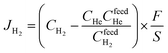Tuning the separation performance of hydrogen permeable membranes using an anion doping strategy

Abstract

Overcoming the dilemma between hydrogen permeability and stability is critical for realizing the widespread application of mixed protonic–electronic conducting (MPEC) membranes. Herein, fluoride-anion doping is for the first time reported for tuning the separation performance of MPEC membranes. Lanthanum tungstate oxyfluoride membranes, La_5.5W_0.6Mo_0.4O_11.25−δF_x (x = 0, 0.025, 0.05, 0.10, 0.20, 0.50), exhibit improved hydrogen permeability and enhanced stability compared to their parent oxides, achieving a maximum value of 0.20 mL min⁻¹ cm⁻² at x = 0.05. Moreover, the declining hydrogen permeability performance of lanthanum tungstate MPEC membranes during high-temperature operation was systematically analyzed and relative solutions are put forward. The anion-doping and stability-improving strategies might accelerate the development and future practical applications of MPEC membranes.

---

Introduction

Nowadays, more than 90% of hydrogen is obtained from hydrocarbon reforming and pyrolysis.^1,2 The produced hydrogen is normally mixed with CO₂, CO and H₂O; thus, it is essential to separate and purify hydrogen from these gas mixtures using appropriate technologies. Cryogenic distillation, pressure swing adsorption (PSA) and membrane separation are common hydrogen separation and purification methods.³ Among them, membrane technology enjoys increasing interest due to its potential for continuous operation and coupling with other reaction processes.^3,4

In the past several decades, many developments have been achieved for hydrogen separation membranes in terms of the materials used, ranging from polymers to inorganic membranes.^5–11 Dense ceramic mixed proton–electron conducting (MPEC) membranes possess 100% hydrogen selectivity in theory because hydrogen is separated as protons instead of molecules.¹² Currently, the state-of-art MPEC ceramics are perovskite-type cerate and zirconate-based solid solutions (ACeO_3−δ and AZrO_3−δ (A = Ca, Sr, Ba)).^13–16 ACeO_3−δ has a high proton conductivity but poor chemical stability in a moist CO₂ atmosphere. AZrO_3−δ possesses better chemical stability, but the total conductivity is relatively low. Additionally, lanthanum tungstate and its related compositions have attracted considerable attentions during the past few years due to their stability in CO₂-containing atmospheres, while their protonic conductivities are only approximately 1 mS cm⁻¹.^17–22 For practical applications, both high conductivity and good stability are urgently required. Consequently, the reported MPEC materials have a dilemma because a compromise should be reached between the conductivity and the stability.

Previously, in order to optimize the conductivity and the stability of MPEC materials, many equivalent or/and aliovalent substitutions on cation sites have been successfully carried out. For instance, in perovskite-type materials, Ce⁴⁺ sites had been partially substituted with Zr,^13,16,23,24 Ta,²⁵ Y,^15,26–28 Yb,^29,30 Tm,³¹ Nd,^32,33 Sm,³⁴ Gd,³⁵ and other rare earth cations.

In lanthanum tungstate oxides (LWOs), the partial substitution of La³⁺ sites with Zr²⁺ or Ca²⁺ and the replacement of W⁶⁺ with Nb⁵⁺, Re⁵⁺ or Mo⁶⁺ have been used to develop dense ceramic MPEC membranes, among which 40% Mo substitution in LWO is the optimized composition.^20,36–39 For instance, the conductivity of undoped La_5.5WO_11.25−δ is approximately 0.003 S cm⁻¹, while it increases to 0.043 S cm⁻¹ at 900 °C when substituting W with 40% Mo.⁴⁰ Moreover, a high hydrogen permeation flux up to 1.36 mL min⁻¹ cm⁻² was obtained for a U-shaped La_5.5W_0.6Mo_0.4O_11.25−δ hollow-fiber membranes at 975 °C when a mixture of 80% H₂–20% He was used as the feed gas and the sweep side was humidified.²⁰ Although the cation substitutions could enhance the conductivity or stability to some extent, it is still difficult to fulfill the requirements of industrial applications.

Aside from cation doping, anion doping in oxygen lattices is also an effective way to modify the properties of MPEC materials. Recently, Shao and his group reported an attractive performance of perovskite-type materials as oxygen reduction electrodes by embedding F⁻ in oxygen sites.⁴¹ Jin et al. found that F-doped perovskite membranes exhibited enhanced oxygen permeation flux at low temperature.⁴² Lacorre and co-workers synthesized and characterized F-doped La₂Mo₂O₉ and presented modified transport properties.⁴³ Therefore, the partial occupation of anions at the oxygen sites could tune the properties of the materials. With the aim of developing MPEC membrane materials with sufficient protonic conductivity and considerable stability to achieve hydrogen separation at high temperatures, we have prepared fluoride anion-doped lanthanum tungstate membranes (La_5.5W_0.6Mo_0.4O_11.25−δF_x, where x = 0, 0.025, 0.05, 0.10, 0.20, and 0.50) for the first time, and the effects of fluorine substitution on the lattice structure, redox stability and hydrogen permeability were investigated in detail.

Experimental

Powder synthesis and membrane preparation

The series of La_5.5W_0.6Mo_0.4O_11.25−δF_x powders (x = 0, 0.025, 0.05, 0.10, 0.20, 0.50, and 1.0) were all prepared using a traditional solid-state reaction method with stoichiometric amounts of La₂O₃, WO₃, MoO₃ and LaF₃. Lanthanum oxide was heated at 1000 °C for 2 h for decarbonation and dehydration before using. The initial powders were mixed in an agate mortar and ball milled for 10 h in the presence of acetone. A subsequent thermal treatment was carried out in an alumina crucible at 900 °C for 10 h. After completion, the powders were ground and pressed into pellets. Then, the pellets were heated in air at 1500 °C for 10 h with a heating and cooling rate of 2 °C min⁻¹ to attain dense membranes. The densities of the sintered disks were determined to be higher than 95% of the theoretical density using the Archimedes method in ethanol. Only those with relative densities higher than 95% were used for hydrogen permeation studies.

Characterization

The sintered La_5.5W_0.6Mo_0.4O_11.25−δF_x disks were characterized using X-ray diffraction (XRD, Bruker D8 Advance and Cu Kα radiation) within the 2θ range from 10° to 80° to confirm the structures. The patterns were analyzed using Total Pattern Solution (TOPAS) software to calculate the cell parameters and volume.

The microstructures of the fresh and spent La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 membranes were observed by scanning electron microscopy (SEM) using a Hitachi SU 8220 at an excitation voltage of 2 kV. The elemental compositions of the membranes were determined by energy dispersive X-ray spectroscopy (EDXS, Horiba, X-MaxN detector) with an ultrathin window at an excitation voltage of 15 kV.

X-ray photoelectron spectroscopy (XPS) analyses of fresh La_5.5W_0.6Mo_0.4O_11.25−δF_x membranes and the spent La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 membrane were performed on a Thermo Fisher Scientific ESCALAB 250Xi spectrometer.

For conductivity tests, two parallel silver wires were bound to the sintered pellets (bars with dimensions ≈10 × 1 × 5 mm) with a silver paste for better contact. After being calcined at 600 °C in air for 2 h, the samples were heated from 50 °C to 900 °C in wet 10% H₂–90% Ar atmospheres with a ramp rate of 5 °C min⁻¹, and the resistance was measured in the 600–900 °C temperature range by using an electrochemical workstation (Zahner IM6ex, German) using a dc two-probe method.

Temperature-programmed reduction (TPR) tests of the La_5.5W_0.6Mo_0.4O_11.25−δ and La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 powders sintered at 1500 °C were carried out by using a chemisorption analyzer (Micromeritics AutoChem II). The powders were pretreated under a dry Ar flow for half an hour and then subjected to reduction under a dry 10% H₂/Ar flow from 50 °C to 900 °C with a heating rate of 10 °C min⁻¹.

Hydrogen permeation measurements

The hydrogen permeation fluxes of the La_5.5W_0.6Mo_0.4O_11.25−δF_x membranes were measured using a homemade corundum reactor following the same methodology as reported elsewhere.^17,18 All the membranes used for the permeation measurements were 0.5 mm-thick gastight disks with a diameter of 13.4 mm sintered at 1500 °C and sealed in the corundum reactor by using a glass ring. Hydrogen was separated from a mixture gas consisting of 50% H₂–50% He with a total flow rate of 80 mL min⁻¹, and Ar was used as the sweep gas with 30 mL min⁻¹. The flow rates of the effluents were measured by using a soap bubble flow meter. A gas chromatograph with a 13X molecular sieve column and thermal conductivity detector (TCD) (GC, Agilent Technologies, 7890A) was connected to the permeation apparatus to detect the composition of the effluents online. The leakage of the hydrogen due to the imperfect sealing at high temperatures was less than 5% during all experiments. Then, the hydrogen permeation fluxes are calculated as follows:
where C_H2^feed and C^feed_He are the hydrogen concentration and helium concentration on the shell side, respectively, which were adjusted by using mass-flow controllers. The C_H2 and C_He are the hydrogen concentration and helium concentration on the sweep side, respectively, which were calculated using a GC instrument, F denotes the flow rate of the exhaust stream, which was measured using a soap flow meter, and S denotes the effective membrane area.

Results and discussion

Characterization of the materials

The X-ray diffraction (XRD) patterns of the La_5.5W_0.6Mo_0.4O_11.25−δF_x (hereafter labelled LWMF_x, x = 0, 0.025, 0.05, 0.10, 0.20, 0.50, and 1.0) materials sintered in air at 1500 °C are shown in Fig. 1(a). The substitution of O²⁻ with F⁻ does not change the crystal symmetry of the compounds; the cubic fluorite structures are retained when lower quantities of F were doped, namely x ≤ 0.2.²¹ In contrast, when the F concentration is further increased, i.e., x = 1.0, the compound is not a single phase and contains additional phases identified as La₆MoO₁₂.³⁹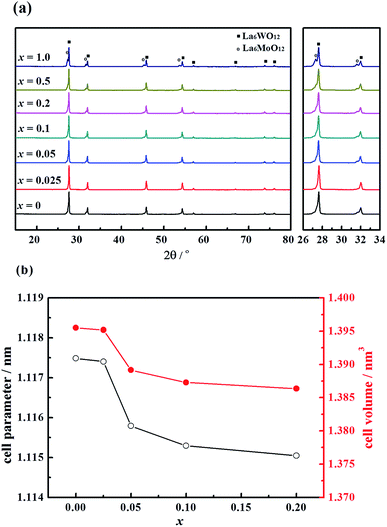

Fig. 1 (a) X-ray diffraction patterns and (b) the cell parameter and the cell volume of the La_5.5W_0.6Mo_0.4O_11.25−δF_x membranes sintered at 1500 °C.

The cell parameters and volume of the single-phase LWMF_x compounds have been calculated based on the XRD results, as shown in Fig. 1(b). The Rietveld refinement results suggest that the LWMF_x (x ≤ 0.2) samples possess a cubic structure and a space group of F4̄3m.¹⁹ The unit cell parameters for the LWMF_x series slightly decrease with increasing fluorine content due to the lower ionic radius of F⁻ (1.33 Å) than that of O²⁻ (1.40 Å).⁴⁴

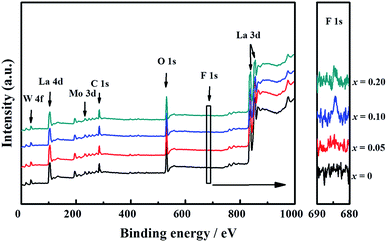
The presence of La, W, Mo, O, and F elements in the LWMF_x (x ≤ 0.2) samples was confirmed using X-ray photoelectron spectra. As shown in Fig. 2, the peaks at the bonding energies of approximately 35 eV, 232 eV, 531 eV, 685 eV and 836 eV are assigned to the W 4f, Mo 3d, O 1s, F 1s and La 3d peaks, respectively.⁴⁵ In particular, the LWMF_0.05 membrane was selected to be characterized using SEM and EDXS tests (Fig. 3), which indicated the uniform distribution of the existing elements in the LWMF_0.05 sample without evident segregation. The theoretical values of the elements in the LWMF_0.05 membrane and the EDXS analysis results are listed in Table 1. The fluorine content of the sintered LWMF_0.05 membrane was further confirmed using a fluoride ion-selective electrode method. The actual x value of the LWMF_0.05 sample from the tests is 0.047, which is approximately the theoretical value.

Fig. 2 XPS wide-scan spectra of La_5.5W_0.6Mo_0.4O_11.25−δF_x (x ≤ 0.2) ceramics.

Fig. 3 SEM-EDXS image of the La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 membrane.

Table 1 The theoretical and experimental values of elemental distribution in the fresh La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 disk. Values in parentheses are standard deviations

Element	Atomic%		Weight%
	Theoretical	Experimental^a	Theoretical	Experimental^b
a EDXS analysis. b Fluoride ion selective electrode method.
O	63.1	63(5)	16.43	—
F	0.3	3.0(6)	0.087	0.082(1)
Mo	2.3	2.0(3)	3.5	—
La	30.9	28(2)	69.9	—
W	3.4	4.0(5)	10.09	—

---

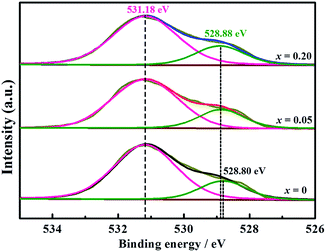
Furthermore, XPS tests through LWMF_x (x = 0, 0.05, 0.2) materials were carried out to study the influence of fluorine doping on the metal–oxygen bond energy (Fig. 4). The peak with a lower binding energy corresponds to the lattice oxygen, while the peak with the higher energy corresponds to the oxygen species absorbed on the surface.^46,47 The O 1s binding energy of the surface oxygen species is 531.18 eV for all original and F-doped samples, while the binding energy for the lattice oxygen of LWMF_0.05 and LWMF_0.2 slightly shift (0.08 eV) toward a higher binding energy compared to that of the original samples. Similar results were also observed in La_1−xSr_xFeO_3−δF_σ and Ca_0.37Sr_0.63CuO_2−δF_σ.^48,49 The increased bonding energy of the lattice oxygen in the F-doped compounds is attributed to the stronger electronegativity of F⁻ (3.98) than that of O²⁻ (3.44). Thus, the fluoride ions attract more valence electrons from the metal ions than the oxygen ions, resulting in the decrease in the valence electron density of O²⁻, which weakening the metal–oxygen bonds and consequently increase the mobility of the lattice oxygen and protons.

Fig. 4 XPS of O 1s peaks for La_5.5W_0.6Mo_0.4O_11.25−δF_x (x = 0, 0.05, 0.2) ceramics.

Hydrogen permeability

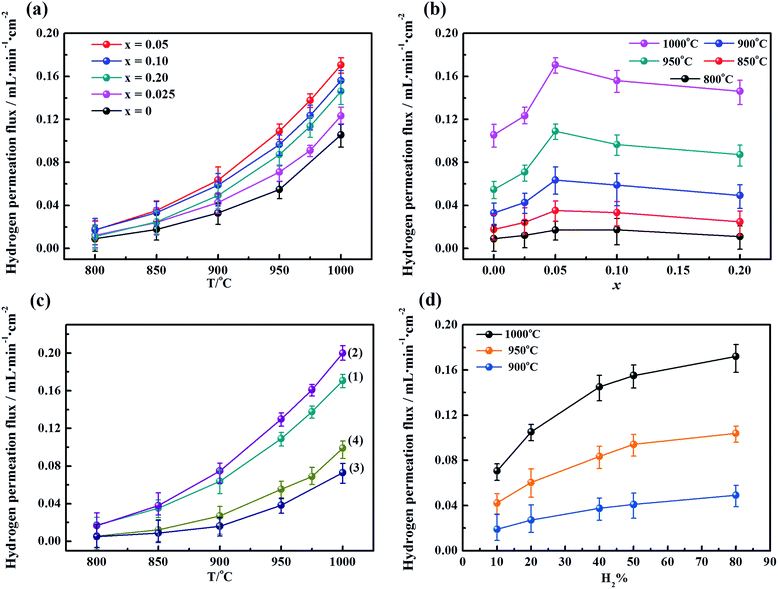
To determine the influence of the fluorine content on the hydrogen permeability, the hydrogen permeation fluxes of the LWMF_x membranes were studied in the temperature range from 800 °C to 1000 °C. As shown in Fig. 5(a), the hydrogen permeation fluxes increase with increasing temperature for all membranes due to the enhancement in the hydrogen bulk diffusion and hydrogen surface reaction rates.^13,20 In addition, the corresponding hydrogen permeation fluxes first increase and then decrease as a function of the fluorine concentration at the same temperature, and the peaks all appear at x = 0.05, as shown in Fig. 5(b). The appropriate introduction of the fluoride ions promotes the mobility of protons as a result of a decrease in the electron density of oxygen. Consequently, the protonic conductivity and hydrogen permeation fluxes of the membranes are improved. However, when the fluorine content is beyond the limit, the excess fluoride ions occupy the oxygen vacancies,⁵⁰ which somehow limits the proton transfer. Therefore, the hydrogen permeation of the LWMF_x (x ≤ 0.2) membranes increases during the early stage and then decreases.

Fig. 5 Hydrogen permeation fluxes for La_5.5W_0.6Mo_0.4O_11.25−δF_x (x ≤ 0.2) membranes at different temperatures (a) and fluorine concentrations (b). (c) Hydrogen permeation fluxes as a function of temperature for the La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 under different reducing environments: (1) with a dry atmosphere on both sides (feed and permeate sides) of the membrane, (2) with only the sweep side humidified (pH₂O = 0.025 atm), (3) with only the feed side humidified (pH₂O = 0.025 atm) and (4) with a wet atmosphere on both sides (pH₂O = 0.025 atm). (d) Hydrogen permeation fluxes for the La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 compound at three temperatures, feeding different H₂ concentrations. Conditions: membrane thickness: 0.5 mm. F_H2+He = 80 mL min⁻¹, F_Ar = 30 mL min⁻¹. Feed gas composition: (a–c) 50% H₂ diluted with 50% He.

Previously, Haugsrud and Norby have reported that protonic conductivity is the predominant conductivity of rare-earth tungstates in wet hydrogen atmospheres up to 800 °C, while electronic conductivity takes over at higher temperature.^51,52 To further confirm the effect of fluoride on protonic conductivity, the conductivity of LWMF₀ and LWMF_0.05 disks was studied as a function of temperature (600–900 °C) in wet hydrogen. As shown in Fig. 6, the conductivity of LWMF_0.05 is greater than that of LWMF₀ under wet hydrogen atmospheres below 800 °C, indicating the enhancement in the protonic conductivity by fluorine doping. With a further increase in temperature to 900 °C, the difference between the LWMF_0.05 and LWMF₀ becomes smaller gradually as electronic conductivity comes into play, which indicates their similar electronic conductivity (at 900 °C).

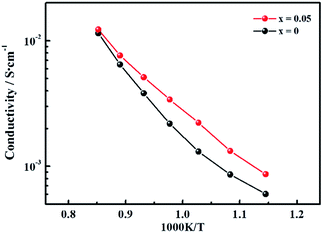Fig. 6 Conductivity as a function of temperature plotted in the Arrhenius form under a wet (pH₂O = 0.025 atm) 10% hydrogen in argon atmosphere for LWMF₀ and LWMF_0.05 specimens.

At an optimized F-doping concentration, the LWMF_0.05 membrane exhibits the highest hydrogen permeability. Thus, LWMF_0.05 was selected to perform hydrogen permeation measurements as a function of temperature under four different reducing environments: (1) with a dry atmosphere on both sides (feed and permeate sides) of the membrane, (2) with only the sweep side humidified (pH₂O = 0.025 atm), (3) with only the feed side humidified (pH₂O = 0.025 atm) and (4) with a wet atmosphere on both sides. The notable effects of the steam on the hydrogen permeation flux are shown in Fig. 5(c). The hydrogen permeation flux of LWMF_0.05 under condition (1) reaches a maximum value of 0.17 mL min⁻¹ cm⁻² at 1000 °C. Nevertheless, the flux suffers a sharp slump when the feed side is humidified (condition 3). This result is attributed to the occupation of the hydrogen adsorption sites on the surface of the membrane by water vapour, which seriously hindered the hydrogen transport in this case. However, the hydrogen permeation flux increased to 0.20 mL min⁻¹ cm⁻² when the sweep side is humidified (condition 2) due to the additional hydrogen production from water splitting and the improved protonic conductivity.⁵³ The improved protonic conductivity is ascribed to the additional formation of protonated oxygen atoms or ions (the essential charge carriers in MPEC membranes), which result from the reaction between water and oxygen vacancies or/and lattice oxygen.¹⁹ In addition, the LWMF_0.05 hydrogen permeation flux using the wet atmosphere on both sides combine the advantages of condition (2) and the disadvantages of condition (3) and exhibit a slightly higher hydrogen permeation flux than that observed under condition (3). Similar phenomena are also observed in the La_5.5W_0.8Mo_0.2O_11.25−δ and La_5.5W_0.8Re_0.2O_11.25−δ membranes.³⁸

Subsequently, the dependence of the hydrogen permeation fluxes on the concentrations of hydrogen on the feed side at three different temperatures was also studied using the LWMF_0.05 membrane. The total flow rate of the feed gases was kept at 80 mL min⁻¹. Fig. 5(d) shows that the hydrogen permeation flux increases with both temperature and the hydrogen concentration in the feed stream, similar to the previously reported results for La_5.5WO_11.25−δ, Nd_5.5W_0.5Re_0.5O_11.25−δ and (Nd_5/6La_1/6)_5.5WO_11.25−δ.^53–55 The improved hydrogen permeation flux can be attributed to the increased hydrogen partial pressure gradient across the membrane with increasing hydrogen concentration on the feed side, leading to an enhanced hydrogen permeation driving force.

Stability study

To evaluate the long-term stability, the hydrogen permeation fluxes were measured as a function of time for the LWMF₀ and LWMF_0.05 membranes at 900 °C, 950 °C and 1000 °C sequentially. As shown in Fig. 7(a), the hydrogen permeation flux of LWMF_0.05 remains relatively stable at 900 °C. When the temperature increases to 950 °C, the hydrogen permeation flux increases to approximately 0.10 mL min⁻¹ cm⁻² as expected, while it declines sharply by 46.12% in 50 h. After further increasing the temperature to 1000 °C, the hydrogen permeation flux only slightly increases and does not reach the expected value (0.17 mL min⁻¹ cm⁻²), and the downward trend continues with time.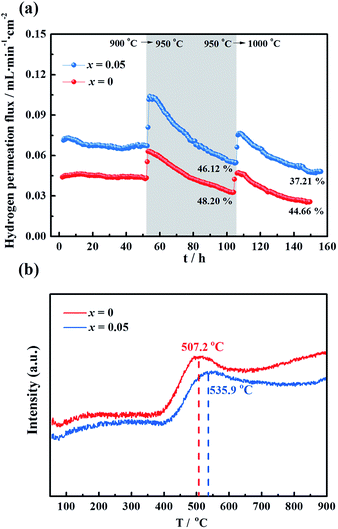

Fig. 7 (a) Hydrogen permeation fluxes for the La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 membrane under dry conditions as a function of time at three temperatures: 900 °C, 950 °C and 1000 °C. Conditions (condition 1 in Fig. 5): F_{50% H2+50% He} = 80 mL min⁻¹, F_Ar = 30 mL min⁻¹. Membrane thickness: 0.5 mm. (b) Temperature programmed reduction profile of La_5.5W_0.6Mo_0.4O_11.25−δ and La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 powders sintered at 1500 °C.

The un-doped LWMF₀ membrane exhibits a similar hydrogen permeation flux to that of LWMF_0.05 during the long-term test, while it suffers a greater percentage of decline, suggesting its weaker redox stability, as demonstrated by the temperature programmed reduction (TPR) results shown in Fig. 7(b). The TPR experiments were performed under a dry 10% H₂/Ar flow from 50 °C to 900 °C to study the reduction behaviour of the LWMF₀ and LWMF_0.05 compounds. The TPR curves plotted in Fig. 7(b) show well-defined reduction peaks at approximately 500 °C, revealing that both LWMF₀ and LWMF_0.05 suffer from an appreciable reduction process. The reduction peak corresponding to LWMF_0.05 appears at a higher temperature than that of LWMF₀, suggesting the slightly stronger redox stability of LWMF_0.05.

To thoroughly investigate the causes of the hydrogen permeation flux attenuation, XPS tests were performed using the LWMF_0.05 membrane samples before and after the hydrogen permeation tests to study the oxidation states of the elements, as shown in Fig. 8 and 9. The results from the analysis show that the binding energy values for the La 3d and W 4f lines fit the XPS databases well and could be assigned to La³⁺ and W⁶⁺, respectively.⁴⁴ As there are no obvious chemical shifts or changes in the peak shapes, it can be concluded that La³⁺ and W⁶⁺ are not affected during the hydrogen permeation process. Moreover, Fig. 8(a) shows the Mo 3d peaks of the fresh, spent and oxidized membranes. The Mo⁵⁺ peaks at 231.0 eV and 234.58 eV are more distinct for the spent membrane, indicating the strong effect of the hydrogen treatment on Mo⁶⁺, which is in agreement with a recent study in which Mo⁶⁺ reduction was observed in La_5.4W_0.7Mo_0.3O_11.1−δ and Nd_5.5W_0.5Mo_0.5O_11.25−δ using XPS.^56,57 This finding can be correlated with the loss of the lattice oxygen of the spent sample in the O 1s spectrum at 528.88 eV (Fig. 9(b)).

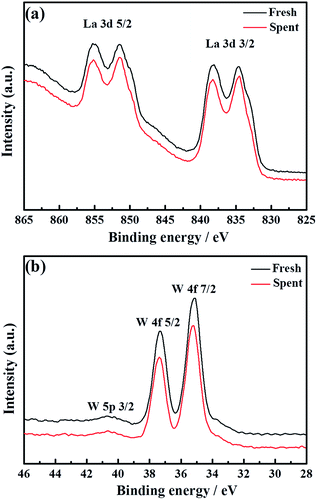Fig. 8 La 3d (a) and W 4f (b) superimposed XPS spectra of fresh and spent La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 membranes.

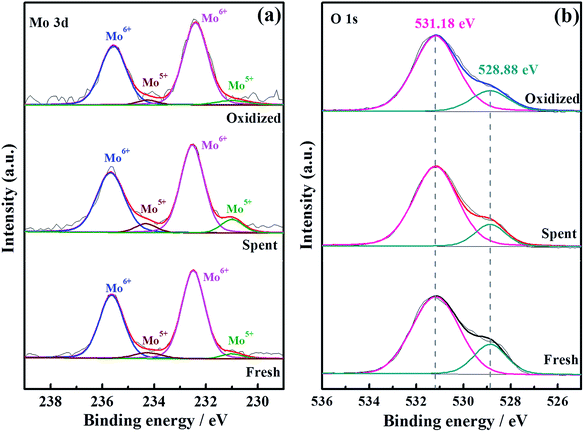Fig. 9 Mo 3d (a) and O 1s (b) XPS spectra of fresh, spent and oxidized La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 membranes.

These results suggest that the decrease of the hydrogen permeation flux at elevated temperatures might have been due to the reduction of Mo⁶⁺. Thus, it is expected that the decreased fluxes could be restored to their original values after oxidization. Herein, when the hydrogen permeation flux of the LWMF_0.05 membrane at 950 °C dropped to approximately 0.05 mL min⁻¹ cm⁻², the feed hydrogen flow was stopped and dry air was applied to oxidize the both sides of the membrane for 10 h. Then, the hydrogen permeation test was restarted. As shown in Fig. 10(a), the hydrogen permeation flux returned to approximately 0.10 mL min⁻¹ cm⁻² (orange line), which is slightly lower than the best hydrogen permeation flux of the LWMF_0.05 membrane at 950 °C. After conducting a 30 h hydrogen permeation test at 1000 °C, the above oxidization procedure was repeated when the temperature cooled down to 950 °C. However, the hydrogen permeation flux remains at a low level and could not reach the initial value (the green line). In addition, to study the oxidization effect at a high temperature, the hydrogen permeation measurement was performed again at 1000 °C after 10 h of oxidization on both sides of the LWMF_0.05 membrane. Different from the case at 950 °C, the hydrogen permeation flux could not recover to its original value, and the attenuation trend cannot be repressed (Fig. 10(b)). The above findings suggest that the diminished hydrogen permeation flux at the elevated temperature might have resulted from both the Mo⁶⁺ reduction and volatilization. In other words, the reversible process at 950 °C is the result of Mo⁶⁺ reduction, while the irreversible process at 1000 °C is mainly attributed to the vaporization of Mo. Similarly, Mo diffusion behaviours were observed in a few Mo-doped tungstate oxides after the permeation tests.^58,59

Fig. 10 (a) The regeneration of hydrogen permeation fluxes for the La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 membrane at 950 °C. (b) The oxidization effect on the permeability of the La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 membrane at 1000 °C.

To further investigate the volatilization of Mo, the structures, SEM morphologies, and elemental compositions of the fresh, spent and oxidized LWMF_0.05 membranes were determined. Despite the possibility of Mo⁶⁺ reduction and volatilization, the samples maintain the fluorite structure after approximately 150 h of continuous hydrogen permeation testing, and obvious phase changes are not detected in the XRD patterns (Fig. 11(a)).

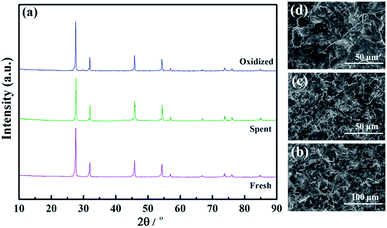Fig. 11 The X-ray diffraction patterns (a) and SEM morphologies of fresh (b), spent (c) and oxidized (d) La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 membranes.

Additionally, similar microstructures are observed in the membrane cross sections, as shown in Fig. 11(b–d). The fresh membrane is dense with occluded porosity before the permeation measurements, and after the permeation measurements, the membrane remained completely dense. Finally, the elemental compositions of the LWMF_0.05 disks obtained from EDXS tests are listed in Table 2. The fresh LWMF_0.05 disk contains higher quantities of molybdenum than the spent disks, which further proves that the Mo evaporated during the high-temperature operation. The oxidized sample contains a higher level of Mo than the spent sample without oxidation, and the lower Mo content of the membrane surface compared to the bulk further suggests the occurrence of Mo evaporation during the long-term high-temperature hydrogen permeation operation. In summary, the LWMF_x membranes exhibit stable hydrogen separation performance at 900 °C; undergo a reversible hydrogen permeability decline at 950 °C during Mo⁶⁺ reduction (which could be regenerated through simple oxidization in air); and experience an irreversible hydrogen permeability diminution due to both the Mo⁶⁺ reduction and the Mo vaporization at 1000 °C.

Table 2 The elemental distribution of La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 disks before and after H₂ permeation and the spent disk treated with oxidation. Values in parentheses are standard deviations

Element	Atomic%
	Fresh membrane	Spent membrane			Spent and oxidized membrane
		Feed side	Middle	Sweep side	Feed side	Middle	Sweep side
O	63(5)	60(5)	62(5)	62(5)	61(5)	62(5)	64(5)
F	2.9(6)	3.2(6)	2.9(6)	2.1(6)	2.1(6)	3.1(6)	2.9(6)
Mo	2.0(3)	1.9(3)	2.4(3)	2.4(3)	2.7(3)	2.8(3)	2.8(3)
La	28.0(2)	31.5(2)	29.3(2)	30.2(2)	30.7(2)	29.0(2)	27.1(2)
W	4.0(5)	3.6(5)	3.1(5)	3.1(5)	3.1(5)	2.7(5)	2.8(5)

---

Conclusions

A series of lanthanum tungstate oxyfluorides, La_5.5W_0.6Mo_0.4O_11.25−δF_x (x = 0, 0.025, 0.05, 0.10, 0.20, and 0.50), were successfully prepared using a traditional solid-state reaction method. By doping an appropriate amount of fluorine (x = 0.05), the obtained La_5.5W_0.6Mo_0.4O_11.25−δF_0.05 (LWMF_0.05) membrane exhibits the highest hydrogen permeability at high temperatures (800–1000 °C) compared to the other F-doped compounds and their parent oxides. The influences of the feed gas concentration and humidification on the hydrogen permeability of LWMF_0.05 are studied in detail. The reasons for the declining hydrogen permeation fluxes at high temperatures are systematically investigated, and the relative regeneration solutions are demonstrated. The fluoride-anion doping strategy and the hydrogen permeation flux regeneration method can boost the development of MPEC membranes and their practical applications in environmental and energy fields.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the financial support from the China Postdoctoral Science Foundation (No. 2017M612665), Fundamental Research Funds for the Central Universities (No. 2017BQ016), National Natural Science Foundation of China (No. 21536005, 51621001, 21606086, 21706076), Natural Science Foundation of Guangdong (2014A030312007), and Guangzhou Technology Project (No. 201707010317).

Notes and references

1. P. Nikolaidis and A. Poullikkas, Renewable Sustainable Energy Rev., 2017, 67, 597–611.
2. I. Dincer and C. Acar, Int. J. Hydrogen Energy, 2015, 4, 11094–11111.
3. S. Adhikari and S. Fernando, Ind. Eng. Chem. Res., 2006, 45, 875–881.
4. R. W. Spillman, Chem. Eng. Prog., 1989, 85, 41–62.
5. Z. Tao, L. Yan, J. Qiao, B. Wang, L. Zhang and J. Zhang, Prog. Mater. Sci., 2015, 74, 1–50.
6. S. Hossain, A. M. Abdalla, S. N. B. Jamain, J. H. Zaini and A. K. Azad, Renewable Sustainable Energy Rev., 2017, 79, 750–764.
7. Z. Zhang, Z. Yao, S. Xiang and B. Chen, Energy Environ. Sci., 2014, 7, 2868–2899.
8. S. Wang, X. Li, H. Wu, Z. Tian, Q. Xin, G. He, D. Peng, S. Chen, Y. Yin, Z. Jiang and M. D. Guive, Energy Environ. Sci., 2016, 9, 1863–1890.
9. B. Ghalei, Y. Kinoshita, K. Wakimoto, K. Sakurai, S. Mathew, Y. Yue, H. Kusuda, H. Imahoriae and E. Sivaniah, J. Mater. Chem. A, 2017, 5, 4686–4694.
10. H. Li, A. Caravella and H. Y. Xu, J. Mater. Chem. A, 2016, 4, 14069–14094.
11. J. S. Fish, S. Ricote, R. O'Hayre and N. Bonanos, J. Mater. Chem. A, 2015, 3, 5392–5401.
12. K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359.
13. E. Rebollo, C. Mortalò, S. Escolástico, S. Boldrini, S. Barison, J. M. Serra and M. Fabrizio, Energy Environ. Sci., 2015, 8, 3675–3686.
14. N. Danilov, J. Lyagaeva, A. Kasyanova, G. Vdovin, D. Medvedev, A. Demin and P. Tsiakaras, Ionics, 2017, 23, 795–801.
15. I. M. Hung, Y. J. Chiang, Y. H. Wang, J. S. C. Jang and S. W. Lee, Int. J. Hydrogen Energy, 2017, 42, 22149–22158.
16. Q. A. Islam, M. W. Raja and R. N. Basu, J. Am. Ceram. Soc., 2017, 100, 1360–1367.
17. S. Escolástico, C. Solís, R. Haugsrud, A. Magrasó and J. M. Serra, Int. J. Hydrogen Energy, 2017, 42, 11392–11399.
18. H. Liu, Y. Chen, Y. Wei and H. Wang, Int. J. Hydrogen Energy, 2017, 42, 4208–4215.
19. Y. Chen, S. Cheng, L. Chen, Y. Wei, P. J. Ashman and H. Wang, J. Membr. Sci., 2016, 510, 155–163.
20. Y. Chen, Q. Liao, Z. Li, H. Wang, Y. Wei, A. Feldhoff and J. Caro, AIChE J., 2015, 61, 1997–2007.
21. A. Magrasó, C. Frontera, D. Marrero-López and P. Núñez, Dalton Trans., 2009, 46, 10273–10283.
22. S. Escolástico, C. Solís, C. Kjølseth and J. M. Serra, Energy Environ. Sci., 2014, 7, 3736–3746.
23. K. Katahira, Y. Kohchi, T. Shimura and H. Iwahara, Solid State Ionics, 2000, 138, 91–98.
24. J. Song, B. Meng and X. Tan, Ceram. Int., 2016, 42, 13278–13284.
25. L. Bi, S. Zhang, S. Fang, Z. Tao, R. Peng and W. Liu, Electrochem. Commun., 2008, 10, 1598–1601.
26. H. Iwahara, H. Uchida, K. Ono and K. Ogaki, J. Electrochem. Soc., 1988, 135, 529–533.
27. G. Ma, T. Shimura and H. Iwahara, Solid State Ionics, 1999, 120, 51–60.
28. N. Sammes, R. Phillips and A. Smirnova, J. Power Sources, 2004, 134, 153–159.
29. H. Iwahara, Solid State Ionics, 1996, 86–88, 9–15.
30. M. Matsuka, R. Braddock and I. Agranovski, Solid State Ionics, 2007, 178, 1011–1019.
31. W. Yuan, L. Mao and L. Li, Chin. Chem. Lett., 2010, 21, 369–372.
32. J. Liu and A. S. Nowick, Solid State Ionics, 1992, 50, 131–138.
33. C. Zhang and H. Zhao, Solid State Ionics, 2010, 181, 1478–1485.
34. H. Iwahara, T. Yajima, T. Hibino and H. Ushida, J. Electrochem. Soc., 1993, 140, 1687–1691.
35. D. Medvedev, V. Maragou, T. Zhuravleva, A. Demin, E. Gorbova and P. Tsiakaras, Solid State Ionics, 2011, 182, 41–46.
36. R. Haugsrud and C. Kjølseth, J. Phys. Chem. Solids, 2008, 69, 1758–1765.
37. M. J. Zayas-Rey, L. dos Santos-Gómez, D. Marrero-López, L. León-Reina, J. Canales-Vázquez, M. A. G. Aranda and E. R. Losilla, Chem. Mater., 2013, 25, 448–456.
38. S. Escolástico, J. Seeger, S. Roitsch, M. Ivanova, W. A. Meulenberg and J. M. Serra, ChemSusChem, 2013, 6, 1523–1532.
39. M. Amsif, A. Magrasó, D. Marrero-López, J. C. Ruiz-Morales, J. Canales-Vázquez and P. Núñez, Chem. Mater., 2012, 24, 3868–3877.
40. A. Magrasó and R. Haugsrud, J. Mater. Chem. A, 2014, 2, 12630–12641.
41. Z. Zhang, Y. Zhu, Y. Zhong, W. Zhou and Z. Shao, Adv. Energy Mater., 2017, 1700242.
42. J. Zhu, G. Liu, Z. Liu, Z. Chu, W. Jin and N. Xu, Adv. Mater., 2016, 28, 3511–3515.
43. A. Arulraj, F. Goutenoire, M. Tabellout, O. Bohnke and P. Lacorre, Chem. Mater., 2002, 14, 2492–2498.
44. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
45. J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy, Physical Electronics. Inc., USA, 1995.
46. S. H. Estemirova, A. V. Fetisov and V. B. Fetisov, J. Appl. Spectrosc., 2009, 76, 394–401.
47. H. Liu, Y. Wei, L. Huang and H. Wang, Funct. Mater. Lett., 2011, 4, 261–264.
48. H. X. Dai, C. F. Ng and C. T. Au, J. Catal., 2000, 189, 52–62.
49. H. X. Dai, H. He, C. F. Ng and C. T. Au, J. Mol. Catal. A: Chem., 2001, 171, 217–227.
50. K. Belova, S. Baskakova, C. Argirusis and I. Animitsa, Electrochim. Acta, 2016, 193, 63–71.
51. R. Haugsrud, H. Fjeld, K. R. Haug and T. Norby, J. Electrochem. Soc., 2007, 154, B77–B81.
52. R. Haugsrud, Solid State Ionics, 2007, 178, 555–560.
53. S. Escolástico, C. Solís, T. Scherb, G. Schumacher and J. M. Serra, J. Membr. Sci., 2013, 444, 276–284.
54. S. Escolástico, S. Somacescu and J. M. Serra, Chem. Mater., 2014, 26, 982–992.
55. S. Escolástico, M. Schroeder and J. M. Serra, J. Mater. Chem. A, 2014, 2, 6616–6630.
56. R. Hancke, Z. Li and R. Haugsrud, J. Membr. Sci., 2013, 439, 68–77.
57. S. Escolástico, S. Somacescu and J. M. Serra, J. Mater. Chem. A, 2015, 3, 719–731.
58. E. Vøllestad, C. K. Vigen and A. Magrasó, J. Membr. Sci., 2014, 461, 81–88.
59. E. Vøllestad, T. Norby and R. Haugsrud, Solid State Ionics, 2013, 244, 57–62.

---