 Open Access Article
Open Access ArticleExploring the reversal of enantioselectivity on a zinc-dependent alcohol dehydrogenase†
Miguel A.
Maria-Solano
,
Adrian
Romero-Rivera
and
Sílvia
Osuna
 *
*
Institut de Química Computacional i Catàlisi (IQCC) and Departament de Quimica, Universitat de Girona, Carrer Maria Aurèlia Capmany 6, 17003 Girona, Spain. E-mail: silvia.osuna@udg.edu
First published on 18th April 2017
Abstract
Alcohol Dehydrogenase (ADH) enzymes catalyse the reversible reduction of prochiral ketones to the corresponding alcohols. These enzymes present two differently shaped active site pockets, which dictate their substrate scope and selectivity. In this study, we computationally evaluate the effect of two commonly reported active site mutations (I86A, and W110T) on a secondary alcohol dehydrogenase from Thermoanaerobacter brockii (TbSADH) through Molecular Dynamics simulations. Our results indicate that the introduced mutations induce dramatic changes in the shape of the active site, but most importantly they impact the substrate–enzyme interactions. We demonstrate that the combination of Molecular Dynamics simulations with the tools POVME and NCIplot corresponds to a powerful strategy for rationalising and engineering the stereoselectivity of ADH variants.
1. Introduction
Biocatalysis is based on the application of natural catalysts for new purposes, for which the enzymes were not designed. The advantages of biocatalysts with respect to traditional catalysts make enzyme-based routes a preferable alternative for the synthesis of optically active compounds.1 The asymmetric reduction of prochiral ketones to yield optically pure alcohols can be achieved with metal-based catalysts,2 but also with enzymes such as alcohol dehydrogenases (ADH). Many studies have been reported in the literature showing the importance of ADH in asymmetric synthesis,3–5 of relevance is their usually high thermostability,6,7 and the ability to operate in non-aqueous media with high activity and selectivity.8,9ADH enzymes catalyse the reversible reduction of prochiral ketones to their corresponding alcohols. They require the presence of NAD(P)H as a cofactor, which delivers its pro-(R) hydride to the usually Re face of the ketone yielding the corresponding (S)-alcohols (see Scheme 1). The stereoselectivity of ADHs towards the formation of (S)-alcohols mainly arises from the shape of the active site of the enzymes that usually present a small and a large binding pocket (see Fig. 1).10 As most ADH follow Prelog's rule (Scheme 1), the engineering of their active sites for the formation of the (R)-enantiomer, i.e. anti-Prelog ADHs, is of great interest. In addition to that, the expansion of the substrate scope of ADH is also highly appealing for broadening their applicability in asymmetric synthesis. To that end, Directed Evolution (DE)1,11–14 and rational site-specific mutagenesis15 have been applied in some ADH enzymes. Reetz et al. developed a powerful strategy for reducing the number of variants to screen by generating a collection of small but ‘smart’ enzyme libraries.16 This was applied on the zinc-dependent secondary ADH from Thermoanaerobacter brockii (TbSADH) for the asymmetric reduction of tetrahydrofuran-3-one towards the (S)-alcohol, which is of importance for the synthesis of the HIV inhibitors amprenavir and fosamprenavir.16,17 Engineered variants of Lactobacillus kefir short-chain alcohol dehydrogenase were also developed for the asymmetric reduction of the same tetrahydrofuran-3-one, but also for the related thiolan-3-one.18 Phillips and coworkers engineered TbSADH for accepting several structurally diverse ketones.19 Similarly, Reetz evolved the same ADH for accepting a set of non-cyclic ketones.6 They also engineered TbSADH for the catalytic asymmetric reduction of prochiral ketones of type 4-alkylidene cyclohexanone with formation of the corresponding axially chiral (R) or (S)-alcohols.20 Interestingly, the singly mutated variants TbSADHW110T and TbSADHI86A were found to yield respectively either the unusual (R)-alcohol or the (S)-alcohol with high conversion rates and selectivity. The same W110 and I86 positions were found to be important in determining the enantioselectivity of the highly homologous secondary ADH from Thermoanaerobacter ethanolicus (TeSADH) enzyme.8,21–23
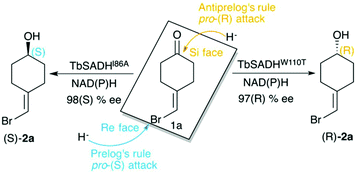 | ||
| Scheme 1 Representation of Prelog and anti-Prelog rules for the studied substrate 1a, together with the stereoselectivity of the engineered variants TbSADHI86A, and TbSADHW110T by Reetz et al.20 | ||
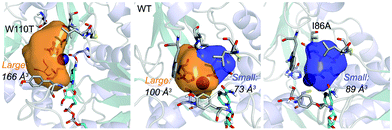 | ||
| Fig. 1 Volume representation of the small and large TbSADH binding pockets for the WT enzyme (middle), W110T (left), and I86A (right) variants. These calculations have been performed with POVME 2.0.31 | ||
The previously mentioned examples highlight the outstanding performance of laboratory-evolution for enhancing activity, and reversing the enantioselectivity of ADHs. Complementary to experimental evolution, computational methods can be used for rationalizing the activity and selectivity of natural and laboratory-engineered enzymes.24 Bocola and coworkers elucidated through Quantum Mechanics and Molecular Mechanics (i.e. QM/MM) calculations the mechanism of hydride and proton transfer of the oxidoreductase from Candida Parapsilosis.25 Electronic structure calculations and Molecular Dynamics (MD) simulations were performed to investigate the mechanism of liver alcohol dehydrogenase (LADH).26 The calculations revealed a lower activation barrier for the hydride transfer step if alcohol deprotonation occurs first. Many computational studies have been devoted to elucidate the fundamental nature of hydrogen tunnelling that occurs in these NAD(P)H-dependent enzymes.27–29 Some of us explored through MD simulations of the Michaelis–Menten and transition state-bound complexes the stereoselectivity of some Lactobacillus kefir short-chain alcohol dehydrogenases.18 These simulations allow rationalising the effect of active site mutations on the selectivity of this Zn(II) free ADH enzyme.
In this study we computationally evaluate the effect of W110 and I86A active site mutations on a series of zinc-dependent TbSADH variants20 through MD simulations. We demonstrate that the introduced mutations induce dramatic changes in the shape of the enzyme active site, which affect the substrate–enzyme interactions thus determining the stereoselectivity of the TbSADH variants.
2. Results and discussion
ADH enzymes present two differently shaped active site pockets, which are responsible for their substrate scope and selectivities (see Fig. 1). By introducing mutations to the ADH active site, both pro-(R) and pro-(S) selectivities can be obtained. In most experimental studies based on TbSADH and the homologous TeSADH published so far two positions, namely I86 and W110, have been found to be key for either enhancing the enzyme activity towards bulky substrates and/or reverting the stereoselectivity of ADHs.9,20,21,23,30 In order to shed some light into the role of the latter mutations in ADH catalytic activity and selectivity, we performed MD simulations on the Wild-Type (WT) TbSADH enzyme, and the variants TbSADHW110T and TbSADHI86A. We restricted our study to the analysis of the prochiral ketone of type 4-alkelidene cyclohexanone (1a, see Scheme 1) studied by Reetz and coworkers.20 This ketone is especially challenging as the steric preferences of the carbon atoms surrounding the carbonyl group are identical. Of importance is the fact that positions I86 and W110 are key to revert the enzyme enantioselectivity even with this non-conventional substrate.We carried out five independent 200 ns MD simulations (i.e. accumulated simulation time of 1 microsecond) in both pro-(R) and pro-(S) conformations of 1a in the WT TbSADH, TbSADHW110T, and TbSADHI86A enzyme variants. In order to maintain the substrate 1a bound to the Zn(II) metal ion, a force constant was applied. This approach allows us to analyse the positioning of 1a for efficient hydride transfer, and thus explain the activity and origin of enantioselectivity observed experimentally.
As shown in Scheme 1, 1a has a bromide atom that can be differently oriented in the small and large binding pockets depending on the variant and the starting pose (pro-(R) and pro-(S) conformation, see Fig. 2–5). The positioning of both the bromide and the cyclohexane ring of 1a and its interactions with the enzyme active site pocket will dictate ADH selectivity. The difference in activity can be predicted by analysing the distance between the carbonyl group of the substrate and the NAD(P)H carbon atom involved in the hydride transfer (see Scheme 2). Our computed hydride transfer Transition State (TS) using DFT and a small subset of the enzyme active site residues, i.e. following the theozyme approach,32 indicates that at the TS it is ca. 2.7 Å for both axial and equatorial attacks (see Scheme 2, and Fig. S8†). This is in line with previous calculations for the hydride transfer. As with classical MD simulations we cannot model the bond-breaking/forming hydride transfer step, we instead evaluate the active site preorganization towards the pro-(S)/pro-(R) enzyme–substrate complexes to shed some light into the enzyme enantioselectivities. We define as catalytically competent poses those MD conformations that present hydride transfer distances shorter than 4.5 Å, whereas those orientations with longer hydride distances were defined as non-catalytic. This allows us to indirectly quantify the number of reactive events along the simulation time, i.e. it provides an estimate of the enzyme catalytic activity.
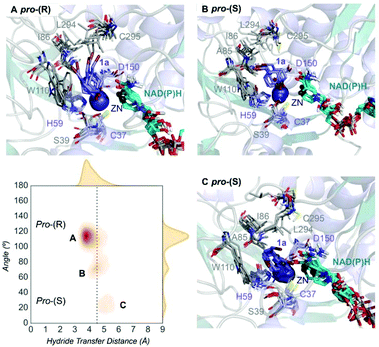 | ||
| Fig. 2 Representation of some representative snapshots of the different conformational states sampled along the MD simulations for TbSADH starting from the pro-(R) orientation of 1a. The histogram of the hydride transfer distance together with the pro-(R)/pro-(S) angle (detailed in Fig. S1†) is displayed. | ||
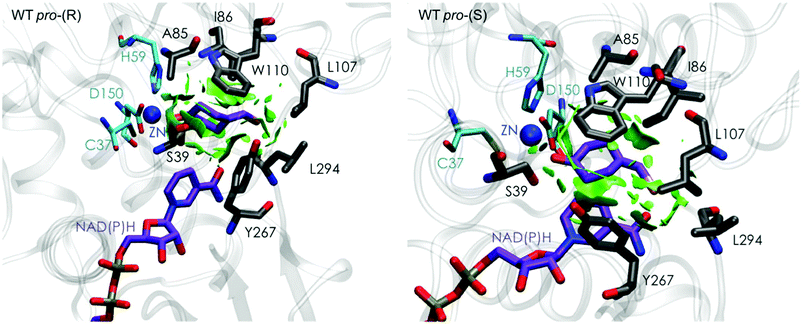 | ||
| Fig. 3 Representation of the non-covalent interactions for the pro-(S) and pro-(R) conformations of 1a in the active site pocket of TbSADH enzyme, computed with the computational tool NCIplot.34,35 | ||
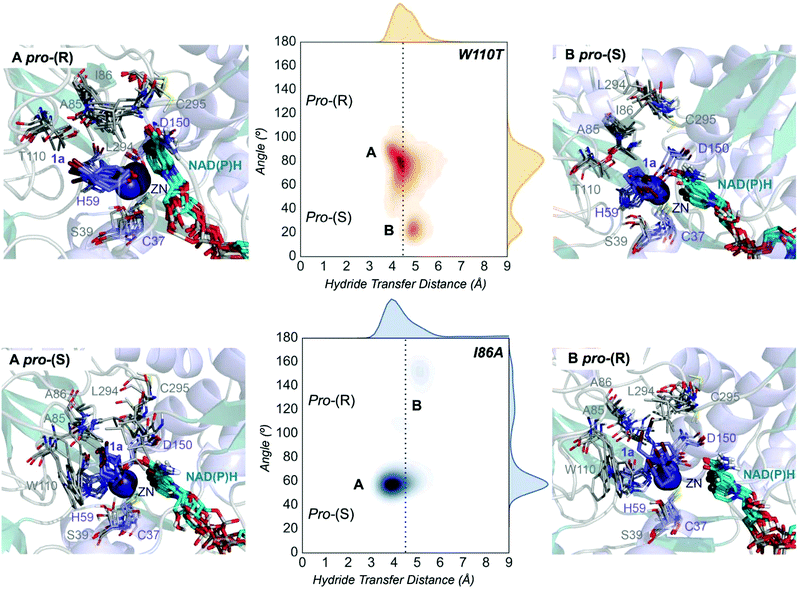 | ||
| Fig. 4 Representation of some representative snapshots of the different conformational states sampled along the MD simulations for the TbSADHW110T and TbSADHI86A starting from the pro-(R) (in orange) and pro-(S) (in blue) orientations of 1a, respectively. The histogram of the hydride transfer distance together with the pro-(R)/pro-(S) angle (detailed in Fig. S1†) is displayed for both variants. | ||
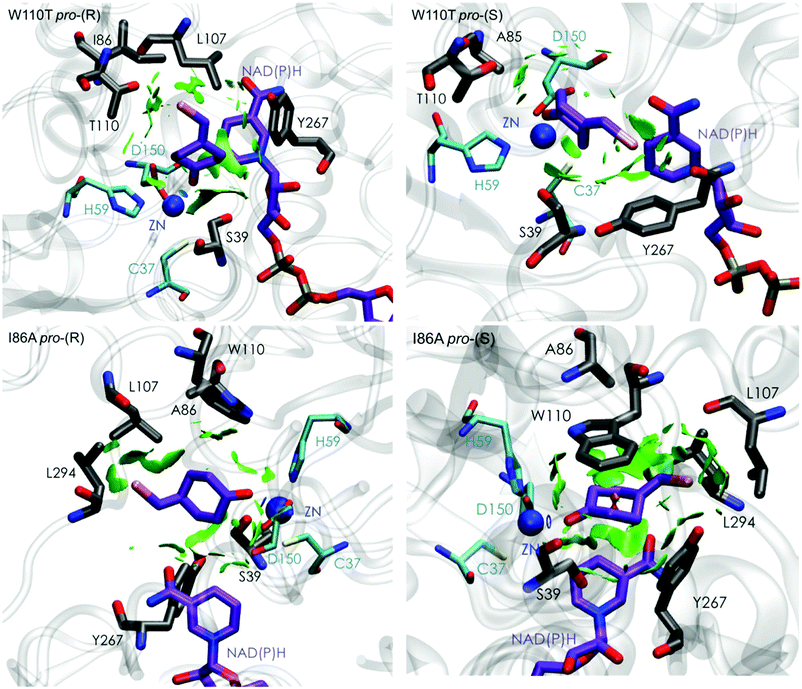 | ||
| Fig. 5 Representation of the non-covalent interactions for pro-(S) and pro-(R) conformations of 1a in the active site pocket of TbSADHW110T (top) and TbSADHI86A (down) enzymes, computed with the computational tool NCIplot.34,35 | ||
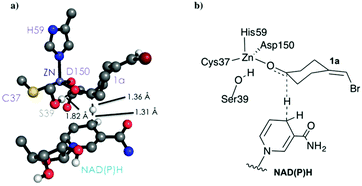 | ||
| Scheme 2 DFT optimized TS structure for the hydride transfer step. For visualization purposes, non-polar hydrogen atoms are hidden. | ||
We evaluate ADH enantioselectivity preferences by comparing the angle formed between the carbonyl group of the active site residue T38 (situated next to C37, one of the Zn(II)-coordinating residues), the C5 and C3 carbon of 1a cyclohexane ring (see Fig. S1†) in all variants. As the NAD(P)H cofactor is in some cases displaced from the active site, the angle provided by the rigid T38 residue together with the measure of the hydride transfer distance allow us to better evaluate the catalytically competent pro-(S) and pro-(R) conformations. As done in previous studies,18 by computing the relative populations of the reactive pro-(S) and pro-(R) poses observed along the MD simulations, the experimental enantiomeric excess ratios can be estimated (see Table S2†).
Evaluation of the TbSADH WT enzyme stereoselectivity
Our analysis starts with the evaluation of the WT TbSADH enzyme activity and selectivity towards 1a. Reetz et al. reported that TbSADH is able to produce the corresponding (R)-alcohol in a 95% conversion, but only with 66 (R) % ee.20 We evaluated the WT enzyme active site pockets in the most populated conformational states (i.e. most visited along the MD simulations) using the computational tool POVME,31 indicating that the small and large active site pockets have an approximated volume of ca. 73 Å3 and 100 Å3 (see Fig. 1 and Table S1†), which evidence their drastic difference in size as observed with X-ray structures.33In our TbSADH MD simulations starting from the pro-(R) orientation of 1a, the bromide atom is forced to fit in the small pocket because the bulky W110 residue does not allow the rotation of the substrate towards the large binding pocket (see Fig. 2, pro-(R) A). This corresponds to the most populated conformation, where 1a remains properly positioned for the hydride transfer to occur towards its Si-face and thus allowing the (R)-alcohol formation. The average hydride distance is ca. 3.9 Å, which coincides with the computed hydride transfer distance at the reactant complex (i.e. 3.8 Å).27 This rather short distance is in agreement with the high conversion rate observed experimentally. The analysis of non-covalent interactions with the NCI plot of 1a in the pro-(R) conformation reveals stabilizing C–H⋯π interactions between H59, Y267, and W110 with the cyclohexane ring of the substrate (see Fig. 3). In contrast, the latter stabilizing interactions are much weaker in the pro-(S) conformations (in particular non-covalent interactions with the residue W110), which evidence how the TbSADH pocket is more complementary to the pro-(R) conformation of 1a to produce the corresponding (R)-alcohol.
In the MD simulations starting from the pro-(S) conformation of 1a, short catalytic distances of ca. 3.9 Å are also observed (see Fig. S2 A†), where 1a is properly positioned for the formation of the (S)-alcohol. However, this pro-(S) catalytically active conformation has a quite low population. This rather low stability of the pro-(S) conformation is also evidenced by analysing the non-covalent interactions of 1a and the active site pocket of TbSADH. The enzyme also adopts some intermediate conformations that present substantially longer unproductive hydride transfer distances. Overall, our MD simulations on TbSADH starting from both pro-(R) and pro-(S) orientations of 1a indicate that the formation of the (R)-alcohol is substantially preferred, although some catalytically competent pro-(S) conformations are also explored. This is in line with the 66% (R) ee observed in the experimental assays.
Evaluation of the TbSADHW110T and TbSADHI86A enzyme stereoselectivity
The substitution of W110 by threonine makes the enzyme large binding pocket even wider. The computed volume is ca. 166 Å3, whereas for the TbSADH it was 100 Å3 (as discussed previously). This mutation therefore gives extra space to 1a for a better accommodation of the bromide substituent in the enzyme active site pocket, and thus allows the substrate to rotate towards the large binding site. Experimentally, it was found that TbSADHW110T was able to convert 1a into the corresponding (R)-alcohol with high conversion rates and high enantioselectivities (99% conversion, and 97 (R) % ee).20 In this enzyme variant, angles of ca. 70° are observed for the pro-(R) conformation, whereas ca. 20° for the pro-(S) attack (see Fig. 4, W110T A and B).In our MD simulations starting from the pro-(R) orientation of 1a, the substrate rapidly rotates to position the bromide into the large binding pocket, and remains in this pro-(R) orientation most of the simulation time (see Fig. 4, W110T). The NAD(P)H cofactor is perfectly positioned to deliver the hydride and allow the (R)-alcohol formation (see Fig. 4, W110T pro-(R) A) displaying catalytically competent hydride distances and angles. Moreover, starting from pro-(S) orientations (Fig. S3†) 1a rapidly rotates towards pro-(R) conformations.
The analysis of non-covalent interactions in the pro-(R) conformations of 1a reveals stabilizing C–H⋯π interactions between the cyclohexane ring of the substrate and residues H59, and Y267, but also with the nicotinamide ring of the NAD(P)H cofactor (see Fig. 5, W110T pro-(R)). The W110T mutation enlarges the active site pocket, but also allows the formation of stabilizing interactions between the bromide and the side-chains of L107 and the newly introduced T110 residue. We also observe during the MD simulations that the substrate can rotate to explore pro-(S) conformations (see Fig. 4, W110T pro-(S) B), however long hydride distances are observed due to the displacement of the NADP(H) cofactor, which interacts with the bromide atom of the substrate (see Fig. 5, W110T pro-(S)).
We finally evaluated the TbSADHI86A enzyme variant, which was found to allow the formation of the opposite (S)-alcohol in high enantiomeric excess (98 (S) % ee), and conversion (95%). Our volume calculations on the most populated conformational states indicate that the small enzyme active site pocket is enlarged from ca. 73 to 89 Å3. In contrast to what we observe in the TbSADH and TbSADHW110T variants, MD simulations starting from the pro-(S) poses of 1a reveal that the substrate stays in the pro-(S) conformations with an angle of ca. 60° most of the simulation time (see Fig. 4, I86A pro-(S) A). In this most populated state, catalytically competent hydride transfer distances are sampled (ca. 4 Å), which fits with the high activity of the variant observed experimentally. This favourable pro-(S) conformations are mainly stabilized by C–H⋯π interactions between the cyclohexane ring and residues W110, H59, and Y267 (see Fig. 5, I86A pro-(S)). As observed in the case of TbSADHW110T, C–H⋯π interactions are also observed within the cyclohexane ring and the nicotinamide ring of NAD(P)H. The mutation introduced at position 86 (i.e. I86A) creates additional space in the small binding pocket, which is occupied by the indole ring of W110. This new conformation of W110 maximizes the C–H⋯π interactions with the cyclohexane ring of 1a, and thus favors the pro-(S) attack (see Fig. 5, I86A pro-(S)).
In the MD simulations, when 1a rotates to explore pro-(R) conformations, long hydride transfer distances are observed due to the displacement of the NAD(P)H cofactor (see Fig. 4, I86A pro-(R) B). MD simulations starting from the pro-(R) conformation (Fig. S4†) show that the substrate stays most of the time in the pro-(R) orientation, but again leads to the displacement of the NAD(P)H cofactor and thus results in a non-catalytic configuration. The analysis of non-covalent interactions in this pro-(R) conformation reveals that most of the above mentioned interactions with W110, H59, and Y267 are lost (see Fig. 5, I86A pro-(R)). These results point out that although 1a can adopt both pro-(R) and pro-(S) orientations, pro-(S) is the catalytically competent pose as only with this orientation both 1a and NAD(P)H are properly positioned for the catalysis.
3. Conclusions
Our MD simulations indicate that the poor selectivity of the WT TbSADH enzyme is due to the possible positioning of the substrate in both pro-(R) and pro-(S) orientations. The pro-(R) conformation is, however, substantially favoured due to stronger non-covalent interactions between the substrate and the enzyme active site. TbSADHW110T presents a substantially wider active site, especially the large binding pocket, which allows the substrate to explore pro-(R) conformations with catalytically active hydride transfer distances. In the pro-(R) conformation, C–H⋯π interactions are observed between the cyclohexane ring and active site residues H59 and Y267. The introduced threonine residue at position 110 also allows the formation of stabilizing interactions between its side-chain and the bromide group of 1a. TbSADHI86A enzyme variant shows a significantly different behaviour revealing a highly pre-organized active site for the pro-(S) conformation with catalytically efficient distances. The introduced I86A mutation enlarges the small binding pocket, and induces a conformational change in W110 that optimally positions the indole group for enhanced C–H⋯π interactions with the cyclohexane ring of the substrate. The combination of MD simulations, theozyme calculations, and in-depth analysis of the active site pocket through the computational tools POVME and NCIplot allows us to rationalise the effect of these two key active site mutations in the enantioselectivity of the zinc-dependent TbSADH enzyme. Given that many studies based on TbSADH and TeSADH target the same active site mutations, we believe that the obtained results are rather general. Our results also highlight the feasibility of MD simulations, coupled with POVME and NCIplot calculations for the engineering of natural enzyme active sites for enhanced activity and selectivity.Computational methods
MD simulations in explicit water were performed using AMBER 16 package4 and starting from the PDB structure: 1YKF.33 The W110T and I86A variants were generated using the mutagenesis tool included in PyMOL (http://www.pymol.org). Parameters for substrate 1a for the MD simulations were generated within the antechamber module of AMBER 16 using the general AMBER force field (GAFF),36 with partial charges set to fit the electrostatic potential generated at the B3LYP/6-31G(d) level by the restrained electrostatic potential (RESP) model.37 The charges were calculated according to the Merz–Singh–Kollman scheme38,39 using Gaussian 09.40 Amino acid protonation states were predicted using the H++ server (http://biophysics.cs.vt.edu/H++).41 We have used the bonded model for Zn and the residues of the first coordination sphere, in particular we used the Seminario approach42 to obtain the metal parameters needed for the simulation as implemented in Prof. Ryde program.43 The optimization, frequencies and charge calculations to obtain the parameters were done at the B3LYP/6-31G(d) level using Gaussian 09.40 The parameters for NAD(P)H were extracted from previous studies by Prof. Ryde.44,45 The WT enzyme (PDB: 1YKF) and variant were solvated in a pre-equilibrated truncated cuboid box with a 10 Å buffer of TIP3P46 water molecules using the AMBER16 leap module, resulting in the addition of ca. 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 solvent molecules. The system was neutralized by the addition of explicit counterions (Na+ and Cl−). All calculations were done using the ff14SB Amber force field.47 A two-stage geometry optimization approach was performed. The first stage minimizes the positions of solvent molecules and ions imposing positional restraints on the solute by a harmonic potential with a force constant of 500 kcal mol−1 Å−2, and the second stage is an unrestrained minimization of all the atoms in the simulation cell. The systems are gently heated using six 50 ps steps, incrementing the temperature 50 K each step (0–300 K) under constant volume and periodic boundary conditions. Water molecules were treated with the SHAKE algorithm such that the angle between the hydrogen atoms is kept fixed. Long-range electrostatic effects were modeled using the particle-mesh-Ewald method.48 An 8 Å cutoff was applied to Lennard-Jones and electrostatic interactions. Harmonic restraints of 10 kcal mol−1 were applied to the solute, and the Langevin equilibration scheme was used to control and equalize the temperature. The time step was maintained at 1 fs during the heating stages, allowing potential inhomogeneities to self-adjust. Each system was then equilibrated without restrains for 2 ns with a 2 fs time step at a constant pressure of 1 atm and a temperature of 300 K. After the systems were equilibrated in the NPT ensemble, 3 independent five hundred nanosecond MD simulations were performed under the NVT ensemble and periodic-boundary conditions.
000 solvent molecules. The system was neutralized by the addition of explicit counterions (Na+ and Cl−). All calculations were done using the ff14SB Amber force field.47 A two-stage geometry optimization approach was performed. The first stage minimizes the positions of solvent molecules and ions imposing positional restraints on the solute by a harmonic potential with a force constant of 500 kcal mol−1 Å−2, and the second stage is an unrestrained minimization of all the atoms in the simulation cell. The systems are gently heated using six 50 ps steps, incrementing the temperature 50 K each step (0–300 K) under constant volume and periodic boundary conditions. Water molecules were treated with the SHAKE algorithm such that the angle between the hydrogen atoms is kept fixed. Long-range electrostatic effects were modeled using the particle-mesh-Ewald method.48 An 8 Å cutoff was applied to Lennard-Jones and electrostatic interactions. Harmonic restraints of 10 kcal mol−1 were applied to the solute, and the Langevin equilibration scheme was used to control and equalize the temperature. The time step was maintained at 1 fs during the heating stages, allowing potential inhomogeneities to self-adjust. Each system was then equilibrated without restrains for 2 ns with a 2 fs time step at a constant pressure of 1 atm and a temperature of 300 K. After the systems were equilibrated in the NPT ensemble, 3 independent five hundred nanosecond MD simulations were performed under the NVT ensemble and periodic-boundary conditions.
The theozyme calculations for the hydride transfer step were performed at the B3LYP/6-31G(d) level of theory using Gaussian 09.40 Active site volume calculations were performed with the computational tool POVME 2.0.31
Acknowledgements
A. R. R. thanks the Generalitat de Catalunya for a PhD fellowship (2015-FI-B-00165), M. A. M. S. is grateful to the Spanish MINECO for a PhD fellowship (BES-2015-074964). S. O. thanks the Spanish MINECO for project CTQ2014-59212-P, Ramón y Cajal contract (RYC-2014-16846), the European Community for CIG project (PCIG14-GA-2013-630978), and the funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (ERC-2015-StG-679001). We are grateful for the computer resources, technical expertise, and assistance provided by the Barcelona Supercomputing Center – Centro Nacional de Supercomputacion.Notes and references
- U. T. Bornscheuer, G. W. Huisman, R. J. Kazlauskas, S. Lutz, J. C. Moore and K. Robins, Nature, 2012, 485, 185–194 CrossRef CAS PubMed.
- R. H. Morris, Chem. Soc. Rev., 2009, 38, 2282–2291 RSC.
- E. García-urdiales, I. Alfonso and V. Gotor, Chem. Rev., 2005, 105, 313–354 CrossRef PubMed.
- W. Kroutil, H. Mang, K. Edegger and K. Faber, Curr. Opin. Chem. Biol., 2004, 8, 120–126 CrossRef CAS PubMed.
- Y.-G. Zheng, H.-H. Yin, D.-F. Yu, X. Chen, X.-L. Tang, X.-J. Zhang, Y.-P. Xue, Y.-J. Wang and Z.-Q. Liu, Appl. Microbiol. Biotechnol., 2017, 101, 987–1001 CrossRef CAS PubMed.
- Z. Sun, G. Li, A. Ilie and M. T. Reetz, Tetrahedron Lett., 2016, 57, 3648–3651 CrossRef CAS.
- D. S. Burdette, V. Tchernajencko and J. G. Zeikus, Enzyme Microb. Technol., 2000, 27, 11–18 CrossRef CAS PubMed.
- M. M. Musa, K. I. Ziegelmann-fjeld, C. Vieille, J. G. Zeikus and R. S. Phillips, Angew. Chem., Int. Ed., 2007, 46, 3091–3094 CrossRef CAS PubMed.
- M. M. Musa, K. I. Ziegelmann-fjeld, C. Vieille and R. S. Phillips, Org. Biomol. Chem., 2008, 6, 887–892 CAS.
- V. Prelog, in Pure Appl. Chem, 1964, vol. 9, p. 119 Search PubMed.
- A. S. Bommarius, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 319–345 CrossRef CAS PubMed.
- M. T. Reetz, Directed Evolution of Selective enzymes: Catalysts for Organic Chemistry and Biotechnology, Wiley-VCH, Weinheim, 2016 Search PubMed.
- A. Currin, N. Swainston, P. J. Day and D. B. Kell, Chem. Soc. Rev., 2015, 44, 1172–1239 RSC.
- S. Lutz and U. T. Bornscheuer, Protein Engineering Handbook, Wiley-VCH Verlag GmbH & Co. KGaA, 2008 Search PubMed.
- J. Pleiss, in Enzyme Catalysis in Organic Synthesis, Wiley-VCH Verlag GmbH & Co. KGaA, 2012, pp. 89–117 Search PubMed.
- Z. Sun, R. Lonsdale, A. Ilie, G. Li, J. Zhou and M. T. Reetz, ACS Catal., 2016, 6, 1598–1605 CrossRef CAS.
- A. Nobili, M. G. Gall, I. V. Pavlidis, M. L. Thompson, M. Schmidt and U. T. Bornscheuer, FEBS J., 2013, 280, 3084–3093 CrossRef CAS PubMed.
- E. L. Noey, N. Tibrewal, G. Jiménez-osés, S. Osuna, J. Park, C. M. Bond, D. Cascio, J. Liang, X. Zhang, G. W. Huisman, Y. Tang and K. N. Houk, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E7065–E7072 CAS.
- C. M. Nealon, M. M. Musa, J. M. Patel and R. S. Phillips, ACS Catal., 2015, 5, 2100–2114 CrossRef CAS.
- R. Agudo, G.-D. Roiban and M. T. Reetz, J. Am. Chem. Soc., 2012, 135, 1665–1668 CrossRef PubMed.
- M. M. Musa, N. Lott, M. Laivenieks, L. Watanabe, C. Vieille and R. S. Phillips, ChemCatChem, 2009, 1, 89–93 CrossRef CAS.
- K. I. Ziegelmann-fjeld, M. M. Musa, R. S. Phillips, J. G. Zeikus and C. Vieille, Protein Eng., Des. Sel., 2007, 20, 47–55 CrossRef CAS PubMed.
- M. M. Musa, K. I. Ziegelmann-fjeld, C. Vieille, J. G. Zeikus and R. S. Phillips, J. Org. Chem., 2007, 72, 30–34 CrossRef CAS PubMed.
- A. Romero-rivera, M. Garcia-borras and S. Osuna, Chem. Commun., 2017, 53, 284–297 RSC.
- G. V. Dhoke, M. D. Davari, U. Schwaneberg and M. Bocola, ACS Catal., 2015, 5, 3207–3215 CrossRef CAS.
- P. K. Agarwal, S. P. Webb and S. Hammes-schiffer, J. Am. Chem. Soc., 2000, 122, 4803–4812 CrossRef CAS.
- D. Roston and A. Kohen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9572–9577 CrossRef CAS PubMed.
- S. R. Billeter, S. P. Webb, P. K. Agarwal, T. Iordanov and S. Hammes-schiffer, J. Am. Chem. Soc., 2001, 123, 11262–11272 CrossRef CAS PubMed.
- D. Roston and A. Kohen, J. Am. Chem. Soc., 2013, 135, 13624–13627 CrossRef CAS PubMed.
- M. M. Musa, J. M. Patel, C. M. Nealon, C. S. Kim, R. S. Phillips and I. Karume, J. Mol. Catal. B: Enzym., 2015, 115, 155–159 CrossRef CAS.
- J. D. Durrant, L. Votapka, J. Sørensen and R. E. Amaro, J. Chem. Theory Comput., 2014, 10, 5047–5056 CrossRef CAS PubMed.
- D. J. Tantillo, C. Jiangang and K. N. Houk, Curr. Opin. Chem. Biol., 1998, 2, 743–750 CrossRef CAS PubMed.
- Y. Korkhin, A. J. Kalb, M. Peretz, O. Bogin, Y. Burstein and F. Frolow, J. Mol. Biol., 1998, 278, 967–981 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-garcía, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- R. Anandakrishnan, B. Aguilar and A. V. Onufriev, Nucleic Acids Res., 2012, 40, W537–W541 CrossRef CAS PubMed.
- J. M. Seminario, Int. J. Quantum Chem., 1996, 60, 1271–1277 CrossRef.
- L. Hu and U. Ryde, J. Chem. Theory Comput., 2011, 7, 2452–2463 CrossRef CAS PubMed.
- U. Ryde, Proteins, 1995, 21, 40–56 CrossRef CAS PubMed.
- U. Ryde, Protein Sci., 1995, 4, 1124–1132 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C7OB00482F |
| This journal is © The Royal Society of Chemistry 2017 |
