Solvent effects on excitation energies obtained using the state-specific TD-DFT method with a polarizable continuum model based on constrained equilibrium thermodynamics
Ting-Jun
Bi
a,
Long-Kun
Xu
a,
Fan
Wang
*b,
Mei-Jun
Ming
a and
Xiang-Yuan
Li
 *a
*a
aCollege of Chemical Engineering, Sichuan University, Chengdu 610065, China. E-mail: xyli@scu.edu.cn
bInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China. E-mail: wangf@scu.edu.cn
First published on 10th November 2017
Abstract
Nonequilibrium solvation effects need to be treated properly in the study of electronic absorption processes of solutes since solvent polarization is not in equilibrium with the excited-state charge density of the solute. In this work, we developed a state specific (SS) method based on the novel nonequilibrium solvation model with constrained equilibrium manipulation to account for solvation effects in electronic absorption processes. Time-dependent density functional theory (TD-DFT) is adopted to calculate electronic excitation energies and a polarizable continuum model is employed in the treatment of bulk solvent effects on both the ground and excited electronic states. The equations based on this novel nonequilibrium solvation model in the framework of TDDFT to calculate vertical excitation energy are presented and implemented in the Q-Chem package. The implementation is validated by comparing reorganization energies for charge transfer excitations between two atoms obtained from Q-Chem and those obtained using a two-sphere model. Solvent effects on electronic transitions of coumarin 153 (C153), acetone, pyridine, (2E)-3-(3,4-dimethoxyphenyl)-1-(2-hydroxyphenyl)prop-2-en-1-one (DMHP), and uracil in different solvents are investigated using the newly developed code. Our results show that the obtained vertical excitation energies as well as spectral shifts generally agree better with the available experimental values than those obtained using the traditional nonequlibrium solvation model. This new model is thus appropriate to study nonequilibrium excitation processes in solution.
1. Introduction
It is well known that solvent effects have an important effect on spectral shifts, and it is necessary to deal with them properly. In general, solvation models to handle interactions between the solute molecule and the surrounding solvent can be classified into two groups. The first class of the solvation model is the explicit solvation model,1,2 which explicitly treats the solvent molecules around the solute molecule. This model is effective in dealing with specific solute–solvent interactions and obtaining optimized structures including solvent molecules around the compound of interest. Nevertheless, potentials representing interactions between the solvent and the solute molecules play a vital role in reliability of such computations. Alternatively, a supermolecular model3 is adopted to consider the influence of solvent molecules from the first solvation shell, where a very small amount of solvent molecules may be clustered with the solute molecule in electronic structure calculations. The second class of the solvation model is the implicit solvation model. A solute cavity from a union of atom-centered spheres is constructed, and the solvent is regarded as a continuous medium characterized by the dielectric constant. The most popular implicit solvation model is the polarizable continuum model (PCM) developed firstly in Pisa.4,5 There are various versions of PCMs, such as the IEF-PCM6 (integral equation formalism-polarizable continuum model), C-PCM7 (conductor-like polarizable continuum model) and D-PCM (the dielectric version of the PCM). In this work, we use the SSVPE8 (Surface and Simulation of Volume Polarization for Electrostatics) method. SSVPE is developed by Chipman,8 which is equivalent in principle to a modification of the original IEF-PCM. In this model, the contribution of volume polarization due to electronic charge density of the solute penetrating outside the cavity is considered.9Considering the fact that a finite time is needed for the solvent to respond to the change in charge density of the solute due to electronic transitions,10 there exist two regimes, i.e., a non-equilibrium and an equilibrium regime.11 In the equilibrium regime, all the solvent degrees of freedom are in equilibrium with the electron density of the state of interest. On the other hand, only solvent electronic polarization, or a fast degree of freedom, is in equilibrium with the excited-state electron density of the solute in the non-equilibrium regime, while the slow degrees of freedom remain in equilibrium with the ground-state electron density of the solute. Within the PCM model, this effect is taken into account by two different dielectric constants. Regarding the equilibrium regime, the static dielectric constant (εs) is employed to describe solvent effects. On the other hand, the reaction field due to the fast solvent degrees of freedom is determined through the optical dielectric constant εopt, which corresponds to the square of the refractive index, in the non-equilibrium regime.12 Recognition of time scales is critical with regard to electronic excitations in solution and electronic transition of the solute is much faster than the reorientation of solvent molecules. It is thus improper to treat both the initial and the final states of the solvent as an equilibrium state.13,14 Consequently, it is a great challenge to establish an appropriate non-equilibrium thermodynamics for such a process.
The study of nonequilibrium solvation theory has attracted enormous scientific interests. Free energy expression of nonequilibrium polarization was proposed initially by Ooshika,15 Marcus,16 Lippert,17 and Mataga et al.,18 and then followed by Lee, Hynes,19 Kim20 and Aguilar et al.21 based on Felderhof's energy expression for medium polarization.22 Recently, we proposed a new formula for the solvation energy of nonequilibrium polarization using a constrained equilibrium approach in the continuum model.23,24 The new formula has been applied successfully to vertical ionization energies of hydrated electrons,25 reorganization energies of electron transfer reactions,26–28 and spectral shifts of the electronic spectrum.29–34
Time-dependent density functional theory (TD-DFT)35 is nowadays the most commonly used method in calculating electronic excitation energies. TDDFT with implicit solvation models has been developed previously to account for solvation effects on excitation energies.35–37 To account for solvent effects on electronic excitations such as absorption or emission processes with nonequilibrium solvation effects considered, state specific (SS) and linear response (LR) quantum mechanical methods are introduced in TDDFT calculations.38–40 LR provides a direct determination of excitation energies and calculation of the excited-state electron density is not required. On the other hand, SS affords the change of solvation free energies caused by the change of the electron density upon excitation. Unrelaxed density for the excited states can readily be obtained from eigenvectors of the random-phase-approximation (RPA) equation in TDDFT, while it is much more involved in calculating the relaxed density. However, it is demonstrated that solvent shifts obtained using unrelaxed density are too large, while the results obtained with relaxed density are improved.41 We thus use relaxed densities in calculating solvation effects. In this work, we implement the state-specific vertical excitation model for electronic excitation in solution based on the new formula for the solvation energy of nonequilibrium polarization.
This paper is organized in the following manner: a concise introduction on constrained equilibrium manipulation to establish an appropriate nonequilibrium state is provided in Section 2. The new formulas for the solvation energy of nonequilibrium polarization as well as vertical excitation energy are given in this section. Computational details are described in Section 3. Validation of the implementation is carried out by comparing the results of charge transfer excitations between two atoms with those of a two-sphere model in Section 4. A proper exchange–correlation functional is chosen based on excitation energies of the C153 molecule in various polar and non-polar solvents. Solvent effects on electronic transitions of four other molecules are explored subsequently. Conclusion remarks and outlook on future directions of research are given in Section 5.
2. Theory
2.1 General considerations
Vertical excitation energy in a solution is defined as the difference between the free energy of the electronic excited state and that of the electronic ground state:| ΔE = G2 − G1. | (1) |
| Gi = Ei + Fi, | (2) |
Within the frame work of a PCM, the solute is placed in a cavity surrounded by the solvent and the surface of the cavity is partitioned into the so-called “tesserae”. On the other hand, the solvent is described by a homogeneous continuum medium and is polarized by the solute. Polarization of the solvent is characterized by the apparent solvation charges on the cavity surface. The apparent solvation charges on the cavity surface are calculated using the following equation:
| DQ = V, | (3) |
| DεsQeq1 = V1. | (4) |
In ground state calculations, the self-consistent reaction field (SCRF) approach is employed to determine the solute charge, the electrostatic potential of the solute charge V1, and the apparent solvation charges Qeq1. This indicates that the electrostatic potential of the solute charge depends implicitly on the static dielectric constant of the solvent. For the ground state, the solvation free energy is calculated using
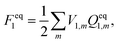 | (5) |
2.2 The nonequilibrium solvation free energy of the excited state
In our previous papers,33,34,43,44 we have established a novel expression for the nonequilibrium solvation free energy by introducing the constrained equilibrium approach proposed by Leontovich.45 By means of imposing a suitable extra electric field Vex, a nonequilibrium state of an isothermal system can always be mapped to a constrained equilibrium state, which has the same solvent polarization as the nonequilibrium state. Detailed comparisons between the formula of nonequilibrium solvation free energy with the constrained equilibrium approach and that of the traditional theory as well as analytical results obtained using these two theories have been discussed in detail in ref. 43. We focus on the corresponding equations pertinent to the PCM model in electronic absorption processes here.As an equilibrium state, the solvation free energy of the constrained equilibrium state can easily be obtained as
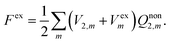 | (6) |
The constrained equilibrium approach can be clarified by the following three assumptions.23–25,31 First of all, a nonequilibrium state of the closed isothermal system without flow can always be mapped to a constrained equilibrium state by means of imposing suitable external conservative forces, and the constrained equilibrium state has the same internal variables as those of the nonequilibrium state. Secondly, differences in state functions between the constructed constrained equilibrium and any other equilibrium state can be calculated simply based on classical thermodynamics. Finally, in order to recover the true nonequilibrium state, the external forces can be removed suddenly without friction from the constrained equilibrium system. Upon removing the external electric field suddenly, the solvent system retains the real nonequilibrium polarization and the work done by the system is given by
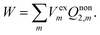 | (7) |
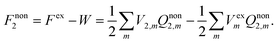 | (8) |
| DεsQnon2 = V2 + Vex. | (9) |
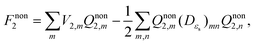 | (10) |
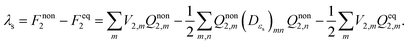 | (11) |
| DεsQeq2 = V2. | (12) |
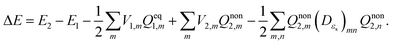 | (13) |
2.3 Vertical excitation energies of solute molecules in TDDFT
In TDDFT calculations, the energy difference between the excited and ground states in the presence of a frozen ground state solvent state, ΔEGS, can be obtained from the eigenvalue of the following RPA equation: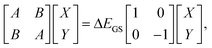 | (14) |
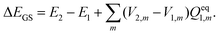 | (15) |
Vertical excitation energy of absorption in a solute based on the constrained equilibrium state approach in TDDFT calculations can thus be achieved as:
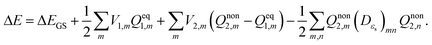 | (16) |
The purpose of the present work is to propose a state specific method using the novel nonequilibrium solvation model based on the constrained equilibrium approach. It is necessary to compare the present formula with those of the traditional theory proposed by Marcus.
Nonequilibrium solvation free energy in the traditional form43 is obtained based on a reversible work method, and it can be expressed as
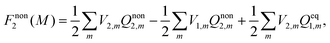 | (17) |
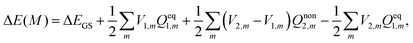 | (18) |
It can readily be seen from eqn (16) that vertical excitation in a solution is composed of two parts. The first part is the difference between excited- and ground-state energies with a frozen ground-state solvent. The second part, i.e. the last three terms on the right hand side of eqn (16), describes the interaction between the polarization charges of the solvent and the electrostatic potential of the solute. The apparent solvation charges corresponding to the nonequilibrium excited state are required to calculate this second part, and they are determined by taking into account the fast and slow partition of the solvent response.
There exist two partition schemes in determining the nonequilibrium apparent solvation charges and defining the fast and slow polarization charges, i.e. the Marcus and Pekar partitions. The apparent solvation charges are divided into the electronic polarization charges and the orientational polarization charges in Marcus' partition scheme, denoted by “el” and “or” respectively. On the other hand, they are partitioned into dynamic polarization charges and inertial polarization charges in Pekar's scheme and these two parts are represented by “dyn” and “in”, respectively.
The total nonequilibrium apparent solvation charges for the excited state on each tessera of the cavity surface are divided into electronic and orientational polarization charges according to Marcus's partition scheme:
| Qneq2,m = Qel2,m + Qor1,m, | (19) |
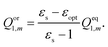 | (20) |
| DεoptQel2,m = V2,m + ΩQor1,m, | (21) |
By contrast, the total nonequilibrium apparent solvation charges for the excited state on each tessera of the cavity surface are composed of dynamic and inertial polarization charges according to Pekar's partition scheme, i.e.,
| Qneq2,m = Qdyn2,m + Qin1,m. | (22) |
| Qin1,m = Qeq1,m − Qdyn1,m, | (23) |
| DεoptQdyn1,m = V1,m. | (24) |
| DεoptQdyn2,m = V2,m, | (25) |
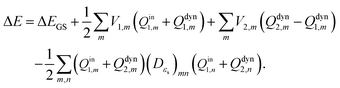 | (26) |
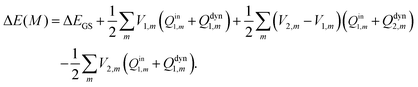 | (27) |
3. Details of computations
DFT and TDDFT calculations are carried out to determine ground state geometries, ground and excited state electronic structures as well as the absorption spectra. To verify the correctness of our implementations, solvent reorganization energies for charge transfer from one atom to another one in water are calculated using Q-Chem and compared with those obtained from a two-sphere model. Next, we tested the accuracy of three different exchange–correlation functionals in describing the spectral shifts of C153, namely, the Becke-3-Lee–Yang–Parr (B3LYP) density functional, the Perdew–Burke–Ernzerhof hybrid functional (PBE0), and the coulomb attenuated functional (CAM-B3LYP). The PBE0 functional is chosen for the rest of the calculations. In our calculations, the 6-31+G(d,p) basis set is employed for geometry optimization of the ground state and the more extended 6-311+G(2d,2p) basis set is adopted for calculations of excitation energies. In gas-phase calculations, excitation energies were determined at the gas-phase ground-state geometries. Similarly, excitation energies were considered at the liquid-phase ground-state geometries in liquid-phase calculations. The SSVPE model is employed to account for bulk solvent effects. The cavity surface is discretized using atom-centered Lebedev grids with a radius of 1.2 times the van der Waals atomic radii. The static dielectric constants at 298 K have been used, namely, 1.91 (heptane), 20.49 (acetone), 35.69 (acetonitrile), 78.35 (water), and 46.8 [dimethyl sulfoxide (DMSO)]. On the other hand, the optical dielectric constants required for the nonequilibrium calculations are 1.926 (heptane), 1.846 (acetone), 1.807 (acetonitrile), 1.778 (water), and 2.008 (DMSO), respectively. All the calculations were performed using a locally modified version of Q-Chem.484. Results and discussion
4.1 Solvation effects on charge transfers between two atoms
To validate the implementation of the nonequilibrium solvation free energy, charge transfer excitations from one atom to another at different inter-atomic distances are calculated using the above equations and the CAM-B3LYP functional. A diatomic system is an ideal system to apply the two-sphere model when the two atoms are well separated. In our work, solvent reorganization energies for the charge transfer excitation from a Mg atom to a C atom at various C–Mg separations are calculated to verify our implementation by comparing numerical values from our modified Q-Chem with the results of the two-sphere model. According to our previous work,43 solvation reorganization energy λs for charge transfer with the two-sphere model can be calculated using the following equation: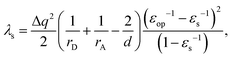 | (28) |
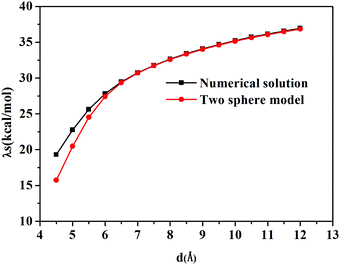
In our calculations with Q-Chem, the solute cavity surface was discretized with Lebedev spheres using 302 Lebedev grid points for each atom, and van der Waals radii of the involving atoms scaled by 1.2 are adopted to construct the cavity. Solvent reorganization energies for charge transfer excitation from Mg to C in water are calculated, where the static and the optical dielectric constants are 78.5 and 1.778, respectively. If the two atoms are too close to each other, the cavity will be composed of two intersected spheres. When the distance between two atoms is larger than 7.0 Å, the cavity will be two independent spheres (see Fig. 1).
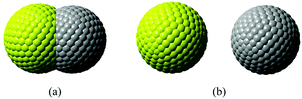 | ||
| Fig. 1 Segmentation of the C–Mg dimmer cavity. (a) The intersected spheres, and (b) the separated spheres. | ||
TDDFT calculations are carried out to obtain charge transfer states in this Mg–C system at different inter-atomic distances. According to our results, the S3 state is an excited state with transition from an occupied orbital of Mg to a virtual orbital on C. Solvent reorganization energy for this state is calculated using eqn (11) as implemented in Q-Chem (Fig. 2).
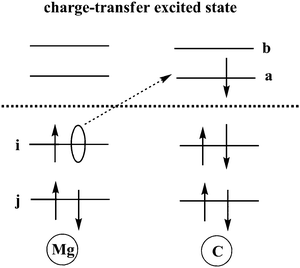 | ||
| Fig. 2 Schematic sketch of a charge-transfer excitation in which an electron is transferred from an occupied orbital on Mg to a virtual orbital on C. | ||
The calculated solvent reorganization energies with the inter-atomic distance ranging from 4.5 Å to 12.0 Å from numerical solutions using Q-Chem and the two-sphere model are illustrated in Fig. 3. It can be seen from this figure that numerical values match better with the results of the two-sphere model when the inter-atomic distance gets longer. When the distance is larger than 7.0 Å, the numerical solution is almost the same as those of the two-sphere model. Thus we can safely draw the conclusion that the subroutines implemented in the Q-Chem package provide correct nonequilibrium solvation free energy based on the constrained equilibrium approach.
4.2 Coumarin 153
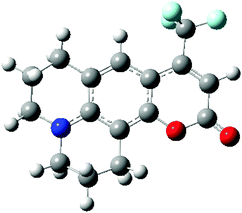
In order to investigate the performance of different exchange–correlation functionals in describing spectral shifts, a benchmark molecule C153 has been adopted to study the dynamic aspects of solvation. This molecule has a significant difference in the dipole moment between the ground and the first excited electronic states. Owing to the huge number of available experimental and computational data,11,14,50–53 the study of C153 becomes a good practice for methodology verifications. In this work, state-specific PCM/TD-DFT calculations on C153 using different XC functionals are carried out and dynamic solvent effects on the absorption process are investigated.C153 is a sizable molecule with substantial electrons, which increases the difficulty in selecting the basis set and the level of calculations. Its ground state geometry is optimized using PBE0/6-31+G(d,p) and the obtained cis-conformation is illustrated in Fig. 4. It should be noted that ground state geometries of C153 in different solvents are optimized separately. The electronic transition S0 → S1 in C153 is calculated and the corresponding solvatochromic shift will be compared with the experimental values. It should be noted that the electronic transition S0 → S1 of C153 has a partial π → π* character,11 and a significant oscillator strength according to our calculations. This excitation mainly corresponds to transition from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO).50
The dipole moments of both the ground and the excited states of C153 are rather large, which indicates that C153 should be strongly solvated in solution. Table 1 summarizes some theoretical results together with the experimental data for comparison. As shown in Table 1, the excited-state dipole moment of C153 is larger than that of the ground state dipole moment in both the gas phase and the liquid phase. The dipole moment changes from 7.61 D in the ground state to 13.15 D in the excited state in the gas phase. It can be seen that the calculated ground state dipole moment in the gas phase is overestimated compared with the experimental value of 6.55 D. However, our value of 7.61 D is close to the previous theoretical results of 7.68 D and 7.0 D obtained at the B3LYP/6-311G(d) level10 and the BHLYP/VTZP level,54 respectively. In addition, the dipole moment of the excited state 13.15 D is in reasonable agreement with experimental observation14 as well as other theoretical results of 13.64 D and 14.3 D obtained in AM155 and PM354 calcultaions.
| Solvent | Ground | Excited | ||
|---|---|---|---|---|
| This work | Expt | This work | Expt | |
| a Calculated at the PBE0/6-311+G(2d,2p) level. b Dielectric measurements in chloroform solution from ref. 56. c Experimental data from ref. 14, and values of the dipole moment difference between the ground and excited states from ref. 53. | ||||
| Vacuum | 7.61 | 6.55b | 13.15 | 12.4–13.6c |
| Heptane | 8.92 | 14.43 | ||
| Acetone | 11.16 | 16.25 | ||
| Acetonitril | 11.29 | 16.36 | ||
| DMSO | 11.34 | 16.39 | ||
When the dipole moment of the ground state is larger than that of the excited state, solute–solvent interactions of the ground state are stronger than those of the excited state and a blue shift of absorption maximum will be observed.31 Similarly, a larger dipole moment of the excited state will suggest a red shift of the absorption maximum. It can be seen from Table 1 that the dipole moment of the ground state is smaller than that of the excited state and this indicates a red shift for the π → π* transition. In addition, the presence of solvent increases dipole moments of both the ground and the excited state and solvation effects on the dipole moment are more pronounced in the ground state than that in the excited state. Moreover, the excited-state dipole moments of C153 in DMSO and other polar solvents are rather similar, leading to the dipole moment of the excited state of around 16.3 D.
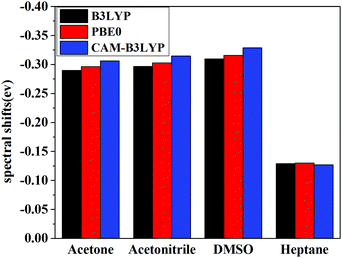
Vertical excitation energies based on the present theory for π → π* transition of C153 in various solvents using different XC functional are compared with the available experimental results51,52 in Fig. 5. It can be seen that the most popular XC functional, B3LYP, underestimates excitation energies by about 0.1–0.2 eV, while the CAM-B3LYP functional, which is designed to deal with the long-range charge transfer excitations, overestimates excitation energies by about 0.3 eV. On the other hand, excitation energies with PBE0 agree the best with the available experimental results among these three XC functionals with an average error of 0.03 eV. In fact, PBE0 is an ab initio hybrid functional due to the absence of adjustable parameters and it has been shown previously that it can usually afford reliable excitation energies for medium/large-sized molecules,57 thus making it a widely applicable method in calculating excitation energies. One can see that the excitation energy for this state in a vacuum computed by PBE0 of 3.36 eV is in good agreement with the experimental value of 3.37 eV,51 whereas the excitation energies obtained using B3LYP and CAM-B3LYP are less accurate in this case. This again shows reliability of PBE0 in describing the excitation energy for this state of C153. Spectral shifts for this transition of C153 in acetone, acetonitrile, DMSO and heptane using these XC functionals are illustrated in Fig. 6. It can be seen from this figure that spectral shifts with different XC functionals are quite similar and their difference is within 0.02 eV. This is probably because the functional dependencies on excitation energies in a vacuum are similar to those in solution.
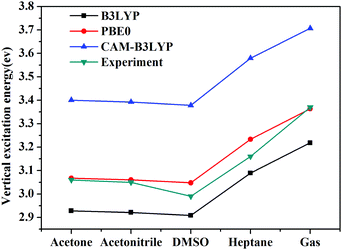 | ||
| Fig. 5 Vertical excitation energies of C153 in different solvents using different XC functionals as well as experimental values.51,52 | ||
Solvent shifts are rather significant in polar solvents such as acetone, acetonitrile, and DMSO, due to the large difference in the dipole moment between the ground and the excited state. The present spectral shifts obtained based on the constrained equilibrium manipulation with the PBE0 functional, namely, −0.29 eV, −0.30 eV, and −0.32 eV for acetone, acetonitrile, and DMSO are in slightly better agreement with the experimental values, i.e. −0.31 eV, −0.32 eV, and −0.38 eV,50 than those obtained with the traditional nonequilibrium solvation model: −0.26 eV, −0.27 eV and −0.28 eV. The other two functionals show the same tendency (see Fig. 6). These results indicate that although XC functionals can have some effects on vertical excitation energies, spectral shifts obtained based on our novel nonequilibrium solvation model generally agree better with the experimental results than those obtained using the traditional nonequilibrium solvation model. On the other hand, the solvent effect in a nonpolar solvent, heptane,60 is small and the nonequilibrium solvation effect is negligible. With regard to nonpolar solvents, effects of non-electrostatic contributions play a more important role. In the present work, solvent effects are calculated by treating the solvent as a dielectric continuum, which implies that only electrostatic contribution is considered. Other factors such as dispersion-repulsion effects are not considered in this work, and we will mainly focus on polar solvents where the electrostatic contribution accounts for the dominant part of solvation effects on vertical energies.
It has been widely accepted that PBE0 is able to provide reasonable results for local valence excitations, while underestimate excitation energies of charge-transfer states pronouncedly. On the other hand, range-separated hybrid functionals such as CAM-B3LYP describe charge transfer excited states more reliably.58,59 For transitions of C153 and the other four molecules considered in the present work, excitation energies with CAM-B3LYP are not much larger than those with PBE0 and the charge-transfer character is probably insignificant. In addition, solvent effects are not sensitive to the employed functional and spectral shifts obtained with different XC functionals are quite similar. We only present the PBE0 results on the absorption spectra and the spectral shifts of the other molecules in the remaining discussions.
Solvatochromic studies show that contributions to the solvent shift can be classified into different categories, such as nonspecific and specific solvent effects.61 In fact, solvation dynamics is a complex phenomenon, and sometimes it is insufficient to be treated simply in the framework of pure continuum models.62 Inevitably, there are limitations in the polarizable continuum model, such as hydrogen bonds which cannot be addressed properly using the PCM model. In addition, vibrational characteristics of ground and excited electronic states through Franck–Condon factors can also influence the position of the maximum of an absorption band. Effective procedures have been developed to deal with this issue, however, it falls outside the scope of this contribution. The focus of this study is on nonequilibrium solvent effects.
4.3. Results of acetone, pyridine, uracil and DMHP
In this section we investigate the solvent effects on the lowest n → π* electronic transition of acetone, pyridine and uracil, as well as the π → π* transition of DMHP (Fig. 7).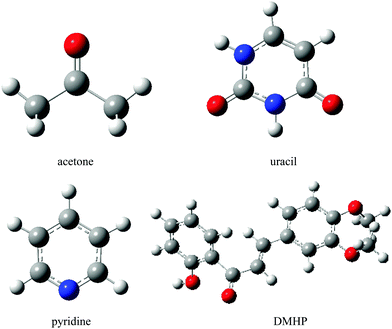 | ||
| Fig. 7 Molecular structures of the solutes. Hydrogen, carbon, nitrogen and oxygen atoms are represented by white, grey, blue and red balls, respectively. | ||
The dipole moments of acetone, pyridine and uracil decrease in solution upon the lowest n → π* electron transition, which indicates blue shifts of the absorption maximum of the corresponding excitation. On the other hand, red shifts are suggested to the lowest π → π* electronic transition for DMHP due to an increase in the dipole moment upon excitation, which implies stronger solute–solvent interactions in the excited state than those of the ground state.
Vertical excitation energies and spectral shifts obtained based on the present theory of the first allowed electronic transitions for the four molecules in various polar solvents are compared with those obtained using traditional theory as well as the available reference data in Tables 2 and 3, respectively.
| Gas | Acetonitrile | Water | DMSO | |
|---|---|---|---|---|
| a Data from ref. 63. b From ref. 64 in 1-methyl uracil. c From ref. 65. d From ref. 66. e From ref. 67; n/a means not available. | ||||
| Acetone | ||||
| Present | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 753 753 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 633 633 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682 682 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623 623 |
| Traditional | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 753 753 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 741 741 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 790 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
| Ref.a | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975 975 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 847 847 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760 760 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 767 |
| Uracil | ||||
| Present | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 487 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208 208 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306 306 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 161 |
| Traditional | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 487 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 530 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506 506 |
| Ref. | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 746b 746b |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100c 100c |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600c 600c |
n/a |
| Pyridine | ||||
| Present | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212 212 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266 266 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 168 |
| Traditional | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 439 439 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 494 494 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411 411 |
| Ref.d | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521 521 |
n/a | n/a | n/a |
| DMHP | ||||
| Present | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 355 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 323 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249 249 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 158 158 |
| Traditional | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 355 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863 863 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 826 826 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 741 741 |
| Ref.e | n/a | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 409 409 |
n/a | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 397 397 |
| Acetonitrile | Water | DMSO | |
|---|---|---|---|
| Acetone | |||
| Present | 880 | 929 | 870 |
| Traditional | 988 | 1037 | 987 |
| Uracil | |||
| Present | 1721 | 1819 | 1674 |
| Traditional | 2043 | 2142 | 2019 |
| Pyridine | |||
| Present | 871 | 926 | 827 |
| Traditional | 1099 | 1154 | 1071 |
| DMHP | |||
| Present | −32 | −105 | −197 |
| Traditional | 507 | 470 | 385 |
For acetone, a comparison between the calculated results and experimental values is made, since the experimental values of vertical excitation energy are observed in both gas and liquid phases. In the gas phase, the calculated vertical absorption energy of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 753 cm−1 for the lowest n → π* electronic transition agrees rather well with the experimental value, with a deviation of 222 cm−1.63 The blue shifts based on the constrained equilibrium manipulation, namely, 880 cm−1 and 870 cm−1 for this molecule in acetonitrile and DMSO are in slightly better agreement with the experimental values, i.e. 872 cm−1 and 792 cm−1,63 than those with the traditional theory: 988 cm−1 and 987 cm−1. For acetone in water, both the constrained equilibrium theory and the traditional theory underestimated the solvent shift pronouncedly compared with the experimental value of 1785 cm−1.63 It is probably because the hydrogen-bonding effect is fairly important in protic solvents as discussed by Han and Zhao.68–70 Spectral shifts should be predicted more accurately in protic solvents if the hydrogen-bonding effect is taken into account as shown in abundance theoretical studies of Truhlar et al.71,72
753 cm−1 for the lowest n → π* electronic transition agrees rather well with the experimental value, with a deviation of 222 cm−1.63 The blue shifts based on the constrained equilibrium manipulation, namely, 880 cm−1 and 870 cm−1 for this molecule in acetonitrile and DMSO are in slightly better agreement with the experimental values, i.e. 872 cm−1 and 792 cm−1,63 than those with the traditional theory: 988 cm−1 and 987 cm−1. For acetone in water, both the constrained equilibrium theory and the traditional theory underestimated the solvent shift pronouncedly compared with the experimental value of 1785 cm−1.63 It is probably because the hydrogen-bonding effect is fairly important in protic solvents as discussed by Han and Zhao.68–70 Spectral shifts should be predicted more accurately in protic solvents if the hydrogen-bonding effect is taken into account as shown in abundance theoretical studies of Truhlar et al.71,72
Similar to the case of acetone, the blue shift for uracil in acetonitrile based on the constrained equilibrium manipulation, i.e. 1721 cm−1, brings the prediction closer to the experimental value, i.e. 1354 cm−1,64,65 than those obtained with traditional theory: 2043 cm−1. The predicted shift in water is not consistent with the experimental value, which is probably due to neglect of the hydrogen bonding effect as has been discussed.
The experimental value of vertical excitation energy of pyridine is available only in the gas phase,66 and the calculated vertical absorption energy of 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 cm−1 for the lowest n → π* electronic transition agrees rather well with the experimental value, with a deviation of 181 cm−1. We only compare spectral shifts in various polar solvents obtained using the two theories. The differences between the results obtained with the present theory and those of traditional ones are minor, but we can still see slightly smaller shifts based on constrained equilibrium manipulation compared with the results of the traditional theory. Baba et al.73 first studied the importance of hydrogen bonding on n → π* transition of pyridine experimentally and Del Bene74,75 pioneered computational studies on hydrogen bonding effects. Those works demonstrate that forming of hydrogen bond gives a large blue shift in the n → π* transition. The explicit solvation model is required to treat hydrogen bonding effects. A detailed discussion of hydrogen bonding effects on this transition is given in a review reported by Reimers et al.76
340 cm−1 for the lowest n → π* electronic transition agrees rather well with the experimental value, with a deviation of 181 cm−1. We only compare spectral shifts in various polar solvents obtained using the two theories. The differences between the results obtained with the present theory and those of traditional ones are minor, but we can still see slightly smaller shifts based on constrained equilibrium manipulation compared with the results of the traditional theory. Baba et al.73 first studied the importance of hydrogen bonding on n → π* transition of pyridine experimentally and Del Bene74,75 pioneered computational studies on hydrogen bonding effects. Those works demonstrate that forming of hydrogen bond gives a large blue shift in the n → π* transition. The explicit solvation model is required to treat hydrogen bonding effects. A detailed discussion of hydrogen bonding effects on this transition is given in a review reported by Reimers et al.76
It is interesting to compare the spectral shifts based on constrained equilibrium manipulation with those of the traditional theory for DMHP,67 An opposite sign of the shift is obtained and red shifts are predicted in a polar solvent using the present approach, however, blue shifts are obtained based on the traditional theory when the PBE0 functional is employed. In fact, spectral shifts for this molecule are relatively small according to the results shown in Table 3. This means that the solvent has only an insignificant effect on this excited state. Since the experimental value in the gas phase is unavailable, the calculated shift cannot be directly compared with the experimental values, and comparison can only be made between the present theory and the traditional one. Notably, the x-direction dipole moment changes sign between the ground and excited electronic states, and the total dipole moment of the excited state is larger than that of the ground state with the PBE0 functional. This implies that the present theory provides a reasonable description on this molecule. On the other hand, the red shift is obtained with both the present theory and the traditional theory when the CAM-B3LYP functional is adopted and the shift with the present theory is somewhat larger. This is because the dipole moment of the excited state is calculated to be larger than that of the ground state with CAM-B3LYP.
From an overall perspective, the results obtained based on our novel nonequilibrium solvation model by introducing constrained equilibrium manipulation are generally more reliable than those with traditional one compared with reference values. Inevitably, there exists some difference between the theoretical results and reference values due to deficiency of the employed implicit solvation model. On the other hand, poorly defined maxima of broad spectral envelopes also give rise to uncertainty in the experimental excitation energies.42
5. Conclusion
Due to different time-scales of slow and fast polarization, the solvent is not in equilibrium with the solute charge density upon electronic excitation of solute molecules. A constrained equilibrium approach proposed previously is employed to achieve the nonequilibrium solvation energy and to calculate vertical excitation energy for the absorption process in this work. Compared with the traditional strategy where nonequilibrium solvation energy is derived through reversible work, a new expression for the nonequilibrium solvation energy is given by invoking the constrained equilibrium principle of classical thermodynamics. A state-specific procedure in the framework of a continuous medium model is adopted together with TDDFT to determine excitation energies. The obtained equations are implemented into the electronic structure program package Q-Chem. Correctness of the implementation is verified by comparing reorganization energies for charge transfer between two atoms obtained with Q-Chem and those obtained using the two-sphere model.State-specific PCM/TD-DFT calculations have been carried out to study the excited states of chromophore C153 and four other molecules in various solvents. Contributions to solvent shifts are discussed and the present approach is applicable only to cases where electrostatic polarization is the key factor for the spectral shift of the electronic absorption spectra in polar solvents. Our results indicate that solvatochromic shifts obtained using our model usually agree well with the available experimental results in various solvents than those obtained using the traditional nonequlibrium solvation model. This new model thus presents an appropriate method to study excitation processes in solution.
Finally, it is noteworthy that non-electrostatic interactions play a significant role in situations such as non-polar solvents, and solvation dynamics there is too complicated to simply consider long-range electrostatic interactions within the continuum model.11 Furthermore, effects of hydrogen bonds play a crucial role in solvent effects in some cases,77 but the continuum model cannot treat these effects sufficiently. More details on this aspect are beyond the subject of this report, and will be given in a more technical paper under preparation. Possible future works also include extension of the present state-specific PCM/TD-DFT method based on the constrained equilibrium approach to geometry relaxations of excited states and emission processes.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Project No. 21573152).References
- C. J. Cramer and D. G. Truhlar, Science, 1992, 256, 213–217 CAS.
- A. Eilmes, Theor. Chem. Acc., 2014, 133, 1538 CrossRef.
- K. Coutinho and S. Canuto, J. Chem. Phys., 2000, 113, 9132–9139 CrossRef CAS.
- B. Mennucci, Int. J. Quantum Chem., 2015, 115, 1202–1208 CrossRef CAS.
- B. Mennucci, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386–404 CrossRef CAS.
- E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- D. M. Chipman, J. Chem. Phys., 2000, 112, 5558–5565 CrossRef CAS.
- P. C. Couto and D. M. Chipman, J. Phys. Chem. A, 2010, 114, 12788–12793 CrossRef PubMed.
- F. Ingrosso, B. M. Ladanyi, B. Mennucci, M. D. Elola and J. Tomasi, J. Phys. Chem. B, 2005, 109, 3553–3564 CrossRef CAS PubMed.
- R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103 CrossRef PubMed.
- V. Barone and A. Polimeno, Chem. Soc. Rev., 2007, 36, 1724–1731 RSC.
- M. Cossi and V. Barone, J. Phys. Chem. A, 2000, 104, 10614–10622 CrossRef CAS.
- D. V. Matyushov and M. D. Newton, J. Phys. Chem. A, 2001, 105, 8516–8532 CrossRef CAS.
- Y. Ooshika, J. Phys. Soc. Jpn., 1954, 9, 594–602 CrossRef.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 979–989 CrossRef CAS.
- V. E. Lippert, Z. Naturforsch., 1955, 10a, 541–546 Search PubMed.
- N. Mataga, Y. Kaifu and M. Koizumi, Bull. Chem. Soc. Jpn., 1956, 29, 465–470 CrossRef CAS.
- S. Lee and J. T. Hynes, J. Chem. Phys., 1988, 88, 6853–6862 CrossRef CAS.
- H. J. Kim, J. Chem. Phys., 1996, 105, 6818–6832 CrossRef CAS.
- M. A. Aguilar, F. J. Olivares del Valle and J. Tomasi, J. Chem. Phys., 1993, 98, 7375–7384 CrossRef CAS.
- B. U. Felderhof, J. Chem. Phys., 1977, 67, 493–500 CrossRef CAS.
- X. Y. Li, F. C. He, K. X. Fu and W. J. Liu, J. Theor. Comput. Chem., 2010, 9, 23–27 CrossRef CAS.
- X. Y. Li, Q. Zhu, F. C. He and K. X. Fu, in Thermodynamics, ed. T. Mizutani, InTech Publisher, Shanghai, 2011, vol. 11, pp. 205–232 Search PubMed.
- X. J. Wang, Q. Zhu, Y. K. Li, X. M. Cheng, X. Y. Li, K. X. Fu and F. C. He, J. Phys. Chem. B, 2010, 114, 2189–2197 CrossRef CAS PubMed.
- H. Y. Wu, H. S. Ren, Q. Zhu and X. Y. Li, Phys. Chem. Chem. Phys., 2012, 14, 5538–5544 RSC.
- H. S. Ren, M. J. Ming, J. Y. Ma and X. Y. Li, J. Phys. Chem. A, 2013, 117, 8017–8025 CrossRef CAS PubMed.
- T. J. Bi, M. J. Ming, H. S. Ren, J. Y. Ma and X. Y. Li, Theor. Chem. Acc., 2014, 133, 1557 CrossRef.
- J. Y. Ma, J. B. Wang, X. Y. Li, Y. Huang, Q. Zhu and K. X. Fu, J. Chem. Phys., 2008, 29, 198–210 CAS.
- Y. K. Li, H. Y. Wu, Q. Zhu, K. X. Fu and X. Y. Li, Comput. Theor. Chem., 2011, 971, 65–72 CrossRef CAS.
- H. S. Ren, Y. K. Li, Q. Zhu, J. Zhu and X. Y. Li, Phys. Chem. Chem. Phys., 2012, 14, 13284–13291 RSC.
- H. S. Ren, M. J. Ming, J. Zhu, J. Y. Ma and X. Y. Li, Chem. Phys. Lett., 2013, 583, 213–217 CrossRef CAS.
- L. K. Xu, T. J. Bi, M. J. Ming, J. B. Wang and X. Y. Li, Chem. Phys. Lett., 2017, 679, 158–163 CrossRef CAS.
- M. J. Ming, L. K. Xu, F. Wang, T. J. Bi and X. Y. Li, Chem. Phys., 2017, 492, 27–34 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- M. E. Casida, in Recent Advances in Density Functional Theory, ed. D. P. Chong, World Scientific, Singapore, 1995, vol. 1, p. 155 Search PubMed.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- R. Improta, G. Scalmani, M. J. Frisch and V. Barone, J. Chem. Phys., 2007, 127, 074504 CrossRef PubMed.
- C. A. Guido, G. Scalmani, B. Mennucci and D. Jacquemin, J. Chem. Phys., 2017, 146, 204106 CrossRef PubMed.
- J. M. Mewes, J. M. Herbert and A. Dreuw, Phys. Chem. Chem. Phys., 2017, 19, 1644–1654 RSC.
- J. M. Mewes, Z. Q. You, M. Wormit, T. Kriesche, J. M. Herbert and A. Dreuw, J. Phys. Chem. A, 2015, 119, 5446–5464 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer, D. G. Truhlar, C. A. Guido, B. Mennucci, G. Scalmani and M. J. Frisch, Chem. Sci., 2011, 2, 2143–2161 RSC.
- X. Y. Li, Int. J. Quantum Chem., 2015, 115, 700–721 CrossRef CAS.
- X. Y. Li and K. Y. Fu, J. Theor. Comput. Chem., 2005, 4, 907–983 CrossRef CAS.
- M. Leontovich, Introduction to Thermodynamics: Statistical Physics, Nauka, Moscow, 1983, pp. 99–108 Search PubMed.
- M. Caricato, B. Mennucci, J. Tomasi, F. Ingrosso, R. Cammi, S. Corni and G. Scalmani, J. Chem. Phys., 2006, 124, 124520 CrossRef PubMed.
- B. Mennucci, C. Cappelli, C. A. Guido, R. Cammi and J. Tomasi, J. Phys. Chem. A, 2009, 113, 3009–3020 CrossRef CAS PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Ku, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. GolubevaZadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- Z. Q. You, J. M. Mewes, A. Dreuw and J. M. Herbert, J. Chem. Phys., 2015, 143, 204104 CrossRef PubMed.
- J. Xu, J. Chen, S. Dong, A. Fu, H. Li and T. Chu, J. Phys. Org. Chem., 2016, 29, 305–311 CrossRef CAS.
- N. P. Ernsting, M. Asimov and F. P. Schafer, Chem. Phys. Lett., 1982, 91, 231 CrossRef CAS.
- T. Gustavsson, L. Cassara, V. Gulbinas, G. Gurzadyan, J. C. Mialocq, S. Pommeret, M. Sorgius and P. van der Meulen, J. Phys. Chem. A, 1998, 102, 4229–4245 CrossRef CAS.
- A. Chowdhury, D. A. Locknar, L. L. Premvardhan and L. A. Peteanu, J. Phys. Chem. A, 1999, 103, 9614–9625 CrossRef CAS.
- A. Muhlpfordt, R. Schanz, N. P. Ernsting, V. Farztdinova and S. Grimme, Phys. Chem. Chem. Phys., 1999, 1, 3209–3218 RSC.
- P. K. McCarthy and G. J. Blanchard, J. Phys. Chem., 1993, 97, 12205–12209 CrossRef CAS.
- C. R. Moyland, J. Phys. Chem., 1994, 98, 13513 CrossRef.
- R. Improta, V. Barone and F. Santoro, J. Phys. Chem. B, 2007, 111, 14080–14082 CrossRef CAS PubMed.
- S. El-Taher and M. Metwaly, J. Mol. Struct., 2017, 1134, 840–850 CrossRef CAS.
- D. Jacquemin, E. A. Perpete, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135 CrossRef CAS PubMed.
- P. Hazra, D. Chakrabarty and N. Sarkar, Chem. Phys. Lett., 2003, 371, 553–562 CrossRef CAS.
- X. Liu, J. M. Cole and K. S. Low, J. Phys. Chem. C, 2013, 117, 14731–14741 CAS.
- T. Schwabe, J. M. H. Olsen, K. Sneskov, J. Kongsted and O. Christiansen, J. Chem. Theory Comput., 2011, 7, 2209–2217 CrossRef CAS PubMed.
- I. Renge, J. Phys. Chem. A, 2009, 113, 10678–10686 CrossRef CAS PubMed.
- W. A. Eaton and T. P. Lewis, J. Chem. Phys., 1970, 53, 2164–2172 CrossRef CAS PubMed.
- F. Santoro, V. Barone, T. Gustavsson and R. Improta, J. Am. Chem. Soc., 2006, 128, 16312–16322 CrossRef CAS PubMed.
- Z. L. Cai and J. R. Reimers, J. Phys. Chem. A, 2000, 104, 8389–8408 CrossRef CAS.
- A. M. Asiri, T. R. Sobahi, O. I. Osman and S. A. Khan, J. Mol. Struct., 2017, 1128, 636–644 CrossRef CAS.
- Hydrogen Bonding And Transfer In The Excited State, ed. K. L. Han, G. J. Zhao, John Wiley & Sons Ltd, Chichester, 2011, vol. I Search PubMed.
- HydrogenBonding And Transfer In The Excited State, ed. K. L. Han, G. J. Zhao, John Wiley & Sons Ltd, Chichester, 2011, vol. II Search PubMed.
- G. J. Zhao and K. L. Han, Acc. Chem. Res., 2012, 45, 404 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2829–2844 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2015, 119, 958–967 CrossRef CAS PubMed.
- H. Baba, L. Goodman and P. C. Valenti, J. Am. Chem. Soc., 1966, 88, 5410 CrossRef CAS.
- J. E. Del Bene, J. Am. Chem. Soc., 1975, 97, 5330 CrossRef.
- J. E. Del Bene, Chem. Phys., 1976, 15, 463–472 CrossRef.
- J. R. Reimers and Z. L. Cai, Phys. Chem. Chem. Phys., 2012, 14, 8791–8802 RSC.
- X. Zhou, J. W. Kaminski and T. A. Wesolowski, Phys. Chem. Chem. Phys., 2011, 13, 10565–10576 RSC.
| This journal is © the Owner Societies 2017 |