Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Characterising the evaporation kinetics of water and semi-volatile organic compounds from viscous multicomponent organic aerosol particles†
Stephen
Ingram
a,
Chen
Cai
 b,
Young-Chul
Song
a,
David R.
Glowacki
b,
Young-Chul
Song
a,
David R.
Glowacki
 ac,
David O.
Topping
d,
Simon
O’Meara
d and
Jonathan P.
Reid
ac,
David O.
Topping
d,
Simon
O’Meara
d and
Jonathan P.
Reid
 *a
*a
aSchool of Chemistry, University of Bristol, Cantock's Close, Bristol BS8 1TS, UK. E-mail: j.p.reid@bristol.ac.uk
bDepartment of Atmospheric and Oceanic Sciences, School of Physics, Peking University, Beijing 100871, China
cDepartment of Computer Science, University of Bristol, BS8 1UB, UK
dSchool of Earth and Atmospheric Sciences, University of Manchester, Williamson Building, Oxford Road, Manchester M13 9PL, UK
First published on 13th November 2017
Abstract
The physicochemical changes experienced by organic aerosol particles undergoing dehydration into the surrounding gas phase can be drastic, forcing rapid vitrification of the particle and suppressing internal diffusion. Until recently, experimental studies have concentrated on quantifying diffusional mixing of either water or non-volatile components, while relatively little attention has been paid to the role of semivolatile organic component (SVOC) diffusion and volatilisation in maintaining the equilibrium between the gas and particle phases. Here we present methods to simultaneously investigate diffusivities and volatilities in studies of evolving single ternary aerosol particle size and composition. Analysing particles of ternary composition must account for the multiple chemical species that volatilise in response to a step change in gas phase water activity. In addition, treatments of diffusion in multicomponent mixtures are necessary to represent evolving heterogeneities in particle composition. We find that the contributions to observed size behaviour from volatilisation of water and a SVOC can be decoupled and treated separately. Employing Fickian diffusion modelling, we extract the compositional dependence of the diffusion constant of water and compare the results to recently published parametrisations in binary aerosol particles. The treatment of ideality and activity in each case is discussed, with reference to use in multicomponent core shell models. Meanwhile, the evaporation of an SVOC into an unsaturated gas flow may be treated by Maxwell's equation, with slow diffusional transport manifesting as a suppression in the extracted vapour pressure.
I. Introduction
In recent years, a diverse range of laboratory and ambient aerosol measurements have supported the existence of a moisture driven glass transition in secondary organic aerosol (SOA) particles.1–4 Vitrification proceeds via the removal of water from the particle following a change in gas relative humidity (RH) and reduction in temperature, which in turn leads to large increases in organic solute concentration close to the surface.5,6 The increasing dehydration arrests molecular diffusion and confines the system to a metastable, amorphous ‘solid-melt’ type structure with no available kinetic pathway to undergo a phase transition and form an equilibrium crystal phase.7,8 Current work is focused on quantifying the influence of functional group chemistry on both the mesoscopic properties of single droplets (for example, the influence of aerosol composition on particle viscosity and phase),9–11 and the diffusional dynamics and reactivity of molecules residing within viscous particles.12,13 Such a fundamental understanding of the underlying physical chemistry may be essential to help qualify (or quantify) the environmental impacts of ensembles of glassy and semisolid particles.Recent studies have investigated the influence of ultraviscous and glassy aerosol on concentrations of highly reactive species in the atmosphere,12,14 and on cloud/ice nucleation.15,16 In addition, the influence of glassy and ultraviscous aerosol on the partitioning of semi-volatile organic compounds (SVOCs) between the condensed particle and gaseous phases is not clear, with studies suggesting that the partitioning may not be governed by equilibrium thermodynamics, but may instead be kinetically determined.6 Although numerous studies have shown that water diffusion in SOA may progress faster than would be expected from the Stokes–Einstein (SE) relationship based on the high viscosity of glassy aerosol,17 numerous other studies have shown that the diffusional transport of large organic molecules is hindered and follows much more closely the expected trend from the SE equation.13,18 The range of atmospheric conditions over which these phenomena may lead to a slowing of particle phase mixing have begun to be investigated,19–21 with some consensus emerging that diffusive limitations to water transport rarely occur in SOA in the planetary boundary layer.22 In contrast, kinetically limited mass transport of SVOC in SOA could have ramifications for mass concentrations and size distributions of aerosol23 and the lifetime of species in the particle phase.24 Indeed, there is considerable interest from a more fundamental perspective on the relationship between diffusion on the molecular scale and viscosity on the mesoscale of particles.8,15 The purpose of this paper is to explore methods for quantifying the competing contributions arising from the simultaneous evaporative mass transport of water and SVOCs in single-particle studies of viscous and glassy aerosol.
There are currently two single particle strategies by which the dependence of the diffusion constant of water on composition in viscous aerosol can be determined. In the first strategy, particles are exposed to step decreases in water activity driving the formation of internal concentration gradients. The rate of water loss from the surface is extremely rapid; often, the core of the particle cannot respond rapidly enough to equalise the water activity before diffusion is effectively arrested near the surface. Such radial heterogeneity is well documented,6,25 and modelling the subsequent internal water transport phenomena is central to extracting diffusion coefficients from experiments conducted on optically trapped and electrodynamically levitated particles.16,26,27 Indeed, we have shown that care must be taken in interpreting kinetic measurements from radially inhomogeneous particles: the radial inhomogeneity at any moment in time is a complex function of the processing history of the particle and so very rarely even starts in a uniform homogeneous form.28 To the best of our knowledge, most studies that assess the impact of aerosol microphysics on the composition of atmospheric aerosol do not account for this process history within an evolving gas phase environment, although some do account for diffusion using a core–shell model.
In a second strategy, the water activity is maintained at a constant value but the gas phase water is instantaneously switched from normal to deuterated water, leading to progressive isotopic exchange within the particle.27,29 The change in isotopic ratio can then be used to extract the water activity dependence of the diffusion constant of water. This method has been used to study particles either deposited on a substrate or optically trapped.30 Indeed, a similar approach has been extended to study the slow diffusional mixing of non-deuterated and deuterated sucrose between two contacting phases at low water activity, examining the conformity of sucrose diffusion constants to the SE equation.18 More broadly, the diffusion constants of large organic molecules in viscous aerosol or through viscous shells on aerosol particles have been inferred from kinetic measurements of the rates of volatilisation of tracer compounds including, for example, pyrene.24
In this publication, we will describe a framework for assessing the coupled evaporation kinetics of water and an SVOC from a viscous particle, allowing both a determination of the diffusion constant of water and the degree of suppression in the volatility of the SVOC with varying particle viscosity. We first review the framework for representing the compositional dependence of diffusion constants and the expected timescales for particle-gas partitioning of water and SVOCs in Section II. In Section III, we review the experimental methods used here. In Section IV we present a method for characterising the variation in particle size with time using the Kohlrausch–Williams–Watts equation,31 separating out the timescales for water transport and for volatile loss of the SVOC. Further, we provide the first direct determinations of diffusion constants of water in ternary component aerosol. This benefits from the application of a new algorithm for routinely fitting multiple kinetic events to yield a compositionally dependent diffusion constant averaged over many events, a considerable step forward from previous work where computational demands restricted the analysis of only individual events. Finally, we examine measurements of the inferred loss rates of a prototypical SVOC (malonic acid) from viscous aerosol, exploring the variation in evaporation rate with moisture content and providing a qualitative examination of the dependence on particle viscosity.
II. The compositional dependence of diffusion constants and the relative timescales for SVOC and water partitioning
A comparison of the reported water activity dependencies of the diffusion constant of water inferred from isotope exchange and RH step experiments suggests that they are incompatible, with qualitatively different shapes.30 Recently, it has been common to adopt the Vignes parametrisation to express the diffusion constant of water in the mixture, Dw(xw), where it has a mole fraction of xw, in terms of the limiting diffusion constants of water in pure water, Dw,w, and at infinite dilution in pure solute, Dw,org:12,16,27,30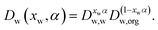 | (1) |
When defining the dependence of the diffusion constant on composition, as in eqn (1), the dimensionless constant α is dependent on composition and is frequently referred to as an activity coefficient.26,27 We have chosen to express this compositional dependence using a cubic dependence on mole fraction,
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = C(1 − xw)3, α = C(1 − xw)3, | (2) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = (1 − xw)2·(C(T) + 3D(T) − 4D(T)·(1 − xw)). α = (1 − xw)2·(C(T) + 3D(T) − 4D(T)·(1 − xw)). | (3) |
Compared to the binomial expansion, the cubic parametrisation of α produces an almost identical shape for Dw(xw), in eqn (1), but with a much less pronounced plateau at the bulk water value of Dw at high water activity. Many techniques, including aerosol optical tweezers experiments, are insensitive to transitions within this region of activity, as the timescale for water transport is comparable to the timescale for the instrumentally limited change of RH. As such, it cannot be said with any confidence which of these parametrisations, (2) or (3), is a more realistic approximation to the binary diffusion coefficients in such particles. Instead, we are seeking the most accurate method to represent data recorded for highly dehydrated droplets that experience large kinetic limitations, and access compositions governed by the shape of the curve at much lower water mole fractions.
The utility, drawbacks, and recent uses of Fickian modelling for characterising diffusional transport in binary viscous aerosol have been discussed in a previous publication.31 We have chosen to use the recently developed partial differential model, Fi-PaD, described by O’Meara et al.35 and a brief description is provided below. Fi-PaD represents the particle by a vector containing compositional information, with each element describing a radial shell within the particle bulk; here 400 shells are used, corresponding to a shell resolution of around 10 nm for typical particle radii in our single-particle measurements, 4 μm. The model assumes an initial homogeneous concentration profile at equilibrium with a user specified gas phase RH, which can then undergo an immediate transition to another (or several consecutive) humidities. After initialisation, the model begins to simulate the immediate aftermath of the first such activity change, where only the concentration of water in the outermost shell has equilibrated with the gas phase RH. The concentrations in every shell are then evaluated iteratively as time progresses by solving Fick's second law in spherical coordinates with the diffusion coefficient varying across the shells (i.e. dependent on local composition of each shell). Time dependent radius data may then be generated, covering the precise residence time of the droplet being modelled. Further details of the operation and implementation of Fi_PaD may be found in the initial publication.35
The simplified treatment of α (eqn (2)) described above greatly decreases the computational expense of the data analysis as it removes one dimension from the fitting space when compared with fitting to the more complex dependence of eqn (3). By iteratively varying log(Dw,org) and C it is possible to improve the overlay between the simulated radius responses and the data. This was achieved using the Matlab interior-point algorithm, within the fmincon function, starting from four randomly selected starting points in (Dw,org, C) space. The extent of agreement between each simulation and the experiment is quantified by calculation of the residual between the two response functions at each simulated timestep:
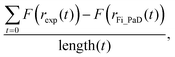 | (4) |
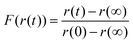 | (5) |
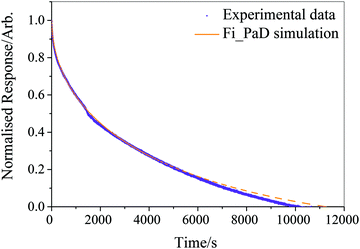
Running on a single Intel i7-4790 core, simulation of a typical experimental RH step change (8000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s in length) was found to take approximately 500 s, with typically around one hundred simulations required to converge the fit parameters and reproduce the measured response in size. The model was considered to have fit when all four independent fitting runs had found the nearest minimum in residual space, and the mean deviation from experiment was less than 3% of the magnitude of the experimental data. We provide an example of the fitting in Fig. 1 for a ternary aqueous-sucrose–glucose droplet experiencing a change in RH from 20 to 6% RH. As in our previous work, we represent the relaxation in size following the RH step by a response function (eqn (5)) that is calculated from the time-dependence in wavelength of a whispering gallery mode (WGM) in the Raman spectrum.31 The initial droplet size prior to the step in RH is calculated explicitly from the fingerprint of WGMs appearing in the Raman signature. The value of Dw,org is the limiting value of the diffusion coefficient of water in the fully dry limit of an isolated water molecule diffusing in a viscous matrix of sucrose and glucose present in a 1
000 s in length) was found to take approximately 500 s, with typically around one hundred simulations required to converge the fit parameters and reproduce the measured response in size. The model was considered to have fit when all four independent fitting runs had found the nearest minimum in residual space, and the mean deviation from experiment was less than 3% of the magnitude of the experimental data. We provide an example of the fitting in Fig. 1 for a ternary aqueous-sucrose–glucose droplet experiencing a change in RH from 20 to 6% RH. As in our previous work, we represent the relaxation in size following the RH step by a response function (eqn (5)) that is calculated from the time-dependence in wavelength of a whispering gallery mode (WGM) in the Raman spectrum.31 The initial droplet size prior to the step in RH is calculated explicitly from the fingerprint of WGMs appearing in the Raman signature. The value of Dw,org is the limiting value of the diffusion coefficient of water in the fully dry limit of an isolated water molecule diffusing in a viscous matrix of sucrose and glucose present in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio. The methods applied here offer improvements over similar diffusion models both in terms of accuracy (varying the fit parameters and parallelising over multiple CPU cores reduces the likelihood of becoming trapped in a local minimum in the parameter space) and throughput (see above).
1 mass ratio. The methods applied here offer improvements over similar diffusion models both in terms of accuracy (varying the fit parameters and parallelising over multiple CPU cores reduces the likelihood of becoming trapped in a local minimum in the parameter space) and throughput (see above).
Most studies establish experimental conditions such that the volatilisation of water or an SVOC can be studied in isolation, allowing the estimation of diffusion constants of water or the diffusion constants of the organic species. For water transport studies, this has often been achieved by examining the evaporation of water or condensation of water from a binary component particle that contains an involatile solute as the second component, for example sucrose or citric acid.30,36
In measurements of the suppression in volatility of an organic component due to slow bulk diffusion, the focus has usually been on the rates of evaporation of a volatile under dry conditions where fluctuations in RH and water content (i.e. the presence of water as a plasticiser) can be avoided.37–39 Alternatively, the volatilities of the organic components have been assumed to be so low that water transport can be studied in isolation, for example in the studies of water transport in SOA samples.27 However, it should be expected that the mass transfer of water and SVOC would happen concurrently in any ambient aerosol. For example, both water and SVOC evaporation would be expected to be convoluted in the size and compositional response when the aerosol contains these two volatile components. Indeed, we have recently examined the evaporation kinetics of water (vapour pressure ∼ 2 kPa) and maleic acid (vapour pressure ∼ 10−3 Pa) from ternary mixed component aerosol consisting of water, maleic acid and sucrose.13 In this first attempt to examine the coupled loss of water, SVOCs, and the correlation with explicit measurements of particle viscosity, we showed that water loss remained fast while the SVOC loss could be suppressed by many orders of magnitude relative to its pure component vapour pressure.
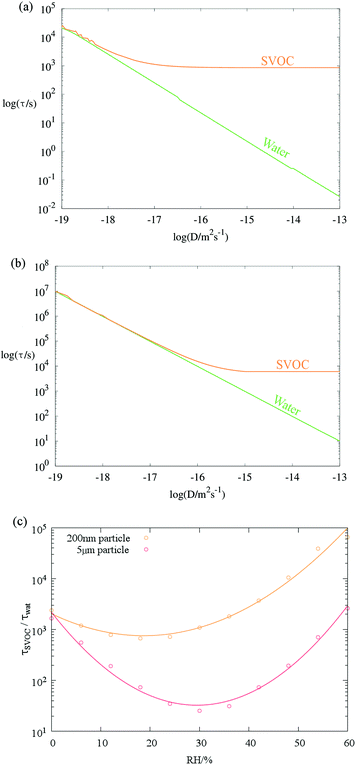
An analytical treatment of the gas-particle partitioning of semi-volatile species has been described by Mai et al.,23 allowing an estimate of the timescale for evaporation of components of varying volatility. It is appropriate at this point to use this model to assess the relative timescales of water and SVOC volatilisation from an aerosol particle. Such an assessment should allow us to identify the conditions under which the water loss rate is dominant, thereby justifying the use of the treatment described above for retrieving the diffusion constants of water. Conversely, this would also allow us to identify the timescales over which the water fraction equilibrates and the loss of the SVOC drives a measured size change. Thus, the Mai et al.23 model was used to simulate the depletion kinetics of water or a hypothetical SVOC (with the same molecular mass as malonic acid) from a particle experiencing a small, but nonzero, change in external gas phase saturation of each species. Timescales were estimated for values of Dw and DSVOC varied logarithmically within atmospherically relevant bounds (10−13–10−19 m2 s−1). Timescales τSVOC and τwat are determined as the e-folding time of the concentration of each component remaining in the particle. The results indicate that for a 200 nm radius particle, SVOC evaporation timescales will only become separable from those of water (τSVOC ≥ 10τwat) at around Dw = 10−17 m2 s−1 (Fig. 2a). Interestingly, τw continues to decrease as Dw increases above this value, whereas the SVOC volatilisation remains constant. This is due to the gas diffusional flux being substantially more limiting for an SVOC than water, owing to the lower equilibrium vapour pressure of the SVOC (captured by the inverse dependence of τ on partial pressure, p, via the Henry's Law coefficient in eqn (14) in the original publication23). We also consider the equilibration timescales for particles of radius 5 μm in Fig. 2b, a size of more relevance to particles that may be trapped during many single particle laboratory based studies, such as optical tweezers. The self-diffusion coefficient below which the timescales are found to be indistinguishable is 10−16 m2 s−1, with the same divergence of regimes as observed in the 200 nm case: the SVOC becomes gas transport limited while water retains a bulk kinetic limitation at higher bulk diffusion constants.
For both particle sizes, the timescales for SVOC and water transport (Fig. 2c) remain widely separated at all RHs and particle moisture contents. In producing Fig. 2c we have assumed that Dw varies according to eqn (1), where Dw,org is 10−16 m2 s−1. DSVOC is assumed to follow the Stokes–Einstein relationship with a hypothetical viscosity range of 10−3 Pa s to 107 Pa s between relative humidities of 100% and 0% respectively. The SVOC was defined to have the properties of malonic acid (molecular weight = 104.1 Da, pure component vapour pressure = 10−4 Pa, Stokes flow diameter = 4 Å). Other model parameters are as follows: temperature = 298 K, accommodation coefficient = 1, particle density = 1.4 g cm−3, gas phase diffusion coefficient = 10−5 m2 s−1.
Water transport is consistently more rapid than SVOC transport as a consequence of the higher vapour pressure for water at all RHs and a bulk condensed phase diffusion constant for water that is considerably faster than expected based on the Stokes–Einstein equation. By contrast, the larger organic molecule is impeded more readily by increases in viscosity (Dw > DSVOC).17 An additional consequence of this is that the water content adjusts rapidly to compositional change arising from volatilisation/condensation of an SVOC.
III. Experimental description
We have provided comprehensive accounts of the time-dependent measurements of particle size and refractive index using aerosol optical tweezers (AOTs) in numerous previous publications40,41 and we will provide only a short overview of the instruments and procedures here. Optical tweezers are formed of a tightly focused 532 nm (Laser Quantum, Opus 2W) laser beam, guided onto a vertically aligned oil-immersion objective and into a trapping cell. A mixed flow of ultrapure (dry) and humidified (wet) nitrogen is directed into the trapping cell to control the RH by altering the relative flow rates of both. The RH is measured by a calibrated probe (HUMICAP HMT 330, Vaisala, error = ±2% RH) placed several centimetres before the trapping cell. An aerosol plume is generated using a medical nebuliser and drawn through the cell. Once a particle is captured in the optical trap, brightfield imaging may be used to visually assess the trapping stability. Inelastic backscattered light is diverted to a spectrograph (0.5 m focal length) coupled to a CCD (1 s time resolution, 0.05 nm per pixel).Once the droplet equilibrates with the cell conditions and the radius is stable, a series of step changes of RH can be conducted. Throughout the measurement series, the droplet size and refractive index can be determined from the fingerprint of cavity enhanced Raman scattering at whispering gallery mode wavelengths.42,43 The kinetic responses to changes in RH are examined either by considering the change in particle radius or the change in wavelength of a selected WGM as described in our earlier work.31 The time intervals between RH steps are programmed in advance and were generally chosen to increase as the particles became more kinetically arrested (i.e. longer periods of RH stability at lower RH).
Here, the time-dependent wavelength shifts of individual WGMs in a Raman spectrum are used to infer the relaxation timescale in particle size following a step change in RH. Such data can be represented as a response function F(λ(t)), as in eqn (5), where λ(t) is the time dependent wavelength in nanometers. The response function is then fit to a modified stretched exponential function similar in form to the Kohlrausch–Williams–Watts equation:
| Φ(t) = s·exp(−t/τ)β + a | (6) |
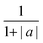 | (7) |
Particle viscosity is determined using a dual trap AOTs, which has also been described in previous publications.17,45 Two particles are independently captured in separate traps, which are formed using a holographic optical tweezer with a 532 nm wavelength laser (Laser Quantum, Opus 3W). By altering the kinoform applied to a spatial light modulator, a diffractive optical component that allows the generation of complex optical landscapes,40 it is possible to manipulate the relative positions of the particles, and therefore to coalesce them. The relaxation of the aspect ratio of the resulting particle (from adjacent spheres to a single sphere) follows an exponential decay with a time constant, τ, that can be related to viscosity by46
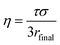 | (8) |
IV. Results and discussion
We first consider the analysis of water diffusion constants in organic aerosol of ternary composition before presenting an approach for characterising and assessing the timescales of water and SVOC loss from viscous aerosol. This is followed by a discussion of the effective suppression in volatility of the SVOC from viscous aerosol and the correlation with particle viscosity.IV.a. Kinetics of water evaporation and condensation in ternary aerosol with one volatile component
One hundred and seventy-two RH transitions have been conducted in the atmosphere surrounding twenty-seven ternary component aerosol particles consisting of water, sucrose and glucose. It should be noted that water is the only volatile component in these measurements; sucrose and glucose can be considered involatile. By capturing the non-exponential nature of relaxation in size (i.e. water partitioned to particle) following the RH step47 using eqn (6), the complex multi-exponential time-dependence in droplet radius has been converted into a simple estimate of the timescale of internal water transport.31Time-constant values for all changes in RHs may be found in in Fig. 3a. For the first time, we have also unconstrained the value of β (in eqn (6)) during the fitting process (Fig. 3b). The chemical significance of this parameter is somewhat less clear: in the glass physics community, where stretched exponential relaxation of macroscopic variables is commonplace, there is some consensus48–50 that β is representative of the heterogeneity of the system, i.e. that there is an underlying distribution of mono-exponential events whose width becomes larger as β approaches zero. Previously, we have shown that fixed values of β between 0.4 and 0.6 represent the relaxation of binary sucrose water aerosol at low humidities;31 similarly, a multi-exponential description of ternary systems is also appropriate (β < 1).
In evaporation experiments, the time constant broadly increases as the final state of dehydration of the particle increases (i.e. as the RH change moves towards the bottom left of Fig. 3(a)), unless the particle begins in a very low viscosity state at high RH. In addition, the slow release of water over long time is consistent with a value of β < 1. Tentatively we can say that this is due to the larger variance in molecular evaporation timescales that together make up the observed radius response. However, we must be careful: stretched exponential behaviour is observed in every transition, including those that take place for viscous liquid aerosol above the moisture driven glass transition RH of the organic components. This suggests that we are using the stretched exponential to represent a fundamentally different physical process to that usually just ascribed to glasses.
The condensation experiments are somewhat more complex to characterise, involving the condensation of a pure water layer on the dehydrated particle surface.44 Induction behaviour is observed in the first several hundred seconds of condensation for many of the measurements, where a thin water layer is likely to have formed on, but not yet been absorbed by, the dehydrated particle. This leads to values of β in excess of 1.31 For purely gas-diffusion limited condensation, the size response should be independent of the internal composition with a value of β close to unity.51
In order to successfully determine diffusion coefficients of water in the ternary mixture using the Fi_PaD model it is essential that an accurate radius response is inferred. The fully equilibrated droplet size and refractive index are determined by fitting the WGM fingerprint at a high initial RH (typically 70–80%) at which the droplet can be assumed to be in equilibrium with the gas phase and to be homogeneous in refractive index. Then, the droplet radius response following an RH change is inferred from the relative change in wavelength of a WGM; in such a kinetically limited system, it is inappropriate to rely on radius data produced by Mie theory fitting to a radially homogeneous sphere.42 Instead, we must assume that the refractive index of the outer micron or so of the droplet is approximately constant throughout the transition and use the approach of Krieger and coworkers, who estimate radius changes from experimental wavelength shifts.52
We consider, as an example, the diffusion constants of water in ternary particles containing glucose and sucrose at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio, along with transitions in pure sucrose and pure glucose. Each transition (see Table 1) has been simulated with the Fi_PaD model to produce diffusion dependences, modelling the droplet as a two component system with the non-volatile component molecular mass taken as the weighted average of glucose and sucrose. As diffusion coefficients are assumed symmetrical (the same for all components at any given composition), no extra information may be gained by explicitly modelling the separate movements of the two organic components. The constants (Dw,org, C) within eqn (1) were floated within the model as described earlier, until simulated radius responses agreed with experiment. The sigmoidal dependencies of Dw on mole fraction resulting from these individual optimal fits for binary aqueous/sucrose aerosol are shown in Fig. 4 retrieved from 4 transitions in RH.
1 mass ratio, along with transitions in pure sucrose and pure glucose. Each transition (see Table 1) has been simulated with the Fi_PaD model to produce diffusion dependences, modelling the droplet as a two component system with the non-volatile component molecular mass taken as the weighted average of glucose and sucrose. As diffusion coefficients are assumed symmetrical (the same for all components at any given composition), no extra information may be gained by explicitly modelling the separate movements of the two organic components. The constants (Dw,org, C) within eqn (1) were floated within the model as described earlier, until simulated radius responses agreed with experiment. The sigmoidal dependencies of Dw on mole fraction resulting from these individual optimal fits for binary aqueous/sucrose aerosol are shown in Fig. 4 retrieved from 4 transitions in RH.
Sucrose![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose mixing ratio glucose mixing ratio |
RH change/% | τ/s | Radius/nm | C | log(Dw,org/cm2 s−1) | D w,org range/cm2 s−1 |
|---|---|---|---|---|---|---|
| Pure sucrose | 30–5 | 3794 | 3657 | −2.02 | −11.74 | 1.60–2.40 × 10−12 |
| 30–10 | 2277 | 4308 | −2.10 | −11.76 | 1.49–2.59 × 10−12 | |
| 50–10 | 1076 | 4954 | −2.49 | −11.79 | 1.06–2.30 × 10−12 | |
| 50–20 | 244 | 3796 | −2.05 | −11.64 | 1.96–4.71 × 10−12 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
20–5 | 2542 | 5205 | −9.71 | −11.42 | 3.10–4.17 × 10−12 |
| 27–0 | 1702 | 4863 | −2.51 | −11.39 | 3.20–4.99 × 10−12 | |
| 0–25 | 1387 | 4770 | −5.81 | −11.16 | 5.86–8.17 × 10−12 | |
| Pure glucose | 50–20 | 37 | 3707 | −2.16 | −10.73 | 1.41–3.69 × 10−11 |
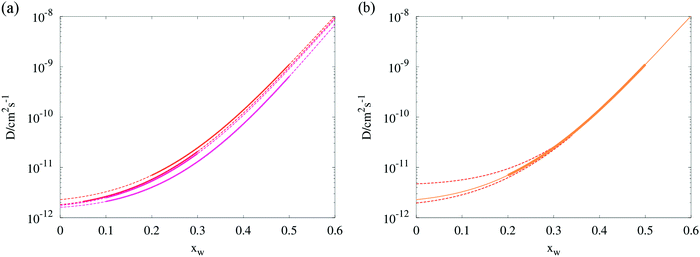 | ||
| Fig. 4 (a) Composition dependent diffusion coefficients estimated from four RH transitions in binary aqueous/sucrose droplets. Solid lines indicate the mole fraction range within which the model was evaluated, dashed lines represent the Vignes extrapolations. (b) Isolation of the 50–20% RH transition (“top-most” curve in panel a) showing the error envelope in the region 0 < xw < 0.35, as determined by eqn (9) (red dotted lines). Exact values of the uncertainties in Dw,org for all four transitions may be inspected in Table 1. | ||
A new method of error analysis has been employed to complement the Fickian modelling, allowing the uncertainty in Dw,org within the sensitivity of the tweezers measurement to be determined over many droplets and step changes in RH, as shown in Fig. 4. As total dehydration of the droplets is often not achieved, one must consider that significant deviations in the values of eqn (1) extrapolated to zero water content may be possible whilst maintaining a similar shape at higher water mole fractions. A rigorous method to investigate this would involve systematically simulating a physically appropriate region of the (Dw,org, C) kinetic parameter space, and comparing the predicted and observed radius response. Unfortunately such a procedure would be too computationally expensive to attempt, even for one single transition.
Instead, the plausible range of the intercepts Dw,org has been determined for all transitions by evaluating a merit function
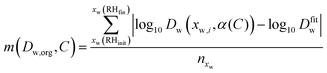 | (9) |
Here, we have used the merit function method described to estimate the diffusion constants Dw,org, with associated uncertainties in ternary sucrose/glucose/water aerosol prepared at a mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the two saccharides (Fig. 5 and Table 1). As might be expected, the fitted Dw,org coefficients and uncertainty envelopes for water the ternary mixture are found to be above the values for water in binary water/sucrose aerosol particles also determined in this work (Fig. 5). In addition, the value for water in sucrose agrees well with recently reported values inferred from aerosol size response in an electrodynamic balance6 (1 × 10−12 cm2 s−1) while comparison with more recent H/D isotope exchange measurements30 (2.6 × 10−17 cm2 s−1) reveals the frequently observed disparity between the two experimental methods described in Section 1, and presented in Fig. 6. Finally, increasing the relative molecular mass of the non-volatile component (i.e. comparing pure glucose to 1
1 for the two saccharides (Fig. 5 and Table 1). As might be expected, the fitted Dw,org coefficients and uncertainty envelopes for water the ternary mixture are found to be above the values for water in binary water/sucrose aerosol particles also determined in this work (Fig. 5). In addition, the value for water in sucrose agrees well with recently reported values inferred from aerosol size response in an electrodynamic balance6 (1 × 10−12 cm2 s−1) while comparison with more recent H/D isotope exchange measurements30 (2.6 × 10−17 cm2 s−1) reveals the frequently observed disparity between the two experimental methods described in Section 1, and presented in Fig. 6. Finally, increasing the relative molecular mass of the non-volatile component (i.e. comparing pure glucose to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 glucose
1 glucose![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose to pure sucrose) inhibits water diffusion more greatly and the diffusion constant of water decreases.
sucrose to pure sucrose) inhibits water diffusion more greatly and the diffusion constant of water decreases.
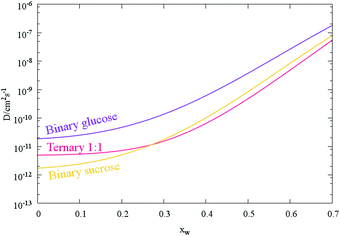 | ||
| Fig. 5 Mean composition dependent diffusion coefficient parametrisations for binary and ternary saccharide aerosol (as in Fig. 4a). Each curve is produced from the mean Dw,org and C values of the transitions tabulated in Table 1. | ||
A comprehensive comparison of our results applying this method to binary sucrose aerosol with previous optical tweezers and isotope exchange parametrisations is also shown in Fig. 6a. We have chosen to plot diffusion coefficients against mole fraction rather than gas phase activity, as previously reported, in recognition of the fact that this is the composition parameter used internally to evaluate D within Fi-PaD, and within any Fickian based framework. Additionally, it is noted that activity does not appear anywhere in eqn (1), and so a choice of thermodynamic model must then be used to implicitly relate particle phase mole fractions, xw, to water activity, in order to determine the range over which the model output is valid in each case. In addition, it is not clear whether current core–shell models are applicable in multicomponent mixtures with more than 3 components that are non-ideal. To clarify this, Fickian based diffusion models can account for non-ideal behaviour by combining Maxwell-Stefan diffusion coefficients with ‘thermodynamic correction’ factors through the following:53
| [D] = [B]−1[Γ] | (10) |
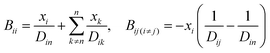 | (11) |
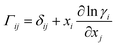 | (12) |
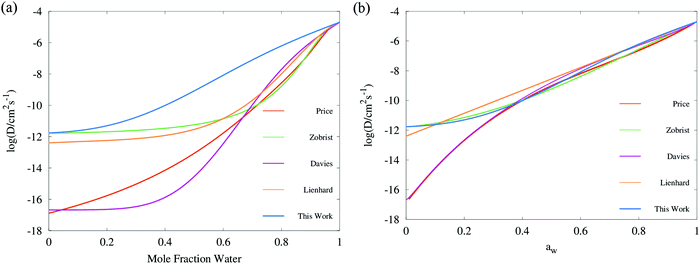 | ||
| Fig. 6 Comparison of diffusion coefficient parameterisations for sucrose aerosol plotted in (a) mole fraction space, and (b) water activity space: mean trend of Vignes functions (ideality assumed, with cubic treatment of α coefficients) simulated with Fi_PaD, as shown in Fig. 4a (Blue); third order polynomial parametrisation of Dw(aw) in log space by Price et al.,59 converted to mole fraction using the AIOMFAC model; Vogel–Fulcher–Tammann (VFT) parameterisation by Zobrist et al.6 to RH step experiments in an electrodynamic balance (Green); temperature dependent Vignes functions (with binomial expansion of α coefficients) fit to RH step experiments in an electrodynamic balance by Lienhard et al.26 (orange); temperature independent Vignes functions (with cubic treatment of α coefficients) fit to isotope exchange experiments by Davies et al.30 (purple). | ||
Whilst Maxwell Stefan diffusion coefficients are symmetric, Fickian diffusion coefficients are not, unless the mixture is ideal or binary. By representing, and fitting, diffusion coefficients in terms of water activity, their use to then account for the compositional dependence of diffusion in non-ideal multicomponent mixtures is questionable. Expressing diffusion coefficients as a function of mole fractions allow the above expressions to be used, provided the matrix of activity coefficient derivatives can be calculated. In the above expressions, Fickian diffusion coefficients can be negative if the chemical potential gradient is such that solubility limitations drive diffusion. The efficacy of available numerical methods in modelling such multicomponent mixtures needs to be reviewed, and will form the basis of future work. For now, presenting diffusion coefficients as a function of mole fraction rather than water activity facilitates future investigations and is consistent with the assumption of ideality.
Following on from this, we stress that representing the diffusion coefficient as a function of mole fraction is distinct from presenting the Vignes dependence as a function of relative humidity, as previously reported.30 We suggest that, based on the previous discussion, this latter form is less rigorous and necessarily requires an assumption that the thermodynamic relationships used for activity coefficient are entirely accurate. Therefore, the choice of activity coefficients can have a substantial influence on the appearance of Dw data if (either particle or gas phase) activity is chosen as the x axis. For example, the frequently observed difference in curvature of Dw parametrisations at low activity between isotope exchange and optical tweezers data can be accounted for if it is recognised that α and xw(RH) models are different; in mole fraction space, the most recent sucrose isotope exchange data30 appears similar in shape to that presented in Fig. 6 although the irreconcilable difference in the Dw,org intercept remains. By contrast, the Fi-PaD model treats activity coefficients as unity, and so particle phase activity is equal to xw.
IV.b. Kinetics of water loss in ternary aerosol with 2 volatile components
As we previously reported for sucrose![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) maleic acid mixtures,13 a complicating factor in assessing the time dependent size response when SVOCs are present is the exact deconvolution of the evaporation rates of competing volatiles from the droplet, water and the SVOC. In the limiting case in which the vapour pressure of the SVOC differs from that of water by a factor of 106 and when there is no kinetic impairment of water loss from the aerosol particle, rapid water evaporation will dominate the first several tens of seconds, after which an underlying linear time-dependent loss in r2 becomes apparent.54 Indeed, Fig. 2 confirms the relative ranges in diffusion coefficients at which this separation in timescale occurs.
maleic acid mixtures,13 a complicating factor in assessing the time dependent size response when SVOCs are present is the exact deconvolution of the evaporation rates of competing volatiles from the droplet, water and the SVOC. In the limiting case in which the vapour pressure of the SVOC differs from that of water by a factor of 106 and when there is no kinetic impairment of water loss from the aerosol particle, rapid water evaporation will dominate the first several tens of seconds, after which an underlying linear time-dependent loss in r2 becomes apparent.54 Indeed, Fig. 2 confirms the relative ranges in diffusion coefficients at which this separation in timescale occurs.
By simply fitting the stretched exponential function to the radius data, eqn (6), normalised to the initial and final radii, the long tail can be assumed to have a constant gradient in r2 with time once the water evaporation has ceased. This causes the r2 loss to appear exactly in the residual between the data and the best fit, from which the gradient can easily be determined. In order to determine this gradient, it has been found that removing the data up to 30% of the way through an experiment provides a good compromise between fitting the largest number of points and ensuring the water loss is excluded (see ESI†). If we assume that the SVOC loss begins immediately at the RH transition, and is masked by the water evaporation, a new function
| r2(t) = r(∞)2 + A·exp(−t/τ)β − dr2/dt | (13) |
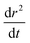 , is kept constant at the value fit to the residual in the previous step, and A, r(∞), τ and β are allowed to vary. r(∞) is the final particle size containing the involatile solute and solvating water at equilibrium with the gas phase. The deviation between this function and the experimental data is found to decrease by several orders of magnitude when compared to fits carried out using a standard stretched exponential on the same dataset (eqn (6)).
, is kept constant at the value fit to the residual in the previous step, and A, r(∞), τ and β are allowed to vary. r(∞) is the final particle size containing the involatile solute and solvating water at equilibrium with the gas phase. The deviation between this function and the experimental data is found to decrease by several orders of magnitude when compared to fits carried out using a standard stretched exponential on the same dataset (eqn (6)).
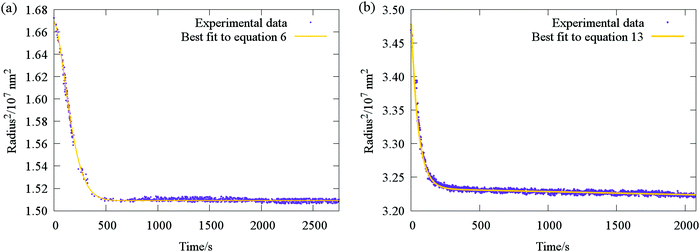 | ||
| Fig. 7 Typical evaporative profile (purple points) for ternary aerosol with (a) two involatile components (sucrose and glucose), and (b) one volatile and one semivolatile component (sucrose and malonic acid). Comparison with fit functions (yellow lines) based on the stretched exponential eqn (6) and (13) are also shown. | ||
The accuracy with which eqn (13) reproduces radius responses for particles containing SVOCs (Fig. 7b and Section IVc) suggests it is valid to assume that transitions between differing semi-volatile loss rates occur rapidly upon relative humidity changes within the trapping cell. This is a consequence of the typical disparities in the time constants for SVOC and water loss illustrated in Fig. 2c (typically more than a factor of 20), effectively allowing the two processes to be decoupled in the analysis.
Therefore, it is possible to probe the water loss response occurring simultaneously with the SVOC loss in the early stages of the particle response by simply subtracting the known r2 profile from the experimental data. This produces a hypothetical ‘water loss only’ radius response. These data may then be modelled using Fi-PaD, making this the first instance of precise water diffusion coefficients being extracted from a ternary system with this distribution of volatilities. From a dataset of seventeen sucrose![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) malonic acid transitions, prepared at a 5
malonic acid transitions, prepared at a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio, four were deemed to not be limited by the timescale of RH changes within the trapping cell (τ > 200 s), and therefore ideal candidates for this analysis. The results are tabulated in Table 2. The assumed involatile molecular mass was once again the weighted average of the two organic components, with the composition assumed to be constant at its initial value throughout the experiment.
2 molar ratio, four were deemed to not be limited by the timescale of RH changes within the trapping cell (τ > 200 s), and therefore ideal candidates for this analysis. The results are tabulated in Table 2. The assumed involatile molecular mass was once again the weighted average of the two organic components, with the composition assumed to be constant at its initial value throughout the experiment.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) malonic acid aerosol, alongside fit values for Dw,org, C (eqn (1)), the uncertainty in the Dw,org estimate (determined viaeqn (7)), the stretched exponential time constant τ (eqn (5)) and the gradient of radius change due to SVOC loss,
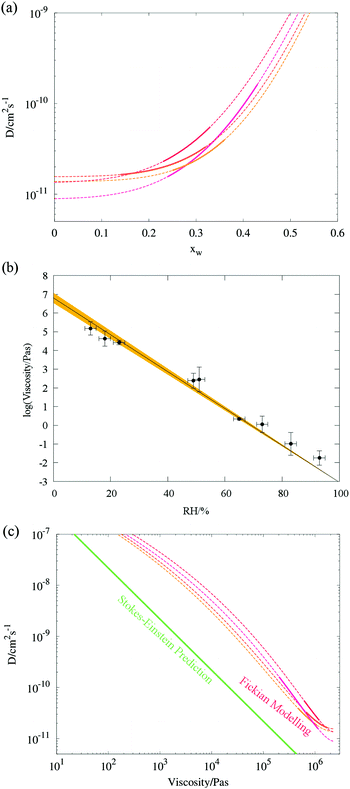
malonic acid aerosol, alongside fit values for Dw,org, C (eqn (1)), the uncertainty in the Dw,org estimate (determined viaeqn (7)), the stretched exponential time constant τ (eqn (5)) and the gradient of radius change due to SVOC loss, 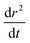 (eqn (13))
(eqn (13))
| Radius/nm | RH change/% | τ/s | dr2/dt/nm2 s−1 | C | log(Dw,org/cm2 s−1) | D w,org range/cm2 s−1 |
|---|---|---|---|---|---|---|
| 4531 | 36–25 | 288.8 | −20.5 | −6.02 | −10.86 | 4.42 × 10−13–4.32 × 10−10 |
| 3822 | 43–24 | 133.9 | −5.5 | −4.18 | −11.05 | 1.05 × 10−12–8.51 × 10−10 |
| 4614 | 32–14 | 698.5 | −9.3 | −5.68 | −10.81 | 4.99 × 10−13–1.10 × 10−10 |
| 4623 | 33–23 | 346.8 | −0.6 | −4.00 | −10.87 | 1.92 × 10−12–1.07 × 10−10 |
The compositional dependence of the diffusion constant (Fig. 8a) indicate a substantial plasticising effect of malonic acid – just under a 30% molar component within the organic matter enhances Dw,org by the same amount (relative to pure sucrose) as a one to one mass ratio of glucose (cf.Fig. 5). This is also borne out by presenting the diffusion dependences against viscosity data, collected via the particle coalescence methods described in Section II. Nine coalescence events were conducted between 13% and 93% RH, which we have chosen to represent with a log-linear trend line constrained to the water viscosity at 100% RH (Fig. 8b). In comparison with pure sucrose, a nearly six order of magnitude suppression of the extrapolated viscosity at 0% RH (ηorg = 2.58 × 106 Pa s) is observed by the presence of a mole fraction of 0.3 of malonic acid. In Fig. 8c, we present the diffusion constant parameterisations in terms of viscosity instead of RH based on these viscosity measurements. As observed in our previous work,13,17 the diffusion constants of water have values at least one order of magnitude larger than expected from the Stokes–Einstein equation when the viscosity is ∼105 Pa s. Note that since the model treats diffusion as symmetric, curves are (within the Fickian framework being employed here) valid for all three components. However, it would be unwise to infer anything about the diffusivity of malonic acid from this treatment.
 | ||
| Fig. 8 Stokes Einstein deviations of water diffusion in ternary aerosol containing sucrose, malonic acid and water. (a) As in Fig. 4a, composition dependent diffusion coefficients fit to four radius responses using Fi-PaD (further details can be found in Table 2). (b) Single particle viscosity measurements, with a loglinear parametrisation. (c) Combination plot of data from (a) and (b) showing correlation between D and η. A comparison of the Stokes–Einstein predicted diffusivity for malonic acid (green) is also provided in panels (b) and (c). | ||
IV.c. Kinetics of SVOC loss in ternary component aerosol with 2 volatile components
Finally, we consider the volatilisation kinetics of a malonic acid from an aqueous sucrose/malonic acid droplet, rather than water. Malonic acid is similar in size and chemical functionality to many organic molecules of atmospheric importance, as well as exhibiting a vapour pressure typical of an SVOC that may partition into the particle phase (10−4 Pa).55 The gradient determined for the SVOC loss can be converted into an effective vapour pressure using the equation56 (we refer the reader to the ESI† for further details):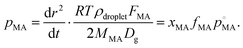 | (14) |
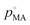 , by xMA, the mole fraction in the droplet, and fMA, the activity coefficient at that mole fraction. These quantities, in addition to the mass fraction of malonic acid, FMA, were calculated using an activity/mole fraction relationship generated from the UManSysProp prediction tools.58 Once pMA is corrected by these terms, we designate the calculated vapour pressure value as an ‘effective pure component’ value.
, by xMA, the mole fraction in the droplet, and fMA, the activity coefficient at that mole fraction. These quantities, in addition to the mass fraction of malonic acid, FMA, were calculated using an activity/mole fraction relationship generated from the UManSysProp prediction tools.58 Once pMA is corrected by these terms, we designate the calculated vapour pressure value as an ‘effective pure component’ value.
A gas flow removes evaporated SVOC from the trapping cell and maintains a background gas phase partial pressure that can be considered to be zero in the vicinity of the droplet. The gas velocity is sufficiently slow that no enhancement in evaporation rate from the droplet need be considered (i.e. the Sherwood number is ∼2). Thus, in Fig. 9 we report the RH dependence of the effective pure component vapour pressure. As the correction to the pure component value accounts for the unique mole fraction of malonic acid at each RH and after each transition, this normalising of the observed values allows meaningful comparisons to be made. Therefore, the ratio of the pure component (4.3 × 10−4 Pa)55 to the effective pure component values can be used to quantify any kinetic suppression in the evaporation. Even though a pure component vapour pressure should remain independent of RH, the effective values for the vapour pressure show an approximate 2.5 decade suppression of the vapour pressure of MA as the particle is dried. This is a broadly similar level of variance at low RHs to that reported in our previous publication13 for the volatility suppression of maleic acid in aqueous maleic acid/sucrose particles and reflects the increasing kinetic limitation imposed on volatilisation as the particle becomes more viscous.13
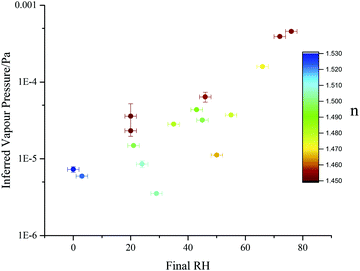 | ||
Fig. 9 Effective pure component vapour pressure estimates, determined for sucrose![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) malonic acid particles (prepared with a 5 malonic acid particles (prepared with a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio) viaeqn (13) and (14) (closed circles). Points are coloured by the mean refractive index recorded after the initial water loss had ceased. 1 mass ratio) viaeqn (13) and (14) (closed circles). Points are coloured by the mean refractive index recorded after the initial water loss had ceased. | ||
One potential inaccuracy that may arise when examining inferred vapour pressures is the fact that particle composition is continuously changing as volatilisation proceeds. Indeed, the magnitude of the diffusive limitation to volatilisation will change as the relative proportion of remaining SVOC changes. This necessarily produces a large degree of variation of both the pure component vapour pressure estimate and retrieved refractive index at any given RH. Fig. 9 shows an example of this: each point is a unique single particle transition, with some droplets trapped and consecutively dried over multiple RH steps, while others were caught and rapidly dried just once. Data are coloured by the final retrieved refractive index to give an indication of droplet composition (see ESI†). Particles in which less malonic acid has previously volatilised exhibit refractive indices further from the pure sucrose value (nmelt = 1.546257) and higher effective vapour pressures, due to a decreased diffusive limitation. This trend leads to the spread in observed volatility for the five experiments with final RHs between 20 and 30%.
V. Conclusion
In the immediate aftermath of a rapid change in surrounding RH, a single optically tweezed organic aerosol particle will begin to vitrify, impeding the dynamics of its constituent molecules, both in the particle phase and at the droplet interface. Using Fickian diffusion modelling, we have determined the compositional dependence of the diffusion constants of water; from analysis of the particle radius behaviour at long time scales (∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s) we have examined the suppression of semi-volatile vapour pressure by a viscous matrix of sucrose.
000 s) we have examined the suppression of semi-volatile vapour pressure by a viscous matrix of sucrose.
This publication marks the first use of the Fi-PaD model developed by O’Meara et al., which allows high throughput determination of both Dw,org, the extrapolated water diffusion coefficient in an amorphous organic matrix, and α, the so called ‘activity coefficient’, which we represent by a cubic parameterisation of composition. By assuming a sigmoidal dependence of diffusion on composition, exact uncertainties of fit values of Dw,org can be determined for each step change experiment.
Further studies suggest that the slow evaporation of malonic acid from ternary droplets is correlated with the conditioning history that the particle experiences, in addition to the composition of the starting solution and the ambient RH. Repeat experiments reveal substantial variation in this volatilisation. Future publications will apply these methodologies to probing diffusion and volatility in increasingly complex systems, both in a ‘bottom-up’ sense, using multicomponent aerosol with well-defined starting compositions, and in a ‘top-down’ sense, through analysis of secondary organic matter produced via chamber oxidation of common VOCs. We will also begin to quantify the regional impacts of kinetic limitations to gas particle partitioning in dry air parcels, by embedding Fickian diffusion methods explicitly within a box model, to probe the evolving dynamics of an ensemble of particles.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. I. acknowledges funding from GW4 + DTP from NERC (NE/L002434/1). J. P. R. gratefully acknowledges support from the NERC through the award of grant NE/M004600/1. D. O. T. and S. O’M. acknowledge support from the NERC through award NE/J02175X/1, and D. O. T. also acknowledges award NE/M003531/1. C. C. acknowledges support from the China Scholarship Council. The experimental data are provided through the University of Bristol data repository: Reid, J. P. Viscous Aerosol, University of Bristol, 2016, DOI: 10.5523/bris.x7uci2pgyizq2ukrs0j00xmjc.References
- B. J. Murray, Atmos. Chem. Phys., 2008, 8, 5423–5433 CrossRef.
- B. Zobrist, C. Marcolli, D. a. Pedernera and T. Koop, Atmos. Chem. Phys., 2008, 8, 5221–5244 CrossRef CAS.
- A. Virtanen, J. Joutsensaari, T. Koop, J. Kannosto, P. Yli-Pirilä, J. Leskinen, J. M. Mäkelä, J. K. Holopainen, U. Pöschl, M. Kulmala, D. R. Worsnop and A. Laaksonen, Nature, 2010, 467, 824–827 CrossRef CAS PubMed.
- A. P. Bateman, A. K. Bertram and S. T. Martin, J. Phys. Chem. A, 2015, 119, 4386–4395 CrossRef CAS PubMed.
- N. A. Hosny, C. Fitzgerald, C. Tong, M. Kalberer, M. K. Kuimova and F. D. Pope, Faraday Discuss., 2013, 165, 343 RSC.
- B. Zobrist, V. Soonsin, B. P. Luo, U. K. Krieger, C. Marcolli, T. Peter and T. Koop, Phys. Chem. Chem. Phys., 2011, 13, 3514–3526 RSC.
- E. Mikhailov, S. Vlasenko, S. T. Martin, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2009, 9, 9491–9522 CrossRef CAS.
- T. Koop, J. Bookhold, M. Shiraiwa and U. Pöschl, Phys. Chem. Chem. Phys., 2011, 13, 19238–19255 Search PubMed.
- J. W. Grayson, M. Song, E. Evoy, M. A. Upshur, M. Ebrahimi, F. M. Geiger, R. J. Thomson and A. K. Bertram, Atmos. Chem. Phys. Discuss., 2016, 1–25 CAS.
- N. A. Hosny, C. Fitzgerald, A. Vyšniauskas, A. Athanasiadis, T. Berkemeier, N. Uygur, U. Pöschl, M. Shiraiwa, M. Kalberer, F. D. Pope and M. K. Kuimova, Chem. Sci., 2016, 1357–1367 RSC.
- Y. C. Song, A. E. Haddrell, B. R. Bzdek, J. P. Reid, T. Bannan, D. O. Topping, C. Percival and C. Cai, J. Phys. Chem. A, 2016, 120, 8123–8137 CrossRef CAS PubMed.
- T. Berkemeier, S. S. Steimer, U. K. Krieger, T. Peter, U. Pöschl, M. Ammann and M. Shiraiwa, Phys. Chem. Chem. Phys., 2016, 18, 12662–12674 RSC.
- F. H. Marshall, R. E. H. Miles, Y.-C. Song, P. B. Ohm, R. M. Power, J. P. Reid and C. S. Dutcher, Chem. Sci., 2016, 7, 1298–1308 RSC.
- M. L. Hinks, M. V. Brady, H. Lignell, M. Song, J. W. Grayson, A. K. Bertram, P. Lin, A. Laskin, J. Laskin and S. A. Nizkorodov, Phys. Chem. Chem. Phys., 2016, 18, 8785–8793 RSC.
- T. Berkemeier, M. Shiraiwa, U. Pöschl and T. Koop, Atmos. Chem. Phys., 2014, 14, 12513–12531 Search PubMed.
- D. M. Lienhard, A. J. Huisman, U. K. Krieger, Y. Rudich, C. Marcolli, B. P. Luo, D. L. Bones, J. P. Reid, A. T. Lambe, M. R. Canagaratna, P. Davidovits, T. B. Onasch, D. R. Worsnop, S. S. Steimer, T. Koop and T. Peter, Atmos. Chem. Phys. Discuss., 2015, 15, 24473–24511 CrossRef.
- R. M. Power, S. H. Simpson, J. P. Reid and A. J. Hudson, Chem. Sci., 2013, 4, 2597 RSC.
- H. C. Price, J. Mattsson and B. J. Murray, Phys. Chem. Chem. Phys., 2016, 18, 19207–19216 RSC.
- A. P. Bateman, Z. Gong, P. Liu, B. Sato, G. Cirino, Y. Zhang, P. Artaxo, A. K. Bertram, A. O. Manzi, L. V. Rizzo, R. A. F. Souza, R. A. Zaveri and S. T. Martin, Nat. Geosci., 2015, 9, 34–37 CrossRef.
- Q. Ye, E. S. Robinson, X. Ding, P. Ye, R. C. Sullivan and N. M. Donahue, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12649–12654 CrossRef CAS PubMed.
- T. Yli-Juuti, A. Pajunoja, O.-P. Tikkanen, A. Buchholz, C. Faiola, O. Väisänen, L. Hao, E. Kari, O. Peräkylä, O. Garmash, M. Shiraiwa, M. Ehn, K. Lehtinen and A. Virtanen, Geophys. Res. Lett., 2017, 44, 2562–2570 CAS.
- A. M. Maclean, C. L. Butenhoff, J. W. Grayson, K. Barsanti, J. L. Jimenez and A. K. Bertram, Atmos. Chem. Phys. Discuss., 2017, 1–17 Search PubMed.
- H. Mai, M. Shiraiwa, R. C. Flagan and J. H. Seinfeld, Environ. Sci. Technol., 2015, 49, 11485–11491 CrossRef CAS PubMed.
- E. Abramson, D. Imre, J. Beránek, J. Wilson and A. Zelenyuk, Phys. Chem. Chem. Phys., 2013, 15, 2983 RSC.
- S. Takahama, S. Liu and L. M. Russell, J. Geophys. Res., 2010, 115, D01202 CrossRef.
- D. M. Lienhard, A. J. Huisman, D. L. Bones, Y.-F. Te, B. P. Luo, U. K. Krieger and J. P. Reid, Phys. Chem. Chem. Phys., 2014, 16, 16677 RSC.
- H. C. Price, J. Mattsson, Y. Zhang, A. K. Bertram, J. F. Davies, J. W. Grayson, S. T. Martin, D. O’Sullivan, J. P. Reid, A. M. J. Rickards and B. J. Murray, Chem. Sci., 2015, 6, 4876–4883 RSC.
- J. W. Lu, A. M. J. Rickards, J. S. Walker, K. J. Knox, R. E. H. Miles, J. P. Reid and R. Signorell, Phys. Chem. Chem. Phys., 2014, 16, 9819–9830 RSC.
- K.-K. Li, F. Wang, G. Zeng, J. P. Reid and Y.-H. Zhang, J. Phys. Chem. B, 2011, 115, 14397–14403 CrossRef CAS PubMed.
- J. F. Davies and K. R. Wilson, Anal. Chem., 2016, 88, 2361–2366 CrossRef CAS PubMed.
- A. M. J. Rickards, Y.-C. Song, R. E. H. Miles, T. C. Preston and J. P. Reid, Phys. Chem. Chem. Phys., 2015, 17, 10059–10073 RSC.
- M. Starzak and S. D. Peacock, Zuckerindustrie, 1997, 122, 380–387 CAS.
- M. L. McGlashan, J. Chem. Educ., 1963, 40, 516–518 CrossRef CAS.
- M. Starzak and M. Mathlouthi, Food Chem., 2006, 96, 346–370 CrossRef CAS.
- S. O’Meara, D. Topping and G. McFiggans, Atmos. Chem. Phys. Discuss., 2016, 16, 5299–5313 CrossRef.
- A. A. Zardini, S. Sjogren, C. Marcolli, U. K. Krieger, M. Gysel, E. Weingartner, U. Baltensperger and T. Peter, Atmos. Chem. Phys. Discuss., 2008, 8, 5235–5268 CrossRef.
- C. D. Cappa and K. R. Wilson, Atmos. Chem. Phys., 2011, 11, 1895–1911 CrossRef CAS.
- T. D. Vaden, D. Imre, J. Beranek, M. Shrivastava and A. Zelenyuk, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 2190–2195 CrossRef CAS PubMed.
- V. Perraud, E. A. Bruns, M. J. Ezell, S. N. Johnson, Y. Yu, M. L. Alexander, A. Zelenyuk, D. Imre, W. L. Chang, D. Dabdub, J. F. Pankow and B. J. Finlayson-Pitts, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2836–2841 CrossRef CAS PubMed.
- J. B. Wills, K. J. Knox and J. P. Reid, Chem. Phys. Lett., 2009, 481, 153–165 CrossRef CAS.
- D. L. Bones, J. P. Reid, D. M. Lienhard and U. K. Krieger, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11613–11618 CrossRef CAS PubMed.
- T. C. Preston and J. P. Reid, J. Opt. Soc. Am. B, 2013, 30, 2113 CrossRef CAS.
- T. C. Preston and J. P. Reid, J. Opt. Soc. Am. A, 2015, 32, 2210 CrossRef PubMed.
- D. L. Bones, J. P. Reid, D. M. Lienhard and U. K. Krieger, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11613–11618 CrossRef CAS PubMed.
- R. M. Power and J. P. Reid, Rep. Prog. Phys., 2014, 77, 74601 CrossRef PubMed.
- B. R. Bzdek, L. Collard, J. E. Sprittles, A. J. Hudson and J. P. Reid, J. Chem. Phys., 2016, 145, 54502 CrossRef PubMed.
- P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267 CrossRef CAS PubMed.
- S. Sengupta, S. Karmakar, C. Dasgupta and S. Sastry, J. Chem. Phys., 2013, 138, 12A548 CrossRef PubMed.
- M. Potuzak, R. C. Welch and J. C. Mauro, J. Chem. Phys., 2011, 135, 214502 CrossRef PubMed.
- J. C. Phillips, Rep. Prog. Phys., 1996, 59, 1133–1207 CrossRef CAS.
- J. F. Davies, A. E. Haddrell and J. P. Reid, Aerosol Sci. Technol., 2012, 46, 666–677 CrossRef CAS.
- S. S. Steimer, U. K. Krieger, Y.-F. Te, D. M. Lienhard, A. J. Huisman, B. P. Luo, M. Ammann and T. Peter, Atmos. Meas. Tech., 2015, 8, 2397–2408 CrossRef.
- R. Krishna and J. A. Wesselingh, Chem. Eng. Sci., 1997, 52, 861–911 CrossRef CAS.
- U. K. Krieger, C. Marcolli and J. P. Reid, Chem. Soc. Rev., 2012, 41, 6631 RSC.
- V. Soonsin, A. A. Zardini, C. Marcolli, A. Zuend and U. K. Krieger, Atmos. Chem. Phys., 2010, 10, 11753–11767 CrossRef CAS.
- B. J. Dennis-Smither, F. H. Marshall, R. E. H. Miles, T. C. Preston and J. P. Reid, J. Phys. Chem. A, 2014, 118, 5680–5691 CrossRef CAS PubMed.
- C. Cai, R. E. H. Miles, M. I. Cotterell, A. Marsh, G. Rovelli, A. M. J. Rickards, Y. H. Zhang and J. P. Reid, J. Phys. Chem. A, 2016, 120, 6604–6617 CrossRef CAS PubMed.
- D. Topping, M. Barley, M. K. Bane, N. Higham, B. Aumont, N. Dingle and G. McFiggans, Geosci. Model Dev., 2016, 9, 899–914 Search PubMed.
- H. C. Price, B. J. Murray, J. Mattsson, D. O’Sullivan, T. W. Wilson, K. J. Baustian and L. G. Benning, Atmos. Chem. Phys., 2014, 14, 3817–3830 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05172g |
| This journal is © the Owner Societies 2017 |