Biosorption of Zn2+, Ni2+ and Co2+ from water samples onto Yarrowia lipolytica ISF7 using a response surface methodology, and analyzed by inductively coupled plasma optical emission spectrometry (ICP-OES)
Arash Asfarama,
Mehrorang Ghaedi*a and
Gholam Reza Ghezelbash*b
aChemistry Department, Yasouj University, Yasouj 75918-74831, Iran. E-mail: m_ghaedi@mail.yu.ac.ir; m_ghaedi@yahoo.com; Fax: +98 741 2223048; Tel: +98 741 2223048
bBiology Department, Faculty of Science, Shahid Chamran University of Ahvaz, 61357-83135, Ahvaz, Iran. E-mail: gh.r.ghezelbash@gmail.com; Tel: +98 611 33331045
First published on 9th February 2016
Abstract
A response surface methodology (RSM) based on a central composite design with five variables and five levels was employed to interpret the biosorption efficiency of Zn2+, Ni2+ and Co2+ ions onto Yarrowia lipolytica ISF7. Independent variables, viz. pH, temperature, and Zn2+, Ni2+ and Co2+ ion concentrations were transformed into coded values and a quadratic model was built to predict the responses. Analysis of variance (ANOVA) and t-test statistics were used to test the significance of the independent variables and their interactions. The predicted maximum biosorption efficiencies (99.65, 99.30 and 98.78% for Zn2+, Ni2+ and Co2+ ions, respectively) under the optimum recommended conditions (pH 6.0, 25 °C, 30, 25 and 30 mg L−1 of Zn2+, Ni2+ and Co2+ ions) following 24 h mixing were very close to the experimental values (99.65, 99.30 and 98.78% for Zn2+, Ni2+ and Co2+ ions, respectively). The equilibrium equation was extensively investigated and found to be efficiently represented by a Langmuir model with maximum monolayer biosorption capacities of 31.96, 24.40 and 25.77 mg g−1 for Zn2+, Ni2+ and Co2+, respectively. The biosorption data trend closely followed a pseudo-second-order kinetic model. FTIR and scanning electron microscopy coupled with X-ray energy dispersed analysis (SEM-EDX) provided proof of progress of ion biosorption on the yeast surfaces.
1. Introduction
Water pollution caused by heavy metal ions and organic compounds remains a serious problem for the environment and public health.1–4 Heavy metal ions (antimony, arsenic, beryllium, cadmium, chromium, copper, lead, mercury, nickel, selenium, silver, thallium and zinc) are non-biodegradable, toxic and carcinogenic compound harmful to organisms even at very low concentrations and lead to the generation of hazards and injury to public health.5–8Ni2+ ions are a major concern because of their extensive application in developing countries and their potential pollution effects. This metal is released into the environment by many processes such as electroplating, leather tanning, wood preservation, pulp processing, steel manufacturing, plastic pigmentation, mining and metallurgical processes.9–11 Excess Zn2+ ion intake leads to respiratory problems with breathing rate, volume and frequency of ventilation, coughing, and a decrease in oxygen uptake efficiency.12–14 Co2+ ions as used in the manufacture of super alloys, lithium ion batteries, oxidation catalysts and as pigments in paints15,16 can lead to the discharge of high levels of cobalt contaminated effluents into the aquatic environment, which has encouraged researchers to design and develop effective clean up technologies to remove heavy metals from aquatic media.17,18
Conventional heavy metal ion removal protocols viz. adsorption, precipitation, ion exchange, biosorption, membrane filtration, electrochemical processes and reverse osmosis have their unique advantages but also suffer from disadvantages such as non-quantitative removal efficiency, high energy consumption and the generation of toxic sludge, which needs proper recycling disposal that is limited from a financial view point.19–22 Easy to operate and cheap materials that have selective binding with alkaline metals compared to physicochemical processes and that have high efficiency for heavy metal ion biosorption using various waste biomaterials from different parts of world are described below:23–25 Aspergillus niger (for Ni, Co and Zn);26,27 Saccharum bengalense (for Ni and Co);28,29 brown algae (for Zn and Ni);30 cross-linked metal-imprinted chitosans with epichlorohydrin (for Zn and Ni);31 Chrysanthemum indicum (for Co);16 Sophora japonica pod powder (for Zn and Ni);32 Sargassum glaucescens nanoparticles (for Zn and Ni);33 Hizikia fusiformis (for Zn, Ni, Cd and Pb);34 and Saccharomyces cerevisiae (for Zn and Ni) are same good choices for such purposes.35
Yarrowia lipolytica is non-conventional yeast with significant biological relevance and biotechnological applications. This yeast is a good candidate36 for biosorption and remediatory degradation of different wastes and complicated materials.37,38 Yarrowia lipolytica is able to utilize a variety of renewable carbon sources and the biomass of the yeast has been used as a single cell protein or single cell oil.39 Our literature survey through most documents did not show any reports nor applications of Yarrowia lipolytica to biomass for the simultaneous biosorption of metal ions, while surviving in presence of metal ions like Cr6+, Ni2+, Co2+, Cu2+, Cd2+, Zn2+ and Au2+ that cause stress and accumulate.40–43 This yeast displays potential for the bioremediation of metal ion polluted environments.
Inductively coupled plasma mass spectrometry (ICP-MS),44 inductively coupled plasma optical emission spectrometry (ICP-OES),45–47 flame atomic absorption (FAAS),48 electrothermal atomic absorption spectrometry (ETAAS),49 and molecular spectrophotometry and other atomic and molecular conventional instrumental techniques have been applied to quantify metals in many samples. Among the available analytical techniques to quantify the elements present in water samples, inductively coupled plasma optical emission spectrometry (ICP-OES) is a multi-element analysis technique that can lead to the achievement of relatively low detection limits and has a practical linear range that makes possible simultaneous and precise determinations in short times over wide concentration ranges.50,51
Optimization of heavy metal ion biosorption efficiencies and their correlation to variables (i.e., pH, temperature and heavy metal concentration) – separately known as a “one factor at a time optimization approach” – is based on maintaining all others at a fixed level. This method is extremely time consuming and expensive for a large number of variables and this limitation can simply be eliminated or lowered by simultaneous and collective optimization using a Central Composite Design (CCD) under a response surface methodology (RSM).26 The CCD model was based on the statistical evaluation of the following tests: the root-mean-square error (RMSE), bias index and accuracy factor and the lack-of-fit test. The CCD minimizes the number of factor combinations and maintains good precision of the predicted response.52
The main objectives of the present study include the following:
(1) in the present investigation, Yarrowia lipolytica ISF7 was isolated from wastewater and subsequently applied for Zn2+, Ni2+ and Co2+ ion removal from aqueous solution;
(2) to construct a mathematical equation following statistical optimization to maximize the metal ion sorption efficiency (%) using RSM; and
(3) to investigate isotherm and kinetic models that describe the biosorption process.
2. Materials and methods
2.1. Preparation of the biomass
Yarrowia lipolytica ISF7 was isolated from wastewater and registered at the NCBI Gene bank with accession number JX010454.1 and was used laterally for the biosorption of the metal ions under study. Yarrowia lipolytica ISF7 was streaked on Yeast–Peptone–Glucose (YPG; 1% yeast extract, 2% peptone, 1% glucose) agar and incubated overnight at 30 °C. Then a single colony was inoculated into a 100 mL Erlenmeyer flask containing 25 mL of YPG broth (pH: 7.0) incubated on a shaker (160 rpm) for 24 h at 30 °C.2.2. Metals and chemicals
The yeast extract, peptone, glucose, agar and Zn(NO3)2·6H2O, Ni(NO3)2·6H2O and Co(NO3)2·6H2O used in all the experiments were obtained from Sigma-Aldrich. NaOH and HCl with the highest purity available were purchased from Merck (Darmstadt, Germany). Several stock solutions of Zn, Ni and Co in deionized water were prepared, ranging from 10 to 100 mg L−1, from their water-soluble metallic salts (Zn(NO3)2·6H2O, Ni(NO3)2·6H2O and Co(NO3)2·6H2O) and stored in 500 mL volumetric flasks for posterior metal ion biosorption experiments.2.3. Instrumentation
Fourier transform infrared spectroscopy (FT-IR) studies were investigated using 1 mg samples in strained cells before and after metal ion biosorption, respectively. Infrared spectra were recorded using a Perkin-Elmer spectrometer, RX-IFTIR, USA) in the range of 4000–300 cm−1. Inductively coupled plasma optical emission spectrometry (ICP-OES, Optima 8300, Perkin Elmer) was used for the determination of analytes with transitions at 213.854 nm (4s), 231.604 nm (5s) and 228.613 nm (4s), i.e. Zn2+, Ni2+ and Co2+, respectively. The spectroscopic technique EDAX, which uses a scanning electron microscope (Oxford INCA II energy solid state detector), was used to characterize the material used, before and after equilibration with the metal ions. The pH measurements were carried out using a digital pH meter (Ino Lab pH 730, Germany). A HERMLE bench centrifuge (2206 A, Germany) was used to accelerate the phase separation. The samples were agitated in an incubator shaker (Labcon, FSIM-SPO16, United States) at 160 rpm. Response surface analysis was performed with the STATISTICA software version 10.0 (Stat Soft Inc., Tulsa, USA). The significance of all the terms in the polynomial equation were analyzed statistically by computing the F-value at a probability (p) of 0.05.2.4. Batch biosorption studies
Following growth on YPG agar, a single colony was inoculated into a 100 mL Erlenmeyer flask containing 25 mL of YGC broth together with 10–40 mg L−1 of Zn2+, Ni2+ and Co2+ ions. The flasks were agitated in a shaker at 160 rpm over various temperatures and times and biosorption equilibrium was reached after 24 h. The required pH value of the solutions was adjusted with HCl and/or NaOH solutions. In the batch biosorption experiments, samples were taken at given time intervals and were centrifuged at 3000 rpm for 10 min. Subsequently the supernatant part was analyzed for the non-sorbed metal ions being studied by inductively coupled plasma optical emission spectrometry (ICP-OES). The sediment phase (yeast) was again centrifuged and the remaining biomass was dried at 65 °C for 24 h. Biosorption isotherm studies were examined over 10–100 mg L−1 of the target compounds. The biosorption capacity (qe), i.e. the amount of metal ion (mg) biosorbed per gram of the biomass, and the efficiency of biosorption (R%) were calculated using eqn (1) and (2), respectively:
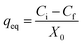 | (1) |
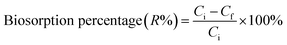 | (2) |
The applicability of each model was judged by a chi-square (χ2) test and the coefficient of determination (R2) as criteria to obtain the best isotherm and kinetic models for describing the experimental equilibrium data in non-linear regression analysis.53
The following non-linear chi-square test (χ2)54 was carried out on the best-fitted isotherm:
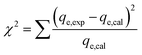 | (3) |
2.5. Statistical analysis
The optimum conditions for maximum Zn2+, Ni2+ and Co2+ ion biosorption by yeast were determined by means of a five factor test which selected at five levels namely lowest, low, medium, high and highest, coded as −α, −1, 0, +1 and +α in a central composite experimental design (CCD) combined with a response surface methodology. Five critical parameters of concern for biosorption, pH (X1), temperature (X2), and Zn2+, Ni2+ and Co2+ concentration (X3, X4 and X5, respectively), were selected as independent variables based on preliminary experiments while removal biosorption % (Y) was the dependent variable (response). The experimental range and levels of independent variables for metal ion biosorption are given in Table 1 and subsequently were analyzed using STATISTICA 10.0, following which the regression model was proposed. In the optimization process, the responses can be simply related to the chosen factors by linear or quadratic models. A quadratic model, which also includes the linear model, is given below as eqn (4):55
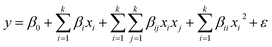 | (4) |
| Factors | Units | Levels | α = 2 | |||
|---|---|---|---|---|---|---|
| Low (−1) | Central (0) | High (+1) | −α | +α | ||
| a Experimental values of response.b Predicted values of response by the proposed RSM model.c (C): center point. (F): factorial point. (A): axial point. | ||||||
| X1: pH | — | 5.0 | 6.0 | 7.0 | 4.0 | 8.0 |
| X2: temperature | °C | 25 | 30 | 35 | 20 | 40 |
| X3: Zn2+ concentration | mg L−1 | 25 | 30 | 35 | 20 | 40 |
| X4: Ni2+ concentration | mg L−1 | 15 | 20 | 25 | 10 | 30 |
| X5: Co2+ concentration | mg L−1 | 15 | 20 | 25 | 10 | 30 |
| Run | Factors | R%Zn2+ | R%Ni2+ | R%Co2+ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | Exp.a | Pred.b | Exp.a | Pred.b | Exp.a | Pred.b | |
| 1 (F) | 5.0 | 25 | 25 | 15 | 25 | 89.34 | 89.09 | 91.56 | 90.88 | 84.71 | 84.39 |
| 2 (F) | 7.0 | 25 | 25 | 15 | 15 | 88.90 | 88.54 | 95.68 | 95.01 | 97.26 | 96.75 |
| 3 (F) | 5.0 | 35 | 25 | 15 | 15 | 85.63 | 85.34 | 91.21 | 90.76 | 91.84 | 91.53 |
| 4 (F) | 7.0 | 35 | 25 | 15 | 25 | 90.64 | 90.39 | 95.65 | 95.19 | 92.82 | 92.28 |
| 5 (F) | 5.0 | 25 | 35 | 15 | 15 | 90.45 | 89.82 | 93.67 | 93.20 | 91.92 | 91.58 |
| 6 (F) | 7.0 | 25 | 35 | 15 | 25 | 94.76 | 94.16 | 97.89 | 97.41 | 89.28 | 88.72 |
| 7 (F) | 5.0 | 35 | 35 | 15 | 25 | 84.65 | 84.12 | 88.34 | 88.09 | 86.84 | 86.48 |
| 8 (F) | 7.0 | 35 | 35 | 15 | 15 | 86.73 | 86.10 | 90.34 | 90.10 | 92.73 | 92.18 |
| 9 (F) | 5.0 | 25 | 25 | 25 | 15 | 92.66 | 92.24 | 90.23 | 89.83 | 90.07 | 89.82 |
| 10 (F) | 7.0 | 25 | 25 | 25 | 25 | 98.77 | 98.38 | 96.64 | 96.23 | 95.06 | 94.59 |
| 11 (F) | 5.0 | 35 | 25 | 25 | 25 | 88.34 | 88.02 | 83.43 | 83.25 | 77.44 | 77.17 |
| 12 (F) | 7.0 | 35 | 25 | 25 | 15 | 85.67 | 85.24 | 94.78 | 94.61 | 97.48 | 97.02 |
| 13 (F) | 5.0 | 25 | 35 | 25 | 25 | 81.67 | 81.01 | 86.34 | 86.14 | 91.71 | 91.42 |
| 14 (F) | 7.0 | 25 | 35 | 25 | 15 | 90.23 | 89.46 | 91.23 | 91.04 | 95.39 | 94.90 |
| 15 (F) | 5.0 | 35 | 35 | 25 | 15 | 85.98 | 85.28 | 87.80 | 87.83 | 85.34 | 85.05 |
| 16 (F) | 7.0 | 35 | 35 | 25 | 25 | 90.23 | 89.57 | 91.21 | 91.23 | 90.61 | 90.10 |
| 17 (A) | 4.0 | 30 | 30 | 20 | 20 | 58.76 | 59.67 | 61.00 | 61.66 | 58.01 | 58.41 |
| 18 (A) | 8.0 | 30 | 30 | 20 | 20 | 65.34 | 66.40 | 71.23 | 71.88 | 69.45 | 70.68 |
| 19 (A) | 6.0 | 20 | 30 | 20 | 20 | 97.35 | 98.41 | 96.89 | 97.99 | 96.15 | 96.95 |
| 20 (A) | 6.0 | 40 | 30 | 20 | 20 | 90.34 | 91.26 | 93.12 | 93.32 | 91.02 | 91.86 |
| 21 (A) | 6.0 | 30 | 20 | 20 | 20 | 97.89 | 98.26 | 97.98 | 99.04 | 97.84 | 98.60 |
| 22 (A) | 6.0 | 30 | 40 | 20 | 20 | 92.21 | 93.82 | 96.12 | 96.36 | 96.94 | 97.82 |
| 23 (A) | 6.0 | 30 | 30 | 10 | 20 | 96.78 | 97.56 | 99.89 | 101.09 | 95.93 | 96.86 |
| 24 (A) | 6.0 | 30 | 30 | 30 | 20 | 96.78 | 97.97 | 95.87 | 95.97 | 95.20 | 95.90 |
| 25 (A) | 6.0 | 30 | 30 | 20 | 10 | 94.88 | 96.01 | 97.90 | 98.53 | 99.89 | 100.67 |
| 26 (A) | 6.0 | 30 | 30 | 20 | 30 | 98.35 | 99.19 | 96.87 | 97.54 | 91.40 | 92.25 |
| 27 (C) | 6.0 | 30 | 30 | 20 | 20 | 94.76 | 95.09 | 90.56 | 91.49 | 89.84 | 89.01 |
| 28 (C) | 6.0 | 30 | 30 | 20 | 20 | 95.64 | 95.09 | 92.62 | 91.49 | 88.41 | 89.01 |
| 29 (C) | 6.0 | 30 | 30 | 20 | 20 | 96.89 | 95.09 | 91.28 | 91.49 | 89.45 | 89.01 |
| 30 (C) | 6.0 | 30 | 30 | 20 | 20 | 95.34 | 95.09 | 92.01 | 91.49 | 90.29 | 89.01 |
| 31 (C) | 6.0 | 30 | 30 | 20 | 20 | 94.67 | 95.09 | 91.88 | 91.49 | 88.77 | 89.01 |
| 32 (C) | 6.0 | 30 | 30 | 20 | 20 | 95.23 | 95.09 | 91.90 | 91.49 | 88.93 | 89.01 |
A total of 32 experiments performed in randomized order were used to construct diagnostic checking tests provided by analysis of variance (ANOVA). The properties of the fit polynomial model are represented by the coefficient of determination R2. The R2 values measure how variability in the observed response values can be clarified by experimental factors and their interactions. These analyses are performed by Fisher’s ‘F’-test and P-value (probability). Based on the experimental data, the levels of the five main parameters investigated in this study are presented in Table 1.
3. Results and discussion
3.1. Effect of contact time on biosorption efficiency
The influence of contact time on the batch biosorption of 10 mg L−1 of the studied analytes at 25 °C, pH 5.5 and different time intervals (6–48 h) are shown in Fig. 1. It is obvious that rising contact time causes a significant increase in the biosorption percentage, which was very rapid at the beginning stage but was found to reach plateau values within 24 h. The trends and magnitudes of their binding to biomass reveal the contribution and participation of the functional groups of the biomass to complex metal ions. Biosorption occurs in two stages: an initial rapid uptake, where the surface of the cell wall components attract metal ions, and a subsequent slow uptake due to their membrane transport. The cell surfaces of many microorganisms consist of polysaccharides, proteins and lipids containing several functional groups which are capable of binding metal ions.57,58 The biosorption rate depends on the structural properties of the sorbate and biosorbent (e.g. protein and carbohydrate composition), surface charge density, topography, surface area, initial concentration of metal ions and the existence of other ions.59,60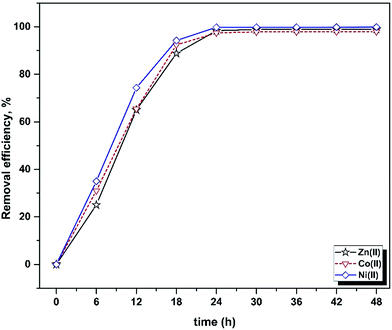 | ||
| Fig. 1 Influence of contact time on the removal efficiency of Yarrowia lipolytica ISF7 (ion concentration = 10 mg L−1, 25 °C, pH = 5.5). | ||
3.2. Fitting the process models
CCD was adopted to study the correlation of the target compound biosorption efficiency with variables like pH, temperature, and Zn2+, Ni2+ and Co2+ ion concentrations. A quadratic model was selected for developing the mathematical relationship between the responses and the five operating variables. The present CCD consists of 16 standard factorial runs, a star configuration (α = ±2) based on 10 experiments and six replicates at the center point, which were finally used to determine the experimental error. The predicted and actual responses (Table 1) reveal that the maximum metal ion biosorptions were 99.65, 99.30 and 98.78% for Zn2+, Ni2+ and Co2+, respectively. Following polynomial regression models correlation of the biosorption of each ion to the corresponding coded values (X1, X2, X3, X4 and X5) of the five different process variables (pH, temperature, Zn2+, Ni2+ and Co2+ ions concentration), finally the best fitted model was obtained as:| R%Zn2+ = −121 + 87.60X1 − 0.70X2 − 0.60X3 − 2.55X5 − 0.42X1X5 − 0.05X3X4 − 0.041X3X5 − 0.008X4X5 − 8.1X12 + 0.03X42 + 0.03X52 | (5) |
| R%Ni2+ = 31.4 + 72.1X1 − 2.62X2 − 2.8X3 − 3.58X4 − 0.12X1X3 + 0.2X1X4 + 0.3X1X5 − 0.012X3X4 − 6.2X12 + 0.042X22 + 0.06X32 + 0.07X42 + 0.07X52 | (6) |
| R%Co2+ = 56.7 + 76.1X1 − 2.71X2 − 5.03X5 + 0.17X1X2 − 0.33X1X3 + 0.22X1X4 − 0.07X2X4 + 0.05X3X5 − 6.12X12 + 0.054X22 + 0.092X32 + 0.074X42 + 0.075X52 | (7) |
The ANOVA results of this quadratic model (Table 2) could be used to navigate the design space. The significance of coefficients was determined from F and P values. The application of ANOVA is found to be the most reliable way for the evaluation of quality of the fitted model.26 By using ANOVA, the variation can be compared among independent variables with respect to response.
| Source of variation | Dfa | Zn2+ | Ni2+ | Co2+ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSb | MSc | F-Value | P-Value | SS | MS | F-Value | P-Value | SS | MS | F-Value | P-Value | ||
| a Degree of freedom: N − 1.b Sum of square: sums of squares, sum of the squared differences between the average values and the overall mean.c Mean of square: sum of squares divided by Df.d F-Value: test for comparing term variance with residual (error) variance. Prob > F: probability of seeing the observed F-value if the null hypothesis is true. Residual: consists of terms used to estimate the experimental error. Lack-of-fit: variation of the data around the fitted model. Pure error: variation in the response in replicated design points. Cor total: totals of all information corrected for the mean. | |||||||||||||
| Model | 20 | 2324.9 | 116.24 | 67.497 | <0.0001 | 1822.6 | 91.128 | 93.498 | <0.0001 | 2155.8 | 107.8 | 92.097 | <0.0001 |
| X1 | 1 | 67.906 | 67.906 | 39.430 | <0.0001 | 156.54 | 156.54 | 160.611 | <0.0001 | 225.95 | 225.95 | 193.056 | <0.0001 |
| X2 | 1 | 76.791 | 76.791 | 44.589 | <0.0001 | 32.713 | 32.713 | 33.564 | 0.000120 | 38.913 | 38.913 | 33.248 | 0.000125 |
| X3 | 1 | 29.504 | 29.504 | 17.131 | 0.00168 | 10.774 | 10.774 | 11.054 | 0.006774 | 0.905 | 0.905 | 0.773 | 0.3981 |
| X4 | 1 | 0.250 | 0.250 | 0.145 | 0.7104 | 39.322 | 39.322 | 40.344 | <0.0001 | 1.382 | 1.382 | 1.181 | 0.3004 |
| X5 | 1 | 15.185 | 15.185 | 8.817 | 0.01276 | 1.470 | 1.470 | 1.508 | 0.2450 | 106.43 | 106.43 | 90.934 | <0.0001 |
| X1X2 | 1 | 6.089 | 6.089 | 3.535 | 0.08680 | 0.152 | 0.152 | 0.156 | 0.7004 | 11.560 | 11.560 | 9.877 | 0.009362 |
| X1X3 | 1 | 7.826 | 7.826 | 4.544 | 0.05641 | 8.702 | 8.702 | 8.929 | 0.01234 | 43.428 | 43.428 | 37.106 | <0.0001 |
| X1X4 | 1 | 1.749 | 1.749 | 1.016 | 0.3352 | 7.952 | 7.952 | 8.159 | 0.01562 | 18.490 | 18.490 | 15.798 | 0.002179 |
| X1X5 | 1 | 70.518 | 70.518 | 40.946 | <0.0001 | 31.922 | 31.922 | 32.753 | 0.000134 | 0.714 | 0.714 | 0.610 | 0.4512 |
| X2X3 | 1 | 6.089 | 6.089 | 3.535 | 0.08680 | 0.360 | 0.360 | 0.369 | 0.5557 | 1.729 | 1.729 | 1.477 | 0.2496 |
| X2X4 | 1 | 0.452 | 0.452 | 0.263 | 0.6185 | 2.280 | 2.280 | 2.339 | 0.1544 | 31.416 | 31.416 | 26.842 | 0.000303 |
| X2X5 | 1 | 3.563 | 3.563 | 2.069 | 0.1782 | 3.168 | 3.168 | 3.251 | 0.09882 | 2.103 | 2.103 | 1.796 | 0.2072 |
| X3X4 | 1 | 23.547 | 23.547 | 13.672 | 0.00352 | 1.346 | 1.346 | 1.381 | 0.2648 | 4.906 | 4.906 | 4.192 | 0.06526 |
| X3X5 | 1 | 16.626 | 16.626 | 9.654 | 0.00998 | 1.796 | 1.796 | 1.842 | 0.2019 | 24.206 | 24.206 | 20.682 | 0.000833 |
| X4X5 | 1 | 0.644 | 0.644 | 0.374 | 0.5533 | 5.018 | 5.018 | 5.148 | 0.04439 | 2.756 | 2.756 | 2.354 | 0.1532 |
| X12 | 1 | 1883.8 | 1883.8 | 1093.8 | <0.0001 | 1120.7 | 1120.7 | 1149.84 | <0.0001 | 1097.0 | 1097.0 | 937.331 | <0.0001 |
| X22 | 1 | 0.124 | 0.124 | 0.072 | 0.7938 | 31.792 | 31.792 | 32.619 | 0.000134 | 53.321 | 53.321 | 45.559 | <0.0001 |
| X32 | 1 | 1.639 | 1.639 | 0.952 | 0.3503 | 70.684 | 70.684 | 72.522 | <0.0001 | 155.11 | 155.11 | 132.524 | <0.0001 |
| X42 | 1 | 13.123 | 13.123 | 7.620 | 0.01854 | 90.844 | 90.844 | 93.207 | <0.0001 | 99.662 | 99.662 | 85.153 | <0.0001 |
| X52 | 1 | 11.554 | 11.554 | 6.709 | 0.02513 | 78.517 | 78.517 | 80.559 | <0.0001 | 101.84 | 101.84 | 87.010 | <0.0001 |
| Residual | 11 | 18.944 | 1.722 | 10.721 | 0.975 | 12.874 | 1.170 | ||||||
| Lack-of-fit | 6 | 15.694 | 2.616 | 4.024 | 0.07404 | 8.231 | 1.372 | 2.754 | 0.1430 | 10.366 | 1.728 | 3.444 | 0.09800 |
| Pure error | 5 | 3.250 | 0.650 | 2.490 | 0.498 | 2.508 | 0.502 | ||||||
| Cor total | 31 | 2343.8 | 1833.3 | 2168.7 | |||||||||
Values of Prob > F less than 0.0500 indicate that the model terms are significant for biosorption of Zn2+, Ni2+ and Co2+ ions. The non-significant lack-of-fit (more than 0.05) supports the validity of the present quadratic model for the present study. The non-significant lack-of-fit shows the goodness of the equation for the prediction of experimental data. The predicted and adjusted R2 values of 0.8427 and 0.9772 for Zn2+ ion, 0.8911 and 0.9835 for Ni2+ ion and 0.8881 and 0.9833 for Co2+ ion has reasonable agreement with the desirable R2 value of 1.0 and indicates the better fitness of the model to the experimental data (see Table 3).
| Quality of quadratic model based on R2 and the standard deviation | |||||||
|---|---|---|---|---|---|---|---|
| Response | SDa | R2b | Adj-R2c | Pred-R2d | Mean | CV%e | APf |
| a Standard deviation: square root of the pure (experimental) error.b Coefficient of determination.c Adjusted coefficient of determination.d Predicted coefficient of determination.e Coefficient of variation, the standard deviation as a percentage of the mean.f Adequate precision: compares the range of predicted values at design points to the average prediction error. | |||||||
| Zn2+ | 1.3120 | 0.9919 | 0.9772 | 0.8427 | 90.180 | 1.455 | 37.170 |
| Ni2+ | 0.9870 | 0.9942 | 0.9835 | 0.8911 | 91.350 | 1.081 | 49.300 |
| Co2+ | 1.0820 | 0.9941 | 0.9833 | 0.8881 | 89.940 | 1.203 | 48.220 |
The residual variation is measured using the coefficient of variance (CV) relative to the size of the mean. A very low value of the CV (<1.4%) implies sufficient precision and reliability of the experimental results. “Adequate Precision” measures the signal to noise ratio, and a ratio greater than 4.0 is desirable. The “Adequate Precision” ratio of this model (>37.00) is far greater than 4.0 which indicates the presence of an adequate signal corresponding to the model.61
Fig. 2a shows the correlation between the predicted and experimental values for prediction of the target compound’s biosorption and their closeness to each other.
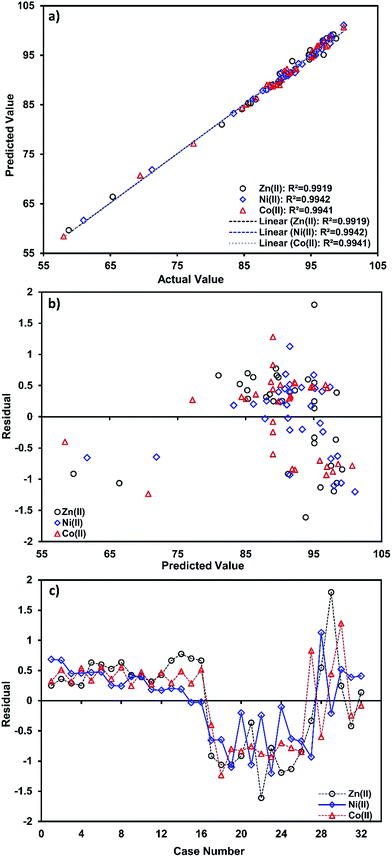 | ||
| Fig. 2 (a) Correlation of predicted and actual values, (b) the studentized residuals and predicted response plot, and (c) studentized residuals and case number value for ion biosorption. | ||
A high value parameter estimate for the variables X1 and X2 indicates a high level of significance and interaction on the biosorption process. The variable X1 (pH) has a positive relation to the studied metal ions’ biosorption, whereas X2 (temperature) shows a negative relationship.
The residual plot for the predicted and experimental values and case number (Fig. 3c and d) reveals that the residual values are uniformly distributed and also suggests that real data are well fitted by eqn (5)–(7),and that it has good agreement with experimental data.
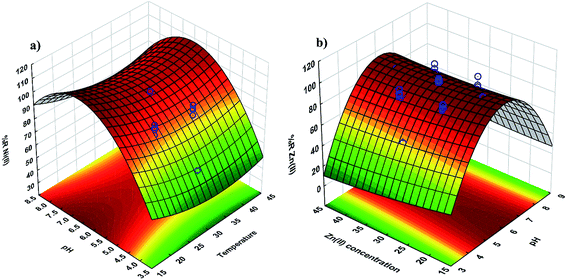 | ||
| Fig. 3 3D surface mapping plot for the multiple effects of (a) pH and temperature and (b) pH and Zn2+ concentration. | ||
3.3. Interactive effects of two variables
The response surface and counter plots for the Ni2+ ion biosorption efficiency of Yarrowia lipolytica ISF7 (Fig. 3a) show the effect of temperature and initial pH on biosorption efficiency. The initial pH and temperature are the most important parameters affecting the biosorption (Fig. 3a) and the maximum efficiency was obtained at pH 6.0 and 25 °C. The Ni2+ ion biosorption efficiency has a positive relation with a pH up to 6.0 though increased values are associated with a decrease in efficiency.The surface plot (Fig. 3b) confirms the contribution of the interaction between pH and initial Zn2+ ion concentration on Zn2+ ion removal efficiency and the results presented in Fig. 3b shows that the maximum removal efficiency of 98% was achieved at pH of 6.0 and 40 mg L−1 Zn2+ ions. This result is due to the influence of pH on the sorption.
3.4. Optimization based on desirability functions
In this study, multi-response optimizations by the desirability function of the response surface methodology were implemented to find optimal cutting parameters to determine the maximum biosorption in the least time. First, each response is converted into an individual desirability function that varies over the range from 0 to 1. The unit value indicates the maximum desirable response while a zero value means one or more responses are outside the acceptable region.62 Finally, the individual desirability functions are combined to provide a measure of the composite desirability of the multi-response system. For multi-response optimization (Table 4), the optimum conditions were pH (6.0), temperature (25 °C) and Zn2+, Ni2+ and Co2+ ion concentrations were 30, 25 and 30 mg L−1, leading to the achievement of biosorption efficiency responses of 99.65, 99.30 and 98.78%, which are in close agreement with the predicted values of 100.18, 99.63 and 99.43%. Comparing the experimental and predicted responses, it is evident that the biosorption efficiencies are in reasonable agreement with the predicted responses, Table 4. A maximum of a 2.5% deviation between the model predictions and experimental average results occurs for Zn2+, Ni2+ and Co2+ ions.| Exp. | Optimum conditions | Biosorption efficiency (R%) | Desirability | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | Response | Experimental | Predicted | ||
| 1 | 6.0 | 25 | 30 | 25 | 30 | Zn2+ | 99.65 ± 1.38 | 100.18 | 0.9967 |
| 2 | 6.0 | 25 | 30 | 25 | 30 | ||||
| 3 | 6.0 | 25 | 30 | 25 | 30 | Ni2+ | 99.30 ± 1.65 | 99.62 | 0.9967 |
| 4 | 6.0 | 25 | 30 | 25 | 30 | ||||
| 5 | 6.0 | 25 | 30 | 25 | 30 | Co2+ | 98.78 ± 2.11 | 99.43 | 0.9967 |
| 6 | 6.0 | 25 | 30 | 25 | 30 | ||||
3.5. Biosorption isotherm model analysis
The equilibrium isotherm is crucial to understand the interaction between sorbate and biosorbent. The data obtained from the batch experiments were applied to some commonly used isotherm models: Langmuir, Freundlich, Temkin and Dubinin–Radushkevich. The equations and linearized forms of these isotherm models are given in Table 5.| Isotherms | Linear expressions | Plot | Parameters | Parameters | Zn2+ | Ni2+ | Co2+ |
|---|---|---|---|---|---|---|---|
| Langmuir | 1/qe = 1/(KLQmaxCe) + 1/Qmax | Ce/qe vs. Ce | Qmax = (slope)−1 | Qmax (mg g−1) | 31.96 | 24.40 | 25.77 |
| KL = slope/intercept | KL (L mg−1) | 2.376 | 0.9995 | 0.8928 | |||
| R2 | 0.9962 | 0.9959 | 0.9952 | ||||
| RL = (1/(1 + KLC0)) | RL | 0.0042–0.0404 | 0.0099–0.0910 | 0.0111–0.1010 | |||
| χ2 | 0.0023 | 0.0019 | 0.0026 | ||||
| Freundlich | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KF + (1/n)ln KF + (1/n)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce Ce |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. log qe vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce Ce |
n = (slope)−1 | n | 4.548 | 4.943 | 5.160 |
| KF = exp(intercept) | KF (L mg−1) | 3.381 | 2.968 | 3.053 | |||
| R2 | 0.9018 | 0.8814 | 0.8993 | ||||
| χ2 | 4.8620 | 6.7023 | 6.3240 | ||||
| Temkin | qe = B1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KT + B1 KT + B1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce Ce |
qe vs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce Ce |
B1 = (slope) | B | 3.870 | 2.748 | 2.787 |
| KT = exp(intercept/slope) | KT (L mg−1) | 153.66 | 177.78 | 221.84 | |||
| R2 | 0.9382 | 0.9345 | 0.9562 | ||||
| χ2 | 2.2450 | 2.400 | 2.003 | ||||
| Dubinin–Radushkevich | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qs − βε2 Qs − βε2 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. ε2 qe vs. ε2 |
Qs = exp(intercept) | Qs (mg g−1) | 27.798 | 21.115 | 21.309 |
| β = −slope | β × 10−8 | 2.3 | 2.8 | 2.4 | |||
| E = (1/(2β)0.5) | E (kJ mol−1) | 4.663 | 4.226 | 4.564 | |||
| R2 | 0.8775 | 0.8871 | 0.8820 | ||||
| χ2 | 6.6231 | 6.0321 | 5.7801 |
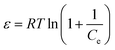 | (8) |
The results for the linear coefficients of determination (R2) and non-linear chi-square tests (χ2) for all biosorption isotherms (Table 5) show that smaller χ2 and higher R2 values simultaneously support the superiority of the Langmuir model for best representation of the experimental data over the whole concentration range. The maximum biosorption capacity of the yeast biomass according to the Langmuir isotherm model was 31.96, 24.40 and 25.77 mg g−1 for Zn2+, Ni2+ and Co2+ ions, respectively. The magnitudes of RL for the biosorption process studied at different initial ions concentrations changed in the range of 0 and 1 and confirm favorable sorption of Zn2+, Ni2+ and Co2+ ions onto the yeast. The value of the Freundlich constants, n, for all ions Zn2+, Ni2+ and Co2+ are greater than 1 and lie in the range of 2–10 indicating more favorable biosorption. The n values for metal ions were between 4.548 and 5.160 suggesting their favorable biosorption onto the yeast biomass. The values of the calculated mean energy (E) of biosorption for the metal ions were less than 8 kJ mol−1 and confirm the high contribution of physical force on the biosorption efficiency.
3.6. Kinetic models
The pseudo-first-order,67 second order,68 intraparticle diffusion69 and Elovich70 kinetic models were used in this work. The equations presented in Table 6 were used for interpretation and explanation of experimental data.| Model | Zn2+ (30 mg L−1) | Ni2+ (25 mg L−1) | Co2+ (30 mg L−1) |
|---|---|---|---|
| Pseudo-first-order-kinetics | |||
| Equation: log(qe − qt) = log(qe) − k1/2.303t | |||
| Plot: log(qe − qt) vs. t | |||
| k1 (min−1) | 0.1163 | 0.0796 | 0.0804 |
| qe(calc) (mg g−1) | 11.428 | 5.442 | 6.994 |
| R2 | 0.9692 | 0.9583 | 0.9051 |
| χ2 | 0.8970 | 2.5760 | 3.4531 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Pseudo-second-order-kinetics | |||
| Equation: (t/qt) = 1/(k2qe2) + 1/qe(t) | |||
| Plot: (t/qt) vs. t | |||
| k2 (min−1) | 0.0092 | 0.0274 | 0.0197 |
| qe(calc) (mg g−1) | 19.120 | 14.663 | 17.667 |
| R2 | 0.9977 | 0.9989 | 0.9998 |
| χ2 | 0.0063 | 0.0112 | 0.0235 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Intraparticle diffusion | |||
| Equation: qt = Kdift1/2 + C | |||
| Plot: qt vs. t1/2 | |||
| Kdif (mg g−1 min−1/2) | 1.516 | 0.8824 | 0.8666 |
| C (mg g−1) | 7.347 | 8.492 | 11.085 |
| R2 | 0.9109 | 0.9353 | 0.9462 |
| χ2 | 3.7504 | 3.4310 | 2.8731 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Elovich | |||
Equation: qt = 1/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(αβ) + 1/β ln(αβ) + 1/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(t) ln(t) |
|||
| Plot: qt vs. ln(t) | |||
| β (mg g−1 min−1) | 0.2927 | 0.7092 | 0.5192 |
| α (g mg−1) | 19.544 | 24.658 | 30.450 |
| R2 | 0.9655 | 0.9771 | 0.9762 |
| χ2 | 0.4751 | 0.3202 | 0.3643 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Experimental data | |||
| qe(exp) (mg g−1) | 18.925 | 14.018 | 16.758 |
The pseudo-second order gave a good fit to the biosorption data (R2 = 0.999 for Zn2+, Ni2+ and Co2+ ions). According to the correlation coefficients, the kinetic models reveal that the pseudo-second order with its high correlation coefficients (Zn2+: 0.9977, Ni2+: 0.9989 and Co2+: 0.9998) and lower χ2 values (Zn2+: 0.0063, Ni2+: 0.0112 and Co2+: 0.0235) has a better ability to represent the fitting model for the kinetics of Zn2+, Ni2+ and Co2+ ions onto Yarrowia lipolytica ISF7. The qe(exp) values of 18.925 for Zn2+, 14.018 for Ni2+, and 6.758 mg g−1 for Co2+ were in close agreement with qe(calc) (19.120 for Zn2+; 14.663 for Ni2+; 17.667 mg g−1 for Co2+) for the pseudo-second order model.
The Weber–Morris intraparticle diffusion model gives idea about mass transfer resistance corresponding to biosorption of Zn2+, Ni2+ and Co2+ ions. The R2 values for this diffusion model were 0.9109, 0.9353 and 0.9462 for Zn2+, Ni2+ and Co2+ ions. This result indicates that the biosorption of ions onto Yarrowia lipolytica ISF7 follows an intraparticle diffusion model. The Elovich rate equation uses constants for biosorption and desorption to describe the kinetics of chemisorption on highly heterogeneous surfaces. The results obtained by applying this model reveal the presence of acceptable correlation coefficients (R2 of 0.9655 for the Zn2+ ion biosorption of Zn2+).
3.7. FTIR and scanning electron microscopy/energy dispersed analysis of X-rays (SEM/EDAX)
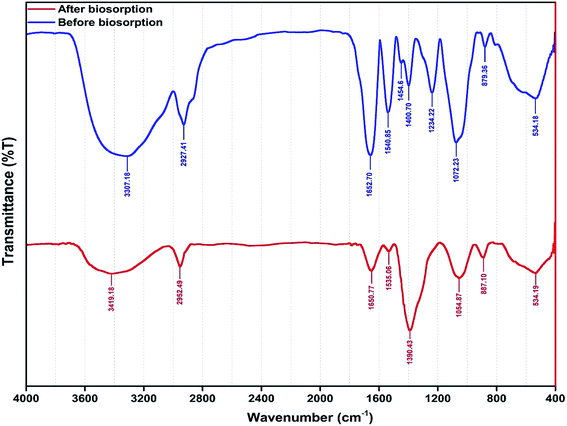
The functional groups involved in metal ion biosorption were studied by FTIR spectra (Fig. 4) before and after metal ion biosorption. There was a change in the intensity of the bands in the FTIR spectra of the yeast biomass after binding with the Zn2+, Ni2+ and Co2+ ions.Fig. 4 shows the presence of broad and strong bands at 3000–3600 cm−1 corresponding to hydroxyl groups (–OH). The peaks at 1500–1750 cm−1 are related to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretches of aromatic rings, while the peaks at 900–1125 cm−1 are assigned to the C–O stretching of alcohols and carboxylic acids. The peaks observed at 1250–1500 cm−1 are assigned to C–H groups. The results indicate that the functional groups mentioned above are mainly involved in the biosorption of the studied metal ions. In addition, the frequency change observed in the functional groups of the biomass after metal ion biosorption show a high contribution of biomass functional groups on biosorption process efficiency. The asymmetric stretching vibration of N–H was shifted from 1540.85 to 1535.06 cm−1. The stretching vibration of δCH2 + δOCH + δCCH group was shifted from 1400 to 1390.43 cm−1 in the yeast. The band shift from 1234.2 to 1390.43 cm−1 was assigned to δCCH + δOCH group involvement. The strong C–O band is due to alcohol primary –CH2OH shifting 1072 from 1076 cm−1. The band shift from 879.36 to 887.10 cm−1 was assigned to N–H group involvement.
C stretches of aromatic rings, while the peaks at 900–1125 cm−1 are assigned to the C–O stretching of alcohols and carboxylic acids. The peaks observed at 1250–1500 cm−1 are assigned to C–H groups. The results indicate that the functional groups mentioned above are mainly involved in the biosorption of the studied metal ions. In addition, the frequency change observed in the functional groups of the biomass after metal ion biosorption show a high contribution of biomass functional groups on biosorption process efficiency. The asymmetric stretching vibration of N–H was shifted from 1540.85 to 1535.06 cm−1. The stretching vibration of δCH2 + δOCH + δCCH group was shifted from 1400 to 1390.43 cm−1 in the yeast. The band shift from 1234.2 to 1390.43 cm−1 was assigned to δCCH + δOCH group involvement. The strong C–O band is due to alcohol primary –CH2OH shifting 1072 from 1076 cm−1. The band shift from 879.36 to 887.10 cm−1 was assigned to N–H group involvement.
The FTIR spectra corresponding to the biosorption of metal ions onto the biomass revealed the involvement of hydroxyl, carboxyl, carbonyl and amino groups which supply suitable sites for complexation,40,71,72 assuming that coordination bonds are formed between metal ions and the functional groups (amino and carboxyl groups) of cell walls which account for the biosorption of Zn2+, Ni2+ and Co2+ ions onto Yarrowia lipolytica ISF7.41 The shifts of the peaks to new values of 1390.43, 1535.06, 1054.87 and 887.10 cm−1 after metal ion biosorption (Fig. 4) confirm the interaction between the corresponding functional groups and metal ions.
The SEM images of the incubated Yarrowia lipolytica ISF7 cells (Fig. 5a) at a magnification of 5000× show the presence of characteristic budding oval yeast cells.
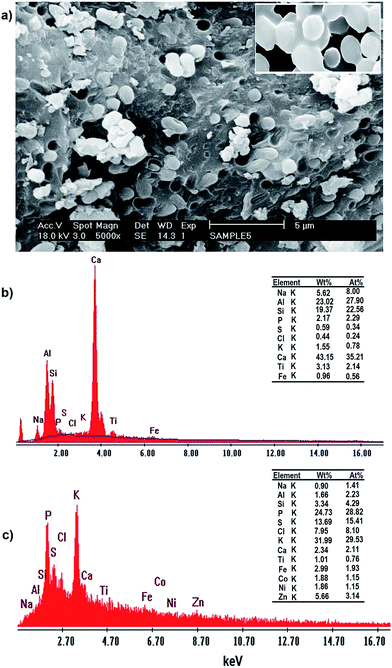 | ||
| Fig. 5 (a) SEM micrographs and EDAX spectra of Yarrowia lipolytica ISF7: (b) in the absence of metal ions and (c) after metal ion biosorption (C0 = 20 mg L−1). | ||
The EDAX analysis conclusively identified them as: Ca, Al, Si, Na, P, S, Cl, K, Ti and Fe with no signal corresponding to Zn2+, Ni2+ and Co2+ (see Fig. 5a). The yeast contains both inorganic and organic matter, mainly in the forms of iron, alumina, silica and carbonates. The EDAX spectrum of these nodules shows the presence of Zn2+, Ni2+ and Co2+ signals and other elemental signals (Fig. 5b) consistent with the uptake isotherm. The analysis results confirm the biosorption of Zn2+, Ni2+ and Co2+ by Yarrowia lipolytica ISF7, and that the ions are mainly located superficially in the biosorbent structure.
3.8. Comparison with other biosorbents
The maximum sorption capacities (Qmax) of Zn2+, Ni2+ and Co2+ ions on various biosorbents in the literature are listed in Table 7. The sorption capacity increased when the initial concentration of the metals increased. It is seen that the sorption capacity of the yeast is higher than that of other biosorbents. Hence, it can be concluded that yeast could be employed as effective low-cost adsorbent for biosorption of Zn2+, Ni2+ and Co2+ ions from aqueous solution.| Adsorbent | Sorption capacity (mg g−1) | pH | Ref. | ||
|---|---|---|---|---|---|
| Zn2+ | Ni2+ | Co2+ | |||
| Aspergillus niger | — | 6.80 | — | 6.0 | 26 |
| Saccharum bengalense | — | 15.79 | — | 5.0 | 28 |
| M. hiemalis | — | 15.83 | — | 8.0 | 73 |
| Aspergillus niger | — | 4.82 | — | 6.3 | 11 |
| Saccharum bengalense | — | — | 1.7 | 6.5 | 29 |
| Brown algae | 1.42 | 1.13 | — | 6.0 | 30 |
| Baker’s yeast | — | 11.40 | — | 6.8 | 10 |
| Cross-linked metal-imprinted chitosans with epichlorohydrin | 14.74 | 29.23 | — | 5.0 | 31 |
| Aspergillus niger | 22.62 | — | 19.881 | 5.0 | 27 |
| Chrysanthemum indicum | — | — | 14.84 | 5.0 | 16 |
| Brown algae C. indica | — | — | 54.640 | 5.0 | 19 |
| Jania rubens | 32.600 | 5.0 | 17 | ||
| Sophora japonica pod powder | 25.71 | 30.3 | — | 6.0–7.0 | 32 |
| Coconut shell | 1.56 | 3.68 | — | 6.0 | 74 |
| Sargassum glaucescens nanoparticles | — | 28.73 | 10.11 | 6.0 | 33 |
| Aspergillus awamori | — | 7.13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
— | 5.0 | 75 |
| Mucor hiemalis | — | 13.60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
— | 8.0 | 76 |
| Hizikia fusiformis | 10.56 | 13.90 | — | 4.0–6.0 | 34 |
| Myriophyllum spicatum L. | 3.00 | 6.80 | — | 5.0 | 77 |
| Activated sludge | 7.78 | 15.69 | — | 5.0–6.0 | 78 |
| Lime stone | 0.038 | 0.012 | — | 4.0–6.0 | 9 |
| Lignin | 5.99 | 11.25 | — | 4.8 | 79 |
| Geobacillus toebii sub sp. decanicus | 29.0 | 42.0 | — | 4.0–5.0 | 21 |
| Geobacillus thermoleovorans sub sp. stromboliensis | 21.1 | 21 | — | 4.0–5.0 | 21 |
| Rhizopus oryzae (bread mold) | — | — | 13.56 | 7.0 | 18 |
| Saccharomyces cerevisiae | 16.94 | — | 21.52 | 4.0–6.0 | 35 |
| Yarrowia lipolytica ISF7 | 31.96 | 24.40 | 25.77 | 6.0 | This work |
4. Conclusion
The use of an experimental design allowed the rapid screening of a large experimental domain for optimization of the Zn2+, Ni2+ and Co2+ removal efficiency of Yarrowia lipolytica ISF7. Using a central composite design, quadratic and interaction terms were revealed and the location of the optimum set of experimental conditions was determined. The P and F-values and model adequacy were tested through lack-of-fit (LOF) and verified successfully by the validation of experimental data. The multiple correlation coefficient of determination (R2) was found to be 0.9919 for Zn2+, 0.9942 for Ni2+ and 0.9941 for Co2+ which suggests that the actual data fitted well with the predicted data. The equilibrium biosorption data are correlated with Langmuir, Freundlich, Temkin and D–R isotherm equations. The statistical parameters indicate that the Langmuir equation is the best fit. The maximum monolayer biosorption capacities for Zn2+, Ni2+ and Co2+ are found to be 31.96, 24.40 and 25.77 mg g−1 respectively. The kinetic study indicates that the rate of biosorption conforms to the Lagergren rate equation. FTIR studies revealed the possible involvement of hydroxyl and carboxyl groups in Zn2+, Ni2+ and Co2+ biosorption. FTIR and SEM-EDAX analyses also suggested a possible coordination between heavy metals and the functional groups on the yeast surfaces.Acknowledgements
The authors thank the Research Council of the Yasouj University and Iran National Science Foundation for financially supporting this work.References
- A. H. Sulaymon, S. E. Ebrahim and M. J. Mohammed-Ridha, Environ. Sci. Pollut. Res. Int., 2013, 20, 175–187 CrossRef CAS PubMed.
- M. M. Areco, S. Hanela, J. Duran and S. Afonso Mdos, J. Hazard. Mater., 2012, 213–214, 123–132 CrossRef CAS PubMed.
- S. Hajati, M. Ghaedi and S. Yaghoubi, J. Ind. Eng. Chem., 2015, 21, 760–767 CrossRef CAS.
- J. Sun, Z. Liu, Y. Wang, S. Xiao, M. Pei, X. Zhao and G. Zhang, RSC Adv., 2015, 5, 100873–100878 RSC.
- Y. Shuhong, Z. Meiping, Y. Hong, W. Han, X. Shan, L. Yan and W. Jihui, Carbohydr. Polym., 2014, 101, 50–56 CrossRef PubMed.
- T. Liu, Y. Dong, X. Wan, W. Li and Y. Yao, RSC Adv., 2015, 5, 76939–76942 RSC.
- R. Shen, D. Liu, C. Hou, J. Cheng and D. Bai, Anal. Methods, 2016, 8, 83–88 RSC.
- S. B. Khan, M. M. Rahman, H. M. Marwani, A. M. Asiri and K. A. Alamry, J. Taiwan Inst. Chem. Eng., 2014, 45, 2770–2776 CrossRef CAS.
- H. A. Aziz, M. N. Adlan and K. S. Ariffin, Bioresour. Technol., 2008, 99, 1578–1583 CrossRef CAS PubMed.
- V. Padmavathy, P. Vasudevan and S. C. Dhingra, Process Biochem., 2003, 38, 1389–1395 CrossRef CAS.
- D. H. K. Reddy, K. Seshaiah, A. V. R. Reddy and S. M. Lee, Carbohydr. Polym., 2012, 88, 1077–1086 CrossRef CAS.
- X. C. Song, Y. F. Zheng, H. Y. Yin, J. N. Liu and X. D. Ruan, New J. Chem., 2016, 40, 130–135 RSC.
- T. Itakura, S. Horike, M. Inukai and S. Kitagawa, Dalton Trans., 2016 10.1039/c5dt03286e.
- R. Alam, T. Mistri, R. Bhowmick, A. Katarkar, K. Chaudhuri and M. Ali, RSC Adv., 2016, 6, 1268–1278 RSC.
- S. B. Khan, A. M. Asiri, M. M. Rahman, H. M. Marwani and K. A. Alamry, Phys. E, 2015, 70, 203–209 CrossRef CAS.
- S. Vilvanathan and S. Shanthakumar, Process Saf. Environ. Prot., 2015, 96, 98–110 CrossRef CAS.
- W. M. Ibrahim, J. Hazard. Mater., 2011, 192, 1827–1835 CrossRef CAS PubMed.
- M. Gharieb, A. Al-Fakih and M. Ali, Arabian J. Sci. Eng., 2014, 39, 2435–2446 CrossRef CAS.
- M. Akbari, A. Hallajisani, A. R. Keshtkar, H. Shahbeig and S. Ali Ghorbanian, J. Environ. Chem. Eng., 2015, 3, 140–149 CrossRef CAS.
- N. R. Shinde, A. V. Bankar, A. R. Kumar and S. S. Zinjarde, J. Environ. Manage., 2012, 102, 115–124 CrossRef CAS PubMed.
- S. Özdemir, E. Kilinc, A. Poli, B. Nicolaus and K. Güven, Chem. Eng. J., 2009, 152, 195–206 CrossRef.
- S. B. Khan, K. A. Alamry, H. M. Marwani, A. M. Asiri and M. M. Rahman, Composites, Part B, 2013, 50, 253–258 CrossRef CAS.
- S. Y. Kim, M. R. Jin, C. H. Chung, Y. S. Yun, K. Y. Jahng and K. Y. Yu, J. Biosci. Bioeng., 2015, 119, 433–439 CrossRef CAS PubMed.
- M. Ghaedi, S. Hajati, B. Barazesh, F. Karimi and G. Ghezelbash, J. Ind. Eng. Chem., 2013, 19, 227–233 CrossRef CAS.
- M. M. Rahman, S. B. Khan, H. M. Marwani and A. M. Asiri, Superlattices Microstruct., 2014, 71, 93–104 CrossRef CAS.
- M. Amini, H. Younesi and N. Bahramifar, Chemosphere, 2009, 75, 1483–1491 CrossRef CAS PubMed.
- Z. Hajahmadi, H. Younesi, N. Bahramifar, H. Khakpour and K. Pirzadeh, Water Resourc. Ind., 2015, 11, 71–80 CrossRef.
- M. I. Din and M. L. Mirza, Int. J. Biol. Macromol., 2013, 54, 99–108 CrossRef CAS PubMed.
- M. Imran Din, M. L. Mirza, S. Ata, M. Athar and I. U. Mohsin, J. Chem., 2012, 2013, 1–11 Search PubMed.
- Y. Liu, Q. Cao, F. Luo and J. Chen, J. Hazard. Mater., 2009, 163, 931–938 CrossRef CAS PubMed.
- C. Y. Chen, C. Y. Yang and A. H. Chen, J. Environ. Manag., 2011, 92, 796–802 CrossRef CAS PubMed.
- M. Amer, R. Ahmad and A. Awwad, Int. J. Ind. Chem., 2015, 6, 67–75 CrossRef CAS.
- A. Esmaeili and A. Aghababai Beni, Int. J. Environ. Sci. Technol., 2015, 12, 2055–2064 CrossRef CAS.
- W.-S. Shin and Y.-K. Kim, Environ. Earth Sci., 2014, 71, 4107–4114 CrossRef CAS.
- S. Farhan and A. Khadom, Int. J. Ind. Chem., 2015, 6, 119–130 CrossRef CAS.
- S. Zinjarde, M. Apte, P. Mohite and A. R. Kumar, Biotechnol. Adv., 2014, 32, 920–933 CrossRef CAS PubMed.
- M. Jain, S. Zinjarde, D. Deobagkar and D. Deobagkar, Mar. Pollut. Bull., 2004, 49, 783–788 CrossRef CAS PubMed.
- R. Lanciotti, A. Gianotti, D. Baldi, R. Angrisani, G. Suzzi, D. Mastrocola and M. Guerzoni, Bioresour. Technol., 2005, 96, 317–322 CrossRef CAS PubMed.
- S. Papanikolaou, I. Chevalot, M. Komaitis, I. Marc and G. Aggelis, Appl. Microbiol. Biotechnol., 2002, 58, 308–312 CrossRef CAS PubMed.
- N. R. Shinde, A. V. Bankar, A. R. Kumar and S. S. Zinjarde, J. Environ. Manag., 2012, 102, 115–124 CrossRef CAS PubMed.
- A. V. Bankar, A. R. Kumar and S. S. Zinjarde, J. Hazard. Mater., 2009, 170, 487–494 CrossRef CAS PubMed.
- S. García, M. Prado, R. Dégano and A. Domínguez, J. Biological Chem., 2002, 277, 37359–37368 CrossRef PubMed.
- P. S. Pimprikar, S. S. Joshi, A. R. Kumar, S. S. Zinjarde and S. K. Kulkarni, Colloids Surf., B, 2009, 74, 309–316 CrossRef CAS PubMed.
- C.-Y. Tai, S.-J. Jiang and A. Sahayam, Food Chem., 2016, 192, 274–279 CrossRef CAS PubMed.
- É. F. Batista, A. dos Santos Augusto and E. R. Pereira-Filho, Talanta, 2016, 150, 206–212 CrossRef PubMed.
- B. Feist and B. Mikula, Food Chem., 2014, 147, 302–306 CrossRef CAS PubMed.
- M. M. Rahman, S. B. Khan, H. M. Marwani and A. M. Asiri, PLoS, 2014, 9, 4084 Search PubMed.
- V. C. D. Peronico and J. L. Raposo, Food Chem., 2016, 196, 1287–1292 CrossRef CAS PubMed.
- X. Wen, S. Yang, H. Zhang and Q. Deng, Microchem. J., 2016, 124, 60–64 CrossRef CAS.
- G. Luis, C. Rubio, C. Revert, A. Espinosa, D. González-Weller, A. Gutiérrez and A. Hardisson, J. Food Compos. Anal., 2015, 39, 48–54 CrossRef CAS.
- X. Zhu, Y. Cui, X. Chang and H. Wang, Talanta, 2016, 146, 358–363 CrossRef CAS PubMed.
- A. Asfaram, M. Ghaedi, A. Goudarzi and M. Rajabi, Dalton Trans., 2015, 44, 14707–14723 RSC.
- J. Zolgharnein and A. Shahmoradi, J. Chem. Eng. Data, 2010, 55, 3428–3437 CrossRef CAS.
- A. Asfaram, M. Ghaedi, S. Hajati and A. Goudarzi, RSC Adv., 2015, 5, 72300–72320 RSC.
- E. A. Dil, M. Ghaedi, A. M. Ghaedi, A. Asfaram, A. Goudarzi, S. Hajati, M. Soylak, S. Agarwal and V. K. Gupta, J. Ind. Eng. Chem., 2016, 34, 186–197 CrossRef CAS.
- A. Asfaram, M. Ghaedi, S. Hajati, A. Goudarzi and A. A. Bazrafshan, Spectrochim. Acta, Part A, 2015, 145, 203–212 CrossRef CAS PubMed.
- G. Yan and T. Viraraghavan, Water Res., 2003, 37, 4486–4496 CrossRef CAS PubMed.
- C. Gao, H. Zhu, M. Zhang, T. Tan, J. Chen and H. Qiu, Anal. Methods, 2015, 7, 8172–8176 RSC.
- D. Bansal and R. Gupta, Dalton Trans., 2016, 45, 502–507 RSC.
- A. M. Hessels, K. M. Taylor and M. Merkx, Metallomics, 2016, 8, 211–217 RSC.
- F. N. Azad, M. Ghaedi, K. Dashtian, S. Hajati and V. Pezeshkpour, Ultrason. Sonochem., 2016, 31, 383–393 CrossRef CAS PubMed.
- A. Asfaram, M. Ghaedi, S. Agarwal, I. Tyagi and V. Kumar Gupta, RSC Adv., 2015, 5, 18438–18450 RSC.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38, 2221–2295 CrossRef CAS.
- H. Freundlich, Z. Phys. Chem., 1906, 57, 385–471 CAS.
- M. Temkin and V. Pyzhev, Acta Physicochim. URSS, 1940, 12, 217–222 Search PubMed.
- A. Elmaci, T. Yonar and N. Ozengin, Water Environ. Res., 2007, 79, 1000–1005 CrossRef CAS PubMed.
- S. Lagergren, K. Sven. Vetenskapsakad. Handl., 1898, 24, 1–39 Search PubMed.
- Y.-S. Ho and G. McKay, Process Biochem., 1999, 34, 451–465 CrossRef CAS.
- W. J. Weber and J. C. Morris, J. Sanit. Eng. Div., Am. Soc. Civ. Eng., 1963, 89, 53–61 Search PubMed.
- C.-Y. Chen, C.-Y. Yang and A.-H. Chen, J. Environ. Manage., 2011, 92, 796–802 CrossRef CAS PubMed.
- N. Ahalya, T. Ramachandra and R. Kanamadi, Res. J. Chem. Environ., 2003, 7, 71–79 CAS.
- M. Riaz, R. Nadeem, M. A. Hanif, T. M. Ansari and K. U. Rehman, J. Hazard. Mater., 2009, 161, 88–94 CrossRef CAS PubMed.
- J. P. K. Wong, Y. S. Wong and N. F. Y. Tam, Bioresour. Technol., 2000, 73, 133–137 CrossRef CAS.
- F. Sousa, A. Oliveira, S. Moreira, R. Cavalcante, M. Rosa and R. Nascimento, Quim. Nova, 2008, 30, 1153–1157 CrossRef.
- F. Shahverdi, M. Ahmadi, S. Avazmoghadam and M. A. Faramarzi, Environ. Prog. Sustainable Energy, 2015, 34, 1356–1364 CrossRef CAS.
- K. A. Shroff and V. K. Vaidya, Eng. Life Sci., 2011, 11, 588–597 CrossRef CAS.
- E. Lesage, C. Mundia, D. Rousseau, A. Van de Moortel, G. Du Laing, E. Meers, F. Tack, N. De Pauw and M. Verloo, Ecol. Chem. Eng. A, 2007, 30, 320–325 CrossRef.
- A. Hammaini, F. González, A. Ballester, M. Blázquez and J. Munoz, J. Environ. Manage., 2007, 84, 419–426 CrossRef CAS PubMed.
- X. Guo, S. Zhang and X.-Q. Shan, J. Hazard. Mater., 2008, 151, 134–142 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |