Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The treatment of uncertainties in reactive pollution dispersion models at urban scales
A. S.
Tomlin
*a,
T.
Ziehn†
a,
P.
Goodman‡
b,
J. E.
Tate
b and
N. S.
Dixon
c
aEnergy Research Institute, School of Chemical and Process Engineering, University of Leeds, Leeds, UK. E-mail: A.S.Tomlin@leeds.ac.uk
bInstitute for Transport Studies, University of Leeds, Leeds, UK
cSchool of Earth and Environment, University of Leeds, Leeds, UK
First published on 30th November 2015
Abstract
The ability to predict NO2 concentrations ([NO2]) within urban street networks is important for the evaluation of strategies to reduce exposure to NO2. However, models aiming to make such predictions involve the coupling of several complex processes: traffic emissions under different levels of congestion; dispersion via turbulent mixing; chemical processes of relevance at the street-scale. Parameterisations of these processes are challenging to quantify with precision. Predictions are therefore subject to uncertainties which should be taken into account when using models within decision making. This paper presents an analysis of mean [NO2] predictions from such a complex modelling system applied to a street canyon within the city of York, UK including the treatment of model uncertainties and their causes. The model system consists of a micro-scale traffic simulation and emissions model, and a Reynolds averaged turbulent flow model coupled to a reactive Lagrangian particle dispersion model. The analysis focuses on the sensitivity of predicted in-street increments of [NO2] at different locations in the street to uncertainties in the model inputs. These include physical characteristics such as background wind direction, temperature and background ozone concentrations; traffic parameters such as overall demand and primary NO2 fraction; as well as model parameterisations such as roughness lengths, turbulent time- and length-scales and chemical reaction rate coefficients. Predicted [NO2] is shown to be relatively robust with respect to model parameterisations, although there are significant sensitivities to the activation energy for the reaction NO + O3 as well as the canyon wall roughness length. Under off-peak traffic conditions, demand is the key traffic parameter. Under peak conditions where the network saturates, road-side [NO2] is relatively insensitive to changes in demand and more sensitive to the primary NO2 fraction. The most important physical parameter was found to be the background wind direction. The study highlights the key parameters required for reliable [NO2] estimations suggesting that accurate reference measurements for wind direction should be a critical part of air quality assessments for in-street locations. It also highlights the importance of street scale chemical processes in forming road-side [NO2], particularly for regions of high NOx emissions such as close to traffic queues.
A Introduction
Although European directives to reduce NOx emissions from vehicles have been in operation for well over a decade, many urban areas across Europe are still failing to meet the NO2 air quality standards set by the EU Directive 2008/50/EC. Within the UK there are a large number of Air Quality Management Areas (AQMAs) which have been declared on the basis of NO2, a large proportion of which are in highly trafficked urban areas. Strategies must therefore be put in place to address potential reductions in NO2 concentrations, particularly focussed on traffic sources. To aid in this AQM process, models can be developed which aim to predict road-side NO2 as a function of important traffic characteristics and can therefore be used to assess the potential impact of traffic management or emissions based intervention measures. Such models should also include relevant features of the urban environment that affect pollution formation and dispersion such as wind speed and direction, rapid chemical transformations and street topologies. The latter feature should be included since it is well understood that urban buildings interact with background winds to modify the turbulent flow structures within the streets, restricting the dispersion of traffic related pollutants out of the street network,1–5 and potentially allowing time for in-street chemical processing of emissions. Models aiming to achieve road-side predictions therefore should contain representation of this potentially circulating flow occurring within the street canyons, as well as vertical and horizontal fluxes into and out of the street network.3 Representations of chemical transformations are also required, in particular those relevant to the formation of secondary NO2. A number of modelling approaches have been suggested to address the dispersion part of the problem including Gaussian based models such as OSPM (Operational Street Pollution Model),6 network models such as SIRANE,7 and compartment based models where pollutant exchange rates are parameterised according to canyon aspect ratios,8 as well as high resolution computational fluid dynamics (CFD) approaches.9,10 Several studies have attempted to couple models of the complex turbulent flow with chemical sub-models, albeit for single or small networks of streets.11–15 These studies have highlighted the influence of incomplete mixing on the formation of secondary pollutants in regions of high primary NOx emissions. This suggests that coarse resolution models (e.g. urban air shed models) are unlikely to be of direct relevance for the study of road-side concentrations and exposure, although they may provide boundary conditions for higher resolution studies at the street scale. However, detailed representations of the interplay between emissions, chemical transformations and dispersion within the street network will be critical for near field exposure. Few models, however, have attempted to couple this modelling of dispersion at the micro-scale with both chemical transformation processes and high resolution traffic emissions models. The current work aims to present such an integrated system which couples a micro-scale traffic emissions model with a turbulent reactive dispersion model based on a combined CFD and reactive Lagrangian particle dispersion approach.16,17The use of such models within the AQM framework requires an understanding of the confidence that can be placed in their predictions. Lack of confidence, or uncertainty, can result from a lack of detailed knowledge of the model parameterisations. It follows that model evaluation will benefit from the inclusion of sensitivity studies that highlight the impact of uncertain input parameters on predicted output concentrations. As part of an uncertainty/sensitivity study we might ask questions such as: (i) how robust are predicted road-side NO2 concentrations, i.e. how wide are the predicted distributions if we properly account for uncertainties within the model input parameters, and (ii) taking into account uncertainties in the model parameters, can we trace the effects of potential traffic management strategies such as reductions in demand, reductions in emissions, and changes in emissions profiles, or are these effects swamped by uncertainties due to the model itself?
Within CFD based approaches, the use of Reynolds Averaged Navier Stokes (RANS) models in particular has raised questions as to their suitability for accurately describing turbulent chemical interactions when they contain only averaged representations of turbulent length and time-scales. On the plus side, such models allow the representation of reactive dispersion within complex street topologies at lower computational cost than, for example, Large Eddy Simulations (LES). On the negative side, they require parameterisation of mixing lengths rather than resolving eddies in an explicit way. They do however, provide much more realistic descriptions of in-street processing of pollutants than urban air shed type models which are too coarse to capture complex street geometries and the effects of buildings on in-street flow profiles. Given the potential utility of such RANS models, it is worth considering how robust their simulations are to the parameterisations chosen. We attempt to address some of these questions here and present an approach for the assessment of sensitivities for a complex multi-component model aiming to predict time-averaged road-side concentrations of NO2 as a function of street topologies, background meteorology, traffic characteristics and temperature dependent parameterisations of chemical reactions.
B Methodology
(i) Case study and dispersion model structure
The location modelled in this study is that of Gillygate, York, UK, the site of an extensive measurement campaign2,18 that has provided observations used in previous evaluations of some of the model components used here.10 Gillygate is a relatively narrow street with an aspect ratio (building height to street width) of approximately 0.8, leading to cross-street recirculating flow under a range of background wind directions, restricting the dispersion of pollutants out of the street. The traffic flow along Gillygate is quite high with significant periods of congestion, and it therefore represents a potential pollution hot spot. It was included within the stated AQMAs by the City of York Council in 2014.19 19 exceedances of the hourly limit value for NO2 of 200 μg m−3 were noted in 2011, and annual average [NO2] values varied between 30 and 50 μg m−3 from (2010–2015) based on data from the air quality monitoring site which is situated away from the congested junction at the Northern end of the street. Diffusion tube data from various points within Gillygate19 showed significant variation in concentrations along the street, with annual average values exceeding 50 μg m−3 in some locations. It therefore provides a useful polluted road-side case study on which to demonstrate the approach adopted for model uncertainty analysis in this work.Fig. 1 (top) shows the grid and the building configuration of Gillygate and the surrounding area that were used for the simulations in this study. The building heights in metres are indicated in the legend. Fig. 1 (bottom) provides an aerial view of the main part of the modelling domain. The basis for the underlying flow and turbulence model under consideration is the k–ε RANS model MISKAM.20 This model was chosen on the basis that it is commonly used as an operational model9 and has undergone previous evaluation for street canyon case studies.10 It has been shown to substantially improve the representation of dispersion in built up areas due to improved representation of turbulent flow patterns compared to more general dispersion models such as those used in compliance assessment.21 In this study, a non-equidistant grid was used to enable a higher resolution within the area of interest.
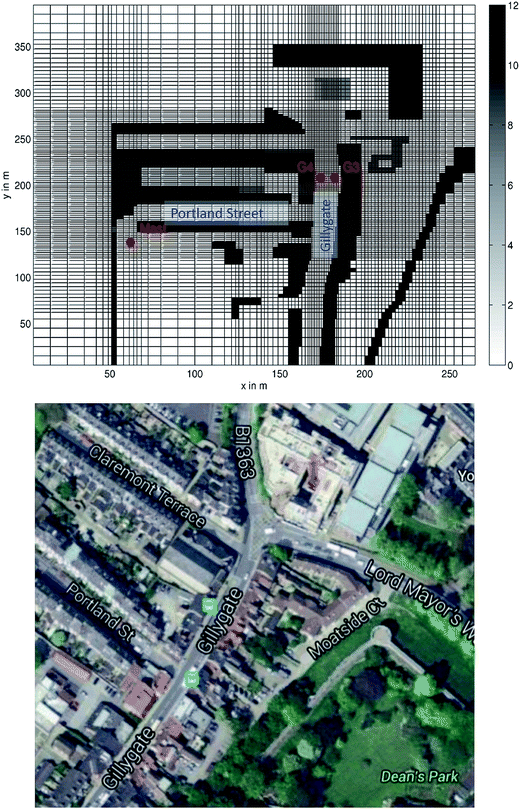 | ||
| Fig. 1 Top: Site schematic for the York Gillygate site showing the grid and building configuration as used in MISKAM. Bottom: Aerial view of the site. ©2015 Infoterra Ltd. & Bluesky, ©2015 Google. | ||
Fig. 1 shows the two locations G3 and G4 that were used in the original measurement campaign as well as the mast location that was used to obtain reference wind speed and direction. The experimental measurements were of concentrations of the non-reactive tracer carbon monoxide. Unfortunately no measurements of [NO2] are available from the campaign but previous evaluations with respect to [CO] highlighted the ability of the model to capture the main flow and dispersion characteristics within the street.10 The uncertainty analysis here allows additional investigation into the robustness of the model with respect to the chemical parameterisations. We use the same locations here as in the previous study for investigating [NO2] predictions, as well as three other sites on each side of the street at 20 m intervals to the South of G3 and G4. A wind direction of 0° represents channelled flow from North to South along the street canyon. The wind directions sampled in the case study (110–130°) represent oblique flow over the building adjacent to G3 towards the North of the domain and lead to a helical in-street recirculating flow with a northerly channelled component.2 We focus on a single wind sector here due to the computational cost of the random sampling approach required for the global sensitivity calculations. In reality of course, many different wind directions would be used within an air quality assessment. Since model validation is usually performed using concentrations normalised by a reference wind speed, the inflow wind speed is kept to a constant value of 5 m s−1 at a height of 50 m, with the vertical profile then determined using a log-law which is based on the sampled values of the roughness length for the incoming flow.
The output from MISKAM is used as the underlying turbulent flow structure for a dispersion model based on the Lagrangian stochastic particle dispersion approach with micro-mixing and chemical sub-models (for a full description and evaluation see ref. 16 and 17). The complex dispersion modelling system was used previously to investigate a reactive plume of nitrogen oxides (NOx) released into an approximately homogeneous turbulent grid flow doped with ozone (O3) for comparison against wind tunnel experiments.17 The chemical and micro-mixing sub-models used here are the same as those specified in the photolysis extended case described in Ziehn et al.17 The chemical reactions included are detailed in Table 1. In summary, only simple reactions between NO, NO2 and O3 are included in the chemical model but these include the photolysis of NO2 and O3. Quite broad ranges have been included for photolysis rates reflecting variation in daytime conditions. No organic reactions are included in the analysis. Rather, any reactions occurring at longer time-scales are represented implicitly within the description of above-roof O3 concentration which is considered as an uncertain parameter. A high sensitivity with respect to this parameter would indicate the importance of long range chemical processes for the net formation of NO2. For the current study the coupled dispersion model is further linked to a traffic micro-simulation model and a zero background concentration of [NO2] is assumed so that the modelled concentrations represent road-side increments above background.
| Parameter | Nominal value | Minimum | Maximum | Unit | Source |
|---|---|---|---|---|---|
| A factor, R1 O + O2 + N2 = O3 + N2 | 5.60 × 10−34 | 4.991 × 10−34 | 6.283 × 10−34 | cm6 per molecule2 per s | 33 |
| A factor, R2 O + O2 + O2 = O3 + O2 | 6.00 × 10−34 | 5.348 × 10−34 | 6.732 × 10−34 | cm6 per molecule2 per s | 33 |
| A factor, R3 O + O3 = 2O2 | 8.00 × 10−12 | 6.654 × 10−12 | 9.618 × 10−12 | cm3 per molecule per s | 33 |
| A factor (k0), R4 O + NO + M = NO2 + M | 1.00 × 10−31 | 0.794 × 10−31 | 1.259 × 10−31 | cm6 per molecule2 per s | 33 |
| A factor R4 (k1) | 3.00 × 10−11 | 1.504 × 10−11 | 5.986 × 10−11 | cm3 per molecule per s | 33 |
| A factor, R5 O + NO2 = NO + O2 | 5.50 × 10−12 | 4.790 × 10−12 | 6.315 × 10−12 | cm3 per molecule per s | 33 |
| A factor, R6 NO + O3 = NO2 + O2 | 1.40 × 10−12 | 1.165 × 10−12 | 1.683 × 10−12 | cm3 per molecule per s | 33 |
| Photolysis rate J O3, R7 O3 = O + O2 | 2.75 × 10−5 | 1.0 × 10−5 | 4.5 × 10−5 | s−1 | 34 |
| Photolysis rate J NO2, R8 NO2 = NO + O | 0.0075 | 0.004 | 0.011 | s−1 | 35 |
| n for reaction R1 | 2.6 | 2.1 | 3.1 | — | 33 |
| n for reaction R2 | 2.6 | 2.1 | 3.1 | — | 33 |
| E/R for reaction R3 | 2060 | 1860 | 2260 | K−1 | 33 |
| n 0 for reaction R4 | 1.6 | 1.3 | 1.9 | — | 33 |
| n ∞ for reaction R4 | −0.3 | −0.6 | 0 | — | 33 |
| E/R for reaction R5 | −188 | −268 | −108 | K−1 | 33 |
| E/R for reaction R6 | 1310 | 1110 | 1510 | K−1 | 33 |
(ii) Traffic micro-simulation modelling
Vehicle flows within the study area were modelled using an established, commercial traffic micro-simulation package AIMSUN 5.1.10 (ref. 22) which represents the movement of individual vehicles through a road network using discrete time intervals of the order of one second. Individual components within the micro-simulation govern the interaction of vehicles with one another, the interaction of vehicles with traffic signals, how vehicles make lane-changing manoeuvres and how vehicles accept gaps in traffic streams. Within each time-step individual components are called, using information from the previous time step, to assign new kinematic information (acceleration, speed and position) to every vehicle. Vehicle and driver parameters which are considered static within a given run (e.g. maximum vehicle acceleration rates) are generated on vehicle entry to the network, and sampled from appropriate distributions. Given the fine spatial and temporal resolution of traffic micro-simulation, output statistics may be aggregated over a wide variety of scales, for use within appropriate environmental models. A substantial body of literature already exists on methodologies detailing such approaches, e.g.ref. 23 and 24.(iii) Traffic emissions modelling
Using the AIMSUN model, total NOx emissions were calculated using the polynomial emissions functions proposed by Int Panis et al.25 based on vehicle type, instantaneous speed, and acceleration parameters. Instantaneous emissions rates (g s−1) were calculated for each vehicle at each model time-step (∼1 s) using polynomial functions. These were converted to mass values, based on initial vehicle velocity, and the assumption of linear acceleration over the time-step. Given the position of the vehicle at the start and end of a time-step, contributions were then apportioned to the individual sections, through which the vehicle had passed. The final output from the bespoke software was the emission rates (g h−1) for each 10 m road section, based on the integrated total of all contributions from vehicles passing through the sections in that period. These were then converted to g m−1 s−1 for input into the dispersion model.The specific fraction of NO2 within the total NOx was treated as an uncertain parameter as discussed later. Calculated emissions were then linked by vehicle position to a particular 10 m section of road giving spatial-profiles of emissions along Gillygate via bespoke software external to AIMSUN.26 The overall traffic network consisted of 4 km of roads surrounding Gillygate and 8 intersections, including 2 which were signalised. Four categories of vehicles were considered: cars, vans, HGVs and buses, for compatibility with Int Panis et al.25 The dynamic demand in the network (the number of vehicles desiring to travel through the network within the simulated hour) was varied over two sets of normalised ranges. The first is an “off-peak” case from 0.8–1.2 with the mean value of 1.0 representing ‘typical’ inter-peak demand. The second was a “peak” case with demand varying from 1.2–1.6. Each simulation run therefore represented 1 h at a particular level of demand using a random sampling approach within the specified ranges.
The normalised demand level was derived from a year of traffic flow data obtained from York's urban traffic control system equating to a two-way flow of ∼880 veh per h along Gillygate. Additional to the dynamic demand was a fixed level of demand from buses based on timetable information. At the base demand level, the network is considered as busy, but in an ‘under-saturated’ state, i.e. able to cope with the level of demand, with only transient queues forming at junctions. At demand levels above 1.1, modelled speeds begin to decline rapidly from ∼20 km h−1 to ∼10 km h−1 at a demand of 1.4. At these higher demand levels, substantial over-saturated queues form as vehicles are unable to clear signalised junctions within a single signal period. For off-peak, under capacity periods, total emissions increase in a slightly non-linear fashion with the volume of traffic as shown for a typical section of Gillygate in Fig. 2a. Some of the non-linearity may be explained by the increasing relative fraction of HGVs present, whose contribution to NOx emissions starts to dominate those of passenger cars. This phase is followed by a transitional period as demand approaches and exceeds network capacity, where emissions stabilise at a high overall level as shown in Fig. 2b. The influence of these characteristics on modelled road-side mean NO2 levels is discussed in the next section.
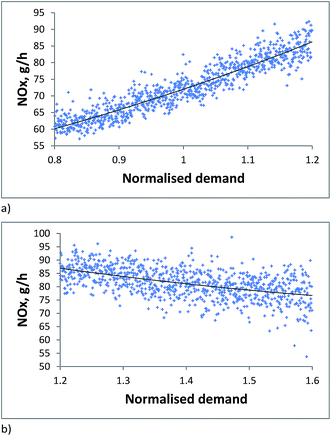 | ||
| Fig. 2 Total exhaust emissions of NOx for a sample section of Gillygate for (a) off-peak and (b) peak demand scenarios. | ||
(iv) Model parameterisations and ranges of uncertainty
Close to a surface the effects of turbulence in a RANS model need to be modelled using boundary conditions that reflect the surface roughness. MISKAM represents these boundary conditions using an idealised log-law based on three surface roughness lengths zo for the incoming boundary flow, the urban surface and wall surfaces, respectively. It follows that parameterisations of these roughness lengths will be a possible source of uncertainty in the final output predictions since they determine the near surface velocity profiles and therefore influence both dispersion and deposition27 processes. A study by Benson et al.,28 based on the application of MISKAM to a street canyon scenario, showed that overall, the uncertainty in the predicted mean and turbulent flow fields due to roughness lengths was small in comparison to the mean outputs. The study concluded that the model was well defined even with large ranges of input parameter uncertainty. In general, at a particular receptor, the closest surface was found to be most influential on the model output except when a recirculating canyon flow pattern was strongly present. In this latter case background wind angle was found to dominate.The turbulent flow field is used as an input to the Lagrangian particle dispersion model where it is assumed that the velocity of a fluid element, for times larger than the Kolmogorov time-scale, is a Markov process that is a continuous function of time.29 Within the Lagrangian particle model framework, the two important parameterisations are the Lagrangian structure coefficient c0, and the mixing time-scale coefficient α. The Lagrangian structure function is defined as the ensemble average of the square of the change in Lagrangian velocity and the definition of c0 is therefore important in determining the effective turbulent diffusion in velocity space. There is some debate within the literature as to whether its value can be universally defined for all types of turbulent flows with a range of values between 2 and 10 quoted from different studies.30–32 It is interesting to establish therefore how sensitive concentration predictions are to the chosen value. Within the model tested, a simple particle mixing model is adopted, that of interaction by exchange with the mean (IEM) concentration.29 In order to provide generality, the mixing model uses a coefficient α which defines the relationship between the turbulent time-scales (total turbulent kinetic energy and its dissipation rate) and the mixing time-scale at every point in the flow as defined by the following equation:
The specification of α should also be considered to be uncertain and the relative time-scales of the chemical processes compared to the mixing time-scale could have an important influence on the formation of secondary species such as NO2.
Uncertainties in the traffic emissions model have been adopted for the level of traffic demand as discussed above, and the NO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NOx ratio for the emissions source which determines the fraction of NO vs. primary NO2 assumed at source. The range adopted was chosen to reflect levels of primary NO2 estimated for UK vehicle fleets,36 taking into account a range of possible fuel types as well as engine exhaust treatment methodologies (15–25% primary NO2). The 26 model parameters varied within the sensitivity/uncertainty analysis can therefore be summarised as:
NOx ratio for the emissions source which determines the fraction of NO vs. primary NO2 assumed at source. The range adopted was chosen to reflect levels of primary NO2 estimated for UK vehicle fleets,36 taking into account a range of possible fuel types as well as engine exhaust treatment methodologies (15–25% primary NO2). The 26 model parameters varied within the sensitivity/uncertainty analysis can therefore be summarised as:
• Velocity structure function coefficient c0 [4–6].
• Mixing time-scale coefficient α [0.6–3].
• Surface roughness length zo for inflow, surface and wall [5–50, 0.5–50, 0.5–10 cm].
• Temperature dependent Arrhenius rate parameters for NO/NO2/O3 reactions, photolysis rate parameters for J O3 and J NO2 [see Table 1 for details].
• Background wind direction θ [110–130°].
• Temperature [273–298 K].
• Background ozone concentration [7.35 × 1011 to 1.23 × 1012, molecules cm−3 or 30–50 ppb].
• NO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NOx ratio for traffic emissions [0.75–0.85].
NOx ratio for traffic emissions [0.75–0.85].
• Normalised traffic demand [off peak 0.8–1.2, peak 1.2–1.6]. Where the ranges used are shown in the square brackets except for the Arrhenius and photolysis parameters which were detailed in Table 1. Of these parameters, most relate to uncertainties in the model formulation. For a given urban morphology, it is mainly the last three, background O3 concentration, NO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NOx ratio and traffic demand, that could be affected by the implementation of pollution mitigation strategies. Therefore if the model were to be highly robust, we would like to see the overall sensitivities of the model dominated by these last three parameters. In a wider study it would of course be possible to assess the impact of changes to urban form including “urban greening8” which may impact on roughness lengths and therefore dispersion and deposition.
NOx ratio and traffic demand, that could be affected by the implementation of pollution mitigation strategies. Therefore if the model were to be highly robust, we would like to see the overall sensitivities of the model dominated by these last three parameters. In a wider study it would of course be possible to assess the impact of changes to urban form including “urban greening8” which may impact on roughness lengths and therefore dispersion and deposition.
(v) Global uncertainty and sensitivity analysis methods
Within a global uncertainty analysis the aim is to determine the possible range of predicted outputs (in this case time-averaged road-side NO2 concentration increments) given the ranges of uncertainty within the model input parameters. Often a Monte Carlo type approach is adopted where random or quasi-random samples of the inputs are used within the adopted ranges of uncertainty, and many model simulations are performed; one for each random sample. The result is a predicted distribution of outputs instead of a single value. The width of this distribution gives the modeller an idea of the robustness of the model given the model input uncertainties. Statistical parameters such as standard deviation can be used to provide simple quantified measures of the output uncertainty in cases where the distribution does not deviate too far from being Gaussian. Otherwise higher moments may also be useful. The aim of improving model robustness is to provide better and better quantification of the model inputs such that the predicted output distribution becomes as narrow as possible i.e. the predicted output uncertainty is low.In order to assist in the model improvement processes it is useful to determine which of the uncertain model inputs have the largest influence of predicted output uncertainties. This is achieved here through a global sensitivity analysis based on the ANalysis Of VAriance (ANOVA) approach.37 In such methods, the output variance is decomposed into component functions representing the effects of individual and groups of parameters whose importance can then be ranked according to global sensitivity indices.
The global sensitivity analysis has been achieved using the RS-HDMR (Random Sampling High Dimensional Model Representation) method introduced by Rabitz et al.38 to express the input–output relationship of complex models with large numbers of input parameters, and further developed into a user friendly Matlab package GUI-HDMR by Ziehn and Tomlin.39 The mapping between input parameters x1, …, xn and output variables f(x) = f(x1, …, xn) in the domain Rn is written in the form:
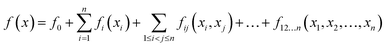 | (1) |
Due to its formulation as a set of hierarchical component functions, the HDMR expansion provides the possibility to determine sensitivity indices for each of the input parameters in an automatic way for selected model outputs. For given input parameter ranges, these indices indicate the relative contribution of each parameter to the predicted output variance. Thus they can be directly used to rank the importance of each individual parameter in determining the model output variance and to explore parameter interactions. The HDMR expansion is computationally very efficient if higher order input parameter interactions are weak and can therefore be neglected. For many systems a HDMR expression up to second-order already provides satisfactory results and a good approximation of f(x) (e.g.ref. 28).
In RS-HDMR, a number of model simulations are performed using a quasi-random set of input samples. This set of model simulations is then used to fit polynomial expressions for each component function in eqn (1). The sensitivity coefficients for individual parameters or for interaction terms can then be easily calculated from the coefficients of the polynomial expansion (see Ziehn and Tomlin39 for details). For the current studies, the 26 dimensional input space is sampled 512 times using a quasi-random approach from uniform distributions within the parameter ranges specified. The RS-HDMR meta-model fit is then generated where the output function f(x) represents the NO2 concentration at the 8 in-street locations discussed above. In practice, the larger the sample size, the better the fitted representation of the component functions and therefore the more accurate the sensitivity indices will be. In reality sample size is often limited by computational resources, particularly for complex high resolution models with substantial individual run times. When using a limited sample size such as used here, it is very important to assess the accuracy of the functional fit to eqn (1) and the GUI-HDMR code provides the facility to do this. Previous applications of the method in chemical kinetics problems40 has shown that large sample sizes (>1000) are usually only needed where significant second-order terms are present (i.e. important parameter interactions exist).
C Results and discussion
(i) Overall uncertainty of predicted [NO2] and accuracy of HDMR fits
The predicted [NO2] distributions for sites G3 and G4 are shown in Fig. 3 for the off-peak case study. The most frequently predicted [NO2] at G3 is around 1 × 1012 molecules cm−3 which equates to ∼76 μg m−3 and is twice that at G4 confirming the influence of the in-street recirculation on the concentration profiles across the canyon. Direct comparison with high time resolution measured data is not possible but data from the diffusion tube network operated by the City of York Council offers a qualitative comparison.19 In 2013, their measurement site in Gillygate opposite Portland street (close to G3, see Fig. 1) gave an annual average for [NO2] of 48.4 μg m−3 compared to only 21 μg m−3 at various sites along Portland street itself. It is clear therefore that due to the in-street dispersion processes large variations in NO2 concentration can be seen over quite short distances. The distributions show that, given the uncertainties adopted for the input parameters, the predicted [NO2] on both sides of the street can vary by up to a factor of 2. This suggests that more accurate parameterisations of the inputs are necessary to improve the robustness of the model predictions. | ||
| Fig. 3 Predicted [NO2] distributions for sites (a) G3 and (b) G4 based on a quasi-random sample of 512 runs and the uncertainty limits described in Section B. | ||
By decomposing the predictive variance into contributions from each of the uncertain inputs, the global sensitivity methodology allows us to target such model improvement strategies on the most important parameters. However, in order to exploit the HDMR component functions for sensitivity analysis purposes, it is first important to establish that the HDMR meta-model gives a reasonable fit to the outputs from the full model runs. This test is especially important for the current example since the combined model simulation time was of the order of an hour and therefore the sample size of 512 was limited by available computer resources. The coefficient of determination or R2 values comparing the fitted second-order HDMR meta-model with the data from the full model simulations vary between 0.905 and 0.951 illustrating that the second-order meta-model gives a good fit despite the limited sample size. This provides confidence in the accuracy of the HDMR component functions and the sensitivity results derived from them. The percentage of total variance accounted for by first-order effects ranges from 79–94% for the different sites indicating that the variance is dominated by sensitivities to individual parameters, and that the effects of parameter interactions are quite small. Where second- or higher-order effects do exist they tend to lead to tails in the predicted output distributions which can be seen to some extent in Fig. 3.
(ii) Sensitivity coefficients – overall parameter importance
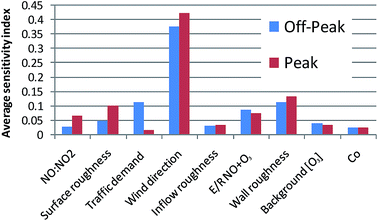
In terms of the influence of traffic characteristics, there are clear differences between the two modelled demand scenarios. For off-peak conditions, there is clearly a response to the levels of traffic demand with an average contribution of ∼11% to the predicted [NO2]. Under peak conditions where the network saturates, road-side [NO2] is relatively insensitive to changes in demand and more sensitive to the primary NO2 fraction (see Fig. 4). The results show that in order to have a substantial effect on road-side NO2 through traffic demand reduction measures, it would be necessary to reduce demand to the lower end of the sensitive region, i.e. by 60% or more.
(iii) Sensitivity coefficients – site to site variation
In this section we focus on the off-peak traffic demand scenario and investigate the responses to changes in selected parameters at individual sites. First we compare sites G3 and G4 which lie on opposite sides of the canyon close to the signalled junction on the leeward and windward sides of the canyon, respectively. Fig. 3 shows that G3 displayed the higher NO2 concentrations due to the in-canyon helical circulation present. At G3 the highest sensitivity (Si = 0.3) is to the wall roughness length zo with the response shown in Fig. 5a. The greater the assumed roughness length, the higher the predicted [NO2], since a higher roughness leads to lower in-canyon flow velocities as the boundary is approached. In these figures the red line displays the first-order component function for the selected parameter (see eqn (1)). Were the response to depend only on a single parameter with an Si of 1, then all points would lie on the red line. In reality, several parameters contribute to the output variance and hence the scatter points in the plots represent the effects of the other important parameters. For the wall zo, the range spanned by the component function for this parameter (shown in red) is about 5 × 1011 molecules cm−3i.e. almost 40 μg m−3 and suggests that the near wall flow is highly influential on pollutant exposure within street canyon type geometries. Depending on the type of wall, windows, street furniture etc. the zo value may vary significantly from site to site and is a difficult parameter to estimate causing problems for improving model robustness.The second most influential parameter is traffic demand (Si = 0.15) as shown in Fig. 5b. Changes in demand of 40% lead to a range of NO2 concentrations of a width of about 3 × 1011 molecules cm−3i.e. 23 μg m−3. This illustrates that within the off-peak flow regime, reductions in demand could lead to substantial reductions in road-side mean [NO2] levels. The figure shows that as the demand levels increase, the slope of the sensitivity decreases which is consistent with the fact that overall emissions flatten off under highly congested conditions. The pay-off is therefore greater for the lower demand scenarios.
Lower [NO2] concentrations are seen at G4 since the flow has circulated around the canyon before reaching this receptor point and hence primary emissions of NOx have dispersed to a certain extent. At G4 the most dominant parameter is now the normalised demand (Si = 0.25) which suggests that the model is relatively robust to the flow and turbulence parameterisations at this receptor. Chemical processes are, however, more dominant at this windward location than they were at G3. The activation energy for reaction NO + O3 = NO2 + O2 has a high sensitivity (Si = 0.24) at this site, as does the background ozone concentration (Si = 0.08). The component functions and scatter plots for these two parameters are shown in Fig. 6a and b respectively. As the activation energy is lowered, the production of NO2 across the canyon increases and assumed uncertainties in this parameter can account for differences in predicted [NO2] of around 15 μg m−3 based on the predicted range of the component function (shown in red). The influence of background [O3] is about half as strong based on the assumed uncertainties.
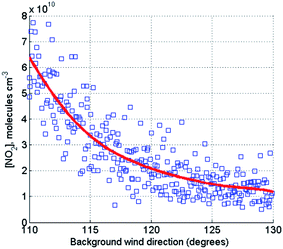
Wind direction was not highly influential at sites G3 and G4 since the most important dispersion process is the recirculating flow which is driven by a strong cross-street wind component for all reference directions tested. However, as we move down the canyon away from the congested junction, then it begins to play a more and more dominant role as it affects the along street dispersion of emissions from the heavily trafficked junction. At sites A and B, 60 and 40 m to the South of G4 respectively, the sensitivity coefficients with respect to wind angle are >0.7, and the response to background wind direction is highly non-linear as shown in Fig. 7 for site A. The complex interplay between the topology of the street network and the flow patterns established means that the concentrations of NO2 at site A are mostly dominated by primary emissions, and therefore as the wind direction takes on an increasingly southerly component, the concentration decreases. The relative importance of in-street chemical processes will be discussed further in the next section.
(iv) Discussion of chemical processes
In-street NO2 concentration increments above background will be affected by both primary NO2 emissions being dispersed from vehicle exhausts, and the formation of secondary NO2 from primary NO through its reaction with ozone which is mixing into the street from the background. The relative importance of these processes will vary with location within the street and can be explored via analysis of the sensitivity coefficients. In this section we therefore also consider the sensitivity of in-street time-averaged ozone concentrations ([O3]) to the model parameterisations.The main first-order sensitivity indices for sites G3 (leeward close to junction), G4 (windward close to junction), A (windward 60 m South of G4), and D (leeward 60 m South of G3) are shown in Fig. 8 for both ozone and NO2 concentrations. In-street ozone is mainly controlled by the background concentration except for at site G3 where high concentrations of NOx are expected due to its close proximity to queueing traffic and the in-street recirculation patterns. However, this sensitivity to background ozone is not seen for [NO2] which suggests that concentration increments of NO2 above background within congested street networks of the street canyon type are unlikely to be dominated by long range transport of ozone. Instead, in-street NO2 tends to be dominated by the effects of wind direction, traffic demand, local secondary NO2 formation rates, and near wall velocity profiles governed by roughness parameterisations. The importance of local NO2 formation is indicated by the importance of the rate parameters for the inorganic chemical reactions with the activation energy for NO + O3 being the dominant parameter. This parameter is particularly influential at sites G3 and G4 close to the junction where NOx concentrations are high. It is also the dominant parameter affecting in-street [O3] at site G3 since a higher rate for this reaction increases the titration of ozone by NO.
 | ||
| Fig. 8 Main first-order sensitivity indices for sites G3, G4, A and D. An index of 1 implies that a single parameter totally determines the variance in predicted concentrations. | ||
(v) Uncertainties in model structure and issues of “uniqueness of place”
The approach for uncertainty assessment used here is parameter based and therefore assumes that the chosen model structure is appropriate for the intended application. It assesses uncertainties in prediction due to lack of knowledge of parameter values but not due to missing processes within the model. There are a number of challenges in choosing an appropriate model structure. The first is computational cost. It is unlikely that a high resolution CFD model that resolves all eddy structures formed within the complex geometry (e.g. using LES or direct numerical simulation), as well as all possible chemical transformations, can be used within the context of compliance assessment due to computational requirements. Even such highly detailed models require accurate boundary and initial conditions. At the other end of the spectrum, semi-empirical models such as those based on a Gaussian or multi-compartment approaches are based on parameterisations informed by street topologies, rather than detailed representations of in-street flow characteristics. The use of parameters based on geometric features such as canyon width to height ratios has provided a way of generalising the use of such models within different city geometries. However, site specific features such as complex intersections and roof shapes cannot be captured by such models and yet the DAPPLE (Dispersion of Air Pollution and its Penetration into the Local Environment) field campaigns highlighted the importance of a number of these features in determining in-street flow and dispersion.41,42 Such models then may contain structural uncertainties that limit their generality. This raises the issue of “uniqueness of place” for models that has been previously highlighted within the field of hydrological modelling.43 LES models may require less site specific parameterisation, but may be unaffordable from a computational perspective.The RANs CFD approach adopted in this work attempts to seek the middle ground, but each simulation still takes of the order of 10 minutes to an hour on a standard PC, and hence the use of such models is difficult within the context of rapid screening. These models, however, can capture the average effects of flows within complex geometries that lead to spatial variation in pollutant concentrations over small scales. A key question that remains is whether uncertainties within their parameterisations can be reduced significantly or whether they still suffer from issues of “uniqueness of place”, where parameterisations are highly site specific and difficult to quantify. Background wind direction ranked highly amongst the sensitive parameters affecting in-street [NO2]. In principle, above-roof measurements could be obtained for all sites of interest but in reality this would be practically difficult. The need for a reference site free of interference from local flow features was discussed by Barlow et al. for the case of London.44 Roughness lengths were also important, in particular those of the nearest surface to the receptor site studied. Roughness lengths cannot be measured directly and whilst approaches have been recently suggested to estimate these for complex city-scale surfaces,45 in reality canyon wall roughness lengths will always have to be estimated and may be site specific.
D Conclusions
A global uncertainty and sensitivity study was used to investigate the robustness of predictions of road-side time averaged NO2 concentrations based on a Reynolds averaged flow model coupled with a reactive Lagrangian particle dispersion model using NOx emission rates calculated from a traffic micro-simulation model. Overall, predicted [NO2] at a number of in-street sites was uncertain to within approximately a factor of 2. The predictions were fairly robust with respect to the parameterisations of turbulent dispersion and mixing time-scales. Uncertainties in the parameterisation of these processes did not greatly affect the time-averaged predictions. At near wall sites close to the high emission traffic junction, however, predictions were strongly influenced by the parameterisation of near boundary flows determined by the wall roughness length zo. This is a difficult parameter to estimate but could strongly influence the prediction of in-street exposure within narrow street canyons such as the one studied here. Further away from the traffic junction, reference wind direction was the most dominant parameter affecting predicted [NO2]. Whilst this parameter could be measured above-roof, it is not a routine measurement that is carried out within UK urban areas. Rather, reference meteorological measurements are commonly obtained from nearby rural sites or local airports. The direction of above-roof winds has been shown to strongly affect in-street flow and dispersion processes5,44 and thus it is not surprising that it influences the transport of NOx emissions from the congested junction to other in-street receptors in this case. However, obtaining long term appropriate reference measurements is a difficult challenge for most cities.With respect to chemical processes, it is the short time-scale, in-street processes that seem to most strongly affect road-side [NO2]. In particular the activation energy for the reaction of NO with O3 is the most critical parameter. Better quantification of the rate of this reaction would help to improve model robustness.
In terms of mitigation strategies, two patterns emerge. Under peak traffic conditions the model suggests that even moderate reductions in traffic demand are unlikely to reduce in-street [NO2]. For such congested conditions, the fraction of NO2 in total NOx was shown to be more influential than demand, indicating that reducing primary NO2 could be a key factor in reducing NO2 in congested street canyon situations. For lower demand scenarios, there were demonstrable benefits to reducing traffic demand, mainly at sites close to the traffic queue. Overall, despite the scatter in the data due to uncertainties within the model parameterisations, there were clearly discernible effects of possible demand or emissions management measures suggesting that the model set up was robust enough to be useful within the context of exposure mitigation.
Acknowledgements
This work was supported by EPSRC grant GR/S90881/01.References
- S. K. Park, S. D. Kim and H. Lee, Sci. Total Environ., 2004, 323, 263–271 CrossRef CAS PubMed.
- J. W. D. Boddy, R. J. Smalley, N. S. Dixon, J. E. Tate and A. S. Tomlin, Atmos. Environ., 2005, 39, 3147–3161 CrossRef CAS.
- P. Louka, S. E. Belcher and R. G. Harrison, Atmos. Environ., 2000, 34, 2613–2621 CrossRef CAS.
- A. S. Tomlin, R. J. Smalley, J. E. Tate, J. F. Barlow, S. E. Belcher, S. J. Arnold, A. Dobre and A. Robins, Atmos. Environ., 2009, 43, 5027–5037 CrossRef CAS.
- A. Dobre, S. J. Arnold, R. J. Smalley, J. W. D. Boddy, J. F. Barlow, A. S. Tomlin and S. E. Belcher, Atmos. Environ., 2005, 39, 4647–4657 CrossRef CAS.
- R. Berkowicz, Environ. Monit. Assess., 2000, 65, 323–331 CrossRef CAS.
- M. Carpentieri, P. Salizzoni, A. Robins and L. Soulhac, Environ. Modell. Softw., 2012, 37, 110–124 CrossRef.
- T. A. M. Pugh, A. R. MacKenzie, J. D. Whyatt and C. N. Hewitt, Environ. Sci. Technol., 2012, 46, 7692–7699 CrossRef CAS PubMed.
- M. Ketzel, R. Berkowicz and A. Lohmeyer, Environ. Monit. Assess., 2000, 65, 363–370 CrossRef CAS.
- N. S. Dixon, J. W. D. Boddy, R. J. Smalley and A. S. Tomlin, Atmos. Environ., 2006, 40, 958–972 CrossRef CAS.
- J. J. Baik, Y. S. Kang and J. J. Kim, Atmos. Environ., 2007, 41, 934–949 CrossRef CAS.
- A. Garmory, I. S. Kim, R. E. Britter and E. Mastorakos, Atmos. Environ., 2009, 43, 4670–4680 CrossRef CAS.
- V. B. Bright, W. J. Bloss and X. M. Cai, Atmos. Environ., 2013, 68, 127–142 CrossRef CAS.
- J. Baker, H. L. Walker and X. M. Cai, Atmos. Environ., 2004, 38, 6883–6892 CrossRef CAS.
- J. Zhong, X. M. Cai and W. J. Bloss, Environ. Pollut., 2015, 200, 42–52 CrossRef CAS PubMed.
- N. S. Dixon and A. S. Tomlin, Atmos. Environ., 2007, 41, 8114–8127 CrossRef CAS.
- T. Ziehn, N. S. Dixon and A. S. Tomlin, Atmos. Environ., 2009, 43, 5978–5988 CrossRef CAS.
- J. W. D. Boddy, R. J. Smalley, P. S. Goodman, J. E. Tate, M. C. Bell and A. S. Tomlin, Atmos. Environ., 2005, 39, 3163–3176 CrossRef CAS.
- City of York Council, 2014 Air Quality Progress Report for City of York Council, 2014 Search PubMed.
- J. Eichhorn and A. Kniffka, Meteorol. Z., 2010, 19, 81–90 CrossRef.
- M. O. Letzel, T. Flassak and D. Angel, Gefahrstoffe - Reinhalt. Luft, 2012, 72, 329–334 Search PubMed.
- TSS, AIMSUN – The Integrated Transport Modelling Software, http://www.aimsun.com/wp/ Search PubMed.
- F. An, M. Barth, J. Norbeck and M. Ross, Transp. Res. Rec., 1997, 1587, 52–62 CrossRef.
- M. Zallinger, J. Tate and S. Hausberger, 16th International Transport and Air Pollution Conference, Graz, Austria, 2008 Search PubMed.
- L. I. Panis, S. Broekx and R. H. Liu, Sci. Total Environ., 2006, 371, 270–285 CrossRef CAS PubMed.
- P. S. Goodman and G. Rhys Tyler, 6th AIMSUN User Group Meeting, Capri, Italy, 2008 Search PubMed.
- M. W. Gallagher, E. Nemitz, J. R. Dorsey, D. Fowler, M. A. Sutton, M. Flynn and J. Duyzer, J. Geophys. Res.: Atmos., 2002, 107 Search PubMed.
- J. Benson, T. Ziehn, N. S. Dixon and A. S. Tomlin, Atmos. Environ., 2008, 42, 1874–1891 CrossRef CAS.
- B. L. Sawford, Flow, Turbulence and Combustion, 2004, 72, 133–160 CrossRef.
- D. Anfossi, G. Degrazia, E. Ferrero, S. E. Gryning, M. G. Morselli and S. T. Castelli, Bound.-Lay. Meteorol., 2000, 95, 249–270 CrossRef.
- S. M. Du, Bound.-Lay. Meteorol., 1997, 83, 207–219 CrossRef.
- A. M. Reynolds, Bound.-Lay. Meteorol., 1998, 89, 161–170 CrossRef.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2004, 4, 1461–1738 CrossRef CAS.
- R. E. Shetter, C. A. Cantrell, K. O. Lantz, S. J. Flocke, J. J. Orlando, G. S. Tyndall, T. M. Gilpin, C. A. Fischer, S. Madronich, J. G. Calvert and W. Junkermann, J. Geophys. Res.: Atmos., 1996, 101, 14631–14641 CrossRef CAS.
- R. E. Shetter, A. H. McDaniel, C. A. Cantrell, S. Madronich and J. G. Calvert, J. Geophys. Res.: Atmos., 1992, 97, 10349–10359 CrossRef CAS.
- D. C. Carslaw, Atmos. Environ., 2005, 39, 4793–4802 CrossRef CAS.
- I. M. Sobol, Math. Comput. Simulat., 2001, 55, 271–280 CrossRef.
- H. Rabitz, O. F. Alis, J. Shorter and K. Shim, Comput. Phys. Commun., 1999, 117, 11–20 CrossRef CAS.
- T. Ziehn and A. S. Tomlin, Environ. Modell. Softw., 2009, 24, 775–785 CrossRef.
- T. Turányi and A. S. Tomlin, Analysis of Kinetic Reaction Mechanisms, Springer, 2014 Search PubMed.
- A. A. Balogun, A. S. Tomlin, C. R. Wood, J. F. Barlow, S. E. Belcher, R. J. Smalley, J. J. N. Lingard, S. J. Arnold, A. Dobre, A. G. Robins, D. Martin and D. E. Shallcross, Bound.-Lay. Meteorol., 2010, 136, 489–513 CrossRef.
- C. R. Wood, S. J. Arnold, A. A. Balogun, J. F. Barlow, S. E. Belcher, R. E. Britter, H. Cheng, A. Dobre, J. J. N. Lingard, D. Martin, M. K. Neophytou, F. K. Petersson, A. G. Robins, D. E. Shallcross, R. J. Smalley, J. E. Tate, A. S. Tomlin and I. R. White, Bull. Am. Meteorol. Soc., 2009, 90, 955–970 CrossRef.
- K. J. Beven, Hydrol. Earth Syst. Sci., 2000, 4, 203–213 CrossRef.
- J. F. Barlow, A. Dobre, R. J. Smalley, S. J. Arnold, A. S. Tomlin and S. E. Belcher, Atmos. Environ., 2009, 43, 5536–5544 CrossRef CAS.
- J. T. Millward-Hopkins, A. S. Tomlin, L. Ma, D. B. Ingham and M. Pourkashanian, Bound.-Lay. Meteorol., 2013, 146, 447–468 CrossRef.
Footnotes |
| † Current address: CSIRO, Oceans and Atmosphere, Aspendale, Australia. |
| ‡ Current address: School of Civil Engineering and Geosciences, Newcastle University, UK. |
| This journal is © The Royal Society of Chemistry 2016 |