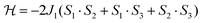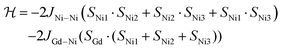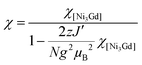A family of fourteen soluble stable macrocyclic [NiII3LnIII] heterometallic 3d–4f complexes†
Humphrey L. C.
Feltham
a,
Sébastien
Dhers
a,
Mathieu
Rouzières
bc,
Rodolphe
Clérac
*bc,
Annie K.
Powell
*de and
Sally
Brooker
*a
aDepartment of Chemistry, University of Otago, PO Box 56, Dunedin, New Zealand. E-mail: sbrooker@chemistry.otago.ac.nz; Fax: +64 3 479 7906; Tel: +64 3 479 7911
bCNRS, CRPP, UPR 8641, F-33600 Pessac, France. E-mail: clerac@crpp-bordeaux.cnrs.fr; Fax: +33 5 56 84 56 00; Tel: +33 5 56 84 56 50
cUniv. Bordeaux, CRPP, UPR 8641, F-33600 Pessac, France
dInstitute of Inorganic Chemistry, Karlsruhe Institute of Technology, Engesserstr.15 Geb. 30.45, 76131 Karlsruhe, Germany. E-mail: annie.powell@kit.edu
eInstitute for Nanotechnoly, Karlsruhe Institute of Technology, Hermann-von-Helmholtz Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
First published on 7th September 2015
Abstract
A family of fourteen tetranuclear, 3d–4f heterometallic nickel(II)–lanthanide(III) complexes of the hexaimine macrocycle (LPr)6−, with general formula NiII3LnIII(LPr)(NO3)3·xsolvents (LnIII = LaIII, CeIII, PrIII, NdIII, SmIII, EuIII, GdIII, TbIII, DyIII, HoIII, ErIII, TmIII, YbIII or LuIII), were prepared in a one-pot synthesis using a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 reaction of nickel(II) acetate, the appropriate lanthanide(III) nitrate, the dialdehyde 1,4-diformyl-2,3-dihydroxybenzene (H2LAld) and 1,3-diaminopropane. In addition, three tetranuclear heterometallic nickel(II)–lanthanide(III) complexes of H2LAld, with general formula NiII3LnIII(LAld)3(NO3)3·xsolvents, were deliberately prepared (LnIII = LaIII, DyIII or YbIII) as in effect they represent intermediates en route to the above macrocyclic complexes. Whilst single crystals of the macrocyclic complexes were not forthcoming, X-ray crystal structure determinations on NiII3LnIII(LAld)3(NO3)3·xsolvents (LnIII = DyIII or YbIII) confirmed that the large ten-coordinate lanthanide(III) ion is bound in the central O6 pocket while the smaller six-coordinate nickel(II) ions are bound in the outer O4 pockets. In all fourteen cases, addition of the diamine to this intermediate (all in one pot) gives the tetrametallic [3 + 3] macrocyclic product. The magnetic properties of all fourteen macrocyclic complexes were measured down to 1.8 K to check for Single-Molecule Magnet behaviour, but no slow dynamics of magnetisation was observed.
3 reaction of nickel(II) acetate, the appropriate lanthanide(III) nitrate, the dialdehyde 1,4-diformyl-2,3-dihydroxybenzene (H2LAld) and 1,3-diaminopropane. In addition, three tetranuclear heterometallic nickel(II)–lanthanide(III) complexes of H2LAld, with general formula NiII3LnIII(LAld)3(NO3)3·xsolvents, were deliberately prepared (LnIII = LaIII, DyIII or YbIII) as in effect they represent intermediates en route to the above macrocyclic complexes. Whilst single crystals of the macrocyclic complexes were not forthcoming, X-ray crystal structure determinations on NiII3LnIII(LAld)3(NO3)3·xsolvents (LnIII = DyIII or YbIII) confirmed that the large ten-coordinate lanthanide(III) ion is bound in the central O6 pocket while the smaller six-coordinate nickel(II) ions are bound in the outer O4 pockets. In all fourteen cases, addition of the diamine to this intermediate (all in one pot) gives the tetrametallic [3 + 3] macrocyclic product. The magnetic properties of all fourteen macrocyclic complexes were measured down to 1.8 K to check for Single-Molecule Magnet behaviour, but no slow dynamics of magnetisation was observed.
Introduction
Single-Molecule Magnets (SMMs) are coordination complexes in which the individual molecules behave like traditional ‘bulk’ magnets.1 As such they can exhibit slow relaxation of magnetisation after removal of the magnetising field, which may make them useful in nano-scale data storage and processing. This is usually the result of a non-zero spin ground state and significant uniaxial anisotropy of that state which induces an energy barrier to reversing the magnetisation. However, due to the small energy barrier between these two states (in comparison to the temperature) and/or quantum tunnelling of the magnetization, a hysteresis effect in magnetisation (M) vs. field (H) plots is not typically seen above 5 K, with the record currently at 14 K.2 Clearly, for any practical device application of SMMs, the barrier must be raised.A variety of complexes have been shown to display SMM behaviour, including systems based on transition metal,3 lanthanide,4–6 actinide7 and mixed-metal6,8 systems. Combining transition metal and lanthanide ions is also common. However, the majority of SMMs are prepared with polydentate acyclic ligands, which can make characterisation somewhat dependent on growing single crystals, as the structure can be difficult to predict with any certainty. Moreover, small modifications to one aspect of the system may make a dramatic change to the structure of the resultant complex, which can make it impossible to tune the magnetic properties.
An alternative approach is to use a macrocyclic ligand, which allows predictable binding in discrete binding pockets. A macrocyclic ligand also confers stability and helps to prevent undesirable inter-molecule interactions. The advantage of using a macrocyclic ligand to prepare SMMs was first illustrated by Ishikawa, who has demonstrated that a single lanthanide ion can show SMM behaviour when sandwiched between two phthalocyanine macrocycles in an N8 donor environment.9 More examples of macrocyclic SMMs containing a single lanthanide ion have been reported in the literature since then,10 including organometallic species where the single lanthanide ion is sandwiched by the π systems of two cyclic, anionic ligands.5
Recently, we expanded the macrocyclic approach to prepare, in a controlled and predictable manner, mixed 3d–4f [MII3LnIII] SMMs, using the [3 + 3] macrocycle (LPr)6− which features distinct binding pockets tailored for binding to MII (transition metal) vs. LnIII (lanthanide) ions (Fig. 1).11–14 Nabeshima, Kajiwara and co-workers have also utilised this approach using the macrocycle (LPh)6− (Fig. 1).15 More recently we have gone on to demonstrate that linking the axial sites of the robust and soluble SMM building block [CuII3TbIII(LPr)]3+ generates, as anticipated, magnetically interesting chains.16 Pleasingly, we have also found that the template method used to prepare (LPr)6− has proven to be remarkably robust, likewise working for the related, larger macrocycle (LBu)6− (Fig. 1).17 We now further demonstrate the versatility of this system by reporting the synthesis of the nickel(II) series, [NiII3LnIII(LPr)], and selected intermediates, [NiII3LnIII(LAld)3], along with the magnetic properties of all 14 macrocyclic complexes.
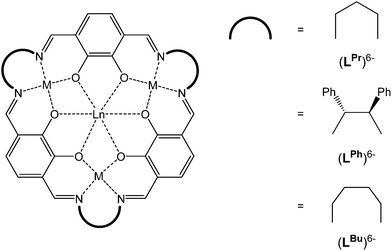 | ||
| Fig. 1 Schematic representation of the [3 + 3] macrocycles (LPr)6−, (LBu)6− and (LPh)6−, all of which are obtained as metal complexes. | ||
Experimental
General
All chemicals were of A.R. Grade and used as received. A working synthesis of H2LAld was developed at Otago University, based on the outline reported by Nabeshima and co-workers18 and with advice from Professor M. J. MacLachlan (UBC). This is practically identical to the detailed method that was subsequently published by Nabeshima and co-workers19 so is not repeated here. IR spectra were recorded as solids on a Bruker Alpha FT-ATR IR spectrometer with a diamond anvil Alpha-P module between 400 and 4000 cm−1. Microanalysis was carried out by the Campbell Microanalytical Laboratory at the University of Otago. Metal analysis was carried out by the Centre for Trace Metal Analysis at the University of Otago. Conductivity measurements were carried out at 25 °C on a Mettler Toledo FE20 FiveEasy Conductivity Meter. Thermogravimetric analysis (TGA) was performed on a TA Instruments Q50 TGA, using nitrogen as a flow gas.Single crystal X-ray measurements were carried out on a Bruker SMART Apex diffractometer using graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å). Structure solution and full-matrix least-squares refinement were carried out using the SHELXTL software package.20 All non-H atoms were refined anisotropically except for the disordered atoms in [NiII3YbIII(LAld)3(NO3)2(MeOH)4.75(H2O)1.25](NO3). H atoms bonded to C atoms were placed in calculated positions whilst those on O atoms were placed in calculated positions that gave the best hydrogen bonds. Due to a non-coordinated nitrate anion being very badly disordered in both structures, SQUEEZE21 was used to account for it. For [NiII3DyIII(LAld)3(NO3)2(MeOH)6](NO3) and [NiII3YbIII(LAld)3(NO3)2(H2O)1.25(MeOH)4.75](NO3) the voids contained 187 and 184 electrons per cell, respectively, both of which are consistent with one nitrate anion and one water molecule per asymmetric unit (expect 164 electrons per cell). For further details see the cif files.
The magnetic susceptibility measurements were obtained with the use of MPMS-XL Quantum Design SQUID magnetometer. The magnetometer operates between 1.8 and 400 K for dc applied fields of up to 70 kOe. Measurements were performed on polycrystalline samples of 13.27, 14.95, 13.54, 17.16, 14.35, 18.06, 8.34 (and 12.25), 12.81, 13.05 (and 19.71), 12.34, 17.92, 11.10, 14.65 and 8.81 (and 9.87) mg respectively for La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb and Lu introduced in a sealed polyethylene bag (3 × 0.5 × 0.02 cm). The ac susceptibility measurements were measured with an oscillating ac field of 3 Oe with frequency between 1 to 1500 Hz (MPMS). The magnetic data were corrected for the sample holder and the diamagnetic contributions (the latter estimated as −0.5 × 10−6 × Mr then adjusted in the fit).
Synthesis
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1614 (s); 1489 (m); 1447 (s); 1413 (m); 1366 (m); 1329 (m); 1245 (s); 1159 (s); 1104 (s); 1030 (m); 834 (s); 796 (w); 770 (w); 736 (w); 703 (s); 596 (s); 561 (s); 521 (m).
/cm−1 = 1614 (s); 1489 (m); 1447 (s); 1413 (m); 1366 (m); 1329 (m); 1245 (s); 1159 (s); 1104 (s); 1030 (m); 834 (s); 796 (w); 770 (w); 736 (w); 703 (s); 596 (s); 561 (s); 521 (m).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1616 (s); 1486 (m); 1445 (s); 1418 (m); 1370 (m); 1332 (m); 1246 (s); 1160 (s); 1112 (s); 1032 (m); 834 (s); 783 (w); 768 (w); 741 (w); 700 (s); 609 (s); 560 (s); 526 (m).
/cm−1 = 1616 (s); 1486 (m); 1445 (s); 1418 (m); 1370 (m); 1332 (m); 1246 (s); 1160 (s); 1112 (s); 1032 (m); 834 (s); 783 (w); 768 (w); 741 (w); 700 (s); 609 (s); 560 (s); 526 (m).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1618 (s); 1491 (m); 1449 (s); 1414 (m); 1369 (m); 1333 (m); 1291 (m); 1248 (s); 1209 (m); 1159 (s); 1111 (s); 1033 (m); 835 (s); 796 (w); 767 (w); 703 (s); 597 (s); 560 (s); 527 (m).
/cm−1 = 1618 (s); 1491 (m); 1449 (s); 1414 (m); 1369 (m); 1333 (m); 1291 (m); 1248 (s); 1209 (m); 1159 (s); 1111 (s); 1033 (m); 835 (s); 796 (w); 767 (w); 703 (s); 597 (s); 560 (s); 527 (m).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1624 (m); 1507 (w); 1446 (m); 1411 (m); 1321 (s); 1230 (m); 1168 (m); 1084 (w); 1027 (w); 832 (w) 770 (m); 718 (m); 657 (w).
/cm−1 = 1624 (m); 1507 (w); 1446 (m); 1411 (m); 1321 (s); 1230 (m); 1168 (m); 1084 (w); 1027 (w); 832 (w) 770 (m); 718 (m); 657 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1617 (m); 1518 (w); 1453 (m); 1410 (m); 1315 (s); 1240 (m); 1194 (m); 1171 (m); 1089 (w); 1055 (m); 1035 (w); 965 (m); 834 (w) 780 (m); 750 (m); 733 (m); 658 (m).
/cm−1 = 1617 (m); 1518 (w); 1453 (m); 1410 (m); 1315 (s); 1240 (m); 1194 (m); 1171 (m); 1089 (w); 1055 (m); 1035 (w); 965 (m); 834 (w) 780 (m); 750 (m); 733 (m); 658 (m).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1624 (m); 1507 (w); 1449 (m); 1407 (m); 1323 (s); 1230 (m); 1170 (m); 1126 (m); 1077 (w); 1021 (w); 828 (w) 769 (m); 718 (m); 657 (w).
/cm−1 = 1624 (m); 1507 (w); 1449 (m); 1407 (m); 1323 (s); 1230 (m); 1170 (m); 1126 (m); 1077 (w); 1021 (w); 828 (w) 769 (m); 718 (m); 657 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1624 (m); 1508 (w); 1449 (m); 1406 (m); 1323 (s); 1230 (m); 1170 (m); 1126 (m); 1076 (w); 1021 (w); 832 (w) 769 (m); 720 (m); 656 (w).
/cm−1 = 1624 (m); 1508 (w); 1449 (m); 1406 (m); 1323 (s); 1230 (m); 1170 (m); 1126 (m); 1076 (w); 1021 (w); 832 (w) 769 (m); 720 (m); 656 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1622 (m); 1507 (w); 1451 (m); 1404 (m); 1321 (s); 1230 (m); 1172 (m); 1125 (m); 1075 (w); 1023 (w); 835 (w) 765 (m); 723 (m); 655 (w).
/cm−1 = 1622 (m); 1507 (w); 1451 (m); 1404 (m); 1321 (s); 1230 (m); 1172 (m); 1125 (m); 1075 (w); 1023 (w); 835 (w) 765 (m); 723 (m); 655 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1621 (m); 1508 (w); 1449 (m); 1411 (m); 1323 (s); 1231 (m); 1168 (m); 1085 (w); 1027 (w); 833 (w) 771 (m); 719 (m); 659 (w).
/cm−1 = 1621 (m); 1508 (w); 1449 (m); 1411 (m); 1323 (s); 1231 (m); 1168 (m); 1085 (w); 1027 (w); 833 (w) 771 (m); 719 (m); 659 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1624 (m); 1508 (w); 1449 (m); 1400 (m); 1321 (s); 1218 (m); 1169 (m); 1125 (m); 1074 (w); 1027 (w); 833 (w); 765 (m); 720 (m); 654 (w).
/cm−1 = 1624 (m); 1508 (w); 1449 (m); 1400 (m); 1321 (s); 1218 (m); 1169 (m); 1125 (m); 1074 (w); 1027 (w); 833 (w); 765 (m); 720 (m); 654 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1621 (m); 1510 (w); 1450 (m); 1407 (m); 1322 (s); 1230 (m); 1170 (m); 1085 (w); 1028 (w); 832 (w) 769 (m); 719 (m); 657 (w).
/cm−1 = 1621 (m); 1510 (w); 1450 (m); 1407 (m); 1322 (s); 1230 (m); 1170 (m); 1085 (w); 1028 (w); 832 (w) 769 (m); 719 (m); 657 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1622 (m); 1508 (w); 1450 (m); 1407 (m); 1324 (s); 1229 (m); 1171 (m); 1131 (m); 1085 (w); 1025 (w); 893 (w); 833 (w); 770 (m); 721 (m); 657 (w).
/cm−1 = 1622 (m); 1508 (w); 1450 (m); 1407 (m); 1324 (s); 1229 (m); 1171 (m); 1131 (m); 1085 (w); 1025 (w); 893 (w); 833 (w); 770 (m); 721 (m); 657 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1617 (m); 1508 (w); 1449 (m); 1408 (m); 1320 (s); 1218 (m); 1170 (m); 1122 (m); 1071 (w); 1026 (w); 898 (w); 827 (w); 769 (m); 714 (m); 669 (w).
/cm−1 = 1617 (m); 1508 (w); 1449 (m); 1408 (m); 1320 (s); 1218 (m); 1170 (m); 1122 (m); 1071 (w); 1026 (w); 898 (w); 827 (w); 769 (m); 714 (m); 669 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1623 (m); 1508 (w); 1451 (m); 1406 (m); 1324 (s); 1229 (m); 1171 (m); 1126 (m); 1085 (w); 1026 (w); 893 (w); 834 (w); 770 (m); 721 (m); 659 (w).
/cm−1 = 1623 (m); 1508 (w); 1451 (m); 1406 (m); 1324 (s); 1229 (m); 1171 (m); 1126 (m); 1085 (w); 1026 (w); 893 (w); 834 (w); 770 (m); 721 (m); 659 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1621 (m); 1508 (w); 1450 (s); 1323 (s); 1253 (m); 1228 (s); 1173 (m); 1085 (w); 1021 (w); 846 (w); 827 (w); 813 (w); 772 (w); 720 (m).
/cm−1 = 1621 (m); 1508 (w); 1450 (s); 1323 (s); 1253 (m); 1228 (s); 1173 (m); 1085 (w); 1021 (w); 846 (w); 827 (w); 813 (w); 772 (w); 720 (m).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1626 (m); 1511 (w); 1455 (m); 1404 (m); 1324 (s); 1230 (m); 1173 (m); 1127 (m); 1086 (w); 1027 (w); 895 (w); 827 (w); 771 (m); 721 (m); 659 (w).
/cm−1 = 1626 (m); 1511 (w); 1455 (m); 1404 (m); 1324 (s); 1230 (m); 1173 (m); 1127 (m); 1086 (w); 1027 (w); 895 (w); 827 (w); 771 (m); 721 (m); 659 (w).
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) /cm−1 = 1624 (m); 1526 (w); 1457 (s); 1323 (s); 1229 (s); 1176 (m); 1086 (w); 1025 (w); 846 (w); 827 (w); 772 (w); 720 (m).
/cm−1 = 1624 (m); 1526 (w); 1457 (s); 1323 (s); 1229 (s); 1176 (m); 1086 (w); 1025 (w); 846 (w); 827 (w); 772 (w); 720 (m).
Results and discussion
Synthesis of the complexes
The fourteen macrocyclic complexes are all prepared in the same manner. Three equivalents of NiII(OAc)2·4H2O and one equivalent of LnIII(NO3)3·xH2O (Ln = La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb or Lu) in methanol are added to a room temperature solution of three equivalents of H2LAld in methanol, forming the ‘intermediate’ complex in situ (Fig. 2). After stirring for one hour, three equivalents of 1,3-diaminopropane in methanol are added dropwise to this solution. After stirring overnight, the solution is diffused with diethyl ether vapour, resulting in the precipitation of a red solid. This solid was isolated, washed with diethyl ether and dried in air, giving complexes of general formula NiII3LnIII(LPr)(NO3)3·xsolvents, referred to hereon by the abbreviated form [NiII3LnIII(LPr)].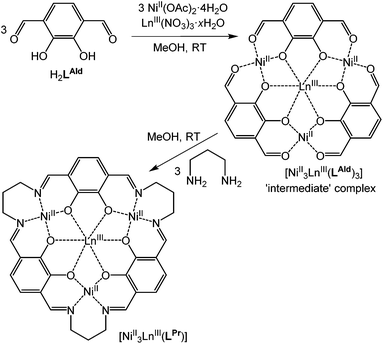 | ||
| Fig. 2 Schematic representation of formation of the macrocyclic complex via the ‘intermediate’ complex. | ||
The formation of the desired macrocyclic complexes was confirmed by elemental analysis, TGA and IR spectroscopy. In all cases the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch of the macrocycle occurred at 1621 cm−1, while no absorptions for unreacted H2LAld (1660 cm−1) or 1,3-diaminopropane (3360 cm−1 and 1601 cm−1) were observed. The presence of nitrate anions was supported by the pronounced band at around 1315–1325 cm−1. The CHN elemental analysis data matched the calculated values expected for complexes of the formula NiII3LnIII(LPr)(NO3)3·xsolvents and were corroborated by nickel and lanthanide metal analysis on three representative samples (LnIII = GdIII, TmIII and LuIII) which confirmed the presence of one lanthanide(III) ion and three nickel(II) ions in all cases. Similarly, thermogravimetric analysis on two representative samples (LnIII = GdIII and LuIII) confirmed the presence of the solvent content determined from the microanalysis data.
N stretch of the macrocycle occurred at 1621 cm−1, while no absorptions for unreacted H2LAld (1660 cm−1) or 1,3-diaminopropane (3360 cm−1 and 1601 cm−1) were observed. The presence of nitrate anions was supported by the pronounced band at around 1315–1325 cm−1. The CHN elemental analysis data matched the calculated values expected for complexes of the formula NiII3LnIII(LPr)(NO3)3·xsolvents and were corroborated by nickel and lanthanide metal analysis on three representative samples (LnIII = GdIII, TmIII and LuIII) which confirmed the presence of one lanthanide(III) ion and three nickel(II) ions in all cases. Similarly, thermogravimetric analysis on two representative samples (LnIII = GdIII and LuIII) confirmed the presence of the solvent content determined from the microanalysis data.
Conductivity values on three representative samples in DMF solution were between 102–120 mol−1 cm2 Ω−1, which is slightly below the expected range27 (130–170 mol−1 cm2 Ω−1) for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes (note: literature ranges for 1
1 electrolytes (note: literature ranges for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes in DMF are 65–90 and 200–240 mol−1 cm2 Ω−1, respectively). This is likely due to the low mobility of the large [NiII3LnIII(LPr)(NO3)x](3−x)+ cations in solution (e.g. as observed for salts of the bulky tetraphenylborate anion27). ESI-MS was not helpful in establishing that the desired complexes had formed, due to extensive fragmentation.
1 electrolytes in DMF are 65–90 and 200–240 mol−1 cm2 Ω−1, respectively). This is likely due to the low mobility of the large [NiII3LnIII(LPr)(NO3)x](3−x)+ cations in solution (e.g. as observed for salts of the bulky tetraphenylborate anion27). ESI-MS was not helpful in establishing that the desired complexes had formed, due to extensive fragmentation.
The very broadened peaks seen in the 1H NMR spectrum of NiII3LaIII(LPr)(NO3)3·11H2O were consistent with paramagnetic octahedral nickel(II) ions in DMF-d7 solution. Although nickel(II) is typically diamagnetic with a square-planar geometry when in the N2O2 pocket of salen- or salpn-like ligands,22 an octahedral geometry (paramagnetic) can be observed if the phenolate oxygen atoms are also coordinated to a second metal ion, such as zinc(II), due to reducing the electron density on these oxygen donor atoms.23 Here, the trivalent lanthanide(III) ion removes electron density from the catecholate oxygen atoms, increasing the tendency of the nickel(II) ion to coordinate axial donors (consistent with the magnetic data, see later). In the related Robson macrocyclic system,24–26 salpn-like pockets bind nickel(II) in an octahedral fashion,24 whereas the smaller macrocycles with tighter salen-like pockets provide a strong enough field to always generate square-planar nickel(II), even when dissolved in pyridine.25 It should be noted that the 1H NMR spectrum of NiII3LaIII(LAld)3(NO3)3·3H2O·5MeOH showed a similar paramagnetically broadened spectrum, which precluded determining if the intermediate complex is present in solution.
These macrocyclic complexes are soluble and stable so can be recrystallised from MeOH (or DMF) by vapour diffusion of diethyl ether, but despite numerous attempts no single crystals were forthcoming. The intermediate complexes (Fig. 2), NiII3LnIII(LAld)3(NO3)3·xsolvents, can be isolated by not adding the 1,3-diaminopropane and diffusing diethyl ether vapour into the reaction solution as usual. Three such complexes (LnIII = LaIII, DyIII or YbIII) were prepared, and the structures of two of them were determined.
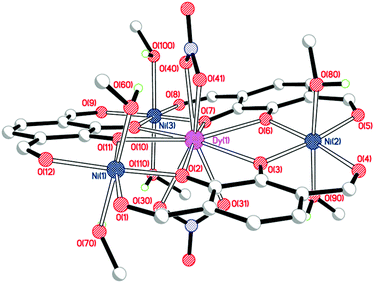
Crystal structures
Single crystals of [NiII3DyIII(LAld)3(NO3)2(MeOH)6](NO3) were grown by vapour diffusion of diethyl ether into a solution of the complex in methanol (Fig. 3, Table 1).| Bond length (Å), angle (°) or distance (Å) | [NiII3DyIII(LAld)3(NO3)2(MeOH)6]+ | [NiII3YbIII(LAld)3(NO3)2(H2O)1.25(MeOH)4.75]+ |
|---|---|---|
| LnIII–Ocatecholate range (average) | 2.479–2.501 (2.489) | 2.449–2.480 (2.464) |
| LnIII–Onitrate range (average) | 2.455–2.511(2.475) | 2.405–2.458 (2.426) |
| NiII–Ocatecholate range (average) | 1.961–1.988 (1.974) | 1.959–1.984 (1.972) |
| NiII–Oformyl range (average) | 2.007–2.019 (2.011) | 2.003–2.011(2.007) |
| NiII–Omethanol range (average) | 2.054–2.107 (2.078) | 2.057–2.203 (2.107) |
| NiII–Owater | — | 1.971–2.061 (2.029) |
| NiII–O–LnIII range (average) | 110.88–109.71 (110.3) | 110.2–111.1 (110.8) |
| NiII⋯NiII range (average) | 6.355–6.371 (6.364) | 6.328–6.353 (6.342) |
| NiII⋯LnIII range (average) | 3.673–3.767 (3.675) | 3.656–3.667 (3.662) |
| Shortest LnIII⋯LnIII distance in lattice | 9.912 | 9.900 |
As expected, the large dysprosium(III) ion is bound to six catecholate oxygen atoms, while the nickel(II) ions are bound to two catecholate and two formyl oxygen atoms each. The dysprosium(III) ion is ten-coordinate with the remaining sites occupied by two nitrate anions binding in a bidentate η2-fashion. The three nickel(II) ions are six-coordinate with methanol molecules in both axial positions. The dysprosium(III) ion is a somewhat distorted tetradecahedron (ChSM (ref. 28) = 1.21) while the nickel(II) ions are regular octahedra (Σ (ref. 29)/ChSM for Ni(1) = 45.3°/0.43; Ni(2) = 34.5°/0.46; Ni(3) = 30.4°/0.41). The complex is quite planar; the angles of the plane made by an arbitrarily chosen catecholate ring to the other two ring planes are 10.7° and 14.6°.
The position of the third, non-coordinated nitrate anion could not be accurately determined due to extensive disorder in that region which resulted in the use of SQUEEZE.21 The resulting electron count for that region was consistent with the presence of one nitrate anion and one water molecule per complex. Furthermore, the microanalysis data are entirely consistent with the presence of three nitrate anions overall: this is particularly clear-cut as in these intermediate complexes the nitrate anions are the only possible source of nitrogen.
Single crystals of [NiII3YbIII(LAld)3(NO3)2(H2O)1.25(MeOH)4.75](NO3) were grown by vapour diffusion of diethyl ether into a solution of the complex in methanol. This structure was also treated with SQUEEZE. Overall, this structure (Fig. S1, ESI†) is very similar to that of the DyIII analogue, but with disorder around the axially-coordinated ligands of the nickel(II) ions.
Magnetic properties
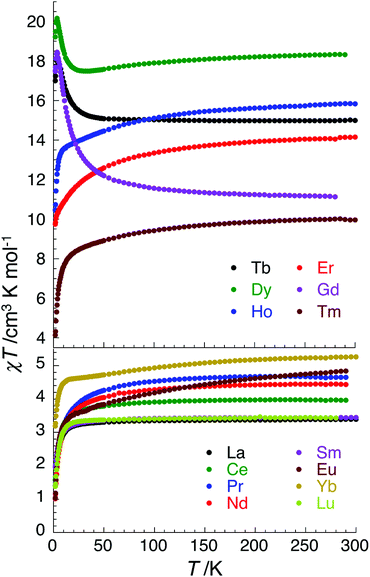
Having discovered SMM behaviour in the complexes [CuII3TbIII(LPr)(NO3)2(H2O)2(MeOH)](NO3)3·3H2O,13 ZnII3ErIII(LPr)(NO3)3·3H2O·2MeOH,12 ZnII3YbIII(LPr)(NO3)3·7H2O12 and [ZnII3DyIII(LPr)(NO3)3(MeOH)3]·4H2O,11,12 we were particularly interested to investigate the magnetic properties of the corresponding nickel(II) analogues, [NiII3LnIII(LPr)], with LnIII = TbIII, ErIII, YbIII or DyIII. However, for completeness (and to rule out the chance that an unexpected member of the family displays SMM behaviour) we have magnetically characterised all fourteen of these [NiII3LnIII(LPr)] complexes (Fig. 4 and S2–S15†).Replacing CuII by NiII will increase the number of unpaired electrons on the 3d ion from 1 to 2, providing the nickel(II) ion is octahedral and high spin (S = 1), not square planar and diamagnetic (i.e. not S = 0 low spin). At room temperature, the χT product for each complex is in agreement with the expected value (Table 2) for three octahedral nickel(II) ions (S = 1, and thus the Curie constant per NiII is equal to 1 cm3 K mol−1 when g = 2; calculated from C = g2S(S + 1)/8) plus the particular lanthanide(III) ion present (the Curie constant is expected to be C = g2J(J + 1)/8, e.g. for DyIIIJ = 15/2 and g = 4/3 so C ≈ 14.2 cm3 K mol−1).
| Complex | g of LnIII ion | Measured/expected (with gNi = 2) χT at 300 K (cm3 K mol−1) | χT at 1.8 K (cm3 K mol−1) | M at 1.8 K and 70 kOe (μB) |
|---|---|---|---|---|
| NiII3LaIII(LPr)(NO3)3·11H2O | — | 3.4/3.00 | 1.44 | 4.8 |
| NiII3CeIII(LPr)(NO3)3·7.5H2O·4MeOH | 6/7 | 4.0/3.80 | 1.58 | 5.6 |
| NiII3PrIII(LPr)(NO3)3·9H2O·2.5MeOH | 4/5 | 4.6/4.60 | 1.39 | 5.1 |
| NiII3NdIII(LPr)(NO3)3·8H2O·3MeOH | 8/11 | 4.4/4.64 | 1.01 | 4.5 |
| NiII3SmIII(LPr)(NO3)3·6.5H2O·2.5MeOH | 2/7 | 3.4/3.09 | 1.96 | 5.0 |
| NiII3EuIII(LPr)(NO3)3·8.5H2O·2MeOH | — | 4.8/3.00 | 1.03 | 3.8 |
| NiII3GdIII(LPr)(NO3)3·7.5H2O | 2 | 11.1/10.88 | 17.5 | 12.2 |
| NiII3TbIII(LPr)(NO3)3·7H2O·2MeOH | 3/2 | 15.0/14.81 | 17.0 | 9.4 |
| NiII3DyIII(LPr)(NO3)3·6H2O·3MeOH | 4/3 | 18.3 /17.17 | 19.2 | 11.0 |
| NiII3HoIII(LPr)(NO3)3·8.5H2O·0.5MeOH | 5/4 | 15.9/17.06 | 10.5 | 9.7 |
| NiII3ErIII(LPr)(NO3)3·7.5H2O·3.5MeOH | 6/5 | 14.0/14.47 | 9.76 | 9.8 |
| NiII3TmIII(LPr)(NO3)3·10H2O·MeOH | 7/6 | 10.0/10.15 | 4.13 | 7.9 |
| NiII3YbIII(LPr)(NO3)3·10H2O | 8/7 | 5.2/5.57 | 3.19 | 6.2 |
| NiII3LuIII(LPr)(NO3)3·7H2O | — | 3.4/3.00 | 1.38 | 4.5 |
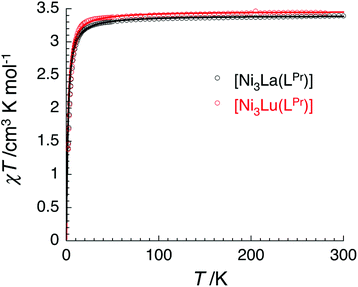
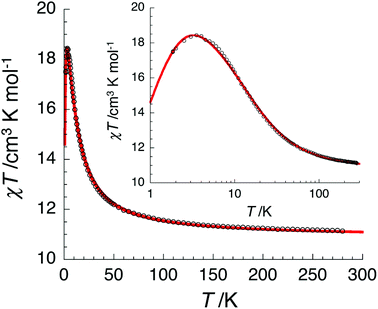
The temperature dependence of the χT product measured for [NiII3LaIII(LPr)] was used to investigate the nickel(II)–nickel(II) interaction without the complications arising from the presence of a paramagnetic lanthanide(III) ion (Fig. 4). Upon lowering the temperature for [NiII3LaIII(LPr)], the χT product is constant until around 50 K, at which point the value decreases to a minimum of 1.4 cm3 K mol−1. This decrease at low temperature suggests that the interaction between the paramagnetic nickel(II) ions is weakly antiferromagnetic. To quantify the nature and magnitude of the nickel(II)–nickel(II) interaction, the experimental magnetic properties of [NiII3LaIII(LPr)] were modelled.
As a first approximation, a simple approach was developed that treats all three paramagnetic nickel(II) ions as equivalent and assumes one interaction, J1, between adjacent metal ion centres (Fig. 5). This model is similar to that used for [CuII3LaIII(LPr)],13 except with nickel(II) ions in place of the copper(II) ions. From this structural motif, the resulting Heisenberg spin Hamiltonian used to calculate the magnetic susceptibility is:
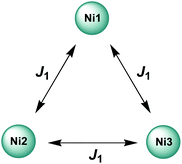 | ||
| Fig. 5 Scheme of the spin and exchange interaction topologies in [NiII3LaIII(LPr)] and [NiII3LuIII(LPr)]. | ||
From this model, the application of the van Vleck equation30 allows a determination of the low field (μBH/kBT ≪ 1) analytical expression of the magnetic susceptibility.31 The temperature dependence of the χT product was reproduced well with weak and equal antiferromagnetic coupling between the nickel(II) ions (J1/kB = −0.50(2) K and g = 2.13(5), Fig. 6). As an aside, [NiII3LuIII(LPr)], which also features a diamagnetic lanthanide ion (lutetium), could also have been used for this analysis (Fig. 6; J1/kB = −0.45(2) K and g = 2.15(5)). The good fit of the experimental data suggests that the simple approximation shown in Fig. 5 is accurate enough for the purposes of the analysis.
The nickel(II)–nickel(II) exchange interactions are similar (and weak) enough that only one coupling parameter is required (rather than JNi1–Ni2, JNi2–Ni3 and JNi3–Ni1) to model the experimental data above 1.8 K. It appears the subtle geometric differences between each NiII–catecholate–NiII moiety are not significant magnetically. The weakness of the interaction is probably because the interaction is via the multi-atom delocalised π system of (LPr)6− rather than via a single atom bridge.
For nine of the complexes, [NiII3CeIII(LPr)], [NiII3PrIII(LPr)], [NiII3NdIII(LPr)], [NiII3SmIII(LPr)], [NiII3EuIII(LPr)], [NiII3HoIII(LPr)], [NiII3ErIII(LPr)], [NiII3TmIII(LPr)] and [NiII3YbIII(LPr)], the χT product is either almost constant down to low temperatures or shows only a slight decrease due to thermal depopulation of excited sublevels (Fig. 4, S3–S7 and S11–S14, ESI†). Below about 50 K, there is a more pronounced decrease of the χT product on further decreasing the temperature, consistent with weak antiferromagnetic nickel(II)–nickel(II) coupling, as observed for [NiII3LaIII(LPr)] and [NiII3LuIII(LPr)], and only weak nickel(II)–lanthanide(III) coupling (otherwise the χT product would be expected to have stronger temperature dependence).
Due to the isotropic nature of the gadolinium(III) ion, the temperature dependence of the χT product of [NiII3GdIII(LPr)] above 5 K is only representative of the interactions between the metal ions (Fig. 7).
The increase in the χT product from a minimum at room temperature to a maximum at 3.5 K is consistent with a dominant ferromagnetic nickel(II)–gadolinium(III) interaction (over the antiferromagnetic nickel(II)–nickel(II) interaction that was identified in [NiII3LaIII(LPr)]), with the subsequent small decrease in the χT product from 3.5 to 1.9 K probably due to the intermolecular antiferromagnetic interactions. As a result of too large a number of adjustable parameters (i.e. overparametrization) attempts to fit both the χT versus T and M versus H experimental data with the same model failed to give a self-consistent set of magnetic parameters even when including intra-complex magnetic interactions and the magnetic anisotropy of the nickel(II) ions. Therefore, only the χT versus T data have been fitted with the following Heisenberg spin Hamiltonian:
The model only produces an acceptable fit to the experimental data when inter-complex magnetic interactions in the frame of the mean field approximation are introduced, keeping in mind that this additional parameter might also include phenomenologically the magnetic anisotropy of the NiII sites. Therefore the susceptibility is given by:
An excellent simulation of the experimental χT vs. T data is obtained with this model, with JNi–Ni/kB = −0.02(2) K, JNi–Gd/kB = +2.6(1) K, g = 2.00(5) and zJ′/kB = −0.021(5) K, down to 1.8 K (Fig. 7). This result is also consistent with the presence of weak antiferromagnetic coupling between the well separated S = 1 NiII spins while ferromagnetic interactions dominate between the NiII spins and the S = 7/2 GdIII spins within the [NiII3GdIII(LPr)] complex, mediated by the single oxygen atom bridge between them, leading to an ST = 13/2 spin ground state (the S = 11/2 excited state lies 5 K above it in energy).
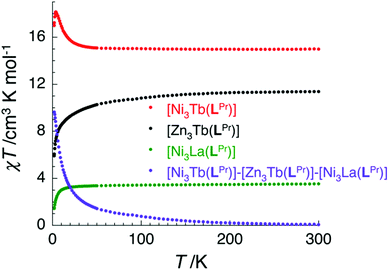
In the case of [NiII3TbIII(LPr)] and [NiII3DyIII(LPr)], the temperature dependence of the χT product is very similar (Fig. 4, 8, S9, S10 and S16†). As the temperature is lowered, the value remains fairly constant until around 50 K, at which point it increases to a maximum at very low temperature. The χT product then decreases slightly until the temperature limit of the measurement (1.8 K). It is usually difficult to determine the nature of the exchange interactions in 3d–4f complexes because of thermal depopulation of excited sublevels of the 2S+1LJ ground state of the lanthanide(III) ion. In our case, comparing the magnetic data with that of the appropriate analogues [NiII3LaIII(LPr)] and [ZnII3LnIII(LPr)]12 allows a qualitative estimation of the 3d–4f interactions by removing the contributions of the 3d–3d interactions and the intrinsic nickel(II) and lanthanide(III) paramagnetism. As shown in Fig. 8 and S16,† the resulting χT product difference plot exhibits a minimum at room temperature before increasing to a maximum at 1.8 K, suggesting that the nickel(II)–terbium(III) and nickel(II)–dysprosium(III) interaction are ferromagnetic.
The field dependence of magnetisation was measured for all fourteen complexes to check for hysteresis of magnetisation, as this is the best evidence of SMM behaviour. However, even at 1.8 K, there is no sign of hysteresis behaviour for any of these complexes when scanning at 100–200 Oe min−1 (Fig. S17–S30, ESI†).
The presence of significant magnetic anisotropy in all of the complexes is confirmed by the field dependence of reduced magnetisation plots (M vs. H/T). In all cases, these show non super-imposable data on a single master curve (Fig. S17–S30, ESI†) and, as expected for significantly anisotropic systems, there is no saturation of the magnetisation at 1.8 K and 70 kOe. Interestingly, the M vs. H/T plots for [NiII3LnIII(LPr)] with LnIII = diamagnetic LaIII/LuIII or isotropic GdIII do not show super-imposable data on a single master curve indicating the presence of low lying excited states and likely a minor contribution from the magnetic anisotropy of the nickel(II) ions (Fig. S17, S23 and S30, ESI†).
The ac susceptibility of all fourteen complexes was measured to check for possible slow relaxation of the magnetisation. At 1.8 K, there was no out-of-phase component for any of the complexes, which indicates there is no appreciable energy barrier to spin reversal (Fig. S21–S44, ESI†).
Conclusions
The template procedure we reported for the generation of large families of [ZnII3LnIII] and [CuII3LnIII] macrocyclic complexes has been extended to the preparation of a family of [NiII3LnIII] macrocyclic complexes. The resulting fourteen complexes vary in the identity of the lanthanide(III) ion present. Although none of the complexes displayed SMM behaviour, this study further illustrates the robustness and versatility of this system in the preparation of a wide range of analogous complexes. Our attention is now focussed on extending this study from the late transition metal ions towards the mid-transition metal ions with a view to elucidating the factors which induce slow relaxation of the magnetisation in 3d/4f blends. Furthermore, it will be of interest to incorporate trivalent 3d ions such as manganese(III) which should provide anisotropy as well as a larger spin.Acknowledgements
This work was supported by grants from the MacDiarmid Institute for Advanced Materials and Nanotechnology (including a PhD scholarship to SD), the University of Otago (including a PhD scholarship to HLCF) as well as the award of a Julius von Haast Fellowship (RSNZ) to AKP, hosted by SB. We also thank the University of Bordeaux, the CNRS, the Région Aquitaine and the Dumont d'Urville NZ-France Science & Technology Support Programme which supported research exchange visits between Bordeaux and Otago (no. 23793PH).Notes and references
- D. Gatteschi, R. Sessoli and F. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236 CrossRef CAS PubMed.
- See for example: G. Aromí and E. K. Brechin, Struct. Bonding, 2006, 122, 1 CrossRef CAS; M. Murrie, Chem. Soc. Rev., 2010, 39, 1986 RSC; T. Glaser, Chem. Commun., 2011, 47, 116 RSC; P. Happ, C. Plenk and E. Rentschler, Coord. Chem. Rev., 2015, 289, 238 CrossRef PubMed; T. Glaser, V. Hoeke, K. Gieb, J. Schnack, C. Schröder and P. Müller, Coord. Chem. Rev., 2015, 289, 261 CrossRef PubMed.
- See for example: R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328 CrossRef CAS PubMed; J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC; J. Luzona and R. Sessoli, Dalton Trans., 2012, 41, 13556 RSC; D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef PubMed; P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2015, 44, 3923 RSC.
- See for example: R. A. Layfield, Organometallics, 2014, 33, 1084 CrossRef CAS.
- See for example: H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1 CrossRef CAS PubMed.
- See for example: K. R. Meihaus and J. R. Long, Dalton Trans., 2015, 44, 2517 RSC.
- See for example: M. Andruh, J.-P. Costes, C. Diaz and S. Gao, Inorg. Chem., 2009, 48, 3342 CrossRef CAS PubMed; K. Liu, W. Shi and P. Cheng, Coord. Chem. Rev., 2014, 289–290, 74 Search PubMed; K. S. Pedersen, J. Bendix and R. Clérac, Chem. Commun., 2014, 50, 4396 RSC; S. Dhers, H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2015, 296, 24 CrossRef PubMed.
- N. Ishikawa, Polyhedron, 2007, 26, 2147 CrossRef CAS PubMed.
- M. Gonidec, E. S. Davies, J. McMaster, D. B. Amabilino and J. Veciana, J. Am. Chem. Soc., 2010, 132, 1756 CrossRef CAS PubMed; M. Gonidec, F. Luis, À. Vílchez, J. Esquena, D. B. Amabilino and J. Veciana, Angew. Chem., Int. Ed., 2010, 49, 1623 CrossRef PubMed; P.-E. Car, M. Perfetti, M. Mannini, A. Favre, A. Caneschi and R. Sessoli, Chem. Commun., 2011, 47, 3751 RSC; M. Gonidec, D. B. Amabilino and J. Veciana, Dalton Trans., 2012, 41, 13632 RSC; G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606 CrossRef PubMed; U. J. Williams, B. D. Mahoney, P. T. DeGregorio, P. J. Carroll, E. Nakamaru-Ogiso, J. M. Kikkawa and E. J. Schelter, Chem. Commun., 2012, 48, 5593 RSC; H. Wang, K. Wang, J. Tao and J. Jiang, Chem. Commun., 2012, 48, 2973 RSC; M.-E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem., Int. Ed., 2013, 52, 350 CrossRef PubMed; C. R. Ganivet, B. Ballesteros, G. d. l. Torre, J. M. Clemente-Juan, E. Coronado and T. Torres, Chem. – Eur. J., 2013, 19, 1457 CrossRef PubMed.
- H. L. C. Feltham, Y. Lan, F. Klöwer, L. Ungur, L. F. Chibotaru, A. K. Powell and S. Brooker, Chem. – Eur. J., 2011, 17, 4362 CrossRef CAS PubMed.
- H. L. C. Feltham, F. Klöwer, S. A. Cameron, D. S. Larsen, Y. Lan, M. Tropiano, S. Faulkner, A. K. Powell and S. Brooker, Dalton Trans., 2011, 40, 11425 RSC.
- H. L. C. Feltham, R. Clérac, A. K. Powell and S. Brooker, Inorg. Chem., 2011, 50, 4232 CrossRef CAS PubMed.
- H. L. C. Feltham, R. Clérac, L. Ungur, V. Vieru, L. F. Chibotaru, A. K. Powell and S. Brooker, Inorg. Chem., 2012, 51, 10603 CrossRef CAS PubMed.
- A. Yamashita, A. Watanabe, S. Akine, T. Nabeshima, M. Nakano, T. Yamamura and T. Kajiwara, Angew. Chem., Int. Ed., 2011, 50, 4016 CrossRef CAS PubMed.
- S. Dhers, H. L. C. Feltham, R. Clérac and S. Brooker, Inorg. Chem., 2013, 52, 13685 CrossRef CAS PubMed.
- H. L. C. Feltham, R. Clérac, L. Ungur, L. F. Chibotaru, A. K. Powell and S. Brooker, Inorg. Chem., 2013, 52, 3236 CrossRef CAS PubMed.
- S. Akine, T. Taniguchi and T. Nabeshima, Tetrahedron Lett., 2001, 42, 8861 CrossRef CAS.
- S. Akine, T. Taniguchi and T. Nabeshima, J. Am. Chem. Soc., 2006, 128, 15765 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- P. van der Sluis and A. L. Spek, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1990, 46, 194 CrossRef.
- S. Yamada, E. Ohno, Y. Kuge, A. Takeuchi, K. Yamanouchi and K. Iwasaki, Coord. Chem. Rev., 1968, 3, 247 CrossRef CAS; M. G. B. Drew, R. N. Prasad and R. P. Sharma, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1985, 41, 1755 CrossRef; Y. Elerman, M. Kabak and O. Atakol, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1993, 49, 1905 CrossRef.
- C. Arici, I. Svoboda, M. Sari, O. Atakol and H. Fuess, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 31 Search PubMed; O. Atakol, H. Nazir, C. Arici, S. Durmus, I. Svoboda and H. Fuess, Inorg. Chim. Acta, 2003, 342, 295 CrossRef CAS.
- N. H. Pilkington and R. Robson, Aust. J. Chem., 1970, 23, 2225 CAS.
- H. Okawa and S. Kida, Bull. Chem. Soc. Jpn., 1972, 45, 1759 CrossRef CAS.
- A. J. Atkins, D. Black, A. J. Blake, A. Marin-Becerra, S. Parsons, L. Ruiz-Ramirez and M. Schroder, Chem. Commun., 1996, 457 RSC; S. Brooker, Coord. Chem. Rev., 2001, 222, 33 CrossRef CAS.
- W. J. Geary, Coord. Chem. Rev., 1971, 7, 81 CrossRef CAS.
- M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, in SHAPE: Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous Shape Measures and Associated Tools, Barcelona, 2013 Search PubMed.
- M. G. B. Drew, C. J. Harding, V. McKee, G. G. Morgan and J. Nelson, J. Chem. Soc., Chem. Commun., 1995, 1035 RSC; F. A. Deeney, J. H. Charles, G. G. Morgan, V. McKee, J. Nelson, S. J. Teat and W. Clegg, J. Chem. Soc., Dalton Trans., 1998, 1837 RSC; P. Guionneau, C. Brigouleix, Y. Barrans, A. E. Goeta, J.-F. Létard, J. A. K. Howard, J. Gaultier and D. Chasseau, C. R. Acad. Sci., Ser. IIc: Chim., 2001, 4, 161 CrossRef CAS.
- J. H. van Vleck, The Theory of Electric and Magnetic Susceptibility, Oxford University Press, 1932 Search PubMed.
- M. Murugesu, R. Clérac, C. E. Anson and A. K. Powell, J. Phys. Chem. Solids, 2004, 65, 667 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional dc and ac magnetic data and selected crystallographic details for [NiII3YbIII(LAld)3(NO3)2(MeOH)4.75(H2O)1.25](NO3). CCDC 913628 and 913629. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00130g |
| This journal is © the Partner Organisations 2015 |