Single-molecule magnet involving strong exchange coupling in terbium(III) complex with 2,2′-bipyridin-6-yl tert-butyl nitroxide

Abstract

A novel terbium(III)-radical complex [Tb^III(hfac)₃(6bpyNO)] (Tb-6bpyNO; 6bpyNO = 2,2′-bipyridin-6-yl tert-butyl nitroxide) was synthesized. The intramolecular antiferromagnetic interaction in Tb-6bpyNO was confirmed by comparison with the magnetic properties of [Tb^III(hfac)₃(6bpyCO)] (Tb-6bpyCO; 6bpyCO = 2,2′-bipyridin-6-yl tert-butyl ketone) together with [Y^III(hfac)₃(6bpyNO)]. Tb-6bpyNO showed a hysteresis loop with negligible coersivity below 1.6 K. The dispersion of the magnetic susceptibility with an applied bias field of 2000 Oe gave the energy barrier E_a/k_B = 21.1(8) K. In contrast, Tb-6bpyCO did not behave as a single-molecule magnet, despite having practically the same crystal field.

---

Introduction

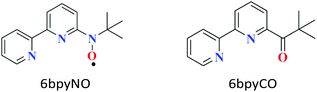
Molecule-based magnetic materials have the advantage of being able to arrange a variety of magnetic orbitals, which results in single-molecule magnets (SMMs) as well as interesting exchange-coupled systems.¹ Recently, 4f-ion-based heterospin compounds have been intensively studied for the development of SMMs,^2,3 because a strong magnetic anisotropy and large magnetic moment are available from lanthanoid (Ln) ions.⁴ When the spin centre of a paramagnetic ligand is bonded to a metal ion, the metal-radical complex shows strong exchange coupling via direct coordination. The 6bpyNO radical (6bpyNO = 2,2′-bipyridin-6-yl tert-butyl nitroxide; Scheme 1) has been synthesized for obtaining strong exchange coupling in transition metal-radical complexes.⁵ Recently, lanthanoid-radical complexes (4f–2p heterospin systems) have been the subject of intense research activity.^6,7 We utilized 6bpyNO as a component of 4f–2p systems and found that [Gd^III(hfac)₃(6bpyNO)] (abbreviated as Gd-6bpyNO hereafter; Hhfac = 1,1,1,5,5,5-hexafluoropentane-2,4-dione) possesses the largest exchange coupling (2J/k_B = –15.9(2) K) of all the Gd-nitroxide coordination compounds ever previously reported.⁸

Scheme 1 Structural formula of 6bpyNO and 6bpyCO.

In the present work, we have synthesized the corresponding Tb analogue, Tb-6bpyNO, and investigated its magnetic properties to understand the role of the ligand spin when introduced to SMMs, which would be useful to create new heterospin compounds and SMMs. The present work also covers the empirical Δ(χ_mT) method⁹ using 2p-spin masked 6bpyCO (2,2′-bipyridin-6-yl tert-butyl ketone; Scheme 1) and clarifies the nature of intramolecular Tb–radical exchange coupling.

Results and discussion

Synthesis and description of the crystal structure

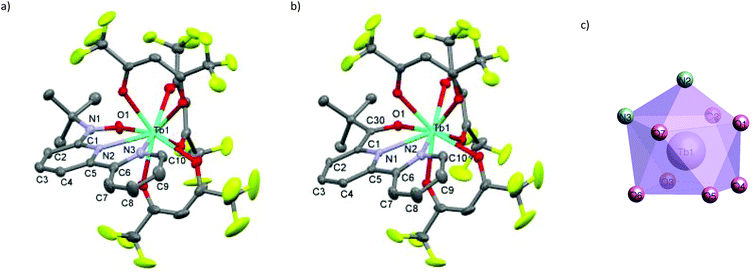
We synthesized RE-6bpyNO (RE = Tb, Y) according to the method developed for the RE = Gd analogue with a slight modification.⁸ The Y³⁺ ion has often been used as a diamagnetic metal centre because the ionic radius is close to those of the heavy lanthanide ions (0.90 Å for Y³⁺vs. 0.94 Å for Gd³⁺ and 0.92 Å for Tb³⁺).¹⁰ The products are stable at room temperature under air. Fine crystals were obtained and subjected without further purification to spectroscopic, X-ray crystallographic and magnetic analyses. The crystallography results are given in Table 1. RE-6bpyNO (RE = Tb, Y) crystallizes in a monoclinic P2₁/n space group, being completely isomorphous to Gd-6bpyNO (Fig. 1a).

Fig. 1 X-ray structures of (a) Tb-6bpyNO and (b) Tb-6bpyCO. Thermal ellipsoids are drawn at the 50% probability level. Hydrogen atoms are omitted for the sake of clarity. (c) Capped square antiprism structure in Tb-6bpyNO.

Table 1 Selected crystallographic data, bond lengths (Å), bond angles (°) and torsion angles (°) for RE-6bpyNO (RE = Gd^a, Tb, Y) and Tb-6bpyCO

Compound	Gd-6bpyNO	Tb-6bpyNO	Y-6bpyNO		Tb-6bpyCO
a Ref. 8. b R = ∑||Fo| − |Fc||/∑|Fo|. c R w = [∑w(Fo^2 − Fc^2)^2/∑w(Fo^2)^2]^1/2.
Formula	C29H19F18N3O7Gd	C29H19F18N3O7Tb	C29H19F18N3O7Dy		C30H19F18N2O7Tb
Formula weight	1020.71	1022.38	952.36		1020.39
T/K	100	100	100		100
Crystal system	Monoclinic	Monoclinic	Monoclinic		Monoclinic
Space group	P21/n	P21/n	P21/n		P21/n
a/Å	13.467(3)	13.433(2)	13.392(2)		13.456(3)
b/Å	17.045(4)	17.068(3)	17.074(3)		17.130(3)
c/Å	16.692(4)	16.695(2)	16.648(2)		16.654(3)
β/°	105.43(1)	105.208(7)	105.114(7)		105.460(8)
V/Å^3	3694(2)	3693.8(9)	3675.0(9)		3700(1)
Z	4	4	4		4
D calc/g cm^−3	1.835	1.838	1.721		1.832
μ (MoKα)/mm^−1	1.939	2.049	1.728		2.045
R(F)^b (I > 2σ(I))	0.0463	0.0424	0.0633		0.0340
R w (F^2)^c (all data)	0.0482	0.0530	0.0855		0.0434
Goodness-of-fit	1.148	1.098	1.037		1.077
RE1–O1/Å	2.373(4)	2.365(4)	2.333(3)	Tb1–O1/Å	2.396(3)
RE1–N2/Å	2.560(4)	2.550(3)	2.539(3)	Tb1–N1/Å	2.569(3)
RE1–N3/Å	2.568(4)	2.547(4)	2.539(4)	Tb1–N2/Å	2.559(3)
RE1–O1–N1/°	126.2(3)	126.3(3)	126.1(3)	Tb1–O1–C30/°	127.8(2)
RE1–O1–N1–C1/°	–16.5(5)	–16.6(5)	–15.4(5)	Tb1–O1–C30–C1/°	–13.1(4)

---

The RE³⁺ centre is nine-coordinate including two RE–N and one RE–O bond from the chelate ligand 6bpyNO. The other six bonds involve oxygen atoms from three hfac coligands. The coordination polyhedron can be best described as a capped square antiprism (CSAPR) with N2 as a cap (Fig. 1c). We further confirmed the CSAPR structure around the Tb and Y ions‡ using the SHAPE program.¹¹ A magnetic axial anisotropy is expected in the CSAPR structure. Important geometrical parameters possibly relating to the intramolecular 4f–2p exchange coupling, such as bond lengths (RE–O1, RE–N1 and RE–N2), bond angles (RE1–O1–N1) and torsion angles (RE1–O1–N1–C1), are summarized in Table 1.

We also prepared and characterized Tb-6bpyCO (Fig. 1b) as a radical-spin silent reference. Crystallographic analysis clarified that it is isostructural to the 6bpyNO analogues (Table 1). A carbonyl group (C30–O1 in Fig. 1b) provides a ligating oxygen atom in place of the nitroxide group (N1–O1 in Fig. 1a). The Tb ion in Tb-6bpyCO also has a CSAPR structure. Furthermore the shape measurement results for Tb-6bpyNO and Tb-6bpyCO are quite close to each other,‡ in particular 0.241 and 0.249, respectively, for the CSAPR, according to the SHAPE program.¹¹ This finding suggests that Tb-6bpyCO is a suitable model for reproducing the crystal field around the Tb ion in Tb-6bpyNO.

Magnetic properties

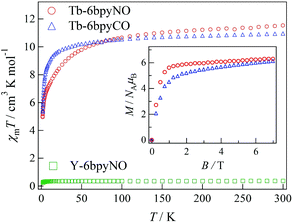
The direct current (dc) magnetic susceptibilities of Tb-6bpyNO, measured at an applied magnetic field of 5000 Oe in a temperature range of 1.8–300 K, are displayed in Fig. 2. The specimen was fixed with a small amount of mineral oil. At 300 K, the χ_mT value was 11.5 cm³ K mol⁻¹ for Tb-6bpyNO. This is close to the theoretical value at the high-temperature limit (12.2 cm³ K mol⁻¹ as the sum from J^z = 6, g_J = 3/2 for a free Tb³⁺ ion and S = 1/2, g = 2 for an organic radical). On cooling, the χ_mT value monotonically decreased to 5.17 cm³ K mol⁻¹ at 2 K. Since we used powder samples, the major part of the reduction is caused by the anisotropy of the Ln ions. It should be noted that the χ_mT value of a radical spin is as small as 0.38 cm³ K mol⁻¹ and is minor compared to the large reduction.

Fig. 2 Temperature dependence of χ_mT for Tb-6bpyNO (red circle), Y-6bpyNO (green square) and Tb-6bpyCO (blue triangle), measured at 5000 Oe. Inset: magnetization curves for Tb-6bpyNO (red circle) and Tb-6bpyCO (blue triangle), measured at 1.8 K.

We tried to obtain a clue for the nature of the magnetic coupling using a conventional approach. For 4f–3d heterospin systems there has been an empirical method known, where the χ_mT difference between the heterospin compound and 3d-spin masked reference is evaluated.⁹ On the other hand, corresponding researches for 4f–2p systems are somewhat rare.¹² Some “nitronyl nitroxide” complexes have been modelled with nitrone complexes^12,13 (“nitronyl nitroxide” stands for 4,4,5,5-tetramethylimidazolin-1-oxyl 3-oxide). Alternatively, a succinimide has also been proposed as a diamagnetic model.¹⁴ In the present case, 6bpyCO is rationally assumed as a diamagnetic reference for 6bpyNO.

Actually, Tb-6bpyCO was found to be isomorphous to Tb-6bpyNO (see above). The results of magnetic susceptibility for the two model compounds are superimposed in Fig. 2. The data on Tb-6bpyCO involve only the contribution of Tb³⁺ with the single-ion magnetic anisotropy regulated by the crystal field, and the data on Y-6bpyNO contain only the contribution of the radical spin affected by the radical–radical intermolecular interactions. Hence, the difference Δ(χ_mT) = (χ_mT)_Tb-6bpyNO − (χ_mT)_Y-6bpyNO − (χ_mT)_Tb-6bpyCO implies the nature of the overall exchange interactions between Tb³⁺ and the radical spins. Positive and negative values of Δ(χ_mT) are directly related to ferro- and antiferromagnetic interactions, respectively. The temperature dependence of Δ(χ_mT) is displayed in Fig. 3. The Δ(χ_mT) shows a large negative value in the wide range below ca. 250 K. At the lowest temperature region below 10 K, an upturn appeared, possibly ascribed to the effect of intermolecular interactions or slight differences of the crystal fields between Tb-6bpyNO and Tb-6bpyCO.

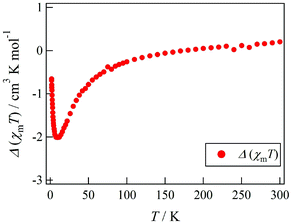Fig. 3 Temperature dependence of Δ(χ_mT) as defined by Δ(χ_mT) = (χ_mT)_Tb-6bpyNO − (χ_mT)_Y-6bpyNO − (χ_mT)_Tb-6bpyCO.

The field dependence of the magnetizations measured using SQUID at 1.8 K is shown in the inset of Fig. 2. The specimens were not fixed, so that the microcrystalline specimens would be aligned in the field direction. The magnetizations tend to saturate in higher fields and the value was 6.28μ_B at 7 T for Tb-6bpyNO. The expected value is 8 μ_B from the subtraction of those values for a free Tb³⁺ ion and 6bpyNO radical. There are two molecular directions in a unit cell, and the CSAPR principal axes are canted by 43° to each other, which was estimated using the Tb1–N2 bond directions. Thus, we have to reduce the saturation moments by about 7% from those of the single site values, giving 7.4μ_B. The reduction in the measured magnetization may be caused by the imperfect field-alignment. The magnetization of Tb-6bpyCO also shows gradual saturation and the value was 6.12μ_B at 7 T. The larger slope found around 7 T is compatible with the uncompensated magnetization of the Tb³⁺ ions. However, it is difficult to distinguish between the effect of intramolecular exchange coupling and that of the Tb³⁺ single ion anisotropy from these magnetization curves.

Let us compare the strong antiferromagnetic coupling found in the present system with the results of a similar system. Another 4f–2p heterospin system, [RE^III(hfac)₃(2pyNO)] (RE-2pyNO), has been developed through the use of tert-butyl 2-pyridyl nitroxide (2pyNO).^15,16 Relatively strong antiferromagnetic 4f–2p exchange coupling was characterized in Gd-2pyNO¹⁵ like Gd-6bpyNO.⁸ The antiferromagnetic coupling in Tb-2pyNO was precisely evaluated by means of inelastic neutron scattering and high-frequency electron paramagnetic reasonance.¹⁷ In the 6bpyNO system, although conventional experimental methods were utilized, Gd- and Tb-6bpyNO were both clarified to have intramolecular antiferromagnetic coupling. It is likely that the antiferromagnetic coupling is considerable in Tb-6bpyNO from the notably negative Δ(χ_mT) even around 100 K. This notion is consistent with the empirical rule that the sign of exchange coupling is common among the heterospin molecules of Gd³⁺ and heavy lanthanide ions coupled with 3d transition metal ions¹⁸ and radicals.¹⁷ Unfortunately, the Δ(χ_mT) method could not afford any further quantitative information.

Dynamic magnetic properties

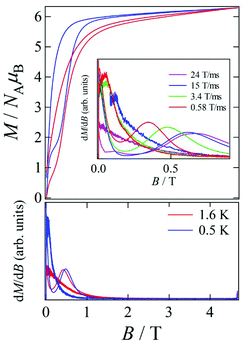
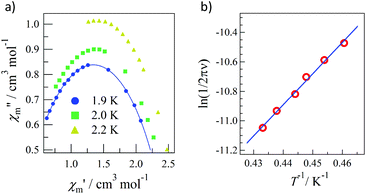
Pulsed-field magnetization experiments¹⁹ on Tb-6bpyNO were carried out using a ³He cryostat (Fig. 4). Hysteresis and magnetization jumps were found at 0.5 and 1.6 K, and the derivative of the magnetization clarifies the apparent coercive field of about 0.5 T. The field position depends slightly on temperature and field-sweeping rate, which shows the role of thermal relaxation.

Fig. 4 Pulsed-field magnetization curves (top) and the corresponding dM/dB vs. B plots (bottom) for Tb-6bpyNO measured at 0.5 and 1.6 K. The inset shows the corresponding dM/dB vs. B plots for Tb-6bpyNO at various field-sweeping rates.

As the applied field was removed, the magnetization quickly disappeared (Fig. 4); namely, the coersivity does not appear from a bulk origin. It should be noted that the downward sweep is much slower than the upward sweep for the non-symmetric pulse shape. To investigate the dynamics of the magnetization reversal, we measured the alternating current (ac) magnetic susceptibility. Fig. 5a shows the in-phase and out-of-phase portions of the ac magnetic susceptibility (χ^′_m and χ^′′_m, respectively) for Tb-6bpyNO, measured without any applied dc field. No appreciable χ^′′_m was recorded, consistent with the fast relaxation of magnetization found in the pulsed-field experiments. On the other hand, when a direct current (dc) bias field²⁰ of 2000 Oe was applied, a decrease in χ^′_m and concomitant increase in χ^′′_m were recorded (Fig. 5b). Frequency dependence was also observed. When we plotted the χ^′′_m against χ^′_m for various temperatures according to Cole–Cole analysis,²¹ a semicircle was drawn for 1.9 K with α = 0.236(2) (Fig. 6a). The α value in the Debye model is relatively small in χ(ω) = χ_S + (χ_T − χ_S)/(1 + (1ωτ)^1−α), where χ_T and χ_S are the isothermal and adiabatic susceptibilities, respectively.²² This finding guarantees a single relaxation process in each molecule. The Arrhenius plot for Tb-6bpyNO (Fig. 6b) shows a straight line for the data of the χ′′ peak in Fig. 5b, and the activation energy (E_a) for the magnetization reversal was estimated as E_a/k_B = 21.1(8) K with τ₀ = 1.7(6) × 10⁻⁹ s, where τ₀ stands for the pre-exponential factor in the Arrhenius equation, ln(2πν) = ln(τ₀) + E_a/k_B.²³

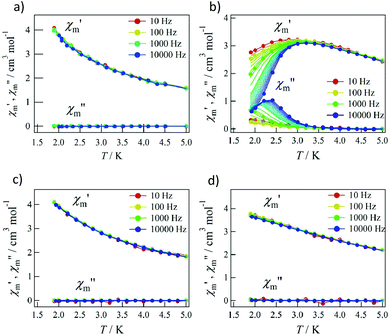Fig. 5 The ac magnetic susceptibilities for Tb-6bpyNO at applied dc bias fields of (a) 0 Oe and (b) 2000 Oe and for Tb-6bpyCO at applied dc bias fields of (c) 0 Oe and (d) 2000 Oe.

Fig. 6 (a) Cole–Cole plot and (b) Arrhenius plot for Tb-6bpyNO.

In the magnetic field, splitting of the lowest doublet causes a Zeeman energy gap. For 7.4μ_B per molecule and 2000 Oe the gap is about 2 K. This gap is minor compared to the energy gap obtained using the Arrhenius plot, and the main cause of the activation energy is the anisotropy of the Tb-6bpyNO molecule as a SMM.

A square antiprismatic (SAPR) coordination polyhedron seems to be suitable from the strong axial anisotropy and the energy gap is quite large between the ground state (J^z = 6) and lowest-excited state (J^z = 5) for a Tb³⁺ ion.^4,24,25 It has already been clarified that SAPR-configured Tb-2pyNO was a SMM.¹⁶ In the present work, the coordination structure of Tb-6bpyNO belongs to CSAPR, which is similar to SAPR. It is natural that both Tb-6bpyNO and Tb-2pyNO behave as SMMs. However, the crystal field effect is not a decisive factor, as follows.

Tb-6bpyNO affords one of the best opportunities where we can assess the role of paramagnetic ligands in SMMs through comparing with a reference compound with the 2p-spin masked. The ac magnetic susceptibility measurements on Tb-6bpyCO displayed no χ^′′_m at 0 Oe or even at a 2000 Oe dc bias field (Fig. 5c and d). This remarkable difference is hard to understand because the energy barrier caused by the Tb³⁺ anisotropy should be nearly identical between Tb-6bpyNO and Tb-6bpyCO. Long et al. have noted that the bistability is not guaranteed for a non-Kramers Tb³⁺ ion and accordingly a suitable crystal field is required so that Tb³⁺ can acquire axial magnetic anisotropy.²⁴ If strong axial magnetic anisotropy is present, both Tb-6bpyNO and Tb-6bpyCO should behave as SMMs, which contradicts the present experimental results. At this point it is noticed that the even/odd components of the total magnetic moment are different between the two species, which is related to the Kramers theorem. The ground total spin of Tb-6bpyNO is 5/2 (a Kramers molecule) whilst that of Tb-6bpyCO is 3 (a non-Kramers molecule), assuming that the spin–spin coupling is strong enough, compared with cryogenic temperatures.

The presence of a 2p spin is critical for SMM performance in the present study. One may be reminded of the studies on [Tb(pc)₂]⁰ and [Tb(pc)₂]⁻ (pc = phthalocyaninate).^4,26 Only the former has a delocalized π spin on the (pc)₂ moiety. The SMM performance of the former was found to be better,²⁶ which can be also interpreted from an odd/even nature of the ground state moments. Another example is found in the fact that SMM behaviour of non-Kramers Dy-2pyNO or Dy-6bpyNO has never been reported.¹⁶ In fact, no meaningful χ^′′_m was observed for Dy-2pyNO or Dy-6bpyNO (Fig. S1 and S2, ESI†). Establishment of the spin-parity effect²⁷ may need further theoretical clarification, but control of the relaxation by radical spin modification would lead to a new functionality of molecule-based magnets.

Finally we comment on the comparison with Tb-2pyNO, showing large coercivity and slow magnetization reversal in the ac magnetic susceptibility.¹⁶ It is known that magnetization reversal is sensitive to the relaxations caused by hyperfine couplings,²⁸ dipolar interactions in Ln ions,²⁹ and weak f–d and f–p exchange couplings.^30,31 It is noticed that the CSAPR principal axes of monoclinic Tb-6bpyNO are canted by 43° between neighbouring molecules. On the other hand, Tb-2pyNO crystallizing in a triclinic P_1̄ space group¹⁶ exhibits a cant angle of only ca. 5° between two independent molecules. This difference may affect the relaxation along with the dipolar interactions and the intramoleculer interactions. This is because the transverse components of fluctuating magnetic fields dominating the relaxation are enhanced by the tilting of the principle axes.

Conclusions

We have successfully prepared Tb-6bpyNO as an exchange-involving SMM or single-ion magnet. Intramolecular antiferromagnetic coupling was indicated using the empirical Δ(χ_mT) method after a corresponding carbonyl compound was proposed as a 2p-spin-masked reference. Tb-6bpyNO behaved as a SMM with E_a/k_B = 21.1(8) K and τ₀ = 1.7(6) × 10⁻⁹ s at the external dc bias of 2000 Oe. The 4f–2p heterospin approach seems to be one of the promising strategies toward novel SMMs. Relaxation by the parity effect is also discussed in terms of the marked differences of the SMM characteristics with and without a radical spin.

Experimental section

Synthesis

6bpyNO was synthesized using the method reported in the literature.⁵ The complexes RE-6bpyNO (RE = Tb, Y) were prepared from [RE^III(hfac)₃(H₂O)₂] (RE = Tb, Y)³² and 6bpyNO in a dichloromethane–n-heptane mixed solvent, according to the procedure known for the Gd analogue.⁸

[Tb^III(hfac)₃(6bpyNO)] (Tb-6bpyNO). The yield was 58%. Mp. 140–146 °C (decomp.). Anal. Calcd for C₂₉H₁₉N₃O₇F₁₈Tb: C, 34.07; H, 1.87; N, 4.11%. Found: C, 33.74; H, 1.70; N, 3.99%. IR (neat, attenuated total reflection (ATR)) 1651, 1488, 1249, 1190, 1133, 1096, 795, 773, 659, 582 cm⁻¹.

[Y^III(hfac)₃(6bpyNO)] (Y-6bpyNO). The yield was 61%. Mp. 168–170 °C (decomp.). Anal. Calcd for C₂₉H₁₉N₃O₇F₁₈Y: C, 36.57; H, 2.01; N, 4.41%. Found: C, 36.07; H, 2.22; N, 4.35%. IR (neat, ATR) 1655, 1491, 1251, 1190, 1137, 1099, 796, 773, 660, 584 cm⁻¹.

2,2′-Bipyridin-6-yl tert-butyl ketone (6bpyCO). 6bpyCO was prepared according to the synthesis of tert-butyl 2-(5-methylpyridyl) ketone,³³ using 6-bromo-2,2′-bipyridine in place of 2-bromo-5-methylpyridine as a starting material. To a suspension of 6-bromo-2,2′-bipyridine (2.52 g, 10.7 mmol) in dry ether (30 mL) was added dropwise n-BuLi (1.60 mol L⁻¹ in n-hexane, 7.4 mL, 12 mmol) at −76 °C. The mixture was stirred at −76 °C for 1 h, and the resultant solution was added dropwise to a solution of pivaloyl chloride (2.6 mL, 21 mmol) in dry THF (5 mL). The mixture was stirred at 0 °C for 15 h and then further stirred at room temperature for 2 h. The reaction mixture was quenched with cooled water followed by cold 40% NaOH aqueous solution, and stirred for 30 min. After the aqueous layer was extracted with ether, the combined organic layer was dried over anhydrous MgSO₄. The filtrate was concentrated under reduced pressure, and the resulting brown oil was purified using HPLC (1H + 2H gel-permeation columns (Japan Analytical Industry), eluted with CHCl₃) to yield a green oil. The yield was 422 mg (1.76 mmol, 16%). ¹H NMR (500 MHz, CDCl₃): δ 8.69 (dd, J = 4.2, 1.6 Hz, 1H), 8.56 (dd, J = 7.7, 1.7 Hz, 1H), 8.42 (d, J = 7.9 Hz, 1H), 7.95 (dd, J = 7.7, 1.7 Hz, 1H), 7.93 (t, J = 7.7 Hz, 1H), 7.86 (td, J = 7.7, 1.6 Hz, 1H), 7.33 (ddd, J = 7.7, 4.2, 1.6 Hz, 1H), 1.55 (s, 9H). ¹³C NMR (126 MHz, CDCl₃): δ 206.4, 155.6, 154.2, 153.7, 149.2, 137.8, 137.0, 124.0, 123.7, 123.2, 121.0, 44.2, 27.7. IR (neat, ATR): 2956, 1685, 1578, 1479, 1428, 1201, 993, 970, 792, 757 cm⁻¹.

[Tb^III(hfac)₃(6bpyCO)] (Tb-6bpyCO). Tb-6bpyCO was prepared according to the procedure of RE-6bpyNO using [Tb^III(hfac)₃(H₂O)₂] and 6bpyCO as starting materials. The yield was 14%. Mp. 191–193 °C (decomp.). Anal. Calcd for C₃₀H₁₉N₂O₇F₁₈Tb: C, 35.31; H, 1.88; N, 2.75%. Found: C, 35.19; H, 1.91; N, 2.62%. IR (neat, ATR) 1651, 1489, 1249, 1189, 1133, 1096, 795, 765, 659, 582 cm⁻¹.

X-ray crystallography

X-ray diffraction data of RE-6bpyNO (RE = Tb, Y) and Tb-6bpyCO were collected on a Rigaku Saturn70 CCD diffractometer with graphite monochromated MoKα radiation (λ = 0.71073 Å). The structures were directly solved using a heavy-atom method and expanded using Fourier techniques in the CrystalStructure program package.³⁴ Numerical absorption correction was used. All of the hydrogen atoms were located at calculated positions and the parameters were refined as “riding”. The thermal displacement parameters of the non-hydrogen atoms were refined anisotropically. Selected crystallographic data and geometrical parameters are listed in Table 1. CCDC numbers 1011564, 1404995 and 1404996.

Magnetic measurements

The dc magnetic susceptibilities and magnetizations of polycrystalline specimens of RE-6bpyNO (RE = Tb, Y) and Tb-6bpyCO were measured on a Quantum Design MPMS-XL SQUID magnetometer equipped with a 7 T coil in the temperature range 1.8–300 K. The magnetic data were corrected using diamagnetic blank data of the sample holder measured separately. The diamagnetic contribution of the sample itself was estimated from Pascal's constants. The ac magnetic susceptibilities were recorded on a Quantum Design PPMS ac magnetometer.

Low-temperature magnetization was measured using a conventional inductive probe in pulsed-magnetic fields, and a temperature as low as 0.5 K was reached using a ³He cryostat.¹⁹ Polycrystalline specimens were mounted in a capillary made of polyimide. The samples were not fixed within the sample tube and they aligned in the magnetic field direction. After we applied the magnetic field several times, the orientation effect was saturated, and the magnetization curves obtained in further shots were found to be identical. The magnetization was calibrated using independent measurements on a SQUID magnetometer.

Acknowledgements

T. K. was supported by the JSPS program for Research Fellowships for Young Scientist (no. 15J11497).

Notes and references

1. O. Kahn, Molecular Magnetism, VCH Publications, New York, 1993; J. S. Miller and M. Eds, Magnetism Molecules to Materials I–V, Wiley-VCH, Weinheim, Germany, 1999–2005; D. Gatteschi, R. Sessoli and J. Villan, Molecular Nanomagnets, Oxford University Press, New York, 2006; D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 2003.
2. S. Osa, T. Kido, N. Matsumoto, N. Re, A. Pochaba and J. Mrozinski, J. Am. Chem. Soc., 2004, 126, 420; F. Pointillart, K. Bernot, R. Sessoli and D. Gatteschi, Chem. – Eur. J., 2007, 13, 1602.
3. F. Mori, T. Ishida and T. Nogami, Polyhedron, 2005, 24, 2588; F. Mori, T. Nyui, T. Ishida, T. Nogami, K.-Y. Choi and H. Nojiri, J. Am. Chem. Soc., 2006, 128, 1440; S. Ueki, T. Ishida, T. Nogami, K.-Y. Choi and H. Nojiri, Chem. Phys. Lett., 2007, 440, 263.
4. N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694.
5. K. Osanai, A. Okazawa, T. Nogami and T. Ishida, J. Am. Chem. Soc., 2006, 128, 14008.
6. S. Demir, L.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149.
7. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538; N. G. R. Hearns, K. E. Preuss, J. F. Richardson and S. Bin-Salamon, J. Am. Chem. Soc., 2004, 126, 9942; A. Caneschi, A. Dei, D. Gatteschi, L. Sorace and K. Vostrikova, Angew. Chem., Int. Ed., 2000, 39, 246; C. Benelli, A. Caneschi, D. Gatteschi, L. Pardi and P. Rey, Inorg. Chem., 1989, 28, 275.
8. T. Kanetomo and T. Ishida, Inorg. Chem., 2014, 53, 10794.
9. J.-P. Costes, F. Dahan, A. Dupuis and J.-P. Laurent, Chem. – Eur. J., 1998, 9, 1616; M. L. Kahn, C. Mathoniére and O. Kahn, Inorg. Chem., 1999, 38, 3692; M. Towatari, K. Nishi, T. Fujinami, N. Matsumoto, Y. Sunatsuki, M. Kojima, N. Mochida, T. Ishida, N. Re and J. Mrozinski, Inorg. Chem., 2013, 52, 6160; A. Okazawa, T. Shimada, N. Kojima, S. Yoshii, H. Nojiri and T. Ishida, Inorg. Chem., 2013, 52, 13351.
10. R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 925; R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1976, 32, 751.
11. M. Lluncll, D. Casanova, J. Circra, J. M. Bofill, P. Alcmany, S. Alvarez, M. Pinsky and D. Avnir, SHAPE, v2.1, University of Barcelona and The Hebrew University of Jerusalem, Barcelona, 2005.
12. J.-P. Sutter, M. L. Kahn and O. Kahn, Adv. Mater., 1999, 11, 863; M. L. Kahn, J.-P. Sutter, S. Golhen, P. Guionneau, L. Ouahab, O. Kahn and D. Chasseau, J. Am. Chem. Soc., 2000, 122, 3413.
13. T. Mochizuki, T. Nogami and T. Ishida, Inorg. Chem., 2009, 48, 2254; F. A. Villamena, M. H. Dickman and D. R. Crist, Inorg. Chem., 1998, 37, 1446.
14. W. Wong and S. F. Watkins, J. Chem. Soc., Chem. Commun., 1973, 888.
15. T. Ishida, R. Murakami, T. Kanetomo and H. Nojiri, Polyhedron, 2013, 66, 183.
16. R. Murakami, T. Ishida, S. Yoshii and H. Nojiri, Dalton Trans., 2013, 42, 1396.
17. M. L. Baker, T. Tanaka, R. Murakami, S. Ohira-Kawamura, K. Nakajima, T. Ishida and H. Nojiri, Inorg. Chem., 2015, 54, 5732.
18. T. Ishida, R. Watanabe, K. Fujiwara, A. Okazawa, N. Kojima, G. Tanaka, S. Yoshii and H. Nojiri, Dalton Trans., 2012, 41, 13609; R. Watanabe, K. Fujiwara, A. Okazawa, G. Tanaka, S. Yoshii, H. Nojiri and T. Ishida, Chem. Commun., 2011, 47, 2110; T. Shimada, A. Okazawa, N. Kojima, S. Yoshii, H. Nojiri and T. Ishida, Inorg. Chem., 2011, 50, 10555; A. Okazawa, T. Shimada, N. Kojima, S. Yoshii, H. Nojiri and T. Ishida, Inorg. Chem., 2013, 52, 13351.
19. H. Nojiri, K.-Y. Choi and N. Kitamura, J. Magn. Magn. Mater., 2007, 310, 1468.
20. S. L. Castro, Z. Sun, C. M. Grant, J. C. Bollinger, D. N. Hendrickson and G. Christou, J. Am. Chem. Soc., 1998, 120, 2365; M. Sugita, N. Ishikawa, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, Inorg. Chem., 2006, 45, 1299.
21. K. S. Cole and H. R. Cole, J. Chem. Phys., 1941, 9, 341.
22. R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328.
23. R. Sessoli, H.-L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804.
24. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078.
25. M. A. AlDamen, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Arino, C. Marti-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467; J. J. Baldovi, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Arino and A. Palii, Inorg. Chem., 2012, 51, 12565; G. F. Xu, Q. L. Wang, P. Gamez, Y. Ma, R. Clérac, J. Tang, S. P. Yan, P. Cheng and D. Z. Liao, Chem. Commun., 2010, 46, 1506; X.-L. Wang, L.-C. Li and D.-Z. Liao, Inorg. Chem., 2010, 49, 4735; V. Chandrasekhar, P. Bag, M. Speldrich, J. van Leusen and P. Kögerler, Inorg. Chem., 2013, 52, 5035.
26. N. Ishikawa, M. Sugita, N. Tanaka, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, Inorg. Chem., 2004, 43, 5498.
27. W. Wernsdorfer, N. E. Chakov and G. Christou, Phys. Rev. Lett., 2005, 95 , 037203 M.-E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, N. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem. Int. Ed., 2013, 52, 350.
28. N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931.
29. T. Fukuda, K. Matsumura and N. Ishikawa, J. Phys. Chem. A, 2013, 117, 10447.
30. E. M. Pineda, N. F. Chilton, F. Tuna, R. E. P. Winpenny and E. J. L. McInnes, Inorg. Chem., 2015, 54, 5930.
31. M. Gonidec, E. S. Davies, J. McMaster, D. B. Amabilino and J. Veciana, J. Am. Chem. Soc., 2010, 132, 1756.
32. M. F. Richardson, W. F. Wagner and D. E. Sands, J. Inorg. Nucl. Chem., 1968, 30, 1275.
33. S. E. Denmark, Y. Fan and M. D. Eastgate, J. Org. Chem., 2005, 70, 5235.
34. CrystalStructure version 4.0, Rigaku Corp., Tokyo, Japan, 2010.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 1011564 (Tb-6bpyNO), 1404995 (Y-6bpyNO) and 1404996 (Tb-6bpyCO). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00098j

‡ Shape measurements were 0.241 (CSAPR) and 1.053 (TCTPR; tricapped trigonal prism) for Tb-6bpyNO, 0.235 (CSAPR) and 1.023 (TCTPR) for Y-6bpyNO, and 0.249 (CSAPR) and 1.019 (TCTPR) for Tb-6bpyCO.

---