Self-assembly of nanoparticles adsorbed on fluid and elastic membranes
Anđela
Šarić
and
Angelo
Cacciuto
*
Department of Chemistry, Columbia University, 3000 Broadway, New York, MC 3123, NY 10027, USA. E-mail: ac2822@columbia.edu
First published on 3rd May 2013
Abstract
In this paper we review recent numerical and theoretical developments of particle self-assembly on fluid and elastic membranes and compare them to available experimental realizations. We discuss the problem and its applications in biology and materials science, and give an overview of numerical models and strategies to study these systems across all length-scales. As this is a very broad field, this review focuses exclusively on surface-driven aggregation of nanoparticles that are at least one order of magnitude larger than the surface thickness and are adsorbed onto it. In this regime, all chemical details of the surface can be ignored in favor of a coarse-grained representation, and the collective behavior of many particles can be monitored and analyzed. We review the existing literature on how the mechanical properties and the geometry of the surface affect the structure of the particle aggregates and how these can drive shape deformation on the surface.
 Anđela Šarić | Anđela Šarić received her Diploma in Chemistry at the University of Zagreb in 2008. Following her MS in Chemical Physics in the Chemistry Department at Columbia University she is now a PhD candidate in the same department (2013). She will soon join D. Frenkel's group at the University of Cambridge as a Human Frontier Science Program Postdoctoral Fellow. Her work focuses on soft matter and biophysics. |
 Angelo Cacciuto | Angelo Cacciuto received his Laurea in Physics at the University of Cagliari (IT) and his PhD in Physics at Syracuse University in 2002. Following two postdoctoral positions at the AMOLF Institute for Atomic and Molecular Physics, and in the Department of Materials Science and Engineering at the University of Illinois at Urbana-Champaign, he is now Associate Professor in the Chemistry Department at Columbia University. He works on soft matter and biological physics. |
I Introduction
Self-assembly is the process by which initially isolated components spontaneously organize into large, ordered and stable structures. The phenomenon is ubiquitous in nature and is observed across all length scales: “from molecules to galaxies”.1 At the nanoscale, self-assembly is usually achieved by a complex balancing act between two factors: the direct or effective interactions among the components, and the random thermal fluctuations of the surrounding medium. While the former factor usually determines the morphology and symmetry of the final aggregate, the latter allows the components to diffuse through the medium and explore the available space. Examples of self-assembly, and more in general self-organization of molecules, proteins and protein complexes in biological systems are numerous and are fundamental for the proper functioning of the cell.2–5 Furthermore, self-assembly is expected to play an important role in the production of materials with novel optical, mechanical, and electronic properties. In fact, whether we are considering organic photovoltaics, photonic crystals with optoelectronic capabilities or energy-saving transistors and LEDs, key to the efficiency of these electronic materials is a regular and precise spatial organization of their building blocks. Because of the large cost associated with nanolithographic patterning, their large-scale production remains prohibitive, and the process of self-assembly has been put forward as an attractive candidate for a cost-effective solution to the next generation of functional materials.Although the field of self-assembly has historically focused on molecular systems interacting via covalent interactions, recent advances in particle synthesis6–12 have significantly extended the structural landscape accessible to colloids that are typically two or three orders of magnitude larger than molecules and interact via dispersion forces. Colloidal particles that are anisotropic both in shape and surface chemistry are today easily synthesized, and provide an unlimited number of building blocks that can potentially organize into an unprecedented variety of structures via the process of self-assembly. Unfortunately, self-assembly is a rather delicate and poorly understood process, and the formation of defect-free structures is hardly achievable unless a careful design of the building blocks is performed beforehand.
In this paper we focus on self-assembly on two dimensional fluctuating surfaces, as they can act as powerful universal templates through which arbitrary building blocks of even larger sizes than colloids can be readily driven close to each other thus favoring their aggregation. Spontaneous organization of components adhering to fluid interfaces is a matter of common experience, and is observed across a wide range of length scales: from the assembly of marine litter into large garbage patches and clustering of cheerios on milk at the macroscopic scale, to the aggregation of proteins embedded in lipid membranes at the nanoscale. The first example of small particles assembling onto the interfaces of liquid droplets was reported over a century ago,13 and has been used ever since in industrial processing,14 as well as to produce supracolloidal structures, such as colloidosomes, capsules and nano-particle-based membranes.15,16 The effectiveness of bottom-up schemes to organize millimeter-size objects at fluid interfaces in a controlled manner was further demonstrated by Whitesides and co-workers.17,18 The origin of particle aggregation driven by fluid interfaces is very well established.19,20 Local deformations in the profile of the interface induced by floating objects adhering to it result in long-range capillary forces that develop to minimize the interfacial free energy that is regulated by its surface tension. By a judicious choice of the interface, and a careful design of the building blocks, a plethora of patterns and even three-dimensional objects can be assembled.21 An extensive body of work is dedicated to self-assembly on fluid interfaces and this topic will not be covered here. For recent reviews we refer the reader to ref. 15,16,22,23.
Here, we focus on self-assembly of nanoobjects on surfaces that are not exclusively dominated by their tension and have richer mechanical properties that give rise to a complex response to deformations and peculiar assembly patterns. Namely, we are interested in fluid and elastic/tethered membranes. While in the former case the elastic properties are controlled by the tension of the surface and by its bending rigidity, in the latter case surfaces are tensionless but have both bending and stretching rigidities.
The simplest and most important example of fluid surfaces is biological membranes. The main constituents of biological membranes are phospholipids – amphiphilic molecules that spontaneously organize in sheets that stack into bilayers and are capable of forming complex and soft two dimensional geometries. They envelop eukaryotic cells and compartmentalize their different subcellular regions.2,24 Under physiological conditions lipid molecules inside each layer are found in the fluid state and can freely diffuse over the membrane surface. Fig. 1(a) illustrates the typical structure of a lipid bilayer. The thickness of biological membranes is t ∼ 5 nm, while their surface area is usually many orders of magnitude larger.24,25 For instance, the total area of a complex network of membranes in a typical liver cell is 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μm2, which gives about 8.2 m2 of membrane area per gram of tissue.2
000 μm2, which gives about 8.2 m2 of membrane area per gram of tissue.2
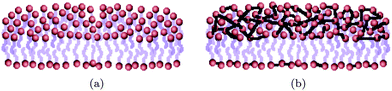 | ||
| Fig. 1 Schematic representation of a fluid (a) and a crosspolymerized (b) membrane. | ||
Biological membranes are constantly in contact with various macromolecules that either reside on their surface, or are being transported between the cell and its environment as well as shuffled between different compartments within eukaryotic cells. Since a lipid membrane is permeable only to water and small uncharged molecules,25 all macromolecules that are required to interact with it or cross it need to do so by locally deforming the surface upon binding and subsequently either organize upon adsorption or possibly vesiculate away from it. Self-assembly on biological membranes is thus a crucial step in cellular transport, signaling and recognition. Being able to control this process is of central interest for designing particles for targeted-drug delivery and for understanding nanotoxicity.26–29 It also has promising applications in nanopatterning and nanotechnology,30 in medical imaging31 and in development of biosensors and functional biomimetic materials.32,33 In addition to phospholipids, many other amphiphilic molecules are capable of building bilayer membranes, for example blockcopolymers and surfactants,34–36 and recently membranes made of colloidal particles have been successfully assembled.37
Unlike their fluid counterparts, the building blocks of elastic membranes do not diffuse, but are tethered to each other as sketched in Fig. 1(b). As a result, the elements of elastic membranes cannot flow and can withstand shear.38 Examples of such surfaces are cross-polymerized membranes,39 gels,40 actin–spectrin networks of red blood cells' cytoskeleton,41,42 membranes made of close-packed nanoparticles,43 graphene and graphite-oxide sheets44–47 and polymer films.48 Their study has seen a drastic increase over the past decade due to their potential use in flexible electronics,49 artificial skin50 and as blood cell substitutes,51 tunable diffraction gratings,52 and in stimulus responsive materials and soft-robotics.53 Although much of the elastic properties of elastic sheets or shells is by now well understood,38 very little is known about their properties as self-assembly templating agents.
The main aim of this paper is to provide an overview of the recent work done on self-assembly of nanoparticles and colloids driven by soft, deformable surfaces, with emphasis on biological and elastic membranes. Specifically we'll focus on adsorbed particles that are at least one order of magnitude larger than the membrane thickness and do not disrupt the molecular structure of the underlying surface or pierce through it in any way. We begin by providing a physical description of fluid and elastic membranes, we proceed by briefly overviewing accepted theories of self-organization on membranes and computer models for their simulation, and finally, we present the most recent advances in the field.
II Physical properties of deformable surfaces
When a particle adhering to a surface is at least one order of magnitude larger than the surface thickness, it is reasonable to neglect the surface molecular details. In this limit a particle will experience the surface as a continuous medium (see Fig. 2(a) for an illustration) having specific mechanical properties. For a lipid membrane the standard elastic representation is given by the Helfrich free energy25,54,55 and contains a curvature Fc and a surface tension Fγ term: | (1) |
 | ||
| Fig. 2 (a) A bending (top panel) and a stretching (bottom panel) deformation of a thin sheet. (b) Stretch-free deformation along a zero-curvature direction on a thin cylinder (left panel). d-cone formed as a result of a stretch-inducing deformation (right panel). | ||
The bending rigidity κ for biological membranes can be estimated as the cost to compress the inner leaflet of the bilayer and stretch the outer one exposing some of its hydrophobic area to water.24,25 Experimentally measured values of κ are found to be in the range of 10–30 kBT, where T is the temperature and kB is the Boltzmann constant; the exact value depends on molecular composition. Unfortunately, no methods are available for a direct measurement of the Gaussian rigidity κG, as a result its value is much more uncertain. To date, the only assessment for a pure phospholipid system yielded κG ≈ −0.9 κ.56 In most treatments of membranes, the Gaussian curvature term of the Helfrich free energy is neglected as κG is a measure of the energy cost associated with topological changes of the surface, and it is constant as long as the surface topology remains unaltered.
The bending rigidity of artificial fluid membranes can be tuned by changing the properties of their building blocks. κ for surfactant membranes grows quadratically with the length of the surfactant molecule, and depends on the surface area per surfactant polar head.34,35,57 Surfactant membranes are relatively soft with 1 kBT ≤ κ ≤ 10 kBT.57 Analogously, the rigidity of block-copolymer membranes greatly depends on the molecular weight of the copolymer58 and can be as low as 10 kBT and as high as 100 kBT.58,59 Fluid membranes made of colloidal rods are reported to be quite stiff and have κ ≈ 150 kBT.37
Although measured values of surface tension γ of lipid membranes vary significantly, most studies assume a negligible or a very small value γ ≈ 10−3 to 10−2 pN nm−1, depending on the conditions of the experiment and the presence of a lipid-reservoir.25,60 The surface tension of polymeric membranes has been shown to be relatively independent of molecular weight, with similar values as those reported for lipid membranes.34 Therefore, the behavior of fluid membranes in the limit of small deformations is mostly governed by the bending energy.
Let us now consider the physical properties of elastic/tethered membranes. They do not have surface tension, but are resistant to stretching and respond to perturbations away from their equilibrium shape in a spring-like fashion. Their free energy can be decomposed into two contributions: a curvature term Fc that has the same form as that introduced for fluid surfaces, and an elastic term, Fe, that accounts for the stretching energy (see Fig. 2(a) for an illustration) and can be expressed in terms of the surface Lamé coefficients μ and λ38 as
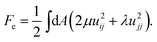 | (2) |
Here uij is the two-dimensional strain tensor that can be written in terms of the in-plane displacement vector field ui and the out-of-plane displacement field h38 with respect to the unstressed planar reference surface
 | (3) |
The last term in the above equation preludes to a non-trivial coupling between in- and out-of plane deformations. In this representation, also known as the Monge gauge,25 the bending free energy can be approximated (for H0 = 0) to
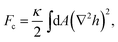 | (4) |
It can be shown that the Lamé coefficients are related to the Young's modulus of the sheet by a simple relation Y = μ(3λ + 2μ)/(λ + μ), while the bending rigidity scales as κ ∼ Yt3; here t is the thickness of the sheet.38
A very important property of thin elastic sheets can be readily obtained by considering the ratio between the cost associated with stretching and that associated with bending deformations. A simple scaling analysis reveals that Fc ∼ Yt3h2/L4 and Fe ∼ Yth4/L4, where L is the lateral length of the surface, and the ratio between the two terms scales as
| q = Fe/Fc ∼ (h/t)2. | (5) |
This equation states that whenever the extent of the deformations applied to an elastic sheet is larger than the surface thickness, bending is the preferred mode of deformation. Furthermore, it is also possible to show that the strain tensor is simply related to the principal radii of curvature, c1 and c2, of a small deformation imposed on a planar surface, namely uxy ≃ c1c2xy.61 This relation, intimately related to the above-mentioned coupling between ui and h, implies that the only stretch-free deformations possible on an elastic sheet are those involving a single axis of curvature, i.e. either c1 or c2 must be equal to zero. These two results have a profound effect on the way thin elastic surfaces respond to deformations, and are at the core of most of the phenomenological behavior experienced with thin elastic materials. For instance, spherical shells have no stretch-free deformations as any perturbation of the spherical shape necessarily involves two axes of curvature. The resulting conformations involve stress-focusing by buckling,61 as readily observed when poking a table tennis ball. Fig. 2(b) shows examples of a stretch-free and a stretch-costly deformation on a cylindrical shell. Skin wrinkling under applied stress62 and stress focusing via d-cone formation of crumpled paper61 are two beautiful examples of this phenomenon that has a strong geometrical dependence.
III Membrane-mediated interactions
Nanoobjects that interact with fluid membranes can be either adsorbed on the membrane surface or embedded in the bilayer, in which case we will call them inclusions. Either way, the adsorption or inclusion of a nanoparticle locally perturbs the membrane surface in a way that depends on the shape and size of the nanoparticle and the nature of its interaction with the membrane. The tendency of the membrane to minimize the size of these perturbations can result in effective interactions between the adsorbed/included nanoparticles. These forces can be either attractive or repulsive as schematically shown in Fig. 3. Theoretical studies of these phenomena for fluid membranes go back over two decades and there are a number of excellent reviews on the subject.63–65 Nonetheless, the field is still developing, and new findings and improvements of the theories are constantly being reported. | ||
| Fig. 3 Illustrations of membrane-induced interactions between inclusions. (a) Casimir-like attractions between particles perfectly included in the bilayer. (b) Hydrophobic mismatch: like deformations attract. (c) Bending-mediated repulsion between like deformations. | ||
There are several ways for a membrane to induce interactions between embedded particles. In the simplest case of an isotropic particle perfectly included in the bilayer (Fig. 3(a)), a Casimir-like interaction is known to develop for a range of particle separations. In general, nanoparticles are much stiffer than the membrane, and their presence perturbs the spectrum of natural membrane fluctuations. The extent of the perturbation depends on the separation r between the nanoparticles, and is minimized when they are brought together, leading to an effective nanoparticle–nanoparticle attraction66–68 of the form V(r) ∼ −1/r4. Although long-ranged, its magnitude and importance are still under debate.
Often the presence of membrane inclusions locally alters the thickness of the hydrophobic core of the bilayer resulting in its distortion near the inclusion perimeter. As illustrated in Fig. 3(b), this typically leads to either a local compression or expansion of the surface.69–71 Whenever two adjacent inclusions deform the bilayer in the same way (both are thinner or thicker than the unperturbed membrane's hydrophobic region), the boundary deformations are minimized upon their aggregation, giving rise to a short-range attraction. When the inclusions alter the membrane thickness in an opposite manner (one thins it out and the other one thickens it), the resulting interaction is repulsive. In both cases the energy cost of the deformation increases as the square of the hydrophobic mismatch length ΔtHP, but it is mainly constant and with a limited range of interaction (several nm).64,70 This interaction is of great importance for the organization of transmembrane proteins and other membrane inclusions.
Another very important membrane-mediated interaction is more readily linked to local bending deformations. Consider for instance the deformation caused by an adsorbing nanoparticle attracted to a membrane as it tries to locally bend it to maximize their surface contact, or the deformations enforced by membrane inclusions that are not symmetric with respect to the bilayer mid-plane (Fig. 3(c)). When the deformation profiles induced by different nanoparticles are close enough to overlap, an effective interaction takes place.66,67,72 In the limit of shallow deformations, like-indentations repel, while oppositely curved indentations attract. The bending mediated interactions are of a longer range than the hydrophobic mismatch and decay with particle separation as V(r) ∼ 1/r4. They are considered to be very important for many membrane-associated aggregation processes. Recently, Deserno and Reynwar have considered interactions between strongly curved deformations, and have showed that a crossover from repulsion to attraction takes place as the deformation deepens.73 Moreover, Fournier and Dommersnes studied anisotropic deformations, and have showed that orientationally dependent attractions are also possible.74 More recently, Deserno and Yolcu have developed an effective field theory that captures in a more transparent manner both entropic and curvature-induced interactions between rigid inclusions, allowing a systematic evaluation of higher-order and multi-body interactions.75
The global shape of the membrane can also be used to sort particles in different regions and favor phase segregation in multi-component systems. For instance, membrane-bending particles tend to aggregate in the regions of the membrane whose curvature is the most similar to their own – thus maximizing their surface contact at a minimum cost in bending.76,77 Analogously, when clustering of like-membrane-bending particles occurs, due, for example, to phase separation between different components,78 large shape deformations on an initially flat region of the membrane can develop for easily bendable surfaces. When the bending energy is non-negligible, micro-phase separation into repulsive bulged phases will occur, resulting in finite-spaced membrane domains, providing yet another mechanism of membrane-induced ordering.79 This complex coupling between particle self-assembly and surface deformability is central to understanding intra- and extra cellular communication in eukaryotic cells.80–84
Unlike fluid membranes, only particle adsorption is possible on elastic surfaces, and they respond to it by bending and stretching. The treatment of the bending part of the deformation is identical to that described for fluid membranes; however, very little is known on the role of the stretching energy in the pair-wise interaction between the deformations. The main difference from fluid membranes is that the topology and the geometry of the surface play a much more important role in the response of elastic surfaces to deformations. Simply put, depending on the elastic parameters and geometry of the surface, different directions on the surface might not be equivalent. Of particular interest are thin elastic surfaces for which the stretching dominates over the bending energy resulting in global constraints involving exclusively (whenever possible) uniaxial deformations. Additionally, the presence of defects in elastic networks may also play an important role, since defects might be more or less prone to deformation compared to the rest of the surface, and might attract or repel particles.85 These phenomena give rise to orientational interactions between deformations and lead to more complex and beautiful aggregation patterns. We hope this review will stimulate further work on exploiting elastic interfaces for studying particle self-assembly.
IV Computer simulations of deformable surfaces
A large number of membrane models have been put forward to describe soft surfaces across all length scales. Not surprisingly, most of them have been developed for biological membranes, although models for surfactant and polymer membranes are also available.86–89 Our goal here is not to review all existing membrane-simulation techniques, but to give a brief overview of representative models at different scales, with focus on their applications in simulating membrane interactions with macromolecules. An overview of representative models is sketched in Fig. 4. For detailed reviews on various techniques and their evaluation we direct the reader to ref. 55, 90–93. | ||
| Fig. 4 From implicit to full atomistic: schematic illustration of representative membrane models at different length scales. From left to right: triangulated network, three-bead per lipid coarse-grained (CG) model, atomistic representation. | ||
Membrane systems can be modeled either as continuous surfaces, using the mathematical functions described in eqn (1) and (2), or with a particle-based representation where each lipid/building-block is depicted explicitly with more or less degree of coarse-graining. A common approach in continuous models includes writing all energy contributions in the framework of the Helfrich elastic description and performing numerical energy minimization with system-dependent constraints. This process is relatively fast and computationally inexpensive, but an analytical expression of all energy contributions in the system is not always trivial. This is especially true in the case of complex membrane–particle systems where multi-body interactions and unexpected geometrical realizations of the membrane and nanoparticles can occur. In addition, this technique does not capture thermal effects or the dynamics of the system, although a few dynamical continuous models have been developed. Let us just mention Fourier space Brownian dynamics,90 which evolves the free energy of a lipid bilayer in the Fourier space in the presence of arbitrary forces, and includes hydrodynamics as well as thermal fluctuations.
Particle-based models are more versatile and can be applied to arbitrary geometries and number of components. However, they need to satisfy the non-trivial task of keeping membrane integrity while maintaining its fluidity. They can be roughly classified into two groups, depending on whether the bilayer structure is described explicitly or implicitly.93 Models in the first group describe each amphiphilic molecule separately and can be fully atomistic or coarse-grained. Implicit models depict a membrane as a coarse-grained surface where a unit segment does not represent a single molecule, but a membrane patch consisting of hundreds to thousands of amphiphilic molecules. The most detailed, full atomistic models explicitly account for each atom of an amphiphilic molecule via molecular mechanics, sometimes employing the united atoms approach to represent nonpolar alkyl groups of the hydrocarbon tails, and a set of interaction parameters are then given by the chosen force field. Such a level of detail is necessary when studying membrane interactions with small molecules or the inner-working of transmembrane channels. Nowadays these simulations are benchmarked at about hundred fully hydrated lipids for 50–100 ns. A nice review on recent developments of membrane force-fields can be found in ref. 94.
To simulate membrane interactions with larger nano-components, this detailed description is unnecessary and unfeasible, and several coarse-graining techniques have been developed. An amphiphilic molecule can be coarse-grained by forming groups consisting of 2–5 heavy atoms into a single coarse-grained (CG) site, with water included either explicitly or implicitly via effective potentials. Further coarse-graining is achieved by a systematic decrease in the number of CG sites – up to two or three segments95–97 or even just one spherocylinder for the whole lipid molecule98 with the solvent represented via an effective attractive potential between hydrophobic parts. Particle-based explicit models that include some degree of depiction of the lipids require a large number of explicit or effective water molecules to provide osmotic pressure and stabilize the surfaces against lipid evaporation. A rough estimate is at least 30 molecules of water per lipid,91 and this increases the computational cost by at least an order of magnitude. For this reason water-free membrane models have become very popular, however, the parametrization of such models is less straightforward and a large variety of ad hoc potentials have been suggested. Most of them are based on modifications of a Lennard-Jones potential.96,97 Although all of the proposed potentials are able to reproduce membrane self-assembly, the resulting values of membrane rigidities are hard to control and range from several kBT up to over 100 kBT.91 Effective potentials for CG simulations of biological membranes can also be derived from atomistic simulations of lipids in water using a multiscaling approach, either via force-matching or by employing hybrid algorithms.99 Each of these approaches has its strengths and weaknesses, see for instance ref. 92,100,101, but all of them have been employed to attack important biophysical questions.
In the second group of particle-based models, the membrane is built from units that represent a coarse-grained surface patch rather than an individual molecule. Since they ignore the details of the bilayer, these models are valid only for a description that involves length-scales sufficiently larger than the membrane thickness (≫5 nm). The mechanical properties of the bilayer are reflected in the values of a set of elastic parameters associated with the Helfrich free energy. The strength of this group of models is that they give access to larger length and time scales unobtainable by explicit-lipid models. The standard physical representation in this class is the triangulated-network model. Here the membrane is described as an infinitely thin elastic surface consisting of hard, spherical beads connected by flexible links to form a triangulated mesh.102–105 Using Monte Carlo (MC) methods, the mesh connectivity is dynamically rearranged to incorporate surface fluidity. The membrane bending energy acts on neighbouring triangles, and has the typical form
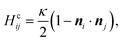 | (6) |
A closely related representation is the meshless model, where membrane beads are polar and are not held together by imposed bonds, but they self-assemble into a membrane by carefully designed potentials. Most of these potentials consist of three distinct interactions: a repulsive part that ensures volume exclusion, an attractive part that drives membrane self-assembly, and an angular part that depends on particle orientation and mimics the membrane bending rigidity. Meshless models can capture membrane topological changes and dynamics, but in the majority of them the membrane elastic properties are not included into the system as external parameters, but are encoded into the details of the pair potentials between the membrane beads and need to be extracted by analyzing the fluctuation spectrum of the surface or by other means. The first meshless model was proposed by Drouffe et al. in 1991 (ref. 106) and has relied on multibody interactions. Recently, a few pair-wise-additive meshless models have been reported.107–109 An alternative meshless model, in which particles have no internal degrees of freedom and the potentials depend only on particle positions, can be found in ref. 110. It is important to emphasize that the size of a surface bead in the triangulated-network model as well as in the meshless model is not related to the membrane thickness, but rather to the coarse-graining length-scale of the membrane surface, and should be large enough, σ ≃ 30–50 nm, so that an elastic description of the membrane is acceptable.
Tethered membranes can also be described employing continuum elastic models, however simulations of elastic membranes in contact with nanoobjects have been mostly performed using particle-based elastic models. The simplest particle-based model for an elastic membrane is a fixed-mesh (network) model.102,105,111 It is a predecessor of the triangulated-network model for fluid membranes, without the bond-flip to maintain the interparticle-connectivity fixed. The bending energy can be incorporated using eqn (6), while the shear elasticity/stretching energy can be accounted for through the strength of harmonic bonds between linked surface beads:
| Hemn = ks(rmn − rb)2 | (7) |
Finally, a full description of the systems of interest requires a representation of the nanoobject–membrane interaction. Adsorption of a nanoobject can take place in different ways, for instance it can be induced by binding of ligands on the nanoparticle to receptors on the surface on the membrane, such as streptavidin–biotin links, but it can also be driven by van der Waals interactions, or by electrostatic physisorption for charged membranes and nanoparticles. Particle inclusion within the bilayer is usually driven by hydrophobic effects. These interactions in atomistic models arise from first principles calculations, while in coarse-grained models they are usually included via a generic short-range attractive potential between a nanoobject and each membrane-building particle, and can be described with simple functional forms ranging from Morse to truncated Lennard-Jones potentials. These short-ranged attractions adequately account for the ligand–receptor or van der Waals interactions. However, it should be noted that specific interactions, not considered by such generic bindings, might in some cases affect the self-assembly behavior. For instance, it is known that highly charged large nanoparticles interacting with zwitterionic lipids may induce a conformational transition in the underlying lipid molecules creating gradients in the lipid density,118 which would affect the way the nanoparticles interact.
V Aggregation on fluid membranes
A large body of work is dedicated to surface-mediated aggregation of membrane inclusion. Here we focus on assembly of large membrane-adsorbed species, such as viruses, colloids and nanoparticles. Specifically, we will discuss how the binding energy associated with adsorbed particles, which depends on the membrane-bound area and on the overall nanoparticle arrangements, leads to a significantly different behavior than that expected from particles or proteins embedded within the bilayer. We will also discuss the role of the size of the membrane-associated species and how it is related to large global membrane deformations, such as tubulation137 or budding.119–130A Small deformations
To best of our knowledge, Safinya et al. have been the first to experimentally investigate membrane mediated attraction of colloidal particles bound to a lipid membrane.77 They studied two systems: streptavidin-grafted latex beads (0.3 and 0.9 μm in diameter) attached to a biotinylated phospholipid giant unilamellar vesicles (GUVs) and negatively charged colloidal DNA–lipid aggregates adsorbed on cationic GUVs. Their experiments revealed that in both cases particles caused deformations of flexible GUVs and experienced membrane mediated attraction. Vesicles with a single attached bead showed distorted contours with a pinched angle around the bead. If the vesicle was not spherical, but had a stomatocyte shape, the bead would preferentially bind to the concave region of the vesicle. This maximizes particle binding energy, with as little bending cost as possible. When a second bead was added to the system, the two beads approached each other over a period of time and eventually bound. The lipid mobility was a prerequisite for aggregation, and particles showed no tendency to aggregate in solution, excluding the possibility of particle attractions without the presence of the membrane. Interestingly, upon addition of the third particle a chain-like triplet was formed on a spherical vesicle, as opposed to a triangular formation which would be expected in isotropic aggregation. Remarkably, in a multi-particle system, a ring shaped string of beads aggregated around the waist of a multilamellar vesicle as shown in Fig. 5, clearly exhibiting a peculiar non-isotropic attraction. A close packed hexagonal cluster of colloids was observed only when the vesicle was not symmetric and had a concave region as a preferred binding site. | ||
| Fig. 5 Latex beads bound to a multilamellar vesicle via biotin–streptavidin interactions forming linear string-like aggregates. Reprinted with permission from ref. 77. | ||
This linear aggregation is quite surprising, especially considering that attraction of symmetric membrane inclusions is always isotropic. Anisotropic, string-like aggregates were predicted only for elongated objects.74 Yue and Zhang have performed computer simulations of receptor-mediated endocytosis of multiple nanoparticles.131 Uptake of nanoparticles in cells and GUVs is often preceded by nanoparticle clustering, as regularly observed in experiments.132 The authors have shown that membrane-mediated interactions between adsorbed nanoparticles are strongly sensitive to their size. They have found small nanoparticles (∼2.5 nm) to exhibit short-range attractions and to aggregate in hexagonal structures. Nanoparticles of intermediate size (∼4.5 nm), once partially wrapped by the membrane, experience longer range interactions that connect them in a linear arrangement, very much like the pearl-like chains observed by Safinya et al.77,133 For larger nanoparticles (∼6.5 nm) the membrane dynamics slows down significantly, as the number of receptors required to be recruited to deform the membrane becomes large. In that case individual-wrapping of each nanoparticle has been observed, except when the nanoparticles were initially next to each other, which leads to wrapping of the whole dimer. Zhang et al. attribute these aggregation patterns to membrane-mediated interactions, which are strongest for small, highly curved particles, and decrease with the particle size. Furthermore, they argue that the interactions are attractive for the small sized particles and repulsive for the big ones. Nanoparticles of size comparable to the membrane thickness can considerably disturb the local lipid packing in a nontrivial way. The resulting deformations induced on the membrane are complicated, and typically lead to the familiar short-range isotropic attraction when like deformations of individual particles overlap. This is often observed in experimental systems of nanoparticles adsorbed on fluid membranes in the small size limit.132,134 Less well studied is the scenario of large particles.
Our group has recently reported a study of aggregation of large membrane-adhered nanoparticles across a wide range of membrane bending rigidities and particle–membrane binding energies for planar and spherical geometries.135 Unlike Zhang et al. who have employed a three-bead-per lipid model to be able to study small nanoparticles comparable to the bilayer thickness, we opted for a less computationally demanding triangulated network representation and have considered exclusively nanoparticles which are at least ∼30 nm in diameter. This enabled us to systematically scan different membrane parameters, as well as to compute free energy profiles of various aggregation pathways to shed light on the mechanism behind the linear aggregation. First of all, no aggregation between the particles was observed unless a sufficient deformation of the surface membrane was achieved by the binding force. For small values of membrane bending rigidities particles create well defined deep-spherical imprints in the membrane and organize into ordered hexagonal arrays. Low cost in bending energy and high gain in surface binding allow for these deep cup-like deformations. Nanoparticles are not in direct contact with each other, but are “bridged” by the pinched parts of the membrane and close-packing maximizes sharing of the pinched regions between neighbouring nanoparticles, thus maximizing the surface-to-nanoparticle contact area (see snapshots in Fig. 6). Weitz et al.136 have experimentally studied adsorption of negatively charged colloids on positively charged surfactant vesicles and have reported very similar two-dimensional aggregates, where colloids are extensively wrapped by the membrane and are not in direct contact with each other. Surfactant membranes have lower bending rigidities than lipid membranes, and we believe that the low κ case in our simulations most resembles this experimental realization. The additional complexity, such as self-limiting colloidal crystal growth observed in that system,136 can only be accounted for by using electrostatic interactions not present in our model.
 | ||
| Fig. 6 Ordered phases of nanoparticles adsorbed on a fluid membrane. From left to right: low-bending hexagonal closed packing, linear aggregates for intermediate bending values, high-bending hexagonal closed packing. The respective membrane profiles underneath the particles are also shown above. On the right panel we show linear aggregates for intermediate κ values on spherical vesicles. Reprinted with permission from ref. 135. | ||
For very large values of κ the nanoparticles reorganize into the familiar hexagonal lattice; however, the membrane now remains almost completely flat and the nanoparticles are in contact with each other. Because of its high stiffness, particles can only weekly deform the membrane to gain in binding energy. As a result the binding is maximized by recruiting the largest number of membrane beads in the vicinity of the nanoparticles. This drives the crystallization of the region of the membrane that directly interacts with the nanoparticles, creating a line tension between crystalline and fluid membrane regions that is minimized when isotropic aggregation takes place.78,137 Local membrane crystallization upon particle adsorption is a known phenomenon,118 making the lipid bilayer effectively a two-component system made of crystalline and fluid domains. Nanoparticle aggregation driven by lipid phase-separation in two-component lipid systems, where nanoparticles prefer to adhere to just one of them, has also been reported in ref. 138.
For intermediate, biologically relevant values of κ, we reported that nanoparticles self-assemble into linear aggregates by creating smooth channel-like distortions on the membrane.135 Results on vesicles strikingly resemble the linear aggregates of colloidal particles on Giant Phospholipid Vesicles (GUVs) obtained by Safinya et al.77 The phenomenon of linear colloidal aggregation being favorable over isotropic aggregation for moderate bending rigidities seems to be experimentally and computationally persistent, and to understand it we computed the free-energy profile of a dimer of nanoparticles bound to the membrane in the field of the third particle, as presented in Fig. 7. When the third particle approaches the other two from infinity to form a linear alignment, we observe a steep free-energy decrease at short distances that drops down to a minimum at contact. When the third particle approaches the dimer from a direction that is perpendicular to the dimer's axis, which would lead to an equilateral triangular arrangement, we observe a repulsive free energy barrier that precedes a shallow minimum at contact. Remarkably the range of the repulsion is felt as far as three nanoparticle diameters, revealing long range correlations in the three-body interactions. These calculations confirm that the linear arrangement is indeed the thermodynamically most stable one, but does not explain why.
 | ||
| Fig. 7 ΔF as a function of the separation when a third nanoparticle approaches a fixed nanoparticle dimer along the direction of the dimer axis (dashed line) and perpendicular to it (full line). Reprinted with permission from ref. 135. | ||
A quick look at the surface deformations in this regime (see snapshots in Fig. 8) suggests that in either the linear or hexagonal configuration the contribution to the system energy can be split into two parts. The first part comes from the overall deformation of the membrane due to the collective arrangement of the particles – either a channel-like or a hexagonal overall imprint. The second part comes from the shallow surface indentations (corrugations) produced by each particle on top of the overall deformation (circled in yellow in Fig. 8). In this regime, the energy due to the corrugations is fairly independent of the overall geometry of the aggregates, since they are relatively shallow. When particles arrange into linear structures (L), the channel-like profiles in the membrane have a length proportional to the number of the nanoparticles N in it, and width proportional to the nanoparticle's diameter. Close-packed hexagonal (H) arrangements form a two-dimensional imprint of the lateral size proportional to  . Now, the bending energy cost is positive and has the same functional form in both cases. It scales with the size of the deformed area, which grows as ∼N in the L case and as
. Now, the bending energy cost is positive and has the same functional form in both cases. It scales with the size of the deformed area, which grows as ∼N in the L case and as  in the H case. This means that the bending energy cost is larger in the linear conformation. The binding energy also scales as the bound area, and it is negative. Most of the binding occurs along the rim of the curved area, which means that the L configuration has more favorable binding than the H formation. The key step is to notice that for any of these phases to be stable, the gain in binding needs to overcome the cost in bending, otherwise particles would not even bind to the membrane. Since the binding energy in the L phase grows much faster with N than that in the H phase, the L phase becomes more stable as more and more particles are added to the surface. The binding energy term, usually and correctly neglected for the case of membrane inclusions, is thus the essential ingredient for understanding the behavior of adsorbed particles.
in the H case. This means that the bending energy cost is larger in the linear conformation. The binding energy also scales as the bound area, and it is negative. Most of the binding occurs along the rim of the curved area, which means that the L configuration has more favorable binding than the H formation. The key step is to notice that for any of these phases to be stable, the gain in binding needs to overcome the cost in bending, otherwise particles would not even bind to the membrane. Since the binding energy in the L phase grows much faster with N than that in the H phase, the L phase becomes more stable as more and more particles are added to the surface. The binding energy term, usually and correctly neglected for the case of membrane inclusions, is thus the essential ingredient for understanding the behavior of adsorbed particles.
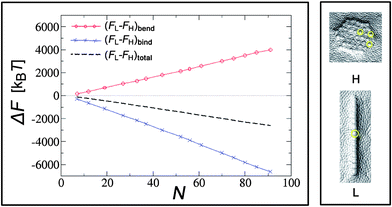 | ||
| Fig. 8 Left panel: difference in bending (FL − FH)bend and binding (FL − FH)bind energies between linear and hexagonal aggregates as a function of the number of nanoparticles N at an intermediate value of bending rigidity (κ = 20 kBT). The dashed line indicates the total energy difference between the two configurations. Right panel: typical membrane profiles underneath the aggregates in this regime. Reprinted with permission from ref. 135. | ||
B Large deformations
So far we have considered only nanoparticles that impose relatively small deformations on the membrane surface. Significant local deformations can occur for sufficiently flexible membranes and large enough binding constants or nanoparticle diameters. Self-assembly in such conditions can lead to large global membrane deformations, and even to topological transitions. Now it is a good time to take a more detailed look at the binding of a single nanoparticle to the membrane. Let us consider a particle of radius Rp ≫ t adsorbed on a fluid membrane. The resulting membrane indentation can be approximated as a spherical cap of height h and area Scap = 2πRph, as illustrated in Fig. 9. According to eqn (1), the cost in bending associated with this configuration is and the cost due to surface tension is γπh2. In the latter expression πh2 is the difference between the area of the spherical cap and its projected area, giving the increase in the membrane area due to particle binding. The free energy gain due to the adhesion energy between particle and membrane scales as −D0Scap, where D0 is the binding constant per surface area. A balance of these terms leads to an equilibrium particle coverage
and the cost due to surface tension is γπh2. In the latter expression πh2 is the difference between the area of the spherical cap and its projected area, giving the increase in the membrane area due to particle binding. The free energy gain due to the adhesion energy between particle and membrane scales as −D0Scap, where D0 is the binding constant per surface area. A balance of these terms leads to an equilibrium particle coverage 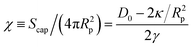 . This suggests that, for small values of surface tension, a particle will become wrapped by the membrane as soon as D0 ≳ 2κ/R2p. At that point the wrapped particle loses the contact with the membrane and buds off. The main point of this simple back-on-the envelope calculation is that for a given binding constant D0, budding is easier for large particles.
. This suggests that, for small values of surface tension, a particle will become wrapped by the membrane as soon as D0 ≳ 2κ/R2p. At that point the wrapped particle loses the contact with the membrane and buds off. The main point of this simple back-on-the envelope calculation is that for a given binding constant D0, budding is easier for large particles.
 | ||
| Fig. 9 Nanoparticle of radius Rp wrapped by the membrane. h is the height of corresponding spherical cap-like deformation induced by the nanoparticle on the membrane. | ||
A variety of more complicated calculations have been put forward to understand the nature of this transition.119–124,141,142 In an early work on the subject,119 Döbereiner and Lipowsky have analyzed vesicles in contact with many colloids and they predicted individual budding of large particles. The authors completely neglected the contribution of the surface tension, in which case the simple analysis shows that the membrane coverage of a particle χ can be either 0 or 1, corresponding to unbound or fully wrapped particles, which clearly does not capture the complete picture since partial wrapping has been observed both in simulations and experiments. In a series of papers Deserno and co-workers have described the membrane profile underneath the bound nanoparticle and in its vicinity using full nonlinear shape equations.120,121 Their analysis reveals continuous nanoparticle binding with increase in D0 followed by a discontinuous envelopment transition, pointing out to the presence of an energy barrier for the complete budding process. These results are in agreement with the particle-based simulations of the same process,125–127,139,140 which in addition provide insight into molecular details of the transition and the different pathways it can take. Simulations have been extended to particles of different shapes143–146 and flexibility,147 and several statistical thermodynamic models have been developed122–124,141,142 in search of optimal conditions for nanoparticle engulfment. Finally, a few experiments have been performed to understand the interaction of a single nanoparticle with a fluid membrane,128–130 with results in line with most of the theoretical findings. All these studies in the large deformation limit considered exclusively single-particle/membrane interactions. In what follows we review recent findings on binding of multiple particles showing that cooperative effects in such systems can lead to significantly different phenomena.
Reynwar et al.148 have investigated aggregation of model virus caps and colloidal virus particles adsorbed on a coarse-grained membrane. They found that both the individual caps and the whole nanoparticles induce large, long range membrane deformations that span throughout the whole simulation box. Subsequently, the overlap of these large deformations drives nanoparticles together and induces membrane budding of several caps or particles without them being in direct contact. Although it is still unclear what is the origin of such large deformations, to the best of our knowledge this was the first explicit simulation study of the important process of collective endocytosis. Recently, the same authors have conducted continuum elasticity study of membrane-mediated interactions between circular particles in the strongly curved regime.73 For large enough deformations they find a crossover from repulsive to attractive pair-interactions, in agreement with their particle-based simulations. Collective budding of many nanoparticles has also been discussed in simulations by Zhang and Yue,131 in the small particle limit. In that case the budding is preceded by isotropic aggregation of nanoparticles into hexagonal structures and driven by increase in binding energy. Their snapshots show no large global deformations as the ones observed by Reynwar et al.
On the experimental side, Yu et al. have studied interaction of cationic nanoparticles enclosed inside spherical phospholipid GUVs.149 In these experiments nanoparticles adsorbed onto the membrane surface and induced shape transformation in the form of tubular protrusions that would break up into pearls over longer periods of time. The tubules were almost uniform in size and approximately an order of magnitude larger than the size of a single nanoparticle. The nanoparticles did not appear to be embedded within lipid tails, but were mobile in the adsorbed state. The authors argue that the adsorption of a cationic nanoparticle increases the headgroup area of lipids causing a mismatch of surface area between the outer and inner leaflets. This would create a local curvature that could drive nanoparticle aggregation and shape change, but no qualitative explanation is available at this time. Similarly, Orwar et al. have investigated adsorption of ∼200 nm CdSe/CdTe nanoparticles inside of surface-supported phospholipid vesicles connected to a multilamellar reservoir of lipids.150 By tuning the concentration of the salt they were able to control the spreading of the phospholipid on the supporting surface. When the vesicle did not preferentially adhere to the surface, they found that nanoparticles create tubular protrusions in the lipid bilayer which grow up to a length of several hundred microns and subsequently retract. They observed nanotubes of different fluorescent intensities, pointing out to a range of possible tube radii. In some occasions, tubes grew large in diameter and exhibited multicompartmentalization, which is beyond the scope of this discussion. Unlike Yu et al., this study did not report tubule pearling.
These results are quite exciting, since they point out to unexplored routes to nanoparticle internalization in biological and artificial membrane compartments.137 To be able to use and control the process, a better understanding of the mechanism behind it is essential. It is well established that tubes can be generated out of lipid membranes by mechanical methods such as by action of motor proteins151 or polymerization of cytoskeletal filaments152 in cells, as well as by pulling by micropipette or optical tweezers in controlled experiments153–156 and by exposure to hydrodynamic flows.157 The size of the tubule in all of these cases is determined by the membrane's mechanical properties, and is given by  .158,159 Tubules can also be generated by curvature-inducing proteins,82,137,160–163 as well as by different chemical means such as by polymer or cholesterol insertion.81,161 But until recently, tubulation induced by adhering nanoparticles has been missing from the large body of work published on nanoparticle–membrane interactions.
.158,159 Tubules can also be generated by curvature-inducing proteins,82,137,160–163 as well as by different chemical means such as by polymer or cholesterol insertion.81,161 But until recently, tubulation induced by adhering nanoparticles has been missing from the large body of work published on nanoparticle–membrane interactions.
For large particles one usually expects budding to be the main mechanism of internalization by membranes. Nevertheless, long tubular protrusions have been observed in infectious pathways of preassembled virus particles. Ewers et al. have performed a thorough study of tubulation induced by simian virus 40 (SV40), both in plasma membranes and GUVs.164 The authors conducted separate experiments on tubulation driven by preassembled virus-like particles (VLP) of 45 nm in diameter, as well as by individual ∼5 nm capsomers. SV40 binds to the membrane via specific ligand–receptor interaction and the experiments show that association of both isolated capsomers and VLPs with membrane receptors was sufficient to induce formation of long tubular invaginations. However, the mechanism by which small membrane-curving capsomers induce tubulation is very different from that of preassembled particles. In both cases adhesion to the membrane creates local regions enriched in lipid receptors, causing line tension between receptor-enriched regions and the surrounding lipids. Decrease in line tension energy drives isotropic aggregation of capsomers enabling curvatures of individual proteins to build up cooperatively and deform the membrane, thus promoting tubulation via isotropic self-assembly. This picture is supported by the fact that tubulation in the case of capsomers is strongly tension-dependent and has a definite lag-time required for the aggregates to nucleate. On the other hand, binding of a single VLP causes sufficiently large local curvature by itself and tubulation happens almost instantaneously. Tubulation of VLPs shows no tension-dependence and fails to occur if not enough membrane receptors are engaged, pointing out to the dependence on binding. The VLPs aggregate into tight-fitting single-file nanotubes, where each VLP is in significant contact with the membrane (see Fig. 10). The authors suggest that VLP aggregation and membrane tubulation is driven by line tension or by means of curvature-mediated attractions, presumably similar to those proposed in simulations of Reynwar et al. However, these experiments suggest a scenario in which colloids are in direct contact with each other and well wrapped by the membrane, in contrast with the floppy invaginations in ref. 148 which are low in nanoparticle density.
 | ||
| Fig. 10 Tubular membrane invaginations induced by binding of SV40 virus particles. (a) Electron micrographs of cells that were incubated with SV40. Note the tight-fitting membrane under SV40 particles. (b) Electron micrographs of polyomavirus-like particles after incubation with cells. The virus-like particles line inside of tubular membrane invaginations like beads on a string (shown by arrowheads). Scale bars are 200 nm. Reprinted with permission from ref. 164. | ||
Our group used computer simulations to investigate the physical mechanism behind the occurrence of nanoparticle-driven tubulation in the system of vesicle-encapsulated nanoparticles.165 The simulations showed that tubulation takes place for intermediate binding constants, above values for which linear aggregation takes place and below those needed for single particle budding (Fig. 11). Tubulation can be thought of as a conformation that maximizes adhesion energy without dramatically bending the surface, and arises upon cooperative interaction of many particles. We measured the pair-interaction between two membrane-adhering colloids and found that the initial elastic cost required to bring together two large membrane deformations is overcome by a large energy gain when the particles are in contact and contained within a membrane tube oriented perpendicularly to the membrane surface. Furthermore, we have measured the free energy as a function of separation between a two-particle-tube and a third isolated particle, and again the lowest free energy is achieved when the three particles are in contact in a tubular formation, as shown in Fig. 12(a). This proves that tubes and free particles bound to the membrane attract each other, and once a tube is formed, its growth by particle addition drives the system towards a lower free energy. Such a behavior occurs for all particle sizes considered in our study (∼50 to 200 nm) and for all bending rigidities analyzed (20–40 kBT), indicating that what sets the tube size is the particle diameter, and not the natural length scale  obtained by pulling experiments.156,158,159 The extent of the mid-way repulsion and short-range attraction is dependent on the specific region of the phase diagram they are computed at, and the characteristic energy barrier at midrange distance becomes more significant as the binding to the membrane increases. For large binding constants particle aggregation becomes rare, making budding the most likely barrier-crossing mechanism. This is a kinetically dominated regime: once the budding threshold is overcome, particles can leave the membrane before having the time to aggregate. Interestingly, we find that preassembly of nanoparticles into linear aggregates facilitates the tubulation process in the regime of high nanoparticle densities, as shown in Fig. 12(b). Long tubules can thus be formed in two ways – by adding nanoparticles to the existing ones, and by collective extrusion of a linear aggregate. We have confirmed that the latter mechanism follows the first-order transition pathway found for particle budding and that longer aggregates lower the energy barrier associated with the process. Nowhere have we observed formation of membrane tubes of a radius larger than one particle diameter; however, these may develop as a result of direct particle–particle interactions or nontrivial long-range electrostatic effects. Working on almost an identical system, Bahrami et al.166 performed energy minimization of two and three particles adsorbed on the outer side of a vesicle. In line with the results of our group, they found that the tubule which encapsulates colloids is indeed the energy minimum also in that case. The authors repeated two-particle simulations for several values of reduced volumes of the vesicle, mimicking conditions of different osmotic pressures obtainable in experiments. Based on the fact that stability of a two-particle tube varied with the reduced value of the vesicle, they suggest that changing osmotic pressure should be enough to reversibly control nanoparticle uptake.
obtained by pulling experiments.156,158,159 The extent of the mid-way repulsion and short-range attraction is dependent on the specific region of the phase diagram they are computed at, and the characteristic energy barrier at midrange distance becomes more significant as the binding to the membrane increases. For large binding constants particle aggregation becomes rare, making budding the most likely barrier-crossing mechanism. This is a kinetically dominated regime: once the budding threshold is overcome, particles can leave the membrane before having the time to aggregate. Interestingly, we find that preassembly of nanoparticles into linear aggregates facilitates the tubulation process in the regime of high nanoparticle densities, as shown in Fig. 12(b). Long tubules can thus be formed in two ways – by adding nanoparticles to the existing ones, and by collective extrusion of a linear aggregate. We have confirmed that the latter mechanism follows the first-order transition pathway found for particle budding and that longer aggregates lower the energy barrier associated with the process. Nowhere have we observed formation of membrane tubes of a radius larger than one particle diameter; however, these may develop as a result of direct particle–particle interactions or nontrivial long-range electrostatic effects. Working on almost an identical system, Bahrami et al.166 performed energy minimization of two and three particles adsorbed on the outer side of a vesicle. In line with the results of our group, they found that the tubule which encapsulates colloids is indeed the energy minimum also in that case. The authors repeated two-particle simulations for several values of reduced volumes of the vesicle, mimicking conditions of different osmotic pressures obtainable in experiments. Based on the fact that stability of a two-particle tube varied with the reduced value of the vesicle, they suggest that changing osmotic pressure should be enough to reversibly control nanoparticle uptake.
 | ||
| Fig. 11 Phase diagram of the membrane aggregates and protrusions induced by colloidal particles placed inside a spherical vesicle in terms of the binding constant (D0) and the nanoparticle diameter (2Rp). Snapshots of the linear (L) and tubular (T) phases are shown on the right. The inset shows a typical single-particle bud conformation (B) that occurs at large D0. The bottom region of the phase diagram is the gaseous phase (G). Reprinted with permission from ref. 165. | ||
 | ||
| Fig. 12 (a) Free energy as a function of the separation of a two-particle tube and a single membrane-bound particle. (b) Onset D0 needed for tubulation to occur as a function of the length of the preformed linear aggregate. The inset shows snapshots of the tubule extrusion process. Reprinted with permission from ref. 165. | ||
Several other mechanisms can be responsible for nanoparticle organization on membranes. Imai et al.167 have reported GUVs of different shapes to transform into smaller multi-bead vesicles when they encapsulate charged colloids. This behaviour is induced by long-range electrostatic repulsions between the colloids and the membrane tendency to increase their free volume. Takagi et al.168 have conducted a very interesting study of size-dependent partitioning of nanoparticles adhered onto two-component membranes. The two components differ in fluidity and thus in the degree of bending stiffness. The authors report that smaller particles prefer the more rigid component, even when not mixed with larger ones, while larger particles persistently adsorb onto the softer component. Large particles gain a lot of membrane contact when wrapped by the membrane, and doing so on the softer component simply costs less in the bending energy. Smaller particles do not deform the membrane, since that would create a large curvature without gaining much in binding energy, but they just lightly attach to it. In that case the only free energy cost is the suppression of membrane thermal fluctuations, which are more pronounced on the floppier component than on the stiffer one. As a result the small particles are driven to the stiff, less fluctuating regions of the membrane. Stachowiak et al.169 have recently reported unexpected membrane tubulation caused by various membrane-adsorbed proteins which do not have hydrophobic helices that are able to penetrate the lipid bilayer. The proteins attached on the outer side of the GUVs and have tubulated outwards. The authors find positive correlation between surface fraction of the adsorbed proteins and the occurrence of membrane tubulation. They rationalize this behavior by protein crowding – at large surface fractions proteins create large surface pressure which can be decreased by curving and stretching the membrane.
VI Aggregation on elastic membranes
We now discuss nanoparticle aggregation on elastic surfaces. The idea to use elastic surfaces to design more complex nanoparticle patterns has come as a response to large number of novel methods in producing elastic sheets and shells at the nano- and microscopic scale. Our group has done extensive work on the subject, predicting the formation of unusual ordered phases of nanoparticles adsorbed on elastic surfaces of different mechanical properties and topologies. Here, we will review results on nanoparticle organization on planar,170 cylindrical171,172 and spherical elastic surfaces.173As already explained, a deformation of an elastic surface comes with costs in bending and stretching energy. The mechanical properties of elastic sheets are specifically controlled by the ratio q = Fe/Fc ∝ (h/t)2 that is intimately related to the thickness, t, of the sheet. Lets first look at the expected limiting behavior. In the bending dominated regime q ≪ 1 particles binding to the surface hardly indent it, but can locally compress it to maximize their interactions with the surface by recruiting as many membrane beads underneath them as the stretching limit allows. As this is mostly an isotropic interaction (in this regime the neighboring bonds are quite flexible), sharing/overlapping of these regions of large nanoparticle–membrane contacts is maximized when the particles are near each other, thus driving their isotropic crystallization into hexagonal structures. These configurations will indeed have lowest bending and stretching energies, however we expect aggregation to only occur for sufficiently long ranged membrane–particle interactions. In the more interesting stretching dominated limit q ≫ 1 (more appropriate for thin sheets/shells), nanoparticles are brought together to minimize their surface deformations, as it is the case for fluid membranes, but the aggregates can only arrange in a way that involves exclusively stretch-free deformations. As we have already discussed, uniaxial bending is the only possible stretch-free deformation, resulting in nanoparticles aligning preferentially into stiff straight lines at any binding energy larger than an onset value which depends on κ and particle radius. In these configurations particles can be fairly wrapped by the membrane, optimizing their binding energy at a minimum stretching cost. A number of other structures are possible when stretching and bending energies become comparable, resulting in a variety of nanoparticle aggregates whose geometry is strongly topology-dependent.
Let us first look at a planar free-standing elastic surface.170 Beyond the isotropic crystals that develop for q ≪ 1, as the stretching rigidity ks is slowly increased, crystalline aggregates are disrupted in favor of a network of short connected lines. This phase is a compromise among stretching, bending and binding energies: the first term preferring the stretch-free uniaxial deformations, the second one driving in-plane isotropic aggregation and the third one preferring isolated particles isotropically wrapped by the membrane. For even larger values of ks, the connected network is fully disrupted and particles arrange into straight parallel fibers, as shown in Fig. 13. Increasing ks at these points only leads to a larger stiffness of the aggregates. This sequence of transitions is completely driven by the stretching energy, and parallel lines make their appearance as soon as q > 1. It is important to stress that the formation of parallel lines, that effectively creates a uniform undulating and one-particle-think corrugation on the surface, is driven by the binding energy. In fact, a stretch free deformation could also be obtained by forming several particles-thick linear aggregates, but these configurations would have a weaker binding to the surface. Sheets with rectangular geometry in which two opposite sides (edges) are kept fixed (clamped) were also considered. The only ordered structure we find in this case are the linear structures and they always appear to be perpendicular to the constrained sides of the membrane with spacing controlled by ks and κ. This kind of pattern is reminiscent of the wrinkle pattern that occurs when a thin elastic sheet is subjected to a longitudinal stretching strain. Instead of having an external force stretching the plane, the particles binding to the surface act as a stress source causing the sheet to wrinkle perpendicularly to the fixed sides of the plane. The lateral distance between the particle lines nicely follows the theoretical prediction of Cerda and Mahadevan174 who analyzed how the wavelengths of wrinkles in the prestretched substrate depend on its elastic constants. This suggests a novel route for producing micro- and nano surfaces with periodical patterning that may serve as components with novel optical, electronic and magnetic properties.175–179 It should be stressed that the discussed mechanism of wrinkle formation is significantly different from the controlled wrinkling methods recently developed for the same purpose.30,180,181 In that case the wrinkles are preformed by compressing the substrate, and particles trivially arrange along the preproduced wrinkles' axis to maximize their binding energy. In our case the wrinkles are induced (in a reversible manner) by the aggregation of the nanoparticles.
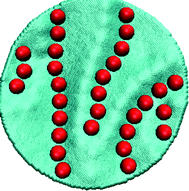 | ||
| Fig. 13 Linear aggregation of nanoparticles on a planar elastic sheet in the stretching dominated regime. | ||
On a curved surface the situation is a bit more complex.171,172 As long as the bending rigidity allows the particles to indent the membrane, they will arrange in linear aggregates that optimize the binding energy. However, the spatial orientation of the lines will change depending on q. Unlike flat sheets, elastic nanotubes have a unique and very well defined way of deforming at zero stretching cost: the deformation must be parallel to its axis and must persevere uniformly along the whole cylinder. Hence in the stretching regime the nanoparticles arrange in straight lines along the cylindrical axis. However, when q < 1, but not too small that out-of-plane deformations become prohibitive, circular lines oriented transversely to the cylinder's axis are promptly observed, as this optimizes the bending energy. In the intermediate regime q ≃ 1 different angles between linear aggregates and the cylinder's axis are possible, as well as a mixture between transversal and axial geometries. Snapshots of possible phases are shown in Fig. 14(a). To obtain more clean results in the intermediate regime, we linearly connected the particles to form a flexible polymer and placed it onto the elastic cylinder. Remarkably, we find that the polymer wraps around the tube in a helical conformation whose pitch is well defined and tunable with q. The angle θ formed between the axis of the cylinder and the direction of the polymer can be related to the two natural length scales of the problem: the radius of the cylinder, R, and the extent of the axial deformation induced by the particle on the cylinder, lp (shown in the inset of Fig. 14(b)).61 Namely, tan(θ) ∼ R/lp ∼ 1/(Dh1/2(ks/κ)1/4) gives the correct limiting behavior by predicting θ → 0 in the stretching dominated regime, and θ → π/2 in the bending dominated regime. This scaling law also nicely follows our results for the direction of the polymer angle for intermediate values of q as shown in Fig. 14(b), proving that it is the ratio of the stretching to bending rigidity that sets the pitch of the linear aggregates on elastic deformable surfaces.
 | ||
| Fig. 14 (a) Aggregation on an elastic cylinder. Nanoparticles self-assemble into ordered linear structures at moderate adhesive strength, switching orientation from rings and helices to axial strings when the stretching energy overcomes the bending. Reprinted with permission from ref. 172. (b) Flexible filament adsorbed on an elastic tube acquires a well defined helical angle. The graph shows variation of the angle that the polymer closes with the cylinder's axis as a function of the membrane stretching rigidity ks, keeping the bending rigidity constant at κ = 150 kBT. The solid line indicates the fit to the scaling law discussed in the text. The left inset illustrates the deformation along the axis of the cylinder of extent lp. The right inset shows the representative helices at different values of ks. Reprinted with permission from ref. 171. | ||
The case of a closed surface, such as a spherical shell, is more complicated. The reason is that any deformation necessarily involves stretching energy. Furthermore, inevitable surface defects in the triangulation of the surface produce a nonuniform elastic background, and on top of that, a buckling transition from a spherical to a faceted icosahedral shape takes place at large stretching energies. The pattern of the aggregates formed on these surfaces in the large stretching regime is therefore far from obvious.
The Föppl–Von Kármán number, defined as γ = YR2/κ, where Y is the Young's modulus of the shell (Y ∝ ks), and R is its radius is the standard way of characterizing the buckling transition of an elastic shell that universally takes place at around γ ≳ 150. Our study shows that, particles binding to elastic shells when γ ≪ 150 (bending regime) organize into hexagonal crystals sitting on top of the sphere173 (Fig. 15 Phase I). As γ becomes larger, at low surface coverage, particles become localized over the twelve disclinations (required by topology when constructing a triangulation on a sphere), and as the number of particles increases linear aggregates initially grow by filling the space between the disclinations on the sphere and finally form a linear network with 3-line joints winding around the disclinations in the shell (Fig. 15 – Phase II). As the templating surface begins to facet, with increasing γ, each segment of the network straightens revealing clear patterns following the seams that a pentagonal tiling of the sphere would generate (a dodecahedron, Fig. 15 – Phase III). At even larger values of γ, once the shell is well faceted, particles arrange into a linear, joint-free aggregate that smoothly winds around and away from the twelve disclinations (Fig. 15 – Phase IV). This pattern is reminiscent of that of the seam on a baseball or tennis ball, the difference being that in our case the geometry of the aggregate is dictated by the presence of 12 topological defects, while in the baseball the seam winds around the location of the four s = 1/2 disclinations that a thin nematic liquid crystal texture would generate on a sphere. Finally, for the largest values of γ studied we found particles arranging into stiff, short rod-like aggregates (rods) with specific orientations173 (Fig. 15 – Phase V).
 | ||
| Fig. 15 Upper panel: representative snapshots of the ordered phases formed on an elastic sphere as a function of the Föppl–Von Kármán number γ. Bottom panel: corresponding bending energy map (top) and stretching energy map (bottom). Different shades indicate the relative strengths as indicated in the color map on the side. Reprinted with permission from ref. 173. | ||
This rich variety of patterns can be easily understood by mapping the bending and stretching energies of an elastic shell as a function of Föppl–Von Kármán number. The bottom panel in Fig. 15 shows the energy map of the two contributions for small, intermediate and large values of γ. These maps provide a simple framework from which the geometry of the aggregates can be understood, and consistently with our understanding of the problem, particle aggregates align to follow the low bending and stretching energy regions on the shell depending on the relative weight of the two interactions.
Inspired by our work, Liang et al.182 performed simulations of long semiflexible polymers adsorbed on a soft elastic shell and have found ordered phases depending on the stage of buckling of the shell. For small values of γ the polymer is attracted to the five disclinations, locally aggregating on them and flattening them, while in the stretching dominated regime the polymer avoids the disclinations, wrapping around them. They also reported different collapsed shell structures in the limit of high binding energies. The same authors repeated these simulations for assembly of stiff nanorods on elastic shells,183 and recovered the ordered pentagonal structures formed around disclinations with short rods, while long nanorods cluster together, in-between the disclinations.
Although this review does not cover the topic of multi-component systems, it is important to mention here the recent work by Olvera de la Cruz and collaborators,184,185 as it bears important implications for the systems described so far. They studied phase separation of two or more component elastic shells using an effective elastic description of their local properties. Unlike most of the previous work on the subject, they also included explicitly the gaussian rigidity term in their energy balance. As explained before, κG is expected to be negative, it is proportional to the bending rigidity, and accounts for the topological changes of the membrane. Because a two component membrane can be described as a system of two surfaces, each constituted by its own component, mixed together and coupled via a line tension between them, arising for instance from different bending rigidities or chemical immiscibility, the energy coming from the Gaussian curvature cannot be considered constant and depends on the specific arrangements of the two components. A positive κG would concur with the line tension to form a large domain with minimal mixing of the components, but κG < 0 leads to the destabilization of such phases promoting demixing. Using these arguments, Olvera de la Cruz and collaborators have studied phase separation and buckling of two component elastic shells as a function of composition and relative bending rigidities, and have reported patterns that are strikingly similar to those found in our study of particle self-assembly on elastic surfaces. These results suggest that the latter system can be described as an effective two-component system where the first component represents the fluctuating surface and the second component, having a larger bending rigidity and an intrinsic curvature, represents the particles. Although such an effective representation would probably be appropriate mostly for intermediate binding strengths (deformations), and it is not obvious how to associate a Gaussian rigidity to these systems, it nevertheless provides an elegant and more general framework of the problem that can be easily generalized to particles interacting on fluid membranes as well as on interfaces.186
VII Conclusions
In this paper we reviewed the most recent theoretical and numerical advances on surface mediated self-assembly of nano-sized particles. Specifically, we described the case of fluid and elastic surfaces. We have given numerous examples of how local deformations of the surface can lead to a variety of particle organizations that are strongly dependent on its mechanical properties. We have discussed how, for sufficiently strong interactions, surface reshaping and/or topological transitions can be driven by nanoparticle interactions, including membrane tube formation and membrane budding. Finally, we discussed some of the different modeling strategies employed to study these systems depending on the length and time scales of interest.Apart from the intrinsically interesting problem of self-assembly and pattern formation of nanocomponents that we have discussed at length throughout the paper, we would like to focus this short conclusion on the surfaces themselves. In fact, by shifting the focus from the particles to the surfaces, one realizes that the adsorbing particles can be thought of as a way of altering the mechanical properties of the surfaces in very predictable ways. The most explicit example can be observed on elastic sheets. An initially planar surface with a uniformly distributed elastic field across its area deforms into a configuration that resembles that of a thin corrugated roof. As a result of this symmetry breaking, the bending modes of deformation of this surface have become anisotropic: the sheet is now softer to bend along the axis formed by the parallel wrinkles, but extremely resistant to bending deformations across the same axis. In a similar manner, particles organizing over a cylindrical surface will also tend to form wrinkles along its axes, and depending on the particle concentration and adhesion energy, it is possible to control the cross-section of the tube.172 By controlling the profile of the nanotube, one has direct access to the effective bending rigidity of the nanoparticle–nanotube composite in the axial direction, as such rigidity depends linearly on the tubes' cross-sectional moment of inertia.
These simple examples suggest that nanoparticles could be used to control the mechanical properties of elastic surfaces in a reversible manner, and this is a very important property that any stimuli responsive material must satisfy. The ability to do so could have several potential applications from fake blood cells, whose elastic properties are very much related to the way they flow in the blood stream, to artificial skin, and more in general in soft micro-robotics, where elastic responses to external stimuli are converted into directed motion. We hope that the results reviewed in this paper can stimulate further work in this direction.
Acknowledgements
This work was supported by the National Science Foundation under Career Grant No. DMR-0846426. The authors thank J. C. Pàmies for many fruitful discussions on the subject.References
- G. M. Whitesides and M. Boncheva, Proc. Natl. Acad. Sci. U. S. A., 2002, 16, 4769 CrossRef.
- B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Science, New York, 5th edn, 2008 Search PubMed.
- F. H. C. Crick and J. D. Watson, Nature, 1956, 177, 473 CrossRef CAS.
- A. Klug and D. L. D. Caspar, Adv. Virus Res., 1960, 7, 225 CrossRef CAS.
- E. Sackmann, J. Phys., 1990, 68, 999 CAS.
- G. Subramanian, V. N. Manoharan, J. D. Thorne and D. J. Pine, Adv. Mater., 1999, 11, 1261 CrossRef CAS.
- G. A. DeVries, et al. , Science, 2007, 315, 358 CrossRef CAS.
- M. Li, H. Schnablegger and S. Mann, Nature, 1999, 402, 393 CrossRef CAS.
- L. Hong, S. Jiang and S. Granick, Langmuir, 2006, 22, 9495 CrossRef CAS.
- H. Weller, Philos. Trans. R. Soc., A, 2003, 361, 229 CrossRef CAS.
- E. K. Hobbie, et al. , Langmuir, 2005, 21, 10284 CrossRef CAS.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525 RSC.
- S. U. Pickering, J. Chem. Soc., Trans., 1907, 91, 2001 RSC.
- C. Zeng, H. Bissig and A. D. Dinsmore, Solid State Commun., 2006, 139, 547 CrossRef CAS and references therein.
- A. Böker, J. Heb, T. Emrick and T. P. Russell, Soft Matter, 2007, 3, 1231 RSC.
- Z. W. Niu, J. B. He, T. P. Russell and Q. A. Wang, Angew. Chem., 2010, 49, 10052 CrossRef CAS.
- N. Bowden, A. Terfort, J. Carbeck and G. M. Whitesides, Science, 1997, 276, 233 CrossRef CAS.
- N. Bowden, I. S. Choi, B. A. Grzybowski and G. M. Whitesides, J. Am. Chem. Soc., 1999, 121, 5373 CrossRef CAS.
- P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- J. N. Israelachvili, Intermolecular And Surface Forces, Academic Press, San Diego, 1992 Search PubMed.
- D. H. Gracias, J. Tien, T. L. Breen, C. Hsu and G. M. Whitesides, Science, 2000, 289, 1170 CrossRef CAS.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418 CrossRef CAS.
- L. Botto, E. P. Lewandowski, M. Cavallaro and K. J. Stebe, Soft Matter, 2012, 8, 9957 RSC.
- D. Boal, Mechanics of the Cell, Cambridge University Press, 2001 Search PubMed.
- S. Safran, Statistical Thermodynamics Of Surfaces, Interfaces, And Membranes, Westview Press, 2003 Search PubMed.
- A. Nel, et al. , Nat. Mater., 2009, 8, 543 CrossRef CAS.
- H. F. Krug and P. Wick, Angew. Chem., 2011, 50, 1260 CrossRef CAS.
- H. L. Karlsson, J. Gustafsson, P. Cronholm and L. Möller, Toxicol. Lett., 2009, 188, 112 CrossRef CAS.
- H. Bouwmeester, et al. , Regul. Toxicol. Pharmacol., 2009, 53, 52 CrossRef CAS.
- S. Hiltl, M.-P. Schürings, A. Balaceanu, V. Mayorga, C. Liedel, A. Pich and A. Böker, Soft Matter, 2011, 7, 8231 RSC.
- T. A.-J. Wafa and K. Kostarelos, Nanomedicine, 2007, 2, 85 CrossRef.
- P. J. Costanzo, E. Liang, T. E. Patten, S. D. Collins and R. L. Smith, Lab Chip, 2006, 5, 606 Search PubMed.
- R. J. Mart, K. P. Liem and S. J. Webb, Pharm. Res., 2009, 26, 1701 CrossRef CAS.
- J. H. Fendler, Acc. Chem. Res., 1980, 13(1), 713 CrossRef.
- J. Oberdisse, C. Couve, J. Appell, J. F. Berret, C. Ligoure and G. Porte, Langmuir, 1996, 12(5), 1212 CrossRef CAS.
- D. E. Discher and A. Eisenberg, Science, 2002, 297, 967 CrossRef CAS.
- E. Barry and Z. Dogic, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 10348 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Pergamon, New York, 1970 Search PubMed.
- J. H. Fendler and P. Tundo, Acc. Chem. Res., 1984, 17, 3 CrossRef CAS.
- P. C. Georges and P. A. Janmey, J. Appl. Physiol., 2005, 98, 1547 CrossRef.
- A. Elgsaeter, B. T. Stokke, A. Mikkelsen and D. Branton, Science, 1986, 234, 1217 CAS.
- C. F. Schmidt, K. Svoboda, N. Lei, I. B. Petsche, L. E. Berman, C. R. Safinya and G. S. Grest, Science, 1993, 259, 952 CrossRef CAS.
- K. E. Mueggenburg, X. M. Lin, R. H. Goldsmith and H. M. Jaeger, Nat. Mater., 2007, 6, 656 CrossRef CAS.
- S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282 CrossRef CAS.
- J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth and S. Roth, Nature, 2007, 446, 60 CrossRef CAS.
- M. S. Spector, E. Naranjo, S. Chiruvolu and J. A. Zasadzinski, Phys. Rev. Lett., 1994, 73, 2867 CrossRef CAS.
- X. Wen, C. W. Garland, T. Hwa, M. Kardar, E. Kokufuta, Y. Li, M. Orkisz and T. Tanaka, Nature, 1992, 355, 426 CrossRef CAS.
- J. Huang, M. Juszkiewicz, W. H. de Jeu, E. Cerda, T. Emrick, N. Menon and T. P. Russell, Science, 2007, 317, 650 CrossRef CAS.
- R. J. Hamers, Nature, 2001, 412, 489 CrossRef CAS.
- K. Efimenko, et al. , Nat. Mater, 2005, 4, 293 CrossRef CAS.
- N. Doshi, A. Zahr, S. Bhaskar, J. Lahann and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21495 CrossRef CAS.
- J. H. Lim, K. S. Lee, J. C. Kim and B. H. Lee, Opt. Lett., 2004, 29, 331 CrossRef.
- F. Ilievski, A. D. Mazzeo, R. F. Shepherd, X. Chen and G. M. Whitesides, Angew. Chem., Int. Ed., 2011, 50, 1890 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., C: Biochem., Biophys., Biol., Virol., 1973, 28, 693 CAS.
- F. L. H. Brown, Annu. Rev. Phys. Chem., 2008, 59, 685 CrossRef CAS.
- M. Hu, J. J. Briguglio and M. Deserno, Biophys. J., 2012, 102, 1403 CrossRef CAS.
- E. Kurtisovski, N. Taulier, R. Ober, M. Waks and W. Urbach, Phys. Rev. Lett., 2007, 98, 258103 CrossRef.
- H. Bermúdez, A. K. Brannan, D. A. Hammer, F. S. Bates and D. E. Discher, Macromolecules, 2002, 35, 8203 CrossRef.
- H. Bermúdez, D. A. Hammer and D. E. Discher, Langmuir, 2004, 20, 540 CrossRef.
- F. Jähnig, Biophys. J., 1996, 71, 1348 CrossRef.
- T. A. Witten, Rev. Mod. Phys., 2007, 79, 643 CrossRef.
- K. Efimenko, M. Rackaitis, E. Manias, A. Vaziri, L. Mahadevan and J. Genzer, Nat. Mater., 2005, 4, 293 CrossRef CAS.
- M. Goulian, Curr. Opin. Colloid Interface Sci., 1996, 3, 358 CrossRef.
- R. Phillips, T. Ursell, P. Wiggins and P. Sens, Nature, 2009, 459, 379 CrossRef CAS.
- T. Gil, J. H. Ipsen, O. G. Mouritsen, M. C. Sabra, M. M. Sperotto and M. J. Zuckermann, Biochim. Biophys. Acta, 1998, 1376, 245 CrossRef CAS.
- M. Goulian, R. Bruisma and P. Pincus, Europhys. Lett., 1993, 22, 145 CrossRef CAS.
- M. Goulian, R. Bruinsma and P. Pincus, Europhys. Lett., 1993, 23, 155 CrossRef , Erratum.
- P. G. Dommersnes and J.-B. Fournier, Europhys. Lett., 1997, 39, 681 CrossRef.
- D. R. Fattal and A. Ben-Shaul, Biophys. J., 1993, 65, 1795 CrossRef CAS.
- H. W. Huang, Biophys. J., 1986, 50, 1061 CrossRef CAS.
- H. Aranda-Espinoza, A. Berman, N. Dan, P. Pincus and S. Safran, Biophys. J., 1996, 71, 648 CrossRef CAS.
- M. S. Turner and P. Sens, Phys. Rev. Lett., 2004, 93, 118103 CrossRef.
- B. J. Reynwar and M. Deserno, Soft Matter, 2011, 7, 8567 RSC.
- P. G. Dommersnes and J.-B. Fournier, Eur. Phys. J. B, 1999, 12, 9 CrossRef CAS.
- C. Yolcu and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031906 CrossRef.
- A. D. Dinsmore, D. T. Wong, P. Nelson and A. G. Yodh, Phys. Rev. Lett., 1998, 80, 409 CrossRef CAS.
- I. Koltover, J. O. Rädler and C. R. Safinya, Phys. Rev. Lett., 1999, 82, 1991 CrossRef CAS.
- T. Baumgart, S. T. Hess and W. W. Webb, Nature, 2003, 425, 821 CrossRef CAS.
- T. S. Ursell, W. S. Klug and R. Phillips, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13301 CrossRef CAS.
- J. E. Rothman, Nature, 1994, 372, 5563 CrossRef.
- K. Farsad and P. De Camilli, Curr. Opin. Cell Biol., 2003, 15, 372 CrossRef CAS.
- R. N. Frese, J. C. Pàmies, J. D. Olsen, S. Bahatyrova, C. D. van Der Weij-De Wit, T. J. Aartsma, C. Otto, N. Hunter, D. Frenkel and R. van Grondelley, Biophys. J., 2008, 94, 640 CrossRef CAS.
- J. T. Groves, Annu. Rev. Phys. Chem., 2007, 58, 697 CrossRef CAS.
- R. Parthasarathy and J. T. Groves, Soft Matter, 2007, 3, 24 RSC.
- D. R. Nelson, Nano Lett., 2002, 2, 1125 CrossRef CAS.
- G. Srinivas, D. E. Discher and M. L. Klein, Nat. Mater., 2004, 3, 638 CrossRef CAS.
- G. Srinivas, J. C. Shelley, S. O. Nielsen, D. E. Discher and M. L. Klein, J. Phys. Chem. B, 2004, 108, 8153 CrossRef CAS.
- S. M. Loverde, D. A. Pantano, D. A. Christian, A. Mahmud, M. L. Klein and D. E. Discher, Curr. Opin. Solid State Mater. Sci., 2011, 15, 277 CrossRef CAS.
- L. Rekvig, B. Hafskjold and B. Smit, Phys. Rev. Lett., 2004, 92, 116101 CrossRef.
- F. L. Brown, Q. Rev. Biophys., 2011, 44, 391 CrossRef CAS.
- M. Deserno, Macromol. Rapid Commun., 2009, 30, 752 CrossRef CAS.
- M. Venturoli, M. M. Sperotto, M. Kranenburg and B. Smit, Phys. Rep., 2006, 437, 1 CrossRef CAS.
- H. Noguchi, J. Phys. Soc. Jpn., 2009, 78, 041007 CrossRef.
- A. P. Lyubartsev and A. L. Rabinovich, Soft Matter, 2011, 7, 25 RSC.
- O. Farago, J. Chem. Phys., 2003, 119, 596 CrossRef CAS.
- Z.-J. Wang and D. Frenkel, J. Chem. Phys., 2005, 122, 234711 CrossRef.
- I. R. Cooke, K. Kremer and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011506 CrossRef.
- G. Brannigan and F. L. H. Brown, J. Chem. Phys., 2004, 120, 1059 CrossRef CAS.
- S. Izvekov and G. A. Voth, J. Phys. Chem. B, 2005, 109, 2469 CrossRef CAS.
- G. Brannigan, L. C.-L. Lin and F. L. H. Brown, Eur. Biophys. J., 2006, 35, 104 CrossRef CAS.
- M. Müller, K. Katsov and M. Schick, Phys. Rep., 2006, 434, 113 CrossRef.
- Y. Kantor, M. Kardar and D. R. Nelson, Phys. Rev. Lett., 1986, 57, 791 CrossRef CAS.
- J.-S. Ho and A. Baumgärtner, Europhys. Lett., 1990, 12, 295 CrossRef.
- A. Baumgärtner and J.-S. Ho, Phys. Rev. A, 1990, 41, 5747 CrossRef.
- G. Gompper and D. M. Kroll, J. Phys.: Condens. Matter, 1997, 9, 8795 CrossRef CAS.
- J. M. Drouffe, A. C. Maggs and S. Leibler, Science, 1991, 254, 1353 CAS.
- M. G. Del Pópolo and P. Ballone, J. Chem. Phys., 2008, 128, 024705 CrossRef.
- H. Yuan, C. Huang, J. Li, G. Lykotrafitis and S. Zhang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 011905 CrossRef.
- T. Kohyama, Phys. A, 2009, 388, 3334 CrossRef CAS.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 021903 CrossRef.
- G. A. Vliegenthart and G. Gompper, Nat. Mater., 2006, 5, 216 CrossRef CAS.
- D. E. Discher, D. H. Boal and S. K. Boey, Biophys. J., 1998, 75, 1584 CrossRef CAS.
- J. Li, M. Dao, C. T. Lim and S. Suresh, Biophys. J., 2005, 88, 3707 CrossRef CAS.
- H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14159 CrossRef CAS.
- J. Li, G. Lykotrafitis, M. Dao and S. Suresh, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4937 CrossRef CAS.
- H. Li and G. Lykotrafitis, Biophys. J., 2012, 102, 75 CrossRef CAS.
- H. Noguchi and G. Gompper, Phys. Rev. Lett., 2004, 93, 258102 CrossRef.
- B. Wang, L. Zhang, S. C. Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18171 CrossRef CAS.
- R. Lipowsky and H. G. Döbereiner, Europhys. Lett., 1998, 43, 219 CrossRef CAS.
- M. Deserno and T. Bickel, Europhys. Lett., 2003, 62, 767 CrossRef CAS.
- M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031903 CrossRef.
- S. Tzlil, M. Deserno, W. M. Gelbart and A. Ben-Shaul, Biophys. J., 2004, 86, 2037 CrossRef CAS.
- H. Gao, W. Shi and L. B. Freund, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9469 CrossRef CAS.
- A. Chaudhuri, G. Battaglia and R. Golestanian, Phys. Biol., 2011, 8, 046002 CrossRef.
- K. A. Smith, D. Jasnow and A. C. Balazs, J. Chem. Phys., 2007, 127, 084703 CrossRef.
- M. Fošnarič, A. Iglič, D. M. Kroll and S. J. May, J. Chem. Phys., 2009, 131, 105103 CrossRef.
- Y. Li and N. Gu, J. Phys. Chem. B, 2010, 114, 2749 CrossRef CAS.
- W. Jiang, B. Y. Kim, J. T. Rutka and W. C. Chan, Nat. Nanotechnol., 2008, 3, 145 CrossRef CAS.
- Y. Roiter, M. Ornatska, A. R. Rammohan, J. Balakrishnan, D. R. Heine and S. Minko, Nano Lett., 2008, 8, 941 CrossRef CAS.
- S. Zhang, A. Nelson and P. A. Beales, Langmuir, 2012, 28, 12831 CrossRef CAS.
- T. Yue and X. Zhang, ACS Nano, 2012, 6, 3196 CrossRef CAS.
- C. Wilhelma, C. Billoteya, J. Rogerc, J. N. Ponsc, J.-C. Bacria and F. Gazeau, Biomaterials, 2003, 24, 1001 CrossRef.
- I. Koltover, T. Salditt and C. R. Safinya, Biophys. J., 1999, 77, 915 CrossRef CAS.
- A. Lesniak, et al. , J. Am. Chem. Soc., 2013, 135, 1438 CrossRef CAS.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 108, 118101 CrossRef.
- L. Ramos, T. C. Lubensky, N. Dan, P. Nelson and D. A. Weitz, Science, 1999, 286, 2325 CrossRef CAS.
- P. Sens, L. Johannes and P. Bassereau, Curr. Opin. Cell Biol., 2008, 20, 476 CrossRef CAS.
- B. J. Reynwar and M. Deserno, Biointerphases, 2008, 3, FA117 CrossRef.
- T. Yue and X. Zhang, Soft Matter, 2011, 7, 9104 RSC.
- T. Ruiz-Herrero, E. Velasco and M. F. Hagan, J. Phys. Chem. B, 2012, 116, 9595 CrossRef CAS.
- S. Zhang, J. Li, G. Lykotrafitis, G. Bao and S. Suresh, Adv. Mater., 2009, 21, 419 CrossRef CAS.
- H. Yuan, J. Li, G. Bao and S. Zhang, Phys. Rev. Lett., 2010, 105, 138101 CrossRef.
- S. Mkrtchyan, C. Ing and J. Z. Y. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 011904 CrossRef.
- K. Yang and Y. Ma, Aust. J. Chem., 2011, 64, 894 CrossRef CAS.
- R. Vacha, F. J. Martinez-Veracoechea and D. Frenkel, Nano Lett., 2011, 11, 5391 CrossRef CAS.
- D. S. Dean, T. C. Hammant, R. R. Horgan, A. Naji and R. Podgornik, J. Chem. Phys., 2012, 137, 144904 CrossRef.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 CrossRef.
- B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Müller, K. Kremer and M. Deserno, Nature, 2007, 447, 461 CrossRef CAS.
- Y. Yu and S. Granick, J. Am. Chem. Soc., 2009, 131, 158 Search PubMed.
- I. Gözen, C. Billerit, P. Dommersnes, A. Jesorka and O. Orwar, Soft Matter, 2011, 7, 9706 RSC.
- R. D. Vale and H. Hotani, J. Cell Biol., 1988, 107, 2233 CrossRef CAS.
- M. Waterman-Storer and E. D. Salmon, Curr. Biol., 1998, 8, 798 CrossRef.
- E. Evans, et al. , Science, 1996, 273, 933 CAS.
- T. Roopa and G. V. Shivashankar, Appl. Phys. Lett., 2003, 82, 1631 CrossRef CAS.
- D. Raucher and M. P. Sheetz, Biophys. J., 1999, 77, 1992 CrossRef CAS.
- D. Cuvelier, N. Chiaruttini, P. Bassereau and P. Nassoy, Europhys. Lett., 2005, 71, 1015 CrossRef CAS.
- R. E. Waugh, Biophys. J., 1982, 38, 29 CrossRef CAS.
- I. Derenyi, F. Jülicher and J. Prost, Phys. Rev. Lett., 2002, 88, 238101 CrossRef.
- G. Koster, A. Cacciuto, I. Derényi, D. Frenkel and M. Dogterom, Phys. Rev. Lett., 2005, 94, 068101 CrossRef.
- W. Römer, et al. , Nature, 2007, 450, 670 CrossRef.
- J. Zimmerberg and M. M. Kozlov, Nat. Rev. Mol. Cell Biol., 2006, 7, 9 CrossRef CAS.
- W. A. Prinz and J. E. Hinshaw, Crit. Rev. Biochem. Mol. Biol., 2009, 44, 278 CrossRef CAS.
- R. Matthews and C. N. Likos, Phys. Rev. Lett., 2012, 109, 178302 CrossRef.
- H. Ewers, et al. , Nat. Cell Biol., 2010, 12, 11 CrossRef CAS.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 109, 188101 CrossRef.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, Phys. Rev. Lett., 2012, 109, 188102 CrossRef.
- Y. Natsume, O. Pravaz, H. Yoshida and M. Imai, Soft Matter, 2010, 6, 5359 RSC.
- T. Hamada, M. Morita, M. Miyakawa, R. Sugimoto, A. Hatanaka, M. C. Vestergaard and M. Takagi, J. Am. Chem. Soc., 2012, 134, 13990 CrossRef CAS.
- J. C. Stachowiak, E. M. Schmid, C. J. Ryan, H. S. Ann, D. Y. Sasaki, M. B. Sherman, P. L. Geissler, D. A. Fletcher and C. C. Hayden, Nat. Cell Biol., 2012, 14, 944 CrossRef CAS.
- A. Šarić and A. Cacciuto, Soft Matter, 2011, 7, 8324 RSC.
- A. Šarić, J. C. Pàmies and A. Cacciuto, Phys. Rev. Lett., 2010, 104, 45702 CrossRef.
- J. C. Pàmies and A. Cacciuto, Phys. Rev. Lett., 2011, 106, 045702 CrossRef.
- A. Šarić and A. Cacciuto, Soft Matter, 2011, 7, 1784 Search PubMed.
- E. Cerda and L. Mahadevan, Phys. Rev. Lett., 2003, 90, 074302 CrossRef CAS.
- Z. Sun and B. Yang, Nanoscale Res. Lett., 2006, 1, 4656 CrossRef.
- S. J. Koh, Nanoscale Res. Lett., 2007, 2, 519 CrossRef CAS.
- S. Mitragotri and J. Lahann, Nat. Mater., 2008, 8, 1523 Search PubMed.
- J. A. Schuller, E. S. Barnard, W. Cai, Y. C. Jun, J. S. White and M. L. Brongersma, Nat. Mater., 2010, 9, 193 CrossRef CAS.
- H. A. Atwater and A. Polman, Nat. Mater., 2010, 9, 205 CrossRef CAS.
- A. Schweikart, A. Fortini, A. Wittemann, M. Schmidt and A. Fery, Soft Matter, 2010, 6, 5860 RSC.
- A. Schweikart, N. Pazos-Pérez, R. A. Alvarez-Puebla and A. Fery, Soft Matter, 2011, 7, 4093 RSC.
- D. Zhang, A. Chai, X. Wen, L. He, L. Zhang and H. Liang, Soft Matter, 2012, 8, 2152 RSC.
- X. Wen, D. Zhang, A. Chai, L. He, S. Ran and L. Zhang, Soft Matter, 2012, 8, 6706 RSC.
- G. Vernizzi, R. Sknepnek and M. Olvera de la Cruz, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4292 CrossRef CAS.
- R. Sknepnek, G. Vernizzi and M. Olvera de la Cruz, Soft Matter, 2012, 8, 636 RSC.
- We could like to thank M. Olvera de la Cruz for pointing out this analogy to us.
| This journal is © The Royal Society of Chemistry 2013 |
