Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Colloidal transport in periodic potentials: the role of modulated-crowding†
Ramón
Castañeda-Priego‡
 a,
Erick
Sarmiento-Gómez
a,
Erick
Sarmiento-Gómez
 ab,
Yasamin Mohebi
Satalsari
ab,
Yasamin Mohebi
Satalsari
 b,
Stefan U.
Egelhaaf
b,
Stefan U.
Egelhaaf
 b and
Manuel A.
Escobedo-Sánchez‡
b and
Manuel A.
Escobedo-Sánchez‡
 *b
*b
aDepartamento de Ingeniería Física, División de Ciencias e Ingenierías, Campus León, Universidad de Guanajuato, Loma del Bosque 103, Lomas del Campestre, 37150 León, Guanajuato, Mexico
bCondensed Matter Physics Laboratory, Heinrich Heine University, Düsseldorf, Universitätsstraße 1, 40225 Düsseldorf, Germany. E-mail: escobedo@hhu.de
First published on 8th April 2025
Abstract
The transport properties of colloids in external potentials are often studied at low concentrations to avoid particle–particle interactions. However, the impact of concentration on colloidal dynamics under external potentials has received limited attention. We examine the effect of concentration on the diffusivity of a quasi-2D colloidal dispersion subjected to a light-induced sinusoidal potential (interference fringes). By measuring particle diffusivity perpendicular to the fringes at various concentrations and laser powers, we find how the particle transport is governed by concentration and the structural organization induced by the external potential. Specifically, we introduce the concept of modulated-crowding for this physical scenario and characterize its influence on the long-time self-diffusion coefficient. These findings are confirmed using Brownian dynamics simulations.
1 Introduction
Soft materials, such as colloidal suspensions, are known to be susceptible to relatively weak external potentials,1 that is, the potential has a magnitude around the thermal energy,2kBT, with kB and T being the Boltzmann constant and the absolute temperature, respectively. Understanding the material response to such potentials has been utilized to design tools that allow us to precisely control or manipulate the material constituents. Colloidal manipulation through different types of external potentials has attracted interest during the last two decades due to its potential technological applications.3,4 Several simulation, theoretical, and experimental studies have found that one simple and effective way to control the properties of a colloidal suspension is to use geometric confinement.4,5 Walls or boundaries act as external potentials that can modify the thermodynamic properties of the suspension. Furthermore, colloids between two parallel plates,6 circular cavities,7 parallel charge colloidal layers8 and even one-dimensional colloidal systems9–11 have been extensively investigated because structural and diffusive properties are strongly influenced by confinement.4,6,12 Thus, confinement has become an important physical mechanism in many different areas of science and technology. Recent reviews highlighting the use and understanding of colloids under confinement can be found in ref. 1, 2, 4, 5 and 13, and references therein.The confinement of a colloidal dispersion between walls can be treated as Brownian particles interacting with an arbitrarily large external potential placed in the position of the confining walls, effectively hindering the movement of the particles out of a given region.4,14,15 Decreasing the energy barrier and adding some spatial variation to the external potential produces an energetic landscape that could induce, for example, freezing-like transitions.6 Furthermore, a directional external field, i.e., gravitational or electric, can produce sedimentation or electrophoretic mobility, leading to interesting non-equilibrium thermodynamic states or transport phenomena not typically seen under homogeneous conditions.16–18 Moreover, a spatially inhomogeneous external field can also promote modifications in the phase behavior of the colloids, e.g., laser-induced phase transitions.6,19–21
The optical force imposed on a dielectric particle by the refraction of light at the particle's interface, known as pressure radiation, is one of the experimental methods to create external potentials to interact with colloidal particles. This mechanism led to the development of optical tweezers.22 It is a suitable option due to the flexibility to induce different spatially dependent light potentials.3,5,13 Inspired by the pioneering work of Ashkin,22 optical tweezers are now a widely used tool in physics and biology.13 This type of light potential has been used to induce structural changes and explore both the influence of external potentials on the diffusion of individual colloidal particles23,24 and the hydrodynamic correlations between a few-body colloidal system.25–28 Currently, arbitrary light potentials are created by manipulating the wavefront of the incident laser using a spatial light modulator, even with a temporal evolution, thus opening the opportunity for spatio-temporal manipulating scenarios.3,5
Although the phase behavior of colloids under the influence of a periodic potential is currently well understood,19–21,29–31 it is interesting to note that much less is known about the particle dynamics of colloidal suspensions under the action of modulated potentials. For example, the dependence of the particle transport of highly charged colloids on the strength of the sinusoidal potential was theoretically reported;23 in that case, the area fraction was fixed ∼0.153 and an interesting non-monotonic variation of particle diffusion emerged due to the competition between particle–particle and particle–potential interactions.23 Moreover, the behaviour of weakly charged dilute colloidal suspensions under the influence of periodic potentials has been experimentally reported.24 In the latter case, the authors focused on how the periodicity and laser power influenced the diffusive properties, specifically the amplitude of the modulated potential and the size of the particles. However, none of the previous contributions dealt with crowding effects. Nevertheless, recent studies have focused on understanding the physical phenomena that arise from the crowding of microparticles suspended in fluids subjected to periodic potentials, see, e.g., ref. 32–40.
In this contribution, we report experimental findings that enhance the understanding of the dynamic behaviour of a confined colloidal dispersion influenced by a periodic energy landscape created by the interference patterns produced by the convergence of two laser beams. Varying the concentration of the sample from very dilute to moderate and adjusting the amplitude of the energetic landscape, we elucidate the impact of concentration on particle transport in periodic light potentials. The periodicity of the external potential was fixed and selected to be greater than the particle size. Specifically, attention has been focused on the effects of concentration (crowding) and amplitude of the modulated periodic potentials on diffusivity. The competition of both mechanisms allows us to introduce the concept of modulated-crowding for this physical scenario. We identify that modulated-crowding effects in the diffusion coefficient can be completely separated into distinct factors. Then, an appropriate external-potential-dependent normalization results in a universal dynamical behavior that is entirely described by the particle concentration and the structure induced by the external light field. This dynamical scenario is accurately described and corroborated by Brownian dynamics simulations.
2 Materials and methods
2.1 Brownian dynamics simulation and external potentials
In Brownian dynamics (BD) simulations, the configuration space of the N particle trajectories is composed of successive displacements![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t + Δτ) −
i(t + Δτ) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t), i = 1,…,N, generated from the following stochastic equation,41
i(t), i = 1,…,N, generated from the following stochastic equation,41![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t + Δτ) = i(t + Δτ) = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) + βD0 i(t) + βD0![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) i(t)Δτ + δ i(t)Δτ + δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(Δτ), i(Δτ), | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(Δτ) a random displacement such that 〈δ
i(Δτ) a random displacement such that 〈δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(Δτ)〉 = 0 and 〈δ
i(Δτ)〉 = 0 and 〈δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(Δτ)δ
i(Δτ)δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j(0)〉 = 2D0δijΔτ, with D0 being the free-particle diffusion coefficient26 and δij the Kronecker delta. In eqn (1),
j(0)〉 = 2D0δijΔτ, with D0 being the free-particle diffusion coefficient26 and δij the Kronecker delta. In eqn (1), ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) i(t) represents the total external force acting on particle i, which includes the particle–particle and particle–potential interactions. The equation does not explicitly include hydrodynamic interactions. The particle–particle interaction is considered a hard-core potential, which is represented by the WCA potential,42
i(t) represents the total external force acting on particle i, which includes the particle–particle and particle–potential interactions. The equation does not explicitly include hydrodynamic interactions. The particle–particle interaction is considered a hard-core potential, which is represented by the WCA potential,42 | (2) |
 | (3) |
The particle–potential coupling is considered to be a periodic field, which can be regarded as a potential that generates energy barriers along the x-direction. Particles must overcome these barriers to move along this axis. This potential is mathematically described by23,24
 | (4) |
The dynamics of the colloidal dispersion is then simulated as follows. We consider a random initial configuration of N = 1024 colloidal particles placed in a rectangular box of dimensions Lx × Ly with  . This condition is required in order to correctly reproduce the density fluctuations of a hard disk suspension.43 Periodic boundary conditions are applied in each direction, with Lx and Ly being the sides of the simulation box along the x and y directions, respectively. We investigated particle concentrations that ranged from extremely low to moderate densities. The number of particles used in the simulations is large enough such that the results are independent of the system size; in most cases reported, every observable is the result of averaging over 5 independent realizations. Then, the particles move according to eqn (1), and the simulated colloidal system evolves from a non-equilibrium state to the equilibrium one.
. This condition is required in order to correctly reproduce the density fluctuations of a hard disk suspension.43 Periodic boundary conditions are applied in each direction, with Lx and Ly being the sides of the simulation box along the x and y directions, respectively. We investigated particle concentrations that ranged from extremely low to moderate densities. The number of particles used in the simulations is large enough such that the results are independent of the system size; in most cases reported, every observable is the result of averaging over 5 independent realizations. Then, the particles move according to eqn (1), and the simulated colloidal system evolves from a non-equilibrium state to the equilibrium one.
The time step, Δτ, in eqn (1) is chosen not to be too large to ensure that the force acting on the particle is approximately constant throughout its duration, but it must not be too small to ensure that we can use the description given by eqn (1), which is valid in the so-called diffusive regime. To do this, we have used a reduced time step of Δτ* ≡ ΔτD0/σ2 = 1 × 10−4, where σ is the diameter of the particles. The time window used in the BD simulations was set to 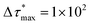 . Fig. 1(c) and (d) shows representative snapshots of the Brownian dynamics computer simulations designed to replicate the experimental conditions.
. Fig. 1(c) and (d) shows representative snapshots of the Brownian dynamics computer simulations designed to replicate the experimental conditions.
2.2 Observables
The mean square displacement (MSD) is a key quantity used to characterize particle motion in systems ranging from simple liquids to soft materials and arrested states.4 The MSD provides a detailed statistical picture of particle motion and bridges the gap between microscopic trajectories and macroscopic transport properties. The trajectories of particles within a periodic potential exhibit pronounced anisotropy. Under such conditions, particles diffuse mainly along the fringes (y-direction) because their movement across (x-direction) them is impeded by potential energy barriers.5,23,31 In this contribution, we do not present data on the motion of particles parallel to the fringes since the external field does not influence particle displacement along this axis. Instead, our focus is on the particle movement perpendicular to the fringes. Hence, we determine the MSD in the x-direction, through a temporal average over all initial times t0 and an ensemble average over all particle trajectories (denoted by E) represented by the following expression:| 〈Δx2(τ)〉 = 〈[x(t0 + τ) − x(t0)]2〉t0,E, | (5) |
Two observables are derived from the MSD. First, the time-dependent diffusivity, D(τ), which describes how the rate of particle displacement evolves with time, capturing dynamic heterogeneity and complex interactions within the system. Second, the anomalous diffusion exponent, α(τ), that shows the scaling of MSD with time, quantifying the transitions between normal, sub-, and super-diffusive behavior. Both quantities are obtained using the following expressions:
 | (6) |
 | (7) |
Therefore, the information obtained from the MSD, time-dependent diffusivity and the anomalous diffusion exponent provides a comprehensive framework for understanding particle transport,44 including transitions between dynamical regimes and the effects of confinement, crowding, or external potentials in complex systems. Despite this, studying directed self-assembly at finite concentrations and its connection to colloid dynamics is far from trivial. This work focuses on unraveling how crowding affects particle transport in colloids subjected to different amplitudes of an external periodic potential, providing evidence that the structure arising from the interplay between crowding and the potential determines long-time diffusivity.
To quantify the structure arising from the interplay between crowding and the external potential, at least two different types of pair-correlation functions can be calculated:23,45 (a) the pair correlation function along the y-direction, g(y); it describes the spatial organization along any fringe, (b) the pair correlation function along the x-direction, g(x); it provides information on the spatial correlation of particles in the direction perpendicular to the fringes.
2.3 Sample preparation, experimental setup and particle tracking
The colloidal suspensions were prepared using polystyrene sulfate latex particles with a radius of 1.48 μm and a polydispersity of ≤10% (Invitrogen Molecular Probes, Cat. No. S37222). The particles were suspended in ultra-pure water with a resistivity of 18.2 MΩ cm (Purelabs Flex, Elga). The suspensions were loaded into custom-made capillary cells of thickness ∼160 μm, and sealed with UV curing glue (Norland Optical Adhesive 61, Norland Products Inc.). Due to their size, the particles settled to the bottom of the sample cell, forming a monolayer and creating a quasi-two-dimensional (quasi-2D) colloidal system. The area fractions (η) studied in this work ranged from 0.015 to 0.45. All samples were allowed to equilibrate for one day prior to measurements. At moderate and higher concentrations, particle interactions occasionally led to vertical stacking, which caused the particles to leave the focal plane. However, this effect disappeared when the particles were subjected to the laser light potential, as the optical force pushed them against the bottom glass plate.The experimental implementation of the periodic external potential is based on the interference of two coherent beams, as detailed in a previous study.46 In summary, light coming from a laser source (Coherent Verdi V5, wavelength = 532 nm, beam diameter 2.25 mm) is expanded 3 times using a telescope and directed to a Köster's prism, providing two beams of almost equal intensity traveling parallel to the optical axis. These beams are focused onto the focal plane of an inverted microscope using a biconvex lens. The periodicity of the potential, determined by the crossing angle of the two beams and thus independent of the laser power, was set to λ = 3.8 μm. To determine the amplitude of the potential V0 as a function of the laser power, the interaction between the particles and the potential must be characterized (see Section 2.4).
Bright-field images of colloidal suspensions were captured using an inverted microscope (Nikon, Ecplise Ti2-U) equipped with a 20× objective (Nikon, CFI Plan Fluor, NA 0.5) and a CMOS camera (Mako U-130, Allied Vision) with pixels of 4.8 × 4.8 μm2. This leads to a pixel pitch of 0.24 μm per px. Images of 1024 × 1024 pixels were acquired at a frequency of 10 Hz. The field of view size was 246 × 246 μm2. Fig. 1(a) and (b) shows representative regions of interest extracted from the experiments. The effective recording time for each concentration and the laser power was carefully limited to ensure that concentration fluctuations, caused by particles entering or leaving the field of view, remained below 10%. The recording durations ranged between 1200 s and 3600 s. To determine the position of the colloidal particles, a modified MATLAB-based particle tracking routines based on the ones from D. Blair and E. Dufresne47 was implemented, which combined with the Michalet algorithm48 led to a localization uncertainty of ±10 nm. The number of extracted trajectories ranged from ∼150 for an area fraction of 0.015 to ∼4000 for an area fraction of 0.45. The trajectories are openly available in Zenodo at https://doi.org/10.5281/zenodo.14514294.
2.4 Connection between laser power and potential amplitude
The external potential defined along the x-direction, uext(x), experienced by the particles is controlled by adjusting the laser power, LP. Its analytical expression is given by13,21,49 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(θ/2)/R2), with R being the radius of the beam and θ the cross angle and the wavevector q = 2π/λ. It is possible to define a simplified external potential as,24
cos2(θ/2)/R2), with R being the radius of the beam and θ the cross angle and the wavevector q = 2π/λ. It is possible to define a simplified external potential as,24uext(x) = V0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(qx) + Vbg, cos(qx) + Vbg, | (9) |
To determine V0 for a series of laser powers, we have used two dynamical approaches based on the long-time self-diffusion coefficient, DL. As a first approach, we employed the one proposed by Festa et al.,50 here referred to as Festa's approach, who solved the Smoluchowski equation for a Brownian-like particle in a periodic potential and obtained the following analytical expression,
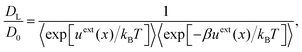 | (10) |
 | (11) |
 | (12) |
Within this approach, a Brownian particle has to overcome an energetic barrier of magnitude 2V0/kBT to escape from the potential well. Interestingly, eqn (12) can also be derived from eqn (11) considering that  for x ≫ 1.54 Therefore, eqn (12), here referred to as Egelhaaf's approach, becomes the exact solution of the Smoluchowski equation for a Brownian-like particle diffusing in a sinusoidal potential in the limit of strong coupling, i.e., V0 ≫ kBT.
for x ≫ 1.54 Therefore, eqn (12), here referred to as Egelhaaf's approach, becomes the exact solution of the Smoluchowski equation for a Brownian-like particle diffusing in a sinusoidal potential in the limit of strong coupling, i.e., V0 ≫ kBT.
To validate the BD simulation scheme with an external field, we have calculated, for a given V0, the normalized long-time self-diffusion coefficient (DL/D0), described by the limit τ → ∞ of eqn (5), represented as a continuous line in the top panel of Fig. 2. In the same figure, the results of the BD simulation (closed symbols) are shown. The excellent agreement found validates our simulation scheme. Additionally, in the top panel of Fig. 2, the dashed line displays the results from the Egelhaaf's approach (eqn (12)), which clearly performs well for external potential barriers of two times the thermal energy of the particles. Then, eqn (12) can be confidently used when V0 > 2kBT, that is, when DL < 0.2D0.
 | ||
| Fig. 2 Top panel: Long-time self-diffusion coefficient, DL, of a single spherical colloid in a periodic potential as a function of V0 for several laser powers, LP. Experiments (open symbols), Brownian dynamics simulations (black symbols), Festa's approach eqn (11) (solid line) and Egelhaaf's approach (12) (dashed line); experiments and BD simulations were performed at an area fraction of 0.015. Bottom panel: Dependence of the potential amplitude, V0, on the laser power, LP. The dashed line was obtained by applying a simple linear regression that allowed us to establish the following relationship V0/LP = (1.41 ± 0.01)kBT/W. | ||
From the previous results, a clear connection emerges between the laser power and the amplitude of the potential experienced by the particles. This connection is mediated through DL/D0. In summary, determining DL/D0 and using Festa's or Egelhaaf's (with its respective limitations) approach, V0 can be experimentally estimated for a given LP in a specific experimental configuration. In general, this relationship is instrument-dependent and varies with the experimental configuration; such dependence is accounted for by the term g in eqn (8).24 The previous description represents the calibration protocol that we have used for our setup.
Finally, the open symbols in the top panel of Fig. 2 correspond to the experimental results for an area fraction of η = 0.015 used as calibration for the periodic light field. The calibration was performed for six different laser powers. These results show excellent agreement with the theoretical predictions from eqn (11) and (12). The explicit dependence of V0 on LP is presented in the bottom panel of Fig. 2. Applying a simple linear regression, we have obtained the following relationship between LP and V0: V0/LP = (1.41 ± 0.01)kBT/W.
It is important to note that in the experiments, D0 is not the bulk diffusion coefficient, as it includes hydrodynamic effects due to particle–wall interactions,14,55 which could be factorized by replacing D0 with the short-time self-diffusion coefficient Ds.15 To simplify the notation and facilitate a direct comparison between the experimental results and the BD simulations, we used the short-time diffusion coefficient Ds instead of D0 from the calibration experiments. This point will be discussed in more detail in Section 3.2. The good agreement between experiments, simulations, and theory allows us not only to highlight the equivalence between the BD simulations and the analytical solution provided by the Smoluchowski equation, but also to make evident that in the dilute limit, the diffusivity is basically driven by the external modulation.
2.5 Mean squared displacement, time-dependent diffusivity and anomalous diffusion exponent: experiments vs. Brownian dynamics simulations
The particle trajectories of a colloidal suspension, with an area fraction of η = 0.015, were analyzed across the fringes (x-direction) to extract the mean squared displacement (MSD, eqn (5)), the time-dependent diffusivity (D(τ), eqn (6)), and the anomalous diffusion exponent (α(τ), eqn (7)). The experimental data was acquired for several values of the laser power, LP, and BD simulations were performed for V0 values calculated with the Festa approach for each LP. In Fig. 3, results from experiments (symbol) and BD simulations (lines) are summarized, showing a very good agreement.As expected for these experiments, the MSD (Fig. 3, top panel) exhibits diffusive behavior at short and long times that depends on LP. In general, at short-time scales, the MSDs increase linearly with time, reflecting the Brownian motion of the particles in the fringes, before the influence of the potential becomes significant. At intermediate-time scales, the MSDs deviate from linearity as particles interact with the barriers formed by the potential, showing sub-diffusive behavior. Finally, at long-time scales, when the particles can overcome the potential barriers (due to thermal fluctuations), the MSD exhibits again a linear dependence on time but with a reduced effective diffusion coefficient. These coefficients are related to the local slope of the MSD, which can be easily quantified through D(τ). In the middle panel of Fig. 3, the values of D(τ) normalized by D0 are explicitly shown. The reduction in the long-time diffusion coefficient is a clear indication of the effect of the particle jumping between fringes.
Furthermore, these time-dependent behaviors are related to the time dependence of the MSD, quantified through α(τ). The results of the analysis of α(τ) are shown in Fig. 3 (bottom panel), where the full dynamical transition from short-time to long-time diffusion (α(τ) = 1) can be observed. Similarly, as before, for intermediate times the dynamics of the particles is subdiffusive, i.e. α(τ) < 1. The observed downward shift in short-time is partially due (particle–wall effects are discussed in Section 3.2) to the increasing restriction in the movement of the particles in the potential minimum, which becomes more attractive with LP. It should be emphasized that although it is widely accepted that when α(τ) = 1 a long-time diffusion coefficient can be obtained, the diffusivity analysis reveals a flattening behaviour for D(τ) where α(τ) < 1 without any significant change for more of an order of magnitude in τ. This ensures that simulations and experiments were conducted under comparable temporal conditions.
3 Particle dynamics: coupling with the external field and concentration effects
Understanding particle dynamics in complex systems, such as crowding in periodic potentials, requires a multifaceted analytical approach. The combined analysis of dynamic and static observables provides valuable insights into particle transport phenomena, revealing how particles navigate through different dynamic regimes.3.1 Pair-correlation-like functions, g(x) and g(y)
As stated above, in this contribution, we investigate the effects of crowding on particle dynamics in a quasi-2D colloidal system subjected to a modulated potential. To explicitly characterize modulated-crowding effects, it is essential to understand how the external potential may affect the spatial organization of particles and, consequently, their transport properties. To achieve this, we investigate the arrangement of particles along the x- and y-axis (with respect to the laboratory frame of reference) at various laser powers. We define pair-correlation-like functions, g(x) and g(y), to analyze spatial particle correlations in directions perpendicular and parallel to the optical fringes, respectively. The pair correlation-like function g(y) was determined for the particles in each potential minima and averaged over all fringes, providing information on the spatial organization of particles within potential wells.Analyzing g(x) and g(y) reveals how particle density fluctuations affect the spatial particle arrangement within the potential landscape. For illustrative purposes, in Fig. 4 and 5, g(x) and g(y), respectively, are shown for LP = 2.5 W and area fractions ranging from 0.015 (dilute) up to 0.45 (intermediate). Our findings reveal that spatial correlations in the direction perpendicular to the fringes (Fig. 4) make it evident that the particles are, on average, pinned to the fringes. Additionally, one can see that the characteristic distance of the particles in the x-direction is determined by the periodicity of the light field (long-dash arrow) and not by the size of the particles σ (short-dash arrow). This is because the periodicity is larger than the diameter of the particles, λ > σ. To facilitate comparison between different area fractions, we have normalized g(x) by g(x = λ). The same phenomenology is also observed for the other laser powers and area fractions (data not shown).
 | ||
| Fig. 4 Pair-correlation-like function, g(x), for a laser power LP = 2.5 W and several values of the area fraction, η, as displayed. Arrows indicate the values at x = σ and x = λ. | ||
 | ||
| Fig. 5 Pair-correlation-like function, g(y), for a laser power LP = 2.5 W and several values of the area fraction, η, as displayed. Arrow indicates the increase in the particle concentration. | ||
In the direction parallel to the fringes, g(y) illustrates the effect of a structured system; see Fig. 5, which presents density correlation peaks that grow in magnitude with increasing concentration and extend over long ranges, as indicated by the arrow. In particular, the contact value, g(y = σ), becomes more pronounced at higher area fractions. A summary of the contact values, g(y = σ), for all laser powers and area fractions is presented in Fig. 6. As seen, g(y = σ) shows a systematic increase with η for all laser powers, revealing the structural evolution of the particles under the effect of the external potential. At low area fractions (η < 0.2), g(y = σ) shows minimal variation between different laser powers, suggesting that direct particle–particle interactions primarily govern particle correlations. However, as η increases beyond 0.2, we observe a marked differentiation in g(y = σ) values across different laser powers. Higher powers (LP ≥ 1.5 W) lead to significantly higher contact values, indicating strong spatial correlations and local ordering induced by the combination of particle crowding and the external periodic potential.
 | ||
| Fig. 6 Contact values, g(y = σ), as a function of the area fraction, η, for all laser powers, LP, as indicated. | ||
The nonlinear growth of g(y = σ) with increasing η, especially seen at higher laser powers, suggests a combined effect between the external field and particle concentration in promoting local structure formation, fundamentally altering the system's spatial organization compared to the unperturbed case (LP = 0.0 W). In other words, g(y = σ) contains both effects that we define here as modulated-crowding, which will be essential to establish a connection between the spatial organization and the particle dynamics, as we discussed further below.
3.2 Long-time self-diffusion coefficient and modulated-crowding effects
The normalized long-time self-diffusion coefficient, DL/D0, is directly obtained from the normalized time-dependent self-diffusivity, D(τ)/D0, for τ > 20 s. As shown in Fig. 7, all functions reach a plateau for τ > 20 s, indicating that the long-time regime has been achieved. In Fig. 7, we present D(τ)/D0 for laser powers ranging from 0 W to 3 W and three area fractions: 0.08, 0.30, and 0.45, corresponding to panels (a), (b), and (c), respectively. Importantly, BD simulations (solid lines) quantitatively capture the experimental data (symbols). However, minor discrepancies are always present, leading to reasonable deviations between experiments and BD simulations. Possible sources of these small discrepancies include: (1) in the simulations, we employ a model pair potential – a short-range repulsive and continuous potential – which, in principle, reproduces the thermodynamic properties of hard disks.42 (2) Simulations do not include hydrodynamic interactions, which mainly influence and reduce the short-time self-diffusion coefficient. However, their effects can be effectively factorized and disentangled from particle–particle contributions at long times; see ref. 14 and 55. Despite these minor approximations, the agreement between experiments and BD simulations remains noteworthy.D(τ) shows the expected and previously reported dynamical behaviour, which can be explained as follows: for short times, the particle moves freely, sampling short distances around a potential minimum with a short-time diffusion coefficient Ds. This is found to be 35% lower than the bulk value (D0) due to the hydrodynamic interaction of the particle with the wall.15 In the dilute case, the short-time diffusion coefficient shows slight variations with laser power. An increase in laser power results in a more pronounced force effect on the particles, pushing them closer to the wall and slowing their dynamics due to the wall–particle hydrodynamic interactions. Therefore, to factor in these effects and establish a connection with the BD simulations,55D0 is considered to be Ds for each corresponding LP in η = 0.015, with the same values used for the dilute case applied to higher concentrations. For higher concentrations, Ds also includes contributions from particle–particle interactions. At intermediate times, the particles become localized due to their interaction with the laser field. This localization resembles the well-known caging effect, where D(τ) decays faster as the laser power increases. However, at long times, normal diffusion is recovered, i.e., D(τ) reaches a plateau, but with a self-diffusion coefficient, DL, smaller than D0 (i.e., DL < D0), which clearly depends on both laser power and particle concentration. Interestingly, the time at which the particles reach the plateau—transitioning from localization to delocalization—is essentially the same in all cases, with τtrans ∼ 20 s (see also Fig. 3). This regime is related to particle hopping across minima, as discussed in other works,23,24,31 resembling a random walk and thus leading to a diffusive regime once again.
The long-time self-diffusivity behavior reveals a complex interplay between laser power (LP) and area fraction (η). Our analysis of D(τ)/D0 at long-time demonstrates that increasing the laser power from 0.0 W to 3.0 W systematically reduces the long-time diffusion coefficient, with the most dramatic effects observed at higher area fractions. At η = 0.45, the normalized long-time diffusivity decreases by three orders of magnitude when exposed to the maximum laser power (3.0 W), indicating strong particle localization within the periodic potential wells. This effect is less pronounced at lower area fractions (η = 0.08), where reduced particle–particle interactions allow greater mobility even under strong field conditions. The relationship between laser power and long-time diffusivity follows a nonlinear trend, with a critical threshold around 1.5 W where significant mobility reduction begins to manifest. Notably, the area fraction acts as a mobility-limiting factor, enhancing the confinement effect of the laser-induced potential landscape. This combined interaction between laser power and area fraction suggests that particle crowding amplifies the effectiveness of the external field in restricting long-time particle diffusion, providing a tunable mechanism for controlling colloidal dynamics in confined geometries.
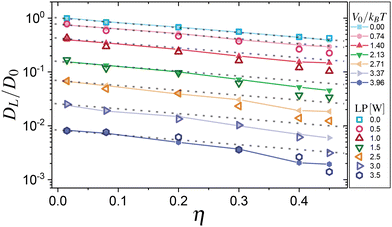
To quantify the effect of both particle–particle and particle–field interactions on particle transport, we extracted the ratio DL/D0 for all laser powers. In Fig. 8 we summarized the experimental results (open symbols) for DL/D0 as a function of area fraction (η) for several laser powers (LP) of the applied periodic potentials. BD simulations for the corresponding amplitude of the potential are shown as closed symbols with solid lines. Again, BD simulations demonstrate excellent agreement with experimental results. The data reveal two key physical mechanisms: first, a systematic decrease in particle mobility with increasing area fraction for all laser powers, evidencing the role of crowding effects; second, a marked reduction in diffusion as the laser power increases from 0 to 3.5 W (corresponding to V0/kBT from 0 to 3.96), demonstrating the enhanced confinement of particles within the optical potential wells.
Notably, at the highest laser power (LP = 3.5 W), the diffusion coefficient drops by two orders of magnitude compared to the particle–potential-free case (LP = 0.0 W), while the impact of crowding becomes more pronounced as evidenced by the steeper decline in DL/D0 with increasing η.
The variation in the data trend is now discussed. As seen in Fig. 9, DL/D0 exhibits a notable deviation from the reference case (particle–potential-free, LP = 0.0 W) as both the area fraction (η) and the laser power increase. This behavior is evidenced by the deviation of the experimental data and the BD simulation results, which are parallel to the particle–potential-free case. It reveals a nontrivial coupling between particle concentration and the periodic potential landscape. At low laser powers (≤1.0 W), the system maintains a trend similar to the particle–potential-free case, where crowding effects dominate the reduction of the particle mobility. However, as the laser power increases (>1.5 W), we observe a pronounced deviation from this trend, particularly at higher area fractions (η > 0.3), where the diffusion coefficient drops more steeply than predicted by simple crowding effects. Furthermore, these variations appear to be similar across all cases, indicating a consistent trend regardless of the specific conditions, much like the behavior of the contact value of g(y) (Fig. 6). This enhanced reduction in particle mobility suggests a combined, synergistic effect between particle–particle (entropy-driven) and particle–potential (energy-driven) interactions, where crowding amplifies the localizing effect of the periodic potential. Brownian dynamics simulations corroborate these experimental findings, accurately capturing the transition from a crowding-dominated regime to one where the interplay between spatial confinement and particle interactions results in a more dramatic dropping of the long-time diffusion. This behavior indicates that the presence of neighboring particles enhances the trapping efficiency of the potential wells, resulting in a nonlinear response to increasing area fraction that becomes more pronounced at higher potential amplitudes.
 | ||
Fig. 9 Ratio  as a function of the area fraction for all the considered laser powers, as indicated. Open symbols are the results from the experiments, closed symbols are the results from Brownian dynamics simulations, and spheres are determined using eqn (14). Inset shows the product as a function of the area fraction for all the considered laser powers, as indicated. Open symbols are the results from the experiments, closed symbols are the results from Brownian dynamics simulations, and spheres are determined using eqn (14). Inset shows the product 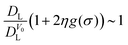 as a function of the particle concentration for V0 ≠ 0. as a function of the particle concentration for V0 ≠ 0. | ||
The results presented in Fig. 8 reveal a remarkable finding in the behavior of the long-time self-diffusion coefficient of colloidal particles confined in a quasi-2D geometry under the combined influence of many-body interactions (crowding) and an external modulated potential; a physical scenario that we refer to as “modulated-crowding.” To analyze the concentration effects in this context, we introduce the normalized long-time self-diffusion coefficient,  , where
, where  represents the long-time diffusion coefficient of a dilute suspension under the influence of the modulated potential (eqn (11)). This quantity is presented as a function of the area fraction, η, for different amplitudes of the periodic potential, V0, and is mathematically expressed as:
represents the long-time diffusion coefficient of a dilute suspension under the influence of the modulated potential (eqn (11)). This quantity is presented as a function of the area fraction, η, for different amplitudes of the periodic potential, V0, and is mathematically expressed as:
 | (13) |
This kind of factorization has been useful for separating or estimating the effects of the direct interactions, i.e., particle–particle interactions, from the indirect ones, i.e., hydrodynamic interactions (see ref. 14, 15 and 55–57).
In Fig. 9, the ratio  as a function of the area fraction for all the considered laser powers (open symbols) is displayed. In this representation, the deviation of the data from the LP = 0.0 W case (blue open squares), discussed in the previous section, is evident. As mentioned above, this deviation results from the competition between particle–particle and particle–potential interactions, which a priori cannot be considered decoupled. However, this competition must, in some way, be related to the structure, which should incorporate concentration effects and a contribution from the periodic potential. The latter disrupts the homogeneity of the material distribution, as we have quantified and demonstrated in Section 3.1.
as a function of the area fraction for all the considered laser powers (open symbols) is displayed. In this representation, the deviation of the data from the LP = 0.0 W case (blue open squares), discussed in the previous section, is evident. As mentioned above, this deviation results from the competition between particle–particle and particle–potential interactions, which a priori cannot be considered decoupled. However, this competition must, in some way, be related to the structure, which should incorporate concentration effects and a contribution from the periodic potential. The latter disrupts the homogeneity of the material distribution, as we have quantified and demonstrated in Section 3.1.
Interestingly, we found that an excellent approximation for quantifying the effects of local structure on diffusivity is the one proposed by Brady,57 which provides a simple relationship between the long-time self-diffusion coefficient, DL, the short-time self-diffusion coefficient, D0, the local structure, g(y), and the concentration, η. It has the following mathematical form:
 | (14) |
We then determined DηL/D0 for all measurements using eqn (14). The results (spheres) are plotted in Fig. 9. Surprisingly, despite the quasi-2D nature of the colloidal system, eqn (14) reproduces the experimental data (open symbols) with remarkable accuracy, which was originally derived for three-dimensional systems. This agreement is particularly significant given that the colloidal system is strongly confined and subject to a periodic external potential. Our physical interpretation of this unexpected behavior is that by imposing spatially periodic energy barriers, the laser potential effectively restricts the configuration space accessible to the particles. This constraint reduces the effective dimensionality of the transport problem by preferentially confining the particles within the potential minima. It is important to note that when the measurements of DL for V0 = 0.00kBT are compared directly with those using eqn (14), do not quantitatively reproduce the experimental data. This aspect was previously noted and reported by Thorneywork et al.14
The inset of Fig. 9 highlights the fact that in the presence of a sinusoidal potential, the product  for all particle concentrations confirms our description. The black closed symbols correspond to the average of all LP values for the same area fraction, with an error bar representing the standard deviation, indicating variations of less than 10 percent. These observations have important implications for understanding and controlling particle dynamics in confined systems, confirming that the imposition of periodic external potentials can be used as a tool to systematically modify transport properties in quasi-2D colloidal dispersions.
for all particle concentrations confirms our description. The black closed symbols correspond to the average of all LP values for the same area fraction, with an error bar representing the standard deviation, indicating variations of less than 10 percent. These observations have important implications for understanding and controlling particle dynamics in confined systems, confirming that the imposition of periodic external potentials can be used as a tool to systematically modify transport properties in quasi-2D colloidal dispersions.
By replacing eqn (14) in eqn (13), the expression becomes,
 | (15) |
The preceding equation accurately describes the diffusivity in the direction perpendicular to the fringes of a colloidal dispersion subjected to a periodic field, allowing us to identify the underlying physical mechanism, called modulated crowding. However, it remains important to clarify the limits of applicability of eqn (15). To address it and motivated by the strong agreement between Brownian dynamics (BD) simulations and experimental data, we conducted an extensive analysis using BD simulations (see Appendix B). Our analysis confirms that eqn (15) quantitatively describes particle dynamics up to an area fraction of approximately η ∼ 0.50. Furthermore, a closer examination of certain limiting cases (also discussed in Appendix B) reveals that at low concentrations (up to η ∼ 0.20), eqn (15) reduces to:  , indicating that, in this dilute regime, diffusivity is essentially determined by the modulation introduced by the periodic potential, as described by eqn (11).
, indicating that, in this dilute regime, diffusivity is essentially determined by the modulation introduced by the periodic potential, as described by eqn (11).
4 Concluding remarks and perspectives
In this work, we have provided experimental and theoretical evidence on the role of crowding in the diffusivity of confined colloids subjected to a light-induced sinusoidal potential with fixed periodicity and variable amplitude. We have also reported and explicitly discussed the dynamical properties along the perpendicular direction of the fringes as a function of the particle concentration and laser power, having introduced the concept of modulated-crowding for this physical scenario.In particular, we focused on the long-time particle dynamics. Our results indicate that, after an appropriate renormalization, the long-time self-diffusion coefficient, crowding effects on particle transport can be fully explained in terms of two main contributions: particle concentration and the structural correlations imposed by the external modulation. This finding highlights that the effects of modulated-crowding on the long-time self-diffusion coefficient of colloids interacting via short-range repulsive forces can be entirely disentangled from the contributions of the external field. A particularly significant aspect of our findings is that, due to particle trapping induced by the periodic potential at any concentration, the Brady relation, originally developed for three-dimensional systems and particularly effective in concentrated regimes, accurately reproduced the experimental results even in low-concentration conditions. This suggests that the underlying dynamics in the presence of modulated-crowding closely resemble those of highly concentrated three-dimensional systems, offering a new perspective on the role of spatial structuring in the diffusion of confined colloidal systems.
Last but not least, we should stress that exploring other types of external potentials, i.e. periodic with other symmetries or nonperiodic potentials, will allow us to better understand the relationship between the static properties and the transport of colloids in well-controlled heterogeneous environments.
Author contributions
MAES and SUE conducted the conceptualization and administration of the project. SUE provided the resources and acquired the funding. MAES, RCP, ESG and SUE worked on the investigation and validation, and MAES worked on the software. MAES and RCP worked on the computer simulations. ESG performed a preliminary analysis of the data. MAES, ESG, YMS worked on the methodology, data curation, visualization, and formal analysis. ESG wrote the original draft. RCP, ESG, YMS, and MAES, reviewed and edited the final version of the manuscript.Data availability
Data for this article, including all particle trajectories analyzed in the manuscript, are available at Zenodo URL: https://doi.org/10.5281/zenodo.14514294.Conflicts of interest
There are no conflicts to declare.Appendices
A Appendix: comparison between dynamic Monte Carlo and Brownian dynamics simulation schemes
To assess the validity of the hard-core potential (eqn (2)),42 we have chosen γ = 50, and ε* ≡ ε/kBT = 0.6816 to reproduce the dynamics of hard disks. The Brownian Dynamics simulations were performed as described in Section 2.1. In Fig. 10, we compare the normalized long-time self-diffusion coefficients of quasi-two-dimensional colloidal hard spheres for area fractions ranging from 0.001 up to 0.68 with previous studies conducted using dynamic Monte Carlo simulations of hard disks.14 The long-time diffusion coefficient was determined following the procedure described in Section 3.2 of the main text. As seen in Fig. 10, excellent agreement between both methods is obtained. | ||
| Fig. 10 Comparison of the normalized long-time self-diffusion coefficients for area fractions ranging from 0.001 up to 0.68 for Brownian dynamics simulations based on the hard-core potential and dynamic Monte Carlo simulations of hard disks.14 | ||
B Analysis of the modulated-crowding approach: testing the limits of Brady's diffusivity formula
As discussed in Section 3, eqn (15) quantitatively describes the long-time diffusion behaviour (along the perpendicular direction of the fringes) of colloids subjected to a light-induced sinusoidal potential up to an area fraction of η ∼ 0.5. To gain a deeper understanding of the physical mechanisms driving this transport behaviour, one should analyze certain intriguing limiting cases of the eqn (15).Let us consider the case where 2ηg(σ) ≪ 1. In that limit, eqn (15) simply reduces to,
 | (16) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (η2) and higher. In that limit, η is very low, so g(σ) is expected to be close to unity because it does not depend strongly on either η nor V0. Hence, eqn (15) reduces to
(η2) and higher. In that limit, η is very low, so g(σ) is expected to be close to unity because it does not depend strongly on either η nor V0. Hence, eqn (15) reduces to  . By explicitly comparing with Brownian dynamics simulations, we conclude that the previous equation is a good estimate up to η < 0.2 and V0 < 4kBT. This means that particle dynamics is given at low concentrations by modulation of the periodic potential, eqn (11), as expected.
. By explicitly comparing with Brownian dynamics simulations, we conclude that the previous equation is a good estimate up to η < 0.2 and V0 < 4kBT. This means that particle dynamics is given at low concentrations by modulation of the periodic potential, eqn (11), as expected.
By means of Brownian dynamics simulations (under the same conditions as previously written), we investigated the limits of validity of eqn (15). Fig. 11 clearly illustrates that for area fractions exceeding 0.50, eqn (15) ceases to be valid. This threshold area fraction ensures sufficient spacing between the fringes, allowing the particles to jump from one fringe to another.
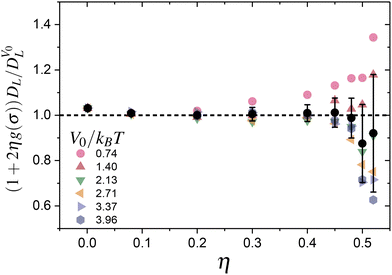 | ||
| Fig. 11 Assessment of the validity of eqn (15) tested by Brownian dynamics simulations. For area fractions (η) exceeding 0.50, deviations from eqn (15) become apparent, indicating its breakdown. Different symbols correspond to different potential barrier heights (V0/kBT), as indicated. | ||
Acknowledgements
Authors thank CONAHCYT-Mexico (Grants No. A1-S-9098, Ciencia de Frontera 102986, CBF2023-2024-3350) and the Deutsche Forschungsgemeinschaft (DFG) – Project number 459399860 for financial support. R. C. P. also acknowledges financial support provided by the Alexander von Humboldt Foundation. MAES and YMS appreciate valuable comments and discussions from Dr Angel B. Zuccolotto-Bernez.Notes and references
- H. Löwen, J. Phys.: Condens. Matter, 2008, 20, 404201 CrossRef.
- R. Castañeda-Priego, Rev. Mex. Fis., 2021, 67, 050101 Search PubMed.
- D. Grier, Nature, 2003, 424, 810–816 CrossRef CAS PubMed.
- C. O. Solano-Cabrera, P. Castro-Villarreal, R. E. Moctezuma, F. Donado, J. Conrad and R. Castañeda-Priego, Annu. Rev. Condens. Matter Phys., 2025, 16, 41–59 CrossRef CAS.
- F. Evers, R. D. L. Hanes, C. Zunke, R. F. Capellmann, J. Bewerunge, C. Dalle-Ferrier, M. C. Jenkins, I. Ladadwa, A. Heuer, R. Castañeda Priego and S. U. Egelhaaf, Eur. Phys. J.-Spec. Top., 2013, 222, 2995 CrossRef.
- H. Löwen, J. Phys.: Condens. Matter, 2009, 21, 474203 CrossRef PubMed.
- K. Mangold, J. Birk, P. Leiderer and C. Bechinger, Phys. Chem. Chem. Phys., 2004, 6, 1623–1626 RSC.
- C. Contreras-Aburto, J. Mendez-Alcaraz and R. Castañeda-Priego, J. Chem. Phys., 2010, 132, 174111 CrossRef CAS PubMed.
- S. Herrera Velarde, A. Zamudio-Ojeda and R. Castaneda-Priego, J. Chem. Phys., 2010, 133, 114902 CrossRef PubMed.
- A. Taloni, O. Flomenbom, R. Castañeda-Priego and F. Marchesoni, Soft Matter, 2017, 13, 1096–1106 RSC.
- A. Villada-Balbuena, A. Ortiz-Ambriz, P. Castro-Villarreal, P. Tierno, R. Castañeda Priego and J. M. Méndez-Alcaraz, Phys. Rev. Res., 2021, 3, 033246 CrossRef CAS.
- U. Gasser, J. Phys.: Condens. Matter, 2009, 21, 203101 CrossRef CAS PubMed.
- M. C. Jenkins and S. U. Egelhaaf, J. Phys.: Condens. Matter, 2008, 20, 404220 CrossRef.
- A. L. Thorneywork, R. E. Rozas, R. P. A. Dullens and J. Horbach, Phys. Rev. Lett., 2015, 115, 268301 CrossRef PubMed.
- E. Sarmiento-Gómez, J. R. Villanueva-Valencia, S. Herrera-Velarde, J. A. Ruiz-Santoyo, J. Santana-Solano, J. L. Arauz-Lara and R. Castañeda Priego, Phys. Rev. E, 2016, 94, 012608 CrossRef PubMed.
- J. A. S. Gallegos, J. Martínez-Rivera, N. E. Valadez-Pérez and R. Castañeda-Priego, J. Chem. Phys., 2023, 158, 114907 CrossRef CAS PubMed.
- V. Lobaskin, B. Dünweg, M. Medebach, T. Palberg and C. Holm, Phys. Rev. Lett., 2007, 98, 176105 CrossRef PubMed.
- J. M. Kim, J. Fang, A. P. R. Eberle, R. Castañeda Priego and N. J. Wagner, Phys. Rev. Lett., 2013, 110, 208302 CrossRef PubMed.
- A. Chowdhury, B. J. Ackerson and N. A. Clark, Phys. Rev. Lett., 1985, 55, 833–836 CrossRef CAS PubMed.
- Q.-H. Wei, C. Bechinger, D. Rudhardt and P. Leiderer, Phys. Rev. Lett., 1998, 81, 2606–2609 CrossRef CAS.
- C. Bechinger, Q. H. Wei and P. Leiderer, J. Phys.: Condens. Matter, 2000, 12, A425–A430 CrossRef CAS.
- A. Ashkin, Phys. Rev. Lett., 1970, 24, 156–159 CrossRef CAS.
- S. Herrera-Velarde and R. Castañeda Priego, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 79, 041407 CrossRef PubMed.
- C. Dalle-Ferrier, M. Krüger, R. D. L. Hanes, S. Walta, M. C. Jenkins and S. U. Egelhaaf, Soft Matter, 2011, 7, 2064–2075 RSC.
- C. Lutz, M. Reichert, H. Stark and C. Bechinger, Europhys. Lett., 2006, 74, 719 CrossRef CAS.
- S. Herrera-Velarde, E. C. Euan-Díaz, F. Córdoba-Valdés and R. Castañeda-Priego, J. Phys.: Condens. Matter, 2013, 25, 325102 CrossRef PubMed.
- E. Cereceda-López, D. Lips, A. Ortiz-Ambriz, A. Ryabov, P. Maass and P. Tierno, Phys. Rev. Lett., 2021, 127, 214501 CrossRef PubMed.
- D. Lips, E. Cereceda-López, A. Ortiz-Ambriz, P. Tierno, A. Ryabov and P. Maass, Soft Matter, 2022, 18, 8983–8994 RSC.
- S. Bleil, H. H. von Grünberg, J. Dobnikar, R. Castañeda-Priego and C. Bechinger, Europhys. Lett., 2005, 73, 450 CrossRef.
- R. F. Capellmann, A. Khisameeva, F. Platten and S. U. Egelhaaf, J. Chem. Phys., 2018, 148, 114903 CrossRef CAS PubMed.
- D. Pérez-Guerrero, J. L. Arauz-Lara, E. Sarmiento-Gómez and G. I. Guerrero-García, Front. Phys., 2021, 9, 635269 CrossRef.
- D. Lips, A. Ryabov and P. Maass, Phys. Rev. Lett., 2018, 121, 160601 CrossRef CAS PubMed.
- D. Lips, A. Ryabov and P. Maass, Phys. Rev. E, 2019, 100, 052121 CrossRef CAS PubMed.
- D. Lips, R. L. Stoop, P. Maass and P. Tierno, Commun. Phys., 2021, 4, 224 CrossRef.
- A. Ryabov, D. Lips and P. Maass, J. Phys. Chem. C, 2019, 123, 5714–5720 CrossRef CAS.
- A. P. Antonov, A. Ryabov and P. Maass, J. Chem. Phys., 2021, 155, 184102 CrossRef CAS PubMed.
- A. P. Antonov, A. Ryabov and P. Maass, Phys. Rev. Lett., 2022, 129, 080601 CrossRef CAS PubMed.
- A. P. Antonov, D. Voráč, A. Ryabov and P. Maass, New J. Phys., 2022, 24, 093020 CrossRef.
- E. Cereceda-Lopez, A. P. Antonov, A. Ryabov, P. Maass and P. Tierno, Nat. Commun., 2023, 14, 6448 CrossRef CAS PubMed.
- D. Voráč, P. Maass and A. Ryabov, J. Chem. Phys., 2023, 159, 114114 CrossRef PubMed.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352 CrossRef CAS.
- C. A. Báez, A. Torres-Carbajal, R. Castañeda-Priego, A. Villada-Balbuena, J. M. Méndez-Alcaraz and S. Herrera-Velarde, J. Chem. Phys., 2018, 149, 164907 CrossRef PubMed.
- B. Li, Y. Nishikawa, P. Höllmer, L. Carillo, A. C. Maggs and W. Krauth, J. Chem. Phys., 2022, 157, 234111 CrossRef CAS PubMed.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164 RSC.
- S. Herrera-Velarde and R. Castañeda Priego, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041407 CrossRef CAS PubMed.
- R. F. Capellmann, J. Bewerunge, F. Platten and S. U. Egelhaaf, Rev. Sci. Instrum., 2017, 88(5), 056102 CrossRef CAS PubMed.
- D. Blair and E. Dufresne, The Matlab Particle Tracking Code Repository, https://site.physics.georgetown.edu/matlab/, visited on 21/01/20.
- X. Michalet, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041914 CrossRef PubMed.
- K. Loudiyi and B. J. Ackerson, Phys. A, 1992, 184, 1–25 CrossRef CAS.
- R. Festa and E. d’Agliano, Phys. A, 1978, 90, 229–244 CrossRef.
- P. Reimann, C. Van den Broeck, H. Linke, P. Hänggi, J. M. Rubi and A. Pérez-Madrid, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031104 CrossRef CAS PubMed.
- J. Spiechowicz, I. G. Marchenko, P. Hänggi and J. Łuczka, Entropy, 2023, 25, e25010042 Search PubMed.
- A. V. Straube and F. Höfling, J. Phys. A: Math. Theor., 2024, 57, 295003 CrossRef CAS.
- B. Geelen, Adv. Eng. Software, 1995, 23, 105–109 CrossRef.
- J. R. Villanueva-Valencia, J. Santana-Solano, E. Sarmiento-Gómez, S. Herrera-Velarde, J. L. Arauz-Lara and R. Castañeda Priego, Phys. Rev. E, 2018, 98, 062605 CrossRef.
- M. Medina-Noyola, Phys. Rev. Lett., 1988, 60, 2705–2708 CrossRef CAS PubMed.
- J. F. Brady, J. Fluid Mech., 1994, 272, 109–134 CrossRef CAS.
Footnotes |
| † This publication is in honor and remembrance of our friend, mentor, and colleague Stefan U. Egelhaaf. |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |