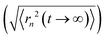Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unravelling chain confinement and dynamics of weakly entangled polymers in one component nanocomposites†
M. Kruteva *a,
M. Monkenbusch
*a,
M. Monkenbusch a,
A. Sharma
a,
A. Sharma ab,
J. Allgaier
ab,
J. Allgaier a,
I. Hoffmann
a,
I. Hoffmann c,
B. Rosi
c,
B. Rosi ad,
M. Dulle
ad,
M. Dulle a,
L. Porcar
a,
L. Porcar c,
O. Matsarskaia
c,
O. Matsarskaia c and
D. Richter
c and
D. Richter *a
*a
aJülich Centre for Neutron Science, Forschungszentrum Jülich GmbH, 52428 Jülich, Germany. E-mail: m.kruteva@fz-juelich.de; d.richter@fz-juelich.de
bCSIR-National Chemical Laboratory, Pune 411008, Maharashtra, India
cInstitut Laue-Langevin (ILL), 38000 Grenoble, France
dEuropean Spallation Source (ESS), Partikelgatan 2, 224 84 Lund, Sweden
First published on 11th March 2025
Abstract
Structure and dynamics of polymer chains grafted to a nanoparticle (NP) surface in one component nanocomposites (OCNC) are investigated by small angle scattering (SAXS, SANS) and neutron spin echo (NSE). The OCNC were realized by self-assembly of block-copolymers and subsequent cross-linking of the core. The sizes of the resulting NPs were narrowly distributed. Owing to equal core and shell volumes the melt structure is that of a concentrated colloidal dispersion of cores. The melt structure could be reasonably well described by a Percus–Yevick structure factor. In order to access more deeply the dynamics, three differently labeled materials with labels at the inner- or outer part and the whole graft were studied. The experimental data were evaluated in terms of models allowing for site dependent friction. For this purpose, the Langevin equation containing a friction profile was solved and the dynamic structure factor in terms of its eigenvalues and eigenvectors was compared to the data. The evaluation shows increased friction towards the grafting points. In addition, topological restrictions of motion due to the dense arrangements of micellar cores and the presence of neighboring chains were considered and compared with those of a corresponding melt. Assuming homogenous relaxation of all grafts did not yield a satisfactory data description, but rather at least two differently relaxing chain ensembles had to be considered.
Introduction
Polymer nanocomposites (PNC) represent a broad class of modern materials with a wide spectrum of possible applications.1–7 Conventional nanocomposites are manufactured by blending nanoparticles (NPs) and polymers. Their properties depend strongly on that of the components: polymers and (typically inorganic) NPs. Applications of PNC in nanotechnology need chemical tuning of components and reliable processing. Conventional nanocomposites consist of NPs (filler) and polymer matrix mixed at different environmental and chemical conditions. The main complexity, especially at relatively high-volume fraction of fillers, relates to the required homogeneous and controlled distribution of the NPs in the polymer matrix. Recently, polymer hybrids such as the novel one component nanocomposites (OCNCs) have drawn much attention both in basic as well as in application-oriented research.8–10 OCNCs consist of NPs that are grafted with polymer chains without any matrix (free) chains. Progress in chemistry facilitates the precise creation of materials with well-defined grafting density, chain length, and functionalization.11 These OCNCs exhibit novel morphologies, dielectric, and mechanical properties, overcome the dispersion challenge, and are expected to display structure-related emergent properties that distinguish them from the more established field of nanocomposites.A number of tuning parameters, e.g. molecular weight of grafted chains, grafting density, size of the NPs (related to NP curvature) lead to different structural and viscoelastic properties allowing variation of applications. There are many studies in the literature which monitor the structural as well as dynamical features of grafted polymer chains at different time and length scales.10,12–26 Changes in the structural and conformational features of grafted polymers were described by a two-phase model for polymer grafted NPs based on volume conservation.25 Theoretically, the properties of grafted layers were described by Alexander27 and de Gennes and Daoud and Cotton.28 Combined theorical modelling and simulations reveal the potential presence of two different polymer layers present next to the NPs depending on polymer molecular weight. For sufficiently high grafting density, the simulations predict the chain sections close to the NP core to be extended and form a dry layer. Such a dry layer was considered earlier and is known as the concentrated polymer brush region (CPB), where the chains are stretched, and the effect of grafting is maximum. As one moves away from the NP core, a transition to a melt like region takes place, which is known as semi dilute polymer brush region (SDPB).29 Small angle neutron scattering (SANS) experiments performed at NIST by Wei et al. found that samples with hydrogen labelled segments in the CPB region demonstrate stretched conformations whereas, those with labelling in SDPB region did not show any signature of stretching.30 These SANS experiments were performed on NPs grafted with polymethylacrylate (PMA) dispersed in solvent with two different polymer labelling schemes at moderate grafting density (0.3 chains per nm2). For the inner labelled chain sections the corresponding polymer layers next to the NPs are claimed to be dry, i.e. without any interpenetration from the polymer chains of neighboring NPs. For outer labelled chain sections, the polymer chains from neighboring particles interpenetrate resulting in the formation of a wet layer. On the other hand, some of us using SANS showed that polyisoprene (PI) chains of a molecular weight of 5 kg mol−1 (about the entanglement molecular weight) grafted at SiO2 NPs at a grafting density of 0.6 chains per nm2 are interpenetrated and do not reveal any change in conformation compared to the neat melt.31 The apparent discrepancy between ref. 16 and 17 may relate to the very different bulkiness (more than factor 3)32 of the PMA and PI monomers. Jhalaria et al. reported that PNC membranes synthesized by grafting poly(methylacrylate) on silica NPs exhibit significantly higher gas separation capability as compared to their respective blended PNCs.33 Grabowski et al. reported that polymer grafted PNCs show enhanced energy storage and reduced dielectric loss than the conventional PNCs.34
Neutron spin echo (NSE) data obtained from the NIST samples were fitted with the phenomenological Kohlrausch Williams Watts (KWW) function.30 The authors reported slower dynamics in the CPB region as compared to the SDPB region, which was attributed to stronger confinements in the CPB region. Holt et al. reported the presence of similar stretched polymer conformation at the interface of NPs and the polymer using dielectric spectroscopy and differential scanning calorimetry (DSC) on solvent free polymer grafted OCNCs.35 Core-modified dissipative particle dynamics (CM-DPD) simulations on grafted polymers under different confinement strengths shows retardation of polymer dynamics as compared to the neat polymer.21 The authors demonstrated the inapplicability of the standard Rouse model to these systems whereas, proper orthogonal decomposition (POD) method calculations show an increasing radius of gyration of the grafted polymers, indicating stretching. Kim et al. attributed the decrease in the relaxation rate of grafted polymers as compared to neat polymers to the requisite of space filling between NPs felt by the polymer.24
Kumar et al. have studied the structure and dynamics of polymer grafted NPs using experiments as well as theory and simulations.25,33 In contrast to the above results Jhalaria et al. reported an acceleration of segmental dynamics in polymer grafted NP membranes as compared to the neat polymers, which controls the diffusion of gas molecules across the membranes.33 The increase of relaxation rate was attributed to a decrease in the friction of polymer chains due to stretching. Using a jump diffusion model, they studied the effect of grafting on the jump length of polymer segments. On the other hand, NSE and backscattering data on SiO2-PI NP indicate that for moderate grafting densities, there is no change in the segmental dynamics of the grafted polymer chains.31 The amplitude of chain motion is diminished due to confinement imposed by neighboring grafts. This confinement restricts the chain dynamics to a conical geometry around the grafting site. In a recent work we showed that the segmental dynamics of grafted polymers exhibits a wide distribution of relaxation rates containing both faster as well as slower components irrespective of the molecular weight.36 All these reports also indicate the presence of an about of 1 nm thick polymer layer around the NPs, which relaxes very slowly. On the other hand, PEO grafted on SiO2 does not develop such a layer.37
Although significant numbers of experiments as well as simulations were performed on unentangled grafted polymers, only a few studies on the dynamics and structure of weakly entangled polymer brushes are reported.38–40
Vladkov et al. used MD simulation to study the dynamics of interfacial polymer chains near a flat wall in non-grafted as well as grafted state.39 They found that for unentangled polymers, in both, grafted and non-grafted state, the dynamics is faster than in the corresponding neat polymer. For weakly entangled polymers, the non-grafted chains display a reduction of entanglements due to presence of surface. Whereas grafted polymers show an increase of entanglements leading to restricted dynamics. Molecular dynamics and Monte Carlo simulations were performed on a system of weakly entangled polymer brushes under good solvent conditions by Reith et al.40 They found that the relaxation time of monomers is dependent on their location along the grafted polymer chain with slowest monomers present close to the grafting site and the fastest ones located in the middle of the chain. Both simulations were performed for flat surfaces.
In this work we focus on the polymer dynamics of grafted polymer chains in one component nanocomposites (OCNC), i.e. without an embedding matrix, in the weakly entanglement regime. The OCNC are built by self-assembly of block-copolymers of cross-linked deuterated 1,2-polybutadiene (dPB) in the core and poly(ethylene oxide) (PEO) grafts at outside. The resulting micellar core has a radius in the order of 12 nm with little dispersity. Using NSE we address following points: (i) chain and segmental mobility of the grafted polymer chain; (ii) the role of the entanglements and confinement on the chain dynamics. (iii) Role of the heterogenous arrangement of micellar cores on the dynamic features.
We use dPB-(h,d)PEO micelles with different hydrogen labelling schemes: labels close to the grafting site, labels at the outer part of the grafts and entire chain labelled grafts (see Fig. 1). As already demonstrated for weakly entangled melts,41 we show that the role of the heterogenous environments created by the dense core melt and the entanglement behavior of grafted polymer chains could be captured using a Rouse mode analysis with suppressed amplitudes for modes with low numbers. Even though the grafting density was low, our results show that the monomeric friction increases significantly close to the grafting point and decreases to constant friction in the direction of the chain ends. Furthermore, we demonstrate that dynamic heterogeneity needs to be assumed, in order to describe the experimental spectra. We relate this heterogeneity to the structural peculiarities of the dense core arrangement.
 | ||
| Fig. 1 Micelles with different deuteration schemes: hydrogenated parts are shown by blue color; deuterated parts are red. | ||
Materials and methods
Synthesis and characterization of polymers
The OCNC materials were synthesized from aqueous micellar solutions of 1,2 dPB-PEO diblock copolymers, having different deuterium labels and all of them having a molecular weight of the dPB block of 6 kg mol−1 and 10 to 12 kg mol−1 for the h- or d-PEO block. The spherical shape of the micelles was fixed by cross-linking the dPB cores with 2,2′-(ethylendioxy)diethanthiol in aqueous solutions using a mild photochemical process. In all OCNC samples, the sulfur content found by elemental analysis corresponded almost exactly with the value for 100% cross-linker incorporation, or in other words, one cross-linking point per every 5 PB monomer units. Even if not all cross-linker molecules might have reacted twice with the polymer chains, it is clear, that the polymer cores were highly cross-linked. In addition, it is important to note that only mild radical cross-linking processes can be used in the presence of PEO. Harsher reaction conditions cause chain scission and decomposition reactions due to the sensitivity of PEO towards radicals. Experiments with a persulfate cross-linking process, described for the PB-PEO system failed.42 Under such reaction conditions, a PEO 5 kg mol−1 polymer was largely decomposed into oligomers in a test experiment, whereas the photochemical thiol cross-linking caused only minor chain scission of the PEO. The details of the synthetic procedures for the block copolymer and the OCNC samples are given in the ESI,† together with the molecular weight characterization results.The molecular characteristics of the different blocks and chains are listed in Tables 1 and 2. The micellar core radius of about 12 nm was identified by solution SAXS performed on OCNC as shown in Fig. 2. To optimize the matching conditions, deuterated PB (d-PB) was used for the core and a mixture of h-PEO and d-PEO in the shell. Moreover, for the NSE experiment also dh- and hdPEO block-copolymers were used as grafts (see Fig. 1), where the hydrogenated portion of chain lies next to or away from the core surface. Again, these block copolymers were mixed with fully deuterated PB-PEO copolymers. Due to the presence of hydrogenated cross-linker in the core the neutron scattering length density (SLD) of the core was different from that of dPB.
| Polymer | Mn [kg mol−1] | Mw/Mn | N | Vmon at 350 K [m3] | |||
|---|---|---|---|---|---|---|---|
| 1,2 dPB | 6.085 | 1.02 | 101 | 1.07 × 10−28 | |||
| hPEO | 10.38 | 1.01 | 236 | 0.65 × 10−28 | |||
| dPEO | 11.07 | 1.02 | 231 | ||||
| hdPEO | 5.16 (h) | 5.95 (d) | 1.01 (h) | 1.01(d) | 117 (h) | 124 (d) | |
| dhPEO | 6.01 (d) | 6.38 (h) | 1.01 (d) | 1.01 (h) | 125 (d) | 145 (h) | |
| Crosslinker | 0.182 | 2.7 × 10−28 | |||||
![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) j2/Vmon, σinc = 4πΣnj(bj2 −
j2/Vmon, σinc = 4πΣnj(bj2 − ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) j2)/Vmon where bj are the spin and isotope dependent scattering lengths and the scattering length densities (SLD) ρmon = NAΣnjbj/Vmon
j2)/Vmon where bj are the spin and isotope dependent scattering lengths and the scattering length densities (SLD) ρmon = NAΣnjbj/Vmon
| Monomer | ρmon [cm−2] × 1010 | σcoh [cm−1] | Vchain × 1024 [cm3] | Density [g cm−3] | σinc [cm−1] |
|---|---|---|---|---|---|
| dPB | 6.2 | 0.52 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
0.96 | 0.12 |
| hPEO | 2.69 | 0.34 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
1.12 | 4.92 |
| dPEO | 7.0 | 0.577 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.22 | 0.13 |
| Crosslinker | 1.92 | 0.25 | 270 | 1.12 | 4.16 |
 | ||
| Fig. 2 Small angle scattering data. SAXS measured (a) in water solution at room temperature, line shows the fitting curve representing the core–shell form factor; inset: corresponding SLD profile; (b) in the melt at 363 K, line shows the fit with a Percus–Yevick structure factor and a sphere form factor; (c) SANS measured on differently labelled polymer grafted NPs hPEO (blue) and hdPEO (green) label (see Table 3) in melt state where the NP core is matched. The PEO melt reference is shown by red symbols. The data were randomly shifted relative to the reference PEO melt. All the data sets follow a Debye form factor (black solid line) Q−2 at high scattering vectors. | ||
The characterization and physical parameter of the basic polymer components is presented in Tables 1 and 2. Table 3 displays the compositions of the various block-copolymers.
Methods
SAXS
Scattering curves were recorded on the SAXS system “Ganesha-Air” from (SAXSLAB, Xenocs), operated at JCNS in the research center Jülich, The X-ray source was a D2-MetalJet (Excillum) with a liquid–metal anode operating at 70 kV and 3.57 mA with Ga-Kα radiation (λ = 0.1341 nm) providing a brilliant and small beam (<100 μm), which was focused with a focal length of 55 cm to a very small and intense beam at the sample using a specifically made X-ray optic from Xenocs. Samples were measured in sealed 2.1 mm borosilicate glass capillaries from Hilgenberg. The scattered intensity was recorded by a movable EIGER2-4M detector from Dectris. A Q-range of 0.1–3 nm−1 was covered. The azimuthally averaged data were normalized in respect to the incident beam, counts per solid angle and measurement time before subtraction of the empty capillary and correction for sample thickness. Intensities were put on absolute scale by standardless absolute intensity calibration.SANS
The SANS experiments were performed on the SANS instruments D22 and D33 at Institute Laue Langevin (ILL)43 in Grenoble (France). The matching experiment was performed on the OCNC carrying the fully labeled shell in aqueous solution of different H2O and D2O concentrations at room temperature on D3344 featuring a sample-detector distance of 12.8 m and a wavelength of 0.8 nm. SANS experiments on the OCNC in a melt state were carried out on the SANS instrument D2245 also at the Institute Laue Langevin (ILL) at a temperature of 363 K, neutron wavelength 0.6 nm, sample-to-detector length 11.2 m. The raw data were corrected by their respective transmissions, the scattering of the empty container and the electronic background (obtained by measuring 10B4C). The data were calibrated to absolute intensity by attenuated empty beam measurements. The data reduction steps were performed using Grasp software.46NSE
The NSE experiments were performed on the spectrometer IN15 at ILL.43 The temperature was fixed at 413 K. The Fourier time range covered 0.1 < t < 500 ns and the Q values accessed were Q = 0.48, 0.77, 0.97, 1.14 and 1.3 nm−1. While the lower Q values (Q ≤ 0.97 nm−1) were studied at a neutron wavelength of λ = 1.35 nm, the higher Q were investigated at λ = 1 nm, at Q = 0.77 nm−1 data from both wavelengths are available.Results
Structure
To determine the scattering length density (SLD) of the cross-linked core we conducted contrast matching experiments. The exact amount of cross-linker (2,2′-(ethylenedioxy)-diethanthiol) was obtained by elemental analysis of the core material yielding a core composition of 77 vol% deuterated PB and of 23 vol% of cross linkers. Using this composition the SLD of the core was calculated as ρcalculatedcore = 5.22 × 1010 cm−2. According to the calculated value the matching conditions for the shell was a mixture of h-PEO (28 vol%) and deuterated (72 vol%) d-PEO. Based on this composition, cross-linked micelles were prepared and dispersed in 6 different D2O/H2O mixtures. The intensity at lowest values of the momentum transfer (Q → 0) was used to determine the proper matching condition and estimate the scattering density of the core. Minimum of scattering intensity the SLD of the core corresponds to ρcore = 5.13 × 1010 cm−2 (see ESI†). This measured value, corrected to the temperature of NSE experiment, led to the contrast matching composition in the shell, at which the scattering from the core is strongly suppressed in the NSE experiment and only dynamics of grafted chains can be studied.To analyze the melt structure built by the micelles, we first need information about the micelle composition. Considering the chain volumes of the constituents, at room temperature we have 15.2 nm3 volume per one PEO chain and accounting for a cross-linker content of 23 vol% in the core an effective volume per one PB chain of 10.8/0.77 = 14.8 nm3. Thus, no matter how large the aggregation number will be, core and shell are occupying very similar volumes.
To obtain the aggregation number, we need to know the micellar size. Using SAXS we looked on 3 vol% solution of the cross-linked micelles in water. There the main contrast is created by the core with a small contribution from the PEO in the shell. Fig. 2a and Table 4 present the result. The data were fitted with a core shell formfactor applying the proper scattering length densities for PEO and PB against water. We arrive at a core radius of 11.6 ± 2.1 nm. The detectable shell thickness is in the order of 6 nm (taken as the decay length, see Fig. 2a inset), in between the radius of gyration (3.4 nm) and the end-to-end distance (8.4 nm) of the PEO chains in the corona. We note that because of the weak scattering contrast between PEO and water the data are prone to some error. From the core radius of R = 11.6 ± 2.1 nm we get an estimation for the aggregation number Nagg from  because of the large uncertainty in the core radius the corresponding aggregation number is between 245 and 730.
because of the large uncertainty in the core radius the corresponding aggregation number is between 245 and 730.
| Formfactor (SAXS in solution) | Structure factor (SAXS/SANS in a melt) | |||||
|---|---|---|---|---|---|---|
| R/nm | dshell/nm | Nagg | d/nm | RPY/nm | HSR/nm | GD/nm−2 |
| 11.6 ± 2.1 | 6 ± 0.5 | 245…730 | 31 | 14.1 ± 3.0 | 15.1 | 0.31…0.32 |
Now, we turn to the melt data: Fig. 2b shows the SAXS result, Fig. 2c, the SANS results, both taken at 363 K. They both display a main peak around Q = 0.2 nm−1 corresponding to an average interparticle distance of d = 31 nm. Depending on the labelling of the corona the SANS spectra show some features at higher Q, which are more pronounced for the inner labeled micelle. We also note that at higher Q the data from all labeling schemes nicely follow the formfactor of a corresponding linear chain, which is well described by a Debye-function. The structures for the fully labelled micelle at Q > 0.3 nm−1 also appears in the SAXS pattern indicating that they are related to the structure factor S(Q).
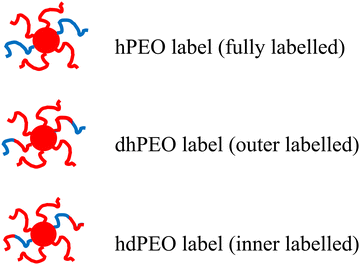
How do we interpret the main peak? (i) the peak may relate to a local crystalline like structure. For a bcc-type arrangement the resulting lattice constant would be 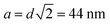 . There would be 2 micelles in the elementary cell taking a volume of 2(14.8 + 15.2)837 = 50
. There would be 2 micelles in the elementary cell taking a volume of 2(14.8 + 15.2)837 = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 nm3 from the largest core radius compatible with the error of dilute solution measurement; the bcc unit cell amounts to 85
220 nm3 from the largest core radius compatible with the error of dilute solution measurement; the bcc unit cell amounts to 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 nm3. Thus, volume filling by far would not be achieved – and a fcc-type structure would make things even worse (
080 nm3. Thus, volume filling by far would not be achieved – and a fcc-type structure would make things even worse ( volume 156
volume 156![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 nm3, 4 micelles in elementary cell: 10
300 nm3, 4 micelles in elementary cell: 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0440 nm3). Thus, we may exclude an ordered crystalline-type structure and have to deal with a disordered dense phase of the micellar cores, where about 50 vol% is taken by the cores and another 50 vol% by the shells acting as a kind of “solvent”. Considering the thermal expansion of about 7 vol% from room temperature to the 393 K of the measurement we get a micellar volume of 25
0440 nm3). Thus, we may exclude an ordered crystalline-type structure and have to deal with a disordered dense phase of the micellar cores, where about 50 vol% is taken by the cores and another 50 vol% by the shells acting as a kind of “solvent”. Considering the thermal expansion of about 7 vol% from room temperature to the 393 K of the measurement we get a micellar volume of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 110 nm3 reasonably close to d3 = 29
110 nm3 reasonably close to d3 = 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 791 nm3. Table 5 summarizes the parameters for the different spatial arrangements. Finally, from the core sizes we may estimate the grafting density:
791 nm3. Table 5 summarizes the parameters for the different spatial arrangements. Finally, from the core sizes we may estimate the grafting density:  . Thus, we conclude that the micellar cores in the melt assume a disordered dense colloidal arrangement with a very heterogenous topological landscape for the corona shells; some will expand into the voids opened by the cores, others in the direction of the next neighbor cores will be more strongly confined.
. Thus, we conclude that the micellar cores in the melt assume a disordered dense colloidal arrangement with a very heterogenous topological landscape for the corona shells; some will expand into the voids opened by the cores, others in the direction of the next neighbor cores will be more strongly confined.
Fig. 2b displace the SAXS results from the melt fitted by combination of a spherical form factor and a Percus–Yevick fluid-like structure factor including a low Q Porod-like power law Q−5.9 in order to describe the surface scattering from air bubbles and other heterogeneities. The power law may also include a contribution from direct beam. The fit resulted in micellar core radii R = 14.1 ± 3.0 nm and an effective interaction radii (HSR) 15.1 nm in good agreement with estimations above.
Apparently, the structural features seen in the low Q-range might appear in the NSE experiment. However, it is worth to note that the NSE experiment was performed at the temperature 413 K, well above the SANS measurement (363 K). Considering the different temperature dependence of polymer density for PEO and PB, the SLD changes and matching conditions are closely reproduced. Remarkably, at Q >1 nm−1, the scattering from PEO chains prevails even at 363 K. In the high scattering vector range, i.e. the NSE range, we notice a Debye dependence of Q−2 in all cases. The observation of a Debye formfactor for the OCNC even for the inner-labeled species indicates that chain stretching is not observed. Thus, the polymer conformation of shell chains in all cases agree with that of the neat melt (Fig. 2c).
Dynamics
Dynamics of OCNC at the conditions described above was measured using NSE. Fig. 3(a)–(f) compare NSE spectra taken for the different Q values taken for the inner, outer and fully labelled shells (Fig. 1).For the smallest Q the relative difference in spectral decay for the different labels is largest. The inner labeled melt decays significantly less than the outer labeled species – the spectral decay of the fully labeled shell lays somewhere in between. This scheme is visible for all Q values even though the spread diminishes with increasing Q. Qualitatively, one may say that larger scale relaxation that dominates at smaller Q-values are sensitive to the position of the label, while the higher Q the difference in the relaxation dynamics is less pronounced.
As derived from NSE, PEO exhibits an entanglement molecular weight of 2 kg mol−1.47 Thus, our grafted chains with a molecular weight around 10 kg mol−1 are in the weakly entangled range of molecular weights, where the classical local reptation process is not yet developed.
To access the influence of entanglements in the transition regime, a bulk PEO melt of slightly smaller molecular weight as that of the grafts i.e. blend of hydrogenated and deuterated PEO with a molecular weight of 8 kg mol−1 was studied separately at different temperatures from 350 K to 450 K.41 To account for the effect of entanglements, the NSE data from the melt sample were evaluated in terms of a Rouse mode analysis.48,49 This analysis allows to scrutinize the spatial confinement of the chain motion in assigning smaller mode amplitudes to the low index Rouse n. We call the associated parameters “topological parameters” since they describe the influence of topological interaction on the chain dynamics. Technically, a modified Fermi function is employed, to systematically describe the change of the Rouse mode amplitudes from low to high mode numbers p as:
 | (1) |
 | (2) |
 the elementary relaxation rate and
the elementary relaxation rate and  the so called “Rouse rate”; with kB the Boltzmann constant; T: the absolute temperature; ξ0: the monomeric friction coefficient. For the neat melt the time dependent center of mass displacement follows a cross over in time from sub-diffusive behavior at short times to Fickian diffusion at longer times as reported previously.41
the so called “Rouse rate”; with kB the Boltzmann constant; T: the absolute temperature; ξ0: the monomeric friction coefficient. For the neat melt the time dependent center of mass displacement follows a cross over in time from sub-diffusive behavior at short times to Fickian diffusion at longer times as reported previously.41
Rouse mode analysis. The NSE data obtained from OCNC were initially evaluated in terms of Rouse mode analysis as described above (eqn (1) and (2)). In contrast to the linear melt, however, the polymer chains in the OCNC are fixed at one end. Therefore, the translational diffusion is that of the full micelle and not visible within the NSE time window. In order to capture the dynamics of polymer chains fixed at one end, we assume a virtual polymer chain of double the molecular weight as that of the real chain. We model the dynamics of half of this virtual chain by considering only the odd modes such that one end of the real chain will always have a node at the grafting point.31 Technically a change of the p-summation in the dynamic structure factor starting from p = 1/2 and continuing to N − 1/2 represents this approach. We fix 〈rcom2(t)〉 = 0 as grafting precludes the possibility of individual chain translational diffusion. Therefore, the modified dynamic structure factor is expressed as:
 | (3) |
 | ||
| Fig. 4 Results from a joint fit with eqn (3) (dashed lines) and eqn (3) and (4) (solid lines) to the spectra with different labels: (a) dhPEO, (b) hdPEO, (c) hPEO, the Q values from above are Q = 0.48, 0.77 (0.76 at λ = 10 nm), 0.97, 1.14, 1.3 nm−1. (d) Friction profile in relative units corresponding to the fit with eqn (3) and (4) (solid lines). The numbers along the abscissae numerate the monomers away from the grafting point at 1. | ||
We further note that the inflection point of fcross(p) (eqn (1)) for the grafted chain is rather similar for a free chain in the PEO melt (pcross = 5.3 compared to pcross = 4.23) – most of this difference may be explained by the larger chain length of about Z = 5 entanglements, while the neat melt corresponded to Z = 4. The crossover width for the grafted chains is significantly broader than that for the melt (pwidth = 2.05 vs. pwidth = 0.61), indicating that (i) the confinement for both, the free and the grafted chain, is of similar origin and (ii) the heterogeneity for the grafted chains in the OCNC appears to be much larger. Nevertheless, we point to the inability of the mode analysis to correctly describe the data.
Spatial variation of friction. Based on the results so far, we hypothesize that the reason for the discrepancies between fits and data most likely arises from the assumption of constant monomeric friction along the chain. The pronounced decay of the dynamics structure factor in particular for the outer labelled dhPEO sample (see Fig. 1 and 3) as compared to the model prediction is in line with this speculation. We have shown in the past that the grafted polymer chains are characterized by a wide distribution of monomeric relaxation times instead of a single value.36 The variation of relaxation times was related to the site dependent constraints experienced by the grafted polymer chains. All these observations encouraged us to modify our approach to include site dependent friction in the description of grafted polymers. This adds further complexity to the Rouse mode analysis approach. The assumption of nonuniform friction is also supported by simulations that predicted a significantly varying monomer density in such OCNCs.17
The related Rouse problem with site dependent Rouse rates was solved numerically delivering the eigenvalues as well as the eigenvectors that are both needed to calculate the dynamic structure factor in an equivalent way as it is done for the standard Rouse problem. Finally, to model the grafting point, the associated friction was set to a very high value.
In order to introduce site dependent friction, we use a diagonal mobility matrix with diagonal values modulated by a function describing the relative segment dependent friction (see ESI†). In order to effectively model a fixed end point we assume H(1,1) = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The friction modulation
000. The friction modulation  as well as the mode modifications fcross(p) (topological parameters) are obtained by fitting.
as well as the mode modifications fcross(p) (topological parameters) are obtained by fitting.
As a first Ansatz for the friction profile, we imposed eqn (4) allowing a large and versatile variation of friction along the chain. The grafting point is located at i = 1.
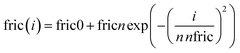 | (4) |
In a next step we investigate whether a more elaborate friction profile could improve the fit. The approach is described in the ESI,† and does not lead to significant improvements.
We conclude that even with a sophisticated very flexible friction profile independent of starting parameters we always find a result (Fig. 4 and Fig. S2, S3, ESI†), where in the neighborhood of the grafting point friction increases by up to a factor of 2; the increased friction encompasses around the first 15% of the grafted chain. From then on, the friction stays constant until the chain ends. Even though allowed by the fitted profile (Fig. S1, ESI†), none of the fits indicated a further decrease of friction towards the chain ends. The details of the fit results using profiles including the option of variable topological parameters pcross and pwidth are displayed in the ESI.†
Motional heterogeneity. Reflecting on the structural peculiarities of densely packed micellar cores with the grafted chains experiencing very different topological environments – some of these chains extend into the voids in between the spherical cores other are strongly confined by the next neighbor cores, we consider motional heterogeneity for the grafted chains (see Fig. 5c). Different chains are situated in different topological environments and will undergo different dynamics. Such a view is also in line with recent simulations17,18 that revealed heterogeneity within the nanocomposite as e.g. pockets of lower density. Lower density always results in higher mobility. We induce dynamic heterogeneity in tentatively allowing for two different groups of topological parameters pcross and pwidth accompanied by two different friction profiles of the relaxing ensembles. We note that the experiment does not resolve the position of an individual graft attached to the core, and therefore, the different chain ensembles could be distributed widely across the outer shell. Furthermore, we point out that naturally one should consider distributions of different topological constraints as well as friction profiles. However, given the expressiveness of the data, such an approach the data do not permit.
Finally, allowing different topological parameters for the two heterogenous fractions, we arrive at an overall goodness of the fit of χ2 = 9.87. This goodness was achieved assuming two equal fractions of differently relaxing grafts. We note that the fit reveals one ensemble with friction variation similar to those found earlier (Fig. 4d). This part is also characterized by a broadly varying cut off function (red line in Fig. 5a), while the other ensemble displays very few topological constraints (blue line in Fig. 5a) and experiences nearly constant friction The minimum in χ2 is not very pronounced – adjacent combinations of relaxing ensembles (0.4 ≤ ϕ ≤ 0.6), where ϕ is volume fraction of the component with a variable friction profile, lead to χ2 = 10.7, and 10.5 respectivly. Thus, we could not evaluate the exact proportion of the two ensembles. Fig. 5a displays the outcome for a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 partition showing the cut off function for the two ensembles.
50 partition showing the cut off function for the two ensembles.
As an alternative, we consider to what extent the assumption of different topological parameters only, for the two ensembles, is able to describe the observed dynamics (χ2 = 11.6). Fig. 5b displays the cut off functions. Qualitatively similar to the former case one component exhibits a broad cut off with a large number of modulated mode amplitudes, the other component shows a mode cut off rather similar to that of the neat melt. Implying different topological environments and keeping friction constant, also a fit of the proportion of the ensembles is possible. We find 58% for the ensemble corresponding to the red line in Fig. 5b, while the other ensemble with the more pronounced cut off assumes a proportion of 42%, well in line with, above result. Finally, Fig. 6 compares the data description by the two approaches. We note that the relatively sharp cut offs for one component are most likely an artifact of the fit that, because of the discreteness of the modes, has difficulties as soon as the pwidth becomes smaller than about 0.5.
 | ||
| Fig. 6 Results from a joint fit with eqn (3) and (4) allowing for heterogeneously relaxing ensembles with two different cut off profiles for the topological constraints and site dependent friction (solid lines); dashed lines shows fitting only the topological parameters with one common constant friction to the spectra; (a) dhPEO, (b) hdPEO, (c) hPEO. The Q values from above are Q = 0.48, 0.77 (0.76) at (λ = 10 nm), 0.97, 1.14, 1.3 nm−1 (d): friction profile for the two heterogeneously relaxing ensembles: cyan line: fraction with broad cut off; blue line: fraction with sharp cut off features. | ||
As the χ2 values indicate, the quality of the data description is somewhat better for the approach employing site dependent friction. For the outer labeled sample, the approach varying only the topological parameters is closest to the data; in particular the plateauing of the spectra at the higher Q-values is well reproduced. For the inner labeled sample and lower Q the site dependent friction approach is somewhat closer to the data, while for the higher Q the reverse holds. Finally, for the fully labeled sample the data description using the site dependent friction approach tends to be closer the measurement. We should note that number of fitted parameter for the first model is 8, while for the second case only 5 parameters are varied.
Fig. 6 also displays the obtained friction profiles. As already observed for the homogenous case, again we find significant site dependent friction, now for the ensemble undergoing the broad cut off feature, while the ensemble with the sharp cut off displays nearly constant friction.
Discussion
The OCNC presented in this study do not demonstrate any visible two-phases structure mentioned by Midya et al.25 In their simulations they observe a dry layer of extended chains, where only few monomers from the surrounding GNPs were present, and an interpenetration layer of unperturbed chains, where significant overlap between grafted chains of the surrounding GNPs occurred, presumably to maximize their conformational entropy. By dielectric spectroscopy and DSC the dynamic suppression at the interface affected by the chain stretching was found.35 Our neutron scattering experiments, performed at comparable grafting density do not evidence either two-phases structure of the grafted chains nor stretched grafted chain conformation.OCNC are heterogenous not only concerning the core–shell structure of the building blocks – in our case: the elementary micelles – but also as a consequence of the inability of the shells to homogenously fill the space in between the core structures. In separation membrane technology this heterogeneous space filling is used to design specific permeabilities.17,18 Also, spatially varying topological constraints related to neighboring chains contribute to the heterogeneity of the chain motions. Interestingly, the slowing down of relaxation modes of tethered polyisoprene (PI) was found to be related to the interchain correlations.24 It suggests the entropic attraction force produced by the space-filling constraint on tethered PI chains in the self-suspended materials produce linkages between individual chains that couples their relaxation dynamics. This, in line with our results, indicates the heterogeneity of chain motion. In this work we have dealt with the modified dynamic properties of the matrix established by polymer grafts in comparison to a neat melt. In the following we elaborate on the measured heterogeneity of the chain dynamics and the associated cross over functions, the associated asymptotic segmental displacements along the chain and the related site dependent friction.
Dynamic heterogeneity
The experiment was designed such as to probe different parts of the polymer matrix from the grafts in labeling different fractions of the grafted chains. An inspection of the measured spectra without any evaluation directly showed the different dynamics of the outer part of the grafts compared to the portion close to the NP core (Fig. 3). These differences were relatively largest at smallest Q, where the experiments probe larger scale motion.By judiciously contrast matching the global scattering between the micellar core (or the NP) and the outer shell we were able to approach contrast matching such that the chain dynamics could be studied without “elastic” contributions from structural features. We note that the SANS experiments (T = 363 K) shown in Fig. 2 were performed well below the temperature of the NSE experiment (T = 413 K). As a consequence of different thermal expansion coefficients of PEO and PB, contrast matching was expected to be valid for the higher temperature. “Elastic” contributions from structural features would add a constant to the spectra that would be very difficult to distinguish from a constraint on the dynamics. The models consistently display spectra that at longer times decay less than the measured spectra. However, if there was some elastic contribution from imperfectly matching the contrast, the experimental spectra (Fig. 3, 4 and 6) would be located above the predicted spectra.
The various approaches undertaken to rationalize the spectra added further complexity to the modelling. First, we performed Rouse mode analysis i.e. we imposed topological constraints on all chains in an equal manner leading to large discrepancies between model and spectra. In particular, the sample with the outer labels could not be described. Adding spatially varying friction improved the fit quality but again could not describe the data from the outer labeling. While the initial decay of these spectra was better described than before, in particular the line-shape of spectra that showed plateauing at longer times was not modelled at all. Also, more sophisticated friction profiles that are presented in the ESI,† could not improve the situation. This result agrees with the simulations of Hore et al.21 reporting about non-applicability of Rouse model to the dynamics of grafted chains.
Guided by the very inhomogeneous structural features, these failures led us to assume heterogenous dynamics: i.e. we considered two different ensembles of relaxing grafts exhibiting different topological constraints (e.g. as presented in Fig. 5c) and different friction profiles. Allowing explicitly for such heterogeneities the fit quality could be significantly improved. As Fig. 6 evidences, the spectra arising from highlighting different parts of the chains now are well described. Thereby, we noticed that apparently the most important difference of the ensembles lies in the topological constraints, which they are undergoing. Looking on the dense colloidal arrangement of cores with its voids such heterogeneity is immediately evident. Employing different constraints at constant friction also provides a reasonably good representation of the spectra. If we compare the solid (modulated friction) and the dashed (different constraints only) lines in Fig. 6 both approaches display strengths and weaknesses, while the overall goodness of the fit favors the combination of different constraints and site dependent friction.
We conclude that the most important ingredient to obtain satisfactory data description is the assumption of heterogeneously relaxing ensembles of grafts. As suggested by the structural features, these ensembles mainly differ in the extent of constraints they undergo. The effect of heterogenous friction appears to be a secondary phenomenon. We hypothesize that at higher grafting densities the influence of site dependent friction might well increase significantly.
Asymptotic segmental displacement
The limiting square root mean squared displacement (MSD) for a segment along the grafts displays the average maximum displacement a segment along the chain may undertake. Note that in contrast to the neat polymer chains, this MSD is not symmetric with respect to the chain center but increases from the grafting point onwards. This is an interesting repercussion of grafting polymer chains on NPs. Rapid increase of asymptotic displacements towards the chain end represents the motional range of the outermost monomers that are not confined by topological constraints. In terms of Rouse mode analysis eqn (3) and (4) provide information about this limiting MSD of each segment along the chain. For the case of eqn (3) we have:
along the grafts displays the average maximum displacement a segment along the chain may undertake. Note that in contrast to the neat polymer chains, this MSD is not symmetric with respect to the chain center but increases from the grafting point onwards. This is an interesting repercussion of grafting polymer chains on NPs. Rapid increase of asymptotic displacements towards the chain end represents the motional range of the outermost monomers that are not confined by topological constraints. In terms of Rouse mode analysis eqn (3) and (4) provide information about this limiting MSD of each segment along the chain. For the case of eqn (3) we have:
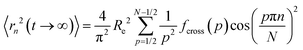 | (5) |
In the Fig. 7 we present the asymptotic square root displacements for the cases of site dependent friction and for topological constraints only. We observe a rapid increase of the limiting displacement starting from the grafting site. The effect of grafting decreases rather quickly and at a length scale of half of the tube diameter, topological constraints take over and this increase is impeded. Blue and red code the effect of only topological constraints. We realize one strongly confined ensemble and a second one, where the constraints are significantly more relaxed. The ensembles with site dependent friction behave similarly. The strongly constrained fraction of chains behaves as those in the former case, while the less confined part exhibits an about twice as large  . At the chain ends all ensembles experience increasing motional freedom. The weak oscillations relate to the Fourier type description of the segmental motion, where finite size effects occur. The average displacement size of the more constraint components amounts to about 1.8–2.0 nm, which corresponds to approximately half of the tube diameter and agrees quite well with the results of a Rouse mode analysis on the neat melt.41 In addition, we observe a less constrained component that in the approach with site dependent friction amounts to about 4 nm, while assuming topological constraints only it gradually increases up to 6 nm. Thus, for both approaches we find a less constraint fraction, which does not appear in the neat melt. Concerning the structure, we may associate these less restricted monomers with chains extending into voids created by the colloidal arrangement of the cores.
. At the chain ends all ensembles experience increasing motional freedom. The weak oscillations relate to the Fourier type description of the segmental motion, where finite size effects occur. The average displacement size of the more constraint components amounts to about 1.8–2.0 nm, which corresponds to approximately half of the tube diameter and agrees quite well with the results of a Rouse mode analysis on the neat melt.41 In addition, we observe a less constrained component that in the approach with site dependent friction amounts to about 4 nm, while assuming topological constraints only it gradually increases up to 6 nm. Thus, for both approaches we find a less constraint fraction, which does not appear in the neat melt. Concerning the structure, we may associate these less restricted monomers with chains extending into voids created by the colloidal arrangement of the cores.
We conclude that in both models we find that the topological constraints acting on the segments along the chain are reduced compared to those in the corresponding linear melt. As suggested by the dense colloidal structure of the core assembly, we also found strong evidence for heterogenous dynamics with chain ensembles that are differently constrained. The separation into two fractions of about equal size has a slight preference with respect to the goodness of the fits, but clearly ensembles governed by a distribution of constraints would be more realistic but would over interpret the data.
Finally, we note that for unentangled grafted chains a similar confinement effect related to neighboring chains was described by Mark et al.31 They hypothesized that longer entangled grafted chains would be the subject of a combination of grafting effect and chain-chain entanglements. From our experiment and analysis, we conclude that the dynamics of grafted weakly entangled polymers is controlled by constraints imposed by neighboring grafts together with topological constraints related to the dense colloidal arrangement of the core NPs.
Friction profile
Our NSE experiments on differently labelled grafted polymer chains and their analysis establishes that the segmental friction coefficient varies depending on the location along the grafted chain. We discuss the friction modulation in terms of the Rouse rate that is directly related to friction: in the first, topological only approach, which was performed by Rouse mode analysis, we had to fix the Rouse rate wl4 and thus friction to the value obtained in the reference melt wl4 = 1.91 nm4 ns−1 – otherwise the fit compensated large mode suppression by choosing unphysically high Rouse rates. With this choice the inflection point of the Fermi type cut off function, defining the mode suppression, increases by one mode and significantly broadens indicating higher heterogeneity of relaxation dynamics compared to the neat melt.
that is directly related to friction: in the first, topological only approach, which was performed by Rouse mode analysis, we had to fix the Rouse rate wl4 and thus friction to the value obtained in the reference melt wl4 = 1.91 nm4 ns−1 – otherwise the fit compensated large mode suppression by choosing unphysically high Rouse rates. With this choice the inflection point of the Fermi type cut off function, defining the mode suppression, increases by one mode and significantly broadens indicating higher heterogeneity of relaxation dynamics compared to the neat melt.
Allowing for site dependent friction using a very flexible friction profile that allowed both for a change (increase or decrease) of friction towards the grafting point as well as an additional further reduction towards the chain end, we consistently found that independent of starting conditions and the number of variable parameters friction always increases towards the grafting point, typically by a factor in the order of 1.5 to 2 (see Fig. S2 of the ESI†). Starting beyond the first 15% to 20% of segments the segmental friction becomes constant and does not further depend on the location along the graft. Thus, again consistently a further decrease of friction towards the chain end was not observed. We like to note that on the basis of site dependent friction alone without considering topological fitting fails completely. Thus, for our OCNC with a high volume fraction of NPs (micellar cores), the consideration of topological hindrance is mandatory. The relatively weak modulation of friction by about a factor of 2 probably owes to the low grafting density of 0.32 chains per nm2.
As was eluded to above, the inability to well describe the spectra within a picture of homogenous relaxation dynamics of all grafts, led us to allow for chain ensembles that relax differently: they were assumed to undergo different spatial constraints and were subject to different friction profiles. As mentioned above, a more realistic assumption of a distribution of differently relaxing ensembles would be pushing the boundaries given by the quality of the data. Fig. 6d displays the best results. Here it was assumed that two equal fractions of grafts relax differently. Aside from the different topological hindrance expressed by the cut off function displayed in Fig. 5a, also the friction profiles, as shown by Fig. 6c, are rather different. While for the topologically more severely restricted ensemble the Rouse rate varies between 1.0080 ≤ wl4 ≤ 1.812 nm4 ns−1 with a significant increase towards the grafting point, the less restricted ensemble undergoes nearly constant friction with 1.3290 ≤ wl4 ≤ 1.442 nm4 ns−1. The combination of more constraints accompanied by stronger friction appears to be very reasonable. The dependence of local monomer relaxation on their location along the grafted polymer chain has been considered by Reith et al. using computer simulations.25 They found the fastest segments located in the middle of the chain with gradual decrease of the relaxation time close to the chain end. Our experiment shows a significant increase of friction in the neighborhood of the grafting point but from then on constant friction.
Conclusion
We studied polymer grafted one component nanocomposites (OCNC) based on self-assembled polymer micelles in the melt, where the PB in the core was densely cross-linked. The grafted polymer chains were labelled at the inner- the outer-part and fully labelled. We studied the chain dynamics of these grafts by neutron spin echo spectroscopy. The molecular weights of the grafts were chosen in the range of about 5 entanglement molecular weights. We employed Rouse mode analysis to capture the dynamics as well as conformational features of the grafted polymers. While this analysis accurately describes the characteristic relaxation and entanglement tube diameter for pure polymer chains, it fails to access the complex features of grafted polymer chains. We demonstrate that the grafted polymer chains can be characterized by a distribution of friction coefficients and hence a distribution of the monomer relaxation rates along the polymer. Stepwise increasing complexity we find that the monomeric friction along the chain increases towards the grafting point. Furthermore, owed to the dense colloidal structure of the OCNC melt, in order to satisfactorily describe the NSE data, we needed to consider motional heterogeneity in the sense that not all grafts undergo the same friction profile and more importantly also undergo different topological constraints. Even with this approach some deficiencies in the description of the spectra from the grafted chains remain. The approach uncovers many interesting features of the grafted polymer dynamics. Although we observe constraints similar to entanglements, there is strong evidence that the constraints do not act equally on the whole chain ensemble. Naturally the assumption of just two different ensembles is an oversimplification and a distribution of different chain environments would have been more realistic, but the determination of the corresponding distribution function could not be extracted from the data. Nevertheless, we note that both the observation of a site dependent friction as well as the evidence of heterogenous chain environments is a novel exploit.Autor contributions
Margarita Kruteva: conceptualization, data curation, investigation, visualization, validation, writing – review & editing, writing – original draft; Michael Monkenbusch: data curation, investigation, formal analysis, methodology, validation, software, writing – review & editing, writing – original draft; Aakash Sharma: data curation, validation, writing – original draft: Jürgen Allgaier: resources, validation, writing – original draft: Ingo Hoffmann: data curation; Benedetta Rosi: formal analysis, investigation; Martin Dulle: data curation, investigation; Lionel Porcar: data curation; Olga Matsarskaia: data curation; Dieter Richter: supervision, conceptualization, formal analysis, investigation, visualization, validation, writing – review & editing, writing – original draft.Data availability
Data for this article are available at ILL at https://doi.ill.fr/10.5291/ILL-DATA.9-12-628.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Institut Laue Langevin (ILL) for granting the neutron beamtime (experiment 9-12-628).References
- Vidya, L. Mandal, B. Verma and P. K. Patel, Mater. Today: Proc., 2019, 26, 3161–3166 Search PubMed.
- E. J. Bailey and K. I. Winey, Dynamics of polymer segments, polymer chains, and nanoparticles in polymer nanocomposite melts: a review, Prog. Polym. Sci., 2020, 105, 101242 CrossRef CAS.
- D. Salatto, J.-M. Carrillo, M. Endoh, T. Taniguchi, B. Yavitt, T. Masui, H. Kishimoto, M. Tyagi, A. Ribbe, V. García Sakai, M. Kruteva, B. Sumpter, B. Farago, D. Richter, M. Nagao and T. Koga, Structural and Dynamical Roles of Bound Polymer Chains in Rubber Reinforcement, Macromolecules, 2021, 54(23), 11032–11046 CrossRef CAS.
- H. M. C. de Azeredo, Nanocomposites for food packaging applications, Food Res. Int., 2009, 42, 1240–1253 CrossRef CAS.
- R. A. Hule and D. J. Pochan, Polymer nanocomposites for biomedical applications, MRS Bull., 2007, 32, 354–358 CrossRef CAS.
- E. N. Zare, P. Makvandi, B. Ashtari, F. Rossi, A. Motahari and G. Perale, Progress in Conductive Polyaniline-Based Nanocomposites for Biomedical Applications: A Review, J. Med. Chem., 2020, 63, 1–22 CrossRef CAS PubMed.
- J. Peng and Q. Cheng, High-Performance Nanocomposites Inspired by Nature, Adv. Mater., 2017, 29, 1702959 CrossRef PubMed.
- M. R. Bockstaller, Progress in polymer hybrid materials, Prog. Polym. Sci., 2015, 40, 1–2 CrossRef CAS.
- D. Vlassopoulos and M. Cloitre, Tunable rheology of dense soft deformable colloids, Curr. Opin. Colloid Interface Sci., 2014, 19, 561–574 CrossRef CAS.
- H. Koerner, L. F. Drummy, B. Benicewicz, Y. Li and R. A. Vaia, Nonisotropic self-organization of single-component hairy nanoparticle assemblies, ACS Macro Lett., 2013, 2, 670–676 CrossRef CAS PubMed.
- J. Che, K. Park, C. A. Grabowski, A. Jawaid, J. Kelley, H. Koerner and R. A. Vaia, Preparation of Ordered Monolayers of Polymer Grafted Nanoparticles: Impact of Architecture, Concentration, and Substrate Surface Energy, Macromolecules, 2016, 49, 1834–1847 CrossRef CAS.
- M. R. Bockstaller, Progress in polymer hybrid materials, Prog. Polym. Sci., 2015, 40, 1–2 CrossRef CAS.
- X. Liu, B. A. Abel, Q. Zhao, S. Li, S. Choudhury, J. Zheng and L. A. Archer, Microscopic Origins of Caging and Equilibration of Self-Suspended Hairy Nanoparticles, Macromolecules, 2019, 52, 8187–8196 CrossRef CAS.
- M. Jhalaria, Y. Huang, E. Ruzicka, M. Tyagi, R. Zorn, M. Zamponi, V. García Sakai, B. Benicewicz and S. Kumar, Activated Transport in Polymer Grafted Nanoparticle Melts, Macromolecules, 2021, 54, 6968–6974 CrossRef CAS.
- S. K. Kumar, N. Jouault, B. Benicewicz and T. Neely, Nanocomposites with polymer grafted nanoparticles, Macromolecules, 2013, 46, 3199–3214 CrossRef CAS.
- P. Voudouris, J. Choi, N. Gomopoulos, R. Sainidou, H. Dong, K. Matyjaszewski, M. R. Bockstaller and G. Fytas, Anisotropic elasticity of quasi-one-component polymer nanocomposites, ACS Nano, 2011, 5, 5746–5754 CrossRef CAS PubMed.
- C. R. Bilchak, E. Buenning, M. Asai, K. Zhang, C. J. Durning, S. K. Kumar, Y. Huang, B. C. Benicewicz, D. W. Gidley, S. Cheng, A. P. Sokolov, M. Minelli and F. Doghieri, Polymer-Grafted Nanoparticle Membranes with Controllable Free Volume, Macromolecules, 2017, 50, 7111–7120 CrossRef CAS.
- C. R. Bilchak, M. Jhalaria, Y. Huang, Z. Abbas, J. Midya, F. M. Benedetti, D. Parisi, W. Egger, M. Dickmann, M. Minelli, F. Doghieri, A. Nikoubashman, C. J. Durning, D. Vlassopoulos, J. Jestin, Z. P. Smith, B. C. Benicewicz, M. Rubinstein, L. Leibler and S. K. Kumar, Tuning Selectivities in Gas Separation Membranes Based on Polymer-Grafted Nanoparticles, ACS Nano, 2020, 14, 17174–17183 CrossRef CAS PubMed.
- T. Ge, M. Rubinstein and G. S. Grest, Effects of Tethered Polymers on Dynamics of Nanoparticles in Unentangled Polymer Melts, Macromolecules, 2020, 53, 6898–6906 CrossRef CAS PubMed.
- G. L. He, H. Merlitz, J. U. Sommer and C. X. Wu, Static and dynamic properties of polymer brushes at moderate and high grafting densities: A molecular dynamics study, Macromolecules, 2007, 40, 6721–6730 CrossRef CAS.
- C. A. Miller and M. J. A. Hore, Simulation of the Coronal Dynamics of Polymer-Grafted Nanoparticles, ACS Polym. Au, 2022, 2(3), 157–168 CrossRef CAS PubMed.
- S. Askar, L. Li and J. M. Torkelson, Polystyrene-Grafted Silica Nanoparticles: Investigating the Molecular Weight Dependence of Glass Transition and Fragility Behavior, Macromolecules, 2017, 50, 1589–1598 CrossRef CAS.
- M. Jhalaria, E. Buenning, Y. Huang, M. Tyagi, R. Zorn, M. Zamponi, V. García-Sakai, J. Jestin, B. C. Benicewicz and S. K. Kumar, Accelerated Local Dynamics in Matrix-Free Polymer Grafted Nanoparticles, Phys. Rev. Lett., 2019, 123, 158003 CrossRef CAS PubMed.
- S. A. Kim, R. Mangal and L. A. Archer, Relaxation Dynamics of Nanoparticle-Tethered Polymer Chains, Macromolecules, 2015, 48, 6280–6293 CrossRef CAS.
- J. Midya, M. Rubinstein, S. K. Kumar and A. Nikoubashman, Structure of Polymer-Grafted Nanoparticle Melts, ACS Nano, 2020, 14, 15505–15516 CrossRef CAS PubMed.
- Y. Huang, Y. Zheng, A. Sarkar, Y. Xu, M. Stefik and B. C. Benicewicz, Matrix-Free Polymer Nanocomposite Thermoplastic Elastomers, Macromolecules, 2017, 50, 4742–4753 CrossRef CAS.
- S. Alexander, Adsorption of chain molecules with a polar head a scaling description, J. Phys., 1977, 38, 983–987 CrossRef CAS.
- M. Daoud and J. P. Cotton, Star shaped polymers: a model for the conformation and its concentration dependence, J. Phys., 1982, 43, 531–538 CrossRef CAS.
- D. Dukes, Y. Li, S. Lewis, B. Benicewicz, L. Schadler and S. K. Kumar, Conformational transitions of spherical polymer brushes: Synthesis, characterization, and theory, Macromolecules, 2010, 43, 1564–1570 CrossRef CAS.
- Y. Wei, Y. Xu, A. Faraone and M. J. A. Hore, Local Structure and Relaxation Dynamics in the Brush of Polymer-Grafted Silica Nanoparticles, ACS Macro Lett., 2018, 7, 699–704 CrossRef CAS PubMed.
- C. Mark, O. Holderer, J. Allgaier, E. Hübner, W. Pyckhout-Hintzen, M. Zamponi, A. Radulescu, A. Feoktystov, M. Monkenbusch, N. Jalarvo and D. Richter, Polymer Chain Conformation and Dynamical Confinement in a Model One-Component Nanocomposite, Phys. Rev. Lett., 2017, 119, 047801 CrossRef CAS PubMed.
- L. J. Fetters, D. J. Lohse and R. H. Colby, Chain Dimensions and Entanglement Spacings, Physical properties of polymers handbook, 2006, ch. 25, pp. 445–452 Search PubMed.
- M. Jhalaria, E. Buenning, Y. Huang, M. Tyagi, R. Zorn, M. Zamponi, V. García-Sakai, J. Jestin, B. C. Benicewicz and S. K. Kumar, Accelerated Local Dynamics in Matrix-Free Polymer Grafted Nanoparticles, Phys. Rev. Lett., 2019, 123, 158003 CrossRef CAS PubMed.
- C. A. Grabowski, H. Koerner, J. S. Meth, A. Dang, C. M. Hui, K. Matyjaszewski, M. R. Bockstaller, M. F. Durstock and R. A. Vaia, Performance of dielectric nanocomposites: Matrix-free, hairy nanoparticle assemblies and amorphous polymer-nanoparticle blends, ACS Appl. Mater. Interfaces, 2014, 6, 21500–21509 CrossRef CAS PubMed.
- A. P. Holt, V. Bocharova, S. Cheng, A. M. Kisliuk, B. T. White, T. Saito, D. Uhrig, J. P. Mahalik, R. Kumar, A. E. Imel, T. Etampawala, H. Martin, N. Sikes, B. G. Sumpter, M. D. Dadmun and A. P. Sokolov, Controlling Interfacial Dynamics: Covalent Bonding versus Physical Adsorption in Polymer Nanocomposites, ACS Nano, 2016, 10, 6843–6852 CrossRef CAS PubMed.
- A. Sharma, M. Kruteva, M. Zamponi, S. Ehlert, D. Richter and S. Förster, Influence of molecular weight on the distribution of segmental relaxation in polymer grafted nanoparticles, Phys. Rev. Mater., 2022, 6, L012601 CrossRef CAS.
- T. Glomann, G. J. Schneider, J. Allgaier, A. Radulescu, W. Lohstroh, B. Farago and D. Richter, Microscopic Dynamics of Polyethylene Glycol Chains Interacting with Silica Nanoparticles, Phys. Rev. Lett., 2013, 110, 178001 CrossRef CAS PubMed.
- G. L. He, H. Merlitz, J. U. Sommer and C. X. Wu, Static and dynamic properties of polymer brushes at moderate and high grafting densities: A molecular dynamics study, Macromolecules, 2007, 40, 6721–6730 CrossRef CAS.
- M. Vladkov and J. L. Barrat, Local dynamics and primitive path analysis for a model polymer melt near a surface, Macromolecules, 2007, 40, 3797–3804 CrossRef CAS.
- D. Reith, A. Milchev, P. Virnau and K. Binder, Computer simulation studies of chain dynamics in polymer brushes, Macromolecules, 2012, 45, 4381–4393 CrossRef CAS.
- A. Sharma, M. Kruteva, J. Allgaier, I. Hoffmann, P. Falus, M. Monkenbusch and D. Richter, Chain Confinement and Anomalous Diffusion in the Cross over Regime between Rouse and Reptation, ACS Macro Lett., 2022, 1343–1348 CrossRef CAS PubMed.
- Y. Y. Won, K. Paso, H. Ted Davis and F. S. Bates, Comparison of original and cross-linked wormlike micelles of poly(ethylene oxide-b-butadiene) in water: Rheological properties and effects of poly(ethylene oxide) addition, J. Phys. Chem. B, 2001, 105, 8302–8311 CrossRef CAS.
- S. Aakash, A. Juergen, F. Stephan, L. S. Fruhner, H. Ingo and K. Margarita, MATSARSKAIA Olga and RICHTER Dieter, Polymer dynamics in one component nanocomposites (OCNC), Institut Laue-Langevin (ILL), 2021 DOI:10.5291/ILL-DATA.9-12-628.
- C. D. Dewhurst, I. Grillo, D. Honecker, M. Bonnaud, M. Jacques, C. Amrouni, A. Perillo-Marcone, G. Manzin and R. Cubitt, The small-angle neutron scattering instrument D33 at the Institut Laue–Langevin, J. Appl. Crystallogr., 2016, 49, 1–14 CrossRef CAS.
- https://www.ill.eu/users/instruments/instruments-list/d22/description/instrument-layout, D22.
- C. D. Dewhurst, Graphical reduction and analysis small-angle neutron scattering program: GRASP, J. Appl. Crystallogr., 2023, 56, 1595–1609 CrossRef CAS PubMed.
- K. Niedzwiedz, A. Wischnewski, W. Pyckhout-Hintzen, J. Allgaier, D. Richter and A. Faraone, Chain Dynamics and Viscoelastic Properties of Poly(ethylene oxide), Macromolecules, 2008, 41, 4866–4872 CrossRef CAS.
- D. Richter, L. Willner, A. Zirkel, B. Farago, L. J. Fetters and J. S. Huang, Polymer Motion at the Crossover from Rouse to Reptation Dynamics, Macromolecules, 1994, 27, 7437–7446 CrossRef CAS.
- D. Richter, L. Willner, A. Zirkel, B. Farago, L. J. Fetters and J. S. Huang, Onset of topological constraints in polymer melts: a mode analysis by neutron spin echo spectroscopy, Phys. Rev. Lett., 1993, 71, 4158–4161 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01505c |
| This journal is © The Royal Society of Chemistry 2025 |