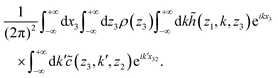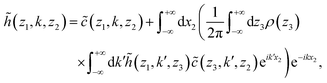Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combining integral equation closures with force density functional theory for the study of inhomogeneous fluids
S. M.
Tschopp
 a,
H.
Vahid
a,
H.
Vahid
 b,
A.
Sharma
c and
J. M.
Brader
b,
A.
Sharma
c and
J. M.
Brader
 a
a
aDepartment of Physics, University of Fribourg, CH-1700 Fribourg, Switzerland
bLeibniz-Institute for Polymer Research, Institute Theory of Polymers, D-01069 Dresden, Germany
cUniversity of Augsburg, Institute of Physics, D-86159 Augsburg, Germany
First published on 7th March 2025
Abstract
Classical density functional theory (DFT) is a powerful framework to study inhomogeneous fluids. Its standard form is based on the knowledge of a generating free energy functional. If this is known exactly, then the results obtained by using standard DFT or its alternative, recently developed version, force–DFT, are the same. If the free energy functional is known only approximately then these two routes produce different outcomes. However, as we show in this work, force–DFT has the advantage that it is also implementable without knowledge of the free energy functional, by using instead liquid-state integral equation closures. This broadens the range of systems that can be explored, since free energy functionals are generally difficult to approximate. In this paper we investigate the utility of using inhomogeneous integral equation closures within force–DFT thus demonstrating the versatility and accuracy of this approach.
I. Introduction
Classical density functional theory (DFT) is a powerful and well-established framework for the study of inhomogeneous fluids in equilibrium.1,2 Traditional applications of DFT require knowledge of the excess Helmholtz free energy functional, which contains all nontrivial information about the interparticle interactions. Functional differentiation then generates the one-body direct correlation function required to solve the Euler–Lagrange (EL) equation for the one-body density. Unfortunately, practical implementation of this standard DFT scheme is often hindered by the limited availability of reliable and accurate approximations to the excess Helmholtz free energy functional. While quantitatively accurate approximations do exist for both hard- and penetrable-particle models (using fundamental measures theory and density expansion functionals,2,3 respectively) the situation is less comfortable when considering either particles with a strongly repulsive soft core or those with an attractive component to the interaction potential (although progress has recently been made in the latter case,4,5 improving upon established approximations6,7).The recently proposed force–DFT approach8 provides an alternative way to obtain one-body density profiles from a given excess Helmholtz free energy functional, by explicitly treating the inhomogeneous two-body correlation functions. Working on the two-body level provides higher resolution of the fluid's internal microstructure. This feature enables direct calculation of the average interparticle forces acting within the system via spatial integration and thus provides access to physical quantities such as the surface tension.9 By identifying the inhomogeneous two-body correlations as functionals of the one-body density,4,5 the force–DFT approach retains the spirit of the traditional DFT framework. If the Helmholtz free energy functional is known exactly, these two approaches become strictly equivalent.
The inhomogeneous correlation functions used in force–DFT are obtained via solution of the inhomogeneous Ornstein–Zernike (OZ) equation. This feature enables versatility in the choice of an implementation route. The one presented in ref. 8 did indeed exploit the second functional derivative of the excess Helmholtz free energy to obtain the two-body direct correlation function and thus permit the solution of the inhomogeneous OZ equation. However, from the field of liquid-state integral equation theory, it is known that the OZ equation can be solved by supplementing it with an approximate closure relation.10–13 This second approach does not involve the knowledge of an excess free energy functional, but still retains the feature that the two-body correlations are functionals of the one-body density (since the latter remains the sole input to the inhomogeneous OZ equation). Information regarding the interparticle interaction potential is contained within the closure relation.
Long experience with closures of the bulk OZ equation has lead to a selection of reliable approximations for the pair correlation functions which, if chosen wisely, can yield accurate results for a broad range of relevant interparticle interaction potentials. For example, hard or other strongly repulsive potentials can be accurately treated using closures due to Verlet,14 Martynov and Sarkisov,15 Rosenfeld and Ashcroft16 or Rogers and Young,17 whereas attractive interactions are well accounted for by the Duh–Haymet closure18,19 or, in certain cases, the powerful self-consistent Ornstein Zernike approximation (SCOZA) of Stell and coworkers.20,21 Since these references represent only the tip of the iceberg regarding the world of integral equation closures, we direct the interested reader to the classic article of Barker and Henderson22 and the more recent work of Pihlajamaa and Janssen23 for an overview and assessment of the various approximations available. In any case, it is fair to say that the number of systems which can be accurately treated in bulk using liquid-state integral equation theory well exceeds the number of systems for which we have a good approximation to the excess Helmholtz free energy functional. It is therefore of interest to investigate the possibility of generalising those closure relations to treat inhomogeneous systems.
In the present paper we choose to focus on a system of soft repulsive particles in two-dimensions, for which the excess Helmholtz free energy functional has at present no truly accurate approximation, but for which there exist a pool of accurate closure relations. We will thereby show that the new route to calculating density profiles using force–DFT presents a powerful alternative to the standard DFT scheme.
II. Theory
A. Density functional theory in a nutshell
 | (1) |
 | (2) |
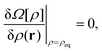 | (3) |
| ρ(r) = e−β(Vext(r)−μ−kBTc(1)(r)), | (4) |
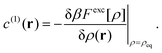 | (5) |
Substitution of the solution of (4) into (1) yields the equilibrium grand potential, and thus provides access to all thermodynamic properties of the system. It is clear that this framework is practically useful only when the excess Helmholtz free energy functional, Fexc, is known.
 | (6) |
The most effective route to generating two-body correlation functions (which are actually all functionals of the one-body density) consists of solving the inhomogeneous OZ equation,
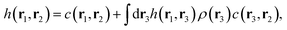 | (7) |
 | (8) |
 | (9) |
If one has access to Fexc, eqn (6)–(9) form a closed set and yield the force–DFT as introduced in ref. 8. In the special case that the excess Helmholtz free energy functional is known exactly, the one-body density profile generated by this scheme is completely equivalent to the one obtained by standard DFT, viaeqn (4) and (5). If Fexc is only known approximately then this is no longer the case. The standard DFT one-body density profiles are consistent with the thermodynamical quantities associated with the compressibility route, while the force–DFT profiles are consistent with the virial route.8
However, there is no need to know the excess Helmholtz free energy functional in order to solve the inhomogeneous OZ eqn (7). One can replace eqn (8) by a closure relation, in the spirit of liquid-state integral equation theory. It is this implementation scheme that we will use in the present work.
In principle, knowledge of both the inhomogeneous one- and two-body densities gives access to all thermodynamic quantities via integration. In that respect force–DFT is not less versatile than standard DFT. If one is interested in the internal micro-structure of the inhomogeneous fluid, then having explicit access to ρ(2) is clearly advantageous.
B. Specification of the interparticle interaction potential
In this work, we choose to focus on (two-dimensional) hard-core Yukawa particles by setting | (10) |
This type of particles are interesting because they have a hard core preventing overlaps, but are softened by a tunable repulsive Yukawa tail. The following exact relation
| g(r1,r2) ≡ h(r1,r2) + 1 = 0, r12 < d, | (11) |
C. Specification of the closure relations
Using the framework of integral equations and generalising it to inhomogeneous systems, the two-body correlation function is formally given by| g(r1,r2) = e−βϕ(r12)eγ(r1,r2)eb(r1,r2), | (12) |
| bHNC(r1,r2) = 0. | (13) |
This is equivalent to imposing
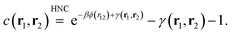 | (14) |
This approximation was originally derived in ref. 24 and 25 and is known to perform well for soft penetrable particles, but is less reliable for strongly repulsive systems.
| bPY(r1,r2) = ln(γ(r1,r2) + 1) − γ(r1,r2). | (15) |
Since g ≡ h + 1, this is equivalent to imposing
 | (16) |
For a system of purely hard particles (hard-disks in two dimensions) this reduces to the well-known relation
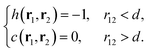 | (17) |
The first line recovers the exact condition (11), while the second line is the hard-disk PY approximation. This closure was originally proposed in ref. 26 and provides good results for strongly repulsive interparticle interactions.
 | (18) |
This is equivalent to imposing
 | (19) |
The form of the bridge function (18) was chosen by Verlet to exactly reproduce the PY virial coefficients up to fourth-order in the bulk density. The fifth- and higher-order virial coefficients predicted by eqn (18) are then found to improve considerably on the PY values. This closure relation was created in order to improve upon the PY approximation for three-dimensional hard spheres. Note that its performance for systems with attractive interactions has not yet been fully investigated.
 | (20) |
 | (21) |
D. Specification of the external fields and geometry
So far, all above mentioned equations hold for any geometry and dimensionality. However, since we wish to focus on inhomogeneous density profiles, we will impose an external field (and a dimensionality).We choose to work in two dimensions, mainly since it is less well-studied than the three-dimensional case. This is largely due to the absence of accurate approximations to the excess Helmholtz free energy functional, Fexc, which has hindered standard DFT studies but poses no difficulties for the force–DFT scheme. Also an open two-dimensional system has the appealing feature that it still conserves the ensemble independence, which would become an issue in one dimension.
We focus on a slit, i.e. particles trapped between two (soft repulsive) walls. The external field is set as follows:
 | (22) |
 , with the slit width L = 8 and the particle diameter d = 1. We fix the amplitude
, with the slit width L = 8 and the particle diameter d = 1. We fix the amplitude 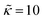 as well as the inverse decay length
as well as the inverse decay length ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) = 3. Despite having set the problem in two dimensions we are using the coordinate z. We are actually taking the natural choice of cartesian coordinates x and y, but we use the symbols x and z instead to respect the DFT community convention that usually employs the coordinate z when working in planar geometry.
= 3. Despite having set the problem in two dimensions we are using the coordinate z. We are actually taking the natural choice of cartesian coordinates x and y, but we use the symbols x and z instead to respect the DFT community convention that usually employs the coordinate z when working in planar geometry.
From the fundamental theorem of DFT1 we know that the external potential uniquely defines the so-induced one-body density profile and that they share the same geometrical symmetries. In our case, this means that the one-body density reduces to ρ(z). Since the one-body density does not vary in the x-direction, the two-body density is fully defined by z1, z2 and x12, the distance between x1 and x2. Without lose of generality, we can choose to fix the coordinate axes such that x1 = 0, as illustrated in Fig. 1. This then yields x12 = x2 and reduces the two-body density to ρ(2)(z1,x2,z2). We note that the distance between the center of particles one and two is now given by  . This is important when evaluating the pair potential (10).
. This is important when evaluating the pair potential (10).
 | ||
| Fig. 1 Sketch of the used geometry and the relevant coordinates. We study a two-dimensional slit, using cartesian coordinates, where we replace the y-coordinate by z to respect standard convention. | ||
E. Numerical implementation
The closure relations (16), (19) and (21) hold for the whole domain. However, since they naturally reduce to the exact hard-core condition (11) in the overlap-domain, we decided to explicitly treat these two cases separately as
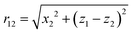 .
.
In our present case of interest, the two-dimensional planar geometry, since the density only varies with respect to the coordinate z, we can use a one-dimensional Fourier transform in the x-dimension. As shown in Appendix A, this yields the following equation:
 | (23) |
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) and
and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) are the Fourier transforms of h and c with respect to the x2-coordinate. Its equivalent form that uses
are the Fourier transforms of h and c with respect to the x2-coordinate. Its equivalent form that uses ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) instead of
instead of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) , namely
, namely | (24) |
Since the closure relation is set in real-space, the computational scheme needs an iterative back and forth Fourier transformation of the inhomogeneous two-body correlation functions, γ and c, until convergence is reached. The issue with this scheme is that discontinuous functions, such as c, are not suited to direct Fourier transformation due to the occurrence of Gibbs phenomena. This difficulty was already encountered in the three-dimensional case and is treated in Appendix C of ref. 4 in the case of hard-spheres.
For our present problem, we use a similar scheme to overcome this issue. First, as already stated, we are using the smooth function γ instead of the discontinuous function h. The discontinuous function c remains to be dealt with. The trick is to separate c into a smooth part, that presents no issue to be Fourier transformed numerically, and a ‘step-slope’ function that can be transformed analytically. When going back to real-space, the closure relation will help to reconstruct c and γ. This technique rests on the fact that Fourier transformation is a linear operation.
Practically, this scheme is implemented as follows: first we define  , the critical x2-value at which the discontinuity occurs. Following the re-written closure relation from the last subsection, we know that inside the core the two-body direct correlation function is defined as cin = −1 − γ, where γ is a smooth function. There is thus no issue to employ interpolation tools on γ and find the value and slope of c at the inner discontinuity (i.e. the inner ‘jump’ and ‘slope’), namely
, the critical x2-value at which the discontinuity occurs. Following the re-written closure relation from the last subsection, we know that inside the core the two-body direct correlation function is defined as cin = −1 − γ, where γ is a smooth function. There is thus no issue to employ interpolation tools on γ and find the value and slope of c at the inner discontinuity (i.e. the inner ‘jump’ and ‘slope’), namely
| cinjump(z1,z2) = −1 − γ(z1,xc,z2), | (25) |
 | (26) |
In contrast to the aforementioned hard-spheres problem, our soft repulsive particles have a non-vanishing c-value outside the core. The present construction is thus a little more complex than in ref. 4 where c was set to zero outside the core and therefore there was no need to define the value and slope at the outer discontinuity. In our soft case, c is defined by the closure relation (16), (19) or (21) outside the core. Since the whole aim of solving the inhomogeneous OZ equation is to determine this part of the two-body direct correlation function, we cannot use it to get the value and slope of c at the outer discontinuity. However, luckily, there is a known first approximation to c outside the core, namely cout ≈ −ϕ. This is part of the mean spherical approximation (MSA), a closure that is known to work well for attractive particles, but that simply is the linearized PY closure (16). Since both the V and MS closures reduce to the PY closure for weak interparticle interactions, using cout ≈ −ϕ in our numerical treatment of the ‘jump’ does not conflict with any of our chosen closures. This approximation, even if not that accurate, is good enough to smooth our numerical scheme. We thus use it to define the value and slope of c at the outer discontinuity, as follows
| coutjump(z1,z2) ≈ −ϕ(d) = −κ, | (27) |
 | (28) |
Finally we are able to assign the ‘step’ and (total) slope,
| cst(z1,z2) = cinjump(z1,z2) − coutjump(z1,z2), | (29) |
| csl(z1,z2) = cinsl(z1,z2) − coutsl(z1,z2), | (30) |
| f(z1,x2,z2) = cst(z1,z2) + csl(z1,z2)(x2 − xc), | (31) |
The procedure is quite straightforward and follows the same steps as in the end of Appendix C of ref. 4. The linear step-function f can be analytically Fourier transformed back and forth. Defining the smoothed out correlation function
| csmooth(z1,x2,z2) ≡ c(z1,x2,z2) − f(z1,x2,z2), | (32) |
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (z1,k,z2). On the other hand γ is a smooth function, which can be numerically Fourier-transformed to
(z1,k,z2). On the other hand γ is a smooth function, which can be numerically Fourier-transformed to ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) (z1,k,z2). Working in the Fourier-space with
(z1,k,z2). Working in the Fourier-space with ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) and
and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) on the transformed inhomogeneous OZ eqn (24) yields updated functions
on the transformed inhomogeneous OZ eqn (24) yields updated functions ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ′ and
′ and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) ′. The only quantity of interest is the latter. This can then be (mixed and) back-transformed to the real-space, where the closure relation will give back an updated c′. This scheme is to be repeated until convergence.
′. The only quantity of interest is the latter. This can then be (mixed and) back-transformed to the real-space, where the closure relation will give back an updated c′. This scheme is to be repeated until convergence.
yields
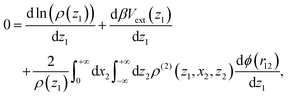 | (33) |
 and, for r12 ≥ d = 1, we have that
and, for r12 ≥ d = 1, we have that | (34) |
 | (35) |
Integration of eqn (33) from 0 to z and exponentiating then leads to
| ρ(z) = ρ0e−βVext(z)ρexp(z) | (36) |
 | (37) |
 | (38) |
 .
.
Eqn (36) is the ‘EL-like’ equation to be solved numerically (using Picard iteration) to obtain the force–DFT density profile for two-dimensional soft repulsive particles in planar geometry.
III. Results
In the following we will compare the outcomes of the (first principles) force–DFT promoted in this work with Brownian dynamics (BD) simulation data. For more details on the simulation, we refer the reader to Appendix B.In Fig. 2 we present numerical results for our chosen two-dimensional system of softened disks (10) between soft walls (22). The first column corresponds to the density profiles. Since they are mirror-symmetric about z = 0, we only show half of them. The profiles, evaluated at different average number of particles per unit length 〈N〉 = 1.40, 1.75, 2.10 and 2.45, are also shifted vertically as follows:
| ρ(z) + ρshift, | (39) |
 | ||
| Fig. 2 Force–DFT with different closures for particles with different softness. We show (half of) the density profiles for a system of soft particles between two soft walls, as given by eqn (10) and (22), respectively. Each row corresponds to a different softness of the particles, while the external potential remains fixed. The first column shows the (shifted) density profiles, ρ(z), and the second column the difference between the obtained density profiles and the simulation data, Δρ(z). The different closures used are given as dashed light orange lines for the hypernetted-chain (14), solid pink lines for Percus–Yevick (16), solid seagreen lines for Verlet (19) and dashed navy blue lines for Martynov–Sarkisov (21). The density profiles generated by Brownian dynamics simulations are given as maroon dots. | ||
The density profiles get more densely packed as we lower the α-value used in the interparticle pair potential (recall that lower values of α generate a longer range Yukawa repulsion). On the other hand, for a given ϕ, an increase of the average number of particles per unit length also yields a higher packing. Therefore, the most oscillatory density profile shown in Fig. 2 is the curve presented in panel G at 〈N〉 = 2.45 and the least oscillatory one is the curve in panel A at 〈N〉 = 1.40. Since all closures used in this work correctly reproduce the exact low-density limit, there is no surprise that the force–DFT density curves coincide for the lower density profiles shown and only become significantly different as the packing grows.
For each of the panels in Fig. 2 we increase 〈N〉 for a given value of the softness parameter, α, and observe an increase in the packing oscillations of the one-body density. In order to better appreciate the packing level of the considered systems we have performed BD simulations of the corresponding bulk systems to roughly estimate the density, ρfrb, at which a freezing transition is to be expected. As α is decreased the Yukawa tail in ϕ becomes longer ranged and thus the particles effectively take more space. This suggests that ρfrb should decrease as α is reduced. From our bulk simulations we estimate the freezing densities to be at ρfrb = 0.80, 0.775, 0.75, 0.70, corresponding to area fractions 0.63, 0.61, 0.59, 0.55, for α = 8, 6, 4, 2 and 〈N〉 = 2.45. However, since in Fig. 2 we are dealing with a highly inhomogeneous system, strongly confined between soft walls and with no flat ‘plateau’ density-value even at the center of the slit, it is hard to draw any straightforward conclusions from simulations of a bulk system. Nevertheless, our bulk freezing estimates can at least be used to give some feeling about whether the parameters we employ constitute a demanding test of the various force–DFT closures.
From the simulation density profiles we read-off the values at the center of the slit, ρ(0), and at the dominant peak close to the wall, max[ρ(z)]. We find ρ(0) = 0.385, 0.372, 0.357, 0.333 and max[ρ(z)] = 0.542, 0.57, 0.638, 0.766 for α = 8, 6, 4, 2. These values enable us to estimate that the most densely packed curves (those for 〈N〉 = 2.45) in Fig. 2 have values of ρ(0) which are 48%, 48%, 47.6%, 47.6% of the freezing density and values of max[ρ(z)] which are 67.75%, 73.55%, 85.07%, 109.43% of the freezing density, for α = 8, 6, 4, 2. Although the values of ρ(0) are all well below bulk freezing, the peak values lie very close to freezing for the smaller values of α. It is important to remember that the self-consistent solution of force–DFT requires solution of the inhomogeneous OZ equation to determine the inhomogeneous two-body correlations at all locations in the slit. In the vicinity of the main density peak, close to the wall, this clearly involves solving the OZ equation at a very high local density, comparable to, or even exceeding, in magnitude the bulk freezing density. We would thus claim that, within this spatial region, the self-consistent solution of force–DFT places considerable stress on the chosen closure relation and really tests the quality of the approximation. Since the force–DFT is a nonlocal theory, a good result for the entire density profile can only be obtained if the two-body closure is capable of handling the regions in which the density is highest. This is the ‘bottleneck’ of the whole calculation. We thus conclude that the density profiles presented for 〈N〉 = 2.45 constitute demanding state points for testing our theory and represent quite ‘highly packed’ situations, despite the fact that the density at the center of the slit is not particularly large. Given these general considerations, we will now proceed to discuss the profiles in detail.
As we can already see in panel A, for the largest α-value considered, α = 8, the density profiles with 〈N〉 = 2.10 and 2.45 generated using the PY and HNC closures differ slightly from those generated by the V or MS closures. The differences between the predictions of each approximation and the simulation data can be seen more clearly in panel B. While the V and MS closures remain very similar and agree well with the simulation data, the PY profile shows some deviations even at these moderate packings. The HNC approximation performs worst, as could be anticipated for this short range Yukawa repulsion.
Although the outcomes of the V and MS closures are almost identical in the case α = 8, they start to differ ever so slightly from each other for α = 6, as shown in panels C and D. However, they both remain in excellent agreement with the simulation data. In contrast, the PY force–DFT profile now exhibits more noticeable deviations from the simulation data. We observe that for 〈N〉 = 2.45 the PY density profile has the wrong shape: at z = 0 the curve decreases to a local minima while the V, MS and simulation profiles all show a local maxima at this location. For this value of α the HNC closure becomes quite unreliable, with somewhat phase-shifted oscillations visible for the higher packings.
For the value α = 4 the Yukawa repulsion begins to slowly change the character of the interparticle potential from hard-disk-like to a more softened interaction. The trends apparent in the profiles are generally similar to those for α = 6, but now become more pronounced as the particles effectively take more space and are thus more strongly subject to packing constraints. The force–DFT profiles calculated using the V and MS closures are in very close agreement with the simulation data, although inspection of panel E indeed reveals some small differences between the two. The PY profiles become quite inaccurate for 〈N〉 = 2.45 and the ‘shape problem’ (i.e. the prediction of an unphysical minima at z = 0) pointed out previously is exacerbated. The HNC gives a generally poor account of the simulation data, although for these strongly softened disks the predictions are not substantially worse than those of the PY theory. It thus appears that both of the ‘classic’ liquid-state closures, PY and HNC, seem to have difficulties. Overall, from inspection of panel F we can conclude that the V closure starts to emerge as the most reliable of the considered approximations.
In panels G and H we consider profiles calculated for strongly softened disks with a Yukawa parameter α = 2. This is the most demanding packing situation we will consider. At 〈N〉 = 2.45 the PY closure is in serious error and erroneously predicts strongly phase-shifted oscillations relative to the simulation data. In contrast, the HNC approximation, although still exhibiting notable errors, gives a fairly reasonable account of the general shape of the simulation density profile. The improving performance of the HNC closure, and the worsening performance of the PY closure, in moving from α = 8 to α = 2 is consistent with experience from bulk integral equation studies, for which the PY and HNC are known to perform best for strongly repulsive and softly repulsive interaction potentials, respectively. However, we note that it is not to be taken for granted that this past experience gained from the investigation of bulk pair correlations will necessarily carry over to the present situation, for which a chosen closure forms part of a self-consistent iteration scheme to determine the one-body density. Profiles from the MS closure are absent from panels G and H at 〈N〉 = 2.45, since the theory becomes unstable and we could not obtain converged solutions. This difficulty is related to an intrinsic limitation of the MS theory, namely the presence of a square root in the approximation to the bridge function, eqn (20), as we mentioned previously.
To conclude, the data presented in Fig. 2 demonstrates that the density profiles generated by the V closure are the most accurate, sitting right under the simulation data points, and stably so for the full range of parameters explored. The MS force–DFT profiles are just behind, at least for the cases where a converged solution could be obtained, with density profiles very close to those generated by the V closure. Only at high packing do the two closures show some small but visible discrepencies, with the V closure proving more accurate in all cases.
The profiles generated using the PY and HNC closures are clearly inferior to the V and MS results. As the level of softness increases the PY closure presents a decrease in quantitative accuracy and, more seriously, the shape of the curves has the tendency to become wrong at higher packing, missing the maxima at z = 0. The HNC approximation is generally the worst of the closures considered, but redeems itself as the softness becomes large (see panels G and H), where it performs far better than the PY.
One should note that our harsh assessment of the PY and HNC closures is only a consequence of the excellently accurate predictions we obtain using the MS and V approximations. When viewed in the broader context of standard DFT predictions, where profiles are often only qualitatively predicted (see e.g. ref. 6), even the PY and HNC results presented here are quite acceptable. Our recommendation for employing force–DFT to treat softened repulsive particles is to use the V closure (which is both accurate and stable) over all the others tested in this work. The numerical scheme to implement any of these closures is the exact same up to one single line of code. There is thus no reason not to choose the best.
IV. Structural inconsistency
Thermodynamic inconsistency is a difficulty which arises in bulk integral equation studies. If the bulk pair correlation functions are known, then the thermodynamic properties of the system can be calculated using one of three routes: the internal energy, the virial or the compressibility.10 Within an exact approach all three yield perfectly consistent results. However, when the pair correlation functions are only known approximately, as is usually the case when using closures of the OZ equation, then the three routes are no longer equivalent.11 Although this feature certainly complicates the application of integral equation approximations, it has been exploited as a means to optimise closure approximations by incorporating adjustable parameters which can be fixed to enforce partial consistency (see ref. 20,21 for a particularly successful example of this approach).In the present work we employ integral equation closures of the inhomogeneous OZ equation and couple this to the YBG eqn (6) to obtain a closed theory. The YBG equation provides an exact relation between ρ(2) and ρ. One can argue that using this equation is the most intuitive choice, since the YBG force-balance emerges in a very natural way when addressing problems of colloidal dynamics.28–30 The YBG is, however, not the only exact equation connecting the one-body density to the two-body correlation functions. For example, the Lovett–Mou–Buff–Wertheim (LMBW) equation,31,32 given in general by
 | (40) |
 | (41) |
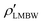 . This will then be compared with
. This will then be compared with  , the numerical derivative of the density profile obtained from our self-consistent force–DFT calculation. Results are shown in Fig. 3. The numerical derivative of the converged density profile (as given in Fig. 2),
, the numerical derivative of the density profile obtained from our self-consistent force–DFT calculation. Results are shown in Fig. 3. The numerical derivative of the converged density profile (as given in Fig. 2),  , is shown as a solid line colored differently according to the used closure, namely light orange for the hypernetted-chain (14), pink for Percus–Yevick (16), navy blue for Martynov–Sarkisov (21) and seagreen for Verlet (19). For each case, the corresponding
, is shown as a solid line colored differently according to the used closure, namely light orange for the hypernetted-chain (14), pink for Percus–Yevick (16), navy blue for Martynov–Sarkisov (21) and seagreen for Verlet (19). For each case, the corresponding  is given by the dashed olive green curve. As a reference, the numerical derivative of the simulation data density profile (also given in Fig. 2) is shown as maroon dots. Each column in Fig. 3 tests a different particle softness, by varying the α-value in the interaction potential (10). There is one row of panels per closure relation.
is given by the dashed olive green curve. As a reference, the numerical derivative of the simulation data density profile (also given in Fig. 2) is shown as maroon dots. Each column in Fig. 3 tests a different particle softness, by varying the α-value in the interaction potential (10). There is one row of panels per closure relation.
 | ||
| Fig. 3 Structural inconsistency. For each panel, taking the corresponding density profile obtained via force–DFT (Fig. 2) and putting it and its, also shown, numerical derivative (solid colored line – light orange, pink, navy blue and seagreen, depending on the applied closure) into the right-hand side of the planar LMBW eqn (41) yields the dashed olive green curve. The discrepency between those two latter curves is a test of the structural inconsistency. The numerical derivative of the simulation data density profile (Fig. 2) is also given as maroon dots, as a reference. Each column represents another type of particle softness, by varying the α-value in the interaction potential (10), while each row gives results for the same closure relation, namely the hypernetted-chain (14), Percus–Yevick (16), Martynov–Sarkisov (21) and Verlet (19). | ||
Let us begin by considering the least demanding situation, namely α = 8 and 〈N〉 = 1.40, and following down the first column of panels to compare the predictions of the various closure relations. Unsurprisingly, the HNC approximation already shows notable structural inconsistency. The PY closure improves upon this, but is still inferior to the results from the MS and V closures, which are almost perfectly self-consistent. The second column shows results for α = 4 and 〈N〉 = 2.45. Here we can see clearly the failings of both the HNC and PY closures, due to the high density but intermediate particle softness. It is interesting to note that the numerical derivative of the self-consistent force–DFT density profile,  , agrees quite well in both cases with the simulation data, whereas the output
, agrees quite well in both cases with the simulation data, whereas the output  deviates significantly from them, albeit in opposite directions. The result for
deviates significantly from them, albeit in opposite directions. The result for 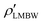 in panel E overestimates the force–DFT prediction, while the one in panel F underestimates it. Finally, results for α = 2 and 〈N〉 = 2.10 (which is the highest packing for which the MS scheme still has a solution) are shown in the last column of Fig. 3. At this higher particle softness the HNC closure gives better results than the PY, for which we observe in panel J a very poor level of structural inconsistency with
in panel E overestimates the force–DFT prediction, while the one in panel F underestimates it. Finally, results for α = 2 and 〈N〉 = 2.10 (which is the highest packing for which the MS scheme still has a solution) are shown in the last column of Fig. 3. At this higher particle softness the HNC closure gives better results than the PY, for which we observe in panel J a very poor level of structural inconsistency with  greatly undershooting both the force–DFT and BD predictions. The HNC result for
greatly undershooting both the force–DFT and BD predictions. The HNC result for  shown in panel I still overshoots, but is considerably better than in the case α = 4 and 〈N〉 = 2.45 (panel E). The level of structural inconsistency from the HNC is now comparable to that of the MS closure, given in panel K. The best closure relation, generating the least amount of structural inconsistency is clearly the V approximation.
shown in panel I still overshoots, but is considerably better than in the case α = 4 and 〈N〉 = 2.45 (panel E). The level of structural inconsistency from the HNC is now comparable to that of the MS closure, given in panel K. The best closure relation, generating the least amount of structural inconsistency is clearly the V approximation.
We observe that all results for 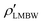 underestimate the force–DFT and BD simulation results, with the exception of those obtained using the HNC approximation. This may reflect the differing types of system for which these closures were intended. The PY, MS and V were targeted at treating hard particles, while the HNC was focused rather on soft penetrable ones. The trends of the inconsistency appear to be linked to this fundamental difference.
underestimate the force–DFT and BD simulation results, with the exception of those obtained using the HNC approximation. This may reflect the differing types of system for which these closures were intended. The PY, MS and V were targeted at treating hard particles, while the HNC was focused rather on soft penetrable ones. The trends of the inconsistency appear to be linked to this fundamental difference.
In this work we have chosen to focus on purely repulsive interactions for which the only phase transition is freezing and we have chosen parameters so as to stay below this value. For such systems we have shown that the best closures (MS and V) exhibit a quite acceptable level of structural inconsistency, which provides a reassuring quality check. However, it is well-known that thermodynamic (and, thus, surely structural) inconsistency will play a more important role for systems exhibiting a liquid-vapour phase transition. In such cases much care in both implementation and interpretation is required. For most closures there exist unphysical ‘no-solutions’ regions of the thermodynamic parameter space which are closely associated with the existence of spinodal lines and which often prevent integral equation theories being applied for the determination of the phase diagram.33 For these reasons we defer to future work the delicate analysis of the force–DFT and structural inconsistency for attractive systems.
V. Discussion
In this paper we have applied force–DFT to calculate the one-body density in (two-dimensional) planar geometry. By generalizing known bulk closures to solve the inhomogeneous OZ equation and coupling this with the exact YBG equation we have shown that this alternative route to force–DFT can provide a robust and accurate method for predicting the one-body density profile from first principles. For the model interaction potential considered here the absence of a good quality approximation to the Helmholtz free energy functional would not permit results of such high precision to be obtained using the traditional implementation of DFT.The versatility of force–DFT lies in its ability to exploit the large body of existing knowledge on closures of the bulk OZ equation, many of which have been assessed and well documented in a recent article by Pihlajamaa and Janssen.23 In contrast, reports in the literature concerning use of generalized closures of the inhomogeneous OZ equation are quite rare and limited almost entirely to studies of three-dimensional hard-spheres using the PY approximation,4,34–36 although there are exceptions (see for example ref. 37 and 38). The investigation of generalized closures within force–DFT thus provides great opportunities for future studies of inhomogeneous fluids and offers the potential to accurately calculate density profiles from first principles in cases where standard (free energy-based) DFT approximations can only make predictions of qualitative accuracy. In short, inhomogeneous OZ closures are powerful, but often overlooked, non-perturbative approximations which can be usefully applied to many problems of interest.
One may well ask why such integral equation closures, which were developed to treat bulk systems, are equally applicable to closing the inhomogeneous OZ equation, and thus the force–DFT. The explanation can be found in the origin of these approximations as diagrammatic cluster expansions.10,39,40 Many of the familiar integral equation closures, such as the Percus–Yevick, hyper-netted-chain etc., can be derived as partial resummations of Mayer cluster expansions to yield closed form expressions.41 The form of the diagrammatic expansions remains the same in the inhomogeneous case as in bulk; factors of ρb associated with integration field points in bulk systems are simply replaced by factors of ρ(r) in the inhomogeneous case. This correspondence means that any resummation scheme employed in bulk will be of equal validity in the presence of spatial inhomogeneity. Closures developed to treat the bulk might therefore be expected to work just as well for closure of the inhomogeneous OZ equation. The results shown in Fig. 2 certainly support this expectation.
Of the four approximations considered, the Verlet closure was found to produce the best results when compared with BD simulation data. In bulk, Verlet found that when applied to three-dimensional hard-spheres the closure (19) produced radial distribution functions which yielded a high level of consistency for the equation of state when comparing the pressure obtained via the virial and compressibility routes (roughly on the 1% level over the entire range of bulk density up to crystallization).14 Given these findings it is perhaps not surprising, although certainly gratifying, to find that application of the inhomogeneous Verlet approximation to close the force–DFT yields density profiles in excellent agreement with simulation data. However, it is important to point out that it is not obvious that residual errors in the two-body Verlet closure would not become amplified as a consequence of coupling to the one-body density via the YBG relation. That this is not the case speaks for the stability of the force–DFT scheme.
In his paper on integral equation closures in which the bulk version of eqn (19) was introduced, Verlet also proposed a slightly modified approximation, incorporating an adjustable parameter. For given values of the bulk density and temperature the value of this parameter is adjusted to enforce perfect virial-compressibility consistency on the pressure. This raises the question of whether it could be possible to generalize the Verlet-modified closure to the inhomogeneous case by replacing the adjustable parameter with a spatially dependent function, which could then be uniquely determined by generalized consistency requirements on the inhomogeneous one- and two-body density. Similar considerations could be applied to inhomogeneous generalizations of other ‘thermodynamically consistent’ bulk closures, such as the well-known Rogers-Young approximation.17 In Fig. 3 we examined the structural inconsistency of the various closures considered in this work. Although the original version of the Verlet closure proved impressively consistent, there is still clearly room for optimisation.
In the present work we have focused on (two-dimensional) planar geometry, however the use of generalized integral equation closures within force–DFT would also be of great interest when applied to (three-dimensional) spherical or (two-dimensional) polar geometries. This would allow for ‘test particle’ calculations in which the external potential is simply a fluid particle fixed at the coordinate origin. The bulk radial distribution function g(r) can then be obtained from the inhomogeneous (radially symmetric) one-body density by using the Percus identity, g(r) = ρ(r)/ρb. With this method any given closure of the bulk OZ equation can be automatically upgraded in accuracy: the inhomogeneous generalization of the closure is used within the force–DFT scheme to obtain the radial density profile and, thus, a new and improved estimate for g(r). For example, we anticipate that applying the Verlet closure (19) to force–DFT for three-dimensional hard-spheres would produce bulk radial distribution functions (and thus pressures) from the test particle method which are more accurate than those reported in ref. 14, where the closure was directly applied to the bulk OZ equation.
Finally, despite the many appealing features of force–DFT, the absence of a free energy functional is a disadvantage when attempting to study phase transitions. The spectre of thermodynamic inconsistency, familiar from bulk liquid-state integral equations, would undoubtedly rise once more via structural inconsistency when applying generalized closures to the inhomogeneous OZ equation. Finding ways to deal with such issues within force–DFT remains a topic for future study.
Data availability
The present work concerns the development and implementation of a first-principles theory for describing the structure of inhomogeneous soft matter systems. No data sets or pre-made software packages were employed and the outputs of this work are solely the equations themselves and their numerical solution, as described in the manuscript.Conflicts of interest
There are no conflicts to declare.Appendices
A: Derivation of the Fourier-transformed OZ equation
We start by rewriting the general form of the inhomogeneous OZ eqn (7) for our specific geometry, namely the two-dimensional planar case as illustrated in Fig. 1. This yields | (A1) |
Since x32 = x2 − x3 and  , it reduces to
, it reduces to
Plugging this last expression into the OZ eqn (A1) and then applying a Fourier transform on the x2-coordinate yields
Using once more that  , we recover eqn (23) in the main text.
, we recover eqn (23) in the main text.
B: Brownian dynamics simulations
The simulations for the density profiles of disks confined between walls were performed in the canonical ensemble using the LAMMPS package42 and a two-dimensional simulation box of size Lx × Lz = 100 × 11d2, with periodic boundaries along the x-axis. The pairwise interactions between particles are modeled via a pseudo-hard-disk potential, which provides a continuous approximation to the idealized hard-disk interaction,43 plus an additional repulsive Yukawa potential, as given by eqn (10). Each system is equilibrated for 107 integration time steps, followed by a production run of 2 × 108 steps. The particle positions are recorded every 5 × 103 steps.Note that, the channel width has been changed from 8d (as used in force–DFT) to 11d, since in simulations, a hard wall cannot be defined at a specific point. Instead, we set harmonic walls with thickness of 1.5 such that particles at z = −4 and 4 see a potential similar to a hard wall. Particles are not able to pass positions z = −3.5 and 3.5 and the density is always zero at z = −4 and 4.
To determine the bulk freezing density, we performed BD simulations for hard disks in a two-dimensional simulation box of the same size as used previously, but with periodic boundary conditions applied along both axes. Other computational details remain consistent with those used for disks confined between walls, except that no walls are present and the external potential, Vext, is absent. As the bulk density of disks increases, the first peak of the radial distribution function, g(r12), shifts towards smaller disk–disk separation distances, r12, while its height decreases. As the bulk density is increased beyond the freezing density the peak position no longer moves, but instead its height increases. We identify this threshold as the freezing density of the bulk system, ρfrb.
References
- R. Evans, Adv. Phys., 1979, 28, 143 CrossRef CAS.
- R. Evans, Fundamentals of Inhomogeneous Fluids, ed., D. Henderson, Marcel Dekker, New York, 1992, ch. 3 Search PubMed.
- R. Roth, J. Phys.:Condens. Matter, 2010, 22, 063102 CrossRef PubMed.
- S. M. Tschopp, H. D. Vuijk, A. Sharma and J. M. Brader, Phys. Rev. E, 2020, 102, 042140 CrossRef CAS PubMed.
- S. M. Tschopp and J. M. Brader, Phys. Rev. E, 2021, 103, 042103 CrossRef CAS PubMed.
- A. Archer, B. Chacko and R. Evans, J. Chem. Phys., 2017, 147, 034501 CrossRef PubMed.
- Y. Rosenfeld, J. Chem. Phys., 1993, 98, 8126 CrossRef CAS.
- S. M. Tschopp, F. Sammüller, S. Hermann, M. Schmidt and J. M. Brader, Phys. Rev. E, 2022, 106, 014115 CrossRef CAS PubMed.
- J. S. Rowlinson and B. Widom, Molecular Theory of Capillarity, Dover, New York, 2003 Search PubMed.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier Science, Amsterdam, 2006 Search PubMed.
- C. Caccamo, Phys. Rep., 1996, 274, 1 CrossRef CAS.
- M. Bomont, Adv. Chem. Phys., 2008, 13, 1 Search PubMed.
- A. Santos, A concise course on the theory of classical liquids, Lecture Notes in Physics, Springer, Heidelberg, 2016 Search PubMed.
- L. Verlet, Mol. Phys., 1980, 41, 183 CrossRef CAS.
- G. Martynov and G. Sarkisov, Mol. Phys., 1983, 49, 1495 CrossRef CAS.
- Y. Rosenfeld and N. W. Ashcroft, Phys. Rev. A:At., Mol., Opt. Phys., 1979, 20, 1208 CrossRef CAS.
- F. J. Rogers and D. A. Young, Phys. Rev. A:At., Mol., Opt. Phys., 1984, 30, 999 CrossRef CAS.
- D. Duh and A. D. J. Haymet, J. Chem. Phys., 1995, 103, 2625 CrossRef CAS.
- D. Duh and D. Henderson, J. Chem. Phys., 1996, 104, 6742 CrossRef CAS.
- D. Pini, G. Stell and J. Høye, Int. J. Thermophys., 1998, 19, 1029 CrossRef CAS.
- D. Pini, G. Stell and N. Wilding, Mol. Phys., 1998, 95, 483 CrossRef CAS.
- J. A. Barker and D. Henderson, Rev. Mod. Phys., 1976, 48, 587 CrossRef CAS.
- I. Pihlajamaa and L. M. C. Janssen, Phys. Rev. E, 2024, 110, 044608 CrossRef CAS PubMed.
- J. van Leeuwen, J. Groeneveld and J. de Boer, Mol. Phys., 1959, 25, 792 Search PubMed.
- T. Morita and K. Hiroike, Prog. Theor. Phys., 1960, 23, 1003 CrossRef.
- J. K. Percus and G. J. Yevick, Phys. Rev., 1958, 110, 1 CrossRef CAS.
- F. Lado, J. Comput. Phys., 1971, 8, 417 CrossRef.
- S. M. Tschopp and J. M. Brader, J. Chem. Phys., 2022, 157, 234108 CrossRef CAS PubMed.
- S. M. Tschopp, H. D. Vuijk and J. M. Brader, J. Chem. Phys., 2023, 158, 234904 CrossRef CAS PubMed.
- S. M. Tschopp and J. M. Brader, J. Chem. Phys., 2024, 160, 214124 CrossRef CAS PubMed.
- R. Lovett, C. Y. Mou and F. P. Buff, J. Chem. Phys., 1976, 65, 570 CrossRef CAS.
- M. S. Wertheim, J. Chem. Phys., 1976, 65, 2377 CrossRef CAS.
- J. Brader, Int. J. Thermophys., 2006, 27, 394 CrossRef CAS.
- P. Attard, J. Chem. Phys., 1989, 91, 3072 CrossRef CAS.
- K. Nygård, S. Sarman and R. Kjellander, J. Chem. Phys., 2013, 139, 164701 CrossRef PubMed.
- K. Nygård, et al. , Phys. Rev. X, 2016, 6, 011014 Search PubMed.
- J. M. Brader, J. Chem. Phys., 2008, 128, 104503 CrossRef PubMed.
- I. Omelyan, F. Hirata and A. Kovalenko, Phys. Chem. Chem. Phys., 2005, 7, 4132 RSC.
- G. Stell, The Equilibrium Theory of Classical Fluids, ed. H. L. Frisch and J. L. Lebowitz, New York, 1992, ch. 3 Search PubMed.
- P. Attard, Thermodynamics and Statistical Mechanics, Academic Press, Amsterdam, 2002 Search PubMed.
- D. A. McQuarrie, Statistical Mechanics, University Science Books, California, 2000 Search PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. Jover, A. Haslam, A. Galindo, G. Jackson and E. Müller, J. Chem. Phys., 2012, 137, 14 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2025 |