Open Access Article
Open Access ArticleGenerative organic electronic molecular design informed by quantum chemistry†
Cheng-Han
Li
 and
Daniel P.
Tabor
and
Daniel P.
Tabor
 *
*
Department of Chemistry, Texas A&M University, College Station, TX 77842, USA. E-mail: daniel_tabor@tamu.edu
First published on 13th September 2023
Abstract
Generative molecular design strategies have emerged as promising alternatives to trial-and-error approaches for exploring and optimizing within large chemical spaces. To date, generative models with reinforcement learning approaches have frequently used low-cost methods to evaluate the quality of the generated molecules, enabling many loops through the generative model. However, for functional molecular materials tasks, such low-cost methods are either not available or would require the generation of large amounts of training data to train surrogate machine learning models. In this work, we develop a framework that connects the REINVENT reinforcement learning framework with excited state quantum chemistry calculations to discover molecules with specified molecular excited state energy levels, specifically molecules with excited state landscapes that would serve as promising singlet fission or triplet–triplet annihilation materials. We employ a two-step curriculum strategy to first find a set of diverse promising molecules, then demonstrate the framework's ability to exploit a more focused chemical space with anthracene derivatives. Under this protocol, we show that the framework can find desired molecules and improve Pareto fronts for targeted properties versus synthesizability. Moreover, we are able to find several different design principles used by chemists for the design of singlet fission and triplet–triplet annihilation molecules.
1 Introduction
Machine learning (ML) methods have emerged as promising tools for accelerating functional materials discovery.1–6 There are two common ways that ML methods are leveraged in molecular design tasks. The first involves using discriminative machine learning models to speed up property prediction tasks, which allows for higher-throughput traversal of targeted chemical libraries. ML models can be trained on existing data to build quantitative structure–property relationship models. These predictions are often sufficiently fast, accurate, and transferable to justify the upfront cost of training the models.6–9 The second way expedites the design process is by using ML methods to select the optimal molecules and materials to simulate (or synthesize). That is, ML is used, either with generative models or optimization methods, to inversely design materials or molecules with specified properties.1–3,10–13The strength of generative models lies in their capability to generate new samples by capturing the underlying patterns from training data.2,3 This approach offers advantages over traditional trial-and-error efforts, as generative models enable efficient search through the multidimensional parameter space with the balance between exploration and exploitation.2,13,14 Through this process, generative models have the potential to discover novel molecules that may not have been previously considered and provide new insights into materials design rules.
In the computational drug discovery community, generative models have received increasing attention due to their advantages over library-based approaches.15,16 From a certain perspective, fragment-based library approaches intrinsically bias the search space, whereas generative models enable searching over broader, more diverse chemical spaces. However, these virtual drug design studies have largely focused on using property prediction tasks that are extremely fast (from a computational perspective) to calculate.17 These cheminformatics-based properties can be, for the purposes of this paper, instantly calculated (e.g., Crippen's log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P18 (solubility estimation through atom-based contributions) and quantitative estimate of drug-likeness (QED)19). In functional materials design, especially for electrochemical or photophysical applications, one cannot solely rely on informatics-based properties.20–23 Instead, quantum chemistry calculations (e.g., semi-empirical methods or density functional theory (DFT)-based calculations) are needed to evaluate the fitness of a given material.
P18 (solubility estimation through atom-based contributions) and quantitative estimate of drug-likeness (QED)19). In functional materials design, especially for electrochemical or photophysical applications, one cannot solely rely on informatics-based properties.20–23 Instead, quantum chemistry calculations (e.g., semi-empirical methods or density functional theory (DFT)-based calculations) are needed to evaluate the fitness of a given material.
Therefore, the sample efficiency of the generative models is important, as it indicates the minimal number of quantum chemistry calculations needed for discovering optimal molecules. Recent studies have examined a series of molecular optimization methods involving combinations of different molecular assembly strategies and optimization algorithms.24,25 The SMILES-based REINVENT scheme, which is the generative model we build upon in this work, remains one of the top-performing methods across all metrics, considering optimization ability and sample efficiency. Usually, a few hundred iterations (64 or 128 molecules sampled per iteration) were involved in applications of REINVENT for drug discovery.26–28 We note that autoencoders have been employed for active search in model studies for searching for specified electronic properties (through iterative retraining of the autoencoder),29 but these methods, if applied with DFT methods as a property predictor, would require hundreds of thousands DFT calculations, or an appropriate surrogate method to estimate their properties. Surrogate models have been employed as electronic property predictors for organic electronic materials discovery tasks using the REINVENT workflow. Marques et al.21 trained reorganization energy predictors based on their previous DFT calculations for a quarter million heteroacenes. Kwak et al.22 trained a glass transition temperature predictor on experimental data, and HOMO/LUMO energy and hole reorganization energy predictors on low-level DFT calculations for selected molecules from an initial library of molecules to train the prior and agent networks for REINVENT.
However, it is often required to pay additional upfront costs to train surrogate models on functional materials discovery projects.1,6,7,11 Additionally, the trained surrogate models risk transferability to molecules out of the training domains,30 which can potentially hamper the power of generative models to explore chemical space. For electrochemical applications, St. John and co-workers23 developed a reinforcement learning framework based on AlphaZero (a system designed by DeepMind to master Chess, Shogi, and Go) to generate organic radical molecules for aqueous redox-flow batteries, considering the task of goal-oriented graph-based molecule generation as a game. They used two ML surrogate models for optimizing radical stability and redox potential. For their optimized organic radicals from the reinforcement learning process, post hoc DFT validation and retrosynthetic analysis are required to yield the final candidates.
To address the challenges of designing organic optoelectronic materials that lack low-cost transferable ML models for the requisite property prediction, we developed a new protocol to incorporate high-throughput excited state electronic structure calculations with the REINVENT workflow. The major advantages of directly using quantum chemistry methods to calculate properties are increased accuracy and transferability. Here, we employ reinforcement learning to find organic molecules with specified electronic properties with our proposed protocol, focusing on leads for singlet fission (SF) and triplet–triplet annihilation (TTA). Both SF and TTA molecular design face challenges due to the complex mechanism of the SF/TTA processes involving electronic transitions, resulting in a lower diversity of candidate molecules.31–34 This molecular design problem offers unique challenges due to the interplay of structure–property relationships of the singlet and triplet energy levels when compared to other molecular property objectives such as redox properties. Thus, we see this problem as a significant molecular design opportunity for ML methods.
The aim of this paper is to showcase the potential of reinforcement learning protocols to explore and exploit uncharted regions of chemical space to discover potential candidates in different functional materials discovery tasks. In the initial exploratory phase, we demonstrate the power of the framework to generate novel molecules that were previously unknown, which allows us to identify a broad range of molecular scaffolds. Subsequently, we employ REINVENT in a more focused manner, targeting a chemical space containing anthracene-containing molecules. Deploying the framework in this context enabled us to optimize further the molecular scaffolds discovered in the exploratory phase and exploit their potential for use in SF/TTA applications without employing brute-force combinatorial screening procedures.
Recent advances for searching SF/TTA molecules mostly focus on strategies for fine-tuning the excited-state energies to make SF/TTA processes thermodynamically more favorable.31,32 Notably, systematic investigations have been conducted to identify potential singlet fission molecules, involving the exploration of various approaches to modify diradical characters or enhance aromaticity to achieve energy-matching conditions.35,36 These same design rules should also be applicable to TTA molecules. Consequently, we examine the REINVENT-generated SF and TTA molecules and compare them with these established design rules.
2 Computational methods
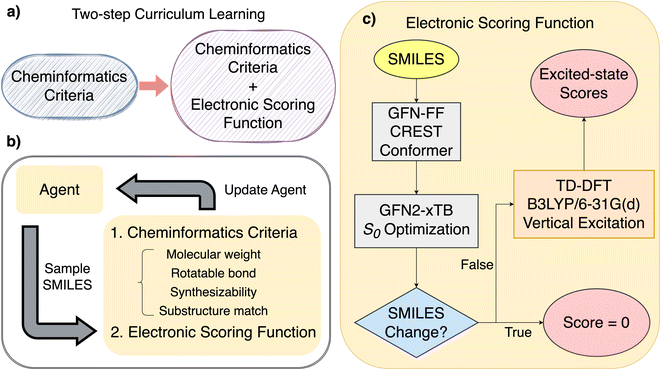
Here, we first describe the details of our implementation of the REINVENT reinforcement learning scheme as applied to organic electronic materials. Second, we discuss the methods that we use to evaluate scores of molecules generated at each iteration of the REINVENT workflow. Both cheminformatics methods and quantum chemistry are used in the scoring evaluation step and are fully integrated into the workflow.2.1 Reinforcement learning toward promising SF and TTA molecules with REINVENT
We implemented REINVENT 3.2,37 a reinforcement learning framework,12,13 which optimizes a SMILES-based, recurrent neural network (RNN) agent to generate novel molecules with targeted properties. The basics of the REINVENT algorithm consist of four parts, a prior network, an agent network, reinforcement learning loops, and scoring functions. Initially, a sequence-generating recurrent neural network is trained on the SMILES representation of over a million molecules from the ChEMBL database38 to generate SMILES strings. To start each reinforcement learning loop, a second RNN capable of SMILES generation is initialized with the trained prior network as the agent network (unless stated otherwise). In each iteration of the reinforcement learning loop, molecules are sampled from the agent network as SMILES strings and scored according to user-defined scoring functions. The agent network is then optimized to generate molecules with desired properties according to the augmented likelihood. The augmented likelihood combines scored values and prior likelihood. More details are provided in Section S2.† This prevents the agent network deviating from the prior network while learning to generate new molecules with higher scores. The property targets are achieved through defining scoring functions, which are, in general, on the continuous interval [0,1]. The agent network is rewarded when the total score is close to one and penalized when the score is closer to zero. Functionally, we take the geometric mean of each score so the total score remains between 0 and 1.To enable REINVENT to learn the complex structure–property relationship for finding ideal SF and TTA molecules, we used a two-step curriculum learning strategy26 as shown in Fig. 1 to train an agent network first on easier objectives and then later on more challenging objectives. In the first step of the curriculum learning strategy, we limited the available chemical space of the agent network such that it is only allowed to generate small and rigid organic molecules, due to these molecules being more likely to be suitable for SF and TTA materials. At this step, the total scoring function (which is derived from the following cheminformatics-calculated properties) is found, with each property resulting in an individual subscore of zero or one:
(1) Molecular weight <400 Dalton
(2) No consecutive rotatable bonds exist
(3) Synthesizability (SCScore39 ≤4)
(4) No matches with a list of forbidden substructures
In this first stage, the total score function is discrete, resulting in a total score of one if all of the criteria are satisfied and zero if any are not satisfied.
It has been shown that goal-directed generation methods are prone to generate unsynthesizable molecules with high scores.40,41 Here, we used the SCScore model developed by Coley et al.39 to assign synthetic complexity score between 1 and 5 to molecules sampled from the agent network, where a higher SCScore corresponds to higher synthetic complexity. Though all synthetic accessibility scoring functions will be influenced by biases that exist in published chemical reactions, the SCScore model is trained on ca. 12 million reactions from the Reaxys database with the assumption that the products from published reaction data should be synthetically more complex than corresponding reactants. Thus, we determined the highest-allowed SCScore during the first step after comparing between SCScore for molecules sampled from REINVENT and the calibration set for the time-dependent DFT (TD-DFT) benchmark in Fig. S1.†
Without synthesizability constraints, a significantly large number of molecules saturate the highest (most complex) SCScore (Fig. S2†). Since we are only interested in small molecules (molecular weight < 400 Dalton) and eventually the generated molecules need to be solved by retrosynthetic planning tools within three steps (Section 2.2), using SCScore is used as a first-step screening criterion before running excited-state calculations.
In addition, we added a list of forbidden substructures (partially motivated by initial substructures generated in our first implementations of the workflow) that are known to be unstable (e.g., unrealistic aromatic or anti-aromatic substructures). If the agent network generates any structures from this forbidden substructure list, it is penalized. The forbidden substructures are given in our implementation on the GitHub repository and in Section S2.† In the exploitative case, the agent network is also be penalized if it fails to generate molecules with the specified substructure. After learning in the first step, the resulting agent network becomes the starting agent network for the second step.
The total scoring function in the second step of the curriculum learning strategy includes excited-state energy gaps in addition to the cheminformatics criteria shown above. The design of scoring functions for excited-state energy gaps are based on evaluating
| |E(S1) − 2E(T1)| ≥0.5 eV | (1) |
| E(T2) − 2E(T1) ≥ −0.3 eV | (2) |
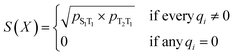 | (3) |
To ensure the diversity of the potential SF/TTA molecules generated at the second step, we used the carbon skeleton diversity filter from the work by Blaschke et al.42 The diversity filter keeps track of the number of sampled molecules with the same carbon skeleton derived from the Bemis–Murcko scaffold43 in the same bucket. The diversity filter starts penalizing molecules with the same carbon skeleton once the bucket for that specific carbon skeleton is full. Inception13 was allowed during the reinforcement learning process, which is an experience replay that can accelerate the learning in the early phase by replaying previous top-scoring sampled molecules to the agent network.
Further implementation details including hyperparameters of the workflow, as tailored for this materials design project, are provided in ESI,† Section S2.
2.2 Synthetic accessibility evaluation with a retrosynthetic planning tool
To sample the chemical space more efficiently, we apply AiZynthFinder,44 a retrosynthetic planning tool to bias the generative model during the second step of the reinforcement learning process with excited-state energy gaps as the objectives. AiZynthFinder utilizes Monte-Carlo tree search to break down a molecule toward purchasable stock molecules with recursion. A molecule is considered “solved” if any one of the reaction routes found by the tree search leads to precursors that are all “in stock”. A policy neural network trained on reaction templates guides the tree search with the probability of each template. Here, we used the policy trained on the US patent office data (USPTO) set,45 reaction templates from the USPTO data, and stock molecules created from ZINC46 database, provided from the original study of AiZynthFinder. We ran the retrosynthetic planning algorithm for each sampled molecule that passed the cheminformatics criteria. The total score for a sampled molecule would become zero and skip the TD-DFT calculation if it could not be solved within 3 steps.2.3 Excited-state methods for electronic scoring functions
To calculate the singlet and triplet energies needed for the evaluation of the scoring function derived from eqn (1) and (2), we implemented a workflow to compute these quantities taking in the SMILES as input, as has been implemented in several library-based high-throughput screening studies.47–50First, we utilized Open Babel 3.1.0 (ref. 51) to generate initial geometries from SMILES strings, which were then subjected to quick conformer searches using CREST 2.1.1 (ref. 52) interfaced with xTB 6.5.1 (ref. 53) to identify the lowest-energy conformers at the GFN-FF level of theory. The resulting geometries were converted back to SMILES strings using Open Babel 3.1.0 and compared with the initial SMILES strings to exclude chemically unstable molecules. The lowest-energy conformers were then optimized at the ground state, followed by TD-DFT calculations to determine the excited-state energies. Ground-state optimizations at the GFN2-xTB level of theory were conducted using xTB 6.5.1, while ground-state optimizations at the PBEh-3c level of theory and all TD-DFT calculations were performed using Q-Chem 5.4.54 The ALPB implicit solvent model was used with xTB 6.5.1, while IEFPCM was used with TD-DFT calculations.
3 Results and discussion
First, we discuss the quantum chemistry results to determine (both semi-empirical and DFT-based) the suitable excited-state method for the REINVENT workflow. Next, we show how REINVENT performs in exploring diverse and promising SF/TTA scaffolds. This was done by analyzing the progression of the optimization curves, the excited-state energy distribution of the sampled molecules, and Pareto front plots between the excited-state scores and SCScore. The Pareto front is defined as the front where one cannot improve either excited-state scores or SCScore without sacrificing the other. We then transition REINVENT into exploitative mode to optimize anthracene derivatives as SF/TTA molecules and examined the results similarly to the exploratory study. We scrutinize the highest-scoring molecules from both studies and infer design rules for SF/TTA molecules from the molecules generated by the framework.3.1 Benchmark results for excited-state methods
In order to strike a balance between accuracy and computational efficiency, we conducted a benchmark study for vertical TD-DFT methods with the Tamm-Dancoff approximation (TDA) that involved three factors (ground state optimization method, level of theory for TD-DFT calculations, and implicit solvent environment), resulting in eight choices. For the ground state optimization method, the choices were PBEh-3c or GFN2-xTB.55,56 The levels of theory tested for TD-DFT calculations were B3LYP/6-31G(d) and ωB97X-D/def2-SV(P). The tested implicit “solvents” were implicit toluene or vacuum. For each vertical TD-DFT method, we made a linear calibration model against experimental S1 and T1 energies.6,31,57 After calibrations against experimental data, we decided to use vertical TD-DFT/B3LYP/6-31G(d) calculation on the GFN2-xTB ground-state optimized geometry in vacuum, which has the lowest mean absolute error in both S1 and T1 energies and is computationally efficient compared to some of the other protocols considered.3.2 Exploratory generative design to hunt for high-value scaffolds
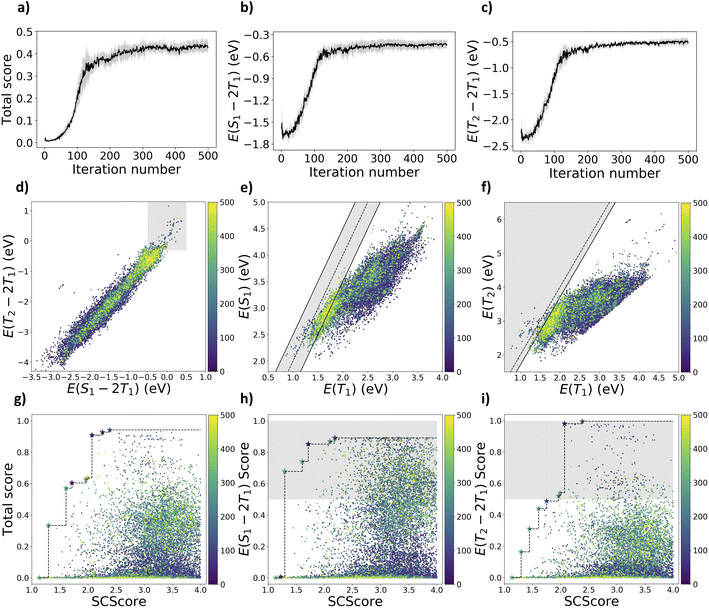
We started the first-step curriculum learning by using cheminformatics criteria mentioned in the computational methods Section 2.1 as the scoring functions. This allows us to break the problem down into multiple objectives for sequential learning. The agent network can learn to sample molecules that meet cheminformatics criteria first. Later, computationally intensive excited-state energy criteria are incorporated in the second step.This provided the agent network with an understanding of valid SMILES syntax, increasing the percentage of synthesizable molecules generated. To prevent overfitting, we extracted the agent network from the 200th iteration in the first-step learning as the starting point for the second step. We repeated the second step of curriculum learning five times, optimization curves are shown in Fig. 2a–c with the mean values as solid lines and standard deviations as the shaded region. The total score converged before it reached 0.5, which is the lowest total score for molecules to meet both S1/T1 and T2/T1 criteria (|E(S1) − 2E(T1)| ≥ 0.5 eV and E(T2) − 2E(T1) ≥ −0.3 eV).
However, there are still 222 molecules satisfying both the excited-state energy criteria in Fig. 2d. It is harder to meet the T2/T1 criterion as there are fewer molecules satisfying the T2/T1 criterion (260) compared to the number of molecules satisfying the S1/T1 criterion (2147). By examining the distribution of molecules on either side of the dashed line under the shaded area in Fig. 2e, there are more potential SF molecules than TTA molecules among those that meet the S1/T1 criterion. This is due to the fact that molecules generally have E(S1) lower than twice E(T1) without specific molecular engineering. The agent network could be guided toward generating potential SF/TTA molecules as molecules sampled from the later iterations are closer to the targeted region in Fig. 2d. For the Pareto plots in Fig. 2g–i, molecules sampled from later iterations generally have higher scores but less synthetic accessibility (higher SCScore). However, the Pareto front can still improve in later iterations, as indicated by some of the pieces of the Pareto front discovered at later iterations.
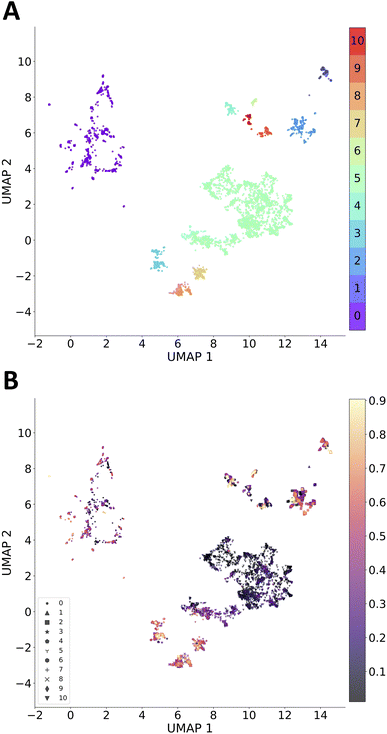
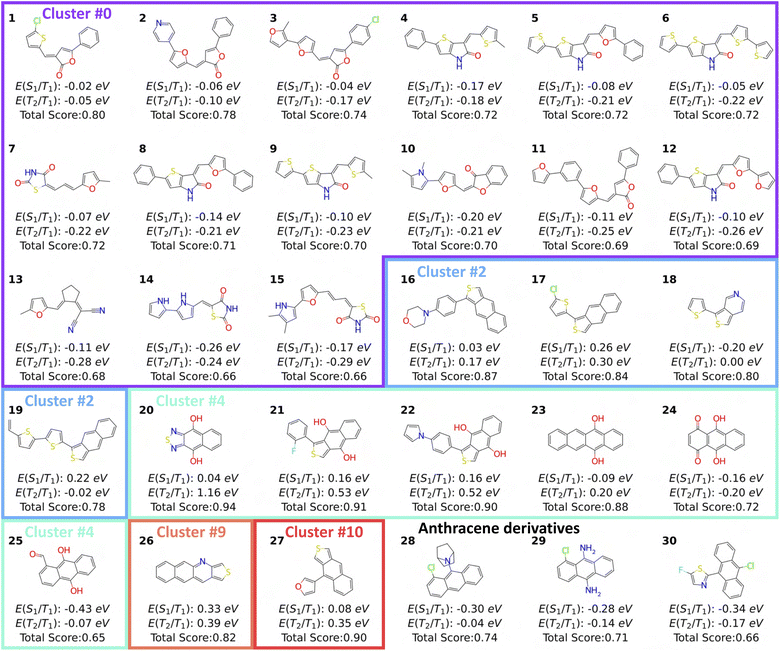
We performed clustering analysis for all molecules generated within five runs, excluding molecules with a total score smaller than 0.01 (the lowest-scoring molecules obscure the analysis). Morgan fingerprints (radius = 3 and 2048 bit) of each molecule were reduced to 2-dimensional vectors using UMAP,58 followed by using HDBScan59 algorithm for building clusters. There are 11 clusters identified among 7959 molecules, including 590 unassigned molecules. As shown in Fig. 3, cluster 5 is the largest cluster where sampled molecules have a lower total score. On the other hand, there are some promising scaffolds that were perturbed locally to reach higher scores (functionalization and heteroatom doping, see Fig. 5). This is more obvious in cluster 0, where a larger spread of low-to-high total scores is present.
3.3 Exploitative generative design for anthracene derivatives
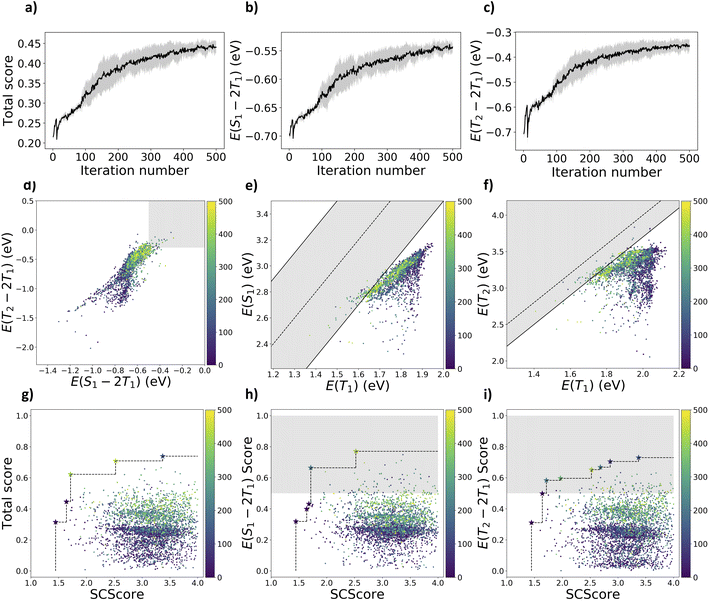
Although the generative search originating from the ChEMBL-trained generative model resulted in some promising molecules, in this next test, we focus on integrating the current body of knowledge on promising singlet fission scaffolds to determine the extent that this framework can leverage current functional materials knowledge to find new high-value candidates, without using combinatorial libraries.We tested using REINVENT to exploit a more focused chemical space by guiding the agent network to generate molecules containing an anthracene scaffold. We note that some anthracene derivatives were found in the exploratory case of Section 3.2, including a top-scoring molecule (molecule 25 in Fig. 5) with some room for improvement in both excited-state energy criteria. In the exploitative case, we followed a similar training procedure as the exploratory case, but we penalized the agent network for sampling molecules without the anthracene scaffold starting from the first-step learning. As shown in Fig. 4a–c, optimization curves evolve slower than the exploratory case but eventually converge around the 400th iteration. The drop in each optimization curve at Step 11 was caused by the default margin guard implemented in REINVENT 3.2, which increased the importance of the total scoring function at Step 10 based on the difference between the augmented and agent likelihood. In a result similar to the exploratory case, although the mean of optimization curves has not passed the excited-state criteria, REINVENT still discovered 29 anthracene derivatives meeting both S1/T1 and T2/T1 criteria, including 82 molecules meeting the S1/T1 criterion and 86 molecules meeting the T2/T1 criterion. The Pareto fronts in Fig. 4 improved throughout the reinforcement learning. With the exploitative strategy, anthracene derivatives with higher S1/T1 and T2/T1 scores were found (molecule 28 to 30 in Fig. 5) compared to molecule 25 from the exploratory case.
3.4 Sample efficiency of REINVENT on electronic properties
Here, we provide an evaluation on the sample efficiency of SMILES-based REINVENT for optimization on electronic properties. Following the approach by Gao et al.,40 we calculated the areas under the curve (AUC) of the top-10 average S1/T1 gap scores and T2/T1 gap scores versus iteration number (each iteration can call up to 64 DFT calculations), for both exploratory and exploitative cases, as shown in Section S6.† Here, AUC is normalized by the maximum possible AUC. For the exploratory case, the S1/T1 gap score has a much larger AUC top-10 average than the T2/T1 gap score, which indicates that the T2/T1 gap is harder to optimize compared to the S1/T1 gap. However, the S1/T1 gap score has a similar AUC top-10 average compared to the T2/T1 gap score for the exploitative case, which is the result of limiting allowed molecular scaffold to anthracene. By comparing the optimization curves of top-10 average between exploratory and exploitative cases, one can see that the exploitative case starts with a larger initial top-10 average but it is later surpassed by the exploratory cases, due to the limited molecular diversity from restricting to anthracene derivatives.3.5 Potential design principles from generated molecules
When using generative schemes to discover new parts of chemical space, we also want to learn design principles for further molecular engineering and to gain direct physical insights into the reasons for the high fitness of some molecules. In this case study, we are able to note several molecular design strategies that have been recently used in the singlet fission community.To this end, we selected top-scoring molecules from the exploratory case (total score > 0.65) that satisfy both excited-state energy criteria. We then grouped these molecules by their carbon skeleton and identified the molecules with the highest total score from each group (Fig. 5). First, in cluster 0, we see that there are many somewhat unconventional (for this application) conjugated species, including lactone or lactam, that could lead to Baird aromaticity in excited states through [4n]-electron rings appearing from resonance structures. We note that excited-state Baird aromaticity was recently used as a guiding principle in recent singlet fission results by Fallon et al.60
Molecules in cluster 2 are fused thiophene derivatives with S1/T1 gaps changing from exothermic to endothermic with longer fused ring systems. The same behavior has been observed for acenes ranging from anthracene to hexacene.61 Molecules in cluster 4 are acenes and heteroacenes substituted with hydroxyl groups. These molecules have large T2/T1 gaps and drive REINVENT for generating similar moieties with hydroxyl substitutions. Interestingly, molecule 24, an isomer of 1,4-dihydroxyanthraquinone, has quinoidal character and undergoes excited state intramolecular proton transfer, which both have been used as design rules for singlet fission.62,63 Although such design rules can not be captured by the reinforcement learning process explicitly, the agent network is driven to generate molecules matching S1/T1 and T2/T1 criteria, which requires molecular engineering to tune excited singlet and triplet energies. Though we are only calculating the vertical excitation energies here, the presence of the neighboring H atom (though not transferred in the calculation), appears to influence the excited state energies. More generally, top-scoring molecules generated by REINVENT have some level of diradical character, as they include common diradicaloids mentioned above and proposed before.60,64 With different combinations of functionalization and scaffold doping, excited-state energies of molecules sampled by REINVENT were tuned to achieve a higher total score. Meanwhile, retrosynthetic planning kept REINVENT from generating exotic molecules with higher excited-state energy scores. Finally, we can see a preference for introducing functional groups at position 9 in the top-scoring anthracene derivatives, which has been shown to alter excited-state energy the most compared to position 1 and 2.65 In addition to electronic effects, a bulky tertiary amino group was introduced for molecule 28 to distort the planarity of anthracene and shift the excited-state energies.
3.6 Excited-state analysis and potential applications of generated molecules
To evaluate the potential use of these generated molecules in the optoelectronic applications, we further examined the excited-state energies (beyond the criteria used in our scoring functions) and interstate properties for SF/TTA candidates meeting both S1/T1 and T2/T1 in exploratory and exploitative cases. Distributions of S1 energies, T1 energies, S0–S1 oscillator strength, and S1–T1 spin–orbital couplings are shown in Fig. S5.† The SF/TTA candidates collected from exploratory and exploitative cases cover broad ranges of S1 (2.08 ∼3.66 eV) and T1 (0.88 ∼1.98 eV) energy levels, which provide a spectral range of ultraviolet-to-near-infrared photon conversion. For example, SF down-conversion and TTA up-conversion allows for improving efficiency of the solar cell, where the triplet energy levels of SF materials and singlet energy levels of TTA materials should be larger than the band gap (Eg) of the solar cell to inject charge carriers. Here, the generated SF/TTA candidates could potentially be applied in the major class of solar cell such as crystalline silicon (Eg ∼1.1 eV), GaAs (Eg ∼1.4 eV), and high-Eg perovskites (Eg ∼1.6 eV).66 In addition, the majority of the S0–S1 oscillator strengths of the generated molecules lies above 0.1, which makes them potentially suitable as SF materials. One of the competing deactivation pathways for SF processes is direct conversion from excited singlet to triplet energy levels through intersystem crossing. S1–T1 spin–orbital couplings are calculated by the one-electron Breit–Pauli Hamiltonian67 to estimate the probability of intersystem crossing. All of the generated molecules exhibit weak S1–T1 spin–orbital couplings (<10 cm−1), which typically holds for organic conjugated molecules.344 Conclusions
We have implemented a framework that uses the REINVENT reinforcement learning framework informed with quantum chemistry calculations to search for lead candidates for SF and TTA organic functional materials. The framework includes a two-step curriculum learning strategy that aims for (1) learning easier and less computationally expensive cheminformatics criteria first, followed by (2) learning cheminformatics criteria together with electronic scoring functions. We applied this framework to a nontrivial task of discovering SF/TTA molecules. REINVENT is capable of finding a series of distinct top-scoring molecules that satisfy both S1/T1 and T1/T2 criteria in the exploratory case. Molecules with higher scores were found and Pareto fronts of electronic scores versus synthesizability were improved throughout the training iterations. To further optimize the molecular scaffolds found in the exploratory case, we ran REINVENT in an exploitative mode, restricting to anthracene derivatives. Anthracene derivatives with higher S1/T1 and T1/T2 scores were found in the exploitative case. Thus, switching between exploratory and exploitative modes provides a potentially more efficient way to discover optimal molecules within the vast chemical space. By inspecting the generated molecules from both cases, we saw that REINVENT has generated molecules that can be interpreted in the context of more general rules of finding molecules with some level of diradical character and fine-tuned excited-state energies with side-group substitutions.Here, our focus was on finding promising initial leads that have the necessary molecular energy levels to be considered leads for SF and TTA applications. The lead molecules can be subjected to further evaluation based on their chemical-, thermal-, and photostability.35 For example, polyacenes found in the exploratory case in Fig. 5 can readily undergo reactions with oxygen to form endo-peroxides and self-dimerize through photoexcitation.68 Using reactivity prediction models69 or providing reaction SMARTS strings to exclude common degradation reactions for SF/TTA motifs can potentially serve as a first-step screening criterion. More detailed quantum chemistry (usually multireference calculations involving dimers of molecules)34,70,71 can be employed to assess the potential efficiency of SF and TTA mechanisms for each individual molecule. The higher computational costs of these calculations make them difficult to incorporate directly into the reinforcement learning framework presented here, though these methods could be used as part of smaller-scale, virtual screening workflows on the initial leads. Further optimization of the framework and additional adjustments and additions to design strategies (e.g., more advanced reward functions) could accelerate the framework as more objectives (and potentially more challenging objectives) are simultaneously considered for different molecular design problems.
Data availability
All the code and data, including the modified REINVENT packages, initial ChEMBL prior network, scripts for setting up configurations and running REINVENT, calibration set along with TD-DFT results and references, and generated molecules in this study are provided at the following GitHub repository: https://github.com/Tabor-Research-Group/reinvent_qc.Author contributions
Cheng-Han Li: writing, conceptualization, developing algorithms, building databases, analyzing data. Daniel P. Tabor: conceptualization, supervision, writing and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the Robert A. Welch Foundation, Grant no. A-2049-20230405 and the Texas A&M Institute of Data Science Career Initiation Fellowship. Portions of this research were conducted with high-performance research computing resources provided by Texas A&M University HPRC.Notes and references
- Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha, R. Q. Snurr and A. Aspuru-Guzik, Nat. Mach. Intell., 2021, 3, 76–86 CrossRef.
- D. M. Anstine and O. Isayev, J. Am. Chem. Soc., 2023, 145, 8736–8750 CrossRef CAS PubMed.
- T. Sousa, J. Correia, V. Pereira and M. Rocha, J. Chem. Inf. Model., 2021, 61, 5343–5361 CrossRef CAS PubMed.
- C. Duan, A. Nandy and H. J. Kulik, Annu. Rev. Chem. Biomol. Eng., 2022, 13, 405–429 CrossRef PubMed.
- C. Suh, C. Fare, J. A. Warren and E. O. Pyzer-Knapp, Annu. Rev. Mater. Res., 2020, 50, 1–25 CrossRef CAS.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120–1127 CrossRef PubMed.
- A. Mahmood and J.-L. Wang, J. Mater. Chem. A, 2021, 9, 15684–15695 RSC.
- Ö. H. Omar, M. del Cueto, T. Nematiaram and A. Troisi, J. Mater. Chem. C, 2021, 9, 13557–13583 RSC.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed.
- J. H. Jensen, Chem. Sci., 2019, 10, 3567–3572 RSC.
- D. E. Graff, E. I. Shakhnovich and C. W. Coley, Chem. Sci., 2021, 12, 7866–7881 RSC.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminformatics, 2017, 9, 48 CrossRef PubMed.
- T. Blaschke, J. Arús-Pous, H. Chen, C. Margreitter, C. Tyrchan, O. Engkvist, K. Papadopoulos and A. Patronov, J. Chem. Inf. Model., 2020, 60, 5918–5922 CrossRef CAS PubMed.
- R. I. Horne, M. H. Murtada, D. Huo, Z. F. Brotzakis, R. C. Gregory, A. Possenti, S. Chia and M. Vendruscolo, J. Chem. Theory Comput., 2023, 19, 4701–4710 CrossRef CAS PubMed.
- H. Chen, J. Med. Chem., 2022, 65, 100–102 CrossRef CAS PubMed.
- Y. Bian and X.-Q. Xie, J. Mol. Model., 2021, 27, 71 CrossRef CAS PubMed.
- A. Tripp, W. Chen and J. M. Hernández-Lobato, ICLR2022 Machine Learning for Drug Discovery, 2022 Search PubMed.
- S. A. Wildman and G. M. Crippen, J. Chem. Inf. Comput. Sci., 1999, 39, 868–873 CrossRef CAS.
- G. R. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Nat. Chem., 2012, 4, 90–98 CrossRef CAS PubMed.
- A. Nandy, C. Duan and H. J. Kulik, Curr. Opin. Chem. Eng., 2022, 36, 100778 CrossRef.
- G. Marques, K. Leswing, T. Robertson, D. Giesen, M. D. Halls, A. Goldberg, K. Marshall, J. Staker, T. Morisato, H. Maeshima, H. Arai, M. Sasago, E. Fujii and N. N. Matsuzawa, J. Phys. Chem. A, 2021, 125, 7331–7343 CrossRef CAS PubMed.
- H. S. Kwak, Y. An, D. J. Giesen, T. F. Hughes, C. T. Brown, K. Leswing, H. Abroshan and M. D. Halls, Front. Chem., 2022, 9, 800370 CrossRef PubMed.
- S. S. V. Sowndarya, J. N. Law, C. E. Tripp, D. Duplyakin, E. Skordilis, D. Biagioni, R. S. Paton and P. C. St. John, Nat. Mach. Intell., 2022, 4, 720–730 CrossRef.
- W. Gao, T. Fu, J. Sun and C. W. Coley, arXiv, 2022, preprint, arXiv:2206.12411, DOI:10.48550/arXiv.2206.12411.
- M. Thomas, N. M. O'Boyle, A. Bender and C. D. Graaf, arXiv, 2022, preprint, arXiv:2212.01385, DOI:10.48550/arXiv.2212.01385.
- J. Guo, V. Fialková, J. D. Arango, C. Margreitter, J. P. Janet, K. Papadopoulos, O. Engkvist and A. Patronov, Nat. Mach. Intell., 2022, 4, 555–563 CrossRef.
- J. Guo, F. Knuth, C. Margreitter, J. P. Janet, K. Papadopoulos, O. Engkvist and A. Patronov, Digital Discovery, 2023, 2, 392–408 RSC.
- V. Fialková, J. Zhao, K. Papadopoulos, O. Engkvist, E. J. Bjerrum, T. Kogej and A. Patronov, J. Chem. Inf. Model., 2022, 62, 2046–2063 CrossRef PubMed.
- N. C. Iovanac, R. MacKnight and B. M. Savoie, J. Phys. Chem. A, 2022, 126, 333–340 CrossRef CAS PubMed.
- M. Glavatskikh, J. Leguy, G. Hunault, T. Cauchy and B. Da Mota, J. Cheminform., 2019, 11, 69 CrossRef PubMed.
- D. Padula, Ö. H. Omar, T. Nematiaram and A. Troisi, Energy Environ. Sci., 2019, 12, 2412–2416 RSC.
- X. Wang, R. Tom, X. Liu, D. N. Congreve and N. Marom, J. Mater. Chem. C, 2020, 8, 10816–10824 RSC.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- D. Casanova, Chem. Rev., 2018, 118, 7164–7207 CrossRef CAS PubMed.
- T. Ullrich, D. Munz and D. M. Guldi, Chem. Soc. Rev., 2021, 50, 3485–3518 RSC.
- R. Casillas, I. Papadopoulos, T. Ullrich, D. Thiel, A. Kunzmann and D. M. Guldi, Energy Environ. Sci., 2020, 13, 2741–2804 RSC.
- REINVENT 3.2, https://github.com/MolecularAI/Reinvent, accessed 2023-05-05.
- J. Arús-Pous, S. V. Johansson, O. Prykhodko, E. J. Bjerrum, C. Tyrchan, J.-L. Reymond, H. Chen and O. Engkvist, J. Cheminform., 2019, 11, 71 CrossRef PubMed.
- C. W. Coley, L. Rogers, W. H. Green and K. F. Jensen, J. Chem. Inf. Model., 2018, 58, 252–261 CrossRef CAS PubMed.
- W. Gao and C. W. Coley, J. Chem. Inf. Model., 2020, 60, 5714–5723 CrossRef CAS PubMed.
- C. Bilodeau, W. Jin, T. Jaakkola, R. Barzilay and K. F. Jensen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1608 Search PubMed.
- T. Blaschke, O. Engkvist, J. Bajorath and H. Chen, J. Cheminform., 2020, 12, 68 CrossRef CAS PubMed.
- G. W. Bemis and M. A. Murcko, J. Med. Chem., 1996, 39, 2887–2893 CrossRef CAS PubMed.
- S. Genheden, A. Thakkar, V. Chadimová, J.-L. Reymond, O. Engkvist and E. Bjerrum, J. Cheminform., 2020, 12, 70 CrossRef PubMed.
- Chemical reactions from US patents (1976-Sep2016), https://figshare.com/articles/dataset/Chemical_reactions_from_US_patents_1976-Sep2016_/5104873, accessed 2023-06-30.
- T. Sterling and J. J. Irwin, J. Chem. Inf. Model., 2015, 55, 2324–2337 CrossRef CAS PubMed.
- K. Chen, C. Kunkel, K. Reuter and J. T. Margraf, Digital Discovery, 2022, 1, 147–157 RSC.
- T. Gensch, G. dos Passos Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. Nigam, M. Lindner-D'Addario, M. S. Sigman and A. Aspuru-Guzik, J. Am. Chem. Soc., 2022, 144, 1205–1217 CrossRef CAS PubMed.
- C.-H. Li and D. P. Tabor, J. Mater. Chem. A, 2022, 10, 8273–8282 RSC.
- S. Axelrod, E. Shakhnovich and R. Gómez-Bombarelli, ACS Cent. Sci., 2023, 9, 166–176 CrossRef CAS PubMed.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminform., 2011, 3, 33 CrossRef PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, A. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, A. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince III, R. A. DiStasio Jr, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard III, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock III, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- T. Froitzheim, S. Grimme and J.-M. Mewes, J. Chem. Theory Comput., 2022, 18, 7702–7713 CrossRef CAS PubMed.
- S. Wang, T. Kind, P. L. Bremer, D. J. Tantillo and O. Fiehn, J. Chem. Inf. Model., 2022, 62, 4403–4410 CrossRef CAS PubMed.
- C. F. Perkinson, D. P. Tabor, M. Einzinger, D. Sheberla, H. Utzat, T.-A. Lin, D. N. Congreve, M. G. Bawendi, A. Aspuru-Guzik and M. A. Baldo, J. Chem. Phys., 2019, 151, 121102 CrossRef PubMed.
- L. McInnes, J. Healy and J. Melville, arXiv, 2020, preprint, arXiv:1802.03426, DOI:10.48550/arXiv.1802.03426.
- R. J. G. B. Campello, D. Moulavi and J. Sander, Advances in Knowledge Discovery and Data Mining, Berlin, Heidelberg, 2013, pp. 160–172 Search PubMed.
- K. J. Fallon, P. Budden, E. Salvadori, A. M. Ganose, C. N. Savory, L. Eyre, S. Dowland, Q. Ai, S. Goodlett, C. Risko, D. O. Scanlon, C. W. M. Kay, A. Rao, R. H. Friend, A. J. Musser and H. Bronstein, J. Am. Chem. Soc., 2019, 141, 13867–13876 CrossRef CAS PubMed.
- V. Gray, L. Weiss and A. Rao, in Singlet Fission: Mechanisms and Molecular Design, ed. J. S. Lissau and M. Madsen, Springer International Publishing, Cham, 2022, pp. 291–311 Search PubMed.
- D. López-Carballeira, D. Casanova and F. Ruipérez, Phys. Chem. Chem. Phys., 2017, 19, 30227–30238 RSC.
- D. López-Carballeira and T. Polcar, ChemPhotoChem, 2023, e202300017 CrossRef.
- I. Paci, J. C. Johnson, X. Chen, G. Rana, D. Popović, D. E. David, A. J. Nozik, M. A. Ratner and J. Michl, J. Am. Chem. Soc., 2006, 128, 16546–16553 CrossRef CAS PubMed.
- S. Abou-Hatab, V. A. Spata and S. Matsika, J. Phys. Chem. A, 2017, 121, 1213–1222 CrossRef CAS PubMed.
- A. J. Carrod, V. Gray and K. Börjesson, Energy Environ. Sci., 2022, 15, 4982–5016 RSC.
- Q. Ou and J. E. Subotnik, J. Phys. Chem. C, 2013, 117, 19839–19849 CrossRef CAS.
- A. J. Baldacchino, M. I. Collins, M. P. Nielsen, T. W. Schmidt, D. R. McCamey and M. J. Y. Tayebjee, Chem. Phys. Rev., 2022, 3, 021304 CrossRef CAS.
- L. C. Gallegos, G. Luchini, P. C. St. John, S. Kim and R. S. Paton, Acc. Chem. Res., 2021, 54, 827–836 CrossRef CAS PubMed.
- H. Kim and P. M. Zimmerman, Phys. Chem. Chem. Phys., 2018, 20, 30083–30094 RSC.
- M. E. Sandoval-Salinas, A. Carreras, J. Casado and D. Casanova, J. Chem. Phys., 2019, 150, 204306 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: ESI contains a description of the contents in all raw data files on the GitHub repository, implementation details for REINVENT, a comparison of SCScore between molecules generated by REINVENT and the initial calibration set, the scoring functions used for evaluating excited state energy gaps, Benchmark results for the excited state quantum chemistry calculations, top-10 average electronic scores for exploratory and exploitative cases, and excited-state analysis for SF/TTA candidates. See DOI: https://doi.org/10.1039/d3sc03781a |
| This journal is © The Royal Society of Chemistry 2023 |