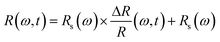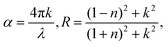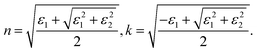Open Access Article
Open Access ArticlePhonon-driven transient bandgap renormalization in perovskite single crystals†
Lijie
Wang
a,
Hong
Wang
ab,
Razan
Nughays
 a,
Wojciech
Ogieglo
a,
Jun
Yin
a,
Wojciech
Ogieglo
a,
Jun
Yin
 c,
Luis
Gutiérrez-Arzaluz
c,
Luis
Gutiérrez-Arzaluz
 ab,
Xinyuan
Zhang
b,
Jian-Xin
Wang
a,
Ingo
Pinnau
ab,
Xinyuan
Zhang
b,
Jian-Xin
Wang
a,
Ingo
Pinnau
 a,
Osman M.
Bakr
a,
Osman M.
Bakr
 b and
Omar F.
Mohammed
*ab
b and
Omar F.
Mohammed
*ab
aAdvanced Membranes and Porous Materials Centre (AMPM), Division of Physical Science and Engineering, King Abdullah University of Science and Technology, Thuwal 23955-6900, Kingdom of Saudi Arabia. E-mail: omar.abdelsaboor@kaust.edu.sa
bKAUST Catalysis Centre, Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology, Thuwal 23955-6900, Kingdom of Saudi Arabia
cDepartment of Applied Physics, The Hong Kong Polytechnic University, Kowloon 999077, Hong Kong, P. R. China
First published on 4th July 2023
Abstract
Tailoring the electronic structure of perovskite materials on ultrafast timescales is expected to shed light on optimizing optoelectronic applications. However, the transient bandgap renormalization observed upon photoexcitation is commonly explained by many-body interactions of optically created electrons and holes, which shrink the original bandgap by a few tens of millielectronvolts with a sub-picosecond time constant, while the accompanying phonon-induced effect remains hitherto unexplored. Here we unravel a significant contribution of hot phonons in the photo-induced transient bandgap renormalization in MAPbBr3 single crystals, as evidenced by asymmetric spectral evolutions and transient reflection spectral shifts in the picosecond timescale. Moreover, we performed a spatiotemporal study upon optical excitation with time-resolved scanning electron microscopy and identified that the surface charge carrier diffusion and transient bandgap renormalization are strongly correlated in time. These findings highlight the need to re-evaluate current theories on photo-induced bandgap renormalization and provide a new approach for precisely controlling the optical and electronic properties of perovskite materials, enabling the design and fabrication of high-performance optoelectronic devices with exceptional efficiency and unique properties.
New conceptsIn this study, we have demonstrated the significant role of phonons in the photo-induced transient bandgap renormalization (BGR) of MAPbBr3 perovskite single crystals, in addition to the contribution from photo-generated hot carriers. This finding provides insights into the fundamental origin of the observed asymmetric spectral evolutions and shifts in transient optical spectroscopy. Moreover, we performed a comprehensive spatiotemporal analysis using state-of-the-art time-resolved scanning electron microscopy. Our results revealed that the excited carriers exhibited diffusion over a distance of approximately 7 μm within 2 ns, with the majority of diffusion occurring within ∼250 ps. Notably, this diffusion time scale coincided perfectly with the phonon-driven BGR observed in our ultrafast spectroscopy measurements, suggesting that the carrier transport behavior, which is influenced by carrier mobility and concentration, can be altered during both nonequilibrium and equilibrium carrier–phonon interactions. Our research provides a novel strategy for precise control over the optical and electronic properties of perovskite crystals, and this knowledge can be harnessed to design and produce high-performance perovskite-based optoelectronic devices. |
Introduction
Lead-halide perovskites have attracted significant attention in recent years in various optoelectronic applications, such as quantum light sources,1 photovoltaics,2 photodetectors,3 and light-emitting diodes,4 because of their extraordinarily long charge carrier lifetimes and diffusion lengths.5–7 Ultrafast spectroscopy enables the measurement of photoexcitation-induced excited-state spectral evolution in real time, while polycrystalline perovskites exhibit spectral features that originate from the localized charge trapping at the impurities and/or defects and hinder the identification of the electronic structures.8,9 Thus, single-crystal grain-free materials with low defect densities are employed to explore and decipher the intrinsic bulk behaviour of perovskites, free from morphological effects.10,11Many-body effects and strong Coulomb interactions occurring after photoexcitation lead to intrinsic bandgap shrinking.12,13 Although this phenomenon is commonly observed in various semiconductor materials, its overall behaviour is dictated by the competition among several different effects, and the exact origin and mechanism remain unclear. Transient spectroscopic characteristics induced by femtosecond (fs) pump and probe laser pulses are sensitive to the initial ultrafast dynamics of photo-generated electron–hole pairs.14 Following photoexcitation, the non-thermal electron–hole distribution typically thermalizes on a sub-picosecond (ps) timescale.15 The initial carrier cooling process is primarily governed by Coulomb-mediated scattering with optical phonons, known as Fröhlich interactions, followed by the less-efficient acoustic phonon scattering driven by deformation potentials.16 These photo-generated charge carriers can ultimately shift the band edge by a few millielectronvolts (meV) within a few ps.17,18 Controlling the electronic properties of materials through these many-body effects is successful but only at ultra-low temperatures.19,20 It was reported that in a two-dimensional (2D) semiconductor,21 room temperature transient absorption (TA) measurements exhibit excitation-density-dependent bandgap renormalization (BGR), which can be explained in terms of repulsive/attractive exciton–exciton interactions at high/low densities. However, the effect of lattice heating via phonon emission is typically disregarded in such cases. Upon photoexcitation, the collisions between electrons and thermally excited lattice vibrations (electron–phonon scattering) play a crucial role in energy transfer.22 Thus, the lattice temperature can potentially affect the carrier distribution and even the electronic structure. Temperature-dependent steady-state photoluminescence (PL) spectra of perovskites exhibit a continuously blueshift of the emission peak with increasing temperature,23–26 while the exact mechanism underlying this phenomenon is still debated. It is noteworthy that all current PL measurements are performed at low temperatures. Therefore, it is crucial to consider the contribution of hot phonons and quantify the impact of electronic and thermal effects on BGR after photoexcitation.
Moreover, directly visualizing the charge carrier diffusion behaviour of perovskites as well as identifying the fundamental physical mechanisms that determine their performance, are of considerable research interest. Thus far, electron–hole diffusion lengths, mostly probed via indirect methods such as time-resolved PL spectroscopy, have been reported to be in the micrometre range.5,6 However, direct spatiotemporal mapping of charge carrier diffusion lengths using TA microscopy, which provides bulk information, has only been reported in fs-scale.27 Ultrafast scanning electron microscopy (SEM), which is sensitive to the uppermost layer (a few to several nm) of a material's surface, has been employed to visualize the charge carrier transport with high spatial resolution in the time-domain.28–32 Further, correlating charge carrier diffusion in a material with alterations to its electronic properties on ultrafast timescales would offer key elements for new material design and discovery for high-performance optoelectronic devices.
In this study, we conducted a systematic investigation to elucidate the effects of hot carriers and phonons on photo-induced BGR in MAPbBr3 single crystals, serving as a model system. Our experimental approach involved a pump-energy and fluence-dependent ultrafast optical spectroscopy, complemented by temperature-dependent steady-state measurements. Our findings clearly demonstrate that, in addition to the contribution from photo-generated hot carriers, phonons also play a significant role in BGR. High-temperature PL and absorption spectra showed consistent band-edge shifting patterns with those observed in transient spectroscopic analysis. Density functional theory (DFT) calculations further confirmed the dependence of the observed bandgap broadening on lattice-expansion. Furthermore, the ultrafast SEM study revealed that excited carriers diffused over a distance of approximately 7 μm within a time frame of 2 ns, with the majority of diffusion occurring within ∼250 ps.
Results and discussion
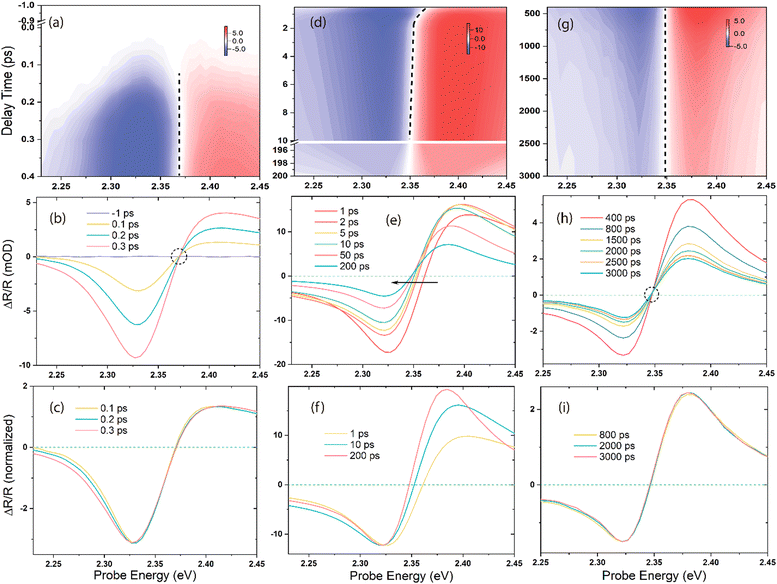
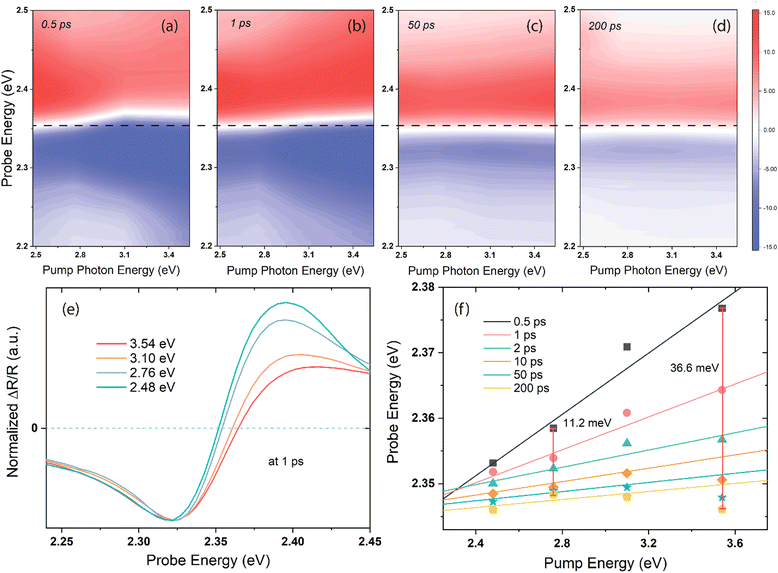
The fs-broadband transient absorption/reflection set-up and MAPbBr3 single-crystal sample (size: ∼5 mm × 5 mm × 2 mm) fabrication methods are described in the ESI† and Methods section. Fig. 1 shows the time-energy transient reflection (TR) maps obtained after different time delays and the corresponding TR and normalized spectra obtained upon 3.10 eV excitation. The red and blue colours indicate the positive and negative TR signals, respectively, while the dashed lines represent the zero-crossing points (ΔOD = 0) at each delay time between the pump and the probe. Initially (stage-i) in Fig. 1a, b, and c, spectral broadening is observed immediately after the photoexcitation within the first few hundreds of fs, accompanied by an isosbestic point on the blue side of the spectral traces. At a later stage (stage-ii) in Fig. 1d, e, and f, there is a significant spectral redshift and narrowing with a delay time of hundreds of ps. The zero-crossing point shifts by ∼14 meV from 1 to 200 ps, and the full width at half maximum (FWHM) of the bleach narrows from ∼63.8 meV at 1 ps to ∼57.1 meV at 200 ps. Subsequently, the spectra exhibit a slight narrowing with no shift, as evidenced by the isosbestic point at ΔOD = 0 (the dashed circle in Fig. 1h, stage-iii), up to nanoseconds (ns) order. The derivative-like spectral response, characterized by positive values above ∼2.35 eV and negative values below this energy, has been well studied and assigned to the excitonic feature induced by bandfilling.33–36 In contrast, the positive feature exhibits a significant asymmetric evolution and differs from the measurements conducted in transmission mode on thin films.34,37 The TR spectra in this regime cannot be explained solely by band filling;38 the presence of free carriers (continuum transitions) also contributes to the bleach of excitonic transitions. Further, the positive feature shows a carrier density dependence distinct from that of the bleach, indicating that it can serve as an indicator of the temperature effect in the material system.38 Briefly, the prominent spectral redshift observed in stage-ii (Fig. 1d, e, and f) can be attributed to the photo-induced change of refractive index, BGR, and Burstein–Moss effect (band filling),34,39,40 although the latter leads to a blueshift by shifting the reflection/absorption onset to higher energies.The BGR is strongly affected by the carrier–carrier interaction,41,42 and the excess energy of the excitation light can determine the extent of the bandgap narrowing, which is confirmed by the pump-energy-dependent TR spectra shown in Fig. 2. Ultrafast 2D pump–probe transient maps at different delay times (0.5, 1, 50, and 200 ps) under an identical pump power are displayed in Fig. 2a–d. All the transients are characterized by a derivative-like signal over the probe range, and two long-lived features are distinctly visible at the positive/negative signal maxima at all the pump energies. The horizontal black dashed line across the four maps represents the reference of the spectral shift with the delay time and pump energies. Fig. 2e shows the spectral cuts of 1 ps for different pump photon energies, with each trace normalized with respect to the minimum of the bleach at ∼2.32 eV. With increasing pump photon energy, the entire spectrum shifts toward the high-energy side, accompanied by a broadening of the bleach signal. The zero-crossing point shifts with the delay time and pump photon energies are plotted in Fig. 2f, in which the solid lines represent the linear fit of the energy positions at ΔOD = 0. These points are clearly nonlinear with the increasing pump photon energies, and the linear fitting has been shown here only to indicate the trend. The vertical red lines indicate the spectral shift energy from 0.5 to 200 ps at each pump photon energy. Within this time period, the zero-crossing point moves 11.2 and 36.6 meV under 2.76 and 3.54 eV excitations, respectively.
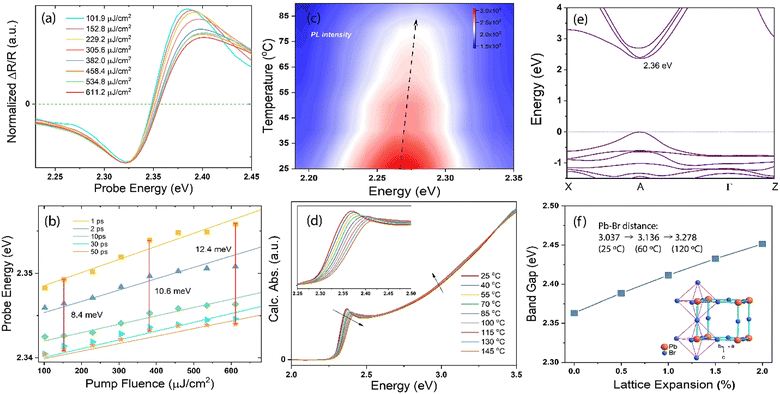
The huge spectral shift observed in the TR spectra cannot be solely attributed to carrier–carrier interaction, considering the timescale involved, which exceeds the rapid cooling of the “hot” carriers (referred to as “hot” due to their initially high temperatures, reaching up to thousands of degrees18). Instead, the complete restructuring of the reflection-edge occurs within a timeframe corresponding to phonon scattering processes.36 Thus, we next performed a pump-fluence-dependent TR experiment under 3.10 eV excitation with fluences ranging from 101.9 μJ cm−2 to 611.2 μJ cm−2. The signal intensities at the maximum bleach positions of ∼2.32 eV show a linear relationship with the pump fluence (Fig. S1, ESI†), thereby confirming that the samples are robust within our excitation power range. Fig. 3a shows the normalized spectral traces cut at 1 ps, and the zero-crossing point shifts at each delay time and pump fluence are depicted in Fig. 3b. With the increasing pump fluence, which generates more hot carriers in the material,43 the overall spectral profile remains the same but becomes broader, especially on the blue side. From 1 to 50 ps of delay times, the spectra shift to high energies with the increasing pump fluence, and the amount of shift does not increase linearly with the pump power; a deviation of ∼4.0 meV from linearity is observed when the number of incident photons is increased to four times (e.g., 8.4 meV at 152.8 μJ cm−2 and 12.4 meV at 611.2 μJ cm−2), suggesting that in addition to the carrier–carrier interactions, the phonons play an integral role in revealing such a giant spectral shift because the hot carriers transfer their energy to the phonons quickly after the photoexcitation.
To verify this phenomenon, we performed careful temperature-dependent PL spectroscopy and spectroscopic ellipsometry, and the results are presented in Fig. 3c and d. The steady-state PL measurements were conducted from 25 to 90 °C; the emission peak at ∼2.27 eV matches well with that reported previously44 and undergoes a slight blue spectral shift upon heating (Fig. S2, ESI†). The PL intensity decreases to half as the temperature increases from 25 to 90 °C. The normalized PL spectra shown in Fig. S3 (ESI†) display an 11 meV peak position difference with respect to the spectra measured at the lowest and highest temperatures, and the corresponding FWHM of the PL peak increases by ∼13% (Fig. S4, ESI†). We measured the dielectric function at different energies and temperatures using variable angle spectroscopic ellipsometry (VASE) at 65°, 70°, and 75° to increase accuracy, and the measured values were simultaneously fitted with an isotropic “B-spline” mode.45 Fig. S5 (ESI†) shows the dielectric function measured at different energies and temperatures, and Fig. S6 (ESI†) shows the VASE data and their fittings at each temperature and angle. Both the real (ε1) and imaginary (ε2) parts of the dielectric function exhibit a downward and blueshifted trend in the range of 2.0–2.5 eV, although the behaviour at the high-energy side is different. Based on these ε1 and ε2, we calculated the temperature-dependent absorption and refractive index in a wide spectral and temperature range from 25 to 145 °C (thermogravimetric analysis confirmed the absence of weight loss until 300 °C, see Fig. S7, ESI†). Fig. 3d shows the absorption spectra calculated at different temperatures, and the inset shows the exciton peak region zoomed-in from 2.25 to 2.50 eV. The exciton peak and onset of the absorption shift toward the high-energy side with the increasing temperature, accompanied by decreased intensity and broadened peak. This result is consistent with the observed TR-analysed derivative-like spectral shape and redshift with lattice cooling (Fig. S8 shows the simulated differential absorption, which was determined by subtracting the absorption at high temperature from that at low temperature, ESI†). It has to be noted that the photo-induced reflectance response can be slightly different with the absorption, as the reflection coefficient R needs to be expressed in terms of the complex index of refraction, and the relation between Δn and the Δk which are the change of the real and imaginary parts of the complex refractive index, is essential for the interpretation of the differential reflectivity signal. Therefore, we retrieved the spectral evolution of R(ω, t), obtained by combining the steady-state Rs(ω) calculated from ellipsometry and the ΔR/R(t) data,33
To further confirm the effect of hot-lattice on the electronic structure of MAPbBr3, we performed density functional theory (DFT) calculations using the generalized gradient approximation (GGA) and Perdew–Burke–Ernzerhof (PBE) functionals. The calculated electronic band structure of cubic-phase MAPbBr3 and its bandgaps, determined as a function of the lattice expansion due to heating, are shown in Fig. 3e, f and Fig. S10 (ESI†). The MAPbBr3 crystal exhibits a direct bandgap at the A-point, where the conduction band minimum originates from the Br-4p and Pb-6p states, and the valence band maximum results from the hybridization of the Br-4p and Pb-6s states. Without lattice expansion, the bandgap of MAPbBr3 is 2.36 eV, which has a deviation of ∼3% with respect to our experimental results obtained by measuring the dielectric function at room temperature. Upon expanding the MAPbBr3 lattice by 2%, a bandgap shift of 90 meV is observed. Such a BGR has been observed in several semiconductors, although most of them show a decreased energy gap with increasing lattice temperature.48–50 The inset in Fig. 3f displays the octahedral structure of the MAPbBr3 crystal, as resolved by single-crystal X-ray diffraction (XRD) measurements, with the MA+ cation removed for simplicity. The measured Pb–Br atomic distance is 3.037 Å at 25 °C, and increases to 3.136 and 3.278 Å at 60 and 120 °C, suggesting a ∼3.2% and ∼7.9% lattice expansion, respectively. The findings collectively indicate that despite the dominant contribution of the hot carrier interactions, the lattice heating/cooling in the stage-ii TR spectra plays a significant role in the observed asymmetric spectral evolution and redshift. This inference is supported by the early time behaviour (Fig. 1), which is governed by the interplay between carrier and lattice temperature exchanges following photoexcitation.
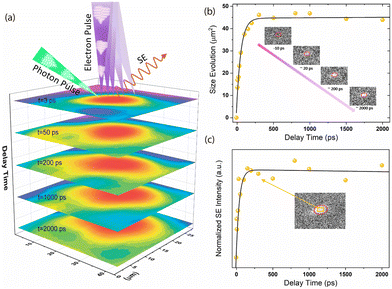
Furthermore, because of the unique phonon-driven BGR that can last for up to hundreds of picoseconds, we investigated its impact on electron–hole diffusion performance, as the ultrafast modification of the electronic structure may affect the transport properties of the photo-generated carriers. Therefore, a time-resolved SEM experiment was performed to evaluate the effect of carrier diffusion on the crystal surface. As shown in Fig. 4a, real-space imaging was performed using photon pump and electron probe pulses. In this experiment, 345 nm ultraviolet (UV) pulses were focused onto the tip of the gun source to generate high-energy (30 keV) pulsed electrons. For the excitation, a 515 nm visible pump beam was irradiated on the sample at 54° with respect to the direction of the pulse electron beam. The time-resolved secondary electron (SE) images were acquired by subtracting the excited signals from the unexcited (at negative time delays) ones. Fig. 4a shows the color-coded ultrafast SEM maps obtained at 3, 50, 200, 1000 and 2000 ps. Fig. 4b and c show the pump-induced spot size evolution and normalized SE kinetics as functions of the delay time. Based on the calculated evolution of these quasi-elliptical areas after the excitation, a ∼7 μm diffusion length within 2 ns was determined on the surface of the MAPbBr3 single crystal. However, the pump-induced SE spot rapidly intensified and expanded almost only within ∼250 ps, and the fitting results suggest a rising time of 60.2 ± 11.9 ps, which well-matches with the decay timescale (67.1 ± 2.8 ps, Table S1, ESI†) at 2.40 eV (obtained by TR spectroscopy). As previously mentioned, the positive TR signal at 2.40 eV could be an indicator of temperature-induced effects in the material. Its shift and decay characteristics align with the time window of electron-hole diffusion, suggesting a strong correlation between the ultrafast modification of electronic structures and charge carrier diffusion. Although the underlying mechanism behind this carrier diffusion, primarily occurring during the photo-induced bandgap renormalization (BGR) period, remains elusive, one hypothesis suggests that carrier mobility and concentration can be altered during both nonequilibrium and equilibrium carrier-phonon interactions.23,51 The temperature dependence of the charge carrier mobility can approach the expected form for acoustic deformation potential scattering (μ ∝ T−3/2),52–54 where mobility increases with decreasing temperature. However, the exact functional dependence typically comprises a combination of multiple scattering mechanisms, making their individual identification challenging. Moreover, electron–phonon scattering imposes an upper limit on free charge mobility,54 potentially prolonging the diffusion time and resulting in a trade-off behaviour. In this context, the carrier transport is initially limited but relative fast until approximately 250 ps, after which diffusion becomes negligible as both the carrier and lattice cool to a temperature that halts their functionality.
Conclusions
Our study unveils the significant role of phonons in the transient restructuring of the band-edge in MAPbBr3 single crystals following photoexcitation, in addition to the well-known contribution of photo-generated hot carriers. This phonon-driven transient BGR, occurring on a timescale commensurate with electron–hole diffusion, has not been previously considered in the context of the ultrafast modification of electronic structures in perovskite materials. Our findings contribute to a deeper understanding of the underlying physical phenomena in perovskite materials and emphasize the need to reassess existing theories regarding photo-induced BGR. By employing a comprehensive approach encompassing time-resolved and steady-state experimental techniques, as well as cutting-edge ultrafast SEM and density functional theory (DFT) analysis, we have made valuable additions to the current knowledge on optoelectronic applications of perovskite materials. Furthermore, our results call for further investigations on other material systems to ascertain whether phonon-driven transient BGR is a general phenomenon in photo-induced processes.Experimental section
Sample preparation and characterization
PbBr2 (99.999%) and anhydrous dimethylformamide were purchased from Sigma-Aldrich, and methylammonium bromine (MABr) was obtained from Luminescence Technology Corp. The precursor MABr (0.748 g) was dissolved in anhydrous dimethylformamide (4 mL) in a 20 mL glass vial to form a clear solution. Then, PbBr2 (2.452 g) was added into the glass vial with stirring to obtain a nearly saturated clear MAPbBr3 solution. The glass vial was then placed onto a hotplate at 50 °C without disturbance for slow evaporation. Bulk MAPbBr3 single crystals with dimensions in the centimetre range (see inset of Fig. S11, ESI†) were obtained from the solution after 12 h. These procedures were all performed inside a fume hood and were previously reported.55 To examine the phase and orientation of the sample, XRD patterns were recorded at room temperature using a Bruker D8 ADVANCE diffractometer and Cu Kα radiation (λ = 1.5406 Å).TR measurements
The TR measurements were performed using a Helios pump–probe setup (Ultrafast Systems), which allowed a broadband visible probe upon a tuneable visible excitation of the samples. A 1 kHz 800 nm ∼150 fs/7 mJ laser pulse was split into two parts for the pump and probe. The pump was obtained using a nonlinear optical parametric amplifier (SpectraPhysics), which delivered pulses from ∼350 nm to ∼700 nm, and the probe was generated by focusing the rest of the 800 nm beam into a 2 mm CaF2 crystal. Particularly, the white-light probe beam was further split into two beams; one was used as a reference to reduce the signal-to-noise ratio significantly. The pump and electronically-delayed probe were then spatially overlapped on the sample, and the reflected signal was collected and focused into a fibre detector. The detailed experimental setup and analysis software of the Helios system can be found elsewhere.56Fluence-dependent measurements
The fluence-dependent experiments were performed using the same TR set-up. The TR was measured at specific time delays, between the pump and probe, in a wide range of pump fluences. Prior to the measurement, we first determined the time zero position at the delay stage by analysing the point at which the signal appeared while electronically moving the delay stage. Next, we converted the desired delay time into distance on the stage and calculated the position of the stage with respect to zero time. Then, we set two time points slightly before and after the desired time, (e.g., the TR responses at ∼9.9 ps and ∼10.1 ps were measured if 10 ps is selected) and averaged the TR values obtained at these two time points.The average incident laser fluence (F; measured in μJ cm−2) is defined as F = P/(r·A), where P is the average laser power, r is the repetition rate of the laser system (500 Hz), and A is the laser beam spot size. The laser beam spot size was measured using a camera-based beam profiling system consisting of a camera and analysis software (Ophir Photonics). The spot-size diameter was determined from the FWHM of the beam profile. We started the measurements with the lowest pump power that yielded a clear signal and used a round continuous neutral density filter to control and increase the power (caution must be taken as the perovskite can be easily damaged by lasers).
Temperature-dependent in situ spectroscopic ellipsometry
Temperature-dependent in situ spectroscopic ellipsometry was performed using an M-2000 DI device (J. A. Woollam, USA), which operated in the 193–1690 nm wavelength range, coupled with an INSTEC heating stage, which allowed thermal scanning from room temperature up to 560 °C under a N2 gas flow. The crystal was measured at a minimum of three angles of incidences (65°, 70°, and 75°), and the data analysis was performed using the Complete EASE 6.51 software package. The dielectric function was extracted using the Kramers–Kronig consistent B-spline optical model45 (node resolution 0.1 eV). To calculate the absorption spectra and the reflectivity we used the relations:33where n and k are, respectively, the real and imaginary parts of the complex refractive index ñ = n + ik:
For consistency, all the samples were modeled using exactly the same model to obtain the absorption coefficients and refractive indices at different temperatures.
Temperature-dependent PL and Raman spectroscopy
The PL spectra were measured using a Horiba Fluoromax-4 spectrofluorometer with a photomultiplier (PMT-928). The crystal was placed into a heating cell with water flow. A temperature controller was installed to heat the water from room temperature to 90 °C. The temperature-dependent Raman spectra were acquired using a confocal Raman instrument (Witec Apyron). The temperature range was set to 25–145 °C, with 15 °C intervals, and a hotplate with liquid nitrogen was used to stabilize the temperature. A continuous-wave laser (wavelength: 633 nm), 300 grooves per mm grating, and Zeiss 50×/0.55 objective lens were used for all the measurements. The laser power was fixed at 15 mW, and the integration time and accumulation number were 0.5 s and 10, respectively.Temperature-dependent single-crystal XRD
Variable-temperature single-crystal X-ray crystallographic data were collected on Bruker D8 Venture, using monochromatic Mo Kα (λ = 0.71073 Å) radiation. Data reduction and cell refinements were performed with the Bruker SAINT Software package using a narrow-frame algorithm. The integration of the data using a cubic unit cell yielded a total of 3276 reflections to a maximum θ angle of 57.41° (0.42 Å resolution). Data were corrected for absorption effects using the Multi-Scan method (SADABS). The ratio of minimum to maximum apparent transmission was 0.283.Time-resolved SEM measurements
A femtosecond pulsed laser (Clark-MXR) with an infrared (IR) wavelength of 1030 nm was integrated with a modified scanning electron microscope (QUANTA 650). The beam generated by the IR laser (repetition rate: 6.25 MHz) was guided by mirrors to a 40/60 beam splitter, which divided the beam into two parts and then used for second and third harmonic generations. The green beam (515 nm) was sent to the scanning electron microscope and focused onto the sample to excite it. The UV beam was directed toward the tip of the gun source in the microscope to generate pulsed electrons rather than using continuously generated thermal electrons. An electronically controlled delay stage was used to move the pump pulse in the time-domain with respect to the probe. The accelerating voltage of the electron beam was 30 kV with a spot size of 7 and pump power of 5.5 mW. The footprint of the pump beam was obtained through a beam-on/beam-off step. The long and short axes were identified as ∼30 and ∼20 μm, respectively. More detailed information about the set-up is available in ref. 57–59. To extract the SE dynamics, we first normalized the image by dividing the maximum value in the whole data matrix to avoid SE intensity fluctuations due to pulsed electrons and crossover propagation. Then, a rectangular area at the centre of the pump spot was selected to calculate the integrated intensity at each delay time to increase the accuracy.DFT calculations
We performed the DFT calculations using the projector-augmented wave method implemented in the Vienna Ab Initio Simulation Package code.60,61 The GGA and PBE exchange-correlation functional were used, and van der Waals interactions were also included in the calculations using the zero-damping DFT-D3 method of Grimme. A uniform grid of 6 × 6 × 6 k-mesh in the Brillouin zone was employed to optimize the crystal structure of cubic-phase MAPbBr3. The energy cutoffs of the wave functions were set to 500 eV for bulk MAPbBr3. The atomic positions of all the structures were fully relaxed until the Hellman–Feynman forces on each atom were less than 0.01 eV Å−1. For evaluating the hot-lattice effect on the electronic structure of MAPbBr3, the lattice parameters were expanded by 0.5, 1.0, 1.5, and 2.0%, respectively, to mimic the crystal structures at different temperatures.Author contributions
L. Wang: conceptualization, data curation, formal analysis, investigation, methodology, writing – original draft, writing – review & editing; H. Wang: investigation, methodology; R. Nughays: data curation, investigation, methodology; W. Ogieglo: data curation, methodology; J. Yin: data curation, formal analysis, methodology; L. Gutiérrez-Arzaluz: data curation, methodology; X. Zhang: methodology; J. Wang: investigation, methodology; I. Pinnau and O. Bakr: supervision, writing – review & editing; O. F. Mohammed: investigation, supervision, writing – original draft, writing – review & editing.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by the King Abdullah University of Science and Technology (KAUST). The authors thank S. Shikin and KAUST Solar Centre for the technical support. The authors also thank Y. Zhang, A. Dikhtiarenko, and KAUST Imaging and Characterization Core Laboratory for the temperature-dependent steady-state measurements.Notes and references
- H. Utzat, W. Sun, A. E. Kaplan, F. Krieg, M. Ginterseder, B. Spokoyny, N. D. Klein, K. E. Shulenberger, C. F. Perkinson and M. V. Kovalenko, Science, 2019, 363, 1068–1072 CrossRef CAS PubMed.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- D. B. Kim, J. Han, Y. S. Jung, K. S. Park, Y. Park, J. Heo and Y. S. Cho, Mater. Horiz., 2022, 9, 1207–1215 RSC.
- Y. Ling, Z. Yuan, Y. Tian, X. Wang, J. C. Wang, Y. Xin, K. Hanson, B. Ma and H. Gao, Adv. Mater., 2016, 28, 305–311 CrossRef CAS PubMed.
- G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar and T. C. Sum, Science, 2013, 342, 344–347 CrossRef CAS PubMed.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344 CrossRef CAS PubMed.
- F. Zu, D. Shin and N. Koch, Mater. Horiz., 2022, 9, 17–24 RSC.
- Y. Tamaki, A. Furube, R. Katoh, M. Murai, K. Hara, H. Arakawa and M. Tachiya, C. R. Chim, 2006, 9, 268–274 CrossRef CAS.
- A. Treglia, F. Ambrosio, S. Martani, G. Folpini, A. J. Barker, M. D. Albaqami, F. De Angelis, I. Poli and A. Petrozza, Mater. Horiz., 2022, 9, 1763–1773 RSC.
- D. R. Ceratti, Y. Rakita, L. Cremonesi, R. Tenne, V. Kalchenko, M. Elbaum, D. Oron, M. A. C. Potenza, G. Hodes and D. Cahen, Adv. Mater., 2018, 30, 1706273 CrossRef PubMed.
- D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger and K. Katsiev, Science, 2015, 347, 519–522 CrossRef CAS PubMed.
- S. Adhikari, J.-H. Kim, B. Song, M.-H. Doan, M. D. Tran, L. Gomez, H. Kim, H. Z. Gul, G. Ghimire and S. J. Yun, Adv. Mater. Interfaces, 2020, 7, 2000835 CrossRef CAS.
- J. Qin, Y. Tang, J. Zhang, T. Shen, M. Karlsson, T. Zhang, W. Cai, L. Shi, W.-X. Ni and F. Gao, Mater. Horiz., 2023, 10, 1446–1453 RSC.
- J. Shah, Ultrafast spectroscopy of semiconductors and semiconductor nanostructures, Springer Science & Business Media, 2013, vol. 115 Search PubMed.
- J. M. Richter, F. Branchi, F. Valduga de Almeida Camargo, B. Zhao, R. H. Friend, G. Cerullo and F. Deschler, Nat. Commun., 2017, 8, 1–7 CrossRef CAS PubMed.
- K. Kaasbjerg, K. S. Bhargavi and S. S. Kubakaddi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 165436 CrossRef.
- V. A. Hintermayr, L. Polavarapu, A. S. Urban and J. Feldmann, ACS Nano, 2018, 12, 10151–10158 CrossRef CAS PubMed.
- J. Yang, X. Wen, H. Xia, R. Sheng, Q. Ma, J. Kim, P. Tapping, T. Harada, T. W. Kee and F. Huang, Nat. Commun., 2017, 8, 14120 CrossRef CAS PubMed.
- J. Katoch, S. Ulstrup, R. J. Koch, S. Moser, K. M. McCreary, S. Singh, J. Xu, B. T. Jonker, R. K. Kawakami and A. Bostwick, Nat. Phys., 2018, 14, 355–359 Search PubMed.
- A. Raja, A. Chaves, J. Yu, G. Arefe, H. M. Hill, A. F. Rigosi, T. C. Berkelbach, P. Nagler, C. Schüller, T. Korn, C. Nuckolls, J. Hone, L. E. Brus, T. F. Heinz, D. R. Reichman and A. Chernikov, Nat. Commun., 2017, 8, 15251 Search PubMed.
- E. J. Sie, A. Steinhoff, C. Gies, C. H. Lui, Q. Ma, M. Rösner, G. Schönhoff, F. Jahnke, T. O. Wehling, Y.-H. Lee, J. Kong, P. Jarillo-Herrero and N. Gedik, Nano Lett., 2017, 17, 4210–4216 CrossRef CAS PubMed.
- N. Del Fatti, R. Bouffanais, F. Vallée and C. Flytzanis, Phys. Rev. Lett., 1998, 81, 922–925 CrossRef CAS.
- A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Pérez-Osorio, H. J. Snaith, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- Z. Zhenfu, J. Liang, W. Zhihai, C. Jiong, Z. Miaomiao and H. Yafei, J. Mater. Sci., 2018, 53, 15430–15441 CrossRef CAS.
- J. Xing, F. Yan, Y. Zhao, S. Chen, H. Yu, Q. Zhang, R. Zeng, H. V. Demir, X. Sun and A. Huan, ACS Nano, 2016, 10, 6623–6630 CrossRef CAS PubMed.
- Y. Guo, O. Yaffe, T. D. Hull, J. S. Owen, D. R. Reichman and L. E. Brus, Nat. Commun., 2019, 10, 1175 CrossRef PubMed.
- J. Sung, C. Schnedermann, L. Ni, A. Sadhanala, R. Chen, C. Cho, L. Priest, J. M. Lim, H.-K. Kim and B. Monserrat, Nat. Phys., 2020, 16, 171–176 Search PubMed.
- B. S. Shaheen, A. M. El-Zohry, J. Zhao, J. Yin, M. N. Hedhili, O. M. Bakr and O. F. Mohammed, ACS Appl. Mater. Interfaces, 2020, 12, 7760–7767 CrossRef CAS PubMed.
- B. S. Shaheen, A. M. El-Zohry, J. Yin, M. De Bastiani, S. De Wolf, O. M. Bakr and O. F. Mohammed, J. Phys. Chem. Lett., 2019, 10, 1960–1966 CrossRef CAS PubMed.
- G. Meizyte, R. Bose, A. Adhikari, J. Yin, M. A. Haque, M. R. Parida, M. N. Hedhili, T. Wu, O. M. Bakr and O. F. Mohammed, J. Phys. Chem. C, 2018, 122, 15010–15016 CrossRef CAS.
- R. Bose, A. Adhikari, V. M. Burlakov, G. Liu, M. A. Haque, D. Priante, M. N. Hedhili, N. Wehbe, C. Zhao and H. Yang, ACS Energy Lett., 2018, 3, 476–481 CrossRef CAS.
- A. M. El-Zohry, B. S. Shaheen, V. M. Burlakov, J. Yin, M. N. Hedhili, S. Shikin, B. Ooi, O. M. Bakr and O. F. Mohammed, Chem, 2019, 5, 706–718 CAS.
- T. Palmieri, E. Baldini, A. Steinhoff, A. Akrap, M. Kollár, E. Horváth, L. Forró, F. Jahnke and M. Chergui, Nat. Commun., 2020, 11, 1–8 CrossRef PubMed.
- J. Fu, Q. Xu, G. Han, B. Wu, C. H. A. Huan, M. L. Leek and T. C. Sum, Nat. Commun., 2017, 8, 1–9 CrossRef CAS PubMed.
- Y. Yang, Y. Yan, M. Yang, S. Choi, K. Zhu, J. M. Luther and M. C. Beard, Nat. Commun., 2015, 6, 1–6 Search PubMed.
- M. Feng, S. Ye, J. W. M. Lim, Y. Guo, R. Cai, Q. Zhang, H. He and T. C. Sum, Small, 2023, 2301831 CrossRef PubMed.
- K. G. Stamplecoskie, J. S. Manser and P. V. Kamat, Energy Environ. Sci., 2014, 8, 208–215 RSC.
- Y. Yang, D. P. Ostrowski, R. M. France, K. Zhu, J. van de Lagemaat, J. M. Luther and M. C. Beard, Nat. Photon, 2016, 10, 53–59 CrossRef CAS.
- M. Feneberg, S. Osterburg, K. Lange, C. Lidig, B. Garke, R. Goldhahn, E. Richter, C. Netzel, M. D. Neumann and N. Esser, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075203 CrossRef CAS.
- K.-F. Berggren and B. E. Sernelius, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 1971–1986 CrossRef CAS.
- M. B. Price, J. Butkus, T. C. Jellicoe, A. Sadhanala, A. Briane, J. E. Halpert, K. Broch, J. M. Hodgkiss, R. H. Friend and F. Deschler, Nat. Commun., 2015, 6, 1–8 Search PubMed.
- A. Chernikov, C. Ruppert, H. M. Hill, A. F. Rigosi and T. F. Heinz, Nat. Photonics, 2015, 9, 466–470 CrossRef CAS.
- H. Zhang, T. Zhang, Y. Wang, Y. Chen, Y. Zhao and J. Chen, Mater. Horiz., 2023, 10, 875–880 RSC.
- K.-H. Wang, L.-C. Li, M. Shellaiah and K. Wen Sun, Sci. Rep., 2017, 7, 13643 CrossRef PubMed.
- B. Johs and J. S. Hale, Phys. Status Solidi A, 2008, 205, 715–719 CrossRef CAS.
- K. Pydzińska, J. Karolczak, M. Szafrański and M. Ziółek, RSC Adv., 2018, 8, 6479–6487 RSC.
- R. R. Tamming, J. Butkus, M. B. Price, P. Vashishtha, S. K. K. Prasad, J. E. Halpert, K. Chen and J. M. Hodgkiss, ACS Photonics, 2019, 6, 345–350 CrossRef CAS.
- W. Bludau, A. Onton and W. Heinke, J. Appl. Phys., 1974, 45, 1846–1848 CrossRef CAS.
- K. P. O’donnell and X. Chen, Appl. Phys. Lett., 1991, 58, 2924–2926 CrossRef.
- J. Wu, W. Walukiewicz, W. Shan, K. M. Yu, J. W. Ager Iii, S. X. Li, E. E. Haller, H. Lu and W. J. Schaff, J. Appl. Phys., 2003, 94, 4457–4460 CrossRef CAS.
- M. Liu, S. D. Verma, Z. Zhang, J. Sung and A. Rao, Nano Lett., 2021, 21, 8945–8951 CrossRef CAS PubMed.
- X.-Y. Zhu and V. Podzorov, J. Phys. Chem. Lett., 2015, 6, 4758–4761 CrossRef CAS PubMed.
- T. M. Brenner, D. A. Egger, A. M. Rappe, L. Kronik, G. Hodes and D. Cahen, J. Phys. Chem. Lett., 2015, 6, 4754–4757 CrossRef CAS PubMed.
- M. Karakus, S. A. Jensen, F. D’Angelo, D. Turchinovich, M. Bonn and E. Canovas, J. Phys. Chem. Lett., 2015, 6, 4991–4996 CrossRef CAS PubMed.
- H. Wang, X. Wang, R. Chen, H. Zhang, X. Wang, J. Wang, J. Zhang, L. Mu, K. Wu, F. Fan, X. Zong and C. Li, ACS Energy Lett., 2019, 4, 40–47 CrossRef CAS.
- A. O. El-Ballouli, E. Alarousu, M. Bernardi, S. M. Aly, A. P. Lagrow, O. M. Bakr and O. F. Mohammed, J. Am. Chem. Soc., 2014, 136, 6952–6959 CrossRef CAS PubMed.
- J. Sun, A. Adhikari, B. S. Shaheen, H. Yang and O. F. Mohammed, J. Phys. Chem. Lett., 2016, 7, 985–994 CrossRef CAS PubMed.
- J. Sun, V. A. Melnikov, J. I. Khan and O. F. Mohammed, J. Phys. Chem. Lett., 2015, 6, 3884–3890 CrossRef CAS PubMed.
- O. F. Mohammed, D.-S. Yang, S. K. Pal and A. H. Zewail, J. Am. Chem. Soc., 2011, 133, 7708–7711 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00570d |
| This journal is © The Royal Society of Chemistry 2023 |