Molecular insights into the hydration of zwitterionic polymers

Abstract

Preventing ice formation and accumulation on solid surfaces has been a great challenge to address for various engineering and technological applications. Recently, the new development of zwitterionic polymer coatings attracted a lot of attention due to their excellent anti-icing performance (i.e., effectively reducing ice formation and adhesion), making them ideal material candidates for anti-icing coating applications. In this study, we employ density functional theory (DFT) to explore the hydration behaviors of two representative zwitterionic polymers, i.e., poly(sulfobetaine-methacrylate) (polySB) and poly(2-methacryloxoethyl-phosphorylcholine) (polyMPC). Through detailed bonding analysis by crystal orbital Hamilton populations (COHP), our results indicate strong interaction and covalent-nature bonds between the hydrogen atoms in water molecules and polymers' oxygen atoms of the anionic group of the polymer. Electron partial density of states (PDOS), Bader charge analysis, and energy calculations further demonstrate the physical and chemical nature of the water–polymer bonds. Interestingly, our modeling results also reveal that the addition of more water molecules will decrease the bonding stability of the bond between adsorbed water molecules to the polymer. Such induced bond instability, along with the polymer's hydrophilic character, suggests that continuous association and dissociation of bonded water molecules serve as the key mechanism which explains the inhibition of water clustering of the hydration layer. Our findings provide valuable insights into the physiochemical nature of water–polymer interaction by unveiling the molecular mechanism of hydration behavior, paving the way for design of next-generation anti-icing materials.

---

Design, System, Application

Zwitterionic polymers have emerged as a promising material for anti-icing applications. However, a lack of fundamental understanding of the interfacial hydration mechanism of these polymers has hindered their design and optimization for improved anti-icing performance. To address this issue, we conducted an atomistic modeling study based on density functional theory (DFT) to investigate how the charge distribution and specific zwitterionic units (i.e., phosphorylcholine and sulfobetaine groups) impact the hydration behaviors of zwitterionic polymers. Our results reveal that the anionic group of the polymer chain plays a crucial role in governing the strength of interaction with water molecules, which ultimately affects the ice formation energy. Specifically, we found that the more negatively charged the anionic group, the stronger the anti-icing effect it will have. These findings highlight the critical role of the zwitterionic unit in the water–polymer interaction and suggest a materials-by-design approach to engineer anti-icing polymers through molecular design.

Introduction

In a harsh and cold environment, ice is a significant problem for many engineering applications, ranging from aircraft,¹ ships,² trains, power lines,³ to renewable systems,⁴ which can cause significant damage and lead to great economic losses. An efficient, environmental, and economical solution to the icing issue is essential. As early as 1946, there have been growing efforts to prevent water icing on surfaces by using ice-phobic, superhydrophobic, and anti-icing coatings.⁵ Up to date, many approaches and strategies have been proposed to develop and optimize efficient and durable anti-icing coatings that can inhibit the formation, propagation, and adhesion of ice.⁶ To reduce ice adhesion, various methods have been employed; for instance, aqueous or organic lubricant coatings have demonstrated relatively good anti-icing performance.^7,8 Additionally, coatings with wetting properties,^9,10 charges, and ions have been used to inhibit and delay the ice nucleation of freezing sessile droplets on the surface.^6,11

Building upon earlier efforts, He et al.¹² studied the effect of counter ions on ice nucleation using cationic poly[2-(methacryloyloxy)-ethyltrimethylammonium] (PMETA) and anionic poly(3-sulfopropylmeth-acrylate) (PSPMA) brushes surfaces. Their study showed that the counter ions affect how fast the water forms ice-like crystals and thus change the ice nucleation temperature. The influence of the surface charge on ice nucleation was studied by Lubomirsky et al.,¹³ who observed that the negatively charged surfaces reduced the ice nucleation temperature while the positively charged surfaces resulted in an increase in ice crystal growth rate. Similar observations were later made by Yang et al.,¹⁴ who investigated the role of surface charges in ice formation dynamics on the supercharged polypeptide surfaces. Inspired by ice skating, Wang et al.^15,16 demonstrated that hydrophilic polymer coating can be better ice-phobic surfaces and anti-icing coatings than hydrophobic coatings that loses its superhydrophobicity under high humidity or at high pressure. They found that paired water molecules on the hydrophilic polymer can act as an aqueous lubricating layer that is naturally replenished from the ambient conditions. Since then, many hydrophilic materials have been investigated as a potential ice-phobic and anti-icing coatings.¹⁷ Yu et al.¹⁸ found that the hydrophilic segment of the amphiphilic lubricant strongly bonded to water molecules through hydrogen bonds and formed non-freezable adsorbed water molecules, leading to decreases in the freezing point of water and delay of the formation of ice crystals on the surface. Lately, Lingru et al.¹⁹ fabricated superior crosslinked anti-icing coatings made of polydimethylsiloxane (PDMS)-dangling zwitterionic polyurethane (ZPU) (PDMS-D + ZPU) and polyhedral oligomeric silsesquioxane (POSS)-dangling ZPU (POSS-D + ZPU) coatings with crosslinked structure that created micropatterned surface that prevented water-induced swelling damage to the coatings.

Recently, zwitterionic polymers have gained considerable attentions as coatings for anti-icing applications. Various zwitterionic polymers have been synthesized and developed, e.g., sulfobetaine (SB), carboxybetaine (CB), or phosphorylcholine (PC), which have the same number of anions and cation (i.e., typically quaternized ammonium) groups on the chains, making them highly hydrophilic and antifouling, i.e., the chains tend to orient towards the surface in contact with water.²⁰ Liang et al.¹⁷ synthesized superhydrophilic polyzwitterion brushes of poly(sulfobetaine methacrylate) (PSBMA) on silicon wafers and showed an excellent anti-icing coating properties arising from the large non-freezable bound water leading to low ice adhesion strength even with film thicknesses as low as ∼100 nm. Furthermore, PC-containing polymers showed strong resistance to protein adsorption and cell adhesion, among them 2-methacryloyloxyethyl phosphorylcholine (MPC) had the best performance.²¹ Inspired by the phospholipid structure on cell membranes, the zwitterionic 2-methacryloyloxyethyl phosphorylcholine (MPC) moiety was developed to yield an excellent antifouling property.²⁰ Feng et al. used atom-transfer radical polymerization (ATRP) to grow MPC brushes from silicon wafers which had significant decrease in protein and cell adhesion.²² MPC antifouling performance is presumably due to the tightly bonded water layer on the brushes which prevents proteins from approaching surfaces.^20,23 Furthermore, recent studies have shown that zwitterionic polymers can be used to create oleophobic coatings for a variety of applications such as self-cleaning surfaces, anti-fouling coatings, and oil–water separation membranes.^24,25

Although zwitterionic polymers have shown great potential for anti-icing applications, the interfacial hydration mechanism of these polymers remains largely elusive at a fundamental level. This limits the design and performance improvement of zwitterionic anti-icing coatings particularly due to a lack of understanding of the effects of charge distribution and specific zwitterionic units on hydration behaviors. Some recent research used molecular dynamics (MD) simulations to provide an in-depth understanding of zwitterionic polymers at atomic level.^26–29 For instance, Shao and coworkers conducted a study where they analyzed the rheological properties of sulfobetaine and carboxybetaine polymers as a function of temperature and their hydrodynamic sizes as a function of salt concentration.²⁹ Their findings revealed that carboxybetaine polymers do not exhibit stimuli responses as expected from the antipolyelectrolyte behavior of zwitterionic polymers as observed in sulfobetaine polymers. According to their simulation results, the difference in stimuli responses between carboxybetaine and sulfobetaine polymers can be attributed to the charge-density difference between their cationic and anionic groups, which determines the associations among the zwitterionic moieties. In another work, Shao et al. used MD simulations to investigate the influence of charged groups on the properties of zwitterionic moieties. All studied zwitterionic moieties exhibit strong hydration, but their structural and dynamic properties differ depending on the cationic and anionic groups present.²⁸ In addition, they found that the charged groups are also present in the self-association and protein interactions of zwitterionic moieties.

To improve the effectiveness of zwitterionic polymers in antifouling and anti-icing applications, an in-depth understanding of the molecular level interactions between zwitterionic polymers and water is required. To bridge this knowledge gap, in this study, we employ atomistic modeling approach based on density functional theory (DFT) to conduct a thorough examination of the fundamental interactions between zwitterionic polymers and water at the molecular and electronic levels, for the first time. DFT is a powerful computational tool that is capable of accurately calculating weak interactions and predicting the electronic structure of adsorbates and adsorbents, which is crucial for understanding the adsorption process. By comparing two representative zwitterionic polymers, polysulfobetaine (polySB) and polyphosphorylcholine (polyMPC), as potential anti-icing coating polymers, we aim to gain in-depth insights into the hydration process and provide a physical and chemical understanding of the water–polymer interaction at a fundamental molecular level, which is needed to develop an extension of structure–property relationships for materials by design.

Methods

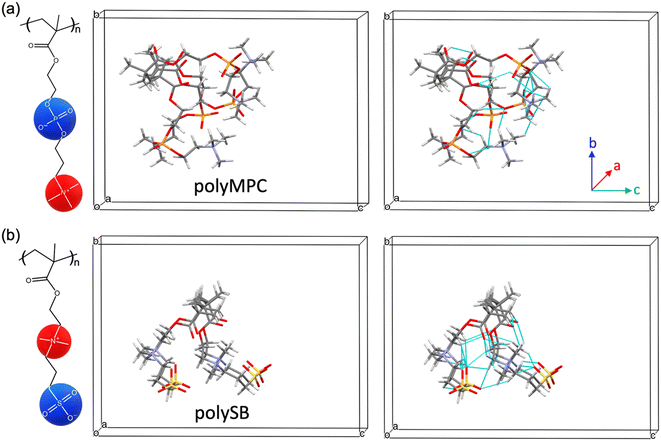
As previously mentioned, polySB and polyMPC demonstrated remarkable resistance to icing and fouling, as shown in experiments.¹⁷ Structurally, they possess a reversed charge distribution, with polySB having an anionic terminal group and polyMPC having a cationic terminal group. Additionally, they have distinct anionic groups, phosphorylcholine in polyMPC and sulfobetaine in polySB. Hence, in this study, we selected these two zwitterionic polymers to gain insights into designing effective anti-icing coatings. For both studied polymers, polySB and polyMPC, we use periodic structure models of one “short” chain with four monomers surrounded by vacuum to avoid any possible interactions between periodic replicas. The atomic structure of the 3D periodic models of polySB and polyMPC are shown in Fig. 1. Then, water molecules are incrementally added to the simulation cell to simulate polymer hydration with different water content. All dry and wet models are fully optimized to the ground structure before hydration and bonding analysis. The Vienna ab initio Simulation Package (VASP)^30–32 is used to perform non-spin-polarized planewave DFT calculations, where the core and valence electrons are described using the projector-augmented wave (PAW)^33,34 and the generalized-gradient approximation in the Perdew–Burke–Ernzerhof (PBE) form is used to describe electron exchange and correlation.³⁵ The Kohn–Sham equations are used to improve the accuracy of self-consistent density functional theory (DFT) calculations. The theoretical single-electron Kohn–Sham equation can be expressed as

(−ℏ²/2m∇² + v[{R⃑_I}, r⃑, ρ(r⃑)])φ^KS_i({R⃑_I}, r⃑) = ε_i({R⃑_I})φ^KS_i({R⃑_I}, r⃑) (1)

where first term corresponds to kinetic energy T and uses symbol of gradient . In the eqn (1), we find a set of one-electron orbital's φ^KS_i({R⃑_I}, r⃑) and their energies ε_i. The orbitals are combined with orbital occupation function f_i for constructing the total density of electrons (ρ) that is composed out of pairs of orbitals with coinciding indicesTotal density determines the potential as following

v[r⃑, ρ] = δ/δρ(E^tot[ρ] − T[ρ]) (3)

Fig. 1 Ground polymer structures with 4 monomers for (a) polyMPC and (b) polySB. The left and right simulation cells show the optimized configurations of models with and without visualization of hydrogen bonds, respectively. Dashed cyan line represents hydrogen bonds. Red, yellow, orange, purple, gray, and white atoms are oxygen, sulfur, phosphorus, nitrogen, carbon, and hydrogen, respectively.

Dispersion interactions are considered by applying Grimme's PBE-D₃ corrections with Becke–Johnson damping function.³⁶ The kinetic energy cutoff is set to 400 eV and the Gaussian smearing of 0.03 eV is used for Brillouin-zone integrations. Atomic positions are optimized using the conjugate-gradient method with energy and force tolerance of 10⁻⁶ eV and 0.01 eV Å⁻¹, respectively. The electron density of states (DOS) is a measure of the number of states within a specific energy range. It is used to analyze the electronic structure of a system. The definition of DOS is

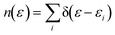where the Dirac delta function is approximated using a Gaussian function of finite width. Then, the Bader method is used to perform partial charges analysis of all atoms in the calculated ground structures.^37–40

To provide a detailed picture of the nature of the bonding between water and polymer, we carry out charge density and chemical bonding analyses by calculating the crystal orbital Hamilton population (COHP)⁴¹ using the Local Orbital Basis Suite Toward Electronic-Structure Reconstruction (LOBSTER) code.⁴² To examine interaction strength, water adsorption energies are calculated using the following equation: ΔE_Ads = (E_surf+H2O − E_surf − E_H2O)/n, where E_surf+H2O is the energy of the wet surface, E_surf is the energy of the initial dry surface, E_H2O is the energy of a free water molecule, and n is the number of water molecules per simulation cell. Furthermore, to include the temperature effect, the Gibbs free energy⁴³ is calculated according to the following equation: ΔG = (ΔH − TΔS)/n, where ΔS is the difference of entropy between the adsorption state of hydrogen and gas phase, ΔH is the change in enthalpy, and T is temperature. If water adsorption is a spontaneous reaction, then ΔG will be negative.

Results and discussion

Electronic structure of zwitterionic polymers

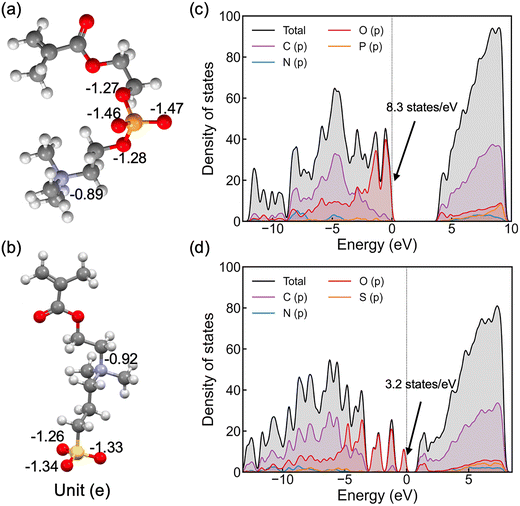
We first examine the atomic and electronic properties of the ground structure of dry zwitterionic polymers, as depicted in Fig. 1. As expected, the simulated ground structures of polySB and polyMPC have “physical” crosslinking in the form of hydrogen bonds between their side chains due to the strong dipole–dipole interaction between their anionic and cationic groups, as shown in the right simulation cells in Fig. 1. PolyMPC has more crumpled ground structure and longer side chains than polySB, which has more straight side chains. However, polySB has a larger number of hydrogen bonds within its side chains, with an average bond length of 2.38 Å, while in polyMPC it is 2.42 Å. Since atomic charges play an important role in the interaction of charged groups, we use Bader charge analysis to calculate the charge of the main atoms in the anionic and cationic groups. The Bader electron population of the atom (Q^Bader_A) is calculated as the integral of the electron density (ρ(r)) over the atomic basin (Ω_A) .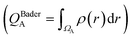

As shown in Fig. 2(a and b), nitrogen atoms in the cationic groups of both polymers have almost the same charge. However, oxygen atoms in the anionic groups of polyMPC are more negatively charged compared to those in polySB. This can be attributed to the fact that phosphorus is less electronegative than sulfur, which results in more localized electrons at the negatively charged oxygen atoms. Furthermore, polyMPC is more polar than polySB with total dipole moments of 51.45 e Å for polyMPC, compared to 48.7 e Å for polySB. The stronger dipole moment of polyMPC makes it more susceptible to interactions with other polar molecules.

Fig. 2 Calculated average Bader atomic charges for (a) polyMPC and (b) polySB. Partial density of states of (c) polyMPC and (d) polySB, where the Fermi level is marked as vertical dotted lines at zero energy.

To gain further insight into the electronic properties of these polymers, we calculate the electron density of states (DOS) (Fig. 2c and d) and find that polyMPC has an intense occupied state at the Fermi level, equals to 8.3 states per eV, compared to 3.2 states per eV for polySB. These states refer to free electrons at the Fermi level and are mainly from the oxygen p orbitals in the anionic group, which tend to overlap with the adsorbate's orbitals. This analysis suggests that the adsorbate (e.g., water) can form a strong bonding interaction with these zwitterionic polymers, especially for polyMPC. To further understand the nature of this bonding, we investigate the interaction between water and the polymers in detail next.

Polymer hydration behavior

The hydrated polymer models are prepared by gradually adding water molecules to the periodic cell of the polymers, starting with 2H₂O/cell and increasing to 16H₂O/cell. This corresponds to a water content (WC) (i.e.,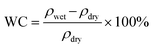 ) of 3.23% to 25.81% for polySB and 3.04% to 24.39% for polyMPC, respectively. From our simulations, it is observed that water molecules form bond to the oxygen atoms of the polymers and prefers those in the anionic group. However, no water molecules are observed to bond to nitrogen atoms in the cationic group. Geometry optimizations are performed for all hydrated models and the resulted ground structures as shown in Fig. S1 and S2.†

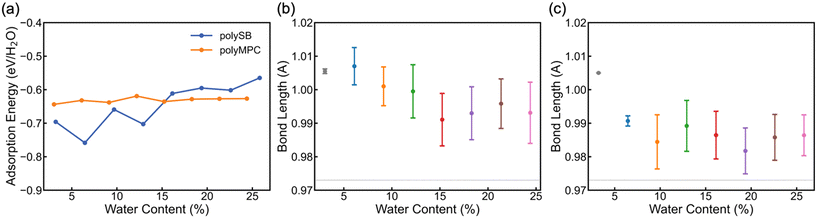
To determine the stability and bond strength of adsorbed water molecules, we calculate the water adsorption energy per H₂O (E_Ads/H₂O) versus water content. Fig. 3a shows that the water molecules are tightly bonded to both polymers with adsorption energy <−0.6 eV (i.e., >58 kJ mol⁻¹ or 14 kcal mol⁻¹) at 0° K. It is important to note that the negative adsorption energy of water molecules on polySB is higher at low water content due to the flexibility of its side chains and the interaction between the side chains, rather than due to a stronger bonding between water and polymer (which will be discussed in more detail later). Also, Fig. S3† shows the calculated water Gibbs adsorption energy for both polymers is negative bellow 0 °C, which indicates a spontaneous adsorption as expected. The average bond length between the polymer oxygen atom and water hydrogen atom (O_poly–H_water) is 1.83 Å, corresponding to the donor–acceptor (O_poly–O_water) distance of 2.8 Å.

Fig. 3 (a) Calculated water adsorption energy per water molecule vs. WC. (b) and (c) The mean and standard of deviation of the O_water–H_water⋯O_poly covalent bond length in the adsorbed water molecules where the H_water atom is bonded to O_poly atom of polyMPC and polySB, respectively. The horizontal dashed line points to O_water–H_water covalent bond length of 0.973 Å in free water molecule.

According to Jeffrey's criterion,⁴⁴ hydrogen bonds with donor–acceptor distances of 2.2–2.5 Å are classified as “strong (mostly covalent)”, 2.5–3.2 Å are classified as “moderate (mostly electrostatic)”, and 3.2–4.0 Å are classified as “weak (electrostatic)”, associated with the bond strengths of 40–14, 15–4, and <4 kcal mol⁻¹, respectively. In comparison, chemical coordinate covalent bonds have a bond strength of ∼50 kcal mol⁻¹ and physical van der Waals interactions have a bond strength of ∼1 kcal mol⁻¹ at room temperature.⁴⁵ Also, G. R. Desiraju⁴⁶ categorizes hydrogen bonds into three types: very strong bonds with pronounced covalency, strong bonds with weak covalency, and weak bonds with no covalency. These bonds have donor-hydrogen lengthening (Å) of 0.05–0.2, 0.01–0.05, and 0.01, respectively. Thus, we calculate the donor-hydrogen bond length in our hydrated models, which is the oxygen–hydrogen covalent bond in adsorbed water molecules where the hydrogen atom is bonded to the polymer's oxygen atoms (O_water–H_water⋯O_poly). Fig. 3b and c shows the mean and the standard deviation of the (O_water–H_water⋯O_poly) covalent bond length in polyMPC and polySB with different water content. The calculated bond length increase is more than 0.02 Å for both polymers, but it is larger for polyMPC than polySB, which indicates a stronger hydrogen bond between polyMPC and water molecules. Therefore, our simulation suggests that the interaction between zwitterionic polymers and water molecules is more than just an electrostatic physical interaction.

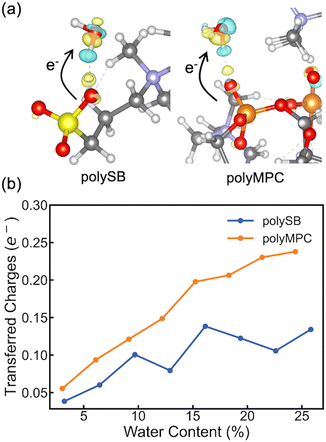
To gain a deeper understanding of the interfacial charge distribution, we calculate the differential charge density and charge transfer after adsorption. This allows us to better analyze the interaction between the polymers and adsorbed water molecules. The differential charge density, Δρ, can be obtained by subtracting the charge density of the isolated polymer and water from the charge density of the polymer structure with bonded water: Δρ = ρ_total − (ρ_poly + ρ_H2O). Here, ρ_total, ρ_poly, and ρ_H2O represent the charge densities of the polymer structure with bonded water, isolated polymer, and water, respectively. As shown in Fig. 4a, the differential charge density plots for both polymers with two adsorbed water molecules reveal some charge accumulation at the interface, as shown by the yellow bubble between the polymer's oxygen atom and the water hydrogen atom. The formation of bonds with chemical/covalent nature and orbital overlap between the polymer and water molecules is confirmed by such significant charge redistribution. To get more quantitative charge redistribution results, we calculate the sum of the atomic charge of adsorbed water molecules that was calculated using both Bader's method and the orbital-based Löwdin charges. Fig. 4b shows that the increase in water content led to more charge transferred to the adsorbed water molecules. There is more charge transferred from polyMPC than polySB, which perfectly agrees with the observed Fermi-level electron state in polyMPC PDOS. Both Bader and Löwdin charges gave the same overall trend. However, in Fig. S4,† the later showed higher charge transfer from the polymers to adsorbed water molecules and an off-trend peak for polySB with a water content of 9.68%.

Fig. 4 (a) Differential charge density plots for both polymers with two adsorbed water molecules (yellow color: charge accumulation; cyan color: charge depletion). (b) Total charge transferred from polymers to the adsorbed water molecules based on Bader charges.

Our results so far indicate that water molecules bond to zwitterionic polymers via strong hydrogen bonds with some covalency, which is quantitatively different from normal hydrogen bonding.^46,47 Other systems that primarily contain ionic species, such as Cl⁻–H₂O, F⁻–H₂O, and H₃O⁺–H₂O, have also shown evidence of strong hydrogen bonds with interaction energies of roughly 15, 30, and 35 kcal mol⁻¹, respectively.⁴⁸ More recently, Dereka et al.⁴⁹ used experimental characterization and DFT simulations to show the chemical nature of the very strong hydrogen bond in F⁻⋯HF complex with interaction energies of ∼40 kcal mol⁻¹. Their results confirmed the covalent nature of strong hydrogen bond, which are consistent with our simulation observations.

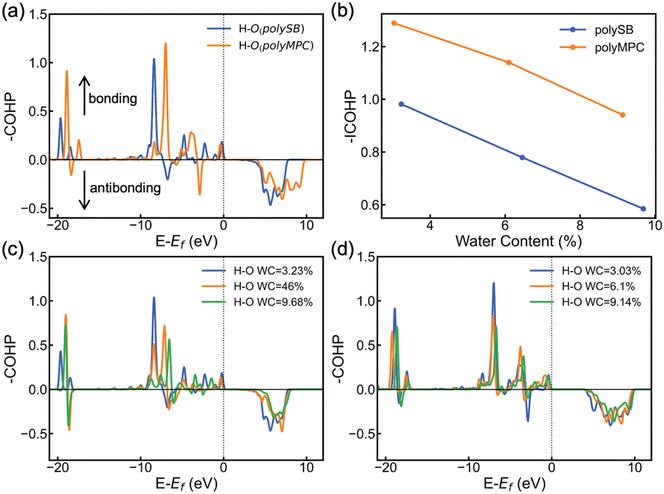
To further understand the stability and covalent nature of the bond between zwitterionic polymers and water, we employ COHP to conduct chemical analysis. COHP analysis indicates bonding and antibonding interactions with negative and positive −COHP values, respectively. The cumulative integration of −COHP up to the Fermi level (E_f), or −ICOHP values, determines the bonding–antibonding balance, and thus characterizes the bonding strength. Fig. 5a shows the calculated −COHP of the bond between the hydrogen atom of adsorbed H₂O and the nearest oxygen atom of the polySB and polyMPC bonds at water content of 3.23% and 3.03%, respectively. This comparison of the two polymers' bonding interactions with adsorbed water molecules reveals the presence of strong and deep positive bonding states below the Fermi level. This indicates the existence of a stable O_poly–H_water bond and confirms the covalent contribution to the bond, as revealed by the topological analysis and adsorption energy results.

Fig. 5 (a) Crystal orbital Hamilton population (−COHP) of the bond between hydrogen atom of the adsorbed H₂O and the nearest oxygen of polySB and polyMPC at WC = 3.23% and 3.03%, respectively. (b) Integrated −COHP (−ICOHP) vs. water content, calculated −COHP for the bond between hydrogen atom of adsorbed H₂O and nearest oxygen atom of the polySB (c) and polyMPC (d) at different WC.

Furthermore, Fig. 5a and b shows that the O_poly–H_water bond in polyMPC is stronger than in polySB, which is consistent with the shorter O_poly–H_water bond length of 1.68 Å in polyMPC compared to 1.84 Å in polySB, as well as the greater charge transferred to the adsorbed water molecules from polyMPC than from polySB. Interestingly, in Fig. 5b, we observe that the increase in water content, which results in a thicker hydration layer, leads to a decrease in the strength of the O_poly–H_water bond of the closest water molecule to the polymer. Such weakening of the O_poly–H_water bond is also evident in the depression of the −COHP bonding states in Fig. 5c and d.

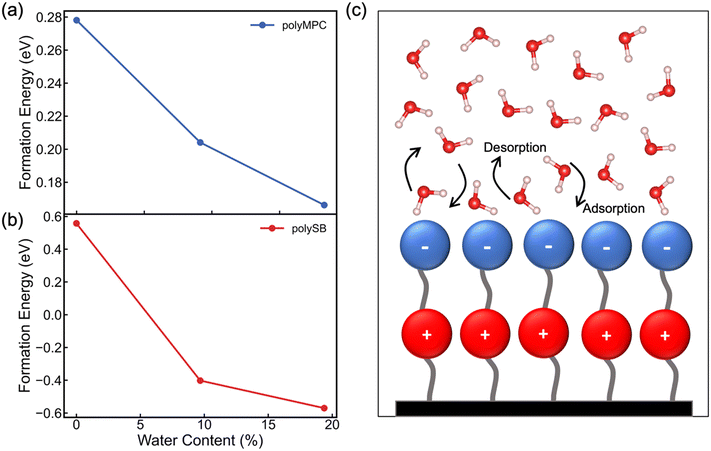
We next evaluate the formation energy (E_form) to further test the hypothesis that the strongly bonded dynamic hydration layer will not likely freeze as informed from our above analysis. In our simulation, E_form is calculated from the energy difference of four H₂O molecules forming a small ice cluster on polymer relative to the same number of adsorbed liquid like water molecules: 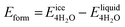, where 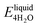is the total energy of the polymer with four adsorbed water molecules and 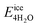is the total energy of the system with adsorbed ice cluster. Ground structures of adsorbed ice cluster are shown in Fig. S5.† The calculated clustering formation energies are +0.28 eV for polyMPC and +0.58 eV for polySB, in the absence of water, as shown in Fig. 6a and b. This result indicates that there is repulsion between the interacting components, making the tightly adsorbed ice clusters right on polymers is energetically unfavorable and unstable.

Fig. 6 Calculated formation energy for small ice cluster of the farther water molecules from the surface of (a) polyMPC and (b) polySB vs. WC of the hydration layer. (c) A schematic illustration showing the expected dynamic of polySB hydration layer.

We further calculate the formation energy needed for small ice clustering on hydrated polymer surface, in the present of hydration layer with water content of approximately 9.5% and 19.5%. The resulting formation energy of the cluster (shown in Fig. 6a and b) significantly decreases on both wet polymers, but remains positive on polyMPC, suggesting that a thicker layer of water molecules needs to be present on the surface of polyMPC before ice formation. These results help to explain the experimental observation that the delayed ice nucleation or formation and the low ice adhesion on polySB, which is likely due to the presence of a non-freezable hydration layer.¹⁷ The similar observation was found with poly(ethylene glycol),⁵⁰ which reduces ice adhesion due to hydrogen-bonded water molecules on the surface that do not freeze and serve as a self-lubricating interfacial layer. Based on our simulation results, it is expected that it will take longer time and more water to form ice on polyMPC compared to polySB and that polyMPC will have much lower ice adhesion strength due to a thick water-lubricating interfacial layer. Our findings suggest polyMPC is an excellent candidate for anti-icing coating applications outperforming polySB. Additionally, the previously indicated bond instability (Fig. 5b) along with the superhydrophilic nature of the polymers suggest that the nearest layer of adsorbed water molecules on the polymer surface has dynamically bond forming and breaking, as illustrated in Fig. 6c. This dynamic hydration layer acts as a non-freezing hydration lubricant, which has been suggested by Yu et al.,¹⁸ who observed similar hydration lubricant on the hydrophilic segment made of strongly bonded water molecules through hydrogen bonds, which forms non-freezable adsorbed water molecules. Built upon our modeling framework established in this study, in the future, it is worth testing a larger number of polymers having diverse chemical structures to further understand the relationship between the anti-icing properties and their molecular characteristics of zwitterionic polymers.

Conclusion

In this study, we investigate the intermolecular interactions between water molecules and two representative superhydrophilic zwitterionic polymers using DFT. We find that polyMPC and polySB have different atomic structures and electronic properties, leading to contrast hydration behaviors associated with interactions with water. Particularly, polyMPC has a more crumpled ground structure, a stronger total dipole moment, and more occupied states at the Fermi level compared to polySB. Detailed bonding analyses demonstrate that the bond between water and polyMPC is stronger compared to polySB, with polyMPC exhibiting more charge transfer to tightly adsorbed water molecules. The partial covalent nature of the polymer–water bond is further confirmed by COHP chemical bonding analysis. The tightly bonded first layer of adsorbed water molecules, known as the hydration layer, does not freeze and acts as a self-lubricating interfacial layer. These characteristics explain the observed delay of ice formation on zwitterionic polymers with relatively low ice adhesion. Our findings suggest that the strong interaction between water and polyMPC make it a promising candidate for anti-icing applications. Our work provides valuable insights into the hydration mechanism of zwitterionic polymers at a fundamental level, paving the way for establishing a materials-by-design strategy for high-performance anti-icing polymers.

Author contributions

W. X. supervised and coordinated all aspects of the project. S. A. T. performed all the calculations and analysis. Both authors contributed to the writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the support from the U.S. Office of Naval Research (ONR) (Award No. N00014-22-1-2129). This work used resources of the Center for Computationally Assisted Science and Technology (CCAST) at NDSU, which were made possible in part of NSF MRI (Award No. 2019077).

References

1. J. Xiao and S. Chaudhuri, Langmuir, 2012, 28, 4434–4446.
2. X. Yao, Y. Song and L. Jiang, Adv. Mater., 2011, 23, 719–734.
3. J. Lv, Y. Song, L. Jiang and J. Wang, ACS Nano, 2014, 8, 3152–3169.
4. O. Parent and A. Ilinca, Cold Reg. Sci. Technol., 2011, 65, 88–96.
5. H. L. Lein, Front. Nanosci., 2019, 14, 257–269.
6. X. Zhou, Y. Sun, J. Liu, X. Zhou, Y. Sun and J. Liu, Adv. Mater. Interfaces, 2021, 8, 2100327.
7. M. J. Kreder, J. Alvarenga, P. Kim and J. Aizenberg, Nat. Rev. Mater., 2016, 1, 15003.
8. T. S. Wong, S. H. Kang, S. K. Y. Tang, E. J. Smythe, B. D. Hatton, A. Grinthal and J. Aizenberg, Nature, 2011, 477, 443–447.
9. D. Richard, C. Clanet and D. Quéré, Nature, 2002, 417, 811–811.
10. L. Wang, Q. Gong, S. Zhan, L. Jiang and Y. Zheng, Adv. Mater., 2016, 28, 7729–7735.
11. A. Dhyani, W. Choi, K. Golovin and A. Tuteja, Matter, 2022, 5, 1423–1454.
12. Z. He, W. J. Xie, Z. Liu, G. Liu, Z. Wang, Y. Q. Gao and J. Wang, Sci. Adv., 2016, 2, e1600345.
13. D. Ehre, E. Lavert, M. Lahav and I. Lubomirsky, Science, 2010, 327, 672–675.
14. H. Yang, C. Ma, K. Li, K. Liu, M. Loznik, R. Teeuwen, J. C. M. van Hest, X. Zhou, A. Herrmann, J. Wang, H. G. Yang, J. Wang, X. Zhou, C. Ma, K. Liu, M. Loznik, A. Herrmann, K. Y. Li, R. Teeuwen and J. C. M. van Hest, Adv. Mater., 2016, 28, 5008–5012.
15. R. Dou, J. Chen, Y. Zhang, X. Wang, D. Cui, Y. Song, L. Jiang and J. Wang, ACS Appl. Mater. Interfaces, 2014, 6, 6998–7003.
16. J. Chen, Z. Luo, Q. Fan, J. Lv and J. Wang, Small, 2014, 10, 4693–4699.
17. B. Liang, G. Zhang, Z. Zhong, Y. Huang and Z. Su, Langmuir, 2019, 35, 1294–1301.
18. Y. Yu, B. Jin, M. I. Jamil, D. Cheng, Q. Zhang, X. Zhan and F. Chen, ACS Appl. Mater. Interfaces, 2019, 11, 12838–12845.
19. Z. Lingru, C. Zhaoyu, H. Ling, J. Juan, M. Tao and L. Junyan, Prog. Org. Coat., 2022, 172, 107135.
20. Y. Zhang, Y. Liu, B. Ren, D. Zhang, S. Xie, Y. Chang, J. Yang, J. Wu, L. Xu and J. Zheng, J. Phys. D: Appl. Phys., 2019, 52, 403001.
21. Z. Jiang, J. Reilly, B. Everatt and N. W. Smith, J. Chromatogr. A, 2009, 1216, 2439–2448.
22. W. Feng, J. Brash and S. P. Zhu, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 2931–2942.
23. A. Erfani, J. Seaberg, C. P. Aichele and J. D. Ramsey, Biomacromolecules, 2020, 21, 2557–2573.
24. Y. Zhang, Y. Liu, B. Ren, D. Zhang, S. Xie, Y. Chang, J. Yang, J. Wu, L. Xu and J. Zheng, J. Phys. D: Appl. Phys., 2019, 52, 403001.
25. L. Qi, T. Jiang, R. Liang and W. Qin, Anal. Chem., 2021, 93, 6932–6937.
26. Z. Chen, M. Liao, L. Zhang and J. Zhou, AIChE J., 2021, 67, e17103.
27. G. Cheng, M. Liao, D. Zhao and J. Zhou, Langmuir, 2017, 33, 1732–1741.
28. Q. Shao and S. Jiang, J. Phys. Chem. B, 2014, 118, 7630–7637.
29. Q. Shao, L. Mi, X. Han, T. Bai, S. Liu, Y. Li and S. Jiang, J. Phys. Chem. B, 2014, 118, 6956–6962.
30. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
31. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
32. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
33. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
34. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
36. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
37. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 64111.
38. G. Henkelman, A. Arnaldsson and H. J. Nsson, Comput. Mater. Sci., 2006, 36, 354–360.
39. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
40. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
41. R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97, 8617–8624.
42. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
43. J. W. Gibbs, Graphical Methods in the Thermodynamics of Fluids, Transactions of the Connecticut Academy, 1873, vol. 2, pp. 309–342.
44. G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York and Oxford, 1997.
45. 2. CHEMICAL AND PHYSICAL BONDING 2.1 Ordinary Bond Types.
46. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond In Structural Chemistry and Biology, Oxford University Press, Oxford and New York, 1999.
47. J. Emsley, Chem. Soc. Rev., 1980, 9, 91–124.
48. K. Szalewicz, Encyclopedia of Physical Science and Technology, 2003, pp. 505–538.
49. B. Dereka, Q. Yu, N. H. C. Lewis, W. B. Carpenter, J. M. Bowman and A. Tokmakoff, Science, 2021, 371, 160–164.
50. D. Chen, M. D. Gelenter, M. Hong, R. E. Cohen and G. H. McKinley, ACS Appl. Mater. Interfaces, 2017, 9, 4202–4214.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3me00020f

---