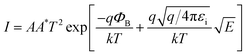Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reservoir computing using back-end-of-line SiC-based memristors†
Dongkai
Guo
 a,
Omesh
Kapur
a,
Omesh
Kapur
 a,
Peng
Dai
a,
Yisong
Han
a,
Peng
Dai
a,
Yisong
Han
 b,
Richard
Beanland
b,
Richard
Beanland
 b,
Liudi
Jiang
c,
C. H. (Kees)
de Groot
b,
Liudi
Jiang
c,
C. H. (Kees)
de Groot
 a and
Ruomeng
Huang
a and
Ruomeng
Huang
 *a
*a
aSchool of Electronic and Computer Science, University of Southampton, Southampton, UK. E-mail: r.huang@soton.ac.uk
bSchool of Physics, Warwick University, Coventry, UK
cSchool of Engineering, University of Southampton, Southampton, UK
First published on 3rd October 2023
Abstract
The increasing demand for intellectual computers that can efficiently process substantial amounts of data has resulted in the development of a wide range of nanoelectronics devices. Reservoir computing offers efficient temporal information processing capability with a low training cost. In this work, we demonstrate a back-end-of-line SiC-based memristor that exhibits short-term memory behaviour and is capable of encoding temporal signals. A physical reservoir computing system using our SiC-based memristor as the reservoir has been implemented. This physical reservoir computing system has been experimentally demonstrated to perform the task of pattern recognition. After training, our RC system has achieved 100% accuracy in classifying number patterns from 0 to 9 and demonstrated good robustness to noisy pixels. The results shown here indicate that our SiC-based memristor devices are strong contenders for potential applications in artificial intelligence, particularly in temporal and sequential data processing.
1. Introduction
Driven by the widespread permeation of artificial intelligence and big data into our society and daily life, there has been a surge in demand for computing systems that can process vast amounts of data quickly and efficiently.1 However, the inherent limitations of digital computing systems where the computing and memory are separated into different units have stimulated a growing interest in developing alternative computing paradigms. Inspired by the human brain where the data processing and storage are unified within the synapses and neurons, the concept of neuromorphic computing has been recognised as one of the most promising solutions for energy-efficient data processing.2Novel two-terminal solid-state memristor devices have been identified as ideal candidates to emulate the synaptic behaviours of synapses and neurons and realize neuromorphic computing. A wide range of materials has been proposed as the electrolyte medium for the memristor-based artificial synapse. Noticeable candidates include chalcogenides,3,4 metal oxides,5,6 and perovskite materials.7,8 In general, the memory model in the human brain can be categorised into long-term memory (non-volatile) and short-term (volatile) memory based on the conductance decay over time.9,10 In long-term memory, the conductance remains constant unless another stimulus is applied. Memristors demonstrating such behaviour have been widely used in constructing feed-forward neural networks for non-temporal data processing.11,12 On the other hand, short-term memory features temporally stored conductance states that decay over time. This volatile switching can be observed in several types of memristor systems with different mechanisms.13 It can be used to directly process temporal data in recurrent neural networks (RNNs) and is particularly attractive for applications such as speech recognition, classification and time series forecasting.14,15 Several memristor devices that demonstrate short-term memory features have been applied in neuromorphic computing for temporal signal processing using functional materials such as WOx,14,16,17 mesoporous silica,18 TaOx,19,20 TiOx,21 HfO2,22 SnOx,23 and perovskite.24
Amorphous silicon carbide (SiC) is a back-end-of-line material in the CMOS industry and is regarded as the interconnection dielectric material for third-generation semiconductors due to its superior electrical properties such as large band gap, high breakdown voltage, and good thermal conductivity.25–27 The development of functional electronic devices based on SiC can be extremely advantageous in consideration of easy integration and large-scale manufacturing in future. Over the past decade, several works have been conducted to develop SiC-based memristors and demonstrate promising resistive and neuromorphic switching behaviours.28–31 Our group also recently developed a SiC-based memristor from a chemical vapour deposition (CVD) process and demonstrated promising short-term memory properties such as short-term potentiation (STP) and spike rate dependent plasticity (SRDP).32 However, neuromorphic computing systems based on the short-term synaptic behaviour of SiC memristors have never been demonstrated before.
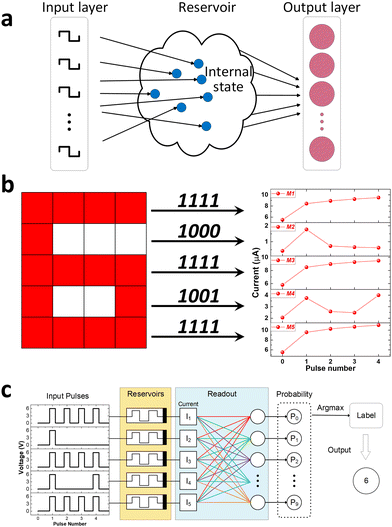
In this work, we will report the unique short-term memory behaviour of SiC memristor for neuromorphic computing applications through constructing a physical reservoir computing (RC) system. Reservoir computing, a subset of RNN, is a unique computational framework that is specifically suited for temporal/sequential data processing. The physical reservoir maps the temporal input signals into a high dimensional space using its nonlinear dynamics and the temporal memory feature which can then be processed using a simple readout network. Comparing with other neuromorphic computing implementation, RC has a key advantage of simplicity as the reservoir itself does not require training whereas only the readout weights are trained with a simple learning algorithm such as linear regression.33 Such simple and fast training process makes it possible to drastically reduce the computational cost of learning. We will demonstrate that our SiC memristor is capable of serving as the physical reservoir in the RC system to perform the task of pattern recognition. After a short training process, the system demonstrates excellent classification performance with an accuracy of 100% as well as good tolerance to the potential input noise. This work paves the way for back-end-of-line SiC memristor devices to be used in the construction of physical RC systems for neuromorphic computing.
2. Results and discussion
2.1 Restive and neuromorphic switching
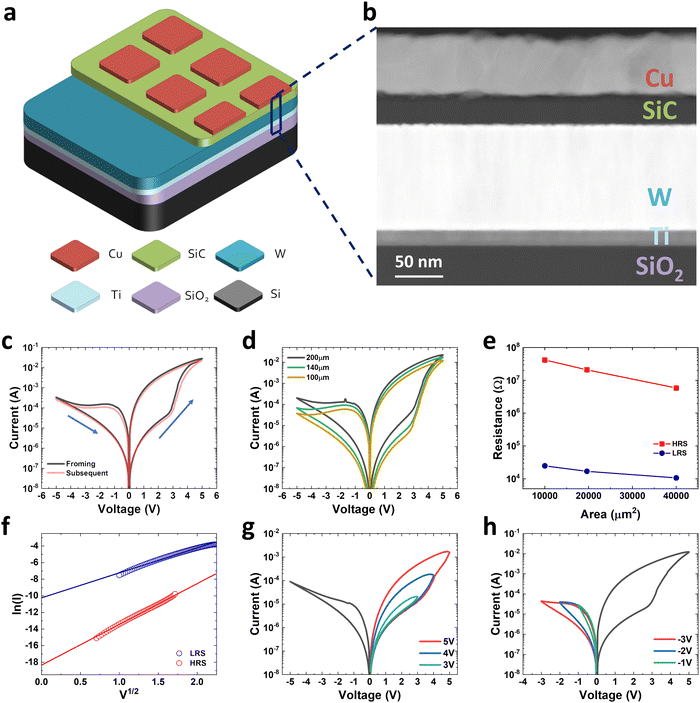
Fig. 1a displays the schematic of the SiC memristor in this work. The patterned Cu top layer serves as the active metal electrode while the W layer underneath acts as the bottom, inert electrode which is adhered to the Si/SiO2 substrate via a Ti adhesion layer. The SiC layer sandwiched between two electrodes serves as the switching electrolyte layer. The Cu/SiC/W/Ti/SiO2/Si structure is confirmed by the transmission electron microscopy (TEM) cross-sectional image (shown in Fig. 1b). It can be observed that the SiC is amorphous with a thickness of ca. 25 nm. The resistive switching properties of the SiC memristor were investigated by DC I–V measurements. The pristine device demonstrates an initial high resistance state (HRS) which can be transformed to a low resistance state (LRS) upon a positive DC sweep from 0 V to 5 V as shown in Fig. 1c. A negative DC sweep from 0 V to −5 V can reset the memristor from LRS to HRS. The subsequent set process manifests a similar pattern with the electro-forming, suggesting an electro-forming-free feature of our SiC memristor. In addition, the memristor also presents itself with compliance-free, self-rectified behaviours, both of which are beneficial for its large-scale integration in 3D cross-bar arrays. The switching performance of devices at different device areas was also investigated as shown in Fig. 1d. While similar I–V characteristics were obtained, the device currents at both ON and OFF states decrease with the scaling of the device area (shown in Fig. 1e). Such area dependence, especially at LRS, suggests that the resistive switching in this memristor is interfacial rather than filamentary. Similar behaviour was also reported in other works.34,35 It is worth noting that these behaviours are different to some of the previously reported SiC-based memristors which feature typical filamentary switching properties with abrupt switching, high ON/OFF ratio and asymmetrical SET and RESET characteristics.29,36 Such differences are likely to be induced by the different composition of the SiC film – while our previous work used stoichiometric SiC film (i.e. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Si to C ratio)29 the SiC film in the current work is silicon-rich with a Si to C ratio of 7
1 Si to C ratio)29 the SiC film in the current work is silicon-rich with a Si to C ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.32 To further explore the current conduction mechanism in our memristor, we fit the I–V characteristics using the Schottky emission equation:
3.32 To further explore the current conduction mechanism in our memristor, we fit the I–V characteristics using the Schottky emission equation:where A is the active device area, A* is Richardson's constant, ΦB is the Schottky Barrier Height (SBH), E is the electrical field, q is the electronic charge, k is the Boltzmann's constant, εi is the dielectric constant of the film and T is the absolute temperature. Linear fittings for both HRS and LRS in Fig. 1f imply that Schottky emission is the dominating current mechanism for both ON and OFF states. A similar mechanism in HRS was also observed in our stoichiometric SiC memristor.37 However, the derived SBH in our Si-rich SiC memristor is 0.624 eV at HRS, which is lower than that in the stoichiometric one (0.79 eV). This is unsurprising as the excess Si in the SiC layer could decrease the bandgap and subsequently reduce the SBH. On the other hand, the current conduction at LRS is very different. While the stoichiometric SiC memristor exhibits an Ohmic conduction due to the formation of Cu filament(s),37 the current conduction in our Si-rich memristor is still Schottky emission dominating, but with a lower SBH of 0.416 eV. It is worth noting that other current conduction such as thermionic emission and field emission may also occur simultaneously under such lowered barrier. Nevertheless, this suggests that the memristive switching in our Si-rich SiC memristor is achieved by the modulation of the Schottky barrier. It is therefore reasonable to suggest that such modulation is a cause of controlled Cu doping in the SiC film during the SET and RESET process. Under a positive bias, the Cu atoms from the top electrode will be oxidised and drift into the SiC layer. Cu ion has a much higher diffusion coefficient in Si than that in SiC with a low diffusion barrier of 0.18 eV.38,39 Compared with the stoichiometric SiC, our Si-rich SiC can further facilitate the movement of Cu ions in the SiC layer over the entire device area. This results in the SiC film being partially doped with Cu, leading to reduced SBH and the resistive switching from HRS to LRS. When a negative bias is applied, the Cu ions will be attracted back to the top electrode and the SBH resumes its original high value. This interfacial switching mechanism also explains the unique switching characteristics of the SiC memristor in this work.
Fig. 1g and h illustrate the characteristics of multi-state switching of the SiC memristor. In Fig. 1g, the memristor was reset into HRS with −5 V sweeps while being switched on with a series of positive sweeps from 1 V to 5 V. It is clear that multiple ON states can be achieved by changing the SET voltages. This is likely due to the controlled modulation of the SBH with different SET voltages. Fig. 1h, the memristor was switched ON into the LRS with 5 V sweeps while a series of negative RESET sweeps with voltage from −1 V to −5 V was applied. Similarly, the memristor can demonstrate multiple OFF states upon different RESET voltages. The capability of gradually tuning the memristor resistance is key for its application in neuromorphic computing.
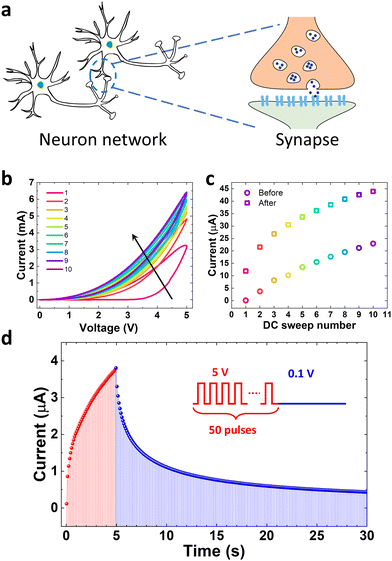
Synaptic plasticity in biology refers to a rise (potentiation) or decrease (depression) in the synaptic weight for information processing as shown in Fig. 2a. Such synaptic behaviour can be emulated by a memristor device where the modulation of its conductive channel by pulsing can precisely control its conductance to represent the change of synaptic weight.40 As shown in Fig. 2b, the device's analogue switching behaviour enables the conductance to be gradually adjusted by applying a series of DC sweeps. As the number of DC stimulus sweeps rises, the conductance (measured at 0.5 V) shifts upwards gradually (shown in Fig. 2c). This shows how the SiC memristor exhibits neuromorphic behaviour, whereby stimulus properties can accurately control multi-state resistances to realise synaptic behaviours. The fact that the conductance is lower before each stimulus than it is after the previous ones is interesting to note. This may imply that the modulated SBH between the electrode and SiC film experienced a spontaneous change in the interval between two subsequent DC sweeps, a feature of short-term plasticity (STP). To verify this behaviour, the SiC memristor is subject to a series of consecutive identical pulses with the current being monitored. Consecutive identical pulses are preferred because it simplifies the peripheral circuitry used to programme the memristor in terms of expected synaptic performances. Fig. 2d shows the typical current response after a series of 50 pulses were applied to the SiC memristor. Each pulse has an amplitude of 5 V with a duration of 50 ms and an interval of 50 ms. The current increases gradually with increasing pulse number, representing a typical potentiation process. However, after the pulse was withdrawn, an automatic current relaxation was observed, confirming the STP behaviour. More detailed results including different types of synaptic plasticity, such as spiking-rate-dependent plasticity (SRDP), spiking-duration-dependent plasticity (SDDP), and spiking-voltage-dependent plasticity (SVDP) can be found in our previously published work.32 In the research that follows, this STP behaviour—the regular fall of current between two stimuli—will be further explored for developing a physical reservoir computing system.
2.2 SiC memristor-based physical reservoir computing system for digit recognition
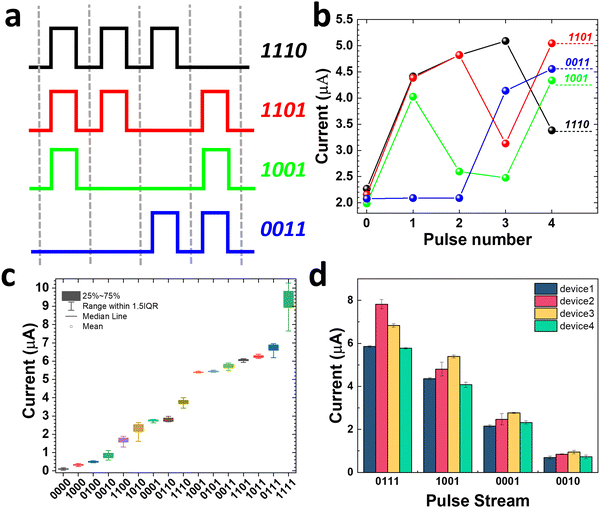
The unique STP property of our SiC memristor enables its capacity to discriminate between input sequences with different temporal orders. We demonstrate this on our SiC memristor by stimulating it with a series of pulse trains. Each pulse train consists of four pulse bits, each of which can be in either a high state (6 V) or low state (0.1 V) of 1 ms duration and 99 ms interval. The high state is denoted by the number “1”, while the low state is denoted by the number “0”. A total number of 16 different types of input pulse streams can be achieved. Fig. 3a presents examples of 4 pulse trains including 1110, 1101, 1001, and 0011. The output current was measured immediately after each pulse throughout the interval using the reading voltage of 0.1 V and is illustrated in Fig. 3b. The first reading (pulse 0) represents the initial state of the memristor while the following readings (pulse 1, 2, 3 and 4) are the currents after each pulse number. It can be observed that the readings for all pulses at high state are always higher than the last readings. This can be understood as a typical potentiation process. On the other hand, the current readings for all pulses of low state are lower than the previous reading. This is the uniqueness of the STP behaviour and the key to the separation of various states. For example, it separates the ‘1110’ signal from ‘1101’ as the potentiation caused by the first three bits in the signal of ‘1101’ attenuated with time, resulting in a much lower final (pulse 4) current from ‘1110’ than that of ‘1101’. Such separation would not be possible if the memristor possesses long-term plasticity instead. The current outputs after pulse 4 for all 16 states are presented in Fig. 3c where it can be observed that all of them are separated. The capability of distinguishing 16 states is clearly beneficial for its application in neuromorphic computing.41 The error bar in Fig. 3c represents the cycle-to-cycle (C2C) variation of our memristor where each pulse was repeated and the statistical output currents are plotted against each signal. The device-to-device (D2D) variation is investigated in Fig. 3d where 4 memristors were subjected to four identical pulse streams of 1110, 1101, 1001 and 0011. Although there are some variations among the devices, all devices show the same trend when subjected to the different input pulse streams. In addition, the reading can be well separated for different inputs for all devices. Additional C2C and D2D variation information of our SiC memristor under these 16 pulse trains are provided in Fig. S1 (ESI†).The capability of encoding temporal information is desirable for the implementation of a reservoir computing system. Fig. 4a shows the schematic for a typical RC system, which consists of an input layer, a reservoir computing layer, and an output layer.16 The input layer interfaces the real-world information with the reservoir network. The input and reservoir layers are connected in a fixed way, but the neurons in the reservoir layer develop dynamically in response to temporal signals. The reservoir layer is made up of a network with randomly connected nodes that nonlinearly maps the temporal time-dependent input signals into a high dimensional space. The reservoir states, which may be read out by a straightforward learning process through the output layer, are recorded as the transient current responses based on the input signals. In order to demonstrate how the STP behaviour of a memristor can be used for neuromorphic computing, we implemented a physical RC system based on our SiC memristor to perform a task of number recognition.
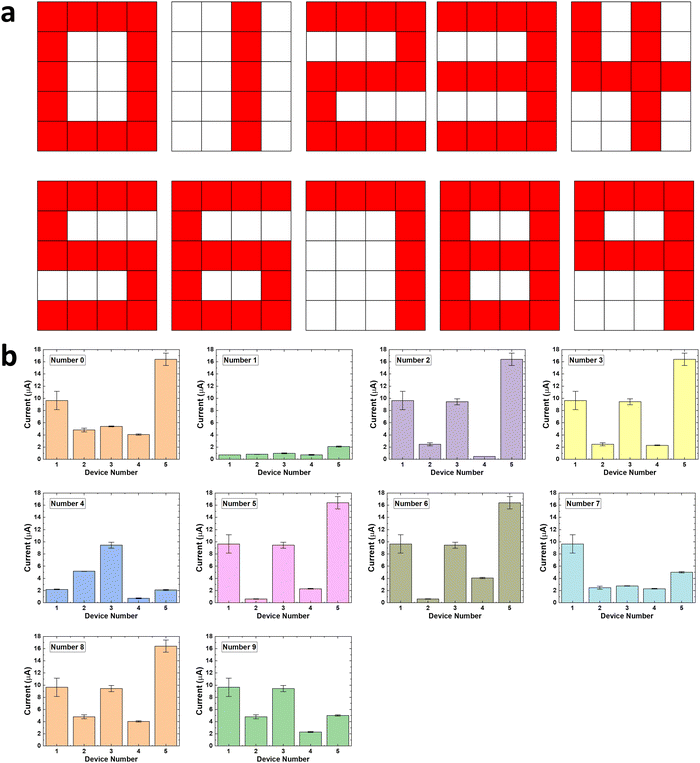
The monochrome images of digits from “0” to “9” were firstly translated into temporal input signals by treating the pattern of numbers as pixels with a size of 5 rows by 4 columns and encoding the pattern using the colour red and white as 1 and 0, respectively. For example, the number “6” can be converted into a 5 × 4 pixel array as shown in Fig. 4b. Based on the spatial distribution of the red and white pixels, the array can be represented by five 4-bit sequences, of “1111”, “1000”, “1111”, “1001” and “1111”, respectively. This information was then encoded into five temporal pulse sequences as the input of our memristor-based RC system where the pulse with a high-level voltage (6 V) represents 1 and a low-level voltage (0.1 V) represents 0 (shown in Fig. 4c). The SiC memristor serves as a physical reservoir that maps the temporal input signal into a high dimensional space using its nonlinear dynamics and the temporal memory feature. Upon the arrival of the pulse sequences, the conductance of the SiC memristor will change according to the temporal order from the pattern as shown in Fig. 4b. The output current, therefore, carries the information of a spatially distributed pattern. The current from the reservoir was then sent to the output layer that consists of a readout network. The readout network is a machine learning network that requires training to read the current from reservoirs (memristors) and perform the pattern classification. To be more specific, the readout network determines how likely it is that the input signal refers to each number by comparing the current from reservoirs (memristors) with the specific details for each of the 10 types of numbers received during the training phase. The readout function then determines which of the 10 different types of number patterns the incoming signal belongs to.
Fig. 5a plots the monochrome images of digits from “0” to “9” in this work. It is worth pointing out that only 6 out of 16 types of pulse trains (i.e. “0010”, “1111”, “0001”, “1000”, “1010” and “1001”) were required for this task. The corresponding reservoir states as well as their distributions measured at the end of the submission of each input pattern are shown in Fig. 5b. The findings demonstrate that, depending on the particular pattern, the reservoir output currents differ substantially despite occasional D2D variations. The final 5 × 1 output state is clearly unique for each input digit, proving the reservoir's capacity to distinguish these 10 situations with clarity.
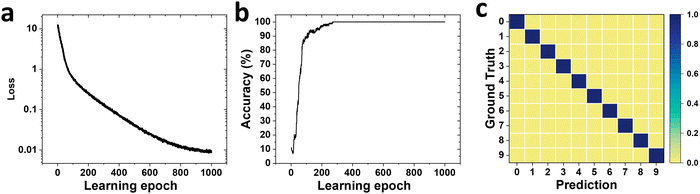
Supervised training of the feedforward readout network was achieved by using the dataset of Fig. 5b (see the Experimental section for the detailed training process). The training loss curve is plotted in Fig. 6a. Within a few training epochs, a dramatic reduction in loss can be obtained. This is accompanied by the increase of the prediction accuracy as shown in Fig. 6b. A training accuracy of 100% was achieved after only 300 epochs, supporting the claim that the RC system has a low training cost than the conventional neural networks.33 After the training process, we evaluate its performance by tasking it to classify number patterns from the test dataset that the system has never seen before. Fig. 6c displays the resulting confusion matrix which compares the experimentally achieved classification results from the RC system to the target outputs. A 100% recognition accuracy rate was attained from the reservoir, highlighting the excellent classification capability of our SiC memristor-based RC system. It is worth noting that an accuracy of 100% is perhaps not surprising in this experiment as the pattern for each digit remains unchanged. The dataset difference mainly resides in the C2C and D2D variations of the memristor rather than the pattern itself. However, this simple pattern recognition task serves as a proof-of-concept experiment, and the fact that our SiC memristor can recognise 10 different patterns with 100% accuracy pave the way for its future application in reservoir computing for more advanced tasks such as MNIST digits classification and voice recognition.
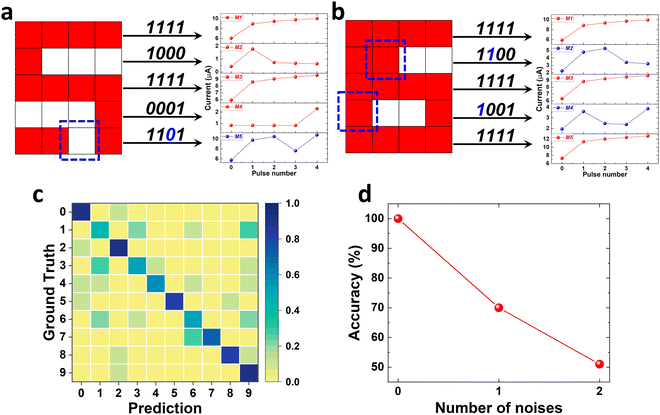
The robustness against the input noise was also assessed by corrupting the monogram images with random noises. The noises are introduced by randomly flipping 1, 2 or 3 pixels to the opposite state (i.e. “1” to “0” or “0” to “1”) in the pattern and converted to the corresponding pulse trains. For example, in Fig. 7a, one corrupted pixel is randomly introduced to the number “5” at the bottom row. The original pulse train changes from “1111” to “1101”, which leads to the drop of the corresponding input current from device 5 (shown in Fig. 7b). Similarly in Fig. 7c where two noisy pixels are introduced to the number “5”, resulting in current changes on devices 2 and 4 (shown in Fig. 7d). These situations, where the noised pattern behaves like a different pattern without noise, reduce the accuracy of the noise test. The predicted accuracy is therefore greater than the measured value. Fig. 7e exhibits the confusion matrix of number patterns with one flipped pixel where an accuracy of 71% was obtained. By adding noisy pixels to the original images, it was shown that the letters may still be recognised by the RC system even though the output signal from the reservoir is disordered. However, as the number of noisy pixels increases to 2, the accuracy will drop to 52%, as shown in Fig. 7f. It is worth mentioning that this reduced accuracy is partially due to the design of the number pattern. For example, the number 5 could be mistaken as the number 6 with one badly placed noisy pixel. Nevertheless, the success of this proof-of-concept experiment has paved the way for the application of our SiC memristor in reservoir computing for more advanced tasks such as MNIST digit recognition, voice recognition and ECG classification.
3. Conclusions
In conclusion, we demonstrate in this work a back-end-of-line SiC-based memristor that offers compliance-free, forming-free, and multi-state resistive switching properties. More importantly, the memristor exhibits a unique short-term plasticity behaviour which is capable of encoding temporal signals. Utilising this unique property, we have implemented a physical reservoir computing system using our SiC-based memristor as the reservoir. This physical reservoir computing system has been experimentally demonstrated to perform the task of pattern recognition. After training, our RC system has achieved 100% accuracy in classifying number patterns from 0 to 9 and demonstrated good robustness to noisy pixels. The results provide promising evidence in support of our SiC-based memristor devices as strong contenders for applications in artificial intelligence, particularly in temporal and sequential data processing.4. Experimental section
4.1 Device fabrication and characterisation
The Cu/SiC/W memristor was fabricated on top of a Si/SiO2 substrate. A Ti adhesion layer of 25 nm was first sputtered on the substrate. A W bottom electrode with a thickness of 100 nm was subsequently sputtered to serve as the bottom electrode. Using a plasma-enhanced chemical vapour deposition (PECVD) method, the SiC electrolyte layer was formed on top of the W layer. The reactive gases utilised were Silane (SiH4) and Methane (CH4), and the flow rates were maintained at 15 sccm and 85 sccm, respectively. A SiC film with a thickness of ca. 25 nm was obtained under a 70 s deposition time. Finally, the top electrode made of the active metal Cu was deposited on the SiC thin film by evaporation and patterned using photolithography and lift-off processes. The dimension of the Cu top electrode is 200 μm each side. Scanning electron microscopy (SEM) has been used to characterize the composition and cross-section of individual devices. The electrical characteristics were measured at room temperature and ambient pressure using a probe connected to a Keysight (B1500) system. For all measurements, the voltage was applied to the top electrode while the bottom electrode was grounded.4.2 Read-out network training
The readout function is trained via the supervised learning algorithm to minimize the cross-entropy loss. Before the training process, a dataset was generated by collecting the current responses of the pattern encoded pulse sequence from different devices for 6000 cycles. The number from 0 to 9 are represented by the digits 0–9 in the dataset, respectively. This created a dataset of 6000 number-current relations. The distribution of the dataset is shown in Fig. S2 (ESI†). For the same number, the output currents from the reservoir (SiC memristor) can still be different due to the C2C and D2D variations. We then randomly selected 5000 of these number-current relations for the readout network training, while the remaining 1000 was used as validation (500) and testing (500). The training set is utilized to train the neural network. The validation set works to monitor whether the neural network is overfitting or underfitting. The testing set, which has not been seen by the network, is used to evaluate the network performance. All currents are scaled to the value with the unit of microamperes (μA) in the dataset. The previously discussed neural network training is processed on a Windows PC with the CPE of Intel Core i7-3770 CPU by the open-source machine learning package PyTorch. More information on the training process can be found in the ESI.†Author contributions
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. H. would like to thank the Royal Society for a Research Grant (RGS/R2/222171). O. K. thanks EPSRC and AWE Ltd for the ICASE studentship No. 16000087. All data supporting this study are openly available from the University of Southampton repository at https://doi.org/10.5258/SOTON/D2725.References
- D. P. Acharjya and K. Ahmed, Int. J. Adv. Comput. Sci. Appl., 2016, 7, 511–518 Search PubMed.
- C. D. Schuman, S. R. Kulkarni, M. Parsa, J. P. Mitchell, P. Date and B. Kay, Nat. Comput. Sci., 2022, 2, 10–19 CrossRef.
- A. Ali, H. Abbas, M. Hussain, S. H. A. Jaffery, S. Hussain, C. Choi and J. Jung, Nano Res., 2021, 15, 2263–2277 CrossRef.
- L. Hu, S. Fu, Y. Chen, H. Cao, L. Liang, H. Zhang, J. Gao, J. Wang and F. Zhuge, Adv. Mater., 2017, 29, 1606927 CrossRef.
- A. Saleem, F. M. Simanjuntak, S. Chandrasekaran, S. Rajasekaran, T.-Y. Tseng and T. Prodromakis, Appl. Phys. Lett., 2021, 118, 112103 CrossRef CAS.
- Y. Lin, J. Liu, J. Shi, T. Zeng, X. Shan, Z. Wang, X. Zhao, H. Xu and Y. Liu, Appl. Phys. Lett., 2021, 118, 103502 CrossRef CAS.
- A. Siddik, P. K. Haldar, T. Paul, U. Das, A. Barman, A. Roy and P. K. Sarkar, Nanoscale, 2021, 13, 8864–8874 RSC.
- J. Lao, W. Xu, C. Jiang, N. Zhong, B. Tian, H. Lin, C. Luo, J. Travas-sejdic, H. Peng and C.-G. Duan, J. Mater. Chem. C, 2021, 9, 5706–5712 RSC.
- E. M. Izhikevich, IEEE Trans. Neural Netw., 2003, 14, 1569–1572 CrossRef CAS PubMed.
- C. Koch, Nature, 1997, 385, 207–210 CrossRef CAS PubMed.
- H. Sak, A. W. Senior and F. Beaufays, Interspeech, 2014, 80, 338–342 Search PubMed.
- C. Raffel and D. P. W. Ellis, arXiv, 2015, preprint, arXiv:1512.08756 DOI:10.48550/arXiv.1512.08756.
- G. Zhou, Z. Wang, B. Sun, F. Zhou, L. Sun, H. Zhao, X. Hu, X. Peng, J. Yan, H. Wang, W. Wang, J. Li, B. Yan, D. Kuang, Y. Wang, L. Wang and S. Duan, Adv. Electron. Mater., 2022, 8, 2101127 CrossRef CAS.
- J. Moon, W. Ma, J. H. Shin, F. Cai, C. Du, S. H. Lee and W. D. Lu, Nat. Electron., 2019, 2, 480–487 CrossRef.
- J. Cao, X. Zhang, H. Cheng, J. Qiu, X. Liu, M. Wang and Q. Liu, Nanoscale, 2022, 14, 289–298 RSC.
- C. Du, F. Cai, M. A. Zidan, W. Ma, S. H. Lee and W. D. Lu, Nat. Commun., 2017, 8, 2204 CrossRef PubMed.
- D. Kim, J. Shin and S. Kim, Appl. Surf. Sci., 2022, 599, 153876 CrossRef CAS.
- A. H. Jaafar, L. Shao, P. Dai, T. Zhang, Y. Han, R. Beanland, N. T. Kemp, P. N. Bartlett, A. L. Hector and R. Huang, Nanoscale, 2022, 14, 17170–17181 RSC.
- R. Midya, Z. Wang, S. Asapu, X. Zhang, M. Rao, W. Song, Y. Zhuo, N. Upadhyay, Q. Xia and J. J. Yang, Adv. Intell. Syst., 2019, 1, 1900084 CrossRef.
- J. Pyo and S. Kim, J. Alloys Compd., 2022, 896, 163075 CrossRef CAS.
- Y. Zhong, J. Tang, X. Li, B. Gao, H. Qian and H. Wu, Nat. Commun., 2021, 12, 408 CrossRef CAS PubMed.
- H. Ryu and S. Kim, Chaos, Solitons Fractals, 2021, 150, 111223 CrossRef.
- O. Kwon, J. Shin, D. Chung and S. Kim, Ceram. Int., 2022, 48, 30482–30489 CrossRef CAS.
- J. Y. Mao, Z. Zheng, Z. Y. Xiong, P. Huang, G. L. Ding, R. Wang, Z. P. Wang, J. Q. Yang, Y. Zhou, T. Zhai and S. T. Han, Nano Energy, 2020, 71, 104616 CrossRef CAS.
- W. Daves, A. Krauss, N. Behnel, V. Häublein, A. Bauer and L. Frey, Thin Solid Films, 2011, 519, 5892–5898 CrossRef.
- S. King, M. French, J. Bielefeld and W. Lanford, J. Non-Cryst. Solids, 2011, 357, 2970–2983 CrossRef CAS.
- M. Cabello, V. Soler, G. Rius, J. Montserrat, J. Rebollo and P. Godignon, Mater. Sci. Semicond. Process., 2018, 78, 22–31 CrossRef CAS.
- J. Fan, O. Kapur, R. Huang, S. W. King, C. de Groot and L. Jiang, AIP Adv., 2018, 8, 095215 CrossRef.
- L. Zhong, L. Jiang, R. Huang and C. De Groot, Appl. Phys. Lett., 2014, 104, 093507 CrossRef.
- Y.-L. Hsu, Y.-F. Chang, W.-M. Chung, Y.-C. Chen, C.-C. Lin and J. Leu, Appl. Phys. Lett., 2020, 116, 213502 CrossRef CAS.
- L. a Liu, J. Zhao, G. Cao, S. Zheng and X. Yan, Adv. Mater. Technol., 2021, 6, 2100373 CrossRef CAS.
- O. Kapur, D. Guo, J. Reynolds, Y. Han, R. Beanland, L. Jiang, C. H. de Groot and R. Huang, Adv. Electron. Mater., 2022, 8, 2200312 CrossRef CAS.
- G. Tanaka, T. Yamane, J. B. Héroux, R. Nakane, N. Kanazawa, S. Takeda, H. Numata, D. Nakano and A. Hirose, Neural Networks, 2019, 115, 100–123 CrossRef PubMed.
- K. Rudrapal, G. Bhattacharya, V. Adyam and A. Roy Chaudhuri, Adv. Electron. Mater., 2022, 8, 2200250 CrossRef CAS.
- S. Bagdzevicius, K. Maas, M. Boudard and M. Burriel, J. Electroceram., 2017, 39, 157–184 CrossRef CAS.
- K. A. Morgan, J. Fan, R. Huang, L. Zhong, R. P. Gowers, L. Jiang and C. H. de Groot, AIP Adv., 2015, 5, 077121 CrossRef.
- L. Zhong, P. Reed, R. Huang, C. de Groot and L. Jiang, Solid-State Electron., 2014, 94, 98–102 CrossRef CAS.
- A. A. Istratov, C. Flink, H. Hieslmair, E. R. Weber and T. Heiser, Phys. Rev. Lett., 1998, 81, 1243–1246 CrossRef CAS.
- A. Suino, Y. Yamazaki, H. Nitta, K. Miura, H. Seto, R. Kanno, Y. Iijima, H. Sato, S. Takeda, E. Toya and T. Ohtsuki, J. Phys. Chem. Solids, 2008, 69, 311–314 CrossRef CAS.
- A. K. McAllister, L. C. Katz and D. C. Lo, Annu. Rev. Neurosci., 1999, 22, 295–318 CrossRef CAS PubMed.
- W. Zhang, B. Gao, J. Tang, X. Li, W. Wu, H. Qian and H. Wu, Phys. Status Solidi RRL, 2019, 13, 1900204 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00141e |
| This journal is © The Royal Society of Chemistry 2023 |