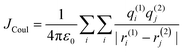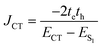DOI:
10.1039/D3CS00176H
(Review Article)
Chem. Soc. Rev., 2023,
52, 6664-6679
Keeping the chromophores crossed: evidence for null exciton splitting
Received
9th March 2023
First published on 22nd August 2023
Abstract
Fundamental understanding of the supramolecular assemblies of organic chromophores and the development of design strategies have seen endless ripples of interest owing to their exciting photophysical properties and optoelectronic applications. The independent discovery of dye aggregates by Jelley and Scheibe was the commencement of the remarkable advancement in the field of aggregate photophysics. Subsequent research warranted an exceptional model for defining the exciton interactions in aggregates, proposed by Davydov, Kasha and co-workers, independently, based on the long-range Coulombic coupling. Fascinatingly, the orthogonally cross-stacked molecular transition dipole arrangement was foretold by Kasha to possess null exciton interaction leading to spectroscopically uncoupled molecular assembly, which lacked an experimental signature for decades. There have been several attempts to identify and probe atypical molecular aggregates for decoding their optical behaviour. Herein, we discuss the recent efforts in experimentally verifying the unusual exciton interactions supported with quantum chemical computations, primarily focusing on the less explored null exciton splitting. Exciton engineering can be realized through synthetic modifications that can additionally offer control over the assorted non-covalent interactions for orchestrating precise supramolecular assembly, along with molecular editing. The task of attaining a minimal excitonic coupling through an orthogonally cross-stacked crystalline architecture envisaged to offer a monomer-like optical behaviour was first reported in 1,7-dibromoperylene-3,4,9,10-tetracarboxylic tetrabutylester (PTE-Br2). The attempt to stitch molecules covalently in an orthogonal fashion to possess null excitonic character culminated in a spiro-conjugated perylenediimide dimer exhibiting a monomer-like spectroscopic signature. The computational and experimental efforts to map the emergent properties of the cross-stacked architecture are also discussed here. Using the null aggregates formed by the interference effects between CT-mediated and Coulombic couplings in the molecular array is another strategy for achieving monomer-like spectroscopic properties in molecular assemblies. Moreover, identifying supramolecular assemblies with precise angle-dependent properties can have implications in functional material design, and this review can provide insights into the uncharted realm of null exciton splitting.

M. P. Lijina
| M. P. Lijina is currently pursuing an integrated PhD in Chemistry with Prof. Mahesh Hariharan at Indian Institute of Science Education and Research Thiruvananthapuram. Her research interests are in exploring exciton interactions and resultant photophysical properties in crystalline organic chromophoric assemblies. |

Alfy Benny
| Alfy Benny is currently a PhD student at Princeton University. He received his integrated BS-MS degree at the Indian Institute of Science Education and Research, Thiruvananthapuram (IISER TVM), majorly investigating charge transport and exciton migration in organic crystalline materials. His current research interests include understanding the complex reaction dynamics of ultrafast excited state processes of molecules and their assemblies utilizing various numerical techniques based on open quantum system formalisms. |

Ebin Sebastian
| Ebin Sebastian is currently a postdoctoral fellow in Prof. Akshay Rao's group at the Cavendish Laboratory, University of Cambridge. He was a PhD scholar at IISER Thiruvananthapuram under the supervision of Prof. Mahesh Hariharan. His research interests are focused on identifying and characterizing null exciton-coupled chromophoric assemblies and exploring their concomitant effects on excited-state dynamics using time-resolved spectroscopy measurements. |

Mahesh Hariharan
| Mahesh Hariharan is a Professor in the School of Chemistry, IISER Thiruvananthapuram. After completing his doctoral research (2002–2007) from CSIR-NIIST India with Dr D. Ramaiah, Dr Hariharan carried out his postdoctoral research (2007–2009) with Prof. F. D. Lewis at Northwestern University. His research efforts focus on understanding the interaction of light with biomolecules and crystalline and twisted organic materials. Prof. Hariharan is the recipient of the Chemical Research Society of India Bronze Medal (2020), and the Japanese Photochemistry Association Lectureship Award for Asian and Oceanian Photochemist Sponsored by Eikohsha (2020). He is a fellow of the Royal Society of Chemistry and the Indian Academy of Sciences. |
Introduction
Invigilation of the photophysical characteristics in chromophores, ranging from retaining the molecular identity to the consideration of overwhelming permutations of molecular packing scenarios, has invoked excitement in the photophysical community from both a fundamental to an applicational level perspective.1–8 The light-matter interactions of π conjugated organic materials are strongly influenced by their three-dimensional ordering.9,10 The molecular organization in π conjugated materials extensively affects their ability to transport charges.11–13 Nature is an eternal motivation with ideal supramolecular architectures designed for performing specific tasks.14–16 Orchestrating supramolecular assemblies is always a challenging and exciting venture owing to its resultant photophysical responses and the enormous possibility of functional material design.17,18 Engineering assemblies with precise molecular stacking is a Herculean task, demanding control over the electronic structure and the resultant non-covalent interactions.19,20 Specific supramolecular assemblies can be rendered through synthetic modifications, which can also offer a hand over the non-covalent interactions.21
The optical response of the crystalline scaffold is the result of electronic communication between the chromophores, governed by the geometrical rulers, including π overlap, intermolecular distance, and relative spatial orientation between the chromophores.22–25 The report by S. E. Sheppard in 1909 is identified as an early documentation of dye aggregation in the solution formed by isocyanine in water, postulated as a reason for the deviation from the Beer–Lambert law.26,27 The independent discoveries by Jelley and Scheibe of the then unusually red-shifted electronic absorption spectrum in a highly concentrated solution of pseudoisocyanine (PIC) chloride is one of the celebrated milestones in the field of aggregate photochemistry.28–30 Later proclaimed as J aggregates, the interesting phenomenon of shifted electronic absorption bands in the aggregate was deciphered by Davydov and Kasha independently in the 1960s.1,2,7,31,32 For the interaction of transition densities of two molecules, which were simplified in terms of transition dipoles, Kasha introduced a form of electronic coupling resulting in the alteration of the excited state photophysical properties of aggregates from a monomer (Fig. 1). The interaction was coined as Coulombic coupling (JCoul), arising from the long-range electrostatic-like interactions where the effect can persist up to hundreds of nanometers. The simplified yet powerful model of interacting transition dipoles in different geometrical arrangements to evaluate the long-range Coulomb interaction (JCoul) has created an outburst of scientific discoveries that continues to extend today. Kasha and co-worker also attempted the investigation of the enhancement of phosphorescence ability upon aggregation of dye molecules with a simultaneous loss in singlet fluorescence.33 Molecules in a cofacial arrangement (H-aggregate) are allowed to undergo transition to the upper state, whereas in molecules with a head to tail arrangement (J-aggregate), transition to the lower state is allowed (Fig. 2).34 Along with the photophysics emerging from the strategical alignment of two transition dipoles, including commonly observed H, oblique and J-aggregates, Kasha predicted a unique class of dipole orientations having electronic states with degenerate energies as a consequence of null Coulombic coupling.1,35,36 Parallelly arranged transition dipoles with a slip angle (θ) of 54.7°, widely known as the magic angle orientation, and an orthogonally cross-stacked transition dipole displayed minimal exciton interactions (Fig. 2).37 The aggregates with shorter intermolecular distance can have significant wave function overlap between the neighbouring molecular orbitals engendering short-range excitonic coupling.38 Spano and co-workers extended the Coulombic coupling-based Kasha's theory by including short-range, charge transfer (CT)-mediated interactions.3 In closely packed aggregates (d ≤ 6 Å), the photophysical behaviour depends on both short-range and long-range couplings. The optical properties of molecular assemblies of π-chromophores encounter challenges, including concentration-dependent fluorescence quenching mediated by trap states and/or exciton coupling.39 Though J-aggregates exhibit strong fluorescence character, such aggregates show weak charge transport efficiencies.40 In spite of the adverse effect on fluorescence, H-aggregates demonstrate excellent charge transport character.41,42 Therefore, an assembly retaining monomer-like properties can significantly contribute to advancing the fundamental understanding of molecular photophysics and emerging properties. In addition to the orthogonal cross and magic angle orientations, the interference between Coulombic coupling and charge transfer-mediated coupling can also result in minimal excitonic coupling.43 The recent attempts to experimentally validate atypical exciton interactions supported by quantum chemical calculations will be discussed in this review, with a primary emphasis on the less investigated null exciton splitting.
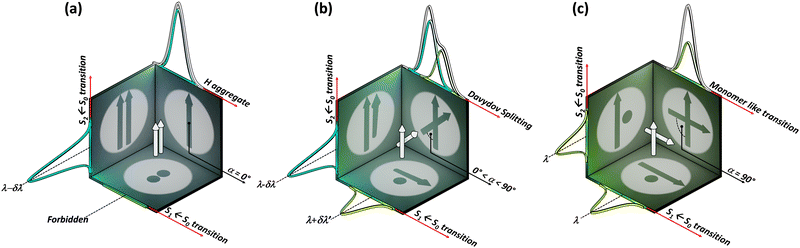 |
| | Fig. 1 Schematic representation of two transition dipoles arranged in (a) parallel (rotational angle, α = 0°), (b) cross (0° < α < 90°), and (c) Greek-cross (α = 90°) orientations with corresponding characteristics in the absorption spectra. | |
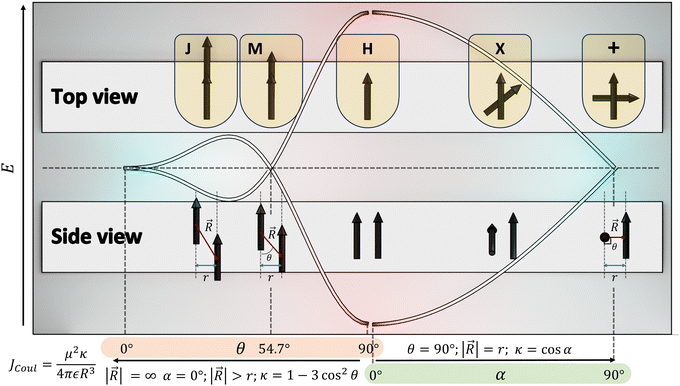 |
| | Fig. 2 Schematic diagram demonstrating the correlation between slip angle (θ), rotational angle (α) and the orientation factor (κ). | |
Exciton theory; beyond the Kasha model
Electronic transition in a classical picture is the absorption of a photon resulting in the oscillating displacement of an electron that creates a change in the spatial distribution of electron density. The instantaneous dipole created by the excitation of the electron in the molecule is the transition dipole moment vector, having magnitude proportional to the intensity of the transition with the orientation corresponding to the direction of the electron displacement.44–46 In molecular aggregates, the interaction of transition dipoles leads to exciton splitting, causing the emergence of distinct spectral shifts or splitting of the absorption bands. The optical response of the molecular aggregate is a direct consequence of its arrangement.47 Inspired by the experimental demonstration by Kautsky and Merkel on dye aggregation instigating fluorescence quenching, which is facilitated as a photophysical sensitizer, Kasha and co-workers theoretically investigated the exciton coupling for diverse transition dipole arrangements.1,48 The exciton model developed by Kasha describes the photophysical properties of molecular aggregates with different geometries based on the Coulombic intermolecular interactions within the scaffold of Frenkel exciton theory (Fig. 2). According to the proposed theory, the molecular dimers stacked side-by-side showing a blue-shifted absorption maximum relative to the monomers with suppressed fluorescence emission are described as H-aggregates. The head-to-tail stacked dimers exhibiting a red-shifted absorption maximum and enhanced radiative decay rate are designated as J-aggregates. In the case of oblique transition dipoles, in-phase and out-of-phase arrangements cause non-vanishing lower and higher energy states, generating a splitting in the absorption band. Assemblies of conjugated organic chromophores invariably face bottlenecks mediated by exciton coupling and trap states.39 Considering the non-planar transition dipole, exciton theory proposed an orthogonal arrangement of molecular transition dipoles exhibiting null exciton coupling, which is less explored. Exciton theory was defined for molecular systems having small intermolecular electron overlap that requires the Coulombic coupling alone in consideration for mapping the exciton splitting. The Coulombic coupling originates from the interaction between two transition dipoles and can be represented using the ideal dipole approximation:1,49,50| | 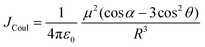 | (1) |
where μ is the magnitude of the transition dipoles of the chromophores, R is the intermolecular distance, θ is the angle between the polarization axes and the line of molecular centers, α is the angle between the two molecular planes and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α − 3
α − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is the orientation factor (κ). The Coulombic coupling can also be calculated using the transition charge from the electrostatic potential method (TrESP) between the molecules and represented as:
θ is the orientation factor (κ). The Coulombic coupling can also be calculated using the transition charge from the electrostatic potential method (TrESP) between the molecules and represented as:| | 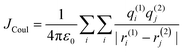 | (2) |
where qi(1) and qj(2) represent the transition charge on the ith atom of the chromophore, ri corresponds to the position vector of the respective transition charge; and ε0 is the vacuum permittivity. The through-space Coulombic coupling operates over long distances (≤10 nm), leading to a direct transfer of excitation between chromophores.38,51 The sign of Coulombic coupling dictates the formation of conventional H and J aggregates when the coupling is coherent.
Conversely, the close packing in molecular systems prompts a charge transfer-mediated exciton coupling (JCT) or superexchange coupling in addition, stemming from the overlap between the HOMOs and LUMOs of the stacked chromophores (Fig. 3). Contributions from many, including Spano and co-workers, Kazmaier and Hoffmann, and Scholes and co-workers, showed the influence of CT-mediated couplings in the aggregate photophysics.3,52–54 The CT-mediated coupling can be calculated as:
| | 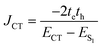 | (3) |
where
te and
th are electron and hole transfer couplings, respectively.
ECT and
ES1 are the energies of the charge-separated state and the first singlet excited state, respectively. The CT-mediated excitonic coupling in molecular systems has been identified as extremely sensitive to interchromophoric orientation due to the inter-orbital phase relationship.
43,55–57 The charge transfer couplings are unpredictable in nature due to the diverse distribution of the wave function in the frontier molecular orbitals (FMOs), which results from the variations in symmetry and atomic composition of the molecular skeleton.
38 The hole (electron) transfer coupling stemmed from the wave function overlaps between the HOMO–HOMO (LUMO–LUMO) orbitals of neighbouring molecules. The charge transfer coupling is recognized as highly sensitive to the slip angle of the molecular dimer instigating an oscillating behaviour in aggregates between H and J due to the recurring nodal and antinodal characteristics of interacting frontier molecular orbitals (FMOs).
35,38 The total coupling in the closely packed system is concluded by the combined effect of short-range charge transfer and long-range Coulombic couplings.
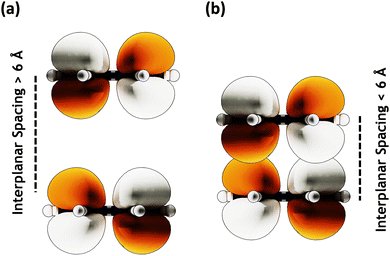 |
| | Fig. 3 MOs with (a) large (≥ 6 Å) interplanar spacing having no orbital overlap and (b) lower (≤ 6 Å) interplanar spacing showing orbital overlap. | |
Subsequent to the exciton theory, the scientific community has witnessed several endeavours to regulate aggregate behaviour by moderating long and short-range interactions. The major limitations of the Kasha's model are that the model considers Coulombic coupling alone and does not account for the vibronic fine structure.52
Atypical supramolecular assemblies
H and J aggregates have gained a great deal of scientific attention due to their outstanding photophysical features and relative ease of attainment. Kasha proposed curious aggregate states at a rotational angle of 90° and slip angle of 54.7° (magic angle), possessing minimal exciton coupling wherein the electronic energy levels of the dimer are the same as that of the corresponding monomer.1 Several attempts were made to attain minimal excitonic coupling in organic chromophores by chemical modifications and crystal engineering backed by theoretical investigations.58 The molecular assembly into different packing modes is dictated by various non-covalent interactions. There have been many theoretical and experimental attempts in order to identify and probe chromophoric aggregates with unique intermolecular angles. Hydrogen bond-assisted crossed dipole π stacking is reported by Lahti and co-worker in a 1,4-bis(phenylethynyl)benzene (Fig. 4; molecule 1).59 The molecule forms π-stacked assemblies with a centroid-to-centroid distance of 3.62 Å and a rotational angle of 99.2° along the π stack, leading to the formation of crossed dipole stacks. Wong and co-workers have synthesized a series of molecularly insulated PDI by adding bulky substituents to the imide position in order to preserve the photoluminescence in the solid state (Fig. 4; molecule 3).60 The intermolecular π–π stacking effects in PDI molecular assembly can be reduced using a molecular insulation strategy by the addition of groups to the planar perylene core through the shoulder of the perylene or through imide positions. The PDI substituted with a bulky group in the imide position crystallized with an angle around 85.6°. Ma and co-workers have reported cross-dipole stacking in distyrylbenzene derivative crystals as an approach for high solid-state luminescence efficiency (Fig. 4; molecule 5).61 The authors have employed the method of adjusting the long axes of adjacent chains such that they are perpendicular in condensed media as an effective arrangement to prevent any drop in luminescence, as per the prediction from theoretical investigations. The crystals of 2,5-diphenyl-1,4-distyrylbenzene (trans-DPDSB) with two trans double bonds adopted a cross-stacking mode with an interchomophoric rotational angle of 70°. Cross dipole stacked 1,4-Bis(2,2-diphenylvinyl)benzene is yet another example of a highly emissive assembly owing to its crystalline architecture (Fig. 4; molecule 2).62 Staggered zigzag nanographene with an inert molecular rotational angle of 90° was synthesized by Müllen and co-workers using a novel strategy to control the helical packing within columnar structures by the substitution pattern PAHs (Fig. 4; molecule 4).20 Spiess and co-workers have reported a discotic liquid crystal of triethyleneglycol (TEG)-substituted PDI, which packs as a stable column with an interchromophoric rotational angle of 90° (Fig. 4; molecule 6).63 The angle between the monomers of alkyl-substituted analogue was found to be approximately 35°, whereas the X-ray study shows that for the system with TEG, the side chains are perpendicular to each other. In another example of anthracene derivatives, upon extending Kasha*s exciton formalism beyond the traditional nearest-neighbour approach, a quantitative estimation of the excimer and dipole shift was demonstrated.64 The exciton interactions tuned in anthracene through acetylation led to the decoded mechanism of the exciton relaxation dynamics. Emergent photophysical properties from the crafted architectures were explored using both experimental tools and state-of-the-art computational methods for understanding the aggregates beyond Kasha's model. The theoretical investigations devoted to the vanishing geometrical points of the exciton couplings gathered a more fundamental understanding of the null aggregates photophysics.65 The diabatization scheme of time-dependent density functional theory was utilized by Tamura to explore singlet exciton coupling, incorporating contributions from Coulomb (Förster) and electron exchange (Dexter) couplings. T-shaped aggregates, the boundary of H- and J aggregates, and cancelled coupling to the bright state of H aggregates in a T-shaped trimer are identified as molecular aggregate topologies causing intermolecular conical intersections with null exciton coupling.
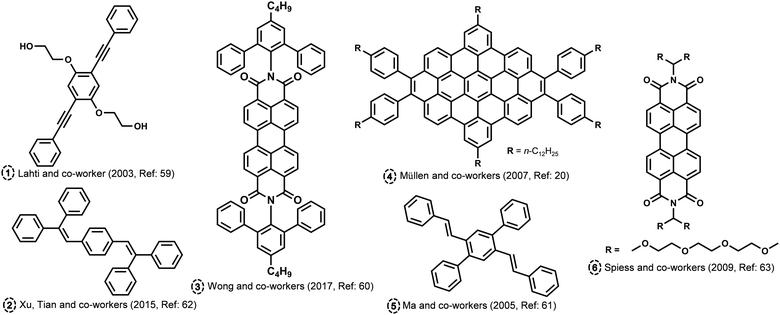 |
| | Fig. 4 Molecular structures of atypical aggregates discussed in the review. | |
The theoretical protocol developed by Engels, Fink, Kaupp and co-workers offers accurate predictions of the packing and optical properties of perylenetetracarboxylicdiimide (PDI).66 PDI dimer geometries with different torsion angles (ϕ) were subjected to ground state energy surface calculations as a function of longitudinal and transversal shifts (Fig. 5). The patterns in the resulting potential energy surface show that a small variation in substitution pattern can result in strong crystal structure alterations. The dimer orientation, having a torsion angle of 30°, displays the minimum potential energy. The orthogonal geometry shows potential energy values lower than those of the 0 and 60° oriented geometries, showing the relative stabilities.
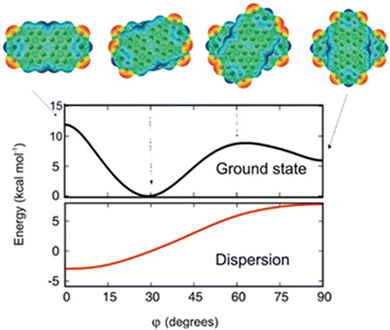 |
| | Fig. 5 Dimer geometries and potential energy curve of the electronic ground state of the geometries (black line) as a function of torsion angle (ϕ). The dispersion contribution to the total energy as a function of the torsion angle is shown in the red trace. Reproduced from ref. 66 with permission from the American Chemical Society, copyright 2023. | |
The experimental evidence for the marginal excitonic coupling for the 54.7° slip-angled (magic angle) system was unveiled by Xie and co-workers in a single crystal of N,N′-bis(4-methoxybenzyl)perylene-3,4,9,10-bis-(dicarboximide) (mb-PBI) (Fig. 6).37 The molecule forms one-dimensional molecular columns along the a axis guided by the intermolecular π–π interactions, and the columns are linked by intermolecular CH⋯O hydrogen bonds. The lower orientation factor in the magic angle stacking (M aggregate) may minimize the exciton migration (Fig. 6) in the system. The equation in Fig. 6 shows the relation between the orientation factor and the slip angle (θ). The value of the orientation factor approaches zero at the magic angle stacking of 54.7°. Therefore, the possibility of fluorescence quenching due to energy transfer reduces, which results in the restricted exciton migration nature of such M aggregates. The experimental results in the PBI crystalline film showed strong and narrow near-infrared (NIR) emission having a fluorescence quantum yield of up to 10%. The stacking of molecular units closer to each other results in strong, red-shifted emission originating from high magnitudes of Frenkel/CT mixing. The M-type stacking, however, results in high fluorescence yield due to the reduction of excitonic energy transfer efficiency.
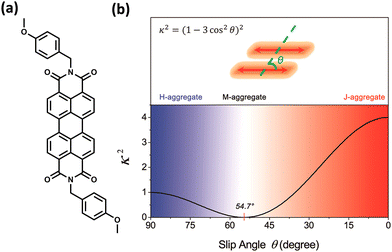 |
| | Fig. 6 (a) Molecular structure of mb-PBI and (b) orientation factor diagram according to Kasha's model for a conventional parallel dimer by considering point dipole approximation. Reproduced from ref. 37 with permission from the American Chemical Society, copyright 2023. | |
Interference between CT-mediated and Coulombic couplings
Spano and co-workers discussed the significance of considering the interference of Coulombic and charge transfer-mediated couplings, which exist simultaneously in the closely packed chromophoric systems.43 In chromophoric assembly with small intermolecular distances, null aggregates can be formed by the existence of destructive interference between equally strong and opposite Coulombic and CT-mediated couplings. The perylenediimide foldamer reported by Würthner and co-workers demonstrates excellent experimental evidence for the null aggregate originating from the interference of long- and short-range couplings (Fig. 7).67 UV-Vis absorption and emission spectra of the perylenediimide foldamer showed unchanged spectral features such as that in the monomeric perylenediimide (Fig. 8). The calculated values of Coulombic and charge transfer mediated couplings converged to a negligible net excitonic coupling, rendering monomer-like optical behaviour (Fig. 7 and 8).
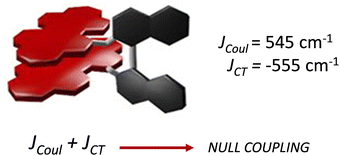 |
| | Fig. 7 Null aggregate of the perylenediimide foldamer originated from the interference between short- and long-range couplings. Reproduced from ref. 67 with permission from the American Chemical Society, copyright 2023. | |
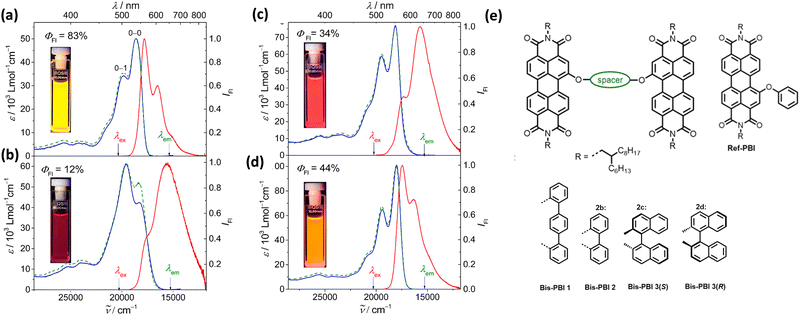 |
| | Fig. 8 Absorption (blue solid line), emission (red solid line) and excitation (green dotted line) spectra of (a) Ref-PBI, (b) Bis-PBI 1, (c) Bis-PBI 2 and (d) Bis-PBI 3(S) in 1,1,2,2-tetrachloroethane (TCE) at room temperature, and (e) molecular structures of Ref-PBI, Bis-PBI 1, Bis-PBI 2, Bis-PBI 3(S) and Bis-PBI 3(R). Reproduced from ref. 67 with permission from the American Chemical Society, copyright 2023. | |
Gopidas and co-worker have reported an effective strategy for the design of null aggregates using the self-assembly of inclusion complexes.68 Supramolecular bolaamphiphiles like bis-inclusion complexes of cyclodextrins (CD), containing two polar head groups connected by a hydrophobic linker, are considered crucial building blocks for creating various nanostructures due to their ability to self-assemble into different morphologies (Fig. 9). In the presence of 2 equivalents of β-CD, the bis-AD (adamantane) derivative of anthracene formed a bis-inclusion complex, where AD groups are connected to anthracene through the 9 and 10 positions in order to induce steric effects (Fig. 9). The β-CD⊂AD–AN–AD⊃β-CD bis-inclusion complex forms a highly crystalline nanofiber network. The tendency of the anthracene core to aggregate in the aqueous environment is anticipated as the root cause of the self-assembly into long fibers. Hydrogen bonding interactions between the fibers are most likely involved in bundling the fibers together. The complex forms a null aggregate, which is packed in a column with a twist angle in the range of 60–72°, which helps to avoid steric hindrance and achieve a π–π stacking distance of 3.64 Å. The complex showed identical absorption and emission spectra as in the molecule AD–AN–AD (Fig. 9). The fluorescence decay profiles were also matching for the AD–AN–AD and its self-assembled complex. This can be used as an effective strategy for designing a null aggregate of planar chromophores in solution and the solid state. The potential applications of aggregates necessitate a meticulous understanding of the properties arising from the assemblies caused even by minute changes in the geometry.
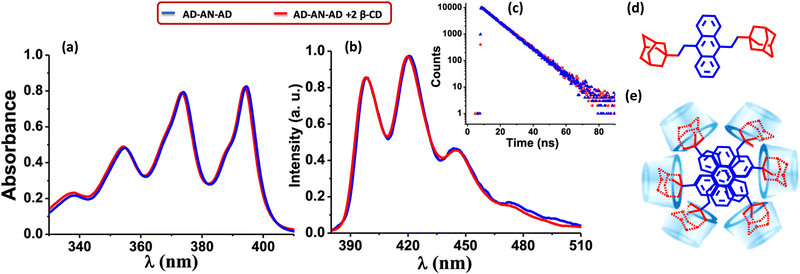 |
| | Fig. 9 (a) Absorption and (b) emission spectra of AD-AN-AD in the absence (blue line) and presence (red line) of 2 equivalents of β-CD, (c) corresponding fluorescence decay profile monitored at 420 nm, (d) molecular structure of AD-AN-AD and (e) stacking of β-CD⊂AD–AN–AD⊃β-CD in the fiber networks. Reproduced from ref. 68 with permission from the American Chemical Society, copyright 2023. | |
Cao, Xie, Guldi and coworkers have synthesised null exciton coupled gridized oligo-diketopyrrolopyrroles via one-pot reaction using bifluorenyls as spacers (Fig. 10).69 Nanogrids are closed-loop molecular building blocks created through covalently linking diarylfluorenes. The molecular design allows targeted studies on DPPs since the C (sp3) nodes break the conjugation between spacers and chromophores. The nanogrids synthesised exhibited monomer-like spectroscopic signatures in steady-state optical measurements. The grid oligomers exhibited symmetry-broken charge-separation (SB-CS) in polar solvent benzonitrile, generating triplet states through charge recombination. Additionally, the [2]Grid showed delayed fluorescence, where SB-CS was found to form an equilibrium with the singlet excited state.
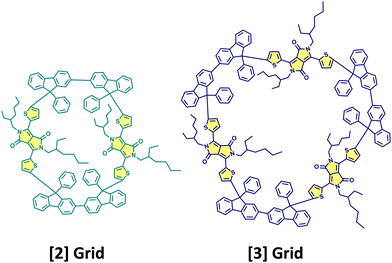 |
| | Fig. 10 Molecular structures of [2]Grid and [3]Grid. | |
Null exciton splitting in greek cross (+) aggregates
Engineering minimal excitonic coupling through orthogonal stacking of chromophores having a precise rotational angle of 90° remains as a challenge, with several attempts reported over the past decades in liquid crystals and theoretical investigations following the prediction of Kasha.20,63 Achieving null exciton coupling in the solid state is challenging due to the close intermolecular distance between the chromophores and the consequent evolution of intermolecular excitonic coupling. The great interest in engineering chromophores into a vanishing excitonic coupling arrangement arises from its exciting physical properties. Greek cross (+) aggregates attained tremendous attention in the past due to proposed charge filtration properties, making the Greek cross aggregate an ideal candidate for the hole or electron transport layer of photovoltaics.70,71 In addition, chromophores in vanishing excitonic coupling arrangements were identified as ideal molecular orientations for long-lived symmetry-broken charge-separated states.72 In order to achieve the desired photophysical properties, methods including functional group substitution and surgery of the molecular core are widely explored.73 Though such strategies give control over the molecular behaviours, the properties become unpredictable when the molecular form is translated to bulk materials such as solids, liquid crystals, etc., for applications. The unpredictability comes from the undesired photophysical pathways generated due to the excitonic interactions resulting from close-packing.64 Therefore, an alternative system is necessary to circumvent the excitonic interactions, thus eliminating unfavourable pathways. The loss of engineered optical properties of molecules experienced in the aggregated state as a result of excitonic communication can be prevented by adopting an orthogonal packing, which results in isolated excitons or null excitons. The null aggregates effectively translate molecular optical behaviours into the bulk material, resulting in photophysical properties that can be reliably predicted. The reported retention of fluorescence quantum yield as in the monomer and exciting charge transport efficiency in the null aggregate, can have far-reaching implications for developing novel optoelectronic properties for device engineering.70
Crystalline evidence for the null exciton splitting
The orthogonally cross-stacked architecture, even though being a promising route for null excitonic interactions, remained uncharted due to the difficulty in self-assembling the molecules into a perfect 90° cross, mainly due to the steric effect-mediated less efficient packing of the chromophores.41–43 The first crystalline evidence for the Greek cross (+) aggregate was deciphered in 1,7-dibromoperylene-3,4,9,10-tetracarboxylic tetrabutylester (PTE-Br2), experimentally substantiated by the observation of monomer-like optical characteristics in the crystalline state (Fig. 11 and 12).71 PTE-Br2 synthesized was crystalized in a columnar organization with the nearest co-facial neighbours oriented in an orthogonal geometry with respect to the long axis of the highly twisted perylene core (dihedral angle = 24.8°) directed by the inter-stack C–H⋯π and dihydrogen (C–H⋯H–C) interactions. The three-dimensional progression of the Greek cross (+) columnar assembly is predominantly directed by the intra-stack C⋯Br (d = 3.54 Å) and inter-stack C–H⋯O (d = 2.65 Å) interactions. Interestingly, the spectroscopic investigations on the crystalline PTE-Br2 having the orthogonally oriented transition dipoles exactly agreed with the theoretical predictions with an unperturbed fluorescence excitation and emission properties (ϕf ≈ 0.20) compared to the monomeric unit (ϕf ≈ 0.23) (Fig. 12). The UV-Vis absorption and fluorescence excitation spectra of orthogonally oriented PTE-Br2 in chloroform showed a typical perylene π–π* (HOMO–LUMO) transition with characteristic vibronic features. The dilute solution of PTE-Br2 exhibited a fluorescence excitation spectrum in the 400–500 nm region and an emission spectrum in the region of 500–600 nm. The monomeric solution of PTE-Br2 retained the fluorescence lifetime (τf = 0.79 and 2.00 ns) as that in the crystalline state (τf = 0.60 and 1.98 ns). Moreover, excellent agreement was observed between the radiative (kr) and non-radiative (knr) decay constant of PTE-Br2 in the solution and crystalline state emphasizing the isolation of transition dipoles (Fig. 12). The photo-excited state properties retained by orthogonally cross stacked molecules in the crystalline state of PTE-Br2 as that in the monomeric solution indicate negligible Coulombic coupling between the cross stacked transition dipoles.
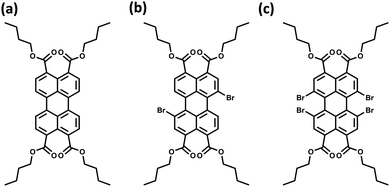 |
| | Fig. 11 Molecular structures of (a) PTE-Br0, (b) PTE-Br2, and (c) PTE-Br4. | |
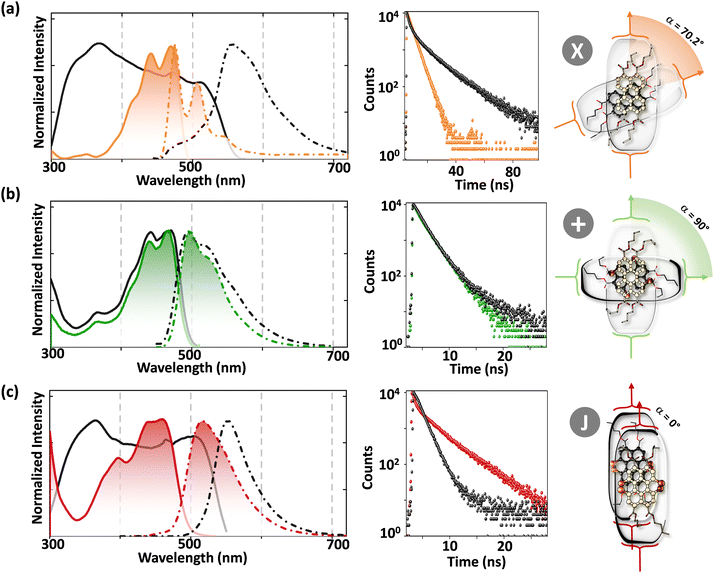 |
| | Fig. 12 Fluorescence excitation (solid) and emission (broken) spectra in the crystalline state (black line) and chloroform solution (colored line), time resolved fluorescence decay profiles and schematic depiction of the molecular structure and close-packing of (a) PTE-Br0, (b) PTE-Br2 and (c) PTE-Br4. Reproduced from ref. 71 with permission from the Wiley-VCH, copyright 2023. | |
Excitingly, the perylene-3,4,9,10-tetracarboxylic tetrabutylester (PTE-Br0) and the tetrabromo substituted derivative (PTE-Br4) formed X-type (α = 70°) and J-type (θ = 48.4°) assemblies respectively in the crystalline state with perturbed optical properties. Compared to the monomeric solutions of PTE-Br0 and PTE-Br4, the crystalline state displayed a broad and bathochromically shifted fluorescence excitation and Kubelka–Munk (K–M) diffuse reflectance spectra in the 300–570 nm region. Crystalline assembly of the PTE-Br0 exhibits a broad, red-shifted fluorescence emission spectrum compared to the monomeric solution in chloroform. The crystalline X-aggregate of PTE-Br0 showed a biexponential decay (τf = 2.18 and 10.9 ns) of the singlet excited state revealed by the picosecond time-resolved lifetime analysis, having a higher average lifetime compared to the monomeric solution in chloroform (Fig. 12). The J-type PTE-Br4 showed red-shifted, moderately narrow emission and increased quantum yield compared to the monomeric state with a reduced lifetime (τf = 0.79 and 1.34 ns) having a nearly ten-fold increase in the radiative decay rate. Thus, spectroscopic investigations in the series with ideal Greek cross (+) PTE-Br2, X-type PTE-Br0 and slip-stacked PTE-Br4 endowed an experimental fabrication of the exciton splitting blueprint proposed by Kasha. Further analysis of the computed charge transport properties revealed exceptional selective hole mobility (μh/μe = 575.8, where μh is hole mobility and μe is electron mobility) in the Greek cross (+) stacked architecture (Fig. 13), unlike the X and J aggregates of PTE-Br0 (μh/μe = 3.86) and PTE-Br4 (μh/μe = 6.36) despite the similar percentage of π stacking interactions.44 The rotational angle-dependent mobility computed reveals the uniqueness of the selective hole transport in the near orthogonal geometry, originating from the negligible electron transfer (te) and high hole transfer (th) integrals.
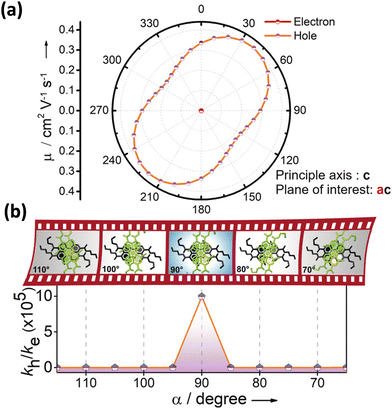 |
| | Fig. 13 (a) Anisotropic mobility computed along the ac plane and (b) schematic depiction of charge filtering demonstrating selective hole transfer in Greek (+) cross PTE-Br2. Reproduced from ref. 71 with permission from Wiley-VCH, copyright 2023. | |
The search for null aggregates in a myriad of chromophoric crystals has revealed a series of Greek cross (+) aggregates in 6,13-bis aryl substituted pentacene derivatives in conjunction with a design strategy for the cross chromophoric assembly (Fig. 14).74 The quantum chemical computations performed in the Greek cross (+) architecture formed by the all carbon 6,13-bisaryl-substituted (4-methylnaphthyl (N2–P); mesityl (M2–P); phenyl (P2–P) groups) pentacene (Ar2–P) derivatives exhibited negligible long-range Coulombic and short-range charge transfer coupling-mediated null exciton splitting with an emergent charge filtering property. The orthogonally cross-stacked orientation at a substantial interplanar distance (di ≥ 4.74 Å) between the stacked dimers of crystalline Ar2–P molecules were directed by the intermolecular C–H⋯C interactions engendered by the sterically bulky aryl substituents in the pentacene. In order to understand the nature of excitonic coupling in orthogonally cross-stacked pentacenes, the contributions from long-range and short-range interactions were calculated. The long-range Coulombic coupling stemming from the transition dipole interaction was calculated using the ideal dipole approximation. All three Ar2–P systems showed negligible Coulombic coupling with values of 0.10, −0.02 and −12.35 cm−1 for N2–P, M2–P and P2–P respectively, reinforcing the perpetual exciton quarantine in the Greek cross (+) pentacene. The investigation on the dependence of Coulombic coupling on the rotational angle between the transition dipoles was analyzed by keeping the dimer molecules of M2–P having an intermolecular distance of 5.99 Å, suggesting a minimal value at an angle of 90° of the order of 10−2 cm−1 (Fig. 15a and d). The JCoul value shows a steady increment with angle and reaches a strongly Coulomb coupled regime with a maximum value of 202.45 cm−1 at a rotation angle of 40°. The variation trend in the JCoul values shows the exclusive role of orthogonal orientation in directing the long-range interaction to a negligible value. The JCT calculated in the Ar2–P systems has an insignificant value reinforcing the irrelevance of charge transfer-mediated coupling in the orthogonally cross-stacked systems, which was further confirmed by calculation of angle-dependent charge transfer integrals (Fig. 15b). The reports by Brédas and co-workers demonstrated that the increase in the interplanar distance leads to an exponential reduction of the charge transfer coupling (Fig. 15c).12 Analogously, cross-stacked pentacene also showed an exponential decline in charge transfer coupling with the increased distance in co-facial dimers. The highest te/th value owned by the orthogonal architecture reinforces the charge filtering in the cross-stacked molecules. The total coupling between the adjacent molecules is defined as the sum of Coulombic and charge transfer mediated couplings (eqn (4)). The insignificant values of Coulombic and CT mediated couplings imply null exciton splitting in Greek cross (+) pentacenes. Analysis of exciton characteristics of the orthogonal dimer using the fragment-based excited state analysis developed by Plasser, executed using TheoDORE, showed that the dimer in the orthogonal orientation possesses two localized nearly degenerate Frenkel states with equal oscillator strength in each fragment.75,76 Deviation from the orthogonal arrangement leads to the mixing of localized Frenkel excitons forming two delocalized Frenkel excitons. It is noted that the Latin cross and T-shape orientations of the dimers at an intermolecular distance of 4 Å displayed minimal excitonic coupling with a slight increase in JCoul, revealing the potential of these architectures that has to be experimentally unveiled. The spectroscopic investigations on the Cross stacked pentacene evidenced unperturbed optical properties, experimentally demonstrating the null exciton splitting in orthogonally cross stacked systems. The UV-Vis absorption spectrum of the chloroform solution of P2–P showed a structured excitation band in the 450–650 nm region and emission spectrum showing resemblance with the absorption and excitation spectra in the crystalline state. Similarly, the other derivatives also showed unperturbed spectroscopic properties in monomeric solution and crystalline states, validating the theoretical predictions. High value for th compared to te, in the Ar2–P systems suggests hole filtering capability through the stacks.
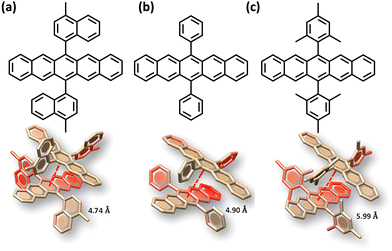 |
| | Fig. 14 Molecular structure and orthogonally stacked dimers of (a) 6,13-bis(4-methylnaphthalen-1-yl)pentacene (N2–P), (b) 6,13-diphenylpentacene (P2–P), and (c) 6,13-dimesitylpentacene (M2–P). Reproduced from ref. 74 with permission from the American Chemical Society, copyright 2023. | |
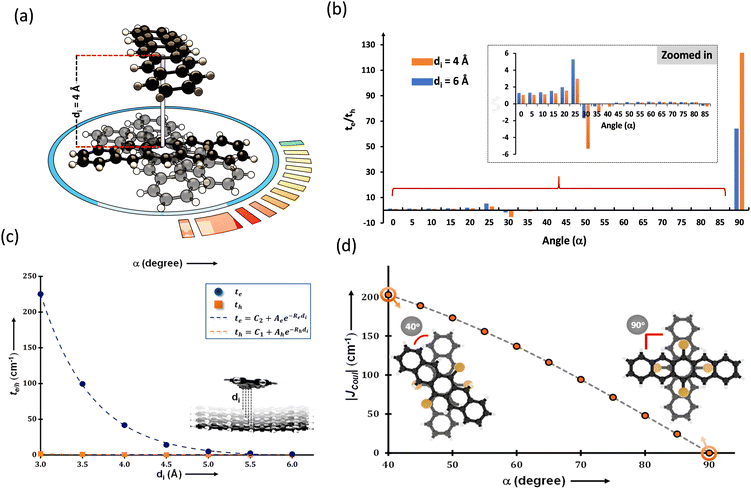 |
| | Fig. 15 (a) Greek cross (+) pentacene with intermolecular distance and angular rotation marked, (b) te/th with varied rotational angle, (c) graph showing the dependence of charge transfer coupling to the interplanar distance and (d) Coulombic coupling variation with respect to the rotational angle. Reproduced from ref. 74 with permission from the American Chemical Society, copyright 2023. | |
Mutually exclusive hole and electron transfer coupling in Greek cross (+) stacks
The theoretical investigation following the trend in the charge transfer coupling of the orthogonal crystalline systems suggests the universality of the cross-stacked architecture as a null coupling inducing chromophore packing even at shorter interplanar distances, as well as possessing selective charge carrier filtering capabilities in the field of charge transport.70 Electronic coupling can lead to the foundation of fascinating optoelectronic properties in organic chromophoric systems.12,77 The influence of electronic coupling through orbital overlap is remarkably susceptible to the relative molecular orientations and sensitive to even sub-angstrom shift.78 The orientation-dependent change arises from the inter-orbital phase relationship. The hole and electron transfer coupling originates from HOMO–HOMO and LUMO–LUMO orbital overlap, respectively. The aggregate architectures with tuned electronic communication can have implications for the design of optoelectronic materials. Diverse geometrical arrangements have been surveyed for the emergent optical and charge transfer properties by altering Coulombic and short-range excitonic coupling through chemical modification and crystal engineering.79,80 The co-facial H-aggregates show high charge carrier mobility where the slip-stacked J-aggregate exhibits comparatively low charge carrier mobility and high fluorescence quantum yield similar to the cross dipole (α = 70°) and magic angle (θ = 54.7°) stacked chromophores.37,61,81,82 Other than the unique 90° arrangement, a rotational angle of 60° is also reported by Müllen, Brédas and co-workers to have an increase in charge transfer mobility for large chromophores.83,84 The Greek cross (+) dimers with eclipsed centroid to centroid arrangement of linear acenes naphthalene (N), anthracene (A), tetracene (T), and pentacene (P) and non-linear acenes pyrene (Py), perylene (Pe), ovalene (Ov), and dibenzo[hi,uV]-phenanthro[3,4,5,6-bcdef]ovalene termed as nanographene (Nn), having a D2h point group were investigated. Interestingly, the scan of electron and hole transfer couplings showed selectivity at orthogonal orientation for all systems under investigation. In the case of naphthalene, the electron transfer coupling reaches a minimum at α = 90° while the hole transfer coupling reaches a maximum (Fig. 16). The magnitude of charge transfer coupling oscillates with α, owing to the interorbital phase relationship between the nodal and antinodal patterns in FMOs. The reason for the observance of hole transfer coupling and negligible electron transfer coupling is attributed to the inherent differences in the orbital symmetry of the monomer. Subsequent analysis on the variation of charge transfer coupling as a function of rotational angle (α) in higher linear acenes revealed a similar trend of mutually exclusive coupling at α = 90°, where either th or te have negligible magnitude. Linear acenes with an even number of benzenoid acenes (naphthalene and tetracene) exhibited higher th and null te, which is in contrast to the odd-numbered benzenoid acenes (anthracene and pentacene). The mutually exclusive behaviour can be traced down to the orbital symmetry of the monomers. Tetracene and naphthalene having gerade symmetry result in zero orbital overlap between LUMOs in a cross-stack, consequently causing a negligible electron transfer coupling. The even-numbered benzenoid acene possessing gerade symmetry in the HOMOs holds an insignificant hole transfer coupling. The selected non-linear acenes having gerade symmetry for the HOMOs (pyrene, ovalene and nanographene) displayed negligible th in the orthogonal architecture, while the acene with gerade symmetry on the LUMO (perylene) revealed null electron transfer coupling. The total coupling (Jtotal) for a Greek cross (+) orientation in these dimers is negligible owing to the minimal inter-orbital overlap in one of the FMOs and the null Coulombic coupling from the orthogonal transition dipoles, resulting in the evolution of two degenerate Frenkel excitons. The specific correlation between geometry and resultant electronic properties in a Greek cross (+) stacked chromophore system highlights the outstanding potential of the Greek cross (+) architectures for emergent optoelectronic properties that call for further investigations.
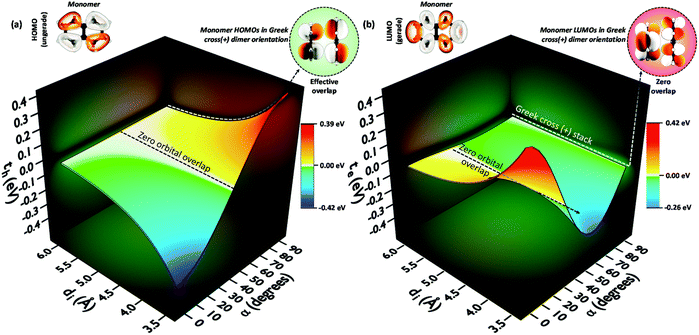 |
| | Fig. 16 (a) Hole transfer coupling (th) and (b) electron transfer coupling (te) of a naphthalene dimer with variation in the rotational angle (α) and interplanar distance (di). Reproduced from ref. 70 with permission from the Royal Society of Chemistry, copyright 2023. | |
Null exciton-coupled spiro-conjugated perylenediimide dimer
The attempt to stitch molecules covalently in an orthogonal fashion to possess null excitonic character culminated in a spiro-conjugated perylenediimide dimer (Sp-PDI2) exhibiting a monomer-like spectroscopic signature.72 An edge-to-edge arranged Greek cross (+)-architecture with a rotational angle (θ) of 87.43° between the chromophores by connecting the two blades of PDI subunits through sp3-hybridized spiro-carbon atom is reported to possess null coupling (Fig. 17).55 Control over the intrinsic excitonic coupling through the cross-architecture and external environment by increasing the solvent polarity led to the evolution of the charge-separated state in the spiro-conjugated perylenediimide dimer. The UV-Vis absorption spectrum of Sp-PDI2 recorded in toluene (Fig. 17) showed virtually unperturbed spectral characteristics as conferred by the Ref-PDI, portraying yet another classic example for Kasha's classic null exciton. The UV-Vis absorption spectrum of Ref-PDI showed an absorption maximum at 533 nm with characteristic spectral features such as that of the monomeric PDI, along with a 10 nm bathochromic shift. The shift observed in the Sp-PDI2 having an absorption maximum at 549 nm is due to the self-energy correction. The fluorescence emission spectrum of Sp-PDI2 in toluene showed a monomer-like signature with well-resolved vibronic bands having an emission maximum of 558 nm and a high fluorescence quantum yield of 90.20%. The reference PDI exhibited an emission maximum at 542 nm with a fluorescence quantum yield of 97.7%. Subsequent theoretical investigations suggested negligible value for the Coulombic and charge transfer couplings, reinforcing the exotic nature of the Greek cross (+) orientation. The obtained JCoul value of 3.34 cm−1 emphasizes the null Coulombic coupling stemming from the Greek cross (+) orientation. The charge transfer coupling calculated revealed the selective hole transfer coupling in the spiro-connected dimer, which is further experimental evidence for the selective charge filtering in the Greek cross (+) stacked architecture. The minimal value (−2.79 cm−1) obtained for the CT coupling warrants the inconsequential short-range interaction at the angle of 90°. The exciton coupling calculated from the UV-Vis absorption spectrum from the ratio of the 0–0 and 0–1 absorption bands reaffirms the null exciton coupling in the system. Coulombic and charge transfer couplings analyzed for different spatial orientations confirmed the exclusive nature of 90° rotational angle in nullifying the excitonic coupling. The emergent excited state dynamics of the null exciton coupled spiro-conjugated PDI dimer exhibited solvent polarity modulated photophysical properties. A significant decrease in fluorescence quantum yield and the evolution of a biexponential fluorescence decay profile with an increase in solvent polarity implied the presence of additional decay pathways. The solvent-dependent femtosecond transient absorption studies revealed the dissociation of the null exciton state facilitated by the selective hole transfer coupling in polar solvents leading to the evolution of a symmetry-breaking charge-separated state. The fragment-based excited state analysis in Sp-PDI2 displayed nearly degenerate localized Frenkel exciton states (S1 and S2) and pure CT state (S3 and S4) (Fig. 18). The high sensitivity of short-range CT coupling to molecular packing geometry leads to the promotion of various photophysical pathways including excimer formation, symmetry-breaking charge-separation (SB-CS), or singlet fission, depending on the molecular arrangement. The photoinduced dynamics of PDI dimers can be categorized based on the long-range Coulombic and short-range CT coupling as: (i) SB-CS state by an incoherent charge separation process in dimers with small Coulombic coupling, (ii) structural relaxation to form an excimer state in the strong Coulomb coupled regime, and (iii) a null coupled regime where both the couplings get cancelled by each other, which can lead to electronic state mixing between Frenkel exciton (FE) and CT states.
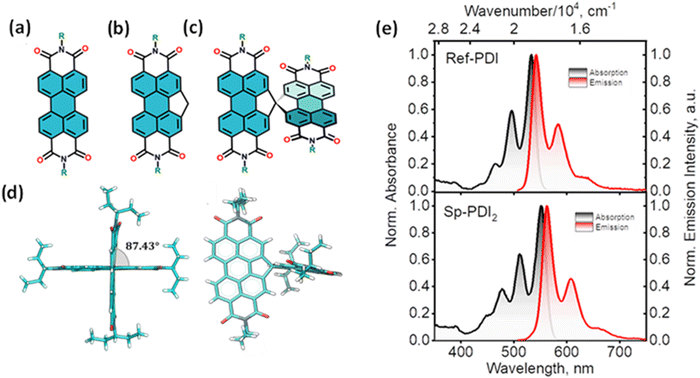 |
| | Fig. 17 Molecular structures of (a) PDI, (b) Ref-PDI and (c) Sp-PDI2 (R-3-pentyl group), (d) single crystal X-ray structure of Sp-PDI2, and (e) normalized absorption (black trace) and emission (red trace) spectra of Ref-PDI (top) and Sp-PDI2 (bottom) in toluene at room temperature. Reproduced from ref. 72 with permission from the American Chemical Society, copyright 2023. | |
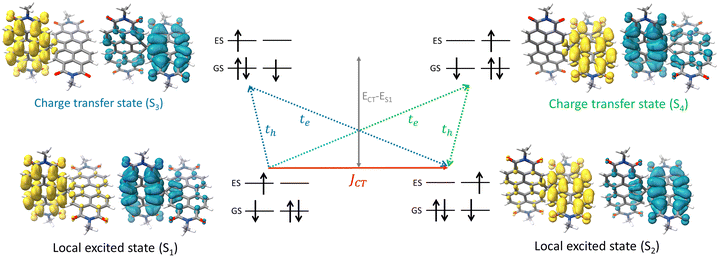 |
| | Fig. 18 Depiction of hole and electron transfer between the neighbouring PDI molecule and corresponding isosurface of the hole (blue) and electron (yellow). Reproduced from ref. 72 with permission from the American Chemical Society, copyright 2023. | |
Wasielewski, Young, and co-workers recently presented null-type exciton coupling in a slip-stack arranged PDI dimer 2 and trimer 3 (Fig. 19).85 The monomeric units 1 of the PDI dimer and trimer connected through a xanthene spacer with 4.3 Å slippage along the longer axes and 3.5 Å average intermolecular distance. The steady-state UV-Vis absorption and fluorescence spectrum of the dimer 2 and trimer 3 indicates the presence of weak excitonic interaction between slip-stacked PDI units. Small bathochromic shifted absorption maxima (12–16 nm), and a slight increase in their I0–1/I0–0 vibronic band ratios support the weak excitonic coupling in 2 and 3 (Fig. 17).
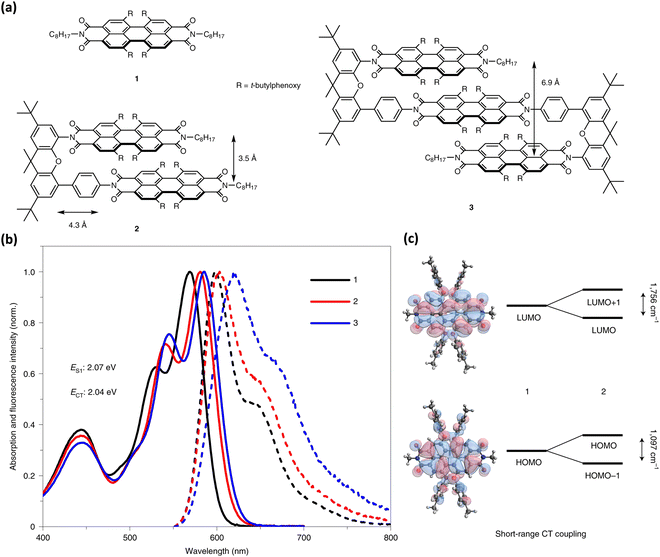 |
| | Fig. 19 (a) Molecular structures of monomer, dimer and trimer (R-4′-tert-butylphenoxy group), (b) absorption (solid line) and emission (dotted line) spectra of 1, 2 and 3 in THF, and (c) energy level splitting between the HOMOs and LUMOs in 2 due to the short-range CT coupling. Reproduced from ref. 85 with permission from Nature, copyright 2023. | |
The excitonic coupling strength (J) calculated from the absorption spectra of 2 and 3 resulted in J = 15 cm−1 and 46 cm−1 for 2 and 3, respectively, signifying the destructive inference between the Coulombic and charge-transfer term contribution. Strong charge-transfer coupling in slip-stacked dimer 2 and dimer 3 could have arisen from the significant frontier molecular orbital wave function overlap between PDI units (Fig. 19). The excited-state dynamics of dimer 2 and trimer 3 in different dielectric environments unveiled the role of vibronic coupling in coherent symmetry-breaking charge separation.
Conclusions
The arrangement of chromophores in the assembly, which determines the electronic coupling, controls the optical characteristics that emerge from supramolecular arrays. It is vital to comprehend electronic couplings and their resulting photophysical properties in order to develop optoelectronic materials of interest. The ease of attainability led to a volume of literature about the H- and J-aggregates that are well understood and can only be seen as the tip of the iceberg. The advancement of aggregate photophysics requires attention to anomalous aggregates with unusual slip and rotational angles. Davydov and Kasha separately established the initial theoretical framework for comprehending the excitonic coupling in molecular assembly. Later the excitonic theory was modified by the incorporation of orbital overlap-mediated coupling. Several attempts were reported in assembling molecules as cross dipoles which enhanced the luminescence efficiency. Atypical aggregates exhibiting minimal exciton interactions have remained elusive owing to the difficulty in achieving them. The M aggregates reported in mb-PBI stacks with 54.7° slip angle minimise the long-distance Föster energy transfer. Yet another phenomenon of null aggregate formation by the interference between Coulombic and CT-mediated couplings was unveiled in a perylenediimide foldamer, where monomer-like absorption features are observed for the foldamer. Null aggregates through orthogonal architectures are a hitherto less explored class of supramolecular assemblies of organic chromophores, which now is in the spotlight with a series of experimental verifications and more theoretical insights unveiled after Kasha's proposal of the exciton isolation in the orthogonal chromophoric arrangement in 1965. The first unambiguous evidence for the null exciton splitting in the crystalline system having a Greek cross (+) architecture is observed in PTE-Br2. Monomer-like optical characteristics are observed for crystalline PTE-Br2 owing to the orthogonal orientation, in contrast to the X-type PTE-Br0 (α = 70.28°) and J-type PTE-Br4 (α = 0°, θ = 48.48°) crystalline assemblies, which rendered perturbed spectroscopic behaviour as compared to the monomeric solutions due to the exciton coupling in the systems. The Greek cross (+) architecture rendered null aggregate was unveiled in a series of 6,13-bisaryl substituted pentacenes, having phenyl, mesityl and methylnaphthyl as substituents, possessing negligible short-range charge transfer and long-range Coulombic couplings. Further theoretical investigations on the charge filtering revealed the mutually exclusive nature of hole and electron transfer couplings as a consequence of Greek cross (+) stacking. The charge filtering capability of the orthogonal system mandates further investigation, which can have applications in supramolecular optoelectronics. Null exciton splitting in the edge-to-edge arranged Greek cross (+) architecture is experimentally verified by the analysis in the spiro-conjugated perylenediimide dimer. Extending the possibilities of null aggregates in the covalently connected system can offer a plethora of design strategies in order to engender molecular assemblies having null coupling. The emergent properties of the aggregate assembly can be structured by tuning the exciton coupling, promising potential applications of less explored architectures for optoelectronic devices.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
M. H. acknowledges the Nanomission project (DST/NM/TUE/EE-01/2019) of the Department of Science and Technology (DST), Government of India, for financial support. MPL acknowledges IISER TVM for financial assistance.
Notes and references
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS.
- A. S. Davydov, Phys.-Usp., 1964, 7, 145 CrossRef.
- N. J. Hestand and F. C. Spano, Acc. Chem. Res., 2017, 50, 341–350 CrossRef CAS PubMed.
-
J.-L. Bredas and S. R. Marder, The WSPC Reference on Organic Electronics: Organic Semiconductors, World Scientific, 2016, vol. 1 Search PubMed.
- O. Ostroverkhova, Chem. Rev., 2016, 116, 13279–13412 CrossRef CAS PubMed.
- J. Gierschner, J. Shi, B. Milián-Medina, D. Roca-Sanjuán, S. Varghese and S. Park, Adv. Opt. Mater., 2021, 9, 2002251 CrossRef CAS.
- M. Kasha, Radiat. Res., 1963, 20, 55–70 CrossRef CAS PubMed.
- J. H. Kim, T. Schembri, D. Bialas, M. Stolte and F. Würthner, Adv. Mater., 2022, 34, 2104678 CrossRef CAS PubMed.
- T. W. Ebbesen, Acc. Chem. Res., 2016, 49, 2403–2412 CrossRef CAS PubMed.
- R. Sethy, J. Kumar, R. Métivier, M. Louis, K. Nakatani, N. M. T. Mecheri, A. Subhakumari, K. G. Thomas, T. Kawai and T. Nakashima, Angew. Chem., Int. Ed., 2017, 56, 15053–15057 CrossRef CAS PubMed.
- J. Cornil, D. Beljonne, J. P. Calbert and J. L. Brédas, Adv. Mater., 2001, 13, 1053–1067 CrossRef CAS.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- S. Varghese and S. Das, J. Phys. Chem. Lett., 2011, 2, 863–873 CrossRef CAS PubMed.
- G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. Van Grondelle, Nat. Chem., 2011, 3, 763–774 CrossRef CAS PubMed.
- D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2001, 34, 40–48 CrossRef CAS PubMed.
- R. G. Saer and R. E. Blankenship, Biochem. J., 2017, 474, 2107–2131 CrossRef CAS PubMed.
- K. Ziach, C. Chollet, V. Parissi, P. Prabhakaran, M. Marchivie, V. Corvaglia, P. P. Bose, K. Laxmi-Reddy, F. Godde, J. M. Schmitter, S. Chaignepain, P. Pourquier and I. Huc, Nat. Chem., 2018, 10, 511–518 CrossRef CAS PubMed.
- E. T. Kool, Acc. Chem. Res., 2002, 35, 936–943 CrossRef CAS PubMed.
- G. R. Desiraju and A. Gavezzotti, Acta Crystallogr., Sect. B, 1989, 45, 473–482 CrossRef.
- X. Feng, W. Pisula and K. Müllen, J. Am. Chem. Soc., 2007, 129, 14116–14117 CrossRef CAS PubMed.
- R. Ramakrishnan, M. A. Niyas, M. P. Lijina and M. Hariharan, Acc. Chem. Res., 2019, 52, 3075–3086 CrossRef CAS PubMed.
- A. Ajayaghosh, C. Vijayakumar, R. Varghese and S. J. George, Angew. Chem., Int. Ed., 2006, 45, 456–460 CrossRef CAS PubMed.
- H. Y. Zhang, Z. L. Zhang, K. Q. Ye, J. Y. Zhang and Y. Wang, Adv. Mater., 2006, 18, 2369–2372 CrossRef CAS.
- T. Hinoue, Y. Shigenoi, M. Sugino, Y. Mizobe, I. Hisaki, M. Miyata and N. Tohnai, Chem. – Eur. J., 2012, 18, 4634–4643 CrossRef CAS PubMed.
- D. Lewis, J. Yang and C. L. Stern, J. Am. Chem. Soc., 1996, 118, 2772–2773 CrossRef.
- S. E. Sheppard, J. Chem. Soc., Trans., 1909, 95, 15–19 RSC.
- B. Heyne, Photochem. Photobiol. Sci., 2016, 15, 1103–1114 CrossRef CAS PubMed.
- E. E. Jelley, Nature, 1936, 138, 1009–1010 CrossRef CAS.
- G. Scheibe, Angew. Chem., 1937, 50, 212–219 CrossRef CAS.
- F. Würthner, T. E. Kaiser and C. R. Saha-Möller, Angew. Chem., Int. Ed., 2011, 50, 3376–3410 CrossRef PubMed.
- M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19 RSC.
- R. M. Hochstrasser and M. Kasha, Photochem. Photobiol., 1964, 3, 317–331 CrossRef CAS.
- E. G. Mcrae and M. Kasha, J. Chem. Phys., 2004, 28, 721 CrossRef.
- J. L. Bricks, Y. L. Slominskii, I. D. Panas and A. P. Demchenko, Methods Appl. Fluoresc., 2017, 6, 012001 CrossRef PubMed.
- F. C. Spano and C. Silva, Annu. Rev. Phys. Chem., 2014, 65, 477–500 CrossRef CAS PubMed.
- S. Ma, S. Du, G. Pan, S. Dai, B. Xu and W. Tian, Aggregate, 2021, 2, e96–e111 CAS.
- J. Zhou, W. Zhang, X.-F. Jiang, C. Wang, X. Zhou, B. Xu, L. Liu, Z. Xie and Y. Ma, J. Phys. Chem. Lett., 2018, 9, 2023 Search PubMed.
- H. Yamagata, C. M. Pochas and F. C. Spano, J. Phys. Chem. B, 2012, 116, 14494–14503 CrossRef CAS PubMed.
- S. Park, J. E. Kwon, S.-Y. Park, O.-H. Kwon, J. K. Kim, S.-J. Yoon, J. W. Chung, D. R. Whang, S. K. Park, D. K. Lee, D.-J. Jang, J. Gierschner and S. Y. Park, Adv. Opt. Mater., 2017, 5, 1700353 CrossRef.
- P. Srujana, P. Sudhakar and T. P. Radhakrishnan, J. Mater. Chem. C, 2018, 6, 9314–9329 RSC.
- U. Rösch, S. Yao, R. Wortmann and F. Würthner, Angew. Chem., Int. Ed., 2006, 45, 7026–7030 CrossRef PubMed.
- N. K. Allampally, A. Florian, M. J. Mayoral, C. Rest, V. Stepanenko and G. Fernández, Chem. – Eur. J., 2014, 20, 10669–10678 CrossRef CAS PubMed.
- N. J. Hestand and F. C. Spano, J. Chem. Phys., 2015, 143, 244707 CrossRef PubMed.
- M. T. Sims, L. C. Abbott, S. J. Cowling, J. W. Goodby and J. N. Moore, Phys. Chem. Chem. Phys., 2017, 19, 813–827 RSC.
- S. G. Telfer, T. M. McLean and M. R. Waterland, Dalton Trans., 2011, 40, 3097–3108 RSC.
- M. B. Oviedo and C. G. Sánchez, J. Phys. Chem. A, 2011, 115, 12280–12285 CrossRef CAS PubMed.
- K. Sugiyasu, N. Fujita and S. Shinkai, Angew. Chem., Int. Ed., 2004, 43, 1229–1233 CrossRef CAS PubMed.
- H. Kautsky and H. Merkel, Naturwissenschaften, 1939, 27, 195–196 CrossRef CAS.
- G. D. Scholes and K. P. Ghiggino, J. Phys. Chem., 1994, 98, 4580–4590 CrossRef CAS.
- B. P. Krueger, G. D. Scholes and G. R. Fleming, J. Phys. Chem. B, 1998, 102, 5378–5386 CrossRef CAS.
- G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57–87 CrossRef CAS PubMed.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- P. M. Kazmaier and R. Hoffmann, J. Am. Chem. Soc., 2002, 116, 9684–9691 CrossRef.
- G. D. Scholes, K. P. Ghiggino, A. M. Oliver and M. N. Paddon-Row, J. Am. Chem. Soc., 2002, 115, 4345–4349 CrossRef.
- H. Yamagata, J. Norton, E. Hontz, Y. Olivier, D. Beljonne, J. L. Brédas, R. J. Silbey and F. C. Spano, J. Chem. Phys., 2011, 134, 204703 CrossRef CAS PubMed.
- J. Vura-Weis, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2010, 132, 1738–1739 CrossRef CAS PubMed.
- A. Benny, D. Sasikumar and M. Hariharan, J. Phys. Chem. C, 2019, 123, 26758–26768 CrossRef CAS.
- J. Cornil, D. A. dos Santos, X. Crispin, R. Silbey and J. L. Brédas, J. Am. Chem. Soc., 1998, 120, 1289–1299 CrossRef CAS.
- N. Sanyal and P. M. Lahti, Cryst. Growth Des., 2006, 6, 1253–1255 CrossRef CAS.
- B. Zhang, H. Soleimaninejad, D. J. Jones, J. M. White, K. P. Ghiggino, T. A. Smith and W. W. H. Wong, Chem. Mater., 2017, 29, 8395–8403 CrossRef CAS.
- Z. Xie, B. Yang, F. Li, G. Cheng, L. Liu, G. Yang, H. Xu, L. Ye, M. Hanif, S. Liu, D. Ma and Y. Ma, J. Am. Chem. Soc., 2005, 127, 14152–14153 CrossRef CAS PubMed.
- S. Ma, J. Zhang, J. Qian, J. Chen, B. Xu and W. Tian, Adv. Opt. Mater., 2015, 3, 763–768 CrossRef CAS.
- M. R. Hansen, T. Schnitzler, W. Pisula, R. Graf, K. Müllen and H. W. Spiess, Angew. Chem., Int. Ed., 2009, 48, 4621–4624 CrossRef CAS PubMed.
- A. M. Philip, S. K. Manikandan, A. Shaji and M. Hariharan, Chem. – Eur. J., 2018, 24, 18089–18096 CrossRef CAS PubMed.
- H. Tamura, J. Phys. Chem. A, 2016, 120, 9341–9347 CrossRef CAS PubMed.
- H.-M. Zhao, J. Pfister, V. Settels, M. Renz, M. Kaupp, V. C. Dehm, F. Würthner, R. F. Fink and B. Engels, J. Am. Chem. Soc., 2009, 131, 15660–15668 CrossRef CAS PubMed.
- C. Kaufmann, D. Bialas, M. Stolte and F. Würthner, J. Am. Chem. Soc., 2018, 140, 9986–9995 CrossRef CAS PubMed.
- N. Nayak and K. R. Gopidas, J. Phys. Chem. B, 2019, 123, 8131–8139 CrossRef CAS PubMed.
- Y. Bo, P. Hou, J. Wan, H. Cao, Y. Liu, L. Xie and D. M. Guldi, Adv. Mater., 2023, 2302664 CrossRef PubMed.
- A. Benny, R. Ramakrishnan and M. Hariharan, Chem. Sci., 2021, 12, 5064–5072 RSC.
- E. Sebastian, A. M. Philip, A. Benny and M. Hariharan, Angew. Chem., Int. Ed., 2018, 57, 15696–15701 CrossRef CAS PubMed.
- E. Sebastian and M. Hariharan, J. Am. Chem. Soc., 2021, 143, 13769–13781 CrossRef CAS PubMed.
- K. Zhao, Z.-F. Yao, Z.-Y. Wang, J.-C. Zeng, L. Ding, M. Xiong, J.-Y. Wang and J. Pei, J. Am. Chem. Soc., 2022, 144, 3091–3098 CrossRef CAS PubMed.
- M. P. Lijina, A. Benny, R. Ramakrishnan, N. G. Nair and M. Hariharan, J. Am. Chem. Soc., 2020, 142, 17393–17402 CrossRef CAS PubMed.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed.
- F. Plasser, J. Chem. Phys., 2020, 152, 084108 CrossRef CAS PubMed.
- C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Chem. Rev., 2012, 112, 2208–2267 CrossRef CAS PubMed.
- J. L. Brédas, J. P. Calbert, D. A. Da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804–5809 CrossRef PubMed.
- A. Pirrotta, G. C. Solomon, I. Franco and A. Troisi, J. Phys. Chem. Lett., 2017, 8, 4326–4332 CrossRef CAS PubMed.
- S. Fratini, S. Ciuchi, D. Mayou, G. T. de Laissardière and A. Troisi, Nat. Mater., 2017, 16, 998–1002 CrossRef CAS PubMed.
- S. Ma, Y. Liu, J. Zhang, B. Xu and W. Tian, J. Phys. Chem. Lett., 2020, 11, 10504–10510 CrossRef CAS PubMed.
- S. Kim, T. K. An, J. Chen, I. Kang, S. H. Kang, D. S. Chung, C. E. Park, Y.-H. Kim and S.-K. Kwon, Adv. Funct. Mater., 2011, 21, 1616–1623 CrossRef CAS.
- X. Feng, V. Marcon, W. Pisula, M. R. Hansen, J. Kirkpatrick, F. Grozema, D. Andrienko, K. Kremer and K. Müllen, Nat. Mater., 2009, 8, 421–426 CrossRef CAS PubMed.
- V. Lemaur, D. A. da Silva Filho, V. Coropceanu, M. Lehmann, Y. Geerts, J. Piris, M. G. Debije, A. M. van de Craats, K. Senthilkumar, L. D. A. Siebbeles, J. M. Warman, J.-L. Brédas and J. Cornil, J. Am. Chem. Soc., 2004, 126, 3271–3279 CrossRef CAS PubMed.
- C. Lin, T. Kim, J. D. Schultz, R. M. Young and M. R. Wasielewski, Nat. Chem., 2022, 14, 786–793 CrossRef CAS PubMed.
Footnote |
| † These authors equally contributed to this work. |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*

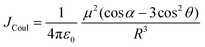
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α − 3
α − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is the orientation factor (κ). The Coulombic coupling can also be calculated using the transition charge from the electrostatic potential method (TrESP) between the molecules and represented as:
θ is the orientation factor (κ). The Coulombic coupling can also be calculated using the transition charge from the electrostatic potential method (TrESP) between the molecules and represented as: