Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Triggering single-molecule qubit spin dynamics via non-Abelian geometric phase effects†
Kieran
Hymas
 a and
Alessandro
Soncini
a and
Alessandro
Soncini
 *b
*b
aCommonwealth Scientific and Industrial Research Organisation (CSIRO), Clayton, Victoria 3168, Australia. E-mail: kieran.hymas@csiro.au
bDepartment of Chemical Sciences, University of Padova, Via Marzolo 1, 35131 Padova, Italy. E-mail: alessandro.soncini@unipd.it
First published on 27th September 2023
Abstract
We illustrate how macroscopic rotations can be utilised to trigger and control a spin dynamics within the ground doublet of both Kramers and non-Kramers-type molecular nanomagnets via the non-Abelian character of the time-evolution operator. For Kramers magnets, we show how this effect can be harnessed to realise single-qubit quantum gates and give the explicit example of a recently reported CoCl2(tu)4 single-molecule magnet (SMM). We demonstrate that gating operations could be performed on this magnet in as fast as 10 ps before the breakdown of adiabaticity, much faster than typical spin–lattice relaxation times. Based on this effect, we also suggest CoCl2(tu)4 as a quantum gyroscope for sensing yaw-axis rotations. For integer spin nanomagnets where non-axial crystal field interactions often lift ground state degeneracy, we show how spin dynamics from the non-Abelian geometric propagator can be recovered using non-adiabatic macroscopic rotations not-necessarily resonant with the tunnel splitting gap. Using the well-known TbPc2 single-ion magnet as a further example, we identify an experimentally plausible non-adiabatic rotation that induces a coherent superposition of tunnelling ground states, tantamount to preparing each member of a TbPc2 ensemble in the maximal angular momentum state |mJ = 6〉. The detection of an ensuing coherent oscillation of the macroscopic magnetisation polarised along the TbPc2 principal magnetic axis after the completed rotation could then proceed via time-resolved magnetisation measurements.
1 Introduction
The rich physics underpinning single-molecule superparamagnetism has been intensely studied since the discovery of single-molecule magnets (SMMs) in 19931 with a mind towards their application as microscopic units in molecular memory devices2–4 and novel quantum information technologies.5–9 While the coherent and incoherent dynamics which result in ‘under-the-barrier’ fast magnetic relaxation has foiled current attempts at room temperature single-molecule magnet memory,10–14 these dynamical processes can instead be harnessed for the manipulation of single-molecule magnet qubit states. Generally, quantum logic gates are implemented in these systems via the application of an external resonant microwave or radio-frequency radiation that coherently prepares the nanomagnet in superpositions of energy eigenstates which oscillate in time when the radiation is switched off.15–17 The time-evolution of these linear combinations is then detectable as Rabi oscillations in time-resolved spin-echo18,19 or non-equilibrium electrical current20 measurements subject to decoherence from the local environment of the qubit. Two-qubit quantum logic gates (e.g. CNOT and ) have also been implemented in coupled paramagnetic qubit architectures via g-factor engineering of lanthanide ions21 and modular supramolecular linkers in paramagnetic rings.22,23 Addressing individual qubits in linked vanadyl–porphyrin dimers has also recently been reported by taking advantage of a weak intramolecular exchange coupling and small homogeneous linewidths intrinsic to the molecule.24
) have also been implemented in coupled paramagnetic qubit architectures via g-factor engineering of lanthanide ions21 and modular supramolecular linkers in paramagnetic rings.22,23 Addressing individual qubits in linked vanadyl–porphyrin dimers has also recently been reported by taking advantage of a weak intramolecular exchange coupling and small homogeneous linewidths intrinsic to the molecule.24
In 1984, Wilczek and Zee showed that the adiabatic transport of a quantum system around a closed path in Hamiltonian parameter space can induce a coherent dynamics between energy eigenstates of a degenerate manifold owing to an emergent non-Abelian gauge structure in the geometric component of the time evolution operator.25 This opened the door for holonomic quantum computation where gating operations correspond to the transport of a degenerate eigenspace (the holonomic qubit computational basis) along holonomies in parameter space.26 When the space of cyclically evolving parameters coincides with the coordinates of real space (e.g. macroscopic rotations), a connection between the Hilbert space of the quantum system and the geometry of the physical space which it occupies, is clearly established. The potential for rotation-induced non-Abelian dynamics in easy-plane Kramers-type spin systems (where time-reversal symmetry enforces an exact ground state degeneracy in the absence of external magnetic perturbations) was first exposed by Zee.27 In that work he pinpointed a mechanism for rotation-induced frequency splitting of nuclear quadrupole resonance spectra obtained for a I = 3/2 35Cl nuclear spin.28
Geometric phase effects have previously been suggested as mechanisms to trigger and control the coherent dynamics of single-molecule magnets29–31 and related spin systems.32–35 As the electronic spin of the SMM adiabatically follows the rotating crystal field potential it can accumulate a non-Abelian geometric phase during the cyclic rotation. Similarly, the generation of a coherent spin dynamics via macroscopic rotations was suggested for ensembles of nitrogen-vacancy (NV) centres where a longitudinal magnetic field (rotating simultaneously with the NV centre quantisation axis) was proposed to enforce degeneracy.36 While largely successful as potential qubits and gyroscopes, NV centres lack the synthetic customisability of molecular nanomagnets. Since the rotation-induced spin dynamics of a SMM is strongly correlated with the microscopic parameters of its associated spin Hamiltonian (vide infra) this offers a bottom-up synthetic pathway to tune geometric effects in SMMs for applications such as holonomic quantum computation and inertial sensing.
In this manuscript we show how macroscopic rotations can trigger a spin dynamics in the degenerate or quasi-degenerate ground doublet of Kramers and non-Kramers molecular nanomagnets, respectively, via the non-Abelian character of their time-evolution operator. We first discuss the sensitivity of the non-Abelian Berry phase to the effective crystal field parameters and, with representative examples for each nanomagnet class, we construct single-qubit Hadamard quantum logic gates using specific rotation paths. In non-Kramers magnets, where non-axial terms in the crystal field Hamiltonian are poised to remove ground state degeneracy through a tunnel splitting between the otherwise bistable ground states, we recover a non-Abelian time evolution operator for the quasi-degenerate ground doublet by relaxing the stringent requirement of adiabatic rotation. In this case, we derive an analytical relationship between the rotation time and rotation axis canting angle which leads to the realisation of all possible Hadamard gates with the tunnelling ground doublet acting as a computational basis. We finally discuss the detection of this effect via the resultant collective magnetic moment oscillation of the non-Kramers nanomagnet crystal.
2 Theoretical model
2.1 Nanomagnet effective spin Hamiltonian
The microscopic origin of magnetic anisotropy in SMMs results from the interplay between electrostatic crystal field effects and spin–orbit coupling mainly affecting the electronic states of the paramagnetic ions’ 3d or 4f unpaired electrons. In polynuclear nanomagnets, intramolecular spin–spin interactions can too influence the overall magnetic anisotropy. For most non-lanthanide SMMs, the effective spin Hamiltonian HS = DSz2 + E(Sx2 − Sy2) is often a good starting point to describe the zero-field splitting of orbital angular momentum quenched magnetic levels within a given ground manifold 2S+1Γ0.37 The first term of HS accounts for an axial magnetic anisotropy of the electronic spin S = (Sx, Sy, Sz) and is always negative for single-molecule magnets. The second term accounts for rhombic magnetic anisotropy and, when Sz is quantised along the principal magnetic axis, we have that 0 ≤ E < D/3. We utilise the aforementioned effective spin Hamiltonian throughout this manuscript except in Section 3.5 where the example of a rotating lanthanide single-ion magnet necessitates the inclusion of higher-order irreducible tensor operators into the effective spin Hamiltonian.In the laboratory frame, the Hamiltonian for the rotating system takes the form H(α, β, γ) = ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (α, β, γ)HS
(α, β, γ)HS ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) †(α, β, γ) where the rotation operator
†(α, β, γ) where the rotation operator
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (α, β, γ) = e−iαSze−iβSye−iγSz (α, β, γ) = e−iαSze−iβSye−iγSz | (1) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (α, β, γ).27 It is thus simple to show that H(α, β, γ) |ηa(α, β, γ)〉 = εa|ηa(α, β, γ)〉 where the eigenvalues εa defined by HS|ϕa〉 = εa|ϕa〉 remain constant throughout the rotation.
(α, β, γ).27 It is thus simple to show that H(α, β, γ) |ηa(α, β, γ)〉 = εa|ηa(α, β, γ)〉 where the eigenvalues εa defined by HS|ϕa〉 = εa|ϕa〉 remain constant throughout the rotation.
For single-molecule magnets with half-odd integer spin length, Kramers theorem guarantees that diagonalisation of HS will always yield a ground state doublet |ϕ±〉 whose instantaneous energy ε+ = ε− = ε0 can be harmlessly shifted to zero.30 As a consequence, ground state degeneracy is maintained throughout any adiabatic rotation and thus triggers the onset of a non-Abelian Berry phase, a unitary transformation producing a linear superposition of the two initial degenerate states. In general this is not the case for integer spin SMMs where the rhombic anisotropy term introduces a tunnel splitting gap between the ground doublet states. We will return to this interesting case in Sections 3.4 and 3.5 but for now, we assume a perfect ground state degeneracy.
2.2 The non-Abelian geometric propagator
Let![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) 0 represent an N-fold dimensional manifold composed of the subset of instantaneous ground states |ηa(λ)〉 of a Hamiltonian H(λ) which remain degenerate throughout a cyclic and adiabatic variation of d classical parameters λ = (λ1, …, λd). For N ≥ 2, an initial wavefunction prepared within this subspace evolves into linear combinations of states from
0 represent an N-fold dimensional manifold composed of the subset of instantaneous ground states |ηa(λ)〉 of a Hamiltonian H(λ) which remain degenerate throughout a cyclic and adiabatic variation of d classical parameters λ = (λ1, …, λd). For N ≥ 2, an initial wavefunction prepared within this subspace evolves into linear combinations of states from ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) 0 according to the Berry phase (see Supplementary Note 1 for a careful derivation, ESI†)
0 according to the Berry phase (see Supplementary Note 1 for a careful derivation, ESI†)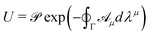 | (2) |
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) denotes path ordering, Γ is the cyclic path traced out in d-dimensional parameter space and
denotes path ordering, Γ is the cyclic path traced out in d-dimensional parameter space and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) μdλμ is the associated non-Abelian gauge potential (here we adopt the Einstein summation convention). The
μdλμ is the associated non-Abelian gauge potential (here we adopt the Einstein summation convention). The ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) μ's are N × N matrices with matrix elements
μ's are N × N matrices with matrix elements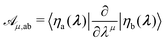 | (3) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) 0.
0.
In this work, we study the spin dynamics triggered within the degenerate ground manifold, ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) 0, of nanomagnets undergoing rotations in physical space parametrised by the Euler angles α, β and γ. The non-Abelian gauge potential (derived explicitly in Supplementary Note 2, ESI†) is defined by the infinitesimal line element
0, of nanomagnets undergoing rotations in physical space parametrised by the Euler angles α, β and γ. The non-Abelian gauge potential (derived explicitly in Supplementary Note 2, ESI†) is defined by the infinitesimal line element ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) μdλμ =
μdλμ = ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) αdα +
αdα + ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) βdβ +
βdβ + ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) γdγ where
γdγ where
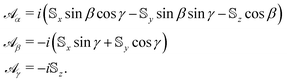 | (4) |
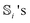 are matrix representations of the angular momentum operators Si on the basis of the ground spin states of HS. Unlike in previous studies of rotation-induced spin dynamics,27,36 we note that the loss of cylindrical symmetry in HS (owing to the inclusion of rhombic anisotropy) necessitates that the gauge potential
are matrix representations of the angular momentum operators Si on the basis of the ground spin states of HS. Unlike in previous studies of rotation-induced spin dynamics,27,36 we note that the loss of cylindrical symmetry in HS (owing to the inclusion of rhombic anisotropy) necessitates that the gauge potential ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) μ be defined in the three-dimensional space spanned by all three Euler angles, rather than just α and β alone.
μ be defined in the three-dimensional space spanned by all three Euler angles, rather than just α and β alone.
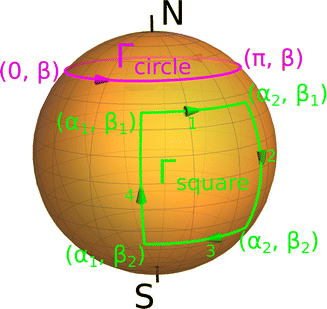
2.3 Rotations about loops enclosing simply and non-simply connected domains
Although the most general rotation is defined by all three Euler angles discussed at the end of last section, we choose here special closed paths in parameter space that are defined by constant, but generally non-zero, values of γ. In particular, we investigate rotations about two topologically distinct closed loops traced out by rotations on the surface of the unit sphere: (i) square paths Γsquare which do not enclose the poles of the sphere and (ii) circular paths Γcircle which do. Examples of each of these paths are depicted schematically in Fig. 1 as green and purple line segments, respectively. Note that the third Euler angle γ could also be allowed to vary along these paths provided that initial and final coordinate axes vectors ex, ey, ez coincide on completion of the rotation. This ensures that the macroscopic rotation forms a true closed loop in parameter space.In the first instance, the geometric propagator Usquare which takes the system around a closed square path on the unit sphere can, due to path-ordering, be decomposed into the ordered product of geometric propagators U(4)squareU(3)squareU(2)squareU(1)square along each of the four legs (enumerated in Fig. 1) in which the system is rotated along constant lines of either latitude or longitude. Explicitly, these four propagators are
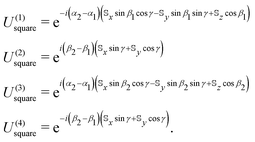 | (5) |
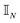 as intuition dictates.
as intuition dictates.
The circular loop Γcircle does not enclose a simply connected domain of the unit sphere. Consequently, the gauge potential defined in eqn (4) is ill-suited for the calculation of the geometric propagator around these kinds of loops for spins with non-integer ground state magnetic moments.27 In order to eliminate this pathology it is necessary to make a change of basis using the unitary operator ρ = exp(i(α + γ)Sz), yielding a gauge transformed potential
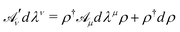 | (6) |
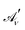 describes precisely the same physics as
describes precisely the same physics as ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) μ (i.e. the potential is gauge invariant) provided that the integration path Γ in eqn (2) is closed.27 While the new potential could in principle make the evaluation of the path-ordered intergal eqn (2) more involved, in practice a slightly modified version of the simpler gauge potential can be used, due to the equivalence
μ (i.e. the potential is gauge invariant) provided that the integration path Γ in eqn (2) is closed.27 While the new potential could in principle make the evaluation of the path-ordered intergal eqn (2) more involved, in practice a slightly modified version of the simpler gauge potential can be used, due to the equivalence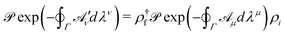 | (7) |
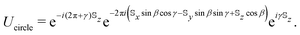 | (8) |
3 Results
3.1 The influence of magnetic anisotropy on non-Abelian dynamics
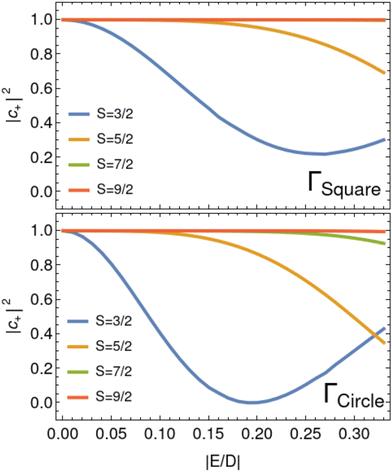
As a consequence of the anisotropic energy landscape of the SMM spin states caused by the interplay between crystal field interactions and spin–orbit coupling, different paths in parameter space will lead to different dynamical properties. It is therefore intuitive that varying the crystal field parameters D and E (which encapsulate this interplay in our model Hamiltonian HS) will influence the non-Abelian spin dynamics discussed here. This simple fact could be used either as a design principle for SMMs optimised for desired quantum dynamical applications, or to indirectly probe crystal field Hamiltonians via quantum dynamics experiments.Given that the most easily measurable effect of the quantum dynamical behaviour in SMMs triggered by a non-Abelian geometric phase is a change in the magnetic moment brought about by the modulation of the degenerate ground state amplitudes, in this section we set out to study the effect of D and E on the achievable population transfer dynamics between the degenerate ground states of Kramers-type SMMs. To achieve this we consider rotations about the square path Γsquare with α1 = 0, α2 = 90°, β1 = 60° and β2 = 120°, and about the circular path Γcircle with β = 90°. For simplicity, we initially set γ = 0° for both rotations. When β = 90° and γ = 0°, the propagator for the great circle (eqn (8)) is
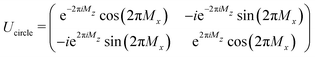 | (9) |
For both rotation paths shown in Fig. 2, the final composition of the ground doublet wavefunction differs the most from the initialised state when S is small and E is near critical. This trend is intuitive since the non-Abelian dynamics here is triggered by the 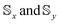 matrices viaeqn (5) and (8). For these matrices to be non-zero, the matrix elements 〈ϕ+|S±|ϕ−〉 (with S± = Sx ± iSy) must be non-vanishing and hence a portion of
matrices viaeqn (5) and (8). For these matrices to be non-zero, the matrix elements 〈ϕ+|S±|ϕ−〉 (with S± = Sx ± iSy) must be non-vanishing and hence a portion of 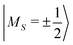 must be recovered in the ground doublet via the rhombic anisotropy term in HS. This condition is most effectively met for small S and large |E|.
must be recovered in the ground doublet via the rhombic anisotropy term in HS. This condition is most effectively met for small S and large |E|.
Interestingly, for the rotation paths chosen here, critical rhombicity does not necessarily lead to maximal population transfer to |ϕ−〉. Instead, maximal transfer occurs for S = 3/2 nanomagnets when |E/D| ∼ 0.2. It turns out that this value of |E/D| leads to a magnetic moment which maximises the off-diagonal matrix elements of eqn (9) and minimises its diagonal elements. An analogous situation is observed for the propagator of the square loop at around |E/D| ∼ 0.25.
It is worthwhile noting that we also investigated the role of the γ rotation in determining the final ground state composition of the magnet after rotation about Γsquare and Γcircle. While the final amplitudes of all spin systems rotated about Γsquare were only imperceptibly changed from those reported in Fig. 2, the choice of γ had some impact on the final wavefunction compositions of the S = 3/2, 5/2 and 7/2 nanomagnets rotated about the great circle Γcircle. The largest change was observed for γ = 90° where population transfer to the |ϕ−〉 state was maximsed for S = 5/2 and S = 7/2 at critical rhombicity, and for S = 3/2 at |E/D| ∼ 0.15.
3.2 Towards a holonomic implementation of Grover's algorithm
We now show how this effect can be utilised to construct single-qubit gates, with a mind towards the holonomic implementation of Grover's search algorithm.39 We follow here an approach to Grover's algorithm proposed by Fahri and Gutman in 199840 which does not require the use of quantum oracles. This version of Grover's algorithm has subsequently been employed using resonant microwave pulses delivered to the I = 3/2 nuclear qudit of a TbPc2 single-molecule magnet.16 In that work, two types of quantum gates were demonstrated (i) a single qubit Hadamard gate which prepared the qudit states in a coherent linear superposition, and (ii) logic gates which selectively populated just one of the four qubit states at a time.We endeavour to show how these gates could be implemented via macroscopic rotations of a recently reported CoCl2(tu)4 single-molecule magnet41 using the ground doublet of the S = 3/2 spin manifold as a computational basis. A rather good agreement was found between experimental magnetic measurements of CoCl2(tu)4 and theoretical simulations using the same effective spin Hamiltonian HS as reported here, with the parameters D = −63 cm−1 and |E/D| = 0.22. We adopt the same values in the following sections.
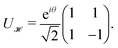 | (10) |
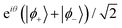 .
.
To investigate in what limit adiabaticity is satisfied for the rotation of this particular system, we numerically integrated the time-reduced Schrödinger equation ∂s|ψ(s)〉 = (−iT/h)H(α, β, γ) |ψ(s)〉 where the Euler angles describing the aforementioned square path have been parameterised by the dimensionless quantity s = t/T (0 ≤ s ≤ 1) with T the total time taken to complete the rotation. In Fig. 3 we show the final amplitudes and relative phases of the ground doublet states as function of rotation duration T. For loops which are completed in T > 10 ps the single-qubit Hadamard gate is implemented with little error. This can be attributed to the rather large axial splitting of the system which separates the ground doublet from the first excited doublet by ΔE = 135 cm−1. In this case, ħ/ΔE ≈ 5 × 10−14 s, so for T = 10−11 s, adiabaticity is satisfied and the formalism presented in Section 2.2 is valid.
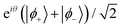 obtained from the previous section, we now demonstrate the selective amplification of |ϕ+〉 and |ϕ−〉 via rotations along the closed square loops Γ±. In general this is achieved by rotating the qubit along different square paths where the rotation parameters are solutions to the relations (Usquare)11 = (Usquare)12 and (Usquare)21 = (Usquare)22, respectively. We find for our CoCl2(tu)4 example that rotation about the square paths Γ+ with α1 = 0, α2 = 70°, β1 = 60°, β2 = 120° and γ = 54° and the path Γ− with α1 = 0, α2 = 163°, β1 = 60°, β2 = 120° and γ = 124° serve to amplify to near unity, the |ϕ+〉 and |ϕ−〉 states, respectively.
obtained from the previous section, we now demonstrate the selective amplification of |ϕ+〉 and |ϕ−〉 via rotations along the closed square loops Γ±. In general this is achieved by rotating the qubit along different square paths where the rotation parameters are solutions to the relations (Usquare)11 = (Usquare)12 and (Usquare)21 = (Usquare)22, respectively. We find for our CoCl2(tu)4 example that rotation about the square paths Γ+ with α1 = 0, α2 = 70°, β1 = 60°, β2 = 120° and γ = 54° and the path Γ− with α1 = 0, α2 = 163°, β1 = 60°, β2 = 120° and γ = 124° serve to amplify to near unity, the |ϕ+〉 and |ϕ−〉 states, respectively.
We again endeavoured to verify the adiabatic limit implicitly assumed in the above calculations by direct numerical integration of the Schrödinger equation. In Fig. 4, we plot the final amplitudes of the ground doublet states after rotations around the two square paths specified in the previous paragraph. Again, after initialisation with the Hadamard gate from the previous section, with T ≥ 10 ps, each member of the ground doublet can be selectively populated to near unity, depending on the choice of rotation along either one of the quite different paths.
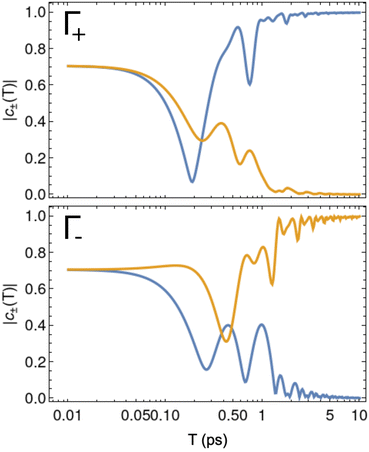 | ||
Fig. 4 Final amplitudes of the ground doublet states of CoCl2(tu)4 after rotation shown as a function of the rotation duration T. The two closed square loops are obtained from eqn (5) with Γ+: α1 = 0, α2 = 70°, β1 = 60°, β2 = 120° and γ = 54° and Γ−: α1 = 0, α2 = 163°, β1 = 60°, β2 = 120° and γ = 124°. The blue and orange curves represent the final populations of the |ϕ+〉 and |ϕ−〉 states respectively. The final wavefunction was obtained from direct numerical integration of Schrödiner's equation with the system initially prepared in the coherent superposition 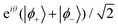 from the previous section. from the previous section. | ||
3.3 Single-ion magnets as quantum gyroscopes
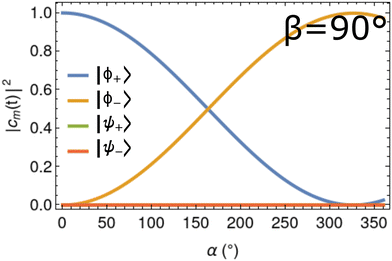
While the non-Abelian geometric propagator formalism developed in Section 2.2 is gauge-invariant only for closed paths in parameter space, macroscopic rotations of nanomagnets along open paths can still lead to a measurable effect provided that the initial state of the system is known a priori, i.e. the gauge has been fixed by the initial measurement. Monitoring a change in amplitudes of the nanomagnet degenerate ground states can hence provide useful information regarding the orientation of the SMM principal magnetic axis in physical space with respect to a known initial direction.In Fig. 5 we plot the squared amplitudes of the ground |ϕ±〉 and first excited |ψ±〉 doublet states of CoCl2(tu)4 as it undergoes a 360° rotation in the xy-plane obtained from numerical integration of the time-dependent Schrödinger equation with α = 2πt/T and T = 10 ns. Note that the squared amplitudes of the ground state doublet are essentially single-valued functions of the angle α. Thus, a measurement of the ground state populations at a given time provides information on how far the molecular magnet has rotated from its initial orientation about the global z or “yaw” axis in the lab frame. We repeated this calculation for shorter timescales and found identical results as shown in Fig. 5 up until T ≤ 10 ps where, from the previous section, adiabaticity begins to breaks down for the particular example of CoCl2(tu)4. For rotations which occur slower than T = 10 ps, the nanomagnet operates as a quantum gyroscope in the xy-plane.
3.4 The case of tunnel-split Ising ground states
For a single-molecule magnet with an integer spin S, small but non-negligible non-axial terms in the crystal field Hamiltonian that can connect the bistable |±S〉 ground states in high-order perturbation theory, lead to a quasi-degenerate tunnelling ground doublet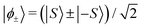 with tunnel splitting Δ. Assuming that the system is initialised in this quasi-degenerate ground manifold and the rotation is not so fast as to activate a dynamics between excited crystal field states, it is possible to write the time-evolution operator of just the quasi-degenerate SMM ground doublet as42
with tunnel splitting Δ. Assuming that the system is initialised in this quasi-degenerate ground manifold and the rotation is not so fast as to activate a dynamics between excited crystal field states, it is possible to write the time-evolution operator of just the quasi-degenerate SMM ground doublet as42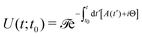 | (11) |
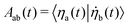 and the matrix Θ has elements Θab = 〈ηa(t)|H(t)|ηb(t)〉/ħ = εaδab/ħ which are time-independent when expressed on the basis of instantaneous eigenstates |ηa(t)〉 of H(t). The integral over time can be converted to a path-ordered integral (see Supplementary Note 1, ESI†) involving the same matrix gauge potential
and the matrix Θ has elements Θab = 〈ηa(t)|H(t)|ηb(t)〉/ħ = εaδab/ħ which are time-independent when expressed on the basis of instantaneous eigenstates |ηa(t)〉 of H(t). The integral over time can be converted to a path-ordered integral (see Supplementary Note 1, ESI†) involving the same matrix gauge potential ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) as in eqn (3) where λμ correspond to the Euler angles α, β and γ. After the system has undergone a complete rotation (when t = T) around the circle path Γcircle specified above, the non-adiabatic time evolution operator is
as in eqn (3) where λμ correspond to the Euler angles α, β and γ. After the system has undergone a complete rotation (when t = T) around the circle path Γcircle specified above, the non-adiabatic time evolution operator is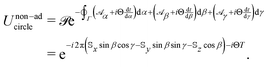 | (12) |
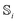 matrices take the simple form
matrices take the simple form 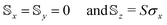 (where σx corresponds to the usual Pauli matrix). Accordingly, the propagator in eqn (12) can be expressed analytically as the 2 × 2 matrix
(where σx corresponds to the usual Pauli matrix). Accordingly, the propagator in eqn (12) can be expressed analytically as the 2 × 2 matrix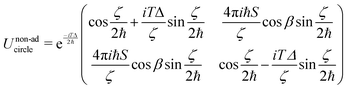 | (13) |
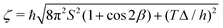 . Note that owing to the simplicity of the gauge potential for this rotation path, eqn (13) is invariant to γ.
. Note that owing to the simplicity of the gauge potential for this rotation path, eqn (13) is invariant to γ.
We now show how eqn (13) can act as a single-qubit Hadamard gate, or in other words can create a coherent linear superposition of the qubit computational basis (here the |ϕ±〉 quasi-degenerate ground doublet states). Supposing that the nanomagnet is initialised in the ground state |ϕ−〉, then a macroscopic rotation specified by eqn (13) creates a coherent linear superposition of |ϕ−〉 and |ϕ+〉 when β and T are chosen such that
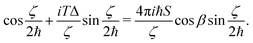 | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ/2ħ = 0 or equivalently that ζ/2ħ = (2n + 1)π/2 for
ζ/2ħ = 0 or equivalently that ζ/2ħ = (2n + 1)π/2 for 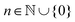 . Using this condition in eqn (14) yields T = (4πSħ/Δ)cos
. Using this condition in eqn (14) yields T = (4πSħ/Δ)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β, so we find that
β, so we find that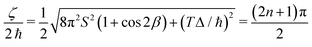 | (15) |
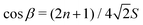 and consequently
and consequently 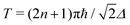 . Interestingly, given the spin quantum number S there are several allowed values of canting angle β, and corresponding rotation times T, that will result in a coherent linear superposition of the non-Kramers SMM ground doublet tunnelling states with the condition that n is a whole number and
. Interestingly, given the spin quantum number S there are several allowed values of canting angle β, and corresponding rotation times T, that will result in a coherent linear superposition of the non-Kramers SMM ground doublet tunnelling states with the condition that n is a whole number and 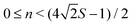 . To maximise the possible choices of rotation speed and canting angle for practical implementations of this effect, molecular magnets with large S spin projections in the quasi-degenerate tunnelling ground states should be favoured.
. To maximise the possible choices of rotation speed and canting angle for practical implementations of this effect, molecular magnets with large S spin projections in the quasi-degenerate tunnelling ground states should be favoured.
The above rotation acting on the tunnelling ground state 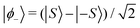 is tantamount to the preparation of the SMM in the |S〉 quantum state. Since we have assumed that Sz does not commute with the nanomagnet Hamiltonian, once the nanomagnet has been prepared in the |S〉 state by the appropriate macroscopic rotation, a periodic tunnelling of the SMM magnetic moment triggered by the non-axial terms of the crystal field potential, will ensue along its principal magnetic axis taking the maximal values μz = ±gμBS. In a crystal of nanomagnets, the collective in-phase oscillation of each molecular magnetic moment will give rise to an oscillating macroscopic magnetisation that can be readily detected. We note en passant that, following a similar line of reasoning as above, the |−S〉 state can also be prepared from |ϕ−〉 with precisely the same macroscopic rotation but now performed clockwise instead of anticlockwise, or equivalently with β → π − β.
is tantamount to the preparation of the SMM in the |S〉 quantum state. Since we have assumed that Sz does not commute with the nanomagnet Hamiltonian, once the nanomagnet has been prepared in the |S〉 state by the appropriate macroscopic rotation, a periodic tunnelling of the SMM magnetic moment triggered by the non-axial terms of the crystal field potential, will ensue along its principal magnetic axis taking the maximal values μz = ±gμBS. In a crystal of nanomagnets, the collective in-phase oscillation of each molecular magnetic moment will give rise to an oscillating macroscopic magnetisation that can be readily detected. We note en passant that, following a similar line of reasoning as above, the |−S〉 state can also be prepared from |ϕ−〉 with precisely the same macroscopic rotation but now performed clockwise instead of anticlockwise, or equivalently with β → π − β.
3.5 TbPc2 as a rotating qubit candidate
Results from the previous section suggest that macroscopic rotations of integer spin single-molecule magnets could be employed to realise single-qubit gating operations for a holonomic implementation of Grover's algorithm where the quasi-degenerate ground doublet acts as the two-dimensional computational basis. In parallel with a recent implementation of Grover's algorithm on the nuclear qudit states of the well-known (bis)-phthalocyanine terbium SMM (TbPc2),16 we demonstrate here how non-adiabatic macroscopic rotations of the same molecule can be utilised to construct logic gates which act instead on the quasi-degenerate 4f tunnelling ground states. In particular, we will demonstrate (i) a single qubit Hadamard gate which prepares the quasi-degenerate ground doublet states into a coherent linear superposition, and subsequently (ii) logic gates which selectively amplify each member of the ground quasi-degenerate doublet beginning from the initialised coherent linear superposition.The [Xe]4f8 electronic configuration of Tb3+ results in an energetically well isolated 7F6 spin–orbit ground multiplet characterised by the J = 6 (S = 3, L = 3) total angular momentum quantum number. The splitting of this multiplet due to the crystal field of the two phthalocyanine ligands which sandwich the Tb3+ ion is captured particularly well with the Hamiltonian43,44
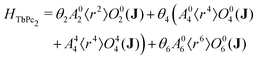 | (16) |
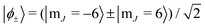 .
.
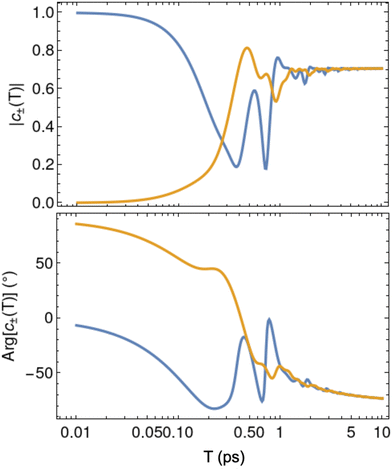
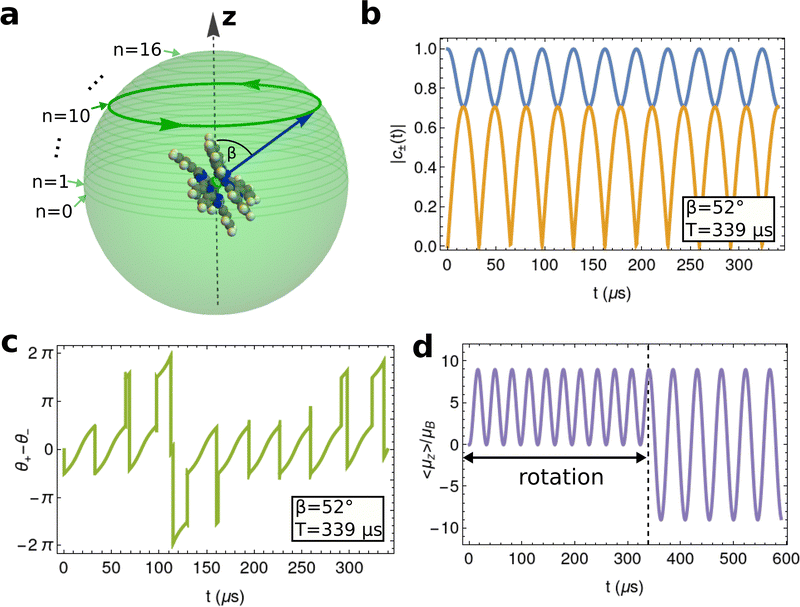
Using the result from the previous section (with S understood as J = 6), n can be chosen as any whole number between 0 ≤ n ≤ 16 resulting in 17 different combinations of β and T that will implement a Hadamard gate on the quasi-degenerate TbPc2 ground doublet. We show each possible path in Fig. 6a but highlight especially the n = 10 path which requires a canting angle β = 52° and a rotation time of T = 339 μs. In principle, one ought to perform the rotation as fast as possible (i.e. choose the path corresponding to minimal n) to ensure that decoherent processes such as spin–lattice relaxation do not interfere with the coherent dynamics of the SMM undergoing rotation. We choose to focus on the n = 10 path here since the required rotation time is in line with similar experimental set-ups which have already exposed Berry phase splittings in a rotating NaClO3 crystal28 as well as measurements of a rapidly rotating diamond qubit.48,49
To investigate the coherent dynamics of the quasi-degenerate tunnelling states during rotation as well as to verify the assumptions leading to eqn (13), we numerically integrated the time-dependent Schrödinger equation for the rotating TbPc2 molecule using the Hamiltonian from eqn (16). The resultant amplitudes |c±(t)| of the tunnelling states |ϕ±〉 are plotted as functions of time t in Fig. 6b in the eigenframe of the rotating TbPc2 quantisation axis as well as the relative phase difference between the |ϕ±〉 states in Fig. 6c. Indeed we find that once a single rotation has been completed, a linear superposition of the tunnelled states is prepared from the initial conditions c−(0) = 1 and c+(0) = 0. Curiously, Fig. 6b and c show that throughout the rotation, the system oscillates eleven times between the |ϕ−〉 tunnelling eigenstate and the linear superposition 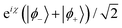 (including some global phase χ). We also checked all other combinations of β and T within the range 0 ≤ n ≤ 16 using the same numerical integration procedure and found consistently that the TbPc2 system undergoes n + 1 oscillations between |ϕ−〉 and
(including some global phase χ). We also checked all other combinations of β and T within the range 0 ≤ n ≤ 16 using the same numerical integration procedure and found consistently that the TbPc2 system undergoes n + 1 oscillations between |ϕ−〉 and 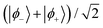 during each rotation.
during each rotation.
In Fig. 6d we plot the time-evolution of the TbPc2 magnetic moment as the SMM undergoes the cyclic macroscopic rotation corresponding to n = 10 (0 μs ≤ t ≤ 339 μs) and is then left stationary (339 μs < t ≤ 600 μs). During rotation, Fig. 6b shows clearly that the TbPc2 wavefunction oscillates between |ϕ−〉 and the coherent linear superposition corresponding to |mJ = 6〉. Naturally, the TbPc2 magnetic moment oscillates between μz = 0 and its maximal value μz = 6gJμB (gJ = 4/3) during this time as well. After the rotation is completed (i.e. the Hadamard gate has been executed) the TbPc2 molecule is prepared in the |mJ = 6 〉 state which is not an energy eigenstate of Hamiltonian (16) due to the θ4A44〈r4〉O44(J) non-axial term. As a result, the nanomagnet tunnels between |mJ = 6〉 and |mJ = −6〉 angular momentum states and thus the magnetic moment oscillates from μz = 6gJμB to μz = −6gJμB accordingly. Notably, from our proof-of-concept model above we have assumed a perfect D4d symmetry of the TbPc2 crystal field and have neglected hyperfine coupling between the TbPc2 electronic spin and its I = 3/2 nuclear spin. With some minor alterations to the experimental protocol, we show in Supplementary Note 4 (ESI†) that this effect persists regardless of crystal field symmetry lowering and hyperfine coupling.
Finally we note that for a given β, T pair specified by n, the same rotation can be performed to amplify the |ϕ−〉 energy eigenstate to unity from the linear combination 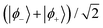 . The |ϕ+〉 state can also be amplified to unity by rotating the quantisation axis along the same path but now clockwise instead of anticlockwise (i.e. with the substitution β → π − β).
. The |ϕ+〉 state can also be amplified to unity by rotating the quantisation axis along the same path but now clockwise instead of anticlockwise (i.e. with the substitution β → π − β).
3.6 Rotation time and angle deviations
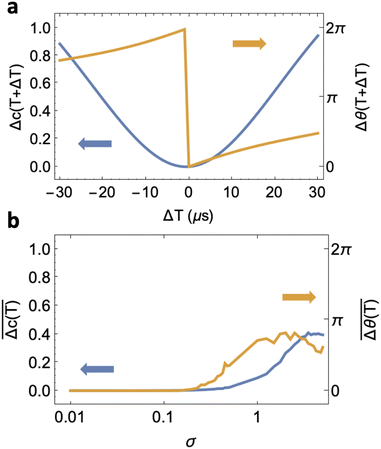
We have so far considered idealised rotation paths and times without concern for errors introduced by experimental/instrumental uncertainties. We use the n = 10 rotation path of the TbPc2 single-molecule magnet described in the last section as a test case to investigate the effect of rotation time and path fluctuation errors on the holonomic implementation of a Hadamard gate on a single-molecule magnet.For the perfect canting angle β and rotation time T, the action of the Hadamard gate should result in equal populations and phases of the tunnelled TbPc2 ground doublet states. In Fig. 7a we show the difference in these populations Δc(T + ΔT) = |c+(T + ΔT)| − |c−(T + ΔT)| and relative phases Δθ(T + ΔT) = θ+(T + ΔT) −θ−(T + ΔT) (mod 2π) at the end of the rotation, due to under/over rotation by a time ΔT. The error in the populations Δc(T + ΔT), grows approximately quadratically with the over/under rotation time ΔT, leading to almost a complete annulment of the Hadamard gate for |ΔT/T| ∼ 10%. The phase error does not grow as rapidly but reaches a maximum of π/2 when |ΔT/T| ∼ 10%.
To approximate the effect of stochastic fluctuations in the rotation path we obtain the mean values of Δc(T) and Δθ(T) from 500 simulations of the TbPc2 rotation described above whereby the Schrödinger equation is numerically integrated up until T = 339 μs. For each of these rotations we pseudo-randomly vary the canting angle β throughout the rotation path by drawing from a normal distribution with mean value 52° and standard deviation σ. Typical fluctuations in the β Euler angle for fixed σ during the TbPc2 rotation are plotted in Note S5 (ESI†). For reference, standard deviations of σ = 0.5 lead to fluctuations in the β canting angle of ∼ 2°. In Fig. 7b we show the mean values of Δc(T) and Δθ(T) as function of the standard deviation σ. Stochastic path fluctuations begin to reduce the fidelity of the Hadamard gate when the β Euler angle fluctuates >2°.
4 Discussion
While we have focused on the specific examples of CoCl2(tu)4 and TbPc2 single-molecule magnets, there are a myriad of alternative candidate molecules reported in the literature which may also show these effects. For example, the tunnel split |J = 8, mJ = ±8〉 ground doublet of a recently reported Ho3 + single-molecule magnet synthesised and characterised by Wu et al.50 In that study, a tunnel splitting of 10−5 cm−1 was obtained from ab initio calculations suggesting that rotations should be carried out on μs timescales to observe the above non-adiabatic rotation-induced spin dynamics of the tunnelling ground states. A further example is a recently reported Ni2+ field-induced single-molecule magnet synthesised and characterised by Miklovic et al.51 In that work, excellent agreement between experimental results and simulations was afforded using the S = 1 effective spin Hamiltonian H = DSz2 + E(Sx2 − Sy2) with D = −13.7 cm−1 and E = 0.07 cm−1. The rhombic magnetic anisotropy term resulted in a zero-field tunnelling ground doublet with splitting Δ = 0.14 cm−1. To observe a rotation-induced coherent dynamics between the tunnel split ground doublet states for such a large Δ, would require rotations to be performed with T < 50 ns which is several orders of magnitude faster than conventional set-ups so far reported in the literature.28,48,49 Nevertheless, more sophisticated molecular rotor systems may in the future be leveraged to achieve such rapid, constrained rotations.52We note in addition, that our theoretical model has not accounted for population transfer between the energy eigenstates of HS mediated by incoherent transitions from the local environment. These could result from lattice phonon-mediated spin transitions in the nanomagnet,37 stray fields from a bath of nuclear dipoles53 or potentially from continuous electrical measurement if the SMM can be realised in a spintronics device.54,55 While we haven’t treated these effects directly, we note that for both explicit examples, the quantum logic gating and gyroscopic applications were based on macroscopic rotations that could be performed on timescales much faster than typical incoherent processes (for example the spin relaxation between TbPc2 doublet states has been measured T1 ∼ 10 s),54 thus reducing the risk for spurious, incoherent population transfer.
While the prototypical results presented in this manuscript represent a first step towards the holonomic implementation of Grover's algorithm using macroscopically rotating single-molecule magnets, since the rotation-induced coherent dynamics is confined to the SMM ground doublet, one is restricted to only ever searching a database of two objects. The database might be expanded however, by the extension of the computational basis to include hyperfine states of the SMM. In addition, the macroscopic rotation of different species of SMM confined to the same unit cell could also offer a way to grow the computational basis for a useful holonomic implementation of Grover's algorithm. The explicit discussion of these more complicated scenarios is beyond the scope of this work and will be considered in a future publication.
5 Conclusions
With a theoretical model, we have demonstrated that a spin dynamics can be triggered in the ground doublet of both half-odd integer and integer spin SMMs by macroscopic rotations of its principal magnetic axis.For half-odd integer spin SMMs, we explored how the crystal field parameters of an effective spin Hamiltonian influence the spin dynamics of the ground Kramers doublet via an emergent non-Abelian gauge potential that arises due to the electronic spin adiabatically following the rotating crystal field. As well as an unconventional probe of the spin Hamiltonian parameters, we suggested how this might be utilised to realise holonomic single-qubit quantum logic gates in a CoCl2(tu)4 single-molecule magnet. Direct numerical integration of Schrödinger's equation revealed that the holonomic gating operations required for such an implementation could be executed on picosecond timescales, orders of magnitude faster than typical spin–lattice relaxation mechanisms. In addition, we demonstrated how this effect could be utilised for a quantum gyroscope inertial sensor based on CoCl2(tu)4. Again, provided that the rotation speed does not exceed 10 ps, the ground doublet squared amplitudes remain single-valued for rotations in the xy-plane and thus their measurement provides direct information about the rotation of the SMM principal magnetic axes.
By lifting the stringent condition that rotations proceed adiabatically, we recovered a tunable non-Abelian spin dynamics in the tunnelling ground (pseudo) doublet of an otherwise general integer spin SMM. We showed that when the quantisation axis is canted by an angle 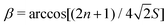 from the lab-frame z axis and rotated along a circular path on the unit sphere for a duration
from the lab-frame z axis and rotated along a circular path on the unit sphere for a duration 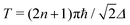 (with n a whole number between 0 and
(with n a whole number between 0 and 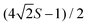 ), the rotation prepares the SMM in a coherent linear superposition of the quasi-degenerate ground doublet states, effectively acting as a single-qubit Hadamard gate. We made a specific example of the well-known single-molecule magnet TbPc2 and showed how this effect could be observed with state-of-the-art set-ups from the current literature. Via numerical integration of Schrödinger's equation, we vindicated the approximations implicit in our non-adiabatic geometric propagator approach and exposed a curious n + 1 oscillation effect in the coherent dynamics of the rotating TbPc2 magnetic moment. We used this prototypical example to explore the effects of rotation time and path fluctuations on the fidelity of a Hadamard gate induced by an SMM macroscopic rotation.
), the rotation prepares the SMM in a coherent linear superposition of the quasi-degenerate ground doublet states, effectively acting as a single-qubit Hadamard gate. We made a specific example of the well-known single-molecule magnet TbPc2 and showed how this effect could be observed with state-of-the-art set-ups from the current literature. Via numerical integration of Schrödinger's equation, we vindicated the approximations implicit in our non-adiabatic geometric propagator approach and exposed a curious n + 1 oscillation effect in the coherent dynamics of the rotating TbPc2 magnetic moment. We used this prototypical example to explore the effects of rotation time and path fluctuations on the fidelity of a Hadamard gate induced by an SMM macroscopic rotation.
Author contributions
Both authors contributed equally to this work.Conflicts of interest
There are no conflicts to declare.Notes and references
- R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816 CrossRef CAS.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197 CrossRef CAS PubMed.
- K. Katoh, H. Isshiki, T. Komeda and M. Yamashita, Chem. Asian J., 2012, 7, 1154–1169 CrossRef CAS PubMed.
- D. Ray, M. S. Oakley, A. Sarkar, X. Bai and L. Gagliardi, Inorg. Chem., 2023, 62, 1642–1658 CrossRef PubMed.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS PubMed.
- B. Zhou, R. Tao, S.-Q. Shen and J.-Q. Liang, Phys. Rev. A, 2002, 66, 010301 CrossRef.
- J. Lehmann, A. Gaita-Arino, E. Coronado and D. Loss, J. Mater. Chem., 2009, 19, 1672–1677 RSC.
- K. Hymas and A. Soncini, Phys. Rev. B, 2019, 99, 245404 CrossRef CAS.
- A. Lunghi and S. Sanvito, Nat. Rev. Chem., 2022, 1–21 Search PubMed.
- M. N. Leuenberger and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 054414 CrossRef.
- L. Lecren, W. Wernsdorfer, Y.-G. Li, O. Roubeau, H. Miyasaka and R. Clérac, J. Am. Chem. Soc., 2005, 127, 11311–11317 CrossRef CAS PubMed.
- R. Schenker, M. N. Leuenberger, G. Chaboussant, D. Loss and H. U. Güdel, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 184403 CrossRef.
- L. Escalera-Moreno, N. Suaud, A. Gaita-Arino and E. Coronado, J. Phys. Chem. Lett., 2017, 8, 1695–1700 CrossRef CAS PubMed.
- K. Irländer and J. Schnack, Phys. Rev. B, 2020, 102, 054407 CrossRef.
- S. Bertaina, S. Gambarelli, T. Mitra, B. Tsukerblat, A. Müller and B. Barbara, Nature, 2008, 453, 203–206 CrossRef CAS PubMed.
- C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef CAS PubMed.
- R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814–9818 CrossRef CAS PubMed.
- A. Ardavan, A. M. Bowen, A. Fernandez, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, npj Quantum Information, 2015, 1, 1–7 CrossRef.
- K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS PubMed.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138 CrossRef CAS PubMed.
- D. Aguila, L. A. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. J. Alonso, J. Sesé, S. J. Teat, F. Luis and G. Arom, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef CAS PubMed.
- G. A. Timco, S. Carretta, F. Troiani, F. Tuna, R. J. Pritchard, C. A. Muryn, E. J. McInnes, A. Ghirri, A. Candini, P. Santini, G. Amoretti, M. Affronte and R. E. P. Winpenny, Nat. Nanotechnol., 2009, 4, 173–178 CrossRef CAS PubMed.
- J. Ferrando-Soria, E. Moreno Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2016, 7, 1–10 Search PubMed.
- D. Ranieri, F. Santanni, A. Privitera, A. Albino, E. Salvadori, M. Chiesa, F. Totti, L. Sorace and R. Sessoli, Chem. Sci., 2023, 14, 61–69 RSC.
- F. Wilczek and A. Zee, Phys. Rev. Lett., 1984, 52, 2111 CrossRef CAS.
- P. Zanardi and M. Rasetti, Phys. Lett. A, 1999, 264, 94–99 CrossRef CAS.
- A. Zee, Phys. Rev. A, 1988, 38, 1 CrossRef PubMed.
- R. Tycko, Phys. Rev. Lett., 1987, 58, 2281 CrossRef CAS PubMed.
- L.-X. Yu, G. Chen and J.-Q. Liang, Commun. Theor. Phys., 2011, 56, 382 CrossRef CAS.
- Y. Liu, A. Roy and M. Stone, J. Phys. A: Math. Theor., 2012, 45, 135304 CrossRef.
- V. A. Mousolou, C. M. Canali and E. Sjöqvist, New J. Phys., 2014, 16, 013029 CrossRef.
- D. Maclaurin, M. Doherty, L. Hollenberg and A. Martin, Phys. Rev. Lett., 2012, 108, 240403 CrossRef CAS PubMed.
- S. Arroyo-Camejo, A. Lazariev, S. W. Hell and G. Balasubramanian, Nat. Commun., 2014, 5, 1–5 Search PubMed.
- K. Nagata, K. Kuramitani, Y. Sekiguchi and H. Kosaka, Nat. Commun., 2018, 9, 1–10 CrossRef PubMed.
- A. A. Wood, L. C. Hollenberg, R. E. Scholten and A. M. Martin, Phys. Rev. Lett., 2020, 124, 020401 CrossRef CAS PubMed.
- M. A. Kowarsky, L. C. Hollenberg and A. M. Martin, Phys. Rev. A, 2014, 90, 042116 CrossRef.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press on Demand, 2006, vol. 5 Search PubMed.
- J. J. Sakurai and E. D. Commins, Modern quantum mechanics, revised edition, 1995 Search PubMed.
- L. K. Grover, Phys. Rev. Lett., 1997, 79, 4709 CrossRef CAS.
- E. Farhi and S. Gutmann, Phys. Rev. A, 1998, 57, 2403 CrossRef CAS.
- S. Tripathi, S. Vaidya, N. Ahmed, E. A. Klahn, H. Cao, L. Spillecke, C. Koo, S. Spachmann, R. Klingeler, G. Rajaraman and M. Shanmugan, Cell Rep. Phys. Sci., 2021, 2, 100404 CrossRef CAS.
- J. Anandan, Phys. Lett. A, 1988, 133, 171–175 CrossRef.
- M. Ganzhorn, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Nat. Nanotechnol., 2013, 8, 165–169 CrossRef CAS PubMed.
- K. Hymas and A. Soncini, Phys. Rev. B, 2020, 102, 125310 CrossRef CAS.
- A. Abragam and B. Bleaney, Electron paramagnetic resonance of transition ions, Oxford University Press, 2012 Search PubMed.
- N. Ishikawa, T. Iino and Y. Kaizu, J. Phys. Chem. A, 2002, 106, 9543–9550 CrossRef CAS.
- N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931–2935 CrossRef CAS PubMed.
- A. A. Wood, E. Lilette, Y. Y. Fein, N. Tomek, L. P. McGuinness, L. C. Hollenberg, R. E. Scholten and A. M. Martin, Science Adv., 2018, 4, eaar7691 CrossRef PubMed.
- A. A. Wood, R. M. Goldblatt, R. E. Scholten and A. M. Martin, Phys. Rev. Res., 2021, 3, 043174 CrossRef CAS.
- S.-G. Wu, Z.-Y. Ruan, G.-Z. Huang, J.-Y. Zheng, V. Vieru, G. Taran, J. Wang, Y.-C. Chen, J.-L. Liu, L. F. Chibotaru, W. Wernsdorfer, X.-M. Chen and M.-L. Tong, Chem, 2021, 7, 982–992 CAS.
- J. Miklovič, D. Valigura, R. Boča and J. Titiš, Dalton Trans., 2015, 44, 12484–12487 RSC.
- T. Matsuno, S. Terasaki, K. Kogashi, R. Katsuno and H. Isobe, Nat. Commun., 2021, 12, 1–7 CrossRef PubMed.
- F. Delgado and J. Fernández-Rossier, Prog. Surf. Sci., 2017, 92, 40–82 CrossRef CAS.
- F. Troiani, C. Godfrin, S. Thiele, F. Balestro, W. Wernsdorfer, S. Klyatskaya, M. Ruben and M. Affronte, Phys. Rev. Lett., 2017, 118, 257701 CrossRef CAS PubMed.
- K. Hymas and A. Soncini, Phys. Rev. B, 2021, 104, 205306 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Derivation of the non-adiabatic non-Abelian Berry phase; effect of crystal field lowering and hyperfine coupling in TbPc2. See DOI: https://doi.org/10.1039/d3cp02939e |
| This journal is © the Owner Societies 2023 |