Theoretical framework and experimental methodology to elucidate the supersaturation dynamics of nanocrystal growth†
Paul Z.
Chen
 a,
Aaron J.
Clasky
a,
Aaron J.
Clasky
 a and
Frank X.
Gu
a and
Frank X.
Gu
 *ab
*ab
aDepartment of Chemical Engineering & Applied Chemistry, University of Toronto, Toronto, Ontario M5S 3E5, Canada. E-mail: f.gu@utoronto.ca
bInstitute of Biomedical Engineering, University of Toronto, Toronto, Ontario M5S 3G9, Canada
First published on 19th January 2022
Abstract
Supersaturation is the fundamental parameter driving crystal formation, yet its dynamics in the growth of colloidal nanocrystals (NCs) remain poorly understood. Here, we demonstrate an approach to characterize supersaturation during classical NC growth. We develop a framework that relates noninvasive measurements of the temporal, size-dependent optical properties of growing NCs to the supersaturation dynamics underlying their growth. Using this approach, we investigate the seed-mediated growth of colloidal Au nanocubes, identifying a triphasic sequence of supersaturation dynamics: rapid monomer consumption, sustained supersaturation, and then gradual monomer depletion. These NCs undergo different shape evolutions in different phases of the supersaturation dynamics. As shown with the Au nanocubes, elucidated supersaturation profiles enable the prediction of growth profiles of NCs. We then apply these insights to rationally modulate NC shape evolutions, decreasing the yield of impurity products. Our findings reveal that the supersaturation dynamics of NC growth can be more complex than previously understood. As our approach is applicable to many types of NCs undergoing classical growth, this work presents an initial step towards more deeply interpreting the phenomena governing nanoscale crystal growth and provides insight for the rational design of NCs.
New conceptsDespite significant interest, supersaturation remains difficult to measure directly in colloidal nanocrystal (NC) syntheses. As such, the field of nanoscience's understanding of how supersaturation progresses during NC growth is based on models, such as the LaMer model and Finke–Watzky model. By developing and then using a methodology to noninvasively characterize supersaturation throughout NC growth, we find that even well-studied reactions, such as the seed-mediated growth of colloidal Au nanocubes, can involve multi-phase supersaturation dynamics that are more complex than previous models indicate. Moreover, we show that elucidated supersaturation profiles can be used to model, and predict, the temporal growth profiles of NCs as well as to identify supersaturation-associated shape evolutions during synthesis. Based on these insights, supersaturation can be altered in these reactions to rationally modulate NC shape evolutions. While this study focuses experimentally on Au NCs, our methodological approach is facile and can be extended to many types of NCs. Thus, this work presents conceptual and methodological advances in understanding and engineering the complex interplay of supersaturation, NC growth, and NC shape evolutions. |
Introduction
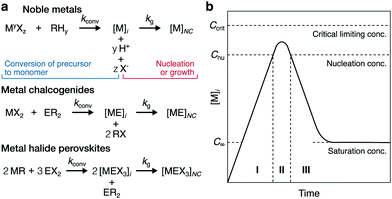
Nanocrystals (NCs) are ordered materials with at least one dimension in the range of 1–100 nm and present physicochemical, electrical, magnetic, and optical properties that can be superior or unavailable to larger crystals.1–3 For colloidal NCs, these properties depend on their size, shape, crystal habit, surface ligands, and elemental composition.3–8 Using the mechanistic insight gained by elucidating reaction pathways, synthesis methods can grow colloidal NCs with precise control over these structural parameters,9–11 potentiating the development of next-generation technologies in heterogeneous catalysis, chemical processing, photonics, sensing, medicine, and environmental remediation.12–19 Hence, a key focus in the fields of chemistry, materials science, and nanoscience has been to understand how colloidal NCs grow.Crystal formation can occur classically or nonclassically, and involves nucleation and growth processes. Primary nucleation refers to the initial formation of condensed phases from monomeric units, whereas growth comprises the integration of monomers into already nucleated crystals.20 Nucleation and growth occur sequentially in crystallization reactions.21 On the other hand, seed-mediated syntheses spatiotemporally separate growth from nucleation.22 In classical nucleation, monomeric units aggregate stochastically in the bulk (vapor, melt, or solution) phase of the reaction and encounter a thermodynamic balance between surface energy and cohesive energy.23 Because the surface-to-volume ratio decreases as size increases, cohesive energy overcomes surface energy above a critical radius, leading to thermodynamically stable nuclei.23 In classical growth, monomers progressively integrate into crystal facets described by the terrace-step-kink (TSK) model.20,23–27 In contrast, crystals nucleate or grow nonclassically when monomers first form intermediate clusters which then coalesce into nuclei or existing crystals, respectively.28,29
While the distinction between classical and nonclassical growth is clear (progressive integration of monomers vs. discrete coalescence of intermediate clusters) and presents a general scheme to classify crystal growth, the growth mechanisms of many colloidal NCs remain unclear. That is, how monomers integrate, or how intermediates attach and coalesce, into NCs is poorly understood, based in part on limited insight into the phenomena underlying NC growth.30,31
Supersaturation is the fundamental, non-equilibrium parameter that drives crystal formation and influences the growth mechanism, shape, exposed facets, crystal habit, size, and uniformity of NCs.8,32–35 It is defined as
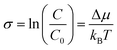 | (1) |
Thus, supersaturation dynamics have yet to be quantitatively characterized during the formation of many types of colloidal NCs, hindering mechanistic understanding. The LaMer model has, since 1950, been one classical interpretation that has guided a qualitative, but incomplete, understanding of how monomer tends to progress during the crystallization of colloidal NCs (Fig. 1b).40 The Finke–Watzky model describes another crystallization process, in which slow, continuous nucleation occurs below the LaMer nucleation limit for monomer concentration (Cnu in Fig. 1b) before autocatalytic surface growth.41 While Finke–Watzky nucleation deviates mechanistically from classical nucleation, these three-dimensional nuclei still form above a critical size described by classical theory.20,41 Moreover, both models describe growth classically; even when growth is kinetically controlled, the NCs grow via the progressive integration of monomeric units into facets which have TSK structures.20,23–25,40,41 Unlike during nucleation, these models generally assume that the bulk, or local, supersaturation dynamics during growth follow a simple, steadily declining profile as the NCs grow (see stage III in Fig. 1b). However, as revealed in this study, the supersaturation dynamics of colloidal NC growth can be more complex than described by these models.
Here, we develop a framework to characterize supersaturation throughout the growth of colloidal NCs. To avoid experimental measurements that disturb the reaction, this approach noninvasively analyzes the temporal, size-dependent optical properties of growing NCs to determine quantitative profiles of the underlying supersaturation dynamics. These profiles facilitate theoretical modeling of, and mechanistic insight into, NC growth. We use our approach to study the growth of Au nanocubes, finding supersaturation dynamics that are more complex than previously understood via the LaMer or Finke–Watzky models. We then input the supersaturation profiles into theoretical equations to predict the temporal growth profile of the nanocubes and identify supersaturation-associated NC shape evolutions. Based on these insights, we rationally modulate the shape evolutions of the nanocubes during growth.
Results and discussion
Framework to characterize supersaturation during NC growth
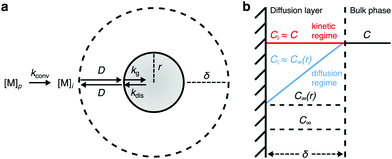
To develop the framework, we first consider the monomer dynamics of colloidal NC growth, as summarized in Fig. 2. Colloidal NCs undergoing classical growth typically involve precursor-limited reactions,21,42,43 in which monomer is converted from precursor before incorporating into a NC (Fig. 1a). This predominantly occurs through one of two pathways: conversion occurs in the bulk phase and monomers diffuse through the stagnant layer of liquid surrounding the NC, or precursors diffuse through the stagnant layer so that the NC surface can catalyze the conversion to monomer.20,40,41,44At the interface of the bulk phase with a NC, the local saturation concentration of monomer increases relative to that of a macroscopic crystal, which is described by the Gibbs–Thomson equation:23
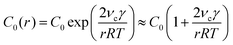 | (2) |
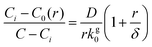 | (3) |
Since directly measuring the concentration of monomer in colloidal syntheses is experimentally difficult and can disturb the reaction, we sought to find another approach to characterize supersaturation. In classical growth, the rate at which monomers incorporate into NCs, RNC(t), is a function of the supersaturation,23 which has been demonstrated previously in colloidal NC syntheses.21,39,42 Moreover, colloidal NCs present a broad range of size-dependent optical properties, such as light scattering, absorbance, and fluorescence, which can be measured in real time by facile, noninvasive techniques.42,46–49 Our framework will interpret the optical progression of growing NCs to determine RNC(t) and then σ(t).
To obtain an expression for RNC(t), we start with an expression based on eqn (2) and (3). As derived by Sugimoto45 and expanded by Talapin et al.,50 the radial rate of classical growth for a colloidal NC is described by
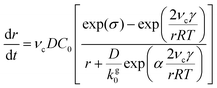 | (4) |
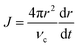 | (5) |
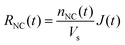 | (6) |
In the diffusion regime, combining eqn (4)–(6) leads to an expression for supersaturation:
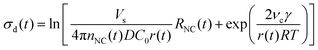 | (7) |
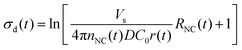 | (8) |
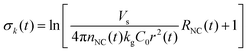 | (9) |
| A = clε | (10) |
Synthesis can affect both c and ε. When changes in ε are small, such as during some crystallization reactions with minor changes in NC size,52ε may be approximated as a constant value,21,42 meaning that c = CNC is the sole variable during the reaction, so that A corresponds directly with CNC. On another hand, seed-mediated syntheses involve a constant c = nNC/Vs but often grow NCs to larger sizes, meaning that ε changes over the reaction. When absorption predominates the overall extinction, ε is proportional to the volume of the NCs,51 which depends on the amount of consumed monomer CNC. Thus, A corresponds with CNC in both cases.
When a synthesis reaction is run to completion, the final monomer concentration approaches C0. If the total concentration of usable monomer added to the closed reaction is CT, then the final concentration of consumed monomer is approximately CT − C0. When colloidal NC syntheses directly introduce monomer or quantitatively convert precursor to monomer before seed addition, some reactions can follow pseudo-first-order kinetics, especially when nNC is large.43,53–55 In both cases discussed above, A corresponds with CNC, and the pseudo-first-order kinetics can be described empirically as
CNC(t) = (CT − C0) − (CT − C0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kgt). exp(−kgt). | (11) |
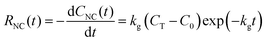 | (12) |
C(t) = (CT − C0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kgt) + C0 exp(−kgt) + C0 | (13) |
When seed-mediated reactions have an induction period, during which precursor is converted into monomer such as in autocatalytic reactions, they often show sigmoidal kinetics.56–58 These kinetics can be represented empirically by the Boltzmann sigmoid function,59
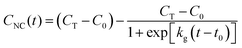 | (14) |
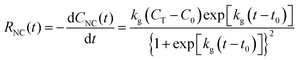 | (15) |
We can further formulate an expression to predict the final size of NCs in the reaction. The concentration of integrated monomer in a population of spherical NCs can be approximated as 4πr3nNC/(3νcVs), where r is the volume–average radius. Since CNC(t → completion) = CT − C0, the average NC size after seed-mediated growth can be estimated with
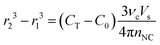 | (16) |
In summary, our framework analyzes the progression of a size-dependent optical property to quantify the underlying supersaturation dynamics in the classical growth of NCs, particularly those with simple geometries in its current form. To implement our approach, the optical measurements should be conducted throughout the entire reaction and are coupled with knowledge of the experimental parameters; these required parameters are listed in Table S2 (ESI†). In its implementation in this study, our framework measures absorbance as this optical property and considers reactions in which absorption predominates the overall extinction. The latter condition is typically valid when colloidal NCs remain smaller than 50–60 nm.46,60 In-line spectrophotometers can rapidly and noninvasively measure absorbance through a transparent synthesis vial, such that high-frequency absorbance measurements yield high-resolution supersaturation dynamics. Moreover, since we characterize σ(t) based on RNC(t), our approach requires neither insight into the source of the monomer nor its molecular structure, limiting the requirements of a priori knowledge and expanding the utility of the methodology. As such, it should be applicable to reactions whether the conversion of precursor to monomer occurs in the bulk phase or is catalyzed by the NC surface.
Our approach can also be extended to additional types of experimental apparatuses and types of NCs. The other size-dependent optical properties of NCs, including light scattering and fluorescence, can also be related with RNC in the framework.46–48 Additionally, the framework can be built upon to interpret anisotropic NC growth more accurately by modifying the dimensionality of eqn (4) and (5) or to interpret crystallization reactions by consider temporal changes in nNC/Vs during nucleation. Lastly, the noninvasive optical methods can be used alongside complementary analytical techniques for additional insight into NC growth, such as in situ X-ray diffraction for the evolution of crystal phases and multimetallic compositions.61
Elucidating supersaturation dynamics throughout the growth of colloidal Au nanocubes
We used our framework to investigate the growth of colloidal Au nanocubes. To assess how supersaturation dynamics influence the shape evolutions of NCs, we chose a seed-mediated synthesis formulation with cetyltrimethylammonium chloride (CTAC) that predominantly grows nanocubes but also grows a small proportion of impurity shapes. To experimentally analyze NCs throughout the aqueous reaction, we arrested growth at various times using ligand exchange with thiol-terminated polystyrene and solvent transfer via tetrahydrofuran into toluene.62 We imaged these samples using high-angle annular darkfield scanning transmission electron microscopy (HAADF-STEM) (Fig. 3a), which showed that the cuboctahedral seeds primarily evolved to truncated cubes and then to cubes along growth (Fig. 3b).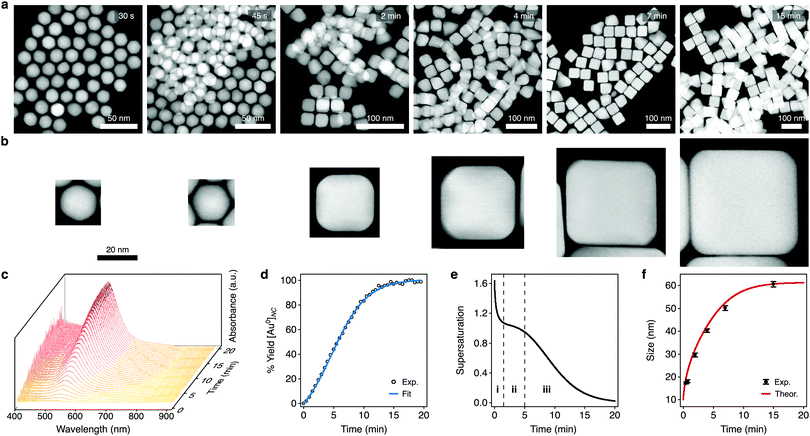 | ||
| Fig. 3 Characterization of the supersaturation-dependent growth of colloidal Au nanocubes. (a) HAADF-STEM images of the NCs found throughout colloidal nanocube growth. Times denote when growth was arrested relative to the initiation of growth. (b) HAADF-STEM images of single NCs from the above samples depicting the transition of cuboctahedra to cubes. The scale bar applies to each micrograph. (c) Time-resolved extinction spectra taken throughout colloidal NC growth. (d) Kinetics of NC growth analyzed via the peak nanoplasmonic extinction. The data were fitted to eqn (14) (r2 > 0.99). (e) Temporal profile of supersaturation dynamics throughout colloidal NC growth, as estimated by eqn (8) and (15). The dashed lines delineate the triphasic sequence of rapid monomer consumption (i), sustained supersaturation (ii), and then gradual depletion (iii). (f) Experimental and theoretically predicted growth of colloidal nanocubes. Theoretical growth was modeled using the supersaturation profile from (e) and eqn (4). Dots and bars represent the mean and SD, respectively. | ||
Towards a high-resolution assessment of supersaturation, we took high-frequency absorbance measurements throughout the reaction (Fig. 3c). The absorbance kinetics had an induction period, and we fitted them to eqn (14) (the equation constants are summarized in Table S2 (ESI†); see Section S1 in the ESI† for additional details). As shown in Fig. 3d, this model showed a strong agreement with the experimental data (coefficient of determination, r2 > 0.99). Since the absorbance of the NCs leads to visually discernible colors, we also took images of the synthesis formulation throughout growth and analyzed the colorimetric development (Fig. S1a and b, ESI†). Imaging and spectrophotometry yielded similar results in their analyses of the absorbance kinetics (Fig. S1c, ESI†), indicating that both approaches can be used to determine the variable parameters of eqn (14).
We applied these fitted parameters to characterize the supersaturation dynamics in the reaction. When D ≪ 1, colloidal NC growth tends to occur in the diffusion regime.20 For our synthesis formulation, D is on the order of 10−10 m2 s−1 (ref. 63), so we used eqn (8) and (15) to determine the supersaturation dynamics (Fig. 3e, the equation constants are summarized in Table S2, ESI†). This revealed a triphasic sequence: an initial phase of rapid monomer consumption (0.0–1.5 min) followed by phases of sustained supersaturation (1.5–5.0 min) and then gradual monomer depletion (>5.0 min). This profile indicates that monomer consumption outpaced the conversion of precursor to monomer in the initial 1.5 min of NC growth. Sustained supersaturation in the second phase suggests that the NCs grew between 1.5–5.0 min while the conversion of precursor to monomer occurred at a rate similar to the rate of monomer consumption. Lastly, the supply of supersaturated monomer was gradually exhausted between 5–20 min as this reaction completed.
Although seed-mediated syntheses of colloidal NCs have been studied heavily, the supersaturation dynamics of these reactions have been assumed to follow the descriptions of the growth stages of the LaMer (see Section III in Fig. 1b) or Finke–Watsky models, in which supersaturation follows a simple, steadily declining profile as the NCs grow.40,41 Notably, the elucidated supersaturation profile for our colloidal nanocubes showed a triphasic sequence with distinct phases of monomer consumption (Fig. 3e and Fig. S2, ESI†), revealing that the supersaturation dynamics of colloidal NC growth can be more complex than previously understood.
We next used the supersaturation profile (Fig. 3e) to model the growth of the colloidal nanocubes using eqn (4) (see Section S2 in the ESI† for additional details). This model estimated that the isometric spherical growth in eqn (4) approximated the isometric cubic growth in our NCs. We also used the HAADF-STEM images of the NCs throughout the reaction to analyze the experimental sizes of the cuboctahedra and cubes (Fig. S3 (ESI†) summarizes the sizing measurements, and the raw sizing data are included in Fig. S4 (ESI†)). As shown in Fig. 3f, the theoretical model demonstrated a strong agreement with the experimental results, predicting the temporal growth profile of the NCs. According to this profile, the NCs grew from 10.0 nm (the seed size) to 29.0 nm in the initial phase of the supersaturation dynamics (0.0–1.5 min), then to 46.5 nm in the intermediate phase (1.5–5.0 min), and finally to approximately 61.2 nm (5.0 min to completion).
To further investigate the influence of the supersaturation dynamics on growth, we artificially simulated a supersaturation profile (Fig. S5a, ESI†) which lacks the initial phase of rapid monomer consumption and more resembles that expected when considering the LaMer model (see Section S3 in the ESI† for additional details). We inputted the simulated supersaturation into eqn (4) for another theoretical growth model, which predicted the final size of the NCs but did not conform to the growth profile during the earlier stages of the reaction (Fig. S5b, ESI†). This distinction reinforced that this reaction involves the complex supersaturation dynamics found in Fig. 3e and further supported the utility of our framework.
Supersaturation-associated shape evolutions of nanocubes during growth
With the supersaturation profile in hand, we sought additional insight into growth by investigating the relationship between the supersaturation dynamics and shape evolutions of the NCs. The HAADF-STEM images and additional scanning electron (SE)-STEM images identified six NC shapes present in this reaction (Fig. 4a). Three of these shapes (cuboctahedra, truncated cubes, and cubes) were involved in the primary growth pathway (Fig. 3b), but the other three shapes (overgrown cubes, tetrahedra, and a small proportion of other, undefined shapes) were undesired. While cuboctahedral seeds grow into tetrahedra and the observed undefined shapes as kinetic impurities of synthesis,64–66 it was unclear how cube overgrowth occurred.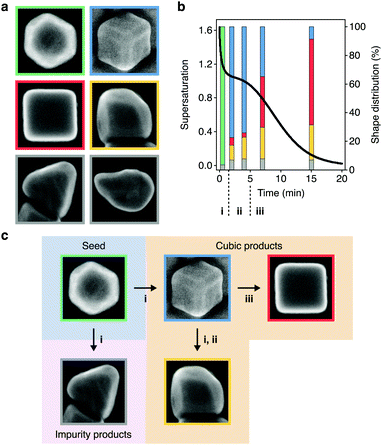 | ||
| Fig. 4 Supersaturation-associated shape evolutions of nanocubes. (a) SE-STEM images showing the NC shapes found throughout colloidal nanocube growth. Cuboctahedra (green), truncated cubes (blue), cubes (red), overgrown cubes (yellow), tetrahedra (grey) and other shapes (grey). The micrographs are not to scale. (b) Temporal profile of supersaturation dynamics taken from Fig. 3e (black curve) overlaid on the distribution of shapes (bars) at 0.5, 2, 4, 7, and 15 min during colloidal growth. These NCs were grown using 0.1 equiv. of NaOH. Shapes are denoted by the outline colors in (a). The triphasic sequence of supersaturation dynamics from Fig. 3e were denoted with i, ii, and iii. (c) Summary of the associations between the supersaturation phases and shape evolutions. | ||
To study the relationship between the supersaturation dynamics and overgrowth, we used the SE-STEM images to analyze the distribution of NC shapes throughout growth (Table S3, ESI†) and overlaid them on the supersaturation profile (Fig. 4b). By doing so, we found associations, which were not necessarily causative, between shape evolutions and supersaturation dynamics. This analysis showed that the population of cuboctahedra predominantly evolved to cubic shapes (truncated cubes, cubes, or overgrown cubes) during the initial phase of rapid monomer consumption. Truncated cubes were the dominant shape shortly after this transition but decreased in proportion as the reaction progressed. The overall yield of NCs with cubic shapes remained consistent throughout growth (92.9, 92.3, 92.1, and 93.0% at 2.0, 4.0, 7.0, and 15 min, respectively) (Table S3, ESI†), suggesting that cubes and overgrown cubes emerged from the truncated cubes rather than directly from cuboctahedra.
Fig. 4b also showed that cubes and overgrown cubes emerged in different phases of monomer consumption, as summarized in Fig. 4c. Cubes primarily emerged in the third phase, gradual monomer depletion. Conversely, overgrowth primarily occurred in the first and second phases. By 2 min, 10.2% of the NCs were overgrown cubes. By 4 and 7 min, this proportion increased to 15.0 and 21.9%, respectively. Between 7–15 min, however, it only increased to 24.4%. That is, cube overgrowth was largely associated with the high supersaturation of the earlier phases of growth (Fig. 4b and c). As described by Fick's first law,45,50
| J = 4πDr(C − Ci) | (17) |
Modulating supersaturation to influence nanocube shape evolutions
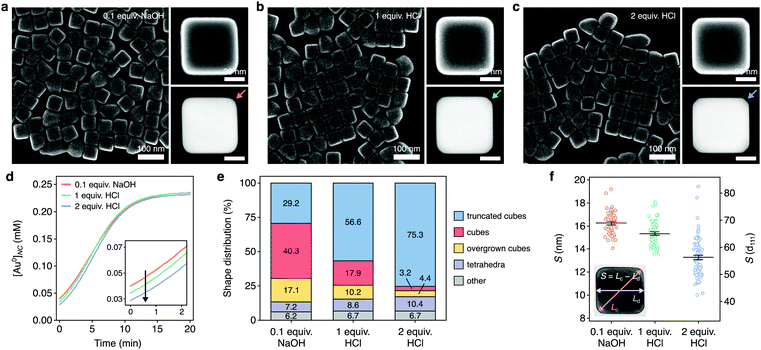
In our synthesis, the reduction of Au precursor to monomer produces H+ and Cl− (Fig. S6, ESI†). The addition of HCl to this reaction should shift the equilibrium and reduce the monomer concentration before the addition of seed. Moreover, H+ and Cl− are labile, weakly binding ions on Au surfaces, and do not promote anisotropic growth.30,67 We hypothesized that adding HCl before the addition of seed would diminish monomer conversion in the early stages of growth and thus limit cube overgrowth. The synthesis formulation for the NCs shown in Fig. 3 and 4 used 0.1 molar equivalents (equiv., relative to Au added) of NaOH. We compared these NCs to the NCs from two syntheses that replaced NaOH with 1.0 or 2.0 equiv. of HCl, small amounts of HCl intended to slightly diminish monomer conversion in the early stages of growth.Fig. 5a–c shows the NCs produced by these syntheses, with larger-area SE-STEM images shown in Fig. S7 (ESI†). As done previously, we took high-frequency absorbance measurements throughout these reactions and analyzed the absorbance kinetics (Fig. S8a–c, ESI†). Fitting them to eqn (14) characterized the monomer conversion kinetics, which showed that the addition of HCl indeed diminished the monomer conversion and supersaturation in the early stages of growth (Fig. 5d and Fig. S8d, ESI†) while yielding nanocubes of similar size (Table S4, ESI†).
To investigate the influence of these different supersaturation dynamics, we analyzed the shape distribution for each sample. The addition of HCl indeed coincided with lower yields of overgrown cubes (Fig. 5e). With 0.1 equiv. of NaOH added, 17.1% of the NCs were overgrown nanocubes. This proportion diminished to 10.2% for 1 equiv. of HCl and then to 4.4% for 2 equiv. of HCl. Moreover, the addition of HCl also coincided with increasingly truncated cubes (Fig. 5a–c and e). Previous research has indicated that decreasing supersaturation during synthesis is expected to dull NC corners.68 To further quantify this in our samples, we measured a sharpness index (S), as defined in the inset of Fig. 5f, for individual nanocubes. With 0.1 equiv. of NaOH added, the mean estimate of S was 16.3 (95% confidence interval [CI]: 15.9–16.6) nm, whereas it was 15.3 (15.0–15.6) nm for 1 equiv. of HCl and 13.3 (12.9-13.7) nm for 2 equiv. of HCl. Thus, diminishing early monomer conversion, especially in the first stage of growth (Fig. 5d), was associated with both lower yields of overgrown cubes (Fig. 5e) and decreased nanocube sharpness (Fig. 5f). Taken together, these results show that altering the supersaturation dynamics during growth can modulate the features as well as shape evolutions of colloidal NCs.
Conclusions
This work developed a theoretical framework and the accompanying experimental methodology to characterize the supersaturation dynamics underlying colloidal NC growth. Our framework relates the temporal, size-dependent optical properties of growing NCs, such as absorbance, light scattering, or fluorescence, to supersaturation throughout the reaction. As such, this approach uses real-time optical measurements, which can be conducted noninvasively, without requiring a priori knowledge into the source of the monomer or its molecular structure. Elucidated supersaturation dynamics can be used to model temporal profiles of, and identify supersaturation-associated shape evolutions during, NC growth. These profiles show the relationships between growth rates and shape changes with the time course of reaction, supersaturation levels, and supersaturation dynamics, revealing specific mechanistic parameters to tune for synthesis development. This also finds concurrent outcomes—aspects of growth or shape evolutions that coincide with the same phase of the reaction—that may not be resolved by tuning supersaturation alone. Reagents and other reaction parameters can then be adjusted rationally based on these insights, including to increase product yields or modulate NC features.By using this approach, our study found that the growth of CTAC-capped Au nanocubes involves a triphasic sequence of supersaturation dynamics. This result demonstrates that the supersaturation dynamics of colloidal NC growth can be more complex than previously understood, including through the LaMer or Finke-Watzky models.40,41 Our analyses also showed that the emergence of cubes and overgrown cubes from truncated cubes were primarily associated with different phases of the supersaturation dynamics: overgrown cubes emerged in the early phases when monomer consumption occurred more rapidly, whereas cubes emerged in the later phase as monomer was gradually depleted. These insights led us to decrease early monomer conversion to modulate the sharpness of nanocube corners and reduce the yield of overgrown cubes. In conclusion, this work presents an initial step towards uncovering the complex thermodynamic and kinetic phenomena underlying NC growth and may guide rational design at the nanoscale.
Experimental
All experimental details for this study are available in the ESI.†Author contributions
P. Z. C., conceptualization, formal analysis, investigation, software, visualization, methodology, writing – original draft, writing – review and editing; A. J. C., formal analysis, investigation, writing – review and editing; F. X. G., funding acquisition, supervision, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank J. Watchorn (UToronto) for helpful comments regarding this manuscript. STEM images were taken at the Ontario Center for the Characterization of Advanced Materials (OCCAM) at the University of Toronto. This work was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery grant (06441). P. Z. C. was supported by the NSERC Vanier Canada Graduate Scholarship. A. J. C. was supported by the Ontario Graduate Scholarship. F. X. G. was supported by the NSERC Senior Industrial Research Chair program.Notes and references
- A. P. Alivisatos, Science, 1996, 271, 933–937 CrossRef CAS.
- J. Shamsi, A. S. Urban, M. Imran, L. De Trizio and L. Manna, Chem. Rev., 2019, 119, 3296–3348 CrossRef CAS PubMed.
- H. Liu and C. Di Valentin, Phys. Rev. Lett., 2019, 123, 186101 CrossRef CAS PubMed.
- M. Zhao, Z. Chen, Y. Shi, Z. D. Hood, Z. Lyu, M. Xie, M. Chi and Y. Xia, J. Am. Chem. Soc., 2021, 143, 6293–6302 CrossRef CAS.
- J. Pan, Y. Shang, J. Yin, M. De Bastiani, W. Peng, I. Dursun, L. Sinatra, A. M. El-Zohry, M. N. Hedhili, A. H. Emwas, O. F. Mohammed, Z. Ning and O. M. Bakr, J. Am. Chem. Soc., 2018, 140, 562–565 CrossRef CAS PubMed.
- M. S. Verma, P. Z. Chen, L. Jones and F. X. Gu, RSC Adv., 2014, 4, 10660–10668 RSC.
- P. C. Chen, M. Liu, J. S. Du, B. Meckes, S. Wang, H. Lin, V. P. Dravid, C. Wolverton and C. A. Mirkin, Science, 2019, 363, 959–964 CrossRef CAS PubMed.
- P. B. Green, P. Narayanan, Z. Li, P. Sohn, C. J. Imperiale and M. W. B. Wilson, Chem. Mater., 2020, 32, 4083–4094 CrossRef CAS.
- Y. Xia, X. Xia and H. C. Peng, J. Am. Chem. Soc., 2015, 137, 7947–7966 CrossRef CAS PubMed.
- B. C. Steimle, J. L. Fenton and R. E. Schaak, Science, 2020, 367, 418–424 CrossRef CAS PubMed.
- C. de Mello Donega, Chem. Soc. Rev., 2011, 40, 1512–1546 RSC.
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- P. Z. Chen, L. Pollit, L. Jones and F. X. Gu, Chem, 2018, 4, 2301–2328 CAS.
- T. Kim, K.-H. Kim, S. Kim, S.-M. Choi, H. Jang, H.-K. Seo, H. Lee, D.-Y. Chung and E. Jang, Nature, 2020, 586, 385–389 CrossRef CAS PubMed.
- E. Ozbay, Science, 2006, 311, 189–193 CrossRef CAS.
- M. S. Verma, P. Z. Chen, L. Jones and F. X. Gu, Biosens. Bioelectron., 2014, 61, 386–390 CrossRef CAS.
- T. Leshuk, A. B. Holmes, D. Ranatunga, P. Z. Chen, Y. S. Jiang and F. X. Gu, Environ. Sci.: Nano, 2018, 5, 509–519 RSC.
- Y. Zhang, A. Malekjahani, B. N. Udugama, P. Kadhiresan, H. Chen, M. Osborne, M. Franz, M. Kucera, S. Plenderleith, L. Yip, G. D. Bader, V. Tran, J. B. Gubbay, A. McGeer, S. Mubareka and W. C. W. Chan, Nano Lett., 2021, 21, 5209–5216 CrossRef CAS.
- A. J. Clasky, J. D. Watchorn, P. Z. Chen and F. X. Gu, Acta Biomater., 2021, 122, 1–25 CrossRef CAS.
- N. T. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630 CrossRef CAS PubMed.
- M. P. Hendricks, M. P. Campos, G. T. Cleveland, I. Jen-La Plante and J. S. Owen, Science, 2015, 348, 1226–1230 CrossRef CAS PubMed.
- N. R. Jana, L. Gearheart and C. J. Murphy, Adv. Mater., 2001, 13, 1389–1393 CrossRef CAS.
- I. V. Markov, Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy, 3rd edn, 2017 Search PubMed.
- X. Ye, M. R. Jones, L. B. Frechette, Q. Chen, A. S. Powers, P. Ercius, G. Dunn, G. M. Rotskoff, S. C. Nguyen, V. P. Adiga, A. Zettl, E. Rabani, P. L. Geissler and A. P. Alivisatos, Science, 2016, 354, 874–877 CrossRef CAS PubMed.
- A. S. Mule, S. Mazzotti, A. A. Rossinelli, M. Aellen, P. T. Prins, J. C. van der Bok, S. F. Solari, Y. M. Glauser, P. V. Kumar, A. Riedinger and D. J. Norris, J. Am. Chem. Soc., 2021, 143, 2037–2048 CrossRef CAS.
- A. Riedinger, F. D. Ott, A. Mule, S. Mazzotti, P. N. Knusel, S. J. P. Kress, F. Prins, S. C. Erwin and D. J. Norris, Nat. Mater., 2017, 16, 743–748 CrossRef CAS.
- W. K. Burton, N. Cabrera and F. C. Frank, Philos. Trans. R. Soc. A, 1951, 243, 299–358 CrossRef.
- J. Lee, J. Yang, S. G. Kwon and T. Hyeon, Nat. Rev. Mater, 2016, 1, 16034 CrossRef CAS.
- R. Takahata, S. Yamazoe, K. Koyasu, K. Imura and T. Tsukuda, J. Am. Chem. Soc., 2018, 140, 6640–6647 CrossRef CAS.
- M. L. Personick and C. A. Mirkin, J. Am. Chem. Soc., 2013, 135, 18238–18247 CrossRef CAS.
- L. M. Liz-Marzan and M. Grzelczak, Science, 2017, 356, 1120–1121 CrossRef CAS PubMed.
- H. X. Lin, Z. C. Lei, Z. Y. Jiang, C. P. Hou, D. Y. Liu, M. M. Xu, Z. Q. Tian and Z. X. Xie, J. Am. Chem. Soc., 2013, 135, 9311–9314 CrossRef CAS PubMed.
- C. S. Tan, Y. Hou, M. I. Saidaminov, A. Proppe, Y. S. Huang, Y. Zhao, M. Wei, G. Walters, Z. Wang, Y. Zhao, P. Todorovic, S. O. Kelley, L. J. Chen and E. H. Sargent, Adv. Sci., 2020, 7, 1903166 CrossRef CAS.
- X. Peng, J. Wickham and A. P. Alivisatos, J. Am. Chem. Soc., 1998, 120, 5343–5344 CrossRef CAS.
- S. A. Morin, M. J. Bierman, J. Tong and S. Jin, Science, 2010, 328, 476–480 CrossRef CAS PubMed.
- M. J. Bierman, Y. K. Lau, A. V. Kvit, A. L. Schmitt and S. Jin, Science, 2008, 320, 1060–1063 CrossRef CAS PubMed.
- J. Zhu, H. Peng, A. F. Marshall, D. M. Barnett, W. D. Nix and Y. Cui, Nat. Nanotechnol., 2008, 3, 477–481 CrossRef CAS PubMed.
- J. Joo, B. Y. Chow, M. Prakash, E. S. Boyden and J. M. Jacobson, Nat. Mater., 2011, 10, 596–601 CrossRef CAS.
- B. Abecassis, F. Testard, Q. Kong, B. Francois and O. Spalla, Langmuir, 2010, 26, 13847–13854 CrossRef CAS.
- V. K. Lamer and R. H. Dinegar, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- M. A. Watzky and R. G. Finke, J. Am. Chem. Soc., 1997, 119, 10382–10400 CrossRef CAS.
- M. P. Hendricks, B. M. Cossairt and J. S. Owen, ACS Nano, 2012, 6, 10054–10062 CrossRef CAS PubMed.
- T. H. Yang, K. D. Gilroy and Y. Xia, Chem. Sci., 2017, 8, 6730–6749 RSC.
- Z. Wu, S. Yang and W. Wu, Nanoscale, 2016, 8, 1237–1259 RSC.
- T. Sugimoto, Adv. Colloid Interface Sci., 1987, 28, 65–108 CrossRef CAS.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, New York, 1983 Search PubMed.
- J. Maes, N. Castro, K. De Nolf, W. Walravens, B. Abécassis and Z. Hens, Chem. Mater., 2018, 30, 3952–3962 CrossRef CAS.
- D. Mutavdzic, J. Xu, G. Thakur, R. Triulzi, S. Kasas, M. Jeremic, R. Leblanc and K. Radotic, Analyst, 2011, 136, 2391–2396 RSC.
- W. Haiss, N. T. Thanh, J. Aveyard and D. G. Fernig, Anal. Chem., 2007, 79, 4215–4221 CrossRef CAS PubMed.
- D. V. Talapin, A. L. Rogach, M. Haase and H. Weller, J. Phys. Chem. B, 2001, 105, 12278–12285 CrossRef CAS.
- K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677 CrossRef CAS.
- W. W. Yu, L. Qu, W. Guo and X. Peng, Chem. Mater., 2003, 15, 2854–2860 CrossRef CAS.
- Y. Wang, H. C. Peng, J. Liu, C. Z. Huang and Y. Xia, Nano Lett., 2015, 15, 1445–1450 CrossRef CAS.
- A. Ruditskiy, M. Zhao, K. D. Gilroy, M. Vara and Y. N. Xia, Chem. Mater., 2016, 28, 8800–8806 CrossRef CAS.
- M. Zhou, H. Wang, M. Vara, Z. D. Hood, M. Luo, T. H. Yang, S. Bao, M. Chi, P. Xiao, Y. Zhang and Y. Xia, J. Am. Chem. Soc., 2016, 138, 12263–12270 CrossRef CAS PubMed.
- A. E. Saunders, M. B. Sigman and B. A. Korgel, J. Phys. Chem. B, 2003, 108, 193–199 CrossRef.
- D. T. Robb and V. Privman, Langmuir, 2008, 24, 26–35 CrossRef CAS PubMed.
- N. Thomas and E. Mani, RSC Adv., 2016, 6, 30028–30036 RSC.
- C. Bullen, P. Zijlstra, E. Bakker, M. Gu and C. Raston, Cryst. Growth Des., 2011, 11, 3375–3380 CrossRef CAS.
- P. K. Jain, K. S. Lee, I. H. El-Sayed and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 7238–7248 CrossRef CAS PubMed.
- H. Fridman, M. Volokh and T. Mokari, Nanoscale, 2021, 13, 19076–19084 RSC.
- K. Park, L. F. Drummy, R. C. Wadams, H. Koerner, D. Nepal, L. Fabris and R. A. Vaia, Chem. Mater., 2013, 25, 555–563 CrossRef CAS.
- M. Harada, K. Okamoto and M. Terazima, J. Colloid Interface Sci., 2009, 332, 373–381 CrossRef CAS PubMed.
- T. K. Sau and C. J. Murphy, J. Am. Chem. Soc., 2004, 126, 8648–8649 CrossRef CAS PubMed.
- J. E. Park, Y. Lee and J. M. Nam, Nano Lett., 2018, 18, 6475–6482 CrossRef CAS PubMed.
- C. Y. Chiu, Y. Li, L. Ruan, X. Ye, C. B. Murray and Y. Huang, Nat. Chem., 2011, 3, 393–399 CrossRef CAS PubMed.
- N. Almora-Barrios, G. Novell-Leruth, P. Whiting, L. M. Liz-Marzan and N. Lopez, Nano Lett., 2014, 14, 871–875 CrossRef CAS PubMed.
- D. Alpay, L. Peng and L. D. Marks, J. Phys. Chem. C, 2015, 119, 21018–21023 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nh00572c |
| This journal is © The Royal Society of Chemistry 2022 |