Open Access Article
Open Access ArticleMicroscale investigation on interfacial slippage and detachment of ice from soft materials†
Kartik
Regulagadda‡
 a,
Julia
Gerber‡
a,
Thomas M.
Schutzius
a,
Julia
Gerber‡
a,
Thomas M.
Schutzius
 *b and
Dimos
Poulikakos
*b and
Dimos
Poulikakos
 *a
*a
aLaboratory of Thermodynamics in Emerging Technologies, Department of Mechanical and Process Engineering, ETH Zurich, Sonneggstrasse 3, Zurich CH-8092, Switzerland. E-mail: dpoulikakos@ethz.ch; Fax: +41 44 632 11 76; Tel: +41 44 632 27 38
bLaboratory for Multiphase Thermofluidics and Surface Nanoengineering, Department of Mechanical and Process Engineering, ETH Zurich, Sonneggstrasse 3, Zurich CH-8092, Switzerland. E-mail: thomschu@ethz.ch; Tel: +41 44 632 46 04
First published on 7th February 2022
Abstract
Surface icing is detrimental to applications ranging from transportation to biological systems. Soft elastomeric coatings can engender remarkably low ice adhesion strength, but mechanisms at the microscale and resulting ice extraction outcomes need to be understood. Here we investigate dynamic ice-elastomer interfacial events and show that the ice adhesion strength can actually vary by orders of magnitude due to the shear velocity. We study the detailed deformation fields of the elastomer using confocal traction force microscopy and elucidate the underlying mechanism. The elastomer initially undergoes elastic deformation having a shear velocity dependent threshold, followed by partial relaxation at the onset of slip, where velocity dependent “stick-slip” micropulsations are observed. The results of the work provide important information for the design of soft surfaces with respect to removal of ice, and utility to fields exemplified by adhesion, contact mechanics, and biofouling.
New conceptsWe present a methodology based on confocal traction force microscopy to investigate in situ ice adhesion on soft elastomeric materials at the microscale. We report unprecedented findings of the in-plane transient heterogeneous deformation field of the elastomer during the ice removal. We study the response of the elastomer at different ice removal rates, and directly relate the determined increase in ice adhesion stress to the applied shear rate. Further, we directly observe and visualize the process of interfacial slippage and subsequent relaxation of a soft surface, including the manifestation of an unexpected stick-slip phenomenon, which we explain. Our findings provide real time insight into the complex process of rate-dependent microscopic deformation in viscoelastic solids during adhesion in general, which is of significance in areas exemplified by adhesion and bonding materials, contact mechanics, bio-fouling control and soft robotic materials. |
Introduction
Soft viscoelastic solids (or simply elastomers) exhibiting both elastic and viscous behavior are ubiquitous in nature and practical applications. Biological tissues mainly comprise viscoelastic components with each tissue having a specific function.1 From a practical point of view, elastomers are traditionally used in foams, adhesives, food additives, and so on.2 With recent technological advances, the applications extend to the exciting domains of soft robotics, tissue engineering, flexible electronics, and so on.3–5 One of the potentially important applications of elastomers is their passive icephobic performance during harsh environmental icing conditions.6–9 Ice adhered to surfaces incurs malfunctioning or a drastic decrease in efficiency in many industrial settings.10 It is previously shown that elastomers offer exceptionally low ice adhesion shear strength, τice = F*/A ≤ 10 kPa, either through interfacial fracture- or slippage mechanisms.6,8,9,11–13 Here, F* indicates the peak ice removal force recorded by a force gauge in a standard ice adhesion shear test at a constant shear velocity, V, and A is the apparent substrate-ice interfacial area.14 In contrast, rigid and liquid impregnated surfaces (which have an intervening lubricant layer in between ice and the base solid) have a lower limit of τice ≈ 50 and 15 kPa, respectively.15–20 On this class of materials, τice can increase significantly due to the highly humid ambient conditions or lubricant depletion over time.21–29 However, elastomers do not have such bottlenecks and are shown to be durable over several (10–20) icing/de-icing cycles.6,8 Other strategies with weakly interacting surface layers using organogel materials to mitigate icing on surfaces are discussed in ref. 30.Interfacial fracture on elastomers can be either stress- or toughness-limited de-bonding of ice, where the elastomer cavitation leads to easy ice removal.6,8 Slippage occurs when the elastomer chains adhered to the ice are sufficiently mobile, which can be realized by either reducing the cross-linking density of the elastomer or infiltrating the elastomer network with a lubricant.6,7,31,32 The latter is unlike liquid impregnated surfaces, because the lubricant is introduced into the bulk of the elastomer, and any lubricant layer on the interface interacting with ice is avoided. During slippage, ice remains adhered to the elastomer but continues to slide away from its initial location as long as shear is applied. Whether ice fractures or slips during an adhesion test is governed by a multitude of parameters: elastomer surface temperature, T, shear velocity, V, type of stress applied in the adhesion test (shear, mixed, and normal), elastomer thickness, h, and Young's modulus, E (also a function of temperature). This illustrates the complexity involved in comprehending the ice removal mechanisms on elastomers across a much broader spectrum of influencing conditions.
The ice adhesion shear strength, τice, is the accepted defining metric for the performance of a surface, with respect to its resistance to ice detachment. In previous studies, τice on elastomers is typically reported for low shear velocities of V ≤ 0.1 mm s−1.6,8,13 Here, we show that τice on soft silicone elastomeric coatings (E = 15.4 kPa at T = −20 °C) can increase by an order of magnitude, depending on the shear velocity, V, which can potentially define the domain of their applicability in practical settings. To understand the reason for this behavior, we first probe into the elastomer deformation using confocal traction force microscopy (cTFM) providing the necessary high-resolution visualization of spatio-temporal in-plane deformation of the elastomer, during shear mode experiments. Therefore, the cTFM technique provides unprecedented detail of the elastomer deformation at the microscopic scale. We then invoke stochastic models involving cyclic adsorption and desorption of elastomer chains near the interface to explain the observed trend of τice with V. Further, we investigate the effect of mode of adhesion test (shear, mixed, and normal) and elastomer temperature on the ice adhesion strength, and show that the trend of τice with V in mixed mode tests is similar to that of shear mode tests while τice decreases with T.
Experimental section
Macroscopic ice adhesion setup
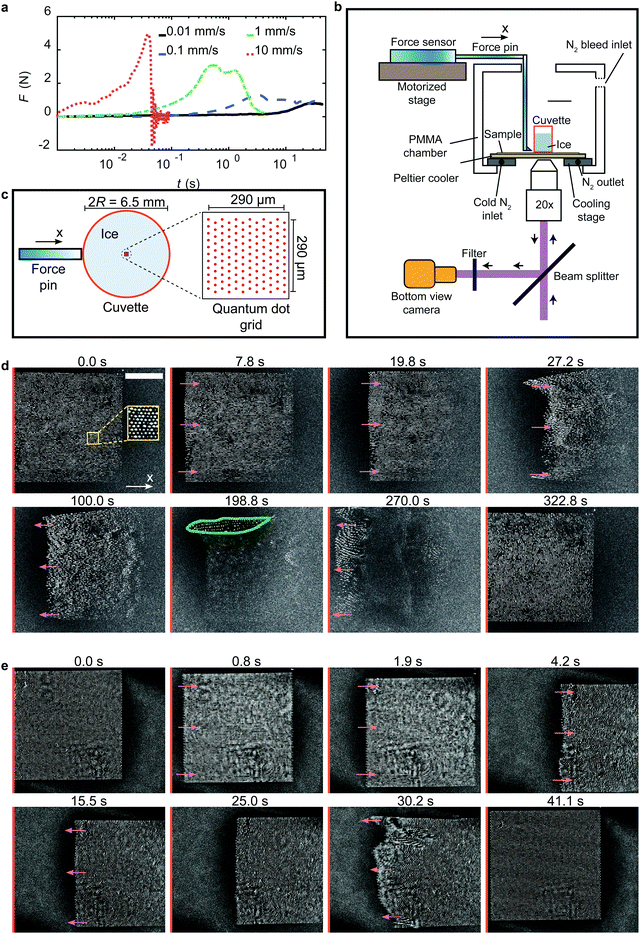
For the macroscopic ice adhesion experiments, we follow a similar protocol as explained in ref. 14. A cryostage (Linkam BCS196) with liquid Nitrogen supply is operated with a temperature controller unit (Linkam TMS93). A cylindrical copper block with a circular groove (diameter 25 mm, depth 0.17 mm) on the top is clamped firmly on the cryostage. A double-sided tape (TESA Doppelband-Fotostrip) is used to fix the spin coated circular cover slips inside the groove. In addition, Kapton tape (3M Polymide Tape 8997) is also used around the edge on the top side of the surface to make sure that the substrate is firmly held in its position during the adhesion test. A cylindrical glass cuvette (outer diameter 8.3 mm, inner diameter 6.5 mm, height 10 mm) which is open on both sides is gently placed on the substrate. The cross-section of the cuvette which comes in contact with the elastomer is polished using wet sand papers with 800, 1200, and 2000 grit in that order to ensure surface flatness. The cuvette is filled with ≈0.25 mL of DI water using a syringe by hand. The experiments are performed in Nitrogen ambient to reduce the relative humidity, RH, so that frost formation on the sample is avoided. An acrylic chamber with slots to accommodate force pin from the top and the side is mounted on the cryostage to ensure the Nitrogen ambient. The slot on the top is sealed while conducting shear or mixed mode adhesion tests. Likewise, the slot on the side is sealed while conducting normal mode tests. The relative humidity, RH, and ambient temperature, Tamb = 21 °C, in the chamber are measured using a sensor (Sensirion Ag SHT31 Smart gadget). Perfect sealing is not a critical aspect of the experiment; in all the macroscopic experiments, RH < 5% even with one slot being fully open.For measuring the force during the adhesion tests, either a Mark 10 force gauge M5-5 (calibration certified) or Tekscan A201 force sensor 0–4 N (calibrated in-house) are used. The force pin comes in contact with the wall of the cuvette at a height of <1 mm and 6.1 mm for the shear and mixed mode tests, respectively. In order to ensure that the contact area of the force pin with the cuvette is minimum, a taper is provided near its end so that the contact width of the pin with the cuvette is ≈85 μm. The force gauge is mounted on top of a manual stage (Thorlabs XR25C) whose axis in the horizontal plane is oriented orthogonal to the shear direction to precisely control the gauge position. This stage is assembled on a lab jack (Thorlabs L490) to control the vertical position of the force gauge. The entire assembly is mounted on a motorized stage (Thorlabs NRT100/M) which is operated at a desired velocity (0.01, 0.1, 1, and 10 mm s−1) for the experiments. The temperature of the elastomer surface is measured using a surface mounted T-type thermocouple (Omega, 5SRTC-TT-TI-40-1M) connected to a thermocouple reader (Lutron TM947SD). The experimental range of elastomer temperature, T, is −33 to −9 °C. The ice adhesion test is also captured optically from the side view using a digital microscope (Celestron Digital Microscope Pro, 5 MP) operated at 9–12 Hz for V ≤ 1 mm s−1. For V = 10 mm s−1, a high-speed camera (Photron SA 1.1) operated at 1000 Hz is used.
The acquisition rate of force gauge is set at 20, 20, 50, and 1000 Hz when the velocities are 0.01, 0.1, 1, and 10 mm s−1, respectively. From the force, F, vs. time, t, plots during the ice adhesion test, the maximum force, F*, is extracted to estimate ice adhesion shear and normal strengths, τice (or σice) = F*/A where A = πR2 is the cross-sectional area of the ice in contact with the elastomer. The estimation of σice in the mixed mode is discussed in ref. 33. The adhesion strengths did not vary significantly with respect to icing/de-icing cycles on a given sample.
cTFM setup
The samples overprinted with regular arrays of brightly emitting QD nanodiscs (as described in Section S2, ESI†) are placed on top of a copper holder with a circular hole at the center to allow bottom view visualization. The copper holder is mounted on an annular Peltier cooler (Laird Thermal Systems, RH14-32-06-L1-W4.5), which is further mounted on a custom-built aluminum cooling stage, which has inlet, outlet, and auxiliary ports for cold Nitrogen flow. By varying the inlet flow rate of the cold Nitrogen gas with a Kaltgas system (KGW Isotherm), and operating the Peltier with a direct current voltage supply, the elastomer surface temperature, T, is maintained at −20 °C. The nitrogen from the outlet port is bled out with a T-junction to the region around the substrate, which is enveloped by the double-walled PMMA chamber to ensure RH < 2%. The other line from the T-junction is routed to the auxiliary port to have nitrogen flow underneath the sample to eliminate condensation obscuring the bottom view. The region between the walls of the PMMA chamber is vacuumed to avoid any condensation on the walls obscuring the side view. For these experiments, we implemented an inverted microscope, which allowed us to acquire images from below. This home-built microscope consisted of a blue laser (wavelength 405 nm), a series of lenses to focus the light on the back-focal plane of the objective, a 20× objective (Nikon Plan Apo), a beamsplitter (Thorlabs, CM1-BP145B1), a lens that focuses the light onto the detector, which is a sCMOS camera (Andor, Zyla 4.2). In this manner, we excited the QD nanodiscs with the blue laser and, captured the emitted light (red) with the sCMOS camera. The exposure time was set to 0.1 s.34Results and discussion
Dynamic ice adhesion
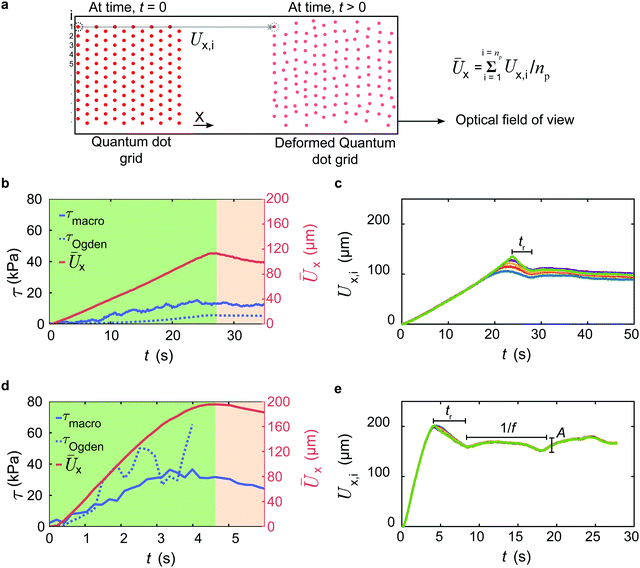
To first understand the effect of shear velocity, V, on the peak ice removal force, F*, we perform macroscopic shear adhesion tests using a standard setup (see Fig. S1, ESI†) on a silicone coating with h = 35 μm, and T = −20 °C at different velocities (see Fig. 1a). Here, the elastomer thickness, h, is sufficiently large to avoid the effects of the underlying rigid substrate. Clearly, F* increases significantly with V, and ice continues to slip as long as shear is applied. Nevertheless, beyond a critical velocity, we can have interfacial fracture even in the shear mode test, due to increase in the normal force at the interface.11 This is because the external force from the finite size force pin (see earlier section) cannot be practically applied in exactly the same plane as the elastomer–ice interface, which results in non-zero torque. At high velocities, the magnitude of this torque becomes significant (implying higher normal stress) leading to interfacial fracture. In our case, we observe fracture at V = 10 mm s−1 for h = 35 μm, and T = −20 °C (see Movie S1, ESI†). As an estimate, F* increases from 0.8 to 6.6 N (see Fig. 1a) over the investigated velocity spectrum (0.01 to 10 mm s−1). An order of magnitude increase in F* (consequently τice) with V emphasizes its importance while designing icephobic surfaces. In contrast, rigid surfaces do not show any such dependence (see Fig. S2, ESI†).14 A remark here is that, in a recent study35 it has been shown that the prolonged application (∼100 s) of constant force (<F*) on ice leads to melting of interfacial ice near substrate which reduces τice significantly. However, in the present case, the condition imposed is a constant shear rate in a given experiment. Therefore, the possibility of local melting of ice and increase in quasi liquid layer thickness is low as the time taken to reach peak ice removal force, F* (thereby τice), in a typical F vs. t plot (see Fig. 1a) even at the lowest velocity, V = 0.01 mm s−1, is typically of the order 10 s; an order of magnitude lower than the time required to melt the interfacial ice.To understand the physics behind this behavior, we employ cTFM (see Fig. 1b, c and Section S2, ESI†), which involves printing and tracking of fluorescent quantum dots (QDs) on the elastomer surface using an electrohydrodynamic drip printing technique reported in previous work.34,36–39 In addition, we also perform bright field experiments to confirm that no undulations persist on the elastomer (i.e. no interfacial fracture) and only interfacial slip occurs during the adhesion test under similar experimental conditions (see Fig. S3 and S4, ESI†). Fig. 1d and e show exemplary bottom view snapshots of the QD grid printed elastomer during ice adhesion test with h = 35 μm, T = −20 °C at V = 0.01 and 0.1 mm s−1, respectively (see Movies S2 and S3, ESI†). The mechanical properties of the selected elastomer are known—established by previous work34,36,39—such that we can use cTFM to reveal the microscopic mechanisms responsible for the rate dependent τice. Time, t = 0 indicates the reference configuration i.e. just before the shear is applied. The grid dimension (290 × 290 μm) is significantly smaller than the diameter of the ice block, 2R = 6.5 mm (see Fig. 1c). The reference configuration grid on the elastomer is located approximately near the center of the initial ice location. In Fig. 1d, as the force pin pushes the ice, the entire QD grid starts to globally translate reaching a maximum displaced configuration around t = 27.2 s. To quantify the displacement of the QDs we track them in time (see Section S3, ESI†), and define the instantaneous mean displacement, 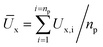 (see Fig. 2a), as the mean of all the tracked QDs displacements in the X-direction (see Fig. 1b–d) at a given time, t. Here, Ux,i represents the X-direction displacement of an ith QD at a time, t, and np represents the number of tracked QDs in each time step. During the adhesion experiments, some of the QDs can undergo out-of-plane motion and go out of focus as seen from t = 19.8 to 270.0 s. This can be attributed to the presence of non-zero normal stresses at the interface as discussed earlier.11 For this reason, np decreases with time. We therefore track the QDs until the time where Ūx approximately reaches a plateau. Fig. 2b shows the variation of Ūx at V = 0.01 mm s−1 with the green region in the plot indicating the deformation regime where Ūx increases approximately linearly with t reaching a peak,
(see Fig. 2a), as the mean of all the tracked QDs displacements in the X-direction (see Fig. 1b–d) at a given time, t. Here, Ux,i represents the X-direction displacement of an ith QD at a time, t, and np represents the number of tracked QDs in each time step. During the adhesion experiments, some of the QDs can undergo out-of-plane motion and go out of focus as seen from t = 19.8 to 270.0 s. This can be attributed to the presence of non-zero normal stresses at the interface as discussed earlier.11 For this reason, np decreases with time. We therefore track the QDs until the time where Ūx approximately reaches a plateau. Fig. 2b shows the variation of Ūx at V = 0.01 mm s−1 with the green region in the plot indicating the deformation regime where Ūx increases approximately linearly with t reaching a peak, 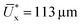 at t = 27.2 s. In addition to the global translation of the QDs, we have simultaneous local distortion i.e. the QD grid layout in each time step is different from the reference configuration. This qualitatively confirms that the transient local displacement and the traction fields are non-uniform. Beyond t = 27.2 s, we observe partial relaxation of the grid i.e. the QDs are displaced back towards the reference axis (orange line in Fig. 1d) slightly. The red region in Fig. 2b indicates the slip regime where Ūx falls below
at t = 27.2 s. In addition to the global translation of the QDs, we have simultaneous local distortion i.e. the QD grid layout in each time step is different from the reference configuration. This qualitatively confirms that the transient local displacement and the traction fields are non-uniform. Beyond t = 27.2 s, we observe partial relaxation of the grid i.e. the QDs are displaced back towards the reference axis (orange line in Fig. 1d) slightly. The red region in Fig. 2b indicates the slip regime where Ūx falls below 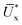 . This explains the dip in τmacro after attaining the peak i.e. τmacro = τice. Here, τmacro = F/A, is the instantaneous shear stress estimated from the force gauge reading at time, t. The partial relaxation of the QD grid marks the beginning of ice slipping on the elastomer, for if interfacial fracture were to occur, the grid should restore completely back to the reference configuration, which does not take place. As mentioned earlier, tracking all the QDs for a long time is difficult. Therefore, in Fig. 2c, we track the displacement of five individual QDs (i = 1–5 in Fig. 2a), Ux,i, for an extended period of time. The partial relaxation of the elastomer is identified by the decrease in Ux,i after attaining the peak. This relaxation continues to take place over a time, tr ≈ 5 s, which is of the same order as the macroscopic relaxation time of the elastomer, trelax = 11.7 s.34 Eventually Ux,i reaches a plateau, and is confirmed by the fact that the QD grid does not translate significantly from its local position (see Fig. 1d and Video S2, ESI†). The edge of the ice starts to crossover the grid at around t = 270.0 s, and once the crossover is complete, the elastomer relaxes fully i.e. the QD grid restores back approximately to the reference configuration with only a slight offset from the reference axis, as shown at t = 322.8 s. The slight offset could be due to the permanent set, which leads to a negligible residual strain in the elastomer after the adhesion test.
. This explains the dip in τmacro after attaining the peak i.e. τmacro = τice. Here, τmacro = F/A, is the instantaneous shear stress estimated from the force gauge reading at time, t. The partial relaxation of the QD grid marks the beginning of ice slipping on the elastomer, for if interfacial fracture were to occur, the grid should restore completely back to the reference configuration, which does not take place. As mentioned earlier, tracking all the QDs for a long time is difficult. Therefore, in Fig. 2c, we track the displacement of five individual QDs (i = 1–5 in Fig. 2a), Ux,i, for an extended period of time. The partial relaxation of the elastomer is identified by the decrease in Ux,i after attaining the peak. This relaxation continues to take place over a time, tr ≈ 5 s, which is of the same order as the macroscopic relaxation time of the elastomer, trelax = 11.7 s.34 Eventually Ux,i reaches a plateau, and is confirmed by the fact that the QD grid does not translate significantly from its local position (see Fig. 1d and Video S2, ESI†). The edge of the ice starts to crossover the grid at around t = 270.0 s, and once the crossover is complete, the elastomer relaxes fully i.e. the QD grid restores back approximately to the reference configuration with only a slight offset from the reference axis, as shown at t = 322.8 s. The slight offset could be due to the permanent set, which leads to a negligible residual strain in the elastomer after the adhesion test.
We observe a small air pocket developing at the interface at t = 198.8 s (region enveloped by the green line in Fig. 1d) where only some of the QDs come into focus. The formation of the air pocket is due to the release of dissolved gases during the freezing of water, which is statistical in nature, and can occur anywhere in the bulk or at the interface.40 Nevertheless, the presence of an air pocket is found to have negligible effect in the present experiments with respect to τice. As V increases (see Fig. 1e), the maximum deformation of the elastomer, 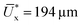 (see Fig. 2d), at t = 4.2 s increases significantly compared to V = 0.01 mm s−1. This explains the reason for the increase in τice with V. As the rate at which the external force applied on the ice increases, the elastomer deformation before slip is higher leading to an increase in adhesion strength. However, the qualitative behaviour of the elastomer i.e. global translation of the QD grid reaching maximum displacement followed by partial relaxation (at t = 15.5 and 25.0 s in Fig. 1e) is similar in both the cases. Here again, we observe that the partial relaxation proceeds over a time, tr ≈ 5 s (see Fig. 2e). However, in this case, we observe pulsations reminiscing of stick-slip behavior; a consequence of higher shear rate.41 The amplitude, A ≈ 10 μm, and the frequency, f ≈ 0.1 Hz, correlates well with the relaxation time of the elastomer i.e. f ∼ 1/trelax. This is in line with the observations reported in the previous works for polymer melts—rather than elastomers.41 However, polymer melts are also viscoelastic, and therefore we believe that their behavior in the slip regime can be used to explain the behavior of our elastomer. Finally, as ice crossover is complete, the QD grid returns back to the reference configuration with only a slight offset at t = 41.1 s.
(see Fig. 2d), at t = 4.2 s increases significantly compared to V = 0.01 mm s−1. This explains the reason for the increase in τice with V. As the rate at which the external force applied on the ice increases, the elastomer deformation before slip is higher leading to an increase in adhesion strength. However, the qualitative behaviour of the elastomer i.e. global translation of the QD grid reaching maximum displacement followed by partial relaxation (at t = 15.5 and 25.0 s in Fig. 1e) is similar in both the cases. Here again, we observe that the partial relaxation proceeds over a time, tr ≈ 5 s (see Fig. 2e). However, in this case, we observe pulsations reminiscing of stick-slip behavior; a consequence of higher shear rate.41 The amplitude, A ≈ 10 μm, and the frequency, f ≈ 0.1 Hz, correlates well with the relaxation time of the elastomer i.e. f ∼ 1/trelax. This is in line with the observations reported in the previous works for polymer melts—rather than elastomers.41 However, polymer melts are also viscoelastic, and therefore we believe that their behavior in the slip regime can be used to explain the behavior of our elastomer. Finally, as ice crossover is complete, the QD grid returns back to the reference configuration with only a slight offset at t = 41.1 s.
Using the digital image correlation method, we estimate the in-plane deformation of the elastomer during the adhesion test at every time step (see Section S3, ESI†).42,43 We calculate the shear stress from a 2nd order Ogden model, τOgden, at any given time, t. Despite the inherent complexities involved in the experiment, a good qualitative match is obtained between τmacro and τOgden (see Fig. 2b and d). Further, the shear stress magnitude reduces after attaining the peak (τice) in our experiments, which indicates that ice already in motion is easier to remove compared to ice at rest. This result is intuitive as the kinetic friction coefficient on any surface is expected to be less than static friction coefficient. Owing to the difficulties involved in tracking QDs at V = 0.1 mm s−1 affecting accuracy, we do not estimate τOgden beyond t = 3.99 s. Experiments with V > 0.1 mm s−1 were not successful due to the limitation of the imaging system.34,35 We also remark here that the alternative method of depositing fluorescent beads44,45 is inferior to our approach as the beads are significantly less bright than QDs during ice adhesion tests, which results in poor image quality. Further, the intrusive effect of QDs is remarkably low as the thickness of each QD <30 nm.36
Mechanism and dynamics of ice removal
The physical reason for the increase in τice with the shear velocity, V, is due to the higher elastomer deformation and higher corresponding force before slip as elucidated with the help of the cTFM experiments. Going beyond this, we seek to obtain a more general relationship quantifying the dependence between τice and V. Intuitively, the slip of ice on an elastomer can be considered analogous to the kinetic friction problem of elastomers sliding on smooth solids. Owing to the complexities involved in the phenomenon, several theories are proposed to explain the observed behavior.46 It has been shown that friction on elastomers is not due to the bulk viscoelastic dissipation, a fact supported by the increase in shear stress with the modulus of the elastomer to start the sliding motion.6,31 Rather, stochastic processes i.e. the cyclic adsorption and desorption of elastomer chains at the interface control the frictional behavior as proposed by Schallamach47 and later refined by Chernyak and Leonov.48 According to these theories, the adhesion of the elastomer with the solid is governed by the van der Waals interactions. When an elastomer slides on a smooth solid, the active load-bearing elastomer chains at the interface stretch, detach, relax, and re-attach to the solid in a cyclic process. Ice stick-slipping on an elastomer is an interesting parallelism for this. In the Chernyak and Leonov model, the tension in each load bearing chain, S, increases monotonically with the shear velocity as S ∼ Vt. Therefore, the frictional force increases with V. The number of active load bearing chains is given by, N = N0tb [tb + td]−1. Here, N0 is the total polymer chains within the ice–elastomer interfacial area, tb is the average bound time of a chain with ice, and td is the average lifetime of the chain in the detached state. The energy required for the adhesive link of the chain to break-off from ice is of the form J = J0 − CS. Here J0 is the break-off energy when V = 0, and C is a constant. Thus, the probability of adhesive failure of a link at any time, t, increases with V, and consequently tb (thereby N) reduces while td remains constant as it is related to the detached state of the chain. The net frictional shear stress is therefore given by the product of the frictional force per unit area and the number of active load bearing chains,48| τfriction = [aG×{VB×(1 − exp(−1/VB))−exp(−1/VB)}][m + 1 − exp(−1/VB)]−1 | (1) |
Here, G is the shear modulus of the elastomer, a is the cotangent of the ultimate angle of a chain at adhesive break-off with respect to the initial position i.e. a = cotψ, B = tb/(aδ), δ is the molecular roughness, and m = td/t0b, where t0b = tb when V = 0. The parameters a, and m are independent of elastomer surface temperature, T, while B and G vary.48 For an incompressible isotropic material, we can estimate the shear modulus as G = E/3 where E is the Young's modulus.49 We measured the Young's modulus of the material using an indentation technique (see Section S4, ESI†) at different elastomer surface temperature, T (Fig. 3a). Interestingly, we found a non-monotonic variation of E with T as opposed to the widely accepted linear relation E ∝ T. This suggests that the elastomer does not behave as an “ideal rubber” and therefore both internal energy and entropic elasticity effects are important.
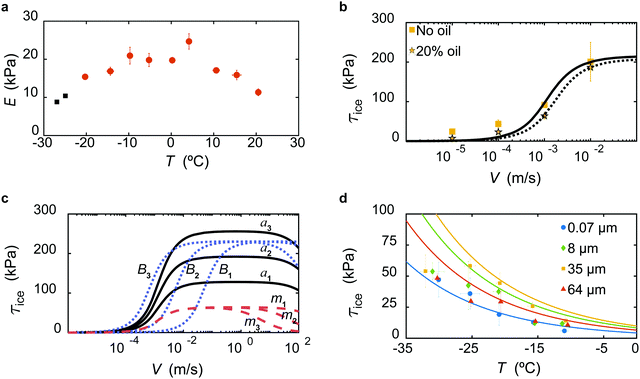 | ||
| Fig. 3 Effect of temperature and shear velocity on ice adhesion in shear mode test. (a) Non-monotonic behaviour of Young's modulus of the elastomer, E, with surface temperature, T. (b) Variation of τice with shear velocity, V, at an elastomer (without and with 20 wt% Silicon oil) surface temperature, T = −20 °C, and thickness, h = 35 μm. The solid and dashed black curves indicate the best fit of Chernyak and Leonov adhesive friction model (eqn (1)) to the experimental data without and with oil, respectively. (c) Variation of τice with shear velocity for different Chernyak and Leonov parameters for arbitrarily selected values of a, B, and m. When only a increases (a1 < a2 < a3), the peak value of τice increases but the velocity at which the peak is obtained remains constant (black solid lines). When only B increases (B1 < B2 < B3), the curve shifts to the left (blue dashed lines) but the peak value of τice remains the same. When only m increases (m1 < m2 < m3), the plateau width after attaining the peak value of τice reduces (red dashed lines). (d) Variation of τice with elastomer surface temperature, T, at V = 0.1 mm s−1. The solid curves indicates the Williams–Landel–Ferry transformation to the experimental data for different elastomer thickness, h. Error bars represent standard deviation for ne ≥ 3 independent experiments in (a, b and d). The black data points in (a) represent individual data points. | ||
The variation of τice with V for h = 35 μm, at T = −20 °C is shown in Fig. 3b. Assuming τfriction = τice with G = 5.13 kPa at T = −20 °C, we obtain the parameters through non-linear curve fitting, a = 83.83, B = 241 s m−1, and m = 2.3 × 10−8, all of which seem quite reasonable.48 We remark here that the viscous retardation in the chains is neglected in our study; due consideration of this phenomenon would result in 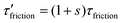 . Here, s represents the ratio of viscous retardation time of the chain with the average bound time in the rest state, t0b. Since s ≤ m ≤ 1,48 we have
. Here, s represents the ratio of viscous retardation time of the chain with the average bound time in the rest state, t0b. Since s ≤ m ≤ 1,48 we have 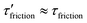 in our case as m ≪ 1. However, as s → 1, i.e. when the viscoelastic effects of each polymer chain are significant, the retardation effects can become significant.
in our case as m ≪ 1. However, as s → 1, i.e. when the viscoelastic effects of each polymer chain are significant, the retardation effects can become significant.
The parameter m correlates with the width of the plateau; increasing m reduces the plateau width. Since a correlates with the maximum stretch of the elastomer chain at the instance of detaching, relatively mobile chains will have lower magnitude of a (see Fig. 3c). Reducing the parameter B (1/B represents a molecular velocity scale) merely shifts the curve to right. Finally, τice ∝ G as described in previous works.6,7 Although, controlling the parameters a, m, and B, is challenging experimentally, the insight their variation provides is valuable. The shear modulus, G, we can easily modify and observe the trend of τice with V. The infusion of oil into the elastomer reduces the cross-linking density (thereby reducing shear modulus, G),6 which leads to a reduction of τice. As an example, with all the experimental conditions being the same as in Fig. 3b, we show that infusing the polymer network with 20% silicone oil leads to a reduction in τice (dashed line in Fig. 3b) with a = 117.7, B = 159.9 s m−1, and m = 1.4 × 10−7. The modified shear modulus when oil is infused is estimated as (1 − ω)5/3G = 3.54 kPa where ω corresponds to the oil weight fraction in the polymer network.7 This indicates that the shear modulus (reduced by 30% in comparison to no oil case) has a dominant effect on τice compared to the interfacial chain mobility (a increased by 40% in comparison to the no oil case). This is also supported from the mathematical form of τfriction (eqn (1)). The areal density of active load bearing chains N ∝G,7 and therefore we conclude that the areal density of chains has a dominant effect than the interfacial mobility of chains. Finally, the curve shifts to the right since B reduced while m increased which is also a desired consequence from oil addition as the plateau width reduces.
We then investigate the effect of elastomer surface temperature, T, on τice at V = 0.1 mm s−1, for h = 35 μm (see Fig. 3d) where τice decreases with T. Employing an analogy from the variation of elastomer friction with temperature, we use the classic empirical Williams–Landel–Ferry (WLF) transformation to explain these results.50,51 The transformation indicates that the temperature dependence of mechanical processes on elastomers can be estimated using a single empirical function. Accordingly, we have log(τice/τref) = [−Y(T − Tref)][Z + T − Tref]−1 where τref = τice at Tref = 253 K, and Y = 30 and Z = 900 K are empirical constants obtained from the data. The solid curves in Fig. 3d represents the estimate from WLF transformation which matches reasonably well with the experimental data for different elastomer thickness, h (discussed next in detail).
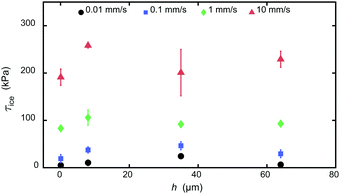
To understand the effect of elastomer thickness, h, we performed experiments by varying it over three orders of magnitude (see Section S2, ESI†). In Fig. 4, we observe that τice is practically independent of h. As h is varied from 0.07 to 64 μm at different shear velocities, V, and elastomer temperature, T = −20 °C, τice remains practically constant. While we do observe a minor variation in τice for V ≤ 0.1 mm s−1, the dependency is not as strong as compared to V and therefore can be neglected. This behavior has its origin in the presence of interfacial slip, and that only the adhesive links of the chains near the ice–elastomer interface (not in the much larger elastomer volume of thickness, h) are expected to play a role on the value of τice. This is also reinforced by the fact that the friction model parameters a, m, and B for all the elastomer thicknesses does not vary significantly as shown in Fig. S5 and Table S1 (ESI†).
Mixed and normal mode tests
To explore the effect of mode of testing, we also conducted macroscopic experiments in mixed (shear and normal), and pure normal modes. The ice removal mechanism in both the modes is due to interfacial fracture as ice clearly de-bonds from the elastomer (see Fig. S1b, ESI†). The elastomer develops instabilities at the interface with a characteristic wavelength in the order equal to the thickness of the film, h.11,12Fig. 5a shows the variation of ice adhesion strength (τice, σice in mixed mode) with V for h = 35 μm at T = −20 °C. The magnitude of τice in mixed mode is lower in comparison to shear mode due to the presence of significant normal stresses. Clearly, the trend in mixed mode is similar to the shear mode although the mechanisms are different. Previous studies reported τice ∼ 1/l where l is the height at which the force pin contacts the ice (see Fig. S1b, ESI†) at the critical shear velocity, where interfacial fracture is observed.11 Therefore, we propose that the relation τice ∼ 1/l holds across the range of shear velocities in the mixed mode when all the other experimental conditions remain the same. This leads to the relation τice,m ∼ (ls/lm)τice,s where the subscripts m and s indicate mixed and shear mode tests. From experiments, we have ls ≈ 0.5 mm, and lm = 6.1 mm obtaining τice,m ∼ 0.1τice,s. The black curve in Fig. 5a represents τice,m = 0.45τice,s where τice,s = τfriction (using eqn (1)) with the model parameters a, B, and m being the same as in Fig. 3b (no oil case). The pre-factor of τice,s varies slightly in the experiments but is of the same order of the ratio ls/lm and more importantly, τice,m and τice,s are directly proportional at all values of V. This remarkably simple proposition also works well for different elastomer thicknesses, h (see Fig. S6, ESI†). By definition, the parameters a, B, and m should not vary in the mixed mode test. We conjecture that the presence of elastic instabilities in the mixed mode test would reduce the number of active load bearing chains, N, as compared to the shear mode test, which leads to a reduction of τice. Fig. 5b shows the variation of ice adhesion strength in the normal mode test, σice, with V for h = 35 μm at T = −20 °C. In this case, V represents the pull up velocity of the force gauge. σice increases with V in a similar fashion as in shear and mixed mode tests. However, the error is significantly higher (see also Fig. S7, ESI†) making it difficult to determine a clear dependency with V. We attribute this behavior to the partial cohesive failure of the elastomer during the adhesion test (see Fig. S8, ESI†).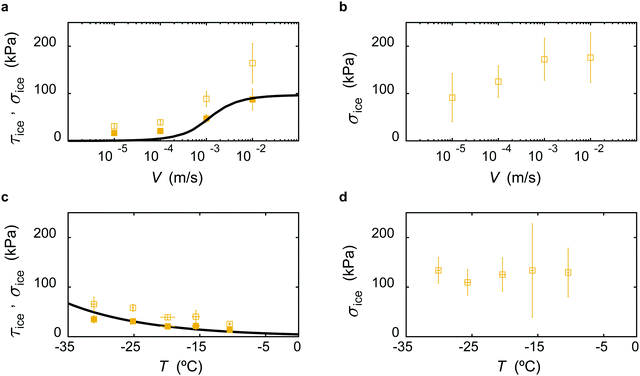 | ||
| Fig. 5 Effect of mode of ice adhesion test. (a and b) Variation of τice (filled) and σice (unfilled) with shear velocity, V, at surface temperature, T = −20 °C, and elastomer thickness, h = 35 μm in mixed and normal mode tests, respectively. The black solid curve in (a) indicates 0.45τice,s where τice,s = τfriction (using eqn (1)) is the ice adhesion strength in the shear mode when all the other experimental conditions are the same. (c and d) Variation of τice (filled) and σice (unfilled) with T, at V = 0.1 mm s−1, and h = 35 μm in mixed and normal mode tests, respectively. The black solid curve in (c) indicates the Williams–Landel–Ferry transformation. Error bars represent standard deviation for ne ≥ 3 independent experiments. | ||
Fig. 5c and d show the variation of ice adhesion strength (τice, σice in mixed mode and σice in normal mode) with T at V = 0.1 mm s−1. Again, using WLF transformation in the mixed mode, we can estimate the temperature dependence of τice with T (see Fig. 5c and Fig. S9, ESI†). σice in the normal mode remains constant in the entire temperature domain for a given h. Further, the magnitude of σice in the normal mode (see Fig. 5d) is much higher than that in the mixed mode. Again, the error is significantly high to predict any conclusive trend (see also Fig. S10, ESI†).
Conclusion
In summary, we show that the velocity at which the force is imposed on ice during ice removal, is an important factor significantly affecting the ice adhesion strength on elastomers. By employing cTFM, we quantified the transient non-uniform elastic deformation fields of the elastomer and related it to the applied external shear stress. The maximum deformation increases significantly with shear velocity, and consequently τice increases with V. Further, we observe pulsations in the slip regime at high velocity, which agrees well with the reported observations in the literature. The capability to visualize the deformation of the elastomer at high resolution is expected to be useful in studies exemplified by bio-fouling control, viscoelastic adhesives, contact mechanics, and soft robotics.Author contributions
T. M. S. and D. P. designed research; K. R. and J. G., performed research and analyzed the data; all the authors contributed in writing the paper.Conflicts of interest
D. P. is participating in Scrona, an ETH spin-off, which is developing the electrohydyodynamic NanoDrip-printing technology towards commercialization. The remaining authors declare no competing interests.Acknowledgements
We thank J. Vidic and P. Feusi for assistance in experimental setup construction. We thank Raoul Hopf for letting us use the femto-tool and having scientific discussions. Partial support by the European Research Council under Advanced Grant 669908 (INTICE) is acknowledged.References
- D. Huang, Y. Huang, Y. Xiao, X. Yang, H. Lin, G. Feng, X. Zhu and X. Zhang, Acta Biomater., 2019, 97, 74–92 CrossRef CAS PubMed.
- R. S. Lakes, Viscoelastic Solids, CRC Press, 2017, pp. 1–476 Search PubMed.
- C. M. Tringides, N. Vachicouras, I. de Lázaro, H. Wang, A. Trouillet, B. R. Seo, A. Elosegui-Artola, F. Fallegger, Y. Shin, C. Casiraghi, K. Kostarelos, S. P. Lacour and D. J. Mooney, Nat. Nanotechnol., 2021, 16, 1019–1029 CrossRef CAS PubMed.
- S. I. Rich, R. J. Wood and C. Majidi, Nat. Electron., 2018, 1, 102–112 CrossRef.
- M. Cianchetti, C. Laschi, A. Menciassi and P. Dario, Nat. Rev. Mater., 2018, 3, 143–153 CrossRef.
- K. Golovin, S. P. R. Kobaku, D. H. Lee, E. T. DiLoreto, J. M. Mabry and A. Tuteja, Sci. Adv., 2016, 2, e1501496 CrossRef PubMed.
- K. Golovin and A. Tuteja, Sci. Adv., 2017, 3, e1701617 CrossRef PubMed.
- K. Golovin, A. Dhyani, M. D. Thouless and A. Tuteja, Science, 2019, 364, 371–375 CrossRef CAS PubMed.
- D. L. Beemer, W. Wang and A. K. Kota, J. Mater. Chem. A, 2016, 4, 18253–18258 RSC.
- M. J. Kreder, J. Alvarenga, P. Kim and J. Aizenberg, Nat. Rev. Mater., 2016, 1, 15003 CrossRef CAS.
- M. K. Chaudhury and K. H. Kim, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 23, 175–183 CrossRef CAS PubMed.
- J. Y. Chung and M. K. Chaudhury, J. Adhes., 2005, 81, 1119–1145 CrossRef CAS.
- P. Irajizad, A. Al-Bayati, B. Eslami, T. Shafquat, M. Nazari, P. Jafari, V. Kashyap, A. Masoudi, D. Araya and H. Ghasemi, Mater. Horiz., 2019, 6, 758–766 RSC.
- A. J. Meuler, J. D. Smith, K. K. Varanasi, J. M. Mabry, G. H. McKinley and R. E. Cohen, ACS Appl. Mater. Interfaces, 2010, 2, 3100–3110 CrossRef CAS PubMed.
- P. Kim, T. S. Wong, J. Alvarenga, M. J. Kreder, W. E. Adorno-Martinez and J. Aizenberg, ACS Nano, 2012, 6, 6569–6577 CrossRef CAS PubMed.
- A. J. Meuler, G. H. McKinley and R. E. Cohen, ACS Nano, 2010, 4, 7048–7052 CrossRef CAS PubMed.
- A. Davis, Y. H. Yeong, A. Steele, I. S. Bayer and E. Loth, ACS Appl. Mater. Interfaces, 2014, 6, 9272–9279 CrossRef CAS PubMed.
- Y. H. Yeong, A. Milionis, E. Loth, J. Sokhey and A. Lambourne, Langmuir, 2015, 31, 13107–13116 CrossRef CAS PubMed.
- R. Dou, J. Chen, Y. Zhang, X. Wang, D. Cui, Y. Song, L. Jiang and J. Wang, ACS Appl. Mater. Interfaces, 2014, 6, 6998–7003 CrossRef CAS PubMed.
- J. Lv, Y. Song, L. Jiang and J. Wang, ACS Nano, 2014, 8, 3152–3169 CrossRef CAS PubMed.
- K. K. Varanasi, T. Deng, J. D. Smith, M. Hsu and N. Bhate, Appl. Phys. Lett., 2010, 97, 234102 CrossRef.
- S. B. Subramanyam, K. Rykaczewski and K. K. Varanasi, Langmuir, 2013, 29, 13414–13418 CrossRef CAS PubMed.
- L. Hauer, W. S. Y. Wong, A. Sharifi-Aghili, L. Kondic and D. Vollmer, Phys. Rev. E, 2021, 104, 044901 CrossRef CAS PubMed.
- X. Liu, H. Zhao, P. Li, Y. Pang, Y. Fan, B. Zhang, L. Wang, Y. Zheng and Z. Wang, ChemNanoMat, 2019, 5, 175–180 CrossRef CAS.
- Y. Hou, M. Yu, Y. Shang, P. Zhou, R. Song, X. Xu, X. Chen, Z. Wang and S. Yao, Phys. Rev. Lett., 2018, 120, 75902 CrossRef CAS PubMed.
- P. Papadopoulos, L. Mammen, X. Deng, D. Vollmer and H.-J. Butt, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3254–3258 CrossRef CAS PubMed.
- J. Liu, M. Kappl and H. J. Butt, Matter, 2020, 3, 981–983 CrossRef.
- Y. Hou, H. Butt and M. Kappl, Ice Adhes., 2020, 55–85 CAS.
- J. Chen, J. Liu, M. He, K. Li, D. Cui, Q. Zhang, X. Zeng, Y. Zhang, J. Wang and Y. Song, Appl. Phys. Lett., 2012, 101, 111603 CrossRef.
- J. Lv, X. Yao, Y. Zheng, J. Wang and L. Jiang, Adv. Mater., 2017, 29, 1703032 CrossRef PubMed.
- K. Vorvolakos and M. K. Chaudhury, Langmuir, 2003, 19, 6778–6787 CrossRef CAS.
- B. Z. Newby, M. K. Chaudhury and H. R. Brown, Science, 1995, 269, 1407–1409 CrossRef CAS PubMed.
- T. Maitra, S. Jung, M. E. Giger, V. Kandrical, T. Ruesch and D. Poulikakos, Adv. Mater. Interfaces, 2015, 2, 1500330 CrossRef.
- J. Gerber, T. Lendenmann, H. Eghlidi and T. M. Schutzius, Nat. Commun., 2019, 10, 4776 CrossRef PubMed.
- L. B. Boinovich, K. A. Emelyanenko and A. M. Emelyanenko, J. Colloid Interface Sci., 2022, 606, 556–566 CrossRef CAS PubMed.
- M. Bergert, T. Lendenmann, M. Zündel, A. E. Ehret, D. Panozzo, P. Richner, D. K. Kim, S. J. P. Kress, D. J. Norris, O. Sorkine-Hornung, E. Mazza, D. Poulikakos and A. Ferrari, Nat. Commun., 2016, 7, 12814 CrossRef CAS PubMed.
- P. Galliker, J. Schneider, H. Eghlidi, S. Kress, V. Sandoghdar and D. Poulikakos, Nat. Commun., 2012, 3, 1891 Search PubMed.
- S. J. P. Kress, P. Richner, S. V. Jayanti, P. Galliker, D. K. Kim, D. Poulikakos and D. J. Norris, Nano Lett., 2014, 14, 5827–5833 CrossRef CAS PubMed.
- T. Lendenmann, T. Schneider, J. Dumas, M. Tarini, C. Giampietro, A. Bajpai, W. Chen, J. Gerber, D. Poulikakos, A. Ferrari and D. Panozzo, Nano Lett., 2019, 19, 6742–6750 CrossRef CAS PubMed.
- A. E. Carte, Proc. Phys. Soc., London, 1961, 77, 757–768 CrossRef.
- V. Mhetar and L. A. Archer, Macromolecules, 1998, 31, 8617–8622 CrossRef CAS.
- R. Hopf, L. Bernardi, J. Menze, M. Zündel, E. Mazza and A. E. Ehret, J. Mech. Behav. Biomed. Mater., 2016, 60, 425–437 CrossRef CAS PubMed.
- B. Pan, K. Qian, H. Xie and A. Asundi, Meas. Sci. Technol., 2009, 20, 062001 CrossRef.
- R. W. Style, R. Boltyanskiy, Y. Che, J. S. Wettlaufer, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2013, 110, 066103 CrossRef PubMed.
- R. W. Style, Y. Che, S. J. Park, B. M. Weon, J. H. Je, C. Hyland, G. K. German, M. P. Power, L. A. Wilen, J. S. Wettlaufer and E. R. Dufresne, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12541–12544 CrossRef CAS PubMed.
- M. K. Chaudhury, K. Vorvolakos and D. Malotky, arXiv:1508.01452, 2015, 1–15.
- A. Schallamach, Wear, 1963, 6, 375–382 CrossRef.
- Y. B. Chernyak and A. I. Leonov, Wear, 1986, 108, 105–138 CrossRef CAS.
- M. H. Sadd, Elasticity: Theory, applications, and numerics, 3rd edn, 2014 Search PubMed.
- M. L. Williams, R. F. Landel and J. D. Ferry, J. Am. Chem. Soc., 1955, 77, 3701–3707 CrossRef CAS.
- W. Gnorich and K. A. Grosch, Rubber Chem. Technol., 1975, 48, 527–537 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1mh01993g |
| ‡ Equally contributing authors. |
| This journal is © The Royal Society of Chemistry 2022 |