Rationalizing energy level alignment by characterizing Lewis acid/base and ionic interactions at printable semiconductor/ionic liquid interfaces

Abstract

Charge transfer and energy conversion processes at semiconductor/electrolyte interfaces are controlled by local electric field distributions, which can be especially challenging to measure. Herein we leverage the low vapor pressure and vacuum compatibility of ionic liquid electrolytes to undertake a layer-by-layer, ultra-high vacuum deposition of a prototypical ionic liquid EMIM⁺ (1-ethyl-3-methylimidazolium) and TFSI⁻ (bis(trifluoromethylsulfonyl)-imide) on the surfaces of different electronic materials. We consider a case-by-case study between a standard metal (Au) and four printed electronic materials, where interfaces are characterized by a combination of X-ray and ultraviolet photoemission spectroscopies (XPS/UPS). For template-stripped gold surfaces, we observe through XPS a preferential orientation of the TFSI anion at the gold surface, enabling large electric fields (∼10⁸ eV m⁻¹) within the first two monolayers detected by a large surface vacuum level shift (0.7 eV) in UPS. Conversely, we observe a much more random orientation on four printable semiconductor surfaces: methyl ammonium lead triiodide (MAPbI₃), regioregular poly(3-hexylthiophene-2,5-diyl (P3HT)), sol–gel nickel oxide (NiO_x), and PbI_x-capped PbS quantum dots. For the semiconductors considered, the ionization energy (IE) of the ionic liquid at 3 ML coverage is highly substrate dependent, indicating that underlying chemical reactions are dominating interface level alignment (electronic equilibration) prior to reaching bulk electronic structure. This indicates there is no universal rule for energy level alignment, but that relative strengths of Lewis acid/base sites and ion-molecular interactions should be considered. Specifically, for P3HT, interactions are found to be relatively weak and occurring through the π-bonding structure in the thiophene ring. Alternatively, for NiO_x, PbS/PbI_x quantum dots, and MAPbI₃, our XPS data suggest a combination of ionic bonding and Lewis acid/base reactions between the semiconductor and IL, with MAPbI₃ being the most reactive surface. Collectively, our results point towards new directions in interface engineering, where strategically chosen ionic liquid-based anions and cations can be used to preferentially passivate and/or titrate surface defects of heterogeneous surfaces while simultaneously providing highly localized electric fields. These opportunities are expected to be translatable to opto-electronic and electrochemical devices, including energy conversion and storage and biosensing applications.

---

New concepts

Interfacial energy level alignment arises from a combination of free charge redistribution (band bending), intermolecular forces, and chemical/electrochemical interactions. These effects have been difficult to characterize in (photo)electrochemical-based energy conversion and energy storage (fuel forming) devices because many (printable) semiconductors exhibit chemical, electronic, and physical structure heterogeneity at the atomic-to-nanoscale. Using vacuum deposition of monolayers of an ionic liquid (IL), we demonstrate the ability to probe reactivity of four prototypical printable semiconductor materials. The IL has unique chemical signatures in photoelectron spectroscopy, independent of the underlying substrates, and thus provide critical insights into interfacial interactions governed by the underlying surface Lewis acid and base sites and the propensity for Stern layer formation. The characterization of these quasi-ordered electrical double layers suggests that there will be much more compact structures at IL/printable electronic materials that are dominated by atomic-level interactions and propagate through multiple monolayers of the IL; in other words, initial layers template the interfacial electronic structure. The molecular nature of IL electrolytes and the number of possible interactions with semiconductor surfaces indicate an exciting new area of materials science, where insights in structure–property relationships could give way to enhanced control over charge transfer and energy conversion processes at interfaces.

1. Introduction

In opto-electronic and (photo)electrochemical platforms and devices, electric field distributions across interfaces that are in electronic equilibrium can control the rate of charge transfer reactions that determine the efficiencies of both electrical and electrochemical energy conversion processes. Thus, understanding the underlying mechanisms by which electronic equilibrium is achieved has been critical for improving the performance of these devices for the last 20+ years.^1,2 Yet to date, there have been no monolayer-level characterizations of energetic alignment at electrolyte/printable semiconductor material interfaces, despite the growing technological interests in energy conversion/storage and biosensing applications and the community's strong interest in semiconductor/semiconductor and semiconductor/metal interfaces.^3–5 Understanding the detailed mechanisms of energy level alignment at these interfaces, and the differences between classes of printable semiconductors, should provide ultimately for control of electric field distributions at complex semiconductor/IL heterojunctions and design guidelines to control rates of charge transfer and efficiencies of energy conversion processes.

Herein we consider the interface electrostatics and surface potential evolution of four familiar printable semiconductor thin film materials: (regio-regular poly(3-hexylthiophene-2,5-diyl)), P3HT; methyl ammonium lead triiodide, MAPbI₃; sol–gel-derived nickel oxide, NiO_x; and PbI_x capped PbS quantum dots). Each material is interfaced with the same prototypical ionic liquid electrolyte (EMIM⁺ (1-ethyl-3-methylimidazolium) and TFSI⁻ (bis(trifluoromethylsulfonyl)-imide) – EMIM⁺/TFSI⁻). This electrolyte was chosen as it is well-characterized and that thin film ionic liquids (ILs) provide some of the same advantages of solvent-based electrolytes, with significantly lower experimental complexity and enhanced technological relevance due to lower vapor pressures and vacuum compatibility.^6–12 For example, we have recently shown that ILs can enable the formation of full dark and photoelectrochemical platforms on printable semiconductors that provide for operando characterization of the energetics and densities of states for defects that ultimately limit energy conversion efficiencies in these materials and their long term stabilities.¹³

Using a layer-by-layer ultra-high vacuum deposition approach to add ILs to the opto-electronic material surfaces, coupled with X-ray and ultraviolet photoelectron spectroscopy characterizations (XPS/UPS), we are able to track the electronic and chemical structure of semiconductor/IL interfaces at monolayer coverages. Such spectroscopic approaches enable unique insights into significant electrostatic interactions and/or charge transfer reactions, facilitated by the strong ion–ion and/or Lewis acid/base interactions of ILs that evolve from different chemical compositions of surfaces. For context, we compare and contrast the energetics and structural order at IL/semiconductor interfaces with previous reports of Au (111) surfaces and structural organization of ILs at nanometer length scales.^6,7,10,14,15 The observed organization of IL cations and anions is very much reminiscent of a subset of electrical double layers associated with compact electrode/electrolyte interfaces termed “Stern layers”, which exhibit significant long-range order arising from strong intermolecular and surface interactions and can create electrostatic potential drops exceeding 10⁸ V cm⁻¹.^3,4,16,17 Yet the gold surface lacks Lewis acid and base sites commonly associated with semiconductor mid-gap states, and by comparison, interactions are relatively weak and confined to within the first 1–2 ML. This system serves as a model reference point to compare the extent of reactivity in each of the four semiconductor/electrolyte interfaces.

Using the complementary shifts in valence band energies, local surface vacuum levels (work functions), and core level binding energies (BE), we demonstrate semiconductor film-dependent electrolyte ionization potentials and local binding energy shifts for IL core levels that reflect underlying unique interfacial microenvironments. Interestingly, each of the different interfaces gives rise to electric fields on the order of 10⁷ eV m⁻¹ but via different pathways to achieve electronic equilibrium. We observe no correlation in Fermi level pinning associated with the different interfaces despite different pre-contact work functions and energetics of valence states, indicating chemical interactions rather than free carrier redistributions are dominant. Rather, energy level alignment and chemical analysis strongly indicates fractional coordination of the electrolyte with underlying defects and or local environments, which we posit provides a generalizable spectroscopic approach to interface interrogation in semiconductor/IL systems. Specifically, we observe a combination of lower binding energy (higher electron density) on both the anion and cation of the IL for Lewis acid/base surfaces (NiO_x, PbI_x-capped PbS, and MAPbI₃), indicating both anionic and cationic species are coordinating with the surface defect states. Alternatively, P3HT, a low dielectric material, shows the reverse trend, with higher binding energies of the anion and cation, representative of a non-polarizing surface.

Collectively, our results demonstrate the need for detailed structure–property understanding to guide molecular design of both the semiconductor surface and the contacting electrolyte, ultimately helping to control rates of interfacial electron transfer and (especially for semiconductors such as perovskites) interfacial and device stabilities. Additionally, strategically chosen ILs, which may exhibit Lewis and/or Brønsted acid–base chemistries, can provide a tactical approach to “titrate” underlying surface defects. One result could be the passivation of unwanted defects. A second result is this could provide much needed guidance in structure–property relationships for synthesis and processing approaches of printable semiconductor materials. We anticipate that this type of measurement science will underpin the development of new device architectures, ranging from alternative charge harvesting contacts in photovoltaics to new contacts and gates in transistor-based sensing platforms.

2. Results and discussion

2.1 Overview of energy level alignment at disordered semiconductor interfaces

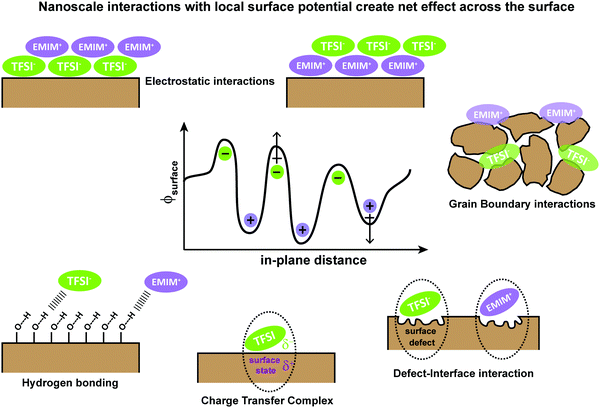
To understand the underlying interactions with IL/semiconductor interfaces, we first collectively consider theories associated with energy level alignment and the role of charge transfer for semiconductor/electrolyte interfaces and metal/semiconductor interfaces. As motivation to this emerging area of interface science, in Fig. 1, we provide an overview of possible interfacial interactions, ranging from Coulombic shielding, evolution of new contact-ion pairs, H-bonding, changes in local anion or cation orientations, and/or redox chemistries. We emphasize that multiple physical and chemical interactions can drive energy level alignment between the IL and the metal or semiconductor, which must be measured and cannot be predicted.

Fig. 1 Schematic of possible nanoscale interactions that can contribute to localized changes in the surface potential (ϕ_surface) at semiconductor/ionic liquid interfaces using EMIM⁺ (1-ethyl-3-methylimidazolium) and TFSI⁻ (bis(trifluoromethylsulfonyl)-imide) ionic liquid as a model.

Briefly, in semiconductor/electrolyte interfaces, large electric field gradients have been connected to nanometer-scale solvent and ion packing in electrical double layers, which have been described as simple Helmholtz planes, diffuse Gouy–Chapman double layers, and compact Stern-like layers.^3–5 Defect states in the semiconductor substrate, near the conduction or valence band edges, or “mid-gap”, can be critically important in these charge transfer processes which lead to electronic equilibrium, but are often hard to characterize due to their ultra-low concentrations.

For metal/semiconductor (organic or inorganic or hybrid materials) interfaces,¹⁸ achieving electronic equilibrium has been described by multiple complementary mechanisms, summarized by Ishii, Sugiyanma, Ito, and Seki¹⁹ and Kahn and Cahen,²⁰ among others. Examples include the formation of image charges in metals, partial-to-full charge transfer to molecular semiconductors, surface rearrangements and charge redistribution, chemical reactions, formation of discrete interface states, and formation of and rearrangement of permanent dipoles, similar to interactions shown in Fig. 1. An important point of each model for these complex interfaces is that, for disordered materials (which can include chemical, electronic, and/or physical disorder), multiple mechanisms to achieve electronic equilibrium can co-exist. This underlying heterogeneity ultimately can lead to local differences in charge injection/extraction barriers and large electric field drops at interfaces that can control opto-electrical device performance.

The unifying component of both semiconductor/metal and semiconductor/electrolyte theories is that due to lower conductivity, semiconductors will redistribute near-surface charge to Fermi level pin to either the Fermi level of the metal or the electrochemical potential of the electrolyte, thus yielding a depletion (or accumulation) region due to band bending.^21–23 Yet, this simplified view overlooks the underlying chemical reactions at molecular length scales which are contributing to charge rearrangement. In printable electronic materials especially, which tend to exhibit surface-correlated defects and/or disorder, energy level alignment at semiconductor/electrolyte interfaces is considerably less well-understood, especially for materials which do not exhibit band-like transport. Most critically, localized electric fields can affect the energetics and chemical/electrochemical stabilities of the semiconductor and/or lead to significant changes in charge transfer processes.^{3–5,20,22,23} The key results from these studies demonstrate that, in addition to Coulombic forces, additional contributions from dipoles, dispersive and inductive processes, charge transfer, and/or hydrogen-bonding can be assessed to understand mechanism(s) of energy level alignment at semiconductor/electrolyte interfaces.^24–26

2.2. Ionic liquid/metal interface

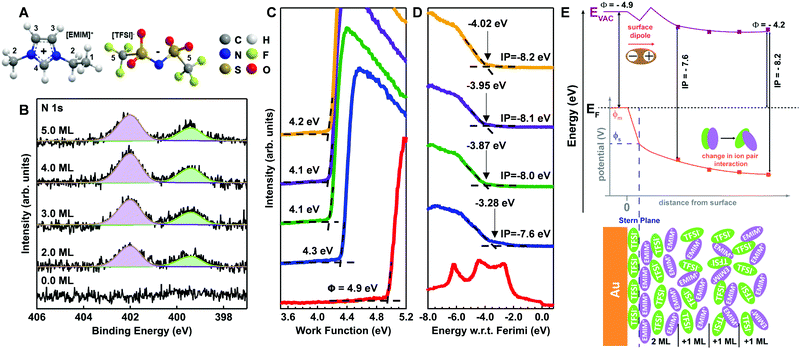
We next turn our attention to a less-disordered system (template stripped gold) as a scaffold on which to build the semiconductor/electrolyte case studies. To date, existing understanding of metal/IL interfaces has been guided by characterizations of ILs on well-ordered single crystal substrates such as Au (111), Au (110), Ag (111), and Ni (111) under ultra-high vacuum (UHV).^27–30 On the Au (111) surface with alkyl-imidazolium cations, such as the ethyl-methyl imidazolium (EMIM⁺) used herein, there is an established in-plane order resulting in alternating anion/cation pairs for anions such as BF₄⁻ and TFSI⁻.^6,7 The extent of this ordering, as a function of IL coverage from single-to-multiple monolayers, is very much controlled by the strength of substrate interactions in the first layer, including length of the alkyl tails in the imidazolium cation, the size and charge density of the anion, the type of structures formed at the interface, and the extrapolation of those structures to the bulk.^6–9,14,15

Fig. 2A shows the molecular structures of the EMIM⁺ and TFSI⁻ (including numeric labelling of the carbon atoms) and Fig. 2B provides the N 1s core level XPS spectra for vacuum deposited EMIM⁺/TFSI⁻ on template-stripped Au surfaces as a function of estimated surface coverage (in monolayers, ML). The other core level spectra for the IL (C 1s, S 2p, F 1s, and O 1s) are provided in Fig. S1 of the ESI.† Fig. S2 (ESI†) gives the respective intensity changes in the Au 4f core levels, the change in Au 4f_7/2 intensity with IL deposition time, and extrapolation to thickness calculations, summarized in Table S1 (ESI†). We note that in Fig. S2 (ESI†), we observe true layer-by-layer growth of the ionic liquid, as determined by exponential decay of the Au 4f_7/2 signal with increasing EMIM⁺/TFSI⁻ coverage, with a coefficient of determination (R²) of >97%. Such conformal coverage is consistent with previous experimental and modelling studies which concluded that TFSI⁻ anions adsorb strongly/preferentially to the Au (111) surface.^6,27,31

Fig. 2 (A) Schematics of cation EMIM⁺⁼ (1-ethyl-3-methylimidazolium) and TFSI⁻ (bis(trifluoromethylsulfonyl)imide) structures. (B) Detailed X-ray photoelectron spectroscopy of N 1s core levels, with fits of EMIM⁺ (purple) and TFSI (green), on Au (111) surface. Ultraviolet photoelectron spectroscopy of (C) secondary edge used to estimate work function and (D) valence region of EMIM⁺/TFSI⁻ on Au (111) as a function of coverage. (E) Energy band diagram (top) and physical packing of IL (bottom) giving rise to 0.6 eV vacuum level shift within the first two monolayers (ML) of coverage.

In Fig. 2B, the cation imidazolium peak is observed at 402.0 eV (purple) and the bistriflimide anion peak (green) is shown at 399.4 eV, with a peak separation of 2.6 eV.^32,33 For all depositions, we observe no binding energy (BE) shifts and a consistent full width half maximum (FWHM) for each peak of 1.2 eV, indicating little change to interionic interactions with increasing surface coverage of the IL.

Fig. 2C and D respectively show the UPS-derived low kinetic energy (LKE) edge and near-valence (high kinetic energy/low BE) region as a function of IL coverage. In Fig. 2C, the data is presented in arbitrary counts as a function of energy for easy benchmarking of the work function, which is the energetic difference between the Fermi level and the local vacuum level. Fig. 2D shows the valence region with respect to the Fermi energy to avoid ambiguity. Table S2 (ESI†) provides average and standard deviation estimations of work function and ionization energy as a function of coverage, summarized in the band diagram inset in Fig. 2E.

In Fig. 2C, for even the lowest coverages (2 ML) of EMIM⁺/TFSI⁻ on Au, we see significant shifts in the LKE edge, consistent with a change in WF of ca. −0.6 eV. Using an approximation of 0.7 nm per monolayer,⁶ this is the equivalent of an electric field gradient of 4 × 10⁸ eV m⁻¹ across the interface, yielding a surface potential (shown in Fig. 2E, Φ_S) that is significantly shifted downward from the initial (pre-contact) metal potential (Φ_M). From the extensive body of work on dipolar self-assembled monolayers on both metals and metal oxides,^34–43 it is understood that these work function changes result from a linear combination of dipolar fields. We can conclude that the initial IL layer on Au must be at least somewhat oriented with the highest positive charge density component (EMIM⁺) dominating at the vacuum interface away from the Au/IL heterojunction, as shown in Fig. 2E (bottom). Such a result is consistent with recent electrochemical/STM and molecular dynamics modelling studies, which suggest that the initial EMIM⁺/TFSI⁻ monolayer is well ordered over short length scales but that more than one orientation of the anion and cation are possible.^{6,7,9,10,14,15} An important caveat is that our surface is template-stripped gold, which has been reported to undergo surface reconstructions due to monolayer adsorption and/or aging^44–46 and is not a true single crystal.

In Fig. 2C, we note that increasing the monolayer coverage of the IL introduces smaller vacuum level shifts and a shift in ionization potential as a function of distance from the surface (from 7.6 eV to 8.2 eV).⁴⁷ Of particular note, the 2 ML IL film has a larger uncertainty in the ionization potential, as there are small contributions from the Au valence band. However, we can see a clear edge that is retained with increasing deposition of the ionic liquid. Such a dramatic change in ionization energy without changes to core levels in Fig. 2B indicates the ionization potential is extremely sensitive to ordering at the surface, possibly due to defects and subsequent screening by additional layers. This is a promising result for connections with semiconductor/IL behaviours described below. Lastly, we note that a change in ionization potential with coverage cannot be formally classified as band bending in the ionic liquid, as we see no change in the XPS core levels of anion or cation (Fig. 2B). However, we note that XPS has typically only parts per thousand sensitivity and typically probes deeper into the interface region (∼5 nm) than UPS (∼2 nm), which could limit sensitivity to core level changes with changes in molecular packing.

2.3 Case studies of IL on P3HT, NiO_x, PbI_x-capped PbS QDs, and MAPbI₃ films

Following a similar protocol for Au (111), we vacuum deposited ∼3 monolayers of the IL on four different printable semiconductors: P3HT, NiO_x, PbI_x-capped PbS quantum dot film, and MAPbI₃. The 3 ML thickness was chosen as it allows for sufficient coverage and ample signal of the IL while also providing for characterization of the changes in the near-surface composition of the underlying semiconductor materials. Additionally, the collective set of materials provide useful case studies for qualifying the effects described in Fig. 1. Briefly, NiO_x, PbI_x-capped PbS quantum dots, and MAPbl₃ films are all expected to have stronger interactions with the IL, relative to P3HT and even Au, due to a combination of both ionic and coordination effects. In particular, PbI_x/PbS and MAPbI₃ surfaces exhibit Lewis acid and base sites and possible surface defects such as under-coordinated species, vacancies or interstitials.^47–50 These sites will have undergone equilibration with the vacuum interface, but are expected to react with the ionic liquid when the interface is changed to semiconductor/electrolyte. Below we summarize our findings in terms of the energy level alignment (Fig. 3), as derived from UPS, the qualitative shifts in core levels for the ionic liquids due to underlying coordination chemistry (Fig. 4) using XPS, and a schematic representation of each of the coordination effects (Fig. 5), ranking each of the surfaces in terms of reactivity relative to one another.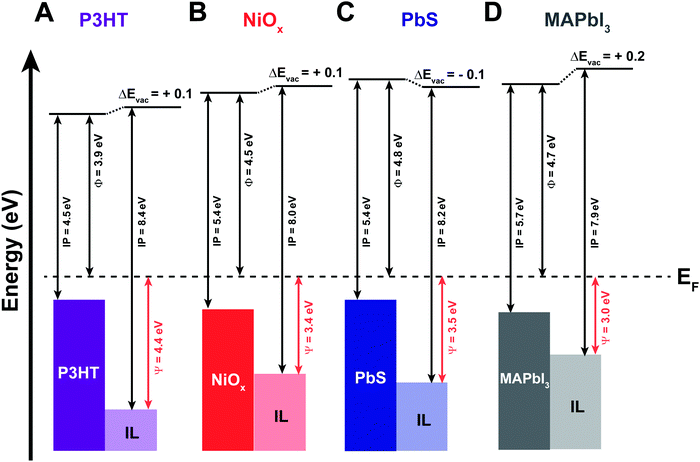

Fig. 3 Energy band diagrams for the four semiconductor/IL interfaces based on UPS data provided in Fig. S4–S7 (ESI†), showing work function (Φ), ionization potential (IP), and vacuum level shifts (ΔE_vac) for as cast (A) P3HT; (B) NiO_x; (C) PbS quantum dot; and (D) MAPbI₃ semiconductor films and after 3 monolayers of EMIM⁺/TFSI⁻. The Ψ value shows the energetic difference between the onset of observable states and the Fermi level (E_F) for the four interfaces.

Fig. 4 X-ray photoelectron spectroscopy of the (A) N 1s and (B) C 1s core levels with 3 ML of EMIM⁺/TFSI⁻ on each of the four substrates. (C) Correlation of the binding energy positions for the C2 carbon on the imidazolium cation, relative to the nitrogen signal and (D) correlation of the binding energy positions for the C5 carbon on the anion imide, relative to the nitrogen signal on each of the substrates. Insets show the labelled carbons for EMIM⁺ and TFSI⁻ referenced in the text.

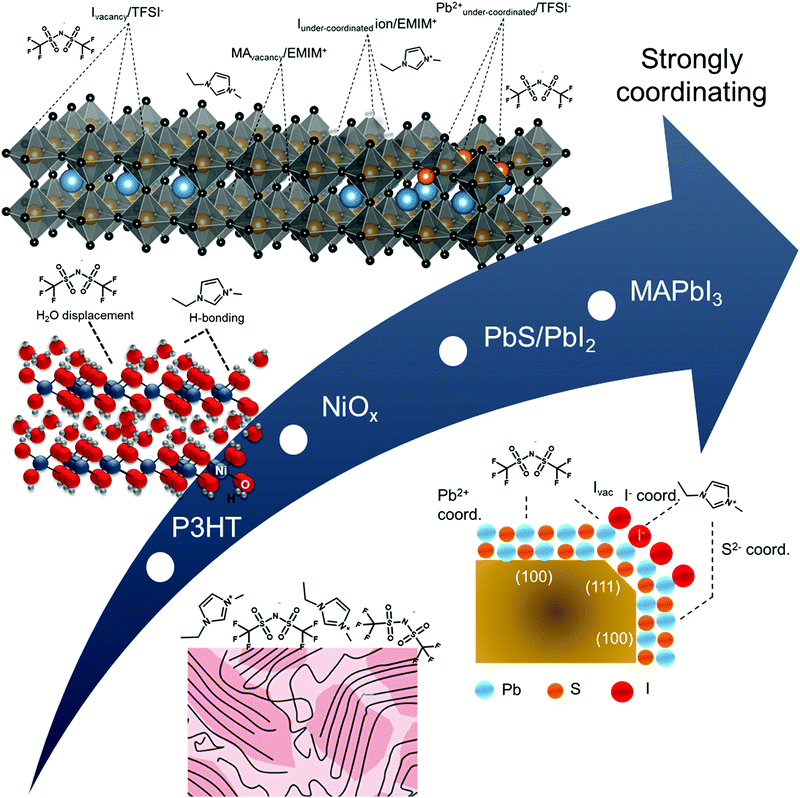Fig. 5 Schematic representation of hypothesized near-surface interactions between ionic liquid and semiconductors from bottom to top: P3HT, NiO_x, PbI_x-capped PbS quantum dots, and MAPbI₃.

2.3.1. Energy level alignment of IL on P3HT, NiO_x, PbI_x-capped PbS QD, and MAPbI₃ films. Fig. 3 shows the energy band diagrams for the four interfaces; Fig. S3–S6 (ESI†) provide the UPS spectra used to construct each of the diagrams. We observe small shifts in local work function via shifts in the surface vacuum level for each of the thin film semiconductors, with work function increases for P3HT (+0.1 eV), NiO_x (+0.1 eV) and MAPbI₃ (+0.2 eV) and a decrease for PbI_x/PbS (−0.1 eV). These smaller shifts versus Au/IL heterojunctions suggest a less organized IL layer on these materials. Specifically, well-ordered electrostatic interactions shown in Fig. 1 would yield very large dipoles and result in work function shifts on the order of 1 eV. However, each of these vacuum level shifts overserved in Fig. 3 still correspond to electric field compensations on the order of 0.1 eV/3 ML, the equivalent of 10⁷ eV m⁻¹. Such electric fields, while smaller than the metal/IL interface, can still provide substantial Coulombic screening (especially between high surface free energy materials such as perovskites and ILs) and large local driving forces to accelerate (or decelerate) charge transfer at grain boundaries and at charge harvesting/injecting electrode heterojunctions.

The collective comparison between surfaces can provide for insights into interfacial phenomena and types of interactions postulated in Fig. 1. We first address the possibility of semiconductor band bending. As previously stated, band bending arises from the redistribution of free carriers to achieve energy level alignment, observed by the same eV shifts (as a function of distance from the interface) in core levels, valence, and conduction bands.⁵⁰ If band bending alone was responsible for interface equilibration, one would expect varying degrees of band bending given the differences in work function for the semiconductors in Fig. 3 (as deposited), relative to the electrolyte potential on Au (111) of ∼4.2 eV: PbI_x-capped PbS quantum dots, Φ = 4.8 eV; MAPbI₃, Φ = 4.7 eV; NiO_x, Φ = 4.5 eV; P3HT, Φ = 3.9 eV. In other words, one would expect “bands” in P3HT to bend upward (towards vacuum) to have a Fermi level pinned at 4.2 eV (Fig. S7, ESI†). If this were realized core levels in carbon and sulfur atoms in P3HT should shift to lower BE (moved closer to the Fermi level). Likewise, given the initial Fermi levels for the other semiconductors, we would expect bands to bend downward to pin to 4.2 eV to varying degrees, with core levels in the reporter atoms are expected to shift to higher BE.

The XPS data for these complex heterojunctions, however, do not suggest band bending is occurring, which, for these materials, are unlikely for a number of reasons. First, we note that the ionization potentials of the IL in Fig. 3 are large, in excess of 8.0 eV, and substrate dependent.⁴⁷ For example, the ionization energy of the EMIM⁺/TFSI⁻ was found to be 8.4 eV on P3HT (0.2 eV greater than Au) but is 0.2–0.3 eV lower than on gold, MAPbI₃ and NiO_x (7.9 and 8.0 eV, respectively). This is a clear indication that the underlying coordination (ionic or covalent) of the IL with the semiconductor is relatively strong and propagates at the molecular scale through subsequent layers of IL to compensate for charge exchange, even if disordered. Second, there is a significant difference in the energy separation between the Fermi level and the onset observed density of states of the IL (Ψ = E_Fermi − IE), depending on the underlying semiconductor. For P3HT, this energy difference is 4.4 eV but as small as 3.0 eV for MAPbI₃, again confirming large changes to relative electrochemical potential of the IL due to underlying substrate. We hypothesize that these reactions are dominated by the strength of Lewis acid and base sites on the relative semiconductors. Thus, we would expect only weak interactions for P3HT, moderate interactions for NiO_x (predominantly Lewis base sites due to surface hydroxyls), and stronger interactions with PbI_x-capped PbS QD and MAPbI₃ films, which exhibit a combination of anion/cation vacancies (ionic interactions) and Lewis acid/base sites (sites with potentially strong coordination with Lewis base/acid moieties within the IL).

2.3.2 Probing ionic interactions and coordination reactions between IL and P3HT, NiO_x, PbI_x-capped PbS QD, and MAPbI₃ films. Before considering the chemical interactions, it is important to note that to date, a number of computational efforts have suggested that IL anions and cations may exhibit non-integer charge transfer.^51–53 Of particular note, a detailed XPS, NMR and theoretical study by Cremer et al. demonstrated that the binding energy environment of the IL is strongly correlated to the coordination strength between anion and cation. For a group of ILs of varying anions, all with the same cation (1-methyl-3-octylimidazolium), they generally concluded that for smaller and more basic/coordinating anions, more charge can be transferred from the anion to the cation, resulting in a decrease in positive charge on the ring and lower binding energies.¹⁷ Thus, changes in the relative binding energies of the EMIM⁺ and TFSI⁻ core levels in XPS can be used to qualitatively identify different reactions with surface species.

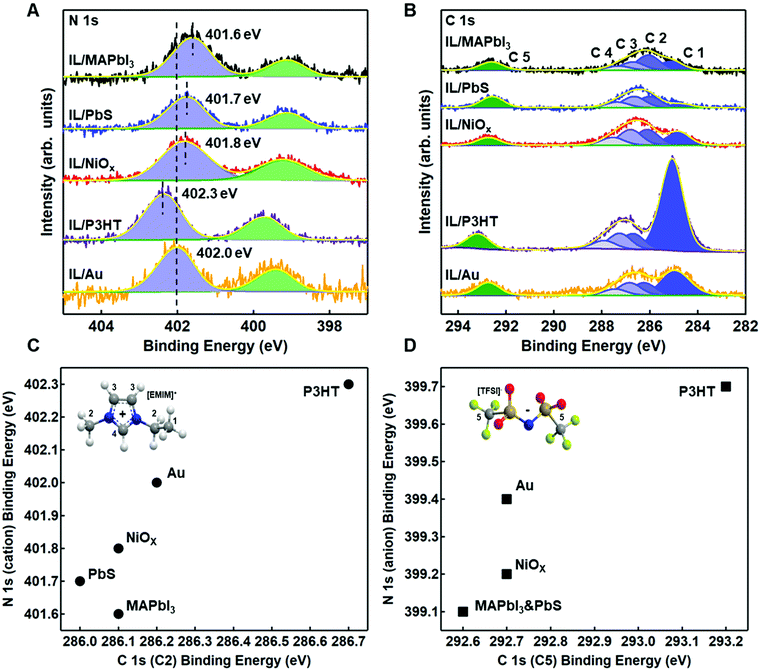
Fig. 4A and B show the relative shifts in the reporter atoms in the N 1s and C 1s spectra for the IL on each of the four substrates, benchmarked against gold/IL interface for comparison. Tables S3 and S4 (ESI†) provide the relative BEs, FWHM, and area ratios for N 1s and C 1s, respectively. Fig. S8–S12 (ESI†) provide changes in select core levels for all four substrates, before and after deposition. Fig. S13–S15 (ESI†) show additional core levels of the ionic liquid (S 2p, F 1s, O 1s), with fitting parameters provided in Tables S5–S7 (ESI†).

In Fig. 4A and B, it is readily observable that shifts are both positive and negative and do not necessarily track equivalently for anion and cation with respect to gold (Fig. 4C and D), a strong indicator of strong intermolecular forces (i.e. Lewis acid/base interactions) at the semiconductor/IL interface. For P3HT, there is a shift towards higher BE (+0.3 eV) of the N 1s core levels for both the imide anion peak (399.7 eV) and the imidazolium cation peak (402.3 eV) in Fig. 4A, relative to gold. Higher binding energy shifts are indicative of a decrease in local electron density on the ionic liquid, consistent with higher ionization potential in Fig. 3. We note that unlike gold, which can polarize through image charge effects, P3HT has a low dielectric constant and is relatively non-polarizable. Thus, the cation appears to have a near +1 charge, while the decrease in electron density of the TFSI⁻ (higher binding energy) we propose arises from weak complexation of TFSI⁻ with the highest electron density aromatic regions of the P3HT chain. We speculate that this interaction is most likely an induced dipole effect, but not necessarily charge transfer. We rationalize this conclusion from an electrochemical perspective. In solution electrochemistry, with standard ion concentrations of 0.1 M or higher, P3HT will undergo an ion intercalation mechanism to support the formation of polarons, resulting from a conformational relaxation of charges and the S 2p core levels shift closer to the Fermi level (negative binding energy shift).^50,54 Here, we observe the opposite, in that the S 2p is shifted +0.1 eV, further from Fermi (Fig. S9, ESI†), which indicates the IL is inducing a small dipole into the aromatic ring. Charging can be ruled out as the S 2p shifts to a different degree from the C 1s and N 1s. We note that in Fig. 5, we have included a longer length scale representation of regio-regular P3HT, which includes a combination of semi-crystalline and amorphous domains which have different oxidation potentials.^55,56 While XPS does not have the sensitivity to resolve interactions between these two domains, the collective changes to higher binding energy of the IL could also indicate different degrees of interaction with these two regions.

By comparison, in Fig. 4A and B, the complex Lewis acid/base surfaces – MAPbI₃, PbI_x/PbS QD, and NiO_x – all show the anion and cation peaks shift towards lower BE, relative to gold. These shifts generally suggest an increase in electron density on both the anion and cation of the IL, consistent with a lowering of the ionization energies (Fig. 3). NiO_x has a weaker coordination effect than the other two materials, as evident in Fig. 4C and D, with smaller shifts in the anion and cation of the IL. We hypothesize that the strongly coordinating I⁻ is dominating the interactions, and we discuss possible interactions on a case by case basis.

NiO_x was chosen as a case study as it has variable Lewis-acid/base properties depending on the local environment and near-surface composition.^57–59 In particular, as-deposited sol–gel NiO_x has been shown to be highly basic. In Fig. S10 (ESI†), we observe both hydroxyl (531.0 eV) and physisorbed water (532.2 eV) contributions to the O 1s core levels of the NiO_x surface, which act as Lewis base sites.^57–60 For the TFSI⁻ anion, relative to the IL on gold and P3HT, we see a decrease in binding energy of the imide nitrogen and a corresponding low binding energy of the sulfonyl (S 2p_3/2 ∼168.7 eV, Table S5, ESI†). Likewise, in Fig. S10 (ESI†), we also observe a displacement of water with the sulfonyl group (532.4 eV) in the O 1s spectra. These three binding energy shifts are all indicative of the anion coordinating with surface. Alternatively, we observe no shift in the carbon of the trifluoromethane group (C5), although we do see a broadening of the F 1s FWHM (Table S6, ESI†), suggesting multiple environments are contributing. To rationalize the decrease in binding energy of the EMIM⁺, consistent with a decrease in overall charge, we suggest coordination with hydroxyl groups on the surface. However, we note that hydrogen-bonding through the most acidic proton on the EMIM⁺ cation is also feasible (C4 in inset of Fig. 4C) through these sites, although this effect is harder to discern. We do observe a decrease in both the imidazolium nitrogen and the carbon attached to the most acidic hydrogen, consistent with an increase in electron density expected from partial proton loss.

For our third case study, we consider the PbS quantum dot surface. The surface structure of colloidal PbS nanocrystals has been studied extensively in the last decade, as the surface chemistry has a strong bearing on functionality. Zherebetskyy et al. demonstrated that oleic acid (the precursor in the dots considered herein) is vital to stabilizing the PbS (111) facets through formation of OH⁻ but is more weakly bound to the (100) nonpolar facets.⁶¹ Counterion exchange with I⁻ containing salts results in a substitution of the carboxylate by the iodide, with improved stability when the supporting cation exhibits non-Brønsted acid properties (ex. tetrabutyl ammonium). For the PbI_x-capped PbS quantum dot films, there is clear evidence of a change in local environment, with a −0.3 eV corresponding shift of the S 2p_3/2 core level associated with the quantum dot (Fig. S11A, ESI†) and a +0.3 eV C 1s peak of adventitious carbon from 284.4 eV to 284.7 eV. This could suggest an ionic interaction between cation to support exposed S sites on the dot surface (i.e. ionic interaction) but could also indicate a coordination effect of the cation with I⁻. Additionally, we observe that the sulfonyl peak of the anion has the lowest binding energy on the QD dot film (168.6 eV for S 2p_3/2, Fig. S13 and Table S5, ESI†), relative to all other surfaces studied, which is indicative of strong interactions between the surface and the IL anion. We hypothesize that this could be due to a combination of I⁻ replacement and/or coordination with underlying Pb sites (perhaps on the (100 plane), but we had insufficient sensitivity in the analysis to definitively support this hypothesis. Future work will focus on more detailed studies using various ligand exchanges.

As the last case study, the MAPbI₃ surface provides a highly defective surface that can undergo a number of reactions. For example, MAPbI₃ has been predicted theoretically to have a number of iodide vacancies (and mobile I⁻) and possible Pb–Pb dimers (under-coordinated Pb) that could yield preferential complexes with the IL components at grain boundaries.^62–64 A recent review from Chen et al. has indicated the following reaction possibilities: (i) ionic interactions between cations and undercoordinated I ions and/or anions interacting with I⁻ vacancies; (ii) undercoordinated I ions and/or Pb–I antisites reactng with Lewis acids; and (iii) undercoordinated Pb²⁺ ions and/or metallic Pb clusters complexing with Lewis bases.⁶⁵ These possible interactions are summarized in Fig. 5.

In Fig. S12A (ESI†), we observe a large BE shift of −0.7 eV in the I 3d_5/2 core level, suggesting that EMIM⁺ may be increasing coordination and/or stabilizing iodide species via charge transfer interactions to provide additional electron density. However, we also observe a negative binding energy shift of the imidazolium nitrogens (−0.4 eV), which is inconsistent with an ionic interaction and rather, suggests the cation is acting as a Lewis acid (or Brønsted acid through most acidic proton and/or hydrogen bonding).⁶⁶ Cremer et al. have speculated that fractional charge transfer could occur between I⁻ and EMIM⁺via Sigma-type molecular orbitals of the imidiazolium ring and the p-orbitals of the anion, thus leading to strong hydrogen bonding for I⁻ over TFSI⁻ in IL films.¹⁷ Additionally, in Fig. 4D, we observe a significant difference in the C 1s and N 1s BEs of the anion, relative to Au, thus indicating the possibility of coordination of the anion with an under-coordinated lead cation on the surface.⁶⁷

3. Conclusions

We have shown here that photoemission spectroscopies, coupled with monolayer growth of vacuum compatible ionic liquids, can reveal molecular-level details about the organization of electrical double layers with the surfaces of printable semiconductor that will be relevant in their use as energy conversion and energy storage technology platforms. Core-level binding energy shifts, changes in work function, and ionization energy have revealed that Lewis acid–base sites and changes to organization of the Stern layer in the IL, rather than simple band bending in the semiconductor, dominate to maintain electroneutrality. These interactions dictate the electric field strength seen by both majority and minority charge carriers, and defects at these surfaces, which ultimately will control efficiencies of charge harvesting, rates of electrochemical reactions leading to fuel formation, and rates of undesired reactions that limit stability of the energy conversion platform. The combined use of these new measurement science approaches, coupled with systematic variation of IL composition matched to the surface chemistry of the underlying semiconductor, will underpin the optimization of these technologies. Overall, our results demonstrate that there is not a “universal” model for semiconductor/ionic liquid energy level alignment. Rather, the molecular nature of ionic liquids is especially useful to probing reactivity of surface defect states on semiconductors, although a significant amount of both experimental and theoretical effort is needed to quantify strengths of interactions. We anticipate more detailed, case-by-case investigations into energy level alignments using a broader class of materials, will provide further insights into strengths of interactions. In particular, we emphasize that both intermolecular and interionic interactions should be considered.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based upon work supported by the US. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0020208, including support for LDH and ELR. MDK and JWH would like to acknowledge the Office of Naval Research for support under award number N00014-20-1-2440 for the preparation of NiO_x and MAPbI₃ films. The Office of Naval Research (ONR) is gratefully acknowledged for financial support by AEC, DP and JEB for synthesis and preparation of PbS/PbI_x films. AEC acknowledges the National Research Council (NRC) Postdoctoral Research Associateship program.

References

1. S. Y. Kim, S. J. Cho, S. E. Byeon, X. He and H. J. Yoon, Adv. Energy Mater., 2020, 10, 1–21.
2. H. Ma, H.-L. Yip, F. Huang and A. K.-Y. Jen, Adv. Funct. Mater., 2010, 20, 1371–1388.
3. D. M. Kolb, Angew. Chemie., Int. Ed., 2001, 40, 1162–1181.
4. D. L. Rath and D. M. Kolb, Surf. Sci., 1981, 109, 641–647.
5. G. J. Hansen and W. N. Hansen, J. Electroanal. Chem., 1983, 150, 193–200.
6. Y. Wang, Y. Sun, Y. Dong and G. Tian, J. Phys. Chem. B, 2021, 125, 3677–3689.
7. A. Ruzanov, M. Lembinen, P. Jakovits, S. N. Srirama, I. V. Voroshylova, M. N. D. S. Cordeiro, C. M. Pereira, J. Rossmeisl and V. B. Ivaništšev, Phys. Chem. Chem. Phys., 2018, 20, 10275–10285.
8. J. W. Yan, Z. Q. Tian and B. W. Mao, Curr. Opin. Electrochem., 2017, 4, 105–111.
9. L. A. Jurado and R. M. Espinosa-Marzal, Sci. Rep., 2017, 7, 1–12.
10. A. Elbourne, S. McDonald, K. Voïchovsky, F. Endres, G. G. Warr and R. Atkin, ACS Nano, 2015, 9, 7608–7620.
11. M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679.
12. J. M. Black, D. Walters, A. Labuda, G. Feng, P. C. Hillesheim, S. Dai, P. T. Cummings, S. V. Kalinin, R. Proksch and N. Balke, Nano Lett., 2013, 13, 5954–5960.
13. M. De Keersmaecker, N. R. Armstrong and E. L. Ratcliff, Energy Environ. Sci., 2021, 14, 4840–4846.
14. J. Le, Ma, Q. Meng and J. Fan, Phys. Chem. Chem. Phys., 2018, 20, 8054–8063.
15. B. Haddad, A. Kachroudi, G. Turky, E. H. Belarbi, A. Lamouri, D. Villemin, M. Rahmouni and A. Sylvestre, J. Mol. Liq., 2021, 324, 114674.
16. D. M. Kolb, J. Solid State Electrochem., 2011, 15, 1391–1399.
17. T. Cremer, C. Kolbeck, K. R. J. Lovelock, N. Paape, R. Wölfel, P. S. Schulz, P. Wasserscheid, H. Weber, J. Thar, B. Kirchner, F. Maier and H. P. Steinrück, Chem. – Eur. J., 2010, 16, 9018–9033.
18. G. Margaritondo, Solid-State Electron., 1983, 26, 499–513.
19. H. Ishii, K. Sugiyama, E. Ito and K. Seki, Adv. Mater., 1999, 11, 605–625.
20. D. Cahen and A. Kahn, Adv. Mater., 2003, 15, 271–277.
21. A. J. Nozik and R. Memming, J. Phys. Chem., 1996, 100, 13061–13078.
22. M. K. Brennaman, R. J. Dillon, L. Alibabaei, M. K. Gish, C. J. Dares, D. L. Ashford, R. L. House, G. J. Meyer, J. M. Papanikolas and T. J. Meyer, J. Am. Chem. Soc., 2016, 138, 13085–13102.
23. M. T. Spitler, M. A. Modestino, T. G. Deutsch, C. X. Xiang, J. R. Durrant, D. V. Esposito, S. Haussener, S. Maldonado, I. D. Sharp, B. A. Parkinson, D. S. Ginley, F. A. Houle, T. Hannappel, N. R. Neale, D. G. Nocera and P. C. McIntyre, Sustainble Energy Fuels, 2020, 4, 985–995.
24. W. Schmickler and E. Santos, in Interfacial Electrochemistry, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 117–131.
25. T. Mayer, M. Lebedev, R. Hunger and W. Jaegermann, Appl. Surf. Sci., 2005, 252, 31–42.
26. J. A. Turner, J. Chem. Educ., 1983, 60, 327–329.
27. M. Meusel, M. Lexow, A. Gezmis, A. Bayer, F. Maier and H. P. Steinrück, Langmuir, 2020, 36, 13670–13681.
28. M. Lexow, T. Talwar, B. S. J. Heller, B. May, R. G. Bhuin, F. Maier and H. P. Steinrück, Phys. Chem. Chem. Phys., 2018, 20, 12929–12938.
29. R. Foulston, S. Gangopadhyay, C. Chiutu, P. Moriarty and R. G. Jones, Phys. Chem. Chem. Phys., 2012, 14, 6054–6066.
30. R. Souda, J. Phys. Chem. B, 2008, 112, 15349–15354.
31. S. Liu, J. Peng, L. Chen, P. Sebastián, J. M. Feliu, J. Yan and B. Mao, Electrochim. Acta, 2019, 309, 11–17.
32. T. Cremer, M. Killian, J. M. Gottfried, N. Paape, P. Wasserscheid, F. Maier and H. P. Steinrück, Chem. Phys. Chem., 2008, 9, 2185–2190.
33. O. Höfft, S. Bahr, M. Himmerlich, S. Krischok, J. A. Schaefer and V. Kempter, Langmuir, 2006, 22, 7120–7123.
34. S. R. Cowan, P. Schulz, A. J. Giordano, A. Garcia, B. A. Macleod, S. R. Marder, A. Kahn, D. S. Ginley, E. L. Ratcliff and D. C. Olson, Adv. Funct. Mater., 2014, 24, 4671–4680.
35. I. Lange, S. Reiter, M. Pätzel, A. Zykov, A. Nefedov, J. Hildebrandt, S. Hecht, S. Kowarik, C. Wöll, G. Heimel and D. Neher, Adv. Funct. Mater., 2014, 24, 7014–7024.
36. B. A. MacLeod, N. E. Horwitz, E. L. Ratcliff, J. L. Jenkins, N. R. Armstrong, A. J. Giordano, P. J. Hotchkiss, S. R. Marder, C. T. Campbell and D. S. Ginger, J. Phys. Chem. Lett., 2012, 3, 1202–1207.
37. H. Li, E. L. Ratcliff, A. K. Sigdel, A. J. Giordano, S. R. Marder, J. J. Berry and J. L. Brédas, Adv. Funct. Mater., 2014, 24, 3593–3603.
38. E. L. Ratcliff, A. Garcia, S. A. Paniagua, S. R. Cowan, A. J. Giordano, D. S. Ginley, S. R. Marder, J. J. Berry and D. C. Olson, Adv. Energy Mater., 2013, 3, 647–656.
39. D. M. Alloway, M. Hofmann, D. L. Smith, N. E. Gruhn, A. L. Graham, R. Colorado, V. H. Wysocki, T. R. Lee, P. A. Lee and N. R. Armstrong, J. Phys. Chem. B, 2003, 107, 11690–11699.
40. A. Asyuda, M. Gärtner, X. Wan, I. Burkhart, T. Saßmannshausen, A. Terfort and M. Zharnikov, J. Phys. Chem. C, 2020, 124, 8775–8785.
41. P. J. Hotchkiss, S. C. Jones, S. A. Paniagua, A. Sharma, B. Kippelen, N. R. Armstrong and S. R. Marder, Acc. Chem. Res., 2012, 45, 337–346.
42. J. Gantz, D. Placencia, A. Giordano, S. R. Marder and N. R. Armstrong, J. Phys. Chem. C, 2013, 117, 1205–1216.
43. R. Rousseau, V. De Renzi, R. Mazzarello, D. Marchetto, R. Biagi, S. Scandolo and U. Del Pennino, J. Phys. Chem. B, 2006, 110, 10862–10872.
44. N. Takeuchi, C. T. Chan and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 13899–13906.
45. P. Wagner, M. Hegner, H. J. Güntherodt and G. Semenza, Langmuir, 1995, 11, 3867–3875.
46. E. Torres and G. A. Dilabio, J. Phys. Chem. C, 2014, 118, 15624–15629.
47. I. Kuusik, M. Kook, R. Pärna and V. Kisand, ACS Omega, 2021, 6, 5255–5265.
48. M. P. Seah and W. A. Dench, Surf. Interface Anal., 1979, 1, 2.
49. Y. Zheng, A. J. Giordano, R. C. Shallcross, S. R. Fleming, S. Barlow, N. R. Armstrong, S. R. Marder and S. S. Saavedra, J. Phys. Chem. C, 2016, 120, 20040–20048.
50. R. C. Shallcross, T. Stubhan, E. L. Ratcliff, A. Kahn, C. J. Brabec and N. R. Armstrong, J. Phys. Chem. Lett., 2015, 6, 1303–1309.
51. E. J. Maginn, J. Phys.: Condens. Matter, 2009, 21, 1–17.
52. B. L. Bhargava and S. Balasubramanian, J. Chem. Phys., 2007, 127, 1–6.
53. T. I. Morrow and E. J. Maginn, J. Phys. Chem. B, 2002, 106, 12807–12813.
54. J. K. Harris, B. Neelamraju and E. L. Ratcliff, Chem. Mater., 2019, 31, 6870–6879.
55. J. K. Harris, B. Neelamraju and E. L. Ratcliff, Chem. Mater., 2019, 31, 6870–6879.
56. S. Hugger, R. Thomann, T. Heinzel and T. Thurn-Albrecht, Colloid Polym. Sci., 2004, 282, 932–938.
57. N. E. Widjonarko, E. L. Ratcliff, C. L. Perkins, A. K. Sigdel, A. Zakutayev, P. F. Ndione, D. T. Gillaspie, D. S. Ginley, D. C. Olson and J. J. Berry, Thin Solid Films, 2012, 520, 3813–3818.
58. E. L. Ratcliff, J. Meyer, K. X. Steirer, A. Garcia, J. J. Berry, D. S. Ginley, D. C. Olson, A. Kahn and N. R. Armstrong, Chem. Mater., 2011, 23, 4988–5000.
59. K. X. Steirer, R. E. Richards, A. K. Sigdel, A. Garcia, P. F. Ndione, S. Hammond, D. Baker, E. L. Ratcliff, C. Curtis, T. Furtak, D. S. Ginley, D. C. Olson, N. R. Armstrong and J. J. Berry, J. Mater. Chem. A, 2015, 3, 10949–10958.
60. C. C. Boyd, R. C. Shallcross, T. Moot, R. Kerner, L. Bertoluzzi, S. Kavadiya, C. Chosy, E. J. Wolf, J. Werner, A. James, C. De Paula, A. F. Palmstrom, Z. J. Yu, J. J. Berry, F. Stacey, Z. C. Holman, J. M. Luther, E. L. Ratcliff and N. R. Armstrong, Joule, 2020, 4, 1759–1775.
61. D. Zherebetskyy, M. Scheele, Y. Zhang, N. Bronstein, C. Thompson, D. Britt, M. Salmeron, P. Alivisatos and L.-W. Wang, Science, 2014, 344, 1380–1384.
62. J. M. Ball and A. Petrozza, Nat. Energy, 2016, 1, 1–13.
63. S. P. Dunfield, L. Bliss, F. Zhang, J. M. Luther, K. Zhu, M. F. A. M. van Hest, M. O. Reese and J. J. Berry, Adv. Energy Mater., 2020, 10, 1–35.
64. R. C. Shallcross, S. Olthof, K. Meerholz and N. R. Armstrong, ACS Appl. Mater. Interfaces, 2019, 11, 32500–32508.
65. B. Chen, P. N. Rudd, S. Yang, Y. Yuan and J. Huang, Chem. Soc. Rev., 2019, 48, 3842–3867.
66. V. Kempter and B. Kirchner, J. Mol. Struct., 2010, 972, 22–34.
67. E. J. Juarez-Perez, L. K. Ono, M. Maeda, Y. Jiang, Z. Hawash and Y. Qi, J. Mater. Chem. A, 2018, 6, 9604–9612.

---

Footnote

† Electronic supplementary information (ESI) available: Materials and methods, additional X-ray and ultraviolet photoelectron spectroscopy data and fitting. See DOI: 10.1039/d1mh01306h

---