Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oxidative addition or Werner coordination complex? Reactivity of β-diketiminate supported main group and first-row transition metal complexes towards ammonia†
Petra
Vasko
 * and
Cheuk W.
Lau
* and
Cheuk W.
Lau
Department of Chemistry, University of Helsinki, A. I. Virtasen aukio 1, P.O. Box 55, 00014 Helsinki, Finland. E-mail: petra.vasko@helsinki.fi
First published on 17th August 2022
Abstract
A series of neutral LM (L = [HC{(H3C)C(Dipp)N}2], Dipp = 2,6-iPr2C6H3, M = group 13: B–In, TM: Fe, Co, Ni, Cu) and L′M (L′ = [HC{(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2)(CCH3)(DippN)2}], M = group 14: C–Pb) compounds including a main group 13/14 and first-row transition metal complexes were studied computationally by density functional theory (DFT). The optimised complexes were assessed in terms of structural parameters and electronic structures to find trends and characteristics that could be used to predict their reactivity towards ammonia. In addition, the differences in oxidative addition and Werner coordination complex formation depending on the identity of the central element were investigated and the Werner complexes were evaluated by QTAIM and EDA-NOCV approaches. The computational results complement the earlier experimental studies and shed light on the feasibility of isolating novel main group Werner complexes or transition metal oxidative addition products.
CH2)(CCH3)(DippN)2}], M = group 14: C–Pb) compounds including a main group 13/14 and first-row transition metal complexes were studied computationally by density functional theory (DFT). The optimised complexes were assessed in terms of structural parameters and electronic structures to find trends and characteristics that could be used to predict their reactivity towards ammonia. In addition, the differences in oxidative addition and Werner coordination complex formation depending on the identity of the central element were investigated and the Werner complexes were evaluated by QTAIM and EDA-NOCV approaches. The computational results complement the earlier experimental studies and shed light on the feasibility of isolating novel main group Werner complexes or transition metal oxidative addition products.
Introduction
In the last few decades, the main group chemistry community has proven that p-block element containing species can achieve reactivity that was previously thought to be the sole domain of transition metal complexes.1,2 A recent example of this is the first main group compound to activate dinitrogen, published by Braunschweig and co-workers.3 Furthermore, in the realm of small molecule activation, main group compounds have shown excellent, and in some cases reversible, reactivity towards inert molecules such as H2,4,5 CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 and NH3.7 The preferred mode of reactivity for low-valent p-block species is oxidative addition. However, as this usually results in highly stable thermodynamic products, achieving reversibility through reductive elimination is in most cases impossible. One of the big challenges for main group chemists is, in fact, evaluating the structure and reactivity relationships between the complexes/catalysts and substrates to achieve efficient and applicable catalysis with high turnover numbers and frequencies.8
6 and NH3.7 The preferred mode of reactivity for low-valent p-block species is oxidative addition. However, as this usually results in highly stable thermodynamic products, achieving reversibility through reductive elimination is in most cases impossible. One of the big challenges for main group chemists is, in fact, evaluating the structure and reactivity relationships between the complexes/catalysts and substrates to achieve efficient and applicable catalysis with high turnover numbers and frequencies.8
In contrast to main group species, transition metal complexes are known for their performance in catalytic applications: the wide range of accessible oxidation states and energetically close frontier molecular orbitals ensure the reversibility of the oxidative addition–reductive elimination catalytic cycle. However, there are reactions that even transition metal complexes struggle with: the activation of ammonia to produce an oxidative addition product instead of a classical Werner coordination complex is a challenge. Thus far, only one complex has been observed to react with ammonia to produce an amido hydride product: Hartwig et al. isolated a RIr(H)NH2-complex (R = 1,5-bis(di-t-butylphosphino)pentan-3-yl) following a reaction of RIr(CH2CHCH3) with ammonia under ambient conditions.9
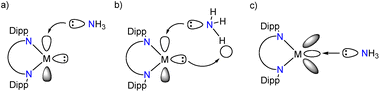
Due to these interesting differences in reactivity with ammonia, we set out to perform a series of computational analyses to investigate the characteristics of main group 13/14 compounds and first-row transition metal complexes stabilised by the ubiquitous β-diketiminate ligand (L, group 13 and TM) or its deprotonated derivative (L′, group 14) (Fig. 1). In addition, we attempted to clarify the nature of the metal–ammonia nitrogen bond in the calculated Werner coordination complexes by QTAIM and EDA-NOCV analyses.
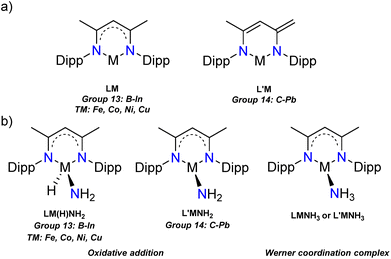 | ||
| Fig. 1 (a) The neutral complexes LM and L′M studied in this work, (b) two activation modes of the LM/L′M species towards ammonia (Dipp = 2,6-iPr2C6H3). | ||
Computational details
All DFT optimizations were performed using Gaussian16 Rev.C.01 programme10 with PBE1PBE hybrid exchange–correlation functional11–13 in combination with Def2-TZVP14,15 basis set. In addition, Grimme's empirical dispersion correction with Becke–Johnson damping (GD3BJ)16 and an ultrafine integration grid were applied. For In, Sn and Pb a pseudopotential (ECP) was used to model the core electrons. Full frequency calculations were performed to the optimised structures to ensure the identity of the stationary points on the potential energy surface (no imaginary frequencies). The Gaussian optimised structures were further used for QTAIM and EDA-NOCV analyses. QTAIM analyses were done using the programme AIMAll17 and EDA-NOCV18–20 calculations using ADF programme21 (PBE0/TZ2P, numerical quality good, no symmetry and no frozen core except ZORA22–24 for In, Sn and Pb). All optimisations were performed in the gas phase and the calculated energies are given in kJ mol−1.Results and discussion
Geometry optimisations and electronic structures
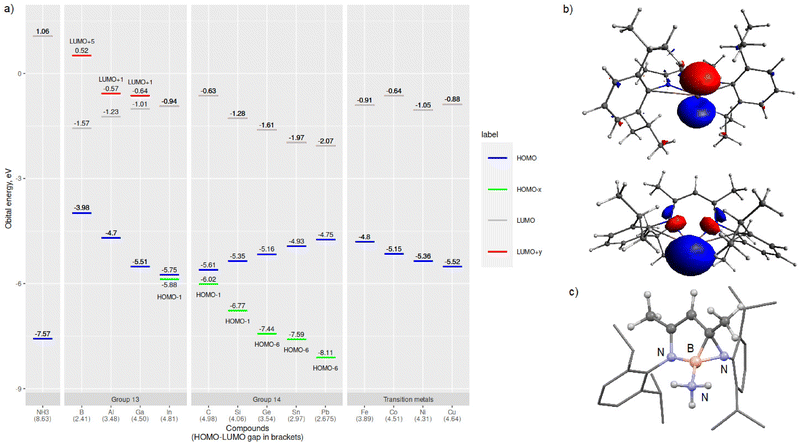
We began our investigations by optimising the LM (L = Nacnac or β-diketiminate, [HC{(H3C)C(Dipp)N}2], Dipp = 2,6-iPr2C6H3, M = group 13: B–In, and TM: Fe, Co, Ni, Cu) and L′M (L′ = [HC{(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2)(CCH3)(DippN)2}], M = group 14: C–Pb) (Fig. 1a) species and their ammonia reaction products, amido hydrides and Werner adducts (Fig. 1b), by density functional theory (DFT). We chose the Nacnac-framework as our supporting ligand because of its extensive experimental use and modest size to facilitate efficient computational resource usage. Moreover, a variety of Nacnac-ligands and their deprotonated derivatives have been shown to stabilise a wide range of both main group and first-row transition metal compounds in the past.25–27 In our study, the main group elements were treated to bear either +I (group 13) or +II (group 14) formal charge to ensure the overall neutral compounds. For the first-row transition metals, we decided to examine LM complexes where the formal charge of the metal is +I (M = Fe, Co, Ni, and Cu). This results in neutral paramagnetic Fe (multiplicity doublet), Co (multiplicity triplet) and Ni (multiplicity doublet) complexes, which may not be isolable experimentally but in our study provide interesting comparison to the main group species.25 The optimised LM and L′M geometries show, that, firstly, the calculated gas phase structures are in good agreement with the structurally characterised ones found in the Cambridge structural database (M = Al,28 Ga,29 In,30 Si,31,32 and Ge7,33 see ESI† for structural comparison). Secondly, the optimised geometries show expected trends in the bond parameters corresponding to the size of the element M: the N–M bond lengths increase going down the groups 13 and 14, and, as expected, there is slightly more variation in the N–M bonds for the group 14 and transition metal species (Table 1). The N–M–N angle decreases going down the groups 13 and 14, most likely due to the increasing lone pair s-character of the heavier analogues. The more acute bond angles also explain the long N–M bonds observed for the heavy group 13 and 14 compounds. However, the transition metal compound structures show less clear trends in the bonding; the M–N bond lengths are significantly shorter than the sum of covalent radii37 of the two elements and the N–M–N angle varies from 94.8° in Fe to 114.2° in the Cu complex. The observed transition metal structural features might be due to the assumed two-coordinate bonding mode in the LM/L′M complexes.
CH2)(CCH3)(DippN)2}], M = group 14: C–Pb) (Fig. 1a) species and their ammonia reaction products, amido hydrides and Werner adducts (Fig. 1b), by density functional theory (DFT). We chose the Nacnac-framework as our supporting ligand because of its extensive experimental use and modest size to facilitate efficient computational resource usage. Moreover, a variety of Nacnac-ligands and their deprotonated derivatives have been shown to stabilise a wide range of both main group and first-row transition metal compounds in the past.25–27 In our study, the main group elements were treated to bear either +I (group 13) or +II (group 14) formal charge to ensure the overall neutral compounds. For the first-row transition metals, we decided to examine LM complexes where the formal charge of the metal is +I (M = Fe, Co, Ni, and Cu). This results in neutral paramagnetic Fe (multiplicity doublet), Co (multiplicity triplet) and Ni (multiplicity doublet) complexes, which may not be isolable experimentally but in our study provide interesting comparison to the main group species.25 The optimised LM and L′M geometries show, that, firstly, the calculated gas phase structures are in good agreement with the structurally characterised ones found in the Cambridge structural database (M = Al,28 Ga,29 In,30 Si,31,32 and Ge7,33 see ESI† for structural comparison). Secondly, the optimised geometries show expected trends in the bond parameters corresponding to the size of the element M: the N–M bond lengths increase going down the groups 13 and 14, and, as expected, there is slightly more variation in the N–M bonds for the group 14 and transition metal species (Table 1). The N–M–N angle decreases going down the groups 13 and 14, most likely due to the increasing lone pair s-character of the heavier analogues. The more acute bond angles also explain the long N–M bonds observed for the heavy group 13 and 14 compounds. However, the transition metal compound structures show less clear trends in the bonding; the M–N bond lengths are significantly shorter than the sum of covalent radii37 of the two elements and the N–M–N angle varies from 94.8° in Fe to 114.2° in the Cu complex. The observed transition metal structural features might be due to the assumed two-coordinate bonding mode in the LM/L′M complexes.
| Compound | M–N (Å) | N–M–N (°) | M–N–C–C (°) | |
|---|---|---|---|---|
| LFe | 1.869 | 1.794 | 94.8 | 5.1 |
| LCo | 1.949 | 1.891 | 99.8 | −13.3 |
| LNi | 1.871 | 1.870 | 105.3 | −0.5 |
| LCu | 1.880 | 1.881 | 114.2 | −0.3 |
| LB | 1.449 | 1.449 | 113.6 | 24.5 |
| LAl | 1.993 | 1.988 | 88.5 | −5.3 |
| LGa | 2.079 | 2.079 | 86.6 | 0.0 |
| LIn | 2.308 | 2.307 | 80.7 | −2.3 |
| L′C | 1.352 | 1.341 | 114.8 | 1.3 |
| L′Si | 1.750 | 1.736 | 98.6 | 0.0 |
| L'Ge | 1.869 | 1.852 | 95.8 | −0.0 |
| L′Sn | 2.068 | 2.047 | 90.6 | 0.0 |
| L′Pb | 2.168 | 2.143 | 88.2 | −0.0 |
Majority of the optimised structures show either planar or near planar arrangements of the Nacnac-heterocycle, one main group exception being LB, which exhibits a highly twisted structure and a B–N–C–C dihedral angle of 24.5°. The boron structure can be explained by a very narrow HOMO–LUMO gap (vide infra). Another interesting geometry can be observed for the transition metal analogue LCo, which exhibits a close contact between the Co–metal and Dipp-substituent's methyl hydrogen (1.871 Å). This close contact twists the heterocycle from planarity which results in a Co–N–C–C dihedral angle of −13.3°.
Next, we turned our attention to evaluating the electronic structures of the LM/L′M complexes. In especially main group chemistry, the magnitude of the HOMO–LUMO gap (or singlet–triplet gap) can be used to evaluate the relative stability and/or reactivity of the compound. Especially for low valent group 13 and 14 species, the HOMO is usually the lone electron pair and LUMO the empty p-orbital, exactly the frontier molecular orbitals involved in formal oxidative addition or adduct forming reactions. Fig. 2 includes a graph of the calculated frontier molecular orbital (FMO) energies of the LM/L′M complexes and an illustration of the LGa HOMO and LUMO+1 orbitals. The calculated HOMO–LUMO gaps for the LM/L′M complexes vary from 2.41 (LB) to 4.98 eV (L′C). For the group 13 compounds, the HOMO–LUMO gap widens in going down the group due to more stabilised HOMO (lower in energy) and at the same time destabilised LUMO (higher in energy). The opposite holds for group 14; the HOMO–LUMO gap gets narrower when the group is descended. However, a closer look at the FMOs reveals that in fact for group 14, the HOMO is a ligand-backbone related bonding orbital and not the group 14 element based lone pair orbital. That said, when the orbital energy gap between the central element lone pair (HOMO−x) and the empty p-orbital (LUMO) is computed, the trends are similar in both groups 13 and 14. For the first row transition metal complexes, the HOMO/SOMO includes a contribution from one of the metal associated 3d-orbitals and Nacnac-backbone while the LUMO is mainly an empty d-orbital (4s-orbital for M = Ni and Cu). In general, the HOMO(−x)–LUMO(+y) gaps are wider for the main group species than for the transition metal complexes.
Reactivity towards ammonia
Based on the electronic structure alone, a mode of reactivity between the LM/L′M compounds and ammonia can be evaluated. The Werner coordination complex formation involves the interaction between the LM/L′M empty p-orbital (groups 13 and 14) or 3d/4s-orbital (transition metals) and the lone pair of nitrogen in ammonia. To achieve oxidative addition, one of the N–H bonds in ammonia needs to be cleaved, which involves the additional participation of the central element M lone pair (Fig. 3). There are few excellent computational studies on the mechanism of the oxidative addition of small molecules by main group species, and in the case of ammonia reacting with group 14 metallylenes, it is speculated that a proton shuttling mechanism involving two different ammonia molecules is the most probable one.34–36 The involvement of two NH3 molecules can lower the associated transition state significantly compared to a mechanism with only one ammonia moiety as there is no need for ammonia dissociation and the H transfer is stabilised by the involvement of the second ammonia molecule. Because of these already published studies on the mechanism of ammonia activation by main group species, we focussed our efforts on investigating the reasons that result in the different modes of reactivity (vide infra).In the main group LM/L′M compounds a highly stabilised HOMO and a wide HOMO–LUMO gap would indicate a relatively unreactive main group element based lone pair. In consequence, this allows facile access to the empty p-orbital (LUMO, provided the ammonia FMO orbital energies match) and hence pronounced tendency to form the ammine adduct LM·NH3. As the lone pair orbital (HOMO−x) and empty p-orbital (LUMO+y) get closer in energy, the compound will become more reactive, and the oxidative addition product should become more favourable. To assess this hypothesis, the oxidative addition products, LM(H)NH2 (M = group 13 or Fe, Co, Ni, Cu) or LMNH2 (M = group 14) and ammine adducts, LM·NH3/L′M·NH3, were optimised computationally. To our knowledge there are only two isolated examples of a reaction between L′M moiety and ammonia reported in the literature: silicon and germanium oxidative addition products L′Si(H)NH2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 32 and LGeNH2.7 The comparison of experimental and calculated bond parameters revealed an excellent agreement of the data (see ESI†).
32 and LGeNH2.7 The comparison of experimental and calculated bond parameters revealed an excellent agreement of the data (see ESI†).
Furthermore, a closer look at the optimised structures of the LM amido hydrides and ammine adducts revealed expected trends and few anomalies. Unsurprisingly, the L′C species does not bind ammonia as the C–N interaction is measured to be over 4.29 Å in the optimised adduct structure. In addition, LB rearranges to a five-membered ring upon reaction with ammonia (Fig. 2c). Both of these observations can be explained by the narrowest (M = B) and widest (M = C) HOMO–LUMO gaps computed for the whole series (Fig. 2). In addition, the boron-compound rearrangement is probably further facilitated by the non-planar structure of LB (vide supra). The calculated main group LM/L′M and ammonia nitrogen M–N interactions in the ammine adducts are significantly longer than the sum of the covalent radii of the two elements (Table 3).37 In contrast, the M–NNH3 bonding interaction is clearly shorter in the computed transition metal ammine adducts as expected based on the electrophilicity of the 3d-metals.
| Compound | Oxidative addition | Werner adduct |
|---|---|---|
| a The 1,1-addition product without proton transfer to the ligand backbone methine carbon is the lowest energy structure. b The 1,4-addition product. | ||
| LFe | −66.5 | −97.2 |
| LCo | 7.8 | −82.8 |
| LNi | 64.8 | −73.6 |
| LCu | 129.0 | −66.7 |
| LB | −260.4 | −82.1 |
| LAl | −173.6 | 23.8 |
| LGa | −34.6 | 31.3 |
| LIn | 73.6 | 15.7 |
| L′C | −67.3a | 9.8 |
| L′Si | −126.6a | 25.6 |
| L'Ge | −46.8b | 15.8 |
| L′Sn | −70.1b | −8.6 |
| L′Pb | −66.2b | −9.9 |
| Compound | q(A) | q(B) | ρ(rbcp) (e Å−3) | ∇2ρ(rbcp) (e Å−5) | DI (A|B) | d(A–B)b (Å) |
|---|---|---|---|---|---|---|
| a No BCP was found between C and N. b Sum of covalent radii according to ref. 37. | ||||||
| LFe·NH3 | +0.76 | −1.13 | 0.0766 | 0.3210 | 0.5324 | 2.064 (2.03) |
| LCo·NH3 | +0.69 | −1.12 | 0.0801 | 0.3342 | 0.5336 | 2.046 (1.97) |
| LNi·NH3 | +0.63 | −1.10 | 0.0818 | 0.3813 | 0.5562 | 2.014 (1.95) |
| LCu·NH3 | +0.61 | −1.09 | 0.0856 | 0.3674 | 0.5536 | 2.005 (2.03) |
| LB·NH3 | +2.05 | −1.25 | 0.1341 | 0.3505 | 0.3449 | 1.581 (1.55) |
| LAl·NH3 | +0.98 | −1.22 | 0.0394 | 0.1187 | 0.2794 | 2.223 (1.92) |
| LGa·NH3 | +0.67 | −1.12 | 0.0308 | 0.0541 | 0.2577 | 2.555 (1.93) |
| LIn·NH3 | +0.68 | −0.11 | 0.0296 | 0.0758 | 0.2620 | 2.678 (2.13) |
| L′C·NH3 | +0.90 | −1.08 | — | — | 0.0007 | 4.294 (1.47) |
| L′Si·NH3 | +1.61 | −1.22 | 0.0635 | 0.0800 | 0.3595 | 2.101 (1.82) |
| L'Ge·NH3 | +1.19 | −1.14 | 0.0607 | 0.0910 | 0.4052 | 2.243 (1.91) |
| L′Sn·NH3 | +1.20 | −1.15 | 0.0494 | 0.1170 | 0.3764 | 2.436 (2.10) |
| L′Pb·NH3 | +1.14 | −1.13 | 0.0451 | 0.1134 | 0.3614 | 2.549 (2.17) |
All optimised structures at hand, we began our analyses by comparing the Gibbs free energies of the reactions resulting in either the oxidative addition product or the Werner adduct (Table 2). For the group 14 compounds, we examined the relative energies of both the 1,1- and 1,4-addition products L′M(H)NH2 and LMNH2 where the proton has migrated to the Nacnac-backbone methine carbon. In line with the experimental observations and the calculated frontier molecular orbital energies,7,32,36 the 1,1-addition was preferred for the carbene and silylene analogues whereas for the other elements M = Ge, Sn and Pb, the 1,4-addition product was more stable. The oxidative addition products were found to be the thermodynamic product for group 13 and 14 compounds, except for LIn, for which both reactions were calculated to be endergonic. The unfavourable oxidative addition reaction for LIn can be explained by the inaccessibility and high energy level of the LUMO. The transition metal congeners expectedly exhibit the opposite reactivity: the Werner coordination complex is the thermodynamic product for all M = Fe, Co, Ni and Cu Nacnac-complexes. Interestingly, the 1,1-addition reaction for LFe was calculated to be exergonic by −66.5 kJ mol−1, indicating that with the correct ligand system and reaction conditions, an amido hydride product might be isolable for Fe-complex.
According to the data in Table 2, it is likely that all of the studied transition metal complexes can form a stable Werner adduct with ammonia. Moreover, the calculations indicate that the oxidative addition products could be isolable for all main group LM/L′M species (except for M = In). Interestingly, the data also suggests that the Werner coordination compounds might be isolable for the main group species M = B, Sn and Pb, for which the adduct is the kinetic product of the reaction between the complex and ammonia. This, however, would require a careful optimisation of reaction conditions and maybe further tuning of the ligand sterics and electronics.
The calculated Werner coordination complex structures, along with the Gibbs free energy calculations of the reactions, suggest that the ammonia moiety in the Werner adducts is more tightly bound in the transition metal complexes than in main group species. To further probe this and the nature of the ammonia adducts and the M–N interactions, we utilised the QTAIM method: the Bader charges of the element M (q(A)) and ammonia nitrogen (q(B)) were calculated as well as the bonding critical point (BCP) properties between the two atoms to shed light on the favourability of the ammine adduct formation depending on the metal M. These results are summarised in Table 3. The calculated atomic charges reveal that the ammonia nitrogen carries a significant negative charge in all adducts as expected based on electronegativities of the atoms.38 The element M, however, is oxidised to a varying extent: group 14 elements carry calculated charges greater than +1 (with C as an exception) and group 13 less than +1 (with B as an exception). The transition metals all carry a positive charge less than +1. A bond critical point for the bond M–NNH3 was located for all LM/L′M complexes, except for M = C. The calculated BCP properties reveal that the electron density at the BCP is very small and has very little covalent character (Laplacian of ρ is small and positive, positive values indicate depletion of electron density at the BCP and are generally related to electrostatic or non-covalent type interactions) in the main group species.39 However, the values grow for M = Fe, Co, Ni and Cu, indicating stronger bonding between the two moieties. This is further corroborated by the greater delocalisation indices, DI(A|B) for the transition metal complexes as DI(A|B) can be used to evaluate the bond order.40
The final bonding analysis we performed for the Werner adducts was the energy decomposition analysis (EDA) in combination with the natural orbitals for chemical valence formalism (NOCV). The EDA-NOCV analysis used the neutral LM/L′M and NH3 fragments as optimised in the respective ammine adducts. The total instantaneous interaction energies were found to range from −43.2 (Ga) to −174.2 kJ mol−1 (Ni) (Table 4). Consistent with the QTAIM results, the LM/L′M and ammonia interactions are strongest for the transition metal analogues. A breakdown of the total interaction energies to repulsive (Pauli repulsion) and attractive (electrostatic, orbital and dispersion interactions) components reveals, that for the transition metal complexes the Pauli repulsion is offset completely by the electrostatic interactions and thus the orbital interactions are the biggest contributor to the total interaction energy. The dispersion component is of similar magnitude for the whole series but becomes more important in stabilising the adducts for the main group species because the Pauli repulsion term is significantly greater than the electrostatic interaction for the group 13 and 14 species. Furthermore, the relatively small orbital interaction values for the M–NNH3 bonds support the non-covalent description from the QTAIM analysis (vide supra).
| Pauli repulsion | Electrostatic interaction | Orbital interactions | Dispersion | Total | |
|---|---|---|---|---|---|
| a LB and L′C were excluded from this analysis due to their different reactivity with ammonia to the rest of the series. | |||||
| LFe·NH3 | 296.5 | −296.5 | −132.5 | −19.4 | −152.0 |
| LCo·NH3 | 315.9 | −308.4 | −122.5 | −15.5 | −130.5 |
| LNi·NH3 | 298.4 | −302.7 | −151.0 | −18.9 | −174.2 |
| LCu·NH3 | 299.0 | −305.6 | −109.9 | −18.5 | −134.9 |
| LAl·NH3 | 349.0 | −245.8 | −136.3 | −17.2 | −50.3 |
| LGa·NH3 | 157.9 | −114.9 | −67.3 | −18.9 | −43.2 |
| LIn·NH3 | 143.7 | −115.9 | −60.3 | −16.9 | −49.1 |
| L′Si·NH3 | 499.4 | −325.0 | −235.3 | −21.5 | −82.4 |
| L'Ge·NH3 | 381.9 | −265.0 | −175.6 | −20.3 | −79.0 |
| L′Sn·NH3 | 293.0 | −229.4 | −134.2 | −19.3 | −89.8 |
| L′Pb·NH3 | 235.2 | −195.2 | −108.6 | −20.3 | −89.0 |
Finally, a closer look at the orbital interactions reveals that the major component in the M–N bonding is composed of the charge flux from the ammonia nitrogen to the element M as expected. For example for the main group adducts, this charge flow constitutes roughly 70% of the overall orbital interactions calculated for the species (see ESI† for further details).
Conclusions
A computational approach to study the reactivity of main group 13/14 and first-row transition metal LM/L′M complexes towards ammonia was exploited. First, the optimised structures were evaluated in terms of their electronic structures and frontier molecular orbital energies to reveal trends in compound stability and reactivity. Next, the difference in reactivity towards ammonia was investigated and as expected, the transition metal complexes were found to prefer the formation of a classical Werner coordination complex over an oxidative addition product. For main group species the reactivity was observed to be the opposite. However, the formation energies along with QTAIM and EDA-NOCV calculations suggest that the isolation of a Werner coordination complex of ammonia might be plausible for few main group element species (B, Sn and Pb), provided that the experimental conditions are optimised.Author contributions
PV: conceptualization, methodology, data curation, funding acquisition, supervision, resources, project administration, writing – original draft, review and editing; CWL: data curation and analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
PV gratefully acknowledges the Jenny and Antti Wihuri Foundation and the Academy of Finland for financial support (grant numbers 338271 and 346565), the Finnish Computing Competence Infrastructure (FCCI) and CSC—IT Center for Science, Finland, for computational and data storage resources.References
- P. P. Power, Nature, 2010, 463, 171–177 CrossRef CAS PubMed.
- C. Weetman and S. Inoue, ChemCatChem, 2018, 10, 4213–4228 CrossRef CAS.
- M.-A. Légaré, G. Bélanger-Chabot, R. D. Dewhurst, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Science, 2018, 359, 896–900 CrossRef PubMed.
- J. Hicks, P. Vasko, J. M. Goicoechea and S. Aldridge, Nature, 2018, 557, 92–95 CrossRef CAS PubMed.
- G. C. Welch, R. R. S. Juan, J. D. Masuda and D. W. Stephan, Science, 2006, 314, 1124–1126 CrossRef CAS PubMed.
- A. V. Protchenko, P. Vasko, D. C. H. Do, J. Hicks, M. Á. Fuentes, C. Jones and S. Aldridge, Angew. Chem., Int. Ed., 2019, 58, 1808–1812 CrossRef CAS PubMed.
- A. Jana, I. Objartel, H. W. Roesky and D. Stalke, Inorg. Chem., 2009, 48, 798–800 CrossRef CAS PubMed.
- O. Planas, F. Wang, M. Leutzsch and J. Cornella, Science, 2020, 367, 313–317 CrossRef CAS PubMed.
- J. Zhao, A. S. Goldman and J. F. Hartwig, Science, 2005, 307, 1080–1082 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand,K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396–1396 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- T. A. Keith, AIMAll, TK Gristmill Software, Overland Parks KS, USA, 2019 Search PubMed.
- T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565 CrossRef CAS.
- T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755–1759 CrossRef CAS.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- P. L. Holland, T. R. Cundari, L. L. Perez, N. A. Eckert and R. J. Lachicotte, J. Am. Chem. Soc., 2002, 124, 14416–14424 CrossRef CAS PubMed.
- T. R. Dugan, X. Sun, E. V. Rybak-Akimova, O. Olatunji-Ojo, T. R. Cundari and P. L. Holland, J. Am. Chem. Soc., 2011, 133, 12418–12421 CrossRef CAS PubMed.
- T. Chu, I. Korobkov and G. I. Nikonov, J. Am. Chem. Soc., 2014, 136, 9195–9202 CrossRef CAS PubMed.
- C. Cui, H. W. Roesky, H.-G. Schmidt, M. Noltemeyer, H. Hao and F. Cimpoesu, Angew. Chem., Int. Ed., 2000, 39, 4274–4276 CrossRef CAS PubMed.
- N. J. Hardman, B. E. Eichler and P. P. Power, Chem. Commun., 2000, 1991–1992 RSC.
- M. S. Hill and P. B. Hitchcock, Chem. Commun., 2004, 1818–1819 RSC.
- M. Driess, S. Yao, M. Brym, C. van Wüllen and D. Lentz, J. Am. Chem. Soc., 2006, 128, 9628–9629 CrossRef CAS PubMed.
- A. Jana, C. Schulzke and H. W. Roesky, J. Am. Chem. Soc., 2009, 131, 4600–4601 CrossRef CAS PubMed.
- M. Driess, S. Yao, M. Brym and C. van Wüllen, Angew. Chem., Int. Ed., 2006, 45, 4349–4352 CrossRef CAS PubMed.
- D. C. H. Do, A. V. Protchenko, M. Á. Fuentes, J. Hicks, P. Vasko and S. Aldridge, Chem. Commun., 2020, 56, 4684–4687 RSC.
- Y. Peng, J.-D. Guo, B. D. Ellis, Z. Zhu, J. C. Fettinger, S. Nagase and P. P. Power, J. Am. Chem. Soc., 2009, 131, 16272–16282 CrossRef CAS PubMed.
- M. E. Alberto, N. Russo and E. Sicilia, Chem. – Eur. J., 2013, 19, 7835–7846 CrossRef CAS PubMed.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838 RSC.
- L. Pauling, J. Am. Chem. Soc., 1932, 54, 3570–3582 CrossRef CAS.
- G. Frenking and S. Shaik, The Chemical Bond: Fundamental Aspects of Chemical Bonding, John Wiley & Sons, Incorporated, Weinheim, GERMANY, 2014 Search PubMed.
- C. Outeiral, M. A. Vincent, Á. M. Pendás and P. L. A. Popelier, Chem. Sci., 2018, 9, 5517–5529 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational details and optimized xyz-coordinates of the structures. See DOI: https://doi.org/10.1039/d2dt02427f |
| This journal is © The Royal Society of Chemistry 2022 |