 Open Access Article
Open Access ArticleOn the vibrations of formic acid predicted from first principles
Anna Klára
Kelemen
a and
Sandra
Luber
 *b
*b
aDepartment of Chemistry, University of Zurich, CH-8057 Zurich, Switzerland. Tel: +41 44 635 42 98
bDepartment of Chemistry, University of Zurich, CH-8057 Zurich, Switzerland. E-mail: sandra.luber@chem.uzh.ch; Tel: +41 44 635 44 64
First published on 17th November 2022
Abstract
In this article, we review recent first principles, anharmonic studies on the molecular vibrations of gaseous formic acid in its monomer form. Transitions identified as fundamentals for both cis- and trans form reported in these studies are collected and supported by results from high-resolution experiments. Attention is given to the effect of coordinate coupling on the convergence of the computed vibrational states.
1 Introduction
Vibrational spectroscopies continue to be a shared interest of both theoretical and experimental approaches in chemistry, with the harmonic approximation1 as the dominating theoretical description in practice. In contrast, methods that describe vibrations from first principles, obey to the rules of quantum mechanics and go beyond the harmonic approximation are far from routine, despite the apparent anharmonicity of many molecular vibrations. Since a clear hierarchy is not well established for these methods, investigating their performance and characteristics in a joint discussion with regard to the accuracy of the predicted vibrations of a selected molecule may be of interest in addition to the comparison to high-accuracy experimental data. Formic acid, the smallest carboxylic acid, emerges as a good candidate in this respect; it exhibits structural cis–trans isomerism and it forms a hydrogen-bonded dimer at room temperature, giving rise to complex nuclear dynamics which are difficult to model accurately.2 In a broader perspective, understanding the nuclear dynamics of carboxylic acids could also give insight into the conformation and folding mechanisms of proteins. After a brief discussion of selected concepts employed in the anharmonic and variational computation of molecular spectra, we review experimental results and discuss ab initio calculations of the anharmonic molecular vibrations of the monomer forms of formic acid in a chronological order.2 Selected concepts of the variational calculation of molecular vibrations
Arguably one of the most difficult aspects of the calculation of molecular vibrations beyond the harmonic approximation is the definition of an appropriate coordinate system and the derivation of the corresponding vibrational Hamiltonian. The separation of the purely vibrational motion of the molecule requires internal coordinates,1,3 but the conditions which define a unique and an optimal coordinate system which is appropriate for various types of nuclear motion are not known.4 The Watson Hamiltonian which was derived for non-linear5 and linear6 reference configurations and defines the rovibrational motion in terms of rectilinear normal coordinates remains to be one of the most popular choices, since its definition ensures minimal rovibrational coupling and an optimal representation of molecular vibrations with small displacements from the reference geometry.1,4 It follows, that difficulties are encountered if vibrations corresponding to e.g. torsional motions or significant displacements from the equilibrium structure are computed in this representation. Slow convergence of the computed vibrational eigenstates or inaccurate results in approximate methods are often encountered in these cases.7 Since the Watson Hamiltonian is invariant under the unitary transformations of the normal modes, attempts for improvement have been made by optimizing8–10 and localizing11 the normal modes. The choice of the vibrational Hamiltonian also affects the ease of interpretation of the computed results. Whereas vibrations which are well described by the harmonic approximation are found to be mostly localized on the respective normal coordinate, anharmonic vibrations which are encountered e.g. in the high-energy region, can have contributions along multiple normal coordinates, leading to increasingly difficult assignments.12 Whereas an ill-defined coordinate system can introduce artificial correlation, a well-choosen one may minimize the correlation between the different degrees of freedom.13The main focus of this section is not a to give a comprehensive review of available vibrational methods, for which already vast literature is available,4,14–19 but rather to give an overview of selected concepts and methods necessary for discussing the literature on formic acid, reviewed below. We also shall not discuss the computation of intensities, but emphasize the importance of the development of e.g. accurate electronic dipole surfaces aiding the interpretation of IR spectra.
In order to present a joint discussion of variational methods and the literature reviewed below, we introduce the following notation for the vibrational coordinates q = {q1,…,qM}. Once defined, the vibrational Hamiltonian may be separated into a kinetic and potential part, where the form of both the kinetic and potential term depends on the employed coordinate system. The potential term, the so called Potential Energy Surface (PES) ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) (q) can be calculated either by direct evaluation of ab initio electronic energies along the vibrational coordinates, or it may be pre-fitted to an appropriate analytic form. Most commonly, either a Taylor expansion20
(q) can be calculated either by direct evaluation of ab initio electronic energies along the vibrational coordinates, or it may be pre-fitted to an appropriate analytic form. Most commonly, either a Taylor expansion20
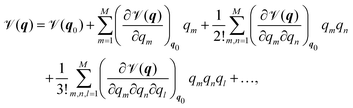 | (1) |
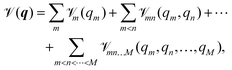 | (2) |
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) m(qm) are the so-called one-,
m(qm) are the so-called one-, ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) mn(qm,qn) are the two-, and
mn(qm,qn) are the two-, and ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) mn…M(qm,qn,…,qM) are the M-body terms, respectively, each dependent on a subset of coordinates. The sum-of product (SOP) form22,23
mn…M(qm,qn,…,qM) are the M-body terms, respectively, each dependent on a subset of coordinates. The sum-of product (SOP) form22,23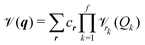 | (3) |
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) r, where the latter is expressed as a product of terms dependent only on coordinate Qk, respectively. The Qks may combine multiple coordinates of q, therefore reducing the computational effort, i.e. f < M and r = [r1,…,rf]. We note, that the accuracy of any vibrational structure calculation is limited by the accuracy of the PES, and therefore the electronic structure method employed for its construction.
r, where the latter is expressed as a product of terms dependent only on coordinate Qk, respectively. The Qks may combine multiple coordinates of q, therefore reducing the computational effort, i.e. f < M and r = [r1,…,rf]. We note, that the accuracy of any vibrational structure calculation is limited by the accuracy of the PES, and therefore the electronic structure method employed for its construction.
Beyond the well-known harmonic approximation, for which the solutions can be obtained exactly due to approximating the potential as a second order Taylor expansion in normal coordinates, variational solutions24 to the vibrational Schrödinger equation require an ansatz. In the Vibrational Self-Consistent-Field (VSCF) method,18,25 the vibrational states are computed in the product form
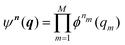 | (4) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
![[n with combining macron]](https://www.rsc.org/images/entities/b_i_char_006e_0304.gif) (qm)
(qm)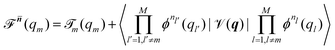 | (5) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) m(qm). n = [n1,…,nM] collects the available quantum numbers associated with the single-coordinate functions ϕnm(qm) determined self-consistently, and
m(qm). n = [n1,…,nM] collects the available quantum numbers associated with the single-coordinate functions ϕnm(qm) determined self-consistently, and ![[n with combining macron]](https://www.rsc.org/images/entities/b_i_char_006e_0304.gif) denotes all quantum numbers but the m-th. The vibrational energies are then the expectation value of the full Hamiltonian with the VSCF wavefunction (eqn (4)) which can be obtained in a state-specific, for a chosen set of quantum numbers, or in a non state-specific fashion. The VSCF approximation has been improved by the correlation-corrected VSCF approach (CC-VSCF) developed by Gerber and co-workers18,27,28 also known as second order vibrational Møller–Plesset (VMP2) theory. In this method, the deviation of the exact wave function from the mean-field solution is assumed to be small, such that a second order perturbation correction is applied for a correlation-corrected energy expression. The latter differs in the zeroth order problem from the well-known second order vibrational perturbation (VPT2) theory in which the harmonic approximation is corrected.
denotes all quantum numbers but the m-th. The vibrational energies are then the expectation value of the full Hamiltonian with the VSCF wavefunction (eqn (4)) which can be obtained in a state-specific, for a chosen set of quantum numbers, or in a non state-specific fashion. The VSCF approximation has been improved by the correlation-corrected VSCF approach (CC-VSCF) developed by Gerber and co-workers18,27,28 also known as second order vibrational Møller–Plesset (VMP2) theory. In this method, the deviation of the exact wave function from the mean-field solution is assumed to be small, such that a second order perturbation correction is applied for a correlation-corrected energy expression. The latter differs in the zeroth order problem from the well-known second order vibrational perturbation (VPT2) theory in which the harmonic approximation is corrected.
Going beyond the product form, a linear combination of configurations
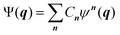 | (6) |
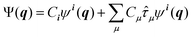 | (7) |
![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) μ generates an excited configuration from the quantum numbers i = [i1,…,iM]. If the full excitation space is used, the method is called full VCI (FVCI). Similarly to CI in electronic structure theory, singles, doubles, and higher excitations are generated, and the expansion is truncated to allow for a subset of the available quantum numbers and/or excitations, therefore introducing a bound on the, in principle, infinite sum. The expansion coefficients Cn of the normalized wavefunction are determined variationally as eigenvectors of the VCI matrix 〈ψn(q)|
μ generates an excited configuration from the quantum numbers i = [i1,…,iM]. If the full excitation space is used, the method is called full VCI (FVCI). Similarly to CI in electronic structure theory, singles, doubles, and higher excitations are generated, and the expansion is truncated to allow for a subset of the available quantum numbers and/or excitations, therefore introducing a bound on the, in principle, infinite sum. The expansion coefficients Cn of the normalized wavefunction are determined variationally as eigenvectors of the VCI matrix 〈ψn(q)|![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (q)|ψl(q)〉. However, the straightforward construction of the untruncated VCI matrix and computation of its eigenvectors is prohibitively expensive and in practice approximations are introduced.33,34 By partitioning the modes into a set of active and a set of bath modes Mizukami and Tew35 have introduced the vibrational active space self-consistent field theory (VASSCF), vibrational active space configuration interaction (VASCI) and vibrational active space second order perturbation theory (VASPT2) methods. These methods employ a product of a CI type ansatz for the active modes and a simple product ansatz for the bath modes. Whereas in their VASSCF approach all CI coefficients and all single-coordinate functions are optimized, only a subset of single-coordinate functions are optimized in their VASCI approach.
(q)|ψl(q)〉. However, the straightforward construction of the untruncated VCI matrix and computation of its eigenvectors is prohibitively expensive and in practice approximations are introduced.33,34 By partitioning the modes into a set of active and a set of bath modes Mizukami and Tew35 have introduced the vibrational active space self-consistent field theory (VASSCF), vibrational active space configuration interaction (VASCI) and vibrational active space second order perturbation theory (VASPT2) methods. These methods employ a product of a CI type ansatz for the active modes and a simple product ansatz for the bath modes. Whereas in their VASSCF approach all CI coefficients and all single-coordinate functions are optimized, only a subset of single-coordinate functions are optimized in their VASCI approach.
In the Multi-configurational time-dependent Hartree22,36 (MCTDH) method a time-dependent ansatz is employed with expansion coefficients Cr
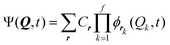 | (8) |
Generally speaking, the underlying coordinate system defines the level of coupling among the coordinates that has to be captured by the Hamiltonian and the wave function of each vibrational state. The convergence of the Hamiltonian with respect to the convergence of the computed energy levels can be tested by e.g. including higher-order terms of a Taylor-expanded PES or higher-order coupling terms in a many-body expanded PES. A systematic improvement of variational wave functions is possible through e.g. the enlargement of the underlying basis set(s) and by employing multiple configurations. Finally, SCF and dynamic methods have the advantage of adapting the single-coordinate functions to a given computed state. Besides obtaining converged states within the respective approach, the accuracy of the latter can be quantified by comparison to high-accuracy experimental frequencies, or a higher level of theory, if available. It follows, that an inaccurate PES computed at a low-level of electronic structure theory or not supportive of the relevant nuclear positions will not yield good results, as will not a single-configurational approach for a coordinate system which is inappropriate for the computed vibration (e.g. rectilinear coordinates for vibrations involving torsional motions). In addition, resonances between states cannot be captured by single-configurational approaches such that any variational or perturbative approach relying only on one configuration will fail in this respect.35 We note, that although multi-configurational approaches can provide the most accurate results, due to their inherent scaling with system-size, they are difficult to apply to larger systems or highly-coupled motions requiring large bases. In this respect, perturbative approaches represent cost-effective alternatives beyond the harmonic approximation.
Once the vibrational states are determined, the interpretation of the computed levels presents the next challenge. In the harmonic approximation the vibrations are decoupled, such that a single quantum number is sufficient for characterizing a molecular vibration, i.e. νn1 corresponds to the n-th solution of the harmonic oscillator in the coordinate q1. If n = 1 the vibration is called a fundamental and otherwise with n > 1 an overtone vibration. As mentioned at the beginning of this section, it is advantageous to find a representation which allows each vibration to be localized along its coordinate and therefore to be decoupled from the remaining degrees of freedom. In this case, the product form is already sufficient and an unequivocal assignment in terms of a single set of quantum numbers is possible. Then, the harmonic or VSCF approximation may already present a satisfactory description of the vibrational state, and the corresponding VCI wave function is characterized by a single large CI coefficient. In the opposite case, the absence of a prevalent configuration may be regarded as the evidence of the vibrational counterpart of the concept of static correlation in electronic structure theory. As a dynamic method, in MCTDH the single-particle functions naturally adapt to the computed state, such that in principle a compact wave function can be achieved. In certain cases a single-configurational description completely fails, as is the case for resonances: in Fermi resonance,38 for instance, an energy splitting, ascribed to the interaction of an overtone and a fundamental accidentally close in energy, is observed.
3 Formic acid
Despite its size, formic acid exhibits a rich structural complexity, which has led to an ongoing theoretical and experimental interest in its nuclear dynamics over the years.30,35,39–57 In its monomer form (Fig. 1), two stable configurations of the Cs point group symmetry, cis and trans have been identified via microwave57–59 and submillimeter spectroscopy60,61 in the gas phase. With a difference of about 1365 cm−1 in zero point energy, as measured by gas-phase microwave relative intensity measurements,57 and 1412 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62 and 1415 cm−1
62 and 1415 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56 determined ab initio, the trans form is significantly more abundant at room temperature. This relative stability has been assumed to be due to an intramolecular hydrogen bond,20 but this idea was discarded later on.20,63 The gas-phase structure of the trans form was determined via electron diffraction.64 Based on the ground-state rotational constants determined by microwave spectroscopy, approximate equilibrium structures have been derived.65 The geometries can be connected via an internal rotation of hydrogen of the OH group around the CO axis,66 where the earliest experiments found a barrier height of 4827 cm−1.57 At low temperatures, proton tunneling through the torsional barrier was found to limit the lifetime of cis-HCOOH as measured in Argon matrix by Petterson et al.,42,67 whereas the deuterium tunneling rate was found to be significanty slower.68
56 determined ab initio, the trans form is significantly more abundant at room temperature. This relative stability has been assumed to be due to an intramolecular hydrogen bond,20 but this idea was discarded later on.20,63 The gas-phase structure of the trans form was determined via electron diffraction.64 Based on the ground-state rotational constants determined by microwave spectroscopy, approximate equilibrium structures have been derived.65 The geometries can be connected via an internal rotation of hydrogen of the OH group around the CO axis,66 where the earliest experiments found a barrier height of 4827 cm−1.57 At low temperatures, proton tunneling through the torsional barrier was found to limit the lifetime of cis-HCOOH as measured in Argon matrix by Petterson et al.,42,67 whereas the deuterium tunneling rate was found to be significanty slower.68
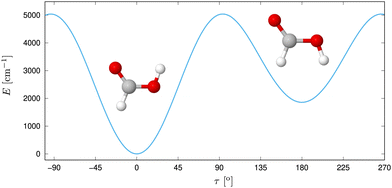 | ||
| Fig. 1 Trans and cis isomer of formic acid with the potential energy displayed along τ, the out-of-plane H motion. Reprinted with permission from ref. 30 from Elsevier, copyright 2022. | ||
The first IR absorption and Raman spectra of gaseous formic acid were measured in 193869 and 194070 by Bonner et al., and numerous experimental studies determining the vibrational transitions have been performed ever since at an increasingly high resolution.39–47,50–52,54,71–79 The signals arising due to the presence of the cis and trans monomers or the dimer have been differentiated experimentally by signal intensification via population control with thermal54 or laser42 excitation. Most variational theoretical methods consider purely the vibrational motion at zero temperature which can be compared to low temperature or high-resolution (e.g. FT absorption) rotationally analysed data. Two popular low temperature spectroscopic methods have emerged in this respect. In matrix isolation spectroscopy80,81 the analyte is condensed with an inert gas, e.g. a noble gas or nitrogen at low temperature, such that the molecules are “trapped” with different local environments in a matrix. This results in a shift of the measured frequencies and a splitting of absorption bands. For high-resolution data, the best agreement with theory is therefore achieved if the matrix-analyte interactions are also modeled in the theoretical description. As opposed to matrix isolation spectroscopy, jet-cooled spectroscopy76 does not suffer from such effects. In this method the analyte is passed through a nozzle with a neutral carrier gas and expanded into an evacuated jet chamber at low temperatures. Population enhancement has been achieved in a jet-setup via thermal control therefore recording and spectra at different temperatures have been compared.54
Complementary high-resolution IR and Raman spectra of partially and fully deuterated formic acid have been recorded for all isotopologues of the cis and trans monomer (DCOOH, HCOOD, DCOOD).41,44,45,50,82–88 Some spectral regions of formic acid are dense and therefore require a careful rotational analysis, hot bands and overlapping dimer signals further complicate the spectrum with the density of states generally increasing in the higher energy region.54,82
Amongst the many experimental studies performed for trans HCOOH,50,55,61,83,88,89 we mention the work of Freytes et al.82, who measured gas-phase room-temperature Fourier-transform (FT) and intracavity laser absorption spectra of trans-HCOOH. They reported band origins from 626 cm−1 to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284 cm−1 and performed a detailed analysis on the rotational structure of the first CH stretching vibrational overtone ν22 and the second OH stretch overtone ν31 of formic acid. Their work built on a previous study of Hurtmans et al., who presented a rovibrational analysis in the range of the first and third overtone of the OH stretching vibration ν21 and ν41 of trans-HCOOH based on FT spectroscopy and intracavity laser absorption spectroscopy measurements.83 Room temperature Raman measurements were performed by Bertie et al.40 in the range from 70 cm−1 to 4000 cm−1 for all isotopologues of the dimer, where the monomer signals could also be identified. Recent work of Nejad, Suhm and Meyer54 provided gas-phase Raman-jet measurements for all four deuterated isotopologues of formic acid monomer of both the cis and trans configuration, where the spectra were recorded with a nozzle temperature of 160 °C. They detected Fermi resonance doublets for the fundamentals ν1 and ν5 of trans-HCOOH, ν3 and ν5 for trans-DCOOH, ν2 and ν5 for trans-HCOOD, and ν2 and ν3 for trans-DCOOD. A summary of available benchmark quality experimental values for the vibrational transitions of trans-HCOOH and deuterated forms up to 4000 cm−1 in the far and mid-IR region with additional Raman-jet measurements has been recently compiled by Nejad and Sibert70 from gas-phase IR and Raman spectra reported in literature.
284 cm−1 and performed a detailed analysis on the rotational structure of the first CH stretching vibrational overtone ν22 and the second OH stretch overtone ν31 of formic acid. Their work built on a previous study of Hurtmans et al., who presented a rovibrational analysis in the range of the first and third overtone of the OH stretching vibration ν21 and ν41 of trans-HCOOH based on FT spectroscopy and intracavity laser absorption spectroscopy measurements.83 Room temperature Raman measurements were performed by Bertie et al.40 in the range from 70 cm−1 to 4000 cm−1 for all isotopologues of the dimer, where the monomer signals could also be identified. Recent work of Nejad, Suhm and Meyer54 provided gas-phase Raman-jet measurements for all four deuterated isotopologues of formic acid monomer of both the cis and trans configuration, where the spectra were recorded with a nozzle temperature of 160 °C. They detected Fermi resonance doublets for the fundamentals ν1 and ν5 of trans-HCOOH, ν3 and ν5 for trans-DCOOH, ν2 and ν5 for trans-HCOOD, and ν2 and ν3 for trans-DCOOD. A summary of available benchmark quality experimental values for the vibrational transitions of trans-HCOOH and deuterated forms up to 4000 cm−1 in the far and mid-IR region with additional Raman-jet measurements has been recently compiled by Nejad and Sibert70 from gas-phase IR and Raman spectra reported in literature.
Vibrational data for cis-HCOOH and isotopologues is more scarce48,66,68,90–95 due to the experimental difficulty of populating the cis state. Matrix-isolation spectroscopy measurements in Argon have been performed for cis-HCOOH by narrowband IR pumping of the first OH stretching overtone of trans-HCOOH ν21 by Pettersson et al.42 Maçôas et al. recorded near- and mid-IR spectra for HCOOH, DCOOH and HCOOD in solid argon matrix at 8 K from 400 cm−1 to 7800 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48 where the cis population was enhanced by pumping a trans to cis transition by narrowband tunable IR radiation. Raman-jet spectra for cis-HCOOH and isotopologues have been recorded recently by Meyer, Nejad and Suhm54,87,96via thermal excitation between 100–190 °C prior to the jet expansion. In Table 1 we summarize transition frequencies of gaseous formic acid monomer from high-resolution experiments, which have been assigned as fundamentals of the cis and trans monomer, respectively. We note, that many of the fundamentals have been found to be affected by rovibrational97 and resonance interactions,20 of which the ν5/ν29 Fermi resonance pair of trans-HCOOH has been the most prominent due to an early experimental misassignment of the more intense overtone band as the fundamental.82
48 where the cis population was enhanced by pumping a trans to cis transition by narrowband tunable IR radiation. Raman-jet spectra for cis-HCOOH and isotopologues have been recorded recently by Meyer, Nejad and Suhm54,87,96via thermal excitation between 100–190 °C prior to the jet expansion. In Table 1 we summarize transition frequencies of gaseous formic acid monomer from high-resolution experiments, which have been assigned as fundamentals of the cis and trans monomer, respectively. We note, that many of the fundamentals have been found to be affected by rovibrational97 and resonance interactions,20 of which the ν5/ν29 Fermi resonance pair of trans-HCOOH has been the most prominent due to an early experimental misassignment of the more intense overtone band as the fundamental.82
| trans-HCOOH | trans-DCOOH | trans-HCOOD | trans-DCOOD | |
|---|---|---|---|---|
| ν 1 | 3570.583 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56641 56641 |
263154 | 2631.8743 |
| ν 2 | 2942.0688 | 2219.6947 | 2938.241 | 2231.840 |
| ν 3 | 1776.8355 | 1725.8785 | 1772.1298 | 1760.041 |
| ν 4 | 1379.0550 | 970.8941 | 1366.4899 | 104241 |
| ν 5 | 1306.261 | 129741 | 972.8645,47 | 945.086 |
| ν 6 | 1104.8598 | 1142.3199 | 1177.0999 | 1170.847 |
| ν 7 | 626.1789 | 620.5775 | 558.2745 | 554.4345 |
| ν 8 | 1033.4798 | 873.3971 | — | 873.086 |
| ν 9 | 640.7389,100 | 631.5475 | 508.1345 | 493.2345 |
Throughout this work, the assignment of the fundamentals in terms of nuclear displacements is discussed with the valence coordinate definition of Richter and Carbonniére56 (Fig. 2), although some of the studies reviewed below employ different coordinates.
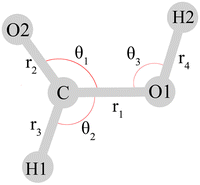 | ||
| Fig. 2 Valence coordinates defined by Richter and Carbonniére56 and adopted in ref. 2, 30, 53 and 79 for the monomeric formic acid molecule. The torsional coordinates τ1 and τ2 (not depicted) describe the out-of-plane motions of H1 and H2, respectively. Reprinted with permission from ref. 56 from AIP Publishing, copyright 2018. | ||
4 Ab initio studies on the formic acid monomer
4.1 First ab initio studies
One of the first ab initio, anharmonic studies on the formic acid monomer was concerned with the overtone series of the OH stretching vibration νn1 of trans-HCOOH.83 Hurtmans et al. recorded rotationally resolved overtone spectra of formic acid with high-resolution gas-phase FT and intracavity laser absorption spectroscopy and performed rovibrational analysis for the first ν21 and third ν41 overtones in the same work. They constructed an effective one-dimensional Hamiltonian dependent on the normal coordinate of the OH stretching mode for the analysis of the OH stretching vibration by relaxing the remaining geometrical parameters along the coordinate. The resulting effective potential was constructed at the MP2/cc-pVTZ level, and the corresponding one-dimensional variational solutions were computed for νn1, n ≤ 4 with an agreement within 50 cm−1 compared to the experimental band origins of the same work. It was found that the excitation of these νn1 vibrations affects the HOC angle with increasing n. The induced electric dipole moment was found to be initially almost parallel to the OH bond and progressively tilted towards the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond with increasing n. Based on these results Hurtmans et al. proposed a possible proton exchange mechanism promoted by the excitation of the OH overtones.
O bond with increasing n. Based on these results Hurtmans et al. proposed a possible proton exchange mechanism promoted by the excitation of the OH overtones.
Subsequently Maçôas et al.48 performed CC-VSCF calculations to support the assignment of the mid- and near-IR transitions measured by matrix-isolation spectroscopy in the same work. The transitions were determined at two trapping sites in solid argon for cis- and trans-HCOOH. Mid-IR spectra of trans and cis-DCOOH and near-IR spectra of trans-DCOOH and trans-HCOOD were also recorded, where the cis transitions were determined by narrowband IR pumping of the first OH overtone transition ν21 of the trans configuration. For cis-HCOOH about half of the expected fundamentals could be recorded and strong matrix effects, such as splitting of the recorded signals, was observed, making the assignments difficult. The CC-VSCF calculations were performed in the normal mode representation without rovibrational coupling terms and the PES was expressed with pairwise coupling terms, constructed directly at the MP2/6-311++G(2d,2p) level of theory for each pair of normal coordinate gridpoints. They computed all fundamentals and selected overtone and combination bands in the mid- and near-IR region for both trans- and cis-HCOOH and -DCOOH. We have included in Tables 2 and 3 the computed transitions identified as fundamentals of cis-and trans-HCOOH reported in their work. Anharmonicity was found to be strongest for the high-frequency stretching vibrations of trans and cis-HCOOH, i.e. ν1 and ν2 were found to have a downshift of up to 200 cm−1 compared to their calculated harmonic counterpart, whereas most fundamentals were found to reproduce the matrix-isolation experiments reasonably well. Exceptions are fundamentals corresponding to torsional and deformation type motions, that is, ν5 and ν9 were predicted to be below the experimental values, e.g. for ν9 around 40 cm−1 and 70 cm−1 for trans-HCOOH and cis-HCOOH, respectively. In the near-IR region, the first overtones ν21 and ν22 of trans-HCOOH and cis-HCOOH were found to be reasonably accurate compared to the measured experimental values. On the other hand, most combination and overtone bands involving ν5 and ν6 were inaccurate. In addition to limitations based on e.g. the level of ab initio theory and the order of coupling in the potential, the reason for this was found to be the normal modes associated with the aforementioned fundamentals. We note, that this inaccuracy may be due to the inability of VSCF to reproduce Fermi resonances. The well-known ν5/ν29 Fermi resonance was observed experimentally for trans-HCOOH and no analogous resonance was identified for cis-HCOOH. For DCOOH an ν3/ν28 Fermi resonance was observed for both the trans and cis form with the involvement of the OH stretching vibration ν1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50,55,61,83,88,89,98 and RMSD with respect to the experimental values. The internal coordinate path Hamiltonian results are abbreviated with an I-prefix
50,55,61,83,88,89,98 and RMSD with respect to the experimental values. The internal coordinate path Hamiltonian results are abbreviated with an I-prefix
| PES & method | ν 1 | ν 2 | ν 3 | ν 4 | ν 5 | ν 6 | ν 7 | ν 8 | ν 9 | RMSD |
|---|---|---|---|---|---|---|---|---|---|---|
| 200348 | 3784 | 3134 | 1789 | 1427 | 1317 | 1123 | 632 | 1065 | 677 | 98.7 |
| Harm.48 | ||||||||||
| 200348 | 3551 | 2951 | 1757 | 1389 | 1268 | 1078 | 621 | 1035 | 598 | 23.5 |
| CC-VSCF48 | ||||||||||
| 200720 | 3783 | 3106 | 1836 | 1429 | 1331 | 1144 | 634 | 1078 | 681 | 96.5 |
| Harm.20 | ||||||||||
| 200720 | 3594 | 2949 | 1801 | 1402 | 1291 | 1114 | 628 | 1042 | 643 | 15.29 |
| PT20 | ||||||||||
| 201335 | 3753 | 3081 | 1809 | 1414 | 1318 | 1137 | 629 | 1048 | 670 | 79.7 |
| Harm.35 | ||||||||||
| 201335 | 3505 | 2915 | 1783 | 1376 | 1296 | 1123 | 636 | 1034 | 687 | 29.3 |
| VSCF35 | ||||||||||
| 201335 | 3587 | 2944 | 1775 | 1365 | 1272 | 1102 | 624 | 1027 | 642 | 13.7 |
| VMP235 | ||||||||||
| 201335 | 3542 | 2915 | 1783 | 1377 | 1321/1226 | 1124 | 629 | 1034 | 635 | 30.6 |
| VASCI35 | ||||||||||
| 201335 | 3560 | 2923 | 1776 | 1364 | 1301/1203 | 1101 | 621 | 1027 | 625 | 36.0 |
| VASPT235 | ||||||||||
| 201662 | 3767 | 3092 | 1818 | 1412 | 1323 | 1140 | 632 | 1056 | 673 | 86.3 |
| Harm.62 | ||||||||||
| 201662 | 3551 | 2918 | 1790 | 1383 | 1305 | 1129 | 683 | 1040 | 648 | 28.2 |
| I-VSCF62 | ||||||||||
| 201662 | 3553 | 2917 | 1790 | 1372 | 1289 | 1127 | 657 | 1042 | 633 | 3.4 |
| I-VMP262 | ||||||||||
| 201662 | 3575 | 2939 | 1783 | 1379 | 1222 | 1108 | 627 | 1034 | 641 | 3.1 |
| I-VCI62 | ||||||||||
| 201662 | 3576 | 2938 | 1783 | 1379 | 1304 | 1108 | 627 | 1034 | 639 | 3.8 |
| GENIUSH30 | ||||||||||
| 201662 | 3576 | 2940 | 1783 | 1380 | 1305 | 1108 | 627 | 1035 | 640 | 2.8 |
| CVPT679 | ||||||||||
| 201856 | 3823 | 3014 | 1845 | 1416 | 1288 | 1124 | 655 | 1036 | 520 | 100.6 |
| Harm.56 | ||||||||||
| 201856 | 3567 | 2937 | 1774 | 1375 | 1301 | 1106 | 623 | 1032 | 637 | 3.6 |
| MCTDH56 | ||||||||||
| 201856 | 3568 | 2939 | 1773 | 1374 | 1300 | 1106 | 623 | 1032 | 637 | 3.7 |
| CVPT679 | ||||||||||
| Exp. | 3570.5 | 2942.06 | 1776.83 | 1379.05 | 1306.1 | 1104.85 | 626.17 | 1033.47 | 640.73 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54,87,90,96 and RMSD with respect to the experimental values. The internal coordinate path Hamiltonian results are abbreviated with an I-prefix
54,87,90,96 and RMSD with respect to the experimental values. The internal coordinate path Hamiltonian results are abbreviated with an I-prefix
| PES & method | ν 1 | ν 2 | ν 3 | ν 4 | ν 5 | ν 6 | ν 7 | ν 8 | ν 9 | RMSD |
|---|---|---|---|---|---|---|---|---|---|---|
| 200348 | 3852 | 3046 | 1829 | 1442 | 1287 | 1113 | 661 | 1043 | 537 | 125.4 |
| Harm.48 | ||||||||||
| 200348 | 3635 | 2863 | 1794 | 1404 | 1204 | 1078 | 647 | 1014 | 431 | 31.0 |
| CC-VSCF48 | ||||||||||
| 201662 | 3829 | 3007 | 1861 | 1428 | 1299 | 1124 | 664 | 1038 | 522 | 108.1 |
| Harm.62 | ||||||||||
| 201662 | — | 2880 | 1824 | 1394 | 1255 | 1103 | 668 | 1038 | 492 | 6.8 |
| I-VCI62 | ||||||||||
| 201856 | 3631 | 2871 | 1810 | 1383 | 1246 | 1097 | 652 | 1011 | 491 | 5.0 |
| MCTDH56 | ||||||||||
| 201662 | — | 2873 | 1821 | 1389 | 1247 | 1096 | 658 | 1021 | 490 | 2.7 |
| GENIUSH30 | ||||||||||
| 201662 | 3653 | 2878 | 1821 | 1389 | 1246 | 1096 | 657 | 1020 | 491 | 7.8 |
| CVPT679 | ||||||||||
| 201856 | 3636 | 2875 | 1810 | 1384 | 1247 | 1097 | 652 | 1014 | 491 | 4.3 |
| CVPT679 | ||||||||||
| Exp. | 3637 | 2873 | 1818 | — | — | 1093 | — | — | 493 |
We also briefly mention the work of Scribano and Benoit,101 who four years later computed the OH stretching frequency ν1 of trans-HCOOH with CC-VSCF, VCI and single-to-all (STA) CC-VSCF and STA-VCI. The STA methods were introduced in their work and rely on the idea that the modes could be partitioned into an active and a “spectator” set. In these calculations, the rovibrational coupling terms were neglected and the potential was expressed with up to two-body coupling terms in normal coordinates. The direct evaluation of the potential was performed at the MP2 and CCSD(T) level with TZP and polarization augmented SBK bases. The OH stretch fundamental ν1 was computed using standard VCI and STA-VCI with only one active degree of freedom. At the CCSD(T)/TZP level of theory a the STA-CC-VSCF and STA-VCI energies were found to be only 8 cm−1 worse compared to the CC-VSCF and VCI calculations for the frequency of the ν1 fundamental, where only singles and doubles excitations were included in the VCI expansion.
4.2 Advanced calculations with analytic potential energy surfaces
A more accurate description of the nuclear dynamics of formic acid has become available due to the development of analytic ab initio PESs, the availability of which leads to a significant speedup in the potential energy evaluation and therefore allows for the use of higher accuracy vibrational structure methods. The first anharmonic ab initio force-fields of formic acid were developed for trans-HCOOH by Demaison et al.20 at the MP2/VTZ, MP2/aVTZ and CCSD(T)/VTZ(ae) level of theory. In addition to analytic harmonic terms, the cubic and semidiagonal quartic force constants were determined via displacements along the normal coordinates with the method of finite differences. With this force field they computed anharmonic fundamentals using vibrational perturbation theory for trans-HCOOH. In Table 2 we included transitions obtained with the CCSD(T)/VTZ(ae) force-field. Vibration-rotation interaction constants as obtained by standard perturbation theory were also reported. The ν7, ν9, and ν3 fundamentals of trans-HCOOH were found to be affected by strong rovibrational interactions. They carried out an analysis of the resonances in terms of the magnitude of the force constants, where the Fermi resonant states were assumed to be connected via the cubic constants of force constants of type kijj and Darling-Dennison type resonances102via the quartic constant kkkll. In contrast to the experimentally derived force constants, several calculated force constants indicating Fermi resonance (e.g. k499 for ν4/ν29, k677 for ν6/ν27) differed significantly in magnitude and sign whereas the ν5/ν29 Fermi resonance matched qualitatively. The resonance interactions were further analyzed by constructing a 5 × 5 symmetric matrix representing interactions involving the ν29, ν27, ν6, ν5, ν4 states and computing the corresponding eigenstates.In 2013, Tew and Mizukami reported their first PES for formic acid, initially fitted for the description of the trans form ref. 35 with 5873 randomly generated configurations within the energy range 0–15 000 cm−1 at the CCSD(T)(F12*)/ccpVDZ-F12 level of theory. With this preliminary surface, they performed VSCF, VMP2, VASCI, and VASPT2 calculations based on the normal-coordinate Watson Hamiltonian for the fundamentals of trans-HCOOH (see Table 2). Rovibrational coupling terms were neglected and up to three body coupling terms were included in the many-body expansion. Up to seven single-mode functions were employed for the state-specific VSCF calculations and for the VASCI calculations an active space of four modes was selected, involving the normal modes associated with the ν1, ν5, ν7, and ν9 fundamentals. The authors note a good performance of VMP2 except for the fundamentals ν1 and ν5, where the former was overestimated by 22 cm−1 compared to the rovibrational-interaction-corrected experimental value. The largest deviations of the VASPT2 calculations were found for the ν2 and ν4 fundamentals. Since the isomerisation barrier was reached already at six quanta of excitation of the single-coordinate function along the torsional mode associated with the ν9 fundamental, only a limited excitation space was available. This led to multiple unconverged states due to the involvement of the torsional mode in multiple states. The authors concluded, that for fully converged values adopting a different coordinate system that can treat both the cis and trans minima would be necessary.
Consequently, two semiglobal PESs capable of describing the cis–trans isomerization have been developed. Tew and Mizukami published a PES in 201662 constructed using LASSO-based regression62 with electronic energies obtained at the CCSD(T)(F12*)/cc-pVTZ-F12 level of theory using 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 random structures in the energy range 0–15
076 random structures in the energy range 0–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 relative to the trans minimum. The structures were generated by random displacements from cis and trans equilibria as well as from the transition state of the OH torsional motion and with points generated in the internal coordinate path (ICP) coordinate system which was constructed for formic acid. The latter corresponds to curvilinear path for the torsional motion and 8 normal coordinate displacements. The analytic potential fit consists of a zeroth order surface, which is a sum of Morse functions of atom–atom separations, and a correction surface, which is a sum of distributed multivariate Gaussian functions which are a combination of atom–atom separations. In the same work, the authors constructed an internal-coordinate path Hamiltonian (ICPH) using their PES, where a curvilinear path was used for the torsional motion connecting the trans and cis rotamers and the remaining mutually orthogonal rectilinear modes were defined such that the rovibrational coupling constant associated with the motion along the path was minimized. Trigonometric functions were used for the expansion of the single-mode functions along the torsional path coordinate, and harmonic oscillator functions were used for the remaining coordinates. State-specific VSCF and VMP2 calculations were carried out with the ICP Hamiltonian of HCOOH, where the potential included up to four-body coupling terms, whereas in the ICPH-VCI calculations up to five-body coupling terms were included with a maximum overall excitation of up to 10 quanta in the VCI expansion. The change of the zero point energy by including, instead of four-body terms, five-body terms in the Hamiltonian was 2 cm−1 and for the fundamentals ν2, ν3, ν5, ν8ν9 it was within 1 cm−1. For the ν1, ν4, ν6, and ν7 fundamentals slower convergence with a change of up to 6 cm−1 was observed with respect to the increase in the coupling. The ICPH-VCI vibrational energies with respect to the trans-minimum were reported up to 4750 cm−1 with respect to the global trans minimum and 14 bands in the region 0–4720 cm−1 were reassigned based on the VCI coefficients compared to the assignment of Freytes et al.82 The cis-zero point energy (ZPE) and cis states were identified from the quantum number of the torsional mode. The authors note the overestimation of the ν26 and ν36 states in their ICPH-VCI calculations compared to experiment. They also discuss the ambiguity of the assignment of some states in the high-energy region and of increasing excitation, further complicated by the high density of states in this region. They observed a coupling between the ν4, ν5, ν6, and ν7cis states and concluded that the coupling could be an artifact from the definition of the coordinate system. Due to this coupling and the associated slow convergence only states with up to two quanta of excitations relative to the cis-ZPE were reported. The highest cis-HCOOH fundamental ν1 was not reported in this work, and the ν24 overtone was identified to be part of a Fermi doublet with ν2. We report only the transitions identified as fundamentals in their work in Tables 2 and 3.
000 cm−1 relative to the trans minimum. The structures were generated by random displacements from cis and trans equilibria as well as from the transition state of the OH torsional motion and with points generated in the internal coordinate path (ICP) coordinate system which was constructed for formic acid. The latter corresponds to curvilinear path for the torsional motion and 8 normal coordinate displacements. The analytic potential fit consists of a zeroth order surface, which is a sum of Morse functions of atom–atom separations, and a correction surface, which is a sum of distributed multivariate Gaussian functions which are a combination of atom–atom separations. In the same work, the authors constructed an internal-coordinate path Hamiltonian (ICPH) using their PES, where a curvilinear path was used for the torsional motion connecting the trans and cis rotamers and the remaining mutually orthogonal rectilinear modes were defined such that the rovibrational coupling constant associated with the motion along the path was minimized. Trigonometric functions were used for the expansion of the single-mode functions along the torsional path coordinate, and harmonic oscillator functions were used for the remaining coordinates. State-specific VSCF and VMP2 calculations were carried out with the ICP Hamiltonian of HCOOH, where the potential included up to four-body coupling terms, whereas in the ICPH-VCI calculations up to five-body coupling terms were included with a maximum overall excitation of up to 10 quanta in the VCI expansion. The change of the zero point energy by including, instead of four-body terms, five-body terms in the Hamiltonian was 2 cm−1 and for the fundamentals ν2, ν3, ν5, ν8ν9 it was within 1 cm−1. For the ν1, ν4, ν6, and ν7 fundamentals slower convergence with a change of up to 6 cm−1 was observed with respect to the increase in the coupling. The ICPH-VCI vibrational energies with respect to the trans-minimum were reported up to 4750 cm−1 with respect to the global trans minimum and 14 bands in the region 0–4720 cm−1 were reassigned based on the VCI coefficients compared to the assignment of Freytes et al.82 The cis-zero point energy (ZPE) and cis states were identified from the quantum number of the torsional mode. The authors note the overestimation of the ν26 and ν36 states in their ICPH-VCI calculations compared to experiment. They also discuss the ambiguity of the assignment of some states in the high-energy region and of increasing excitation, further complicated by the high density of states in this region. They observed a coupling between the ν4, ν5, ν6, and ν7cis states and concluded that the coupling could be an artifact from the definition of the coordinate system. Due to this coupling and the associated slow convergence only states with up to two quanta of excitations relative to the cis-ZPE were reported. The highest cis-HCOOH fundamental ν1 was not reported in this work, and the ν24 overtone was identified to be part of a Fermi doublet with ν2. We report only the transitions identified as fundamentals in their work in Tables 2 and 3.
The second semiglobal ab initio PES was developed by Richter and Carbonnière56 in 2018 who fit 660 single point calculations at the CCSD(T)-F12a/aug-cc-pVTZ level of theory in the energy range 0–6000 cm−1 relative to the trans minimum. The PES was fit in terms of internal valence coordinates1 (i.e. bond stretches, angles and torsions) with the points generated by the Adaptive Generation of Adiabatic PES (AGAPES) procedure.103 The coordinate definition used is depicted in Fig. 2. The barrier between the two minima along the torsional coordinate τ2 was found to be 4442 cm−1, where the barrier height was found to be affected by the bond-length r1 and the bending angle θ2. The barrier of this PES is 20 cm−1 higher compared to the value reported by Tew and Mizukami.56 For the vibrational Hamiltonian, the exact analytical kinetic energy operator was constructed in the SOP form with the TANA program104 in polyspherical coordinates, and the PES was expanded as a many-body expansion in valence coordinate displacements. The “dead branching”105 option of the AGAPES procedure was used, in which only certain coordinate combinations were selected based on a remoteness measure defined by geometric mean values for the potential coupling terms. Out of the 256 possible coordinate combinations in the four-body expansion, 36, 84 and 126 were kept, for two, three and four-body terms, respectively. A maximal number of terms was kept for the coupling between the θ3 and τ2 coordinates, associated with the ν5 and ν9 fundamentals. Below 3500 cm−1 with respect to the trans ZPE only half the period of the grid of the torsional coordinate was used (τ2 ≤ π/2), such that no cis–trans delocalization effects were included in the computation of the trans states. Full-period calculations were performed between 3500 cm−1–3640 cm−1. The high-lying fundamentals associated with the CH and OH stretch vibrations (ν2, ν1) were computed with the improved relaxation scheme of MCTDH, and all states below 3100 cm−1 for trans and 2700 cm−1 for cis with respect to their respective ground state were computed with the block Davidson scheme of MCTDH. We have included the transitions identified as fundamentals in Tables 2 and 3. The MCTDH reference state was found to have only a minor effect on the convergence of the states. All vibrational states below 3796 cm−1 were converged in either the cis or the trans well, as differentiated by the torsional coordinate, and the first delocalized state was found at 3796 cm−1 above trans ZPE, which was labeled as the ν69 overtone of cis-HCOOH. Four states could not be converged to sufficient accuracy, these were the states at (assignments of Richter Carbonnière in brackets) 3086 cm−1 (ν4 + ν3), 3116 cm−1 (ν28 + ν26) for trans-HCOOH and at 2357 cm−1 (ν9 + ν7 + ν5), 2479 cm−1 (ν27 + ν5) for cis-HCOOH. For most states which were previously identified in literature to be involved in Fermi resonances, a single-configurational description was found to be sufficient, except for the well known ν5/ν29 Fermi resonance, where a mixing of the reference configurations was observed. The computed states of trans-HCOOH were in good agreement with the values reported by Tew and Mizukami with a root mean square deviation (RMSD) of 11 cm−1: the RMSD of the fundamentals, two, three and four quanta excited states were 5 cm−1, 8 cm−1, 9 cm−1 and 25 cm−1, respectively with maximal deviations (MAXDs) for ν3, ν32, ν5 + ν27 and ν27 + ν29. The RMSDs of the cis states were about 49 cm−1 compared to the levels of Tew and Mizukami, where the RMSDs for fundamentals, two and three quanta excited states were 14 cm−1, 49 cm−1 and 111 cm−1, respectively, and the MAXDs were found for the ν8, ν4 + ν8 and ν8 + ν29 states. This discrepancy of the cis results compared to the work of Tew and Mizukami was further investigated by the authors.56 For cis-HCOOH the authors validated their results by performing the AGAPES construction referenced on the cis, instead of the trans geometry: the levels computed with the global PES were found to be consistent with the latter. VPT2 and MCTDH calculations were performed with both the present PES and the 2016 PES of Tew and Mizukami, for which the latter was re-fitted in the SOP form. The VPT2 fundamentals were found to compare well with each other and with the original MCTDH values such that the authors concluded that the disagreement for the cis levels stems from the ICPH-VCI calculations, rather than from the PES. For the cis levels, a mixing of the ν5 and ν6 levels was identified.
4.3 Recent developments
Fundamentals, combination bands and overtone transitions up to approximately 3000 cm−1 with respect to the global trans minimum were computed by Aerts et al.53 in 2020 for the deuterated forms of cis and trans formic acid using the above mentioned PES of Richter and Carbonnière56 with the block-improved relaxation method of MCTDH. The assignment of the states was performed via visualization of the reduced densities of the computed vibrational wavefunctions. The RMSDs with respect to experimental data of the fundamental transitions were found to be 8 cm−1, 7 cm−1 and 3 cm−1 for trans-DCOOD, trans-HCOOD and trans-DCOOH, respectively. The calculations were performed by defining modes combining r1 and θ3, θ1 and θ2, and τ1 and τ2, respectively (see Fig. 2). Aerts et al. confirmed the Fermi resonance ν3/ν28 of trans-DCOOH, already reported by Macoas et al., as identified by the reduced density functions along the important coordinates.Vibrational transition energies were computed by Nejad and Sibert79 up to 4000 cm−1 for HCOOH and isotopologues with sixth order Canonical Van Vleck Perturbation theory (CVPT6) employing both surfaces of Tew and Mizukami and Richter and Carbonnière.56 In their work, the PESs were represented as a Taylor expansion in terms of stretch, bend, and dihedral angles with the valence coordinate definition of Richter and Carbonnière.56 Up to four-body coupling terms were used for the PES, and the elements of the exact kinetic energy operator were expanded up to the sixth order in the internal coordinates. The CVPT6 calculations were performed with the Hamiltonian constructed in curvilinear normal coordinates based on only one geometry. As a basis for the matrix representations, a product of harmonic oscillator functions was used where the excitation degree of each oscillator was limited. A slightly faster convergence of the trans-HCOOH states obtained with the 2016 PES of Mizukami and Tew as compared to the 2018 PES of Richter and Carbonnière was observed with regard to the order of perturbation, where fourth and sixth order corrections were found to be especially important for higher lying vibrational transitions. Slower convergence was observed for the cis-HCOOH states on the 2016 compared to the 2018 PES. It was found, that the 2016 surface generally overestimates, whereas the 2018 PES often underestimates the transition energies for all isotopologues as compared to experimental values, where increasing deviations were found for higher lying vibrational states. The CVPT6 fundamentals of trans-HCOOH compared within 2 cm−1 to ICPH-VCI and MCTDH results of the respective surface (see Table 2). For cis-HCOOH it was suggested by the authors that the ICPH-VCI results of Tew and Mizukami were not fully converged. The band assignment was performed based on the leading coefficient in the VCI expansion and in comparison to previous calculations and previously assigned IR and Raman bands reported in literature. 11 new vibrational band centers were assigned for trans-HCOOH and 53 for the deuterated isotopologues by the authors with multiple reassignments in comparison to previous assignments from theory or experiment. For trans formic acid strong coupling among the states which share the polyad quantum number Np = n5 + n9/2 was found, with an involvement of the ν1 fundamental at higher energies.
Most recently, Martín Santa Daría, Avila, and Mátyus performed calculations using the 2016 PES of Tew and Mizukami with a Hamiltonian constructed using the cis–trans torsional coordinate and eight curvilinear normal coordinates defined with respect to an instantaneous reference configuration along the torsional motion.30 The curvilinear normal coordinates were adapted to the cis–trans isomerization of formic acid by relaxing the internal coordinates such that the potential energy was at minimum along the torsional motion. In principle, the kinetic and potential energy coupling among the coordinates was reduced by employing curvilinear normal coordinates. The kinetic energy operator was constructed numerically with the kinetic and potential energy integrals evaluated over the direct product basis with the GENIUSH (general rovibrational code with numerical, internal-coordinate, user-specified Hamiltonians) code.106 For the curvilinear normal coordinates harmonic oscillator basis functions and for the torsional degree of freedom a Fourier basis was used. A Smolyak grid was then used for the truncated direct product basis for the evaluation of the multi-dimensional integrals. The authors computed converged vibrational states up to ca. 4700 cm−1 with respect to the trans-ZPE, slightly above the cis–trans isomerization barrier and therefore the highest-energy cis ν1 fundamental was not computed. The convergence was evaluated by increasing the basis set size. The energy difference between calculations using the same basis set size was performed with rectilinear and relaxed curvilinear normal coordinates and the difference was found to be around 8–10 cm−1, with an increasing difference in the higher energy region. The assignment of the cis-states was performed in terms of the contribution of the 1D torsional basis function, which in the lower energy ranges was localized in either well. A variational improvement of up to 5–10 cm−1 was reported compared to the CVPT6 results and by 10–40 cm−1 compared to the previously computed ICPH-VCI levels. Beyond 3700 cm−1, mixed cis–trans states were reported and the “tunneling splittings” associated with these mixed states were computed to be below 1–5 cm−1, almost within the convergence uncertainty of the calculations. Beyond 3900 cm−1, non-negligible contributions from delocalized torsional states were observed. We note, that although the results of the authors unequivocally indicate the switching of the ν5 and ν6cis-HCOOH states as opposed to previous calculations, in Table 3 we list the labeling to be consistent with previous results.
Finally, we discuss the recent work of Aerts et al., who simulated the intramolecular vibrational redistribution (IVR) dynamics of formic acid on the 2018 PES of Richter and Carbonniére with the goal of identifying a possible laser-induced trans–cis isomerization pathway. The dynamical evolution following the excitation of an infrared-active vibration was simulated by the time-evolution of an initial vibrational wave function which was prepared by the excitation of the single particle function of the torsional mode τ2 associated with the isomerization. The probability of finding the molecule in the trans well, as defined by the value of the torsional coordinate, was followed during the evolution, and local energies were ascribed to each mode. By investigating the time-evolution of the fractional energies defined for each overtone of the local torsional vibration of trans-HCOOH, multiple mode-couplings and resonances were identified and confirmed. The ν5/ν29 Fermi resonance was observed as a strong, reversible energy flow between the two fundamentals, also for states sharing the previously mentioned polyad quantum number Np = n5 + n9/2. A coupling between the modes of the ν9 and ν4 fundamentals was identified. The probability to find the wavepacket in the initial trans well was found to diminish at ν69 at which part of the wavepacket transfered from trans to cis within 100 fs. The non-periodic probability indicated, that this transition between trans and cis is irreversible.
5 Summary
We have reviewed first principles, anharmonic studies on the molecular vibrations of formic acid in its monomer form and collected all reported computed transitions identified as fundamentals for both cis- and trans-HCOOH. Formic acid has been a widely explored albeit challenging system to both experiment and theory. On one hand, the spectrum is dense and complex in certain spectral ranges and requires a careful rovibrational analysis83 and experimental differentiation of the signals arising due to its possible geometries.107 Undistorted, high-resolution experimental data has still not been recorded for all of the available cis transitions predicted by theory. On the other hand, the higher-energy vibrations of the molecule are expected to explore trans and cis geometries or both,30 a formidable task for vibrational methods. The minimal energy path connecting the two minima was found to be a function of the τ2 torsional coordinate,56,57 but possible isomerization pathways involving the excitation of the νn1 OH overtones83 or involving ν6 and ν9 were also suggested.2 Early on, multiple resonances affecting the vibrational levels of formic acid were identified, most notably the ν5/ν29 Fermi resonance of trans-HCOOH.48 Hurtmans et al. reported the involvment of the HOC angle in the νn1 excitations,83 however, the first ab initio studies employed rectilinear normal coordinates which were found to be ill-suited for torsional and deformation vibrations.48 The first PESs were computed directly along the normal coordinates48 or as a Taylor20 or a local many-body expansion,35 such that vibrations with a local trans character could be predicted. The development of analytic semiglobal PESs capable of reproducing transitions both from the cis and trans minima followed.56,62 Transitions of cis- and trans-HCOOH were computed with a Hamiltonian constructed with normal coordinates along the curvilinear isomerisation path, and the computed high-energy cis states were found to be coupled significantly.62 The vibrational transitions were also computed with the dynamical MCTDH method in valence coordinates,56 and the computed cis-states differed significantly from the previously reported results. A comparison between the PESs was made with transitions computed based on a curvilinear normal coordinate Hamiltonian, where the coordinates were defined based on a single geometry.79 The transitions of the deuterated species53,79 and assignments up to 4000 cm−1 with respect to trans-ZPE were also described.79 A curvilinear normal coordinate Hamiltonian adapted to the cis–trans torsional motion was constructed,30 and vibrational states slightly above the isomerisation barrier were reported including cis–trans entangled and delocalized states. Small splittings associated with the high torsional isomerisation barrier were reported. The study of Martín Santa Daría et al. reported the lowest energy variational solutions up to now30 with a good agreement with high-accuracy experimental values for both cis (Table 3) and trans (Table 2) fundamentals.Finally, we discuss the computed vibrations of formic acid which have been identified as fundamentals across the studies mentioned in this work, as compiled in Tables 2 and 3. Although such an analysis is not necessarily warranted considering that different PES and Hamiltonians are used across these approaches, it is still worth analyzing the results in terms of the employed methods. The harmonic analysis performed by many of the studies shows the worst agreement to experimental values with an RMSD ranging from approximately 80–125 cm−1 where generally a better agreement is achieved for the lower energy states. Single-configurational approaches follow with an RMSD ranging from approximately 3.4–31 cm−1. Finally, all multi-configurational methods achieve an RMSD better than 4 cm for the trans-states and better than 8 cm−1 for the cis states, where for the latter conclusions should only be drawn with care due to the few available experimental results.
As a small molecule exhibiting large-amplitude motion, the vibrations of formic acid are comparatively difficult to model, where the computation of converged cis states and highly excited states above the delocalization barrier remains to be challenging due to the strong coupling of the coordinates in this region. We note that these difficulties are illustrative of the challenges faced for larger systems, since the nuclear dynamics of bigger molecules and clusters can become increasingly intricate but multiconfigurational methods become prohibitively expensive due to their scaling with respect to system size.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Swiss National Science Foundation (grant no. 200021_197207).Notes and references
- E. B. Wilson, J. C. Decius and P. C. Cross, Molecular vibrations: the theory of infrared and Raman vibrational spectra, Courier Corporation, 1980 Search PubMed.
- A. Aerts, A. Brown and F. Gatti, J. Chem. Phys., 2022, 5, 0098819 Search PubMed.
- S. Wilson, Handbook of molecular physics and quantum chemistry, Wiley, 2003, vol. 2 Search PubMed.
- A. G. Császár, C. Fábri, T. Szidarovszky, E. Mátyus, T. Furtenbacher and G. Czakó, Phys. Chem. Chem. Phys., 2012, 14, 1085–1106 RSC.
- J. K. Watson, Mol. Phys., 1968, 15, 479–490 CrossRef CAS.
- J. K. Watson, Mol. Phys., 1970, 19, 465–487 CrossRef CAS.
- E. Mátyus, G. Czakó, B. T. Sutcliffe and A. G. Császár, J. Chem. Phys., 2007, 127, 084102 CrossRef PubMed.
- T. C. Thompson and D. G. Truhlar, J. Chem. Phys., 1982, 77, 3031–3035 CrossRef CAS.
- K. Yagi, M. Keçeli and S. Hirata, J. Chem. Phys., 2012, 137, 204118 CrossRef PubMed.
- T. Mathea, T. Petrenko and G. Rauhut, J. Phys. Chem. A, 2021, 125, 990–998 CrossRef CAS PubMed.
- P. T. Panek and C. R. Jacob, J. Chem. Phys., 2016, 144, 164111 CrossRef PubMed.
- T. Mathea and G. Rauhut, J. Chem. Phys., 2020, 152, 194112 CrossRef CAS PubMed.
- A. Aerts, M. R. Schäfer and A. Brown, J. Chem. Phys., 2022, 156, 164106 CrossRef CAS PubMed.
- J. M. Bowman, T. Carrington and H.-D. Meyer, Mol. Phys., 2008, 106, 2145–2182 CrossRef CAS.
- M. Neff and G. Rauhut, J. Chem. Phys., 2009, 131, 124129 CrossRef PubMed.
- V. Barone, M. Biczysko, J. Bloino, M. Borkowska-Panek, I. Carnimeo and P. Panek, Int. J. Quantum Chem., 2012, 112, 2185–2200 CrossRef CAS.
- O. Christiansen, Phys. Chem. Chem. Phys., 2012, 14, 6672 RSC.
- T. K. Roy and R. B. Gerber, Phys. Chem. Chem. Phys., 2013, 15, 9468 RSC.
- T. Carrington, J. Chem. Phys., 2017, 146, 120902 CrossRef PubMed.
- J. Demaison, M. Herman and J. Liévin, J. Chem. Phys., 2007, 126, 164305 CrossRef CAS PubMed.
- Q. Yu, C. Qu, P. L. Houston, R. Conte, A. Nandi and J. M. Bowman, Vibrational Dynamics of Molecules, World Scientific Publishing, 2022, pp. 296–339 Search PubMed.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS.
- F. Gatti, B. Lasorne, H.-D. Meyer and A. Nauts, Applications of Quantum Dynamics in Chemistry, Springer International Publishing, Cham, 2017, vol. 98 Search PubMed.
- R. J. Whitehead and N. C. Handy, J. Mol. Spectrosc., 1975, 55, 356–373 CrossRef CAS.
- J. M. Bowman, J. Chem. Phys., 1978, 68, 608–610 CrossRef CAS.
- O. Christiansen, Phys. Chem. Chem. Phys., 2007, 9, 2942 RSC.
- L. S. Norris, M. A. Ratner, A. E. Roitberg and R. B. Gerber, J. Chem. Phys., 1996, 105, 11261–11267 CrossRef CAS.
- J. O. Jung and R. B. Gerber, J. Chem. Phys., 1996, 105, 10332–10348 CrossRef CAS.
- T. Carrington, Mathematics, 2018, 6, 13 CrossRef.
- A. Martín Santa Daría, G. Avila and E. Mátyus, J. Mol. Spectrosc., 2022, 385, 111617 CrossRef.
- B. Schröder and G. Rauhut, Vibrational Dynamics of Molecules, World Scientific Publishing, 2022, pp. 1–40 Search PubMed.
- J. M. Bowman, K. Christoffel and F. Tobin, J. Phys. Chem., 1979, 83, 905–912 CrossRef CAS.
- T. Mathea and G. Rauhut, J. Comput. Chem., 2021, 42, 2321–2333 CrossRef CAS PubMed.
- T. Mathea, T. Petrenko and G. Rauhut, J. Comput. Chem., 2022, 43, 6–18 CrossRef CAS PubMed.
- W. Mizukami and D. P. Tew, J. Chem. Phys., 2013, 139, 194108 CrossRef PubMed.
- M. Beck, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- S. Heislbetz and G. Rauhut, J. Chem. Phys., 2010, 132, 124102 CrossRef PubMed.
- E. Fermi, Z. Phys., 1931, 71, 250–259 CrossRef CAS.
- V. Z. Williams, J. Chem. Phys., 1947, 15, 243–251 CrossRef CAS.
- J. E. Bertie and K. H. Michaelian, J. Chem. Phys., 1982, 76, 886–894 CrossRef CAS.
- J. E. Bertie, K. H. Michaelian, H. H. Eysel and D. Hager, J. Chem. Phys., 1986, 85, 4779–4789 CrossRef CAS.
- M. Pettersson, J. Lundell, L. Khriachtchev and M. Räsänen, J. Am. Chem. Soc., 1997, 119, 11715–11716 CrossRef CAS.
- K. L. Goh, P. P. Ong, H. H. Teo and T. L. Tan, Spectrochim. Acta, Part A, 2000, 11 Search PubMed.
- O. Baskakov, S. Alanko and M. Koivusaari, J. Mol. Spectrosc., 1999, 198, 40–42 CrossRef CAS PubMed.
- O. Baskakov, H. Bürger and W. Jerzembeck, J. Mol. Spectrosc., 1999, 193, 33–45 CrossRef CAS PubMed.
- T. L. Tan, K. L. Goh, P. P. Ong and H. H. Teo, J. Mol. Spectrosc., 1999, 6 Search PubMed.
- T. L. Tan, K. L. Goh, P. P. Ong and H. H. Teo, J. Mol. Spectrosc., 1999, 5 Search PubMed.
- E. M. Maçôas, J. Lundell, M. Pettersson, L. Khriachtchev, R. Fausto and M. Räsänen, J. Mol. Spectrosc., 2003, 219, 70–80 CrossRef.
- F. Madeja, A. Hecker, S. Ebbinghaus and M. Havenith, Spectrochim. Acta, Part A, 2003, 59, 1773–1782 CrossRef.
- W. Luo, Y. Zhang, W. Li and C. Duan, J. Mol. Spectrosc., 2017, 334, 22–25 CrossRef CAS.
- R. A’dawiah, T. Tan and L. Ng, J. Mol. Spectrosc., 2018, 349, 43–48 CrossRef.
- S. Oswald, E. Meyer and M. A. Suhm, J. Phys. Chem. A, 2018, 122, 2933–2946 CrossRef CAS PubMed.
- A. Aerts, P. Carbonnière, F. Richter and A. Brown, J. Chem. Phys., 2020, 152, 024305 CrossRef CAS PubMed.
- A. Nejad, M. A. Suhm and K. A. E. Meyer, Phys. Chem. Chem. Phys., 2020, 22, 25492–25501 RSC.
- A. Perrin, J. Vander Auwera and Z. Zelinger, J. Quant. Spectrosc. Radiat. Transfer, 2009, 110, 743–755 CrossRef CAS.
- F. Richter and P. Carbonnière, J. Chem. Phys., 2018, 148, 064303 CrossRef PubMed.
- W. H. Hocking, Z. Naturforsch A, 1976, 9 Search PubMed.
- R. G. Lerner, B. P. Dailey and J. P. Friend, J. Chem. Phys., 1957, 26, 680–683 CrossRef CAS.
- E. Willemot, D. Dangoisse and J. Bellet, J. Mol. Spectrosc., 1978, 73, 96–119 CrossRef CAS.
- V. Lattanzi, A. Walters, B. J. Drouin and J. C. Pearson, Astrophys. J., Suppl. Ser., 2008, 176, 536–542 CrossRef CAS.
- O. I. Baskakov, B. P. Winnewisser, I. R. Medvedev and F. C. De Lucia, J. Mol. Struct., 2006, 795, 42–48 CrossRef CAS.
- D. P. Tew and W. Mizukami, J. Phys. Chem. A, 2016, 120, 9815–9828 CrossRef CAS PubMed.
- J. M. Hermida-Ramón and R. A. Mosquera, Chem. Phys., 2006, 323, 211–217 CrossRef.
- A. Almenningen, O. Bastiansen, T. Motzfeldt, D. Heinegård, A. T. Balaban and J. C. Craig, Acta Chem. Scand., 1969, 23, 2848–2864 CrossRef CAS.
- G. H. Kwei and R. F. Curl, J. Chem. Phys., 1960, 32, 1592–1594 CrossRef CAS.
- E. M. S. Maçôas, L. Khriachtchev, M. Pettersson, R. Fausto and M. Räsänen, J. Chem. Phys., 2004, 121, 1331–1338 CrossRef PubMed.
- M. Pettersson, E. M. S. Maçôas, L. Khriachtchev, J. Lundell, R. Fausto and M. Räsänen, J. Chem. Phys., 2002, 117, 9095–9098 CrossRef CAS.
- A. Domanskaya, K. Marushkevich, L. Khriachtchev and M. Räsänen, J. Chem. Phys., 2009, 130, 154509 CrossRef PubMed.
- L. G. Bonner and R. Hofstadter, J. Chem. Phys., 1938, 6, 531–534 CrossRef CAS.
- L. Bonner and J. Kirby-Smith, Phys. Rev., 1940, 57, 1078 CrossRef CAS.
- R. C. Millikan and K. S. Pitzer, J. Am. Chem. Soc., 1958, 80, 3515–3521 CrossRef CAS.
- Y. Maréchal, J. Chem. Phys., 1987, 87, 6344–6353 CrossRef.
- O. Baskakov, J. Mol. Spectrosc., 2001, 208, 194–196 CrossRef CAS.
- O. Baskakov, J. Mol. Spectrosc., 2002, 213, 1–7 CrossRef CAS.
- O. Baskakov, J. Lohilahti and V.-M. Horneman, J. Mol. Spectrosc., 2003, 219, 191–199 CrossRef CAS.
- R. Georges, M. Freytes, D. Hurtmans, I. Kleiner, J. Vander Auwera and M. Herman, Chem. Phys., 2004, 305, 187–196 CrossRef CAS.
- P. Zielke and M. A. Suhm, Phys. Chem. Chem. Phys., 2007, 9, 4528 RSC.
- O. Birer and M. Havenith, Annu. Rev. Phys. Chem., 2009, 60, 263–275 CrossRef CAS PubMed.
- A. Nejad and E. L. Sibert, J. Chem. Phys., 2021, 154, 064301 CrossRef CAS PubMed.
- V. E. Bondybey, A. M. Smith and J. Agreiter, Chem. Rev., 1996, 96, 2113–2134 CrossRef CAS PubMed.
- A. Barnes, W. Orville-Thomas, A. Müller and R. Gaufrès, Matrix isolation spectroscopy, Springer Science\Business Media, 2012, vol. 76 Search PubMed.
- M. Freytes, D. Hurtmans, S. Kassi, J. Liévin, J. Vander Auwera, A. Campargue and M. Herman, Chem. Phys., 2002, 283, 47–61 CrossRef CAS.
- D. Hurtmans, F. Herregodts, M. Herman, J. Liévin, A. Campargue, A. Garnache and A. A. Kachanov, J. Chem. Phys., 2000, 113, 1535–1545 CrossRef CAS.
- A. Nejad and M. A. Suhm, J. Indian Inst. Sci., 2020, 100, 5–19 CrossRef.
- K. Goh, P. Ong and T. Tan, Spectrochim. Acta, Part A, 1999, 55, 2601–2614 CrossRef.
- H. Susi and J. R. Scheker, Spectrochim. Acta, Part A, 1969, 25, 1243–1263 CrossRef CAS.
- K. A. E. Meyer and M. A. Suhm, J. Chem. Phys., 2018, 149, 104307 CrossRef PubMed.
- M. Takami and K. Shimoda, Jpn. J. Appl. Phys., 1974, 13, 1699 CrossRef CAS.
- A. Perrin, J.-M. Flaud, B. Bakri, J. Demaison, O. Baskakov, S. Sirota, M. Herman and J. Auwera, J. Mol. Spectrosc., 2002, 216, 203–213 CrossRef CAS.
- O. I. Baskakov, V.-M. Horneman, J. Lohilahti and S. Alanko, J. Mol. Struct., 2006, 795, 49–53 CrossRef CAS.
- E. M. S. Maçôas, L. Khriachtchev, M. Pettersson, R. Fausto and M. Räsänen, Phys. Chem. Chem. Phys., 2005, 7, 743–749 RSC.
- K. Marushkevich, L. Khriachtchev, J. Lundell and M. Räsänen, J. Am. Chem. Soc., 2006, 128, 12060–12061 CrossRef CAS PubMed.
- K. Marushkevich, L. Khriachtchev and M. Räsänen, J. Chem. Phys., 2007, 126, 241102 CrossRef PubMed.
- L. Khriachtchev, J. Mol. Struct., 2008, 880, 14–22 CrossRef CAS.
- L. O. Paulson, D. T. Anderson, J. Lundell, K. Marushkevich, M. Melavuori and L. Khriachtchev, J. Phys. Chem. A, 2011, 115, 13346–13355 CrossRef CAS PubMed.
- K. A. E. Meyer and M. A. Suhm, Chem. Sci., 2019, 10, 6285–6294 RSC.
- J. Sarka, B. Poirier, V. Szalay and A. G. Császár, Spectrochim. Acta, Part A, 2021, 250, 119164 CrossRef CAS PubMed.
- O. Baskakov and J. Demaison, J. Mol. Spectrosc., 2002, 211, 262–272 CrossRef CAS.
- K. L. Goh, P. P. Ong, T. L. Tan, W. F. Wang and H. H. Teo, J. Mol. Spectrosc., 1998, 5 Search PubMed.
- O. I. Baskakov, E. A. Alekseev, R. A. Motiyenko, J. Lohilahti, V.-M. Horneman, S. Alanko, B. P. Winnewisser, I. R. Medvedev and F. C. De Lucia, J. Mol. Spectrosc., 2006, 240, 188–201 CrossRef CAS.
- Y. Scribano and D. M. Benoit, J. Chem. Phys., 2007, 127, 164118 CrossRef PubMed.
- P. R. Franke, J. F. Stanton and G. E. Douberly, J. Phys. Chem. A, 2021, 125, 1301–1324 CrossRef CAS PubMed.
- F. Richter, P. Carbonniere, A. Dargelos and C. Pouchan, J. Chem. Phys., 2012, 136, 224105 CrossRef CAS PubMed.
- M. Ndong, L. Joubert-Doriol, H.-D. Meyer, A. Nauts, F. Gatti and D. Lauvergnat, J. Chem. Phys., 2012, 136, 034107 CrossRef PubMed.
- F. Richter, P. Carbonniere and C. Pouchan, Int. J. Quantum Chem., 2014, 114, 1401–1411 CrossRef CAS.
- E. Mátyus, G. Czakó and A. G. Császár, J. Chem. Phys., 2009, 130, 134112 CrossRef PubMed.
- A. Nejad, K. A. E. Meyer, F. Kollipost, Z. Xue and M. A. Suhm, J. Chem. Phys., 2021, 155, 224301 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |
