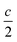Energy storage mechanisms in vacancy-ordered Wadsley–Roth layered niobates

Abstract

Wadsley–Roth (WR) crystallographic shear structures demonstrate high energy and power densities as Li-ion battery anode materials. We report the (de)lithiation behavior of two WR-derived layered niobates: NaNb₃O₈ and KNb₃O₈. Both demonstrate multi-electron (Nb⁵⁺/Nb³⁺) redox on the first discharge, reacting with ≈5 mol Li per mol ANb₃O₈. Li intercalation in NaNb₃O₈ is dominated by Li-diffusion kinetics and evolution of the interlayer structure, with Li initially filling octahedral sites near the interlayer space to draw the layers together to form a (2 × 2)_∞ WR structure. This average structure change pushes Na ions into the square channels, blocking fast Li diffusion down the square channels that provide the fast Li-ion conduction in most WR materials. Upon charge, Li ions incorporated into the octahedral WR sites (ordered vacancies in the layered structure) are extracted, revealing a new, reversible Li site for additional capacity in WR-like materials. The behavior of KNb₃O₈ is similar, but has additional hysteresis associated with its larger counter-cation. While neither layered niobate matches the demonstrated performance of WR materials, by studying them, we identify a route for increased capacity in WR-like frameworks. Additionally, we identify the important role of Li diffusion kinetics and counter-cations in the cycling behavior of WR-derived structures.

---

1 Introduction

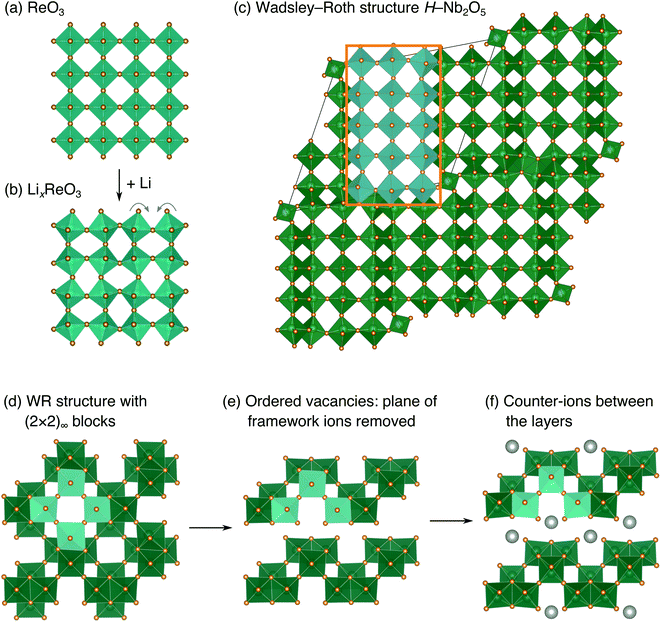
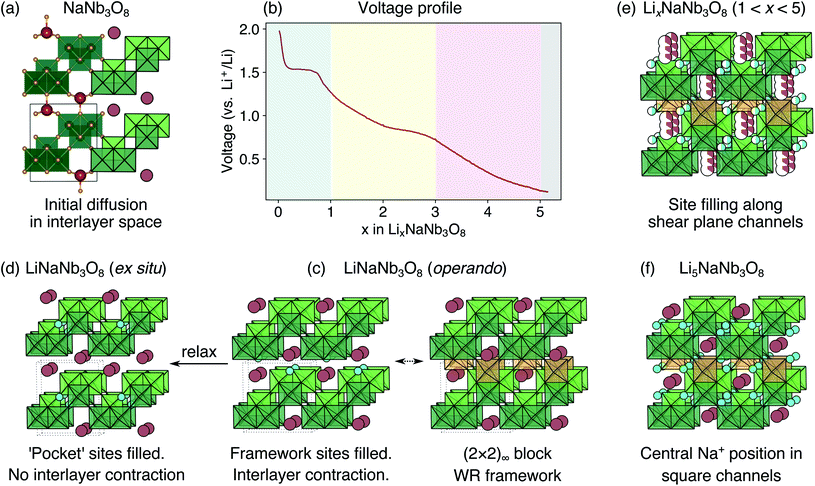
The development of high-power Li-ion batteries requires new anode materials to replace graphite, which fails catastrophically at high cycling rates.^1,2 Transition metal oxides (TMOs) with intermediate potentials relative to Li⁺/Li (termed ‘high potential anodes’) provide fast, reversible Li-ion diffusion, high capacities, and excellent structural and chemical stability.³ Among candidate TMO anodes, Wadsley–Roth (WR) crystallographic shear materials, such as TiNb₂O₇, Ti₂Nb₁₀O₂₉, H–Nb₂O₅, Nb₁₆W₅O₅₅, and Nb₁₈W₈O₆₉, exhibit some of the highest capacities and best power densities.^4–11 WR materials are a broad structural family, primarily consisting of [MO₆] octahedra (where M is a transition metal) forming ReO₃-like units linked in various connectivities, and sometimes containing [MO₄] tetrahedra.^12,13 They are typically oxides based upon Ti, Nb, Mo, V, and/or W, but may be formed with other framework cation species, such as Hf, Fe, P, or Ge, and can exhibit partial occupancy of F on the anion sites.^14–20 The wide composition space of WR materials offers opportunities to chemically and structurally tune Li intercalation behavior to optimize energy storage performance.

The parent structure of WR phases, ReO₃ [Fig. 1a, International Crystal Structure Database (ICSD) 16810 (ref. 21)], is formed of [ReO₆] octahedra in a corner-sharing arrangement. ReO₃ has poor charge storage properties due to correlated rotations of the [ReO₆] octahedra that occur upon Li insertion (Fig. 1b).²² The rotations change the nature of Li-diffusion channels (Fig. 1a and b) and result in an electronically insulating material upon deep discharge.^22–25 In WR materials, ReO₃-like units form (m × n)_∞ blocks [e.g., the (3 × 5)_∞ in H–Nb₂O₅, Fig. 1c].¹² The blocks terminate at shear planes where the octahedra in the ReO₃-like units are linked through their edges to neighboring blocks. These shear planes provide rigidity to the framework, preventing correlated rotations of the octahedra upon lithiation, during which diffusion is predominantly 1D, down square channels in the centers of the blocks.^7,8,23,26 As a result, structural changes across a wide operating composition range are mostly limited to subtle expansions and contractions of lattice parameters.^7,8 Because the WR framework structure does not change significantly during lithiation, Li ions retain similar intercalation geometries across different states of charge that result in fast diffusion.^26,27 Motivated by their excellent anode properties, we investigated the electrochemical energy storage behavior of variations on the WR structure using complex niobates with layered and ordered-cation-vacancy motifs (Fig. 1d–f).

Fig. 1 (a) ReO₃ square channels (b) change shape upon lithiation as [ReO₆] octahedra begin to tilt (ReO₃ framework of Li_0.2ReO₃, Li not shown). (c) Wadsley–Roth crystallographic shear structures can be considered as ReO₃-like blocks connected by shear planes (at the orange block edges), across which neighboring blocks have edge-rather than corner-sharing [MO₆] octahedra. (d) Hypothetical WR structure with (2 × 2)_∞ blocks. (e) Ordered framework cation vacancies leave layers with the composition M₃O₈. (f) Counter-cations reside in sites near the framework vacancies and push the layers apart.

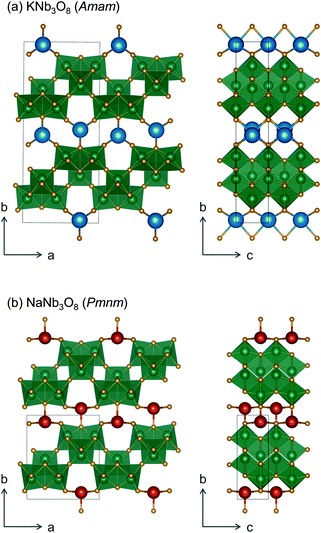
We report the lithiation mechanism, Li-ion diffusion pathways, and average structure evolution in layered niobates NaNb₃O₈ and KNb₃O₈. These are derived from a hypothetical body-centred tetragonal (2 × 2)_∞ WR structure²⁸ by replacing a plane of framework Nb atoms with ordered vacancies, resulting in Nb₃O₈ sheets with a combination of edge- and corner-sharing octahedra (Fig. 2a,b). Large K⁺ or Na⁺ counter-cations reside near the ordered vacancies and prop the sheets apart to form a layered framework [general example in Fig. 1f, specific cases in Fig. 2, ICSD 31994 (ref. 29) and ICSD 202400,³⁰ respectively]. The counter-cation size and preferred coordination impact the layer stacking, both in terms of interlayer distance and stacking sequence. In KNb₃O₈, adjacent Nb₃O₈ layers are off-set from one-another by 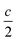, giving AB stacking, while NaNb₃O₈ has AA stacking, approximately halving the unit cell volume (Fig. 2).

Fig. 2 In (a) KNb₃O₈ and (b) NaNb₃O₈, Nb₃O₈ layers are separated by counter-cations. The size and preferred coordination of counter-cation (K or Na) determine the interlayer spacing as well as the stacking sequence of adjacent layers, AB for KNb₃O₈ (with B shifted by ) and AA in NaNb₃O₈.

Electrochemical cycling of KNb₃O₈ as an electrode has been previously reported for Na- and Li-ion-based energy storage.^31–33 To the best of our knowledge, this is the first reported electrochemical cycling of NaNb₃O₈. In the previous electrochemical studies of KNb₃O₈, asymmetric cycling profiles indicate a different path upon discharge and charge, as has been observed for other K–Nb–O compounds.^34,35 Incorporation of specialized carbon additives and reduction of particle dimensions have been reported and show improved rate capabilities and capacity retention,^32,33 but the underlying intercalation mechanisms have not yet been discerned, and are our focus here.

The electrochemical energy-storage behavior of NaNb₃O₈ and KNb₃O₈ as Li-ion electrodes was analyzed using a combination of ex situ and operando X-ray diffraction (XRD), high-resolution transmission electron microscopy (HRTEM), solid-state nuclear magnetic resonance (NMR) spectroscopy of ⁹³Nb, ²³Na, and ⁷Li nuclei, and hybrid-exchange density-functional-theory (DFT) calculations. The work reveals new insights into Li diffusion kinetics, structural transformations, and charge-storage mechanisms in WR-derived materials with layered and vacancy-ordered modifications and counter-cations.

2 Results & discussion

2.1 Synthesis and initial structures

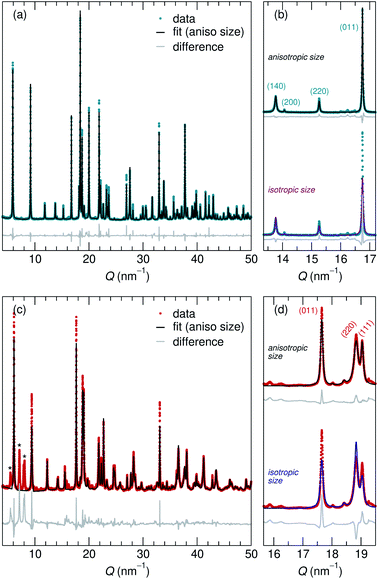
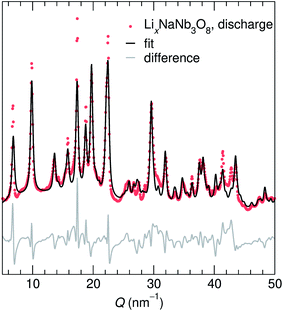
Adapting previously reported molten-salt syntheses,^36,37 we produced KNb₃O₈ by heating K₂CO₃ and Nb₂O₅ in molten KCl at 800 °C for 5 h. High-resolution synchrotron XRD showed agreement with the published Amam structure.²⁹ However, there appeared to be peak intensity mismatch for several reflections, including some at low momentum transfer, Q (Fig. 3a). TEM micrographs indicate rectangular platelets with particle dimensions varying as a function of crystallographic direction (Fig. 4a–c). SAED patterns show well-defined diffraction spots without streaking, consistent with a regular stacking arrangement and the absence of stacking faults.

Fig. 3 High resolution 11-BM XRD data shows crystalline (a) KNb₃O₈ and (c) NaNb₃O₈. (a) Rietveld refinement reveals anisotropic particle size broadening and isotropic strain, and captures the peak shapes and intensities. The importance of these features is highlighted in (b) and (d) by comparing peak intensity mismatch (arising from peak width differences) for models with anisotropic (top) and isotropic (bottom) particle shape for KNb₃O₈ and NaNb₃O₈, respectively. (c) Despite several impurity peaks (marked by *), including the same anisotropic particle size and isotropic strain also captures peak shapes and intensities for NaNb₃O₈. The y-axis in these plots corresponds to the intensity of X-ray scattering, which is shown here on a arbitrary scale.

Fig. 4 (a) SEM reveals rectangular platelets of as-prepared KNb₃O₈ powders. (b) Bright-field TEM image of a KNb₃O₈ crystallite cross-section imaged along the [100] direction. (c) SAED along the [100] direction shows no extended defects, revealing sharp reflections without any diffuse streaking, suggesting a well-ordered layer-stacking sequence along the [010] direction. (d) SEM of NaNb₃O₈ shows a decreased particle size and increased size dispersity, but still a platelet shape.

Rather than extended defects, the apparent peak intensity mismatch was in fact systematic index-dependent width mismatch for several reflections, which resulted from anisotropic particle size along crystallographic directions. Integrated intensity of synchrotron XRD data was overall well-captured using Rietveld refinement with an anisotropic size broadening model (based on linear combinations of spherical harmonics) and an isotropic strain parameter contributing to the Lorentzian line shape (Fig. 3). The dramatic shape anisotropy evident in micrographs is reflected in refined average dimensions for the principal axes of 263.9 nm (h00), 78.6 nm (0k0), and 6511 nm (00l). It is important to note that the method for extracting these quantitative results gives only the average value of particle size along each direction, and does provide information on the distribution of particle sizes. The relative refined particle dimensions are consistent with TEM micrographs, which together indicate the platelets' shortest dimension in the stacking direction (lattice parameter b) and their longest dimension along the chains of edge-sharing polyhedra (lattice parameter c) (Fig. 4). The XRD fit with isotropic size broadening and isotropic strain is shown for comparison in Fig. 3b, which highlights the index-dependent peak broadening.

A survey of other studies on KNb₃O₈ found their XRD data have a variation of maximum peak intensity of the same reflections across samples.^38–40 While these studies did not model microstructure effects in their diffraction data, it is likely that the deviations resulted from anisotropic particle size, preferred orientation, or a combination thereof. These various distributions of peak intensities per reflection character suggest a dependence of morphology on synthesis route (e.g., molten salt, solid state, hydrothermal).

NaNb₃O₈ was prepared from KNb₃O₈ using soft chemical methods, with intermediate hydrate phases.³⁰ In several repetitions of the synthesis, there were variations in the phase purity of intermediate hydrates that resulted in a minor fraction of unidentified phase(s) (≤ 5% by volume) in addition to NaNb₃O₈ (Fig. 3c). High-resolution XRD of NaNb₃O₈ revealed a similar index-dependent variation of peak width as that observed for KNb₃O₈, and the general features were modeled using a similar combination of isotropic strain and anisotropic particle size broadening. SEM (Fig. 4d) shows a larger dispersity of particle dimensions for NaNb₃O₈ than KNb₃O₈. This dispersity, as well as the impurity, leads to less confidence in the quantitative particle size from refinement due to the overall poorer fit. However, the particles once again had their shortest dimension in the stacking direction (lattice parameter b) and their longest in the direction of the polyhedral chains (lattice parameter c). Additional complexity in the analysis of NaNb₃O₈ may also arise from a higher degree of strain, which could be introduced during the low temperature ion-exchange process, though we are not able to quantitatively determine this with the dataset.

Further details about Rietveld analysis of KNb₃O₈ and NaNb₃O₈ are provided in the Methods and ESI† sections, including expanded plots of XRD data and fits (Fig. S1 and S2†).

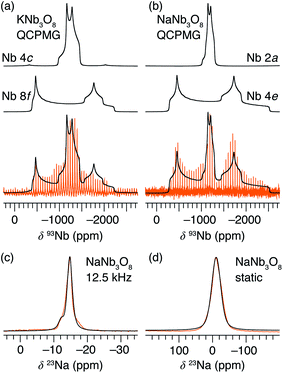
Average structure characterization is complemented by the local structure perspective from solid-state nuclear magnetic resonance (NMR) spectroscopy. Despite the change in stacking sequence upon ion-exchange from K⁺ to Na⁺, and associated decrease in interlayer spacing, the intralayer structure remains very similar, as reflected in the refined average structure as well as the similar features in the ⁹³Nb NMR spectra (Fig. 5a and b). For KNb₃O₈ and NaNb₃O₈, the ⁹³Nb central-transition spectra, collected using the quadrupolar Carr–Purcell–Meiboom–Gill (QCPMG) sequence, span about 2000 ppm at 9.4 T at room temperature (Fig. 5a and b). The two Nb sites in the structures can be fit using two quadrupolar lineshapes with numerical simulations guided by CASTEP PBE DFT calculations^41–44 and fit to within 15% of the calculated quadrupolar coupling magnitudes. The local coordination is consistent with the structure models wherein the Nb(1) site in the double-width chain is considerably more distorted than Nb(2) in the single-width chain (see calculated and experimental NMR parameters in Tables S3 and S4,† respectively). For NaNb₃O₈, the observed ²³Na quadrupolar coupling (0.52(5) MHz; the uncertainty value specified in parentheses refers to a single standard deviation associated with the fitting procedure) is far smaller (< 40%) than the calculated value (1.36 MHz), which suggests fast room-temperature Na-ion dynamics (Fig. 5c and d).^45,46

Fig. 5 Solid-state NMR spectra of layered alkali niobates. The static ⁹³Nb spectra of (a) KNb₃O₈ and (b) NaNb₃O₈, collected using the quadrupolar Carr–Purcell–Meiboom–Gill (QCPMG) sequence. Both sets of data (orange) are overlaid by the fit (black) and deconvoluted into signals from the two crystallographically-distinct Nb sites. (c) MAS and (d) static ²³Na spectra (orange) of NaNb₃O₈ fit to a single Na site (black). The y-axis corresponds to intensity, which is shown here on an arbitrary scale.

2.2 Cycling

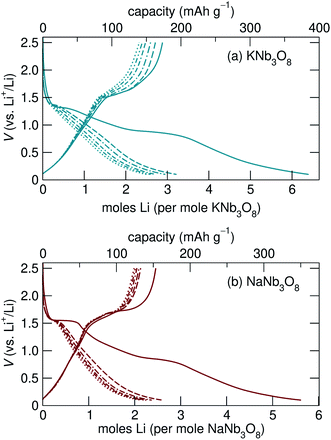
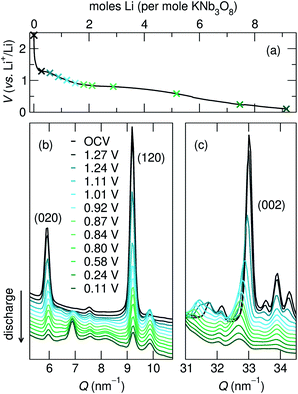
Loose-powder electrodes of the active material mixed with conductive carbon additive (SuperP) were assembled into home-built Swagelok cells for electrochemical cycling against Li metal anodes. As structural evolution rather than absolute cycling performance is the focus of this work, cell construction and cycling parameters were not optimized. The assembled half cells were cycled at slow rates, reacting with 1 mol Li per mol ANb₃O₈ in 30 h; with ≈6 mol Li on the first discharge, this corresponds to roughly C/180; in later cycles reaction with ≈2 mol Li, this corresponds to roughly C/60. The cycling profiles of KNb₃O₈ and NaNb₃O₈ show similar features (Fig. 6). On the first discharge (Fig. 6), both have a plateau near 1.5 V corresponding to a chemical formula of approximately LiANb₃O₈. This high-potential plateau is followed by a sloped region, over which an additional ≈2 mol Li react. A second plateau near 1 V is followed by another sloped region where an additional ≈2 mol Li react.

Fig. 6 Galvanostatic cycling of (a) KNb₃O₈ and (b) NaNb₃O₈, with the first cycle in solid lines and increasingly broken lines for subsequent cycles. In their first cycle, KNb₃O₈ and NaNb₃O₈ have similar cycling profiles, consisting of a combination of plateaued and sloped regions, with asymmetry in the profiles between discharge and charge. Later cycling shows a slow fade in capacity for both compounds.

With the applied cycling conditions, both compounds react with about 6 mol Li per formula unit (or 2 mol Li per mol Nb) on the first discharge. However, as reported by See et al., conductive carbon additives have considerable contributions to capacity during cycling to low potentials.⁴⁷ This effect, in combination with solid electrolyte interphase (SEI) formation, undoubtedly contributes to the measured capacity at low potentials. Future consideration of these materials in applied studies should certainly consider a higher minimum potential limit, but here we focus on identifying charge-storage mechanisms, including at low potentials.

Beyond the first cycle, there is a reversible capacity of ≈3 mol Li per mol KNb₃O₈ (or 1 mol Li per Nb) and ≈2 mol Li per mol NaNb₃O₈, which slowly fades with each cycle in these unoptimized cells (Fig. 6). Second and later discharge cycles have a small plateau and a long sloped region, with the majority of the capacity coming from the latter. Charge cycles begin with a sloped region, which contributes less than half of the reversible capacity, and the majority of the charge capacity takes place over a plateau near 1.5 V. The difference in charge distribution over slopes and plateaus between discharge and charge indicates asymmetric processes, as has been observed for other intercalation electrode materials, including compositionally-related KNb₅O₁₃,³⁵ in which the order of Li sites filling and unfilling varies.

The most notable difference in the cycling of KNb₃O₈ and NaNb₃O₈ is the voltage hysteresis of the high potential plateau between charge and discharge. For KNb₃O₈, the high potential plateaus are separated by about 0.3 V, as opposed to about 0.1 V for NaNb₃O₈. This difference in potentials indicates a difference in the charge-storage processes between these two compounds despite their structural and chemical similarities. To understand this difference, the previously mentioned asymmetric cycling profiles, and generally how these compounds store charge, we detail below the structural evolution at various states of charge using ex situ and operando synchrotron X-ray scattering and DFT, complemented by ex situ NMR and electron microscopy.

2.3 NaNb₃O₈ structural evolution with cycling

2.3.1 First discharge. Operando XRD shows a shift of the 010 and 020 reflections to higher momentum transfer, Q, during the first discharge, indicating a contraction of the b lattice parameter. This is most prominent during the high potential plateau from 0 mol Li to 0.75 mol Li (1.45 V) (Fig. 7). Over the first plateau, there is a discontinuous change of the 002 reflection position to lower Q (Fig. 7c), indicating an expansion of the c lattice parameter. In contrast, ex situ XRD at a similar state of charge shows no apparent evolution from the starting material (NA, discharged to 1.4 V, and NaNb₃O₈, respectively, in Fig. 8, ex situ and operando plotted together in Fig. S3†). After the first plateau, the remainder of the operando discharge reveals only minor changes to the average structure, including some further shifts in peak positions. Both operando and ex situ XRD show qualitatively consistent structures for the first discharge products from cycling (NB, discharged to 0.1 V) (Fig. S3†). Based on their initial and final positions, the 010 and 002 reflections reveal an ≈9% reduction in lattice parameter b (the stacking direction) and a 3.5% increase in c during the first discharge, with an intermediate change in operando XRD data at the end of the high potential plateau (Table 1).

Fig. 7 (a) Galvanostatic discharge of NaNb₃O₈ during operando X-ray scattering and (b and c) operando XRD at select states of charge, marked in (a), shows the evolution of specific reflections during lithiation (* marks a reflection from a component of the operando cell). The y-axis in (b) and (c) corresponds to the intensity of X-ray scattering, which is shown here on a arbitrary scale.

Table 1 The positions of the 010 and 002 reflections of Li_xNaNb₃O₈ at various states of charge, and the their corresponding interplanar spacing, d_hkl, show the progression of these key features of the average structure during discharge

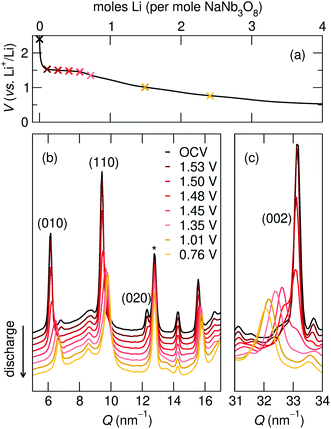
	010 position, (Q, nm^−1)	d 010, (Å)	002 position, (Q, nm^−1)	d 002, (Å)
NaNb3O8 (pre-cycle)	6.2	10.2	33.1	1.9
Operando partial discharge, to 1.35 V	6.6	9.6	32.4	1.9
Operando full discharge, to 0.1 V	6.7	9.3	31.9	2.0
Ex situ full discharge, to 0.1 V	6.7	9.3	32.0	2.0

---

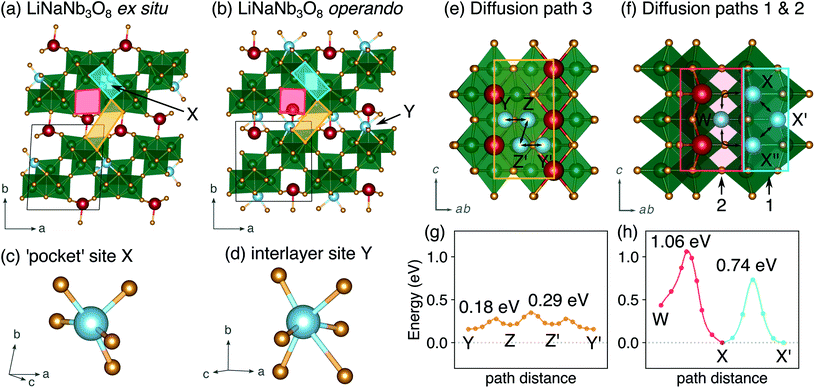
The difference between operando and ex situ XRD results for the intermediate discharge product (approximately LiNaNb₃O₈) are resolved by DFT calculations of the energetics and kinetics of Li site filling. The DFT calculations identify two low-energy sites for Li in NaNb₃O₈ under dilute conditions, labeled X and Y (Fig. 9c and d). Site X is a five-fold coordinated square-pyramidal ‘pocket’ in the Nb₃O₈ layers (Fig. 9a and c) and site Y is a distorted octahedral site in the interlayer space (Fig. 9b and d).

Fig. 8 (a) Galvanostatic cycling of the first 1.5 cycles of NaNb₃O₈ and the states of charge of ex situ samples. (b and c) XRD of pristine NaNb₃O₈ and ex situ cycling products, with (b) structures similar to NaNb₃O₈ at higher potentials and (c) with a distinct average structure from low potentials [data in (c) are scaled up by a factor of 2.5 relative to (b)]. The y-axis in (b) and (c) corresponds to the intensity of X-ray scattering, which is shown here on a arbitrary scale.

Fig. 9 Structures obtained from DFT calculations for intercalation to (LiNaNb)3O₈. (a) Ground-state structure with Li in five-fold coordinate ‘pocket’ sites within Nb₃O₈ layers, corresponding to the structure from ex situ XRD analysis. (b) Metastable structure with Li in distorted octahedral interlayer sites, corresponding to the structure from operando XRD analysis. Figures (c) and (d) show detail of the Li geometry from (a) and (b) respectively. Red, blue, and gold quadrilaterals indicate pathways along the square channels, within the Nb₃O₈ layers, and within the interlayer space, respectively. (e) Diffusion pathway 3 in the interlayer space. (f) Diffusion paths 1 and 2 within the Nb₃O₈ layers. Calculated activation barriers for (g) diffusion along pathway 3 and (h) along paths 1 and 2.

Li ions occupying ‘pocket’ sites are a common feature of WR materials, such as TiNb₂O₇ and Nb₂O₅–WO₃ phases that contain ‘capped’ ReO₃-like units (defined as type II WR cavities by Cava et al.).^6–8,13 To the best of our knowledge, octahedral Li ion sites have not been reported previously in WR-like materials. In the WR phases studied for Li intercalation, framework transition metal (TM) ions typically occupy all of the possible octahedral sites in the defect fcc O²⁻ sublattice.⁴⁸

At a composition of LiNaNb₃O₈, the structure with Li ions filling site X is more stable than with Li ions filling site Y by 0.082 eV per formula unit (f.u.) NaNb₃O₈. The calculated lattice parameters (Table 2) show the framework structure is relatively unchanged with Li ions in the low-energy X sites, consistent with ex situ XRD (Fig. 8 and S3†). In contrast, filling metastable Y sites leads to a contraction of the interlayer space (lattice parameter b) (Fig. 9b), in agreement with operando XRD data (Fig. 7 and S3†). We find the interlayer contraction occurs because the Li ions in Y sites (tucked into voids behind Na⁺) bond to O ions across layers, drawing the Nb₃O₈ layers closer together and pushing Na ions into the square channels.

Table 2 Lattice parameters of key structures obtained from DFT calculations for Li_xNaNb₃O₈. E_{above hull} is the relative energy vs. the most stable structure at that composition

x	Sites	a (Å)	b (Å)	c (Å)	α (°)	β (°)	γ (°)	E above hull (eV f.u.^−1)
a Corresponding to ex situ XRD analysis. b Corresponding to operando XRD analysis.
0		8.853	10.393	3.790	90.000	90.000	90.000	0.000
1	X^a	8.819	10.434	3.887	86.652	90.004	89.995	0.000
	Y^b	8.837	9.342	3.946	90.255	90.004	90.006	0.082
3	Y + Z	8.612	9.254	4.240	90.000	90.006	90.255	0.454
	X + Y	9.133	9.165	4.127	90.000	90.000	86.652	0.000
5	X + Y + X	9.123	9.188	4.262	90.409	91.004	89.987	0.000

---

Using DFT, we compared the kinetics of Li diffusion to fill X and Y sites. Li diffusion in NaNb₃O₈ is one-dimensional and takes place along the c direction, either between or within the Nb₃O₈ layers (Fig. 9e and f). To fill X sites, Li ions must move within the Nb₃O₈ layers either via ‘cross-block’ hops (path 1), which have an activation barrier of 0.74 eV, or through the square channels via a metastable high-energy square-planar site ‘W’ (Fig. S13†), overcoming a barrier of 1.04 eV (path 2) (Fig. 9h). The high barrier for the ‘cross-block’ hop is due to Li–Nb repulsion, while the still higher barrier to move along the square channel results from Li–Na repulsion: Li⁺ must move past Na⁺ to migrate down the channels.

In the interlayer space, Li moves between Y sites following a zig-zag pathway (path 3) through two metastable distorted tetrahedral sites (denoted ‘Z’) (Fig. 9e and g). The activation barrier for mobility in the interlayer space is 0.29 eV, much lower than for paths 1 and 2 within the Nb₃O₈ layers. Diffusion in the interlayer space is therefore kinetically favorable, and leads to the formation of the metastable intermediate cycling product with a contracted interlayer distance and Li in higher energy Y sites, as was observed at the end of the first plateau in operando XRD. In ex situ experiments, Li ions relax to occupy the thermodynamically favorable X sites, allowing the interlayer separation to expand back to a similar distance in the pristine material. We note that Y and Z sites cannot be occupied simultaneously under dilute Li conditions, since the two sites face-share; occupation of a Y site will push an adjacent Li from a Z site into the next Y site. However, under non-dilute conditions, Z sites adjacent to Y sites can be filled, which is discussed in greater detail later.

At the end of the first discharge, ex situ and operando XRD are consistent and indicate a final structure with Li in interlayer and intralayer sites. Rietveld refinement of the ex situ discharge product (NB) using DFT-predicted Li₅NaNb₃O₈ (with all X, Y and Z sites filled) captures the major reflections (Fig. 10). This is in qualitative agreement with our first discharge capacity (≈6 mol Li) with some additional capacity resulting from side reactions at low potentials, a combination of reactions with carbon and solid electrolyte interphase formation.⁴⁷ Additionally, NMR indicates the reduction of all Nb (discussed in detail later), which gives rise to electronic changes in the material and the resulting Nb spectra at the discharged state. Together, the XRD, DFT, and NMR results strongly suggest a complete reaction, or at least homogeneous reactivity, of NaNb₃O₈, even as loose-powder electrodes.

Fig. 10 Ex situ XRD of the first discharge product of NaNb₃O₈ and a fit of the data based on a model with a decreased interlayer spacing and expanded c lattice parameter. The y-axis corresponds to the intensity of X-ray scattering, which is shown here on a arbitrary scale.

2.3.2 First charge. Due to unexpected side reactions at low potentials during the operando discharge of NaNb₃O₈, XRD over the full charge was not captured. However, over the collected potential range, over a slope from 0.1 V to 1.5 V, only minor changes in peak positions and intensities were observed in operando (Fig. S4†) and ex situ XRD (NC, Fig. 8), indicative of a solid solution reaction. In particular, the k-character reflections show that the b lattice parameter remains similar to that of the discharge product (Li₅NaNb₃O₈) over this voltage range. Based on our understanding that occupation of Y sites contracts the interlayer space, this indicates that some Li remains between the layers, even after the removal of ≈2.5 mol Li on charge.

The remainder of the first charge takes place over a plateau at 1.5 V, after which ex situ XRD indicates a final average structure nearly identical to pristine NaNb₃O₈ (ND, Fig. 8) despite some Li remaining in the structure (from NMR, the estimated composition is Li_2.2NaNb₃O₈, see ESI Table S5† for details). This suggests a recovery of the original, larger interlayer spacing, with the remaining Li predominantly occupying ‘pocket’ X sites. Based on our observations of the metastable intermediate discharge product, it is unclear if the ex situ charge product has again evolved between cycling and structural characterization. It is worth noting that operando XRD over only the high potential plateau shows electrochemical and structural reversibility of this interlayer contraction and expansion, as well as a more symmetric galvanostatic profile (Fig. S5†). While the high potential process appears to have symmetric (de)lithiation, the difference in the final composition between the two charge products does not allow for extrapolation of the nature of the charge product following a deeper discharge.

2.3.3 Later cycling. In subsequent cycles, reversible capacity matches that of the first charge. Ex situ XRD to deep on the second cycles shows the same interlayer contraction as the first (NB and NF, Fig. 8). Based on our conclusions from experiment and theory regarding the first charge product, we propose Li that fills the X sites during the first discharge remains there through subsequent cycling, with reversible (de)insertion of Li in the Y and Z sites contributing to the reversible capacity of ≈2 mol Li.

This assignment of X sites as the primary origin of irreversible capacity is supported by our observations for cycling over only the high potential features (using a minimum potential of 1.4 V). Operando XRD over this potential range shows contraction and expansion of the interlayer space, indicating Li (de)insertion into the interlayer Y site and only mild, gradual capacity fade without deep discharge. Likewise, we propose that the reversible capacity in second and later cycles for NaNb₃O₈ arises from the (de)insertion of Li in Z and Y sites.

2.3.4 NMR of Li_xNaNb₃O₈. The local structure during cycling was investigated with ⁹³Nb, ²³Na, and ⁷Li NMR. Upon Li insertion, the two ⁹³Nb resonances corresponding to the two symmetry-independent sites in NaNb₃O₈ do not change position or shape. Instead, they decrease in intensity, until there is no visible feature upon deep discharge (at x ≈ 5) (Fig. 11a, B). This loss of signal can be attributed to the rapid relaxation of the ⁹³Nb nuclei that results from unpaired electrons when the transition metal ions are reduced (to d¹ and d²) upon lithiation, though it cannot be distinguished whether this stems from Curie (localized) or Pauli (delocalized) paramagnetism. On charge, the two ⁹³Nb signals return, indicating that the local structure of some Nb is recovered upon delithiation. As ≈2 mol Li remain at the end of charge, Nb in the vicinity of residual Li remain in a reduced state and are not visible owing to rapid nuclear relaxation.

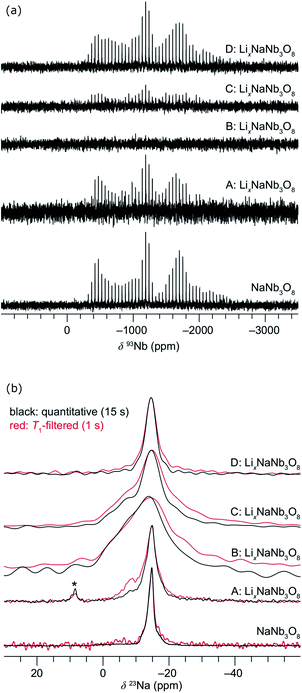Fig. 11 Evolution of the ex situ (a) QCPMG ⁹³Nb MAS NMR and (b) ²³Na MAS NMR of Li_xNaNb₃O₈ at various states of charge. Sample labels correspond to the ex situ cycling and XRD data in Fig. 8: NaNb₃O₈ before cycling, (A) after reaction with 1 mol Li, (B) end of first discharge, (C) halfway through first charge, and (D) at the end of the first charge. The y-axis corresponds to intensity, which is shown here on a relative scale. In (b), quantitative (black) and T₁-filtered (red) spectra are overlaid, recycle delays are given in the legend, and maximum intensities are normalized to highlight the changes in lineshape. A small impurity from sample preparation is denoted with an asterisk.

Upon reaction with Li, the ²³Na resonance broadens and additional intensity is observed at higher frequencies (Fig. 11b, A and B). The full-width at half maximum (FWHM), 2 ppm in pristine NaNb₃O₈ (12.5 kHz MAS), increases to 16 ppm when fully discharged. Upon charge, the ²³Na resonance does not return to its original narrow lineshape and, unlike the Nb local environment, is irreversibly altered from that of the pure compound. This suggests that some Li remains in the structure after charge, affecting the Na local environment.

Another insight from NMR is that no residual ⁹³Nb signal, nor sharp ²³Na signal, is present at the end of discharge, indicating a relatively homogeneous and complete reaction rather than the presence of unlithiated particles or an inhomogeneous distribution of composition across domains. Insights from ⁷Li are limited due to the broad lineshape and narrow shift range; however, two apparent features are (i) the broadened signal at deep discharge and (ii) a resonance that comes in at −7.5 ppm (Fig. S12†). The correlation between line broadening and Li concentration could be due to increased homonuclear dipolar coupling, an increase in the number of sites, or slower kinetics, which limit signal averaging. The negatively shifted resonance is outside the range for diamagnetic Li, but has been observed in other Nb-based oxides, such as WR structure Li_xTiNb₂O₇, where it was correlated with electron localization.⁸

2.4 Site-filling mechanisms in Li_xNaNb₃O₈

2.4.1 (2 × 2)_∞ WR structure of LiNaNb₃O₈ formed during discharge. Guided by insights from ex situ and operando XRD and NMR, DFT calculations were employed to further probe structural changes and site filling during cycling. The interlayer contraction across the first discharge plateau heavily influences the subsequent Li intercalation mechanism, changing the preferred Li diffusion pathways. When viewed along the c-direction, the metastable LiNaNb₃O₈ structure with occupied Y sites resembles a (2 × 2)_∞ WR structure (Fig. 1d), with channels at the edges of the blocks formed by either pairs of [NbO₆] octahedra (cyan) or by one [LiO₆] and one [NbO₆] octahedra (yellow) (Fig. 12, as in Fig. 9a and b). DFT calculations indicate that when octahedral Y sites are filled, Li ions introduced into site Z adopt a new 4- or 5-coordinate geometry, similar to ‘pocket’ type sites at the edges of the WR blocks (Fig. 12b). In total, the crystallographic unit cell containing two formula units of NaNb₃O₈ contains 10 Li intercalation sites; four X, two Y, and four Z sites.

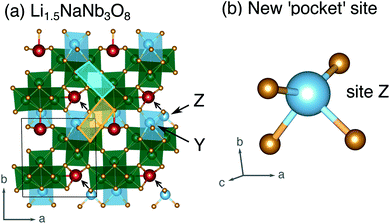Fig. 12 (a) Structure of Li_1.5NaNb₃O₈ with Z sites filled, causing Li–Na repulsion and displacement of Na (red). (b) Geometry of the four-fold-coordinate Li ion in pocket site Z.

In WR materials, rapid Li-ion diffusion typically occurs down the square channels, hopping from window-to-window site with low barriers of ≈0.3 eV to 0.4 eV.^8,26 In pristine NaNb₃O₈, Li–Na repulsion results in a large barrier of 1.04 eV for Li diffusion down the square channels (Fig. 9h). Calculations for Li diffusion along the same path at a composition of LiNaNb₃O₈ with the interlayer sites filled show an increased barrier of 1.48 eV (Fig. S14†). The interlayer contraction causes the Na ions to be pushed into the square channels, further impeding the mobility of Li along this path. Li ions must instead diffuse along the channels at the edges of the blocks, by ‘cross-block’ hops. To fill X sites, Li must move along channels between [NbO₆] octahedra (Fig. 9a, cyan channel), whereas to fill Z sites, the Li ions must move along channels between [LiO₆] and [NbO₆] octahedra (Fig. 9a, gold channel).

Previously published DFT calculations for TiNb₂O₇ revealed the activation barrier for cross-block hops increases as the charge of the framework cation increases, due to greater electrostatic repulsion.⁸ This observation follows a similar principle to the models of Li diffusion in disordered rocksalt compounds, where the activation barrier varies depending on the number of faces the mobile Li shares with Li vs. TMs.^49,50 We therefore expect Li diffusion in Li_xNaNb₃O₈ to be easier between Z sites, down channels formed by [LiO₆] and [NbO₆] octahedra, in which the mobile Li will experience a smaller electrostatic repulsion moving past octahedra containing Li⁺ than Nb^(4+/5+).

2.4.2 Voltage profile from DFT calculations. To examine the site filling mechanisms under dilute conditions and for x > 1 in Li_xNaNb₃O₈, we calculated the energetics of different Li orderings in the range 0 < x ≤ 5, constructed convex hulls, and computed three possible voltage profiles to compare with experiment.

The thermodynamic ground-state hull results from filling X sites between 0 < x ≤ 1 (Fig. 9a), followed by Y sites between 1 ≤ x ≤ 2 (Fig. 13c, structure D), then the remaining X sites between 2 ≤ x ≤ 3 (Fig. 13c, structure G), and finally Z sites between 3 ≤ x ≤ 5 (Fig. 13c, structure I). The calculated voltage curve based on these ground-state hull structures (blue curve in Fig. 13b) shows a plateau at 1.6 V for 0 < x ≤ 2 with a slight step at x = 1, followed by a large step at x = 2 (to 0.7 V), a smaller step at x = 3 (to 0.5 V), and a plateau to x = 5. This is different than the experimental voltage curve, which shows a clear drop just before x = 1, followed by two solid-solution-type regions when 1 ≤ x ≤ 5.

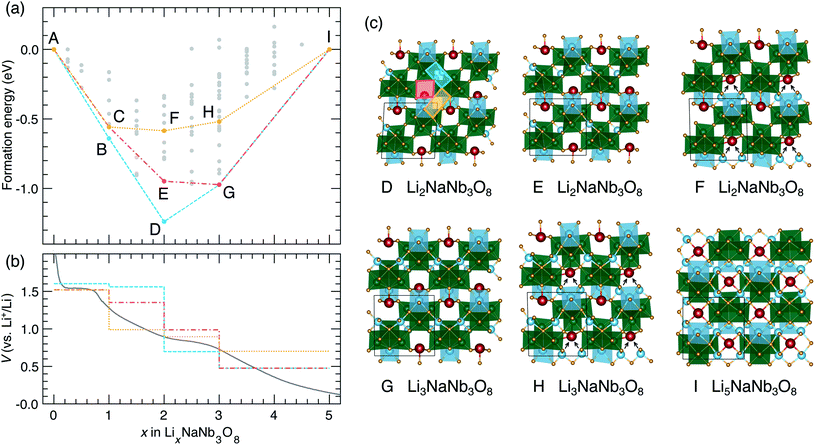Fig. 13 Lithiation of NaNb₃O₈ from DFT calculations. (a) Convex hull, showing the ground-state hull, and two convex hulls based on site filling determined by diffusion kinetics. Letters indicate structures along the hull. Structures B and C are presented in Fig. 9. (b) Experimental and calculated voltage curves, from the convex hulls in (a). (c) Structures along the convex-hulls from (a).

Such a difference between the experimental and computed voltage from the ground-state hull is additional evidence that Li diffusion kinetics determine the site filling in NaNb₃O₈, with metastable Y sites filled before more stable X sites. Two alternative calculated voltage curves are presented in Fig. 13b (red and orange), based on filling Y sites to x = 1, corresponding to the operando XRD product, followed by filling of sites X and Z. From the metastable LiNaNb₃O₈ structure, filling X sites down alternate channels (Fig. 13c, structure E) results in a low-energy structure, however, the step in the computed voltage curve at x = 1 is relatively small. From LiNaNb₃O₈, filling Z sites instead involves Li ions moving down the block-edge channels bordered by [LiO₆] and [NbO₆]. This results in a higher-energy structure (Fig. 13c, structure F), but a larger drop in the voltage curve at x = 1 that better reproduces the experimental voltage.

Even so, none of the calculated voltage profiles match with experiment perfectly. The experimental voltage profile between 1 ≤ x ≤ 5 is sloping, indicating solid-solution-type behavior that cannot be captured in the DFT calculations, which are limited to enumerating configurations within a small unit cell. We speculate that the site-filling mechanism for 1 ≤ x ≤ 3 involves the preferential filling of Z sites, based on the step in the voltage curve and the easier diffusion along channels to access Z sites, but we cannot rule out some diffusion to fill X sites. For 3 ≤ x ≤ 5, a second solid-solution mechanism occurs, filling the remaining empty X or Z sites along the shear planes. At a composition of Li₅NaNb₃O₈, Na ions are pushed into the center of the square channels, as all the pocket sites surrounding the central cavity are occupied by Li ions (Fig. 13c, structure I).

2.5 KNb₃O₈ structural evolution with cycling

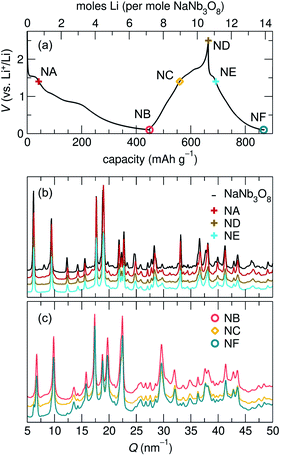
The structural evolution of KNb₃O₈ generally shows similarities to NaNb₃O₈, but a number of differences arise, which likely stem from the different stacking sequence for the two materials in their pristine state.

During the first discharge of Li_xKNb₃O₈, operando XRD shows a decrease in intensity of the 020 reflection concurrent with the growth of a new reflection at slightly higher Q (≈7 nm⁻¹) (Fig. 14a and b). The correlated exchange of intensity between these peaks suggests a two-phase transformation upon lithiation of KNb₃O₈. Based on our findings for NaNb₃O₈, we interpret the new reflection as corresponding to a smaller b lattice parameter arising from a reduction of the interlayer spacing. The position of this new reflection is similar to that of the final 010 reflection for LiNaNb₃O₈, in further support of this proposed change. Also similar to the Na analogue, we see a gradual shift of the 002 reflection to lower angle, indicating an expansion of the c lattice parameter. Similar trends in average structure evolution have been observed during electrochemical cycling of KNb₃O₈ as a Na-ion electrode.³¹

As was found for NaNb₃O₈, we find discrepancies between ex situ and operando characterization of KNb₃O₈ cycling products. From operando XRD, we observe a two-phase coexistence at the end of the first plateau (x ≈ 1) (Fig. 14). However, ex situ XRD shows an average structure nearly identical to the pristine niobate (KNb₃O₈ and KA, Fig. S6†). Likewise, electron diffraction reveals discrete 020 spots at this intermediate state of charge, showing no evidence of a second stacking sequence (Fig. S9†). However, we do find domains within crystallites, separated by low-angle boundaries (≈14°, Fig. 15a and b). The domains themselves maintain crystalline order and a single, well-ordered stacking sequence.

Fig. 14 (a) Galvanostatic discharge of KNb₃O₈ during operando XRD and (b and c) operando XRD patterns at select states of charge [marked in (a)] shows the evolution of specific reflections during lithiation. The y-axis in (b) and (c) corresponds to the intensity of X-ray scattering, which is shown here on a relative scale.

Fig. 15 (a) Dark-field TEM image of a KNb₃O₈ crystallite after partial discharge (to about LiKNb₃O₈) shows segmentation into domains (labeled 1, 2, and 3). (b) As revealed by selected-area electron diffraction patterns from the three domains in (a), the domains share the same crystal structure and are separated by low-angle boundaries. Domain 2 is oriented with its [010] direction parallel to the beam, while domains 1 and 3 are tilted by about 14° from the in-plane [100] direction of domain 2. The contrast in domain 2 is consistent with the presence of twin-like domains. (b) Electron diffraction patterns show that each region is crystalline, with evidence of twin-like domains across region 2. (c, left) STEM high-angle annular dark-field imaging after several cycles shows crack-like channels across the platelets of Li_xKNb₃O₈. (c, right) High-resolution TEM (down the [010] zone axis) shows crystallinity is retained on either side of the ‘crack’ region, and reveals amorphous contrast within these features. EELS spectra in the amorphous channel and its adjacent crystalline areas each indicate K, Nb, and O are present (see Fig. S10†).

Over the remainder of the discharge, operando XRD shows relatively minor average structure changes, and at the end of the discharge some intensity remains at the original 020 reflection position, while the new, higher Q reflection is more intense (Fig. 14). The ex situ discharge product shows three peaks in this low Q range (KB, Fig. S6†), suggesting different stacking sequences are present. The dominant stacking reflection in the operando discharge product supports a reduction of the b lattice constant, as seen for Li₅NaNb₃O₈. TEM of the first discharge product shows lighter-contrast channels across crystallites and ordered stacking, with no sign of multiple stacking sequences within the crystallite (Fig. S9†). While this is inconsistent with XRD data for the discharge product, the two techniques differ by their statistical sampling (i.e., selected particles suitable for electron diffraction and imaging in TEM versus ensemble average in XRD). Thus, one possible interpretation of this discrepancy is that the various reflections associated with the stacking direction (and lithium composition) in XRD arise from variation between, rather than within, particles. Alternatively, such a phenomena could be the result of Li composition gradients within particles, as has been observed in V₂O₅.⁵¹

After several cycles, what appeared as channels after the first discharge resemble cracks in TEM micrographs (Fig. 15c, left). However, high-resolution TEM shows some of these regions have an amorphous structure, rather than being true cracks (Fig. 15c, right). The difference in density, rather than the atomic species present, results in the contrast between the channels and crystalline regions surrounding them. Electron energy loss spectroscopy (EELS) reveals that K, Nb, and O atoms are present in these amorphous channels (Fig. S10†). We propose these channels are the result of defect aggregation (e.g., dislocations) to alleviate strain associated with structure evolution upon (de)lithiation or as a result of relaxation from a higher energy metastable product. Given the similar crystallographic orientation of these channels and the low-angle boundaries in the partial discharge product, it is possible that those boundaries are the origins of the channels observed upon continued cycling.

Upon charge, operando XRD shows the initial average structure is partly recovered, albeit with a decrease of peak intensity and some of the discharge product (with a smaller interlayer spacing) remaining. The former is likely a consequence of reduced domain sizes, as observed in TEM for discharge products. The latter is consistent with ex situ XRD insofar as that various interlayer spacings (corresponding to different Li compositions) co-exist in the sample (KD, Fig. S6†). The multiple peaks in the XRD after discharge and charge indicate an incomplete reaction and heterogeneous products (chemically and structurally), in contrast to NMR and XRD indications of homogeneous NaNb₃O₈ cycling products. This could have several origins, e.g., the generation of phases with sluggish Li diffusion or a loss of electrical conductivity across amorphous channels, each of which could result in electrochemically inactive regions or particles.

Building upon the similarity of the initial structures and average-structure changes indicated by XRD reflections, especially the 0k0 and 002, we propose that the dominant structure evolution during (de)lithiation is the decrease (increase) of the interlayer spacing. There are several open questions regarding this change, for example, does such a change to the interlayer spacing involve a change of the stacking sequence (from AB to AA, Fig. 2a and b)? If so, this could involve staging or relaxation to intermediate stacking sequences, which would be supported by the multiple low Q reflections in ex situ XRD.

Stacking changes in NaNb₃O₈ are associated with Li between the layers, and result from the reduction of the interlayer spacing. In the pristine materials, we see that the counter-cation size and preferred coordination determine the interlayer spacing. Accordingly, it seems that intercalated Li between the layers has a similar effect in the cycling products of both compounds. In KNb₃O₈, however, the high potential plateau has more hysteresis between discharge and charge than NaNb₃O₈, suggestive of a more extensive atomic structure change over this feature during cycling, perhaps even a change of stacking sequence in addition to interlayer spacing. A similar reduction of interlayer spacing (indicated by a new reflection near 7 nm⁻¹) is observed in operando XRD over only the high potential plateau, as is the relatively large voltage hysteresis (Fig. S8†). For KNb₃O₈, the average structure evolution is not as reversible as for the Na analogue, evidenced in the various low angle Bragg peaks in ex situ diffraction as well as the aggregation of defects to form amorphous channels within particles. However, we cannot confirm whether average-structure changes and their irreversibility are the cause or result of separate domains formed within particles during cycling.

Fig. 16 Schematic summary of the intercalation behavior in Li_xNaNb₃O₈. (a) Structure of pristine NaNb₃O₈. (b) Voltage profile for the first discharge with shaded regions indicating the first high-voltage plateau, followed by two solid solution regions, and a low-voltage region where reactions with carbon and SEI are expected to occur. (c) Structure of LiNaNb₃O₈ from operando XRD with Y sites filled, the interlayer space contracted and Na ions pushed into the square channels. Filling Y sites (gold blocks) results in a (2 × 2)_∞ block structure. (d) Structure of LiNaNb₃O₈ from ex situ XRD with ‘pocket’ X sites filled. (e) Structure of Li_xNaNb₃O₈ when 1 ≤ x < 5, with partial occupancy of X and Z sites, filled by ‘cross-block’ Li diffusion along shear-plane channels. Depending on which X and Z pocket sites are filled, the Na ions are displaced within the (2 × 2 × 2) cavity. (f) Structure of Li₅NaNb₃O₈ with all X, Y, and Z sites filled and Na ions in the center of the square channels.

3 Further discussion & context

It is interesting to compare how Li intercalation proceeds in layered, vacancy-ordered NaNb₃O₈, summarized in Fig. 16 (and KNb₃O₈), and conventional WR materials. In TiNb₂O₇, H–Nb₂O₅ and Nb₂O₅–WO₃, Li diffusion is quasi-1D, taking place almost exclusively along square channels in the blocks.^6–8 Some coupling and correlation between Li in different channels, identified in Li₈Nb₁₂WO₃₃ and Li₈Nb₁₄W₃O₄₄, changes the nature of the diffusion from purely 1D.²⁶

In NaNb₃O₈, diffusion does not occur down the square channels, which are blocked by Na ions. Instead, Li ions initially move down channels in the interlayer space, pathways that are absent in conventional WR phases. In the interlayer space, Li-ions fill the ordered octahedral framework vacancies, forming a WR framework with (2 × 2)_∞ blocks. These octahedral ‘vacancy’ sites do not exist in conventional WR materials, where all octahedral sites not face-sharing with tetrahedral cations are occupied by framework cations (typically transition metals). Li-ion insertion sites in conventional WR materials are square-planar or square-pyramidal, except for some ‘in-tunnel’ sites for Li in TiNb₂O₇ under dilute conditions.⁸ Filling framework vacancies is a new charge-storage mechanism for WR-type materials. This results in high theoretical capacities for Li₅NaNb₃O₈ and Li₅KNb₃O₈ of ≈300 mA h g⁻¹.

As the octahedral framework vacancies are filled upon Li intercalation in these layered niobates, the interlayer space contracts as Li ions bond to O in adjacent layers. The layer contraction pushes Na (or K) ions further into the square channels. With the Na ions further into the square channels, Li diffusion down these channels is even more strongly impeded. Li ions are forced to move down shear planes through ‘cross-block’ hops, which have high activation barriers. This is a different diffusion mechanism than in conventional WR materials, where diffusion via cross block hops is always prohibitively sluggish compared to diffusion down square channels.^8,26 The low overall rate performance of NaNb₃O₈ is likely due to Li ions moving down these high-energy pathways. On charge, some Li remains in the structure, which our results suggest is in the X sites; this suggests a charge product similar to the ex situ LiNaNb₃O₈ structure in which Li moves from the metastable Y site to the more stable X site, resulting in an interlayer spacing resembling pristine NaNb₃O₈. We predict that Li is extracted first from the Z sites along shear-plane channels, followed by the Y sites. The Li stuck in the structure lowers the reversible cycling capacity, resulting in an operating range of about 2 ≤ x ≤ 4 in Li_xNaNb₃O₈.

A comparison of the cycling and structure evolution of Li_xNaNb₃O₈ and Li_xKNb₃O₈ shows the general intercalation mechanism and order of Li site filling are similar. However, some subtle differences that arise are associated with the different stacking sequence for KNb₃O₈ (AB) compared to NaNb₃O₈ (AA), and are likely associated with a change in the stacking sequence for Li_xKNb₃O₈ from AB to AA over the high-voltage plateau. We propose this change in stacking sequence is the source of the additional hysteresis of the high-potential feature for KNb₃O₈. The general similarities in the cycling for both compounds highlight the stability of the WR-type Nb₃O₈ layers, leaving the differences to arise from changes to the interlayer structure, dependent on the counter-cation.

The combination of relatively extensive average structure evolution and blocked square-channel diffusion pathways results in the poor rate capabilities of NaNb₃O₈ and KNb₃O₈ for Li transport. However, there may exist layered structures with larger block sizes that allow fast diffusion down square channels while also incorporating Li into framework vacancy sites to achieve high capacity. The incorporation of a lower valent ion (such as Li or Na) rather than high valent d⁰ TMs along the shear plane lowers the electrostatic repulsion for mobile Li ions along these pathways, benefiting ion diffusion, analogous to transport properties in cation-disordered rocksalt cathodes.^49,50 Diffusion of Na ions down square channels in WR and structurally related materials is limited by high activation barriers.^8,27 However, the dynamics of Na apparent in NMR of NaNb₃O₈, as well as the previously reported Na-ion storage in KNb₃O₈,³¹ indicate that Na is mobile between the layers in these materials. Accordingly, WR-derived structures, such as the layered compounds studied here, may also be applicable hosts for other large cation species.

4 Conclusions

In the search for high-rate Li-ion electrode materials and their design rules, we investigated ANb₃O₈ (A = Na, K), which are layered, vacancy-ordered derivatives of Wadsley–Roth materials, to see how these structural modifications influence electrochemical performance. Overall, the rate performance is lower than other WR materials, and not all Li is reversibly extracted after the first cycle. However, this work supports previous studies indicating polyhedral connectivity stabilizes the WR framework against significant structural changes upon cycling. Structure evolution during cycling is dominated by changes to the interlayer, rather than intralayer, structure. Li is incorporated into ordered framework vacancy sites between the layers, contracting the interlayer space and forming a WR framework with (2 × 2)_∞ blocks. The size and preferred coordination of counter-cations (Na, K) is significant to average structure evolution and voltage, with a different hysteresis and suggestions of a stacking sequence change in KNb₃O₈ upon lithiation. While fast Li-ion diffusion takes place down square channels in conventional WR materials, in these niobates the square channels are blocked by the counter-cations and diffusion takes place initially in the interlayer space, and subsequently along the shear planes, leading to the overall moderate performance. These results offer perspective on key motifs for fast ion transport, as well as opportunities to further improve capacity and ion transport in WR-derived electrode materials and beyond.

5 Methods

5.1 Synthesis

KNb₃O₈ powders were prepared using molten salt synthesis adapted from reported methods.^36,37 K₂CO₃ (J. T. Baker, 99.9%), Nb₂O₅ (AlfaAesar, 99.9987%), and KCl (J. T. Baker 99.9%) were combined in a 1 : 3 : 12 molar ratio (about a 1 : 1 mass ratio of reactant and flux). Powders were ball-milled in ethanol and dried at ambient conditions. The resulting fine powder was heated in a new, covered alumina crucible, which went into a 700 °C furnace, was heated at 3 °C min⁻¹ to 800 °C and held for 5 h, cooled at 3 °C min⁻¹ to 700 °C, and then air-quenched to room temperature.‡ The product was isolated using hot distilled water and vacuum-assisted filtration (using Whatman Grade 50 hardened low-ash filter paper).

NaNb₃O₈ was prepared through soft chemical methods through several steps of ion-exchange reactions. KNb₃O₈ was stirred in a nitric acid solution (7 mol HNO₃ per 1 L H₂O) for 3 days, after which the powder was filtered and rinsed with room-temperature distilled water.⁵² While the structure is not known, this intermediate is reported to be HNb₃O₈·H₂O.^30,52 HNb₃O₈·H₂O was then stirred in a NaOH solution (1 mol NaOH per 1 L H₂O) for 3 h, the product was collected by filtration and rinsed with room temperature distilled water; again, while there is not a reported structure, this intermediate is described as NaNb₃O₈·2H₂O based on thermogravimetric analysis.³⁰ The hydrated sodium niobate was heated at 3° min⁻¹ to 140°, held for 3 h, and furnace cooled to room temperature, resulting in NaNb₃O₈.³⁰

5.2 Battery assembly & testing

For battery testing and ex situ characterization, layered niobates and SuperP (conductive carbon additive, Alfa Aesar, 99+%) in a 7 : 3 mass ratio were ground using an agate mortar and pestle. Loose powders were the working electrodes in 1.27 cm (0.5 in.) diameter Swagelok cells against Li metal (Alfa Aesar, 99.9%, 1.5 mm thick), which served as counter and reference electrode. Cells were assembled in an argon-filled glovebox with two Whatman glass filter dryer (GFD) separators and an electrolyte solution of 1 M (mol L⁻¹) lithium hexafluorophosphate (LiPF₆) in an ethylene carbonate : dimethyl carbonate (EC : DMC) (1 : 1 volume ratio) solvent (Sigma Aldrich). Galvanostatic cycling with potential limitations (GCPL) at various rates and potential limitations was carried out using a Bio-Logic VSP-300 potentiostat.

For ex situ samples, after cycling to a select state of charge, powders were collected from disassembled cells, rinsed with DMC in the glovebox, and dried under vacuum without air-exposure. Dried powders were ground using an agate mortar and pestle and loaded into 1.2 mm outer-diameter Kapton tubes sealed with epoxy. Sealed tubes were packed in glass vials under Ar, wrapped with Parafilm, and not exposed to air until just before X-ray scattering data was collected.

5.3 X-ray characterization

Lab diffraction was collected using a Panalytical X'Pert powder diffractometer. High-resolution synchrotron XRD of prepared KNb₃O₈ and NaNb₃O₈ was collected at beamline 11-BM-B (λ = 0.4127 Å) of the Advanced Photon Source (APS) at Argonne National Laboratory through the rapid-access mail-in program (GUP-59538). Finely ground powders were measured in 0.8 mm inner-diameter Kapton tubes sealed with epoxy at both ends. Data was analyzed using Rietveld refinement and Fullprof⁵³ freeware. Additional details of the refinement are provided in the Results and discussion section as well as in the ESI.†

Ex situ and operando X-ray total scattering of high-energy X-rays (λ = 0.2113 Å, E = 58.7 keV) was collected at beamline 11-ID-B of the Advanced Photon Source using a PerkinElmer amorphous Si-based area detector at a sample-to-detector distance of 995 mm for diffraction data suitable for average structure information and analysis. Ex situ cycled powders were loaded into 1.2 mm outer-diameter Kapton capillaries in an argon glovebox and sealed with epoxy at both ends. Capillaries were sealed in vials under argon until just prior to scattering measurements to minimize moisture effects. Ex situ experimental geometries were calibrated using CeO₂ standards and integrated using Fit2D freeware,⁵⁴ and Topas-Academic-v6 was used for ex situ XRD analysis.⁵⁵

For operando data collection, AMPIX cells⁵⁶ were assembled in an argon glovebox. Layered niobate powders were mixed with graphite, VulcanC, and polytetrafluoroethylene (6 : 1 : 1 : 2 ratio by mass) and pressed into a free-standing cathode pellet. Between the cathode and Li metal anode were 1 M LiPF₆ in EC : DMC (1 : 1 volume ratio) electrolyte and one GFD separator. X-ray scattering of assembled AMPIX cells, with all but the cathode, was collected as a background to subtract from operando data. LaB₆ standards were used to calibrate experimental geometries. Due to the time constraints of operando experiments, full potential window cells were cycled at faster rates than ex situ.

5.4 NMR

Solid-state NMR spectra were recorded with a Bruker Avance III HD spectrometer in a Bruker narrow-bore 9.4 T superconducting magnet. The pulse–acquire sequence was used to record ⁷Li and ²³Na spectra while both pulse-acquire and the quadrupolar Carr–Purcell–Meiboom–Gill (QCPMG) sequences were used to record ⁹³Nb spectra. Quantitative relaxation delays (≥5 T₁) were used for all spectra (0.5 s for ⁹³Nb, 15 s for ²³Na, 10 s for ⁷Li), with some additional T₁-filtered measurements with shorter relaxation delays of 1 s for ⁷Li and ²³Na to differentiate between sites experiencing rapid relaxation due to interactions with unpaired electrons. ⁷Li, ²³Na, and ⁹³Nb were referenced to 1.0 M LiCl (aqueous) [1 mol LiCl per L H₂O] at 0 ppm, 1.0 M NaCl (aqueous) [1 mol NaCl per L H₂O] at 0 ppm, and LiNbO₃ at −1004 ppm, respectively. All spectra were recorded at ambient temperature.

NMR chemical shielding and quadrupolar parameters were calculated with plane wave DFT in CASTEP^41–43 (v19.11) after geometry optimization of the experimental structures from the Inorganic Crystal Structure Database (NaNb₃O₈, ICSD 202400;³⁰ KNb₃O₈, ICSD 31994²⁹). Vanderbilt ultrasoft pseudopotentials⁵⁷ were generated on-the-fly in CASTEP. The Perdew–Burke–Ernzerhof (PBE) functional⁴⁴ was used to approximate exchange–correlation effects. A plane wave basis set cut-off energy of 700 eV and Monkhorst–Pack k-point grids⁵⁸ of 4 × 4 × 9 (NaNb₃O₈) and 4 × 2 × 9 (KNb₃O₈) were used in the calculations. The geometry optimization was performed with the limited Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm until the energy and force converged to less than 2 × 10⁻⁵ eV per atom and 1 meV Å⁻¹ respectively. ⁹³Nb calculated isotropic shieldings were converted to shifts using the absolute shielding value of 642 ppm taken from the calculated⁵⁹vs. experimental value for LiNbO₃, δ_iso = −σ_iso − 642 ppm.

5.5 Computational methods

First-principles calculations to investigate structures, energies and Li diffusion in Li_xNaNb₃O₈ (0 < x ≤ 5) were performed using the periodic density-functional-theory (DFT) code CRYSTAL17.⁶⁰ Electronic exchange and correlation were approximated using the hybrid-exchange functional HSE06.⁶¹ All-electron, atom-centered Gaussian basis sets were used for all atoms, with details provided in the ESI.† The Coulomb and exchange series were truncated with thresholds of 10⁻⁷ 10⁻⁷ 10⁻⁷ 10⁻⁷ 10⁻¹⁴. Reciprocal space was sampled using a Pack–Monkhorst net,⁵⁸ with a shrinking factor of IS = 8 along each periodic direction for a total of 125 k-points in the irreducible Brillouin zone of the orthorhombic unit cell of NaNb₃O₈. Modified k-point grids were used for supercell calculations for a consistent sampling of reciprocal space. Dispersion forces were included using Grimme's semiclassical D3 correction.⁶² The self-consistent field (SCF) procedure was performed up to a convergence threshold of ΔE = 10⁻⁸ Hartree per unit cell. Full geometry optimizations (lattice parameters and atomic positions) were performed using the default convergence criteria in CRYSTAL17. Activation barriers for ionic migration were determined using constrained geometry optimisations, with full details of the procedure described in the ESI.† Supercells obtained from a (1 × 1 × 2) expansion of the crystallographic unit cell were used for the calculations of activation barriers to ensure a distance of >7 Å between periodic images. The same (1 × 1 × 2) supercell was used to calculate the site filling and voltage profile. Intercalation voltages in Li_xNaNb₃O₈ between the limits x₁ and x₂ were determined relative to lithium metal using the following equation: ΔE_inse = E_total(Li_x2NaNb₃O₈) − [(x₂ − x₁)E_total(Li_s) + E_total(Li_x1NaNb₃O₈)]. Hybrid-exchange functionals are unsuited for the calculation of metals. To evaluate the energy of lithium metal, we calculated the energy of a single isolated Li ion and added the experimentally determined energy of sublimation (E_sub) and the first ionization energy (E_i(1)): E(Li_(s)) = E(Li⁺) + E_sub(Li_(s)) + E_i(1)(Li). Crystal structures were visualized using VESTA software.⁶³

5.6 Electron microscopy

SEM was performed with powder samples on carbon tape using a Helios NanoLab DualBeam microscope (Thermo Fisher Scientific, Waltham, MA, USA). TEM was performed in an FEI Titan (S)TEM operated at 300 kV and equipped with a high-angle annular dark field detector and EELS spectrometer. In same cases, a tomography sample holder was used to enable sufficiently large tilting angles.

Pristine KNb₃O₈ powder samples were prepared for TEM by mixing the powder with a small amount of epoxy. The mixture was embedded in a slotted brass rod, which was placed inside a tightly fitting brass tube with an outer diameter of 3 mm. After curing the epoxy, the rod-in-tube sample was mechanically sectioned into thin disks, which were subsequently mechanically polished and dimpled to the final thickness of 25 μm, followed by Ar-ion thinning at 4 kV until perforation. Cycled materials were washed with DMC in an argon glovebox and dried under vacuum. The resulting powders were dispersed in ethanol and deposited on copper grids coated with lacey carbon for TEM.

Disclaimer

Any mention of commercial products is for informational purposes only; it does not imply recommendation or endorsement by the NIST.

Author contributions

MMB: conceptualization and project administration; MMB, KM, KJG, JED, IL: investigation; MMB, KM, KJG, RLD: formal analysis; MMB, KM, KJG, IL, RL: visualization; MMB, KM, RLD: writing original draft; RL: data curation; MMB, KM, KJG, KRP, IL, FC: writing – review and editing; KRP, FC, IL: supervision and resources.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was performed while M. M. B., R. L. D., and J. E. D. held NRC Research Associateship awards at the National Institute of Standards and Technology. K. M. and F. C. thank the EPSRC for funding the JUICED project (EP/R023662/1). This work used computational resources provided by the ARCHER UK National Supercomputing Service via K. M. and F. C.'s membership of the UK's HEC Materials Chemistry Consortium, funded by the EPSRC (EP/L000202, EP/R029431). Computational resources were also provided by the UK Materials and Molecular Modeling Hub (MMM Hub), which is partially funded by EPSRC (EP/P020194) and the UCL Kathleen High Performance Computing Facility (Kathleen@UCL). K. J. G. and K. R. P. were supported as part of the Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES). This work made use of the IMSERC NMR facility at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-2025633), Int. Institute of Nanotechnology, and Northwestern University. This research made use of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory (Contract No. DE-AC02-06CH11357). Synchrotron XRD was collected at Argonne National Laboratory on beamline 11-BM through the general user proposal mail-in program (GUP59538). Ex situ and operando X-ray scattering experiments were performed at beamline 11-ID-B at the Advanced Photon Source at Argonne National Laboratory through the general user proposal (GUP58814). The authors are grateful to the support of all of the beamline staff who support on-site beamtime and operando experiments, especially Drs Antonin Grenier, Olaf Borkiewicz, and Karena Chapman.

References

1. P. Arora, R. E. White and M. Doyle, Capacity Fade Mechanisms and Side Reactions in Lithium-Ion Batteries, J. Electrochem. Soc., 1998, 145, 3647–3667.
2. J. Vetter, P. Novàk, M. Wagner, C. Veit, K.-C. Moller, J. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, Ageing mechanisms in lithium-ion batteries, J. Power Sources, 2005, 147, 269–281.
3. M. V. Reddy, G. V. Subba Rao and B. V. R. Chowdari, Metal Oxides and Oxysalts as Anode Materials for Li Ion Batteries, Chem. Rev., 2013, 113, 5364–5457.
4. J.-T. Han, Y.-H. Huang and J. B. Goodenough, New Anode Framework for Rechargeable Lithium Batteries, Chem. Mater., 2011, 23, 2027–2029.
5. Q. Cheng, J. Liang, Y. Zhu, L. Si, C. Guo and Y. Qian, Bulk Ti₂Nb₁₀O₂₉ as long-life and high-power Li-ion battery anodes, J. Mater. Chem. A, 2014, 2, 17258–17262.
6. K. J. Griffith, A. C. Forse, J. M. Griffin and C. P. Grey, High-Rate Intercalation without Nanostructuring in Metastable Nb₂O₅ Bronze Phases, J. Am. Chem. Soc., 2016, 138, 8888–8899.
7. K. J. Griffith, K. M. Wiaderek, G. Cibin, L. E. Marbella and C. P. Grey, Niobium tungsten oxides for high-rate lithium-ion energy storage, Nature, 2018, 559, 556–563.
8. K. J. Griffith, I. D. Seymour, M. A. Hope, M. M. Butala, L. K. Lamontagne, M. B. Preefer, C. P. Koçer, G. Henkelman, A. J. Morris, M. J. Cliffe, S. E. Dutton and C. P. Grey, Ionic and Electronic Conduction in TiNb₂O₇, J. Am. Chem. Soc., 2019, 141, 16706–16725.
9. N. Takami, K. Ise, Y. Harada, T. Iwasaki, T. Kishi and K. Hoshina, High-energy, fast-charging, long-life lithium-ion batteries using TiNb₂O₇ anodes for automotive applications, J. Power Sources, 2018, 396, 429–436.
10. K. J. Griffith, Y. Harada, S. Egusa, R. M. Ribas, R. S. Monteiro, R. B. Von Dreele, A. K. Cheetham, R. J. Cava, C. P. Grey and J. B. Goodenough, Titanium Niobium Oxide: From Discovery to Application in Fast-Charging Lithium-Ion Batteries, Chem. Mater., 2021, 33, 4–18.
11. K. J. Griffith and C. P. Grey, Superionic Lithium Intercalation through 2×2 nm² Columns in the Crystallographic Shear Phase Nb₁₈W₈O₆₉, Chem. Mater., 2020, 32, 3860–3868.
12. S. Andersson and A. D. Wadsley, Crystallographic Shear and Diffusion Paths in Certain Higher Oxides of Niobium, Tungsten, Molybdenum and Titanium, Nature, 1966, 211, 581–583.
13. R. J. Cava, D. W. Murphy and S. M. Zahurak, Lithium Insertion in Wadsley–Roth Phases Based on Niobium Oxide, J. Electrochem. Soc., 1983, 130, 2345–2351.
14. X. Zhu, J. Xu, Y. Luo, Q. Fu, G. Liang, L. Luo, Y. Chen, C. Lin and X. S. Zhao, MoNb₁₂O₃₃ as a new anode material for high-capacity, safe, rapid and durable Li⁺ storage: structural characteristics, electrochemical properties and working mechanisms, J. Mater. Chem. A, 2019, 7, 6522–6532.
15. R. Zheng, S. Qian, X. Cheng, H. Yu, N. Peng, T. Liu, J. Zhang, M. Xia, H. Zhu and J. Shu, FeNb₁₁O₂₉ nanotubes: Superior electrochemical energy storage performance and operating mechanism, Nano Energy, 2019, 58, 399–409.
16. Q. Fu, H. Cao, G. Liang, L. Luo, Y. Chen, V. Murugadoss, S. Wu, T. Ding, C. Lin and Z. Guo, A highly Li⁺-conductive HfNb₂₄O₆₂ anode material for superior Li⁺ storage, Chem. Commun., 2020, 56, 619–622.
17. M. B. Preefer, M. Saber, Q. Wei, N. H. Bashian, J. D. Bocarsly, W. Zhang, G. Lee, J. Milam-Guerrero, E. S. Howard, R. C. Vincent, B. C. Melot, A. Van der Ven, R. Seshadri and B. S. Dunn, Multielectron Redox and Insulator-to-Metal Transition upon Lithium Insertion in the Fast-Charging, Wadsley-Roth Phase PNb₉O₂₅, Chem. Mater., 2020, 32, 4553–4563.
18. F. Ran, X. Cheng, H. Yu, R. Zheng, T. Liu, X. Li, N. Ren, M. Shui and J. Shu, Nano-structured GeNb₁₈O₄₇ as novel anode host with superior lithium storage performance, Electrochim. Acta, 2018, 282, 634–641.
19. N. H. Bashian, M. B. Preefer, J. Milam-Guerrero, J. J. Zak, C. Sendi, S. A. Ahsan, R. C. Vincent, R. Haiges, K. A. See, R. Seshadri and B. C. Melot, Understanding the role of crystallographic shear on the electrochemical behavior of niobium oxyfluorides, J. Mater. Chem. A, 2020, 8, 12623–12632.
20. K. E. Wyckoff, D. D. Robertson, M. B. Preefer, S. M. L. Teicher, J. Bienz, L. Kautzsch, T. E. Mates, J. A. Cooley, S. H. Tolbert and R. Seshadri, High-Capacity Li⁺ Storage through Multielectron Redox in the Fast-Charging Wadsley–Roth Phase (W_0.2V_0.8)₃O₇, Chem. Mater., 2020, 32, 9415–9424.
21. K. Meisel, Rheniumtrioxyd III. Mitteilung. Ueber die Kristallstruktur des Rheniumtrioxyds, Z. Anorg. Allg. Chem., 1932, 207, 121–128.
22. R. Cava, A. Santoro, D. W. Murphy, S. M. Zahurak and R. S. Roth, The Structures of the Lithium Inserted Metal Oxides Li_0.2ReO₃ and Li_0.36WO₃, J. Solid State Chem., 1983, 50, 121–128.
23. R. Cava, A. Santoro, D. W. Murphy, S. M. Zahurak and R. S. Roth, Structural Aspects of Lithium Insertion in Oxides: Li_xReO₃ and Li₂FeV₃O₈, Solid State Ionics, 1981, 5, 323–326.
24. R. Cava, A. Santoro, D. W. Murphy, S. M. Zahurak and R. S. Roth, The Structures of the Lithium-Inserted Metal Oxides LiReO₃ and Li₂ReO₃, J. Solid State Chem., 1982, 42, 251–262.
25. N. H. Bashian, S. Zhou, M. Zuba, A. M. Ganose, J. W. Stiles, A. Ee, D. S. Ashby, D. O. Scanlon, L. F. J. Piper, B. Dunn and B. C. Melot, Correlated Polyhedral Rotations in the Absence of Polarons during Electrochemical insertion of Lithium in ReO₃, ACS Energy Lett., 2018, 3, 2513–2519.
26. C. P. Koçer, K. J. Griffith, C. P. Grey and A. J. Morris, Lithium Diffusion in Niobium Tungsten Oxide Shear Structures, Chem. Mater., 2020, 32, 3980–3989.
27. K. McColl and F. Corà, Fast lithium-ion conductivity in the ‘empty-perovskite’ n = 2 Ruddlesden–Popper-type oxysulphide Y₂Ti₂S₂O₅, J. Mater. Chem. A, 2021, 9, 7068–7084.
28. R. S. Roth and A. D. Wadsley, Multiple phase formation in the binary system Nb₂O₅–WO₃. IV. The block principle, Acta Crystallogr., 1965, 19, 42–47.
29. M. Gasperin, Structure du Triniobate (V) de Potassium KNb₃O₈, un Niobate Lamallaire, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 2024–2026.
30. R. Nedjar, M. M. Borel, A. Leclaire and B. Raveau, The Sodium Niobate NaNb₃O₈: A novel lamellar oxide synthesized by soft chemistry, J. Solid State Chem., 1987, 71, 182–188.
31. H. Nakayama, M. Nose, S. Nakanishi and H. Iba, Electrochemical Reactions of Layered Niobate Material as Novel Anode for Sodium Ion Batteries, J. Power Sources, 2015, 287, 158–163.
32. Q. Deng, M. Li, J. Wang, K. Jiang, Z. Hu and J. Chu, Carbonized Polydopamine Wrapping Layered KNb₃O₈ Nanoflakes Based on Alkaline Hydrothermal for Enhanced and Discrepant Lithium Storage, J. Alloys Compd., 2018, 749, 803–810.
33. Z. Chen, X. Cheng, N. Long, H. Zhu, T. Liu and N. Peng, Lithium Storage Behaviors of KNb₃O₈ Nanowires for Rechargeable Batteries, Ceram. Int., 2018, 44, 5699–5704.
34. J.-T. Han, D.-Q. Liu, S.-H. Song, Y. Kim and J. B. Goodenough, Lithium Ion Intercalation Performance of Niobium Oxides: KNb₅O₁₃ and K₆Nb_10.8O₃₀, Chem. Mater., 2009, 21, 4753–4755.
35. Y. Lu, J. B. Goodenough, G. K. P. Dathar, G. Henkelman, J. Wu and K. Stevenson, Behavior of Li Guest in KNb₅O₁₃ Host with One-Dimensional Tunnels and Multiple Interstitial Sites, Chem. Mater., 2011, 23, 3210–3216.
36. L. Li, J. Deng, R. Yu, J. Chen, X. Wang and X. Xing, Phase evolution in low-dimensional niobium oxide synthesized by a topochemical method, Inorg. Chem., 2010, 49, 1397–1403.
37. F. Madaro, R. Saeterli, J. R. Tolchard, M.-A. Einsarsrud, R. Holmestad and T. Grande, Molten salt synthesis of K₄Nb₆O₁₇, K₂Nb₄O₁₁, and KNb₃O₈ crystals with needle- or plate-like morphology, CrystEngComm, 2011, 13, 1304–1313.
38. G. Zhang, J. Gong, X. Zou, F. He, H. Zhang, Q. Zhang, Y. Liu, X. Yang and B. Hu, Photocatalytic Degradation of Azo Dye Acid Red G by KNb₃O₈ and the Role of Potassium in the Photocatalysis, Chem. Eng. J., 2006, 123, 59–64.
39. Z. Y. Zhan, C. Y. Xu, L. Zhen, W. S. Wang and W. Z. Shao, Large-Scale Synthesis of Single-Crystalline KNb₃O₈ Nanobelts via a Simple Molten Salt Method, Ceram. Int., 2010, 36, 679–682.
40. X. Liu, W. Que and L. B. Kong, Hydrothermal Synthesis of Bamboo-Shaped Nanosheet KNb₃O₈ with Enhanced Photocatalytic Activity, J. Alloys Compd., 2015, 627, 117–122.
41. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First Principles Methods using CASTEP, Z. Kristallogr., 2005, 220, 567–570.
42. C. J. Pickard and F. Mauri, All-electron Magnetic Response with Pseudopotentials: NMR Chemical Shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
43. J. R. Yates, C. J. Pickard and F. Mauri, Calculation of NMR Chemical Shifts for Extended Systems Using Ultrasoft Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. A. A. Savina, V. A. Morozov, A. L. Buzlukov, I. Y. Prapova, S. Y. Stefanovich, Y. V. Baklanova, T. A. Denisova, N. I. Medvedeva, M. Bardet, J. Hadermann, B. I. Lazoryak and E. G. Khaikina, New Solid Electrolyte Na₉Al(MoO₄)₆: Structure and Na⁺ Ion Conductivity, Chem. Mater., 2017, 29, 8901–8913.
46. R. L. Vold and G. L. Hoatson, Effects of jump dynamics on solid state nuclear magnetic resonance line shapes and spin relaxation times, J. Magn. Reson., 2009, 198, 57–72.
47. K. A. See, M. Lumley, G. D. Stucky, C. P. Grey and R. Seshadri, Reversible Capacity of Conductive Carbon Additives at Low Potentials: Caveats for Testing Alternative Anode Materials for Li-Ion Batteries, J. Electrochem. Soc., 2017, 164, A327–A333.
48. J. S. Anderson and R. J. D. Tilley, in Surface and Defect Properties of Solids: Volume 3, ed. M. W. Roberts and J. M. Thomas, The Royal Society of Chemistry, 1974, vol. 3, pp. 1–56.
49. J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Unlocking the Potential of Cation-Disordered Oxides for Rechargeable Lithium Batteries, Science, 2014, 343, 519–522.
50. R. J. Clément, Z. Lun and G. Ceder, Cation-disordered rocksalt transition metal oxides and oxyfluorides for high energy lithium-ion cathodes, Energy Environ. Sci., 2020, 13, 345–373.
51. L. R. De Jesus, P. Stein, J. L. Andrews, Y. Luo, B.-X. Xu and S. Banerjee, Striping Modulations and Strain Gradients within Individual Particles of a Cathode Material upon Lithiation, Mater. Horiz., 2018, 5, 486–498.
52. R. Nedjar, M. M. Borel and B. Raveau, H₃ONb₃O₈ and HNb₃O₈: New protonic oxides with a layer structure involving ion exchange properties, Mater. Res. Bull., 1985, 20, 1291–1296.
53. J. Rodríguez-Carvajal, Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction, Physica B, 1993, 192, 55–69.
54. A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, Two-Dimensional Detector Software: From Real Detector to Idealised Image or Two-Theta Scan, High Pressure Res., 1996, 14, 235–248.
55. A. A. Coelho, TOPAS and TOPAS-Academic: An optimization program integrating computer algebra and crystallographic objects written in C++, J. Appl. Crystallogr., 2018, 51, 210–218.
56. O. J. Borkiewicz, B. Shyam, K. M. Wiaderek, C. Kurtz, P. J. Chupas and K. W. Chapman, The AMPIX Electrochemical Cell: a Versatile Apparatus for in situ X-ray Scattering and Spectroscopic Measurements, J. Appl. Crystallogr., 2012, 45, 1261–1269.
57. D. Vanderbilt, Soft Self-consistent Pseudopotentials in a Generalized Eigenvalue Formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892(R).
58. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
59. E. Papulovskiy, A. A. Shubin, V. V. Terskikh, C. J. Pickard and O. B. Lapina, Theoretical and Experimental Insights into Applicability of Solid-state ⁹³Nb NMR in Catalysis, Phys. Chem. Chem. Phys., 2013, 15, 5115–5131.
60. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360.
61. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215.
62. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
63. K. Momma and F. Izumi, VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta02992d

‡ Products were phase pure when using a new crucible. Subsequent reactions in used crucibles resulted in increasing fractions of secondary products until eventually the crucible cracked. While we have not investigated the cause of this, we anticipate that KCl in combination with rapid cooling contributed to reactants being lost in cracks in the crucible and shifting to other nearby K–Nb–O phases, especially K₄Nb₆O₁₇, K₃Nb₇O₁₉, and ternary bronzes.

---