Energy transfer in ternary blend organic solar cells: recent insights and future directions
Aiswarya Abhisek
Mohapatra
 ,
Vivek
Tiwari
,
Vivek
Tiwari
 * and
Satish
Patil
* and
Satish
Patil
 *
*
Solid State and Structural Chemistry Unit, Indian Institute of Science, Bangalore 560012, India. E-mail: vivektiwari@iisc.ac.in; spatil@iisc.ac.in
First published on 26th November 2020
Abstract
Resonance energy transfer (RET) can potentially improve the device efficiencies of ternary blend organic solar cells (TBSCs). However, several parameters, such as domain morphology, exciton lifetime, energy and charge transfer, influence the resulting photophysics. Owing to this, spectroscopic studies on TBSCs have not unambiguously deconvolved the role of RET in the observed enhancement of photocurrent densities, often downplaying the mechanistic aspects of the RET associated enhancement. In this perspective, we discuss and analyse the role of RET in enhancing the device efficiency by taking a few recent examples of TBSCs. Taking analogy from natural photosynthetic systems, we argue that deviations in the observed RET rates from a Förster type mechanism may be at play. We suggest new strategies to systematically correlate the Förster critical distance (R0) with increments in current density (ΔJSC) in order to gain mechanistic insights to optimize RET enhanced photocurrent for high efficiency organic solar cells.
Broader contextEfficiency and cost are the key parameters that limit the large-scale deployment of photovoltaics. Organic solar cells (OSCs), owing to their inexpensive roll-to-roll fabrication, semi-transparency, solution processability and a wide choice of materials, have emerged as a potential choice for low cost photovoltaics. In OSCs, the concept of ternary blend solar cells (TBSCs) is a promising pathway to further improve light absorption and enhance power conversion efficiencies by harnessing excitons through resonance energy transfer (RET), although the ensuing excited state photophysics is complex. In this perspective, the photophysics of exciton generation, migration and dissociation is discussed in the context of mechanistic insights available from natural photosynthesis. Unlike the ∼100% quantum efficiency of charge separation in photosynthetic proteins, the excitations in TBSCs are impeded by recombination losses, with exciton lifetime and blend morphology playing the key roles. The failure of current studies on TBSCs in correlating Förster critical distance to the measured photocurrent, as compared to their binary counterparts, motivates a closer scrutiny. Experimental strategies to better understand the role of RET in photocurrent enhancement with unambiguous quantification are motivated. Understanding the fundamental parameters that govern the efficiency of OSCs is critical for large-scale deployment of cost-effective photovoltaics. |
Introduction
Resonance energy transfer (RET)1 is a ubiquitous photophysical process across several biological pigment–protein systems. In one such example, the efficient nature of energy delocalization and internal conversion, which are the fastest steps of photosynthesis, has intrigued scientists over the past several decades.1,2 In the recent past, several efforts have been made to understand the mechanistic aspects of the abovementioned process in terms of extensions of the adiabatic RET framework3–5 beyond the point-dipole approximation. Significant non-adiabatic deviations from the RET framework have also been proposed.6 Design principles gained from the above energy transfer frameworks7 have recently found applications in explaining the ultrafast hot exciton delocalization in organic polymers,8,9 as well as singlet exciton fission in organic thin films.10,11 In a related context, ternary blend solar cells (TBSCs) based on notions borrowed from Förster RET mechanism have already shown promising efficiency enhancements,12–15 especially with non-fullerene acceptors (NFAs), in which the reported power conversion efficiencies (PCEs) exceeded ∼16%,16–23 highlighting the need for a mechanistic understanding of the interplay of electronic and vibrational states possibly involved in RET based solar cell designs.Based on the spatial proximity of interacting chromophores, donor D and acceptor A, the electronic energy transfer between them can be classified into two mechanisms based on the point-dipole approximation: Dexter24 and Förster1,25 resonance energy transfer. The expressions for the expected energy transfer rate from both the mechanisms are derived under an adiabatic framework, under the assumption of thermal equilibrium at the D and A sites, and therefore no excitation wavelength dependence of energy transfer. Dexter energy transfer (DET) occurs at very short distances (typically a few Å s), where there is an overlap of the molecular orbitals of neighbouring chromophores. As a result, the excitation can migrate between the chromophores via electron exchange interactions.24 Dependence on overlapping charge densities implies that the DET rates fall off exponentially as ∼e−2R/L, where R is the distance between the neighbouring sites and L is the sum of the effective van der Waals radii of the excited donor and the ground state acceptor.
In contrast, Förster resonance energy transfer (FRET)25 is mediated through long-range Coulomb interactions between the donor and acceptor chromophores in which, for non-zero oscillator strengths for donor emission transition and the corresponding acceptor excitation, the energy is transferred from the electronically excited donor to the ground state acceptor chromophore without the emission of a photon. The rate of FRET from a donor to an acceptor is given by26
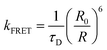 | (1) |
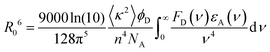 | (2) |
Although the abovementioned mechanisms serve as a good starting point for describing energy transfer, in several situations such as tightly packed chromophores in photosynthetic proteins, or photovoltaic thin films, the approximation of convergent multipole interactions, on which the above expressions are based, becomes invalid. For instance, in the context of photosynthetic proteins, it is known3 that the observed energy transfer rates are much faster than those predicted using the far-field linear spectroscopic information used in the abovementioned framework. This has motivated extensions3,4 beyond point-dipole approximations for situations where the donor and acceptors are aggregates of monomeric transition dipoles such that the physical size of the aggregate becomes comparable to the distance between the donor–acceptor aggregates. In such situations, the transition rates become sensitive to the relative geometry of individual molecules comprising the donor and acceptor aggregates. A surprising finding3,27 from such extensions was that local interactions between a donor and an aggregate acceptor lead to the participation of optically forbidden acceptor states in energy transfer, thus causing enhanced rates. It has also been shown3–5 that, instead of including higher order dipole-quadrupole interactions, etc., a multicentric transition density provides a better description of the aggregate shape.4,5 In addition to the above extensions, it has also been shown that, apart from long-range Coulombic interactions, in tightly packed aggregates where the donor–acceptor orbitals overlap significantly, exciton resonance configurations involving a mixture of excitonic and charge-transfer (CT) basis states28 play a dominant role in through-bond RET mediated by CT configurations compared to the Dexter electron-exchange mechanism. Note that the above extensions assume the validity of Born–Oppenheimer approximation and do not explicitly consider the role of vibrational–electronic couplings. Recently, non-adiabatic vibrational–electronic couplings which can promote energy or charge transport have also been reported6 in the literature, further broadening the scope for deviations from the standard FRET or DET framework.
In the context of mechanistic deviations from the RET framework, we discuss the energy and charge transfer mechanisms and design principles from natural photosynthetic systems in the following section. Comparison of these mechanistic and design aspects with organic photovoltaics allows us to motivate the development of TBSCs.
1. Energy and charge transfer in natural light harvesting systems
Fig. 1 shows some examples of ultrafast energy and charge transfer reported in natural photosynthesis and organic photovoltaics (OPVs). In the case of natural photosynthetic systems,29 extended models such as generalized Förster adiabatic framework25,30,31 and, more recently, non-adiabatic vibrational–electronic couplings32 have been implicated to explain the observed energy or charge transfer rates in closely packed molecular aggregates. In contrast, in the case of OPVs which aim to harvest additional excitons through RET, energy transfer is achieved by employing the standard RET design principle of having D–A spectral overlaps, while several other mechanistic factors described above have been largely ignored. The purpose of drawing an analogy between natural photosynthesis and RET-based OPVs is to underscore the point that the consideration of fundamental design principles from natural photosynthesis, such as the role of transition densities and vibrational–electronic couplings in energy and charge transfer, may also pave the way for efficient OPV designs. Fundamental mechanistic investigations at the same level as conducted in the case of natural photosynthetic systems could be key in applying more extended EET design principles to increase OPV efficiency.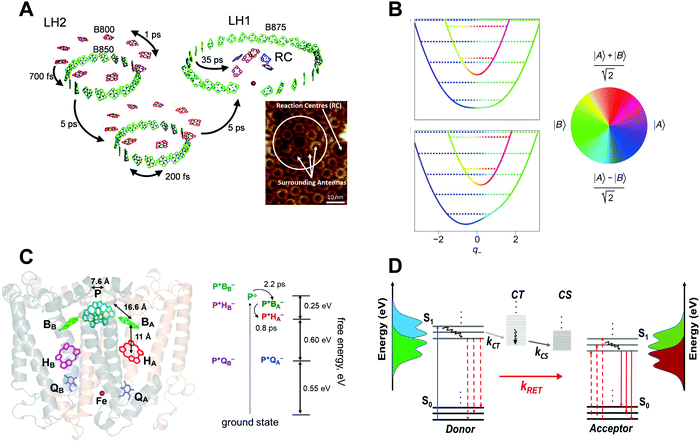 | ||
| Fig. 1 (A) Illustration of energy transfer events in the purple photosynthetic bacteria (adapted from ref. 33). The light harvesting assembly consists of LH2 proteins, seen as little rings in the AFM image of a membrane fragment at the bottom right, which transfer energy to LH1–RC protein complexes, seen as larger rings in the AFM image. The LH2 protein complex consists of a B850 ring (green pigments) and a B800 ring (red pigments). The LH1–RC complex consists of a B875 ring, inside which are located the reaction centre (RC) pigments. At the RC, the charge separation takes place. Lifetimes of these ultrafast energy transfer events are indicated by arrows. Double-headed arrows indicate exciton delocalization within the B800/B850 or B875 pigment rings. The AFM image (inset) is adapted from ref. 34. (B) Vibronic exciton models that extend the FRET adiabatic framework to include vibrational–electronic couplings and associated non-adiabatic effects are now treated in several photosynthetic systems6 (adapted from ref. 35). Colour represents the electronic character of a mixed D–A system which changes upon relative nuclear motions between the pigments, thereby coupling the electronic states. (C) Timescales, length scales and energetics of ultrafast electron transfer in photosynthetic RCs (adapted from ref. 36). Purple bacterial reaction centre (pbRC) pigments responsible for charge separation. Electron transfer intermediates along the B branch are higher in energy compared to the A branch due to a dielectric asymmetry37 created by the protein environment. (D) Photophysical processes in a typical donor/acceptor OPV blend. The singlet excitons S1 excited in the donor domains convert into charge transfer (CT) states and subsequently dissociate into charge separated (CS) states, depicted by respective rate constants. The vertical axis shows the absorption and emission spectra of the D and A molecules. Solid vertical arrows represent optically allowed transitions, and dashed vertical arrows represent virtual transitions in the RET process. Curved lines denote non-radiative relaxation within the respective states. The above schematic does not show the population lifetime decays associated with different electronic states. | ||
Fig. 1A shows the typical electronic energy transfer (EET) timescales33,38 within a photosynthetic purple bacterial ‘antenna’ protein, LH2,39 as well as across a network of LH2 and LH1–RC protein complexes. Intra-band energy delocalization proceeds on sub-picosecond timescales and is ubiquitous across antennas from several different photosynthetic systems. Typical centre-to-centre inter-molecular distances in LH2 complexes range between 10 and 20 Å. As suggested by the AFM image34,40 of a purple bacterial membrane, EET from LH2 antennas to the LH1–RC complex typically occurs on length scales of tens of nanometres within a few picoseconds. Several antennas per reaction centre (RC) ensure enhanced photon capture cross-section. Additionally, the antenna network protects the RC from photodamage through the dissipation of excess electronic energy. In a way, the chromophores embedded within each of the antennas collectively form a giant molecular aggregate, spatio-energetically assembled by the protein scaffold, such that the electronic excitation rapidly diffuses across it until it encounters a RC ‘sink’. At the RC, the electronic energy received from the antenna is utilized to create a long-lived charge separated state across a membrane, which initiates the subsequent ‘light’ and ‘dark’ reactions41 of photosynthesis. Remarkably, the process of photon absorption by the antennas to create a charge-separated state in the RC proteins occurs with an ∼100% quantum efficiency even for low photon fluences.
In the context of the LH2 antenna protein, a weak overlap between the B800 fluorescence and B850 absorption and almost zero oscillator strengths of the overlapping B850 acceptor states implied3 that the sub-picosecond and nearly temperature independent B800–B850 EET significantly deviates from the predictions of the standard FRET framework. In order to quantitatively rationalize the above observations, extensions3,31,42 of the RET framework incorporating tightly packed multi-chromophoric assemblies and the effects of energetic disorder have been successfully utilized. There is also experimental evidence43 suggesting that the transfer from LH2 to LH1–RC ‘sink’ proceeds via a superradiant lowest exciton of LH2.
In general, observations of quantum coherences6,7,29 in photosynthetic proteins on the same timescales as EET has led to the investigation of several other potential EET mechanisms, ranging from electronic quantum coherence between excited electronic states44–46 to the more recent non-adiabatic6 vibrational–electronic (vibronic) enhancement of EET rates. Fig. 1B shows a vibronic exciton model35 which treats vibrational modes of the molecules explicitly as a part of the system. In such models, vibrational motions which change the relative electronic energy gap between the pigments can allow rapid non-adiabatic energy transfer through vibronic mixing between excitons, marking a significant deviation from adiabatic EET frameworks. This effect is most pronounced at vibronic resonance,47 highlighting an interesting role of energetic disorder and vibronic coupling in creating a directional non-adiabatic energy funnel. Strong vibrational coordinate dependence of vibronic mixing is highlighted by rapid changes in electronic character, which is mapped onto the colour wheel, versus vibrational coordinates along which the relative energy gap between the pigments is tuned. In the context of natural photosynthesis, several groups6,7 have recently reported quantum superpositions between such vibronically mixed states with the possibility of exploiting such superposition states in enhancing functionality in artificial light harvesting systems. Discussing these mechanisms in detail is beyond the scope of this focus review as they have been already discussed in recent literature reports.6,7
Fig. 1C summarizes the length scales,48 timescales49 and energetics36 of charge separation in the purple bacterial reaction centre (pbRC). The EET from LH1 complex excites a strongly coupled dimer of bacteriochlorophyll a (BChl a) pigments (termed the excited “special pair” P*). The P* exciton undergoes ultrafast electron transfer to accessory BChl a B and subsequently to pheophytin pigment H and quinone pigment Q. Due to the macroscopically symmetric structure of the RC, electron transfer could proceed along both branches A and B. However, a dielectric asymmetry created by the protein environment arranges the LUMOs of P*, P+BA− and P+BB− states in a way to create a driving force of ∼0.25 eV,37 such that the electron transfer is known to only proceed along the A branch. Interestingly, even though the driving force for the process is only ∼0.25 eV, electron transfer from P* to P+BA− to P+HA− occurs within 3 ps over 3 nm length scales with ∼100% quantum efficiency. The role of charge transfer states49 in the special pair and the functional role of vibronic coherences in the above mechanism are now being actively investigated by several groups.6,50,51
2. Energy and charge transfer in organic photovoltaics – lessons from natural photosynthetic systems
OPVs typically comprise organic donor and acceptor moieties packed tightly in a thin film, where the Coulombically bound electron–hole pairs or the excitons generated upon absorption of photons in the donor and/or acceptor domains are rapidly delocalized into polaron pairs at the donor/acceptor interface, which are thought to be precursors of free charges.8 Subsequently, the polaron or charge transfer (CT) states as shown in Fig. 1D dissociate into charge separated (CS) states. Because of the built-in potential in the device, free charge carriers migrate to respective electrodes to generate photocurrent. Long range exciton migration to donor–acceptor interfaces via EET, and charge separation without loss are necessary to achieve a high PCE. A number of parameters such as the limited exciton diffusion length (∼5–10 nm), geminate and non-geminate recombination of charge carriers and the thin film morphology of donor–acceptor domains lead to the loss of PCE.52,53 The optimization of these parameters in the bulk heterojunction (BHJ) concept overcomes these losses to a certain extent54,55 which results in an ∼18% PCE in a single-junction OPV,22,56–58 albeit still lower than the Shockley–Queisser limit. A typical binary BHJ thin film is made of a conjugated polymer as the donor and very frequently fullerenes as the acceptor, mixed together to form an interdigitating network which facilitates exciton migration to the heterojunction interface. Fig. 1D schematically represents the photophysical pathways of exciton generation in a binary blend of BHJ, followed by the dissociation and separation of free charge carriers at the BHJ interface. When there is a donor–acceptor spectral overlap, RET can occur alongside as a loss process in the form of emission from acceptor excitons as shown. This parallel EET process is commonly observed in recently developed NFAs.59 However, RET is sometimes reported to enhance the overall exciton dissociation efficiency60 by harvesting the excitons that did not convert into CT and CS states, which then subsequently undergo dissociation after transferring to the acceptor domain. Similar to the case of photosynthetic RCs shown in Fig. 1C, the energetic offsets between S1, CT and CS states, although often significantly higher than that in the photosynthetic RC, provide a driving force for interfacial exciton dissociation. In general, the rate processes for energy transfer, charge transfer and charge separation, shown in Fig. 1D, compete with each other. The following section discusses the role of several factors, the interplay among which can tilt the balance in favour of any one of the abovementioned processes.A. Role of exciton lifetime and blend morphology
In the presence of incomplete exciton dissociation, OPVs based on harvesting excitons created in the donor domain through RET can be expected61–63 to exhibit improved photocurrent, provided that (1) they are not competing with the charge transfer processes occurring between the donor and acceptor and (2) the initially created excitons have a sufficiently long population lifetime such that the EET outcompetes population relaxation. This key point is demonstrated in a recent article by Gundogdu and co-workers.64 They choose a thin film of low band-gap polymers blend with different morphology with a typical small molecule acceptor (SMA). The bandgap of SMA is larger than those of the polymers. They investigated the role of blend morphology in dictating whether charge transfer and EET are competing processes.64 When donor–acceptor interfaces are readily available to the excitons transferred from the SMA to the polymer, interfacial charge separation is the dominant process following the initial EET. In contrast, when the transferred excitons in the polymer do not have readily available interfaces due to the coarse nanomorphology of the polymer, exciton recombination in the polymer domains becomes a potential loss channel which inhibits the harvesting of EET channels. Their findings suggest that, in order to harvest the excitons transferred to the lower bandgap material as free charges, the transferred excitons must have longer lifetimes, such that subsequent charge transfer resulting from the transferred excitons can effectively compete against exciton recombination losses.Interestingly, as shown in Fig. 1A, the diffusion timescales of photosynthetic excitons of the order of picoseconds in the antenna network, until they encounter a charge separation site, are much faster than the population lifetimes of the chlorophyll pigments of the order of nanoseconds, essentially highlighting the above findings. Interestingly, in the case of natural photosynthetic designs, the ∼100% charge separation efficiency is not “morphology” dependent. This is evident in the example of purple bacteria as shown in Fig. 1A. The antenna network and also the antenna spectral line shapes (not shown) are strongly dependent on growth conditions. Under low-light (LL) growth conditions, the ratio of RC sinks to antenna proteins is lower such that the excitons have to diffuse up to ∼2× longer33 before encountering a RC sink. Additionally, LL growth conditions lead to more energetic disorder.33 However, the internal quantum efficiency of charge separation is still ∼100% and is not affected by energetic disorder or the presence of a smaller number of sinks. That is so because the exciton lifetimes are at least three orders of magnitude longer than diffusion timescales, making the process less susceptible to growth-dependent changes in morphology and energetic structure. In sharp contrast, in the case of OPVs, the interplay between EET, followed by charge separation, and direct exciton dissociation is intimately connected with morphology, which can then dictate whether or not EET can be beneficial for enhancing device photocurrent.
B. Role of interfacial energetics and driving force
Blend morphology is not the only factor dictating the relative contributions of EET, charge separation and exciton recombination pathways. Several studies have also investigated the role of relative energetics between the donor and acceptor domains at the interface and the possibility of charge transfer being mediated by interfacial CT states. In the context of polymer:fullerene blend films, Durrant and co-workers investigated65 the role of FRET D–A overlap and CT driving force in the competition between EET and charge transfer rates. They have reported a 16× higher efficiency of energy transfer from the polymer to PCBM, compared to electron transfer from the polymer lowest unoccupied molecular orbital (LUMO) to the PCBM LUMO, due to an insufficient driving force for charge separation. Furthermore, the insufficient driving force for the resulting PCBM excitons to dissociate via hole transfer from the PCBM highest occupied molecular orbital (HOMO) to the polymer HOMO results in the exciton recombination loss channel being the dominant pathway for the transfer of the excitons to PCBM.More recently, in the context of TBSCs, Li et al.66 have elucidated the delicate interplay of EET, exciton lifetime and charge separation driving force in blends between two crystalline polymers and PTB7-Th:PCBM host blends. Both polymers lead to similar morphologies – increased phase separation between polymer-rich and fullerene-rich domains, and polymer well-mixed in the PTB7-Th domains. However, only the polymer that exhibits EET to PTB7-Th shows associated improvements in photocurrent due to efficient charge-separation at the PTB7-Th:fullerene interface with a driving force of ∼0.8 eV. Compared to this, the reverse process, in which the polymer receives excitons from PTB7-Th, is less facile because electron transfer from the polymer LUMO to the PTB7-Th LUMO has an insufficient driving force. However, as highlighted by Gundogdu et al.,64 sufficiently long acceptor exciton lifetimes can counter lower driving forces and overcome exciton loss.
In the context of NFA:polymer blends, Neher and co-workers67 have recently reported near-unity efficiency of singlet exciton dissociation into a CT state via an electron transfer pathway with a low driving force of 0.6 eV. Furthermore, their results show that the dissociation of CT into free charge-carriers is independent of temperature, wavelength and external bias. The field independence of CT dissociation directs the attention towards the role of interfacial electrostatic potential and permanent quadrupole moment in the Y6 acceptor in overcoming the Coulombic binding energy of CT states and facilitating the barrierless dissociation of CT states. Their study also supports the idea that charge dissociation proceeds through cold polarons rather than through hot-polaronic states.68 On a similar note, Sini and co-workers performed kinetic Monte Carlo (KMC) simulations to investigate the effect of interfacial energy bending on charge separation.69 They report that, in the presence of optimal interfacial energy bending, the external bias does not influence the rate of charge generation, in line with the report of Neher et al.67
Recent work70 by Banerji et al. also highlights the role of interfacial energetics in driving charge separation. The effect of morphology was first decoupled by optimizing the polymer:NFA blend morphology for maximizing the contribution of the intrinsic hole transfer (HT) rate at the NFA/polymer interface, while minimizing the delayed hole transfer component limited by exciton diffusion within the NFA domain to the interface. Using optimized blends, the intrinsic electron transfer rate was reported to be <60 fs, while the intrinsic hole transfer rate was reported to be 400 fs, both for a comparable driving force as low as 0.05 eV. The order of magnitude of faster electron transfer rates has been attributed to larger electron transfer versus hole transfer integrals (32 meV versus 21 meV). By using different polymers, where the driving force is increased to 0.4 eV, the HT rate becomes faster by an order of magnitude reaching 80 fs. The electron transfer timescale is always faster than the experimental time resolution.
Interestingly, in the case of natural photosynthetic RCs shown in Fig. 1C, even lower amounts of driving forces are at play, but result in ∼100% efficient charge separation in pbRCs on picosecond timescales over ∼3 nm distances.
C. Role of vibrational–electronic couplings with CT states
Mechanistic frameworks which go beyond FRET, such as the vibronic mixing of excitonic and CT states, have been implicated to explain the ∼100% efficiency of photosynthetic energy and charge transfer. For instance, in contrast to the reports69 of the inhibiting role of energetic disorder in interfacial charge separation, vibronic exciton models6 highlight the fact that the presence of energetic disorder of the order of vibrational energies can in fact be responsible for directional energy or charge transfer even for weak electronic couplings or negligible driving forces as in the photosynthetic RCs. Similar physics is now observed in the case of polymer:NFA blends and may have similar mechanistic origins67,71 which remain to be explored.As pointed out in Fig. 1B in the context of photosynthesis, and later by Lienau et al.8 in the context of OPVs, vibrational–electronic coupling can lead to strongly hybridized excitonic and CT states even for moderate to weak Coulomb couplings. Recently, Inganäs and co-workers71 have also reported oscillatory signatures in transient absorption (TA) and nonlinear two-dimensional photocurrent from TBSCs with both fullerene and NFAs. Their study implicates quantum coherence assisted, temperature independent exciton dissociation. Vibronic couplings involving low-frequency vibrational modes coupling the exciton and polaron electronic states have been invoked to explain the sub-200 fs coherent photocurrent generation, mechanistically similar to that reported by Lienau et al. An earlier study by Song and Scholes et al.72 on poly(3-hexylthiophene-2,5-diyl) (P3HT):phenyl-C61-butyric acid methyl ester (PCB61M) blends has also indicated that vibrational coherences exist at the same timescale as that of the charge dissociation process. Recently, the role of vibronic couplings in molecular materials has also been theoretically investigated by Tretiak et al.73 They have performed semi-classical simulations of excited state wavepacket dynamics initiated by non-adiabatic transitions between excited states. They report the possibility of coherence wavepacket motion between electronic states modulated by a coupled asymmetric vibrational mode.
In the case of pbRCs (Fig. 1C), vibrational–electronic states have been extensively investigated.49 The ultrafast charge transfer accompanied by dielectric asymmetry of protein operates over longer length scales (∼3 nm) with a 100% efficiency and minimum driving forces smaller than 0.25 eV. Two key points of energy and charge delocalization proceeding through vibronic states similar to those shown in Fig. 1B are that (1) coupling to vibrations and energetic disorder, which normally impede exciton propagation, can synergistically enhance delocalization even in the presence of weak electronic coupling, and (2) the non-adiabatic energy funnel is directional in nature.
One interesting possibility arises when considering a CT acceptor and an exciton donor. When energetic disorder is of the order of vibrational quanta,32 higher lying CT acceptor states become near-resonant with the exciton donor and strongly hybridize through resonant vibrational–electronic mixing. The electronic excitation received by higher lying CT acceptor states is then directed towards the lowest vibrational level on the CT acceptor, which is only weakly hybridized with the exciton donor, thereby reducing the possibility of charge recombination. An alternate possibility, of interest in designing bright LEDs, arises when the driving forces between bright donor excitons, such as the superradiant k = 0 exciton of the LH2 protein or the bright lower P* exciton in RCs, and CT acceptor states are negligibly small. In such cases, the lowest CT acceptor state can attain substantially bright exciton character through direct electronic coupling, instead of relying on vibronic mixing, and allow for facile radiative exciton recombination without exciton dissociation.
Although several studies have reported74 on slower charge separation due to a lower driving force, and hybridized exciton–polaron states,75 the non-adiabatic vibronic coupling framework, typically employed6 in the case of photosynthetic excitons, may explain the sub-100 fs formation of polaron states even for a negligible driving force.70,76 The role of such hybridized excitonic–CT states in promoting charge dissociation versus exciton recombination needs further investigation in the case of OPVs.
The above parallels between energy and charge transfer in natural light harvesting systems and OPVs serve to highlight the fact that the key design aspects understood in photosynthetic proteins are also the major players in the case of OPVs. For instance, in the case of purple bacteria, exciton diffusion can occur on length scales of tens of nanometres until reaching a RC sink because the rate of exciton diffusion to exciton lifetime is of the order of picoseconds to nanoseconds. In the context of OPVs as well, this basic design principle is the key to ensure EET transferred excitons to be harvested as charges. Similarly, pbRCs exhibit ultrafast charge transfer with a 100% efficiency based on design aspects quite analogous to interfacial driving forces suggested for OPVs.
One aspect that makes OPVs significantly complicated is that the blend morphology dictates photophysics. Important photophysical parameters such as exciton diffusion length, exciton lifetime, energy offset for charge-transfer and interfacial band bending are governed by the morphology of BHJ solar cells. In contrast, in the case of photosynthetic systems such as purple bacteria, unfavourable “morphologies” caused by the increased ratio of the antenna network to the RC sink, along with higher energetic disorder in the presence of low-light growth, does not affect the efficiency of charge separation, even though the exciton diffusion timescales to reach a RC become ∼2× longer.33 This may be due to the nanosecond exciton lifetimes of photosynthetic pigments, as well as lesser overall energetic disorder in photosynthetic membranes compared to OPV thin films, reflected in the respective spectral linewidths.41 Additionally, chlorophylls have a large number of low-frequency (<500 cm−1) vibrations which overlap with the range of energetic disorder. It is not entirely clear which of the above design aspects of photosynthetic energy and charge transfer distinguishes it from similar processes in OPVs. Understanding the natural photosynthetic EET mechanisms is therefore also imperative in order to possibly apply those principles to enhance the overall PCE7 in OPVs.
The above discussion suggests that, in OPVs, thin film morphology and exciton lifetimes regulate the molecular level photophysical parameters such as energy and/or charge transfer versus exciton recombination. The analogies between underlying photophysics in OPVs and photosynthesis advocate a platform to discuss systematic strategies to alleviate the losses in OPVs by harvesting excitons that did not undergo initial charge separation at the D/A interface.
3. Motivation for ternary blend solar cells (TBSCs)
One possible way to take advantage of the RET channel (shown in Fig. 1D) is by maximizing the overlap of the absorbing layer with the solar spectrum by extending from the UV to the NIR region. This can assist in harvesting additional excitons via RET and further augment the PCE. This can be accomplished by utilizing more than two components in the active layer without additional complexity in the OPV device architecture. Experimentally, RET in TBSCs is demonstrated based on the principle of overlap between the emission spectrum of the RET donor and the absorption spectrum of the RET acceptor as shown in Fig. 1D,77 assuming the validity of a Förster type energy transfer framework. Other factors in eqn (1) and (2) such as relative dipole orientations and donor–acceptor distance are highly dependent on the resulting morphology and difficult to control experimentally. Owing to this, several reported studies on TBSCs do not systematically consider the effect of adding the additional component, hereby referred to as the third component or D2, to the existing morphology of the binary D1/A blend. The observed photocurrent enhancements upon the addition of the third component are directly attributed to RET.Keeping the factors discussed in Section 2 in mind, the incorporation of the third component does not necessarily imply improved device performance because the morphology of donor and acceptor domains and the interfacial energetics can play a key role in dictating energy versus charge transfer rates, assuming that other factors such as exciton lifetime and spectral overlaps are favourable. Ideally, the third component should also improve the nanoscale morphology, thus simultaneously promoting light absorption as well as rapid exciton dissociation.60 Binary blend OPVs delivering 18% PCE are very encouraging and by choosing a suitable third component, TBSCs may likely surpass this,21,78,79 with several recent reviews focussing on the role of the third component in TBSCs.60,80,81 Attempts have been made to understand potential mechanisms for morphological stability maintaining the device performance in binary and ternary blend OSCs.82 In order to minimize geminate recombination losses through RET, it is necessary for the donor and acceptor to be in close proximity to each other, i.e. within 2–10 nm,26 which brings them within the typical exciton diffusion length reported for organic materials.58 Phase separation, formation of traps, etc. are common morphology related issues which are addressed using solvent additives pre- and post-treatment of the film by thermal and solvent vapour annealing (SVA), etc.83–85 Using this approach, the short-circuit current density (JSC) of TBSCs can also be improved by harvesting more excitons through RET. To get a perspective of how morphology plays a crucial role in dictating the device performance, a review article by Gasparini et al. is comprehensive.81 The third component alters both the physical and chemical landscapes of the BHJ blend. The crystallinity and purity of donor and acceptor domains and the miscibility of multiple components tune not only the open circuit voltage (VOC), but also the fill factor and photocurrent of the resulting blend.86,87 Photocurrent generating interfaces need to comprise mixed phases and the regions farther from the interface should have pure phase domains to achieve better charge collection with improved VOC.81 However, this is not universal to all ternary blends, and hence any guideline to achieve higher PCEs for TBSCs, by taking components with favourable energetics, has not been established.
In a scenario where TBSCs are primarily based on engineering spectral overlaps between the donor and acceptor components with a lack of morphology control over the individual components in the blend, directly attributing the JSC enhancement in TBSCs to “FRET” not only obfuscates the practical device design guiding principles, but also prevents a mechanistic understanding of femtosecond energy and charge delocalization in such systems. Systematically correlating TBSC morphology with spectroscopic studies to examine fundamental design considerations such as exciton–CT state hybridization, non-adiabatic vibrational–electronic couplings, hot exciton delocalization, and charge transfer with minimized recombination losses even with negligible driving forces is crucial to optimize TBSCs based on rigorous design principles.
In OPVs, the focus of the field to date has been on achieving a high PCE by using TBSC thin films. The discussion of all the TBSC approaches reported in the literature is beyond the scope of this perspective. In the section below, we briefly summarize the key findings of various TBSC approaches. We also attempted to empirically correlate the observed JSC with the R0 for the reported TBSC systems and found no expected correlations. We argue that the lack of such correlations in the current literature motivates a systematic approach for quantifying the EET contribution to JSC enhancement, such that certain guiding design principles could be established for future TBSC development.
4. Approaches to ternary blend organic solar cells
Very recently, TBSCs have exhibited PCEs more than 17%, which is encouraging. Table 1 lists some of the high performing TBSCs from recent studies. Following a recent report on the PM6:Y6 blend which delivers a 15.6% PCE, substantial efforts have been made to improve the PCE further by incorporating the third component. Table 1 shows nine such successful attempts made on the PM6:Y6 blend alone.| Sl no. | Control blend | Third component | PCE (%) | Ref. |
|---|---|---|---|---|
| 1 | PM6:Y6 | PC71BM | 16.67 | 21 |
| 2 | PM6:Y6 | MF1 | 17.22 | 16 |
| 3 | PM6:Y6 | BTF | 16.53 | 88 |
| 4 | PM6:Y6 | J71 | 16.5 | 19 |
| 5 | PM6:Y6 | 3TP3T-4F | 16.7 | 79 |
| 6 | PM6:Y6 | SM1 | 16.55 | 18 |
| 7 | PM6:Y6 | PBDBT-SF | 16.4 | 20 |
| 8 | PM6:Y6 | IT4F | 16.27 | 89 |
| 9 | PM6:Y6 | PC61BM | 16.5 | 90 |
| 10 | PM7:Y6 | PC71BM | 16.2 | 17 |
| 11 | PBDB-T:m-INPOIC | IT-M | 13.7 | 23 |
| 12 | PBTA-PS:6TIC | IDIC-C4Ph | 14.24 | 66 |
| 13 | PBDB-T:ITIC | IDT-T | 12.2 | 91 |
| 14 | PTB7-Th:IEICO-4F | PffBT4T-2OD | 12.12 | 92 |
| 15 | PM6:IT-4F | IDIC | 14.03 | 93 |
| 16 | PBDTTT-EF-T:IDTBR | IDFBR | 11.0 | 94 |
| 17 | PM6:IDIC | TOBDT | 14.0 | 95 |
This shows the viability of the idea of TBSCs, where the third component can either improve the light absorption and nanomorphology of blends or reduce charge recombination.
The most common approach in TBSCs is to introduce chromophores (small molecule or dye) with a high absorption coefficient as the third component in the binary blend of a polymer donor and either fullerene or NFAs.7,8,81,96–100 Initially, the purpose of the addition of the third component is to make the photoactive layer panchromatic. However, several experimental studies observed excitons efficiently harvested in ternary blend donor/acceptor interfaces through long-range energy transfer. For example, the excitons generated in the J71 polymeric domain can get transferred to PM6 by virtue of RET and this can contribute to the photocurrent enhancement of the resulting TBSC.19 Based on the RET design parameters outlined in eqn (1) and (2), fullerenes, being poor absorbers of light, are not ideally suited for harnessing this RET channel. In contrast, low bandgap NIR absorbing NFAs by virtue of their high extinction coefficient and long acceptor exciton lifetimes with minimized non-radiative relaxation can serve as ideal RET acceptors. As mentioned earlier, several ternary blends based on NFAs have already reported encouraging PCE enhancements.
In this section, we will first describe the most notable TBSC approaches that have been recently reported in the literature, with a focus on the key role of energy transfer keeping in mind the specific properties of the third component with the observed RET.
A. Energy transfer in ternary blend organic solar cells
It is required that the third component should have absorption overlapping with the fluorescence spectrum of the polymer donor for efficient energy transfer. The donor–acceptor type conjugated polymers, owing to their comparatively low bandgap, absorb in the far visible and near-IR (NIR) regions of the solar spectrum. They often complement the absorption of the binary blend and hence have been incorporated in many systems to realize a high PCE.81 The composition of the polymers in the optimized blend varies from 10–50 wt% with respect to the other donor. The chemical structures of polymers and oligomers used in recent studies as FRET pairs are shown in Fig. 2. In the very first report on all-polymer TBSCs, Koppe et al. introduced a low band gap polymer, PCPDTBT, in a binary blend of P3HT:PC71BM, which resulted in a ternary blend. PCPDTBT is a NIR sensitizer which provides complementary spectral coverage to P3HT and forms energy cascade promoting charge transfer.61 Photoinduced absorption (PIA) spectroscopy studies revealed a two-step charge transfer process to be dominant in the ternary blend. Initially, the excitons are generated in PCPDTBT, followed by electron transfer to PC71BM. Subsequently, the holes in PCPDTBT get relayed into P3HT and finally to an interface between PCPDTBT and P3HT with negligible bimolecular recombination losses. However, RET was not the primary mechanism for the observed photoluminescence (PL) quenching of P3HT by the addition of 20% PCPDTBT, even though the PL spectrum of P3HT and the absorption spectrum of PCPDTBT overlap considerably.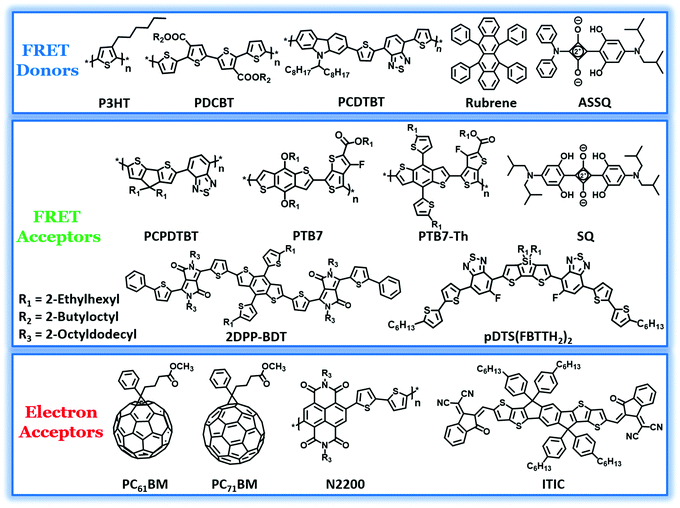 | ||
| Fig. 2 Molecular structures of polymer and small molecule FRET donors and acceptors, fullerene and non-fullerene electron acceptors utilized in TBSCs showing RET. | ||
Furthermore, the dissociation of excitons via photoinduced electron transfer to PC71BM while mutually transferring holes to P3HT was observed as the decisive factor. Such observations demanded more investigations on the excited-state dynamics of the photoactive layer in TBSCs. Goh et al. reported energy transfer in a TBSC consisting of two commonly used polymers, semicrystalline P3HT and amorphous PTB7 as the donor and PC71BM as the acceptor materials.101 Energy level cascading and FRET from P3HT to PTB7 synergistically boosted the PCE by 22.5% as compared to the binary blend of PTB7 and PC71BM. Although P3HT and PTB7 prefer different packing orientations in films, SVA improved the intermixing of both polymers, and as a result both fill factor (FF) and carrier mobility were found to be enhanced. At the optimal loading percentage (5%) of P3HT in the blend, bimolecular recombination was suppressed significantly. Assuming the validity of RET, R0 was found to be 6.5 nm, comparable with the domain sizes obtained from AFM.101 FRET between the two polymers (P3HT and PTB7) was established based on a decreased PL of P3HT with a concomitant increase in the PL of PTB7. In order to establish charge and energy transfer, the authors employed TA spectroscopy.101 Benten et al. utilized two high performing polymer donor materials: PBDTTT-EF-T (hereafter will be referred to as PTB7-Th) and a high bandgap polymer, PCDTBT, along with a non-fullerene polymeric acceptor (N2200) to fabricate an all-polymer TBSC.102 The chemical structures of the polymers are shown in Fig. 2. Only 10 wt% PCDTBT in TBSCs improved the PCE up to 6.65%. The weak absorption by the PTB7-Th:N2200 blend in the visible spectrum is compensated by the third component. Because of the low LUMO offset between PTB7-Th and PCDTBT, the PL of PTB7-Th could not be quenched by PCDTBT as evident from steady state measurements and the observation of very low JSC from the PTB7-Th:PCDTBT device.102 But the excitons generated in PTB7-Th as well as the excitons that were transferred from PCDTBT via RET could be separated at the PTB7-Th:N2200 interface. Moreover, the excitons generated in PCDTBT domains could be transferred energetically to N2200 and get separated at either the PCDTBT:N2200 or the PTB7-Th:N2200 interface. The R0 values of PCDTBT/PTB7-Th and that of PCDTBT/N2200 were calculated to be 3.5 and 3.3 nm, respectively. This enabled the long range transport of PCDTBT excitons into PTB7-Th and N2200 which in turn improved the JSC to 14.4 mA cm−2 for a 10 wt% loading of PCDTBT in the ternary blend. The external quantum efficiency (EQE) spectrum of the ternary blend shows an improvement in the range of 500–650 nm (green open circles), confirming the contribution of PCDTBT to the generation of photocurrent. This caused the highest EQE of the ternary blend to surge towards 65–70% compared to the PTB7-Th:N2200 blend. The same donor FRET pair, PCDTBT/PTB7-Th, was incorporated with a NFA, ITIC, to yield a 7.5% PCE.14
To draw a correlation between the entropy of mixing of two conjugated polymers and harvest the NIR part of the solar spectrum, Gasparini et al. introduced PTB7-Th as the third component in a binary blend of PDCBT and PC71BM.13 The incorporation of PTB7-Th suppressed the trap assisted recombination which was independently confirmed by intensity dependent photovoltage/photocurrent studies and thermally stimulated current measurements. The maximum free charge carrier generation rate was the highest for the ternary blend with an equal amount of polymer donors in the ternary blend. This example is one of the few TBSCs that have an equal amount of polymer donors by weight in the optimized blend. PDCBT and PTB7-Th form a RET pair which manifests in the steady state PL spectra of the blend with complete quenching of PL from PDCBT, and the blend PL resembles that of PTB7-Th.13 A very low concentration of PTB7-Th was sufficient to quench the PL of PDCBT and the time resolved emission of PTB7-Th showed a delayed maximum of PL intensity for low PTB7-Th concentrations, which clearly established FRET from PDCBT to PTB7-Th. Using Flory-Huggins theory, the intermolecular mixing parameter (χ1,2) was calculated for each component with PC71BM and between the two polymers. For PDCBT:PTB7-Th, χ1,2 was calculated to be 0.20, while for PDCBT:PC71BM and PTB7-Th:PC71BM it was 2.29 and 1.23, respectively, suggesting higher affinity of intermixing between two polymers rather than individually mixing with PC71BM. As FRET is distance dependent, this particular observation suggested that there is a higher probability that PDCBT and PTB7-Th would lie in close proximity promoting FRET efficiently. However, the authors have not discussed the role of energy transfer between the two polymers. To generalize the concept of all polymer blends, the authors fabricated ternary devices using these two polymer donors and a NFA, IEICO-4Cl, and reported an 11.2% PCE.
Taylor et al. incorporated squaraine (SQ) in the P3HT:PC61BM binary blend.63 The NIR absorption of SQ combined with P3HT resulted in a 38% increase in PCE. The PL of P3HT and the absorption of SQ overlapped significantly (Fig. 3a) and FRET from P3HT to SQ was confirmed by the increase in the PL intensity of SQ with the increasing amount of SQ in the P3HT:SQ blend upon excitation at the absorption maximum of P3HT (Fig. 3b). The absorption spectra of P3HT:SQ films with varying concentrations of SQ show an increase in the crystallinity of P3HT with a higher loading percentage of SQ, which implies that the incorporation of SQ did not interrupt the interchain ordering of P3HT. The time-resolved decay of the blend films showed faster decay dynamics with an increase in the SQ concentration as compared to that of neat P3HT, confirming FRET between the two. To gain a deeper insight into the photophysical processes in the blend, transient absorption studies were performed. In the blend containing 1 or 5 wt% SQ, ground state bleaching of SQ at 665 nm was observed, confirming energy transfer from P3HT to SQ in sub-ps timescales. The simultaneous improvements of JSC and FF at the optimal loading percentage (1%) of SQ show effective exciton harvesting and better nanophase crystallinity (Fig. 3c). A further increase in the amount of SQ improved the JSC but a drop in FF was observed. The EQE spectra of the blends indicated an increase in photocurrent in the range of 300–620 nm due to resonance energy transfer from P3HT to SQ (Fig. 3d), whereas the improvement in EQE in the 650–700 nm region is due to SQ absorption as it increased with an increase in the loading percentage of SQ in blend.
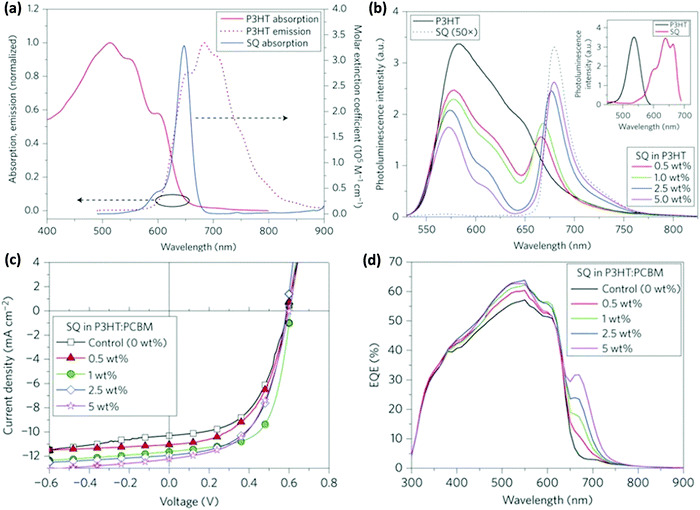 | ||
| Fig. 3 (a) Absorption and emission spectra of P3HT and SQ showing an overlap between the PL of the P3HT film and the absorption of SQ in solution. (b) PL spectra of P3HT (pumping wavelength: 525 nm) and its blend with different weight percentages of SQ in solution. Inset: PL excitation spectra of neat P3HT solution (black) and neat SQ solution (red). The excitation spectrum of P3HT was obtained at an emission wavelength of 600 nm and that for neat SQ was obtained at 700 nm. (c) J–V curves of the photovoltaic devices with the SQ concentration ranging from 0 to 5 wt%. (d) EQE vs. wavelength of devices with the SQ concentration ranging from 0 to 5 wt% (adapted with permission from ref. 63). | ||
Kong et al. have used a dye, 2,4-bis-[(N,N-diisobutylamino)-2,6-dihydroxyphenyl]-4-(4-diphenyliminio) squaraine (ASSQ), in a PTB7-Th (or PCE10):N2200 based binary blend OPV (chemical structure shown in Fig. 2).103 Similar to the previously discussed RET pairs, the ASSQ/PTB7-Th pair exhibited a characteristic spectral overlap as well as sensitized steady state emission from PTB7-Th upon exciting ASSQ, suggesting FRET. Being a NFA based TBSC, all the three components generate excitons upon light illumination, the excitons in ASSQ separated either at the ASSQ:N2200 interface via charge transfer or transferred to PTB7-Th via RET and subsequently separated at the PTB7-Th:N2200 interface. R0, assuming the validity of the FRET mechanism, calculated using eqn (2) is 4.3 nm. TBSCs with 20 weight% ASSQ in PTB7-Th:N2200 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) exhibited a maximum PCE of 5.55% which is 10% higher than that of the binary blend without ASSQ. The JSC increased from 12.4 to a maximum of 13.1 mA cm−2 for the blend containing 20% ASSQ, which is a mere 5% increment. As the control devices comprising ASSQ:PTB7-Th and ASSQ:N2200 yielded negligible JSC > 0.1 mA cm−2, suggesting negligible charge transfer between the sensitizer and the existing donor and acceptor, we can safely attribute this enhancement to the charges generated upon the dissociation of excitons at the PTB7-Th:N2200 interface after getting transferred from ASSQ to PTB7-Th via FRET. Aromatic dyes like rubrene have also been used as the third component in PTB7:PC71BM solar cells to enhance the device photocurrent by 16% by virtue of RET from rubrene to PTB7.104
1) exhibited a maximum PCE of 5.55% which is 10% higher than that of the binary blend without ASSQ. The JSC increased from 12.4 to a maximum of 13.1 mA cm−2 for the blend containing 20% ASSQ, which is a mere 5% increment. As the control devices comprising ASSQ:PTB7-Th and ASSQ:N2200 yielded negligible JSC > 0.1 mA cm−2, suggesting negligible charge transfer between the sensitizer and the existing donor and acceptor, we can safely attribute this enhancement to the charges generated upon the dissociation of excitons at the PTB7-Th:N2200 interface after getting transferred from ASSQ to PTB7-Th via FRET. Aromatic dyes like rubrene have also been used as the third component in PTB7:PC71BM solar cells to enhance the device photocurrent by 16% by virtue of RET from rubrene to PTB7.104
Bi et al. incorporated p-DTS(FBTTH2)2 (structure shown in Fig. 2) in P3HT:PC71BM BHJ solar cells and showed a nearly 24% increase in PCE.105 The absorption spectrum of the third component, p-DTS(FBTTH2)2, complements that of P3HT which is beneficial for harvesting more sunlight and, moreover, the PL of P3HT significantly overlaps with the absorption spectrum of p-DTS(FBTTH2)2 raising the possibility of RET between the two. R0, calculated using eqn (2), was found to be 8.6 nm. To understand the RET timescales in more detail, pump–probe spectroscopy was used. The samples were excited at 400 nm and the PL was probed at 650 nm. The faster decay of P3HT excitons upon the addition of 15 wt% p-DTS(FBTTH2)2 shows that either charge or energy transfer between the two co-exists. Upon close inspection of the biexponential fitting parameters and initial components, it was deduced that the ultrafast decay (<10 ps) is due to energy transfer because, in such short timescales, <10 ps, the charge transfer was not observed by Banerji et al. in a similar system.106 The observation of an increase in the proportion of a shorter time component as the loading percentage of p-DTS(FBTTH2)2 was increased in the blend further confirmed the energy transfer. The JSC increased from 8.47 to 9.35 mA cm−2 as the loading percentage of p-DTS(FBTTH2)2 was increased from 0 to 15 wt% in the P3HT:PC71BM BHJ blend. The EQE spectra at 685 nm show the contribution of p-DTS(FBTTH2)2 to the photocurrent.
We investigated the role of RET in the P3HT:2DPP-BDT:PC71BM ternary system. 2DPP-BDT is a donor–acceptor type molecule, consisting of the diketopyrrolopyrrole and benzodithiophene backbone.107 Based on the substantial overlap of the PL of P3HT and the absorption spectrum of 2DPP-BDT, we chose these materials as the FRET pair (Fig. 4a). In the P3HT:2DPP-BDT blend, the PL intensity of 2DPP-BDT was enhanced in the NIR region even though P3HT was selectively excited. This finding clearly suggests that there is efficient energy transfer from P3HT to 2DPP-BDT (Fig. 4b). The fluorescence quenching of P3HT (∼96%) was observed for a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of P3HT and 2DPP-BDT (Fig. 4c), which implies that there might be processes such as charge and energy transfer operating in tandem. To further establish RET between P3HT and 2DPP-BDT, we performed TA spectroscopy for both neat and 1
50 mixture of P3HT and 2DPP-BDT (Fig. 4c), which implies that there might be processes such as charge and energy transfer operating in tandem. To further establish RET between P3HT and 2DPP-BDT, we performed TA spectroscopy for both neat and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 blend films which resulted in GSB of 2DPP-BDT in earlier time scales (few ps) for a 1
1 blend films which resulted in GSB of 2DPP-BDT in earlier time scales (few ps) for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 blend although it was not directly excited.107
1 blend although it was not directly excited.107
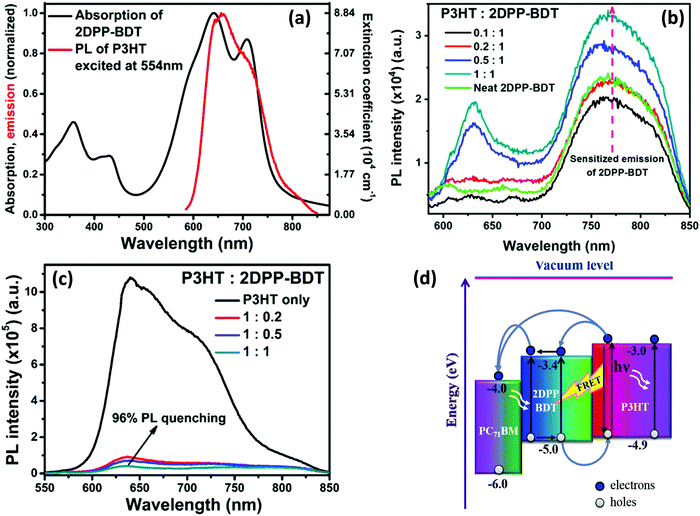 | ||
| Fig. 4 (a) The overlap of the PL spectrum of P3HT with the absorption spectrum of 2DPP-BDT; (b) the sensitized PL of 2DPP-BDT; when P3HT is excited at 554 nm, it increased with an increase in the amount of 2DPP-BDT in the blend film; (c) PL quenching of P3HT by 2DPP-BDT; and (d) the energy level cascading of P3HT, 2DPP-BDT and PC71BM showing charge transfer between P3HT/2DPP-BDT/PC71BM and energy transfer from P3HT to 2DPP-BDT upon light illumination (adapted with permission from ref. 107). | ||
The frontier molecular energy level alignments of the three components are shown in Fig. 4d. It schematically depicts various charge and energy transfer processes between P3HT, 2DPP-BDT and PC71BM upon light illumination. The combination of energy and charge transfer improved the photocurrent (11.88 as compared to 8.45 mA cm−2) and in turn caused a 27% increase in overall PCE. The energy transfer from P3HT to 2DPP-BDT plays a significant role in harvesting excitons at the donor/acceptor interface. To conclude this section, we note that energy transfer is one of the determining factors to improve the PCE of TBSCs.
5. Discussion
The immediate conclusion that can be drawn from the experimental results discussed above is that if the systems are chosen rationally, RET can synergistically work with charge transfer and improve the photocurrent. A relevant question to ask is whether RET is redundant in multi-component blends because, with the development of NFAs which absorb solar light in the visible to NIR region, spectral overlaps between components are practically unavoidable. Furthermore, in many such cases, possible RET contribution is often not discussed rigorously.13,15,23,108 It is understandable that the progress in OSCs is efficiency-driven and, within the last seven years, the PCEs have been doubled.56,57,78,89,90,109–111 Owing to this approach, in many such high-performing ternary systems, RET is just another photophysical phenomenon which is often not investigated to the same extent as has been done for photosynthetic systems. It is important that any scalable solar cell technology must be well-understood in terms of underlying fundamental photophysics, in order to realize and scale its applicability. In this perspective, we have summarized several TBSC approaches reported recently in the literature, where an enhancement in JSC has been attributed to both charge transfer and efficient RET. Although our sample space, in terms of the number of papers discussed, is small, nevertheless, it is worth analysing whether there exist any expected correlations between FRET-based D–A spectral overlap design parameters and the observed device parameters.The striking success of ternary blend approaches is the realization of enhanced JSC with an improved overall PCE of OPVs. The optimized binary systems, except the PTB7-Th:PCDTBT:N2200 TBSC, do not report RET between them. The commonly presented picture in such binary systems is that of charge transfer at the existing donor (D1)/acceptor (A) interface contributing to the JSC. When the third component, D2, is introduced, several research groups have reported improvements in JSC, as summarized in Table 2. In a simplistic description of the ternary blend, the third component is designed to either provide additional excitons to D1 via EET from D2 to D1 (case1 D2/D1/A) or receive additional excitons from D1, which did not undergo dissociation at the D1/A interface, via EET from D1 to D2 (case2 D1/D2/A). In either of the cases presented in Table 2, the amount of the third component D2 is small to avoid the dramatic effect on the existing optimized D1/A morphology. Note that the morphology in the reported studies in Table 2 was optimized for binary and ternary blends to achieve the maximum PCE, whereas R0 for the RET pairs was estimated using D–A spectral overlaps only.
| Reported R0 (nm) | RET donor (D) | RET acceptor (A) | J SC (without/with the RET component) (mA cm−2) | ΔJSC (mA cm−2) | PCEa/ΔPCEb (%) | D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A A |
Ref. |
|---|---|---|---|---|---|---|---|
| a Highest PCEs obtained from TBSCs. b ΔPCE = PCETBSC − PCEBinary. | |||||||
| 1.8 | P3HT | 2DPP-BDT | 8.45/11.88 | 3.43 | 4.11/0.88 | 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 0.2 |
ACS Appl. Energy Mater., 2018, 1, 4874–4882 |
| 3.1 | Rubrene | PTB7 | 14.94/17.35 | 2.41 | 8.03/1.43 | 0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.99 0.99 |
Solar Energy, 2016, 139, 221–227 |
| 3.5 | PCDTBT | PTB7-Th | 12.40/14.40 | 2.00 | 6.65/0.95 | 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.9 0.9 |
Energy Environ. Sci., 2016, 9, 135–140 |
| 4.3 | ASSQ | PTB7-Th | 12.40/13.10 | 0.70 | 5.55/0.55 | 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Nano Energy, 2017, 38, 36–42 |
| 6.5 | P3HT | PTB7 | 14.84/17.25 | 2.41 | 8.72/1.37 | 0.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.95 0.95 |
J. Mater. Chem. A, 2015, 3, 18611–18621 |
| 8.0 | P3HT | SQ | 10.30/11.60 | 1.30 | 4.51/1.24 | 0.99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 0.01 |
Nature Photonics, 2013, 7, 479–485 |
| 8.6 | P3HT | p-DTS(FBTTH2)2 | 8.47/9.35 | 0.88 | 3.71/0.71 | 0.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.15 0.15 |
ACS Appl. Mater. Interfaces, 2016, 8, 23212–23221 |
| — | ASSQ | PBDB-T | 15.50/17.30 | 1.80 | 10.51/1.53 | 0.04![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.96 0.96 |
Mater. Today, 2018, 21, 79–87 |
In both cases mentioned above, exciton dissociation can take place at D1/A, D2/A, and D1/D2 interfaces in parallel with the D1/D2 EET channel. Even without any D1/D2 EET channel, the JSC enhancement can arise from additional contributions from exciton dissociation at D1/D2 and D2/A interfaces, which were absent in either of the binary blends, D1/A or D2/A. In addition to the above JSC enhancement, the TBSC systems in Table 2 are intended to have a complementary energy transfer from D1 to D2, or vice versa, which can contribute to the harvesting of additional excitons as separated charges. The EET transferred excitons would then get dissociated at the interface with the acceptor A. In general, the excitons generated in the ternary blend, localized in the proximity of D1/D2 interface exhibit a low probability of escaping from the dissociation either via charge or energy transfer and hence contribute to the improvement of JSC. In some of the reported examples, it was observed that the D1/D2 interface did not lead to charge separation and hence did not contribute directly to the photocurrent. Although excitons can, in principle, dissociate at the D1/D2 interface, it was found that the contribution to the photocurrent was minimal due to the low mobility of the free charge carriers within the D1/D2 blend. A very low photocurrent was observed when a solar cell was made using PTB7-Th and PCDTBT which form a RET pair.102 Hence, the total observed enhancement in current density (ΔJSC) reported in the literature between the binary and their ternary blend counterparts may be expected to have increased contribution primarily from two channels: the creation of excitons in D2, followed by exciton dissociation at the additional D2/A interface, and energy transfer between D1 and D2, followed by exciton dissociation at the D2/A or D1/A interface. Based on the above reasoning, attributing any enhancement in JSC completely to energy transfer neglects the former channel and overestimates the efficacy of “FRET” in TBSCs. Thus, the EET contribution to JSC enhancement is difficult to reliably assess without systematically probing the excited state relaxation channels.
The assumption of Förster RET framework for the systems studied in the above examples may not be a valid and generalized Förster framework3,42 as vibronic exciton models6 may be more applicable in certain situations. Despite expected mechanistic deviations from a Förster type framework, EET is nevertheless sensitive to distance. The recently reported ternary blend systems in Table 2 have relied on the Förster critical distance R0 as a guiding parameter to achieve JSC enhancement. Note that the R0 values reported in these studies, and shown in Table 2, are solely based on the spectral characteristics of the donor and acceptor, and may not necessarily imply a faster rate of energy transfer unless the morphology determination of the D1/D2 part of the TBSC blend confirms increased spatial proximity of the domains. Based on eqn (1), the exciton population in the donor domains should decay faster with increasing R0, and correspondingly the rate of exciton transfer to the acceptor domains becomes faster. Thus, an additional channel for the excited state relaxation of the donor is created via RET which can compete with the direct interfacial exciton dissociation and exciton population relaxation channels. As discussed in Sections 2A and B, this competition between relaxation channels is dictated by morphology, exciton lifetime and interfacial driving forces. This implies that while a higher R0 and the spatial proximity of donor–acceptor domains can help RET to be the dominant channel, subsequent competition between the acceptor exciton lifetime and exciton dissociation rate will ultimately dictate the achievable JSC enhancement.
Based on the above discussion, Fig. 5 plots the reported JSC enhancement in the studies summarized in Table 2 against the reported R0. Even though RET efficiency is expected to increase with R0, the current TBSC systems in the literature do not reflect any positive correlations between JSC enhancement and R0. This re-emphasizes the point that R0 alone may not be a reliable design parameter for TBSCs because contributions towards JSC enhancement can also arise from direct interfacial exciton dissociation channels instead of increased energy transfer. The stark lack of trends between JSC and Förster critical distance available in the current TBSC literature may not be completely surprising and may be attributed to the shambolic variation of RET parameters (shown in Table 2), such as refractive index, random orientations of the donor and acceptor, variation in interfacial driving forces between varying material combinations, etc. Additionally, as discussed earlier, when the concentration and absorption cross-section of the third component (D2) are substantial, the creation of excitons in D2, followed by exciton dissociation at the D2/A interface, without any EET can also contribute to device photocurrent enhancement and cannot be assumed to be negligible.
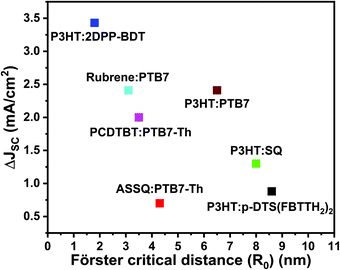 | ||
| Fig. 5 Plot of the reported current density enhancement in TBSCs (ΔJSC) versus the reported Förster critical distance (R0). The enhancement in JSC is compared to the corresponding binary blends. Note that the RET pairs reported in the literature, compared in Fig. 5, do not systematically consider the effect of morphology on RET enhancement. | ||
Most importantly, all the RET pairs considered in Table 2 have been processed under different conditions – different processing solvents, annealing temperatures, additives, etc. This hinders a systematic comparison because morphological differences are expected to not only affect the RET rates due to varying spatial proximity between RET pairs, but also modify the competition between electronic relaxation channels such as RET rates, exciton dissociation and exciton lifetimes. Such differences are also expected in the D1/A binary blend as well as the resulting D1/D2/A ternary blends. Modifications to the resulting nanomorphology of binary blend components upon the addition of the third component have been found to be crucial for efficiency optimization. However, systematic modifications to the morphology have been experimentally challenging.112–114
Apart from insufficient spectroscopic evidence for RET contribution to JSC enhancement and the lack of systematic morphology control, the TBSC literature highlighted in Fig. 5 also comprises different material combinations for RET pairs. As discussed in Section 2A, interfacial energetics and exciton lifetimes critically determine the competition between exciton dissociation across nanostructured interfaces, exciton loss and EET. For the varying set of material combinations shown in Fig. 5, it is not clear how the interfacial energetics affect this interplay.
One possible way to decouple the effects of interfacial energetics and morphology and quantify the RET contribution to JSC enhancement is to keep the material combinations fixed and systematically vary the morphology of the RET pair using different processing conditions to find the optimal solvent and/or additives for realizing a progressively larger RET critical distance. This approach can be well complemented by further correlating the existing morphology characterization techniques, such as AFM and grazing incidence small angle X-ray spectroscopy, with non-linear broadband transient absorption microscopy.115–117 Recent application of fluorescence118 or photocurrent detection119,120 non-linear spectro-imaging techniques is another promising route towards correlating nanomorphology with ultrafast photophysics. The above time-resolved spectroscopic techniques can additionally exploit the timescale and possible spectral separation between direct exciton dissociation and RET channels, in order to deconvolute their contributions to JSC enhancement. When the third component expands the absorption range of TBSC, the above broadband spectro-imaging techniques can potentially help to map out the spatial and wavelength dependence of generated excitons, dissociated excitons, as well as the collected photocurrent if any, thereby addressing the interesting question of whether RET leads to an enhanced internal quantum efficiency and subsequently to an enhanced device photocurrent.
The relative orientation of dipoles is another parameter that is always assumed as 2/3 considering random molecular orientation. The reported importance of dipolar orientation in altering the frontier molecular energy levels and thereby creating an electrostatic landscape conducive to exciton dissociation121 necessitates a rigorous examination of this parameter. Theoretical calculations can be helpful in this regard and illustrate a realistic picture which would help in the precise calculation of R0.
As we have discussed in the context of photosynthesis as well as OPVs, the acceptor exciton lifetime is crucial in determining the balance between exciton dissociation and exciton loss, and optimized morphology and favourable driving forces can assist in charge generation. Interestingly, in the case of photosynthetic RCs, quite low driving forces can lead to sub-picosecond exciton dissociation through vibronic mixing, in contrast to recently reported122 NFA based OSCs, wherein low driving offsets result in long charge dissociation timescales, which then need to be balanced by long acceptor exciton lifetimes to prevent exciton loss. This underscores the possible importance of the vibronic mixing design principle known from natural photosynthetic RCs.
Furthermore, nanosecond acceptor exciton lifetimes versus picosecond EET rates prevent unfavourable morphology, as in low-light grown photosynthetic bacteria, from affecting EET and charge separation efficiency. With a similar analogy, a recent report suggested that high PLQY emitters with low energy offsets will minimize the non-radiative recombination-based voltage loss in NFA based OPVs.122 In TBSCs, the low bandgap NIR absorbing components with a high PLQY and a longer acceptor exciton lifetime will therefore be the key to achieve long range energy transfer with minimum voltage loss. Therefore, rational molecular design is required to synthesize new NIR absorbing organic chromophores with a high PLQY and a longer lifetime to achieve the maximum benefit from RET.
This perspective highlights that, despite achieving a high PCE in TBSCs, a great deal of systematic work is needed to underpin the role of the third component in determining VOC and JSC. The high performance TBSC systems need to be relooked systematically to quantify RET contribution to JSC enhancement and to realize the full potential of TBSCs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. P. acknowledges the support from Science and Engineering Research Board (SERB), IRHPA grant, Department of Science and Technology, New Delhi, India for a Swarnajayanti fellowship and acknowledges the financial support from UKRI Global Challenge Research Fund project, SUNRISE (EP/P032591/1). A. A. M. acknowledges Indian Institute of Science, Bangalore for senior research fellowship. V. T. acknowledges the support from the Indian Institute of Science through a start-up grant (SG/MHRD-18-0020).References
- T. Förster, Delocalized excitation and excitation transfer, Modern Quantum Chemistry, Academic Press Inc., New York, vol. 3, 1965 Search PubMed.
- J. Franck and E. Teller, J. Chem. Phys., 1938, 6, 861–872 CrossRef CAS.
- H. Sumi, J. Phys. Chem. B, 1999, 103, 252–260 CrossRef CAS.
- D. Beljonne, C. Curutchet, G. D. Scholes and R. J. Silbey, J. Phys. Chem. B, 2009, 113, 6583–6599 CrossRef CAS PubMed.
- G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57–87 CrossRef CAS PubMed.
- D. M. Jonas, Annu. Rev. Phys. Chem., 2018, 69, 327–352 CrossRef CAS PubMed.
- G. D. Scholes, G. R. Fleming, L. X. Chen, A. Aspuru-Guzik, A. Buchleitner, D. F. Coker, G. S. Engel, R. van Grondelle, A. Ishizaki, D. M. Jonas, J. S. Lundeen, J. K. McCusker, S. Mukamel, J. P. Ogilvie, A. Olaya-Castro, M. A. Ratner, F. C. Spano, K. B. Whaley and X. Zhu, Nature, 2017, 543, 647–656 CrossRef CAS PubMed.
- A. De Sio and C. Lienau, Phys. Chem. Chem. Phys., 2017, 19, 18813–18830 RSC.
- Y. Song, S. N. Clafton, R. D. Pensack, T. W. Kee and G. D. Scholes, Nat. Commun., 2014, 5, 4933 CrossRef PubMed.
- A. F. Morrison and J. M. Herbert, J. Phys. Chem. Lett., 2017, 8, 1442–1448 CrossRef CAS PubMed.
- C. Schnedermann, A. M. Alvertis, T. Wende, S. Lukman, J. Feng, F. A. Y. N. Schröder, D. H. P. Turban, J. Wu, N. D. M. Hine, N. C. Greenham, A. W. Chin, A. Rao, P. Kukura and A. J. Musser, Nat. Commun., 2019, 10, 1–11 CrossRef CAS PubMed.
- Y. Xie, T. Li, J. Guo, P. Bi, X. Xue, H. S. Ryu, Y. Cai, J. Min, L. Huo, X. Hao, H. Y. Woo, X. Zhan and Y. Sun, ACS Energy Lett., 2019, 4, 1196–1203 CrossRef CAS.
- N. Gasparini, S. Kahmann, M. Salvador, J. D. Perea, A. Sperlich, A. Baumann, N. Li, S. Rechberger, E. Spiecker, V. Dyakonov, G. Portale, M. A. Loi, C. J. Brabec and T. Ameri, Adv. Energy Mater., 2019, 1803394 CrossRef.
- P. Bi, F. Zheng, X. Yang, M. Niu, L. Feng, W. Qin and X. Hao, J. Mater. Chem. A, 2017, 5, 12120–12130 RSC.
- Q. An, J. Wang and F. Zhang, Nano Energy, 2019, 60, 768–774 CrossRef CAS.
- Q. An, J. Wang, W. Gao, X. Ma, Z. Hu, J. Gao, C. Xu, M. Hao, X. Zhang, C. Yang and F. Zhang, Sci. Bull., 2020, 65, 538–545 CrossRef CAS.
- M. A. Pan, T. K. Lau, Y. Tang, Y. C. Wu, T. Liu, K. Li, M. C. Chen, X. Lu, W. Ma and C. Zhan, J. Mater. Chem. A, 2019, 7, 20713–20722 RSC.
- T. Yan, J. Ge, T. Lei, W. Zhang, W. Song, B. Fanady, D. Zhang, S. Chen, R. Peng and Z. Ge, J. Mater. Chem. A, 2019, 7, 25894–25899 RSC.
- G. Xie, Z. Zhang, Z. Su, X. Zhang and J. Zhang, Nano Energy, 2020, 69, 104447 CrossRef CAS.
- Y. Chang, T.-K. Lau, P. C. Y. Chow, N. Wu, D. Su, W. Zhang, H. Meng, C. Ma, T. Liu, K. Li, X. Zou, K. S. Wong, X. Lu, H. Yan and C. Zhan, J. Mater. Chem. A, 2020, 8, 3676 RSC.
- T. Yan, W. Song, J. Huang, R. Peng, L. Huang and Z. Ge, Adv. Mater., 2019, 31, 1902210 CrossRef.
- B. Fan, Z. Zeng, W. Zhong, L. Ying, D. Zhang, M. Li, F. Peng, N. Li, F. Huang and Y. Cao, ACS Energy Lett., 2019, 4, 2466–2472 CrossRef CAS.
- B. Du, R. Geng, W. Li, D. Li, Y. Mao, M. Chen, X. Zhang, J. A. Smith, R. C. Kilbride, M. E. O’Kane, D. Liu, D. G. Lidzey, W. Tang and T. Wang, ACS Energy Lett., 2019, 2378–2385 CrossRef CAS.
- D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850 CrossRef CAS.
- T. Förster, Ann. Phys., 1948, 437, 55–75 CrossRef.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, 3rd edn, 2006 Search PubMed.
- V. Butkus, D. Zigmantas, L. Valkunas and D. Abramavicius, Chem. Phys. Lett., 2012, 545, 40–43 CrossRef CAS.
- R. D. Harcourt, G. D. Scholes and K. P. Ghiggino, J. Chem. Phys., 1994, 101, 10521–10525 CrossRef CAS.
- G. D. Scholes, J. Phys. Chem. Lett., 2018, 9, 1568–1572 CrossRef CAS.
- J. M. Womick and A. M. Moran, J. Phys. Chem. B, 2011, 115, 1347–1356 CrossRef CAS PubMed.
- S. Jang, M. D. Newton and R. J. Silbey, J. Phys. Chem. B, 2007, 111, 6807–6814 CrossRef CAS PubMed.
- V. Tiwari, W. K. Peters and D. M. Jonas, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1203–1208 CrossRef CAS PubMed.
- L. Lüer, V. Moulisová, S. Henry, D. Polli, T. H. P. Brotosudarmo, S. Hoseinkhani, D. Brida, G. Lanzani, G. Cerullo and R. J. Cogdell, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1473–1478 CrossRef PubMed.
- S. Scheuring and J. N. Sturgis, Science, 2005, 309, 484–487 CrossRef CAS PubMed.
- V. Tiwari, W. K. Peters and D. M. Jonas, Nat. Chem., 2014, 6, 173–175 CrossRef CAS PubMed.
- M. Saggu, B. Carter, X. Zhou, K. Faries, L. Cegelski, D. Holten, S. G. Boxer and C. Kirmaier, J. Phys. Chem. B, 2014, 118, 6721–6732 CrossRef CAS PubMed.
- M. A. Steffen, K. Lao and S. G. Boxer, Science, 1994, 264, 810–816 CrossRef CAS.
- V. Novoderezhkin, M. Wendling and R. van Grondelle, J. Phys. Chem. B, 2003, 107, 11534–11548 CrossRef CAS.
- R. J. Cogdell, N. W. Isaacs, A. A. Freer, T. D. Howard, A. T. Gardiner, S. M. Prince and M. Z. Papiz, FEBS Letters, Elsevier, 2003, vol. 555, pp. 35–39 Search PubMed.
- S. Scheuring, J. N. Sturgis, V. Prima, A. Bernadac, D. Lévy and J.-L. Rigaud, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 11293–11297 CrossRef CAS PubMed.
- R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Blackwell Science Ltd, 2002 Search PubMed.
- G. D. Scholes, X. J. Jordanides and G. R. Fleming, J. Phys. Chem. B, 2001, 105, 1640–1651 CrossRef CAS.
- R. Monshouwer, M. Abrahamsson, F. Van Mourik and R. Van Grondelle, J. Phys. Chem. B, 1997, 101, 7241–7248 CrossRef CAS.
- A. Ishizaki and G. R. Fleming, Annu. Rev. Condens. Matter Phys., 2012, 3, 333–361 CrossRef CAS.
- A. Ishizaki and G. R. Fleming, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17255–17260 CrossRef.
- M. H. Vos, F. Rappaport, J.-C. Lambry, J. Breton and J.-L. Martin, Nature, 1993, 363, 320–325 CrossRef CAS.
- V. Tiwari, W. K. Peters and D. M. Jonas, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1203–1208 CrossRef CAS.
- W. D. Schubert, O. Klukas, W. Saenger, H. T. Witt, P. Fromme and N. Krauß, J. Mol. Biol., 1998, 280, 297–314 CrossRef CAS PubMed.
- A. Niedringhaus, V. R. Policht, R. Sechrist, A. Konar, P. D. Laible, D. F. Bocian, D. Holten, C. Kirmaier and J. P. Ogilvie, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 3563–3568 CrossRef CAS PubMed.
- E. Romero, R. Augulis, V. I. Novoderezhkin, M. Ferretti, J. Thieme, D. Zigmantas and R. Van Grondelle, Nat. Phys., 2014, 10, 676–682 Search PubMed.
- F. D. Fuller, J. Pan, A. Gelzinis, V. Butkus, S. S. Senlik, D. E. Wilcox, C. F. Yocum, L. Valkunas, D. Abramavicius and J. P. Ogilvie, Nat. Chem., 2014, 6, 706–711 CrossRef CAS PubMed.
- P. Peumans, A. Yakimov and S. R. Forrest, J. Appl. Phys., 2003, 93, 3693–3723 CrossRef CAS.
- S. M. Menke and R. J. Holmes, Energy Environ. Sci., 2014, 7, 499–512 RSC.
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791 CrossRef CAS.
- J. J. M. Halls, C. A. Walsh, N. C. Greenham, E. A. Marseglia, R. H. Friend, S. C. Moratti and A. B. Holmes, Nature, 1995, 376, 498–500 CrossRef CAS.
- J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H.-L. Yip, T.-K. Lau, X. Lu, C. Zhu, H. Peng, P. A. Johnson, M. Leclerc, Y. Cao, J. Ulanski, Y. Li and Y. Zou, Joule, 2019, 3, 1140–1151 CrossRef CAS.
- B. Fan, D. Zhang, M. Li, W. Zhong, Z. Zeng, L. Ying, F. Huang and Y. Cao, Sci. China: Chem., 2019, 62, 746–752 CrossRef CAS.
- Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, Sci. Bull., 2020, 65, 272–275 CrossRef CAS.
- N. Gasparini, A. Salleo, I. McCulloch and D. Baran, Nat. Rev. Mater., 2019, 4, 229–242 CrossRef.
- T. Ameri, P. Khoram, J. Min and C. J. Brabec, Adv. Mater., 2013, 25, 4245–4266 CrossRef CAS PubMed.
- M. Koppe, H.-J. Egelhaaf, G. Dennler, M. C. Scharber, C. J. Brabec, P. Schilinsky and C. N. Hoth, Adv. Funct. Mater., 2010, 20, 338–346 CrossRef CAS.
- K. Feron, W. J. Belcher, C. J. Fell and P. C. Dastoor, Int. J. Mol. Sci., 2012, 13, 17019–17047 CrossRef CAS PubMed.
- J.-S. Huang, T. Goh, X. Li, M. Y. Sfeir, E. A. Bielinski, S. Tomasulo, M. L. Lee, N. Hazari and A. D. Taylor, Nat. Photonics, 2013, 7, 479–485 CrossRef CAS.
- B. R. Gautam, R. Younts, J. Carpenter, H. Ade and K. Gundogdu, J. Phys. Chem. A, 2018, 122, 3764–3771 CrossRef CAS PubMed.
- Y. W. Soon, T. M. Clarke, W. Zhang, T. Agostinelli, J. Kirkpatrick, C. Dyer-Smith, I. Mcculloch, J. Nelson and J. R. Durrant, Chem. Sci., 2011, 2, 1111–1120 RSC.
- W. Li, Y. Yan, Y. Gong, J. Cai, F. Cai, R. S. Gurney, D. Liu, A. J. Pearson, D. G. Lidzey and T. Wang, Adv. Funct. Mater., 2018, 28, 1704212 CrossRef.
- L. Perdigón-Toro, H. Zhang, A. Markina, J. Yuan, S. M. Hosseini, C. M. Wolff, G. Zuo, M. Stolterfoht, Y. Zou, F. Gao, D. Andrienko, S. Shoaee and D. Neher, Adv. Mater., 2020, 32, 1906763 CrossRef PubMed.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. Van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 335, 1340–1344 CrossRef CAS PubMed.
- L. E. Sousa, V. Coropceanu, D. A. da Silva Filho and G. Sini, Adv. Theory Simul., 2020, 1900230 CrossRef.
- Y. Zhong, M. Causa, G. J. Moore, P. Krauspe, B. Xiao, F. Günther, J. Kublitski, R. Shivhare, J. Benduhn, E. BarOr, S. Mukherjee, K. M. Yallum, J. Réhault, S. C. B. Mannsfeld, D. Neher, L. J. Richter, D. M. DeLongchamp, F. Ortmann, K. Vandewal, E. Zhou and N. Banerji, Nat. Commun., 2020, 11, 1–10 Search PubMed.
- Q. Bian, F. Ma, S. Chen, Q. Wei, X. Su, I. A. Buyanova, W. M. Chen, C. S. Ponseca, M. Linares, K. J. Karki, A. Yartsev and O. Inganäs, Nat. Commun., 2020, 11, 1–9 Search PubMed.
- Y. Song, S. N. Clafton, R. D. Pensack, T. W. Kee and G. D. Scholes, Nat. Commun., 2014, 5, 4933 CrossRef PubMed.
- T. R. Nelson, D. Ondarse-Alvarez, N. Oldani, B. Rodriguez-Hernandez, L. Alfonso-Hernandez, J. F. Galindo, V. D. Kleiman, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X. K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J. L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed.
- F. D. Eisner, M. Azzouzi, Z. Fei, X. Hou, T. D. Anthopoulos, T. J. S. Dennis, M. Heeney and J. Nelson, J. Am. Chem. Soc., 2019, 141, 6362–6374 CrossRef CAS PubMed.
- J. Liu, S. Chen, D. Qian, B. Gautam, G. Yang, J. Zhao, J. Bergqvist, F. Zhang, W. Ma, H. Ade, O. Inganäs, K. Gundogdu, F. Gao and H. Yan, Nat. Energy, 2016, 1, 1–7 Search PubMed.
- R. M. Clegg, Fluorescence resonance energy transfer, 1995, vol. 6 Search PubMed.
- Y. Cui, H. Yao, J. Zhang, T. Zhang, Y. Wang, L. Hong, K. Xian, B. Xu, S. Zhang, J. Peng, Z. Wei, F. Gao and J. Hou, Nat. Commun., 2019, 10, 2515 CrossRef PubMed.
- J. Song, C. Li, L. Zhu, J. Guo, J. Xu, X. Zhang, K. Weng, K. Zhang, J. Min, X. Hao, Y. Zhang, F. Liu and Y. Sun, Adv. Mater., 2019, 1905645 CrossRef CAS PubMed.
- Q. An, F. Zhang, J. Zhang, W. Tang, Z. Deng and B. Hu, Energy Environ. Sci., 2016, 9, 281–322 RSC.
- N. Gasparini, A. Salleo, I. McCulloch and D. Baran, Nat. Rev. Mater., 2019, 4, 229 CrossRef.
- K. Zhou, J. Xin and W. Ma, ACS Energy Lett., 2019, 4, 447–455 CrossRef CAS.
- H. Lee, C. Park, D. H. Sin, J. H. Park and K. Cho, Adv. Mater., 2018, 30, 1800453 CrossRef.
- C. McDowell, M. Abdelsamie, M. F. Toney and G. C. Bazan, Adv. Mater., 2018, 30, 1707114 CrossRef PubMed.
- W. Ma, C. Yang, X. Gong, K. Lee and A. J. Heeger, Adv. Funct. Mater., 2005, 15, 1617–1622 CrossRef CAS.
- K. Jiang, G. Zhang, G. Yang, J. Zhang, Z. Li, T. Ma, H. Hu, W. Ma, H. Ade and H. Yan, Adv. Energy Mater., 2018, 8, 1701370 CrossRef.
- M. Ghasemi, L. Ye, Q. Zhang, L. Yan, J.-H. Kim, O. Awartani, W. You, A. Gadisa and H. Ade, Adv. Mater., 2017, 29, 1604603 CrossRef PubMed.
- Y. Ma, X. Zhou, D. Cai, Q. Tu, W. Ma and Q. Zheng, Mater. Horiz., 2020, 7, 117–124 RSC.
- Q. An, X. Ma, J. Gao and F. Zhang, Sci. Bull., 2019, 64, 504–506 CrossRef CAS.
- R. Yu, H. Yao, Y. Cui, L. Hong, C. He and J. Hou, Adv. Mater., 2019, 31, 1902302 CrossRef PubMed.
- L. Xiao, B. He, Q. Hu, L. Maserati, Y. Zhao, B. Yang, M. A. Kolaczkowski, C. L. Anderson, N. J. Borys, L. M. Klivansky, T. L. Chen, A. M. Schwartzberg, T. P. Russell, Y. Cao, X. Peng and Y. Liu, Joule, 2018, 2, 2154–2166 CrossRef CAS.
- L. Duan, Y. Zhang, R. Deng, H. Yi and A. Uddin, ACS Appl. Energy Mater., 2020, 3, 5792–5803 CrossRef CAS.
- K. Li, Y. Wu, Y. Tang, M. A. Pan, W. Ma, H. Fu, C. Zhan and J. Yao, Adv. Energy Mater., 2019, 9, 1901728 CrossRef.
- D. Baran, R. S. Ashraf, D. A. Hanifi, M. Abdelsamie, N. Gasparini, J. A. Röhr, S. Holliday, A. Wadsworth, S. Lockett, M. Neophytou, C. J. M. Emmott, J. Nelson, C. J. Brabec, A. Amassian, A. Salleo, T. Kirchartz, J. R. Durrant and I. McCulloch, Nat. Mater., 2017, 16, 363–369 CrossRef CAS PubMed.
- X. Chen, B. Kan, Y. Kan, M. Zhang, S. B. Jo, K. Gao, F. Lin, F. Liu, X. Peng, Y. Cao and A. K.-Y. Jen, Adv. Funct. Mater., 2020, 30, 1909535 CrossRef CAS.
- X. Yang, F. Zheng, W. Xu, P. Bi, L. Feng, J. Liu and X. Hao, ACS Appl. Mater. Interfaces, 2017, 9, 618–627 CrossRef CAS PubMed.
- G. M. Paternò, L. Moretti, A. J. Barker, C. D’Andrea, A. Luzio, N. Barbero, S. Galliano, C. Barolo, G. Lanzani and F. Scotognella, J. Mater. Chem. C, 2017, 5, 7732–7738 RSC.
- T. Kumari, S. M. Lee, S. H. Kang, S. Chen and C. Yang, Energy Environ. Sci., 2017, 10, 258–265 RSC.
- W. Zhao, S. Li, S. Zhang, X. Liu and J. Hou, Adv. Mater., 2017, 29, 1604059 CrossRef PubMed.
- V. Gupta, V. Bharti, M. Kumar, S. Chand and A. J. Heeger, Adv. Mater., 2015, 27, 4398–4404 CrossRef CAS PubMed.
- T. Goh, J.-S. Huang, B. Bartolome, M. Y. Sfeir, M. Vaisman, M. L. Lee and A. D. Taylor, J. Mater. Chem. A, 2015, 3, 18611–18621 RSC.
- H. Benten, T. Nishida, D. Mori, H. Xu, H. Ohkita and S. Ito, Energy Environ. Sci., 2016, 9, 135–140 RSC.
- J. Kong, M. Mohadjer Beromi, M. Mariano, T. Goh, F. Antonio, N. Hazari and A. D. Taylor, Nano Energy, 2017, 38, 36–42 CrossRef CAS.
- S. Xing, H. Wang, Y. Zheng and J. Yu, Sol. Energy, 2016, 139, 221–227 CrossRef CAS.
- P. Q. Bi, B. Wu, F. Zheng, W. L. Xu, X. Y. Yang, L. Feng, F. Zhu and X. T. Hao, ACS Appl. Mater. Interfaces, 2016, 8, 23212–23221 CrossRef CAS PubMed.
- N. Banerji, J. Mater. Chem. C, 2013, 1, 3052–3066 RSC.
- A. A. Mohapatra, V. Kim, B. Puttaraju, A. Sadhanala, X. Jiao, C. R. McNeill, R. H. Friend and S. Patil, ACS Appl. Energy Mater., 2018, 1, 4874–4882 CrossRef CAS.
- H. Jiang, X. Li, J. Wang, S. Qiao, Y. Zhang, N. Zheng, W. Chen, Y. Li and R. Yang, Adv. Funct. Mater., 2019, 29, 1903596 CrossRef.
- X. Xu, K. Feng, Z. Bi, W. Ma, G. Zhang and Q. Peng, Adv. Mater., 2019, 1901872 CrossRef PubMed.
- T. Liu, Z. Luo, Y. Chen, T. Yang, Y. Xiao, G. Zhang, R. Ma, X. Lu, C. Zhan, M. Zhang, C. Yang, Y. Li, J. Yao and H. Yan, Energy Environ. Sci., 2019, 12, 2529–2536 RSC.
- R. Wang, J. Yuan, R. Wang, G. Han, T. Huang, W. Huang, J. Xue, H. Wang, C. Zhang, C. Zhu, P. Cheng, D. Meng, Y. Yi, K. Wei, Y. Zou and Y. Yang, Adv. Mater., 2019, 1904215 CrossRef CAS PubMed.
- C. Lee, S. Lee, G. U. Kim, W. Lee and B. J. Kim, Chem. Rev., 2019, 119, 8028–8086 CrossRef CAS PubMed.
- C. Groves, O. G. Reid and D. S. Ginger, Acc. Chem. Res., 2010, 43, 612–620 CrossRef CAS PubMed.
- Y. Huang, E. J. Kramer, A. J. Heeger and G. C. Bazan, Chem. Rev., 2014, 114, 7006–7043 CrossRef CAS PubMed.
- G. Piland and E. M. Grumstrup, J. Phys. Chem. A, 2019, 123, 8709–8716 CrossRef CAS PubMed.
- A. C. Jones, N. M. Kearns, M. Bohlmann Kunz, J. T. Flach and M. T. Zanni, J. Phys. Chem. A, 2019, 123, 10824–10836 CrossRef CAS PubMed.
- C. Schnedermann, J. Sung, R. Pandya, S. D. Verma, R. Y. S. Chen, N. Gauriot, H. M. Bretscher, P. Kukura and A. Rao, J. Phys. Chem. Lett., 2019, 10, 6727–6733 CrossRef CAS PubMed.
- V. Tiwari, Y. A. Matutes, A. T. Gardiner, T. L. C. Jansen, R. J. Cogdell and J. P. Ogilvie, Nat. Commun., 2018, 9, 1–10 CrossRef CAS.
- K. J. Karki, J. R. Widom, J. Seibt, I. Moody, M. C. Lonergan, T. Pullerits and A. H. Marcus, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- J. Chen, K. Žídek, P. Chábera, D. Liu, P. Cheng, L. Nuuttila, M. J. Al-Marri, H. Lehtivuori, M. E. Messing, K. Han, K. Zheng and T. Pullerits, J. Phys. Chem. Lett., 2017, 8, 2316–2321 CrossRef CAS PubMed.
- Y. Dong, V. C. Nikolis, F. Talnack, Y.-C. Chin, J. Benduhn, G. Londi, J. Kublitski, X. Zheng, S. C. B. Mannsfeld, D. Spoltore, L. Muccioli, J. Li, X. Blase, D. Beljonne, J.-S. Kim, A. A. Bakulin, G. D’Avino, J. R. Durrant and K. Vandewal, Nat. Commun., 2020, 11, 4617 CrossRef.
- A. Classen, C. L. Chochos, L. Lüer, V. G. Gregoriou, J. Wortmann, A. Osvet, K. Forberich, I. McCulloch, T. Heumüller and C. J. Brabec, Nat. Energy, 2020, 5, 711–719 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |



