Sequential and alternating RAFT single unit monomer insertion: model trimers as the guide for discrete oligomer synthesis†
Ruizhe
Liu
,
Lei
Zhang
,
Zixuan
Huang
and
Jiangtao
Xu
 *
*
Centre for Advanced Macromolecular Design, School of Chemical Engineering, UNSW Sydney, NSW 2052, Australia. E-mail: j.xu@unsw.edu.au
First published on 22nd April 2020
Abstract
Sequence-defined polymers have garnered increasing attention in a broad range of applications from materials engineering to medical science. Reversible addition–fragmentation chain transfer single unit monomer insertion (RAFT SUMI) technology has recently emerged as a powerful tool for sequence-defined polymer synthesis, which utilizes sequential monomer radical additions occurring one unit at a time to assemble olefins into uniform polymers. The strategy of employing alternating additions of electron-donor and acceptor (D–A) monomers can be used to prepare long chain sequence-defined polymers by the RAFT SUMI technique. However, considering both terminal and penultimate unit effects, complex radical reaction kinetics can result from various monomer addition orders particularly if three or more different families of vinyl monomers are used to build diverse sequences. Simplifying reaction processes and establishing reaction kinetics will be critical for effective synthesis of sequence-defined polymers. Herein, a series of model trimers containing D–A–D and A–D–A triads was thus produced from four families of α,β-disubstituted vinyl monomers (N-phenylmaleimide, fumaronitrile and dimethyl fumarate and indene). Such trimers presented distinct synthesis kinetics (reaction rate and yield). These model trimers and their kinetics data are able to provide full guidance for the synthesis of long chain discrete polymers using sequential and alternating RAFT SUMI processes.
Introduction
Biomacromolecules and synthetic polymers are two diverse groups of materials assembled from natural and petrochemical monomers, respectively, which have changed and will keep changing our daily lives in their own ways. From the viewpoint of structural precision, synthetic polymers are far behind the natural ones in terms of their primary structures constituted by sequential repetition of monomer units.1,2 For instance, nucleic acids have precise monomer sequences along the polymer chains that enable the genetic information to be stored and used for the synthesis of various proteins. Such proteins therefore possess precisely defined chemical constitution and form the basic structural and functional components in life. In contrast, synthetic polymers made from petrochemical monomers are far away from such biological precision and lack specific functions. The monomer sequence control is still a “Holy Grail” in synthetic polymer chemistry.3 However, with the rapid development of modern synthetic chemistry, many innovative approaches have been constantly established for the synthesis of well-defined or precision polymers analogous to biomacromolecules,4,5 which is also fuelled by the potential to access new materials to facilitate our daily life.6–10Living polymerization techniques, notably reversible deactivation radical polymerization (RDRP) are powerful tools for synthesizing precisely controlled polymers, which has allowed the facile preparation of nearly infinite polymer topological architectures.11 However, sequence control by chain growth processes through a radical mechanism in RDRP is very challenging due to the “too active” radical species tending to form dispersed molecular weights and randomly distributed monomer sequences.12 Originating from RDRP (dominantly nitroxide-mediated polymerization (NMP),13 atom-transfer radical polymerization (ATRP),14 and reversible addition–fragmentation chain transfer (RAFT) polymerization),15 single unit monomer insertion (SUMI) technology allows vinyl monomers to be added into the initiator one unit at a time, instead of continuous growth of polymer chains with a large number of monomer units.16–21 Although RDRP enables access to sequenced block and multiblock copolymers, they are still significantly dispersed in molecular weights for each block.12,22 In comparison, SUMI is able to create monodispersed and sequence-defined polymers (also called “uniform or discrete polymers”) with specific monomer sequences. SUMI has been recognized as a powerful tool in engineering radical addition reactions and polymerization, not only in sequence-defined polymer synthesis, but also for organic transformations, stereochemistry regulation and the kinetic investigation of free radical polymerization.16,23
The history of SUMI can be dated back to the 1980s to the discovery of unimer formation from reactions between alkoxyamine and vinyl monomers,24,25 and facile radical generation from xanthates and subsequent radical addition to various alkenes,26 although it was initially not termed “SUMI”. With the advances of RDRP, RDRP SUMI approaches have attracted increasing attentions to prepare functional RDRP initiators,17,27–29 polymer end-group or mid-chain functionalization30–34 as well as sequenced-defined polymers.16,35,36 RAFT SUMI has been demonstrated to be versatile and robust due to its unique degenerative radical transfer mechanism. Moad, Junkers and their co-workers has made significant contributions to this area in the past two decades.37–39,40–42
Our group has been focussing on photochemical approaches to activate and mediate RAFT SUMI (photo-RAFT SUMI) including photoiniferter and photoinduced electron/energy transfer (PET)-RAFT processes by visible light.16,18,19,23,43–45 The photo-activation of RAFT agents to generate initiating radicals is able to effectively suppress exogenous initiator-derived by-products in comparison to conventional RAFT polymerization. Meanwhile, the use of visible light allows the minimization of RAFT decomposition commonly observed under UV light irradiation in photoiniferter polymerization involving xanthates and dithioesters.46 By employing the strategy of selective photo-activation of RAFT agents and sequential monomer additions, discrete oligomers containing up to three units of different monomers (styrene, maleimide, and vinyl acetate or limonene) have been synthesized in high isolated yields (up to 95%).44 An improved approach was developed to prepare longer oligomer chain by sequential and alternating insertion of two families of α,β-disubstituted vinyl monomers, one electron-donor monomer (e.g. indene (Ind)) and the other electron-acceptor monomer (e.g. maleimide (MI)).18 Such monomers have been reported to be non-homopolymerizable or low propagation rate constants (kp) through radical processes, which can effectively restrict multiple monomer insertions (i.e. homopolymer formation). Additionally, this approach allows oligomer production on a gram scale through continuous flow process without pre-deoxygenation steps.19
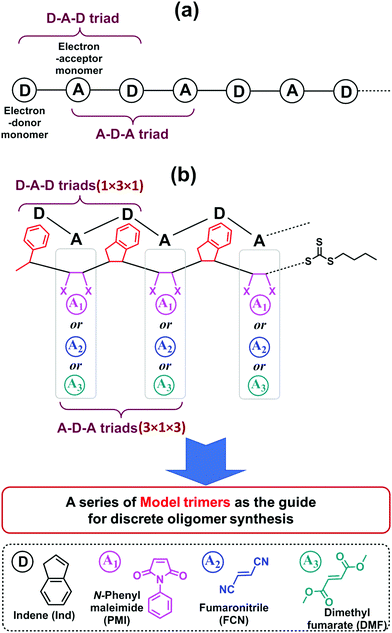
One significant advantage of this sequential and alternating approach is that it is not necessary to explore the reaction conditions and kinetics for all monomer addition steps during the synthesis of the full length of targeted oligomer, as the oligomer is composed of repeating alternative monomer units of MI and Ind.18,19 Taking into account both the terminal and penultimate (the next-to-last) unit effects on the kinetics of radical additions,47,48 only two key SUMI radical reactions are essential for evaluating reaction conditions and kinetic efficiency: (1) the D (electron-donor monomer, e.g. Ind) addition into D–A macroradical to generate a D–A–D triad and (2) the A (electron-accepting monomer, e.g. MI) addition into A–D macroradical to generate an A–D–A triad (Fig. 1a). Therefore, the synthesis of a model oligomer (D–A–D–A) containing these two triads (D–A–D and A–D–A) is able to represent the preparation of whole chain of polymers. The reaction conditions and kinetics of this model oligomer synthesis can be applied into the subsequent SUMI processes. In this study, this methodology is applied to different families of monomers to build more complex oligomers with diverse monomer sequences. A complete set of model trimers containing D–A–D and A–D–A triads and their SUMI kinetics data are established based on four different families of vinyl monomers and a trithiocarbonate RAFT agent (Fig. 1b) using a combinatorial approach,49–51 which provides guidance for the synthesis of long chain discrete oligomers via sequential and alternating RAFT SUMI processes.
Four α,β-disubstituted vinyl monomers (Fig. 1b), including three electron-acceptor monomers (N-phenylmaleimide (PMI), fumaronitrile (FCN) and dimethyl fumarate (DMF)) and one electron-donor monomer (indene (Ind)), are employed as examples for sequence-defined polymer synthesis. The FCN and DMF monomers meet the basic requirements of the SUMI process; the propagation rate constants (kp) are relatively low but they can copolymerize with many other monomers.52–56 Furthermore, these monomers have been used to prepare special polymer materials which exhibit unique mechanical or thermal properties such as high glass transition temperature when copolymerized with divinylbenzene.57–60 The other electron-accepting monomer, PMI, has been demonstrated to be a good monomer for discrete oligomer synthesis through sequential and alternating SUMI, which is used for comparison with FCN and DMF. Ind is employed as the only electron-donating monomer to simplify the kinetic discussion.
As shown in Fig. 1b, nine model trimers (1 × 3 × 1 × 3) containing three D–A–D triads (1 × 3 × 1) and nine A–D–A triads (3 × 1 × 3) are required to fully cover the SUMI reactions for long chain oligomer synthesis. The reaction conditions (monomer and RAFT agent concentration) and kinetics data (reaction time, reaction yield and reaction rate) can determine the best monomer sequences with highest atom efficiency. Further chain growth (tetramer, pentamer and longer oligomer) using the same monomers can be guided by the kinetic data due to the repetitiveness of alternating monomer insertions. In this approach, high throughput online NMR spectroscopy is used to collect kinetic data. Rapid and efficient automated flash chromatography is employed for isolation and purification of SUMI products and measuring isolated yields. NMR and ESI-MS techniques are used for the structural confirmation of synthetic oligomers.
Results and discussion
Synthesis and SUMI kinetics of nine model trimers
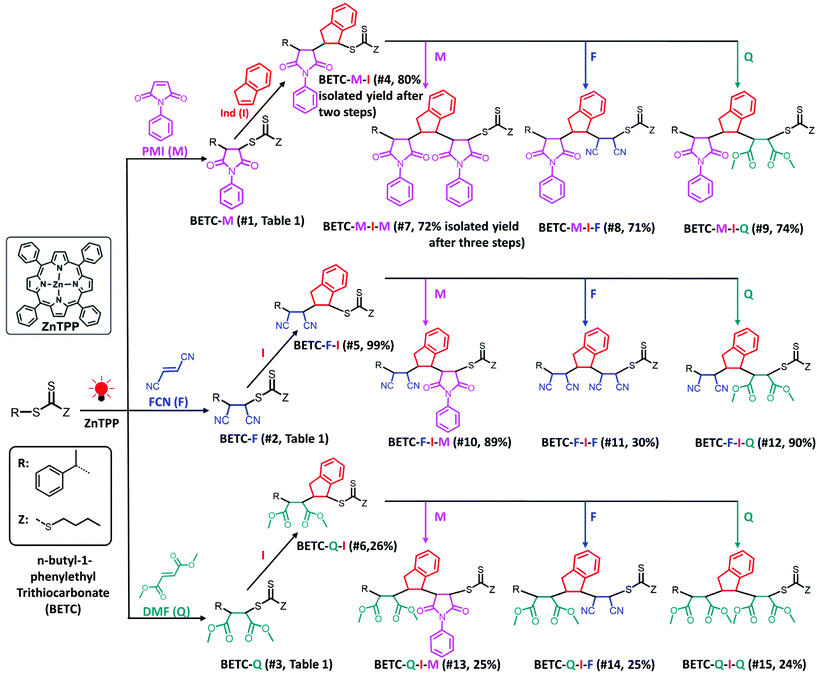 | ||
| Scheme 1 Synthetic chemistry for the complete set of model trimers. Total isolated yields of three dimer and nine trimers after two or three steps of PET-RAFT SUMI are shown in parentheses, which are calculated by multiplying the respective values of two or three steps isolated yields in Table 1. The solvent (DMSO), light source (red LED, λmax = 635 nm, 0.46 mW cm−2) and photocatalyst (ZnTPP) were employed for all investigated SUMI reactions. | ||
| # | [Monomer]/[RAFT] | RAFT | Monomer | SUMI Product | Time (h) | RAFT Conv.b (%) | Isolated yieldc (%) | k appRAFT (h−1) |
|---|---|---|---|---|---|---|---|---|
| a Reaction conditions: DMSO as solvent, ZnTPP as photocatalyst, red LED light (λmax = 635 nm, 0.46 mW cm−2), [monomer]/[RAFT]/[ZnTPP] = x/1/0.005. The kinetic experiments were conducted in NMR tubes which showed higher reaction rates than those in glass vials due to lower reagent concentrations and higher light penetration (see more details in the ESI †). b RAFT conversions were measured by 1H NMR spectroscopy. c Isolated yields were measured by weighing the purified products and comparing the theoretical masses. d BETC-M-I (#4) SUMI products include 7.0 mol% of unreacted BETC-M determined by 1H NMR, which has been excluded for calculation of the isolated yields. BETC-F-I-M-I (#16) SUMI product contains small amount of unreacted BETC-F-I-M verified by 1H NMR (ESI, Fig. S35†) and ESI-MS spectrum (Fig. 6A). However, the exact amount is difficult to calculate due to overlap of the proton signals. It was thus assumed that BETC-F-I-M-I is of 100% purity for calculation of yields and for uses in the further steps of SUMI reaction. e The values were not calculated due to substantial overlap of the proton signals from the initial RAFT agents and respective SUMI products with multiple diastereoisomers. f Apparent reaction rate coefficients were calculated on RAFT conversion versus reaction time using pseudo-first order reaction kinetics (Fig. 3B and 4B). | ||||||||
| 1 | 1/1 | BETC | PMI (M) | BETC-M | 24 | 99 | 95 | 1.84 |
| 2 | 5/1 | BETC | FCN (F) | BETC-F | 24 | 93 | 92 | 0.18 |
| 3 | 5/1 | BETC | DMF (Q) | BETC-Q | 24 | 98 | 97 | 0.41 |
| 4d | 5/1 | BETC-M | Ind (I) | BETC-M-I | 18 | 83 | 80 | 0.55 |
| 5 | 1/1 | BETC-F | Ind (I) | BETC-F-I | 24 | 99 | 99 | 0.17 |
| 6 | 5/1 | BETC-Q | Ind (I) | BETC-Q-I | 48 | 54 | 26 | 0.04 |
| 7 | 1/1 | BETC-M-I | PMI (M) | BETC-M-I-M | 24 | 99 | 95 | — |
| 8 | 5/1 | BETC-M-I | FCN (F) | BETC-M-I-F | 24 | —e | 93 | — |
| 9 | 5/1 | BETC-M-I | DMF (Q) | BETC-M-I-Q | 24 | — | 98 | — |
| 10 | 1/1 | BETC-F-I | PMI (M) | BETC-F-I-M | 24 | — | 98 | — |
| 11 | 10/1 | BETC-F-I | FCN (F) | BETC-F-I-F | 48 | — | 33 | — |
| 12 | 5/1 | BETC-F-I | DMF (Q) | BETC-F-I-Q | 24 | — | 99 | — |
| 13 | 1/1 | BETC-Q-I | PMI (M) | BETC-Q-I-M | 24 | — | 98 | — |
| 14 | 5/1 | BETC-Q-I | FCN (F) | BETC-Q-I-F | 24 | — | 98 | — |
| 15 | 5/1 | BETC-Q-I | DMF (Q) | BETC-Q-I-Q | 24 | — | 97 | — |
| 16d | 5/1 | BETC-F-I-M | Ind(I) | BETC-F-I-M-I | 18 | — | 80 | — |
| 17 | 5/1 | BETC-F-I-M-I | FCN (F) | BETC-F-I-M-I-F | 24 | — | 94 | — |
| 18 | 5/1 | BETC-F-I-M-I | DMF (Q) | BETC-F-I-M-I-Q | 24 | — | 96 | — |
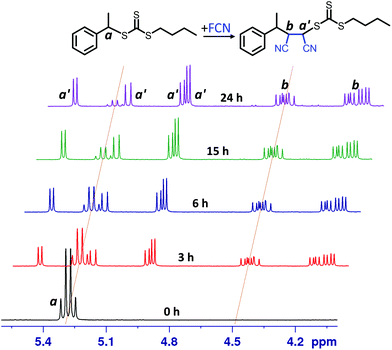
The kinetic experiments were performed using online 1H NMR spectroscopy as reported in previous studies.18,191H NMR spectra for FCN SUMI (Fig. 2) collected at different light irradiation duration clearly showed the gradual consumption of BETC (decrease of the quartet signal centered at δ 5.28 ppm assigned to proton a from BETC) and the ready formation of the monoadduct BETC-F (increase of the four doublet signals centred at δ 4.93, 4.97, 5.22 and 5.47 ppm assigned to proton a′ from the monoadduct). Meanwhile, the signals for proton b from BETC-F (four quartets at δ 4.10, 4.20, 4.46 and 4.50 ppm) also presented a simultaneous increase to that for proton a′ during the reaction period, which confirmed the generation of the SUMI product of BETC-F. It is worth noting that there were no observable unassigned peaks in the spectra which indicates negligible by-products generated during the reaction. The four groups of signals for both protons a′ (four doublets) and b (four quartets) are attributed to four different diastereoisomers of the BETC-F monoadduct, which is confirmed by the 1H & 13C, HMBC and HSQC NMR spectra (ESI, Fig. S3–S6†) of the purified monoadduct. The DMF SUMI presented similar reaction behaviour with clear 1H NMR spectra at different reaction time points (ESI, Fig. S7†). The BETC-Q monoadduct is confirmed by 1H & 13C NMR, HMBC and HSQC analysis (ESI, Fig. S8–S11†).
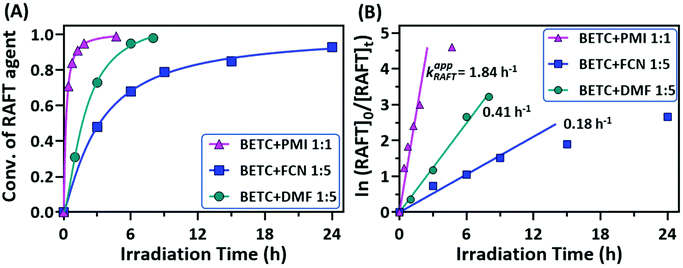
The conversions of RAFT agent (BETC) for the three monomers measured at different irradiation time points were plotted in Fig. 3A. The BETC conversions for FCN SUMI were estimated to be 51% after 3 h of light irradiation and reached 93% after 24 h. In contrast, the BETC conversions for DMF SUMI were faster with 74% after 3 h of light irradiation and 98% after 8 h under identical reaction conditions. In the case of PMI SUMI into BETC with [PMI]/[BETC] = 1/1, 99% of BETC was consumed after 5 h (the data see ref. 19). Although BETC in FCN SUMI could not completely be consumed within 24 h, increasing the molar ratio of [FCN]/[BETC] to 10/1 could push BETC conversion to 99% within 24 h (ESI, Fig. S12†). The quartet proton signal at δ 5.28 ppm assigned to BETC completely disappeared. These results clearly indicated the order of reaction rates: PMI > DMF > FCN. To quantify the reaction rates for each SUMI, the reaction rate coefficients were calculated based on pseudo-first order kinetics. For a SUMI reaction, RAFT agent + monomer → RAFT-monomer, it is supposed to be a second order reaction. The reaction rate is proportional to both [RAFT] and [monomer] (eqn (1)):
| R = k[RAFT][monomer] | (1) |
There are two plausible explanations for the different rates of the three monomer insertions. The first is that the addition rate constants (kadd, see ESI, Scheme S1† for the detailed mechanism of RAFT SUMI process) of 1-phenylethyl to these three monomers are different, with PMI being the highest (strong electron donor–acceptor complexation) and FCN the lowest. The second reason is the reaction equilibrium in the RAFT process which has been discussed in our previous publication.18,19 This can explain why FCN SUMI gave the lowest reaction rate. The dissociation rate constant (k′d) of BETC-F is the highest among the three SUMI monoadducts (BETC-M, BETC-F and BETC-Q) and even higher than that of BETC (kd,BETC) due to the lower C–S bond dissociation energy of BETC-F when compared to BETC, leading to a better leaving group (R group) in BETC-F than that in BETC. Therefore, with the consumption of BETC, the concentration of BETC-F increased and reached an equilibrium stage. The conversion of BETC cannot reach to 100% unless a high monomer concentration is employed. Specifically, the detailed reaction mechanism (ESI, Scheme S1†) suggests that the light activation and addition/fragmentation process of BETC-F competes with that of BETC, i.e., kd,BETC[BETC] competes with k′d[BETC-F], while ktr[BETC] competes with k−tr[BETC-F]. As we discussed above, the dissociation rate constant of BETC-F is higher than that of BETC (k′d > kd,BETC). The chain transfer rate k−tr is higher than ktr in this SUMI, which suggests that the fragmentation to produce SUMI product of BETC-F is unfavorable. If higher FCN concentration is used ([FCN]/[BETC] = 10/1), the equilibrium can be shifted to the full consumption of BETC as shown in ESI, Fig. S12.† For PMI and DMF SUMI, their dissociation rate constants are lower than that of BETC-F, maintaining the reaction equilibrium in the stage of full consumption of BETC.
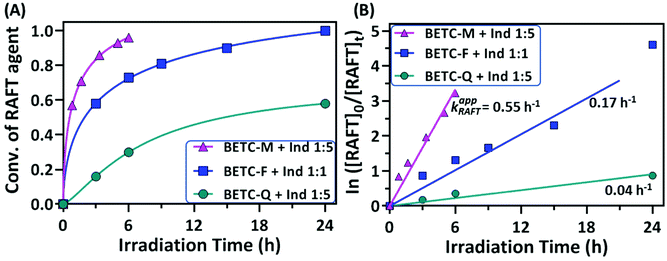
It is interesting to observe that the Ind insertion into the other two macro-RAFT agents, BETC-F and BETC-Q, displayed quite different reaction results (#5 and #6, Table 1) and SUMI kinetics (Fig. 4). The reaction between BETC-F and Ind presented high efficiency with 99% BETC-F conversion after 24 h light irradiation and an apparent rate coefficient of 0.17 h−1 in a stoichiometric ratio (#5, Table 1 and Fig. 4). The 1H NMR spectra at different irradiation time points (ESI, Fig. S13†) revealed that the four doublet peaks at δ 4.93, 4.97, 5.22 and 5.47 ppm rapidly disappeared within 6 h and a number of doublet peaks from δ 5.47 to 6.20 ppm increased in signals with reaction time. The kinetic plot of BETC-F conversion versus irradiation time showed a very quick SUMI reaction (blue line, Fig. 4A). The Ind monomer was also observed to be completely consumed along with the BETC-F. Such results demonstrated a quantitative reaction between BETC-F and Ind. No purification step was required for the crude product, BETC-F-I, after removal of the solvent (DMSO). The final SUMI product was analysed by 1H & 13C, HMBC NMR (ESI, Fig. S14–S16†) and ESI-MS (ESI, Fig. S17†), respectively. The 1H NMR spectrum shows that eight doublet peaks located at δ 5.46–5.90 ppm (ESI, Fig. S14†), which are assigned to the terminal –CH– proton (proton 5) of eight diastereoisomers with trans-Ind unit in BETC-F-I confirmed by HMBC (ESI, Fig. S16†). The other group of peaks located at δ 6.0–6.2 ppm are assigned to the terminal –CH– proton (proton 5) of specific diastereoisomers with cis-Ind unit in BETC-F-I. The ESI-MS spectrum shows that the molar mass of purified SUMI product ionized with Na+ to be 487.13 g mol−1, which corresponds to the SUMI product, BETC-F-I (Fig. S17†).
The SUMI of Ind into the other macro-RAFT agent, BETC-Q, with the molar ratio [Ind]/[BETC-Q]/[ZnTPP] = 5/1/0.005 revealed slow consumption of BETC-Q and reached 54% after 48 h light irradiation (#6, Table 1). The kinetics results showed an apparent rate coefficient of 0.04 h−1 (Fig. 4B). 1H NMR spectra at different time points (0, 3 and 48 h) presented the decrease of four doublet peak signals at δ 4.58, 5.0, 5.18 and 5.46 ppm assigned to the terminal –CH– proton (proton a) of four diastereoisomers in BETC-Q, along with the increase of several doublet peaks ranging from δ 5.44 to δ 6.0 ppm assigned to the terminal –CH– proton (proton a′) of different diastereoisomers in BETC-Q-I (ESI, Fig. S18†). A large number of the signals for proton a in BETC-Q were retained even after extended reaction time (48 h) indicating relatively low BETC-Q conversion, which was hypothesized to the low addition rate of Ind to the radical generated from BETC-Q. Alternatively, the dissociation rate of BETC-Q is much lower than that of BETC-Q-I and thus the reaction reaches the equilibrium. Unfortunately, the SUMI products BETC-Q-I and the unreacted macro-RAFT agents BETC-Q were difficult to separate due to the similar molecular polarity causing substantial overlap (ESI, Fig. S19†). Only the collected fraction for the elution from 17–19 column volume (CV) was the pure product of BETC-Q-I which was verified by NMR analysis and ESI-MS (ESI, Fig. S20–S23†). Four doublet peak signals at δ 5.43, 5.52, 5.88 and 5.94 ppm in 1H NMR (ESI, Fig. S20†) were assigned to the terminal -CH- proton (proton 5) of the four diastereoisomers in BETC-Q-I. Theoretically, there are eight diastereoisomers in the product. Other diastereoisomeric product is most likely separated out during the column purification. Therefore, the isolated yield is only 26% (#6, Table 1). To improve reaction yield, the increased [Ind]/[BETC-Q] ratio of 20/1 was also carried out. Unfortunately, the 1H NMR spectra showed (ESI, Fig. S24†) that a lot of abnormal peaks were observed after 18 h when the initial RAFT agent BETC-Q was completely consumed, which can most likely be attributed to the degradation of SUMI product BETC-Q-I and radical combination/disproportionation. Therefore, increasing monomer concentration did not result in a corresponding increment of the reaction yield for the SUMI of Ind into BETC-Q. To conclude, although the SUMI of Ind into BETC-F presented a moderate reaction rate in comparison to the SUMI of Ind into BETC-M, it offered a maximum atom economy with full conversions of all reagents, significantly much better than BETC-Q.
One of the challenges is to quantitatively measure the conversions of macro-RAFT agents by 1H NMR except for the SUMI of PMI into BETC-M-I, ascribed to the substantial overlaps of the terminal proton signals for macro-RAFT agents and their respective SUMI products (see illustrative examples in ESI, Fig. S25 and S26†). Therefore, the kinetic data of RAFT conversion versus time for these SUMI reactions was not collected. However, the isolated yield of each reaction after the same reaction time could be obtained by weighing the purified product to compare with its theoretical masses (Table 1), which are able to provide rough information on reaction rates. Meanwhile, 1H NMR can also qualitatively show how the reaction proceeds with the consumption of starting materials and product generation.
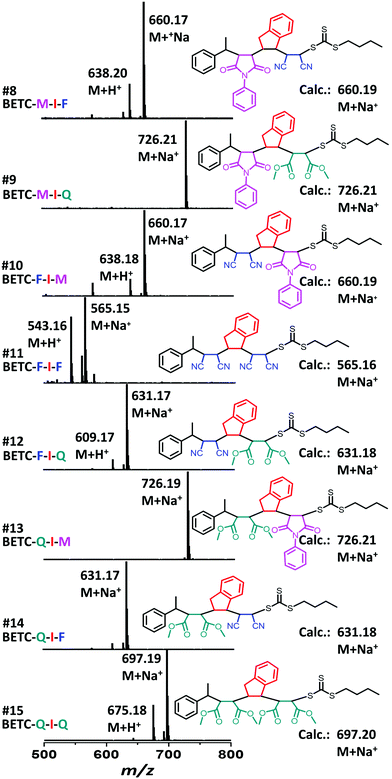
As shown in Table 1 (#7–#15), all nine combinatorial reactions presented high isolated yields (>90%) after 24 h light irradiation, except for the case of SUMI of FCN into BETC-F-I (#11, Table 1) which showed 33% after 48 h reaction attributed to strong steric hindrance or electrostatic repulsion between the penultimate FCN unit and approaching FCN monomer during the addition reaction. Such highly negative penultimate effect for FCN monomer has been reported by many groups while using FCN as a comonomer to copolymerize with other monomers such as divinylbenzene and styrene.66,67 In our study, the low reaction yield for FCN insertion into BETC-F-I most likely stemmed from steric hindrance or electrostatic repulsion between FCN penultimate unit and FCN monomer, since the effect was neither observed in the cases of FCN as penultimate unit and PMI or DMF as the monomer (#10 and #12 in Table 1) nor was effect observed in the systems of PMI or DMF as penultimate units and FCN as the monomer (#8 and #14 in Table 1). Two 1H NMR spectra for the SUMI reactions at different time points (DMF SUMI into BETC-M-I in ESI, Fig. S25† and PMI SUMI into BETC-F-I in ESI, Fig. S26†) clearly demonstrate the successful SUMI processes. The purified products for the eight trimers (BETC-M-I-M has been previously reported) were verified by ESI-MS (Fig. 5) and 1H NMR (ESI Fig. S27–S34† for the eight trimers).
Effective synthesis of long chain discrete oligomers
Based on the established nine model trimers and their SUMI kinetics data, the trimer sequences with the highest isolated yields are BETC-F-I-M (89%) and BETC-F-I-Q (90%) (Scheme 1). As demonstrated in the previous sections, FCN monomer is excellent to be the first unit, as it possesses a high reaction rate for insertion into BETC RAFT agent (#2, Table 1). Most importantly, it prepared a macro-RAFT agent (BETC-F) that was able to effectively react with electron-donating monomer (Ind) in a stoichiometric ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to generate BETC-F-I dimer in the subsequent SUMI step (#5, Table 1). This result makes FCN surpass the other two monomers, PMI and DMF. In the third step, FCN unfortunately failed to provide high reaction yield due to steric hindrance (#11, Table 1). DMF again faced the same issue of the subsequent Ind insertion which has been demonstrated in the second step. Therefore, PMI is the only choice for the third SUMI step to prepare the discrete oligomers. The insertion of PMI also presented highly efficient SUMI process in a stoichiometric ratio to generate BETC-F-I-M trimer, although the subsequent Ind insertion is still flawed with the cap of macro-RAFT conversion (∼80%, #16, Table 1) to supress double Ind insertion. Overall, in all three steps the trimer product, BETC-F-I-M, was obtained in high isolated yields (89%) with an effortless purification process.
1) to generate BETC-F-I dimer in the subsequent SUMI step (#5, Table 1). This result makes FCN surpass the other two monomers, PMI and DMF. In the third step, FCN unfortunately failed to provide high reaction yield due to steric hindrance (#11, Table 1). DMF again faced the same issue of the subsequent Ind insertion which has been demonstrated in the second step. Therefore, PMI is the only choice for the third SUMI step to prepare the discrete oligomers. The insertion of PMI also presented highly efficient SUMI process in a stoichiometric ratio to generate BETC-F-I-M trimer, although the subsequent Ind insertion is still flawed with the cap of macro-RAFT conversion (∼80%, #16, Table 1) to supress double Ind insertion. Overall, in all three steps the trimer product, BETC-F-I-M, was obtained in high isolated yields (89%) with an effortless purification process.
Next, there was an encouragement to select the proper monomers to prepare longer oligomer chains, such as pentamers with specific five units monomer sequences (Scheme 2). Meanwhile, relatively high efficiency reaction yields were also targeted as well. The tetramer, BETC-F-I-M-I was prepared using identical reaction conditions as for the second step (#4, Table 1) due to having the same I-M-I triads. After 18 h light irradiation, 80% of isolated yield was obtained after purification (#16, Table 1). The purified product was subjected to 1H NMR (ESI, Fig. S35†) and ESI-MS (Fig. 6A) analysis for the structural and purity verification. The selection of the fifth monomers could refer to the data in #7–#9, Table 1, which presents the same triads. Therefore, the reaction conditions and kinetics are the same. High isolated yields were thus obtained with 94% for FCN insertion and 96% for DMF insertion (#17 and #18, Table 1). The resultant pentamers, BETC-F-I-M-I-F and BETC-F-I-M-I-Q were confirmed by ESI-MS (Fig. 6B and C) and 1H NMR (ESI, Fig. S36 and S37†), revealing the pure products were prepared with matched theoretical masses. It is evident that the last monomer unit being FCN starts to repeat the sequence from the beginning (BETC-F-I-M-I-F-I-M-I…), and high reaction yields for longer chain polymers are thus expected.
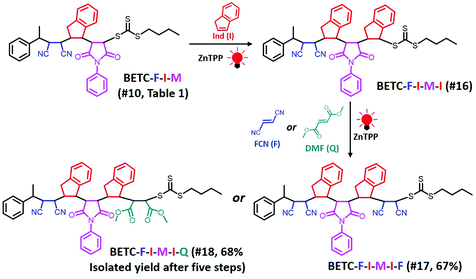 | ||
| Scheme 2 Synthetic chemistry of pentamers, BETC-F-I-M-I-F (#17, Table 1) and BETC-F-I-M-I-Q (#18, Table 1), using sequential SUMI processes. The total isolated yields of the pentamers after five iterations of SUMI are shown in parentheses. | ||
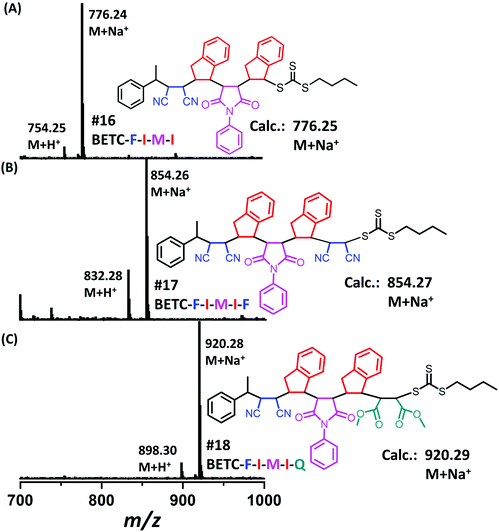 | ||
| Fig. 6 ESI-MS spectra for the tetramer BETC-F-I-M-I (A), the pentamers BETC-F-I-M-I-F (B) and BETC-F-I-M-I-Q (C). | ||
Conclusions
This article described a methodology using model trimers containing D–A–D and A–D–A triads as the guide for the synthesis of sequence-defined polymers through sequential and alternating PET-RAFT SUMI technology. The reaction conditions and kinetics data for the synthesis of these trimers were applied into subsequent chain growth due to repeated monomer triads. Four different families of α,β-disubstituted vinyl monomers (N-phenylmaleimide (PMI or M), fumaronitrile (FCN or F) and dimethyl fumarate (DMF or Q) and indene (Ind or I)) were employed to prepare nine model trimers. The monomer sequences in synthetic trimers have been demonstrated to have significant effects on SUMI reaction rate coefficients and reaction yields, and the best monomer sequence with a high yield (89%) was BETC-F-I-M. The kinetics data was successful to guide the synthesis of longer chain oligomers (tetramer and pentamers) in high isolated yields (>67%). The optimal monomer sequence from the investigated monomers for a pentamer could be BETC-F-I-M-I-Q or BETC-F-I-M-I-F, although the insertion of Ind into BETC-F-I-M is flawed with relatively low reaction yield (80–90%) and the potential of multiple Ind insertions. Therefore, longer chain polymers can be expected to be synthesized using the reaction conditions and kinetics data. It can be envisioned that the established model trimers and pentamers can be efficiently prepared in gram scale within several days by using a continuous flow process, as demonstrated in our previous reports on Ind and PMI monomers.19It is worth noting that this method can also be applied into any other vinyl monomers and different RAFT initiation in SUMI processes. The kinetics of more families of monomers including both electron-acceptor and electron-donor monomers are currently under investigation. Additionally, the established model trimers and kinetics data could provide the experimental and theoretical guidance for the synthesis of alternating polymers and investigation of mechanism and kinetics of radical copolymerization. It will also be very useful to select different monomers for synthesizing sequence-controlled macromolecules to build new functional materials with unique physical and chemical properties.
Conflicts of interest
The author declares no competing financial interest.Acknowledgements
J. X. acknowledges the Australian Research Council (ARC) and UNSW Sydney for the financial support under the schemes of Future Fellowship (FT160100095) and Startup Fund.Notes and references
- J.-F. Lutz, J.-M. Lehn, E. W. Meijer and K. Matyjaszewski, Nat. Rev. Mater., 2016, 1, 16024 CrossRef CAS.
- J.-F. Lutz, M. Ouchi, D. R. Liu and M. Sawamoto, Science, 2013, 341, 1238149 CrossRef PubMed.
- N. Badi and J.-F. Lutz, Chem. Soc. Rev., 2009, 38, 3383–3390 RSC.
- M. Ouchi and M. Sawamoto, Polym. J., 2018, 50, 83–94 CrossRef CAS.
- J. Lawrence, E. Goto, J. M. Ren, B. McDearmon, D. S. Kim, Y. Ochiai, P. G. Clark, D. Laitar, T. Higashihara and C. J. Hawker, J. Am. Chem. Soc., 2017, 139, 13735–13739 CrossRef CAS PubMed.
- R. K. Roy, A. Meszynska, C. Laure, L. Charles, C. Verchin and J. F. Lutz, Nat. Commun., 2015, 6, 7237 CrossRef CAS PubMed.
- M. Porel, D. N. Thornlow, N. N. Phan and C. A. Alabi, Nat. Chem., 2016, 8, 590–596 CrossRef CAS PubMed.
- M. Ouchi, N. Badi, J. F. Lutz and M. Sawamoto, Nat. Chem., 2011, 3, 917–924 CrossRef CAS PubMed.
- J.-F. Lutz, Macromolecules, 2015, 48, 4759–4767 CrossRef CAS.
- M. G. T. A. Rutten, F. W. Vaandrager, J. A. A. W. Elemans and R. J. M. Nolte, Nat. Rev. Chem., 2018, 2, 365–381 CrossRef.
- A. D. Jenkins, R. G. Jones and G. Moad, Pure Appl. Chem., 2009, 82, 483–491 Search PubMed.
- G. Gody, P. B. Zetterlund, S. Perrier and S. Harrisson, Nat. Commun., 2016, 7, 10514 CrossRef CAS PubMed.
- G. Moad and E. Rizzardo, in Nitroxide Mediated Polymerization: From Fundamentals to Applications in Materials Science, The Royal Society of Chemistry, 2016, pp. 1–44 Search PubMed.
- T. G. Ribelli, F. Lorandi, M. Fantin and K. Matyjaszewski, Macromol. Rapid Commun., 2019, 40, 1800616 CrossRef PubMed.
- S. Perrier, Macromolecules, 2017, 50, 7433–7447 CrossRef CAS.
- J. Xu, Macromolecules, 2019, 52, 9068–9093 CrossRef CAS.
- S. Houshyar, D. J. Keddie, G. Moad, R. J. Mulder, S. Saubern and J. Tsanaktsidis, Polym. Chem., 2012, 3, 1879–1889 RSC.
- Z. Huang, B. B. Noble, N. Corrigan, Y. Chu, K. Satoh, D. S. Thomas, C. J. Hawker, G. Moad, M. Kamigaito, M. L. Coote, C. Boyer and J. Xu, J. Am. Chem. Soc., 2018, 140, 13392–13406 CrossRef CAS PubMed.
- Z. Huang, N. Corrigan, S. Lin, C. Boyer and J. Xu, J. Polym. Sci., Part A: Polym. Chem., 2019, 57, 1947–1955 CrossRef CAS.
- J. J. Haven, J. Vandenbergh, R. Kurita, J. Gruber and T. Junkers, Polym. Chem., 2015, 6, 5752–5765 RSC.
- E. Maron, J. H. Swisher, J. Haven, T. Y. Meyer, T. Junkers and H. G. Börner, Angew. Chem., 2019, 58, 10747–10751 CrossRef CAS PubMed.
- S. Harrisson, Polym. Chem., 2018, 9, 1366–1370 RSC.
- S. Lin, L. Zhang, Z. Huang, P. V. Kumar and J. Xu, Macromolecules, 2019, 52, 7157–7166 CrossRef CAS.
- G. Moad, E. Rizzardo and D. H. Solomon, Macromolecules, 1982, 15, 909–914 CrossRef CAS.
- D. H. Solomon, E. Rizzardo and P. Cacioli, Polymerization Process and Polymers Produced Thereby, Google Patents, US4581429A, 1986.
- P. Delduc, C. Tailhan and S. Z. Zard, J. Chem. Soc., Chem. Commun., 1988, 308–310 RSC.
- M. Chen, K. P. Ghiggino, A. W. H. Mau, E. Rizzardo, W. H. F. Sasse, S. H. Thang and G. J. Wilson, Macromolecules, 2004, 37, 5479–5481 CrossRef CAS.
- M. Chen, K. P. Ghiggino, E. Rizzardo, S. H. Thang and G. J. Wilson, Chem. Commun., 2008, 1112–1114 RSC.
- C. J. Hawker, J. Am. Chem. Soc., 1994, 116, 11185–11186 CrossRef CAS.
- T. Gruendling, M. Kaupp, J. P. Blinco and C. Barner-Kowollik, Macromolecules, 2011, 44, 166–174 CrossRef CAS.
- S. M. Henry, A. J. Convertine, D. S. W. Benoit, A. S. Hoffman and P. S. Stayton, Bioconjugate Chem., 2009, 20, 1122–1128 CrossRef CAS PubMed.
- S. Tanaka, H. Nishida and T. Endo, Macromolecules, 2009, 42, 293–298 CrossRef CAS.
- X.-S. Feng and C.-Y. Pan, Macromolecules, 2002, 35, 4888–4893 CrossRef CAS.
- N. Isahak, G. Gody, L. R. Malins, N. J. Mitchell, R. J. Payne and S. Perrier, Chem. Commun., 2016, 52, 12952–12955 RSC.
- J. De Neve, J. J. Haven, L. Maes and T. Junkers, Polym. Chem., 2018, 9, 4692–4705 RSC.
- M. A. R. Meier and C. Barner-Kowollik, Adv. Mater., 2019, 31, 1806027 CrossRef PubMed.
- J. Vandenbergh, G. Reekmans, P. Adriaensens and T. Junkers, Chem. Commun., 2013, 49, 10358–10360 RSC.
- J. J. Haven, J. Vandenbergh and T. Junkers, Chem. Commun., 2015, 51, 4611–4614 RSC.
- J. J. Haven and T. Junkers, Eur. J. Org. Chem., 2017, 6474–6482 CrossRef CAS.
- M. Chen, M. Haussler, G. Moad and E. Rizzardo, Org. Biomol. Chem., 2011, 9, 6111–6119 RSC.
- A. Aerts, R. W. Lewis, Y. Zhou, N. Malic, G. Moad and A. Postma, Macromol. Rapid Commun., 2018, 39, 1800240 CrossRef PubMed.
- Y. Zhou, Z. Zhang, C. Reese, D. Patton, J. Xu, C. Boyer, A. Postma and G. Moad, Macromol. Rapid Commun., 2019, 40, 1900478 CrossRef PubMed.
- J. Xu, S. Shanmugam, C. Fu, K.-F. Aguey-Zinsou and C. Boyer, J. Am. Chem. Soc., 2016, 138, 3094–3106 CrossRef CAS PubMed.
- J. Xu, C. Fu, S. Shanmugam, C. J. Hawker, G. Moad and C. Boyer, Angew. Chem., Int. Ed., 2017, 56, 8376–8383 CrossRef CAS PubMed.
- C. Fu, Z. Huang, C. J. Hawker, G. Moad, J. Xu and C. Boyer, Polym. Chem., 2017, 8, 4637–4643 RSC.
- J. F. Quinn, L. Barner, C. Barner-Kowollik, E. Rizzardo and T. P. Davis, Macromolecules, 2002, 35, 7620–7627 CrossRef CAS.
- M. L. Coote and T. P. Davis, Prog. Polym. Sci., 1999, 24, 1217–1251 CrossRef CAS.
- A. K. Nanda and K. Matyjaszewski, Macromolecules, 2003, 36, 8222–8224 CrossRef CAS.
- M. Mondal and A. K. H. Hirsch, Chem. Soc. Rev., 2015, 44, 2455–2488 RSC.
- H. Xue, Y. Zhao, H. Wu, Z. Wang, B. Yang, Y. Wei, Z. Wang and L. Tao, J. Am. Chem. Soc., 2016, 138, 8690–8693 CrossRef CAS PubMed.
- P. Frei, R. Hevey and B. Ernst, Chem. – Eur. J., 2019, 25, 60–73 CrossRef CAS PubMed.
- R. G. Fordyce and G. E. Ham, J. Am. Chem. Soc., 1951, 73, 1186–1189 CrossRef CAS.
- T. Itoh, I. Katoh, T. Satoh and S. Iwatsuki, J. Polym. Sci., Part A: Polym. Chem., 1995, 33, 1537–1543 CrossRef CAS.
- H. Ohnishi and T. Otsu, J. Macromol. Sci., Chem., 1978, 12, 1491–1500 CrossRef.
- M. G. Mikhael, A. B. Padias and H. Hall Jr., Macromolecules, 1993, 26, 5835–5839 CrossRef CAS.
- W. Mormann, K. Schmalz and A. Grimm, Macromol. Chem. Phys., 1997, 198, 419–429 CrossRef CAS.
- F. Xie, W. Hu, L. Ding, K. Tian, Z. Wu and L. Li, Polym. Chem., 2017, 8, 6106–6111 RSC.
- S. N. A. M. Jamil, R. Daik and I. Ahmad, J. Polym. Res., 2007, 14, 379–385 CrossRef CAS.
- S. Jamil, R. Daik and I. Ahmad, Materials, 2014, 7, 6207–6223 CrossRef PubMed.
- R. Malacea, C. Fischmeister, C. Bruneau, J.-L. Dubois, J.-L. Couturier and P. H. Dixneuf, Green Chem., 2009, 11, 152–155 RSC.
- J. Phommalysack-Lovan, Y. Chu, C. Boyer and J. Xu, Chem. Commun., 2018, 54, 6591–6606 RSC.
- S. Shanmugam, J. Xu and C. Boyer, J. Am. Chem. Soc., 2015, 137, 9174–9185 CrossRef CAS PubMed.
- K. Matyjaszewski, Macromolecules, 2002, 35, 6773–6781 CrossRef CAS.
- B. Klumperman, Polym. Chem., 2010, 1, 558–562 RSC.
- D. Bertin, P.-E. Dufils, I. Durand, D. Gigmes, B. Giovanetti, Y. Guillaneuf, S. R. A. Marque, T. Phan and P. Tordo, Macromol. Chem. Phys., 2008, 209, 220–224 CrossRef CAS.
- G. E. Ham, J. Polym. Sci., 1954, 14, 87–93 CrossRef CAS.
- W. Barb, J. Polym. Sci., 1953, 11, 117–126 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details of reaction setup, NMR and ESI-MS characterization of macro-RAFT agents, and flash chromatograph. See DOI: 10.1039/d0py00390e |
| This journal is © The Royal Society of Chemistry 2020 |