Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Advances towards programmable droplet transport on solid surfaces and its applications
Robert
Malinowski
 ,
Ivan P
Parkin
,
Ivan P
Parkin
 and
Giorgio
Volpe
and
Giorgio
Volpe
 *
*
Department of Chemistry, University College London, 20 Gordon Street, WC1H 0AJ London, UK. E-mail: g.volpe@ucl.ac.uk
First published on 5th June 2020
Abstract
Droplets moving on solid surfaces are at the heart of many phenomena of fundamental and applied interest in chemistry, physics and materials science. On the fundamental side, as they are often subject to evaporation, these droplets are a beautiful and complex example of non-equilibrium physical chemistry, whose explanation and understanding still capture the imagination of multiple researchers around the world. In technology, droplets on solid surfaces are of widespread use for handling small amounts of matter, for harvesting energy, for manufacturing materials and for sensing chemical and biological analytes. A key underlying factor of their widespread applicability is the degree of control that can be achieved over their transport on surfaces. This tutorial review provides an overview of recent progress towards the programmable transport of droplets on solid surfaces. We will first present the physical principles behind the main experimental strategies for droplet transport. We will then review the most inspiring applications where these strategies have been employed in chemistry, materials science and engineering. Finally, we will outline possible future research directions for the programmable transport of droplets. Beyond projecting the reader at the forefront of this exciting field of physical chemistry, we believe that this tutorial review will inspire diverse, multidisciplinary scientific communities to devise novel ways of manipulating the flow of matter, energy and information on solid surfaces using programmable droplets as vessels.
Key learning points• The hysteresis of a droplet's contact angle represents the major hindrance to its motion on a solid surface. Most strategies for droplet transport therefore aim to minimise or overcome it.• On a solid surface, the velocity of a moving droplet is determined by the balance between driving forces and viscous forces. • Body forces, wettability gradients and Marangoni flows are among the main driving mechanisms for droplet transport on solid surfaces. • The programmable motion of droplets has found application in manipulating matter and information, in harvesting matter and energy, in manufacturing and processing materials, and in the preparation and analysis of chemical and biological systems. |
1 Introduction
Every time it rains, an extremely large number of droplets form in the air and land on all sorts of surfaces, ultimately having an impact on several aspects of our everyday life. In general, droplets are small volumes of liquid separated from their surroundings by at least one interface. Beyond these meteorological considerations, droplets display a range of very curious, yet useful behaviours which make the field concerned with their study intrinsically multidisciplinary, spanning across several areas of physics, chemistry and engineering. Much of the richness in the behaviours of droplets which we will discuss here is due to their small size. Because of their typically small volumes, droplets' dynamics are indeed strongly determined by their surface energy, i.e. the excess energy available due to a disruption of the intermolecular forces between liquid molecules compared to the bulk when an interface is created. Moreover, droplets of different liquids play key roles in several industrial processes, such as heat transfer, water harvesting, energy generation, printing and even clinical diagnostics, to name a few. Often, these processes require the controlled transport of these droplets on solid surfaces, which presents both fundamental and technical challenges of its own.This tutorial review provides an overview of recent progress made towards the programmable transport of droplets on solid surfaces and lays the foundations for further in-depth study on the topic. After discussing typical barriers to droplet motion on solid surfaces (Section 2), we will highlight different mechanisms that have been proposed to overcome them, including the use of body forces, gradients in surface energy and the generation of Marangoni flows (Section 3). We will introduce a unified pedagogical formalism to present the physical principles behind these strategies. We will then discuss examples where droplets moving on solid substrates have found application in chemistry, materials science and engineering (Section 4), including the manipulation of matter and information, the harvesting of matter and energy, the manufacture and processing of materials, and the preparation and analysis of chemical and biological samples. Finally, we will conclude by drawing a picture of the possible future for both fundamental and applied research in the field of droplet transport on surfaces (Section 5).
2 Wetting and contact angle hysteresis
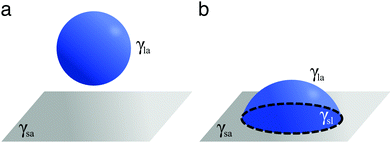
A droplet resting on a surface is said to wet it. Wetting can indeed be defined as the ability of a liquid to keep contact with a solid substrate.1 This phenomenon is driven by the surface energy at the interface between the liquid and the solid as a result of intermolecular interactions between the two. The degree to which a surface will be wetted, also known as its wettability, depends on the balance between forces of adhesion (driving the spreading of the liquid on the solid surface) and forces of cohesion (trying to minimise the surface area of the liquid), with favourable (unfavourable) interactions leading to more (less) wetting. In particular, three interfaces are involved in how a droplet wets a solid surface (Fig. 1): a solid–air, a solid–liquid and a liquid–air interface. Each of these interfaces is associated to a surface tension: γsa, γsl and γla, respectively (Fig. 1). Surface tension is surface energy per unit area, and it is equivalent to a force per unit length exerted on the droplet's contact line.Different wetting behaviours can be distinguished based on the value of the spreading coefficient1
| S = γsa − γsl − γla. | (1) |
In the case of partial wetting, a contact angle θc can be defined as the angle formed between the solid surface and the plane tangent to the liquid surface at the point of contact (Fig. 2). This angle is given by the Young–Dupré equation as a function of the three surface tensions involved
γsa = γsl + γla![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θc. θc. | (2) |
S = γla(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θc − 1). θc − 1). | (3) |
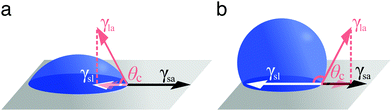 | ||
| Fig. 2 Definition of contact angle. According to the Young–Dupré equation (eqn (2)), the contact angle θc of a liquid droplet on a solid surface is determined by the vectorial balance at the contact line between the forces associated to the three surface tensions involved: γsa at the solid–air interface, γsl at the solid–liquid interface and γla at the liquid–air interface. For a liquid on a surface, the value of θc determines whether wetting is (a) favourable (θc < 90°) or (b) less so (θc > 90°). For water, the surface is said to be hydrophilic or hydrophobic, respectively. | ||
According to this picture, if the contact line of the droplet is not pinned (i.e. it is free to move on the solid substrate), the contact angle θc is constant in time. In practice, this is rarely the case. A liquid droplet resting on a solid surface can take a whole range of metastable contact angles as allowed by the lateral adhesion forces between the liquid and the solid. This phenomenon is known as contact angle hysteresis and it is often attributed to surface roughness and other physicochemical surface inhomogeneities down to the atomic scale that can pin the contact line to the substrate (contact line pinning).1 In particular, hysteresis is typically due to an interplay between the elasticity of the contact line and the force exerted by microscopic pinning defects on it.1 Although the precise cause of hysteresis is beyond the scope of this tutorial review, this phenomenon has a large impact on the dynamics of droplets: in particular, the hysteresis of the contact angle represents the main barrier to droplet motion on solid surfaces, as any force exerted on a droplet, rather than moving it, will first deform it within its range of acceptable contact angles.
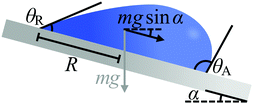
This hindrance to motion can be understood by using the intuitive example shown in Fig. 3, where a droplet of mass m and basal radius R rests on an incline (e.g. rain droplets on a glass window). The minimum tilt angle α of the incline at which the droplet will move can be estimated as1,2
mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = κRγla(cos α = κRγla(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR − cos θR − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA) θA) | (4) |
3 Strategies for droplet transport
As seen in the previous section, the main barrier to the motion of a droplet on a solid surface comes from the lateral adhesion forces responsible for the hysteresis of its contact angle θc.1 All mechanisms of droplet transport on solid surfaces therefore aim to either directly overcome hysteresis or decrease it to reduce the threshold for motion. Either way, a droplet will start moving as long as the initial net applied force is strong enough to defeat the initial static lateral adhesion forces, which are proportional to Rγla(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR − cos
θR − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA) on a given surface (eqn (4)).2
θA) on a given surface (eqn (4)).2
Once motion is initiated, a smaller driving force FD is needed to keep the droplet moving by balancing the kinetic viscous force FV due to the viscous stress at the base of the droplet on the solid surface (Fig. 4).2 The balance between these two forces (FD = FV) can then be used to estimate the velocity v of the droplet.3 Examples of typical speeds for different transport strategies are provided in Table 1. For instance, assuming small constant contact angles (as often the case in this tutorial), the velocity of a small droplet that, when moving, maintains the shape of a spherical cap of radius R can be obtained as3
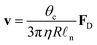 | (5) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) n are respectively the dynamic viscosity and an adimensional cutoff (with a typical value between 10 and 15) determined by the geometry of the droplet and the liquid constituting it.3
n are respectively the dynamic viscosity and an adimensional cutoff (with a typical value between 10 and 15) determined by the geometry of the droplet and the liquid constituting it.3
 | ||
| Fig. 4 Force balance on a moving droplet. When a droplet is set in motion on a solid surface by a driving force FD, its velocity v can be estimated by balancing forces with respect to the droplet's centre of mass (CM). In particular, the driving force FD is counteracted by a kinetic viscous force FV at the solid–liquid interface, which is proportional to v (eqn (5)). | ||
| Transport mechanism | Droplet composition | Surface type | Maximum speed |
|---|---|---|---|
| Surface acoustic waves4 | Water | Piezoelectric | ∼10 cm s−1 |
| Electrostatic repulsion5 | Water | Patterned PDMS substrate with superhydrophobic coating | ∼35 mm s−1 |
| Light-induced pyroelectric trapping6 | Water | Cu substrate with Ag nanocrystals rendered superhydrophobic with a monolayers of fluorinated thiols | ∼1 mm s−1 |
| Texture gradient and vibration7 | Water | Patterned Si wafer rendered superhydrophobic by coating with Teflon | ∼15 mm s−1 |
| Capillarity8 | Water | Hydrophilic PDMS substrate reproducing the microstructure of the peristome of the pitcher plant N. alata | ∼0.1 cm s−1 |
| Capillarity9 | Water, ethylene glycol, 2-propanol, ethanol, hexane | Si wafer patterned with U-shaped cavity arrays | ∼15 mm s−1 |
| Surface hydrophobicity gradient10,11 | Water | Si wafer functionalised with alkylsilanes via vapour diffusion | ∼0.3 cm s−1 |
| Photoisomerization of surface azobenzenes12 | Oil, liquid crystals | SiO2 plate functionalised with azobenzene moieties | ∼50 μm s−1 |
| Light-responsive surface rotaxanes13 | Diiodomethane | Au surface functionalised with light-switchable rotaxanes with fluoroalkane moieties | ∼1 μm s−1 |
| Surface charge density gradients14 | Water, various organic liquids | Charged thin nanoporous silica layer rendered superamphiphobic with fluorinated alkyltrichlorosilanes | ∼1 m s−1 |
| Electrowetting15 | Water | ITO substrate coated with a dielectric superhydrophobic layer with an inbuilt ground electrode | ∼3 cm s−1 |
| Optoelectrowetting16 | Water | Photoconductive substrate coated with a superhydrophobic dielectric layer | ∼5 mm s−1 |
| Thermal Marangoni flows17 | Silicone oil | Si wafer functionalised with alkylsilanes subject to a temperature gradient | ∼40 μm s−1 |
| Solutal Marangoni flows18,19 | Binary mixtures of water and propylene glycol | Glass | ∼1 mm s−1 |
| Leidenfrost effect20 | Nitrogen, acetone, methanol, ethanol, water, hexadecane | Ratchet-like surfaces of different materials at much hotter temperatures than the liquid's boiling point | ∼5 cm s−1 |
In this section, we will review the main mechanisms that have been proposed to achieve droplet transport on solid surfaces. For pedagogical reasons, the theoretical description of the different strategies will be based on droplets of small θc that move along linear gradients maintaining a spherical cap shape. Beyond body forces (e.g. gravity) (Fig. 5a and Section 3.1), a driving force FD can also be induced by direct action on the droplet's contact line either using a gradient in surface wettability (Fig. 5b and Section 3.2) or by generating Marangoni flows with imbalances of surface tension at the droplet's liquid–air interface (Fig. 5c and Section 3.3). Finally, in Sections 3.4 and 3.5, we will briefly mention popular alternatives for droplet transport based on the Leidenfrost effect and on Slippery Liquid-Infused Porous Surfaces (SLIPSs), respectively.
 | ||
| Fig. 5 Simplified schematics of the main driving mechanisms for droplet transport on solid surfaces. A droplet can be put into motion on a solid substrate at a velocity v because of three main driving mechanisms (alone or in combination): (a) body forces Fbody, e.g. gravity on an incline (Fig. 3), exerted on the droplet centre of mass CM (Section 3.1), (b) wettability gradients ∇γsl at the solid–liquid interface (Section 3.2) or (c) recirculating Marangoni flows within the droplet due to gradients of surface tension ∇γla at the droplet's liquid–air interface (Section 3.3). | ||
3.1 Motion due to body forces
Body forces are forces acting on the entire volume of an object. Continuing with the example of Fig. 3, the simplest and most commonly observed case of moving droplets due to body forces are raindrops rolling down a glass window (or incline) because of gravity. Under their own weight, droplets start deforming into a tear-like shape, but they will only move if they are heavy enough to overcome the inherent high contact angle hysteresis on glass. The threshold for droplet motion due to gravity on an incline can, however, be reduced significantly by making its surface superhydrophobic. Droplet motion on such surfaces has been extensively discussed in other reviews.21 When it comes to the programmable transport of droplets on surfaces, gravity has obvious limitations as it relies on controlling the tilt of the underlying surface.Surface acoustic waves induced by, e.g., a vibrating piezoelectric substrate can be used for the fast and fine actuation of small droplets on solid substrates.4 Because of the different sound propagation velocities in the solid and liquid, momentum is transferred from the acoustic wave to the droplet, thus generating a body force that moves the droplet in the wave propagation direction. Beyond surface acoustic waves, magnetic fields have also been heavily employed to exert programmable body forces on droplets loaded with, for example, magnetic cargoes.22 Alternatively, electric fields have been proposed to initiate transport of polarisable liquids, such as water, on low hysteresis surfaces.5,6 Recently, for example, small charged water droplets were remotely manoeuvred on superhydrophobic surfaces with repulsive electric fields.5 Similarly, water droplets could be manipulated on superhydrophobic surfaces in a contactless manner by generating dielectrophoretic attractive forces with a light-absorbing pyroelectric material, i.e. a surface capable of generic a temporary electric field upon illumination-induced heating.6
3.2 Motion due to wettability gradients
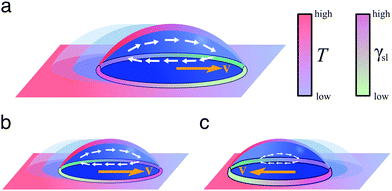
On homogeneous solid surfaces, droplets experience the same wetting behaviour in all directions, thus they spread isotropically until an equilibrium is reached and Young-Dupré equation (eqn (2)) is satisfied. In this case, the total energy Uγ of the droplet associated to its three interfaces (solid–liquid, liquid–air and solid–air) is constant on the substrate. However, when lying on a surface energy gradient (Fig. 5b), Uγ varies in space and the droplet will experience a net driving force FD towards lower energies, i.e. towards areas of higher wettability, given in the most general case by| FD = −∇Uγ | (6) |
 | ||
| Fig. 6 Simplified schematic of droplet transport due to gradients in surface texture. Space-varying structural features can lead to directional droplet transport at a velocity v towards areas of lower surface energy by influencing the contact angle that the droplet assumes on it. For example, an array of pillars of varying width and separation can induce a droplet to move towards areas of larger surface coverage when contact angle hysteresis is overcome.7 | ||
 | ||
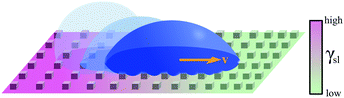
| Fig. 7 Simplified schematics of droplet transport due to chemical gradients. A gradient in surface energy can be generated by functionalising the surface with tailored molecular interactions. In (a), a permanent wettability gradient is obtained by controlling the density of hydrophobic groups (–R) available on the surface, thus biasing the droplet's motion in the direction of increased hydrophilicity (–OH).10 In (b), an on-demand wettability gradient can be obtained using photoisomerisable compounds containing, e.g., azobenzene moieties, which become more hydrophilic when irradiated with UV light, and return to a more hydrophobic state when illuminated with blue light.12 Alternatively, in (c), controllable charge gradients can be generated on a surface to induce directional droplet motion.14 | ||
 | ||
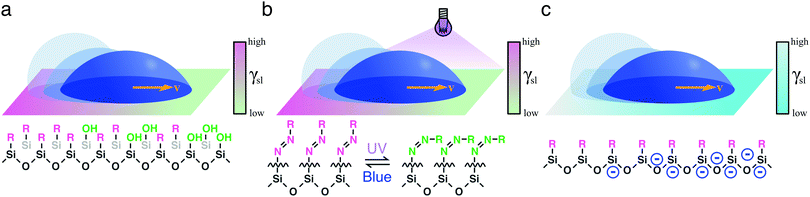
| Fig. 8 Simplified schematics of droplet transport due to electrowetting. The wetting properties of a hydrophobic dielectric surface can be modulated by applying a voltage (eqn (12) and (13)), thus inducing a droplet of a polarisable liquid to move towards its more hydrophilic side at a velocity v. In an on-plate configuration, the voltage applied to the dielectric can be modulated (a) directly with electrodes15 or (b) indirectly by exposing a photoconductive material to light.16 In the schematics, the droplet's impedance is represented by a parallel RC circuit and the dielectric material is represented as parallel capacitors. In (a), these capacitors can be independently connected to a voltage source or grounded. In (b), each of these capacitors follows a photoresistor whose resistivity is modulated with the incident light by, e.g., a projector: if all photoresistors but one underneath the droplet near its edge are illuminated, the resistance of the nonilluminated photoresistor increases, thus inducing a local drop in voltage that makes the droplet move.16 | ||
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θW = r θW = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θc θc | (7) |
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θCB = ϕ(cos θCB = ϕ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θc + 1) − 1 θc + 1) − 1 | (8) |
Independent of the model, according to both eqn (7) and (8), the contact angle and, thus, the wettability change with surface roughness. As both r and ϕ are indeed functions of surface texture, gradients in these parameters can lead to surface energy gradients and, thus, to directional droplet transport.7 For example, a linear gradient in contact angle can be obtained by systematically varying both the width and the spacing of etched micropillars on a silicon surface (Fig. 6).7 These rough hydrophobic surfaces are designed so that air is trapped underneath a droplet wetting them in a Cassie–Baxter configuration. By overcoming the strong contact angle hysteresis of such surfaces with the aid of mechanical vibration,7 droplets could then be transported down these linear wettability gradients responding to a net driving force FD derived from eqn (6) as
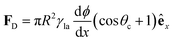 | (9) |
For completeness, it is worth mentioning that other types of surfaces displaying space-varying spatial features have also been extensively studied and considered for the transport of droplets on solids.8,9,24,25 For more details, we refer the reader to a recent review, which covers theory, fabrication and applications of such surfaces in depth.26 Briefly, beyond any influence from wettability gradients, these surfaces often exploit wedge-like and conical features to drive a droplet in a directional manner relying on various mechanisms. For example, a driving force can be generated thanks to a gradient in Laplace pressure at both ends of the droplet exploiting the asymmetric shape of the underlying wedge-like/conical structure.
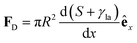 | (10) |
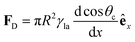 | (11) |
An example of such principle was reported at the beginning of the 90's, when a water droplet was shown to move along a treated silicon wafer, even uphill against gravity.10 A wettability gradient was generated by exposing the silicon wafer to a vapour of a volatile alkyltrichlorosilane in a diffusion-controlled process, thus creating a spatial variation of the surface hydrophobicity. The motion towards the direction of increased hydrophilicity was therefore caused by an imbalance in the forces acting on the solid–liquid contact line at opposite sides of the droplet (Fig. 7a). Droplets moved with relatively low average velocities of around 1–2 mm s−1 (Table 1), as the driving force due to surface tension was reduced by the need to overcome contact angle hysteresis. More sustained motion was later achieved on similarly treated surfaces through either coalescence of condensing droplets11 or, once more, through the aid of mechanical vibration,27 reaching velocities up to hundreds of mm s−1.
Stimulus responsive molecules can also be used to functionalise solid surfaces, thus enabling the generation of wettability gradients on demand. In fact, substrates can be functionalised with chemical moieties that can be controllably switched between two conformations with different wetting properties in response to an external stimulus, such as magnetic fields.22 This is also the case for molecules with azobenzene moieties capable of cis–trans isomerisation on exposure to different wavelengths of light (Fig. 7b).12 These photoisomerisable compounds become more hydrophilic when irradiated with UV light, and return to a more hydrophobic state when illuminated with blue light. As each isomer has a different surface energy, the wettability of these surfaces can therefore be locally controlled to transport droplets of liquids of low contact angle hysteresis over large distances by irradiating one edge of the droplet with UV light. Both direction and velocity of the motion can be tuned by modulating the spatial distribution in the light intensity. Being readily controllable in time and space, light has indeed been frequently used as a stimulus to trigger programmable droplet motion. Another such example was implemented by functionalising a gold surface with light-switchable rotaxanes capable of exposing or concealing a hydrophobic residue (i.e. a fluoroalkane) upon light exposure, thus generating a gradient of surface tension γsl at the solid–liquid interface.13 By covering the gold surface with a monolayer of such molecules, it was possible to transport a small diiodomethane droplet directionally for a few millimetres, even on an incline against gravity.
As an alternative to light and magnetic fields, gradients in surface charge density have also been recently suggested to modulate and control droplet transport on superamphiphobic surfaces.14 These surfaces were realised by coating glass slides with a thin nanoporous silica layer, which was subsequently rendered hydrophobic by chemical vapour deposition of fluorinated alkyltrichlorosilanes. On such surfaces, controllable charge density gradients can be created due to the contact electrification generated by the impact of water droplets. In particular, these gradients can be regulated by controlling the kinetic energy and surface tension at which the droplets impact on the surface. By controlling these surface charge density gradients, the transport velocity of the droplet could also be regulated as a consequence, reaching values around 1 m s−1, orders of magnitude higher than those achieved with most other strategies so far (Table 1).
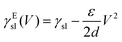 | (12) |
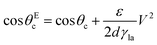 | (13) |
In order to modulate the wetting properties of a surface, an alternative to the use of independently addressable electrodes relies on the use of photoconductive materials (optoelectrowetting).16 In this case, an electric field parallel to the surface is applied with two external electrodes to generate a linear decrease of voltage along the photoconductive material; the local voltage can then be modulated by light illumination, thus inducing a change of contact angle according to eqn (13) (Fig. 8b).16 This approach offers some advantages over more traditional electrowetting devices mainly connected to the use of light to trigger droplet motion: compared to the pixellation introduced by any electrode, light control of surface wettability appears continuous even for the smallest droplet sizes; moreover, complex manipulation patterns can be easily generated by shaping the incident light with, e.g., commercial projectors.
3.3 Motion due to Marangoni flows
In Section 3.2, we have seen how droplet transport on solid surfaces can be initiated by a spreading coefficient S varying in space due to surface wettability gradients (eqn (10)). According to the definition of spreading coefficient (eqn (1)), however, a droplet can also be driven into motion on a solid surface because the surface tension γla at the liquid–air interface is not uniform, thus giving rise to Marangoni flows (Fig. 5c).3 These flows always cause the liquid to flow away from regions of low surface tension. In their presence, eqn (10) cannot be simplified to eqn (11), and the droplet will be subject to an additional drive imposed by the viscous stress that the Marangoni flows generate at its base.3 In the case of linear gradients, the driving force is then given by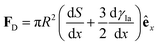 | (14) |
This principle for droplet transport can be enacted by inducing surface tension gradients at the liquid–air interface in different ways. Two of the most common strategies include the generation of temperature gradients (Section 3.3.1) and, more recently, of concentration gradients (Section 3.3.2).
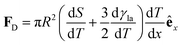 | (15) |
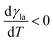 (Fig. 9a).3,17 A second contribution is due to the spreading coefficient S and always drives the droplet towards regions of lower surface energy (i.e. of larger S).3,17 Whether this direction is towards colder or warmer regions of the surface will depend on the actual material that the surface is made of. When the two terms are comparable, the net displacement of a droplet is not obvious and will depend on the exact experimental implementation (Fig. 9b and c);17 however, if there is no or negligible contribution from the solid (as often the case), then droplets always move towards colder regions (Fig. 9a) according to
(Fig. 9a).3,17 A second contribution is due to the spreading coefficient S and always drives the droplet towards regions of lower surface energy (i.e. of larger S).3,17 Whether this direction is towards colder or warmer regions of the surface will depend on the actual material that the surface is made of. When the two terms are comparable, the net displacement of a droplet is not obvious and will depend on the exact experimental implementation (Fig. 9b and c);17 however, if there is no or negligible contribution from the solid (as often the case), then droplets always move towards colder regions (Fig. 9a) according to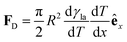 | (16) |
 | ||
| Fig. 9 Simplified schematics of droplet transport due to thermal gradients. When a liquid droplet rests on a solid surface in the presence of a linear thermal gradient, (a) the droplet typically moves towards colder regions due to Marangoni flows, unless (b and c) the surface is designed so that the surface energy is lower towards warmer regions. The motion of the droplet then depends on the balance between the two terms induced by the Marangoni flows and the spreading coefficient S (eqn (15)): the droplet can move either (b) towards colder regions if the Marangoni term predominates or (c) towards warmer regions if the spreading coefficient term predominates. | ||
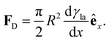 | (17) |
The necessary gradient can, for example, be induced by variations of composition along the liquid–air interface (Fig. 10). This naturally occurs in evaporating droplets of two or more miscible liquids: as liquids typically display different volatilities and evaporation tends to proceed faster near the droplet's edge, a gradient in concentration of the more volatile liquid can form between the droplet's apex (higher concentration) and its edge (lower concentration). If the liquids have also different surface tensions, this concentration gradient translates in a surface tension gradient and drives the formation of Marangoni flows towards higher γla.29 When radially symmetric, these flows either favour or prevent the droplet from spreading on the surface depending on whether they point outwards or inwards. In the latter case, the contracted droplet shows a significantly lower contact angle hysteresis than droplets made of its individual components, so that, when biased by, e.g., a second droplet evaporating nearby, these flows can lead to motion (Fig. 10).18 This is, for instance, the case for mixtures of water and propylene glycol, with water being the component of higher volatility and surface tension. Droplets of this mixture can sense each other and can display a wealth of emerging spontaneous behaviours, including attraction, chasing, coalescence and repulsion.18 More intricate and controllable motion patterns have recently been demonstrated by inducing deterministic concentration gradients on the droplet's liquid–air interface by means of nearby localised sources of vapour, thus enabling the precise contactless long-range manipulation of droplets on pristine substrates (Fig. 10).19
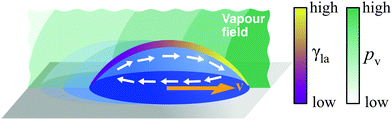 | ||
| Fig. 10 Simplified schematic of droplet transport due to concentration gradients. A concentration gradient along the liquid–air interface induces a gradient of surface tension γla. If the contact angle hysteresis is low, this gradient can lead to droplet motion due to Marangoni flows. Control over such a gradient in concentration can be achieved with solvent vapours induced by nearby droplets18 or, in a more precise fashion, by localised vapour sources (pv represents the partial vapour pressure).19 The direction of the motion will depend on the actual concentration profile of the vapour field around the droplet and can be towards the source or away from it.19 | ||
3.4 The Leidenfrost effect
A liquid droplet can hover over a surface whose temperature is much higher than the liquid's boiling point Tb (Fig. 11a). This is due to the formation of a thermally insulating vapour layer between the liquid and the solid that prevents the fast evaporation of the droplet. This phenomenon, known as the Leidenfrost effect, causes a reduction of the liquid–solid drag thanks to the intermediate vapour layer and was exploited to spontaneously transport droplets over asymmetric ratchet-like surfaces (Fig. 11b).20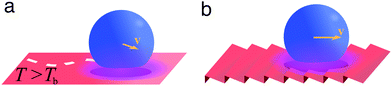 | ||
| Fig. 11 Simplified schematics of droplet transport due to the Leidenfrost effect. (a) A liquid droplet can hover over a surface maintained at a temperature T higher than the liquid's boiling point Tb due to the formation of a thermally insulating vapour layer between the liquid and the hot solid. This vapour layer reduces the liquid–solid drag, thus easing the spontaneous motion of droplets on the surface. (b) On a ratchet-like surface, the droplet motion can be biased in a direction determined by the underlying structure.20 | ||
3.5 SLIPSs
Slippery Liquid-Infused Porous Surfaces (SLIPSs) are special surfaces created by filling a solid porous material with a lubricating liquid (Fig. 12a). They were originally inspired by the carnivorous Venezuelan Nepenthes pitcher plants which exploit microscopic hairs to create a water slide causing ants to slip to their death and nourish the plant. The resulting thin layer of liquid covering the surface of the porous substrate determines its properties at the interface. As discussed in depth in a recent review on the topic,30 SLIPSs have been the subject of intensive research because of their self-healing, anti-icing, anticorrosion and anti-biofouling characteristics as well as for their excellent liquid repellency. In fact, SLIPSs are often characterised by a low contact angle hysteresis (≤10°), thus easing the transport of droplets made of a liquid immiscible with the infused liquid (Fig. 12b). Beyond the use of body forces (Section 3.1), the dynamical manipulation of liquid droplets on SLIPSs has also been achieved either by using stimulus-responsive liquids for infusing the porous substrate or by using stimuli-responsive materials for fabricating it.304 Applications of droplet transport
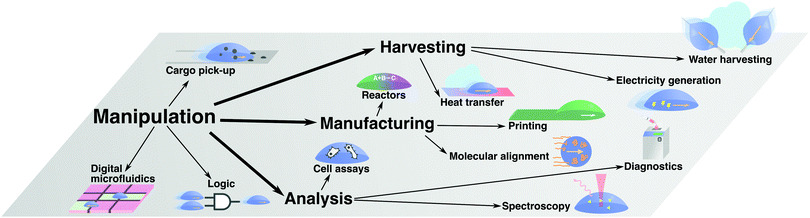
In the previous section, we have reviewed the main principles that have been put forward to control droplet transport on surfaces. The range of applications where these strategies have been employed is broad (Fig. 13). Often, these applications rely on a liquid droplet's inherent nature as a tiny self-contained compartment, thus allowing the handling of small volumes of liquids and materials within it. In this section, we will review some major examples of such applications, which we have broadly classified in four main categories: manipulation of matter and information (Section 4.1), harvesting of matter and energy (Section 4.2), manufacturing and materials processing (Section 4.3), and chemical and biological analysis (Section 4.4).4.1 Manipulation of matter and information
Transporting materials and information in small volumes is one of the simplest tasks that can be performed with moving droplets (Fig. 13). This simple task has formed the core of droplet-based technologies such as:• Digital microfluidics
Digital microfluidics is a technology for liquid-handling based on the parallel manipulation of individual droplets on an array of electrodes (Fig. 14a).31 This technology can be considered as one of the first examples of application for the programmable transport of droplets on solid surfaces, and it developed in parallel to the advancements in electrowetting research (Section 3.2.3). By employing an array of independent electrodes beneath the dielectric, the solid surface can be discretised into pixels of controllable wettability, so that multiple small liquid droplets can be generated, moved, merged and split simultaneously relying on electrical control.31 Due to its unique selling points (e.g. instrumental simplicity, flexible device geometry and compatibility with other technologies), digital microfluidics has found broad appeal as an alternative to traditional microfluidics for the generation, manipulation, mixing and compositional analysis of microdroplets.31 Since the first experimental demonstrations, significant and constant research effort, as reviewed elsewhere,32 has indeed allowed digital microfluidics to evolve into a mature technology for lab-on-a-chip applications, some of which are discussed in the following sections due to their interest in chemistry, physics, materials science and clinical medicine.33–40
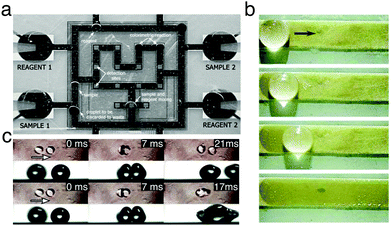 | ||
| Fig. 14 Examples of manipulation of matter and information with moving droplets. (a) A digital microfluidic device capable of creating droplets from reservoirs (“Reagent 1”, “Reagent 2”, “Sample 1” and “Sample 2”), and transporting them to be mixed, analysed and discarded. Reproduced from V. Srinivasan et al., Lab Chip, 2004, 4, 310–31533 with permission from The Royal Society of Chemistry, copyright 2004. (b) Surface cleaning by a droplet moved using surface acoustic waves. Stains formed by melamine microparticles on a strip are collected when the droplet moves along its surface. Reproduced from M. K. Tan et al., Lab Chip, 2007, 7, 618–5254 with permission from The Royal Society of Chemistry, copyright 2007. (c) When propelled towards each other, droplets can either rebound (top) or coalesce (bottom) depending on their velocity and impact geometry. These discrete phenomena, when combined with tracks to lead droplets, can be used to create AND/OR and NOT/FANOUT logic gates. Adapted and reproduced with permission from H. Mertaniemi et al., Rebounding Droplet–Droplet Collisions on Superhydrophobic Surfaces: from the Phenomenon to Droplet Logic, Adv. Mater., 2012, 24, 5738–5743.41 Copyright © 2012 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
• Cargo pick-up and removal
During their motion, droplets can collect other liquids or solids encountered in their path, such as dust particles, stains and/or solvents (Fig. 14b).4 Because of this feature, moving droplets have therefore become an important aid in many self-cleaning technologies as reviewed elsewhere.21 Droplets can indeed help remove fouling substances, thus leaving the underlying surface clean and in full working conditions. As seen in Section 3.1, modifying the chemical and physical properties of the surface can significantly reduce the threshold for droplets' motion due to, e.g., gravity, thus favouring self-cleaning applications. This approach can also be enhanced with the use of SLIPS surfaces (Section 3.5) and active transport phenomena mediated by, e.g., electrowetting (Section 3.2.3).
• Droplet logic
Two or more moving droplets can also be exploited to implement simple logic operators on a surface. On superhydrophobic surfaces, for example, the collisions of two pure water droplets can be controlled to lead to either coalescence or rebouncing based on their velocity and impact geometry (Fig. 14c).41 By designing superhydrophobic tracks crossing at desired impact parameters on a copper plate, different logic elements could therefore be demonstrated based on this droplet bouncing mechanism: namely, AND/OR and NOT/FANOUT Boolean operators as well as a flip-flop memory.41
4.2 Harvesting of matter and energy
Beyond manipulating materials suspended or dissolved within them, moving droplets can also be employed to harvest matter, generate energy or transfer it during their transport (Fig. 13). This principle has, for example, been employed for the following applications:• Water harvesting
Water harvesting is the collection of water from the environment for its reuse. This is possibly one of the simplest applications where the directional transport of droplets has been successfully employed as water must simply be directed to a collection point without requiring high levels of droplet transport programmability. In nature, many organisms, including plants, insects, reptiles and birds, have developed surfaces and structures that allow them to harvest water (often in harsh environmental conditions) by exploiting the directional transport of droplets.26 Examples are varied and, among others, include spider web silk fibres24 and cactus spines to capture water from fog condensation (Fig. 15a)25 as well as the peristome of carnivorous pitcher plants for enhancing prey-trapping mechanisms.8 These natural structures typically exploit chemical and structural gradients in surface energy or asymmetric geometries for the directional collection of water droplets (Sections 3.2.1 and 3.2.2), and have been the inspiration for the realisation of manmade surfaces and materials for the harvesting of liquids,26e.g. for harvesting fog from air25 or for the directional pumping of water and oil droplets on SLIPSs (Section 3.5).43
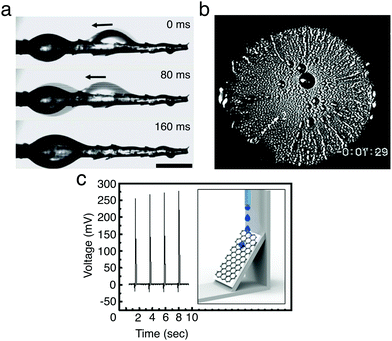 | ||
| Fig. 15 Examples of water and energy harvesting with moving droplets. (a) A droplet moving and coalescing with another near the base of a cactus spine. Adapted by permission from Springer Nature Customer Service Centre GmbH: Springer Nature, J. Ju et al., Nat. Commun., 2012, 3, 1247,25 Copyright 2012 Springer Nature. (b) Water condensing on a cooled silicon 1 cm wafer bearing a wettability gradient. The wafer is most hydrophobic in the centre and becomes more hydrophilic towards the edges. The condensing droplets move outwards towards the edges, visible as radial streaks, carrying thermal energy with them. Adapted with permission from S. Daniel et al., Science, 2001, 291, 633–636.11 Reprinted with permission from AAAS. (c) Voltage generated by droplets moving down a graphene/PTFE surface under gravity due to the triboelectric effect (setup schematically shown in the inset). Each spike corresponds to a new droplet sliding down the surface. Adapted with permission from S. S. Kwak et al., ACS Nano, 2016, 10, 7297–7302.42 Copyright 2016 American Chemical Society. | ||
• Heat transfer
Droplet motion can be harnessed to enhance the performance of industrial heat exchangers.11 In such devices, a cold liquid flow is typically used to extract heat from a hot vapour. The heat exchange is mediated by a thermally conductive wall which separates the two phases. However, vapour condensation at this wall can strongly hamper the performance of the heat exchanger by forming a thin thermally insulating liquid film. This phenomenon can be moderated by using substrates with wettability gradients to remove the droplets away from the point of condensation (Section 3.2.2), thus continuously renewing the surface of the exchanger and improving the overall heat transfer through it (Fig. 15b).11
• Electricity generation
The possibility of generating electricity by moving droplets of rain, seawater, sweat or ionic liquids on an appropriate surface is an exciting application of droplet transport that has emerged more recently. One of the first demonstrations of this concept was obtained by reversing electrowetting (Section 3.2.3):37 high power densities (up to a few kW m−2) could be generated by moving an array of droplets of a conductive fluid on multilayered dielectric surfaces made of tantalum pentoxide coated with a thin fluoropolymer film.37 Alternatively, electricity can be generated by dragging liquid droplets of salt (NaCl), acid and alkali solutions on a graphene surface at controllable speeds with a SiO2/Si wafer.44 In this case, the interface between the moving droplet and the underlying graphene substrate forms a pseudocapacitor due to the generation of an electrical double layer. This pseudocapacitor, which charges and discharges at the front and rear of the moving droplet, can generate an electric power on the order of a few tens of nanoWatts (<20 nW), enough to demonstrate several prototype devices such as velocity and handwriting sensors44 and, more recently, an all-weather solar cell that can be triggered both by sunlight and raindrops.45 When using graphene, the production of electric power can be increased by modifying the properties of the underlying surface. For example, a boost of two orders of magnitude in the generated electric power compared to the previous case can be achieved when droplets are moved on graphene monolayers deposited on polytetrafluoroethylene (PTFE) substrates, due to the strong negative triboelectric potential characterising these surfaces (Fig. 15c).42
4.3 Manufacturing and materials processing
While transporting materials, droplets can also be employed for manufacturing, either by working as self-contained chemical reactors or by modifying the underlying substrate (Fig. 13). Often, in these applications, droplets leave behind trails of material during their motion. An intrinsic downside is therefore the higher risk of surface defect formation that can pin the contact line and increase contact angle hysteresis (Section 2). This risk can be mitigated with a careful design of the substrate–droplet system employed for the specific application:• Compartmentalised reactions
Because of their self-contained nature, small droplets spontaneously lend themselves to act as mesoscopic mixers and/or reactors of materials dissolved or suspended within them. Their small scale means that droplets are particularly convenient for efficiently screening reaction conditions. The collision and coalescence of two (or more) droplets can therefore be harnessed to initiate a reaction controllably in space and time,41 such as for acid–base neutralisation and for monitoring pH.19 Another example includes the formation of inorganic salts by merging droplets containing precursor compounds (Fig. 16a).5 Furthermore, nylon 6-6 was recently synthesised by combining magnetically actuated droplets on a SLIP surface compatible with both aqueous and organic liquids:48 the two reactants, hexamethyl diamine and adipoyl chloride, were respectively contained in droplets based on water and heptane, and reacted at the interface between the two liquids upon merging.
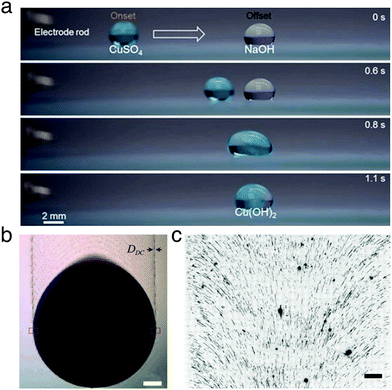 | ||
| Fig. 16 Examples of materials manufacturing and processing with moving droplets. (a) A droplet containing copper(II) sulfate is propelled towards a second stationary droplet containing sodium hydroxide by electrostatic repulsion from an electrode rod. Upon merging, copper hydroxide is formed. Reproduced with permission from H. Dai et al., Controllable High-Speed Electrostatic Manipulation of Water Droplets on a Superhydrophobic Surface. Adv. Mater., 2019, 31, 1905449.5 © 2019 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. (b) A binary liquid droplet of toluene and nonane containing gold nanoparticles moves down an inclined silicon wafer due to gravity. As the droplet moves, it leaves a trail of nanoparticles. Scale bar 300 mm. Adapted and reproduced with permission from G. Konvalina et al., Printing Nanostructures with a Propelled Anti-Pinning Ink Droplet. Adv. Funct. Mater., 2015, 25, 2411–2419.46 © 2015 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. (c) Fluorescence microscopy image of human DNA deposited by dragging a droplet (downwards in frame) on a Zeonex-coated microscope slide. The motion of the droplet imparts directionality on the deposited DNA, which is aligned perpendicularly to the droplet edge. Scale bar 200 kilobase pairs in length (108 mm). Adapted with permission from G. Deen et al., ACS Nano, 2015, 9, 809–81647 under an ACS AuthorChoice License. Permission for further reuse should be sought directly with the ACS. | ||
• Deposition and printing
Moving droplets can be used to deposit continuous trails of materials (such as colloids and polymers) contained within them along their path, thus offering alternatives to conventional ink-jet printing techniques for printing 2D and 3D patterns on both planar and curved surfaces.4 The main obstacle for this sort of applications is the pinning of the contact line, which is typically aggravated in the presence of any material suspended or dissolved within the droplet (Section 2). Binary droplets are a good candidate to mitigate this issue due to their low threshold to motion and increased compatibility with different chemical species due to their multicomponent nature (Section 3.3.2). In this context, binary droplets of toluene and nonane were employed to deposit gold nanoparticles in controllable patterns (Fig. 16b), and even to realise working sensors capable of detecting strain and volatile organic compounds.46 Binary droplets have also been employed to print organic materials, such as polymers: arbitrary macroscopic 2D patterns of polyvinyl alcohol or polyethylene glycol were indeed deposited on pristine substrates by manipulating binary droplets of water and propylene glycol containing different concentrations of either polymer.19
• Molecular alignment and self-assembly
While depositing, moving droplets can also impart a preferential direction to the deposited material, thus favouring processes of molecular alignment and self-assembly. This is, for example, useful in DNA technology, where the deposition of linear DNA molecules is key for several single-molecule genomic approaches, from DNA mapping to sequencing. DNA-containing water droplets can indeed efficiently deposit, combine and align DNA molecules on different substrates (Fig. 16c) when driven either by body forces47 (Section 3.1) or chemical wettability gradients49 (Section 3.2.2). Similarly, the speed at which a binary droplet containing crystallising polymers (such as polyethylene glycol) moves on a pristine substrate can be used as a tuneable parameter to control how the polymer crystallites orient on it, thus determining the texture of the final deposition patterns.19
4.4 Chemical and biological analysis
Moving droplets can be exploited to implement fully operational chemical and biological assays relying on their capability of transporting and concentrating small quantities of analytes (Fig. 13). Because of this, they have been broadly embraced in the following areas:• Spectroscopy of molecules and biomolecules
The ability to handle and process small liquid volumes makes moving droplets ideal for the detection and in situ analysis of molecules and biomolecules when combined, e.g., with spectroscopy techniques. This is also augmented by the fact that droplets are often evaporative systems. Evaporation indeed aids to concentrate small quantities of analytes, thus improving the signal-to-noise ratio in the measurement. For example, a digital microfluidic device was used to implement an efficient in-line sample purification method of droplets with contaminated peptides for their analysis with matrix-assisted laser desorption/ionisation mass spectrometry (MALDI-MS).34 More recently, magnetically actuated butanol droplets were employed to extract natural molecules with antibacterial properties produced by two strains of marine bacteria (prodigiosin from Pseudoalteromonas rubra and violacein from Pseudoalteromonas luteoviolacea) before also being analysed with MALDI-MS.48 Similarly, droplet transport was employed to realise a high-throughput surface-enhanced Raman scattering (SERS) sensor for the real-time control and detection of dye-containing droplets on SERS-active surfaces made with superhydrophobic silver dendritic substrates (Fig. 17a and b):50 much like in a conveyor belt, droplets were employed to transport rhodamine 6G, Nile blue A and malachite green under a laser spot on the surface, where the molecule's Raman fingerprint could be measured.
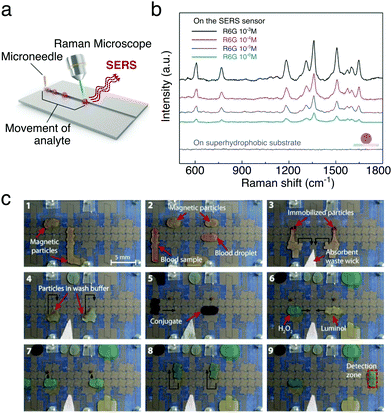 | ||
| Fig. 17 Examples of chemical and biological analysis with moving droplets. (a and b) Droplets containing analytes can be transported to a location illuminated with a laser in order to perform sequential SERS measurements as schematically depicted in (a). Examples of Raman spectra measured from droplets containing different concentrations of rhodamine 6G are shown in (b). Adapted and reproduced with permission from S. Shin et al., A Droplet-Based High-Throughput SERS Platform on a Droplet-Guiding-Track-Engraved Superhydrophobic Substrate, Small, 2017, 13, 1602865.50 © 2016 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. (c) Sequence of images showing the working of a digital micofluidic platform for detecting antibodies for measles and rubella in human blood. (1 and 2) Paramagnetic particles functionalised with the virus antigens are mixed with the blood sample. (3 and 4) Any antibodies present bind to the particles and a magnet can be used to immobilise them while the mother liquid is removed and the particles washed in buffer. (5) The attached antibodies are reacted with an anti-human IgG–horseradish peroxidase conjugate, which binds to the antibodies. (6–8) After further washing, the attached antibodies can then be detected by mixing with luminol and H2O2 (9) after moving the droplet to the detection zone. The black arrows show droplet motion. Reprinted with permission from A. H. C. Ng et al., Sci. Transl. Med., 2018, 10, eaar6076.39 Reprinted with permission from AAAS. | ||
• Cell-based assays and clinical diagnostics
In parallel with the progress of digital microfluidics technology (Section 4.1), droplet transport has found broad application in the development of in vitro biological and clinical assays. Digital microfluidics was proven to be compatible with the manipulation of many physiological fluids quite early on, including blood, serum, plasma, urine, saliva, sweat and tears.33 Moreover, digital microfluidics platforms have also been applied to grow, transport and analyse various types of cells, such as mammalian cells,35 as well as microorganisms, such as bacteria, algae and yeast cells.36 The literature on the topic is therefore vast and includes immunoassays, nucleic acid assays and cell-based assays, as can be appreciated from references herein.38–40 Among recent developments, a smartphone integrated portable optoelectrowetting device was employed to monitor water quality based on the real-time detection of target cells in water samples.38 Excitingly, a digital microfluidics platform has recently been used as the core technology to demonstrate a compact, portable, field-deployable, point-of-care system to perform serological immunoassays for measles and rubella from human blood samples in remote settings (Fig. 17c).39 Similarly, in the wake of antimicrobial resistance, digital microfluidics has proven valuable in developing a platform to facilitate detection of antimicrobial resistance genes in human urine for the diagnosis of antimicrobial resistant urinary tract infections.40
5 Conclusions and outlook
In this tutorial review, we have summarised both pioneering work and recent progress on the programmable transport of droplets on solid surfaces and its applications. Beyond offering a current snapshot of this exciting and fast developing research area in physical chemistry, this tutorial review aims at providing a pedagogical introduction for anybody approaching the field ex novo. Due to the field's ample breadth, we decided to focus on some fundamental and applied aspects centred on the motion of droplets on hard surfaces. Even if beyond the scope of this tutorial review, droplet motion on soft and liquid surfaces is indeed the object of intensive research too. From a fundamental point of view, due to the fact that droplets are often evaporating, their motion is a beautiful example of non-equilibrium physics.19,29 As such, understanding and controlling motion mechanisms on a microscopic level still poses challenges due to the (often) transient nature and molecular scale of the forces at play.18,19 Among the various applications of droplet transport highlighted herein, we would like to outline a few future directions that we envisage will reinforce existing research areas or open new ones. Firstly, the study of self-propelling droplets (i.e. droplets capable of triggering their own motion without external control) is still in its infancy,18 and could lead to the emergence of collective motion, self-organisation and other non-equilibrium phenomena useful for the development of life-inspired microreactors. Secondly, expanding the operations enabled by droplets beyond reactions and deposition to include, e.g. etching, could boost their potential for processing mesoscopic materials and find use, for example, in microfabrication. Thirdly, while digital microfluidics is an emerging technology for portable applications in clinical diagnostics,39,40 the integration of such platforms with portable devices and wearable electronics can boost the development of physiological sensors and all-weather energy harvesting devices.38,42 Finally, the computational capabilities of liquid droplets are particularly interesting as a way to boost automatisation on digital microfluidics platforms: computation based on droplet logic could indeed reduce the amount of external input and feedback required in order to manipulate droplets in parallel on such devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Giorgio Volpe acknowledges funding from the HEFCE's Higher Education Innovation Fund (KEI2017-05-07). Robert Malinowski and Ivan P. Parkin acknowledge funding from EPSRC (EP/G036675/1).References
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739–805 CrossRef CAS.
- N. Gao, F. Geyer, D. W. Pilat, S. Wooh, D. Vollmer, H.-J. Butt and R. Berger, Nat. Phys., 2018, 14, 191–196 Search PubMed.
- F. Brochard, Langmuir, 1989, 5, 432–438 CrossRef CAS.
- M. K. Tan, J. R. Friend and L. Y. Yeo, Lab Chip, 2007, 7, 618–625 RSC.
- H. Dai, C. Gao, J. Sun, C. Li, N. Li, L. Wu, Z. Dong and L. Jiang, Adv. Mater., 2019, 31, 1905449 CrossRef CAS PubMed.
- X. Tang and L. Wang, ACS Nano, 2018, 12, 8994–9004 CrossRef CAS PubMed.
- A. Shastry, M. J. Case and K. F. Böhringer, Langmuir, 2006, 22, 6161–6167 CrossRef CAS PubMed.
- H. Chen, P. Zhang, L. Zhang, H. Liu, Y. Jiang, D. Zhang, Z. Han and L. Jiang, Nature, 2016, 532, 85–89 CrossRef CAS PubMed.
- J. Li, X. Zhou, J. Li, L. Che, J. Yao, G. McHale, M. K. Chaudhury and Z. Wang, Sci. Adv., 2017, 3, eaao3530 CrossRef PubMed.
- M. K. Chaudhury and G. M. Whitesides, Science, 1992, 256, 1539–1541 CrossRef CAS PubMed.
- S. Daniel, M. K. Chaudhury and J. C. Chen, Science, 2001, 291, 633–636 CrossRef CAS PubMed.
- K. Ichimura, S.-K. Oh and M. Nakagawa, Science, 2000, 288, 1624–1626 CrossRef CAS PubMed.
- J. Berná, D. A. Leigh, M. Lubomska, S. M. Mendoza, E. M. Pérez, P. Rudolf, G. Teobaldi and F. Zerbetto, Nat. Mater., 2005, 4, 704–710 CrossRef PubMed.
- Q. Sun, D. Wang, Y. Li, J. Zhang, S. Ye, J. Cui, L. Chen, Z. Wang, H.-J. Butt, D. Vollmer and X. Deng, Nat. Mater., 2019, 18, 936–941 CrossRef CAS PubMed.
- C. G. Cooney, C.-Y. Chen, M. R. Emerling, A. Nadim and J. D. Sterling, Microfluid. Nanofluid., 2006, 2, 435–446 CrossRef.
- D. Jiang and S.-Y. Park, Lab Chip, 2016, 16, 1831–1839 RSC.
- J. B. Brzoska, F. Brochard-Wyart and F. Rondelez, Langmuir, 1993, 9, 2220–2224 CrossRef CAS.
- N. J. Cira, A. Benusiglio and M. Prakash, Nature, 2015, 519, 446–450 CrossRef CAS PubMed.
- R. Malinowski, I. P. Parkin and G. Volpe, 2019, arXiv:1909.05221.
- H. Linke, B. J. Alemán, L. D. Melling, M. J. Taormina, M. J. Francis, C. C. Dow-Hygelund, V. Narayanan, R. P. Taylor and A. Stout, Phys. Rev. Lett., 2006, 96, 154502 CrossRef CAS PubMed.
- D. Sun and K. F. Böhringer, Micromachines, 2019, 10, 101 CrossRef PubMed.
- Y. Zhang and N.-T. Nguyen, Lab Chip, 2017, 17, 994–1008 RSC.
- Z. Zhang, F. Zhang, Q. Huang, G. Cheng and J. Ding, Appl. Surf. Sci., 2020, 515, 145976 CrossRef CAS.
- Y. Zheng, H. Bai, Z. Huang, X. Tian, F.-Q. Nie, Y. Zhao, J. Zhai and L. Jiang, Nature, 2010, 463, 640–643 CrossRef CAS PubMed.
- J. Ju, H. Bai, Y. Zheng, T. Zhao, R. Fang and L. Jiang, Nat. Commun., 2012, 3, 1247 CrossRef PubMed.
- J. Li and Z. Guo, Nanoscale, 2018, 10, 13814–13831 RSC.
- S. Daniel and M. K. Chaudhury, Langmuir, 2002, 18, 3404–3407 CrossRef CAS.
- M. G. Pollack, R. B. Fair and A. D. Shenderov, Appl. Phys. Lett., 2000, 77, 1725–1726 CrossRef CAS.
- R. Malinowski, G. Volpe, I. P. Parkin and G. Volpe, J. Phys. Chem. Lett., 2018, 9, 659–664 CrossRef CAS PubMed.
- D. P. Regan and C. Howell, Curr. Opin. Colloid Interface Sci., 2019, 39, 137–147 CrossRef CAS.
- S. K. Cho, H. Moon and C.-J. Kim, J. Microelectromech. Syst., 2003, 12, 70–80 CrossRef.
- E. Samiei, M. Tabrizian and M. Hoorfar, Lab Chip, 2016, 16, 2376–2396 RSC.
- V. Srinivasan, V. K. Pamula and R. B. Fair, Lab Chip, 2004, 4, 310–315 RSC.
- A. R. Wheeler, H. Moon, C. A. Bird, R. R. Ogorzalek Loo, C.-J. C. J. Kim, J. A. Loo and R. L. Garrell, Anal. Chem., 2005, 77, 534–540 CrossRef CAS PubMed.
- I. Barbulovic-Nad, H. Yang, P. S. Park and A. R. Wheeler, Lab Chip, 2008, 8, 519–526 RSC.
- S. H. Au, S. C. C. Shih and A. R. Wheeler, Biomed. Microdevices, 2011, 13, 41–50 CrossRef CAS PubMed.
- T. Krupenkin and J. A. Taylor, Nat. Commun., 2011, 2, 448 CrossRef PubMed.
- D. Jiang, S. Lee, S. W. Bae and S.-Y. Park, Lab Chip, 2018, 18, 532–539 RSC.
- A. H. C. Ng, R. Fobel, C. Fobel, J. Lamanna, D. G. Rackus, A. Summers, C. Dixon, M. D. M. Dryden, C. Lam, M. Ho, N. S. Mufti, V. Lee, M. A. M. Asri, E. A. Sykes, M. D. Chamberlain, R. Joseph, M. Ope, H. M. Scobie, A. Knipes, P. A. Rota, N. Marano, P. M. Chege, M. Njuguna, R. Nzunza, N. Kisangau, J. Kiogora, M. Karuingi, J. W. Burton, P. Borus, E. Lam and A. R. Wheeler, Sci. Transl. Med., 2018, 10, eaar6076 CrossRef PubMed.
- S. Kalsi, M. Valiadi, C. Turner, M. Sutton and H. Morgan, Lab Chip, 2019, 19, 168–177 RSC.
- H. Mertaniemi, R. Forchheimer, O. Ikkala and R. H. A. Ras, Adv. Mater., 2012, 24, 5738–5743 CrossRef CAS PubMed.
- S. S. Kwak, S. Lin, J. H. Lee, H. Ryu, T. Y. Kim, H. Zhong, H. Chen and S.-W. Kim, ACS Nano, 2016, 10, 7297–7302 CrossRef CAS PubMed.
- J. Jiang, J. Gao, H. Zhang, W. He, J. Zhang, D. Daniel and X. Yao, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 2482–2487 CrossRef CAS PubMed.
- J. Yin, X. Li, J. Yu, Z. Zhang, J. Zhou and W. Guo, Nat. Nanotechnol., 2014, 9, 378–383 CrossRef CAS PubMed.
- Q. Tang, X. Wang, P. Yang and B. He, Angew. Chem., Int. Ed., 2016, 55, 5243–5246 CrossRef CAS PubMed.
- G. Konvalina, A. Leshansky and H. Haick, Adv. Funct. Mater., 2015, 25, 2411–2419 CrossRef CAS.
- J. Deen, W. Sempels, R. De Dier, J. Vermant, P. Dedecker, J. Hofkens and R. K. Neely, ACS Nano, 2015, 9, 809–816 CrossRef CAS PubMed.
- P. Agrawal, T. T. Salomons, D. S. Chiriac, A. C. Ross and R. D. Oleschuk, ACS Appl. Mater. Interfaces, 2019, 11, 28327–28335 CrossRef CAS PubMed.
- D. Giri, Z. Li, K. M. Ashraf, M. M. Collinson and D. A. Higgins, ACS Appl. Mater. Interfaces, 2016, 8, 24265–24272 CrossRef CAS PubMed.
- S. Shin, J. Lee, S. Lee, H. Kim, J. Seo, D. Kim, J. Hong, S. Lee and T. Lee, Small, 2017, 13, 1602865 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |