Graphene foam-embedded epoxy composites with significant thermal conductivity enhancement†
Zhiduo
Liu‡
ab,
Yapeng
Chen‡
ab,
Yifan
Li
c,
Wen
Dai
 a,
Qingwei
Yan
a,
Fakhr E.
Alam
a,
Shiyu
Du
a,
Qingwei
Yan
a,
Fakhr E.
Alam
a,
Shiyu
Du
 *c,
Zhongwei
Wang
d,
Kazuhito
Nishimura
e,
Nan
Jiang
ab,
Cheng-Te
Lin
*c,
Zhongwei
Wang
d,
Kazuhito
Nishimura
e,
Nan
Jiang
ab,
Cheng-Te
Lin
 *ab and
Jinhong
Yu
*ab and
Jinhong
Yu
 *ab
*ab
aKey Laboratory of Marine Materials and Related Technologies, Zhejiang Key Laboratory of Marine Materials and Protective Technologies, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo, 315201, China. E-mail: linzhengde@nimte.ac.cn; yujinhong@nimte.ac.cn
bCenter of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
cDivision of Functional Materials and Nanodevices, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo, Zhejiang 315201, China. E-mail: dushiyu@nimte.ac.cn
dCollege of Materials Science and Engineering, Shandong University of Science and Technology, Qingdao, 266590, China
eAdvanced Nano-processing Engineering Laboratory, Mechanical Engineering, Kogakuin University, Tokyo, 192-0015, Japan
First published on 17th June 2019
Abstract
High thermal conductivity polymer composites at low filler loading are of considerable interest because of their wide range of applications. The construction of three-dimensional (3D) interconnected networks can offer a high-efficiency increase for the thermal conductivity of polymer composites. In this work, a facile and scalable method to prepare graphene foam (GF) via sacrificial commercial polyurethane (PU) sponge templates was developed. Highly thermally conductive composites were then prepared by impregnating epoxy resin into the GF structure. An ultrahigh thermal conductivity of 8.04 W m−1 K−1 was obtained at a low graphene loading of 6.8 wt%, which corresponds to a thermal conductivity enhancement of about 4473% compared to neat epoxy. This strategy provides a facile, low-cost and scalable method to construct a 3D filler network for high-performance composites with potential to be used in advanced electronic packaging.
Introduction
Thermal management is critical to the performance, lifetime, and reliability of electronic devices. With the miniaturization and integration of electronics and the emergence of new applications such as light-emitting diodes, thermal dissipation has become a challenging problem.1,2 Solving this problem requires the development of novel polymer composites with high thermal conductivity.3,4 Traditional high thermal conductivity polymer composites are always achieved by incorporating an extremely high loading of high thermal conductivity inorganic fillers, such as graphene, boron nitride nanosheets and alumina. Among the current high thermal conductivity nanofillers, graphene exhibits the highest thermal conductivity, which is 2000–5000 W m−1 K−1.5 However, high loading always results in high cost, heavy weight and deterioration of mechanical properties. Current polymeric thermally conductive composites produced by simple blending can hardly achieve high thermal conductivity with a low filler content. The reasons can be attributed to the difficulty of thermal conduction path formation in the polymer matrix at low filler loading.6 Research showed that the thermal conductivity of the polymer can be greatly improved when the filler content reached the percolation threshold, which is usually a relatively high filler loading.7,8 So far, preparation of high thermal conductivity composites with low loading is not only of great significance but also a challenge for the next generation electronics encapsulation.9A number of attempts have been made to realize the high-efficiency thermal conductivity enhancement at a relatively low filler loading, such as through using a functionalized filler,10,11 hybrid filler,12–14 rational orientation of fillers and self-assembly into three-dimensional (3D) networks.15,16 Recently prepared 3D foam-like materials have been reported as a new way of building up two-dimensional (2D) nanomaterials into 3D architectures as a thermally conductive path, which has been proved to be a promising strategy to achieve the high thermal conductivity enhancement efficiency.17 In comparison with the composite with randomly distributed fillers, 3D foam-like materials are favourable for the formation of a thermally conductive network at an extremely low filler loading.18 For example, a 3D vertically aligned and interconnected graphene network was prepared via the oriented freeze-casting method. The obtained epoxy composites exhibit a high thermal conductivity of 2.13 W m−1 K−1 at an ultralow graphene loading of 0.92 vol%.19 Kim et al. reported that the continuous chemical vapour deposition (CVD) growth of graphene networks within the epoxy composites leads to an exceptional in-plane thermal conductivity of 8.8 W m−1 K−1 at the filler loading of 8.3 wt%.20 Although the preparation of 3D networks can easily achieve obvious thermal conductivity enhancement at low filler loading, the preparation methods including ice-templating and CVD are always time-consuming and involve processing, hardly meeting the requirement of large-scale production. In comparison with the above methods, the template method is the most promising and attractive method due to its ability to produce well-defined and shaped architectures.21
Herein, we have developed a facile and scalable method to prepare graphene foam (GF) via sacrificial commercial polyurethane (PU) sponge templates. Highly thermally conductive composites were then prepared by impregnating epoxy resin into the GF structure. The three-dimensional GF thermal conductive path improves the thermal conductivity to 8.04 W m−1 K−1 for a low graphene loading of 6.8 wt%, which corresponds to a thermal conductivity enhancement of about 4473% compared to neat epoxy. These results could provide new insights into the design and preparation of polymer composites with excellent heat-conducting properties that are promising for applications in electronic packaging, such as thermal interface materials, underfills and molding compounds.
Experimental
Materials
Polyurethane (PU) foam used for kitchen supplies was utilized in this work. Graphene nanoplatelets (GNPs) as the filler were supplied by Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences (China). A cycloaliphatic epoxy resin (6105) and the hardener of methyl-hexahydrophthalic anhydride (MHHPA) were obtained from Dow Chemicals (USA) and Shanghai Li Yi Science & Technology Development Co. Ltd (China), respectively. Neodymium(III) acetylacetonate trihydrate (Nd(III)acac) purchased from Aldrich Chemicals was used as a latent catalyst. All other chemicals were of analytical reagent grade and used without further purification.Preparation of GF/epoxy composites
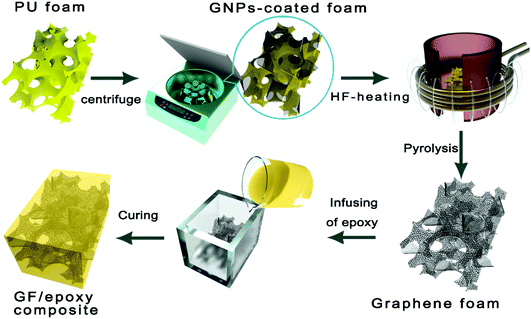
GNPs were firstly uniformly dispersed in ethanol through a general ultrasonic treatment. A pristine foam skeleton (about 2 × 2 × 2 cm3) diced from the commercial PU sponge was subsequently immersed and squeezed in the above dispersion. Followed by a suction filtration or centrifugation process, the foam was taken out and then dried. The above procedure was repeated several times to get different filler contents. The surface of the PU foam skeleton was assembled with graphene nanosheets after the above processes. The GNP-coated foam was rapidly pyrolyzed in the graphite crucible by medium frequency induction heating to completely decompose the polymer in 10 s and a free-standing graphene foam was obtained. A cycloaliphatic epoxy resin was mixed with its curing agent (MHHPA) with a ratio of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95 and degassed in a vacuum chamber at room temperature for 30 min. Then, the mixture solution was infused into GF. Finally, GF immersed in epoxy solution was degassed and cured by a typical curing process and a bulk-like GF/epoxy composite was obtained. The overall preparation procedure of GFs and their impregnation with epoxy resin are carried out as shown in Fig. 1. Compared to the widely used CVD-based methods, the proposed GNP-coated foam strategy in this work provides a simple and scalable fabrication of GF. The GF was encapsulated by epoxy resin to prepare the epoxy composites, denoted as the GF/epoxy composite.
95 and degassed in a vacuum chamber at room temperature for 30 min. Then, the mixture solution was infused into GF. Finally, GF immersed in epoxy solution was degassed and cured by a typical curing process and a bulk-like GF/epoxy composite was obtained. The overall preparation procedure of GFs and their impregnation with epoxy resin are carried out as shown in Fig. 1. Compared to the widely used CVD-based methods, the proposed GNP-coated foam strategy in this work provides a simple and scalable fabrication of GF. The GF was encapsulated by epoxy resin to prepare the epoxy composites, denoted as the GF/epoxy composite.
Characterization
The morphology was obtained using field emission scanning electron microscopy (FE-SEM, QUANTA FEG250, USA) at an acceleration voltage of 10 kV. Raman spectroscopy was performed on a Renishaw inVia Reflex with a laser wavelength of 532 nm (RENISHAW plc, Wotton-under-Edge, UK). Fourier transform infrared spectroscopy (FT-IR) was performed on a Nicolet 6700 spectroscopy (Thermo Fischer Scientific, USA). X-Ray diffraction patterns (XRD, D8 Advance, Bruker AXS, Germany) were used to analyze the matter phase of GNP-coated foam and GF. The optical micrograph (OM) image was captured using an optical microscope (OM, Leica DM2500 M, Germany). Thermal diffusivity (TD) of the composites was measured by the laser flash method using an LFA 447 Nanoflash apparatus (NETZSCH, Germany) at room temperature and at gradual temperature for the specific heat. Thermal conductivity λ (W m−1 K−1) was calculated as a multiplication of thermal diffusivity (α, mm2 s−1), specific heat (Cp, J g−1 K−1), and density (ρ, g cm−3). Namely, λ = α × Cp × ρ. For the heating and cooling cycle test, the composite and neat epoxy were heated up to 100 °C with 5 °C min−1 and cooled to room temperature naturally. Thermal imaging analysis was performed using a hand-held infrared camera (Fluke, Ti400, USA). A smart digital multimeter (UNI-T, UT71B, Hongkong, China) with a thermocouple probe was used to collect real-time temperature data of the samples in the Thermal imaging analysis. Thermogravimetric analysis (TGA) was carried out using a NETZSCH TG-209 (NETZSCH, Germany). The temperature range was from 30 to 800 °C at a ramp rate of 10 °C min−1 under a nitrogen atmosphere.Results and discussion
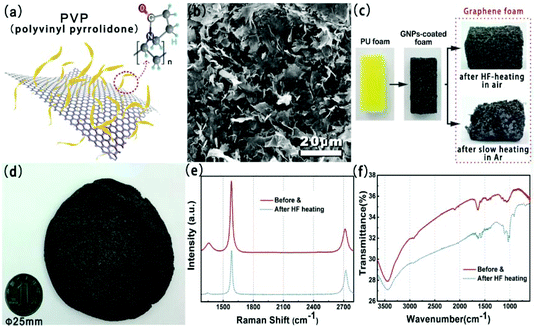
Fig. 2(a) shows the chemical structures of polyvinyl pyrrolidone (PVP) and the schematic illustration of the PVP-functionalized graphene powder. The SEM image for the prepared GPNs is shown in Fig. 2(b). GNPs have a laminar configuration and a flaky sheet structure in shape. In order to obtain the size distribution of the GNPs, the optical microscopy image and high magnification SEM image of GNPs are presented in Fig. S1(a) and S1(b),† respectively. The average lateral size and average thickness of GNPs are around 5.4 ± 0.3 μm and 10.6 ± 0.3 nm, which we calculated.22,23Fig. 2(c) shows the optical image of pristine PU foam, the GNP-coated foam and the GF. Complete three-dimensional GF could not be obtained after slow heating whether under a protective atmosphere or air. The skeleton remains unscathed after decomposition suffering rapid high-frequency induction heating, which reveals the advantage of this heat treatment process in comparison with other heat-treatment methods (shown in Fig. S2†). Fig. 2(d) presents the photographs of large scale GF. Raman and XRD spectra of GNPs obtained before and after HF-heating treatment are shown in Fig. 2(e) and Fig. S1(c),† respectively. In Raman spectra, the D band at near 1350 cm−1, which corresponds to the defects in the graphene unit, obviously decreased after HF heating. This result suggest that the nanostructure defects of graphene were partly restored via HF heating, which could also enhance thermal conductivity of GNPs. Fig. 2(f) shows the FT-IR spectra of GNPs obtained before and after HF-heating treatment. The peak at 3437 cm−1 is attributed to the O–H stretching mode of H2O absorbed on the surface of the sample. Peaks between 1250 and 1650 cm−1 correspond to the C–N stretching motion and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching motion of PVP, as can be seen in the FT-IR spectra of GNPs before HF heating.24,25 The TGA result of the GNP powder is shown in Fig. S1(d).† There were two main weight loss steps for the pristine GNPs, one of which, at around 200–350 °C, was from the decomposition of oxygen-containing functional groups on the GNPs and the other, at around 350–800 °C, was from the thermal decomposition of the PVP and GNP structure.26
O stretching motion of PVP, as can be seen in the FT-IR spectra of GNPs before HF heating.24,25 The TGA result of the GNP powder is shown in Fig. S1(d).† There were two main weight loss steps for the pristine GNPs, one of which, at around 200–350 °C, was from the decomposition of oxygen-containing functional groups on the GNPs and the other, at around 350–800 °C, was from the thermal decomposition of the PVP and GNP structure.26
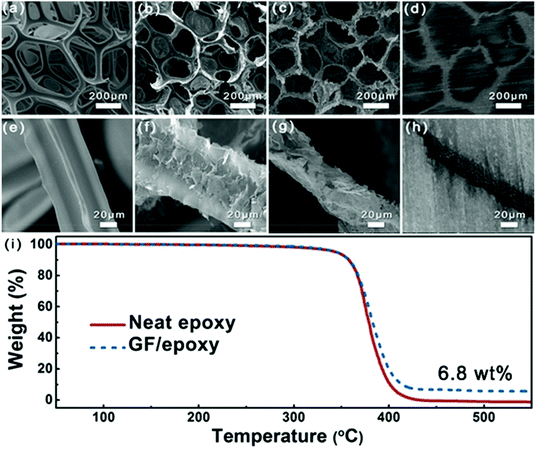
Fig. 3(a–h) show the SEM images of PU foam, GNP-coated foam, GF and GF/epoxy composite at different resolutions. Fig. 3(a) and (e) show the morphology of PU foam with an interconnected structure, which was used as a template for the fabrication of GF. Such a big average cellular size of the PU foam, which is approximately 300 μm, could ensure that a low graphene content maximized the mechanical properties of the polymer matrix. Fig. 3(b) and (f) show the morphology of GNP-coated PU foam. It is apparent that GNPs evenly covered the skeleton of PU foam. Meanwhile, only a thin layer of GNPs was coated on the PU foam and it maintains the maximum extent possible for the mechanical properties of the composite. Fig. 3(c) and (g) display the microstructure of GF after removing the PU template via HF heating. It can be clearly seen that the GF maintains the cellular structure of the PU framework. Interconnected GNPs constitute the skeleton of the GF and construct an effective thermal conductive path, which is the key for the high thermal conductivity of the composites. Meanwhile, amorphous carbon from the pyrolysis of PVP reduces the interfacial thermal resistance.27 After impregnating with epoxy, low- and high-magnification cross-sectional SEM images of the GF/epoxy composite with 6.8 wt% graphene loading after polishing can be seen in Fig. 3(d) and (h). The cellular graphene structure in the matrix reveals that GF is interconnected through the epoxy matrix. In addition, GF and epoxy exhibit excellent interfacial compatibility, and no obvious pore or debonding is observed, as can be seen in Fig. S3.† The well-maintained cellular GF framework and good interfacial binding are the key factors for the high thermal conductivity of the GF/epoxy composite at a low filler content. The GNP content in the composite can be investigated from the TGA result, as can be seen in Fig. 3(i). It can be seen that neat epoxy totally decomposed after 440 °C. Meanwhile, GNPs will not lose weight below 800 °C under a N2 atmosphere. Therefore, the GNP content in the GF/epoxy composite was calculated by comparing the weight loss in neat epoxy and the GF/epoxy composite after 440 °C, which is noted to be 6.8 wt%. The construction of an efficient phonon transport path at such a low GNP content can be attributed to the support of the porous PU foam template.
In order to evaluate the effect of different GNP contents and temperatures on the heat transfer ability of the composites, the thermal diffusivity of GF/epoxy composites with various GNP loadings was measured using the laser flash method and the results are shown in Fig. 4(a) and (b). Detailed information on test principles can be seen in the ESI.† Both thermal diffusivity and thermal conductivity increased with GNP loading, as expected. Meanwhile, there exists an obvious thermal percolation threshold between 3.03 and 4.05 wt%. Below the percolation threshold, GNPs, which are interconnected with amorphous carbon from the pyrolysis of PU and PVP, do not reveal sufficient contact between GNPs. Therefore, the thermal conductivity of the GF/epoxy composites exhibits lower speed under the thermal percolation threshold. Once the GNP content reached the percolation threshold, the sharp increase in thermal conductivity illustrated the construction of continuous three-dimensional GNP foam. Above the thermal percolation threshold, the thermal conductivity of the GF/epoxy composites demonstrates a higher growth ratio and the thermal conductivity of the composite reaches 8.04 W m−1 K−1 at a GNP content of only 6.8 wt%. The thermal diffusivity of epoxy and GF/epoxy composites with various GNP contents reduced as temperatures increased, as shown in Fig. 4(b). In epoxy and epoxy composites, thermal resistivity is dominated by Umklapp processes, and therefore, the temperature increase will lead to a reduction of the mean free phonon path length, causing a decrease in thermal diffusivity.38Fig. 4(c) shows the 15 heating and cooling cycles for neat epoxy and the GF/epoxy composite with 6.8 wt% between 25 and 100 °C. Both of them reveal a small deviation, suggesting the stable capability of heat conduction after long-term device operation. Fig. 4(d) shows the thermal conductivity comparison and TCE of the solution blending prepared GNP/epoxy and GF/epoxy composites at the same GNP loading. As can be clearly seen in Fig. 4(e), GNPs randomly dispersed in the GNP/epoxy composite, and GNPs could not interconnect at such a low filler content, which is far from reaching the thermal percolation threshold. Therefore, the thermal conductivity of the GNP/epoxy composite is only 0.85 W m−1 K−1 with 387% TCE compared to that of neat epoxy. As for the GF/epoxy composite, GNPs could easily reach the thermal percolation threshold with the help of the porous PU template. A thin layer GNP coated on the PU foam could construct continuous cellular GF after removing the PU template. Interconnected GNPs provide an efficient heat transfer path, and amorphous carbon from PVP could also reduce the interface thermal resistance, as shown in Fig. 4(e). All these factors result in a high thermal conductivity up to 8.04 W m−1 K−1 of GF/epoxy at only 6.8% fillers. Fig. 4(f) illustrates the comparison of thermal conductivity of the GF/epoxy composite with other graphene-epoxy composites. It is apparent that our GF/epoxy has the highest thermal conductivity at various graphene loadings below 10 wt%.18,20,26,28–37 This cellular PU template provides an ideal framework of GNPs, which converts the Kapitza resistance from the heat transport path in the composite to graphene–graphene contact resistance. The graphene–graphene contact resistance is related to the thermal conductive barrier at the contact surface of the same phonon density of state which shows a significantly lower level than Kapitza resistance between graphene and the matrix.39 Therefore, GF in the epoxy matrix could observably reduce the thermal percolation threshold skeleton that is kept in this posture with the assistance of amorphous carbon from PVP after removing PU at a high GNP loading. These interconnected flatting structures greatly utilize the axial of the composite. Otherwise, because graphene is thermal conductive anisotropic, interconnected flatting GNPs on the PU greatly utilize the axial high thermal conductivity of GNPs and significantly enhance the thermal conductivity of the epoxy matrix with a TCE surpassing 4400%.
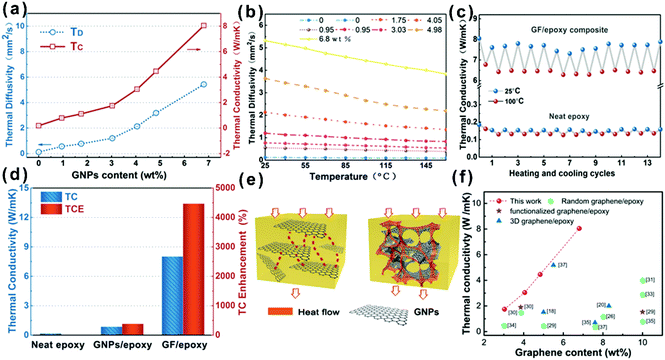 | ||
| Fig. 4 (a) Thermal conductivity (TC) and thermal diffusivity (TD) of the GF/epoxy composite. (b) Experimentally determined dependence of thermal diffusivity on temperature for the GF/epoxy composite with different loading contents. (c) Thermal conductivity upon multiple heating and cooling cycles for the GF/epoxy composite and neat epoxy. (d) Thermal conductivity and TCE of neat epoxy, the GNP/epoxy composite, and the GF/epoxy composite. (e) Heat conduction model of the GNP/epoxy and GF/epoxy composites. (f) Comparison of thermal conductivity of the GF/epoxy composite with other graphene-epoxy composites.18,20,26,28–37 | ||
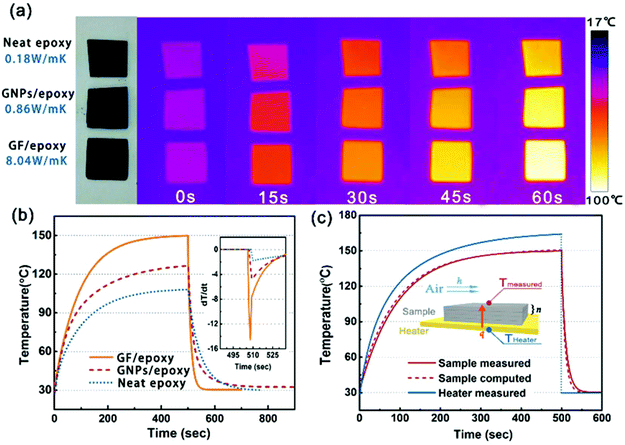
In order to visually verify and compare the thermal transport performance of neat epoxy, the GNP/epoxy composite and the GF/epoxy composite, an infrared camera was used to record temperature distribution of the composites and neat epoxy, as shown in Fig. 5(a). Samples were placed on an alumina heater in the order of neat epoxy, GNP/epoxy composite and GF/epoxy composite. The surface temperature of the hot plate increased from room temperature to 150 °C. It is obvious that the surface temperature of GF/epoxy increased the fastest. After 30 s, the surface temperatures of neat epoxy, the GNP/epoxy composite and the GF/epoxy composite were 55, 65 and 71.4 °C, respectively. Another 30 s later, they reach 80, 94.3 and 104.3 °C, respectively, suggesting that the thermal transport ability of epoxy is greatly enhanced by introducing GF and GNPs. Furthermore, GF reveals much efficient enhancement than GNPs at the same filler content. The quantitative temperature heating and cooling process is recorded to further demonstrate the effect on thermal conductive performance, displayed in Fig. 5(b). A system with a hot plate, a thermocouple element and a versatile voltmeter are employed. In the heating region, GNP/epoxy and GF/epoxy display a much faster and higher temperature rise than neat epoxy, which is a bad thermal conductor. The GF/epoxy composite exhibits the fastest temperature increase ratio and the highest temperature value at any moment. In the cooling region, the temperature of both the composites drops faster than neat epoxy and GF/epoxy shows the highest cooling ratio, as can be seen in Fig. 5(b), particularly, with differential treatment ranging from 485 to 535 s shown in the inset of Fig. 5(b). This result further proves the high efficiency of heat transfer by the interconnected cellular graphene. Based on the classic thermoelastic theory and computational method, we can get the sample computed line shown in Fig. 5(c) and Fig. S4.† In the simulation, the thermal conduction model can be considered as an unsteady one-dimensional heat transfer in a flat solid body without inner heat sources under the third boundary conditions, as shown in the inset in Fig. 5(c). The computed lines of the sample are obtained using the time forward difference and interpolation method. The temperature on the top surface is expressed by the following formula:
| Tk+1i = f*Tki+1 + (1 − 2*f)*Tki + f*Tki−1, | (1) |
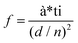 | (2) |
Conclusions
In summary, a novel epoxy composite with significant thermal conductivity enhancement efficiency was prepared by infiltrating 3D GF with epoxy resin. An ultrahigh thermal conductivity of 8.04 W m−1 K−1 was obtained at a low graphene loading of 6.8 wt%, which corresponds to a thermal conductivity enhancement of about 4473% compared to neat epoxy. The presented GF and its polymeric composites have excellent heat-conducting properties that are promising for applications in electronic packaging, such as thermal interface materials, underfills, and molding compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the financial support of the National Natural Science Foundation of China (51573201), the NSFC-Zhejiang Joint Fund for the Integration of Industrialization and Informatization (U1709205), the Public Welfare Project of Zhejiang Province (2016C31026), The Scientific Instrument Developing Project of the Chinese Academy of Sciences (YZ201640), the Project of the Chinese Academy of Sciences (KFZD-SW-409), and the Science and Technology Major Project of Ningbo (2016S1002 and 2016B10038). We also thank the Chinese Academy of Sciences for the Hundred Talents Program, the Chinese Central Government for the Thousand Young Talents Program, and the 3315 Program of Ningbo.References
- Y. Guo, C. Dun, J. Xu, J. Mu, P. Li, L. Gu, C. Hou, C. Hewitt, Q. Zhang, Y. Li, D. Carroll and H. Wang, Small, 2017, 13, 1702645 CrossRef PubMed.
- N. Wang, M. Samani, H. Li, L. Dong, Z. Zhang, P. Su, S. Chen, J. Chen, S. Huang, G. Yuan, X. Xu, B. Li, K. Leifer, L. Ye and J. Liu, Small, 2018, 14, 1801346 CrossRef PubMed.
- H. Chen, V. Ginzburg, J. Yang, Y. Yang, W. Liu, Y. Huang, L. Du and B. Chen, Prog. Polym. Sci., 2016, 59, 41–85 CrossRef CAS.
- Y. Yao, J. Sun, X. Zeng, R. Sun, J. Xu and C. Wong, Small, 2018, 14, 1704044 CrossRef PubMed.
- D. L. Nika and A. A. Balandin, Rep. Prog. Phys., 2017, 80, 036502 CrossRef PubMed.
- M. Wang, Z. Jiao, Y. Chen, X. Hou, L. Fu, Y. Wu, S. Li, N. Jiang and J. Yu, Composites, Part A, 2018, 109, 321–329 CrossRef CAS.
- F. Kargar, Z. Barani and R. Salgado, ACS Appl. Mater. Interfaces, 2018, 10, 37555–37565 CrossRef CAS PubMed.
- F. Kargar, Z. Barani and M. Balinskiy, Adv. Electron. Mater., 2019, 5, 1800558 CrossRef.
- X. Wang and P. Wu, Chem. Eng. J., 2018, 348, 723–731 CrossRef CAS.
- A. Xie, Y. Wang, P. Jiang, S. Li and X. Huang, Compos. Sci. Technol., 2018, 154, 154–164 CrossRef CAS.
- K. Wu, J. Fang, J. Ma, R. Huang, S. Chai, F. Chen and Q. Fu, ACS Appl. Mater. Interfaces, 2017, 9, 30035–30045 CrossRef CAS PubMed.
- F. An, X. Li, P. Min, H. Li, Z. Dai and Z. Yu, Carbon, 2018, 126, 119–127 CrossRef CAS.
- S. Ramirez, K. Chan and R. Hernandez, Mater. Des., 2017, 118, 75–80 CrossRef CAS.
- J. Lewis, Z. Barani and A. S. Magana, Mater. Res. Express, 2019, 6, 085325 CrossRef.
- C. Yuan, B. Duan, L. Li, B. Xie, M. Huang and X. Luo, ACS Appl. Mater. Interfaces, 2015, 7, 13000–13006 CrossRef CAS PubMed.
- L. Shao, L. Shi, X. Li, N. Song and P. Ding, Compos. Sci. Technol., 2016, 135, 83–91 CrossRef CAS.
- M. Loeblein, R. Tay, S. Tsang, W. Ng and E. Teo, Small, 2014, 10, 2992–2999 CrossRef CAS PubMed.
- Z. Liu, D. Shen, J. Yu, W. Dai, C. Li, S. Du, N. Jiang, H. Li and C. Lin, RSC Adv., 2016, 6, 22364–22369 RSC.
- G. Lian, C. Tuan, L. Li, S. Jiao, Q. Wang, K. Moon, D. Cui and C. Wong, Chem. Mater., 2016, 28, 6096–6104 CrossRef CAS.
- X. Shen, Z. Wang, Y. Wu, X. Liu, Y. He, Q. Zheng, Q. Yang, F. Kang and J. Kim, Mater. Horiz., 2018, 5, 275–284 RSC.
- C. Tang, B. Li, Q. Zhang, L. Zhu, H. Wang, J. Shi and F. Wei, Adv. Funct. Mater., 2016, 26, 577–585 CrossRef CAS.
- F. Alam, J. Yu, D. Shen, W. Dai, H. Li, X. Zeng, Y. Yao, S. Du, N. Jiang and C. Lin, Polymers, 2017, 9, 662 CrossRef PubMed.
- F. Alam, W. Dai, M. Yang, S. Du, X. Li, J. Yu, N. Jiang and C. Lin, J. Mater. Chem. A, 2017, 5, 6164–6169 RSC.
- H. Reveron, C. Elissalde, C. Aymonier, C. Bousquet, M. Maglione and F. Cansell, Nanotechnology, 2006, 17, 3527–3532 CrossRef CAS PubMed.
- X. Lu, L. Li, W. Zhang and C. Wang, Nanotechnology, 2005, 16, 2233–2237 CrossRef CAS PubMed.
- Y. Wang, J. Yu, W. Dai, Y. Song, D. Wang, L. Zeng and N. Jiang, Polym. Compos., 2015, 36, 556–565 CrossRef CAS.
- J. Ma, X. Zhou, S. Ding and Z. Liu, RSC Adv., 2017, 7, 15469–15474 RSC.
- S. Wang, M. Tambraparni, J. Qiu, J. Tipton and D. Dean, Macromolecules, 2009, 42, 5251–5255 CrossRef CAS.
- S. Song, K. Park, B. Kim, Y. Choi, G. Jun, D. Lee, B. Kong, K. Paik and S. Jeon, Adv. Mater., 2013, 25, 732–737 CrossRef CAS PubMed.
- C. Teng, C. Ma, C. Lu, S. Yang, S. Lee, M. Hsiao, M. Yen, K. Chiou and T. Lee, Carbon, 2011, 49, 5107–5116 CrossRef CAS.
- Y. Fu, Z. He, D. Mo and S. Lu, Int. J. Therm. Sci., 2014, 86, 276–283 CrossRef CAS.
- F. Wang, L. Drzal, Y. Qin and Z. Huang, J. Mater. Sci., 2015, 50, 1082–1093 CrossRef CAS.
- K. Shahil and A. Balandin, Nano Lett., 2012, 12, 861–867 CrossRef CAS PubMed.
- F. Wang, L. Drzal, Y. Qin and Z. Huang, Composites, Part A, 2016, 87, 10–22 CrossRef CAS.
- H. Kim, H. Bae, J. Yu and S. Kim, Sci. Rep., 2016, 6, 26825 CrossRef PubMed.
- C. Liang, H. Qiu, Y. Han, H. Gu, P. Song, L. Wang, J. Kong, D. Cao and J. Gu, J. Mater. Chem. C, 2019, 7, 2725–2733 RSC.
- H. Hou, W. Dai, Q. Yan, L. Lv, F. Alam, M. Yang, Y. Yao, X. Zeng, J. Xu, J. Yu, N. Jiang and C. Lin, J. Mater. Chem. A, 2018, 6, 12091–12097 RSC.
- P. Li, X. Zhen, L. Zheng, G. Yan, L. Peng and G. Chao, Adv. Mater., 2017, 29, 1700589 CrossRef PubMed.
- Y. Su, J. Li and G. Weng, Carbon, 2018, 137, 222–233 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr03968f |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |