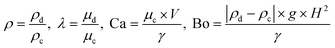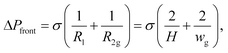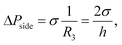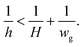Grooved step emulsification systems optimize the throughput of passive generation of monodisperse emulsions

Abstract

Microfluidic step emulsification passively produces highly monodisperse droplets and can be easily parallelized for high throughput emulsion production. The two main techniques used for step emulsification are: i) edge-based droplet generation (EDGE), where droplets are formed in a single, very wide and shallow nozzle, and ii) microchannel emulsification (MCE), where droplets are formed in many separated narrow nozzles. These techniques differ in modes of droplet formation that influence the throughput and monodispersity of produced emulsions. Here we report a systematic study of novel grooved step emulsifying geometries, a hybrid of MCE and EDGE architectures. We introduce partitions of different heights to a wide (EDGE-like) slit to establish optimal geometries for high-throughput droplet production. We demonstrate that the volume and monodispersity of the produced emulsion can be tuned solely by changing the height of these partitions. We show that the spacing of the partitions influences the size of the produced droplets, but not the population monodispersity. We also determine the moment of transition between two distinct droplet generation modes as a function of the geometrical parameters of the nozzle. The optimized grooved geometry appears to combine the advantages of both MCE and EDGE, i.e. spatial localization of droplet forming units (DFUs), high-throughput formation of tightly monodisperse droplets from parallel DFUs, and low sensitivity to variation in the flow rate of the dispersed phase. As a proof-of-concept we show grooved devices that for a 260-fold increase of flow rate produce droplets with volume increased by just 75%, as compared to 91% increase in volume over a 180-fold increase of flow rate of the dispersed phase in MCE devices. We also present the optimum microfluidic device geometry that almost doubles the throughput of an MCE device in the generation of nanoliter droplets.

---

Introduction

In this paper we report on the interplay between a wide range of geometries of a step emulsification microfluidic device and the quality of droplet formation. We identify the key parameters that optimize passive emulsification of nanoliter-sized droplets and present devices that outperform state-of-the-art chips.

Emulsions, metastable systems of droplets dispersed in an immiscible fluid, are of high interest to many industries, especially cosmetic, food and pharmaceutical companies.^1–4 The key requirements for industrial-scale emulsifiers are minimal cost of their operation and the quality of the emulsion. Droplet monodispersity is a crucial parameter of droplet libraries, because highly monodisperse droplet populations are not only less prone to degradation, via e.g. Ostwald ripening,⁵ but also allow maintaining of the reproducibility of the experiments on multiple separate compartments.^6–8

A number of emulsification techniques, such as rotor–stator, high pressure or ultrasonic homogenization, are used to generate emulsions on an industrial scale. While these techniques allow high throughput of the process, the size distribution of the emulsion is rather high (CV > 20%). Droplet microfluidics – an interdisciplinary field of science that deals with controlled manipulation of discrete portions of fluids suspended in immiscible fluids in microdevices^8,9 – is a powerful tool to produce highly monodisperse emulsions containing one to trillions of pico- or nanoliter droplets.^10,11 Droplet microfluidics allows minimization of the time and resources required to perform typical laboratory assays when compared to batch methods.^9,12

Encapsulation of various objects in droplets provided the possibility to use droplet microfluidic systems in high-throughput screening, both in research and industry. Biological research is a staple application field of droplet systems: starting from digital assays (e.g. droplet digital PCR¹³), through drug-discovery research (e.g. determination of effective antibiotic treatments¹⁴) to performing operations on single cells (e.g. high-throughput single cell genome sequencing¹⁵). The high-throughput capabilities of droplet microfluidics have not only biological research benefits, but have also found use in industrial applications such as production of a variety of materials, including functional materials (e.g. biodegradable, magnetically or temperature-responsive microparticles¹⁶) and monodisperse micro- and nanoparticles,¹⁷ as well as capsules that can be loaded with various active ingredients.¹⁸

From the point of view of how the droplets are generated, droplet microfluidic devices can be generally divided into active and passive.⁷ In active devices, both the droplets and the continuous phases are continuously pressed through a droplet generation junction (e.g. a T-junction¹⁹ or a flow-focusing junction²⁰). The main feature of the active droplet generators is that the volume of the droplets depends on the flow rates of both phases.^21,22 While this allows tuning of the droplet volume and parallelized active systems can be engineered to generate emulsions at kg h⁻¹ rates, the dependence of the droplet volume on the flow rates is a disadvantage in mass production. Even small fluctuations in the flow rates or in the distribution of resistance in the channels may spoil the otherwise highly monodisperse character of the emulsion.²³ Passive devices are primarily dependent on the geometry of the droplet generating units and allow large variation of the flow rate of the dispersed phase, with minimum impact on the droplet volumes.^24,25

For less stringent requirements on the input flow and higher robustness, passive emulsification methods are fundamentally better suited for mass production. Step emulsification is a popular and widely used passive emulsification method due to its simplicity of fabrication and parallelization.²⁶ Recently, a lot of effort has been put into developing new geometrical variants of step emulsification devices (so-called step emulsifiers) that may increase the throughput of droplet formation. Some solutions change the geometry of a single step emulsifier in order to decouple the dependency of the droplet size from the flow rate of the droplet phase.^25,27 Another approach is to parallelize a large number of step emulsifiers in one microfluidic device, as shown e.g. in the ‘millipede’ device²⁸ or in an up-scaled microchannel emulsifier.²⁹

Two well-known passive emulsification methods are microchannel emulsification (MCE)³⁰ and edge-based droplet generation (EDGE),^31,32 both shown in Fig. 1. MCE employs one up to thousands of independent droplet forming units (DFUs), microchannels with a rectangular cross-section that enter the deep outer phase reservoir.^25,29,33 The aspect ratio of the channel width to height is relatively small, in the order of ∼1–10.²⁹ DFU positions are fixed, as microchannels are separated by solid walls. Each DFU operates independently and the process is highly reproducible. MCE produces highly monodisperse emulsions for low droplet phase flow rates. When a critical flow rate is reached, the droplet size and dispersion sharply rise.^33–35 The EDGE geometry features a single, wide channel with a shallow slit, which enters the deep reservoir filled with the continuous phase. The emulsifying channel has a high aspect ratio of width to height, as it can exceed 100.³¹ The wide channel results in a wide channel–reservoir junction, along which the droplet phase splits into droplets in multiple places (DFUs). An EDGE system self-tunes the number and position of the DFUs and allows for reaching higher flow rates than MCE systems.³⁶ Constant self-adjustment of the positions of the DFUs dynamically changes the conditions during the droplet formation process. Thus, the polydispersity of produced droplet populations is higher than that in MCE devices.⁷

Fig. 1 A. Difference between step emulsifiers based on the height of the partition between droplet forming units. From left to right: Microchannel emulsification module (MCE), our grooved device, EDGE-based emulsification module. B. Front view of the render of the grooved device showing the operation of the microchip. Aqueous droplets (blue) are produced when extruded from a slit to the reservoir filled with the continuous phase (transparent); w – width of the emulsifying slit. C. Scheme of the geometrical parameters in the grooved geometry: h – height of the partition, H – height of the groove, L_g – width of the partition, w_g – width of the groove, w – width of the device.

In this paper we investigate the transition between two well-established step emulsification techniques: MCE and EDGE. To the best of our knowledge, no work has been previously undertaken to explain why two step emulsifying techniques yield droplets in different modes, where the transition point between those modes is observed, and what the optimal wide step emulsification geometry is. We identify the source of the transition between the two modes in the geometry of the emulsifying slit. Testing a wide range of geometrical variants allowed us to design and characterize a new type of geometry: the grooved step emulsifier (Fig. 1). This architecture combines the advantages of EDGE and MCE, i.e. producing droplets at a high throughput with a narrow size distribution. Moreover, grooved devices show lower dependence on the flow rate than the compared MCE and EDGE geometries. The principles of droplet formation and sensitivity to the flow rate are hardwired in the geometry of the devices. The grooved geometry allows fine tuning of the interplay between the emulsion monodispersity, size, and device throughput at the level of device fabrication. As a result, we deliver devices that produce monodisperse emulsions of known volume independent of the flow rate of the to-be-dispersed phase.

Results

Investigated parameters

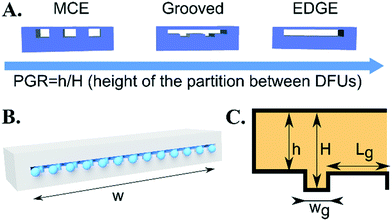
In our research, we investigated the influence of the geometry of the device on the droplet formation and introduced a number of geometrical parameters, such as the groove width (w_g) and height (H), partition width (L_g) and height (h) and device total width (w). The used fluids (droplet phase – labeled with subscripts d, continuous phase – labeled with subscripts c) are characterized by their viscosities (μ_d, μ_c), densities (ρ_d, ρ_c), to-be-dispersed phase flow rate (Q), and interfacial tension (γ). Independent parameters that could be investigated in this work form multidimensional space that is virtually impossible to fully scan.

We chose two geometrical parameters to scan: i) the partition to groove ratio, 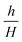, and ii) distance between grooves, 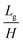(for more details see the ESI†). These parameters offer insight into the influence of the height and spacing of the grooves and the height of partitions between them on droplet formation. Fluid parameters such as densities, viscosities, interfacial tension, and flow rate enter hydrodynamic equations through four dimensionless independent parameters: density ratio ρ, viscosity ratio λ, bond (Eötvös) number Bo, and capillary number Ca:

where V is the characteristic speed of the fluid [m s⁻¹], and g is the gravitational acceleration [m s⁻²].

Microfluidic experiments are performed for a small bond number – in our case Bo ≈ 0.002. It means that the emulsification process is governed by surface tension, not gravity. As a consequence we did not scan fluid densities.

The capillary number defines the ratio of viscous to interfacial forces. It can be used to determine the mode of droplet formation, whether they are produced in the dripping or jetting regime. The value of Ca for which the regime changes is called the critical capillary number (Ca_cr).³⁵ Since the interfacial tension, viscosity and flow rate are part of the capillary number, therefore scanning over one of these parameters is equivalent to scanning all of them. This is why the scan of the devices over the flow rate of the to-be-dispersed phase is equivalent to the scan over the interfacial tension and viscosity of the continuous phase (for other parameters fixed). In the ESI,† we also included a test of fluids of different viscosities, confirming our assumptions (see Fig. S1†).

Geometry of the devices

We modify the droplet-generating step by introducing elevations (partitions) along the length of the slit (Fig. 1A): from no partitions (EDGE), through semi-full partitions (grooves), to full floor-to-ceiling partitions (MCE). The key parameter is referred to as the partition-to-groove ratio (PGR). It describes the ratio of the height of the partition to the height of the channel (PGR = h/H, h – height of the partition; H – height of the channel, see Fig. 1C). The PGR ranges from 0 (MCE, full partitions, h = 0) to 1 (EDGE, no partitions, h = H).

In our experiments, we used a range of devices with different heights of partitions. We investigated narrow devices (step width w = 1.1 mm) that produced one droplet at a time and wide devices (step width w = 15 mm) that featured multiple DFUs. The height (H) and width (w_g) of the grooves were kept constant at 100 and 120 μm, respectively. The partition height (h) and width (L_g) varied across experiments.

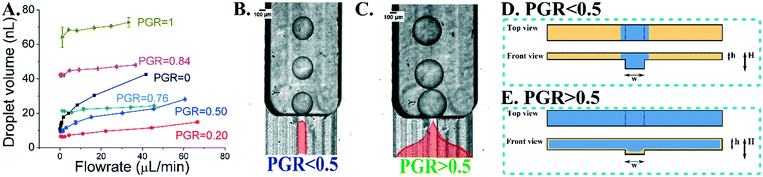
PGR determines the mode of droplet generation

In the first set of experiments, we tested devices with narrow channels (w = 1.1 mm), comprising a single groove surrounded by elevated partitions. The devices differed only by the height of the partition, with their PGR value changing from 0 to 1. We observed that the volume of the droplet is correlated with the device PGR value, e.g. the change of the PGR from 0.2 to 1 causes the droplet volume to increase approximately 6 times (see Fig. 2A). In systems with shallow partitions around the groove (PGR from 0 to 0.5), we observed that the droplet phase remains within the groove and the emulsification yields droplets of small volume (see Fig. 2B). We called this mode of operation of the device an ‘in-groove’ droplet generation mode.

Fig. 2 Droplet production in microfluidic devices with a single groove. The height of all of the channels and grooves is H = 100 μm, and the width is w_g = 120 μm. A: Droplet size as a function of the droplet phase flow rate for devices with various PGRs and a single groove. B and C: Spreading of the droplet phase over the partition for different PGR values (scale bar 100 μm). D and E: Schematic representation of the in-groove (D) and spilled (E) droplet phase. H is the height of the groove, h is the height of the partition, and w_g is the width of the groove.

In the second case, for devices with PGR > 0.5, the droplet phase plug is not confined to the groove but spreads onto the partitions. We called this second mode a ‘spilt-groove’ droplet generation mode (see Fig. 2C). In the in-groove mode, the volume of the generated droplet is more affected by the volumetric flow rate than in the spilt-groove mode – for PGR = 0.76 the volume of the produced droplets is almost constant for the investigated flow rates (see Fig. 2A).

PGR controls the monodispersity of droplets and the rate of generation

We investigated how the introduction of grooves impacted the droplet generation of parallelized DFUs. We tested wide step emulsifiers with multiple DFUs (15 mm long emulsifying edge with 23 grooves for L_g = 0.5 mm, and 17 grooves for L_g = 0.75 mm). The height of the partition was varied resulting in PGRs ranging from 0 to 1. The sizes of the droplets were measured in the dripping mode,³⁷ which corresponded to flow rates of 5–1300 μL min⁻¹ (0.3–78.0 mL h⁻¹), unless transition to the jetting mode occurred at a lower flow rate (see Fig. 3). We observed that the manipulation of the PGR and flow rates visibly impacts the size and monodispersity of emulsions. In the wide microfluidic chips, the increase of the PGR is followed by the increase of the average size of the droplet, slowly for a PGR close to 0, and very fast for a PGR over 0.5 (Fig. 3 and S2†). Reducing the PGR from 1 to 0.2 decreases the volume of produced droplets by a factor of 6, exactly like in the case of the single-groove devices (Fig. 3 and 2A, respectively). Despite this, narrow devices of the same PGR produce ca. 2 times smaller droplets than wide chips. For example, for PGR = 0.5 and a flow rate of 30 μL min⁻¹, we obtain ∼20 nL and ∼39 nL droplets for narrow and wide devices, respectively.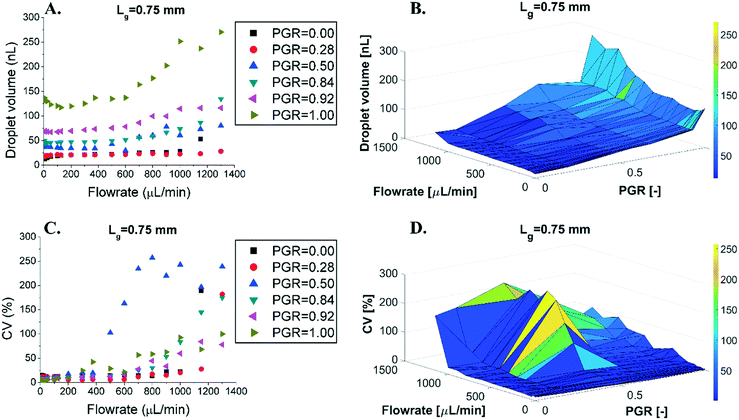

Fig. 3 Droplet size (A and B) and droplet dispersion reported as the CV of the droplet volume (C and D) as a function of the flow rate of the droplet phase for devices with L_g = 0.75 mm. Data for other devices can be found in the ESI† (Fig. S1 and S2).

Monodispersity is measured by the coefficient of variation of droplet population sizes, CV (CV = SD_size/d_size × 100%, where SD_size is the standard deviation of the droplet size and d_size is the mean of the droplet size, either volume or diameter; CV_diameter = 1% corresponds to CV_volume = 3%). Devices with PGR = 0–0.3 exhibited a very wide range of flow rates at which the CV_volume was <10% (CV_diameter < 3.3%), with a sharp increase of the polydispersity when reaching a certain threshold, around 1000 μL min⁻¹ (see Fig. 3 and ESI† Fig. S2 and S3). For devices with PGR = 0.5–1.0, the polydispersity rapidly increased at much smaller flow rates than those with small PGRs (around 500 μL min⁻¹) and for the highest tested flow rates large values were reached, up to CV_volume = 300% (see Fig. 3 and the ESI†).

The grooves not only affect the size and dispersion of the generated droplets, but also alter the dependence of the droplet size on the change of the flow rate. For PGR < 0.5, the droplet size changes with the flow rate much less than that for PGR > 0.5. Devices with PGR = 0.2 produce the smallest droplets, with the smallest monodispersity, and are the most resistant to variation in the flow rate for almost the whole range of the volumetric flow which we investigated.

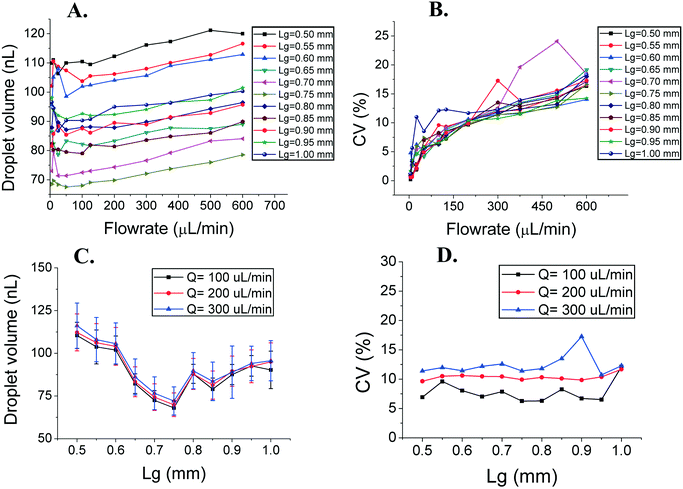
L _g controls the size, but not the dispersion of the emulsions

We studied the droplet size as a function of groove spacing, L_g. It is possible to normalize the L_g parameter by dividing it by the height of the groove, H. However, as H is kept constant, it wouldn't change the results except for transforming the data from dimensional to dimensionless units. We ran the experiments for PGR = 0.9 – in the spilt-groove mode. As shown in Fig. 4A, the droplet size depends on the flow rate and on L_g. The correlation between the change of L_g and droplet volume is not monotonic – there is a local minimum for L_g = 0.75 mm. For this value, droplets are the smallest for all flow rates (see Fig. 4C). The monodispersity of the droplets for every L_g is almost identical, usually CV_volume < 15% (CV_diameter < 5%). However, the dispersion of the produced emulsion increases with the increase of the flow rate of the droplet phase (see Fig. 4B and D).

Fig. 4 Droplet size (A) and droplet dispersion reported as the CV of the droplet volume (B) as a function of flow rates for varying DFU spacings, L_g. Droplet size (C) and dispersion of volumes (D) as a function of L_g for chosen flow rates. For all experiments, PGR = 0.9.

Discussion

Mechanism of step emulsification

In this work we expand the description of a quasi-static mechanism of step emulsification.^24,37 Briefly, the mechanism of droplet formation describes the interface shapes on the release of the droplet phase from the confined microchannel to a big reservoir. The quasi-static model assumes that at any given moment the interface is at equilibrium. When the head of the droplet phase expands after crossing the step, the Laplace pressure decreases in the head region. The pressure drop inflicts additional pull on the dispersed phase still in the confined microchannel and locally depletes the droplet phase faster than it is supplied by the applied flow. This leads to the formation of the so-called ‘neck’, a region where the interface is thinned. When the depletion of the droplet phase causes the interface to lose contact with all of the microchannel walls, the system is pushed out of equilibrium and the Rayleigh–Plateau instability snaps the droplet off.²⁴

Access of the continuous phase to the necking region is crucial for the droplet formation process. Increasing the access of the continuous phase and fixing the position of the necking region can be realized by adding side channels that deliver the continuous phase to the necking zone.^25,27 This leads to increased stability of the droplet size against variation of the flow rate over a wide range.²⁵ Here, we show that partitions of appropriate height may serve as bypasses and that their presence improves the performance of step emulsifiers.

To optimize the emulsifier parameters we systematically screened the geometries with varying partition dimensions. We observed two behaviors of the droplet phase stream which are associated with the geometry of the device. For small PGR values (<0.5), the dispersed phase prefers to stay in the grooved area, while for larger PGR values (>0.5) the droplet phase spreads over partitions (in detail in Fig. 2D). By calculating the Laplace pressures at the interface in the equilibrium configuration, we explained the reason for the transition as follows.

Droplet phase spreads over partitions for ΔP_front > ΔP_side

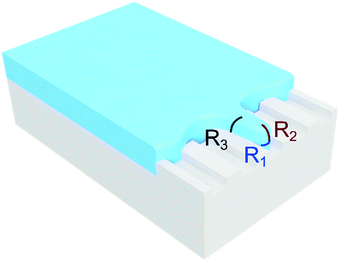
The Laplace pressure at the front tip of the droplet (ΔP_front) is calculated as in the case of a pancake-shape droplet squeezed inside a microchannel (see Fig. 5):
where w_g is the width of the droplet (yielding the radius of curvature R₂ = w_g/2), H is the microchannel height (yielding the radius of curvature R₁ = H/2), and σ is the interfacial tension. The Laplace pressure at the side of the droplet (ΔP_side) is calculated as in the case of a long and flat droplet invading a gap (partition) (see Fig. 5):
where h is the partition height (yielding the radius of curvature R₃ = h/2), and σ is the interfacial tension. From the pressure balance, the droplet phase spreads outside the groove only when the side Laplace pressure is smaller than the pressure at the front of the liquid thread,

ΔP_side < ΔP_front

Thus, the condition of spreading can be defined as

For w_g ≈ H, the condition for the droplet spreading out of the groove becomes

h > H/2,

which is the case we experimentally tested. Such spreading conditions match our observations that increasing the value of h (and consequently, PGR) over a certain threshold eventually enables expansion of the droplet phase over the partitions (see Fig. 2A).

As mentioned, the presence of the continuous phase next to the neck of a forming droplet facilitates droplet pinch-off and formation of highly monodisperse droplet populations. Hence, the geometrical structures facilitating the contact of the neck of the droplet phase with the continuous phase promote the monodispersity of the produced droplets by influencing the hydrodynamics of the droplet formation process. Depending on the PGR, partitions of our geometries may act as: i) bypasses constantly supplying the outer phase to the necking point for the in-groove (MCE-like) mode, or ii) storage rooms for more droplet phase to accumulate before each droplet formation process for the spilt (EDGE-like) mode. That is why for the in-groove mode, the produced droplets were more monodisperse and smaller than emulsions from devices operating in the spilt-mode.

Fig. 5 Visualization of the grooved device with three principal radii of curvature of the droplet phase. R₁ and R₂ are the principal radii of curvature of the front of the droplet. R₃ is the principal radius of curvature of the side of the plug. There is no other radius of curvature for the side of the droplet, as the plug lies flat against the ceiling of the device.

Groove spacing controls interactions between DFUs

We observed that for every tested L_g value, the curves describing the flow rate–droplet volume relationship were parallel. It would be intuitive that in the spilt-mode for the largest groove spacing, the droplets would be the largest, as they should pull the droplet phase from the largest area. However, we see in Fig. 4C that the relationship between the droplet size and L_g is not monotonous with the local minimum (smallest droplets produced) for L_g = 0.75 mm. This can be explained if we consider that the number and location of the DFUs are not constant. Potential DFUs, places where the droplet phase begins to leave the channel, compete between themselves for the droplet phase. The droplet forms in the area with the lowest pressure, withdrawing the liquid from the competing low-pressure areas nearby. The existence of the optimum groove spacing value for a wide step emulsifier, in our case L_g = 0.75 mm (6.25 × w_g, 7.5 × H), suggests that there is a ‘range of interaction’ for the groove. For systems with L_g < 0.75 mm, the DFUs strongly compete for the same portion of fluid, which leads to a decrease of the number of DFUs operating simultaneously. If a smaller number of DFUs emulsify the same portion of fluid, the droplets are visibly larger. For L_g > 0.75 mm, the competition decreases, and individual DFUs can draw more liquid, which results in an increase of the droplet volumes.

Grooved systems outperform MCE and EDGE in terms of throughput

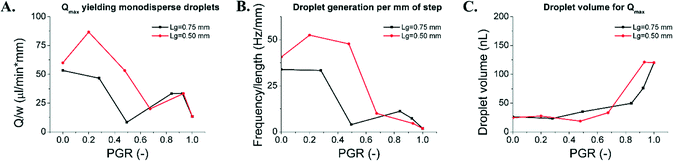
We compared the throughput of droplet production using two parameters: i) the maximum volumetric flow rate (Q_max, μL min⁻¹) per unit length of the step (w, mm), at which devices produce monodisperse droplets (CV of volumes <15%, Fig. 6A), and ii) the frequency of droplet production (f, Hz) per unit length of the step (w, mm; see Fig. 6B). Microfluidic devices with a long droplet-generating edge performed at the highest throughput for PGR between 0 and 0.5. Their maximum operational flow rate as well as number of droplets produced was the highest around PGR = 0.2–0.3. The flow rates were 53 μL min⁻¹ mm⁻¹ and 87 μL min⁻¹ mm⁻¹, for devices with L_g = 0.75 mm and L_g = 0.5 mm, respectively. The droplet production rates were 30 Hz mm⁻¹ and 50 Hz mm⁻¹, for devices with L_g = 0.75 mm and L_g = 0.5 mm, respectively. The sharp drop in the system throughput for PGR > 0.5 can be attributed to the increase of the average droplet volume with the Q_max for PGR > 0.5 (see Fig. 6C). Droplets produced from systems with PGR < 0.5 were roughly 25 nL, while for PGR > 0.5 the obtained droplets were roughly 50–100 nL, depending on L_g. For comparison, MCE devices (PGR = 0) and EDGE devices (PGR = 1) yielded droplets up to 25 nL and 120 nL, respectively. They operated up to 50 μL min⁻¹ mm⁻¹ (MCE) and 13 μL min⁻¹ mm⁻¹ (EDGE). The frequencies of the droplet production were ∼30 Hz mm⁻¹ (MCE) and 4 Hz mm⁻¹ (EDGE). The decrease of sensitivity of the droplet volume to the variation of the flow rate for the investigated devices is greatest for the grooved device (PGR = 0.2, L_g = 0.5 mm), i.e. 75% increase of droplet volume (15.8 ± 1 nL to 27.5 ± 4 nL) with a 260-fold increase of flow rate (from the lowest tested Q = 5 μL min⁻¹ to the highest Q yielding monodisperse droplets Q_max = 1300 μL min⁻¹ per device). In comparison, for MCE the increase in volume was 91% (12.9 ± 3 nL to 24.6 ± 5 nL) for a 180-fold increase of flow rate (5 to 900 μL min⁻¹). For EDGE, the volume actually decreased by 12% (from 137.2 ± 7 nL to 120.2 ± 12 nL) for a 40-fold increase of flow rate (5 to 200 μL min⁻¹).

Fig. 6 A: Maximum flow rate Q_max at which devices produced monodisperse droplets (CV_volume < 15%) per unit length of the step, w. B: Frequency of droplet generation for Q_max per unit length of the step, w. C: Droplet size for Q_max per device.

Choice of emulsifier depends on the desired droplet volume

Depending on the geometrical parameters, we can obtain a wide range of droplet sizes in high throughput. To select an appropriate emulsification system, we need to consider if we wish to produce droplets of diameter roughly 3 times larger than the DFU height (25 nL for H = 100 μm) or 6 times larger than the DFU height (>100 nL for H = 100 μm). For production of small droplets (∼25 nL), both MCE and grooved emulsifiers (PGR = 0.2, L_g = 0.5 mm) could be used. The grooved device outperforms MCE in terms of the operational flow rate (87 μL min⁻¹ mm⁻¹ for grooved, 50 μL min⁻¹ mm⁻¹ for MCE) and the frequency of droplet production (50 Hz mm⁻¹ for grooved, 30 Hz mm⁻¹ for MCE).

Production of large droplets (∼100 nL for H = 100 um) can be carried out by both EDGE and grooved emulsifiers (PGR = 0.3, L_g = 0.75 mm). The grooved device outperforms EDGE in terms of the operational flow rate (53 μL min⁻¹ mm⁻¹ for grooved, 13 μL min⁻¹ mm⁻¹ for EDGE) and the frequency of droplet production (30 Hz mm⁻¹ for grooved, 4 Hz mm⁻¹ for EDGE).

Comparison with current state-of-the-art devices

Numerous passive high-throughput droplet production techniques have been described, each featuring a unique set of advantages and drawbacks,⁷ for example MCE,^29,38 EDGE^31,32 or ‘millipede’.^28,39 Parallel passive emulsifying chips can be operated both horizontally (if the continuous phase is continuously supplied to transport the droplets away from the DFU^29,31) and vertically (aligning the DFU with the gravitational field allows buoyancy to evacuate the droplets away from the step, as shown here and by Stolovicki et al.⁴⁰).

The throughput of droplet generation is a function of multiple parameters, the most fundamental of which is the geometry of the junctions and the connections between them.²⁴ The presented grooved design features parallelized step emulsifying DFUs that rely on the geometry of the microchannels rather than on actuating the flow rates of the liquids. We provide insight into the relationship between the geometry of the DFU and the produced emulsions. Application of our findings allows the throughput of emulsification to be increased with respect to the known geometries, such as MCE and EDGE. We directly compare our geometry with state-of-the-art emulsifiers (grooved devices compared with EDGE and MCE devices, see Fig. 6).

We obtained a higher throughput of droplet production (e.g. grooved: up to 87 μL min⁻¹ mm⁻¹, MCE: up to 50 μL min⁻¹ mm⁻¹ for 25 nL droplets), a higher frequency of droplet generation (e.g. grooved: up to 50 Hz mm⁻¹, MCE: up to 30 Hz mm⁻¹ for 25 nL droplets) and a lower sensitivity of droplet volumes to changes in flow rates (e.g. grooved: 75% increase of droplet volume with a 260-fold increase of flow rate, MCE: 91% increase in volume for a 180-fold increase of flow rate, EDGE: the volume decreased by 12% for a 40-fold increase of flow rate, above which the volume rose sharply). Thus, we provide guidelines on how to design parallelized passive emulsification systems in order to maximize the throughput of desired emulsion production.

While in this paper we focus on passive high-throughput methods of droplet production, it is important to stress that progress has been made in the development of active methods. For instance, using a novel and very complex fabrication method it is possible to obtain a microfluidic device with over 10 000 active droplet generators operating at extremely high pressures.¹¹ It allows for impressive high-throughput emulsion production (>trillions of droplets per hour), higher than that in currently existing grooved devices. However, besides the complex fabrication and need to actuate the flows, the device requires the use of a considerable excess amount of the continuous phase, unlike in passive droplet production methods. Thus, we expect that both active and passive methods will undergo further optimization and find their select uses, also in industry.

Fluid supply to the device

There are two main ways of supplying liquids to microfluidic devices: either by applying constant volumetric flow (supplied by e.g. syringe pumps or electronic pipettes²⁵) or constant pressure (e.g. by pressure-controlled valves⁴¹). In our research, we used syringe pumps, unlike pressure-driven MCE and EDGE.^31,42 This raises a question if there is a difference in the supply method.

If there are no substantial changes in the total hydrodynamic resistance of the supplying tubing and microfluidic chip (e.g. if they clog or fill up with the produced emulsion) then both ways are equivalent. Small pressure fluctuations are caused by the droplet formation process. When the curvature of the interface inside a chip changes, the Laplace pressure changes as well. As a result in constant pressure mode, there appear fluctuations of the flow rate. As reported for EDGE, they are negligible and do not influence the device operation.³¹ Such fluctuations can be eliminated by taking larger hydrodynamic resistance of the supplying tubing. What is more, as stated before, the passive microfluidic device can be placed in an unconfined reservoir filled with the continuous phase, which eliminates the influence of newly formed droplets on hydrodynamic resistance. Keeping this in mind, it is up to the researcher to pick the fluid supply method for the grooved step emulsifier.

Downscaling possibilities

To produce smaller droplets, the optimum grooved geometry should be scaled down. Manufacturing a downscaled grooved system would require employing a more precise and accurate fabrication method than CNC-milling, e.g. glass-etching, soft-lithography or 3D-printing, preferentially injection molding.

The droplet volume scales with the cube of the DFU height;²⁸ thus to produce 1 nL droplets (reduce the volume by 25 times) the approximate geometrical parameters would need to be downscaled by 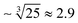times. The suggested dimensions would be: h ∼ 10 μm, H ∼ 30 μm, w_g ∼ 40 μm, and L_g ∼ 0.17 mm. Since the maximum injection rate scales with h², we estimate Q_max/w to be of the order 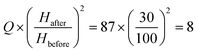μL min⁻¹ mm⁻¹.²⁸ The single DFU width is 0.174 mm (w_g + L_g), yielding 5.71 DFUs per mm. The theoretical throughput of 1 nL droplet production from the grooved device is around 80 μL h⁻¹ per DFU.

The state-of-the-art ‘millipede’ device produces droplets at 150 mL h⁻¹ in 550 DFUs, (roughly 275 μL h⁻¹ per single DFU), which is 3 times the rate per groove in our device.²⁸ At the same time, however, the footprint of the millipede nozzle is 3 times larger than the footprint of the DFU in the grooved device (approximately 0.2 mm² and 0.06 mm², respectively). Thus, the two designs offer a similar throughput per surface area of the chip, since the DFUs in the grooved system can be placed 3 times denser than in the millipede system.

Conclusions

In this work we investigated step emulsification devices with partitions of different heights h separated by grooves of height H and introduced a partition-to-groove ratio defined as PGR = h/H. Our devices in the limits PGR = 0 and PGR = 1 are known as MCE and EDGE step emulsification devices, respectively. We fabricated devices with intermediate PGRs to observe the transition between MCE and EDGE emulsification techniques. This transition includes the change of the liquid–liquid interface shape, from the sharp in-groove mode (for small h, the droplet phase is inside the grooves) to the spilt-groove mode (for h > H/2 the droplet phase spreads outside grooves). Our results often show a non-monotonic and hard to systematize droplet generation mechanism.

In our study we established optimal geometries for high-throughput droplet formation using paralleled step emulsifying units, DFUs. The choice of appropriate emulsifier depends on the volume of the droplet that we want to obtain. The optimal geometry features an intermediate ratio of PGR ∼0.2–0.3 for grooves spaced by 4–6.25 times the width of a groove (0.5 or 0.75 mm for 120 μm wide grooves). The groove geometry appears to combine the advantages of both MCE and EDGE, i.e. spatial localization of DFUs, high-throughput formation of tightly monodisperse droplets from parallel DFUs, and low sensitivity to variation in the flow rate.

The presented microsystems share the benefits of previously shown passive droplet generation systems, such as no need for control over the continuous phase flow, low consumption of the outer phase and production of highly monodisperse droplets. Our study shows how altering the geometry of the microfluidic nozzles and the connection between them can substantially change the throughput of the emulsification process and the size distribution of the produced emulsion. We propose a way to further optimize the throughput of existing highly parallel passive systems in order to produce vast amounts of monodisperse emulsions.

The droplet production schemes shown in this study might find use in any field of industry dealing with monodisperse emulsions or particles.⁸ As the findings that we report here are scale-free, the optimum geometry can in principle be scaled down to produce picoliter droplets. Consequently, the variants of the presented device would be extremely useful for biological-assay studies, such as single molecule or single cell studies requiring ultra-high throughput of encapsulation and investigation, coupled with the need for monodispersity and stability (e.g. single cell genome sequencing¹⁵ or expression profiling⁴³).

Author contributions

A. S. O., K. M., and P. G. designed the experiments. A. S. O. and Y.-K. L. performed the experiments. A. S. O., K. M., Y.-K. L., L. D., and P. G. analysed the data. A. S. O. and Y.-K. L. provided the graphics. A. S. O., K. M., Y.-K. L., L. D., and P. G. discussed and wrote the manuscript.

Conflicts of interest

A. S. O., K. M., Y.-K. L. and P. G. are authors of Polish patent application describing the chip design (P.425543).

Acknowledgements

The authors would like to thank Patryk Adamczuk, Bogdan Dąbrowski and Karol Patyrak for microfabrication of the devices, Leszek J. Opalski for discussion and help with writing MATLAB routines, and Witold Postek for discussion. A. S. O. and L. D. were supported by the Foundation for Polish Science within the project TEAM TECH POIR.04.04.00-00-2159/16-00. A. S. O., K. M. and P. G. were supported by the National Science Centre, Poland, within the projects Preludium 2016/23/N/ST4/01020, Sonata 2016/21/D/ST3/00988 and Symfonia 2014/12/W/NZ6/00454, respectively. Y.-K. L. was supported by the NaMeS research training programme (Horizon 2020 grant agreement No. 711859, Ministry of Science and Higher Education grant agreement No. 3549/H2020/COFUND/2016/2).

Notes and references

1. A. Ammala, Int. J. Cosmet. Sci., 2013, 35, 113–124.
2. F. Sarghini, Adv. Food Biotechnol., 2015, 539–564.
3. J. Lu, J. D. Litster and Z. K. Nagy, Cryst. Growth Des., 2015, 15, 3645–3651.
4. D. Z. Gunes, Curr. Opin. Food Sci., 2018, 21, 57–65.
5. F. Leal-Calderon and P. Poulin, Curr. Opin. Colloid Interface Sci., 1999, 4, 223–230.
6. H. N. Joensson and H. Andersson Svahn, Angew. Chem., Int. Ed., 2012, 51, 12176–12192.
7. P. Zhu and L. Wang, Lab Chip, 2017, 17, 34–75.
8. A. S. Opalski, T. S. Kaminski and P. Garstecki, KONA Powder Part. J., 2019, 36, 50–71.
9. S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220.
10. T. S. Kaminski, S. Jakiela, M. A. Czekalska, W. Postek and P. Garstecki, Lab Chip, 2012, 12, 3995–4002.
11. S. Yadavali, H. H. Jeong, D. Lee and D. Issadore, Nat. Commun., 2018, 9, 1222.
12. J. J. Agresti, E. Antipov, A. R. Abate, K. Ahn, A. C. Rowat, J.-C. Baret, M. Marquez, A. M. Klibanov, A. D. Griffiths and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4004–4009.
13. B. J. Hindson, K. D. Ness, D. A. Masquelier, P. Belgrader, N. J. Heredia, A. J. Makarewicz, I. J. Bright, M. Y. Lucero, A. L. Hiddessen, T. C. Legler, T. K. Kitano, M. R. Hodel, J. F. Petersen, P. W. Wyatt, E. R. Steenblock, P. H. Shah, L. J. Bousse, C. B. Troup, J. C. Mellen, D. K. Wittmann, N. G. Erndt, T. H. Cauley, R. T. Koehler, A. P. So, S. Dube, K. A. Rose, L. Montesclaros, S. Wang, D. P. Stumbo, S. P. Hodges, S. Romine, F. P. Milanovich, H. E. White, J. F. Regan, G. A. Karlin-Neumann, C. M. Hindson, S. Saxonov and B. W. Colston, Anal. Chem., 2011, 83, 8604–8610.
14. A. Kulesa, J. Kehe, J. E. Hurtado, P. Tawde and P. C. Blainey, Proc. Natl. Acad. Sci. U. S. A., 2018, 201802233.
15. F. Lan, B. Demaree, N. Ahmed and A. R. Abate, Nat. Biotechnol., 2017, 35, 640–646.
16. A. Ofner, D. G. Moore, P. A. Rühs, P. Schwendimann, M. Eggersdorfer, E. Amstad, D. A. Weitz and A. R. Studart, Macromol. Chem. Phys., 2017, 218, 1600472.
17. J. T. Wang, J. Wang and J. J. Han, Small, 2011, 7, 1728–1754.
18. E. Amstad, ACS Macro Lett., 2017, 6, 841–847.
19. T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Phys. Rev. Lett., 2001, 86, 4163–4166.
20. S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364–366.
21. P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–446.
22. P. Garstecki, H. A. Stone and G. M. Whitesides, Phys. Rev. Lett., 2005, 94, 164501.
23. P. M. Korczyk, O. Cybulski, S. Makulska and P. Garstecki, Lab Chip, 2011, 11, 173–175.
24. R. Dangla, E. Fradet, Y. Lopez and C. N. Baroud, J. Phys. D: Appl. Phys., 2013, 46, 114003.
25. F. Dutka, A. S. Opalski and P. Garstecki, Lab Chip, 2016, 16, 2044–2049.
26. N. Mittal, C. Cohen, J. Bibette and N. Bremond, Phys. Fluids, 2014, 26, 082109.
27. A. G. Håti, T. Szymborski, M. Steinacher and E. Amstad, Lab Chip, 2018, 18, 648–654.
28. E. Amstad, M. Chemama, M. Eggersdorfer, L. R. Arriaga, M. P. Brenner and D. A. Weitz, Lab Chip, 2016, 16, 138–155.
29. G. T. Vladisavljević, E. E. Ekanem, Z. Zhang, N. Khalid, I. Kobayashi and M. Nakajima, Chem. Eng. J., 2018, 333, 380–391.
30. S. Sugiura, M. Nakajima, J. Tong, H. Nabetani and M. Seki, J. Colloid Interface Sci., 2000, 227, 95–103.
31. K. van Dijke, G. Veldhuis, K. Schroën and R. Boom, Lab Chip, 2009, 9, 2824–2830.
32. S. Sahin and K. Schroën, Lab Chip, 2015, 15, 2486–2495.
33. S. Sugiura, M. Nakajima and M. Seki, Langmuir, 2002, 18, 5708–5712.
34. S. Sugiura, M. Nakajima and M. Seki, Langmuir, 2002, 18, 3854–3859.
35. S. Sugiura, M. Nakajima, N. Kumazawa, S. Iwamoto and M. Seki, J. Phys. Chem. B, 2002, 106, 9405–9409.
36. K. van Dijke, R. de Ruiter, K. Schroën and R. Boom, Soft Matter, 2010, 6, 321–330.
37. Z. Li, A. M. Leshansky, L. M. Pismen and P. Tabeling, Lab Chip, 2015, 15, 1023–1031.
38. T. Kawakatsu, Y. Kikuchi and M. Nakajima, J. Am. Oil Chem. Soc., 1997, 74, 317–321.
39. M. L. Eggersdorfer, W. Zheng, S. Nawar, C. Mercandetti, A. Ofner, I. Leibacher, S. Koehler and D. A. Weitz, Lab Chip, 2017, 17, 936–942.
40. E. Stolovicki, R. Ziblat and D. A. Weitz, Lab Chip, 2018, 18, 132–138.
41. K. Churski, P. Korczyk and P. Garstecki, Lab Chip, 2010, 10, 816–818.
42. S. Sugiura, M. Nakajima, H. Itou and M. Seki, Macromol. Rapid Commun., 2001, 22, 773–778.
43. E. Z. Macosko, A. Basu, R. Satija, J. Nemesh, K. Shekhar, M. Goldman, I. Tirosh, A. R. Bialas, N. Kamitaki, E. M. Martersteck, J. J. Trombetta, D. A. Weitz, J. R. Sanes, A. K. Shalek, A. Regev and S. A. McCarroll, Cell, 2015, 161, 1202–1214.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8lc01096j

---