Open Access Article
Open Access ArticleRuthenium nanoparticles on covalent triazine frameworks incorporating thiophene for the electrocatalytic hydrogen evolution reaction†
Lars
Rademacher
 a,
Thi Hai Yen
Beglau
a,
Bahia
Ali
a,
Linda
Sondermann
a,
Till
Strothmann
a,
Thi Hai Yen
Beglau
a,
Bahia
Ali
a,
Linda
Sondermann
a,
Till
Strothmann
 a,
István
Boldog
a,
István
Boldog
 a,
Juri
Barthel
a,
Juri
Barthel
 b and
Christoph
Janiak
b and
Christoph
Janiak
 *a
*a
aInstitut für Anorganische Chemie und Strukturchemie, Heinrich-Heine Universität Düsseldorf, Universitätsstraße 1, D-40225 Düsseldorf, Germany. E-mail: Janiak@uni-duesseldorf.de
bErnst Ruska-Zentrum für Mikroskopie und Spektroskopie mit Elektronen, Forschungszentrum Jülich GmbH, 52425 Jülich, Germany
First published on 15th December 2023
Abstract
In this study, 2 to 4 nm ruthenium nanoparticles (Ru-NPs) were loaded (21 to 33 wt%) by decomposition of triruthenium dodecacarbonyl, Ru3(CO)12, through microwave heating on the prototypal CTF-1 and on thiophene-containing CTFs to access the influence of the thiophene content on the electrocatalytic properties in the hydrogen evolution reaction (HER). The CTFs were synthesized ionothermally with heating at 400 °C and 600 °C (CTF_400/600) using thiophene- (Th-CTF), phenylthiophene- (PhTh-CTF), bithiophene- (BTh-CTF) or quaterthiophene- (QTh-CTF) dinitrile precursors. The homogenous nature of the Ru/CTF composite materials was confirmed by transmission electron microscopy (TEM) and scanning electron microscopy (SEM) combined with energy-dispersive X-ray spectroscopy (EDX). X-ray photoelectron spectroscopy (XPS) revealed the successful introduction of thiophene units and the deposition of Ru-NPs. The Ru/CTF composite materials retained their porosity with calculated Brunauer–Emmett–Teller (BET) surface areas being between 540 to 1326 m2 g−1. Low overpotentials and Tafel slopes towards HER down to 30 mV at 10 mA cm−2 and 55 mV dec−1 were recorded in 0.5 mol L−1 H2SO4 with the lowest (i.e. best) value observed for Ru/BTh-CTF_600. Notably, Ru/CTF composite materials based on CTFs synthesized at 600 °C are generally superior compared to the ones at 400 °C by exhibiting lower overpotentials due to more pronounced carbonization during synthesis. In 1 mol L−1 KOH the Ru/CTFs demonstrate even lower overpotentials down to 3 mV with Ru/PhTh-CTF_600 and Ru/QTh-CTF_600 as the two best materials. Tafel slopes down to 39 mV dec−1 indicate fast kinetics. Durability tests of Ru/BTh-CTF_600, Ru/PhTh-CTF_600 and Ru/QTh-CTF_600 with 2000 voltammetry cycles show minor to no alterations in the electrocatalytic performances.
Introduction
The hydrogen evolution reaction (HER) is the cathodic half-reaction for water splitting and the electrocatalytic method of hydrogen generation, a key resource for numerous industrial and energy related processes.1–4 Developing energy-efficient electrocatalysts for HER is crucial for implementing a hydrogen economy.5 In this regard, electrocatalysts based on noble metals are receiving much attention due to their unparalleled activity in the HER.6,7 However, cost impediments focus the attention on the nanoparticular state of noble metals.6,8,10 Nanoparticles (NPs) possess high activities due to their large surface to volume ratio, which is accompanied by a larger number of outer atoms acting as active sites.6,8 Ruthenium (Ru), one of the comparatively less expensive noble metals, shows a competitive catalytic performance towards HER among its noble peers with properties similar to platinum (Pt), thus constituting an area of active research.5,6,11 In particular, composite-catalysts based on carbon materials are in demand due to their enhanced performance and durability.12,13The primary prerequisite for high electrocatalytic performance of metallic Ru in HER is its strong affinity towards hydrogen. However, excessive binding strength might decelerate the kinetics according to the principle of Sabatier (i.e. that the binding of the substrates and the products should be of intermediate strength).5,6,13,14 The introduction of nitrogen (N) donor ligands, which coordinate to Ru, is a means to stabilize the NPs against aggregation as well as to tune the local chemical environment, thereby facilitating the desorption of hydrogen.5,13–15 The introduction of other heteroatoms, particularly sulfur (S), could have similar effects for additional fine-tuning the electrocatalytic performance.5,6,16–18 The efficiency of the HER reaction also strongly depends on the nature of the electrolyte, which essentially affects the reaction mechanism (Table 1).
| Step | Condition | Pathway | Tafel slope (mV dec−1) |
|---|---|---|---|
| Volmer (adsorption) | Acidic | M + e− + H3O+ → M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + H2O H + H2O |
>120 |
| Neutral, alkaline | M + e− + H2O → M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + OH− H + OH− |
||
| Heyrovsky (desorption) | Acidic | Had/M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + e− + H+ → M + H2 H + e− + H+ → M + H2 |
40–120 |
| Neutral, alkaline | M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + e− + H2O → M + H2 + OH− H + e− + H2O → M + H2 + OH− |
||
| Tafel (desorption) | Acidic | M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + M H + M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H → 2M + H2 H → 2M + H2 |
∼30 |
| Neutral, alkaline |
In alkaline electrolytes further improvement is possible by accelerating the dissociation of water, a challenging step within the mechanism.13,19 Here, an enhanced water adsorption and breakage of the O–H bond can facilitate the HER performance.13,20 Sulfur in the form of sulfides, actually a known catalyst poison for many chemical reactions catalyzed by noble metals,21,22 is, on the other hand, known for its active site- and dissociation-promoting properties and its benign role in some cases of electrocatalysis (e.g. metal sulfides23,24), and thereby could be beneficial for HER.13,17,25 Supported by density functional theory (DFT) calculations, several studies report a greatly reduced dissociation barrier of adsorbed H2O by increasing the electron deficiency of Ru in S-doped carbon supports, which is further connected with an optimized adsorption/desorption of hydrogen.14,17,20
Thus, both N- and S-ligands are introduced into carbon supports by doping strategies commonly using sulfuric acid, nitric acid, thioacetamide and other precursors, which result in catalytic materials with (often) poorly defined active sites, but nevertheless with improved performance.20,25–28 Alternatively, both elements can be incorporated directly in the form of repeating structural moieties into the materials. In this regard, thiophene-containing compounds have emerged as promising candidates for applications in electrocatalysis.29–34 Towards HER, Li et al. tested sulfur-doped carbon nanosheets derived from polythiophene as support for Ru nanoclusters demonstrating a very low overpotential of 19 mV in an alkaline electrolyte.17 Ru nanoclusters decorated on S,N-doped carbon prepared from an aniline-thiophene-copolymer by Li et al. exhibit a 14 mV overpotential.35 Chakrabartty et al. applied a Pt-NP/poly(α-terthiophene) composite, which shows a 67 mV overpotential in 0.5 mol L−1 H2SO4.36 Zhang et al. synthesized a cobalt containing polythiophene composite by electropolymerization achieving an overpotential of 75 mV.37
Another requirement for electrocatalysts is a high porosity, thereby enhancing the exposure of active sites.6,13 Covalent triazine frameworks (CTFs) form a promising group of ideally regular, but often rather amorphous porous organic polymers, based on linked triazine nodes. CTFs can be synthesized by cyclotrimerization of molecular di- or polynitrile precursors.38–41 They are of particular interest due to their high structural variety and tunability, depending primarily on the structure of the precursor and the method of synthesis.38 Various studies concerning thiophene-containing CTFs are published, since the triazine moiety as an electron withdrawing group together with electron donating thiophene could constitute donor–acceptor (DA) polymers with low band gap and improved conductivity.42–56 The primary route of CTF synthesis, the cyclotrimerization of oligo-nitrile precursors, is achieved via various ways, like ionothermal (ZnCl2) or superacid-catalyzed polymerization, or amide condensation. Each way offers different advantages depending on the desired properties and intended applications.42,46,48,57,58 These properties render CTFs highly suitable for energy storage and conversion applications.42,59–62 CTFs synthesized by ionothermal processes, without the use of expensive catalysts or toxic solvents, present tunable high surface area materials.41 Importantly, ionothermal synthesis produces CTFs with sufficient electrical conductivity as a result of partial carbonization.38,63,64
Especially metal NPs deposited on CTFs as composites are promising electrode materials, demonstrating improved performances over their individual components.63–66 While there are some existing studies, the research on M-NP/CTF composites targeting electrocatalytic HER remains relatively limited, especially concerning thiophene-based CTFs. As a singular example, Yau et al. synthesized a CTF-related nickel containing microporous organic polymer incorporating triazine and thiophene moieties by polycondensation of 2,5-thiophenedicarboxaldehyde and melamine; the resulting material demonstrated an overpotential of 597 mV.67 Among non-thiophene CTF work, Siebels et al. deposited Rh- and Pt-NPs on 1,4-dicyanobenzene-based CTF-1 and the materials demonstrated overpotentials of 58 and 111 mV, respectively, in 0.5 mol L−1 H2SO4.68 Qiao et al. tested molybdenum sulfide NPs on CTF-1 achieving 93 mV.69 Zhang et al. synthesized composite materials with Cu, Ni, Co, Pd, Pt ions and clusters on a 2,6-dicyanopyridine-based (DCP-)CTF and on a 5,5′-dicyano-2,2′-bipyridine-based (BPY-)CTF with overpotentials from 46 to 470 mV.65 Ju et al. prepared a triazine-ring doped carbon material from a tetracyanoquinodimethane-based CTF decorated with Ru-NPs, achieving an ultralow overpotential of only 2 mV in 1 mol L−1 KOH.70
In this study, we report the synthesis of novel Ru-NP decorated thiophene-containing covalent triazine frameworks (Fig. 1) and their electrocatalytic activities towards the HER in an acidic and in an alkaline electrolyte. The deposition of Ru-NPs on the preformed CTFs was carried out by a microwave-assisted thermal decomposition of Ru3(CO)12 in propylene carbonate (PC) without any stabilizing additives.9,10,63 The respective CTFs were synthesized by ionothermal reactions in ZnCl2 from dinitrile precursors and constitute triazine moieties connected by thiophene (Th-CTF), phenylthiophene (PhTh-CTF), bithiophene (BTh-CTF) or quaterthiophene (QTh-CTF) bridges (Fig. 1). To the best of our knowledge the ionothermal synthesis of these CTFs is not known (except for Th-CTF).39 However, analogous porous organic polymers, which were non-ionothermally synthesized, have been published.45,71–75 A PhTh-based CTF has been obtained through a Brønsted acid route with very low BET surface area.45 BTh-cross-linked triazine polymers were prepared via electropolymerization and Yamamoto-type Ullmann coupling.72–74 A QTh-cross-linked triazine polymer with a low BET surface was synthesized through a Stille coupling reaction.75
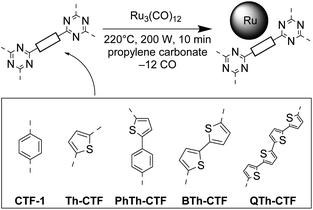 | ||
| Fig. 1 Schematic synthesis of Ru-NPs on CTFs in propylene carbonate (PC) by microwave-assisted thermal decomposition of Ru3(CO)12. | ||
Results and discussion
Synthesis and characterization of the CTFs
The selection of targeted CTFs involved mono-, bi-, and quaterthiophene bridges between the triazine moieties, to elucidate the influence of the thiophene moiety and of the bridge length on the properties of the resultant materials, as well as of a mixed phenylthiophene bridge to assess the ‘dilution’ of the bridge by a non-specific aromatic entity (cf.Fig. 1). The nitrile groups of the precursors thiophene-2,5-dicarbonitrile (leading to Th-CTF), 5-(4-cyanophenyl)thiophene-2-carbonitrile (leading to PhTh-CTF), 2,2′-bithiophene-5,5′-dicarbonitrile (leading to BTh-CTF), and 2,2′:5′,2′′:5′′,2′′′-quaterthiophene-5,5′′′-dicarbonitrile (leading to QTh-CTF) were in an ideal view trimerized to triazine rings via ionothermal synthesis in ZnCl2 at temperatures of 400 or 600 °C (_400 or _600 suffix in the code) (cf. Fig. S1 and S2†). The same conditions were used for the synthesis of the paradigmatic CTF-1 with phenylene bridges being a reference CTF material (Table S1†). All of the synthesized CTFs were mostly non-crystalline (Fig. S3†).39 Broad reflexes at around 8° and 26° correspond to the (100) and (001) planes and support the typical layered structure of the CTFs.38–41,48The CHNS elemental analysis (EA) confirms the presence of nitrogen and sulfur in the CTF samples, albeit significantly less than the theoretical amount for the idealized CTF structure (Table S2†). As expected, and typically observed for ionothermally synthesized CTFs, the contents of N and S were lower compared to the theoretical values due to partial carbonization of the intermediates or the CTF at 400 and particularly at 600 °C, releasing HCN and other volatiles.40,41,76 Already at 400 °C, which is a normal temperature for ionothermal CTF synthesis, usually about half of the theoretical N content is lost, while at significantly higher temperature the products rather represent N-doped porous carbons.63,64,77,78 The decreased content of the triazine and thiophene functionalities with increase of the synthesis temperature is also reflected by the increase of the carbon to heteroatom ratio, C/(S + N), given in Table S2.† The loss of N and S varied strongly with the monomer. For Th-CTF and BTh-CTF_400 over 50% of the theoretical N and S percentage was found. For PhTh-CTF_400, both N and S content dropped to less than 20% of the theoretical value. While the N content in QTh-CTF_400 was at 25%, over 50% of the theoretical S content was preserved here. The latter is an example that the loss of N and S do not have to occur in parallel.
PhTh-CTF_400 and PhTh-CTF_600 show the lowest N and S contents with absolute amounts down to ∼1 wt%, which can be explained by the high amount of hydrogen atoms in the formula benefitting the formation of gaseous HCN, H2S, HSCN and related products. The thiophen units in the CTF_400 samples (except Th-CTF) seemed to be more stable during synthesis in comparison to the triazine units as demonstrated by the higher S/N ratios compared to the theoretical ratios (Table S2†). With increasing temperature to 600 °C the loss of S becomes more significant and an enhanced loss of sulfur at higher temperatures increases the relative amount of carbon and nitrogen, comparable to findings in the literature.28 As will be seen, the carbonization is beneficial in the context of electrical conductivity and increased micro- and meso-porosity.59,64 However, compared to other carbon supports for electrocatalysts having ∼3 wt% sulfur, the obtained amount of sulfur in the ionothermally synthesized CTFs is very high.20,25,79
Scanning electron microscopy, SEM illustrated a largely shard-like morphology of particles with dimensions of 5 to 50 μm (Fig. S4†). A combination with energy-dispersive X-ray spectroscopy, EDX mapping reveals the homogenous distribution of sulfur near the surface of the CTF particles (Fig. S4 and S5†).
Thermogravimetric analysis, TGA (Fig. S6a and b†) indicated a varied stability of the CTFs in synthetic air. Except for CTF-1_400 and Th-CTF_400, which give a 10% mass loss up to 300 °C, the CTF_400 compounds were stable at least up to ∼300 °C and show only slight degradation until decomposition at 400 °C. Among the CTF_600 samples, Th-CTF_600 starts a continuous mass loss at 150 °C while the others possess a stability until ∼500 °C. Residual masses at 1000 °C were below 8 wt% and within the range published in the literature but are indicative of inorganic residues.39,41 Coupled TGA-mass spectrometry for gas analysis of formed volatiles was exemplarily done for Th-CTF and BTh-CTF samples and indicated the formation of NO2 and SO2 between ∼300 to ∼700 °C with maxima around 550–600 °C (Fig. S6c–f†).
Nitrogen gas adsorption measurements yielded IUPAC Type I(b) to Type II isotherms for almost all CTFs typical for materials having wider micropores (<2 nm) and mesopores (2–50 nm) (Fig. S7a and b†).80 The desorption curves show usually a H4 hysteresis loop in a P/P0 range characteristic for mesopores and small macropores with a step-down at P/P0 < 0.5 common for this hysteresis type. For PhTh-CTF_600 the isotherm is of Type IV(a), indicating a more mesoporous adsorbent with a H2(b) hysteresis.80 Accordingly, most of the pores are larger than 2 nm (Fig. S7c and d†). Interestingly, in case of Th-CTF_400 and Th-CTF_600 the isotherms are only of Type I(b) with essentially no hysteresis indicating a distinctive microporous character. To some extend this character is also present in QTh-CTF_600 having a narrow hysteresis and a more pronounced Type I(b) portion. The calculated BET surface areas range from 485 to 2236 m2 g−1 depending on the dinitrile CTF precursors, and the synthesis temperature (Table 2).
| Material | BET surface areaa (m2 g−1) | Total pore volumeb (cm3 g−1) | Micropore volumec (cm3 g−1) | Average pore width (nm) |
|---|---|---|---|---|
| a From nitrogen sorption measurements at 77 K, cf. Fig. S7a and b. Calculated BET area based on the adsorption points between P/P0 = 0.05–0.2. b Determined at P/P0 = 0.95. c Calculated by NLDFT for ≤2 nm pores. | ||||
| CTF-1_400 | 978 | 0.57 | 0.33 | 2.3 |
| CTF-1_600 | 1752 | 1.59 | 0.52 | 3.6 |
| Th-CTF_400 | 935 | 0.44 | 0.34 | 1.9 |
| Th-CTF_600 | 1532 | 0.81 | 0.49 | 2.1 |
| PhTh-CTF_400 | 485 | 0.36 | 0.15 | 3.0 |
| PhTh-CTF_600 | 1177 | 1.64 | 0.18 | 5.5 |
| BTh-CTF_400 | 1336 | 0.80 | 0.43 | 2.4 |
| BTh-CTF_600 | 1846 | 1.39 | 0.48 | 3.0 |
| QTh-CTF_400 | 1651 | 1.27 | 0.43 | 3.1 |
| QTh-CTF_600 | 2236 | 1.37 | 0.64 | 2.4 |
As expected and in accordance to the literature,38–41,77 the synthesis temperature of 600 °C gave significantly higher surface areas than at 400 °C, with values becoming approximately twice as large at 600 °C for CTF-1 and PhTh-CTF. The values of 978 and 1756 m2 g−1 for CTF-1 are in the expected range of the literature (791 (400 °C) to 1750 m2 g−1 (600 °C), depending on the actual conditions).38–41,81 The highest surface areas were observed for the QTh-CTFs at their respective temperature. More thiophene units in the precursor and hence longer inter-triazine bridges led, as expected, to an increased surface area. Th-CTF_400 with 935 m2 g−1 exceeded the literature value of 584 m2 g−1.41,64 PhTh-CTF_400 with 485 m2 g−1 and PhTh-CTF_600 with 1177 m2 g−1 feature the lowest surface areas at the given temperatures. A possible reason may be is the evident asymmetry of the PhTh-dinitrile precursor.
Generally, with increasing temperature, the relative proportion of the mesopores increases at the expense of the micropore volume, which leads to hierarchical porosity beneficial for the mass transport and diffusion.59,82,83 The total pore volumes range from 0.32 to 1.64 cm3 g−1 and show a similar trend within the samples as the BET surface areas, except that PhTh-CTF_600 demonstrates the highest total pore volume which is also characterized by a larger fraction of mesopores in the pore size distribution (Fig. S7d†). Fourier transform infrared (FTIR) spectra of the CTFs and the underlying dinitrile precursors reveal the triazine ring formation with a broad band at 1567 cm−1 while the characteristic band of the nitrile groups at 2245 cm−1 (–CN stretching vibration) disappears (Fig. S8†).39,59,63
Characterization of Ru/CTF
Preparation of metal NPs by the microwave-assisted thermal decomposition of a precursor in solvents with considerable dielectric losses (i.e. solvents, which are good absorbers of microwave radiation) is an efficient synthesis method of NPs.10,84 Propylene carbonate is a suitable polar solvent with high boiling point, low toxicity, environmental sustainability, and has been established for metal nanoparticle synthesis.9,10,85–89 The Ru/CTF composites were prepared by microwave induced heating of a slurry of Ru3(CO)12 and the CTF in a ratio to aim for 33 wt% of Ru content in the product (Fig. S9†). The actual content of Ru in the composites was post-synthetically determined by AAS between 21 and 33 wt% and the molar Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio from AAS/CHNS elemental analysis (EA) and EDX. Noteworthy, the latter gave a reasonable to good agreement (Table 3). Due to the loss of heteroatoms the proportion of Ru increases from the Ru/CTF_400 to the respective Ru/CTF_600 samples. The highest Ru
S ratio from AAS/CHNS elemental analysis (EA) and EDX. Noteworthy, the latter gave a reasonable to good agreement (Table 3). Due to the loss of heteroatoms the proportion of Ru increases from the Ru/CTF_400 to the respective Ru/CTF_600 samples. The highest Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratios with 17
S ratios with 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 43
1 and 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are present in the Ru/PhTh-CTF samples due to the low S contents in the PhTh-CTFs (cf. Table S2†). Overall, the deposition was quite efficient, leaving only a minor part of non-deposited Ru, mostly in the form of metal NPs dispersed in PC, which are removed during the purification.
1 are present in the Ru/PhTh-CTF samples due to the low S contents in the PhTh-CTFs (cf. Table S2†). Overall, the deposition was quite efficient, leaving only a minor part of non-deposited Ru, mostly in the form of metal NPs dispersed in PC, which are removed during the purification.
| Material | Metal contenta (wt%) | Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S molar ratio by AAS/EA S molar ratio by AAS/EA |
Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S molar ratio by EDX S molar ratio by EDX |
NP sizeb (nm) | BET surface area (est. value)c,d (m2 g−1) | Total pore volume (est. value)c,e (cm3 g−1) |
|---|---|---|---|---|---|---|
| a As determined by AAS (the ratio of precursors corresponded to a potential 33 wt% metal content in the case of quantitative reaction). b NP size determined from TEM, cf. Fig. S10–S14. c From nitrogen sorption measurements, cf.Fig. 5a and b. d BET calculation based on the adsorption points between P/P0 = 0.05–0.2. In parentheses estimated BET surface area from the percent content of the CTF in the composite (eqn (2)). e Determined at P/P0 = 0.95. Estimated pore volume in parentheses derived according to eqn (2). | ||||||
| Ru/CTF-1_400 | 32 | — | — | 3 ± 1 | 631 (665) | 0.40 (0.39) |
| Ru/CTF-1_600 | 21 | — | — | 9 ± 2 | 871 (1384) | 1.13 (1.26) |
| Ru/Th-CTF_400 | 27 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
4 ± 1 | 850 (683) | 0.43 (0.32) |
| Ru/Th-CTF_600 | 26 | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
4 ± 1 | 1326 (1134) | 0.88 (0.60) |
| Ru/PhTh-CTF_400 | 30 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
3 ± 1 | 540 (306) | 0.45 (0.23) |
| Ru/PhTh-CTF_600 | 25 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2 ± 1 | 788 (883) | 1.01 (1.23) |
| Ru/BTh-CTF_400 | 32 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2 ± 1 | 667 (908) | 0.37 (0.54) |
| Ru/BTh-CTF_600 | 30 | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2 ± 1 | 1072 (1292) | 0.79 (0.97) |
| Ru/QTh-CTF_400 | 21 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2 ± 1 | 959 (1304) | 0.60 (1.00) |
| Ru/QTh-CTF_600 | 33 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2 ± 1 | 794 (1498) | 0.48 (0.92) |
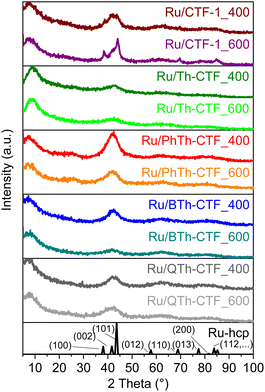
The formation of Ru-NPs with hexagonal close packed (hcp) phase was supported by powder X-ray diffraction (PXRD) measurements albeit showing only broad reflexes because of the very small particle size (Fig. 2, Table 3).9,90 Narrower reflexes were only seen in the case of Ru/CTF-1_600, yielding crystallites with 7 nm average size from the Scherrer equation based on the (100) reflex which is in good agreement with the transmission electron microscopy (TEM) derived average size of 9 ± 2 nm. The poorly crystalline CTF-materials do not contribute much to the PXRD. Only in the patterns of the Ru/PhTh-CTFs there is a broader reflex at ∼25° visible, which is attributed to the interlayer spacings between the aromatic layers in the CTF. Compared to the PXRDs of the neat CTFs, the (001) reflections have strongly decreased in intensity, which could be caused by the exfoliation or intercalation of Ru-NPs inbetween the CTF sheets during the Ru-NP deposition in PC (cf. Fig. S1†). The exfoliation is an often-observed process, which emerges during thermal treatment of materials which are morphologically similar to graphite and enhances the accessibility of the surface for the in situ formed NPs as well as of active sites.63,64,91,92
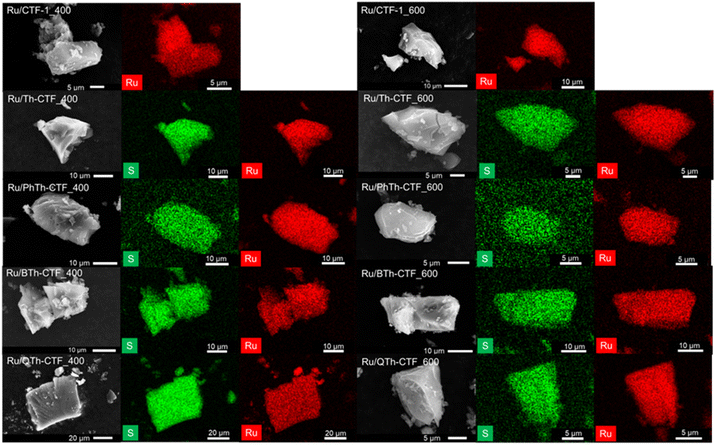
TEM images show a rather uniform distribution of Ru-NPs on the CTF flakes (Fig. 3). The high-resolution image of an Ru-NP on CTF-1_600 exhibits a lattice spacing of ∼0.23 nm belonging to the (100) planes of Ru-hcp.90,93 Selected area electron diffraction (SAED) conducted for Ru@CTF-1_600 demonstrates the characteristic ring pattern of Ru-NPs, with rings assignable to (100), (101), (110), (013) and (112) planes of the hcp phase, similar to the PXRD results (cf.Fig. 2).17 In general, smaller NP sizes are often associated as dominating parameter for a high electrocatalytic activity towards the HER.6,8 The determined average NP size of many Ru/CTFs of 2 ± 1 nm (Table 3, Fig. S10–S14†) is close to the scale of some small discrete nanoclusters. Moreover, the Ru-NP sizes exhibit no difference among these samples indicating that the presence of larger pore sizes in the micro- to mesoporous thiophene-containing CTFs does not lead to larger NPs. In Ru/CTF-1_600 larger NPs were found (av. size 9 nm) while in the thiophene-CTF_600s the average size lies below 4 nm, indicating that the thiophene containing materials enable a better stabilization of small NPs. A smaller size of the Ru-NPs can understandably lead to a higher activity as their surface area will be overproportionally increased. SEM-EDX mapping confirms the homogeneous distribution of Ru and S on the shard-like CTF particles (Fig. 4) and yield a matching molar Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio to AAS/CHNS analysis (Table 3).
S ratio to AAS/CHNS analysis (Table 3).
 | ||
| Fig. 3 TEM images of Ru-NP/CTF materials. A high-resolution TEM (HRTEM) image and selected area electron diffraction (SAED) is shown for Ru@CTF-1_600. | ||
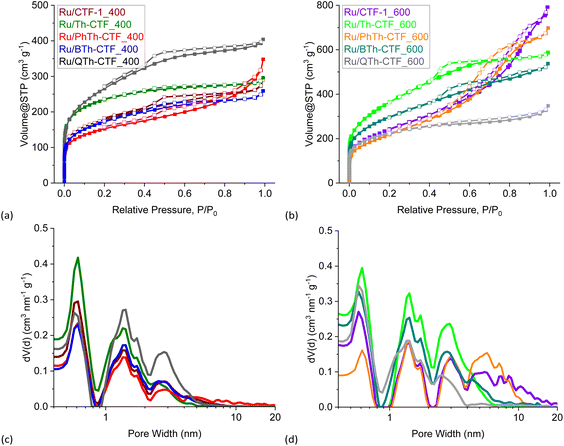 | ||
| Fig. 5 (a and b) Nitrogen adsorption (filled boxes) and desorption isotherms (empty boxes) and (c and d) pore size distribution curves of the Ru/CTF materials. | ||
Nitrogen gas adsorption measurements confirm the expected decrease in the specific surface area and pore volume in Ru/CTFs compared to the pristine CTFs due to the additional mass of non-porous Ru-NPs. The isotherms of the metal loaded CTFs resemble the isotherms of the neat CTFs, with lower specific uptake. Most composites exhibit also a IUPAC Type I(b) isotherm with contribution of a Type II isotherm at higher relative pressures, typical for microporous (<2 nm) materials with narrow mesopores (2–50 nm).80 Furthermore, Ru/PhTh-CTF_600 still exhibits a Type IV(a) isotherm with an H2(b) hysteresis. Contrary to the pristine CTFs, Ru/Th-CTF_400 and Ru/Th-CTF_600 now exhibit small H4 hysteresis loops. Table 3 also lists the estimated BET surface areas based on the CTF weight percentage. Most experimental surface areas are smaller than expected, except for the Ru/Th-CTFs and for Ru/PhTh-CTF_400. Possibly, for these latter CTFs, an exfoliation during the microwave reaction may occur and/or the intercalation of NPs enhance the porosity of the structure.63,94–96 The usually lower experimental values can be explained by more distinct pore-blocking effects caused by the deposited NPs or remaining PC in the pores.63
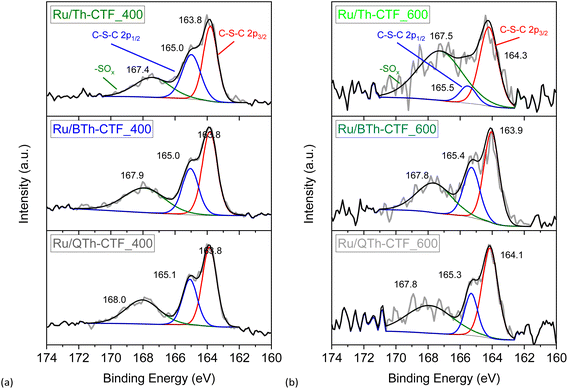
High-resolution X-ray photoelectron spectra (XPS) of the Ru 3p3/2 and 3p1/2 orbital states (∼465 and ∼486 eV, respectively) illustrate the multi-valent oxidation states of the Ru-NPs (Fig. 6). The Ru(0) state can be assigned to the binding energies of ∼462 and ∼484 eV for the 3p3/2 and 3p1/2 peaks, respectively. The presence of Ru(n+) species is evidenced by peaks at ∼465 and ∼487 eV and attributed to surface oxidation during exposure to air.20,97 However, the Ru(0) state exhibits the largest relative contribution with at least ∼58 at% (Table S3†). The N 1s high-resolution spectra (Fig. S15†) can be deconvoluted into four peaks corresponding to pyridinic, pyrrolic, graphitic and oxidized nitrogen (based on the nomenclature used for N-doped carbon materials) with maxima at ∼398, ∼399, ∼400, and ∼402 eV, respectively.63,76,98 Notably the peak at ∼398 eV is also referred to the nitrogen in the formed triazine ring.97 According to the peak fitting, the nitrogen species exhibit variations in their relative proportions, as summarized in Table S3.† Ru/QTh-CTF_600 and Ru/Th-CTF_400 demonstrate the highest proportions of pyridinic nitrogen and pyrrolic nitrogen, respectively, while Ru/Th-CTF_600 exhibits the highest amount of graphitic nitrogen. Furthermore, with an additional temperature step at 600 °C during ionothermal synthesis, the amount of oxidized nitrogen tends to increase in the materials with up to ∼26 at% in the Ru/PhTh-CTF_600. Notably, graphitic and pyridinic nitrogen are discussed as causes for an improved electrical conductivity and activity in CTFs and N-doped carbon materials.28,59,64 Peak fitting of the S 2p high-resolution spectra (Fig. 7) reveals the presence of thiophene moieties (organic sulfide species, C–S–C) in the CTF evidenced by peaks at ∼164 and ∼165 eV. Peaks at ∼168 eV correspond to different organic sulfur oxide species (–SOx–, with x = 1–4), such as sulfinyl, sulfone, sulfonate, or sulfate.20 Nevertheless, the organic sulfide species is dominating in all Ru/CTFs with around 60–70 at% except in Ru/Th-CTF_600 where the sulfur oxide species exceeds 50 at% (Table S3†).
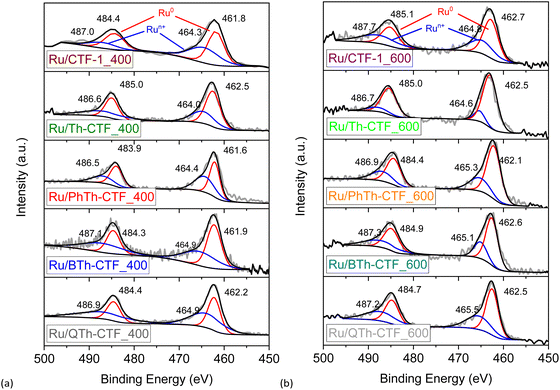 | ||
| Fig. 6 High resolution X-ray photoelectron spectra of Ru 3p orbitals from (a) Ru/CTF_400 and (b) Ru/CTF_600. | ||
Hydrogen evolution reaction in H2SO4
The electrocatalytic performance of the Ru/CTF composites towards HER was tested with a three-electrode setup (see Experimental section for details). Polarization curves of the composites tested in 0.5 mol L−1 H2SO4 are presented in Fig. 8a and b. Generally, samples for which the underlying CTF is synthesized at 400 °C lie towards higher potentials. This is seemingly due to a lower electrical conductivity of these CTFs.59,64 In accordance with literature findings, the synthesis temperature can exert a predominant influence on the electrocatalyst performance despite the loss of thiophene.28,63,64 The polarization curves of Ru/BTh-CTF_600, Ru/QTh-CTF_600 and Ru/PhTh-CTF_600 are located close to the equilibrium potential of the HER at 0 mV vs. RHE similar to Pt/C, used as benchmark (Fig. 8b). Fig. 8c presents the overpotentials at a current density of 10 mA cm−2. Here, Ru/BTh-CTF_600 and Ru/QTh-CTF_600 demonstrate remarkably low overpotentials with 30 and 42 mV. Ru/PhTh-CTF_600 with the lowest thiophene content also has a remarkably low 56 mV overpotential. For comparison, Pt/C possesses an overpotential of 9 mV in good agreement with the literature (∼10 mV).99,100 The introduction of thiophene-bridges into the CTF has no straightforward trend for the electrocatalytic activity of the Ru/CTF samples since parameters such as the elemental composition (by at% and species distribution), Ru-NP size, Ru metal content, the CTF surface area and the porosity vary independently with the underlying monomer. Nevertheless, the thiophene containing samples can reach low overpotentials down to 30 mV whereas the non thiophene containing Ru/CTF-1_600 sample exhibits 90 mV.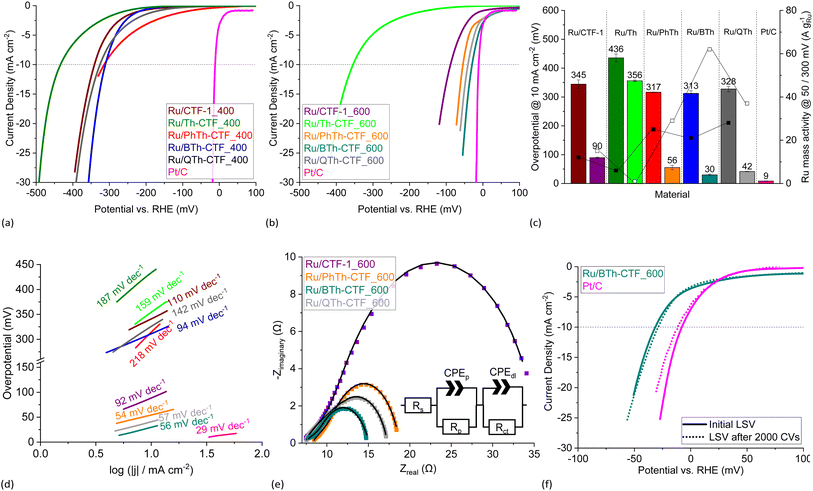 | ||
| Fig. 8 HER LSV polarization curves in 0.5 mol L−1 H2SO4 of (a) Ru/CTF_400 and (b) Ru/CTF_600. (c) Overpotentials (left bars for _400, right bars for _600 samples), Ru mass activities (filled boxes @ 300 mV, empty boxes @ 50 mV) and (d) Tafel plots of Ru/CTFs. (e) Nyquist plots at −100 mV vs. RHE and fitted EEC models (solid lines) of Ru/CTF_600 with resistors for the electrolyte resistance, Rs, the electrode porosity, Rp, and the charge transfer, Rct, as well as constant phase elements assigned to the electrode porosity, CPEp, and double layer capacitance, CPEdl.109–111 (f) LSV polarization curves of Ru/BTh-CTF_600 after 2000 CV cycles durability test. | ||
Furthermore, subsequent coating of the Ru/CTF-1_600 electrode with molecular thiophene does not show signs of catalyst poisoning to the Ru active sites for low molar Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratios (Fig. S17†). Until molar Ru
S ratios (Fig. S17†). Until molar Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratios of 1
S ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 the measured overpotentials remain nearly unchanged despite the affinity of Ru towards sulfur and the possibility of molecular thiophene to occupy the active Ru sites.101,102 The incorporated thiophene units in the CTF support are probably not small enough to reach all active Ru sites. Thus, the results indicate that small amounts of sulfur species do not act as catalyst poison towards Ru.
2.5 the measured overpotentials remain nearly unchanged despite the affinity of Ru towards sulfur and the possibility of molecular thiophene to occupy the active Ru sites.101,102 The incorporated thiophene units in the CTF support are probably not small enough to reach all active Ru sites. Thus, the results indicate that small amounts of sulfur species do not act as catalyst poison towards Ru.
For Ru/CTF_400 composites with thiophene-bridges, overpotentials from 313 to 328 mV were measured evidencing a slight positive effect of phenyl-, di- and tetrathiophene units compared to Ru/CTF-1_400 having 345 mV. Only for Ru/Th-CTF higher overpotentials were measured, possibly caused by the low carbon content or a larger band gap by the bridging thiophene units affecting the electronic properties of the support.103–106 As reported by Gershoni-Poranne et al. already a few additional repeating units in thiophene oligomers can advantageously decrease the electronic band gap drastically.103 The introduction of a donor–acceptor system and a three dimensional layered structure can further narrow the band gap of the support.104,106 Ru mass activities in Fig. 8c correlate with the measured overpotentials. In particular, Ru/PhTh-CTF_600, Ru/QTh-CTF_600 and Ru/BTh-CTF_600 demonstrate high activities with up to 62 A gRu−1 at 50 mV. Ru/CTF-1_600 possesses 15 A gRu−1. Ru/Th-CTF_600 shows the lowest mass activity among the Ru/CTF_600 samples with 1 A gRu−1. Furthermore, for samples with CTFs synthesized at 400 °C Ru mass activities range from 6 to 28 A gRu−1 at 300 mV overpotential. Notably, the metal content can also determine the overpotentials of the composites. A series of Ru/BTh-CTF_600 samples with 12, 22, 30 and 43 wt% Ru shows an optimum at a loading of 30 wt% metal content (Fig. S18 and S19†).
Tafel slopes of Ru/PhTh-CTF_600, Ru/BTh-CTF_600 and Ru/QTh-CTF_600 show similar values between 54 and 57 mV dec−1 significantly lower than Ru/CTF-1_600 having 92 mV dec−1 (Fig. 8d). Here, kinetics could be approximated by the Heyrovsky reaction as rate determining step (∼40 mV dec−1) for the thiophene containing CTFs, where an H-atom (either adsorbed Had or as metal-hydride) binds with another proton and an extra electron to form a hydrogen molecule (in acidic media: Had/M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + e− + H+ → M + H2).7 Ru/Th-CTF_600 demonstrates the highest slope among the Ru/CTF_600 composites correlating with the lower overall performance. The Tafel slope is not only an indicator for the rate determining reaction mechanism, but it is also an evaluation approach for electrocatalysts. A higher Tafel slope means an unfavorable stronger increase of the potential difference with increase of current density.7,13 Pt/C, known for its close-to-thermoneutral hydrogen binding, exhibits an expected low Tafel slope of 29 mV dec−1 (lit.: ∼23 mV dec−1)100 indicating a stronger influence by the Tafel step on the reaction kinetics.7,107,108
H + e− + H+ → M + H2).7 Ru/Th-CTF_600 demonstrates the highest slope among the Ru/CTF_600 composites correlating with the lower overall performance. The Tafel slope is not only an indicator for the rate determining reaction mechanism, but it is also an evaluation approach for electrocatalysts. A higher Tafel slope means an unfavorable stronger increase of the potential difference with increase of current density.7,13 Pt/C, known for its close-to-thermoneutral hydrogen binding, exhibits an expected low Tafel slope of 29 mV dec−1 (lit.: ∼23 mV dec−1)100 indicating a stronger influence by the Tafel step on the reaction kinetics.7,107,108
The Tafel reaction is the chemical recombination of two H-atoms (adsorbed or metal hydride) (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + M
H + M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H → 2M + H2).7 The performances of the Ru/CTF_400 composites are more sluggish than those with CTFs obtained at 600 °C and range from 94 to 218 mV dec−1. For Ru/PhTh-CTF_400, Ru/Th-CTF_400 and Ru/QTh-CTF_400 the Volmer step (>120 mV dec−1), which is the electrochemical adsorption of protons (M + e− + H+ → M
H → 2M + H2).7 The performances of the Ru/CTF_400 composites are more sluggish than those with CTFs obtained at 600 °C and range from 94 to 218 mV dec−1. For Ru/PhTh-CTF_400, Ru/Th-CTF_400 and Ru/QTh-CTF_400 the Volmer step (>120 mV dec−1), which is the electrochemical adsorption of protons (M + e− + H+ → M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + H2O), is potentially determining in the reaction rate.18,112 In this case, the coverage with hydrogen on the metal surface is limited and the adsorbed hydrogen is converted to molecular hydrogen by the Heyrovsky and/or Tafel step.19 However, a slope of ∼120 mV dec−1 can also be attributed to the Heyrovsky reaction as rate determining step but only in case of a high hydrogen coverage (i.e. ≫60%) on the electrode surface.107,113 However, theoretical calculations by Li et al. postulate an optimization of the strong hydrogen adsorption on Ru clusters by an N,S-doped carbon support due to an improved charge distribution around the active sites.17
H + H2O), is potentially determining in the reaction rate.18,112 In this case, the coverage with hydrogen on the metal surface is limited and the adsorbed hydrogen is converted to molecular hydrogen by the Heyrovsky and/or Tafel step.19 However, a slope of ∼120 mV dec−1 can also be attributed to the Heyrovsky reaction as rate determining step but only in case of a high hydrogen coverage (i.e. ≫60%) on the electrode surface.107,113 However, theoretical calculations by Li et al. postulate an optimization of the strong hydrogen adsorption on Ru clusters by an N,S-doped carbon support due to an improved charge distribution around the active sites.17
Exchange current densities were extracted from the Tafel plots to evaluate the reaction rate (i.e. transfer of electrons) of the electrocatalyst at the equilibrium potential (Table S4†).7,19,20 Calculated values range from 0.1 to 3.0 mA cm−2. The highest value was determined for Ru/BTh-CTF_600 followed by Pt/C with 2.7 mA cm−2 located in a commonly found magnitude indicative for a fast reaction rate.7,20 Generally, Ru/CTF_600 samples reveal higher exchange current densities compared to the other samples in good correlation with the estimated overpotentials.
Electrochemical impedance spectroscopy (EIS) was performed at −100 mV vs. RHE, and the Nyquist plots are illustrated in Fig. 8e. Impedance profiles are almost entirely dominated by depressed arcs decreasing in size from Ru/CTF-1_600 to Ru/BTh-CTF_600 which can be attributed to an improved HER processes.109–111,114 Moreover, Ru/CTF_600 samples clearly show an additional small semi-circle at high frequencies. For evaluation, these data points were fitted to an electrical equivalent circuit (EEC) model with two series connected time constants, commonly used to interpret the contribution of the electrode porosity at higher frequencies (Rp-CPEp) and of the HER charge transfer located at lower frequencies (Rct-CPEdl).109–111 Constant phase elements were used to describe the deviation from idealized capacitors caused by different types of inhomogeneities giving better fittings.109–111 Determined parameters from the fittings are listed in Table S4† and present a comparable trend to the overpotentials. Ru/BTh-CTF_600 shows the lowest charge transfer resistance with 5.2 Ω, while Ru/QTh-CTF_600, Ru/PhTh-CTF_600 and Ru/CTF-1_600 have higher resistances with up to ∼23 Ω. Samples with CTFs, which were heated only to 400 °C during synthesis show almost no apparent hydrogen production at −100 mV vs. RHE resulting in broader Nyquist plots (Fig. S20a†). A cyclic voltammetry (CV) durability test with 2000 cycles was carried out for Ru/BTh-CTF_600 (Fig. 8f) having the lowest overpotential in 0.5 mol L−1 H2SO4 among the Ru/CTF composites. Even after 2000 CV cycles the tested sample demonstrated a robust overpotential of 29 mV and a Tafel slope of 56 mV dec−1. In case of the benchmark material Pt/C the overpotential increases slightly from 9 to 12 mV and the Tafel slope from 29 to 32 mV dec−1. Subsequent TEM measurements showed no apparent changes in the morphology and average size of the Ru particles, which remained at 2 ± 1 nm (Fig. S21†).
Hydrogen evolution reaction in KOH
In 1 mol L−1 KOH the Ru/CTF composites indicate a more distinct behavior. In particular composites with thiophene synthesized at 600 °C demonstrate polarization curves that are very close to the potential of the HER at 0 V vs. RHE (cf.Fig. 9a and b). Overpotentials derived from the polarization curves were presented in Fig. 9c, whereby the thiophene containing Ru/CTF_600 samples demonstrate overpotentials down to 3 mV in comparison to Ru/CTF-1_600 having 26 mV and Pt/C with 26 mV (lit.: 25 mV).25 Ru/Th-CTF_600 exhibits again the highest overpotential among the CTF_600 series, albeit lower than in the acidic electrolyte. The good performance of Ru-based electrocatalysts in alkaline electrolyte is known especially when these materials contain organic supports featuring moieties with N and/or S heteroatoms (see comparison of materials, Table S5†). Typical for many electrocatalysts, the performance of Pt/C in 1 mol L−1 KOH is lower compared to the performance in 0.5 mol L−1 H2SO4.6,13,99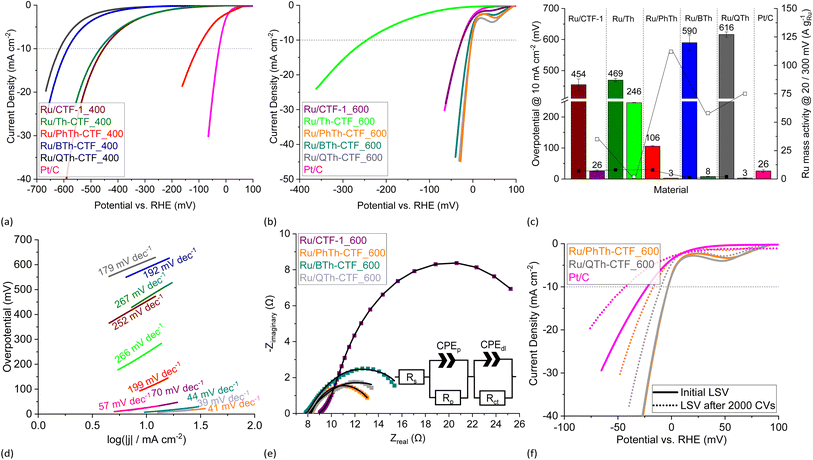 | ||
| Fig. 9 HER LSV polarization curves in 1 mol L−1 KOH of (a) Ru/CTF_400 and (b) Ru/CTF_600. (c) Overpotentials (left bars for _400, right bars for _600 samples), Ru mass activities (filled boxes @ 300 mV, empty boxes @ 20 mV) and (d) Tafel plots of Ru/CTFs. (e) Nyquist plots at −20 mV vs. RHE and fitted EEC models (solid lines) of Ru/CTF_600 with resistors for the electrolyte resistance, Rs, the electrode porosity, Rp, and the charge transfer, Rct, as well as constant phase elements assigned to the electrode porosity, CPEp, and double layer capacitance, CPEdl.109–111 (f) LSV polarization curves of Ru/PhTh-CTF_600 and Ru/QTh-CTF_600 after 2000 CV cycles durability test. | ||
In our tests, the highest overpotentials with up to 616 mV were observed for Ru/Th-CTF_400, Ru/BTh-CTF_400 and Ru/QTh-CTF_400 which could possibly be assigned to the very high sulfur content since Ru/PhTh-CTF_400 and non-thiophene-containing Ru/CTF-1_400 demonstrate lower overpotentials. Here, the results indicate a trade-off behavior between the sulfur content (as well as the temperature during CTF synthesis) and the HER performance. Samples with sulfur contents below ∼6 wt% in the CTF can exhibit improved performances while high amounts always cause weaker performances in the alkaline electrolyte (cf. Fig. S17†).
An outlier is the low performance of Ru/Th-CTF_600. The electrocatalytic performance does not follow the increase in surface area or pore volume, as otherwise Ru/Th-CTF_600 would have to be among the best performing composites. Th-CTF_600 has a sulfur content of only 4.8 wt%, yet, the Th-CTF_600 sticks out with at very high nitrogen content (18.4 wt%) while the other CTF_600's have at the most 7.8 wt% (for BTh-CTF_600) (Table S2†). This suggests that a too high nitrogen content in the CTF support can be disadvantageous. Further, XPS analysis (Table S3†) points for Ru/Th-CTF_600 to a significantly higher percentage of pyrrolic N species (30.4% vs. <20.6%), lower percentage of pyridinic N species (9.1% vs. >21.7%), higher Ru(0) (85% vs. <67.3%) and lower Ru(n+) species (15.0% vs. >32.7%) than for the other Ru/CTF_600 composites. In this context we note that the lower active Ru/Th-CTF_600 has an average Ru-NP size of 3.9 nm, while the other Ru/thiophene-CTF_600s fall below 2.3 nm with their average. Hence, their higher activity can then be a consequence of the better stabilization of smaller Ru-NPs sizes through an optimal sulfur and nitrogen content.
Ru mass activities in Fig. 9c demonstrate a very high activity at 20 mV overpotential for Ru/PhTh-CTF_600 with 114 A gRu−1 followed by Ru/QTh-CTF_600, Ru/BTh-CTF_600, and Ru/CTF-1_600, whereas Ru/CTF_400 samples show Ru mass activities below 8 A gRu−1 at 300 mV.
Tafel analysis reveals again low slopes in the range of 39 to 44 mV for Ru/PhTh-CTF_600, Ru/QTh-CTF_600 and Ru/BTh-CTF_600 implying the Heyrovsky reaction (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + e− + H2O → M + H2 + OH−) as rate determining step (Fig. 9d). For comparison, Pt/C and Ru/CTF-1_600 have much higher slopes of 57 (lit.: 56 mV dec−1)25 and 70 mV dec−1, respectively. Ru/CTF_400 samples all exceed 120 mV dec−1, which is indicative for the Volmer reaction as rate determining step (M + e− + H2O → M
H + e− + H2O → M + H2 + OH−) as rate determining step (Fig. 9d). For comparison, Pt/C and Ru/CTF-1_600 have much higher slopes of 57 (lit.: 56 mV dec−1)25 and 70 mV dec−1, respectively. Ru/CTF_400 samples all exceed 120 mV dec−1, which is indicative for the Volmer reaction as rate determining step (M + e− + H2O → M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H + OH−). Notably, Sun et al. and Wang et al. postulate an improved dissociation of H2O on the surface of Ru clusters on S-doped or N,S-doped graphene oxide compared to the undoped material based on theoretical density functional theory (DFT) and nudged elastic band (NEB) calculations.14,20 Exchange current densities were in the range of 0.1 to 11.0 mA cm−2 (Table S4†). Here, Ru/PhTh-CTF_600 demonstrated the highest exchange current density of 11.0 mA cm−2 followed by Ru/QTh-CTF_600 with 9.3 mA cm−2. For comparison, Pt/C has an exchange current density of 3.2 mA cm−2.20
H + OH−). Notably, Sun et al. and Wang et al. postulate an improved dissociation of H2O on the surface of Ru clusters on S-doped or N,S-doped graphene oxide compared to the undoped material based on theoretical density functional theory (DFT) and nudged elastic band (NEB) calculations.14,20 Exchange current densities were in the range of 0.1 to 11.0 mA cm−2 (Table S4†). Here, Ru/PhTh-CTF_600 demonstrated the highest exchange current density of 11.0 mA cm−2 followed by Ru/QTh-CTF_600 with 9.3 mA cm−2. For comparison, Pt/C has an exchange current density of 3.2 mA cm−2.20
Nyquist plots of the performed EIS measurements at −20 mV vs. RHE are presented in Fig. 9e. Within the tested samples the diameter of the arcs decreases from Ru/CTF-1_600 to Ru/PhTh-CTF_600. Comparable to the results in H2SO4, Ru/CTF_600 samples partially show a small semi-circle at higher frequencies attributed to the influence of the electrode porosity. For evaluation, impedance profiles were fitted to a Voigt model with two time constants.109–111 Ru/PhTh-CTF_600 and Ru/QTh-CTF_600 show the lowest charge transfer resistances while Ru/BTh-CTF_600 and Ru/CTF-1_600 have higher resistances (Table S4†). Furthermore, a strong manifestation of the hydrogen adsorption can be found in the Ru/Th-CTF_600 sample if the Armstrong model is applied, as evidenced by the shoulder of the semicircle at Zreal = >50 Ω (Fig. S20b†), which is also supported by the high Tafel slope of 266 mV dec−1 (Fig. 9). The remaining Ru/CTF_400 samples are generally dominated by large open arcs in the Nyquist plots which can be attributed to an overall sluggish HER accompanied with high resistances and weak capacitive effects. CV stability tests with 2000 cycles were carried out for Ru/PhTh-CTF_600 and Ru/QTh-CTF_600 demonstrating the lowest overpotentials in 1 mol L−1 KOH (Fig. 9f). After 2000 CV cycles the recorded polarization curves show an increase in the overpotential from 3 to 21 mV for Ru/PhTh-CTF_600, from 3 to 11 mV for Ru/QTh-CTF_600 and from 26 to 42 mV for Pt/C. Obviously, the performance of Ru/QTh-CTF_600 is more stable. Tafel slopes increase slightly to 43 mV dec−1 for Ru/QTh-CTF_600, to 52 mV dec−1 for Ru/PhTh-CTF_600 and from 57 to 80 mV dec−1 for Pt/C. TEM measurements after the stability tests show no significant changes in the size and morphology of the particles. In case of Ru/PhTh-CTF_600 the Ru-NP average size has slightly increased from 2 ± 1 to 3 ± 1 nm while for Ru/QTh-CTF_600 the particle size remains unchanged at 2 ± 1 nm (Fig. S21†).
Conclusion
Ionothermally synthesized CTFs with thiophene (Th), phenylthiophene (PhTh), bithiophene (BTh) and quaterthiophene (QTh) building units were successfully decorated with 21 to 33 wt% of Ru-NPs by an efficient decomposition reaction of Ru3(CO)12 in propylene carbonate under microwave-induced heating. TEM images show the stabilization of small 2 to 4 nm NPs while SEM-EDX mapping demonstrates a uniform distribution of Ru and S without local accumulations, which suggests that CTFs are promising as supports for homogenous nanoparticular electrocatalysts. Electrochemical measurements reveal a high performance of Ru-NP decorated CTFs towards HER with overpotentials down to 30 mV in 0.5 mol L−1 H2SO4 and as low as 3 mV in 1 mol L−1 KOH. Importantly, CTFs which were ionothermally synthesized at 600 °C exhibit in general better electrocatalytic performances as at 400 °C. The graphitization or more extended carbonization at 600 °C yields an increased surface area and porosity and a higher electrical conductivity in the CTF framework. At the same time, the sulfur content in the thiophene containing CTFs decreases with temperature while the relative amount of nitrogen remains nearly unaffected. The best performance in the H2SO4 electrolyte towards the HER was found for Ru/BTh-CTF_600 with a nearly unchanged overpotential of 29 mV after 2000 CVs while Ru/QTh-CTF_600 and Ru/PhTh-CTF_600 demonstrate the lowest overpotentials in KOH at 11 and 21 mV after 2000 CVs. Depending on the electrolyte, Tafel slopes range from 54 to 218 mV dec−1 in H2SO4 and from 39 to 267 mV dec−1 in KOH. The comparison of the low active Ru/Th-CTF_600 to the higher active Ru/CTF_600 composites demonstrates that it is not a single parameter that controls the activity but the interplay of parameters that influence and fine-tune the electronic structure and the number of the active sites. Thorough analyses showed that the elemental composition (by at% and species distribution), Ru-NP size, Ru metal content, the CTF surface area and the porosity vary simultaneously with the change in monomer. Still, we have here for the first time demonstrated that thiophene-based CTFs used as carbon support materials for the deposition of metal nanoparticles can reach very low overpotentials and good electrocatalytic properties. Obviously, the introduction of thiophene-bridges into the CTF shows no clear trend in the electrocatalytic tests since other parameters vary simultaneously but independently with the choice of the underlying CTF monomer, the temperature during ionothermal synthesis and the electrolyte.Part of the problem with CTFs lies in the successful but high-temperature ionothermal synthesis conditions which lead to monomer-dependent degradation. Thus, in future work we aim to decouple the correlation of these parameters by testing other synthesis routes for thiophene-CTFs for a more in depth understanding of the origin behind a possible high performance of Ru/CTF composites. Furthermore, heightened attention should be directed to varying heteroatom quantities and heteroatom species in electrocatalysts since the influence on the electrocatalytic performance could involve trade-off dynamics. To conclude, this study reveals the promising opportunity to synthesize tunable thiophene-containing CTFs with anchored Ru-NPs demonstrating high electrocatalytic activities and optimizable properties towards the HER in an acidic and an alkaline electrolyte.
Experimental
Materials
2,5-Thiophenedicarbonitrile (97%) was purchased from BLD Pharm; 1,4-dicyanobenzene (97%), triruthenium dodecacarbonyl, Ru3(CO)12 (99%), graphitized carbon containing 20 wt% platinum, Pt/C, and Nafion 1100 W containing solution from Sigma-Aldrich; 0.5 mol L−1 sulfuric acid solution, H2SO4, and 1.0 mol L−1 potassium hydroxide solution, KOH, from VWR chemicals; anhydrous zinc chloride, ZnCl2 (98%), from Alfa Aesar. Propylene carbonate, PC (99.7%), from Carl Roth was dried for 16 h under high vacuum (<10−6 mbar) before use. Water was purified with a Sartorius Arium Mini ultrapure water system. The synthesis and characterization of the thiophene dinitrile precursors is described in the ESI.†Methods
1H- and 13C-NMR spectra were acquired using a Bruker Avance III-600 spectrometer. Mass spectrometry with electron impact ionization (EI) was performed by a Finnigan Trace DSQ spectrometer with direct sample inlet. Fourier-transform infrared spectroscopy (FT-IR) spectra from 4000 to 400 cm−1 were acquired using a Bruker TENSOR 37 IR on samples in KBr pellets. Elemental analyses (CHNS) were performed using a Elementar Vario MICRO Cube analyzer. Powder X-ray diffractometry (PXRD) was conducted on a Bruker D2 Phaser diffractometer, operated with a scan time of 30 min between 5° and 100° 2θ using Cu-Kα radiation (λ = 1.54182 Å, 30 kV) and equipped with a rotating low-background silicon sample holder. The crystallite size L was calculated using the Match! Version 3.3.0 software according to the Scherrer equation (eqn (1))| L = (K × λ)/(B × cod(θ)) | (1) |
Nitrogen sorption experiments were carried out on a Belsorp MAX-II automatic gas adsorption analyzer and the samples were activated at 120 °C for 5 h under a dynamic vacuum down to ∼10−5 mbar before the measurements. Data evaluation was done with the BELMaster7 software. For calculating the Brunauer–Emmett–Teller (BET) surface areas, adsorption points in the relative pressure range P/P0 of 0.05–0.2 were selected.80 The pore size distributions were calculated based on non-local density functional theory (NLDFT) using the “N2 at 77 K on carbon, slit pore, (NLDFT) equilibrium model”.80,115 Expected specific BET surface areas for the M/CTF composites SBET(M/CTF)theo. were estimated by multiplying the weight percentage of CTF in the composite with the surface area of the neat CTF (eqn (2)), assuming that the non-porous metal nanoparticles do not significantly contribute to the surface area.63
| SBET(M/CTF)theo = (wt% CTF/100) × SBET(CTF) | (2) |
For thermogravimetric analysis (TGA) of the pure CTFs a Netzsch TG 209 F3 Tarsus was used and operated with synthetic air atmosphere and a heating rate of 10 K min−1. TGA curves were baseline corrected with a blank run.116 Gaseous products were analyzed with a GAM 200 mass spectrometer from InProcess Instruments. Flame atomic absorption spectroscopy (AAS) analysis for the ruthenium content in Ru/CTF was measured on a PinAAcle 900T from PerkinElmer. For the AAS sample preparation, exactly weighted amounts (∼3 mg) of the sample were decomposed completely in 20 mL of boiling aqua regia. The solution was concentrated by evaporation to a minimal amount of liquid then diluted with 20 mL of concentrated HCl (36 wt%). The evaporative concentration procedure was repeated, the residue dissolved in 20 mL of semi-concentrated HCl (18 wt%) and diluted with deionized water in a 100 mL volumetric flask. Scanning electron microscopy (SEM) was done on a JEOL JSM-6510 advanced electron microscope equipped with a LaB6 cathode at 5–20 keV in combination with energy-dispersive X-ray spectroscopy (SEM-EDX) for elemental mapping using an Xflash 410 silicon drift detector from Bruker (the samples were not gold-sputtered because the CTFs ensured sufficient conductivity. This way the sulfur content could be quantified without interference from an otherwise overlapping gold signal). Transmission electron microscopy (TEM) was performed using an FEI Tecnai G2 F20 electron microscope operated with an accelerating voltage of 200 kV and an EDAX detector system for EDX analysis. The TEM images were recorded with a Gatan UltraScan 1000P detector.117 The average size and size-distribution were calculated from over 300 manually measured individual particle sizes using the Gatan Digital Micrograph software. X-Ray photoelectron spectroscopy (XPS) was done with a ULVAC-PHI VersaProbe II microfocus spectrometer with an Al Kα X-ray source (1486.8 eV). As reference for the binding energy scale the Cu 2p3/2 signal at 932.6 eV of a Cu standard was used, since the commonly used C 1s signal and the Ru 3d signal overlap.118 The spectra were evaluated using the Casa XPS software, version 2.3.19PR1.0.
Synthesis of CTFs
The ionothermal synthesis of CTF-1 and Th-CTF was carried out according to Kuhn et al.39–41 The preparation of the new ionothermally synthesized thiophene-CTFs was carried out by adapting published CTF procedures.38–41,48,64,119 The amount of 0.3 g of the dinitrile CTF precursor (‘monomer’) was mixed with 10 molar equivalents of anhydrous ZnCl2 in a glovebox under argon atmosphere (see Table S1† for details). The mixture was transferred into a quartz glass ampoule, the ampoule was evacuated, sealed, and then placed in a tube furnace. Warning: high pressure builds up during the synthesis, which necessitate the use of quartz ampules even at 400 °C. Subpar quality of the sealing can lead to explosion. Two treatment protocols were used. In both cases the treatment started by heating up to 400 °C at 3 °C min−1 and holding at this temperature for 40 h. For the first protocol, with the resultant materials designated as “_400”, the thermal treatment was finished at that point. According to the second protocol, with the resultant materials noted as “_600”, the samples were additionally heated at 600 °C for 20 h. The ampoules were opened carefully after cooling down to room temperature and the formed black residue was collected. The product was subsequently ground in a mortar and vigorously stirred in 250 mL of deionized ‘ultrapure’ water for 5 days. Then the product was filtered, dispersed in 200 mL of 2 mol L−1 HCl and left stirring for 1 day. The residue was filtered, washed with water (3 × 75 mL), tetrahydrofuran (3 × 75 mL), and acetone (3 × 75 mL). All samples were dried under high vacuum (<10−6 mbar) for 16 h and stored under Ar atmosphere. The thiophene-based CTFs were designated as X-CTF_400 or X-CTF_600 according to the used thiophene monomer X with X = Th (thiophene), PhTh (phenylthiophene), BTh (bithiophene) and QTh (quaterthiophene) (cf.Fig. 1) and the used temperature (400 or 600 °C). For the case of the phenylene bridge (1,4-dicyanobenzene monomer) the standard CTF-1 acronym was used.39Synthesis of Ru/CTF composites
Ru3(CO)12 (21.1 mg, 0.33 mmol) and 20 mg of CTF were dispersed with stirring in 1.65 mL (2.0 g) of dried propylene carbonate (PC) in a thick-walled microwave pressure vial for 30 min under inert conditions (Ar). The amount of metal precursor was set to yield a Ru/CTF composite with approximately 33 wt% metal content upon quantitative decomposition. The vials were processed in a CEM Discover microwave at 220 °C with a dynamic power of 200 W for 10 min (the auto-relieve for the pressure was set at 7 bar, which was not reached under standard synthetic conditions). The product was suspended in acetonitrile (4 mL) and the solvent, together with unreacted dissolved Ru3(CO)12 and unsupported, still dispersed M-NPs, was separated as the supernatant by centrifugation at 3500 rpm (∼5500×g) for 7 min. This separation procedure was repeated two more times. The final centrifugate residue was dried under vacuum (<10−2 mbar) overnight and stored at ambient conditions under air atmosphere.For the series of Ru/BTh-CTF_600 samples with AAS-determined 12, 22, 30 and 43 wt% Ru, 6.3, 12.8, 21.1 and 31.7 mg, respectively, of Ru3(CO)12 and 20 mg of CTF were dispersed with stirring in 1.65 mL (2.0 g) and treated as described above.
Electrochemical measurements
Electrochemical measurements were performed using a three-electrode setup on an RRDE-3A station from ALS Japan, which included a platinum counter electrode, a rotating glassy carbon (GC) working electrode with a geometric area of 0.196 cm2 and an Interface 1010E potentiostat (Gamry Instruments). For the catalyst ink 2.50 mg of the sample were dispersed in a solution of 20 μL Nafion (∼5 wt%) in 0.50 mL of ethanol. Subsequently, 10 μL of the ink were transferred on the GC electrode for an electrocatalyst loading of 0.255 mg cm−2. The electrolytes were purged with nitrogen for 10 min before measurements and replaced after each sample. The measurements in 0.5 mol L−1 H2SO4 were performed using an Ag/AgCl reference electrode (stored in 3 mol L−1 NaCl). Measured potentials, EAg/AgCl, were subsequently related to the potential, ERHE, of a reversible hydrogen electrode (RHE; ‘Mini-Hydroflex’, Gaskatel). For calibration, the open circuit voltage (OCV) between both electrodes was measured in 0.5 mol L−1 H2SO4 and was subsequently used for determining the relation ERHE = EAg/AgCl + OCV, with OCV = 248 mV.120 In the case of alkaline conditions, samples were tested in 1 mol L−1 KOH electrolyte using the RHE. The linear sweep voltammetry (LSV) curves were recorded from 150 to −600 mV vs. RHE with a scan rate of 10 mV s−1. All measurements were performed twice to ensure reproducibility. Gas bubble formation and mass transport limitations at the electrode surface were prevented by applying an electrode rotation of 3600 rpm. The uncompensated ohmic electrolyte resistance (Ru) was found to be in the range of ∼8 Ω. All polarization curves were corrected after the scan individually by complete Ru compensation according to Ecomp. = Euncomp. − I × Ru.121,122 Measured currents I were normalized to the geometrical surface area of the GC electrode after the measurement. Overpotentials (at 10 mA cm−2 by default), η, were calculated according to η = ERHE − EHER, where EHER = 0 V. Ru mass activities were normalized to the Ru content determined by AAS. The Tafel plots were derived from the LSV curves. For determination of Tafel slopes, b, and exchange current densities, j0, a line, conforming to the Tafel equation, η = b × log(j/j0), with the current density j, was fitted to the linear portion of the Tafel plots. Electrochemical impedance spectroscopy (EIS) was performed at fixed potentials of −100 mV vs. RHE in H2SO4 and of −20 mV vs. RHE in KOH.114 Measurements were conducted in a frequency range from 1 to 100 kHz with an alternating current (AC) amplitude of 10 mV. Fittings, based on an electrical equivalent circuit (EEC) model with series connected branches (simplified porous electrode with one time constant related to HER kinetics) or parallel connected branches (two time constants related to HER kinetics), were generated using a non-linear least-squares routine.109–111,114,123 CV stability tests for the best samples were performed using a graphite counter electrode and a scan rate of 100 mV s−1.Author contributions
Conceptualization, L. R.; methodology, L. R.; validation, L. R.; formal analysis, L. R.; investigation, L. R., T. H. Y. B., B. A., L. S. and T. S.; resources, J. B. and C. J.; writing—original draft preparation, L. R.; writing—review and editing, L. R., I. B. and C. J.; visualization, L. R. and C. J.; supervision, C. J.; project administration, L. R. and C. J.; funding acquisition, C. J.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research of C. J. was supported by a joint National Natural Science Foundation of China-Deutsche Forschungsgemeinschaft (NSFC-DFG) project (DFG JA466/39-1). The authors would like to thank the CeMSA@HHU (Center for Molecular and Structural Analytics @ Heinrich Heine University) for recording the NMR-spectroscopic and mass spectrometric data. We thank Birgit Tommes and Annette Ricken for their help with the IR and AAS measurements.References
- W. Liu, H. Zuo, J. Wang, Q. Xue, B. Ren and F. Yang, Int. J. Hydrogen Energy, 2021, 46, 10548–10569, DOI:10.1016/j.ijhydene.2020.12.123.
- J. A. Okolie, B. R. Patra, A. Mukherjee, S. Nanda, A. K. Dalai and J. A. Kozinski, Int. J. Hydrogen Energy, 2021, 46, 8885–8905, DOI:10.1016/j.ijhydene.2021.01.014.
- R. Ramachandran and R. K. Menon, Int. J. Hydrogen Energy, 1998, 23, 593–598, DOI:10.1016/S0360-3199(97)00112-2.
- S. Sharma and S. K. Ghoshal, Renewable Sustainable Energy Rev., 2015, 43, 1151–1158, DOI:10.1016/j.rser.2014.11.093.
- S. Y. Bae, J. Mahmood, I. Y. Jeon and J. B. Baek, Nanoscale Horiz., 2020, 5, 43–56, 10.1039/C9NH00485H.
- J. Zhu, L. Hu, P. Zhao, L. Y. S. Lee and K.-Y. Wong, Chem. Rev., 2020, 120, 851–918, DOI:10.1021/acs.chemrev.9b00248.
- M. Zeng and Y. Li, J. Mater. Chem. A, 2015, 3, 14942–14962, 10.1039/C5TA02974K.
- D. Woitassek, T. Strothmann, H. Biller, S. Lerch, H. Schmitz, Y. Song, S. Roitsch, T. Strassner and C. Janiak, Molecules, 2023, 28, 405, DOI:10.3390/molecules28010405.
- R. Marcos Esteban, K. Schütte, D. Marquardt, J. Barthel, F. Beckert, R. Mülhaupt and C. Janiak, Nano-Struct. Nano-Objects, 2015, 2, 28–34, DOI:10.1016/j.nanoso.2015.07.002.
- C. Vollmer, R. Thomann and C. Janiak, Dalton Trans., 2012, 41, 9722–9727, 10.1039/C2DT30668A.
- W. Luo, Y. Wang and C. Cheng, Mater. Today Phys., 2020, 15, 100274, DOI:10.1016/j.mtphys.2020.100274.
- H. Wang, W. Fu, X. Yang, Z. Huang, J. Li, H. Zhang and Y. Wang, J. Mater. Chem. A, 2020, 8, 6926–6956, 10.1039/C9TA11646J.
- Y. Yang, Y. Yu, J. Li, Q. Chen, Y. Du, P. Rao, R. Li, C. Jia, Z. Kang, Y. Shen and X. Tian, Nano-Micro Lett., 2021, 13, 1–20, DOI:10.1007/s40820-021-00679-3.
- M. J. Wang, M. Ji, X. Zheng, C. Jiang, H. Zhao, Z. X. Mao, M. Zhang, C. Zhu and J. Xu, Appl. Surf. Sci., 2021, 551, 148742, DOI:10.1016/j.apsusc.2020.148742.
- X. Huang, R. Lu, Y. Cen, D. Wang, S. Jin, W. Chen, I. Geoffrey, N. Waterhouse, Z. Wang, S. Tian and X. Sun, Nano Res., 2023, 16, 9073–9080, DOI:10.1007/s12274-023-5711-1.
- Y. Ito, W. Cong, T. Fujita, Z. Tang and M. Chen, Angew. Chem., Int. Ed., 2015, 54, 2131–2136, DOI:10.1002/anie.201410050.
- C. F. Li, J. W. Zhao, L. J. Xie, Y. Wang, H. B. Tang, L. R. Zheng and G. R. Li, J. Mater. Chem. A, 2021, 9, 12659–12669, 10.1039/D1TA02568F.
- Y. Jiao, Y. Zheng, K. Davey and S. Z. Qiao, Nat. Energy, 2016, 1, 16130, DOI:10.1038/nenergy.2016.130.
- Z. Chen, X. Duan, W. Wei, S. Wang and B. J. Ni, J. Mater. Chem. A, 2019, 7, 14971–15005, 10.1039/C9TA03220G.
- X. Sun, X. Gao, J. Chen, X. Wang, H. Chang, B. Li, D. Song, J. Li, H. Li and N. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 48591–48597, DOI:10.1021/acsami.0c14170.
- J. Oudar, Catal. Rev.: Sci. Eng., 1980, 22, 171–195, DOI:10.1080/03602458008066533.
- J. K. Dunleavy, Platinum Met. Rev., 2006, 50, 110, DOI:10.1595/147106706X111456.
- J. Yu, Y. Guo, S. Miao, M. Ni, W. Zhou and Z. Shao, ACS Appl. Mater. Interfaces, 2018, 10, 34098–34107, DOI:10.1021/acsami.8b08239.
- P. Li, X. Duan, S. Wang, L. Zheng, Y. Li, H. Duan, Y. Kuang and X. Sun, Small, 2019, 15, 1904043, DOI:10.1002/smll.201904043.
- C. Ling, H. B. Li, C. Z. Yuan, Z. Yang, H. B. Chong, X. J. Qian, X. J. Lu, T. Y. Cheang and A. W. Xu, Catal. Sci. Technol., 2021, 11, 3865–3872, 10.1039/D1CY00621E.
- R. K. Shervedani and A. Amini, Carbon, 2015, 93, 762–773, DOI:10.1016/j.carbon.2015.05.088.
- Z. Li, Y. Yao, Y. Niu, W. A. Zhang, B. Chen, X. Zeng and J. Zou, Chem. Eng. J., 2021, 418, 129321, DOI:10.1016/j.cej.2021.129321.
- Y. M. Zhao, T. Z. Ren, Z. Y. Yuan and T. J. Bandosz, Microporous Mesoporous Mater., 2020, 297, 110033, DOI:10.1016/j.micromeso.2020.110033.
- Y. Tian, Z. Wei, X. Wang, S. Peng, X. Zhang and W. M. Liu, Int. J. Hydrogen Energy, 2017, 42, 4184–4192, DOI:10.1016/j.ijhydene.2016.09.142.
- M. T. Giacomini, M. Balasubramanian, S. Khalid, J. McBreen and E. A. Ticianellia, J. Electrochem. Soc., 2003, 150, A588, DOI:10.1149/1.1562932.
- R. Schrebler, M. A. Del Valle, H. Go, C. Veas and R. Co, J. Electroanal. Chem., 1995, 380, 219–227, DOI:10.1016/0022-0728(94)03628-G.
- C. H. Ng, O. Winther-Jensen, C. A. Ohlin and B. Winther-Jensen, Int. J. Hydrogen Energy, 2017, 42, 886–894, DOI:10.1016/j.ijhydene.2016.10.105.
- J. Niedbała, Mater. Chem. Phys., 2009, 118, 46–50, DOI:10.1016/j.matchemphys.2009.06.034.
- S. Elmas, W. Beelders, S. J. Bradley, R. Kroon, G. Laufersky, M. Andersson and T. Nann, ACS Sustain. Chem. Eng., 2017, 5, 10206–10214, DOI:10.1021/acssuschemeng.7b02198.
- T. Li, X. Zhang, Y. Chen, L. Zhong, S. Li, P. Zhang and C. Zhao, J. Mater. Chem. A, 2021, 9, 16967–16973, 10.1039/D1TA04917H.
- S. Chakrabartty, C. S. Gopinath and C. R. Raj, Int. J. Hydrogen Energy, 2017, 42, 22821–22829, DOI:10.1016/j.ijhydene.2017.07.152.
- X. Zhang, X. Zhang, W. Zhu and X. Liang, Dalton Trans., 2022, 51, 6177–6185, 10.1039/D2DT00515H.
- C. Krishnaraj, H. S. Jena, K. Leus and P. Van Der Voort, Green Chem., 2020, 22, 1038–1071, 10.1039/C9GC03482J.
- P. Kuhn, M. Antonietti and A. Thomas, Angew. Chem., Int. Ed., 2008, 47, 3450–3453, DOI:10.1002/anie.200705710.
- P. Kuhn, A. Forget, D. Su, A. Thomas and M. Antonietti, J. Am. Chem. Soc., 2008, 130, 13333–13337, DOI:10.1021/ja803708s.
- P. Kuhn, A. Thomas and M. Antonietti, Macromolecules, 2009, 42, 319–326, DOI:10.1021/ma802322j.
- R. Caballero, B. Cohen and M. Gutiérrez, Molecules, 2021, 26, 7666, DOI:10.3390/molecules26247666.
- K. Wang, Y. Tang, Q. Jiang, Y. Lan, H. Huang, D. Liu and C. Zhong, J. Energy Chem., 2017, 26, 902–908, DOI:10.1016/j.jechem.2017.07.007.
- W. Huang, Q. He, Y. Hu and Y. Li, Angew. Chem., 2019, 131, 8768–8772, DOI:10.1002/ange.201900046.
- W. Huang, J. Byun, I. Rörich, C. Ramanan, P. W. Blom, H. Lu, D. Wang, L. Caire da Silva, R. Li, L. Wang, K. Landfester and K. A. Zhang, Angew. Chem., Int. Ed., 2018, 57, 8316–8320, DOI:10.1002/anie.201801112.
- W. Huang, B. C. Ma, H. Lu, R. Li, L. Wang, K. Landfester and K. A. Zhang, ACS Catal., 2017, 7, 5438–5442, DOI:10.1021/acscatal.7b01719.
- H. Chai, S. Wang, X. Wang, J. Ma and J. Jin, ACS Catal., 2022, 12, 3700–3709, DOI:10.1021/acscatal.2c00285.
- L. Liao, M. Li, Y. Yin, J. Chen, Q. Zhong, R. Du, S. Liu, Y. He, W. Fu and F. Zeng, ACS Omega, 2023, 8, 4527–4542, DOI:10.1021/acsomega.2c06961.
- L. Liao, D. Ditz, F. Zeng, M. Alves Favaro, A. Iemhoff, K. Gupta, H. Hartmann, C. Szczuka, P. Jakes, P. J. C. Hausoul, J. Artz and R. Palkovits, ChemistrySelect, 2020, 5, 14438–14446, DOI:10.1002/slct.202004115.
- L. Frey, J. F. Pöhls, M. Hennemann, A. Mähringer, S. Reuter, T. Clark, R. T. Weitz and D. D. Medina, Adv. Funct. Mater., 2022, 32, 2205949, DOI:10.1002/adfm.202205949.
- H. Liu, X. Zheng, J. Xu, X. Jia, M. Chao, D. Wang and Y. Zhao, ACS Appl. Mater. Interfaces, 2023, 15, 16794–16800, DOI:10.1021/acsami.3c01154.
- Y. Ma, Y. Fu, W. Jiang, Y. Wu, C. Liu, G. Che and Q. Fang, J. Mater. Chem. A, 2022, 10, 10092–10097, 10.1039/D2TA00659F.
- B. Cai, L. Cao, R. Zhang, N. Xu, J. Tang, K. Wang, Q. Li, B. Xu, Y. Liu and Y. Fan, ACS Appl. Energy Mater., 2022, 6, 930–938, DOI:10.1021/acsaem.2c03322.
- R. Sun and B. Tan, Chem. Res. Chin. Univ., 2022, 38, 310–324, DOI:10.1007/s40242-022-1468-4.
- X. Xue, J. Luo, L. Kong, J. Zhao, Y. Zhang, H. Du, S. Chen and Y. Xie, RSC Adv., 2021, 11, 10688–10698, 10.1039/D0RA10862F.
- M. S. Kim, C. S. Phang, Y. K. Jeong and J. K. Park, Polym. Chem., 2017, 8, 5655–5659, 10.1039/C7PY01023K.
- M. Liu, K. Yang, Z. Li, E. Fan, H. Fu, L. Zhang, Y. Zhang and Z. Zheng, Chem. Commun., 2022, 58, 92–95, 10.1039/D1CC05619K.
- C. B. Meier, R. Clowes, E. Berardo, K. E. Jelfs, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, Chem. Mater., 2019, 31, 8830–8838, DOI:10.1021/acs.chemmater.9b02825.
- Y. Li, S. Zheng, X. Liu, P. Li, L. Sun, R. Yang, S. Wang, W. Zhong-Shuai, X. Bao and W. Q. Deng, Angew. Chem., 2018, 130, 8124–8128, DOI:10.1002/ange.201711169.
- Y. Zhang and S. Jin, Polymers, 2018, 11, 31, DOI:10.3390/polym11010031.
- Y. Zheng, N. A. Khan, X. Ni, K. A. Zhang, Y. Shen, N. Huang, X. Y. Kong and L. Ye, Chem. Commun., 2023, 59, 6314–6334, 10.1039/D3CC00712J.
- Z. Xiang, D. Cao, L. Huang, J. Shui, M. Wang and L. Dai, Adv. Mater., 2014, 26, 3315–3320, DOI:10.1002/adma.201306328.
- L. Rademacher, T. H. Y. Beglau, T. Heinen, J. Barthel and C. Janiak, Front. Chem., 2022, 10, 945261, DOI:10.3389/fchem.2022.945261.
- S. Öztürk, Y. X. Xiao, D. Dietrich, B. Giesen, J. Barthel, J. Ying, X.-Y. Yang and C. Janiak, Beilstein J. Nanotechnol., 2020, 11, 770–781, DOI:10.3762/bjnano.11.62.
- B. Zhang, Y. Zhang, M. Hou, W. Wang, S. Hu, W. Cen, X. Cao, S. Qiao and B. H. Han, J. Mater. Chem. A, 2021, 9, 10146–10159, 10.1039/D1TA00589H.
- J. D. Yi, R. Xu, G. L. Chai, T. Zhang, K. Zang, B. Nan, H. Lin, Y. L. Liang, J. Lv, J. Luo, Y. B. Huang and R. Cao, J. Mater. Chem. A, 2019, 7, 1252–1259, 10.1039/C8TA09490J.
- A. M. Yau, A. Khaligh and D. Tuncel, J. Appl. Polym. Sci., 2023, 140, e53492, DOI:10.1002/app.53492.
- M. Siebels, C. Schlüsener, J. Thomas, Y. X. Xiao, X. Y. Yang and C. Janiak, J. Mater. Chem. A, 2019, 7, 11934–11943, 10.1039/C8TA12353E.
- S. Qiao, B. Zhang, Q. Li, Z. Li, W. Wang, J. Zhao, X. Zhang and Y. Hu, ChemSusChem, 2019, 12, 5032–5040, DOI:10.1002/cssc.201902582.
- Q. Ju, R. Ma, Y. Pei, B. Guo, Z. Li, Q. Liu, T. Thomas, M. Yang, G. J. Hutchings and J. Wang, Adv. Energy Mater., 2020, 10, 2000067, DOI:10.1002/aenm.202000067.
- L. Liu, C. Song and A. Kong, Mater. Lett., 2020, 277, 128291, DOI:10.1016/j.matlet.2020.128291.
- H. Chai, S. Wang, X. Wang, J. Ma and J. Jin, ACS Catal., 2022, 12, 3700–3709, DOI:10.1021/acscatal.2c00285.
- Y. Zhang, H. Lv, Z. Zhang, L. Wang, X. Wu and H. Xu, Adv. Mater., 2021, 33, 2008264, DOI:10.1002/adma.202008264.
- Z. Wang, J. Liu, Y. Fu, C. Liu, C. Pan, Z. Liu and G. Yu, Chem. Commun., 2017, 53, 4128–4131, 10.1039/C7CC00704C.
- X. Han, Y. Zhang, Y. Dong, J. Zhao, S. Ming and J. Zhang, RSC Adv., 2022, 12, 708–718, 10.1039/D1RA07916F.
- D. Y. Osadchii, A. I. Olivos-Suarez, A. V. Bavykina and J. Gascon, Langmuir, 2017, 33, 14278–14285, DOI:10.1021/acs.langmuir.7b02929.
- S. Dey, A. Bhunia, H. Breitzke, P. B. Groszewicz, G. Buntkowsky and C. Janiak, J. Mater. Chem. A, 2017, 5, 3609–3620, 10.1039/C6TA07076K.
- S. Dey, A. Bhunia, I. Boldog and C. Janiak, Microporous Mesoporous Mater., 2017, 241, 303–315, DOI:10.1016/j.micromeso.2016.11.033.
- Y. Wang, W. Luo, H. Li and C. Cheng, Nanoscale Adv., 2021, 3, 5068–5074, 10.1039/D1NA00424G.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069, DOI:10.1515/pac-2014-1117.
- Y. Zhao, K. X. Yao, B. Teng, T. Zhang and Y. Han, Energy Environ. Sci., 2013, 6, 3684–3692, 10.1039/C3EE42548G.
- D. Schneider, D. Mehlhorn, P. Zeigermann, J. Kärger and R. Valiullin, Chem. Soc. Rev., 2016, 45, 3439–3467, 10.1039/C5CS00715A.
- L. Zu, W. Zhang, L. Qu, L. Liu, W. Li, A. Yu and D. Zhao, Adv. Energy Mater., 2020, 10, 2002152, DOI:10.1002/aenm.202002152.
- H. Duan, D. Wang and Y. Li, Chem. Soc. Rev., 2015, 44, 5778–5792, 10.1039/C4CS00363B.
- B. Schäffner, S. P. Verevkin and A. Börner, Chem. Unserer Zeit, 2009, 43, 12–21, DOI:10.1002/ciuz.200900468.
- M. Siebels, L. Mai, L. Schmolke, K. Schütte, J. Barthel, J. Yue, J. Thomas, B. Smarsly, A. Devi, R. A. Fischer and C. Janiak, Beilstein J. Nanotechnol., 2018, 9, 1881–1894, DOI:10.3762/bjnano.9.180.
- K. Schütte, J. Barthel, M. Endres, M. Siebels, B. Smarsly, J. Yue and C. Janiak, ChemistryOpen, 2017, 6, 137–148, DOI:10.1002/open.201600105.
- R. Marcos Esteban, H. Meyer, J. Kim, C. Gemel, R. A. Fischer and C. Janiak, Eur. J. Inorg. Chem., 2016, 13–14, 2106–2113, DOI:10.1002/ejic.201500969.
- K. Schütte, H. Meyer, C. Gemel, J. Barthel, R. A. Fischer and C. Janiak, Nanoscale, 2014, 6, 3116–3126, 10.1039/C3NR05780A.
- Y. Li, L. A. Zhang, Y. Qin, F. Chu, Y. Kong, Y. Tao, Y. Li, Y. Bu, D. Ding and M. Liu, ACS Catal., 2018, 8, 5714–5720, DOI:10.1021/acscatal.8b01609.
- D. Marquardt, F. Beckert, F. Pennetreau, F. Tölle, R. Mülhaupt, O. Riant, S. Hermans, J. Barthel and C. Janiak, Carbon, 2014, 66, 285–294, DOI:10.1016/j.carbon.2013.09.002.
- Y. Tao, W. Ji, X. Ding and B. H. Han, J. Mater. Chem. A, 2021, 9, 7336–7365, 10.1039/D0TA12122C.
- J. Oh, J. S. Lee and J. Jang, Polymers, 2020, 12, 1427, DOI:10.3390/polym12061427.
- M. Cai, D. Thorpe, D. H. Adamson and H. C. Schniepp, J. Mater. Chem., 2012, 22, 24992–25002, 10.1039/C2JM34517J.
- S. Im, Y. R. Park, S. Park, H. J. Kim, J. H. Doh, K. Kwon, W. G. Hong, B. Kim, W. S. Yang, T. Kim and Y. J. Hong, Appl. Surf. Sci., 2017, 412, 160–169, DOI:10.1016/j.apsusc.2017.03.282.
- Y. Si and E. T. Samulski, Chem. Mater., 2008, 20, 6792–6797, DOI:10.1021/cm801356a.
- Z. Zhang, S. Yao, X. Hu, F. Okejiri, K. He, P. Liu, Z. Tian, V. P. Dravid, J. Fu, X. Zhu and S. Dai, Adv. Sci., 2021, 8, 2001493, DOI:10.1002/advs.202001493.
- A. Vesel, R. Zaplotnik, G. Primc and M. Mozetič, Nanomaterials, 2020, 10, 2286, DOI:10.3390/nano10112286.
- R. Y. Shao, L. W. Chen, Q. Q. Yan, W. J. Zeng, P. Yin and H. W. Liang, ACS Appl. Energy Mater., 2021, 4, 4284–4289, DOI:10.1021/acsaem.1c00308.
- J. Yang, Y. Ji, Q. Shao, N. Zhang, Y. Li and X. Huang, Adv. Funct. Mater., 2018, 28, 1803722, DOI:10.1002/adfm.201803722.
- J. M. Badano, M. Quiroga, C. Betti, C. Vera, S. Canavese and F. Coloma-Pascual, Catal. Lett., 2010, 137, 35–44, DOI:10.1007/s10562-010-0336-x.
- J. N. Stanley, P. Benndorf, F. Heinroth, A. F. Masters and T. Maschmeyer, RSC Adv., 2014, 4, 28062–28071, 10.1039/C4RA03474K.
- R. Gershoni-Poranne, A. P. Rahalkar and A. Stanger, Phys. Chem. Chem. Phys., 2018, 20, 14808–14817, 10.1039/C8CP02162G.
- A. Ajayaghosh, Chem. Soc. Rev., 2003, 32, 181–191, 10.1039/B204251G.
- S. Rasmussen, in Encyclopedia of Polymeric Nanomaterials, ed. S. Kobayashi and K. Müllen, Springer, Berlin, Heidelberg, 2013, pp. 1–13, DOI:10.1007/978-3-642-36199-9_5-1.
- R. Gutzler, Phys. Chem. Chem. Phys., 2016, 18, 29092–29100, 10.1039/C6CP06101J.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 13801, DOI:10.1038/srep13801.
- X. Peng, H. Bao, J. Sun, Z. Mao, Y. Qiu, Z. Mo, L. Zhuo, S. Zhang, J. Luo and X. Liu, Nanoscale, 2021, 13, 7134–7139, 10.1039/D1NR00795E.
- V. Bachvarov, E. Lefterova and R. Rashkov, Int. J. Hydrogen Energy, 2016, 41, 12762–12771, DOI:10.1016/j.ijhydene.2016.05.164.
- A. Lasia, in Modern Aspects of Electrochemistry, ed. B. E. Conway, J. O. Bockris and R. E. White, Springer, Boston, 2002, vol. 32, pp. 143–248, DOI:10.1007/0-306-46916-2_2.
- A. Laszczyńska, W. Tylus and I. Szczygieł, Int. J. Hydrogen Energy, 2021, 46, 22813–22831, DOI:10.1016/j.ijhydene.2021.04.103.
- Y. Zheng, Y. Jiao, L. H. Li, T. Xing, Y. Chen, M. Jaroniec and S. Z. Qiao, ACS Nano, 2014, 8, 5290–5296, DOI:10.1021/nn501434a.
- F. Bao, E. Kemppainen, I. Dorbandt, R. Bors, F. Xi, R. Schlatmann, R. Van de Krol and S. Calnan, ChemElectroChem, 2021, 8, 195–208, DOI:10.1002/celc.202001436.
- S. Anantharaj and S. Noda, ChemElectroChem, 2020, 7, 2297–2308, DOI:10.1002/celc.202000515.
- W. J. Roth, B. Gil, W. Makowski, B. Marszalek and P. Eliášová, Chem. Soc. Rev., 2016, 45, 3400–3438, 10.1039/C5CS00508F.
- R. L. Gibson, M. J. Simmons, E. H. Stitt, L. Horsburgh and R. W. Gallen, Chem. Eng. Technol., 2022, 45, 238–248, DOI:10.1002/ceat.202100120.
- M. Luysberg, M. Heggen and K. Tillmann, J. Large-Scale Res. Facil., 2016, 2, A77, DOI:10.17815/jlsrf-2-138.
- J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-Ray Photoelectron Spectroscopy, Perkin-Elmer Corp., Eden Prairie, 1992 Search PubMed.
- A. Bhunia, S. Dey, M. Bous, C. Zhang, W. von Rybinski and C. Janiak, Chem. Commun., 2015, 51, 484–486, 10.1039/C4CC06393G.
- D. Yoon, B. Seo, J. Lee, K. S. Nam, B. Kim, S. Park, H. Baik, S. H. Joo and K. Lee, Energy Environ. Sci., 2016, 9, 850–856, 10.1039/C5EE03456F.
- S. Anantharaj and S. Noda, J. Mater. Chem. A, 2022, 10, 9348–9354, 10.1039/D2TA01393B.
- W. Zheng, ACS Energy Lett., 2023, 8, 1952–1958, DOI:10.1021/acsenergylett.3c00366.
- R. D. Armstrong and M. Henderson, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39, 81–90, DOI:10.1016/S0022-0728(72)80477-7.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and characterization of the thiophene dinitrile CTF precursors. Additional data from CTF and Ru/CTF characterization. Comparison of electrocatalysts. See DOI: https://doi.org/10.1039/d3ta05597c |
| This journal is © The Royal Society of Chemistry 2024 |