Open Access Article
Open Access ArticleCells function as a ternary logic gate to decide migration direction under integrated chemical and fluidic cues†
Hye-ran
Moon
 a,
Soutick
Saha
b,
Andrew
Mugler
a,
Soutick
Saha
b,
Andrew
Mugler
 bcd and
Bumsoo
Han
bcd and
Bumsoo
Han
 *ace
*ace
aSchool of Mechanical Engineering, Purdue University, West Lafayette, IN, USA. E-mail: bumsoo@purdue.edu
bDepartment of Physics and Astronomy, Purdue University, West Lafayette, IN, USA
cPurdue Center for Cancer Research, Purdue University, West Lafayette, IN, USA
dDepartment of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA 15260, USA
eWeldon School of Biomedical Engineering, Purdue University, West Lafayette, IN, USA
First published on 16th December 2022
Abstract
Cells sense various environmental cues and subsequently process intracellular signals to decide their migration direction in many physiological and pathological processes. Although several signaling molecules and networks have been identified in these directed migrations, it still remains ambiguous to predict the migration direction under multiple and integrated cues, specifically chemical and fluidic cues. Here, we investigated the cellular signal processing machinery by reverse-engineering directed cell migration under integrated chemical and fluidic cues. We imposed controlled chemical and fluidic cues to cells using a microfluidic platform and analyzed the extracellular coupling of the cues with respect to the cellular detection limit. Then, the cell's migratory behavior was reverse-engineered to build a cellular signal processing system as a logic gate, which is based on a “selection” gate. This framework is further discussed with a minimal intracellular signaling network of a shared pathway model. The proposed framework of the ternary logic gate suggests a systematic view to understand how cells decode multiple cues and make decisions about the migration direction.
Introduction
Directed cell migration is ubiquitous in many physiological and pathological processes, including cancer metastasis, embryonic development, inflammation, wound healing, and angiogenesis.1–5 During these processes, cells sense multiple and often heterogeneous environmental cues. These cues are chemical, mechanical, and fluidic ones.3,6,7 For instance, cancer cells were induced by various chemokines or growth factors such as TGF-β to have a biased direction in their migration.8–10 Interstitial fluid flow also plays a key role in inducing directed migration of cancer, endothelial, and immune cells.11–15 However, it is still puzzling how cells decipher simultaneous heterogeneous cues and decide their migration direction.Directed cell migration by chemical or fluidic cues has been studied to identify key signaling molecules. Cells sense a chemical cue as a concentration gradient of various chemokines or growth factors through corresponding receptors on the cell surfaces, including G-protein coupled receptors (GPCR) and receptor tyrosine kinases (RTK).10,16,17 After sensing the chemicals, cells transduce the cues into the migratory signal via intracellular pathways to execute the directed migration. It has been reported that RTKs locally activate GTPases through the Rho subfamily, phosphoinositide3-kinase (PI3K), and ROCK/LIMK/cofilin pathways when detecting corresponding chemical cues to regulate actin polymerization, microtubule dynamics, and adhesion dynamics, eventually governing cellular polarization and asymmetric force generation for directed migration.17–22 Fluidic cue can also lead to the directed migration by activating focal adhesion kinases (FAK) through integrin, ERK, and PI3K.23–26 Indeed, cell trajectories were mostly aligned to the flow streamlines with FAK activation, where the FAK are signaling networks governing mechanotransduction involved in local activation of the Rac pathway to govern actin dynamics.23,24 T lymphocytes could also sense the fluidic cue and showed directed migration toward the upstream direction of blood flow requiring LFA-1 of T-cell integrins and corresponding pathways such as PI3K and ERK.13,27
Besides biochemical aspects of directed migration, quantitative biophysical aspects of the migration also have been investigated and provide complementary understanding on the behavior of cellular sensing and processing machinery. Cellular sensory precision for detecting shallow chemical gradients has been analyzed considering biochemical relations of the ligand–receptor binding kinetics.28–31 The physical limits to cellular processing ability have also been approached when cells sense and process multiple chemical cues concurrently.32,33 In cellular signal processing, the spatial and temporal variations for the intracellular signaling molecules' diffusion and activation have been modeled to understand better the cellular sensing and processing machinery.34–36
Despite advances in understanding the signaling networks regulating directed migration, it is still difficult to predict migration direction when cells are exposed to multiple heterogeneous cues, such as chemical and fluidic cues. Cellular response to multiple cues has been studied in the context where both cues are chemical. In many cases, exposing cancer cells to two growth factors showed a synergistic effect on cell motility.37–40 When one of the growth factors stimulates cells in the form of a gradient, the other can have either a synergistic41,42 or antagonistic9 effect on directional accuracy or motility for directional migration. While the synergistic combination of the chemical cues was shown from the cooperative effect of their downstream pathways,43,44 antagonistic results were illustrated with cells' signal-processing capacity.9 The cell's ability to sense and process multiple chemical cues simultaneously has been physically modeled to predict the cellular capability32,33,45 or to distinguish one chemical from another.46–48 The integration of chemical and fluidic cues, however, still remains elusive to predict how and which direction is determined, although cells are frequently exposed to both chemical and fluidic cues in vivo.49,50
In the present study, we reverse-engineer the cellular signal processing system for directed migration under integrated chemical and fluidic cues and construct a minimal functional system capable of predicting the cell's migration direction. To elucidate a biophysical understanding of how cells decipher integrated chemical and fluidic cues to determine migration direction, we initially investigate the extracellular coupling of the chemical and fluidic cues. Specifically, by applying pressure-driven flow simultaneously with the chemical concentration gradient in the microfluidic platform, we assess two scenarios: 1) parallel flow as an additive cue with the chemical gradient and 2) counter flow as a competing cue to the chemical gradient. The extracellular complication of the integrated two cues is analyzed concerning the cellular detection limit. Then, we expose the controlled TGF-β gradient with the fluidic cue on a murine pancreatic cancer cell line (KIC) embedded in the collagen matrix in the microfluidic platform. Under these integrated cues, we characterize the directional accuracy of cell migration. The results are reverse-engineered to construct a minimal intracellular signaling network with a shared pathway model9,51 and illustrate it with a logic gate. This framework is further discussed to lay the groundwork for a systematic approach to understanding how cells decode multiple cues to decide their migration direction.
Materials and methods
Cells and reagents
KIC is a murine pancreatic cancer cell line isolated from genetically engineered mouse model for pancreatic adenocarcinoma in which Kras was combined with deletion of the Ink4a locus (Ink4a/ArfL/L).52–54 The KIC cells showed mesenchymal phenotype in response to TGF-β, whose invasion potential increased and directed migration was induced.8,9 These cells were cultured in RPMI 1640 with 2.05 mM L-glutamine (GE Healthcare Bio-Sciences Corp., MA, USA) supplemented by 5% v/v fetal bovine serum (FBS) and 100 μg ml−1 penicillin/streptomycin (P/S). The cells were regularly harvested by 0.05% trypsin and 0.53 mM EDTA (Life technologies, CA, USA) when grown to ∼80% confluency in 25 cm2 T-flasks and incubated at 37 °C with 5% CO2. Harvested cells were used for experiments, or sub-cultured while maintaining them below 15th passage.Convection-driven signal environment in a microfluidic platform
In this study, we use the in vitro microfluidic platform to engineer microenvironment involving both chemical and pressure variances. The in vitro microfluidic device is composed of center, source, and sink channels with 100 μm in thickness.9,55 The center channel is 1 mm wide compositing collagen matrix with cells where the conditions of chemical and fluidic cues are controlled through the adjacent 300 μm wide channels of source and sink. We manipulate concentration of transforming growth factor beta-1 (TGF-β, Invitrogen, CA, USA) between source and sink channels to develop chemical gradients in the center channel. Meanwhile, we engineer the pressure variance between source and sink channels so that the pressure driven flow is generated in the center channel. The concentration profile in the center channel could be determined by its diffusion and advection. To apply the interstitial flow in a presence of TGF-β gradient, we always filled the source channel with 10 nM of TGF-β while the sink channel was filled with normal culture medium. The concentration range is selected not to saturate the cell's signal processing capacity.9 The concentration profile of TGF-β was analyzed with simple mathematical approach through the governing equation and corresponding boundary conditions, providing structural intuition of the gradient features. We simplified the device geometry as a 1-D, used constant parameters of diffusivity (Deff) and flow velocity (vf = U), and evaluated the steady state (∂Ci/∂t = 0).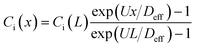 | (1) |
In the center channel of the microfluidic platform, KIC cells were uniformly implanted in 2 mg ml−1 type I collagen mixture (Corning Inc., NY, USA) supplemented with 10X PBS, NaOH, HEPES solution, FBS, Glu, P/S, and cell-culture level distilled water. Initial cell density was 8 × 105 cells per ml consistently for all groups. After loading, the cells in the collagen matrix were cultured with basic mediums for 24 hours. Then, cells were exposed by engineered signal environment accordingly.
Pressure driven flow in the microfluidic platform
We controlled the low Reynolds flow through the collagen matrix (0.5–4 μm s−1) that corresponded to the interstitial flow rate of the tumor microenvironment.56,57 In controlling the flow rate inside the collagen matrix, we considered the Brinkman equation: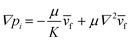 | (2) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) f is the average flow velocity, μ is a dynamic viscosity, and K is the permeability of the culture medium in a type I collagen matrix of 2 mg ml−1.57,58 In the literatures, the permeability K in a type I collagen matrix of 2 mg ml−1 has been reported to the range of 10−14–10−13 m2.59–61 Based on that, we averaged the value range of reported permeability, calculated as K = 5 × 10−14 m2. To control the flow velocity of around 1 μm s−1, we considered the pressure differences between the source and sink channels as ΔP (Psource − Psink) = ∼2 mm H2O, adapting ∇p ∼ 19.6 Pa mm−1 in the center channel. The hydrostatic pressure differences are controlled by applying the medium level differences between two channel reservoirs with a presence of drain flow. The drain flow was applied aiming to maintain the pressure difference between the channels consistently. Here, we assumed that the drain flow at the sink channel is not critically interrupted the interstitial flow at the center channel with relatively small area of the interface. The consistent drain flow at the channel in lower pressure (Qdrain = 10 μl h−1) was applied considering potential pressure drop caused by the flow. The drain flow was achieved by connecting the sink channel with syringe pump (NE-1000-ES, New Era pump system, USA).
f is the average flow velocity, μ is a dynamic viscosity, and K is the permeability of the culture medium in a type I collagen matrix of 2 mg ml−1.57,58 In the literatures, the permeability K in a type I collagen matrix of 2 mg ml−1 has been reported to the range of 10−14–10−13 m2.59–61 Based on that, we averaged the value range of reported permeability, calculated as K = 5 × 10−14 m2. To control the flow velocity of around 1 μm s−1, we considered the pressure differences between the source and sink channels as ΔP (Psource − Psink) = ∼2 mm H2O, adapting ∇p ∼ 19.6 Pa mm−1 in the center channel. The hydrostatic pressure differences are controlled by applying the medium level differences between two channel reservoirs with a presence of drain flow. The drain flow was applied aiming to maintain the pressure difference between the channels consistently. Here, we assumed that the drain flow at the sink channel is not critically interrupted the interstitial flow at the center channel with relatively small area of the interface. The consistent drain flow at the channel in lower pressure (Qdrain = 10 μl h−1) was applied considering potential pressure drop caused by the flow. The drain flow was achieved by connecting the sink channel with syringe pump (NE-1000-ES, New Era pump system, USA).
To verify the scale of the controlled flow rate, we measured fluorescent beads' (0.2 μm diameter) trajectories. The average ± standard error of the collected particle velocities was 1.5 ± 0.048 μm s−1 (Fig. S1†). By using the measured value of the flow velocity, the permeability K for 2 mg ml−1 type I collagen matrix was calculated as 8 × 10−14 m2 where μ = 0.84 cP for DMEM,57 which is within comparable scale with the reported permeability range of 10−14–10−13 m2.59–62
Characterization of the directed cell migration
Live-cell time-lapse imaging with an inverted microscope (Olympus IX71, Japan) is utilized to characterize the cell migration. A stage top incubator allows maintaining the microfluidic platform at 37 °C with 5% CO2 condition during imaging as described in our previous studies.55 Migrating KIC cells were captured every 5 minutes for 3 hours. The time-lapse images are captured 3 hours after applying either chemical or pressure variances to give an adjustment time for stable environmental condition. The bright-field time lapse images are segmented to analyze cell trajectories by using ImageJ. A specific cell region is determined by the image contrasts which provides clear boundaries between cells and background. Then, cell centroids are collected in the converted monochrome images. A collection of the centroids of cell areas at different time points are defined as a cell trajectory. In collecting cell trajectories, we reject trajectories of cells under division and the stationary cells. This is because the dividing cells could affect for cell polarity63 and the stationary cells could underestimate the cell movement characteristics. The stationary cells were defined when a cell's total trajectories were less than the estimated cell diameter.The directed cell migration is characterized by motility and directional accuracy.55 The direction of the cell trajectories is analyzed based on the direction of environmental signals. We measure directional accuracy using the directional accuracy index (DAI)
DAI = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (3) |
Statistical analysis for experiments
All experimental controls were repeated until the number of trajectories in each case >50 trajectories. A trajectory was evaluated with a quantified DAI and a speed. To compare the directional accuracy, the distribution of DAIs was reported in box plots with distribution of data points. A data point in the box plots indicates the metric of a cell trajectory. Median values of the distribution were statistically examined with Mann–Whitney nonparametric test where the statistical significance was evaluated when U < 0.05 in Fig. 1D and 3C.Results
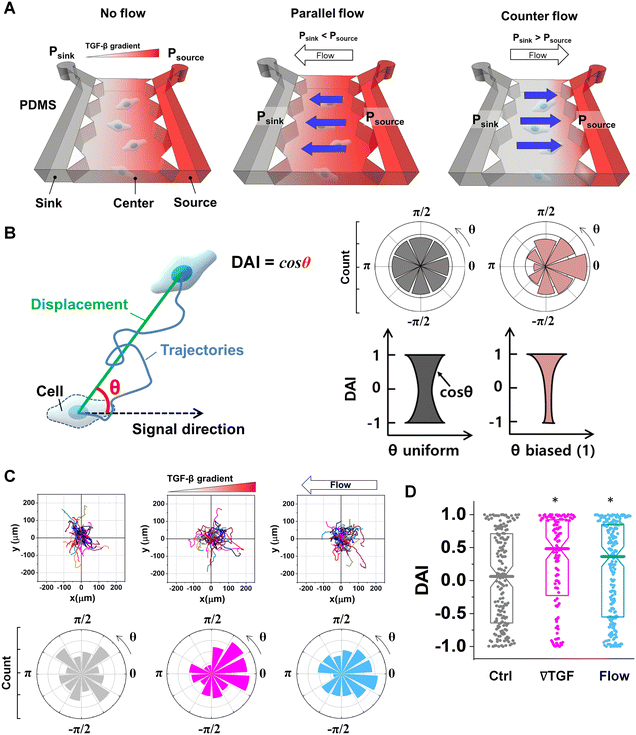
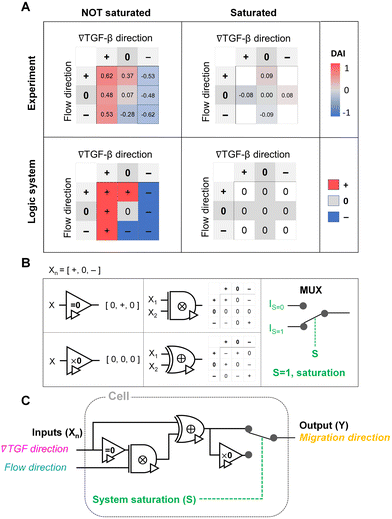
Creation of a cellular microenvironment with controlled chemical and fluidic cues
To evaluate the effect of the integrated chemical and fluidic cues, we engineer the cellular microenvironment by using a microfluidic platform having a center and two side channels.9,55 A center channel contains cells embedded in a type I collagen mixture in the platform, where two adjacent source and sink channels are filled with the medium. The chemical gradient and pressure-driven flow are simultaneously developed in the center channel by manipulating both chemical concentration and pressure variances between source and sink channels as described in Materials and methods. Here, we consider two combinations based on the flow direction: parallel and counter flow (Fig. 1A). A parallel flow is represented as a positive direction (+) to the chemical gradient where the flow direction is from the higher to lower concentration of the chemical. On the other hand, the direction of the counter flow is represented as a negative direction (−) to the chemical gradient flowing from lower to higher concentration. By using the platform, we investigate the migration behaviors of cells under the engineered environment of integrated chemical and fluidic cues. We use murine pancreatic cancer cells (KIC cells) whose directed migration is stimulated by the TGF-β gradient.8–10 The directed cell migration is often characterized by its directional accuracy, directional persistence, and motility.55,64 In this study, we focus on the directional accuracy, representing how cells accurately follow the cue direction. In order to quantify the cellular directional accuracy to an environmental cue, we use a directional accuracy index (DAI; see Materials and methods) as defined in Fig. 1B. Here, we note that the DAI distribution of the control is concentrated at the extremes of −1 and 1, this is an expected and well-known consequence of the cosine in its definition, as a uniform distribution of angles produce a nonuniform distribution of cosines that is more concentrated at the extremes.9,55,65,66Extracellular combination of the chemical and fluidic cues creates regions where the chemical cue becomes below the cellular sensing limit
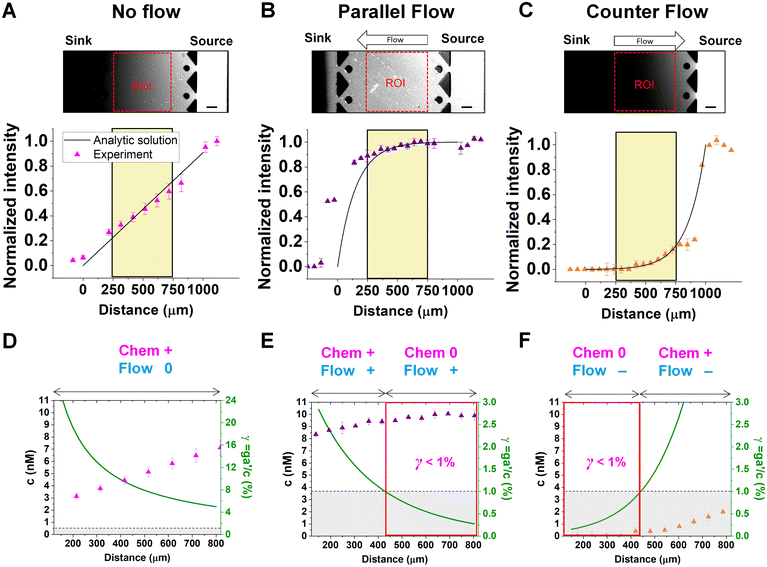
Chemical cues in the cellular microenvironment are transported by not only diffusion but also interstitial fluid flow.56,57,67 To characterize this complex extra-cellular environment, the concentration profiles of a chemical cue in the presence of the flow on the microfluidic platform are measured and predicted by using FITC-conjugated dextran of 10 kDa in Fig. 2. The 10 kDa FITC-dextran is selected to simulate the diffusion transport of TGF-β based on the hydrodynamic radius comparison.55,68 The intensity measurement is considered as concentration of the FITC-dextran. Without flow, the concentration gradient of a chemical cue is a linear profile (Fig. 2A). When the interstitial fluid flow of 1.5 μm s−1 was imposed along the chemical cue (i.e., parallel flow configuration in Fig. 2B), the gradient becomes shallow in the region of interest (ROI) except the edge region (x ∼ 250 um). Since the parallel flow augments the advection of the molecules along the chemical cue gradient, the overall concentration value increases (Fig. 2B). On the contrary, the counter flow suppresses the chemical cue gradient and lower the overall chemical cue concentration. Near the edge of source side (x ∼ 750 um), the gradient grows and becomes steep (Fig. 2C). This result demonstrates that the concentration gradient of chemical cues in the microenvironment is significantly altered by the presence of the interstitial flow. Considering the interstitial flow can also regulate the directed cell migration as a fluidic cue, cells under chemical and fluidic cues need to process much more complex extra- and intra-cellular signals.Then, we analyze the complication of the integrated chemical and fluidic cues asking if the non-linear cue profiles fulfill the physical detection limit for chemical cue. The physical detection limit for chemical cue is a cellular capacity physically governed for a shallow chemical gradient.29,30 Although the exponential profiles (either parallel or counter flow) provided a steep gradient near the source or sink, most of cells are located in the area where a relatively shallow gradient is present. The physical detection limit was roughly determined with a relative gradient of the chemical concentration across the cell body (γ) as follows:30,55,69
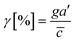 | (4) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) is an average concentration (see Materials and methods and Fig. S2†). We determined the cellular detection precision with γ ∼ 1% as a physical detection limit, as the cells may not be capable of sensing the chemical gradient below this limit based on knowledge of the sensory precision threshold for Dictyostelium70,71 and cancer cells.55,72 Here, we define the cue directions as forward (+ state), backward (− state), and no-cue (0-state). If a gradient is present but below the detection limit for the cells (γ < 1%), the gradient is neglected by the cells. Consequently, it is also considered as a 0-state, indicating that there is no gradient which cells can sense.
is an average concentration (see Materials and methods and Fig. S2†). We determined the cellular detection precision with γ ∼ 1% as a physical detection limit, as the cells may not be capable of sensing the chemical gradient below this limit based on knowledge of the sensory precision threshold for Dictyostelium70,71 and cancer cells.55,72 Here, we define the cue directions as forward (+ state), backward (− state), and no-cue (0-state). If a gradient is present but below the detection limit for the cells (γ < 1%), the gradient is neglected by the cells. Consequently, it is also considered as a 0-state, indicating that there is no gradient which cells can sense.
In the no-flow condition (Fig. 2D), all regions were above the physical detection limit, indicating that the cells are capable of sensing the chemical gradient. On the other hand, both parallel and counter flow conditions presented in Fig. 2E and F display ‘0-state’ regions where the relative gradient is below the cells' physical detection limit, leading to differential signal environment in two ways. For the parallel flow, the γ value drops down as the location is close to source channel and gets to the detection limit (γ ∼ 1%) in the middle of ROI shown in Fig. 2E. Consequently, it divides the region into two where the chemical cue is detectable (chem + state) and not detectable (chem 0-state). When the chemical cue is detectable, cells are exposed by additive combination of the chemical gradient and the flow. Interestingly, 0-state in parallel flow, the background concentration of chemoattractant is close to 10 nM. We anticipate that it is equivalent to the situation of cells exposed to a uniform chemoattractant with flow. On the other hand, γ for the counter flow increases as it is close to source channel while the detection limit (γ ∼ 1%) is in the middle of ROI (Fig. 2F). At the location where the chemical cue is detectable, the combination of the chemical and fluidic cues is competitive, having opposite direction (chem +/flow − state). Unlike the parallel flow, the counter flow washes the chemoattractant mostly away from the ROI showing the background concentration as close to 0 nM where the chemical cue is below the detection limit in Fig. 2F.
Intra-cellular processing of two cues simultaneously
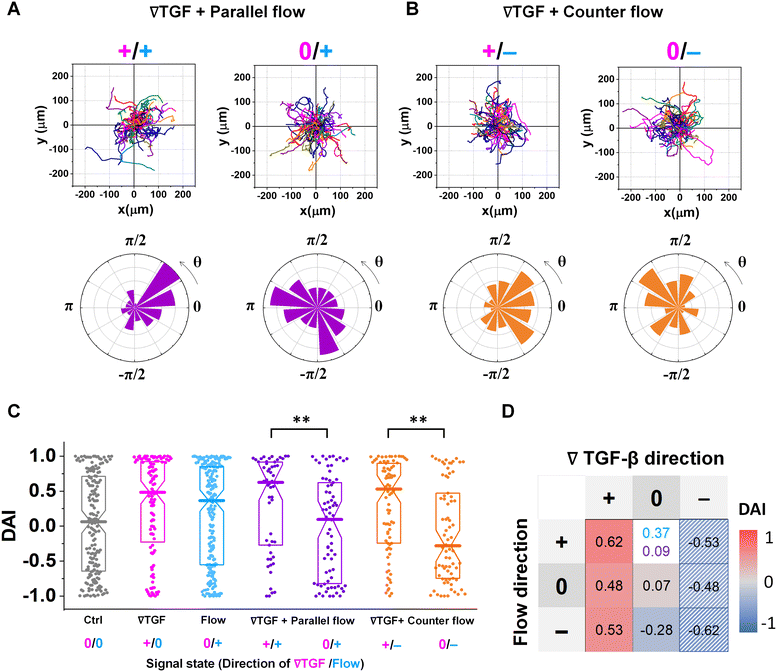
Fig. 3 shows the directed migration behaviors of KIC cells under integrated chemical and fluidic cues. The cells' migration trajectories and the angular distribution of corresponding displacement are presented in Fig. 3A and B. The results are divided into sub-regions considering the signal states of (TGF-β gradient/flow). For parallel flow (Fig. 3A), the trajectories and angle (θ) are distributed biased features toward the chemical cue direction in the sub-region of the additively integrated chemical and fluidic cues (+/+), whereas the trajectories and their angles in the other sub-region of 0/+ are randomly distributed. For the counter flow presented in Fig. 3B, the trajectories and angular distribution are biased toward the chemical cue direction in the sub-region of the competitively integrated cues (+/−) whereas those are biased toward the flow direction in the other sub-region of 0/−.Resulting directional accuracy is further analyzed with directional accuracy index (DAI) of all experimental cases in Fig. 3C. DAI of the cell trajectories under a single cue either TGF-β gradient (Fig. 3C, magenta) or flow (Fig. 3C, dark cyan) are biased toward each cue direction whereas control DAIs (Fig. 3C, grey) show a distribution with median close to 0. In the parallel flow, the directional accuracy is significantly enhanced toward the chemical cue direction in +/+ as shown in Fig. 3C (purple, left). Indeed, the DAI distribution is highly biased toward 1, with a median as 0.62 in this case. Although the gradient strength is ∼10% shallower than a linear TGF-β gradient, directional accuracy under +/+ state is still significantly biased toward the cue direction comparable to the linear gradient (median DAI = 0.46). On the other hand, cells lose their directional accuracy completely under 0/+ state where 0-state for the TGF-β gradient despite the flow presence shown in Fig. 3C (purple, right).
The TGF-β gradient and the counter flow compete in their directions when stimulating the cells. Here, we define reference direction for DAI as TGF-β gradient direction, resulting in a negative sign for the directed migration stimulated by the flow. Cells under the counter flow in the region with the TGF-β gradient above the limit (+/−) show bias in their DAI distribution toward 1, showing a median DAI = 0.53 (Fig. 3C, orange, left). Although the counter flow direction is the opposite of the TGF-β gradient, cells remain significantly biased toward the TGF-β gradient. On the other hand, cells under the counter flow with 0-state of TGF-β gradient (0/−) have biased distribution of DAI toward −1 with a median as −0.28 (Fig. 3C, orange, right). It implies that cells are not capable of sensing the shallow chemical gradient in the 0-state region, consequently, they respond only to the flow.
We summarize the median DAI from distributions of each signal state in the heat map (Fig. 3D) to show how each signal state induces the directional accuracy. The signal states with negative chemical cue direction (−/+, −/0, and −/−) are simply reflected by the signal states (+/−, and +/0, and +/+, respectively). The heat map shows two distinct features. Regardless of the fluidic cue, cells seem to follow the chemical cue direction when the chemical cue is not 0-state. Indeed, the cells seem to neglect the flow when they are exposed to a competing combination of TGF-β gradient and the counter flow. If the cellular response simply follows the signal state hypothesizing that the chemical and fluidic cues have comparable level in cellular processing machinery, the signal state of (+/−) would be anticipated as an antagonism showing lower DAI than TGF-β gradient only, but this was not shown in our results. Also, the 0/+ state can be represented in two distinct ways: flow only (dark cyan) and 0/+ state of chemical cue with parallel flow under the integrated chemical and fluidic cues (purple) (Fig. 3D). The median DAI under the flow only was 0.37, which was significantly biased toward the upstream direction of the flow. However, cells under for 0/+ of the integrated chemical and fluidic cues lose their bias completely with the median DAI = 0.09, indicating the cells do not respond to the flow stimulation. Unlike cells in 0/+, the cells in 0-state with counter flow (0/−) were induced by the flow. Thus, a quantitative comparison of effectiveness between chemical and the fluidic cues is required to address the results. Since the 0-state with parallel flow includes the high background concentration of TGF-β, we hypothesize that cells are receiving strong information about an ungraded chemical cue, and this overpowers the weaker fluidic cue.
A shared pathway model successfully predicts the cellular response to integrated cues
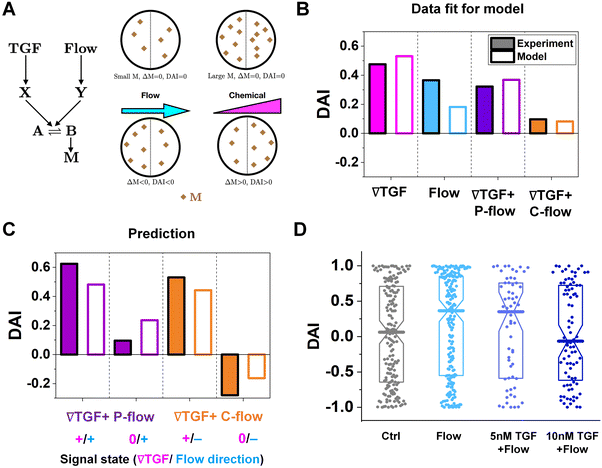
To further understand the cell's integrated response to both flow and chemical cues, we turn to mathematical modeling. Recent findings from Artemenko et al. suggest that the convergent signaling from the chemical and fluidic stimuli regulates cellular migratory behaviors.73 We adapt a model that we previously introduced to describe a cell's integrated response to two chemical signals9 that relies on the convergence of the two response pathways at a common intracellular component. Specifically, here we suppose that TGF-β induces the production an internal chemical species X, whereas flow induces (e.g., via pressure-sensitive receptors) the production of a second internal species Y (Fig. 4A). X and Y converge to jointly catalyze the conversion of a third species A into an activated state B, which is responsible for initiating the migration machinery downstream, described in the model as species M. The net result is that a rightward TGF-β gradient, or a leftward flow (corresponding to a rightward pressure gradient), produces more M molecules on the right side than on the left side of the cell, inducing rightward migration. Simplifying the cell to just these two halves, the rate equations corresponding to the reaction network in Fig. 4A give a steady-state molecule number difference of (see ESI†).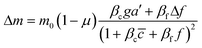 | (5) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) is the background TGF-β concentration in the region of interest, g is its gradient, and a′ is the cell length; and here a′g(=Δc) is the difference of chemical molecules between two halves of the cell and f and Δf is the corresponding effect due to the flow. Intracellular pathway parameters are denoted as μ and βi, where m0(1 − μ) intuitively sets the overall molecule number scale and βi indicates an intracellular reaction efficiency corresponding to each cue (see ESI† for details).
is the background TGF-β concentration in the region of interest, g is its gradient, and a′ is the cell length; and here a′g(=Δc) is the difference of chemical molecules between two halves of the cell and f and Δf is the corresponding effect due to the flow. Intracellular pathway parameters are denoted as μ and βi, where m0(1 − μ) intuitively sets the overall molecule number scale and βi indicates an intracellular reaction efficiency corresponding to each cue (see ESI† for details).
To describe the resulting migration, we use a biased random walk model55 to relate the migration angle θ to the molecule number difference Δm,
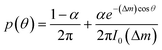 | (6) |
The median of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ values drawn from p(θ) gives the DAI from the model in terms of the parameters
θ values drawn from p(θ) gives the DAI from the model in terms of the parameters ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) , g, a′, μ, βc, ϕ, ηf, and α, where ϕ and ηf represent βfΔf and βff respectively. We compare the model with the experiments in two steps. First, we calibrate the model parameters using the experimental data. Specifically, we set
, g, a′, μ, βc, ϕ, ηf, and α, where ϕ and ηf represent βfΔf and βff respectively. We compare the model with the experiments in two steps. First, we calibrate the model parameters using the experimental data. Specifically, we set ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) , g, and a′ directly from the experiments as above; we set the four parameters, m0(1 − μ), βc, ϕ, and ηf using the median DAI in the four experimental conditions (TGF-β gradient only, flow only, parallel flow, and counter flow); and we set the last parameter α using the maximum mean DAI observed across all of these experimental conditions (see ESI†). We see in Fig. 4B that the model is able to capture the median DAI from experiments well. Second, we use the calibrated model parameters, with no further fitting, to predict the median DAI when the parallel and counter flow conditions are separated based on the detection limit as above. We see in Fig. 4C that the model prediction agrees well with the observed median DAI values, even without further fitting.
, g, and a′ directly from the experiments as above; we set the four parameters, m0(1 − μ), βc, ϕ, and ηf using the median DAI in the four experimental conditions (TGF-β gradient only, flow only, parallel flow, and counter flow); and we set the last parameter α using the maximum mean DAI observed across all of these experimental conditions (see ESI†). We see in Fig. 4B that the model is able to capture the median DAI from experiments well. Second, we use the calibrated model parameters, with no further fitting, to predict the median DAI when the parallel and counter flow conditions are separated based on the detection limit as above. We see in Fig. 4C that the model prediction agrees well with the observed median DAI values, even without further fitting.
Beyond validating the experiments, the model offers an intuitive explanation for the cell responses. When the TGF-β and flow signals are coherent (parallel flow), and above the TGF-β gradient detection limit, the DAI is large, as expected (Fig. 4C, left purple). Below the detection limit, one might expect that flow should dominate, and the DAI would still be positive. However, the large TGF-β background concentration in this regime (Fig. 2E and large ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) in eqn (5)) saturates the signaling network, leading to a small Δm and thus a small DAI (Fig. 4C, purple right). When the TGF-β and flow cues are incoherent (counter flow), and above the TGF-β gradient detection limit, the DAI is large and positive (Fig. 4C, orange left), indicating that chemical detection overpowers flow detection. Indeed, in the model we find that Δf/f, which is the analog of α′g/
in eqn (5)) saturates the signaling network, leading to a small Δm and thus a small DAI (Fig. 4C, purple right). When the TGF-β and flow cues are incoherent (counter flow), and above the TGF-β gradient detection limit, the DAI is large and positive (Fig. 4C, orange left), indicating that chemical detection overpowers flow detection. Indeed, in the model we find that Δf/f, which is the analog of α′g/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) for flow sensing (see ESI†) is 0.1%, which always less than α′g/
for flow sensing (see ESI†) is 0.1%, which always less than α′g/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) in regimes where it is above its detection limit of 1%. Finally, below the chemical detection limit, the DAI is negative (Fig. 4C, orange right), i.e., aligned with the flow, because here the TGF-β background concentration is negligible, allowing flow to dominate.
in regimes where it is above its detection limit of 1%. Finally, below the chemical detection limit, the DAI is negative (Fig. 4C, orange right), i.e., aligned with the flow, because here the TGF-β background concentration is negligible, allowing flow to dominate.
To confirm a key prediction of the model, namely that the large TGF-β background concentration is responsible for the suppression of flow sensing in the parallel flow regime below the chemical detection limit (Fig. 3C, right purple), we perform further experiments. Specifically, we combine flow with a uniform TGF-β concentration at either 5 or 10 nM. At 5 nM, which is roughly half of the background level in this regime (Fig. 2E), we see that the DAI is not suppressed (Fig. 4D). However, at 10 nM, which is roughly equal to the background level in this regime, we see that the DAI is indeed suppressed (Fig. 4D).
Cellular signal processing machinery can be modeled as a ternary logic gate
The shared pathway model addresses cellular processing capacity, and it successfully predicts the cellular response. However, this theoretical model is computationally intensive to predict a cell's migration direction under multiple cues. To address this gap, we digitize the direction of cues and cell migration and propose a reverse-engineered form of the cell's signal-processing system. We construct a logic gate model to reconstitute the function of the cellular signal processing machinery (Fig. 5). The cellular response to the cues (+, 0, or −) presents three variables as outputs, allowing us to develop a ternary logic system. For consistency, we define the output direction based on the chemical cue. When the cell migration direction is aligned to the chemical cue direction with positive DAIs, cell direction can be represented as a forward (+ state). On the other hand, the repulsive response to the cue with negative DAI can be denoted as − state. Cells' random movement not showing any bias in their direction with DAI close to 0 are defined as 0-state. In this way, the heat map presented in Fig. 3D can be converted to a ternary logic table. We convert the positive or negative DAIs to + or − respectively when the DAI distribution fulfills the statistical significance (p < 0.05) in their comparison with control (Fig. 5A). The DAIs close to 0 with no significant bias in their distribution is converted to 0. We present two separate ternary logic tables based on the system saturation caused by the high background TGF-β concentration resulting in suppression of the directional accuracy as we presented in the prior section. By separating the results depending on the system saturation, the present inconsistency presented in 0/+ (Fig. 3D) is resolved.The ternary logic gate is composed of the five ternary operators, whose operating functions are presented in Fig. 5B. The monadic operator “=0” returns 0 input to + output whereas + and − input to 0 output. Another monadic operator “×0” returns all zero regardless of the input states. We also used dyadic operators represented as ⊗ and ⊕, which simply multiply and add two inputs to return the corresponding outputs respectively. To stop misguided migration when the machinery capability is saturated, we apply a circuit breaker for the system saturation with a multiplexer. The multiplexer switches the circuit path based on an additional intracellular input S. We apply two intracellular inputs; S = 1 where the system is saturated by high background TGF-β concentration, and S = 0 where the system is not saturated. By using the basic operators, the ternary logic circuit to address the ternary logic tables is developed in Fig. 5C. When the system is not saturated (S = 0), the cells tend to select their migration direction primarily along TGF-β gradient, regardless of the flow's existence (i.e., “selection” gate). The path for S = 0 mimics an absorption logic gate which selectively choose one particular input to decide their output. In contrast, the path for S = 1 for system saturation leads to returning all zero. Consequently, the circuit successfully represents the experimental results. The ternary logic gate in Fig. 5C implies a corresponding mathematical expression in terms of ternary variables (−, 0, or +) which, self-consistently, agrees with our expression for Δm (eqn (5)) when looking only at its sign (−, 0, or +); see Fig. S3.†
Discussion
The present results unravel the complications in the extracellular signal environment, specifically caused by the integrated chemical and fluidic cues. We investigated signaling environments where the Péclet number (Pe) ∼ 1 in cases that flow runs parallel or counter to a TGF-β gradient. As the fluidic cue becomes stronger (i.e., a higher Pe environment, Pe ≫ 1), the transport of TGF-β becomes convection-dominant, whereas weaker fluidic cues (i.e., lower Pe, Pe ≪ 1) correspond to diffusion-dominant transport. Corresponding changes of the gradient of chemical cue depending on the flow direction and Pe are shown in Fig. S4.† In fact, Pe varies from 0.1 to 2 with slow interstitial flow velocities in various tissue interstitium, including cancer.56,57,67 The combination of the TGF-β gradient and the flow displays two important aspects. First, the TGF-β concentration profiles are non-linear exponentials, where the cells experience spatially differential gradient strengths, including a shallow gradient region close to the cellular sensing limit. The exponential profiles of the concentration could be either shallow or steep where the background concentration could be higher or lower depending on the direction of flow and chemical gradient, causing a spatially differential response of cells.55,69,70 Second, cells are exposed to integrated cues of the chemical gradient and the flow as either additive or competitive depending on the flow direction, increasing the complexity of the cellular sensing and processing machinery both intrinsically and extrinsically.We streamlined the complication of the integrated cues by implicating cellular sensing capability for the chemical cue. The spatially varied gradient is developed by imposing convection in the microenvironment, including shallow gradient regions below the cellular detection limit.30 Indeed, the physical limit of cells in sensing chemical gradient allowed us to decouple the integrated chemical and fluidic cues into the fluidic cue only, indicating 0-state. Consequently, the cells ruled out the effect of the TGF-β gradient in their decision-making for migration direction where it was below the detection limit.
Additionally, we demonstrated the cellular response to the combination of chemical and fluidic cues. The flow impacts the cellular behaviors as a transport medium and as a fluidic cue to induce migration potential of various cell types, including immune cells and cancer.11,74,75 In the presented experiment results, we have observed that cells effectively select a cue to follow in processing the mixed chemical and fluidic cues. When cells are capable of sensing both chemical and fluidic cues, cells tend to follow a chemical gradient direction in both the additive combination with the parallel flow and the competing with the counter flow, as shown in Fig. 3. The cells were biased toward the upstream direction of the fluidic cue, only when the chemical gradient was too shallow for cells to detect it (Fig. 3 orange right). Another striking result was that the cellular response was completely unbiased when the processing capacity was saturated (Fig. 3 purple). When cells were exposed to a higher background concentration of TGF-β, cell migration direction was not determined even though they were exposed to the fluidic cue (Fig. 3 purple right and 4D), demonstrating the physical implication of the cells' innate capability of processing the integrated cues. Based on the experimental observation, we proposed the framework of the cellular sensing machinery by using the ternary logic gate model in Fig. 5.
Our results suggest that the cells preferentially select the chemical cue over the fluidic cue if the cellular processing capacity is not saturated, as illustrated in the presented ternary logic gate model. How does the cellular processing machinery preferentially select the chemical cue to the fluidic cue when both cues are presented simultaneously?
The proposed shared pathway model can explain the fact that the cellular migration direction is determined by the cells' relative sensing and processing capability for the cues (Fig. 6). In the model, the cell migration direction is determined by the sign of Δm (+, 0, or −). Intuitively, the selection of the migration direction can be illustrated with a competing relation between the sensing and processing capability for chemical (γcηc) and fluidic (γfηf) cues, specifically when the counter flow is applied. Here, we define the relative extracellular cue strength ε = γf/γc and the relative intracellular pathway strength ρ = ηf/ηc in the parameters of eqn (5).
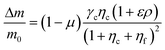 | (7) |
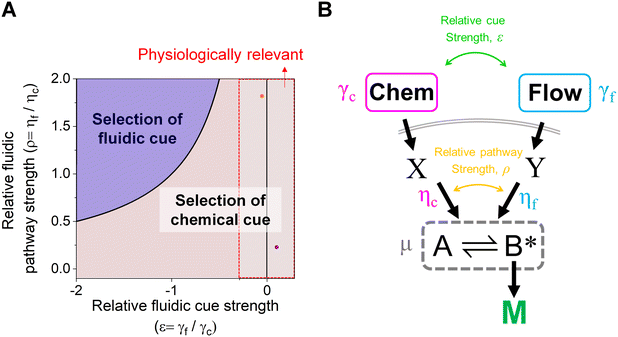 | ||
| Fig. 6 Schematic of cellular decision making to preferentially select a chemical cue in their migration direction. (A) The shared pathway model predicts cellular selection of a specific cue under the spontaneously applied chemical and fluidic cues, determined with the sign of Δm. Dot: an estimated experimental condition of the counter flow (+/−, orange) and the parallel flow (+/+, purple) (see ESI† for details). (B) Illustration of the parameters in the general context of a signaling network defined by the shared pathway. | ||
The proposed framework of the cellular sensing machinery using the ternary logic gate (Fig. 5) illustrates the cellular signal processing capability. Previously, we have shown that saturation of the intracellular signal transduction capacity causes antagonism in their chemotaxis, where the two different chemical cues not sharing their receptors induce cell directed migration.9 A recent study also demonstrated that the limited source of intracellular translational or transcriptional factors results in poor performance and predictability in synthetic biology.77 In this sense, our results demonstrate that the saturation of the shared pathway to manipulate cellular migration direction completely removes cells' biased movement, indicating that the cellular processing capacity could limit cellular performance.
Our results and proposed physical implications demonstrate that the shared pathway of the chemical and fluidic cues governs cellular migration direction. Indeed, studies have reported that the downstream networks of the flow cue overlap with the chemotaxis signaling transduction.20,73,78 The shared downstream signaling transduction regulates actin cytoskeletal dynamics, which are thought to manipulate the cell biased movement. The proposed physical implications contribute to understanding the cellular sensing and processing machinery for the integrated cues.
Although the present study demonstrates how cells decipher integrated chemical and fluidic cues, the type of environmental cues for the investigation is limited. Multiple chemoattractants may induce directed cell migration besides TGF-β. Besides the chemical or fluidic cues, mechanical cues such as matrix stiffness gradient can also affect migration. The present study used one cell type, but further validation using multiple cell types is warranted.
Conclusions
The present study lays a framework for understanding how cells decode chemical and fluidic cues to determine migration direction by proposing a ternary gate circuit. Cellular decision-making is a systematic result from sensing to deciphering the cues with complex downstream signal processing. Our results suggest a simple circuit to address the complex process based on our observation showing the cellular innate sensing and processing capacity.9 The proposed framework of the gate circuit implies the potential use of the ternary system to model cellular sensory machinery for environmental cues with heterogeneous origins. The proposed ternary logic gate may provide a blueprint to synthesize functional signal processing machinery for engineered cells. Recent advances in synthetic biology to engineer genetic circuits of the cells offer great potential in developing engineered cellular systems as sensors, therapeutics, and delivery vehicles.79–82 The microbials (e.g., Escherichia coli and virus) have been engineered to target pathogenic sites for diagnosis and therapeutics.83,84 Recent development in synthetic mammalian cells pursued the immune cell (T-cell) chemotaxis85 and anti-cancer targeting purposes.86,87 Nonetheless, it is required to have an effective genetic circuit design to regulate the directed migration of the delivery vehicles based on a profound understanding of cellular sensory machinery with both extrinsic and intrinsic considerations. Accordingly, the proposed ternary gate model provides insight to develop potential targeting vehicles in various ways.Author contributions
HM was responsible for conceptualization, investigation, analysis, and writing – original draft preparation. SS was responsible for investigation, analysis, writing – original draft preparation. AM and BH were responsible for conceptualization, analysis, and writing – review and editing.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was partially supported by grants from the National Institutes of Health (U01 HL143403, R01 CA254110, R61 HL 159948, U01 CA274304, and P30 CA023168) and National Science Foundation (MCB-2134603, MCB-1936761, and PHY-1945018).Notes and references
- T. Worbs, S. I. Hammerschmidt and R. Förster, Nat. Rev. Immunol., 2017, 17, 30–48 CrossRef CAS.
- A. D. Luster, R. Alon and U. H. von Andrian, Nat. Immunol., 2005, 6, 1182–1190 CrossRef CAS.
- M. J. Oudin and V. M. Weaver, Cold Spring Harbor Symp. Quant. Biol., 2017, 81, 189–205 CrossRef.
- K. Kohli, V. G. Pillarisetty and T. S. Kim, Cancer Gene Ther., 2021, 1–12 Search PubMed.
- B. de Lucas, L. M. Pérez and B. G. Gálvez, J. Cell. Mol. Med., 2018, 22, 746–754 Search PubMed.
- M. A. Swartz, N. Iida, E. W. Roberts, S. Sangaletti, M. H. Wong, F. E. Yull, L. M. Coussens and Y. A. DeClerck, Cancer Res., 2012, 72, 2473–2480 CrossRef CAS.
- A. Ozcelikkale, J. C. Dutton, F. Grinnell and B. Han, J. R. Soc., Interface, 2017, 14, 20170287 CrossRef PubMed.
- M. J. Bradney, S. M. Venis, Y. Yang, S. F. Konieczny and B. Han, Small, 2020, 1905500 CrossRef CAS PubMed.
- H.-R. Moon, S. Saha, A. Mugler and B. Han, iScience, 2021, 24, 103242 CrossRef CAS PubMed.
- E. T. Roussos, J. S. Condeelis and A. Patsialou, Nat. Rev. Cancer, 2011, 11, 573–587 CrossRef CAS PubMed.
- J. M. Munson and A. C. Shieh, Cancer Manage. Res., 2014, 6, 317 CrossRef PubMed.
- H. J. Lee, M. F. Diaz, K. M. Price, J. A. Ozuna, S. Zhang, E. M. Sevick-Muraca, J. P. Hagan and P. L. Wenzel, Nat. Commun., 2017, 8, 1–14 CrossRef PubMed.
- M.-P. Valignat, O. Theodoly, A. Gucciardi, N. Hogg and A. C. Lellouch, Biophys. J., 2013, 104, 322–331 CrossRef CAS PubMed.
- P. Campinho, A. Vilfan and J. Vermot, Front. Physiol., 2020, 11, 552 CrossRef PubMed.
- A. H. Chang, B. C. Raftrey, G. D'Amato, V. N. Surya, A. Poduri, H. I. Chen, A. B. Goldstone, J. Woo, G. G. Fuller and A. R. Dunn, Genes Dev., 2017, 31, 1308–1324 CrossRef CAS PubMed.
- T. Miyagawa, H. Koteishi, Y. Kamimura, Y. Miyanaga, K. Takeshita, A. Nakagawa and M. Ueda, Nat. Commun., 2018, 9, 1–13 CrossRef CAS PubMed.
- K. F. Swaney, C.-H. Huang and P. N. Devreotes, Annu. Rev. Biophys., 2010, 39, 265–289 CrossRef CAS.
- P. G. Charest and R. A. Firtel, Biochem. J., 2007, 401, 377–390 CrossRef CAS PubMed.
- H. Li, L. Yang, H. Fu, J. Yan, Y. Wang, H. Guo, X. Hao, X. Xu, T. Jin and N. Zhang, Nat. Commun., 2013, 4, 1–12 CAS.
- S. SenGupta, C. A. Parent and J. E. Bear, Nat. Rev. Mol. Cell Biol., 2021, 22, 529–547 CrossRef CAS.
- A. J. Ridley, Curr. Opin. Cell Biol., 2015, 36, 103–112 CrossRef CAS PubMed.
- K. M. Byrne, N. Monsefi, J. C. Dawson, A. Degasperi, J.-C. Bukowski-Wills, N. Volinsky, M. Dobrzyński, M. R. Birtwistle, M. A. Tsyganov and A. Kiyatkin, Cell Syst., 2016, 2, 38–48 CrossRef CAS PubMed.
- H. E. Steele, Y. Guo, B.-Y. Li and S. Na, Biochem. Biophys. Res. Commun., 2019, 514, 524–529 CrossRef CAS PubMed.
- W. J. Polacheck, A. E. German, A. Mammoto, D. E. Ingber and R. D. Kamm, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 2447–2452 CrossRef CAS PubMed.
- S. Mao, A. Sarkar, Y. Wang, C. Song, D. LeVine, X. Wang and L. Que, Lab Chip, 2021, 21, 3128–3136 RSC.
- I. Xanthis, C. Souilhol, J. Serbanovic-Canic, H. Roddie, A. C. Kalli, M. Fragiadaki, R. Wong, D. R. Shah, J. A. Askari and L. Canham, J. Cell Sci., 2019, 132, jcs229542 CrossRef CAS.
- N. H. Roy, S. H. J. Kim, A. Buffone Jr, D. Blumenthal, B. Huang, S. Agarwal, P. L. Schwartzberg, D. A. Hammer and J. K. Burkhardt, J. Cell Sci., 2020, 133, jcs248328 CrossRef CAS.
- P. J. Thomas and A. W. Eckford, IEEE Trans. Inf. Theory, 2016, 62, 7358–7382 Search PubMed.
- B. Hu, W. Chen, W.-J. Rappel and H. Levine, Phys. Rev. Lett., 2010, 105, 048104 CrossRef PubMed.
- J. Varennes and A. Mugler, Mol. Pharmaceutics, 2016, 13, 2224–2232 CrossRef CAS PubMed.
- G. Malaguti and P. R. Ten Wolde, eLife, 2021, 10, e62574 CrossRef CAS.
- W. de Ronde, F. Tostevin and P. R. Ten Wolde, Phys. Rev. Lett., 2011, 107, 048101 CrossRef PubMed.
- V. Singh and I. Nemenman, PLoS Comput. Biol., 2017, 13, e1005490 CrossRef.
- S. Soh, M. Byrska, K. Kandere-Grzybowska and B. A. Grzybowski, Angew. Chem., Int. Ed., 2010, 49, 4170–4198 CrossRef CAS.
- S. Gupta, S. Fancher, H. C. Korswagen and A. Mugler, Phys. Rev. E, 2020, 101, 062420 CrossRef CAS PubMed.
- Y. Cao, E. Ghabache and W.-J. Rappel, eLife, 2019, 8, e48478 CrossRef CAS.
- H. Y. Zhou, Y. L. Pon and A. S. Wong, Endocrinology, 2007, 148, 5195–5208 CrossRef CAS.
- J. M. Buonato, I. S. Lan and M. J. Lazzara, J. Cell Sci., 2015, 128, 3898–3909 CAS.
- A. Badache and N. E. Hynes, Cancer Res., 2001, 61, 383–391 CAS.
- N. C. Schlegel, A. von Planta, D. S. Widmer, R. Dummer and G. Christofori, Exp. Dermatol., 2015, 24, 22–28 CrossRef CAS PubMed.
- B. Mosadegh, W. Saadi, S. J. Wang and N. L. Jeon, Biotechnol. Bioeng., 2008, 100, 1205–1213 CrossRef CAS PubMed.
- B. J. Kim, P. Hannanta-Anan, M. Chau, Y. S. Kim, M. A. Swartz and M. Wu, PLoS One, 2013, 8, e68422 CrossRef CAS PubMed.
- S. Uttamsingh, X. Bao, K. T. Nguyen, M. Bhanot, J. Gong, J. L. K. Chan, F. Liu, T. T. Chu and L. H. Wang, Oncogene, 2008, 27, 2626–2634 CrossRef CAS.
- M. Pang, A. Georgoudaki, L. Lambut, J. Johansson, V. Tabor, K. Hagikura, Y. Jin, M. Jansson, J. Alexander and C. M. Nelson, Oncogene, 2016, 35, 748–760 CrossRef CAS PubMed.
- H. Nunns and L. Goentoro, eLife, 2018, 7, e33617 CrossRef PubMed.
- M. Carballo-Pacheco, J. Desponds, T. Gavrilchenko, A. Mayer, R. Prizak, G. Reddy, I. Nemenman and T. Mora, Phys. Rev. E, 2019, 99, 022423 CrossRef CAS PubMed.
- T. Mora, Phys. Rev. Lett., 2015, 115, 038102 CrossRef PubMed.
- J.-B. Lalanne and P. François, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 1898–1903 CrossRef CAS PubMed.
- Q. Huang, X. Hu, W. He, Y. Zhao, S. Hao, Q. Wu, S. Li, S. Zhang and M. Shi, Am. J. Cancer Res., 2018, 8, 763 CAS.
- N. Baeyens, C. Bandyopadhyay, B. G. Coon, S. Yun and M. A. Schwartz, J. Clin. Invest., 2016, 126, 821–828 CrossRef PubMed.
- S. Saha, H.-R. Moon, B. Han and A. Mugler, arxiv, 2022, preprint, arXiv:2205.02699, DOI:10.48550/arXiv.2205.02699.
- L. F. Sempere, J. R. Gunn and M. Korc, Cancer Biol. Ther., 2011, 12, 198–207 CrossRef CAS PubMed.
- C. A. Whipple, A. L. Young and M. Korc, Oncogene, 2011, 31, 2535 CrossRef PubMed.
- H.-R. Moon, A. Ozcelikkale, Y. Yang, B. D. Elzey, S. F. Konieczny and B. Han, Lab Chip, 2020, 20, 3720–3732 RSC.
- J. Varennes, H.-R. Moon, S. Saha, A. Mugler and B. Han, PLoS Comput. Biol., 2019, 15, e1006961 CrossRef CAS PubMed.
- G. Follain, D. Herrmann, S. Harlepp, V. Hyenne, N. Osmani, S. C. Warren, P. Timpson and J. G. Goetz, Nat. Rev. Cancer, 2019, 1–18 Search PubMed.
- M. A. Swartz and M. E. Fleury, Annu. Rev. Biomed. Eng., 2007, 9, 229–256 CrossRef CAS.
- D. Huber, A. Oskooei, X. Casadevall i Solvas, A. Demello and G. V. Kaigala, Chem. Rev., 2018, 118, 2042–2079 CrossRef CAS PubMed.
- W. J. Polacheck, J. L. Charest and R. D. Kamm, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11115–11120 CrossRef CAS PubMed.
- V. L. Cross, Y. Zheng, N. W. Choi, S. S. Verbridge, B. A. Sutermaster, L. J. Bonassar, C. Fischbach and A. D. Stroock, Biomaterials, 2010, 31, 8596–8607 CrossRef CAS PubMed.
- P. A. Galie and J. P. Stegemann, Tissue Eng., Part C, 2011, 17, 527–536 CrossRef CAS PubMed.
- C. P. Ng and M. A. Swartz, Am. J. Physiol., 2003, 284, H1771–H1777 CAS.
- B. A. Harley, H.-D. Kim, M. H. Zaman, I. V. Yannas, D. A. Lauffenburger and L. J. Gibson, Biophys. J., 2008, 95, 4013–4024 CrossRef CAS PubMed.
- J. B. Beltman, A. F. Marée and R. J. De Boer, Nat. Rev. Immunol., 2009, 9, 789–798 CrossRef CAS PubMed.
- M. Skoge, H. Yue, M. Erickstad, A. Bae, H. Levine, A. Groisman, W. F. Loomis and W.-J. Rappel, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14448–14453 CrossRef CAS PubMed.
- R. Karmakar, M.-H. Tang, H. Yue, D. Lombardo, A. Karanam, B. A. Camley, A. Groisman and W.-J. Rappel, Phys. Rev. E, 2021, 103, 012402 CrossRef CAS PubMed.
- M. W. Dewhirst and T. W. Secomb, Nat. Rev. Cancer, 2017, 17, 738–750 CrossRef CAS.
- D. Venturoli and B. Rippe, Am. J. Physiol., 2005, 288, F605–F613 CAS.
- D. Ellison, A. Mugler, M. D. Brennan, S. H. Lee, R. J. Huebner, E. R. Shamir, L. A. Woo, J. Kim, P. Amar and I. Nemenman, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E679–E688 CrossRef CAS PubMed.
- P. J. Van Haastert and M. Postma, Biophys. J., 2007, 93, 1787–1796 CrossRef CAS PubMed.
- D. Fuller, W. Chen, M. Adler, A. Groisman, H. Levine, W.-J. Rappel and W. F. Loomis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9656–9659 CrossRef CAS PubMed.
- J. D. Shields, M. E. Fleury, C. Yong, A. A. Tomei, G. J. Randolph and M. A. Swartz, Cancer Cell, 2007, 11, 526–538 CrossRef CAS PubMed.
- Y. Artemenko, L. Axiotakis, J. Borleis, P. A. Iglesias and P. N. Devreotes, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E7500–E7509 CrossRef CAS PubMed.
- H. D. Moreau, M. Piel, R. Voituriez and A.-M. Lennon-Duménil, Trends Immunol., 2018, 39, 632–643 CrossRef CAS PubMed.
- X. Zhang, T.-H. Kim, T. J. Thauland, H. Li, F. S. Majedi, C. Ly, Z. Gu, M. J. Butte, A. C. Rowat and S. Li, Curr. Opin. Biotechnol., 2020, 66, 236–245 CrossRef CAS PubMed.
- G. Follain, D. Herrmann, S. Harlepp, V. Hyenne, N. Osmani, S. C. Warren, P. Timpson and J. G. Goetz, Nat. Rev. Cancer, 2020, 20, 107–124 CrossRef CAS PubMed.
- T. Frei, F. Cella, F. Tedeschi, J. Gutiérrez, G.-B. Stan, M. Khammash and V. Siciliano, Nat. Commun., 2020, 11, 1–14 CrossRef PubMed.
- D. J. Sieg, C. R. Hauck, D. Ilic, C. K. Klingbeil, E. Schaefer, C. H. Damsky and D. D. Schlaepfer, Nat. Cell Biol., 2000, 2, 249–256 CrossRef CAS PubMed.
- W. Weber and M. Fussenegger, Nat. Rev. Genet., 2012, 13, 21–35 CrossRef CAS PubMed.
- S. M. Brooks and H. S. Alper, Nat. Commun., 2021, 12, 1–16 CrossRef PubMed.
- T. Ozdemir, A. J. Fedorec, T. Danino and C. P. Barnes, Cell Syst., 2018, 7, 5–16 CrossRef CAS PubMed.
- D. T. Riglar and P. A. Silver, Nat. Rev. Microbiol., 2018, 16, 214–225 CrossRef CAS PubMed.
- I. Y. Hwang, M. H. Tan, E. Koh, C. L. Ho, C. L. Poh and M. W. Chang, ACS Synth. Biol., 2014, 3, 228–237 CrossRef CAS PubMed.
- C. A. Miller, J. M. Ho, S. E. Parks and M. R. Bennett, ACS Synth. Biol., 2021, 10, 258–264 CrossRef CAS PubMed.
- J. S. Park, B. Rhau, A. Hermann, K. A. McNally, C. Zhou, D. Gong, O. D. Weiner, B. R. Conklin, J. Onuffer and W. A. Lim, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 5896–5901 CrossRef CAS PubMed.
- H. Ye and M. Fussenegger, FEBS Lett., 2014, 588, 2537–2544 CrossRef CAS PubMed.
- M.-R. Wu, B. Jusiak and T. K. Lu, Nat. Rev. Cancer, 2019, 19, 187–195 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc00807f |
| This journal is © The Royal Society of Chemistry 2023 |