Theoretical investigation of the optoelectronic response of highly correlated Cu₃P photocatalyst

Abstract

Photocatalytic materials attract immense scientific interest due to their possible applications in energy harvesting. These applications are strongly dependent on the material's band gap and efficient visible light absorption, which ultimately relies on the underlying electronic structure of the material. In this work, we have theoretically studied the electronic and optical response of a Cu₃P semiconductor. We have used Density Functional Theory (DFT), and the Many-Body Perturbation Theory (MBPT) based Bethe–Salpeter Equation (BSE). Cu₃P has intriguing band gap nature, as DFT predicts a semi-metallic state which was corrected by employing the Hubbard potentials. Only astronomically large values of Hubbard potentials reproduced the semiconducting state of Cu₃P. The optical response of the material is computed within a Random Phase Approximation (RPA) and using the BSE on top of DFT+U wavefunctions and on the ground state computed with the PBE0 functional. The BSE captures the excitonic physics, and the optical absorption obtained from it was red-shifted compared to the RPA, which shows the significance of electron–hole interactions in Cu₃P. The comparison of the BSE with experiments suggests that BSE@PBE0 reproduces the optical absorption much more closely to the experimental data.

---

1 Introduction

Photocatalytic materials have drawn considerable scientific interest in water splitting since TiO₂ emerged as a pioneering material in this field.¹ TiO₂ possesses promising characteristics such as low-cost and a non-toxic nature; however, pure TiO₂ is hardly employed in actual photocatalytic applications due to its wide band gap. Although significant efforts have already been made to tune the TiO₂ band gap via doping² and altering its surface properties,³ the need to probe for new potential photocatalytic materials has been profoundly felt, worked on in the past,⁴ and still continues. Various semiconductors like Bi₂WO₆ and other tungsten oxides have recently evolved as photocatalytic systems,⁵ but most materials exhibit suppressed photocatalytic activity compared to TiO₂.⁶ Apart from designing new undoped materials, combining two semiconductors to form a heterostructure is another popular method. There are several heterostructures that have been studied; for instance, Bi₂WO₆–Cu₃P has been experimentally studied to be a conducive system for photocatalysis.⁷ Substantial research has been conducted on pure Bi₂WO₆, both experimentally and theoretically,^7–9 to find its electronic and optical response. However, interestingly, Cu₃P, which shows promising photocatalytic performance under irradiation, has not been investigated in much detail experimentally and is yet to be studied theoretically.

Copper phosphide (Cu₃P) has been found to be a semiconductor with a lower band gap than TiO₂ and even lower than Bi₂WO₆, which ensures sizeable optical absorption in the visible portion of the electromagnetic spectrum, which has also experimentally been observed.⁷ Cu₃P has shown promise as an electrode material for batteries due to its cyclability and capacity¹⁰ and was recently found to be an excellent fluorescent material due to its excellent fluorescence properties,¹¹ hence is also suitable as a photodetector. Furthermore, Cu₃P as a p-type semiconductor has been combined with several other wide band gap n-type semiconductors such as Bi₂WO₆,⁷ SnO₂,¹² and very recently with TiO₂ (ref. 13) to form heterostructures which enhanced the photocatalytic properties of the overall system under solar light irradiation. The internal electric field that develops near the p–n junction area helps to segregate generated electron–hole pairs and prevents recombination, ultimately improving the photocatalytic efficiency.¹⁴

Besides experimental studies, theoretical calculations on Cu₃P heterostructures have already been performed.^15,16 However, the theoretical study of pure Cu₃P, mainly electronic and optical properties, is often overlooked, and there are unanswered questions about the absorption and emission spectroscopy of this material. The electronic and optical response is vital for any photocatalytic material, and theoretical computation has become a valuable tool to predict these properties with comparable results to experiments. Electronic structure methods such as DFT have found enormous success in finding the lattice structure¹⁷ or phonon vibration in solids.¹⁸ However, inherently complex and spurious interactions between electrons, named self-interaction, which is not treated in the GGA type of functionals, cause severe band gap underestimation.¹⁹ Experimentally, Cu₃P has been found to have a small band gap; however, PBE predicts a metallic state suggesting a strong underestimation of gap or physically wrong ground state at the PBE level. The significant underestimation of the gap has also been manifested in other copper-based materials such as chalcopyrites.²⁰ To mitigate the band gap underestimation and to deal with onsite correlation effects, we have used the DFT+U method.²¹ Quasi-particle corrections,²² like the GW approximation,²³ based upon the Many-Body Perturbation Theory (MBPT) followed by a BSE calculation is often used as a state-of-the-art approach to compute electronic and optical spectra.²⁴ However, we have avoided GW here because this method might give ambiguous corrections if the ground state wavefunctions computed from DFT are fundamentally unphysical;²⁵ therefore, the Hubbard correction (DFT+U) is considered in this work. The hybrid functional starting point for GW or BSE calculations is one popular choice known to give reasonable results,^25,26 but employing large k-points with a hybrid functional becomes unfeasible due to the massive computational and memory costs.

Nevertheless, a band gap calculation was carried out employing the PBE0 hybrid functional using a 3 × 3 × 3 k-grid, which yielded a 0.55 eV band gap. The band gap of Cu₃P with the PBE0 functional is comparable to earlier studies using the same functional.²⁷ Furthermore, meta-GGA types of functionals are prevalent, and they perform significantly better than the GGA functionals to yield band gaps close to experiment,²⁸ and they have not been employed for Cu₃P in the past; we have used a SCAN functional²⁹ to compute the band gap. However, still, the semiconducting state was not achieved. Therefore, Hubbard potentials and hybrid functional calculations were performed in all further computations. We have taken DFT+U, or PBE0 computed wavefunctions in the optical calculations to solve the BSE. Furthermore, a significant effort was made to determine Hubbard parameters for Cu₃P from first-principles; however, those calculations did not yield promising results due to a well-known limitation in the theory, which is discussed in Section 3.

In this work, we have performed theoretical calculations to investigate optoelectronic properties using DFT and post-DFT methods like the BSE. In the past, the optical calculations were carried out within the Independent Particle Approximation (IPA) only, and therefore, no electron–hole interaction was taken into account.²⁷ Since excitonic physics plays a significant role in describing the optical absorption of semiconductors, we have computed optical properties from the BSE as well as with IPA levels of theories. Furthermore, a comparison of these two theories with the experimental data was also studied, which was missing in the earlier studies. These theoretical calculations will help in understanding the optoelectronic properties of highly correlated Cu₃P and pave the way for further studies to fine-tune its properties.

2 Computational details

Ground-state wave functions were computed using DFT³⁰ employing Generalized Gradient Approximation (GGA) to account for the exchange and correlational effects between electrons as implemented in the Perdew–Burke–Ernzerhof (PBE)³¹ functional using the Quantum ESPRESSO code.³² Norm-conserving pseudopotentials³³ were used to model the ions–electrons interaction without Non-Linear Core Correction (NLCC) taken from the SG15 library.³⁴ In optical calculations, we have also included the non-local part of the pseudopotentials.³⁵ A plane-wave basis set up to the cutoff energy 80 Ry was used to expand the electronic wavefunctions, at which the total energy convergence of 3.1 × 10⁻⁵ Ry per atom is achieved. A k-points sampling under the Monkhorst–Pack³⁶ scheme was used for the first Brillouin zone integration using the 6 × 6 × 6 k-mesh. All the calculations are performed using the non-spin-polarized DFT to save computational time, as we had determined that Cu₃P has an identical DOS for spin-up and spin-down configurations (Fig. S1†). To achieve the minimum potential energy configuration of the system, the atomic positions and structure constants are optimized by computing the Hellmann–Feynman forces using the Broyden–Fletcher–Goldfarb–Shanno procedure (BFGS).³⁷ Optimization is performed until the total force on the system becomes as low as 3 × 10⁻⁴ Ry per a.u. To correct the band gap energies and to account for the onsite Coulombic repulsion, we have applied Hubbard potentials (U) not only to Cu-3d but also to the P-3p states (DFT + U_d + U_p) with values of 22 eV and 10 eV respectively.²⁷ It has already been extensively studied for various materials that applying Hubbard corrections to p-orbitals has a prominent effect on the band gap,^9,27,38,39 and it signifies the localized nature of the p states. In the hybrid functional (PBE0) calculations, 25% exact exchange was considered as the exchange parameter.

The density of states (DOS) and optical calculations require a dense k-mesh grid; therefore, in DOS calculations, we have chosen an 18 × 18 × 18 k-grid, while for optical calculations, a 9 × 9 × 9 grid in the BSE was found to give convergent results. Optical calculations have been computed using the Yambo code,⁴⁰ within RPA theory, including local field effects and using the Bethe Salpeter Equation (BSE) incorporating electron–hole interaction effects. The static screening calculation considered four hundred bands (212 unoccupied). To build the exchange part of the BSE kernel comprising local field effects, 10 Ry of Hartree potential components and 3 Ry for the screened interaction block size for electron–hole interaction term proved to be perfectly convergent for the BSE kernel. Optical absorption was computed by averaging out values of dielectric function along with three spatial directions, and a 0.1 eV damping coefficient was used as the width of the Lorentzian peak.

3 Results and discussion

3.1 Electronic properties

The hexagonal unit cell of Cu₃P with space group P6₃cm was considered with experimental lattice parameters a = b = 6.959 and c = 7.143 (in angstrom). All the properties were calculated from the optimized geometrical structure from the PBE functional (Fig. S3†), and the optimized lattice constants are given in Table S1 (ESI). † Since the geometrical structure can influence the optoelectronic properties, relaxing the structure is vital in electronic structure calculations. The PBE lattice constants were within 1% of experimental parameters and were closer to experimental values than the PBEsol optimized structure. Some reports suggest Cu₃P is a semiconductor with an energy gap in the range 1.3–1.4 eV measured from scanning tunneling spectroscopy⁴¹ or around 0.8 eV according to optical DRS spectroscopy⁴² and 1.6 eV from another DRS spectroscopy,⁷ while a study using the NMR technique shows it to be metallic.⁴³ However, many experimental studies have shown Cu₃P is a semiconductor. Moreover, the metallic state obtained by theoretical calculations at the PBE level²⁷ can be attributed to the band gap problem in Kohn–Sham DFT formalism. We also obtained the metallic state at the PBE level in this study. In order to circumvent the band gap problem of DFT, we have tried to employ the DFT+U method, where Hubbard (U) values are taken empirically, but the same “U” values have been used in the previous study on this material. The Hubbard values taken in all the calculations (unless explicitly mentioned) were 22 eV and 10 eV for Cu-3d and P-3p, respectively. These surprisingly large values seem unusual at first glance. However, the same were used in the previous study to open up the gap, close to the experimental value²⁷ and it indicates strong localization and correlational effects of Cu-3d and P-3p electrons in Cu₃P. The lattice constants at these U values (22 eV and 10 eV) are also given in Table S1 (ESI),† which is not too far from the PBE result and the band gap against a different set of “U” values is presented in Table S2 (ESI).†

Interestingly, the gap does not open unless we apply Hubbard on P-3p, no matter how large the “U” is for Cu-3d alone (up to U_d = 30 eV has been tested).²⁷ The DFT + U_d + U_p with the chosen U values opens the gap as the states around the Fermi level start to re-shift, causing the gap to open up, Fig. 1, 2 and S3† show this shifting. Moreover, the band gap opening is strongly dependent on the U_p value (Fig. S4†). Furthermore, we also tried to use the DFT + U + V method⁴⁴ (“U” signifies the onsite correlation, the “V” term accounts for the inter-site electronic interactions) and tried to compute “U and V” using the linear response method within Density Functional Perturbation Theory (DFPT).⁴⁵ However, DFPT was not successful for the Cu₃P system. It has been found that for closed d-shell transition metals, this approach gives unphysical “U” values that continue to rise astronomically after each iteration;⁴⁶ therefore, self-consistency cannot be attained. We also got similar behavior for the Cu-3d state, as shown in Table S3 (ESI).†

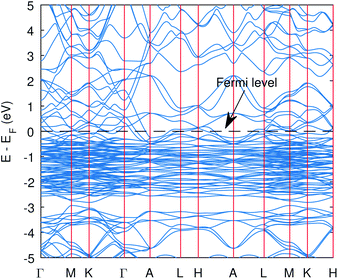Fig. 1 The band structure of Cu₃P from the PBE functional without Hubbard potentials. The valence and conduction states overlap and hence the metallic state was obtained.

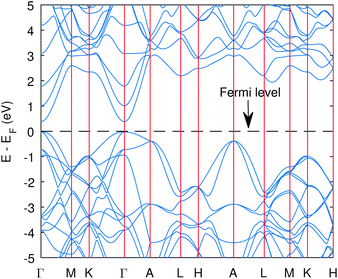Fig. 2 The band structure of Cu₃P from the PBE functional with Hubbard potentials. The gap opened up with value of 0.41 eV. However, the band curvatures are almost identical to without Hubbard case.

The computed band structure of Cu₃P is shown in Fig. 1, which shows the metallic state due to bands of top valence states overlapping with some of the conduction states. The band structure with the Hubbard potential, as depicted in Fig. 2, shows the band gap opening and yields a 0.41 eV band gap value, which is quite similar to what has already been obtained using these Hubbard values in the past.²⁷ However, the effect of these large Hubbard potentials on optical calculations, especially using the BSE, has not been studied in the past. We tried to use these Hubbard parameters to find optical properties and also employed hybrid functional PBE0 in optical calculations (BSE@PBE0). Furthermore, the curvature of the bands is identical in both cases, which shows that the effective mass and hence carrier dynamics of the electron and holes will not be influenced much by applying these enormous Hubbard potentials.

3.2 Partial density of states (PDOS)

The significant change in applying the Hubbard was observed at the top of the valence state, where those states shifted to lower energies, as depicted in Fig. 2. The partial density of states (PDOS) plot in Fig. 3 with applied Hubbard values suggests that the top of the valence band is mainly composed of P-3p and Cu-3d orbitals, so these two states primarily constitute the total density of states of valence states, while the bottom of the conduction state is comprised mainly of Cu 4s. Thus, the significant impact on valence states in the band structure corresponds to applying Hubbard on P-3p and Cu-3d. Furthermore, the nature of the band gap is direct; as evident in Fig. 2, the top of the valence band and the bottom of the conduction band exist at the gamma point, and experimental studies also suggest a direct band gap.⁷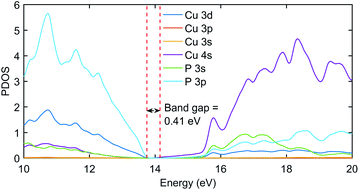

Fig. 3 The PDOS plot of Cu₃P with Hubbard potentials (22, 18). The gap value of 0.41 eV was obtained as it was in the band structure diagram using the same Hubbard values.

4 Optical properties

4.1 Dielectric function

Many optical parameters for a material can be deduced from dielectric function, such as absorption coefficient, refractive index, reflectivity, and extinction coefficient. A material might show no significant response at much lower energies than the visible; however, we might have a resonant response resulting from the inter-band transitions at higher energies. In this study, we are considering interband transitions only to study the optical absorption of Cu₃P, and phonon-assisted optical transitions were also omitted due to the direct nature of the band gap. The imaginary part of the dielectric function describes the transition probability from occupied to unoccupied states and is related to optical absorption.

The imaginary part of the dielectric function shown in Fig. 4 was computed using RPA and BSE theories. Independent Particle Approximation (IPA) including Local Fields Effects (LFE) constitutes the RPA.⁴⁷ Local fields in the material result from polarization caused by the applied electric field and describe the density inhomogeneity of the material. On the other hand, the Bethe–Salpeter equation (BSE) also deals with neutral excitations but takes electron–hole interaction into account.^48,49 The BSE is an eigenvalue problem solved by finding eigenvalues of the electron–hole Hamiltonian.⁴⁸ The obtained eigenvalues of the BSE are then used to find the optical properties.⁵⁰ The dielectric function in Fig. 4 shows the enlarged absorption up to 5 eV from the BSE and has a low absorption onset than the RPA curve. This shows that the BSE curve is red-shifted and signifies the optical excitation caused by the excitonic states present in the band gap.

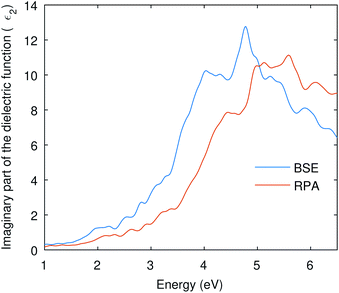Fig. 4 The imaginary part of the dielectric function is computed from RPA and BSE theories. The BSE curve shows a red-shift due to electron–hole interactions.

4.2 Absorption coefficient

To see the effect of the large Hubbard values used in all our calculations, we have computed the optical absorption at two different sets of “U” values. One with (22, 10) and the other with (18, 8) for (Cu-3d, P-3p), as shown in Fig. 5. The electronic band gap with (22, 10) Hubbard values was 0.41 eV, and we obtained 0.07 eV with (18, 8) values. Both curves in Fig. 5 are pretty similar, while the (18, 8) curve is red-shifted almost the same amount as the difference in electronic band gap using these two different sets of Hubbard values. This signifies that the large Hubbard values help open the band gap but do not drastically impact the shape of the optical spectrum. Moreover, the identical optical absorption calculated from the BSE with these two sets of Hubbard values also validates the resemblance of the band structures because the optical spectrum directly correlates with underlying electronic structure calculations.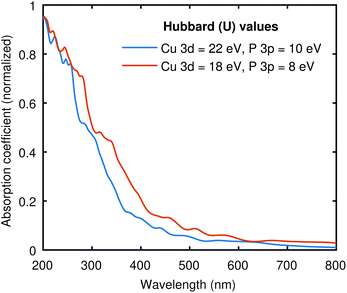

Fig. 5 The absorption coefficient of Cu₃P at two different sets of Hubbard values. The results are qualitatively similar to the expected shift across the x-axis due to the difference in the band gap.

Fig. 6 compares the theoretically obtained absorption coefficient with the experimental data for the absorption. The BSE can be solved on top of the Kohn–Sham wavefunction with the band gap corrected by rigid scissor shift, or quasiparticle wavefunctions like GW corrections, or the ground state wavefunction calculated using hybrid functionals. In this work, we have tested the PBE0 hybrid functional as a starting point for the BSE, and conventional DFT+U. Fig. 6 shows that BSE@DFT+U has the correct optical absorption onset compared to the experimental curve. However, it misses some features; for instance, the peak close to 800 nm is not present in the DFT+U curve. The BSE@PBE0 performs much better in terms of qualitatively reproducing the experimental data. The comparison shows that BSE@PBE0 is closer to the experimental data, which shows that the exact exchange present in PBE0 plays a vital role in Cu₃P. However, the need for a more involved theory like GW corrections might be helpful to obtain even better agreement with the experimental data and to understand the behavior of subtle exchange and correlation effects present in Cu₃P.

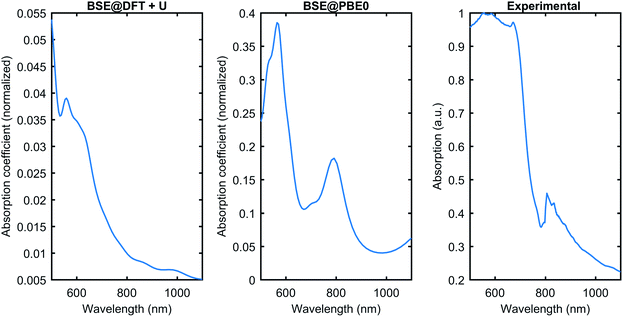Fig. 6 The optical absorption comparison was obtained from the BSE on top of DFT+U and PBE0 with the experimental data. BSE@PBE0 gives better agreement with the experiment.

5 Conclusions

The electronic and optical response of Cu₃P is correctly reproduced by applying DFT+U followed by the BSE. The semiconducting state can be obtained in ground state Kohn–Sham calculations using the Hubbard potentials or more computationally expansive hybrid functional, PBE0. The first-principles determination of Hubbard values from the self-consistent DFPT approach was unsuccessful due to the full-shell d-block transition metal (Cu). Furthermore, optical calculation suggests the electron–hole interaction plays a significant role in the optical response of Cu₃P, as the optical onset for the RPA and BSE curves differs. BSE@PBE0 gives much better agreement with the experimental data as compared to BSE@DFT+U. Our study provides an improved understanding and application of BSE theory on Cu₃P; however, further studies using more advanced theories incorporating quasiparticle calculations will further pave the way in understanding the electronic structure of Cu₃P.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

All the calculations for this work were performed using the LUMS HPC resources.

References

1. A. Fujishima and K. Honda, Nature, 1972, 238(5358), 37–38.
2. S. A. Ansari, M. M. Khan, M. O. Ansari and M. H. Cho, New J. Chem., 2016, 40, 3000–3009.
3. J. Low, B. Cheng and J. Yu, Appl. Surf. Sci., 2017, 392, 658–686.
4. N. Mosleh, M. Mohammadikish and M. Masteri-Farahani, Langmuir, 2020, 36, 14224–14233.
5. B. Huang and J. N. Hart, Phys. Chem. Chem. Phys., 2020, 22, 1727–1737.
6. T. Saison, P. Gras, N. Chemin, C. Chanéac, O. Durupthy, V. Brezová, C. Colbeau-Justin and J. P. Jolivet, J. Phys. Chem. C, 2013, 117, 22656–22666.
7. A. Rauf, M. Ma, S. Kim, M. S. A. S. Shah, C. H. Chung, J. H. Park and P. J. Yoo, Nanoscale, 2018, 10, 3026–3036.
8. F. Ren, J. Zhang and Y. Wang, RSC Adv., 2015, 5, 29058–29065.
9. H. Ahmad, A. Rauf, A. Ahmad, A. Ulhaq and S. Muhammad, RSC Adv., 2021, 11, 32330–32338.
10. A. F. Harper, M. L. Evans and A. J. Morris, Chem. Mater., 2020, 32, 6629–6639.
11. X. Peng, Y. Lv, L. Fu, F. Chen, W. Su, J. Li, Q. Zhang and S. Zhao, RSC Adv., 2021, 11, 34095–34100.
12. H. Shi, T. Zheng, Y. Zuo, Q. Wu, Y. Zhang, Y. Fan and P. Tontiwachwuthikul, RSC Adv., 2021, 11, 33471–33480.
13. Q. Wang, L. Xiao, X. Liu, X. Sun, J. Wang and H. Du, J. Alloys Compd., 2022, 894, 162331.
14. F. Meng, J. Li, S. K. Cushing, M. Zhi and N. Wu, J. Am. Chem. Soc., 2013, 135, 10286–10289.
15. Z. Yang, L. Shao, L. Wang, X. Xia, Y. Liu, S. Cheng, C. Yang and S. Li, Int. J. Hydrogen Energy, 2020, 45, 14334–14346.
16. L. Zhang and Z. Jin, Nanoscale, 2021, 13, 1340–1353.
17. G. X. Zhang, A. M. Reilly, A. Tkatchenko and M. Scheffler, New J. Phys., 2018, 20, 063020.
18. S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515.
19. L. J. Sham and M. Schlter, Phys. Rev. Lett., 1983, 51, 1888–1891.
20. S. Conejeros, P. Alemany, M. Llunell, I. D. P. Moreira, V. Sánchez and J. Llanos, Inorg. Chem., 2015, 54, 4840–4849.
21. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943.
22. M. S. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390–5413.
23. L. Hedin, Phys. Rev., 1965, 139, A796.
24. A. Schleife and F. Bechstedt, J. Mater. Res., 2012, 27, 2180–2189.
25. F. Bruneval and M. A. Marques, J. Chem. Theory Comput., 2013, 9, 324–329.
26. A. Schleife, M. D. Neumann, N. Esser, Z. Galazka, A. Gottwald, J. Nixdorf, R. Goldhahn and M. Feneberg, New J. Phys., 2018, 20, 053016.
27. R. Gaspari, F. Labat, L. Manna, C. Adamo and A. Cavalli, Theor. Chem. Acc., 2016, 135, 73.
28. P. Borlido, J. Schmidt, A. W. Huran, F. Tran, M. A. Marques and S. Botti, npj Comput. Mater., 2020, 6, 1–17.
29. J. Sun, A. Ruzsinszky and J. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
30. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
33. D. R. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494–1497.
34. D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117.
35. A. F. Starace, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 3, 1242–1245.
36. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
37. H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218.
38. O. K. Orhan and D. D. O'Regan, Phys. Rev. B, 2020, 101, 245137.
39. S.-G. Park, B. Magyari-Köpe and Y. Nishi, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115109.
40. D. Sangalli, A. Ferretti, H. Miranda, C. Attaccalite, I. Marri, E. Cannuccia, P. Melo, M. Marsili, F. Paleari, A. Marrazzo, G. Prandini, P. Bonfà, M. O. Atambo, F. Affinito, M. Palummo, A. Molina-Sánchez, C. Hogan, M. Grüning, D. Varsano and A. Marini, J. Phys.: Condens. Matter, 2019, 31, 325902.
41. G. Manna, R. Bose and N. Pradhan, Angew. Chem., Int. Ed., 2013, 52, 6762–6766.
42. J. Ann Aitken, V. Ganzha-Hazen and S. L. Brock, J. Solid State Chem., 2005, 178, 970–975.
43. I. Furo, I. Bakonyi, K. Tompa, E. Zsoldos, I. Heinmaa, M. Alla and E. Lippmaa, J. Phys.: Condens. Matter, 1990, 2, 4217.
44. V. Leiria Campo and M. Cococcioni, J. Phys.: Condens. Matter, 2010, 22, 055602.
45. I. Timrov, N. Marzari and M. Cococcioni, Phys. Rev. B, 2018, 98, 085127.
46. K. Yu and E. A. Carter, J. Chem. Phys., 2014, 140, 121105.
47. D. Bohm and D. Pines, Phys. Rev., 1951, 82, 625–634.
48. G. Onida, L. Reining and A. Rubio, Electronic excitations: density-functional versus many-body Green's-function approaches, 2002, https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.74.601.
49. E. E. Salpeter and H. A. Bethe, Phys. Rev., 1951, 84, 1232–1242.
50. S. Albrecht, L. Reining, R. Del Sole and G. Onida, Phys. Rev. Lett., 1998, 80, 4510–4513.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra02472a

---