Open Access Article
Open Access ArticlePreparation, characterization and DFT+U study of the polar Fe3+-based phase Ba5Fe2ZnIn4S15 containing S = 5/2 zigzag chains†
Batoul
Almoussawi
,
Victor
Duffort
 ,
Angel M.
Arevalo-Lopez
,
Angel M.
Arevalo-Lopez
 ,
Maxime
Braun
,
Nora
Djelal
and
Houria
Kabbour
,
Maxime
Braun
,
Nora
Djelal
and
Houria
Kabbour
 *
*
Univ. Lille, CNRS, Centrale Lille, ENSCL, Univ. Artois, UMR 8181 – UCCS – Unité de Catalyse et Chimie du Solide, F-59000 Lille, France. E-mail: houria.kabbour@univ-lille.fr
First published on 18th May 2022
Abstract
The polar magnetic chalcogenide phase Ba5Fe2ZnIn4S15 was synthesized and its structure was solved by single crystal XRD. It is the first member with a 3d magnetic metal (Fe3+) in the Pb5ZnGa6S15-type structure family of wide bandgap materials with non-linear optical properties. The three-dimensional framework possesses a low dimensional magnetic character through the presence of weakly interacting zig-zag chains made of corner-sharing FeS4 tetrahedra forming chain 1, [FeS2]−∞. The latter chains are separated by InS4 tetrahedra providing weak magnetic super-super exchanges between them. The framework is also constituted by chain 2, [In3Zn1S9]7−∞ (chain of T2-supertetrahedra) extended similarly to chain 1 along the direction c and connected through InS4 tetrahedra. Symmetry analysis shows that the intrinsic polarization observed in this class of materials is mostly due to the anionic framework. Preliminary magnetic measurements and density functional theory calculations suggest dominating antiferromagnetic interactions with strong super-exchange coupling within the Fe-chains.
Introduction
The interest in the search and study of transition metal chalcogenide compounds is due to their structural diversity and compositional complexity.1 These characteristics lead to appealing properties.2,3 For instance, superconductivity coexists with ferromagnetism in layered iron-based chalcogenide Cr-doped FeTe0.8S0.2.4 Multiferroicity has also been found in several Fe-based systems.5–7 On the other hand, polar chalcogenides with second harmonic generation (SHG) responses are being investigated for their nonlinear optical properties.An interesting strategy to target new multiferroic phases is to substitute these strongly polar systems using magnetic cations in order to induce magnetic interaction on top of the polar distortion. Therefore, in this work, we focused on the polar structure type A5ZnM6S15 with the reported members Sr5ZnGa6S15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 and Pb5ZnGa6S15
8 and Pb5ZnGa6S15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 phases (space group Ama2). They are wide bandgap semiconductors and exhibit a strong SHG response. Thus, we attempt to insert Fe3+ (3d5, S = 5/2) providing strong magnetic coupling. They are characterized by interconnected Ga4S10 T2-supertetrahedra, dimeric Ga2S7 tetrahedra and ZnS4 tetrahedra to form a complex 3D non-centrosymmetric (NCS) anionic framework with a large cation residing in the irregular voids (Sr2+ or Pb2+ in the later examples). Here we have synthesized the first magnetic member Ba5Fe2ZnIn4S15. Besides, a few polar magnetic sulfides are found in the literature with Fe3+ as the magnetic ion, such as the chain compounds RE3MInS7 (RE = rare earth and M = Fe, Co, and Ni in an octahedral environment) related to the La3CuSiS7-type which exhibits antiferromagnetic interactions.10 With other magnetic ions, one can cite the polar sulfide Na8Mn2(Ge2Se6)2 which was mainly studied for its non-linear optical properties and is a paramagnetic semiconductor.11 The polar chalcogenides BaLnSn2Q6 (Ln = Ce, Pr, Nd and Q = S and Se) were reported as well with paramagnetic behaviour obeying the Curie–Weiss law.12
9 phases (space group Ama2). They are wide bandgap semiconductors and exhibit a strong SHG response. Thus, we attempt to insert Fe3+ (3d5, S = 5/2) providing strong magnetic coupling. They are characterized by interconnected Ga4S10 T2-supertetrahedra, dimeric Ga2S7 tetrahedra and ZnS4 tetrahedra to form a complex 3D non-centrosymmetric (NCS) anionic framework with a large cation residing in the irregular voids (Sr2+ or Pb2+ in the later examples). Here we have synthesized the first magnetic member Ba5Fe2ZnIn4S15. Besides, a few polar magnetic sulfides are found in the literature with Fe3+ as the magnetic ion, such as the chain compounds RE3MInS7 (RE = rare earth and M = Fe, Co, and Ni in an octahedral environment) related to the La3CuSiS7-type which exhibits antiferromagnetic interactions.10 With other magnetic ions, one can cite the polar sulfide Na8Mn2(Ge2Se6)2 which was mainly studied for its non-linear optical properties and is a paramagnetic semiconductor.11 The polar chalcogenides BaLnSn2Q6 (Ln = Ce, Pr, Nd and Q = S and Se) were reported as well with paramagnetic behaviour obeying the Curie–Weiss law.12
Here, we present the in-depth structural characterization of the polar magnetic chalcogenide Ba5Fe2ZnIn4S15, using multiple cations with different scattering factors to provide new insights into the chemical speciation of each cationic site. Symmetry analysis of the structure is used to emphasize the origin of the non-centrosymmetry and polarity of this structure type. Finally, a low dimensionality magnetism is proposed based on the preliminary magnetic study combined with DFT calculations.
Experimental section
Synthesis
The synthesis was carried out with a stoichiometric mixture of the precursors BaS/In2S3/Zn/Fe/S. These precursors were mixed and thoroughly ground in an agate mortar before being pressed into pellets and heated in an evacuated sealed quartz tube. The heat treatment consisted of heating up to 1000 °C at a rate of 250 °C h−1 for 7 hours and then cooling down to 700 °C at a 30 °C h−1 rate, after which the furnace was switched off.X-ray diffraction of single crystals was performed on an X8 diffractometer equipped with a bi-dimensional CCD 4 K detector and an Ag Kα source.
Mode symmetry analysis was performed using the ISODISTORT software13 and the representation of the atomic shifts was drawn using the Vesta 3 software.14
The powder X-ray diffraction pattern was obtained on a Bruker D8 diffractometer equipped with a linear detector Lynxeye (CuKα) in the Bragg–Brentano geometry at room temperature.
Magnetic measurements were performed on a 7 T Dynacool PPMS from Quantum Design by field cooled (FC) and zero field cooled (ZFC) procedures under an external field of 0.1 T.
DFT calculations were carried out by employing the projector augmented wave (PAW)15,16 method encoded in the Vienna ab initio simulation package (VASP)17 and the generalized gradient approximation of Perdew, Burke and Ernzerhof18 (PBE) for the exchange–correlation functionals. A plane wave cutoff energy of 550 eV and a threshold of self-consistent-field energy convergence of 10−6 eV were used, with 74 k points in the irreducible Brillouin zone for the spin polarized GGA+U (Ueff = 4 eV) calculations of Ba5Fe2ZnIn4S15.
For the site preference calculations in Sr5ZnGa6S15 and Pb5ZnGa6S15, full geometry optimizations were carried out using a plane wave energy cutoff of 550 eV and 30 k points in the irreducible Brillouin zone. It converged with residual Hellman–Feynman forces on the atoms smaller than 0.03 eV Å−1 and led to a good match with the experimental structure, i.e. within a reasonable error expected for the GGA method. The relaxed structure was used for calculations of the electronic structure. For the latter, a plane wave cutoff energy of 550 eV and a threshold of self-consistent-field energy convergence of 10−6 eV were used, with 90 k points in the irreducible Brillouin zone.
Scanning electron microscopy (SEM) experiments and EDX analysis were carried out on a Hitachi S400N.
Results and discussion
Structure solution and description
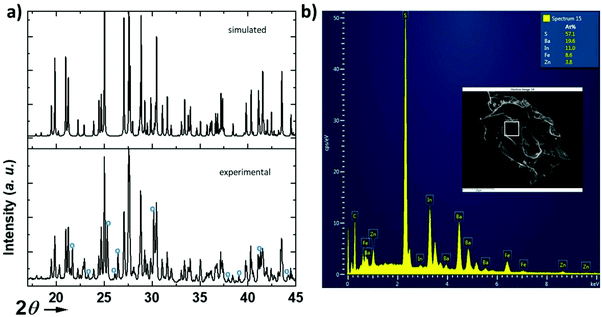
The structure (Fig. 1) was solved using single crystal XRD data (CCDC deposition number 2148490†) obtained from a black platelet crystal. It crystallizes in the orthorhombic system with cell parameters a = 23.4580(19) Å, b = 18.551(6) Å, and c = 6.464(5) Å and the polar space group Ama2 (40). The data collection and refinement details are given in Table 1. The refinement was carried out using the JANA2006![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 software based on a structure solution obtained using the charge flipping method.20 The EDS analysis of the single crystals (Fig. 2) revealed an average atomic ratio of 19.6/8.6/3.8/11.0/57.1 for Ba/Fe/Zn/In/S. This is in good agreement with the theoretical ratio expected for the refined formula Ba5Fe2ZnIn4S15, i.e. 18.5/7.4/3.7/14.8/55.6 for Ba/Fe/Zn/In/S. In particular, the Fe ratio is about twice the Zn ratio which is consistent with their refined distribution.
19 software based on a structure solution obtained using the charge flipping method.20 The EDS analysis of the single crystals (Fig. 2) revealed an average atomic ratio of 19.6/8.6/3.8/11.0/57.1 for Ba/Fe/Zn/In/S. This is in good agreement with the theoretical ratio expected for the refined formula Ba5Fe2ZnIn4S15, i.e. 18.5/7.4/3.7/14.8/55.6 for Ba/Fe/Zn/In/S. In particular, the Fe ratio is about twice the Zn ratio which is consistent with their refined distribution.
| Formula | Ba5Fe2In4ZnS15 |
| Molecular weight (g mol−1) | 1804 |
| Symmetry | Orthorhombic |
| Space group | Ama2 (40) |
| Unit cell dimensions (Å) | a = 23.458(2) |
| b = 18.551(6) | |
| c = 6.464(5) | |
| Volume (Å3) | 2813(2) |
| Z | 4 |
| Data collection | |
| Equipment | Bruker CCD |
| λ [Ag Kα; Å] | 0.56087 |
| Calculated density (g cm−3) | 4.2599 |
| Crystal shape | Platelet |
| Crystal dimensions (μm) | 65 × 50 × 5 |
| Color | Black |
| Absorption correction | Analytical |
| Scan mode | ω, ϕ |
| θ (min–max) (°) | 1.73–19.72 |
| μ (mm−1; for λ Kα = 0.56087 Å) | 6.841 |
| F(000) | 3192 |
| Reciprocal space recording | −28 ≤ h ≤ 28 |
| −22 ≤ k ≤ 22 | |
| −7 ≤ l ≤ 7 | |
| No. of measured reflections | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 736 |
| No. of independent reflections | 2633 |
| I > 3σ(I) (total) | 2325 |
| Refinement | |
| Number of refined parameters | 245 |
| Refinement method | Least-squares |
| Weighting scheme | Sigma |
| R 1(F) [I > 3σ(I)]/R1(F2) (all data, %) | 0.0315/0.0382 |
| wR2(F2) [I > 3σ(I)]/wR2(F2) (all data, %) | 0.0374/0.0386 |
| Goodness of fit | 1.42 |
| Flack parameter | 0.05(5) |
| Max/Min residual electronic density (e−/Å3) | 1.39/−1.86 |
| T min/Tmax | 0.6607/0.7387 |
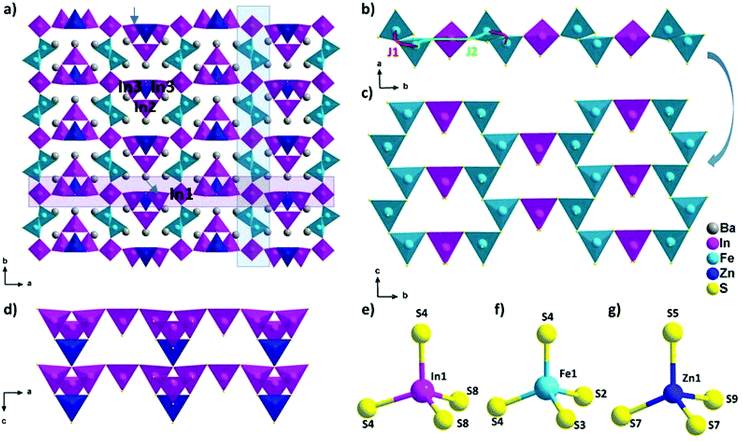
The new phase Ba5Fe2ZnIn4S15 is a 3D framework (Fig. 1, Tables 2–5) combining three different types of tetrahedra InS4, FeS4 and ZnS4 (Fig. 1e, f and g). The standard description of this family has been reported for several non-magnetic chalcogenides, e.g. SHG active compounds Sr5ZnGa6S15 and Pb5Ga6ZnS5 with wide bandgaps.8,9 The atomic positions are very close to those reported in the previous compositions with the exception of the zinc position, as discussed later. Please note that due to the polar nature of the space group, multiple origin choices are possible. The transformation matrices to apply in the reported atomic positions8,9 for straightforward comparison can be found in Table S1.†
The structural model can be described as the stacking of two distinct 1D building blocks. The [FeS2]−∞ zigzag chain (1) extending along the c axis is built from corner-sharing [Fe1S4]5− tetrahedra (Fig. 1c) and the T2 supertetrahedron (made of 4 tetrahedra forming M4X10 with M as the cation and X as the anion) based chain (2) [In3Zn1S9]7−∞ which also extends along the c axis (Fig. 1d). In the latter chain, the corner sharing [In3ZnS10]8− T2-supertetrahedra are composed of one [In2S4]5−, two [In3S4]5− and one [Zn1S4]6− tetrahedra. In the FeS4 tetrahedra, the distances dFe–S are found to be between 2.238 Å and 2.266 Å and lead to a BVS of 3.02(5) which is consistent with the Fe3+ oxidation state calculated from the charge balance. This range is comparable to the one reported for instance in Ba5Fe4S11 which also has Fe3+ in the FeS4 tetrahedra, with d(Fe3+–S2−) = 2.214–2.306 Å.21 The In–S bond lengths ranging from 2.377 Å to 2.484 Å are comparable to the range of bond lengths in Ba2In2S5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 (from 2.386 Å to 2.503 Å). The Ba2+ cations are localized in the voids.
21 (from 2.386 Å to 2.503 Å). The Ba2+ cations are localized in the voids.
The two chains are interconnected via [In1S4]5− tetrahedra along the a and b axis respectively to form the three-dimensional framework of the structure (Fig. 1a). The heterogeneous cation composition of the T2-supertetrahedra, i.e. [In3ZnS10]8−, is observed for the first time. In previous studies on this structure type (ref. 8 and 9), the [ZnS4]6− tetrahedron was reported as the connecting unit between the two chains that were composed purely of [GaS4]5− tetrahedra. We would like to emphasize here that Zn2+ and Ga3+ being isoelectronic species, X-rays crystallography is a poor tool to resolve the chemical composition of Ga/Zn sites and therefore such structures are possibly ambiguous. Yet, the chemical speciation of the different sites is not discussed in previous studies. While our composition only has Zn2+ as the common cation with the other two previously reported structures, the atomic positions are remarkably similar. Therefore, the speciation information obtained in the case of BaZnFe2In4S15, thanks to the different electron counts in Fe3+, Zn2+ and In3+, could also be relevant to help resolve the natural ambiguity of the Ga/Zn speciation in the other two structures.
Recently, the IR NLO phase Ba5CdGa6Se15 with a strong SHG response has also been reported22 with the Pb5ZnGa6S15-type structure. In this phase there is no ambiguity concerning the repartition of Cd/Ga, but interestingly they suggest a site preference (4a site) for Zn in the parent phase Pb5ZnGa6S15 without excluding Zn/Ga disorder.
In our study, reinvestigation of the reported structures of Pb5ZnGa6S15 and Sr5ZnGa6S15 shows evidence of a Zn/Ga inversion. In particular, in both structures the thermal displacement of Zn2+ is significantly smaller than that of other cations while the thermal parameter of the Ga site corresponding to the location of the Zn site in our structure is the largest of all Ga3+ cations. While all reported parameters are within an acceptable range, this is exactly the effect one would expect if a slightly larger Zn2+ was squeezed in a Ga3+ position and vice versa. Finally, the hypothesis of Ga/Zn in previously reported structures was probed using geometry optimization by DFT calculations. In both Pb5ZnGa6S15 and Sr5ZnGa6S15, the energy of the optimized structure (see Tables S2–S5†) is significantly lower when the [ZnS4]6− tetrahedron is part of the T2-supertetrahedra (−461.5 eV and −491.4 eV respectively) rather than in the reported position (−460.1 eV and −488.5 eV respectively).
None of the above elements are direct proof of the Zn position in (Pb,Sr)5ZnGa6S15; however, we report here clear evidence that this question is still pending. It should be addressed with caution until powders with sufficient purity or large enough single crystals for neutron diffraction can be obtained.
| Atom | Wyck. | x | y | z | U eq |
|---|---|---|---|---|---|
| Ba1 | 4b | 3/4 | 0.34541(7) | 0.147(2) | 0.0128(4) |
| Ba2 | 8c | 0.61457(3) | 0.13332(2) | 0.068(2) | 0.0110(2) |
| Ba3 | 8c | 0.10987(3) | 0.16031(4) | 0.102(2) | 0.0126(2) |
| In1 | 4a | 1/2 | 1/2 | 0.078(2) | 0.0118(4) |
| In2 | 4b | 3/4 | 0.69547 | 0.183(2) | 0.0125(4) |
| In3 | 8c | 0.66016(4) | 0.5262(2) | 0.055(2) | 0.0203(3) |
| Fe1 | 8c | 0.47101(7) | 0.6962(1) | 0.130(2) | 0.0071(5) |
| Zn1 | 4b | 3/4 | 0.52836(12) | 0.531(2) | 0.0079(6) |
| S1 | 4b | 3/4 | 0.8245(3) | 0.142(2) | 0.0122(14) |
| S2 | 8c | 0.37633(11) | 0.69643(16) | 0.088(2) | 0.0100(9) |
| S3 | 8c | 0.51069(14) | 0.70254(19) | −0.186(2) | 0.0125(10) |
| S4 | 8c | 0.49966(15) | 0.60120(19) | 0.323(2) | 0.0125(10) |
| S5 | 4b | 3/4 | 0.6575(2) | 0.551(2) | 0.0112(13) |
| S6 | 8c | 0.65417(12) | 0.65980(17) | 0.066(2) | 0.0121(9) |
| S7 | 8c | 0.66700(13) | 0.47875(19) | 0.391(2) | 0.0133(10) |
| S8 | 8c | 0.58174(14) | 0.4932(2) | −0.158(2) | 0.0137(11) |
| S9 | 4b | 3/4 | 0.4937(3) | −0.113(2) | 0.0143(15) |
Origin of the non-centrosymmetry and the polarization of the structure
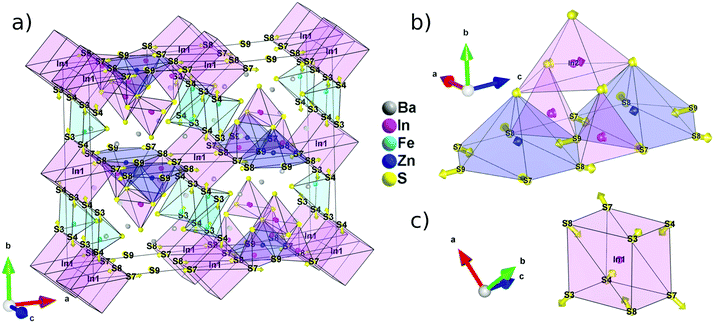
With at least three compositions with the same structure type, sulphides with the A5ZnM6S15 stoichiometry appear as a very promising family for the discovery of new polar materials. Understanding of the geometrical origin of the spatial inversion breaking appears as a critical element to improve the properties of these materials. To visualize the origin of the non-centrosymmetry and polarity observed in A5ZnM6S15, we constructed a hypothetical centrosymmetric high-symmetry structure (aristotype) and used symmetry mode analysis23 to decompose the atomic shifts, relating the aristotype to the lower-symmetry structure (hettotype), into centrosymmetric and non-centrosymmetric displacements.Looking at the cationic framework of Ba5Fe2ZnIn4S15, we found that the structure is composed of 8 layers along a, 6 along b and only 2 along c. The positions of each cation can therefore be rounded off to the closest fractional coordinate with the form (nx/8, ny/6, nz/2) to construct a high symmetry structure. The resulting arrangement has the Cmcm (#63) centrosymmetric space group; note that to avoid permutation of the basis vectors when transforming the aristotype to the hettotype, the non-standard setting Amam (#63-4) is used in the rest of the article. Similarly, the anion framework can be described using 8 layers along a, 6 along b and 4 along c, and the resulting atomic positions, also compatible with the Amam space group, are listed in Table S6.†
The decomposition of the different modes and the evaluation of their amplitude (Table S7†) were achieved using the ISODISTORT software (ref. 10). The 43 modes belong to two irreducible representations Γ1+ and Γ3− with isotropic subgroups Amam and Ama2, respectively. This allows the differentiation between the atomic shifts breaking the inversion symmetry, i.e. belonging to Γ3−, and the displacements compatible with the inversion center, i.e. belonging to Γ1+. By applying the atomic shifts of the Γ1+ irreducible representation to the aristotype we can generate the best possible centrosymmetric model and represent the remaining atomic shifts using arrows (Fig. 3a). It is then easy to visualize that it is mostly the anionic framework that breaks the inversion symmetry. The cations have atomic shifts less than 0.4 Å with respect to the centrosymmetric Amam structure, with the exception of In2 that shows a shift of about 0.7 Å. Positions S3, S4, S7, S8 and S9 require a displacement greater than 1 Å to reach their actual position with a maximum of 1.2 Å for S9.
Because In1 lies on an inversion center in the aristotype structure, the deviation from a centrosymmetric structure is most obvious in the evolution of its coordination polyhedra (Fig. 3c). The pseudo-cubic environment imposed by the inversion center can be relaxed into a tetrahedral environment by pulling in atoms that are on the diagonal of each face since S3/S4 and S7/S8 are no longer equivalent positions in the Ama2 space group. Then, using the centrosymmetric and non-centrosymmetric models, the calculated polarization via point charge is found to be high with a value of 63.7 μC cm−2.
The polarity of the structure, on the other hand, originates from the displacements along the polar axis, c. In this regard, the evolution of the T2 super-tetrahedral subunit (Fig. 3b) is much more relevant. The large shift of the S9 position along c is only partially compensated by a much smaller shift of the In1 position in the opposite direction. Several substitution strategies can then be devised to increase the polarization of this structure type. In particular, the effective charge carried by the anion in the S9 position is maximized by increasing the ionicity of its chemical bonds.
DFT calculations
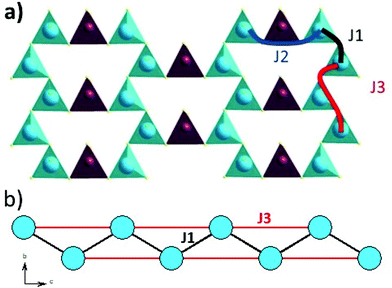
The magnetic interactions within the title phase were investigated using DFT+U calculations at the GGA level. We have investigated several magnetic configurations using Ueff = 4 eV which is in the typical range of similar systems.24 The structure was not relaxed to avoid slight geometrical changes in the spin chain that may affect the results.Using the energy mapping analysis25 and the magnetic configurations presented in (Fig. 4), we extracted from our DFT+U calculations the magnetic interaction constants J1, J2 and J3 (Table 3) (Fig. 5). We consider decoupled 2D layers containing the spin chains weakly interacting. Based on the geometrical configuration we can propose and estimate a super-exchange mechanism within the chains (intra-chain, J1 coupling) and a super-super exchange mechanism between the chains (inter-chains couplings) as well as for the next-nearest neighbour interaction within the chains (J2 and J3 respectively). Another inter-chain path exists through the T2 supertetrahedra but is not considered due to its exceedingly long inter-chain distance (a path of four successive InS4 tetrahedra between Fe atoms) providing a complete structural disconnection.
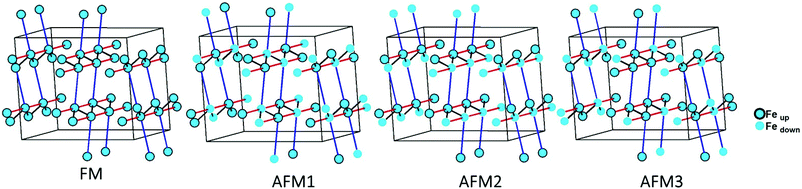 | ||
| Fig. 4 Different magnetic configurations of Ba5Fe2In4Zn1S15 used in the DFT+U calculations; J1, J2 and J3 are represented in black, red and blue, respectively. | ||
| Atom 1 | Atom 2 | d[1,2] (Å) | Fe–S–Fe (Å) | Fe–S⋯S–Fe (Å) | Fe–S–Fe (°) | Number of coupling | |
|---|---|---|---|---|---|---|---|
| J1 | Fe1 | Fe1 | 4.0349(149) | Fe–S3 = 2.2478(167) | 126.8(4) | 2 + 8/2 = 6 | |
| J2 | Fe1 | Fe1 | 6.464(57) | Fe1–S7 = 2.265(5) | 16/2 | ||
| S7–S7 = 3.7094(67) | |||||||
| J3 | Fe1 | Fe1 | 7.4054(35) | Fe1–S4⋯S4–Fe1 | 1 + 9/2 = 5.5 | ||
| Fe–S4 = 2.2614(106) | |||||||
| S4–S4 = 3.7548(5) |
E 0: sum of the nonmagnetic parts.
J ij : the exchange interactions between spin Si and Sj at sites i and j, respectively.
The positive (negative) Jij represents FM (AFM) coupling. For one formula unit, the total energies associated with different magnetic orders can be calculated using:
| E(FM) = E0 − 16J1S2 − 8J2S2 − 16J3S2 | (1) |
| E(AFM1) = E0 + 8J2S2 + 16J3S2 | (2) |
| E(AFM2) = E0 + 16J1S2 + 8J2S2 − 16J3S2 | (3) |
| E(AFM3) = E0 − 8J2S2 + 8J3S2 | (4) |
Here, we use S = 5/2, accordingly with the charge of Fe assumed in this work (d5) corresponding to high spin Fe3+. The latter allows the J calculations using a defined spin state on each site. Using the equations above and the energies of the magnetic configurations presented in (Fig. 4), we extracted from our DFT+U calculations the magnetic interactions constants J1 = −206 K, J2 = −9.08 K and J3 = −6.62 K, considering Ueff = 4 eV. The DFT calculated local magnetic moment on the Fe sites is found to be around 3.9μB with slight variations depending on the magnetic configuration; such a value agrees with a high spin state of Fe3+. All J couplings are found to be antiferromagnetic but J1 is largely dominating which avoids any competition between J1 and J3 (both in-chains and cannot be AFM at the same time) with |J1| ≫ |J3|. J2, inter-chain, is also very weak compared to J1 and in the same range than J3. Therefore, this system can be described as an S = 5/2 AFM spin chain. For such a low dimensional magnetic system with highly disconnected 2D magnetic layers made of weakly interacting spin chains (with the strong J1 in chain), a clear establishment of a long-range magnetic ordering may not occur. Considering the large value of J1, we should keep in mind that it would be affected by Ueff applied for the calculations. We cannot adjust more accurately the Ueff value in the absence of experimental magnetic data on a pure sample (see the discussion below) to compare with the calculation results. Nevertheless, the trend and the dominating J1 are clear. Then, the large value of J1 may be related to the high spin configuration of d5 (Fe3+) which provides a maximal spin-only magnetic moment thus enabling greater magnetic interactions between the spin sites. Additionally, the role of the more covalent bonding with the sulfide anions (compared to oxides) should be further investigated. It is difficult to make a straightforward comparison with other systems but one can cite Ba2FeS3 with quasi one-dimensional (1D) spin chains built with corner sharing FeS4 as found in our phase but not in a zigzag manner and with Fe2+ (S = 2) instead of Fe3+ (S = 5/2). In these cases, a long-range antiferromagnetic transition is found at 54 K (56 K, for a similar high pressure (HP) phase). In the latter phases, the intrachain coupling Jintra is calculated as −24 K (−18 K for HP) from the Wagner-Friedberg model.26 In the centrosymmetric compound BaFe3+2S4, the AFM 1D chains are made of Fe3+S4 with AFM SE but through edge-sharing, it exhibits a magnetic susceptibility which fits a classical S = 5/2 Heisenberg Hamiltonian.27
Powder sample and magnetic measurements
We have attempted to synthesize a pure powder phase. Numerous efforts allowed the increase of the purity of the sample and the powder XRD pattern of our best sample is presented in (Fig. 2). An impurity that could not be indexed to known phases persists. Although the title phase is the major phase as shown in the simulated and superimposed XRD pattern, the impurity is significant which makes the magnetic characterization and its interpretation difficult. Nevertheless, we have carried out a preliminary study.Fig. 6 shows the temperature dependence of the magnetic susceptibilities. At around 2–3 K, a slight divergence of the ZFC/FC is observed; however it is difficult to attribute it to a specific phenomenon such as a spin glass state, low dimensional short-range magnetic correlations and/or a complex long-range magnetic order because of the significant amount of the unidentified impurity. Considering the DFT calculations which suggest that this system can be described as a low dimensional magnetic system (S = 5/2 AFM spin chain), the expected susceptibility for such behaviour would be a broad maximum; however the presence of the impurity hampers its observation. As shown in the ESI (Fig. S1†), we attempted fitting the magnetic susceptibility which shows AFM interactions dominating but it is impossible to fully interpret the magnetic data with the amount of unidentified impurity.
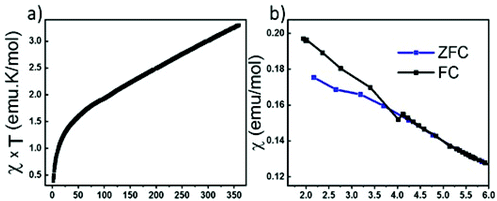 | ||
| Fig. 6 (a) Temperature dependence of magnetic susceptibility χxT. (b) Zoom-in view of ZFC/FC at low temperature. | ||
Conclusion
We describe here the synthesis and the structural and physical characterization of the new sulfide material Ba5Fe2ZnIn4S15. It adopts a polar structure type isostructural with a family of wide bandgap SHG materials, A5ZnM6S15, containing chains of T2-supertetrahedra and [MS2]∞ chains made of corner-sharing tetrahedra. The multi-element substitution on the M-site, M = In and Fe, allowed us to gain insights into the chemical speciation of each cationic site highlighting the ambiguities in previously reported structures with the same structure type. In the title phase, the magnetic high-spin Fe3+ (d5) transition metal lies in the (MS2)∞ chains and the Zn2+ cation is part of the T2 super-tetrahedra. In-depth symmetry analysis of the structure shows that the intrinsic polarization observed in this class of materials is mostly due to the anionic framework and most particularly due to the S9 site.A powder sample could be obtained but a significant unidentified impurity hampers deep physical characterization. Preliminary magnetic measurements reveal a divergence of the ZFC/FC at a very low temperature around 3 K and dominant antiferromagnetic interactions. DFT calculations suggest a stable antiferromagnetic state with strong AFM intrachain Fe–S–Fe super exchanges and very weak interchain Fe–S–S–Fe coupling (via InS4). It thus represents an AFM S = 5/2 spin chain system. A pure powder and magnetic measurements based on single crystals are required to further investigate this sample. It represents a promising platform to measure electric polarization and tune the magnetic interactions toward multiferroic systems.
| Atom | U 11 | U 22 | U 33 | U 12 | U 13 | U 23 |
|---|---|---|---|---|---|---|
| Ba1 | 0.0048(5) | 0.0219(7) | 0.0116(7) | 0.0000(0) | 0.0000(0) | 0.0002(5) |
| Ba2 | 0.0075(3) | 0.0119(4) | 0.0136(5) | 0.0006(3) | 0.0016(4) | −0.0010(4) |
| Ba3 | 0.0081(3) | 0.0193(4) | 0.0105(5) | −0.0001(3) | 0.0006(4) | −0.0027(4) |
| In1 | 0.0110(6) | 0.0133(7) | 0.0112(7) | −0.0004(5) | 0.00000 | 0.00000 |
| In2 | 0.0084(6) | 0.0123(8) | 0.0169(8) | 0.000000 | 0.00000 | 0.0014(6) |
| In3 | 0.0194(5) | 0.0229(6) | 0.0187(6) | 0.0010(4) | −0.0019(5) | 0.0003(6) |
| Fe1 | 0.0044(8) | 0.0100(10) | 0.0069(10) | −0.0004(7) | 0.0007(8) | −0.0002(8) |
| Zn1 | 0.0046(9) | 0.0120(11) | 0.0072(13) | 0.000000 | 0.000000 | −0.0008(9) |
| S1 | 0.008(2) | 0.015(3) | 0.014(3) | 0.000000 | 0.000000 | 0.003(2) |
| S2 | 0.0031(13) | 0.0142(16) | 0.0127(18) | −0.0009(11) | −0.0011(15) | −0.0018(18) |
| S3 | 0.0128(17) | 0.0128(19) | 0.0118(19) | −0.0004(14) | 0.0050(14) | 0.0038(16) |
| S4 | 0.0110(15) | 0.0120(19) | 0.0144(19) | 0.0031(12) | −0.0032(14) | 0.0014(15) |
| S5 | 0.0065(19) | 0.013(2) | 0.014(3) | 0.000000 | 0.000000 | 0.000(2) |
| S6 | 0.0100(14) | 0.0135(16) | 0.0129(18) | −0.0004(12) | −0.0043(15) | −0.0005(19) |
| S7 | 0.0111(16) | 0.0161(19) | 0.0127(19) | −0.0021(14) | 0.0004(15) | 0.0016(16) |
| S8 | 0.0112(16) | 0.015(2) | 0.0147(19) | −0.0014(14) | 0.0062(15) | −0.0016(16) |
| S9 | 0.008(2) | 0.022(3) | 0.012(3) | 0.000000 | 0.000000 | 0.003(2) |
| Atoms 1,2 | d 1,2 [Å] | Atoms 1,2 | d 1,2 [Å] |
|---|---|---|---|
| Ba1–S1 | 3.29(2) | In1–S4 | 2.454(13)*2 |
| Ba1–S1 | 3.22(2) | In1–S8 | 2.456(12)*2 |
| Ba1–S2 | 3.087(4)*2 | In2–S1 | 2.407(6) |
| Ba1–S9 | 3.224(11) | In2–S5 | 2.484(19) |
| Ba2–S2 | 3.168(4) | In2–S6 | 2.461(6)*2 |
| Ba2–S3 | 3.179(10) | In3–S6 | 2.417(4) |
| Ba2–S4 | 3.184(10) | In3–S7 | 2.380(18) |
| Ba2–S5 | 3.210(1) | In3–S8 | 2.395(11) |
| Ba2–S7 | 3.323(8) | In3–S9 | 2.463(9) |
| Ba2–S8 | 3.236(11) | Fe–S2 | 2.237(4) |
| Ba3–S1 | 3.309(2) | Fe1–S3 | 2.246(18) |
| Ba3–S2 | 3.232(19) | Fe1–S3 | 2.265(11) |
| Ba3–S3 | 3.239(9) | Fe1–S4 | 2.263(11) |
| Ba3–S4 | 3.324(11) | Zn1–S5 | 2.399(5) |
| Ba3–S7 | 3.209(9) | Zn1–S7 | 2.335(8)*2 |
| Ba3–S8 | 3.310(10) | Zn1–S9 | 2.387(19) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the French government through the Programme Investissement d'Avenir (I-SITE ULNE/ANR-16-IDEX-0004 ULNE) managed by the Agence Nationale de la Recherche (Project ANION-COMBO). X-rays diffractometers were funded by Région NPDC, FEDER, CNRS and MESR. The regional computational cluster supported by Lille University, CPER Nord-Pas-de-Calais/CRDER, France Grille CNRS and FEDER is acknowledged for providing computational resources.References
- A. Abudurusuli, K. Wu, J. Li, A. Yalikun, Z. Yang and S. Pan, LiBa 2 M, 2019, vol. 4. DOI:10.1021/acs.inorgchem.9b01810.
- N. Nakayama, Studies on the Compounds in the Ba-Fe-S Antiferromagnetism of Ba, FeS, and Related System. I. Linear Chain Compounds Ba & OS, 1980, vol. 356, pp. 351–356 Search PubMed.
- J. T. Lemley, Ba, Fe, S, and Ba, FeS: Crystal Structures, Miissbauer, Magnetic, and Electrical Behavior, 1976, vol. 128, pp. 117–128 Search PubMed.
- T. Li, Z. Feng, Q. Hou, H. Wu, K. Wang, J.-Y. Ge, S. Cao, J. Zhang and N.-C. Yeh, Effects of Cr doping on the superconductivity and magnetism of FeTe0.8S0.2, Solid State Commun., 2020, 309, 113846, DOI:10.1016/j.ssc.2020.113846.
- P. Paul, A. K. Rajarajan, S. Kuila, P. N. Vishwakarma, B. Mandal and T. V. C. Rao, Plausible Multiferroic and Magneto-Electric Behaviour of Polycrystalline Bi0.85Gd0.05La0.1FeO3 at Room Temperature, J. Magn. Magn. Mater., 2021, 538, 168253, DOI:10.1016/j.jmmm.2021.168253.
- J. Chen, L. Liu, X. L. Zhu, Z. V. Gareeva, A. K. Zvezdin and X. M. Chen, The Involvement of Pna 21 Phase in the Multiferroic Characteristics of La/Lu Co-Substituted BiFeO3 Ceramics, Appl. Phys. Lett., 2021, 119(11), 112901, DOI:10.1063/5.0059793.
- P. Augustine, N. Yerol, N. Kalarikkal, B. Raneesh, M. T. Rahul and S. K. Chacko, Room Temperature Multiferroic Properties of BiFeO3−MnFe2O4 Nanocomposites, Ceram. Int., 2021, 47(11), 15267–15276, DOI:10.1016/j.ceramint.2021.02.090.
- H. Lin, B.-X. Li, H. Chen, P.-F. Liu, L.-M. Wu, X.-T. Wu and Q.-L. Zhu, Sr5ZnGa6S15: A New Quaternary Non-Centrosymmetric Semiconductor with a 3D Framework Structure Displaying Excellent Nonlinear Optical Performance, Inorg. Chem. Front., 2018, 5(6), 1458–1462, 10.1039/C8QI00322J.
- R.-H. Duan, J.-S. Yu, H. Lin, Y.-J. Zheng, H.-J. Zhao, S.-X. Huang-Fu, M. A. Khan, L. Chen and L.-M. Wu, Pb5Ga6ZnS15: A Noncentrosymmetric Framework with Chains of T2-Supertetrahedra, Dalton Trans., 2016, 45(31), 12288–12291, 10.1039/C6DT02404A.
- B. W. Rudyk, S. S. Stoyko and A. Mar, Rare-Earth Transition-Metal Indium Sulphides RE3FeInS7 (RE=La–Pr), RE3CoInS7 (RE=La, Ce), and La3NiInS7, J. Solid State Chem., 2013, 208, 78–85, DOI:10.1016/j.jssc.2013.09.035.
- S. Balijapelly, A. J. Craig, J. Bin Cho, J. I. Jang, K. Ghosh, J. A. Aitken, A. V. Chernatynskiy and A. Choudhury, Building-Block Approach to the Discovery of Na8Mn2(Ge2Se6)2: A Polar Chalcogenide Exhibiting Promising Harmonic Generation Signals with a High Laser-Induced Damage Threshold, J. Alloys Compd., 2022, 900, 163392, DOI:10.1016/j.jallcom.2021.163392.
- K. Feng, X. Zhang, W. Yin, Y. Shi, J. Yao and Y. Wu, New Quaternary Rare-Earth Chalcogenides Ba Ln Sn 2 Q 6 (Ln = Ce, Pr, Nd, Q = S; Ln = Ce, Q = Se): Synthesis, Structure, and Magnetic Properties, Inorg. Chem., 2014, 53(4), 2248–2253, DOI:10.1021/ic402934m.
- B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, ISODISPLACE: A Web-Based Tool for Exploring Structural Distortions, J. Appl. Crystallogr., 2006, 39, 607–614 CrossRef CAS.
- K. Momma and F. Izumi, VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276, DOI:10.1107/S0021889811038970.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979, DOI:10.1103/PhysRevB.50.17953.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- G. Kresse, et al., Vienna Ab-Initio Simulation Package (VASP) Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- V. Petříček, M. Dušek and L. Palatinus, Crystallographic Computing System JANA2006: General Features, Z. Kristallogr. – Cryst. Mater., 2014, 229(5), 345–352, DOI:10.1515/zkri-2014-1737.
- A. van der Lee, Charge Flipping for Routine Structure Solution, J. Appl. Crystallogr., 2013, 46(5), 1306–1315, DOI:10.1107/S0021889813020049.
- S. Cohen, N. Kimizuka and H. Steinfink, The Crystal Structure and Stability of Ba5Fe4S11, J. Solid State Chem., 1980, 35(2), 181–186, DOI:10.1016/0022-4596(80)90491-0.
- W. Yin, A. K. Iyer, C. Li, J. Yao and A. Mar, Ba5CdGa6Se15, a Congruently-Melting Infrared Nonlinear Optical Material with Strong SHG Response, J. Mater. Chem. C, 2017, 5(5), 1057–1063, 10.1039/C6TC05111A.
- J. M. Perez-Mato, D. Orobengoa and M. I. Aroyo, Mode Crystallography of Distorted Structures, Acta Crystallogr., Sect. A: Found. Crystallogr., 2010, 66(5), 558–590, DOI:10.1107/S0108767310016247.
- J. K. Shenton, D. R. Bowler and W. L. Cheah, Effects of the Hubbard U on Density Functional-Based Predictions of BiFeO3 Properties, J. Phys.: Condens. Matter, 2017, 29(44), 445501, DOI:10.1088/1361-648X/aa8935.
- X. Li, H. Yu, F. Lou, J. Feng, M.-H. Whangbo and H. Xiang, Spin Hamiltonians in Magnets: Theories and Computations, Molecules, 2021, 26(4), 803, DOI:10.3390/molecules26040803.
- L. Duan, J. Zhang, X. Wang, Z. Zhao, C. Xiao, X. Li, Z. Hu, J. Zhao, W. Li, L. Cao, G. Dai, C. Ren, X. He, R. Yu, Q. Liu, L. H. Tjeng, H.-J. Lin, C.-T. Chen and C. Jin, High Pressure Phase of Ba2FeS3: An Antiferromagnet with One-Dimensional Spin Chains, J. Alloys Compd., 2021, 859, 157839, DOI:10.1016/j.jallcom.2020.157839.
- J. S. Swinnea and H. Steinfink, Mössbauer Spectra, Magnetic and Electrical Behavior of Ba1+xFe2S4 Phases, J. Solid State Chem., 1982, 41(2), 124–131, DOI:10.1016/0022-4596(82)90192-X.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2148490. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt00733a |
| This journal is © The Royal Society of Chemistry 2022 |