Development of magnetocaloric coordination polymers for low temperature cooling

Abstract

Caloric materials have attracted significant interest as replacements for conventional refrigeration, which is becoming increasingly important in our daily lives, yet poses issues for sustainability due to both energy consumption and loss of refrigerants into the atmosphere. Among caloric materials, which are key to solid state cooling technologies, those exhibiting the magnetocaloric effect (MCE), an entropy-driven phenomenon under cycled applied magnetic fields, are promising candidates for cryogenic cooling. These have potential to replace conventional cryogenics, particularly liquid He – an increasingly scarce and expensive resource. Amongst magnetocalorics, coordination polymers containing polyatomic ligands have been shown to be very promising materials due to their large entropy changes at low temperatures. One of the contributing factors to this peformance is their unique structural flexibility, as they can adopt a wide range of structures usually not accessible for conventional materials, such as close-packed metal oxides. The most researched materials for magnetocaloric applications are those containing Gd as their magnetic centre, as the combination of structure and the weakly interacting 4f orbitals of Gd³⁺ in these materials enables the fabrication of promising magnetocalorics that contain a high density of cations and thus exhibit a high entropy change as a function of their weight and volume at ultra-low cryogenic temperatures. Alongside this, there is a growing interest in magnetocaloric coordination polymers with their magnetocaloric effect optimised for lower applied fields that can be generated using permanent magnets through incorporating other magnetic cations, including lanthanides with greater magnetic anisotropy. When combined with tailored magnetic interactions this leads to promising entropy changes above 4 K, a typical base temperature for many cryogenic applications. This review discusses the most promising magnetocalorics among coordination polymers and MOFs, highlighting their structural characteristics, and concluding with a brief perspective on the future of this field.

---

Mario Falsaperna

Mario Falsaperna obtained his MSc in Materials Chemistry in 2018 from the University of Catania, Italy. He is currently a PhD student in the Functional Coordination Frameworks group at the School of Physical Sciences, University of Kent, UK. Since 2019, he has been working on coordination polymers exhibiting magnetocaloric properties and their optimisation for low-temperature magnetic refrigeration, with a key interest in the frustrated and low dimensional magnetic states featured in these materials.

Paul J.Saines

Dr Paul Saines has a BSc. (2004) and PhD (2008) from the University of Sydney, studying solid state chemistry with Prof. Brendan Kennedy. He then completed postdoctoral research on new magnetic metal–organic frameworks with Prof. Anthony Cheetham at the University of Cambridge and a Glasstone fellowship at the University of Oxford hosted by Prof. Andrew Goodwin on ferroic and magnetocaloric frameworks. In 2015 he was appointed to his current post at the University of Kent and is currently a Senior Lecturer. His group's research focuses on the synthesis and characterisation of coordination polymers, with a particular interest in exploiting low dimensional and frustrated magnetism to optimise magnetocalorics.

---

1. Introduction

1.1 Conventional refrigeration and the alternative of solid-state caloric materials

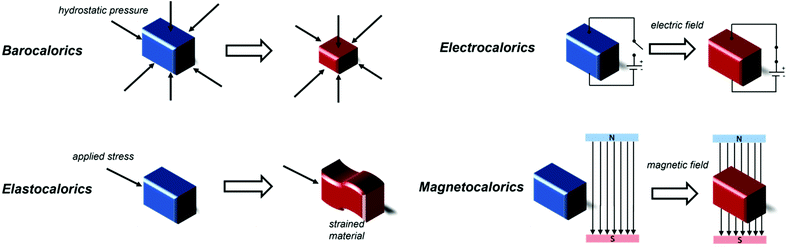
One of the major challenges of the past thirty years is combating climate change, which requires the reduction of energy consumption and of environmentally harmful greenhouse gas emissions. The International Institute of Refrigeration (IIR) estimates that, as of 2019, there are approximately 5 billion refrigeration, air conditioning and heat pump units worldwide that contribute to climate change, with 63% of this contribution being indirect due to the electricity consumption required for the functioning of the apparatuses and around 37% of it directly caused by leakage of refrigerant gases, e.g. fluorinated molecules.¹ With refrigeration becoming increasingly important both in our daily lives as well as for more specific applications, such as in the food industry and food transportation,² medicine and science,^3,4 it is vital to find alternatives to traditional gas compression\expansion refrigeration technologies,⁵ for which, in general, energy efficiencies are typically limited to a maximum of 40–50% of Carnot efficiency;⁶ a theoretical thermodynamic cycle which provides insight into the upper limit a thermodynamic system achieves during conversion of heat into work. Limitations to their efficiency are often determined by technological limitations of the components of the refrigerating device, such as the compressor.⁶

Solid-state caloric materials are an alternative for gas-based refrigeration, avoiding emissions of environmentally harmful or non-renewable gases. Furthermore, the predicted cooling efficiency for some of these materials is higher than that of traditional gas cooling, with above 60% of Carnot efficiency attained by some prototypes.⁷ It is possible to identify four main classes of materials for refrigeration depending on the external factors that drive their caloric effects, i.e. their heating and cooling process. These are namely barocalorics, elastocalorics, electrocalorics and, finally, magnetocalorics, on which this review focuses (see Fig. 1). In all cases, the cooling step typically occurs via an entropically driven process when the applied stimulus is removed. Electrocaloric materials are solids exhibiting the electrocaloric effect (ECE), where adiabatic depolarization upon the application of an external electric field results in a temperature change of the material.⁸ Polymeric materials such as the copolymer polyvinylidene fluoride-tetrafluoroethylene (PVDF-TFE) have shown to be promising candidates for electrocaloric applications,⁹ along with Rochelle salt (KNaC₄H₄O₆·4H₂O),¹⁰ KTaO₃,¹¹ BaTiO₃ and SrTiO₃,^12,13 and NH₄HSO₄.¹⁴ It is also possible to achieve cooling with the application of mechanical stress or pressure when elastocaloric or barocaloric (BCE) materials are used. In materials exhibiting the elastocaloric effect (eCE), the change in temperature is caused by the uniaxial stress-induced Martensitic phase transformation process. Application of mechanical stress decreases the entropy of the material and releases latent heat, this is reversed when the mechanical stress is removed enabling the material to absorb heat from its surroundings.¹⁵ Elastocaloric materials focus on alloys, including Ni–Ti and Cu–Zn–Al,¹⁶ alongside Cu-, Fe- and Ni–Ti-based superelastic alloys.¹⁷ Barocalorics materials exhibit a thermal response due to isotropic compression from hydrostatic pressure, typically associated with a concurrent first-order phase transition.¹⁸ The BCE has been identified in many materials,^19–21 including elastomeric polymers,^22,23 including natural rubber,^24,25 plastic crystals,²⁶ magnetic memory shape alloys²⁷ and coordination polymers, particularly inorganic–organic perovskites that have shown the so-called giant barocaloric effect, including [TPrA][Mn(dca)₃],^28,29 [(CH₃CH₂CH₂)₄N]Cd[N(CN)₂]₃([TPrA]Cd[dca]₃)³⁰ and [(CH₃)₄N]Mn[N₃]₃.³¹

Fig. 1 Different types of caloric materials and the stimuli responsible for their caloric effects.

The final group of caloric solids are magnetocalorics, which were first discovered by Weiss and Picard in 1917.^32,33 The magnetocaloric effect (MCE) is driven by the application and removal of an external magnetic field. Many magnetocalorics show promising magnetocaloric effects, with some prototype devices existing for applications such as domestic refrigeration and air-conditioning,³⁴ and as established candidates for subkelvin cooling with predicted energy efficiencies higher than 60% of the Carnot cycle.^35,36 The so-called giant MCE (GMCE) is associated with first-order magneto-structural transitions that enable significantly higher magnetocaloric effects than known materials near ambient temperatures and modest applied magnetic fields, enabling their use in near ambient temperature applications. This term was first coined for Gd₅Si₂Ge₂ at nearly 15 J kg⁻¹ K⁻¹ for a 2–0 T field change, double that of the best near ambient temperature magnetocalorics then known.³⁷ Conversely magnetocalorics for low temperature cooling rely on gradual field induced magnetic ordering of paramagnetic spins.^36,37

Amongst caloric materials magnetocalorics are particularly promising and thermodynamically efficient candidates for low temperature cooling. Cryogenic cooling has become increasingly relevant recently for technologies that are dependent on cooling to low and ultra-low temperatures such as hydrogen liquefaction,³⁸ quantum computing,³⁹ spintronics,⁴⁰ medical imaging,³ and high-performance infrared sensing.⁴¹ Liquid cryogenics are conventionally used for this purpose, with liquid helium vital for reaching temperatures below the boiling point of liquid nitrogen (77 K), including the millikelvin regime. In particular, ⁴He can reach 2 K, while mixtures with ³He can be used in dilution refrigerators to reach temperatures below 0.1 K. With liquid helium becoming an increasingly scarce and expensive resource, it is essential to find alternatives suitable for low-temperature cryogenic cooling.⁴²

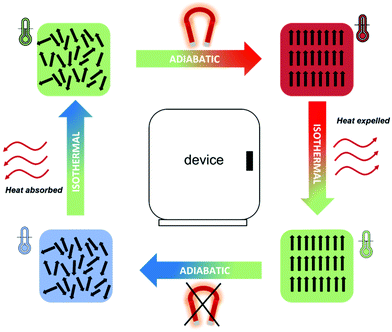
In magnetocalorics used at low temperatures, the application of an externally applied magnetic field induces a transition from a disordered paramagnetic state to an ordered magnetic state; the orientation of the magnetic moments along the direction of the field in magnetocaloric materials leads to a temperature change, ΔT_ad, in an adiabatic process. Heat can then be removed from the system whilst keeping the spins aligned with the magnetic field under isothermal conditions. In a subsequent step, removing the magnetic field under adiabatic conditions will result in the material cooling down due to the disordering of the spins. Due to this final temperature change, which results in the material having a lower temperature than its initial state, the material can then be used as a heat sink for cooling utilising the magnetic refrigeration process (see Fig. 2). The biggest accomplishment of magnetic refrigeration lies in the fact that the cooling process does not rely on the use of gases, therefore no refrigerant leakage or CO₂ emission is possible, resulting in a much more environmentally friendly process.

Fig. 2 Scheme of the magnetic refrigeration cycle of a magnetocaloric.

1.2 Theory and measurements of the magnetocaloric effect

The MCE is an intrinsic property of all magnetic materials,⁴³ but in order to classify them in terms of their magnetocaloric effect some parameters are necessary.⁴⁴ The most commonly reported parameter in literature is the maximum magnetic entropy change, −ΔS^max_m (where the negative stems from the entropy conventionally decreasing when the field is applied) for a given applied magnetic field change, typically reported with respect to the mass in J kg⁻¹ K⁻¹. A second parameter, the volumetric entropy change, is easily obtained by considering the product between the former and the density of the material (−ΔS^max_m × ρ) and is reported as mJ cm⁻³ K⁻¹. The magnetic entropy change can be determined by either direct or indirect measurements. In the former case, the total heat capacity C_T of the material is measured, with this being the result of electronic C_e, lattice C_l and magnetic C_m contributions. Therefore, it is necessary to isolate the magnetic contribution, C_m, to determine the magnetic entropy change ΔS_m, the relationship between the two given by ΔS_m = ∫(C_m/T)dT. Indirect measurement of ΔS_m requires determining the isothermal magnetisation of a material and applying the Maxwell relation, ΔS_m(T,ΔH) = ∫[δM(T,H)/δT]_HdH, therefore requiring measurements to be carried out as a function of temperature for a variety of magnetic fields. The indirect approach is the more commonly used approach in the initial characterisation of magnetocalorics. While the Clausius–Clapeyron method is an indirect method for calculating ΔS_m for magnetocalorics that rely on first order transitions, as is the case for “giant” magnetocalorics such as Gd₅Si₂Ge₂,⁴⁵ this is largely not relevant for magnetocalorics for low temperature applications that rely on more gradual changes. A third parameter, the aforementioned adiabatic temperature change ΔT_ad, is a more direct measure of magnetocaloric effect. Nevertheless, this parameter is less well characterised for most new magnetocalorics as determining the adiabatic temperature, ΔT_ad, requires a detailed understanding of how its heat capacity changes as a function of temperature and applied field. This additional information often limits the availability of ΔT_ad for new materials, whose magnetocaloric effect parameters have been assessed by indirect measurements.

Theoretically, the maximum entropy change −ΔS^max_m that can be extracted from a material corresponds to nRln(2J + 1), where R is the universal gas constant, n the number of unpaired spins and J the total angular momentum.⁴⁶ Increasing the magnetic moment is then essential to increase the maximum realisable −ΔS^max_m, as well as minimising the diamagnetic components of the material, such as non-magnetic cations and coordination ligands, which negatively affects the entropy change with respect to its weight and volume. As a non-zero orbital angular momentum might result in zero-field splitting (ZFS) effects, which are responsible for splitting the ground spin state into a number of degenerate states and, as a consequence, lowering the magnetic entropy change, most magnetocalorics studied have negligible orbital momentum. Thus their maximum expected entropy corresponds to nRln(2S + 1), and it is therefore entirely dependent on the magnetic degrees of freedom, as expressed by the term (2S + 1), the spin multiplicity. Therefore, when choosing an appropriate metal for the fabrication of magnetocaloric materials, gadolinium is considered the best candidate, as the 4f orbitals of the Gd³⁺ cation are exactly half-filled, resulting in a total spin quantum number of S = 7/2, and due to it being strongly isotropic, i.e. it possesses zero orbital angular momentum and its magnetism is determined only by its spins, preventing any ZFS effects. As a result, considerable effort has been put into the design and characterization of gadolinium-based materials with oxides such as gadolinium gallium garnet Gd₃Ga₅O₁₂ (GGG) and the iron-substituted derivatives Gd₃(Ga_1−xFe_x)₅O₁₂ (GGIG) well established as candidates for low-temperature cooling, superseding traditional metal salts due to the higher −ΔS^max_m, which stems from the higher density of magnetic cations in these oxides.⁴⁷

More recently, molecule-based magnetic materials have been proposed for low- and ultra-low temperature applications.⁴⁷ Molecule-based materials can adopt a wide variety of structures that are not easily obtained with traditional oxides due to the tendency of these to adopt close-packed structures. This, combined with their lack of significant intermolecular magnetic interactions, enables these molecule-based magnetocalorics to be used at lower temperatures. However, research on these materials has recently lost traction as their −ΔS^max_m with respect to their weight and, particularly, volume, is limited due to the use of large ligands for the fabrication of their structures.^47,48

1.3 Beyond conventional materials: coordination polymers

In contrast to discrete complexes and metal oxides, there has recently been significant interest in dense coordination polymers, including metal–organic frameworks (MOFs), as potential magnetocaloric materials.^47,49–51 IUPAC provisionally defines coordination polymers as a coordination compound continuously extending in 1, 2 or 3 dimensions through coordination bonds.⁵² While according to IUPAC the definition of coordination bond is a covalent bond where two of the electrons forming the bond come from the same chemical entity, as the IUPAC definition itself acknowledges, the term “coordination” is also used with a wider connotation, generally to define the ligands surrounding a metal centre regardless of whether the character of the bond is covalent or ionic. With this in mind, and with the balance of covalent and ionic bonds being difficult to clearly discern for many materials, in this review we have used the term coordination polymers to describe any extended structures in which metals are linked by polyatomic ligands. The focus on polyatomic ligands is to avoid considering those more well-known compounds with monodentate ligands that would be generally considered salts e.g. oxides or halides. In doing so, we acknowledge this restriction is somewhat arbitrary and some of the materials reviewed here will likely possess predominantly ionic bonds and that some of the materials included may be considered by others to simply be salts. The varied structural topologies of coordination polymers offer more freedom in the tuning of their magnetic properties than is commonly found in oxides due to the structure directing effect of their polyatomic ligands leading to a variety of structures rather than the close packed arrays typically adopted by simple salts.⁵³

The variety of structures accessible with coordination polymers makes it possible to design three-dimensional structures containing low-dimensional motifs, such as one-dimensional magnetic chains or two-dimensional magnetic sheets, via the structure direct effect of the ligand.^47,53 When these structural motifs are well isolated from one another, structures with a higher density of magnetic cations with long-range order occurring at very low temperatures can be realised due to the resulting weak interactions between these units. In addition to this, it is possible to design structures featuring competing magnetic interactions due to the arrangement of the cations in the crystal lattice, so-called geometric frustration,⁵⁴ to further suppress the onset of long-range magnetic order to much lower temperatures and, therefore, allow for an even higher density of magnetic cations in the structure. Typically, this implies designing structures containing triangular motifs, responsible for the competition of antiferromagnetic interactions, such as the two-dimensional triangular or Kagome lattices,^54,55 as well as pyrochlore structures,⁵⁴ such as that of Gd₂Ti₂O₇.⁵⁶ While conventional materials can exhibit geometric frustration, GGG being a classic example,⁵⁷ coordination polymers expand the scope for this through the plethora of topologies they can adopt. Coordination polymers featuring low dimensional units and/or magnetic frustration have been suggested to be excellent candidates for low-temperature cooling, highlighting that attention to the structural characteristics of materials plays a key role in the optimisation of their MCE. The combination of lower ordering temperatures in coordination polymers compared to metal oxides, which enables them to remain useful magnetocalorics at lower temperatures, and higher density of magnetic cations than is possible in molecular complexes, greatly enhances their −ΔS^max_m as a function of weight and volume, making them very promising candidates as magnetocalorics materials.⁴⁷ Furthermore many coordination polymers have already been reported to have greater −ΔS^max_m than the benchmark oxides, such as GGG.

The coordination polymers and dense MOFs with the highest −ΔS^max_m, approximately 40 J kg⁻¹ K⁻¹ or higher for large field changes, tend to be found amongst materials with either purely inorganic (in which there are no C–H bonds) or carboxylate ligands. The majority of the magnetocaloric coordination polymers studied to date incorporate only lanthanides, primarily Gd³⁺, as their magnetic centres, although there has been recent interest in a handful of systems that feature both 3d and 4f metals as a future potential route to enhancing their magnetocaloric properties as seen previously in molecular magnetocalorics.⁴⁷ In this review we will discuss the most promising magnetocalorics coordination polymers and dense MOFs known to date across these categories.

2. Coordination polymers containing inorganic ligands

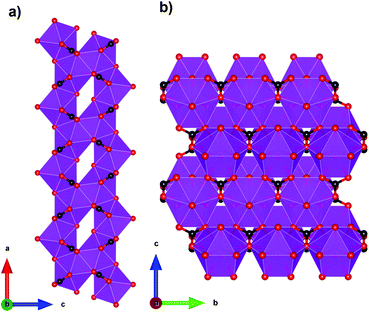
Coordination polymers with inorganic ligands are attractive as their smaller polyatomic anions typically allow denser packing of their magnetic cations than systems with larger organic ligands, increasing the magnetocaloric entropy change as a function of volume. Among inorganic coordination polymers, GdPO₄ has attracted significant interest for having a higher −ΔS^max_m than GGG.⁵⁸ At room temperature, this material adopts a monoclinic P2₁/n structure in which the nine-coordinate Gd³⁺ node is bound to four oxygens from the distorted tetrahedral phosphate groups (see Fig. 3), with an average Gd–O distance of 2.47 Å, and linked together in a chain-like fashion.⁵⁹ The reported magnetic entropy change −ΔS^max_m for this material is 62.0 J kg⁻¹ K⁻¹ (376 mJ cm⁻³ K⁻¹) at 2.1 K and an applied field change of 7 T, higher than that of the benchmark material, GGG, under the same conditions.^47,58 The magnetic properties, including the MCE, of this material are largely attributed to the high density of Gd³⁺ cations in the structure, coupled with the presence of weak magnetic interactions and the low magnetocrystalline anisotropy, allowing for magnetic order only below 60 mK as a dipolar antiferromagnet.⁵⁸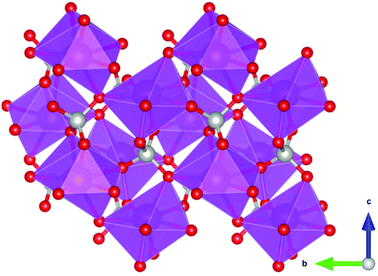

Fig. 3 Crystal structure of GdPO₄. The GdO₉ polyhedra are bridged by the tetrahedral phosphate groups. Colour codes: Gd: purple, P: grey, O: red.

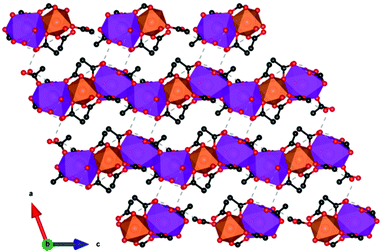
More recently, a Gd(OH)SO₄ coordination polymer has been synthesised and it has been shown to exhibit a −ΔS^max_m comparable to that of GGG.⁶⁰ This material crystallises in a monoclinic P2₁/n structure with the asymmetric unit consisting of one Gd³⁺ cation, one sulfate ion and a single hydroxy anion. The Gd cations are nine-coordinate and form a capped square antiprism coordination geometry, with six oxygens from the SO₄²⁻ ligands, with two of the sulfate oxygens being μ₂-bridging and three oxygens from the OH⁻ anion, this being μ₃-bridging.⁶¹ The Gd³⁺ cations are connected to form 1D-chains along the a-axis, and these further extend via hydroxy oxygens along the bc direction to form a three-dimensional framework (see Fig. 4).⁶¹ The magnetic coupling is negligible in this material with a Weiss constant, θ_W, of about −0.2 K. The magnetic entropy change −ΔS_m of this material was extracted from magnetisation data using the Maxwell relation, with a −ΔS^max_m value of 53.5 J kg⁻¹ K⁻¹ (276 mJ cm⁻³ K⁻¹) obtained at 2 K and for a 7 T field change, demonstrating a higher gravimetric −ΔS^max_m than GGG, but a comparable volumetric −ΔS^max_m to the benchmark material.^47,62

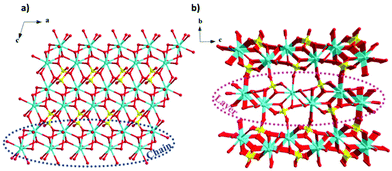Fig. 4 (a) Crystal structure of Gd(OH)SO₄, with one-dimensional chains propagating along the a-axis and forming layers along the ac-plane, (b) with the latter stacking along the b-axis. Colour codes: Gd: cyan, O: red, S: yellow. The hydrogen atoms have been omitted for clarity. Reproduced from ref. 60 with permission from the Chinese Chemical Society (CCS), Institute of Chemistry of Chinese Academy of Sciences (IC), and the Royal Society of Chemistry.

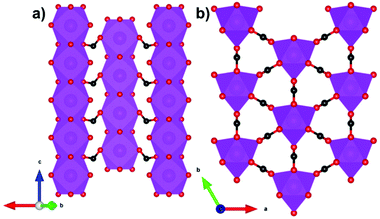
Another family of coordination polymers, the lanthanide orthoborates LnBO₃, have proven to be viable magnetocalorics for liquid helium temperature regimes at both high and low applied magnetic fields.⁶³ These materials adopt a monoclinic C2/c structure with triangular layers of Ln³⁺ cations separated by sheets of three-membered rings of corner sharing BO₄⁵⁻ tetrahedra that form isolated B₃O₉⁹⁻ units.⁶³ While the existence of antiferromagnetic interactions within triangular layers suggest the possibility of geometric frustration, the monoclinic symmetry results in the triangles being scalene and the difference in Ln–Ln distances among different triangles make this less likely than in higher symmetry systems.^64,65 Consistent with this it was found that GdBO₃ has a low frustration index, f, (θ_W, divided by Néel temperature) of f = 5.4/1.7 = 3.1, and although the Er and Dy analogues possess f > 10, consistent with highly frustrated systems it cannot be ruled out that this is partly due to crystal field effects on θ_W.⁶³ In GdBO₃, the average in-plane Gd–Gd distance is 3.84 Å, while the average interplane distance is 4.52 Å. The maximum magnetic entropy change −ΔS^max_m for this material is found to be 57.8 J kg⁻¹ K⁻¹ (366 mJ cm⁻³ K⁻¹) for a field change of 9 T at 2 K.⁶³ While this value is higher than the benchmark material, GGG, under the same conditions, the high magnetic field strength would limit its application to where superconducting magnets are employed. For a 2 T field change, −ΔS^max_m drops significantly, reaching values below 10 J kg⁻¹ K⁻¹ (about 60 mJ cm⁻³ K⁻¹). Amongst other members of the LnBO₃ series, it is worth noting that DyBO₃ has been shown to outperform the Gd analogue at lower applied fields, with a −ΔS^max_m of 13.9 J kg⁻¹ K⁻¹ (92.5 mJ cm⁻³ K⁻¹) for a field change of 2 T at 2 K.

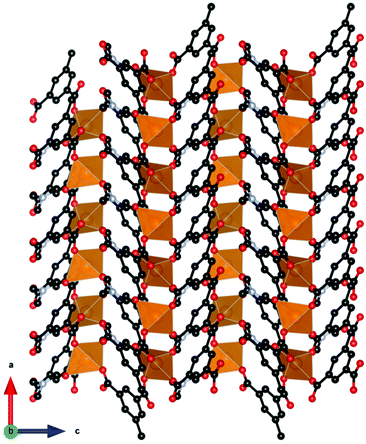
Among inorganic coordination polymers, the LnOHCO₃ frameworks have the highest −ΔS^max_m as a function of weight. Work on these compounds started with GdOHCO₃,^66,67 which adopts an orthorhombic P2₁2₁2₁ structure in which the Gd³⁺ cation is 10-coordinate, binding to five carbonate anions, three in a chelating fashion, and two hydroxide groups. These polyhedra connect in a face-sharing fashion to form zig-zag chains with short 3.82 Å Gd–Gd contacts (see Fig. 5). These chains are packed in a dense and distorted triangular lattice via edge-sharing connectivity. The MCE effect was determined via the Maxwell equation from the magnetisation data to give a −ΔS^max_m of 66.4 J kg⁻¹ K⁻¹ (355 mJ cm⁻³ K⁻¹) at 1.8 K for a field change of 7 T, which is very similar to that determined from heat capacity measurements, 67.1 J kg⁻¹ K⁻¹ (359 mJ cm⁻³ K⁻¹). An impressive ΔT_ad of 24 K was determined for a field change of 9 T from heat capacity measurements, which is the highest reported for a coordination polymer.

Fig. 5 (a) Crystal structure of GdOHCO₃ with face-sharing GdO₁₀ polyhedra forming zig-zag chains along the a-axis and (b) packing of the distorted triangular lattice along the bc-plane. Colour codes: Gd: purple, C: black, O: red. The hydrogen atoms have been omitted for clarity.

Interest in the magnetocaloric properties of GdOHCO₃ led Dixey et al.⁶⁸ to an investigation of other heavier lanthanides from Tb–Er, which were confirmed to adopt orthorhombic P2₁2₁2₁ symmetry via neutron diffraction.⁶⁸ Among these materials, TbOHCO₃ and DyOHCO₃ demonstrated promising magnetocaloric properties with higher entropy change than GdOHCO₃ for field changes lower than 2 T, the maximum field strength achievable using a permanent magnet at temperatures above 4 K, where they could be potentially used to replace liquid He for a wider range of cryogenic cooling temperatures. Specifically, DyOHCO₃ has a −ΔS^max_m of 33.3 J kg⁻¹ K⁻¹ (186 mJ cm⁻³ K⁻¹) at 4 K and a field change of 2 T while TbOHCO₃ has a −ΔS^max_m of 301.0 J kg⁻¹ K⁻¹ (169 mJ cm⁻³ K⁻¹) compared to a value of 29.5 J kg⁻¹ K⁻¹ (158 mJ cm⁻³ K⁻¹) for GdOHCO₃ under the same conditions. The differences in −ΔS^max_m values between these compounds are even greater for a field change of 1 T (17.6 and 20.8 J kg⁻¹ K⁻¹, respectively for Dy and Tb; cf. 11.7 J kg⁻¹ K⁻¹ for Gd). These results are impressive when compared to the benchmark garnet oxides, with DyOHCO₃ showing improved magnetocaloric properties than GGG's maximum for a 2 T field change up to 8 K. Unfortunately, attempts to optimise magnetocaloric entropy change further through synthesising solid solutions Gd_1−xTb_xOHCO₃ and Gd_1−xDy_xOHCO₃ were unsuccessful, with heterometallic compounds having lower entropy changes compared to the homometallic materials.

A further study by Dixey et al.⁶⁹ indicated that the LnOHCO₃ compounds with improved magnetocaloric properties above 4 K all exhibited significant magnetic diffuse scattering in their correlated paramagnetic phases. Reverse Monte Carlo (RMC) fits indicated this was a result of having non-collinear ferromagnetic coupled Ising-like spins within the zig-zag chains packed into a frustrated antiferromagnetic lattice. They suggested such arrangements allows the ferromagnetic Ising chains to be readily aligned with low applied magnetic fields once the antiferromagnetic interactions are supressed by it, therefore maximising the change in magnetisation under these conditions, resulting in a higher MCE, as expressed by the Maxwell relation. This is in contrast to GdOHCO₃, which, as is typical in Gd coordination polymers, has predominantly antiferromagnetic coupling with a θ_W of about −1 K.⁵⁵ Therefore, geometric frustration likely plays a key role in the optimisation of the MCE for this material, and indicates the important role structure plays in achieving such an optimisation, suggesting particular attention needs to focused on fabricating materials with similar structural motifs.

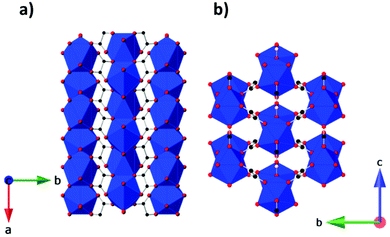
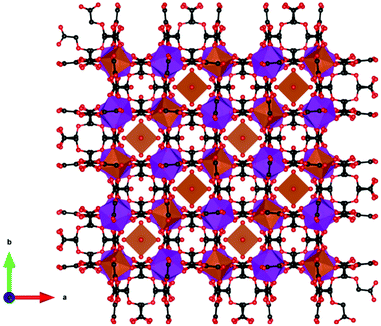
Other inorganic coordination polymers have also been reported to have high magnetic entropy changes. This includes weakly antiferromagnetically coupled Gd(OH)₃ whose −ΔS^max_m is comparable to GdOHCO₃ at 62.0 J kg⁻¹ K⁻¹ (346 mJ cm⁻³ K⁻¹) at 2 K and 7 T, as determined from magnetisation data.⁷⁰ This material adopts P6₃/m hexagonal symmetry with nine-coordinate Gd³⁺ connected via 9 different μ₃-OH⁻ groups into a 3D structure with 1D hexagonal channels (see Fig. 6). Gd₂O(OH)₄(H₂O)₂ is another promising material,⁷⁰ with −ΔS^max_m values, determined from magnetisation data, of 59.1 J kg⁻¹ K⁻¹ at 2 K and 7 T, although its lower density leads to a significant decreased value as a function of volume of 217 mJ cm⁻³ K⁻¹. This orthorhombic Cmcm structure features two distinct Gd³⁺ ions which are eight and nine coordinate. These are connected to form a 2D structure via connection of adjacent Gd2 ions through two OH⁻ and one O²⁻ bridges along the c-axis with adjacent Gd1 ion connected through two OH⁻ bridges along the same direction; adjacent Gd1 and Gd2 ions are connected through three OH⁻ bridges along the b-axis. These 2D structures are held together along the a-axis via hydrogen-bonding between the coordinated water molecules from adjacent 2D layers thus generating a 3D framework. A final inorganic polymer with −ΔS^max_m above 40 J kg⁻¹ K⁻¹ is [Gd₆(μ₆-O)(μ₃-OH)₈(μ₄-ClO₄)₄(H₂O)₆](O)₄,⁷¹ which crystallises in a monoclinic C2/c structure with relatively significant antiferromagnetic coupling (θ_W = −5.5 K) and has a −ΔS^max_m equal to 46.6 J kg⁻¹ K⁻¹ (207 mJ cm⁻³ K⁻¹) at 2.5 K for a field change of 7 T, based on magnetisation data. This material has a complex structure comprised of hexanuclear octahedral clusters and four crystallographically distinct Gd cations. The [Gd₆(μ₆-O)(μ₃-OH)₈]⁸⁺ distorted octahedral clusters have six Gd³⁺ around one central μ₆-oxo central atom and are connected by eight face-capping μ₃-OH bridges. All Gd³⁺ cations are coordinated to nine oxygen atoms in a mono-capped square antiprism geometry. The octahedral clusters are connected to each other to form a 3D framework through ClO₄⁻ bridges, with every cluster bridged via twelve ClO₄⁻ ligands with every ligand linking three Gd₆ clusters.

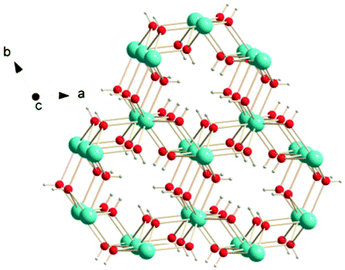Fig. 6 Crystal structure of Gd(OH)₃. Colour codes: Gd: cyan, O: red, H: white. Reproduced from ref. 70 with permission from the Royal Society of Chemistry.

3. Carboxylate-based coordination polymers

The other family of promising lanthanide coordination polymers that have shown significant promise as magnetocaloric materials are carboxylate-based frameworks. Amongst these materials those with extended 2D and 3D structures can generally be considered to be MOFs, albeit most of these are dense and, thus, lack significant porosity. Generally, these materials can be thought of as containing either small monocarboxylate ligands, slightly larger linear dicarboxylates or bulker aromatic carboxylates; where materials in this review contain more than one of these ligand types we have classified them according to the largest ligand type. The larger ligands involved in these materials, compared to purely inorganic coordination frameworks, leads to less densely packed structures, therefore, while their −ΔS^max_m as a function of weight are often similar, these coordination polymers typically have lower entropy changes as a function of volume.

3.1 Monocarboxylate-based polymers

The denser monocarboxylate frameworks, which amongst the polymers containing organic ligands are generally reported to have the highest −ΔS^max_m, are either based on acetate or formate ligands. Acetate compounds commonly adopt 1D chain structures with coordination bonding only within these chains, with three such materials being reported to have high magnetocaloric entropy changes. Two examples of this are Gd(OAc)₃(MeOH) and Gd(OAc)₃(H₂O)_0.5, which adopt monoclinic P2₁/c and Cc symmetry, respectively (see Fig. 7).⁷² In Gd(OAc)₃(MeOH), the Gd³⁺ are in a nine-coordinate capped square-antiprism geometry, while in Gd(OAc)₃(H₂O)_0.5 there are two Gd in nine-coordinate, capped square-antiprismatic, and eight-coordinate, square antiprismatic, geometries. In both cases, the Gd within the chains are bridged by three acetate ligands, in a mixture of η₂:η₁ and syn–syn acetate geometries with Gd–Gd distances of 4.06 Å and 6.46 Å for Gd(OAc)₃(MeOH) and Gd(OAc)₃(H₂O)_0.5, respectively. In Gd(OAc)₃(H₂O)_0.5 there are interchain hydrogen bond interactions between the water and acetate carboxylate groups while Gd(OAc)₃(MeOH) only has weaker interchain interactions. Gd(OAc)₃(MeOH) and Gd(OAc)₃(H₂O)_0.5 have very weak ferromagnetic and antiferromagnetic coupling, respectively, with θ_W of −0.22 and 0.34 K. Magnetisation measurements indicate a −ΔS^max_m = 45.0 J kg⁻¹ K⁻¹ (96.8 mJ cm⁻³ K⁻¹) and 47.7 J kg⁻¹ K⁻¹ (106 mJ cm⁻³ K⁻¹) for a 7 T field change at 1.8 K for Gd(OAc)₃(MeOH) and Gd(OAc)₃(H₂O)_0.5, respectively.

Fig. 7 Chain structures of (a) Gd(OAc)₃(MeOH) and (b) Gd(OAc)₃(H₂O)_0.5, shown with thermal ellipsoids at 30% probability. (c) Three-dimensional hydrogen-bonded network of Gd(OAc)₃(H₂O)_0.5. Adapted with permission from Inorg. Chem., 2012, 51(1), 405–413. Copyright 2011 American Chemical Society.

A third 1D acetate compound reported to have high magnetocaloric entropy change is weakly antiferromagnetically coupled Gd(HCO₂)(OAc)₂(H₂O)₂,⁷³ which adopts monoclinic P2₁/m symmetry. Here it is the formate co-ligand which connects Gd within the chain, with Gd–Gd distances of 6.58 Å (see Fig. 8). Adjacent chains are rotated by 180° which allows for the formation of a dense network of hydrogen bonds in one direction perpendicular to the chain while chains in the third dimension are separated by methyl groups for the acetate ligand resulting in only weak intermolecular forces in this direction. The magnetocaloric properties of this compound were evaluated through both magnetisation and heat capacity data, both determining that −ΔS^max_m has a maximum of 45.9 J kg⁻¹ K⁻¹ (110 mJ cm⁻³ K⁻¹) at 1.8 K for a field change of 7 T.

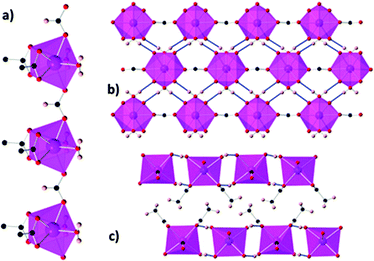Fig. 8 (a) Coordination chains of Gd(HCO₂)(OAc)₂(H₂O)₂ along the b-axis; (b) hydrogen-bonded chains forming sheets on the bc-plane; (c) packing of the sheets along the b-axis. Colour codes: Gd: purple, O: red, C: black, H: pink. Reproduced from ref. 73 with permission from the Royal Society of Chemistry.

The other formate-containing compound in this grouping reported to have significant magnetocaloric properties is Gd(HCO₂)₃,⁷⁴ which adopts an R3m rhombohedral structure featuring face-sharing chains with neighbouring chains connected through the formate ligand to yield a triangular lattice (see Fig. 9). The Gd cations are nine-coordinate in a tricapped trigonal prismatic geometry. The MCE of Gd(HCO₂)₃ is evaluated both indirectly from the magnetisation data and directly from heat capacity measurements. In the former case, the magnetic entropy changes for different applied field changes are obtained, which are similar to those from heat capacity data. At ∼1 K and for a field change of 7 T, the −ΔS^max_m is 55.9 J kg⁻¹ K⁻¹ or 216 mJ cm⁻³ K⁻¹, with the large volumetric entropy change enabled by the dense structure. ΔT_ad was estimated to be approximately 22 K from heat capacity measurements. Direct measurements under quasi-adiabatic conditions suggest values of 2.47 and 0.51 K during magnetisation and demagnetisation for a 1–0 T field change, consistent with the values obtained from the indirect entropy-based measurements for such changes. The relative cooling power (RCP) of Gd(HCO₂)₃ was also estimated to be 522 mJ cm⁻³ K⁻¹, which is higher than the 479 mJ cm⁻³ K⁻¹ reported for Gd₃Ga₅O₁₂.

Fig. 9 (a) Crystal structure of Gd(HCO₂)₃ with chains propagating along the c-axis and (b) arranged in a triangular lattice on the bc-plane. Colour codes: Gd: purple, C: black, O: red. The hydrogen atoms have been omitted for clarity.

The high entropy change of Gd(HCO₂)₃ has led to the investigation of analogues containing heavier lanthanides from Tb–Er.⁷⁵ While the −ΔS^max_m of these compounds is lower at high fields than for Gd(HCO₂)₃, for field changes less than 2 T and for temperatures above 4 K Tb(HCO₂)₃ and, to a smaller extent, Ho(HCO₂)₃, have higher −ΔS_m compared to the Gd analogue. Specifically, Tb(HCO₂)₃ outperforms Gd(HCO₂)₃ above 6 K for a 2–0 T field change and both Tb(HCO₂)₃ and Ho(HCO₂)₃ do so above 4 K for a 1–0 T field change, although the difference between Ho(HCO₂)₃ and Gd(HCO₂)₃ is very modest. Unlike the LnOHCO₃ series the mixing of lanthanide cations is shown to be a promising route to optimising higher temperature and lower applied field MCE behaviour. In the series Gd_1−xTb_x(HCO₂)₃, for x = 0.2 and 0.4 and a field change of 1 T, there is improvement in the magnetic entropy change above 4 K compared to Gd(HCO₂)₃ with only a minimal loss in −ΔS^max_m at 2 K.

Strong diffuse magnetic scattering is observed from neutron diffraction of the paramagnetic phase of Tb(HCO₂)₃ with RMC fits indicating the presence of Ising-like spins parallel to the chain direction with strong ferromagnetic correlations within these units.⁷⁵ There are also weaker frustrated antiferromagnetic interchain correlations within the triangular lattice. It has been suggested that the high entropy change of Tb(HCO₂)₃ under low applied fields is caused by ready alignment of the ferromagnetic Ising chains with the applied field once the interchain antiferromagnetic interactions are supressed. Further work has shown that this combination of interactions in Tb(HCO₂)₃ leads to a unique triangular Ising antiferromagnetic state below 1.6 K, which has long range 1D magnetic order with only short range antiferromagnetic correlations between these chains.⁷⁶ Strong magnetic diffuse scattering has also been uncovered in Ho(HCO₂)₃ indicating the presence of similar magnetic interactions as in Tb(HCO₂)₃ while all other Ln(HCO₂)₃ lack such correlations, suggesting the ferromagnetic Ising chains in these systems is key to improving their −ΔS_m at higher temperatures as opposed to the predominantly antiferromagnetic interactions in Gd(HCO₂)₃.⁷⁷

3.2 Linear dicarboxylate-based polymers

Another extensively studied family of carboxylate magnetocalorics are those with linear dicarboxylate ligands, principally those containing the relatively small oxalate, succinate and citrate ligands. The oxalate ligand is the simplest of these, being comprised of two connected carboxylate groups. The first promising magnetocaloric to be reported using the oxalate ligand was very weakly antiferromagnetically coupled Gd(C₂O₄)(H₂O)₃Cl.⁷⁸ This adopts a P2₁/n monoclinic structure with the Gd in a nine-coordinate capped squared antiprismatic geometry. Gd dimers, formed by edge-sharing polyhedra with an intradimer separation of 4.42 Å, are connected into 2D layers with shorter Gd–Gd distances of 5.84 Å along the a-axis, through μ₄–η₁:η₂:η₁:η₂ bonded oxalates, and 6.31 Å along the c-axis, through μ–η₂:η₂ oxalates (see Fig. 10). The structure includes O_water–H⋯O_oxalate intralayer and O_water–H⋯O_water and O_water–H⋯Cl interlayer hydrogen bonds. Indirect methods indicate a −ΔS^max_m of 48.0 J K⁻¹ kg⁻¹ (144 mJ cm⁻³ K⁻¹) at 2.2 K for a 7 T field change. Direct determination of the MCE effect via heat capacity measurements shows that the −ΔS^max_m values are consistent with those obtained from magnetisation data and that ΔT_ad is 16.9 K for the same magnetic field change.

Fig. 10 Crystal structure of Gd(C₂O₄)(H₂O)₃Cl, with (a and b) 2D layers on the ac-plane and (c) packing along the b-axis. Colour codes: Gd: cyan, C: grey, O: red. The hydrogen atoms have been omitted for clarity. Adapted with permission from Inorg. Chem., 2014, 53(17), 9052–9057. Copyright 2014 American Chemical Society.

Another oxalate family shown to have good magnetocaloric properties are the Gd(pda)(ox)_0.5(H₂O)_x (x = 0, 1, 2, pda = propionate) phases.⁷⁹ All three compounds adopt P1̄ triclinic symmetry with nine coordinate Gd cations in the anhydrous form, which increase to 10 in the hydrated forms. The increase in the hydration state leads to a change from a 3D structure made of pillared layers in the anhydrous and monohydrate form to a 2D dihydrate structure with only weak C–H⋯O hydrogen bonding interactions between them. The layers in the 3D structure are connected by the carboxylate groups of the pda²⁻ ligands with the oxalates pillaring the layers. In the dihydrate, the layers are comprised of cationic zig-zag Gd(pda) chains, which are connected to form 2D layers by the oxalate ligands. Despite the changes in dimensionality, all three materials retain similar weak ferromagnetic coupling, with θ_W between 0.3 and 0.7 K. Magnetisation measurements indicate −ΔS^max_m for these compounds are similar with regards to mass density at 46.8 J kg⁻¹ K⁻¹, 46.1 J kg⁻¹ K⁻¹ and 45.0 J kg⁻¹ K⁻¹ for the x = 0, 1 and 2 phases for a 7 T field change at 2 K, although the greater density of the hydrated phases increases their volumetric entropy change (cf. 128 mJ cm⁻³ K⁻¹, 1512 mJ cm⁻³ K⁻¹ and 159 mJ cm⁻³ K⁻¹ for x = 0, 1 and 2, respectively).

More recently, the magnetocaloric properties of the Ln(HCO₂)(C₂O₄) phases have been assessed, specifically for the members where Ln = Gd³⁺, Tb³⁺, Dy³⁺ and Ho³⁺, and the oxalate ligand C₂O₄²⁻ is present. These coordination polymers adopt an orthorhombic Pnma structure, featuring face-sharing polyhedra forming zig-zag chains with adjacent chains connected by the formate and oxalate ligands forming a triangular lattice, hence exhibiting a similar topology to the Ln(HCO₂)₃ family of coordination polymers (see Fig. 11).⁸⁰ The Ln³⁺ cations are nine-coordinate with a distorted monocapped square antiprism geometry, with three oxygen atoms from three formates and six from three oxalates, with these acting as a bichelating ligand utilizing both carboxylate groups. Among the members of this family, weakly antiferromagnetically coupled Gd(HCO₂)(C₂O₄) has proven to be an interesting candidate for magnetic cooling with the magnetic entropy change determined via isothermal magnetisation measurements, indicating a −ΔS^max_m of 56.0 J kg⁻¹ K⁻¹ (218 mJ cm⁻³ K⁻¹) for a 5 T field change at 2 K,⁸¹ with these values being the highest known for a dense MOF and higher than that of the closely related Gd(HCO₂)₃.⁷⁴ The other members of this family have a lower −ΔS^max_m at high fields and, with the exception of Dy(HCO₂)(C₂O₄) above 5 K for a 1–0 T field change and above 7 K for a 2–0 T field change, do not exceed Gd(HCO₂)(C₂O₄) at lower applied fields.⁸¹ For the Tb and Ho phases, this is in direct contrast with the LnOHCO₃ and Ln(HCO₂)₃ frameworks, which have similar face-sharing chains packed in distorted triangular lattices.^68,75 Neutron diffraction experiments on Tb(HCO₂)(C₂O₄) and Ho(HCO₂)(C₂O₄) have shown these lack significant magnetic correlations above 1.5 K, this likely being the cause of a significantly poorer entropy change compared to their LnOHCO₃ and Ln(HCO₂)₃ analogues; this highlights the importance of local magnetic interactions in determining the magnetocaloric properties at lower applied fields, and suggests small changes in structures influence these significantly.⁸¹

Fig. 11 (a) Crystal structure of Ln(HCO₂)(C₂O₄) with infinite one-dimensional chains grow along the a-axis. (b) Arrangement of the chains in a triangular lattice on the bc-plane. Colour codes: Ln: blue, C: black, O: red, H: pink.

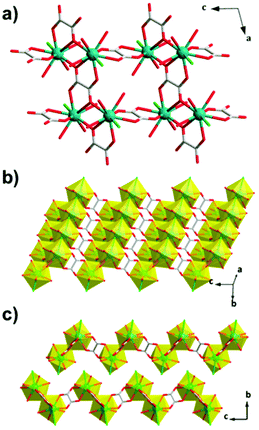
The succinate (suc) ligand is expanded from an oxalate by inclusion of two CH₂ groups between its carboxylates. Two succinate frameworks have been reported to have promising magnetocaloric entropy changes, viz. Gd₂(OH)₂(suc)₂(H₂O)·2H₂O and Gd₆(OH)₈(suc)₅(H₂O)₂·4H₂O, which adopt C2/c and P2₁/c symmetry, respectively.⁸² Gd₂(OH)₂(suc)₂(H₂O)·2H₂O and Gd₆(OH)₈(suc)₅(H₂O)₂·4H₂O both adopt ladder-like structures with two and six distinct Gd cations, respectively, with one gadolinium in an eight coordinate environment in both structures and the remainder in nine coordinate environments (see Fig. 12). Gd₂(OH)₂(suc)₂(H₂O)·2H₂O crystallises as a Gd–OH ladder that grows parallel to the b-axis and is comprised of two rows of Gd³⁺ ions with Gd–Gd distances ranging from 3.655 to 4.065 Å. These ladders are then connected along the a-axis and the c-axis via succinate ligands which serve as pillars to form the 3D network. Similarly, Gd₆(OH)₈(suc)₅(H₂O)₂·4H₂O adopts a three rail Gd–OH ladder where three rows of Gd³⁺ ions, connected by the succinate ligand, form the rungs of the ladder. The ladders extend along the b-axis and neighbouring Gd⋯Gd separations range from 3.656 and 4.049 Å. Magnetisation measurements of these weakly antiferromagnetically coupled phases indicate a −ΔS^max_m of 42.8 J kg⁻¹ K⁻¹ (120 mJ cm⁻³ K⁻¹) and 48.0 J kg⁻¹ K⁻¹ (144 mJ cm⁻³ K⁻¹) for a field change of 7 T at 2.6 K and 1.8 K, with ΔT_ad of 17 and 15 K, respectively.

Fig. 12 (a) Crystal structure of Gd₂(OH)(suc)₂H₂O·2H₂O with a two-rail Gd–OH ladder parallel to the b-axis and (b) the packing of the ladders on the ac-plane. (c) Crystal structure of Gd₆(OH)₈(suc)₅(H₂O)₂·4H₂O showing the three-rail Gd–OH ladder parallel to the b-axis and (d) the packing of the three-rail ladders on the ac-plane. Colour codes: Gd: purple, C: black, O: red. Hydrogens are omitted for clarity.

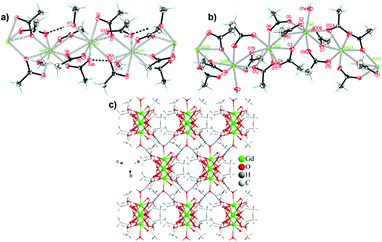
One citrate (cit) coordination polymer, which is related to the succinate ligand via replacement of a CH₂ group with a C(OH)(CHCO₂) group, has been reported to have potentially promising magnetocaloric entropy changes, namely Gd(cit)(H₂O).⁸³ This compound adopts monoclinic C2/c symmetry with GdO₉ polyhedra connected by carboxylate O atoms in a μ₂–η₂ bridging mode to form a dimer (see Fig. 13). Neighbouring dimers are then bridged through carboxylate groups to form 1D ladder Gd³⁺ chains which are bridged by citrate ligands to from a 2D layer structure with weak ferromagnetic coupling indicated by a θ_W of 1.1 K. Magnetisation measurements indicate a −ΔS^max_m of 43.6 J kg⁻¹ K⁻¹ (115 mJ cm⁻³ K⁻¹) for field change of 7 T at 2 K.

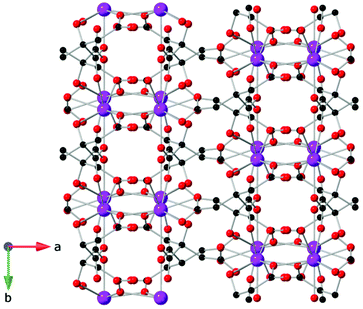Fig. 13 Two-dimensional layer structure of Gd(cit)(H₂O) showing two Gd ladder chains propagating along the b-axis. Colour codes: Gd: purple, C: black, O: red. Hydrogens are omitted for clarity.

3.3 Cyclic carboxylate-based polymers

Compounds incorporating cyclic carboxylate ligands, which are amongst the most common ligands utilised in MOFs, have also been investigated as magnetocalorics. Amongst the first of these was Gd(C₄O₄)(OH)(H₂O)₄,⁸⁴ which adopts a monoclinic P2₁/c structure with six coordinate Gd, which are bridged by the squarate ligand to form a 2D sheet in the bc-plane with an intralayer Gd–Gd separation of 6.48 Å (see Fig. 14). Interlayer coupling is via extensive hydrogen bonding between squarate oxygen atoms and water ligands. This phase has negligible magnetic interactions with indirect measurements of MCE properties indicating a −ΔS^max_m of 47.3 J kg⁻¹ K⁻¹ or 210 mJ cm⁻³ K⁻¹ for a field change of 9 T at ∼3 K, with the volumetric density particularly high for a MOF containing a cyclic unit due to the dense structure enabled by the smaller squarate ligand. Another high performing magnetocaloric framework containing a cyclic carboxylate Gd(HCO₂)(bdc),⁸⁵ where bdc is the aromatic 1,4-benzenedicarboxylate ligand found in many MOFs structures. Here it leads to a monoclinic P2₁/c structure with edge-sharing dimeric GdO₈ distorted trigonal dodecahedra, which are connected through the oxygen atoms of two formate ligands with intradimer Gd–Gd distances of 3.95 Å. These dimers are connected through the bdc carboxylate groups to generate layers that are pillared through the bdc linker. Gd(HCO₂)(bdc) was found to be very weakly antiferromagnetically coupled. The −ΔS^max_m, calculated from magnetisation data, gives a value of 42.4 J kg⁻¹ K⁻¹ (113 mJ cm⁻³ K⁻¹) for a 5 T field change at 2.25 K, with this increasing to 47.0 J kg⁻¹ K⁻¹ (125 mJ cm⁻³ K⁻¹) for a field change of 9 T.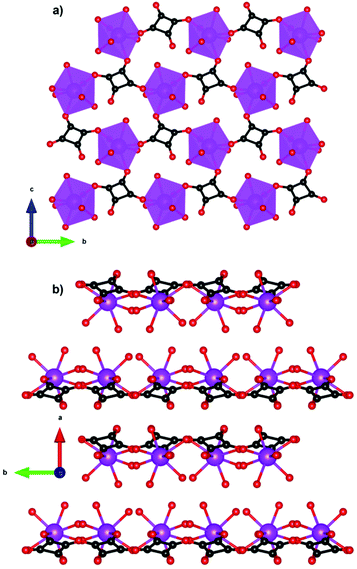

Fig. 14 (a) Two-dimensional layers of Gd(C₄O₄)(OH)(H₂O)₄ on the bc-plane and (b) packing of the layers along the a-axis. Colour codes: Gd: purple, C: black, O: red. Hydrogens are omitted for clarity.

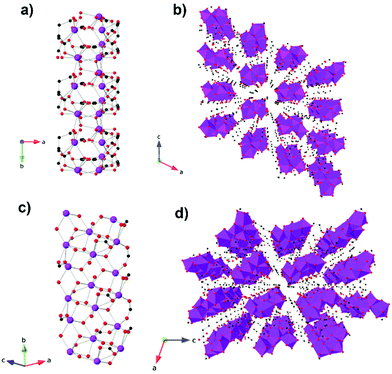
More recently an evacuated porous benzenetricarboxylate (btc) framework, Gd(btc)(H₂O),⁸⁶ has been reported to have a surprisingly high θ_W of −6.2 K and good magnetocaloric entropy change at 1.8 K for a 5 T field change as a function of weight, 42 J kg⁻¹ K⁻¹. Its entropy change as a function of volume is, however, very modest at about 68 mJ cm⁻³ K⁻¹, due to its low density structure. This structure, which adopts the chiral space groups of P4₁22 and P4₃22,⁸⁷ features Gd cations connected via carboxylate groups of btc linkers to give 1D helical chains with Gd–Gd distances of 4.30 Å. These rods pack to give a 3D structure thanks to the connectivity of Gd³⁺ ions and btc³⁻ ligands and features helical-shaped channels, with well-spaced Gd cations between chains with a minimum separation of 8 Å.

Two other frameworks with potential voids featuring cyclic carboxylates and with −ΔS^max_m above 40 J kg⁻¹ K⁻¹ have been reported, namely the weakly antiferromagnetically coupled Gd₅(μ₃-OH)₆(TZI)₃(DMA)_1.5(H₂O)_9.5·DMA⁸⁸ (where H₃TZI is 5-(1H-tetrazol-5-yl)isophthalic acid and DMA is dimethylcetamide) and [Gd(2,5-FDA)_0.5(Glu)(H₂O)₂]·xH₂O⁸⁹ (where FDA²⁻ is furan-2,5-dicarboxylate and Glu²⁻ is glutarate). Indirect measurements indicate a −ΔS^max_m of 41.3 J kg⁻¹ K⁻¹ and 40.6 J kg⁻¹ K⁻¹ at 2 K for a 7 T field change but, again, their porosity leads to a very modest volumetric −ΔS^max_m of 93.7 mJ cm⁻³ K⁻¹ and 70.6 mJ cm⁻³ K⁻¹ respectively. Gd₅(μ₃-OH)₆(TZI)₃(DMA)_1.5(H₂O)_9.5·DMA forms a 3D framework in monoclinic C2/m symmetry. Its structure is based on the [Gd₅(OH)₆]⁹⁺ trigonal bipyramidal core built from eight and nine coordinate Gd linked together by six μ₃-OH bridges and five syn–syn carboxylate bridges. These clusters are then connected by a μ₂-H₂O bridge to form 1D chains which are in turn connected by carboxylate groups of the TZI ligand to create the 3D framework. Gd(2,5-FDA)_0.5(Glu)(H₂O)₂·xH₂O adopts orthorhombic Pnma symmetry consisting of nine-coordinate Gd in monocapped square-antiprismatic polyhedra.⁸⁹ These Gd are linked into Gd₂O₁₆ dimers by two bidentate chelating-bridged carboxylates. The dimers connected into 1D zig-zag chains via the 2,5-FDA ligand with neighbouring chains bridged together by two Glu ligands per dimer.

4. 4f–3d mixed-metal polymers

The other general group of magnetocaloric coordination polymers that should be considered are those containing transition metals, with the highest performing materials amongst these typically combining d⁵ Mn²⁺ with f⁷ Gd³⁺ to maximise their magnetic spin. Mn²⁺ is the transition metal of choice in 3d–4f systems due to it being readily available and having the most unpaired electrons possible in a transition metal. Indeed, despite their lower number of unpaired electrons (cf. to Gd³⁺), Mn²⁺ complexes can have high −ΔS^max_m, with respect to weight even in the absence of a lanthanide, as seen in Mn(Me-ip)(DMF) (where Me-ipH₂ is 5-methylisophthalic acid).⁹⁰ This material adopts a Pna2₁ orthorhombic structure which contains distorted octahedral Mn²⁺ in a coordination polymer comprised of chains of Mn cations connected by two carboxylate ligands with a Mn–Mn intrachain distance of 3.88 Å (see Fig. 15). Each chain is then connected to four adjacent ones via the Me-ip²⁻ ligand with interchain Mn–Mn distance of 7.49 Å. The −ΔS^max_m for this system is calculated at 42.4 J kg⁻¹ K⁻¹ (66.7 mJ cm⁻³ K⁻¹) for a field change of 8 T at 2 K. This is accompanied by weak antiferromagnetic coupling, with a θ_W of −0.59 K, indicating that despite the presence of only 3d cations the emergence of magnetic order should not prevent its use as a magnetocaloric until much lower temperatures.

Fig. 15 Crystal structure of Mn(Me-ip)(DMF) with MnO₈ octahedra forming chains along the a-axis, connected by the Me-ip2-ligand. Colour codes: Mn: orange, C: black, O: red. Hydrogens are omitted for clarity.

An interesting 3d–4f mixed coordination polymer is GdMn_0.5(OAc)₄(H₂O)₂·3H₂O,⁹¹ which contains a low-dimensional motif, specifically the Gd³⁺–Mn²⁺ acetate chains with only very weak antiferromagnetic coupling within them. This compound has a −ΔS^max_m of 38.7 J kg⁻¹ K⁻¹ (78.7 mJ cm⁻³ K⁻¹) for a field change of 7 T at 2.5 K It should be noted that this compound also shows an interesting −ΔS^max_m of 31.1 J kg⁻¹ K⁻¹ (63.2 mJ cm⁻³ K⁻¹) for a field change of 3 T at ∼2 K, which is higher than that of the commercially available GGG under the same conditions. This compound crystallises in a triclinic P1̄ structure where each Gd ion is in a capped square-antiprism geometry and each Mn adopts an octahedral geometry. Two adjacent Gd³⁺ ions are bridged by two acetates while adjacent Gd³⁺ and Mn²⁺ ions are bridged by three acetates (see Fig. 16). This generates a 1D chain structure where pairs of Gd ions are separated by one Mn along the chain. Within the chains, the Gd–Gd distance is 4.277 Å whereas the Gd–Mn distance is 4.030 Å. Intrachain hydrogen bonds are present between one coordinated water molecule and two acetate ligands. Water tetramers, formed by two guest water molecules, support the main interactions between chains by enabling hydrogen bonding between coordinating carboxylate and water molecules.

Fig. 16 Crystal structure of [GdMn_0.5(OAc)₄(H₂O)₂]·3H₂O with chains of Mn and Gd polyhedra bridged together in a 2D network via hydrogen bonds. Colour codes: Gd: purple, Mn: orange, C: black, O: red. Hydrogens are omitted for clarity.

The remaining mixed 3d–4f coordination polymers with promising magnetocaloric properties are 3D frameworks with a net charge that is balanced by the presence of counterions in the pore space. These compounds all have respectable magnetocaloric entropy changes as a function of weight but, as for other porous magnetocalorics, they are much more modest as a function of volume. [Mn(H₂O)₆][MnGd(oda)₃]₂·6H₂O (where oda²⁻ is oxydiacetetate) is the only reported example of a promising magnetocaloric framework with an anionic charge.^92,93 The framework is composed of nine coordinate Gd in a distorted tricapped trigonal prismatic geometry while Mn in an octahedral environment, with each 3d cation connected via carboxylate oxygen atoms to six 4f cations and vice versa (see Fig. 17). This leads to a cubic lattice with voids of alternatingly broad and narrow cavities that are occupied by [Mn(H₂O)₆]²⁺ units, which both balance the anionic charge of the framework and enhance the MCE of the material, and solvent water molecules, respectively. This weakly coupled ferromagnetic material (θ_W of 1.2) has been determined indirectly to exhibit −ΔS^max_m of 50.1 J kg⁻¹ K⁻¹ (114 mJ cm⁻³ K⁻¹) at 1.8 K for field changes of up to 7 T. Heat capacity measurements under fields of up to 3 T were also performed giving properties that were consistent with those obtained from bulk magnetisation measurements with a ΔT_ad of 10.1 K for an applied field of 3 T.

Fig. 17 Crystal structure of [Mn(H₂O)₆][MnGd(oda)₃]₂·6H₂O. The structure presents broad and narrow cavities, occupied by [Mn(H₂O)₆]²⁺ and water molecules, respectively. Colour codes: Gd: purple, Mn: orange, C: black, O: red. Hydrogens are omitted for clarity.

Weakly antiferromagnetically coupled [Gd₄Mn(L)₃(H₂O)₃(μ₃-OH)₄(HCOO)_1.5](NO₃)_2.5·6H₂O (where H₂L is 2,2′-dipyridine-4,4′-dicarboxylic acid) has the highest −ΔS^max_m amongst a series of cationic mixed 3d–4f frameworks, between which L is varied, with a value of 46.0 J kg⁻¹ K⁻¹ (70.0 mJ cm⁻³ K⁻¹) for a field change of 7 T at 2 K.⁹⁴ This compound adopts a cubic I2₁3 symmetry with Gd³⁺ having two distinct coordination environments where Gd1 is eight coordinated with a dicapped trigonal prism geometry whereas Gd2 is six coordinated. These distinct cations are linked by OH⁻ groups into a distorted cubane [Gd₄O₄] cluster six coordinate and three eight coordinate Gd with intracluster in which the Gd are arranged in a trigonal prism containing one Gd–Gd distances of 3.78 Å and 3.87 Å. The L²⁻ ligands both link each [Gd₄O₄] cluster to three others but also to the octahedral Mn, which is coordinated only to nitrogen atoms from these ligands to six [Gd₄O₄] clusters, forming a 6,9-connected sqc topology. The clusters are bridged by formate ligands into a 3D framework with two unusual types of helical channels. The first of these is a larger L-helix with a pore diameter of 10.4 Å while the latter is an R-helix with the same helix pitch – that is the height of one complete helix turn of 20.7 Å, but a smaller pore diameter of 5.0 Å. Residual electron density has been used to suggest the pores of this compound are occupied by disordered H₂O molecules and NO₃⁻ anions, the latter being required for charge balancing, but there is no direct confirmation of this through other techniques. Weakly antiferromagnetically coupled [Gd₅Mn(L)₃(H₂O)₁₀(μ₃-OH)₆](NO₃)₅·13H₂O,⁹⁴ (where H₂L is 2,2′-dipyridine-4,4′-dicarboxylic acid) is another example of a 3D cationic framework with a high −ΔS^max_m of 38.3 J kg⁻¹ K⁻¹ (57.3 mJ cm⁻³ K⁻¹) at 3 K for a field change of 7 T. This compound adopts hexagonal P3₁2₁ symmetry and contains [Gd₅(COO)₆(H₂O)10(OH)₆]³⁺ cluster nodes in which the five Gd cations are arranged in a distorted trigonal bipyramidal geometry, with the Gd cations bridged by six μ₃-OH groups and encapsulated by the six carboxyl groups of three L²⁻ ligands. Each cluster contains three crystallographically independent Gd³⁺ cation all of which are eight-coordinated with dicapped trigonal prismatic geometries in the apical positions and square antiprism geometries in the equatorial plane of the cluster. Every cluster connects to six adjacent ones through the L²⁻ ligand which also connects the octahedral Mn to the Gd clusters, forming an overall 6,6-connected topology. The resulting channels in the structure contain free water molecules and NO₃⁻ counter anions.

5. Summary and perspective

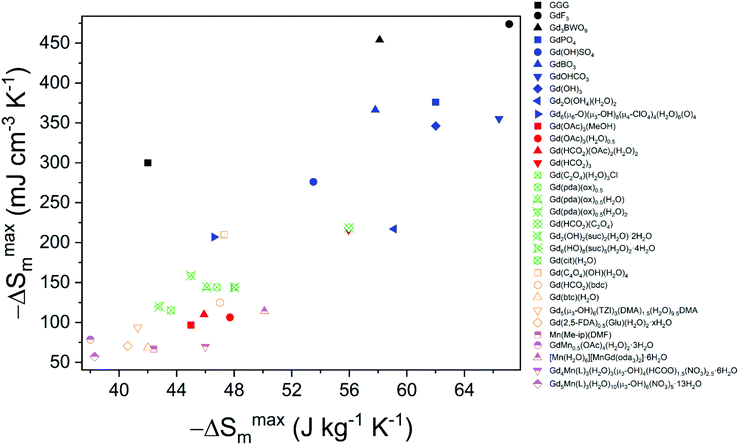
This review has presented coordination polymers, based on polyatomic ligands, exhibiting MCE showing a high −ΔS^max_m, the most readily available measure of their potential magnetic cooling. These are dominated by materials in which Gd is the magnetic cation and have been grouped across four categories, based on the ligand type, i.e. inorganic, monocarboxylate, linear carboxylate and cyclic carboxylate (see Fig. 18). Among these, the best performing magnetocaloric materials are typically found to incorporate only inorganic-based ligands, such as phosphates, borates and carbonates to name a few, likely because these smaller ligands yield structures containing higher densities of Gd³⁺ cations. One of the best performing magnetocalorics in this category is GdPO₄,⁵⁸ which features a high density of Gd³⁺ in combination with weak magnetic interactions and low magnetocrystalline anisotropy, with a magnetocaloric entropy change of up to 62.0 J kg⁻¹ K⁻¹ (376 mJ cm⁻³ K⁻¹) for a field change of 7 T, making this a very promising material for high field applications. Comparable materials are GdBO₃,⁶³ Gd(OH)₃,⁷⁰ and GdOHCO₃,⁵⁵ with the latter two having comparable and higher gravimetric magnetic entropy changes, respectively, but presenting a slightly lower volumetric entropy change.

Fig. 18 Plot of gravimetric and volumetric maximum entropy changes −ΔS^max_m of the materials discussed in this review. Presented here are inorganic-based (blue), monocarboxylate-based (red), linear carboxylate-based (green), cyclic carboxylate-based (orange) and mixed 3d–4f (purple) materials along with selected high-performance conventional materials (black). The values presented here are for field changes of 7 T with the exception of those for which 9 T (GGG, Gd₃BWO₉, GdBO₃, Gd(HCO₂)(bdc)), 8 T (Mn(Me-ip)(DMF) and only 5 T (GdF₃, Gd(HCO₂)(C₂O₄), Gd(btc)(H₂O)) values were available.

While there are a number of compounds associated with the other ligand groupings that exhibit −ΔS^max_m above 40 J kg⁻¹ K⁻¹, and thus comparable to the commonly used benchmark material GGG, they generally exhibit more modest entropy change values with respect to those incorporating only inorganic ligands. There are, however, some notable exceptions to this, specifically Gd(HCO₂)₃ and Gd(C₂O₄)(HCO₂),^74,81 that highlight that magnetocalorics with simple carboxylates can offer comparable entropy changes to purely inorganic frameworks. It can be seen that coordination frameworks with more complex ligands, particularly where these lead to more porous structures, generally have much lower MCE due to their relatively low density of magnetic cations. Such MOFs, however, retain scope for multifunctionality that could be either used to enhance their magnetocaloric properties, e.g. via inclusion of simple magnetic guests in their pores such as simple neutral lanthanide complexes analogous to [Mn(H₂O)₆][MnGd(oda)₃]₂·6H₂O,^92,93 or couple another function with good, if not excellent, magnetocaloric properties. In the pursuit of such multifunctionality, the use of simpler cyclic carboxylates, such as squarates,⁸⁴ and relatively small pore sizes that provide space for the desired guest or functionality, but do not unnecessarily reduce overall density, appear a sensible route forward.

In contrast to the wide number of coordination polymers whose −ΔS_m have been characterised further characterisation of the thermodynamic properties of even the most promising materials is very limited. It will be important to rectify this to enable the full potential of the most promising magnetocalorics to be determined. This can be emphasised by examination of Table 1, which compares the −ΔS^max_m and ΔT_ad of coordination polymers, for the limited number of materials where the later has been reported. This shows that some materials with high −ΔS^max_m have relatively more modest ΔT_ad, which is often considered a more direct measure of a magnetocalorics performance.

Table 1 Available values of ΔT_ad for the compounds discussed in this review

Compound	ΔTad (K)	−ΔS^maxm (J kg^−1 K^−1)	T max (K)	ΔH (T)
GdPO4	24.6	62.0	2.1	7
GdOHCO3	24	66.4	2	9
Gd(HCO2)3	22	55.9	∼1	7
Gd(C2O4)(H2O)3Cl	16.9	48.0	2.2	7
Gd2(OH)2(suc)2(H2O)·2H2O	∼17	42.8	2.6	7
Gd6(OH)8(suc)5(H2O)2·4H2O	15	48	1.8	7
Gd(btc)(H2O)	∼14	42	∼20	5
[Mn(H2O)6][MnGd(oda)3]2·6H2O	10.1	42.6	∼2	3

---

Looking beyond Gd-based materials, it has been noted that, amongst the 4f coordination polymers, there are a handful of examples where metal cations with significant magnetocrystalline anisotropy feature improved entropy changes for lower field changes and higher temperatures compared to their Gd analogues. This renders these materials good candidates for a broader range of applications that require cooling above 4 K, as He is commonly used to do, rather than the <2 K temperatures at which Gd materials excel. This is particularly the case when lower applied fields are needed, which are more readily achieved and offer the potential of using a permanent magnet rather than a more energy demanding superconducting magnet.

Notably amongst these are DyOHCO₃ and TbOHCO₃,⁶⁸ which have higher −ΔS_m changes at and above 4 K than GdOHCO₃ for field changes below 2 T, and Tb(HCO₂)₃ and Ho(HCO₂)₃,⁷⁵ which offer similar improved magnetocaloric properties compared to Gd(HCO₂)₃. In contrast, in the Ln(HCO₂)(C₂O₄) phases only the Dy analogue has a similar entropy change for low field applications compared to Gd(HCO₂)(C₂O₄),⁸¹ with this enhancement found to be modest.⁸¹ The materials with improved −ΔS_m for low applied fields also tend to exhibit strong diffuse magnetic scattering originating from a combination of low dimensional ferromagnetic coupling and geometrically frustrated magnetic interactions.⁷⁷ This suggests such properties are dependent on a combination of the single ion anisotropy and tailored magnetic interactions and thus designing structures where local magnetic interactions are optimised might be key to improving the magnetocaloric properties for cooling using low applied fields. Examples thus far focus on cases where there are strong ferromagnetic interactions in chains but competing interactions between the chains due to geometric frustration. This enables the facile alignment of the moment on the chains along the direction of a modest external magnetic field while the frustration suppresses order to very low temperatures in the absence of an applied field. Similar behaviour might also be expected for well isolated chains in coordination polymers, such that the interchain interactions are weak enough that magnetic order does not occur until below the temperature at which these are useful magnetocalorics, although this would likely lead to lower −ΔS^max_m as a function of volume and, to a lesser extent, weight due to the dilution of the magnetic cations required by this additional spacing. It is also possible that other magnetic motifs may exhibit similar properties with anisotropic magnetic centres as indicated by the performance of DyBO₃ compared to its Gd analogue.⁶³ Thus investigation of the analogues of inorganic frameworks with anisotropic lanthanides offers a potential opportunity for improvement of magnetocaloric properties under lower fields with such materials, including Gd(OH)₃, Gd(OH)SO₄ and Gd₂O(OH)₄(H₂O)₂.

Finally, 3d–4f mixed-metal coordination polymers have been briefly reviewed, with Gd–Mn polymers showing −ΔS^max_m comparable to the other classes of materials discussed with respect to weight. Although the lower density of these mixed metal MOFs leads to their entropy change as a function of volume being quite modest, it should also be considered that the materials reported thus far commonly have cyclic dicarboxylates that, even in purely 4f materials, commonly lead to poorer MC properties. The greater availability and lower cost of transition metals, however, makes 3d–4f frameworks or, as seen in Mn(Me-ip)(DMF),⁹⁰ even 3d frameworks attractive as a way of enabling the use of magnetocalorics with a reduced dependence on the use of lanthanides. Thus, the magnetocaloric properties of 3d–4f and 3d frameworks based on inorganic ligands or small carboxylates, e.g. formate and oxalate, are worth further exploration. While it is possible these will have stronger magnetic coupling than the 3d containing polymers explored in this review, this should not prove an impediment to their application as magnetocalorics, provided magnetic order is supressed to below the desired order temperature by e.g. geometric frustration. Additionally, through the promising −ΔS^max_m of GdMn_0.5(OAc)₄(H₂O)₂·3H₂O for 3 T field changes,⁹¹ there is some indication of there being a potential route for maximising properties at lower applied magnetic fields.

In conclusion, a variety of coordination polymers featuring promising magnetocaloric properties have been reviewed, highlighting the influence of a material's structure, including incorporation of smaller polyatomic ligands and optimising magnetic interactions, through use of low dimensional motifs and magnetic frustration, as important factors to consider when designing materials for low-temperature magnetic cooling applications.

Author contributions

MF lead the investigation which PJS also contributed to, with both authors contributing to the writing of the manuscript. PJS conceptualised the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank the Leverhulme Trust and Engineering and Physical Sciences Research Council for supporting this work through RPG-2018-268 and EP/T027886/1, respectively.

References

1. J.-L. DuPont, P. Domasnki, P. Lebrun and F. Ziegler, 38th Informatory Note on Refrigeration Technologies, 2019.
2. S. A. Tassou, J. S. Lewis, Y. T. Ge, A. Hadawey and I. Chaer, Appl. Therm. Eng., 2010, 30, 263–276.
3. L. P. Ichkitidze, N. A. Bazaev, D. V. Telyshev, R. Y. Preobrazhensky and M. L. Gavrushina, Biomed. Eng., 2015, 48, 305–309.
4. J. C. Doane and H. D. Stein, J. Int. Coll. Surg., 1951, 16, 346–349.
5. A. H. Olafsdottir and H. U. Sverdrup, Biophys. Econ. Sustain., 2020, 5, 6.
6. O. Sari and M. Balli, Int. J. Refrig., 2014, 37, 8–15.
7. V. Franco, J. S. Blázquez, B. Ingale and A. Conde, Annu. Rev. Mater. Res., 2012, 42, 305–342.
8. J. F. Scott, Annu. Rev. Mater. Res., 2011, 41, 229–240.
9. P. F. Liu, J. L. Wang, X. J. Meng, J. Yang, B. Dkhil and J. H. Chu, New J. Phys., 2010, 12, 023035.
10. G. G. Wiseman and J. K. Kuebler, Phys. Rev., 1963, 131, 2023.
11. W. N. Lawless, Phys. Rev. B: Solid State, 1977, 16, 433–439.
12. H.-X. Cao and Z.-Y. Li, J. Appl. Phys., 2009, 106, 094104.
13. W. N. Lawless and A. J. Morrow, Ferroelectrics, 1977, 15, 159–165.
14. I. N. Flerov and E. A. Mikhaleva, Phys. Solid State, 2008, 50, 478–484.
15. S. Qian, Y. Geng, Y. Wang, J. Ling, Y. Hwang, R. Radermacher, I. Takeuchi and J. Cui, Int. J. Refrig., 2016, 64, 1–19.
16. J. Tušek, K. Engelbrecht, R. Millán-Solsona, L. Mañosa, E. Vives, L. P. Mikkelsen and N. Pryds, Adv. Energy Mater., 2015, 5, 1500361.
17. K. Otsuka and C. M. Wayman, Shape memory materials, Cambridge university press, 1999.
18. C. M. Miliante, A. M. Christmann, E. O. Usuda, W. Imamura, L. S. Paixão, A. M. G. Carvalho and A. R. Muniz, Macromolecules, 2020, 53, 2606–2615.
19. S. Crossley, N. D. Mathur and X. Moya, AIP Adv., 2015, 5, 067153.
20. L. Mañosa and A. Planes, Adv. Mater., 2017, 29, 1603607.
21. C. Cazorla, Appl. Phys. Rev., 2019, 6, 041316.
22. W. Imamura, É. O. Usuda, L. S. Paixão, N. M. Bom, A. M. Gomes and A. M. G. Carvalho, Chin. J. Polym. Sci., 2020, 38, 999–1005.
23. A. M. G. Carvalho, W. Imamura, E. O. Usuda and N. M. Bom, Eur. Polym. J., 2018, 99, 212–221.
24. E. O. Usuda, N. M. Bom and A. M. G. Carvalho, Eur. Polym. J., 2017, 92, 287–293.
25. N. M. Bom, W. Imamura, E. O. Usuda, L. S. Paixão and A. M. G. Carvalho, ACS Macro Lett., 2017, 7, 31–36.
26. B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole, T. Hattori, T. Kikuchi, S. Yano, Z. Zhang, Z. Zhang, W. Ren, S. Lin, O. Sakata, K. Nakajima and Z. Zhang, Nature, 2019, 567, 506–510.
27. L. Mañosa, D. González-Alonso, A. Planes, E. Bonnot, M. Barrio, J.-L. Tamarit, S. Aksoy and M. Acet, Nat. Mater., 2010, 9, 478–481.
28. J. M. Bermúdez-García, M. Sánchez-Andújar, S. Yáñez-Vilar, S. Castro-García, R. Artiaga, J. López-Beceiro, L. Botana, Á. Alegría and M. A. Señarís-Rodríguez, Inorg. Chem., 2015, 54, 11680–11687.
29. J. M. Bermúdez-García, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga and M. A. Señarís-Rodríguez, Nat. Commun., 2017, 8, 15715.
30. J. M. Bermúdez-García, S. Yáñez-Vilar, A. García-Fernández, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga, M. Dilshad, X. Moya and M. A. Señarís-Rodríguez, J. Mater. Chem. C, 2018, 6, 9867–9874.
31. J. Salgado-Beceiro, A. Nonato, R. X. Silva, A. García-Fernández, M. Sánchez-Andújar, S. Castro-García, E. Stern-Taulats, M. A. Señarís-Rodríguez, X. Moya and J. M. Bermúdez-García, Adv. Mater., 2020, 1, 3167–3170.
32. E. Warburg, Ann. Phys., 1881, 249, 141–164.
33. P. Weiss and A. Piccard, C. R. Acad. Sci., 1918, 166, 352–354.
34. A. Waske, M. E. Gruner, T. Gottschall and O. Gutfleisch, MRS Bull., 2018, 43, 269–273.
35. C. Zimm, A. Jastrab, A. Sternberg, V. Pecharsky, K. Gschneidner, M. Osborne and I. Anderson, Advances in Cryogenic Engineering, Springer US, Boston, MA, 1998, pp. 1759–1766.
36. K. A. Gschneidner and V. K. Pecharsky, Int. J. Refrig., 2008, 31, 945–961.
37. V. K. Pecharsky and K. A. Gschneidner, Phys. Rev. Lett., 1997, 78, 4494–4497.
38. U. Cardella, L. Decker and H. Klein, Int. J. Hydrogen Energy, 2017, 42, 13329–13338.
39. L. Gyongyosi and S. Imre, Comput. Sci. Rev., 2019, 31, 51–71.
40. C. Mitra, Nat. Phys., 2015, 11, 212–213.
41. P. Martin, A. S. Royet, F. Guellec and G. Ghibaudo, Solid-State Electron., 2011, 62, 115–122.
42. A. Cho, Science, 2009, 326, 778–779.
43. V. K. Pecharsky and K. A. Gschneidner Jr., J. Magn. Magn. Mater., 1999, 200, 44–56.
44. I. Niknia, P. V. Trevizoli, T. V. Christiaanse, P. Govindappa, R. Teyber and A. Rowe, J. Appl. Phys., 2017, 121, 064902.
45. A. Giguère, M. Foldeaki, B. Ravi Gopal, R. Chahine, T. K. Bose, A. Frydman and J. A. Barclay, Phys. Rev. Lett., 1999, 83, 2262–2265.
46. A. M. Tishin, J. Alloys Compd., 1997, 250, 635–641.
47. Y. Z. Zheng, G. J. Zhou, Z. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014, 43, 1462–1475.
48. M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672–4676.
49. N. R. Ram, M. Prakash, U. Naresh, N. S. Kumar, T. S. Sarmash, T. Subbarao, R. J. Kumar, G. R. Kumar and K. C. B. Naidu, J. Supercond. Novel Magn., 2018, 31, 1971–1979.
50. K. A. Gschneidner and V. K. Pecharsky, Annu. Rev. Mater. Sci., 2000, 30, 387–429.
51. Y. Mozharivskyj, Magnetocaloric Effect and Magnetocaloric Materials, Elsevier Inc., 2016.
52. S. R. Batten, N. R. Champness, X.-M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Öhrström, M. O'Keeffe, M. P. Suh and J. Reedijk, CrystEngComm, 2012, 14, 3001.
53. M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353–1379.
54. A. P. Ramirez, Annu. Rev. Mater. Sci., 1994, 24, 453–480.
55. M. Mekata, Phys. Today, 2003, 56, 12–13.
56. S. S. Sosin, L. A. Prozorova, A. I. Smirnov, A. I. Golov, I. B. Berkutov, O. A. Petrenko, G. Balakrishnan and M. E. Zhitomirsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 094413.
57. O. A. Petrenko, D. M. K. Paul, C. Ritter, T. Zeiske and M. Yethiraj, Physica B: Condens. Matter, 1999, 266, 41–48.
58. E. Palacios, J. A. Rodríguez-Velamazán, M. Evangelisti, G. J. McIntyre, G. Lorusso, D. Visser, L. J. de Jongh and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214423.
59. D. F. Mullica, D. A. Grossie and L. A. Boatner, Inorg. Chim. Acta, 1985, 109, 105–110.
60. Y. Han, S.-D. Han, J. Pan, Y.-J. Ma and G.-M. Wang, Mater. Chem. Front., 2018, 2, 2327–2332.
61. R. A. Zehnder, C. S. Wilson, H. T. Christy, K. S. Harris, V. Chauhan, V. Schutz, M. Sullivan, M. Zeller, F. R. Fronczek, J. A. Myers, K. Dammann, J. Duck, P. M. Smith, A. Okuma, K. Johnson, R. Sovesky, C. Stroudt and R. A. Renn, Inorg. Chem., 2011, 50, 836–846.
62. B. Daudin, R. Lagnier and B. Salce, J. Magn. Magn. Mater., 1982, 27, 315–322.
63. P. Mukherjee, Y. Wu, G. I. Lampronti and S. E. Dutton, Mater. Res. Bull., 2018, 98, 173–179.
64. L. C. Chapon, P. Manuel, F. Damay, P. Toledano, V. Hardy and C. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 024409.
65. A. I. Smirnov, L. E. Svistov, L. A. Prozorova, A. Zheludev, M. D. Lumsden, E. Ressouche, O. A. Petrenko, K. Nishikawa, S. Kimura, M. Hagiwara, K. Kindo, A. Y. Shapiro and L. N. Demianets, Phys. Rev. Lett., 2009, 102, 037202.
66. T. Tahara, I. Nakai, R. Miyawaki and S. Matsubara, Z. Krist., 2007, 222, 326–334.
67. Y.-C. Chen, L. Qin, Z.-S. Meng, D.-F. Yang, C. Wu, Z. Fu, Y.-Z. Zheng, J.-L. Liu, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, J. Mater. Chem. A, 2014, 2, 9851–9858.
68. R. J. C. Dixey and P. J. Saines, Inorg. Chem., 2018, 57, 12543–12551.
69. R. J. C. Dixey, G. B. G. Stenning, P. Manuel, F. Orlandi and P. J. Saines, J. Mater. Chem. C, 2019, 7, 13111–13119.
70. Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long, L.-S. Zheng, Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long and L.-S. Zheng, Chem. Commun., 2015, 51, 7317–7320.
71. Y.-L. Hou, G. Xiong, P.-F. Shi, R.-R. Cheng, J.-Z. Cui and B. Zhao, Chem. Commun., 2013, 49, 6066.
72. F.-S. Guo, J.-D. Leng, J.-L. Liu, Z.-S. Meng and M.-L. Tong, Inorg. Chem., 2012, 51, 405–413.
73. G. Lorusso, M. A. Palacios, G. S. Nichol, E. K. Brechin, O. Roubeau and M. Evangelisti, Chem. Commun., 2012, 48, 7592–7594.
74. G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656.
75. P. J. Saines, J. A. M. Paddison, P. M. M. Thygesen and M. G. Tucker, Mater. Horiz., 2015, 2, 528–535.
76. D. R. Harcombe, P. G. Welch, P. Manuel, P. J. Saines and A. L. Goodwin, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 174429.
77. R. J. C. Dixey, F. Orlandi, P. Manuel, P. Mukherjee, S. E. Dutton and P. J. Saines, Philos. Trans. R. Soc., A, 2019, 377, 20190007.
78. Y. Meng, Y.-C. Chen, Z.-M. Zhang, Z.-J. Lin and M.-L. Tong, Inorg. Chem., 2014, 53, 9052–9057.
79. S.-J. Liu, C. Cao, S.-L. Yao, T.-F. Zheng, Z.-X. Wang, C. Liu, J.-S. Liao, J.-L. Chen, Y.-W. Li and H.-R. Wen, Dalton Trans., 2017, 46, 64–70.
80. S. Romero, A. Mosset and J. C. Trombe, J. Solid State Chem., 1996, 127, 256–266.
81. M. Falsaperna, G. B. G. Stenning, I. da Silva and P. J. Saines, J. Mater. Chem. C, 2021, 9, 13209–13217.
82. Y.-C. Chen, F.-S. Guo, Y.-Z. Zheng, J.-L. Liu, J.-D. Leng, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, Chem. – Eur. J., 2013, 19, 13504–13510.
83. S.-J. Liu, C.-C. Xie, J.-M. Jia, J.-P. Zhao, S.-D. Han, Y. Cui, Y. Li and X.-H. Bu, Chem. – Asian J., 2014, 9, 1116–1122.
84. S. Biswas, A. Adhikary, S. Goswami and S. Konar, Dalton Trans., 2013, 42, 13331–13334.
85. R. Sibille, T. Mazet, B. Malaman and M. François, Chem. – Eur. J., 2012, 18, 12970–12973.
86. V. Zeleňák, M. Almáši, A. Zeleňáková, P. Hrubovčák, R. Tarasenko, S. Bourelly and P. Llewellyn, Sci. Rep., 2019, 9, 15572–15580.
87. L.-H. Xie, Y. Wang, X.-M. Liu, J.-B. Lin, J.-P. Zhang and X.-M. Chen, CrystEngComm, 2011, 13, 5849–5857.
88. F. Liu, H. Huang, W. Gao, X.-M. Zhang and J.-P. Liu, CrystEngComm, 2017, 19, 3660–3665.
89. M. Kumar, L.-H. Wu, M. Kariem, A. Franconetti, H. N. Sheikh, S.-J. Liu, S. C. Sahoo and A. Frontera, Inorg. Chem., 2019, 58, 7760–7774.
90. C.-B. Tian, R.-P. Chen, C. He, W.-J. Li, Q. Wei, X.-D. Zhang and S.-W. Du, Chem. Commun., 2014, 50, 1915–1917.
91. Y. Y. Pan, Y. Yang, L. S. Long, R. Bin Huang and L. S. Zheng, Inorg. Chem. Front., 2014, 1, 649–652.
92. T. K. Prasad, M. V. Rajasekharan and J.-P. Costes, Angew. Chem., Int. Ed., 2007, 46, 2851–2854.
93. F. S. Guo, Y. C. Chen, J. L. Liu, J. D. Leng, Z. S. Meng, P. Vrábel, M. Orendác, M. L. Tong, M. Orendáč and M. L. Tong, Chem. Commun., 2012, 48, 12219–12221.
94. P.-F. Shi, C.-S. Cao, C.-M. Wang and B. Zhao, Inorg. Chem., 2017, 56, 9169–9176.

---