Open Access Article
Open Access ArticleHow general is the effect of the bulkiness of organic ligands on the basicity of metal–organic catalysts? H2-evolving Mo oxides/sulphides as case studies†
Anna
Rovaletti
 *a,
Ulf
Ryde
*a,
Ulf
Ryde
 b,
Giorgio
Moro
b,
Giorgio
Moro
 c,
Ugo
Cosentino
a and
Claudio
Greco
c,
Ugo
Cosentino
a and
Claudio
Greco
 *a
*a
aDepartment of Earth and Environmental Sciences, Milano-Bicocca University, Piazza della Scienza 1, Milano, Italy. E-mail: anna.rovaletti@unimib.it; claudio.greco@unimib.it
bDepartment of Theoretical Chemistry, Lund University, Chemical Centre, P.O. Box 124, SE-221 00 Lund, Sweden
cDepartment of Biotechnology and Biosciences, Milano-Bicocca University, Piazza della Scienza 2, Milano, Italy
First published on 8th November 2022
Abstract
Tailoring the activity of an organometallic catalyst usually requires a targeted ligand design. Tuning the ligand bulkiness and tuning the electronic properties are popular approaches, which are somehow interdependent because substituents of different sizes within ligands can determine inter alia the occurrence of different degrees of inductive effects. Ligand basicity, in particular, turned out to be a key property for the modulation of protonation reactions occurring in vacuo at the metals in complexes bearing organophosphorus ligands; however, when the same reactions take place in a polar organic solvent, their energetics becomes dependent on the trade-off between ligand basicity and bulkiness, with the polarity of the solvent playing a key role in this regard [Bancroft et al., Inorg. Chem., 1986, 25, 3675; Rovaletti et al., J. Phys. Org. Chem., 2018, 31, e3748]. In the present contribution, we carried out molecular dynamics and density functional theory calculations on water-soluble Mo-based catalysts for proton reduction, in order to study the energetics of protonation reactions in complexes where the incipient proton binds a catalytically active ligand (i.e., an oxide or a disulphide). We considered complexes either soaked in water or in a vacuum, and featuring N-based ancillary ligands of different bulkiness (i.e. cages constituted either by pyridine or isoquinoline moieties). Our results show that the energetics of protonation events can be affected by ancillary ligand bulkiness even when the metal center does not play the role of the H+ acceptor. In vacuo, protonation at the O or S atom in the α position relative to the metal in complexes featuring the bulky isoquinoline-based ligand is more favored by around 10 kcal mol−1 when compared to the case of the pyridine-based counterparts, a difference that is almost zero when the same reactions occur in water. Such an outcome is rationalized in light of the different electrostatic properties of complexes bearing ancillary ligands of different sizes. The overall picture from theory indicates that such effects of ligand bulkiness can be relevant for the design of green chemistry catalysts that undergo protonation steps in water solutions.
1 Introduction
The search for renewable, carbon-neutral energy sources remains one of the central challenges for scientists in the 21st century.1 In this regard, H2 is considered to be an ideal alternative for the future energy supply due to its high energy density and eco-friendly combustion to water.2 As far as H2 production is concerned, it is desirable to obtain it by clean and environmentally friendly routes such as the splitting of water molecules. Efficient hydrogen production from water by means of inexpensive catalysts exploiting the redox-chemistry of Earth-abundant metals in conjunction with green electron donors3 exemplifies one of the alternatives to water electrolysis, which usually requires precious metals such as Pt to be carried out. A notable example in such context is represented by molybdenum-based oxo and sulphide catalysts that can produce H2 from water at neutral pH and even from sea water.4,5In the design of metal–organic catalysts, great attention is usually paid to tailoring the metal coordination sphere in order to control reactivity. The electronic properties of the ligands, which can easily be tuned via substitutions, constitute the main focus of synthetic strategies as they are directly correlated with the activity of the system. At the same time, reaction rates are rarely considered to be controlled by the steric properties of the coordinating ligands, unless the bulkiness of the latter lets one foresee the possible occurrence of interactions that prevent substrate(s) from binding the catalytically active metal center(s) or ligand(s).
Experimental studies on metal protonation in mononuclear transition metal complexes having the formula [W(CO)5(PR3)] (R = Me, Ph) suggested an inversion of the reactivity as a function of the polarity of the medium in which the reaction is conducted.6 Notably, the usage of bulky phosphine ligands for the fine tuning of the stereoelectronic properties is a popular approach in the case of biomimetic modeling of hydrogenases,7–10 the active sites of which involve CO ligands bound to iron ion(s).
In a previous study,11 we investigated the effects of phosphine ligand bulkiness on metal protonation in the case of biomimetic models of [FeFe]-hydrogenases.12,13 By means of density functional theory (DFT) calculations, we demonstrated that differences in reactivity toward metal protonation between a biomimetic diiron catalyst [Fe2((μ-adt)(CO)4(PMe3)2] and its bulkier counterpart [Fe2(μ-adt)(CO)4(PPh3)2] (adt = N-benzylazadithiolate) can be rationalized based on differences in the overall electrostatic properties of the complexes, which acquire key relevance upon changing the nature of the surrounding medium (vacuum vs. acetonitrile). In fact, electrostatic contributions turned out to play a significant role in determining the solvation energies of these complexes, which in turn influences their protonation energetics.
These results prompted us to extend the study to other classes of metal–organic catalysts, e.g. [(PY5Me2)MoO]+2, [(PY5Me2)MoS2]+2 (PY5Me2 = 2,6-bis(1,1-bis(2-pyridyl)ethyl)pyridine), which work in an even more polar medium, such as water, and H2 is evolved without the direct involvement of the metal in the protonation reactions. More specifically, our aim is to analyze the role of the bulkiness of the ligands in the reactivity of the metal-bound oxide and sulphide groups, these being the centres that undergo the protonation reactions underlying dihydrogen evolution in water.4,5 By the combined application of DFT and molecular dynamics, we show that the energetics of the catalytic protonation events can be affected by ligand bulkiness even when H2 formation occurs without direct involvement of the metal center. Furthermore, our results indicate that such effects of ligand bulkiness can be relevant for the design of better catalysts for H2 evolution in water solution. This study can bear relevance also for a better understanding of the role of ligands in ligand-protected atomic metal clusters.14
2 Methods
2.1 Quantum chemical calculations
All calculations were performed within the framework of density functional theory (DFT) at the BP86-D3(BJ)/def2-TZVP level,15–18 an approach which has already proved successful for the modelling of Mo complexes in the presence of oxo and sulphide ligands.19–22 Calibration of the method employed was also assessed by testing different DFT functionals and basis sets as reported in Table S2 in the ESI.† Geometry optimizations of all models were carried out both in a vacuum and in a water-like solvent, described by the conductor-like polarizable continuum model (C-PCM).23,24 The universal solvation model based on solute electron density and on a continuum model of the solvent (SMD)25 was also tested by running single point calculations on vacuum-optimized geometries. For all the optimized models, atomic charges were computed by means of natural population analysis.26Energy differences discussed in the following refer to differences in total energies. In particular, the protonation energies reported consider proton transfer reactions towards the α-ligand of Mo in the monocationic species, with the H3O+ cation acting as the proton donor in all cases for a convenient evaluation of relative basicities of the organometallic assemblies. Solvation energies were computed by calculating total energy differences between model energies in vacuo and in the presence of the solvent. All quantum chemical calculations were performed with the G16 version of the Gaussian suite of programs.27
2.2 Classical mechanics simulations
In order to evaluate solvation of the molybdenum catalysts, molecular dynamics (MD) simulations were run in the presence of explicit water solvent. Only the Mo-oxo monocationic ([PY5Me2MoO]+, [QY5Me2MoO]+) and dicationic species ([PY5Me2MoOH]+2, [QY5Me2MoOH]+2) were treated in these simulations.Validation of the employed force field was conducted based on a comparison between key structural parameters of Mo first coordination sphere obtained by classical MD, and by DFT as a reference (see Table S6 in the ESI†).
3 Results and discussion
In the present study two Mo(IV) complexes, recently reported in the literature as a promising inexpensive alternative for the electrocatalytic hydrogen production in water, were considered: a molybdenum-oxo and a molybdenum-disulphide, coordinated to the PY5Me2 ligand.4,5 As for the Mo![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O complex, the first step of the mechanism for the H2 generation was reported to involve a one-electron reduction of the catalyst, followed by protonation of the oxygen ligand atom to form [PY5Me2MoOH]+2.40 Therefore, the energetics involved in the [PY5Me2MoO]+ → [PY5Me2MoOH]+2 reaction were computed.
O complex, the first step of the mechanism for the H2 generation was reported to involve a one-electron reduction of the catalyst, followed by protonation of the oxygen ligand atom to form [PY5Me2MoOH]+2.40 Therefore, the energetics involved in the [PY5Me2MoO]+ → [PY5Me2MoOH]+2 reaction were computed.
Since a detailed reaction mechanism for the most recent catalyst, PY5Me2MoS2, has not been reported in the literature, we assumed that the first steps of its catalytic cycle are analogous to those of the corresponding oxo species, e.g. one-electron reduction followed by protonation of the α-ligand.
In order to analyse the effect of the bulkiness of the ligands on the reactivity of the catalysts, the PY5Me2 ligand was made bulkier by addition of a phenyl ring to the four pyridine that substitute the central pyridine, i.e. QY5Me2, = 2,6-bis(1,1-bis(2-quinolinyl)ethyl)pyridine, see Fig. 1. Since the catalysts were reported to work in neutral or slightly acidic water, the effect of the medium was considered by comparing the properties of the complexes both in a water-like continuum solvent and in a vacuum.
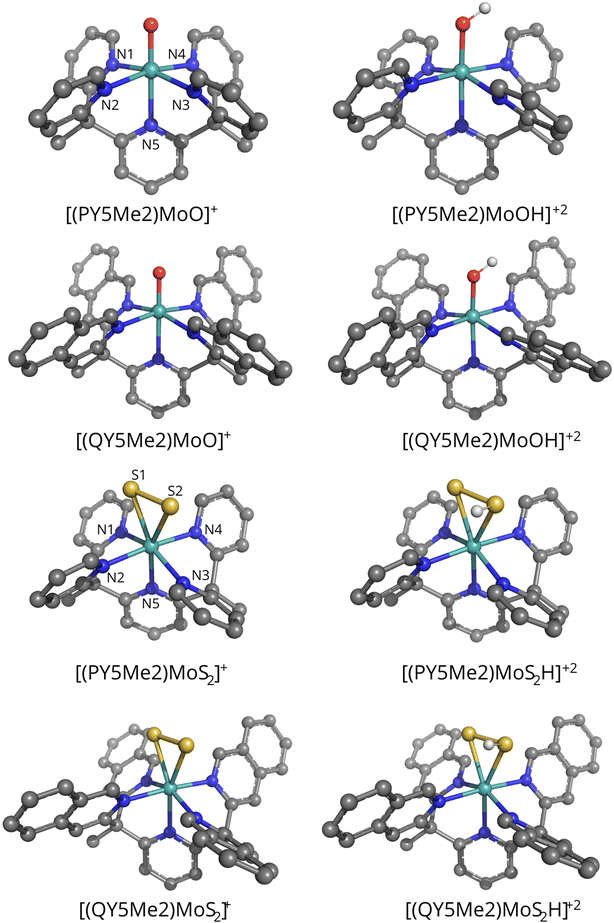
The vacuum-optimized geometries of the monocationic species [PY5Me2MoO]+, [QY5Me2MoO]+, [PY5Me2MoS2]+ and [QY5Me2MoS2]+, as well as those of the corresponding protonated products (protonated either on the oxo or on one of the sulfido ligands) [PY5Me2MoOH]+2, [QY5Me2MoOH]+2, [PY5Me2MoS2H]+2 and [QY5Me2MoS2H]+2, are shown in Fig. 2, whereas some key bond distances and angles of the vacuum- and solvent-optimized geometries are shown in Tables 1 and 2. As reported in the Methods section, different levels of theory were tested for the geometry optimization. However, deviations in the relevant geometry parameters turned out to be small (maximum deviation in coordination distances: 0.06 Å; maximum deviation in angles: 2.4°. See Table S1 in the ESI†). Therefore, only the BP86-D3(BJ)/def2-TZVP geometries will be discussed in the main text.
| [PY5Me2MoO]+ | [QY5Me2MoO]+ | |||
|---|---|---|---|---|
| Vacuo | Solvent | Vacuo | Solvent | |
| Mo–O | 1.72 | 1.73 | 1.72 | 1.73 |
| Mo–N1 | 2.14 | 2.14 | 2.14 | 2.14 |
| Mo–N2 | 2.14 | 2.14 | 2.14 | 2.14 |
| Mo–N3 | 2.14 | 2.14 | 2.14 | 2.14 |
| Mo–N4 | 2.14 | 2.14 | 2.14 | 2.14 |
| Mo–N5 | 2.26 | 2.25 | 2.27 | 2.28 |
| [PY5Me2MoS2]+ | [QY5Me2MoS2]+ | |||
|---|---|---|---|---|
| Vacuo | Solvent | Vacuo | Solvent | |
| Mo–S1 | 2.43 | 2.42 | 2.44 | 2.41 |
| Mo–S2 | 2.46 | 2.51 | 2.44 | 2.50 |
| Mo–N1 | 2.16 | 2.17 | 2.15 | 2.17 |
| Mo–N2 | 2.20 | 2.19 | 2.21 | 2.19 |
| Mo–N3 | 2.14 | 2.11 | 2.15 | 2.21 |
| Mo–N4 | 2.22 | 2.22 | 2.21 | 2.11 |
| Mo–N5 | 2.13 | 2.16 | 2.14 | 2.17 |
| [PY5Me2MoOH]+2 | [QY5Me2MoOH]+2 | |||
|---|---|---|---|---|
| Vacuo | Solvent | Vacuo | Solvent | |
| Mo–O | 1.89 | 1.89 | 1.90 | 1.90 |
| O–H | 0.98 | 0.98 | 0.98 | 0.98 |
| Mo–O–H | 127.6 | 124.5 | 125.2 | 124.0 |
| [PY5Me2MoS2H]+2 | [QY5Me2MoS2H]+2 | |||
|---|---|---|---|---|
| Vacuo | Solvent | Vacuo | Solvent | |
| Mo–S(H) | 2.51 | 2.51 | 2.50 | 2.51 |
| Mo–S | 2.44 | 2.45 | 2.45 | 2.45 |
| S–H | 1.38 | 1.37 | 1.38 | 1.37 |
| Mo–S–H | 109.0 | 108.2 | 109.1 | 108.7 |
The vacuum-optimized [PY5Me2MoO]+ and [QY5Me2MoO]+ species show an octahedral molecular geometry where the oxygen ligand is found in the axial position (dMo–O = 1.72 Å for both catalysts) opposite to the nitrogen atom of the pyridyl ring (dMo–N = 2.26 and 2.27 Å for [PY5Me2MoO]+ and [QY5Me2MoO]+ respectively). The equatorial azo-ligands are all bound at the same distance from the metal, at 2.14 Å for both complexes. For the Mo–S2 catalysts, the vacuum-optimized complexes show a pseudo-octahedral geometry with the S2 ligand positioned in a side-on manner in the equatorial plane (dMo–S = 2.46 and 2.43 Å for [PY5Me2MoS2]+, and 2.44 and 2.44 Å for [QY5Me2MoS2]+) along with three nitrogen atoms (dMo–Neq = 2.13, 2.14 and 2.16 Å for [PY5Me2MoS2]+ and 2.14, 2.15 and 2.15 Å for [QY5Me2MoS2]+). The axial substituents lie at a distance of 2.20 and 2.22 Å from Mo in the pyridine species and 2.21 Å in the quinoline complex. Protonation of the oxo or S2 ligand led to formation of species with very similar MoOH, or MoSSH, moiety geometry (maximum deviation in coordination distances: 0.01 Å, maximum deviation in Mo–O/S–H angles: 2.4° and 0.1° for the oxo and sulphide species, respectively).
Full geometry optimization in water – modelled as a C-PCM continuum solvent – was also performed on each structure. Comparison of the optimized geometries for the monocationic species does not evidence any significant changes due to the change of the medium (maximum deviation in coordination distances: 0.01 Å and 0.05 Å for the oxo and sulphide species, respectively, see Tables 1 and 2). Soaking of the dicationic catalysts only led to a decrease of the Mo–O–H angle by 3°, while the rest of the coordination sphere remains essentially identical to the one of the vacuum-optimized structure (maximum deviation in coordination distances: 0.01 Å).
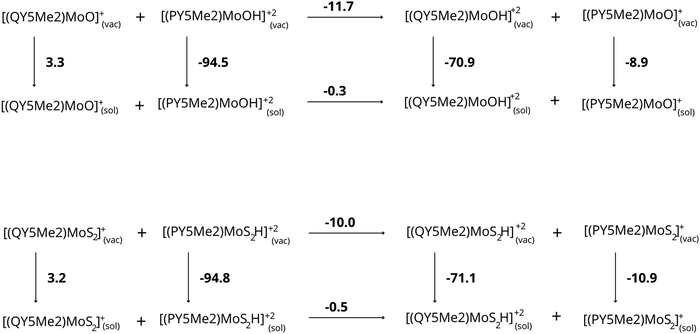
Despite the pronounced structural similarity in the two different media, the resulting protonation energies for [PY5Me2MoO]+ and [QY5Me2MoO]+ with or without the continuum solvent representation showed a peculiar trend. As can be seen in Table 3, protonation of the oxygen atom in α-position is strongly favoured in the presence of the bulky isoquinoline ligand (QY5Me2) compared to the pyridine one (PY5Me2) in vacuum (−11.7 kcal mol−1), but the difference is nearly zero when the reaction is performed in water (−0.3 kcal mol−1). The same trend is observed for the molybdenum-disulphide analogues. Protonation of the disulphide is favoured in a vacuum when the QY5Me2 ligand is coordinated to the Mo ion (−10.1 kcal mol−1) but in the polarizable solvent the difference is minimal (−0.4 kcal mol−1).
| Proton acceptor | Vacuum | Solvent |
|---|---|---|
| [PY5Me2MoO]+ | −16.3 | −30.2 |
| [QY5Me2MoO]+ | −28.0 | −30.5 |
| (−11.7) | (−0.3) | |
| [PY5Me2MoS2]+ | −11.4 | −23.7 |
| [QY5Me2MoS2]+ | −21.5 | −24.1 |
| (−10.1) | (−0.4) | |
To check the dependency of the computed protonation energies on the selected level of theory, we calculated protonation energies for the [PY5Me2MoO]+ species with six different DFT methods (BP86, BLYP, B3LYP*, TPSS, TPSSh, and M06L), and four basis sets (def2-SVP, def2-TZVP, def2-TZVPD, and def2-QZVP), while also turning dispersive corrections on and off (see Table S2 in the ESI†). The results show that the dispersion correction has little influence on the protonation energetics. However, more significant differences are seen for the basis sets; in particular, the protonation energies increase with the size of the basis set. Moreover, the density functional significantly influences the protonation energies; in particular, the magnitude of protonation energy decreases as the amount of Hartree–Fock exchange increases. However, difference in the energy for the protonation reaction between vacuum and solvent is remarkably stable at the various theory levels. The [PY5Me2MoO]+ species is more favourably protonated in water by 13.0 (TPSSH/def2-TZVP) to 14.4 kcal mol−1 (BLYP/def2-TZVP; see Table S2 in the ESI†). In the present work, the main focus is not on the absolute value of protonation energies but on the comparison between differences in protonation energies in a vacuum or in a solvent, as explained in the Introduction. Therefore, only energies obtained at the BP86-D3(BJ)/def2-TZVP will be discussed in the main text.
The pyridine ring can bind to the metal by σ-donation of the nitrogen lone pair and also by interaction of the ring antibonding orbitals through π-backbonding.41 Different substituents on the azo-rings may influence such interplay42 and consequently modify the electron density of the α-positioned oxygen or sulfur atom. For this reason, the atomic charges for both oxo and sulfide complexes were computed using the natural population analysis approach (see Tables S3 and S4 in the ESI†) and analysed by comparing the values of the corresponding atoms of the monocationic species, as well as of the protonated products. Deviations of atomic charges turned out to be small (maximum deviation 0.03 e both for the oxo and the sulfide species). Such picture is analogous to what was found in the above-mentioned study on [FeFe]-hydrogenase biomimetic models11 whose atomic charges varied only slightly as a function of the presence of phosphine ligands of different size and nature (PCH3, PPh3).
Furthermore, the solvation energies of each species were computed in order to verify whether the protonation energies are affected by different affinities of the complexes for the water medium. The resulting values, reported in Tables 4 and 5, do not show very large differences in solvation energies for the monocationic catalysts (ΔΔEsolv = 12.2 and 14.1 kcal mol−1 for the oxo and sulfide species, respectively where ΔΔEsolv is the difference in solvation energy for compounds with difference bulkiness). However, the differences increase significantly when solvation energies of dications are compared: in this case, the catalysts featuring the PY5Me2 ligand exhibit higher affinity for the water medium compared to those coordinated by the bulky QY5Me2 ligand by 23.6 kcal mol−1 for Mo![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and by 23.7 kcal mol−1 for Mo–S2. In addition to calculations carried out with the C-PCM solvation model, the SMD solvation model developed by Cramer and Truhlar was also tested on the set of molybdenum-oxo species (see Table S5 in the ESI†). Interestingly, a noticeable analogy is found when the C-PCM results above are compared to the SMD ones: with the latter solvation model, the monocationic species show small differences in solvation energies (ΔΔEsolv = 0.6 kcal mol−1 for the bulkier species compared to the smaller one at the BP86-D3(BJ)/def2-TZVP:SMD level on BP86-D3(BJ)/def2-TZVP optimized geometries) whereas a significantly larger deviation in solvation energies is again observed for the [RY5Me2MoOH]+2 species (ΔΔEsolv = 12.1 kcal mol−1 for complex featuring the bulky QY5Me2 compared to the one bound to PY5Me2).
O and by 23.7 kcal mol−1 for Mo–S2. In addition to calculations carried out with the C-PCM solvation model, the SMD solvation model developed by Cramer and Truhlar was also tested on the set of molybdenum-oxo species (see Table S5 in the ESI†). Interestingly, a noticeable analogy is found when the C-PCM results above are compared to the SMD ones: with the latter solvation model, the monocationic species show small differences in solvation energies (ΔΔEsolv = 0.6 kcal mol−1 for the bulkier species compared to the smaller one at the BP86-D3(BJ)/def2-TZVP:SMD level on BP86-D3(BJ)/def2-TZVP optimized geometries) whereas a significantly larger deviation in solvation energies is again observed for the [RY5Me2MoOH]+2 species (ΔΔEsolv = 12.1 kcal mol−1 for complex featuring the bulky QY5Me2 compared to the one bound to PY5Me2).
| [PY5Me2MoO]+ | [PY5Me2MoOH]+2 | [QY5Me2MoO]+ | [QY5Me2MoOH]+2 | |
|---|---|---|---|---|
| ΔEsolv | −8.9 | −94.5 | 3.3 | −70.9 |
| Total non-electrostatic | 25.8 | 26.0 | 37.0 | 37.9 |
| Cavitation | 60.2 | 60.7 | 85.2 | 86.1 |
| Dispersion | −36.8 | −37.0 | −51.5 | −51.5 |
| Repulsion | 2.3 | 2.3 | 3.2 | 3.2 |
| Total electrostatic | −34.6 | −120.5 | −33.7 | −108.8 |
| (Unpolarized solute)-solvent | −33.9 | −119.6 | −32.2 | −106.0 |
| (Polarized solute)-solvent | −35.8 | −121.8 | −35.7 | −113.0 |
| Solute polarization | 1.1 | 1.3 | 2.0 | 4.2 |
| [PY5Me2MoS2]+ | [PY5Me2MoS2 H]+2 | [QY5Me2MoS2]+ | [QY5Me2MoS2 H]+2 | |
|---|---|---|---|---|
| ΔEsolv | −10.9 | −94.8 | 3.2 | −71.1 |
| Total non-electrostatic | 24.8 | 25.0 | 37.2 | 37.2 |
| Cavitation | 61.4 | 61.8 | 86.9 | 87.0 |
| Dispersion | −39.1 | −39.2 | −53.1 | −53.2 |
| Repulsion | 2.5 | 2.5 | 3.4 | 3.4 |
| Total electrostatic | −35.7 | −119.8 | −34.0 | −108.4 |
| (Unpolarized solute)–solvent | −33.9 | −118.7 | −32.0 | −105.5 |
| (Polarized solute)–solvent | −38.8 | −121.2 | −37.2 | −112.7 |
| Solute polarization | 3.1 | 1.4 | 3.2 | 4.3 |
To get a deeper insight into the solvation process, solvation energies calculated by C-PCM were separated into their electrostatic and non-electrostatic contributions, as shown in Tables 4 and 5. The non-electrostatic contributions account for the cost of creating a cavity in the solvent with the size of the solute, which includes change of the solvent–solvent interaction energy and the solvent entropy, and for the solute–solvent van der Waals dispersion and exchange repulsion interactions. The electrostatic contributions are divided into the polarization of the medium due to the electric charge distribution of the solute as well as the polarization of the solute by the solvent. The analysis of the contributions to the solvation energy of the various species shows that the total non-electrostatic contributions do not differ significantly between the protonated and non-protonated species (ΔEnon-el = 0.2 kcal mol−1 for both PY5Me2MoO and PY5Me2MoS2; 0.9 and 0.0 kcal mol−1 for QY5Me2MoO and QY5Me2MoS2). In contrast, the electrostatic contributions vary significantly. In particular, the solvation energies of protonated species are greatly affected by the bulkiness of the substituents, resulting in less negative solvation energies for systems that carry a bulkier ligand (ΔEel = 85.9 and 84.1 kcal mol−1 for PY5Me2MoO and PY5Me2MoS2, respectively; ΔEel = 75.1 and 74.4 kcal mol−1 for QY5Me2MoO and QY5Me2MoS2).
Further investigation of the solvation of the molybdenum catalysts was performed by considering explicit solvent modelling. In this context, MD simulations were run in order to evaluate possible differences in the distribution of the solvent molecules around the complexes with ligands of different sizes. The radial distribution function, g(r), was employed to analyse the density of solvent molecules around the Mo-bound oxygen atom of the monocationic ([PY5Me2MoO]+ and [QY5Me2MoO]+) and dicationic species ([PY5Me2MoOH]+2 and [QY5Me2MoOH]+2). The exposure of the Mo-bound oxygen atom to the solvent for all the considered species is shown in Fig. 3 and Fig. S1 in the ESI.† As highlighted by the overlapping graphs, no substantial differences are observed between the radial distribution functions, neither by comparing mono- and dicationic species nor by comparing species of different sizes.
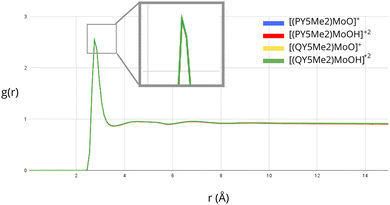 | ||
| Fig. 3 Radial distribution function of the water oxygen atoms around the oxo α-ligand of Mo derived from MD simulations. The four curves corresponding to each solvated compound essentially coincide. | ||
Based on all these results, we can suggest that the difference in protonation energy between the [PY5Me2MoO]+ and [QY5Me2MoO]+ complexes is caused by the difference in solvation energy of the complexes, in particular by the different electrostatic contribution to the solvation energy of the protonated complexes. These effects are evident considering the proton-transfer reaction from the species with less bulky substituents to the species featuring bulkier substituents (see Fig. 4). While this reaction is energetically favored in a vacuum (−11.7 and −10.0 kcal mol−1 for complexes with oxo and disulfide ligand, respectively), highlighting the greater basicity of the more bulky species, in aqueous solution the reaction gives an energy difference of only −0.3 and −0.5 kcal mol−1 for the complexes with oxo and disulfide ligand, respectively, making the basicity of the two complexes comparable. The electrostatic contribution to the solvation energies of the various species plays the main role for this difference, which disfavors the protonated species of the compounds with bulkier substituents by about 11 kcal mol−1.
4 Conclusions
The design of new metal–organic complexes for catalytic purposes requires careful consideration of electronic and steric effects in order to tune the activity of such species. In a previous theoretical study of organometallic diiron catalysts for proton reduction,11 we showed that the protonation of Fe ions in complexes bearing bulky and strongly electron-donating PPh3 ligands is highly favoured compared to the analogous reaction involving the PMe3-containing species when studied in a vacuum. However, the trend is inverted when the models instead are studied in a continuum solvent. In the present contribution, we show that such an effect of ligand bulkiness is general: in fact, we found it to be significant even for mononuclear Mo catalysts including N-based ligands in which the catalytically relevant protonation reactions do not occur directly at the metal, but in the α-position on an oxo or disulfide ligand.As far as one can say on a comparative basis, the effects of the bulkiness of ligands on protonation energetics do not seem to be impacted by the difference in nuclearity between the complexes investigated in the present study and the diiron coordination compounds considered previously.11 Therefore, we expect that our results can have relevance for the design of low-nuclearity, sub-nanometric cluster catalysts encompassing ligands whose bulkiness can be object of modulation. Actually, establishing a detailed parallel between the results here reported and those we presented previously is informative at other levels as well. In fact, a comparison between protonation of the complexes considered in the present study and terminal protonation of dinuclear iron complexes in ref. 11 highlights a peculiar fact, namely that complexes with ligands featuring markedly different electronic properties (N-heterocycles/oxo vs. phosphines) and different protonation regiochemistry have, in vacuo, a similar variation in the protonation energies as a function of the increase in the bulkiness of ligands (the bulkier systems show a proton affinity larger than the small ones by about 12 kcal mol−1 in both cases). Despite the fact that in the previous work, the solvent had a dielectric constant smaller than that considered in the present work (acetonitrile vs water), for the iron complexes we even observed an inversion of the protonation energies going from vacuum to solvent11 as also noticed above. However, in the case of the Mo complexes, no inversion of protonation energy is observed in water. Considering that the increase in the bulkiness of ligands on the Fe center is comparable with the increase in the bulkiness in the Mo complex, it seems reasonable to suggest that the main difference between the two series of complexes lies in the regiochemistry of protonation (on the metal in one case, in alpha to the metal in the other). This suggestion will be scrutinized in future investigations.
In the context of green chemistry, this study shows that cost-effective computations with density functional theory can help modelling a key aspect in molecular catalyst design, i.e. the effect of ligands bulkiness on the basicity of metal–organic catalysts. Considering that running a reaction in a solvent is often essential to facilitate mass and heat transfer and that the most sustainable reaction medium is water, the present work evidenced that – for catalysts design purposes – it is important to take into account the electrostatic properties of both reactants and products within the medium in which protonation reactions are going to be conducted.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computations were performed on computer resources provided by CINECA as part of the agreement with the University of Milano-Bicocca.Notes and references
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef PubMed.
- B. Johnston, M. C. Mayo and A. Khare, Technovation, 2005, 25, 569–585 CrossRef.
- F. Dawood, M. Anda and G. Shafiullah, Int. J. Hydrogen Energy, 2020, 45, 3847–3869 CrossRef.
- H. I. Karunadasa, C. J. Chang and J. R. Long, Nature, 2010, 464, 1329–1333 CrossRef CAS PubMed.
- H. I. Karunadasa, E. Montalvo, Y. Sun, M. Majda, J. R. Long and C. J. Chang, Science, 2012, 335, 698–702 CrossRef CAS.
- G. M. Bancroft, L. Dignard-Bailey and R. J. Puddephatt, Inorg. Chem., 1986, 25, 3675–3680 CrossRef CAS.
- C. Greco, P. Fantucci, L. De Gioia, R. Suarez-Bertoa, M. Bruschi, J. Talarmin and P. Schollhammer, Dalton Trans., 2010, 39, 7320–7329 RSC.
- J. M. Camara and T. B. Rauchfuss, Nat. Chem., 2012, 4, 26–30 CrossRef CAS PubMed.
- S. Ghosh, S. Rana, N. Hollingsworth, M. G. Richmond, S. E. Kabir and G. Hogarth, Inorganics, 2018, 6, 122 CrossRef CAS.
- T. Shimamura, Y. Maeno, K. Kubo, S. Kume, C. Greco and T. Mizuta, Dalton Trans., 2019, 48, 16595–16603 RSC.
- A. Rovaletti and C. Greco, J. Phys. Org. Chem., 2018, 31, e3748 CrossRef.
- J. A. Birrell, V. Pelmenschikov, N. Mishra, H. Wang, Y. Yoda, K. Tamasaku, T. B. Rauchfuss, S. P. Cramer, W. Lubitz and S. DeBeer, J. Am. Chem. Soc., 2019, 142, 222–232 CrossRef PubMed.
- M. Sensi, C. Baffert, C. Greco, G. Caserta, C. Gauquelin, L. Saujet, M. Fontecave, S. Roy, V. Artero and P. Soucaille, et al. , J. Am. Chem. Soc., 2016, 138, 13612–13618 CrossRef CAS PubMed.
- J. Jašk, A. Fortunelli and Š. Vajda, Phys. Chem. Chem. Phys., 2022, 24, 12083–12115 RSC.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. Rovaletti, M. Bruschi, G. Moro, U. Cosentino and C. Greco, Front. Chem., 2019, 6, 630 CrossRef PubMed.
- A. Rovaletti, M. Bruschi, G. Moro, U. Cosentino, C. Greco and U. Ryde, Inorganics, 2019, 7, 135 CrossRef CAS.
- A. Rovaletti, C. Greco and U. Ryde, J. Mol. Model., 2021, 27, 68 CrossRef CAS PubMed.
- A. Rovaletti, G. Moro, U. Cosentino, U. Ryde and C. Greco, ChemPhysChem, 2022, 23, e202200053 CrossRef CAS PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef.
- J. M. Seminario, Int. J. Quantum Chem., 1996, 60, 1271–1277 CrossRef.
- K. Nilsson, D. Lecerof, E. Sigfridsson and U. Ryde, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2003, 59, 274–289 CrossRef PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly and P. A. Kollman, J. Am. Chem. Soc., 1993, 115, 9620–9631 CrossRef.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef.
- D. A. Case, R. M. Betz, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao and P. A. Kollman, AMBER 2016, University of California, San Francisco, 2016 Search PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef.
- E. J. Sundstrom, X. Yang, V. S. Thoi, H. I. Karunadasa, C. J. Chang, J. R. Long and M. Head-Gordon, J. Am. Chem. Soc., 2012, 134, 5233–5242 CrossRef PubMed.
- S. Pal, Pyridine: A useful ligand in transition metal complexes, IntechOpen, London, UK, 2018 Search PubMed.
- R. S. Hosmane and J. F. Liebman, Struct. Chem., 2009, 20, 693–697 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03996f |
| This journal is © the Owner Societies 2022 |