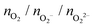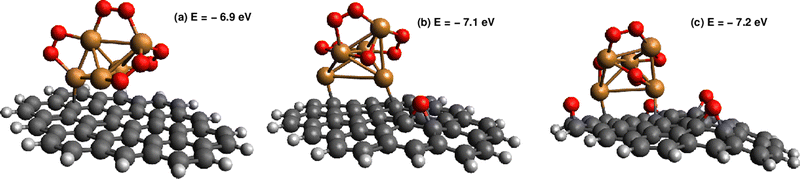Open Access Article
Open Access ArticleAggregation and support effects in the oxidation of fluxional atomic metal clusters. The paradigmatic Cu5 case†
Jaime
Garrido-Aldea
and
María Pilar
de Lara-Castells
 *
*
Institute of Fundamental Physics (AbinitSim Unit), Madrid, Spain. E-mail: Pilar.deLara.Castells@csic.es
First published on 13th September 2022
Abstract
The recent development of new synthesis techniques has allowed the production of monodisperse metal clusters composed of a few atoms. Follow-up experimental spectroscopic characterization has indicated the stability of these atomic metal clusters (AMCs). Despite the common assumption that the occurrence of an irreversible oxidation becomes more likely as the cluster size decreases, its quenching and reversible nature has been experimentally identified in the particular case of Cu5 clusters, making them paradigmatic. This work aims to address the influence of aggregation and the effects of a chemically inert carbon-based support on the oxidation of AMCs, considering the case of Cu5 as a model system. For this purpose, we present an extended first-principles study of the oxidation of Cu5–Cu5 and circumpyrene-supported Cu5, comparing it with that of unsupported Cu5, and combine dispersion-corrected density-functionals, first principles thermochemistry, and ab initio molecular dynamics (AIMD) simulations within an adiabatic approach. Our results indicate that a molecular chemisorption/desorption model is sensible upon consideration of aggregation and support effects in such a way that the predicted (p–T)-phase diagrams do not differ significantly from those obtained for unsupported Cu5. We also provide insights into the decoupling of the Cu5–Cu5 dimer into Cu5 sub-units through activated fluxional rotational motion, upon heating, as well as the adsorption of multiple O2 molecules at high oxygen gas pressures. Furthermore, numerical evidence shows the likelihood of a support-mediated mechanism leading to the dissociation of chemisorbed peroxo O22− species, delivering states with very similar energies to those characterized by molecular chemisorption. A Boltzmann-weighted average of the free energies of formation is computed as well, coming up with a diagram of the dominant copper oxidation states as a function of temperature and oxygen gas pressure.
1 Introduction
This work is motivated by the impact that aggregation and the effects of a chemically inert support might have on the oxidation of atomic metal clusters (AMCs) composed of a few atoms. The recent development of new synthesis techniques has allowed the production of monodisperse AMCs such as, for instance, Cu5 clusters.1 Previous works have shown their catalytic applications in, e.g., CO oxidation,2,3 CO2 reduction,4 and methanation,5 as well as their ability to modify the properties of a relevant semiconductor (TiO2), making it a visible photo-active material6 (see, e.g., ref. 7 and 8 for recent reviews). One major concern has been on the stability of Cu5 clusters in an O2-rich atmosphere as it is generally assumed that nanoparticles suffer from an increasing susceptibility to oxidation with decreasing size. In contrast to that assumption, recent works have indicated that Cu5 clusters experience reversible oxidation,7,9–13 making them paradigmatic.The possibility of reversible oxidation of Cu5 clusters has been pointed out through ex situ experimental measurements at temperatures below 423 K14 as well as theoretical studies considering the chemisorption of either single9,11,14 or multiple12 oxygen molecules into Cu5 clusters in the two structures identified by first-principles theory: planar trapezoidal (2D) and trigonal bipyramidal (3D). Thus, for a planar structure, a multireference ab initio treatment11 has indicated that a high energy barrier prevents the Cu5–O2 collisional pair to access the precursor charge-transfer state for irreversible oxidation of Cu5. In contrast, for a bipyramidal structure, the potential energy landscape has revealed a reversible transition from physisorption to chemisorption states, with the energetically costly O–O splitting remaining as the rate determining step for irreversible oxidation to occur. The most recent experimental evidence has shown a reversible oxidation of surface-supported Cu5 clusters at thermodynamic equilibrium using in situ X-ray absorption spectroscopy and X-ray photoelectron spectroscopy.13 Highly oriented pyrolytic graphite (HOPG) was considered as a chemically inert support, at different oxygen gas pressures, and in the temperature range going from room-temperature (RT) up to 773 K.13
In general, the interaction of molecular oxygen with metal and metal oxides such as TiO2 rutile (110) has been a long-standing problem over the last few decades as extensively reviewed by Yates's15–17 and Henderson's18,19 groups from an experimental perspective. As shown in the earliest first-principles studies,20–24 molecular oxygen can be adsorbed onto TiO2 rutile (110) as either a superoxo O2− radical or a peroxo O22− species, both in molecular and dissociative forms, existing in several (photo-)desorption channels as well. The existence of multiple stable charged species and reaction pathways becomes even more challenging in the case of AMCs due to their fluxional nature. In fact, when the size of a metal cluster is reduced to a very small number of atoms, the d-band of the metal splits into a network of molecular orbitals with the interconnections between different atoms having the length of a chemical bond (1–2 Å).7 The ‘floppy’ character of the resulting ACM geometries invokes the concept of structural fluxionality. This concept has been recently advocated to explain the catalytic activities of AMCs (see, e.g., ref. 4, 7, 25 and 26). The occurrence of fluxional dynamics has also been suggested from recent spectroscopic observations.27 This characteristic might lead to the existence of many local minima, having very similar energies, when AMCs interact with multiple O2 molecules. Such an energy landscape is implicitly associated with fluxional dynamics and wide amplitude AMC–AMC and AMC–O2 motions.
Despite the attention that AMCs have recently attracted, little is known about the effects that their aggregation might have in the most fundamental process (i.e., their oxidation). Interestingly, previous work on TiO2-supported atomic copper clusters has shown that oxidation might quench their aggregation.28 Besides complementing previous research on the interaction of O2 molecules with the Cu5 monomer,7,9–13 we have selected the unsupported Cu5–Cu5 dimer as a model system to explore the aggregation effects in the oxidation of AMCs. Next, the interaction of the circumpyrene-supported Cu5 monomer with multiple O2 molecules has been analyzed as well with the main purpose of providing insight into the role of a chemically inert support in the oxidation of a model AMC. As reported in ref. 6, graphene has very little impact on the electronic structure of supported Cu5 due to the dispersion nature of the Cu5–graphene interaction. This way, the net charge donation from the copper cluster to the support was found to be insignificant (less than 0.02 |e−|). In this work, the consideration of circumpyrene as a molecular model of a carbon-based surface has aided in the analysis of its influence on the interaction of supported Cu5 with the environmental gas-phase O2 molecules.
This article is structured as follows. In Section 2, we provide a detailed description of the computational methods. The results are presented in Section 3 as follows: first, we compare the stability of (Cu5)–(O2)n and (Cu5–Cu5)–(O2)2n (n < 9) clusters as a function of temperature and oxygen gas pressure. Second, we analyze the stability of circumpyrene-supported Cu5–(O2)n (n < 9) complexes, comparing it with that of unsupported Cu5−n (n < 9) complexes. Finally, our findings are summarized and conclusions are presented in Section 4.
2 Methods
2.1 Electronic structure calculations and ab initio molecular dynamics simulations
Structural optimizations and frequency calculations have been carried out using the atom-centered def2-TZVPP41 basis set for copper and oxygen atoms, while the def2-SVP basis set has been used for carbon and hydrogen atoms of circumpyrene. Binding energies Ebind of n and 2n O2 molecules binding into the bare Cu5 monomer and the Cu5–Cu5 dimer are defined as
| Ebind = ECu5–(O2)n − ECu5 − n·EO2 | (1) |
| Ebind = E(Cu5–Cu5)–(O2)2n − ECu5–Cu5 − 2n·EO2, | (2) |
| Ebind = E(Cu5/support)–(O2)n − ECu5/support − n·EO2, | (3) |
These binding energies have been calculated using the def2-QZVPP basis set,41 including the Boys-Bernardi counterpoise correction.42 The reduction states of the adsorbed O2 molecules (neutral O2, O2−, and O22−) as well as each copper metal atom [Cu(0), Cu(I), and Cu(II)] have been assigned from a correlated analysis of Mulliken charges,43 atomic spin populations of the molecular orbitals using the Hirshfeld method,44,45 and the values of the optimized O–O distances, comparing the latter with those corresponding to gas-phase O2, O2−, and O22− species. The adequacy of our analysis has been assessed for the case of the Cu5–(O2)3 complex by comparing it with that reported in ref. 12 through an analysis of the Mulliken charges and atomic spin populations of the natural orbitals obtained at a high-level of ab initio theory. All dispersion-corrected DFT-based calculations have been performed using the ORCA suite of programs46–48 (version 5.0.1).
For assessment purposes, density fitting single-state multi-configurational self-consistent-field (DF-CASSCF) calculations have also been carried out, as implemented in the most updated version of the MOLPRO code.49 Since the CASSCF wave-function is built on a basis of configuration state functions and separate calculations have been carried out for different spin states, no spin contamination has been identified. The MOLPRO implementation of the internally contracted RS2C method50 has been applied on top of DF-CASSCF calculations to cover dynamical correlation effects. We have used the polarized correlation-consistent triple-ζ basis set of Dunning and collaborators51 (cc-pVTZ) for oxygen atoms and the cc-pVTZ-PP basis set for copper atoms,52 including a small (10-valence-electron) relativistic pseudopotential. For density fitting, the associated MP2FIT and JKFIT bases have been used in DF-CASSCF and R2SC calculations, respectively. For the sake of comparison, the domain-based pair natural orbital coupled-cluster approach DLPNO-CCSD(T)53 has been applied as well, as implemented in the ORCA code (version 4.0.1.2).
2.2 Equilibrium thermodynamics: thermodynamic potential
At a given temperature (T) and partial oxygen gas pressure (p), considering that we are dealing with an open system with an arbitrary number of gas-phase O2 molecules, the relative stability of Cu5–(O2)n (or (Cu5–Cu5)–(O2)2n) complexes is determined by calculating the thermodynamic potential ω57–60 (referred to as the (Gibbs) free energy of formation in, e.g., ref. 58 and 59).ω(T,μO2,n) = ΔEF,corr(T) − T·SCu5–(O2)n(T) + T·SCu5(T) − n·![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O2(p,T) O2(p,T) | (4) |
It should be stressed that the Cu5 clusters are thus treated as immobilized on the support, therefore not contributing to the enthalpy and are coupled to a heat bath of temperature T and an infinite reservoir of O2 gas-phase molecules at pressure p. Under these idealized conditions, the ω potential becomes minimal at thermodynamic equilibrium. ΔEF,corr, the first term on the right-hand side of eqn (4), corresponds to the formation energy of the Cu5–(O2)n complex and is defined as
| ΔEF,corr(T) = ECu5–(O2)n − ECu5 − nEO2 + Ecorr(T,n), | (5) |
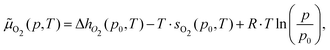 | (6) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O2. This way, the T, p-independent contribution to the O2 chemical potential, EO2, is shifted to the ΔEF,corr(T) term (eqn (5)). The change of enthalpy is given by ΔhO2 = h(p0,T) − h(p0,T = 0 K). For maximum accuracy, values for hO2 and sO2 from the NIST database have been used.61,62 Next, the (p,T)-phase diagram has been created by determining the number n of adsorbed O2 molecules which minimizes ω at a specified temperature and a given oxygen gas pressure. The thermodynamic potential ω can also be expressed as the difference between the Helmholtz free energies of the Cu5–(O2)n complex and the Cu5 cluster [FCu5–(O2)n–FCu5] minus n × μO2 as reported in ref. 58 and 59.
O2. This way, the T, p-independent contribution to the O2 chemical potential, EO2, is shifted to the ΔEF,corr(T) term (eqn (5)). The change of enthalpy is given by ΔhO2 = h(p0,T) − h(p0,T = 0 K). For maximum accuracy, values for hO2 and sO2 from the NIST database have been used.61,62 Next, the (p,T)-phase diagram has been created by determining the number n of adsorbed O2 molecules which minimizes ω at a specified temperature and a given oxygen gas pressure. The thermodynamic potential ω can also be expressed as the difference between the Helmholtz free energies of the Cu5–(O2)n complex and the Cu5 cluster [FCu5–(O2)n–FCu5] minus n × μO2 as reported in ref. 58 and 59.
We emphasize that our methodological protocol to analyze the stability of supported copper clusters holding multiple adsorbed O2 molecules can be extended to other relevant processes such as hydrogen storage onto AMCs as a function of temperature and hydrogen gas pressure.63 For this purpose, we have provided a general code, delivering phase diagrams using the thermochemistry output of the ORCA package (see the ESI†).
3 Results and discussion
3.1 Oxidation of unsupported Cu5 and Cu5–Cu5
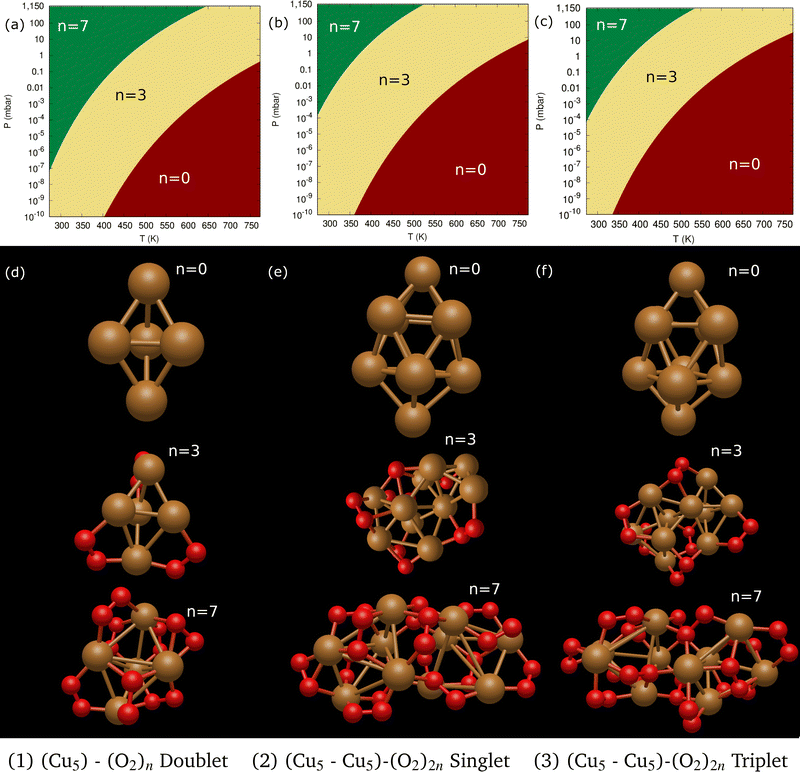
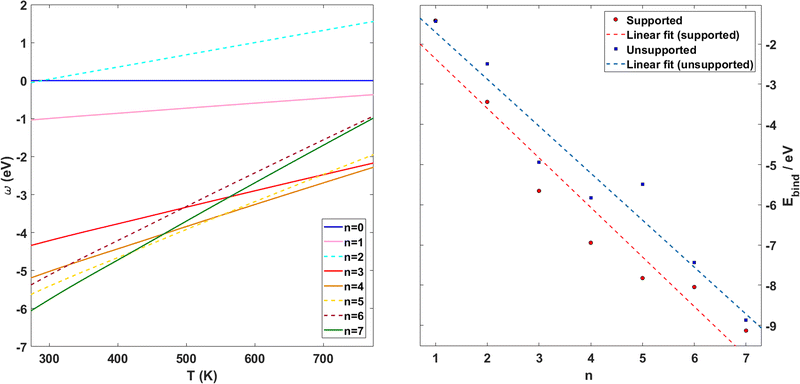
Following previous work on individual Cu5 clusters,12,13 we start by assuming that the Cu5 monomer and the Cu5–Cu5 dimer can form complexes with multiple gas-phase O2 molecules and calculate the number of O2 molecules that can be adsorbed depending on the oxygen gas pressure and temperature. As theoretically shown in ref. 11 and 12, we also consider that the energy barriers from physisorption to chemisorption states are very low (ca. 0.1 in ref. 11 and 12), while those associated with O2 bond breaking are very high (of a few eV for the unsupported Cu5–O2 and Cu5–(O2)3 complexes11,12). This assumption holds true for the reaction pathway to chemisorption states exhibiting the lowest activation energies for O2 adsoprtion into both planar and bipyramidal Cu5 structures.11Table 1 and Fig. 1 (upper left-hand panel) show the values of the binding energies as a function of the number of the adsorbed O2 molecules onto the Cu5–Cu5 dimer, considering singlet and triplet spin states. For the sake of comparison, they are also shown for the Cu5 monomer in the lowest-energy doublet spin state (see also ref. 13). The bottom panels of Fig. 1 present the free energies of formation at ambient pressure (1 atm), while the most likely adsorption states as a function of oxygen gas pressure and temperature appear in the phase diagrams (upper panels of Fig. 2). The optimized structures for bare Cu5 and Cu5–Cu5 along with the most stable Cu5–(O2)n and (Cu5–Cu5)–(O2)n complexes are shown in the bottom panels of Fig. 2 instead.
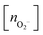 , and peroxo
, and peroxo 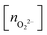 species is also indicated. The ‘*’ quotation indicates the dissociation of one peroxo species in two O2− ions
species is also indicated. The ‘*’ quotation indicates the dissociation of one peroxo species in two O2− ions
| Cu5–(O2)n (doublet) | (Cu5–Cu5)–(O2)2n (singlet) | (Cu5–Cu5)–(O2)2n (triplet) | ||||
|---|---|---|---|---|---|---|
| E bind/eV | E bind/eV | E bind/eV | ||||
| n = 1 | 0/1/0 | −1.4 | 0/2/0 | −0.4 | 2/0/0 | −1.2 |
| n = 2 | 0/2/0 | −2.5 | 1/2/1 | −4.1 | 1/2/1 | −5.1 |
| n = 3 | 0/3/0 | −4.9 | 0/2/4 | −8.1 | 0/2/4 | −9.1 |
| n = 4 | 0/4/0 | −5.8 | 0/4/4 | −9.2 | 0/4/4 | −10.3 |
| n = 5 | 2/3/0 | −5.5 | 2/4/3 | −9.6 | 4/3/3 | −10.7 |
| n = 6 | 1/5/0 | −7.4 | 2/8/2 | −11.0 | 1/7/4* | −13.8 |
| n = 7 | 0/5/2 | −8.9 | 0/10/4 | −15.0 | 0/9/5 | −16.2 |
| n = 8 | 1/5/2 | −9.0 | 2/8/6 | −12.7 | — | — |
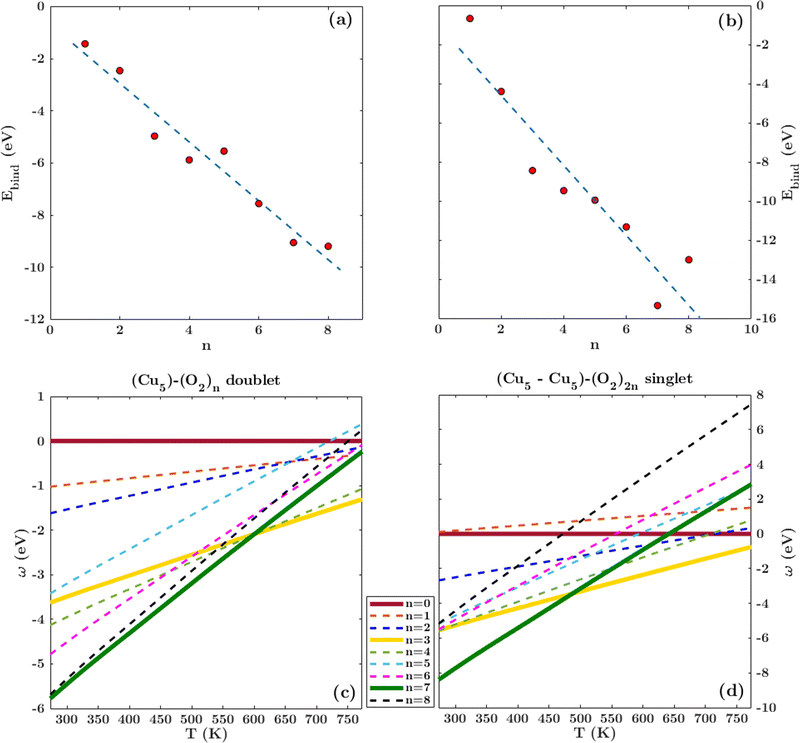 | ||
| Fig. 1 Free energies of formation of Cu5–(O2)n and (Cu5–Cu5)–(O2)n complexes. Upper panels: electronic binding energies of the clusters as a function of the number of O2 molecules attached to Cu5 (panel a) and (Cu5–Cu5) (panel b) complexes in doublet and singlet spin states, respectively. Bottom panels: free energies of formation (w potential) comparison at 1 atm for Cu5–(O2)n (panel c) and (Cu5–Cu5)–(O2)2n (panel d) complexes. The color coding in solid lines follows dot colors in the predicted phase diagrams (see Fig. 2). The energy values corresponding to less stable complexes are plotted with dashed lines. The predicted phases can be retrieved from the convex hull of the lowest-energy curves. | ||
Let us first compare how differently the Cu5–Cu5 dimer and the Cu5 monomer interact with the surrounding O2 molecules. As can be observed in Table 1, binding energies per Cu5 cluster are smaller for the Cu5–Cu5 dimer. However, the most stable complexes shown up in the phase diagram (see Fig. 2) have 3 and 7 adsorbed O2 molecules per Cu5 cluster for either the monomer or the dimer.
The optimized structures for both Cu5–(O2)n and (Cu5–Cu5)–(O2)2n complexes show enhanced stability when the O2 molecules attach to bridge Cu5 positions. Depending on their number, the O2 molecules are absorbed as neutral (O2) or charged superoxo (O2−), or peroxo (O22−) species (see Table 1). The copper clusters thus donate electron charge to the O2 molecules but the entire system remains neutral. Upon stretching of the Cu–Cu distances, Cu5 and Cu5–Cu5 adapt their shape to accommodate the charged O2 species, featuring larger O–O bonds, at its bridge sites.
A clear difference between the Cu5 and Cu5–Cu5 cases is on the major contribution of adsorbed peroxo O22− species over superoxo O2− radicals for the latter. This outcome can be simply explained by considering that the O2 molecule adsorbed in between the two Cu5 clusters tends to elongate its O–O distance to benefit from the attractive interaction with both copper clusters. This enlargement might cause its dissociation even at 0 K, as shown in Table 1 for the (Cu5–Cu5)–(O2)12 complex in the singlet spin state. For the triplet state, the binding energies are slightly larger but hardly compensate for the singlet-triplet energy splitting on the bare Cu5–Cu5 dimer (see below).
For assessment purposes, DF-CASSCF and R2SC calculations have been carried out for the structures corresponding to both the global and the local minimum identified at the DFT-D4 level. Using CAS active spaces of increasing size [from (4,4), with four electrons in four orbitals, to (10,10), with ten electrons in ten orbitals], it is found that the lowest-energy structure is that predicted via the DFT-D4 ansatz. Its re-optimization using the DF-CASSCF method modifies the Cu–Cu bond length by less than 0.1 Å on average.
The interaction energy between the two Cu5 monomers is very large (−4.9, −5.2, and −5.4 eV at LCPNO-CCSD(T), R2SC, and DFT-D4 levels, respectively). This attractive interaction is mainly determined by the dynamical correlation contribution (by about 70%), as covered by the R2SC approach. The large values of Mulliken charges on each Cu atom (larger than 0.1 |e−|) suggest that strong electrostatic contributions favor the stabilization of the Cu5–Cu5 dimer. With values above 0.1 |e−|, the analysis of Mulliken charges on copper atoms reveals that the interaction is favored by electrostatic contributions. A detailed investigation into the reorganization of the Cu5 electronic charge upon dimerization is a topic of future prospect.
At DFT-D4 and R2SC levels, the triplet state is 0.8 and 1.0 eV above the singlet spin state, respectively. The optimized structures are very similar (see Fig. 2), with the average Cu–Cu bond length being just 0.02 Å larger for the triplet spin state. This similarity can be understood by considering that the dynamical correlation contribution to the attractive Cu5–Cu5 interaction differs very little (by only 0.2 eV) in singlet and triplet spin states. The energy difference in the interaction energy arises from non-dynamical correlation effects and can be explained as follows: the single-electron occupied s-type orbitals of each Cu5 cluster lead to the formation of bonding and anti-bonding orbitals when the two Cu5 clusters come together. Two electrons with opposite spins occupy the resulting bonding orbital in the singlet spin state of the Cu5–Cu5 dimer. Contrarily, two electrons with the same spin cannot occupy the same orbital. This way, both bonding and anti-bonding orbitals become single occupied in the triplet state of the Cu5–Cu5 dimer, destabilizing the system.
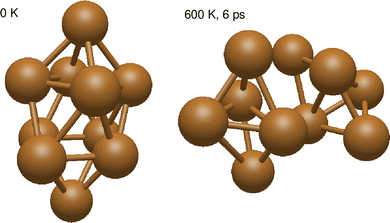
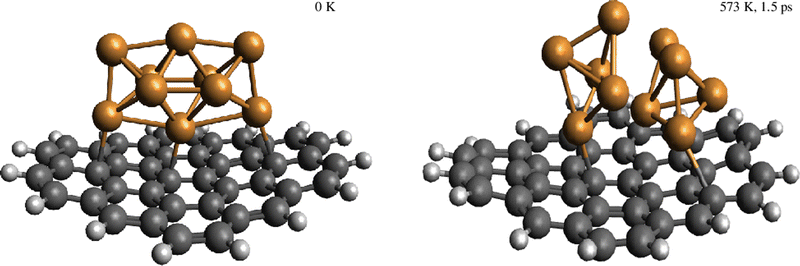
Despite the strongly attractive nature of the Cu5–Cu5 interaction, our results indicate that a quenching of the Cu5–Cu5 aggregation might occur in an O2-rich environment. As mentioned in the Introduction section, previous work on TiO2-supported atomic copper clusters has shown that ACMs’ oxidation is preferred over their sintering, with the AMC–surface interaction playing a key role.28 These outcomes suggest strategies to individualize Cu5 clusters. This way, a clear spatial separation between the Cu5 monomers happen when the energy gained by the adsorption of O2 molecules is larger than the Cu5–Cu5 interaction energy itself (e.g., for n = 7 in Fig. 2). The decoupling of the two Cu5 monomers through fluxional rotational motion is favored by an increase in the temperature as well (see Fig. 3).
3.2 Oxidation of circumpyrene-supported Cu5 clusters
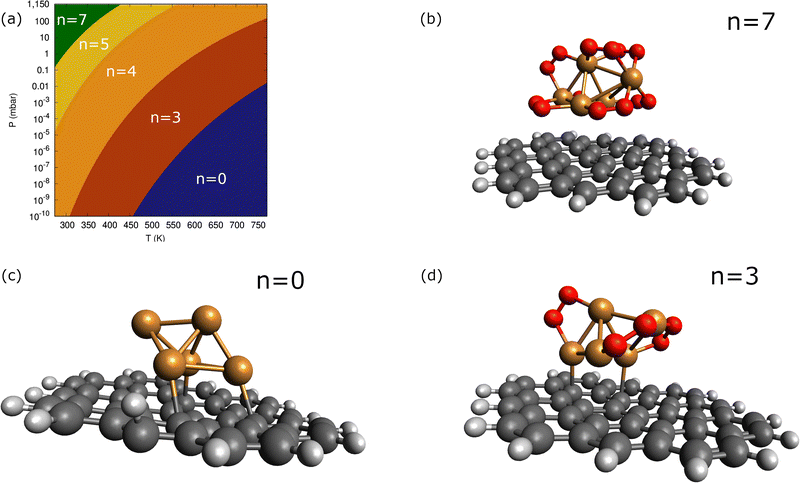
In order to consider the effect of a carbon-based support, the PAH circumpyrene has been used (see Fig. 4). The dispersion D4 correction accounts for 82% of the attractive Cu5-circumpyrene interaction at the optimized geometry. For the sake of comparison, a dispersion-dominated nature of the ACM–PAH interaction has been also found for the Au12 cluster but is less pronounced (45% vs. 82%).Let us now analyze the contribution of a carbon-based support to the interaction of molecular oxygen with Cu5. Considering the molecular chemisorption model, Fig. 5 shows the binding energies as a function of the number of adsorbed O2 molecules onto circumpyrene-supported Cu5. The values of the binding energies can be compared with those obtained for bare Cu5 in Table 2. The left-hand panel of Fig. 5 presents the corresponding free energies of formation at ambient pressure (1 atm), while the most likely adsorption states as a function of oxygen pressure and temperature are depicted in the phase diagram of Fig. 4 (upper left-hand panel). The optimized structures of circumpyrene-supported Cu5, as well as the most stable (Cu5/circumpyrene)–(O2)n complexes are shown in Fig. 4.
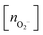 , and peroxo
, and peroxo 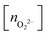 species is also specified. The ‘*’ and ‘**’ quotations indicate the dissociation of a single and all the adsorbed peroxo species, respectively. These species dissociate in three-fold coordinated O2− ions and carbon-supported ad-atoms (or ad-ions)
species is also specified. The ‘*’ and ‘**’ quotations indicate the dissociation of a single and all the adsorbed peroxo species, respectively. These species dissociate in three-fold coordinated O2− ions and carbon-supported ad-atoms (or ad-ions)
| Cu5–(O2)n | ||
|---|---|---|
| E bind/eV | ||
| n = 1 | 0/1/0 (0/1/0) | −1.4 (−1.4) |
| 0/0/1* | −1.7 | |
| n = 2 | 0/2/0 (0/2/0) | −3.4 (−2.5) |
| 0/0/2* | −3.9 | |
| 0/0/2** | −4.8 | |
| n = 3 | 0/3/0 (0/3/0) | −5.6 (−4.9) |
| 0/1/2* | −4.7 | |
| n = 4 | 0/4/0 (0/4/0) | −6.9 (−5.8) |
| 0/1/3* | −7.1 | |
| 0/1/3** | −7.2 | |
| n = 5 | 0/5/0 (2/3/0) | −7.8 (−5.8) |
| 0/3/2* | −7.6 | |
| 0/1/4** | −8.4 | |
| n = 6 | 0/6/0 (1/5/0) | −8.0 (−7.4) |
| 0/5/1* | −8.6 | |
| n = 7 | 0/7/0 (0/5/2) | −9.1 (−8.9) |
Except for single O2 adsorption, it can be observed from Table 2 that the support stabilizes the Cu5–(O2)n complexes so that the binding energies become 2–26% larger. As a result, additional phases do appear with n = 4 and 5, and the inter-phase boundaries for n = 7 and 3 become shifted to lower pressures and higher temperatures as compared with unsupported Cu5. As expected from the dispersion-dominated nature of the Cu5-circumpyrene interaction, the Cu5 trigonal bipyramidal structure is slightly modified by the support, with one side face becoming almost parallel to the circumpyrene plane. The same holds true for the adsorption of three O2 molecules (see Fig. 2). When the number of adsorbed O2 increases further up to 7, however, the Cu5 pyramidal structure becomes much elongated along one of their vertices due to the stretching of Cu–Cu distances to host additional O2 molecules. Concurrently, the binding of the complex to the support becomes weaker.
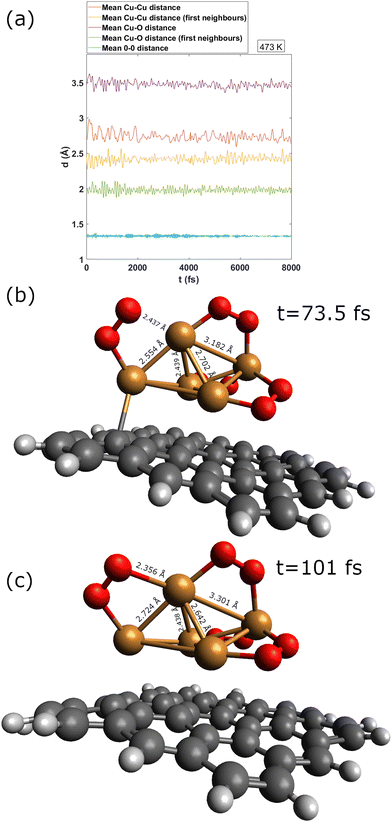
To gain insights into the fluxional nature of the complexes, we have carried out an AIMD simulation of the Cu5–(O2)4 motion at 473 K (see Fig. 6). As indicated in Table 2, the four adsorbed O2 molecules become charged as superoxo O2− ions. The conversion of the four O2 molecules in superoxo radicals causes the enlargement of the O–O bond lengths (ca. 1.3 Å) upon that corresponding to the neutral O2 molecule (ca. 1.2 Å). During the 12 ps of the AIMD simulation, no desorption of neutral O2 molecules is observed. Accordingly, the O–O distance (shown in blue) changes very little. In contrast, the fluctuations of the Cu–O distances (to within 0.2 Å) are noticeable. They are associated with Cu–O bond breaking/formation which is concurrent to concerted contractions/elongations of Cu–Cu distances. The wide amplitude nature of the AMC motifs is also reflected in the large fluctuations (within 0.5 Å) of the Cu–Cu distances (shown in yellow and red in panel a of Fig. 6).
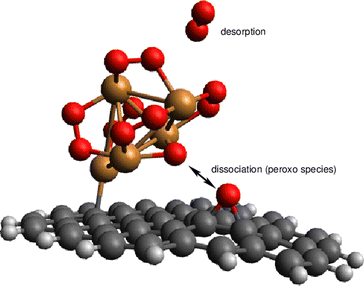 | ||
| Fig. 7 Picture illustrating the support-mediated dissociation of one peroxo O22− species along with the desorption of one neutral O2 molecule. | ||
As can be observed in Fig. 8, the states characterized by the adsorption of O2 molecules as superoxo radicals are very close to those arising from the occurrence of support-mediated dissociation. The lowest energy state (see Table 2) corresponds to a complex that can be characterized as Cu5O5. As typically found for fluxional atomic metal clusters, the energy differences between global and local minima are very small (to within 0.3 eV). Therefore, it seems sensible that the inter-conversion between them be reversible at experimentally relevant ranges of temperatures and oxygen gas pressures as discussed for single O2 chemisorption on bare Cu5 in ref. 11. In order to include the likelihood of inter-conversion between these energetically close-lying adsorption states (see Fig. 8), we have computed the Boltzmann-weighted average of free energies of formation for each circumpyrene-supported Cu5–(O2)n complex as well as their associated distributions of copper oxidation states [Cu(0), Cu(I), Cu(II)].
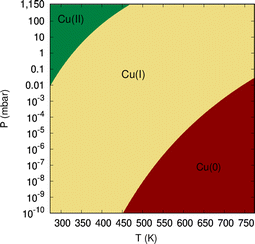 | ||
| Fig. 9 Diagram showing the dominant oxidation states of copper atoms of circumpyrene-supported Cu5 as a function of temperature and oxygen gas pressure. | ||
(1) The aggregation of two Cu5 clusters into the Cu5–Cu5 dimer induces a shift of the inter-phase boundaries to higher pressures and lower temperatures. This outcome might suggest that a portion of Cu5 clusters might experience an aggregation process upon surface deposition.
(2) Strong non-adiabatic effects featured by AMCs7,12 induce a ‘trapping’ of O2 molecules approaching Cu5 in an electronic state correlating with the neutral O2 and Cu5 fragments at the asymptotic limit. These effects prevent the system to access the charge-transfer chemisorption state, thus favoring the dominance of the Cu(0) metallic state over that predicted through the consideration of chemisorption states only.
4 Concluding remarks and future perspectives
We have identified aggregation and the role of a chemically inert support in the interaction of gas-phase O2 molecules with Cu5 as a paradigmatic case of a fluxional AMC. Our results can be summarized as follows:(1) The aggregation of two Cu5 clusters into a Cu5–Cu5 dimer formed by coupled bipyramidal 3D structures is predicted to be energetically much favored, with the attractive Cu5–Cu5 interaction being about −5.2 eV. However, the decoupling of the Cu5–Cu5 dimer into two Cu5 clusters has been apparent in the corresponding (p, T)-phase diagram upon increasing the oxygen gas pressure. Molecules of O2 adsorb in between Cu5 clusters, causing an enlargement of their O–O bonds, the formation of peroxo species, and even their dissociation. AIMD simulations have illustrated the rotational decoupling of the Cu5–Cu5 dimer into two Cu5 sub-units, with and without including support effects, upon heating.
(2) Without including support effects, Cu5–(O2)n and (Cu5–Cu5)–(O2)2n complexes with n = 3 and 7 are the most stable. The phase diagrams of Cu5 and Cu5–Cu5 are very similar, differing just in an overall shifting of the inter-phase boundaries to higher pressures and lower temperatures for the Cu5–Cu5 dimer.
(3) Considering circumpyrene as a molecular model of a carbon-based surface, the role of an inert support has been manifested in the overall stabilization of Cu5–(O2)n complexes in such a way that additional (p,T)-phases do appear. Moreover, lower pressures and higher temperatures are necessary for the desorption of neutral O2 molecules when the copper clusters are supported.
(4) An AIMD simulation has illustrated the fluxionality and wide amplitude nature of the Cu–Cu and Cu–O motions in circumpyrene-supported Cu5–(O2)4. We have identified the contraction of Cu–Cu distances upon Cu–O bond breaking and their enlargement upon Cu–O bond formation.
(5) A support-mediated mechanism for dissociation of peroxo species adsorbed onto Cu5 has been revealed, with the energies of the dissociative states being very close to those characterized by molecular chemisorption. Considering both molecular and dissociative reaction channels, a diagram has been provided to show the dominant copper oxidation states as a function of temperature and oxygen gas pressure, being consistent with recent experimental measurements.13
Through first-principles modelling, we have shown that gas-phase O2 molecules can be adsorbed as either superoxo or peroxo species onto atomic metal clusters (AMCs) and that both molecular and dissociative chemisorption can occur. The energetically favored aggregation of AMCs and occurrence of multiple energetically closely lying chemisorption states upon their interaction with O2 molecules have the potential of impacting both their stability and catalytic properties, either under aggregation and/or oxidation conditions. On the one hand, the structural fluxionality of ACMs allows their rotational decoupling from formed aggregates, such as the Cu5 dimer both upon heating, and their spatial separation at exposition into an O2-rich environment. On the other hand, the same properties might be the one responsible for the appearance of many reaction channels, such as support-mediated dissociative chemisorption, with the resulting adsorption states having very similar energies to those characterized by, e.g., molecular chemisorption. This characteristic might favor a reversible inter-conversion between different adsorption states at experimentally relevant ranges of temperatures and oxygen gas pressures. Considering circumpyrene-supported Cu5 as a model system, we have shown that a Boltzmann average of a representative ensemble of close-lying states and their corresponding copper oxidation states allow reaching a sensible agreement with recent in situ experimental measurements on HOGP-supported Cu5 clusters.13 In order to gain further insights into the oxidation of Cu5, it is, however, necessary to consider additional channels for chemisorption of O2 both in molecular and dissociative forms, particularly those involving peroxo species. The achievement of a complete picture of the aggregation process for two Cu5 clusters, with and without O2 molecules, requires extensive AIMD simulations as a function of temperature. Future work is planned to address them, using periodic models of graphene, properly addressing the diffusion of Cu5 clusters as well. An investigation of the influence of the ACMs’ aggregation in the electronic structures and geometries of individual ACMs is also a future perspective. Despite the need for further research, we consider that our study provides a solid support to previous works addressing the reversible nature of the oxidation of the smallest copper clusters,7,9–13 including in situ experimental measurements.13
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Andreas W. Hauser for having provided Python and MATLAB codes that have served to write a general-purpose code, delivering phase diagrams. We are also thankful to Alexandre Zanchet, Lyudmila Moskaleva, Berta Fernández, and Alexander O. Mitrushchenkov for very fruitful discussions, and Mehrdad R. Osanloo for the proof-reading of the revised manuscript. This work was supported by the Spanish Agencia Estatal de Investigación (AEI) under Grant No. PID2020-117605GB-I00. This publication is also based upon work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology). J. A.-G. acknowledges the ‘JAE-Intro 2021’ program for having provided a scholarship at CSIC. The CESGA super-computer center (Spain) and the CTI-CSIC are acknowledged for having provided computational resources. We also acknowledge the support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI). The EU project of reference HORIZON-MSCA-2021-DN-01 is acknowledged as well.Notes and references
- S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908 CrossRef CAS.
- A. Halder, L. A. Curtiss, A. Fortunelli and S. Vajda, J. Chem. Phys., 2018, 148, 110901 CrossRef PubMed.
- S. Hirabayashi and M. Ichihashi, Phys. Chem. Chem. Phys., 2014, 16, 26500–26505 RSC.
- P. López-Caballero, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074 CrossRef PubMed.
- A. Halder, C. Lenardi, J. Timoshenko, A. Mravak, B. Yang, L. K. Kolipaka, C. Piazzoni, S. Seifert, V. Bonačić-Koutecký, A. I. Frenkel, P. Milani and S. Vajda, ACS Catal., 2021, 11, 6210–6224 CrossRef CAS.
- M. P. de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500 RSC.
- M. P. de Lara-Castells, J. Colloid Interface Sci., 2022, 612, 737–759 CrossRef CAS PubMed.
- J. Juraj, A. Fortunelli and S. Vajda, Phys. Chem. Chem. Phys., 2022, 120, 12083–12115 Search PubMed.
- E. Fernández, M. Boronat and A. Corma, J. Phys. Chem. C, 2015, 119, 19832–19846 CrossRef.
- P. Concepción, et al. , ACS Catal., 2017, 7, 3560–3568 CrossRef.
- A. Zanchet, P. López-Caballero, A. O. Mitrushchenkov, D. Buceta, M. A. López-Quintela, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 27064–27072 CrossRef CAS PubMed.
- A. O. Mitrushchenkov, A. Zanchet, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. A, 2021, 125, 9143–9150 CrossRef CAS PubMed.
- D. Buceta, S. Huseyinova, M. Cuerva, H. Lozano, L. J. Giovanetti, J. M. Ramallo-López, P. Lóopez-Caballero, A. Zanchet, A. O. Mitrushchenkov, A. W. Hauser, G. Barone, C. Huck-Iriart, C. Escudero, J. C. Hernández-Garrido, J. Calvino, M. Lopez-Haro, M. P. de Lara-Castells, F. G. Requejo and M. A. López-Quintela, ChemRxiv, 2021, 1–36, DOI:10.26434/chemrxiv.13661081.v1.
- P. Concepción, M. Boronat, S. García-García, E. Fernández and A. Corma, ACS Catal., 2017, 7, 3560–3568 CrossRef.
- T. L. Thomson and J. T. Yates, Jr., Chem. Rev., 2006, 106, 4428–4453 CrossRef PubMed.
- J. T. Yates Jr., Surf. Sci., 2009, 603, 1605–1612 CrossRef.
- Z. Zhang and J. T. Yates Jr., Chem. Rev., 2012, 112, 5520–5551 CrossRef CAS.
- M. A. Henderson, Surf. Sci. Rep., 2011, 66, 185–197 CrossRef CAS.
- M. A. Henderson, M. M. Shen, Z. T. Wang and I. Lyubinetsky, J. Phys. Chem. C, 2013, 117, 5774–5784 CrossRef CAS.
- C. Shu, N. Sukumar and C. P. Ursenbach, J. Chem. Phys., 1999, 110, 10539–10544 CrossRef CAS.
- M. P. de Lara-Castells and J. L. Krause, J. Chem. Phys., 2001, 115, 4798–4810 CrossRef CAS.
- M. P. de Lara-Castells and J. L. Krause, Chem. Phys. Lett., 2002, 354, 483–490 CrossRef CAS.
- M. P. de Lara-Castells and J. L. Krause, J. Chem. Phys., 2003, 118, 5098–5105 CrossRef CAS.
- M. P. de Lara-Castells, A. O. Mitrushchenkov, O. Roncero and J. L. Krause, Isr. J. Chem., 2005, 45, 59–76 CrossRef CAS.
- H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911 CrossRef CAS.
- Q.-Y. Fan, Y. Wang and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 3891–3897 CrossRef CAS.
- O. V. Lushchikova, H. Tahmasbi, S. Reijmer, R. Platte, J. Meyer and J. M. Bakker, J. Phys. Chem. A, 2021, 125, 2836–2848 CrossRef CAS PubMed.
- S. K. Iyemperumal, T. G. Fenton, S. L. Gillingham, A. D. Carl, R. L. Grimm, G. Li and N. A. Deskins, J. Chem. Phys., 2019, 151, 054702 CrossRef.
- Q. Chen, D. Schollmeyer, K. Müllen and A. Narita, J. Am. Chem. Soc., 2019, 141, 19994–19999 CrossRef CAS PubMed.
- M. P. de Lara-Castells, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 102804 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- P. E. Blöch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- A. Muñoz-Castro, T. Gomez, D. M. Carey, S. Miranda-Rojas, F. Mendizabal, J. H. Zagal and R. Arratia-Perez, J. Phys. Chem. C, 2016, 120, 7358–7364 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchenkov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20, 19110–19119 RSC.
- P. López-Caballero, J. M. Ramallo-López, L. J. Giovanetti, D. Buceta, S. Miret-Artés, M. A. López-Quintela, F. G. Requejo and M. P. de Lara-Castells, J. Mater. Chem. A, 2020, 8, 6842–6853 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1962, 36, 3428–3439 CrossRef CAS.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606 Search PubMed.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS.
- P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244 CrossRef CAS.
- A. Kubas, D. Berger, H. Oberhofer, D. Maganas, K. Reuter and F. Neese, J. Phys. Chem. Lett., 2016, 7, 4207–4212 CrossRef CAS PubMed.
- M. Mukherjee, D. Tripathi, M. Brehm, C. Riplinger and A. K. Dutta, J. Chem. Theory Comput., 2021, 17(1), 105–116 CrossRef CAS PubMed.
- M. Weiβ and M. Brehm, Molecules, 2020, 25(24), 5861 CrossRef PubMed.
- C. Slawik, C. Rickmeyer, M. Brehm, A. Böhme and G. Schüürmann, Environ. Sci. Technol., 2017, 51(7), 4018–4026 CrossRef CAS PubMed.
- A. W. Hauser, J. Gomes, M. Bajdich, M. Head-Gordon and A. T. Bell, Phys. Chem. Chem. Phys., 2013, 15, 20727–20734 RSC.
- X. Yu, A. R. Oganov, Q. Zhu, F. Qi and G. Qian, Phys. Chem. Chem. Phys., 2018, 20, 30437–30444 RSC.
- S. Bhattacharya, S. V. Levchenko, L. M. Ghiringhelli and M. Scheffler, Phys. Rev. Lett., 2013, 111, 135501 CrossRef PubMed.
- Y. Xu, W. A. Shelton and W. F. Schneider, J. Phys. Chem. B, 2006, 110, 16591–16599 CrossRef CAS PubMed.
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 2019, p. 20899 DOI:10.18434/T4D303.
- M. W. Chase, Jr., NIST-JANAF Themochemical Tables, Fourth Edition, J. Phys. Chem. Ref. Data, Monograph 9, 1998, 1–1951.
- P. L. Rodríguez-Kessler, A. R. Rodríguez-Domínguez, D. MacLeod-Carey and A. Muñoz-Castro, Adv. Theory Simul., 2021, 4, 2100043 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Complementary code written in Octave/MATLAB to extract (p–T)-phase diagrams from the thermochemistry output of the ORCA code. See DOI: https://doi.org/10.1039/d2cp02169b |
| This journal is © the Owner Societies 2022 |