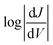Controlling destructive quantum interference in tunneling junctions comprising self-assembled monolayers via bond topology and functional groups

Abstract

Quantum interference effects (QI) are of interest in nano-scale devices based on molecular tunneling junctions because they can affect conductance exponentially through minor structural changes. However, their utilization requires the prediction and deterministic control over the position and magnitude of QI features, which remains a significant challenge. In this context, we designed and synthesized three benzodithiophenes based molecular wires; one linearly-conjugated, one cross-conjugated and one cross-conjugated quinone. Using eutectic Ga–In (EGaIn) and CP-AFM, we compared them to a well-known anthraquinone in molecular junctions comprising self-assembled monolayers (SAMs). By combining density functional theory and transition voltage spectroscopy, we show that the presence of an interference feature and its position can be controlled independently by manipulating bond topology and electronegativity. This is the first study to separate these two parameters experimentally, demonstrating that the conductance of a tunneling junction depends on the position and depth of a QI feature, both of which can be controlled synthetically.

---

Introduction

Molecular electronics is concerned with the transport of charge through molecules spanning two electrodes,¹ the fabrication of which is a challenging area of nanotechnology.^2–4 In such junctions, π-conjugated molecules influence transport more than a simple, rectangular tunneling barrier; when a tunneling electron traverses the region of space occupied by orbitals localized on these molecules, its wave function can undergo constructive or destructive interference, enhancing or suppressing conductance. When the presence of different pathways in molecular system affects conductance, it is typically described as quantum interference (QI),⁵ which was originally adapted from the Aharonov–Bohm effect⁶ to substituted benzenes.^7,8 The concept “quantum interference effect transistor” was also proposed using meta-benzene structures for device application.⁹ Solomon et al. further refined the concept in the context of molecular electronics where it is now well established that destructive QI leads to lower conductance in tunneling junctions.^10–15 We previously demonstrated QI in SAM-based junctions using a series of compounds based on an anthracene core; AC, which is linearly-conjugated; AQ, which is cross-conjugated via a quinone moiety; and AH, in which the conjugation is interrupted by saturated methylene bridges (Fig. S1†).¹⁶ Subsequent studies verified these findings in a variety of experimental platforms and a consensus emerged that, provided the destructive QI feature (anti-resonances in transmission) is sufficiently close to the Fermi level, E_F, cross-conjugation leads to QI.^17–24 However, experimental studies on conjugation patterns other than AC/AQ are currently limited to ring substitutions such as meta-substituted phenyl rings^,25–32 or varied connectivities in azulene,^33–35 which differ fundamentally^5,11,36–38 from cross-conjugated bond topologies^23,39,40 because they change tunneling pathways, molecular-lengths and bond topology simultaneously (Table S1†). Isolating these variables is however important because the only primary observable is conductance, which varies exponentially with molecular length. More recent work has focused on “gating” QI effects by controlling the alignment of π-systems through-space^37,41,42 and affecting the orbital symmetry of aromatic rings with heteroatoms.^43–45 These studies exclusively study the effects of the presence and absence of QI features; to date—and despite recent efforts⁴⁶—the specific effects of bond topology and electronegativity on the depth and position of QI features have not been isolated experimentally.

To address this issue, we designed and synthesized the series of benzodithiophene derivatives (BDT-n); benzo[1,2-b:4,5-b′]dithiophene (BDT-1, linearly-conjugated), benzo[1,2-b:4,5-b′]dithiophene-4,8-dione (BDT-2, cross-conjugated with quinone), and benzo[1,2-b:5,4-b′]dithiophene (BDT-3, cross-conjugated and an isomer of BDT-1). These compounds separate the influence of cross-conjugation (bond topology) from that of the electron-withdrawing effects of the quinone functionality while controlling for molecular formula and length. We investigated the charge transport properties of these molecules in tunneling junctions comprising self-assembled monolayers (SAMs), which are relevant for solid-state molecular-electronic devices.^47–49 Through a combination of density functional theory (DFT) and transition voltage spectroscopy (TVS) we show that cross-conjugation produces QI features near occupied molecular states and that the position and depth of the QI feature is strongly influenced by the strongly electron-withdrawing quinone functionality, which places these features near unoccupied states while simultaneously bringing those states close to E_F. Thus, by controlling bond topology and electronegativity separately, the conductance can be tuned independently of length and connectivity via the relative positions of the QI features and molecular states and not just the presence or absence of such features.

Results and discussion

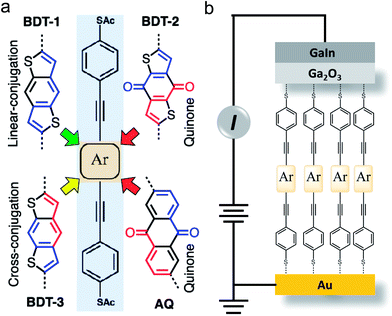
To isolate molecular effects on transport, it is important to control for changes to the width of the tunneling barrier which, in SAMs, is typically defined by the end-to-end lengths of the molecules. Conductance G generally varies exponentially with the barrier-width d such that G = G₀ exp(–βd), where G₀ is the theoretical value of G when d = 0, and β is the tunneling decay coefficient. Since β depends on the positions of molecular states relative to E_F and we are comparing compounds with very different redox potentials (orbital energies) we can only ascribe changes to G if d is invariant across the series. Furthermore, to isolate the variable of bond topology experimentally, the electronic properties of the linear- and cross-conjugated compounds must be nearly identical. Fig. 1a shows the structures of the BDT-n series and AQ; the “arms” are linearly-conjugated phenylacetylenes (highlighted in the light blue background) and the cores (Ar, highlighted in the brown background) are substituted by the structures indicated. The variation in the end-to-end lengths of these compounds is within 1 Å and the linear- and cross-conjugated compounds BDT-1 and BDT-3 differ only by the relative position of sulfur atoms; they have the same molecular formula. The synthesis, full characterization and a detailed discussion of their properties are provided in the ESI.† Note that we include AQ in the series as a benchmark for destructive QI effects.

Fig. 1 (a) Structures of BDT-1, BDT-2 and BDT-3 with linearly and cross-conjugated pathways of the cores drawn in blue and red, respectively. The phenylacetylene arms (highlighted in blue) are linearly conjugated. BDT-1 is linearly-conjugated, BDT-2 contains a cross-conjugation imposed by the central quinone ring analogous to AQ and BDT-3 is similarly cross-conjugated, but the cross-conjugation separating the two linearly-conjugated pathways arises from the positions of the sulfur atoms relative to the central phenyl ring (there are no exocyclic bonds). (b) Schematic of Au/SAM//EGaIn junction (“/” and “//” denote a covalent and van der Waals interfaces, respectively).

We measured tunneling charge transport through metal–molecule–metal junctions comprising BDT-1, BDT-2, BDT-3 and AQ using conformal eutectic Ga–In (EGaIn) contacts as top electrodes.⁵⁰ We utilized an established procedure of the in situ deprotection of thioacetates^41,51 to form well-defined SAMs on Au substrates; these substrates served then as bottom electrodes. We refer to the assembled junctions as Au/SAM//EGaIn where “/” and “//” denote a covalent and van der Waals interfaces, respectively. The geometry of the junctions is shown in Fig. 1b. To verify that the structural similarities of the compounds carry over into the self-assembly process, we characterized the SAMs of BDT-n by several complementary techniques, including (high-resolution) X-ray photoelectron spectroscopy (HRXPS/XPS) and angle-resolved near-edge X-ray absorption fine structure (NEXAFS) spectroscopy. These data are discussed in detail in the ESI† and summarized in Table 1. The characterization of SAMs of AQ is reported elsewhere.^16,41 The XPS and NEXAFS data suggest that the molecules in the BDT-n SAMs are assembled upright with the tilt angle of approximately 35°. The molecules are packed densely on the order of 10¹⁴ molecules per cm² as are similar conjugated molecular wire compounds.⁴¹

Table 1 Summary of the properties of SAMs of BDT-n and Au/BDT-n//EGaIn junctions

Compound	BDT-1	BDT-2	BDT-3	C18 reference
XPS thickness (Å)	17 ± 3	18 ± 4	19 ± 4	n.d.
HRXPS thickness (Å)	19.81 ± 0.40	22.30 ± 0.45	17.17 ± 0.34	20.9
Averaged XPS thickness (Å)	18.4	20.2	18.4	n.d.
Water contact angle (°)	68.3 ± 4.8	65.8 ± 4.0	62.8 ± 4.6	104.2 ± 2.2
Density (10^14 molecules per cm^2)	2.05	3.30	2.33	4.63
Area molecules per Å^2	48.8 ± 2	30.3 ± 2	43.0 ± 2	21.6
log|J|@0.5 V (A cm^−2)	−2.34 ± 0.17	−4.09 ± 0.23	−3.53 ± 0.20	−4.96 ± 0.87 (ref. 41)
Yield of working junctions (%)	88.9	93.8	84.2	79 (ref. 41)
Num. working EGaIn junctions	32	30	32	28 (ref. 41)
Total J/V traces	643	626	666	280 (ref. 41)

---

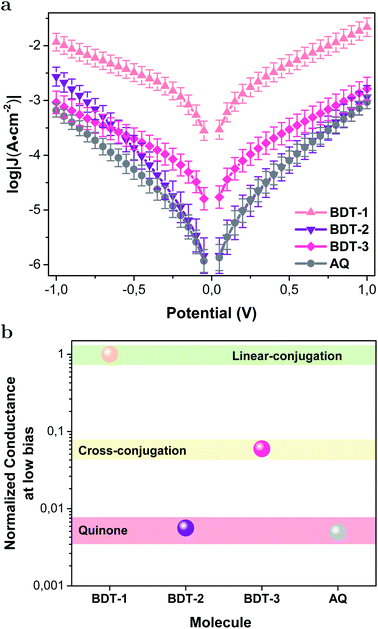
Fig. 2a shows the current–density versus voltage (J/V) curves for the BDT-n series and AQ using EGaIn top contacts. BDT-1 is the most conductive across the entire bias window. The conductance of linearly-conjugated BDT-1 and AC (Fig. S1;† a linearly-conjugated analog of AQ), are almost identical (Fig. S21†), meaning that the low-bias conductivity and/or values of J are directly comparable between the AC/AQ and BDT-n series. As expected, the cross-conjugated BDT-2, BDT-3 and AQ are all less conductive than BDT-1 (and AC). The low-bias conductivity (from the ohmic region, −0.1 V to 0.1 V) of the quinones (BDT-2 and AQ), however, is even more suppressed than the cross-conjugated BDT-3, while the magnitudes of J for BDT-2, BDT-3 and AQ are similar beyond −0.5 V. We observed similar behavior in QI mediated by through-space conjugation in which the compound with an interference feature very close to E_F exhibited a sharp rise in J, eventually crossing J/V curve of the compound with a feature further from E_F.⁴¹ This observation suggests that, as the junction is biased, the transmission probability “climbs” the interference feature rapidly, bringing highly transmissive conduction channels into the bias window at sufficiently low values of V to meet and exceed the total transmission of the compound for which the interference feature is far from E_F at zero bias. Further discussion on the asymmetry of J/V curves is included in the ESI.†

Fig. 2 (a) Plots of log|J (A cm⁻²)| versus V for Au/SAM//EGaIn junctions comprising SAMs of BDT-1 (salmon up-triangles), BDT-2 (purple down-triangles), BDT-3 (pink diamonds) and AQ (grey circles). Each datum is the peak position of a Gaussian fit of log|J| for that voltage. The error bars are 95% confidence intervals taking each junction as a degree of freedom. (b) Normalized low bias conductance, linearly conjugated BDT-1 (salmon ball) features the highest values, the quinone BDT-2 (purple ball) and AQ (grey ball) the lowest and cross conjugated BDT-3 (pink ball) is in between.

To better compare the conductance of the molecules, we calculated the low-bias conductivities and normalized them to BDT-1. These values are plotted in Fig. 2b, showing that cross-conjugation lowers the conductance of BDT-3 by an order of magnitude compared to BDT-1 and the quinone functionality of BDT-2 and AQ lowers it by two orders of magnitude, in agreement with the analogous behavior of AC and AQ.²⁰ To control for large-area effects (e.g., if there are defects in the SAM), we measured BDT-n series by conducting-probe atomic force microscopy (CP-AFM) with Au electrodes and found the same trend: BDT-1 > BDT-3 > BDT-2, however, a direct comparison of low-bias conductivities was precluded by the extremely high resistance of BDT-2 and AQ at low bias. These data are discussed in detail in the ESI.† Thus, we conclude that quinones suppress conductance more than cross-conjugation alone, irrespective of the measurement/device platform.

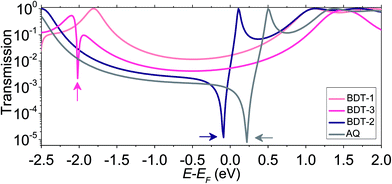
For insight into the shapes of the J/V curves and the conductance, we simulated the transmission spectra, T(E) vs. E − E_F (E_F value of −4.3 eV, see Experimental section), of the BDT-n series using density functional theory (DFT) and compared the resulting curves with AQ (Fig. 3). These calculations, which are discussed in more detail in the Computational methodology section of the ESI,† simulate the transmission spectra through isolated molecules in vacuum at zero bias and are useful for predicting trends in conductance. There are three important features of these curves: (1) only the compounds with cross-conjugation (including quinones) show sharp dips (anti-resonances or QI features)^13,18 in the frontier orbital gap; (2) the dips occur near E_F only for the two quinones; and (3) the QI features are more pronounced for the molecules in which the cross-conjugation is caused by a quinone moiety as opposed to the carbon–carbon bond topology. When bias is applied to a junction, the x-axis of the transmission plot shifts and E_F broadens such that an integral starting at E − E_F = 0 eV and widening to larger ranges of E − E_F is a rough approximation of how T(E) translates into current, I(V). This relationship is apparent in the slightly lower conductance of AQ compared to BDT-2 (Fig. 2b) and the slightly lower values of T(E) for AQ compared to BDT-2 across the entire range of E − E_F. The proximities of the QI features to E_F are also apparent in the J/V curves (Fig. 2a). As the junction is biased, the minimum of the QI feature shifts such that, by 0.5 V, the transmission probabilities are roughly equal for BDT-n and AQ.

Fig. 3 Transmission spectra for isolated molecules of BDT-n and AQ. The spectrum of BDT-1 (salmon) is featureless between the resonances (T(E) → 1) near the frontier orbitals. The sharp dips in the spectra of BDT-2 (purple), BDT-3 (pink) and AQ (grey) indicated with arrows are destructive QI features. The energies on the bottom axis are with respect to the E_F value of −4.3 eV.

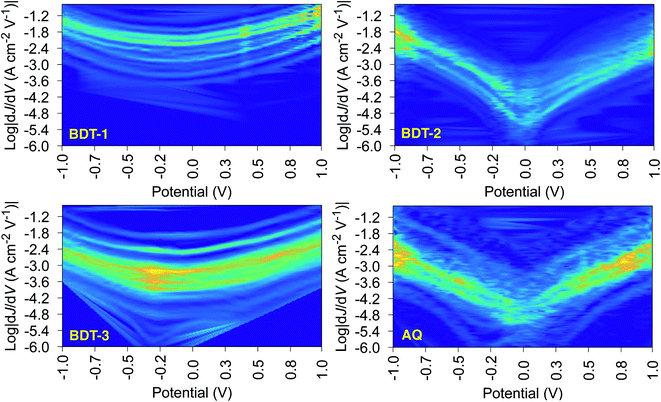
The shape of T(E) near E − E_F = 0 eV is roughly traced by differential conductance plots of 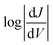vs. V, allowing QI features near E_F to be resolved experimentally.^18,41,52Fig. 4 shows heatmap plots of differential conductance of Au/SAM//EGaIn constructed from histograms binned to 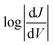for each value of V (note that these are histograms of J/V curves with no data-selection, thus, brighter colors correspond to mean values of J and are not related to conductance histograms of single-molecule break-junctions; see ESI† for details). Both BDT-1 and BDT-3 exhibit ordinary, U-shaped plots characteristic of non-resonant tunneling. By contrast, both AQ and BDT-2—the two compounds bearing quinone functionality—show V-shaped plots with negative curvature. These results are in agreement with Fig. 3, which places the QI features for the quinone moieties, AQ and BDT-2, much closer to E_F than for BDT-3. The positions of these features are related to the positions of highest-occupied and lowest-unoccupied π-states (HOPS and LUPS), which are in good agreement between DFT and experiment (Tables S2 and S3†). Thus, the differential conductance heatmaps (experiment) and DFT (simulation) both indicate that cross-conjugation suppresses conductance because it creates a dip in T(E) in the frontier orbital gap, but that the electron-withdrawing nature of the quinone functionality simultaneously pulls the LUPS and the interference features close to E_F such that the J/V characteristics and transmission plots of AQ and BDT-2 are nearly indistinguishable despite the presence of two thienyl groups in BDT-2. These results also suggest that tunneling transport is mediated by the HOPS (hole-assisted tunneling) for BDT-1 and BDT-3 and by the LUPS (electron-assisted tunneling) for BDT-2 and AQ because tunneling current is dominated by the resonance(s) closest to E_F.

Fig. 4 Differential conductance heatmap plots of Au/SAM//EGaIn junctions comprising BDT-1 (top-left), BDT-2 (top-right), BDT-3 (bottom-left) and AQ (bottom-right) showing histograms binned to (differential conductance, Y-axis) versus potential (V, X-axis). The colors correspond to the frequencies of the histograms and lighter (more yellow) colors indicate higher frequencies. The bright spots near ±1 V are due to the doubling of data that occurs in the forward/return J/V traces. The plots for both BDT-2 and AQ, which contain quinones, are V-shaped at low bias and exhibit negative curvature, indicating a destructive QI feature near E_F, while the plots of BDT-1 and BDT-3 are U-shaped.

To further investigate the mechanism of transport, we measured transition voltages, V_trans (Table S3, Fig. S17 and S18†), which provide information about the energy offset between E_F and the dominant frontier orbital.^53,54Fig. 5a shows the levels for the BDT-n series calculated by DFT with respect to E_F (−4.3 eV), clearly predicting LUPS-mediated tunneling for BDT-2 and AQ. Fig. 5b compares the experimental values of V_trans to the energy differences between E_F and the frontier orbitals. The salient feature of Fig. 5b is that the trend in |E_HOPS − E_F| opposes the trend in V_trans such that the trend in experimental values of V_trans agrees with DFT only when we compare V_trans with |E_HOPS − E_F| for BDT-1 and BDT-3, and with |E_LUPS − E_F| for BDT-2 and AQ. Thus, DFT calculations combined with experimental values of V_trans predict electron-assisted tunneling for BDT-2 and AQ. This degree of internal consistency between the experiment and theory is important because, ultimately, the only primary observable is conductance, which we plot as J/V curves, differential conductance heatmaps and Fowler–Nordheim plots (from which we extract V_trans). And we find remarkable agreement between these direct and indirect observations and DFT calculations on model junctions comprising single molecules.

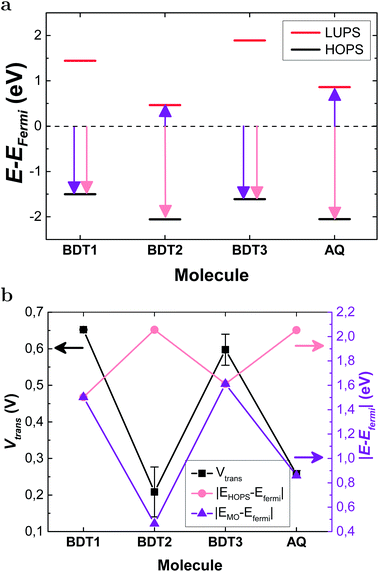Fig. 5 (a) Energy offsets of the frontier orbitals calculated using DFT with respect to E_F value of −4.3 eV. (b) The energy offsets (salmon and purple lines, right axis) plotted with the measured values of V_trans (black line, left axis). The salmon line plots the energy offsets of the HOPS. The purple line plots the smallest energy difference (purple arrows in (a)); |E_HOPS – E_Fermi| for BDT-1 and BDT-3, |E_LUPS − E_Fermi| for BDT-2 and AQ. The exact values of V_trans and the orbital energies are shown in Tables S3 and S5.†

Conclusion

The key question of this work is how cross-conjugation and electronegativity affect QI features.^{11,20,52,55,56} Based on our experimental observations and calculations, we assert that destructive QI induced by cross-conjugation is highly sensitive to the functional groups that induce the cross-conjugation and that quinones are, therefore, a poor testbed for tuning QI effects (beyond switching them on and off⁵⁷) because their strong electron-withdrawing nature places a deep, destructive feature near E_F irrespective of other functional groups (in our case, two fused thiophene rings barely make a difference). Comparing a quinone to a hydrocarbon also compares HOPS-mediated tunneling to LUPS-mediated tunneling between molecules with significantly different band-gaps and absolute frontier orbital energies. In contrast, BDT-1 and BDT-3 are heterocyclic isomers with no functional groups, identical molecular formulas, nearly-identical HOPS, identical lengths that translate into SAMs of identical thicknesses, and transport is dominated by the HOPS. They isolate the single variable of conjugation patterns, allowing us to separate bond topology (cross-conjugation) from electronic properties (functional groups), giving experimental and theoretical insight into the relationship between bond topology and QI. Our results suggest that there is a lot of room to tune the conductance of moieties derived from BDT-3 by including pendant groups (e.g., halogens, CF₃ groups or acidic/basic sites) that shift the QI feature gradually towards E_F synthetically and/or in response to chemical signals.

Experimental

Synthesis

Reagents. All reagents and solvents were commercial and were used as received. Benzo[1,2-b:4,5-b′]dithiophene was purchased from TCI. 2,6-dibromobenzo[1,2-b:4,5-b′]dithiophene-4,8-dione,⁵⁸ 2,6-dibromobenzo[1,2-b:5,4-b′]dithiophene,⁵⁹ 4-ethynyl-1-thioacetylbenzene⁶⁰ and 1-tert-butylthio-4-ethynylbenzene⁶¹ were synthesized according to literature procedures.

NMR and mass spectra. ¹HNMR and ¹³CNMR were performed on a Varian Unity Plus (400 MHz) instrument at 25 °C, using tetramethylsilane (TMS) as an internal standard. NMR shifts are reported in ppm, relative to the residual protonated solvent signals of CDC1₃ (δ = 7.26 ppm) or at the carbon absorption in CDC1₃ (δ = 77.0 ppm). Multiplicities are denoted as: singlet (s), doublet (d), triplet (t) and multiplet (m). High Resolution Mass Spectroscopy (HRMS) was performed on a JEOL JMS 600 spectrometer.

UV-Vis and cyclic voltammetry. UV-Vis measurements were carried out on a Jasco V-630 spectrometer. Cyclic voltammetry (CV) was carried out with a Autolab PGSTAT100 potentiostat in a three-electrode configuration.

General. Unless stated otherwise, all crude compounds were isolated by bringing the reaction to room temperature, extracting with CH₂C1₂, washing with saturated NaHCO₃, water and then brine. The organic phase was then collected and dried over Na₂SO₄ and the solvents removed by rotary evaporation. Synthetic schemes and NMR spectra are provided in the ESI.†

2,6-Dibromobenzo[1,2-b:4,5-b′]dithiophene (1). Benzo[1,2-b:4,5-b′]dithiophene (540 mg, 2.84 mmol) were dissolved in 70 mL anhydrous THF under an atmosphere of N₂, cooled to −78 °C and n-butyllithium (8.5 mmol, 5.3 mL, 1.6 M in hexane) was added drop-wise. The solution was stirred for 30 min in the cold bath before being warmed to room temperature and stirred for and additional 20 min. The mixture was cooled to −78 °C again and a solution of CBr₄ (2.8 g, 8.5 mmol) in 5 mL anhydrous THF was added. The solution was stirred for 30 min in the cold bath before being quenched with concentrated sodium bicarbonate solution (10 mL) at −78 °C. The crude solid was purified by recrystallization from CHC1₃ to give 1 (890 mg, 90%) as colorless platelets. ¹HNMR (400 MHz, CDC1₃) δ: 8.03 (s, 2H); 7.33 (s, 2H). ¹³CNMR (100 MHz, CDC1₃) δ: 138.36, 136.88, 125.63, 116.00, 115.10.

2,6-Bis[(4-acetylthiophenyl)ethynyl]benzo[1,2-b:4,5-b′]dithiophene (BDT-1). 2,6-Dibromobenzo[1,2-b:4,5-b′]dithiophene (125 mg, 0.36 mmol) and 4-ethynyl-1-thioacetylbenzene (176 mg, 1 mmol) were dissolved in mixture of fresh distilled Et₃N (5 mL) and anhydrous THF (10 mL). After degassing with dry N₂, the catalysts Pd(PPh₃)₄ (58 mg, 0.05 mmol) and CuI (10 mg, 0.05 mmol) were added. The reaction mixture was refluxed overnight under N₂. The crude solid was purified by column chromatography to give BDT-1 (78 mg, 40%). ¹HNMR (400 MHz, CDC1₃) δ: 8.17 (s, 2H), 7.59 (d, J = 8.2, 4H), 7.55 (s, 2H), 7.43 (d, J = 8.2, 4H), 2.45 (s, 6H). ¹³CNMR (100 MHz, CDC1₃) δ: 195.88, 140.66, 140.46, 136.90, 134.76, 131.51, 130.89, 126.53, 126.25, 119.27, 97.57, 87.31, 32.97. HRMS (ESI) calcd for C₃₀H₁₈O₂S₄ [M + H]⁺: 539.02624, found: 539.02457.

2,6-Bis[(4-tert-butylthiophenyl)ethynyl]benzo[1,2-b:4,5-b′]dithiophene-4,8-dione (5). 2,6-Dibromobenzo[1,2-b:4,5-b′]dithiophene-4,8-dione (3; 200 mg, 0.53 mmol) and 1-tert-butylthio-4-ethynylbenzene (4; 230 mg, 1.21 mmol) were dissolved in mixture of fresh distilled Et₃N (5 mL) and anhydrous THF (10 mL). After degassing, the catalysts Pd(PPh₃)₄ (30 mg, 0.03 mmol) and CuI (5 mg, 0.03 mmol) were added. The reaction mixture was refluxed for overnight under N₂. The crude solid was purified by column chromatography to give 5 (100 mg, 32%). ¹HNMR (400 MHz, CDC1₃) δ: 7.71 (s, 2H), 7.55 (d, J = 8.2, 4H), 7.50 (d, J = 8.2, 4H), 1.31 (s, 18H). ¹³CNMR (100 MHz, CDC1₃) δ: 173.33, 143.91, 142.55, 137.24, 135.17, 131.73, 131.56, 130.31, 121.70, 98.14, 82.55, 46.81, 31.02.

2,6-Bis[(4-acetylthiophenyl)ethynyl]benzo[1,2-b:4,5-b′]dithiophene-4,8-dione (BDT-2)⁶². TiCl₄ (0.04 mL, 0.364 mmol) was added drop-wise to a solution of compound 5 (100 mg, 0.167 mmol) and CH₃C(O)C1 (0.03 mL, 0.377 mmol) in CH₂C1₂ at 0 °C. The resulting mixture was stirred at room temperature for 1 h and the conversion was monitored by TLC (hexanes/CH₂C1₂, 2 : 1). Upon completion, the reaction was quenched with water (10 mL). The crude solid was purified by column chromatography to give BDT-2 (50 mg, 53%). ¹HNMR (400 MHz, CDC1₃) δ: 7.73 (s, 2H), 7.59 (d, J = 8.2, 4H), 7.45 (d, J = 8.2, 4H), 2.46 (s, 6H). ¹³CNMR (100 MHz, CDC1₃) δ: 195.59, 175.96, 145.20, 136.95, 134.87, 134.20, 133.15, 132.57, 132.50, 125.24, 100.42, 85.49, 33.01. HRMS (ESI) calcd for C₃₀H₁₇O₄S₄ [M + H]⁺: 569.00042, found: 568.99887.

2,6-Bis[(4-tert-butylthiophenyl)ethynyl]benzo[1,2-b:5,4-b′]dithiophene (7). 2,6-Dibromobenzo[1,2-b:5,4-b′]dithiophene (6; 50 mg, 0.143 mmol) and 1-tert-butylthio-4-ethynylbenzene (4; 68 mg, 0.358 mmol) were dissolved in mixture of fresh distilled Et₃N (5 mL) and anhydrous THF (10 mL). After degassing, the catalysts Pd(PPh₃)₄ (16 mg, 0.014 mmol) and CuI (2.7 mg, 0.014 mmol) were added. The reaction mixture was refluxed overnight under N₂. The crude solid was purified by column chromatography to give 7 (40 mg, 49%). ¹HNMR (400 MHz, CDC1₃) δ: 8.16 (s, 1H), 8.14 (s, 1H), 7.56 (s, 2H), 7.54 (d, J = 4, 4H), 7.51 (d, J = 4, 4H), 1.31 (s, 18H). ¹³CNMR (100 MHz, CDC1₃) δ: 141.35, 140.05, 139.89, 136.77, 134.10, 131.29, 125.64, 125.38, 120.85, 117.39, 97.51, 86.99, 49.30, 33.67.

2,6-Bis[(4-acetylthiophenyl)ethynyl]benzo[1,2-b:5,4-b′] dithiophene (BDT-3)⁶². TiCl₄ (0.042 mL, 0.388 mmol) was added drop-wise to a solution of compound (7) (100 mg, 0.176 mmol) and CH₃C(O)C1 (0.03 mL, 0.397 mmol) in CH₂C1₂ at 0 °C. The resulting mixture was stirred at room temperature for 10 min and the conversion was monitored by TLC (hexanes/CH₂C1₂ 2 : 1). Upon completion the reaction was quenched with water (10 mL). The crude solid was purified by column chromatography to give BDT-3 (25 mg, 26%). ¹HNMR (400 MHz, CDC1₃) δ: 8.17 (s, 1H), 8.15 (s, 1H), 7.59 (d, J = 7.2, 4H), 7.58 (s, 2H), 7.43 (d, J = 8.2, 4H), 2.45 (s, 3H). ¹³CNMR (100 MHz, CDC1₃) δ: 195.88, 141.43, 140.03, 136.90, 134.76, 131.51, 131.48, 126.27, 126.50, 120.94, 117.42, 97.22, 87.15, 32.97. HRMS(ESI) calcd for C₃₀H₁₈O₂S₄ [M + H]⁺: 539.02624, found: 539.02476.

Self-assembled monolayers

The SAMs of BDT-n were formed via in situ deprotection^41,51 on template-stripped Au substrates.⁶³ Freshly template-stripped substrates were immersed into 3 mL of 50 μM solutions of the thioacetate precursors in freshly distilled toluene inside a nitrogen-filled glovebox and sealed under a nitrogen atmosphere. The sealed vessels were kept inside a nitrogen flow box⁶⁴ (O₂ below 3%, RH below 15%) overnight; all subsequent handling and EGaIn measurements were performed inside the flowbox. 1.5 h prior to measurement, 0.05 mL of 17 mM diazabicycloundec-7-ene (DBU) in toluene was added to the precursor/substrate solution. The substrates were then rinsed with toluene and allowed to dry for 30 min before performing the measurements.

Characterization

The SAMs of BDT-n were characterized by XPS (laboratory and synchrotron), NEXAFS spectroscopy, UPS and water contact angle goniometry. In some cases, SAMs of CH₃(CH₂)₁₅SH or CH₃(CH₂)₁₇SH on Au were used as a reference. See ESI† for details.

Transport measurements

EGaIn. For each SAM, at least 10 junctions were measured on each of three different substrates by applying a bias from 0.00 V → 1.00 V → −1.00 V → 0.00 V with steps of 0.05 V. At least 20 trace/re-trace cycles were measured for each junction; only junctions that did not short over all 20 cycles were counted as “working junction” for computing yields.

CP-AFM. I–V measurements were performed on a Bruker AFM Multimode MMAFM-2 equipped with a Peak Force TUNA Application Module. The Au on mica substrates were removed from the flowbox immediately prior to measurement, which occurred under ambient conditions by contacting the SAM with a Au-coated SI₃N₄ tip with a nominal radius of 30 nm (NPG-10, Bruker; resonant frequency: 65 kHz, spring constant: 0.35 N m⁻¹). The AFM tip was grounded and the samples were biased from −1.0 V → 1.0 V → −1.0 V on Au^Mica. 11 trace/re-trace cycles per junction were performed and the top electrode was removed from SAMs between junctions.

Processing. All raw data were processed algorithmically using Scientific Python to generate histograms, Gaussian fits, extract transition voltages and construct differential conductance heatmap plots.

DFT calculations

Calculation were performed using the ORCA 4 software package^65,66 and the ARTAIOS-030417 software package.^67,68 The molecules terminating with thiols were first minimized to find the gas-phase geometry and then attached to two 18-atom Au(111) clusters via the terminal sulfur atoms with a distance of 1.75 Å at hexagonal close-pack hollow sites (hydrogen atom from the thiol was deleted before attaching the electrodes). Single-point energy calculations were performed on this model junction using B3LYP/G and LANL2DZ basis sets according to literature procedures to compute the energy levels.⁶⁷ Transmission curves and isoplots of the central molecular orbitals, for isolated molecules without electrodes and terminal hydrogen atoms, were generated using the ARTAIOS-030417 software package and the energy axis was scaled using the E_F of −4.3 eV. The use of this E_F value for comparing transmission trends to the experimental tunneling conduction in Au/SAM//EGaIn junction is supported by the UPS measurements that also give a similar E_F value (see ESI Section 1.3.3†). It is has also been established experimentally that SAMs of aliphatic and conjugated molecules on Au shift the E_F values by 0.85 and 0.98 eV, respectively, (i.e., to −4.2 eV to −4.4 eV) from −5.2 eV for a clean gold surface.^69–71 This value of E_F was used for all DFT calculations. Further rational for choosing this value of E_F and the detailed step-wise procedure for all the calculations involved is further described in ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

R. C. C., Y. Z. and M. C. acknowledge the European Research Council for the ERC Starting Grant 335473 (MOLECSYNCON). G. Y. acknowledges financial support from the China Scholarship Council (CSC): No. 201408440247. X. Q. acknowledges the Zernike Institute for Advanced Materials “Dieptestrategie.” E. S. and M. Z. thank the Helmholtz Zentrum Berlin for the allocation of synchrotron radiation beamtime at BESSY II and A. Nefedov and Ch. Wöll for the technical cooperation during the experiments there; a financial support of the German Research Society (Deutsche Forschungsgemeinschaft; DFG) within the grant ZH 63/22-1 is appreciated. We thank the Center for Information Technology of the University of Groningen for their support and for providing access to the Peregrine high performance computing cluster.

References

1. A. Vilan, D. Aswal and D. Cahen, Large-Area, Ensemble Molecular Electronics: Motivation and Challenges, Chem. Rev., 2017, 117, 4248–4286.
2. N. Xin and X. Guo, Catalyst: The Renaissance of Molecular Electronics, Chem, 2017, 3, 373–376.
3. E. Lörtscher, Reaction: Technological Aspects of Molecular Electronics, Chem, 2017, 3, 376–377.
4. L.-Y. Hsu, B.-Y. Jin, C.-h. Chen and S.-M. Peng, Reaction: New Insights Into Molecular Electronics, Chem, 2017, 3, 378–379.
5. C. J. Lambert, Basic Concepts of Quantum Interference and Electron Transport in Single-Molecule Electronics, Chem. Soc. Rev., 2015, 44, 875–888.
6. R. a. Webb, S. Washburn, C. P. Umbach and R. B. Laibowitz, Observation of He Aharonov-Bohm Oscillations in Normal-Metal Rings, Phys. Rev. Lett., 1985, 54, 2696–2699.
7. P. Sautet and C. Joachim, Electronic Interference Produced by a Benzene Embedded in a Polyacetylene Chain, Chem. Phys. Lett., 1988, 153, 511–516.
8. L.-Y. Hsu and B.-Y. Jin, An investigation of quantum transport by the free-electron network model: resonance and interference effects, Chem. Phys., 2009, 355, 177–182.
9. D. M. Cardamone, C. A. Stafford and S. Mazumdar, Controlling Quantum Transport through a Single Molecule, Nano Lett., 2006, 6, 2422–2426.
10. G. C. Solomon, D. Q. Andrews, R. P. Van Duyne and M. A. Ratner, When Things Are Not as They Seem: Quantum Interference Turns Molecular Electron Transfer “Rules” Upside Down, J. Am. Chem. Soc., 2008, 130, 7788–7789.
11. G. C. Solomon, D. Q. Andrews, R. H. Goldsmith, T. Hansen, M. R. Wasielewski, R. P. Van Duyne and M. a. Ratner, Quantum Interference in Acyclic Systems: Conductance of Cross-Conjugated Molecules, J. Am. Chem. Soc., 2008, 130, 17301–17308.
12. D. Q. Andrews, G. C. Solomon, R. H. Goldsmith, T. Hansen, M. R. Wasielewski, R. P. V. Duyne and M. A. Ratner, Quantum Interference: The Structural Dependence of Electron Transmission Through Model Systems and Cross-Conjugated Molecules, J. Phys. Chem. C, 2008, 112, 16991–16998.
13. G. C. Solomon, C. Herrmann, T. Hansen, V. Mujica and M. A. Ratner, Exploring Local Currents in Molecular Junctions, Nat. Chem., 2010, 2, 223–228.
14. E. Maggio, G. C. Solomon and A. Troisi, Exploiting Quantum Interference in Dye Sensitized Solar Cells, ACS Nano, 2014, 8, 409–418.
15. K. G. L. Pedersen, A. Borges, P. Hedegård, G. C. Solomon and M. Strange, Illusory Connection Between Cross-Conjugation and Quantum Interference, J. Phys. Chem. C, 2015, 119, 26919–26924.
16. D. Fracasso, H. Valkenier, J. C. Hummelen, G. C. Solomon and R. C. Chiechi, Evidence for Quantum Interference in SAMs of Arylethynylene Thiolates in Tunneling Junctions With Eutectic Ga-In (EGaIn) Top-Contacts, J. Am. Chem. Soc., 2011, 133, 9556–9563.
17. W. Hong, H. Valkenier, G. Mészáros, D. Z. Manrique, A. Mishchenko, A. Putz, P. M. García, C. J. Lambert, J. C. Hummelen and T. Wandlowski, An MCBJ Case Study: The Influence of Π-Conjugation on the Single-Molecule Conductance at a Solid/Liquid Interface, Beilstein J. Nanotechnol., 2011, 2, 699–713.
18. C. M. Guedon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. Van Der Molen, Observation of Quantum Interference in Molecular Charge Transport, Nat. Nanotechnol., 2012, 7, 305–309.
19. V. Kaliginedi, P. Moreno-García, H. Valkenier, W. Hong, V. M. García-Suárez, P. Buiter, J. L. H. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, Correlations Between Molecular Structure and Single-Junction Conductance: A Case Study With Oligo(phenylene-Ethynylene)-Type Wires, J. Am. Chem. Soc., 2012, 134, 5262–5275.
20. H. Valkenier, C. M. Guedon, T. Markussen, K. S. Thygesen, S. J. van der Molen and J. C. Hummelen, Cross-Conjugation and Quantum Interference: A General Correlation?, Phys. Chem. Chem. Phys., 2014, 16, 653–662.
21. M. Koole, J. M. Thijssen, H. Valkenier, J. C. Hummelen and H. S. J. van der Zant, Electric-Field Control of Interfering Transport Pathways in a Single-Molecule Anthraquinone Transistor, Nano Lett., 2015, 15, 5569–5573.
22. J. P. Bergfield, H. M. Heitzer, C. Van Dyck, T. J. Marks and M. A. Ratner, Harnessing Quantum Interference in Molecular Dielectric Materials, ACS Nano, 2015, 9, 6412–6418.
23. T. Markussen, R. Stadler and K. S. Thygesen, The Relation Between Structure and Quantum Interference in Single Molecule Junctions, Nano Lett., 2010, 10, 4260–4265.
24. C. Salhani, M. L. Della Rocca, C. Bessis, R. Bonnet, C. Barraud, P. Lafarge, A. Chevillot, P. Martin and J. C. Lacroix, Inelastic Electron Tunneling Spectroscopy in Molecular Junctions Showing Quantum Interference, Phys. Rev. B, 2017, 95, 165431.
25. M. Mayor, H. B. Weber, J. Reichert, M. Elbing, C. von Hänisch, D. Beckmann and M. Fischer, Electric Current Through a Molecular Rod—Relevance of the Position of the Anchor Groups, Angew. Chem., Int. Ed., 2003, 42, 5834–5838.
26. M. Taniguchi, M. Tsutsui, R. Mogi, T. Sugawara, Y. Tsuji, K. Yoshizawa and T. Kawai, Dependence of Single-Molecule Conductance on Molecule Junction Symmetry, J. Am. Chem. Soc., 2011, 133, 11426–11429.
27. J. S. Meisner, S. Ahn, S. V. Aradhya, M. Krikorian, R. Parameswaran, M. Steigerwald, L. Venkataraman and C. Nuckolls, Importance of Direct Metal π Coupling in Electronic Transport Through Conjugated Single-Molecule Junctions, J. Am. Chem. Soc., 2012, 134, 20440–20445.
28. C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. M. Woerde, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Signatures of Quantum Interference Effects on Charge Transport Through a Single Benzene Ring, Angew. Chem., Int. Ed., 2013, 52, 3152–3155.
29. J. R. Quinn, F. W. Foss, L. Venkataraman, M. S. Hybertsen and R. Breslow, Single-Molecule Junction Conductance Through Diaminoacenes, J. Am. Chem. Soc., 2007, 129, 6714–6715.
30. M. Kiguchi, H. Nakamura, Y. Takahashi, T. Takahashi and T. Ohto, Effect of Anchoring Group Position on Formation and Conductance of a Single Disubstituted Benzene Molecule Bridging Au Electrodes: Change of Conductive Molecular Orbital and Electron Pathway, J. Phys. Chem. C, 2010, 114, 22254–22261.
31. S. V. Aradhya, J. S. Meisner, M. Krikorian, S. Ahn, R. Parameswaran, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Dissecting Contact Mechanics From Quantum Interference in Single-Molecule Junctions of Stilbene Derivatives, Nano Lett., 2012, 12, 1643–1647.
32. D. Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. a. Al-Owaedi, H. Sadeghi, V. Kaliginedi, W. Hong, M. Gulcur and T. Wandlowski, et al., A Quantum Circuit Rule for Interference Effects in Single-Molecule Electrical Junctions, Nat. Commun., 2015, 6, 6389.
33. J. Xia, B. Capozzi, S. Wei, M. Strange, A. Batra, J. R. Moreno, R. J. Amir, E. Amir, G. C. Solomon and L. Venkataraman, et al., Breakdown of Interference Rules in Azulene, a Nonalternant Hydrocarbon, Nano Lett., 2014, 14, 2941–2945.
34. F. Schwarz, M. Koch, G. Kastlunger, H. Berke, R. Stadler, K. Venkatesan and E. Lörtscher, Charge Transport and Conductance Switching of Redox-Active Azulene Derivatives, Angew. Chem., Int. Ed., 2016, 55, 11781–11786.
35. G. Yang, S. Sangtarash, Z. Liu, X. Li, H. Sadeghi, Z. Tan, R. Li, J. Zheng, X. Dong and J.-Y. Liu, et al., Protonation Tuning of Quantum Interference in Azulene-Type Single-Molecule Junctions, Chem. Sci., 2017, 8, 7505–7509.
36. R. Baer and D. Neuhauser, Phase Coherent Electronics: A Molecular Switch Based on Quantum Interference, J. Am. Chem. Soc., 2002, 124, 4200–4201.
37. G. C. Solomon, C. Herrmann, J. Vura-Weis, M. R. Wasielewski and M. A. Ratner, The Chameleonic Nature of Electron Transport Through Π-Stacked Systems, J. Am. Chem. Soc., 2010, 132, 7887–7889.
38. A. A. Kocherzhenko, F. C. Grozema and L. D. A. Siebbeles, Charge Transfer Through Molecules With Multiple Pathways: Quantum Interference and Dephasing, J. Phys. Chem. C, 2010, 114, 7973–7979.
39. N. F. Phelan and M. Orchin, Cross Conjugation, J. Chem. Educ., 1968, 45, 633–637.
40. P. a. Limacher and H. P. Lüthi, Cross-Conjugation, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 477–486.
41. M. Carlotti, A. Kovalchuk, T. Wächter, X. Qiu, M. Zharnikov and R. C. Chiechi, Conformation-Driven Quantum Interference Effects Mediated by Through-Space Conjugation in Self-Assembled Monolayers, Nat. Commun., 2016, 7, 13904.
42. A. Borges, J. Xia, S. H. Liu, L. Venkataraman and G. C. Solomon, The Role of Through-Space Interactions in Modulating Constructive and Destructive Interference Effects in Benzene, Nano Lett., 2017, 17, 4436–4442.
43. S. Sangtarash, H. Sadeghi and C. J. Lambert, Exploring Quantum Interference in Heteroatom-Substituted Graphene-Like Molecules, Nanoscale, 2016, 8, 13199–13205.
44. X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z.-Y. Xiao, W. Hong, C. J. Lambert and S.-X. Liu, Gating of Quantum Interference in Molecular Junctions by Heteroatom Substitution, Angew. Chem., Int. Ed., 2017, 56, 173–176.
45. Y. Tsuji, T. Stuyver, S. Gunasekaran and L. Venkataraman, The Influence of Linkers on Quantum Interference: A Linker Theorem, J. Phys. Chem. C, 2017, 121, 14451–14462.
46. H. Lissau, R. Frisenda, S. T. Olsen, M. Jevric, C. R. Parker, A. Kadziola, T. Hansen, H. S. J. van der Zant, M. B. Nielsen and K. V. Mikkelsen, Tracking molecular resonance forms of donor–acceptor push–pull molecules by single-molecule conductance experiments, Nat. Commun., 2015, 6, 10233.
47. Z. Wang, H. Dong, T. Li, R. Hviid, Y. Zou, Z. Wei, X. Fu, E. Wang, Y. Zhen and K. Norgaard, et al., Role of redox centre in charge transport investigated by novel self-assembled conjugated polymer molecular junctions, Nat. Commun., 2015, 6, 7478.
48. P. Pourhossein, R. K. Vijayaraghavan, S. C. J. Meskers and R. C. Chiechi, Optical Modulation of Nano-Gap Tunnelling Junctions Comprising Self-Assembled Monolayers of Hemicyanine Dyes, Nat. Commun., 2016, 7, 11749.
49. S. Seo, E. Hwang, Y. Cho, J. Lee and H. Lee, Functional Molecular Junctions Derived From Double Self-Assembled Monolayers, Angew. Chem., Int. Ed., 2017, 56, 12122–12126.
50. R. C. Chiechi, E. A. Weiss, M. D. Dickey and G. M. Whitesides, Eutectic Gallium–Indium (EGaIn): A Moldable Liquid Metal for Electrical Characterization of Self-Assembled Monolayers, Angew. Chem., Int. Ed., 2008, 120, 148–150.
51. H. Valkenier, E. H. Huisman, P. A. van Hal, D. M. de Leeuw, R. C. Chiechi and J. C. Hummelen, Formation of High-Quality Self-Assembled Monolayers of Conjugated Dithiols on Gold: Base Matters, J. Am. Chem. Soc., 2011, 133, 4930–4939.
52. J. Lykkebo, A. Gagliardi, A. Pecchia and G. C. Solomon, IETS and Quantum Interference: Propensity Rules in the Presence of an Interference Feature, J. Chem. Phys., 2014, 141, 124119.
53. J. M. Beebe, B. Kim, C. D. Frisbie and J. G. Kushmerick, Measuring Relative Barrier Heights in Molecular Electronic Junctions With Transition Voltage Spectroscopy, ACS Nano, 2008, 2, 827–832.
54. Y. Zhang, X. Qiu, P. Gordiichuk, S. Soni, T. L. Krijger, A. Herrmann and R. C. Chiechi, Mechanically and Electrically Robust Self-Assembled Monolayers for Large-Area Tunneling Junctions, J. Phys. Chem. C, 2017, 121, 14920–14928.
55. K. G. L. Pedersen, M. Strange, M. Leijnse, P. Hedegard, G. C. Solomon and J. Paaske, Quantum Interference in Off-Resonant Transport Through Single Molecules, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 125413.
56. G. C. Solomon, Cross Conjugation, Wiley-VCH Verlag GmbH & Co. KGaA, 2016, pp. 397–412.
57. M. Baghernejad, X. Zhao, K. Baruël Ørnsø, M. Füeg, P. Moreno-García, A. V. Rudnev, V. Kaliginedi, S. Vesztergom, C. Huang and W. Hong, et al., Electrochemical Control of Single-Molecule Conductance by Fermi-Level Tuning and Conjugation Switching, J. Am. Chem. Soc., 2014, 136, 17922–17925.
58. C.-Y. Kuo, W. Nie, H. Tsai, H.-J. Yen, A. D. Mohite, G. Gupta, A. M. Dattelbaum, D. J. William, K. C. Cha and Y. Yang, et al., Structural Design of Benzo[1,2-b:4,5-b]dithiophene-Based 2D Conjugated Polymers With Bithienyl and Terthienyl Substituents Toward Photovoltaic Applications, Macromolecules, 2014, 47, 1008–1020.
59. R. Rieger, D. Beckmann, A. Mavrinskiy, M. Kastler and K. Müllen, Backbone Curvature in Polythiophenes, Chem. Mater., 2010, 22, 5314–5318.
60. Z.-F. Shi, L.-J. Wang, H. Wang, X.-P. Cao and H.-L. Zhang, Synthesis of Oligo(phenylene Ethynylene)s With Dendrimer “Shells” for Molecular Electronics, Org. Lett., 2007, 9, 595–598.
61. E. H. van Dijk, D. J. T. Myles, M. H. van der Veen and J. C. Hummelen, Synthesis and Properties of an Anthraquinone-Based Redox Switch for Molecular Electronics, Org. Lett., 2006, 8, 2333–2336.
62. T. C. Pijper, J. Robertus, W. R. Browne and B. L. Feringa, Mild Ti-Mediated Transformation of T-Butyl Thio-Ethers Into Thio-Acetates, Org. Biomol. Chem., 2015, 13, 265–268.
63. E. A. Weiss, G. K. Kaufman, J. K. Kriebel, Z. Li, R. Schalek and G. M. Whitesides, Si/SiO₂-Templated Formation of Ultraflat Metal Surfaces on Glass, Polymer, and Solder Supports: Their Use as Substrates for Self-Assembled Monolayers, Langmuir, 2007, 23, 9686–9694.
64. M. Carlotti, M. Degen, Y. Zhang and R. C. Chiechi, Pronounced Environmental Effects on Injection Currents in EGaIn Tunneling Junctions Comprising Self-Assembled Monolayers, J. Phys. Chem. C, 2016, 120, 20437–20445.
65. F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
66. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
67. C. Herrmann, L. Gross, T. Steenbock, M. Deffner, B. A. Voigt and G. C. Solomon, ARTAIOS - A Transport Code for Postprocessing Quantum Chemical Electronic Structure Calculations, https://www.chemie.uni-hamburg.de/ac/herrmann/software/index.html. 2016.
68. C. Herrmann, G. C. Solomon, J. E. Subotnik, V. Mujica and M. A. Ratner, Ghost Transmission: How Large Basis Sets Can Make Electron Transport Calculations Worse, J. Chem. Phys., 2010, 132, 024103.
69. O. M. Cabarcos, S. Schuster, I. Hehn, P. P. Zhang, M. M. Maitani, N. Sullivan, J.-B. Gigure, J.-F. Morin, P. S. Weiss and E. Zojer, et al., Effects of Embedded Dipole Layers on Electrostatic Properties of Alkanethiolate Self-Assembled Monolayers, J. Phys. Chem. C, 2017, 121, 15815–15830.
70. T. AbuHusein, S. Schuster, D. A. Egger, M. Kind, T. Santowski, A. Wiesner, R. Chiechi, E. Zojer, A. Terfort and M. Zharnikov, The Effects of Embedded Dipoles in Aromatic SelfAssembled Monolayers, Adv. Funct. Mater., 2015, 25, 3943–3957.
71. A. Kovalchuk, T. Abu-Husein, D. Fracasso, D. A. Egger, E. Zojer, M. Zharnikov, A. Terfort and R. C. Chiechi, Transition voltages respond to synthetic reorientation of embedded dipoles in self-assembled monolayers, Chem. Sci., 2016, 7, 781–787.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc00165k

‡ These authors contributed equally to this work.

---