Open Access Article
Open Access ArticleNew insights into aromatic pathways of carbachlorins and carbaporphyrins based on calculations of magnetically induced current densities†
Isaac
Benkyi
*a,
Heike
Fliegl
*b,
Rashid R.
Valiev
*cd and
Dage
Sundholm
*a
aUniversity of Helsinki, Department of Chemistry, P. O. Box 55 (A.I. Virtanens plats 1), FIN-00014 University of Helsinki, Finland. E-mail: Dage.Sundholm@helsinki.fi
bCentre for Theoretical and Computational Chemistry (CTCC), Department of Chemistry, University of Oslo, P. O. Box 1033 Blindern, 0315 Oslo, Norway. E-mail: Heike.Fliegl@kjemi.uio.no
cTomsk Polytechnic University, 43a Lenin Avenue, Building 2, Tomsk 634050, Russian Federation
dTomsk State University, Lenina Avenue 36, Tomsk, Russian Federation. E-mail: valievrashid@mail.ru
First published on 25th February 2016
Abstract
Magnetically induced current densities have been calculated and analyzed for a number of synthesized carbachlorins and carbaporphyrins using density functional theory and the gauge including magnetically induced current (GIMIC) method. Aromatic properties have been determined by using accurate numerical integration of the current flow yielding reliable current strengths and pathways that are related to the degree of aromaticity and the aromatic character of the studied molecules. All investigated compounds are found to be aromatic. However, the obtained aromatic pathways differ from those previously deduced from spectroscopic data and magnetic shielding calculations. For all studied compounds, the ring current divides into an outer and an inner branch at each pyrrolic subring, showing that all π-electrons of the pyrrolic rings take part in the delocalization pathway. The calculations do not support the common notion that the main share of the current takes the inner route at the pyrrolic rings without an inner hydrogen and follows an 18π aromatic pathway. The aromatic pathways of the investigated carbaporphyrins and carbachlorins are very similar, since the current strength via the Cβ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cβ′ bond of the cyclopentadienyl ring of the carbaporphyrins is almost as weak as the current density passing the corresponding saturated Cβ–Cβ′ bond of the carbachlorins.
Cβ′ bond of the cyclopentadienyl ring of the carbaporphyrins is almost as weak as the current density passing the corresponding saturated Cβ–Cβ′ bond of the carbachlorins.
1 Introduction
Carbaporphyrinoids are porphyrin analogues in which one of the nitrogen atoms of the porphyrin macroring is replaced by an isoelectronic CH moiety.1–6 Carbachlorins are similar molecules with a saturated Cβ–Cβ′ bond of the cyclopentadienyl ring. This class of organic compounds is interesting for chemists due to their potential use in catalysis as they are able to bind metals in unusual oxidation states.1,6 In particular carbaporphyrinoid compounds such as carbachlorins with strong absorption bands at around 650 nm or even at longer wavelengths have the potential to be used as photosensitizers in photodynamic therapy.7A clear picture of the full utilization of these compounds cannot be obtained without elucidating their aromatic properties. In spite of their unusual structure and chemistry, carbaporphyrinoids can be expected to be aromatic like most planar organic (heterocylic) compounds that exhibit conjugation pathways fulfilling the Hückel 4n + 2π rule for aromaticity. However, very little is known about their aromatic character and electron delocalization pathways,8,9 mainly because it is challenging to experimentally quantify the electron delocalization of complicated multiring molecules, and computational studies of the aromatic character of porphyrinoids are also demanding. By using the gauge-including magnetically induced current (GIMIC) method,10–12 it is though possible to determine current strength susceptibilities and current pathways by explicitly calculating the susceptibility of the magnetically induced current density passing selected chemical bonds. A careful analysis of the current density provides information about how electronic charge can be transported around molecular rings of fused multiring molecules.10,12–19 Comprehensive and detailed current-density studies have proven to be very helpful in elucidating the aromatic properties of porphyrinoids.20–28 Current density calculations carried out using the GIMIC program are an invaluable computational means for designing carbaporphyrinoids or other compounds with distinct aromaticity and electron delocalization features, since they can accurately predict aromatic pathways and ring-current strengths along different routes in the molecule.10–12,29 The GIMIC program, which is a stand-alone code, has been employed in a number of aromaticity studies of porphyrinoids.10,22–28 The studies have shown that numerical integration of the current strength susceptibilities passing selected chemical bonds is a reliable tool for quantifying molecular aromaticity according to the magnetic criterion.30–32 By calculating the current strength susceptibilities of selected chemical bonds one obtains information about the electron-delocalization pathways. The approach has proven to be very useful for determining current pathways in multiring molecules, where many other approaches are prone to fail.22,33–47
In this work, we have employed the GIMIC method at the density functional theory (DFT) level to investigate the aromatic character of a number of traditional carbaporphyrinoids and modified carbaporphyrinoids such as oxybenziporphyrin,48–50 benzocarbaporphyrin,51,52 azuliporphyrin51,53,54 and tropiporphyrin.55,56 In addition, we have also studied a number of carbachlorins that have been synthesized and characterized.9 The proton nuclear magnetic resonance (1H NMR) and ultraviolet-visible (UV-Vis) spectra have been recorded to assess the aromatic properties of the synthesized carbachlorins and carbaporphyrins.9 The calculated values for nucleus independent chemical shifts (NICS)57 have been previously used for assessing the aromatic character and delocalization pathways of carbaporphyrinoids,9 concluding that all the investigated carbaporphyrinoids are aromatic with a similar 18π aromatic pathway as the classical aromatic pathway of free-base porphyrin.9 Nowadays it is well known that the NICS approach has difficulties in accurately determining the degree of aromaticity of single molecular rings.33–43 Furthermore, NICS has even larger problems to provide reliable current pathways in multiring molecules such as free-base porphyrin.22,58–62 Here we aim at providing novel insights regarding the aromatic pathways and electron delocalization pathways of the investigated compounds using the reliable current-density integration technique for analyzing the current flow.
The computational methods are described in Section 2. The molecular structures of the carbaporphyrinoids are discussed in Section 3, whereas the results of the current density calculations are presented in detail for all studied molecules in Section 4. The results of the study are summarized in Section 5 where the main conclusions are also drawn.
2 Computational methods
The optimization of the molecular structures as well as the calculations of the NMR shieldings were performed at the density functional theory (DFT) level using the Becke-three-parameter functional combined with the Lee–Yang–Parr exchange–correlation functional (B3LYP)63,64 as implemented in Turbomole 6.6.65,66 The Karlsruhe triple-ζ quality basis set (def2-TZVP) was used for all atoms.67,68 The NMR shielding calculations were performed using the mpshift module of Turbomole.69,70 Benchmark calculations have shown that B3LYP/def2-TZVP calculations of 1H NMR and 13C NMR chemical shifts are close to the basis-set limit and agree qualitatively with experimental data for organic molecules.71The magnetically induced current densities were calculated at the B3LYP/def2-TZVP level using the GIMIC program.10–12 GIMIC is an independent program that uses the atomic orbital density matrix as well as the corresponding first-order magnetically perturbed density matrices from the NMR shielding calculations and basis-set information as input data.10,11 GIMIC employs gauge-including atomic orbitals (GIAOs), which imply that the basis set convergence is faster than with magnetic-field independent basis functions.10,72,73 When GIAOs are employed, the obtained gauge-origin independent current densities were close to the complete basis-set limit already when standard basis sets are used.72,73 The current densities can be analyzed by determining the current pathways, which are obtained by the numerical integration of the current-strength susceptibilities (in nA T−1) flowing along the chosen chemical bonds. The current pathways are visualized using the XMakemol74 and paint.net75 programs. The pictures of the molecules have been drawn using the Marvin program.76 The streamline representations of the current density have been obtained using PyNgl77 and the schematic ring labeling displayed in Fig. 15 has been done using ChemBioDraw78 and Gimp.79
The effects of dispersion corrections80 on the geometry and the current strength were investigated for oxybenziporphyrin. No significant changes in the molecular structure or the ring-current strength were observed. See ESI.†
3 Molecular structures and nomenclature
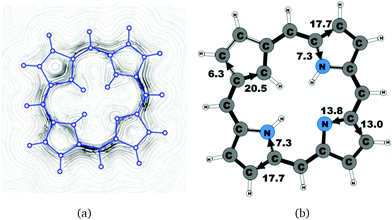
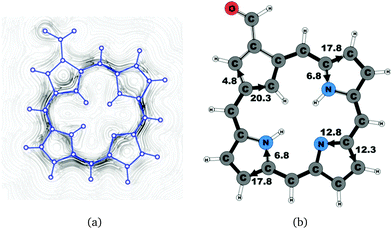
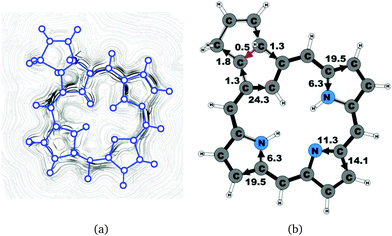
A number of recently synthesized carbaporphyrins and carbachlorins9 have been investigated computationally. The alkyl substituents have been omitted to save computational costs, since previous current density studies have shown that alkyl substituents do not significantly influence the current pathways and current strengths of aromatic porphyrinoids,25 whereas for antiaromatic porphyrinoids substituents such as ethylformate or pentafluorophenyl may significantly reduce the strength of the ring current.24–26 The labeling of the investigated molecules follows the one in ref. 9, which inspired us to perform the present study. The common notation enables easier comparison of the present results with previously published ones.9,50Carbaporphyrin 20 (Fig. 1) is the most simple carbaporphyrin without any substituents. The carbaporphyrin cation 20H+ (Fig. 2) is the protonated form of 20 with one extra inner hydrogen and a positive charge. The doubly protonated carbaporphyrin dication 20H22+ (Fig. 3) has five inner hydrogens of which two saturate the inner carbon of the cyclopentadienyl ring. Carbaporphyrin 14 (Fig. 4) has an aldehyde group substituted in one of the Cβ positions of the cyclopentadienyl ring of the carbaporphyrin.
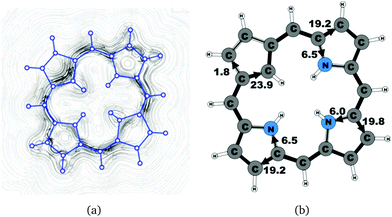
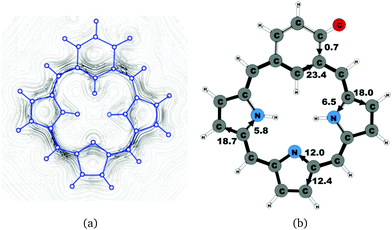
Carbachlorin 19 is the most simple carbachlorin with a saturated Cβ–Cβ′ bond of the cyclopentadienyl ring and without any substituents. Carbachlorin 19 (Fig. 5) lacks the inner hydrogen in the trans position to the cyclopentadienyl ring, whereas carbachlorin 19′ (Fig. 6) is the corresponding cis tautomer. The carbachlorin cation 19H+ (Fig. 7) is the protonated form of 19 and 19′ with four inner hydrogens.
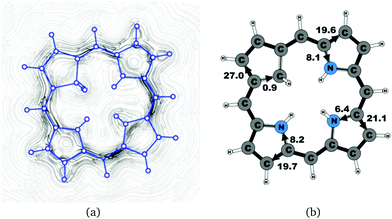
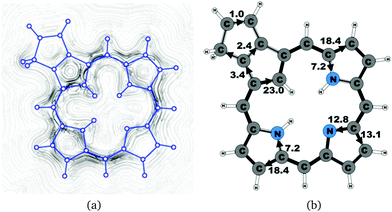
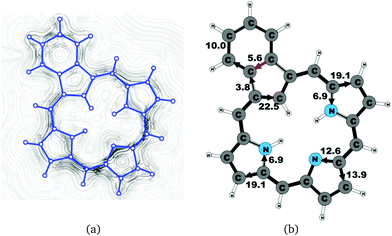
In compound 6b, a propene moiety is fused to the cyclopentadienyl ring forming a fused nonaromatic cyclopentene ring. The two ends of the propene moiety can bind to the cyclopentadienyl ring in the cis6b (Fig. 8) or trans6b (Fig. 9) position. Compounds 6b are propencarbachlorins, because the Cβ–Cβ′ bond of the cyclopentadienyl ring becomes saturated when binding the propene moiety to the cyclopentadienyl. Carbaporphyrins like compound 9 (Fig. 10) could in principle be obtained by oxidizing the corresponding carbachlorin. However, experimentally this is not straightforward since Li and Lash reported that they were not able to oxidize 6b,9 which would have yielded the corresponding carbaporphyrin 9.
Compounds 1–4 are modified carbaporphyrinoids. In oxybenziporphyrin 1 (Fig. 11), the cyclopentadienyl ring is replaced by a cylohexadienone moiety. In benzocarbaporphyrin 2 (Fig. 12), a benzoic ring is fused to the cyclopentadienyl ring. In azuliporphyrin 3 (Fig. 13), a cycloheptatriene ring is fused to the cyclopentadienyl ring, and in tropiporphyrin 4 (Fig. 14), the cyclopentadienyl ring is replaced by a cycloheptatrienyl ring.
4 Current-density calculations
All the investigated compounds are found to be aromatic according to the magnetic criterion. Streamline representations of the current densities obtained in a plane placed 1 bohr above the molecular plane and the calculated current density pathways that are obtained through explicit integration of the current flow across several chemical bonds are given in Fig. 1–14. An overview of the calculated results is given in Table 1 and the respective labeling of the pyrrolic rings is shown in Fig. 15.| Ring → molecule | Total | A | B | C | D | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 20 | 26.8 | 6.3 | 20.5 | 17.7 | 7.3 | 13.0 | 13.8 | 17.7 | 7.3 |
| 20H+ | 25.7 | 1.8 | 23.9 | 19.2 | 6.5 | 19.8 | 6.0 | 19.2 | 6.5 |
| 20H22+ | 27.8 | 27.0 | 0.9 | 19.6 | 8.1 | 21.1 | 6.4 | 19.7 | 8.2 |
| 14 | 24.8 | 4.8 | 20.3 | 17.8 | 6.8 | 12.8 | 12.3 | 17.8 | 6.8 |
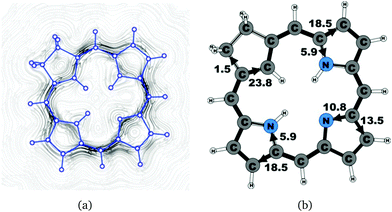
| 19 | 24.6 | 1.5 | 23.8 | 18.5 | 5.9 | 13.5 | 10.8 | 18.5 | 5.9 |
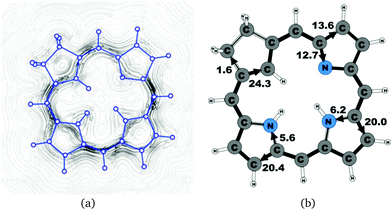
| 19′ | 26.1 | 1.6 | 24.3 | 13.6 | 12.7 | 20.0 | 6.2 | 20.4 | 5.6 |
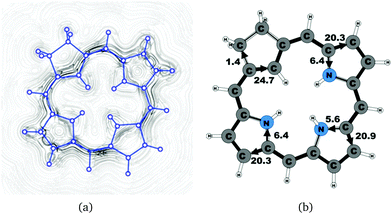
| 19H+ | 26.5 | 1.4 | 24.7 | 20.3 | 6.4 | 20.9 | 5.6 | 20.3 | 6.4 |
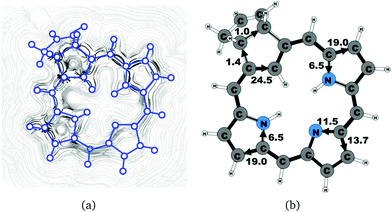
| 6b (cis) | 25.5 | 1.4 | 24.5 | 19.0 | 6.5 | 13.7 | 11.5 | 19.0 | 6.5 |
| 6b (trans) | 25.7 | 1.3 | 24.3 | 19.5 | 6.3 | 14.1 | 11.3 | 19.5 | 6.3 |
| 9 | 25.9 | 3.4 | 23.0 | 18.4 | 7.2 | 13.1 | 12.8 | 18.4 | 7.2 |
| 1 | 24.4 | 0.7 | 23.4 | 18.0 | 6.5 | 12.4 | 12.0 | 18.7 | 5.8 |
| 2 | 26.5 | 3.8 | 22.5 | 19.1 | 6.9 | 13.9 | 12.6 | 19.1 | 6.9 |
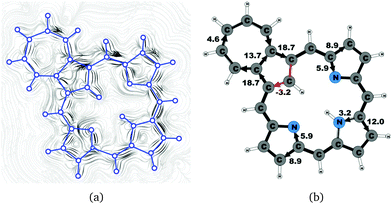
| 3 | 15.1 | 18.7 | −3.2 | 8.9 | 5.9 | 12.0 | 3.2 | 8.9 | 5.9 |
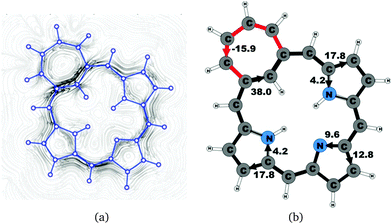
| 4 | 22.1 | −15.9 | 38.0 | 17.8 | 4.2 | 12.8 | 9.6 | 17.8 | 4.2 |
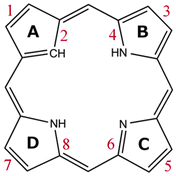 | ||
| Fig. 15 The numbering of the current pathways of the carbaporphyrinoids. Odd numbers indicate outer routes. | ||
The current density calculations show that the aromatic pathway of the studied carbaporphyrinoids does not follow the classical 18π aromaticity route of porphyrinoids as suggested by Li and Lash.9 This is not surprising, since the classical 18π aromatic pathway of porphyrins and chlorins might not even be correct.10,22,59,81 The aromatic pathways of the studied carbaporphyrins and carbachlorins are indeed very reminiscent of the aromatic pathway of porphyrins and chlorins as previously obtained in current density calculations.22 Similar current pathways as obtained for the carbaporphyrinoids have also been obtained in a number of current density studies on other porphyrinoids.20–28
For all studied compounds, the ring current divides into an outer and an inner pathway at each pyrrolic subring. Thus, all π-electrons of the pyrrolic rings take part in the delocalization pathways. The calculations show that the resistance of the inner NH group is generally larger than for the inner nitrogen without a hydrogen. Thus, a stronger current passes the inner N than the inner NH moiety of the pyrrolic rings. For the pyrrolic rings without an inner hydrogen, the current strengths via the outer and inner pathways are almost the same, whereas for the pyrrolic rings with an inner hydrogen roughly 25% of the current takes the inner route. Thus, the common notion that the main part of the current takes the inner route at the pyrrolic rings without an inner hydrogen is incorrect. One of the main conclusions of this work is that all current pathways for the carbaporphyrinoids suggested by Li and Lash are not completely correct.9 A comparison of the diatropic and paratropic contributions to the net current strength passing the meso-carbon with the ones passing via the inner and outer routes of the pyrrolic rings show that the pyrrolic rings do not sustain any strong local ring currents. In the following, we discuss in more detail the current pathways at the all-carbon subrings of the studied carbaporphyrinoids.
4.1 Carbaporphyrins 20, 20H+ and 20H22+
Molecule 20 is the unsubstituted trans-carbaporphyrin lacking the inner hydrogen in the trans position relative to the cyclopentadienyl ring. The calculations of the current density for 20 have recently been reported,27 whereas in this work we have also studied the current densities of the protonated 20H+ and diprotonated 20H22+ forms of 20. The current pathways are shown in Fig. 1–3. At the cyclopentadienyl ring the inner pathway dominates for 20 and 20H+. For 20, only 6.3 nA T−1 of the total ring current of 26.8 nA T−1 takes the outer route.27 For the protonated form, the current strength of 1.8 nA T−1 along the outer pathway is even weaker, whereas the total ring-current strength of 25.7 nA T−1 is practically the same as for the unprotonated 20. The doubly protonated 20H22+ has five inner hydrogens implying that the inner carbon of the all-carbon five-membered subring is saturated. For 20H22+, the ring current of 27.8 nA T−1 is slightly larger than for 20 and mainly takes the outer route, whose current strength is 27.0 nA T−1 as compared to the tiny 0.9 nA T−1 along the inner pathway. For these molecules, Li and Lash suggested an 18π aromaticity, where the inner NH groups and the Cβ atoms of the pyrrolic ring without an inner hydrogen do not belong to the aromatic pathway.9 Proton and carbon NMR spectroscopy suggest that 20 is planar,9 whereas according to the calculations the planar form is a transition state. The small barrier of 1.9 kcal mol−1 does not prevent the thermal motion across the barrier implying that the molecule is on the average planar. The ring-current strength of planar 20 is 26.2 nA T−1 showing that the small nonplanarity of 20 does not significantly affect the aromatic properties.4.2 Carbaporphyrin 14
Substituent effects were studied by adding an aldehyde group to one of the Cβ positions of the cyclopentadienyl ring. Carbaporphyrin 14 with an aldehyde group in the Cβ position as shown in Fig. 4 sustains a net ring-current whose strength is 24.8 nA T−1. The net ring-current is 2.0 nA T−1 smaller than the one obtained for 20,27 whereas the current strength of 20.3 nA T−1 along the inner pathway at the cyclopentadienyl ring is almost the same for 14 and 20. Substitution of the aldehyde group to the Cβ position of the cyclopentadienyl ring decreases the current strength along the outer pathway by 1.5 nA T−1, which is probably due to the electron withdrawing effect of the aldehyde group. However, the substitution does not influence the current pattern of the rest of the molecule.4.3 Carbachlorins 19, 19′ and 19H+
The studied carbachlorins 19, 19′ and 19H+ are identical to 11, 11′ and 11H+ that were synthesized by Li and Lash,9 when the alkyl substituents in the Cβ positions are omitted. The calculated ring-current strength of 19 is 24.6 nA T−1. As expected, most of the ring current (23.8 nA T−1) passes on the inside of the cyclopentadienyl ring, whereas only 1.5 nA T−1 takes the outer route via the saturated Cβ carbons. A current-density plot and the current strengths are shown in Fig. 5. The current-density analysis reveals that the current pathway of 19 is very similar to the ones obtained for the other carbachlorin compounds. However, the ring current is somewhat stronger along the outer route at the pyrrolic rings than for the carbaporphyrins. For example, 56% of the ring current passes the Cβ carbons of the pyrrolic ring without an inner hydrogen. Li and Lash suggested that the ring current takes the outer pathway at the pyrrolic rings with inner hydrogens and the inner one at the pyrrolic ring without the inner hydrogen,9 which is the traditional but incorrect aromatic pathway of porphyrins and chlorins. Thus, the suggested aromatic pathway of carbachlorin 19 is not completely correct.9The current pathway of tautomer 19′ is very similar to that of 19. The largest difference in the current pattern is obtained for the pyrrolic ring without the inner hydrogen, where current strengths along the outer and inner routes are almost equal in this case. The net current strength of 26.1 nA T−1 is about 1.5 nA T−1 larger than for 19. The current strengths are shown in Fig. 6. The aromatic pathway at each of the pyrrolic rings looks like the aromatic pathway for 19 and 19′ at the pyrrolic rings with an inner hydrogen. Thus, the ring current flows mainly along the outer bonds of the protonated carbachlorin 19H+. The current pathways are shown in Fig. 7. Li and Lash suggested that the aromatic pathway for 19H+ can be considered as a superposition of three pathways because the NICS values in the three pyrrolic rings are practically the same.9 Since the total ring-current strength is 26.5 nA T−1, each of these pathways would have a current strength of almost 9 nA T−1. The superposed current pattern would then be 17.7 nA T−1 along the outer pathway and 8.8 nA T−1via the inner route, which can be compared to the calculated combined current of 20.3–20.9 nA T−1 along the outer route and 5.6–6.4 nA T−1 takes the inner one. When applying the superposition principle, the current flow of 1.4 nA T−1 passing the saturated Cβ atoms of the all-carbon five-membered ring introduces uncertainties of 0.5 nA T−1 and 1.0 nA T−1 in the current strengths of the inner and outer pathways, respectively. Thus, the ratio between the current strengths of the outer and inner pathways is too large for validating the superposition principle.
4.4 Carbachlorin 6b
Carbachlorin 6b (cis) sustains a net current strength of 25.5 nA T−1 of which 24.5 nA T−1 takes the inner pathway at the all-carbon five-membered ring. At the pyrrolic rings, the ring current follows largely the same pattern as in the corresponding unsubstituted carbachlorin 19. The calculated current pattern at the pyrrolic rings of compound 6b (trans) is very similar to the one obtained for 6b (cis). The net current strength is 25.7 nA T−1. The current flow at the propene substituted all-carbon five-membered ring of 1.3 nA T−1 takes the outermost route. In addition the fused cyclopentene ring due to the propene substitution sustains a tiny local ring current of 0.5 nA T−1.4.5 Carbaporphyrin 9
Carbaporphyrin 9 can in principle be obtained by oxidizing carbachlorin 6. However, that reaction step was unsuccessful.9 Current-density calculations show that carbaporphyrin 9 is expected to have similar ring-current pathways as obtained for the unsubstituted carbaporphyrin 20. The net ring-current strength is 25.9 nA T−1 as compared to 26.8 nA T−1 for 20 and 25.5–25.7 nA T−1 for 6b. A small current of 1.0 nA T−1 passes the saturated CH2 group of the cyclopentene ring fused to the cyclopentadienyl ring of the carbaporphyrin, whereas a current strength of 2.4 nA T−1 passes the common bond of the two five-membered rings.4.6 Oxybenziporphyrin 1
Oxybenziporphyrin 1 is a carbaporphyrinoid where the cyclopentadienyl ring is replaced by a cylohexadienone ring.521 sustains a net ring-current strength of 24.4 nA T−1 around the macrocycle, which is 3 nA T−1 (10%) smaller than for porphyrin.22 The current pattern at the pyrrolic rings is the same as for porphyrin and the other carbaporphyrinoids studied in this work. The current strengths along the different routes are shown in Fig. 11. The carbonyl group of the cylohexadienone ring prevents the ring-current to take the outer route. Thus, only 0.7 nA T−1 flows on the outside of the cylohexadienone ring and 23.4 nA T−1 takes the inner pathway. The net ring-current strength calculated for the molecular structure of 1 optimized at the same level of theory using also the D3 correction differs by only 0.3 nA T−1 from the value of 24.4 nA T−1 as obtained without the D3 correction. Thus, the use of the D3 correction has almost no effect on the ring current strengths of the investigated class of molecules.4.7 Benzocarbaporphyrin 2
Benzocarbaporphyrin 2 is a carbaporphyrin with a benzoic ring fused to the Cβ bond of the cyclopentadienyl ring.49 The current pattern at the pyrrolic rings is very similar to that of the other carbaporphyrinoids of this work. The ring-current strength around the macrocycle of 26.5 nA T−1 is almost as large as for unsubstituted carbaporphyrin 20. At the cyclopentadienyl ring, the current prefers the inner route whose strength is 22.5 nA T−1, whereas a current of 3.8 nA T−1 flows outwards passing on the outside of the benzoic ring. The benzoic ring sustains a local ring current of 5.6 nA T−1. The current pathway and current strengths are shown in Fig. 12. The current density calculations show that the proposed 18π aromatic pathway is not completely correct.49,524.8 Azuliporphyrin 3
Azuliporphyrin 3 consists of a cycloheptatriene ring fused to the cyclopentadienyl ring of carbaporphyrin 20. Lash et al. proposed that it has some aromatic character, because the structure can formally be described by two resonance structures.49,52 The zwitterionic form is thought to sustain a ring current around the carbaporphyrin macrocycle, whereas in the other form the ring current circles only around the azulene moiety.49 However, the current density calculations yield a somewhat different picture of the aromatic character. The strength of the ring current circling around the carbaporphyrin macroring is 15.1 nA T−1, which is about 55% of the ring-current strength of porphyrin. At the azulene moiety the main current of 18.7 nA T−1 takes the outer route around the cyclopentadienyl ring, whereas a weaker current of 4.6 nA T−1 passes on the outside of the cycloheptatrienyl ring. The cyclopentadienyl ring sustains a weak local ring current of 3.2 nA T−1. At the pyrrolic rings, the main current flow passes the Cβ carbons. At the pyrrolic rings without an inner hydrogen, 40% of the current takes the inner route, whereas at the pyrrolic ring with an inner hydrogen only 20% of the current passes the NH moiety. The current pathways and current strengths are shown in Fig. 13.4.9 Tropiporphyrin 4
The calculated structure of tropiporphyrin 4, which is obtained from carbaporphyrin by replacing the cyclopentadienyl ring with a cycloheptatrienyl ring,55 is found to be almost planar with the largest out-of-plane torsional angle of 3° at the cycloheptatrienyl ring. The current strength of tropiporphyrin is 22.1 nA T−1, which is 82% of the ring-current strength of carbaporphyrin 20. The ring current around the macrocycle mainly passes along the outer routes at the pyrrolic rings. The pattern of the current flow around the carbaporphyrin ring is similar to the one for the other carbaporphyrins with about 20% of the ring current passing the NH moiety of the two pyrrolic rings with an inner hydrogen, whereas 43% of the ring current passes the nitrogen of the pyrrolic ring without an inner hydrogen. The cycloheptatrienyl ring is antiaromatic sustaining a strong local paratropic ring current of −15.9 nA T−1, thus forming a strongly antiaromatic ring fused to the aromatic one. Fused rings with opposite tropicity have previously been found for thienopyrrole modified 20π-electron porphyrinoids and thieno-bridged porphyrins.23,25 The current pathways and current strengths in Fig. 14 show that the calculations yield a different aromatic character as compared to the one deduced from the measured NMR chemical shifts.555 Summary and conclusions
Magnetically induced current densities of a number of synthesized as well as spectroscopically and theoretically characterized carbachlorins and carbaporphyrins9 have been studied computationally at the DFT level and analyzed using the gauge including magnetically induced current (GIMIC) method. The investigated compounds are found to be aromatic with calculated ring-current strength susceptibilities ranging from 15 nA T−1 to 27 nA T−1. Thus, they can be considered aromatic according to the magnetic criterion. Tropiporphyrin 3 has the weakest aromaticity among the studied molecules with a ring-current strength of 15.1 nA T−1, which can be compared to the ring-current strength of 12.0 nA T−1 for benzene.29 The calculated ring-current strengths and the current strengths of different pathways are summarized in Table 1 and the numbering of the bonds and rings are shown in Fig. 15.For most of the investigated carbaporphyrinoids, the inner pathway at the five membered all-carbon ring (A) is the preferred route and only a small current of 0.7 nA T−1 to 4.2 nA T−1 passes on the outer side of the ring, regardless of whether the bond is saturated or not. The only exceptions are 20H22+, 3 and 4, where the inner pathway is blocked by the saturated CH2, a cycloheptatriene ring is fused to the cyclopentadienyl ring, and a cycloheptatrienyl ring replaces the cyclopentadienyl ring, respectively. Previous studies on aromatic molecules have also shown how the insertion of CH2 moieties leads to changes in the current flow around porphyrinoids.22,27,28 Insertion of an aldehyde group to the cyclopentadienyl ring of carbaporphyrin 14 did not significantly affect the current density pattern and current strengths as compared to the unsubstituted carbaporphyrin 20. For azuliporphyrin 3 a cycloheptatriene ring is fused to the cyclopentadienyl ring, the ring current prefers the outer route. The current even splits into one branch passing around the cycloheptatrienyl ring, whereas the main current streams along the common bond between the cycloheptatrienyl and cyclopentadienyl rings. Tropiporphyrin 4 consists of an antiaromatic cycloheptatrienyl ring fused to the aromatic porphyrinoid macroring leading to a weaker ring-current strength of 21.9 nA T−1 as compared to 26.8 nA T−1 for carbaporphyrin 20. Similar current-strength trends were obtained for the pyrrolic rings as previously reported for other porphyrinoid compounds.22,27,28 For the investigated compounds the ring current divides at the pyrrolic rings into the inner and outer branches showing that all π-electrons of the pyrrolic rings participate in the current pathway. For pyrrolic rings B and D with an inner hydrogen, the main share of the current flows on the outside of the ring, whereas at the pyrrolic rings without an inner hydrogen. At ring C without an inner hydrogen, the current is almost equally split into the inner and outer branches or the main current pathway is along the outer route.
In conclusion, for the investigated compounds the calculated current pathways disagree with previously proposed ones. Lash et al. have proposed that the aromatic pathway of the studied carbaporphyrinoids follow an 18π-electron aromaticity route that excludes the Cβ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cβ′ bond of ring C, whereas the explicit current-density calculations of this work show that the ring current is generally stronger along the outer pathway of ring C than for the inner route.9,49,52,55 Furthermore, we show that all π-electrons of the pyrrolic rings participate in the electron delocalization pathway. For tropiporphyrin 4, the current-density analysis shows that the fused cycloheptatrienyl ring is antiaromatic. In general, the integration based current-density analysis provides accurate and reliable information about the aromatic character and the aromatic pathways of the studied multiring molecules. We suggest that one should not merely use spectroscopic data in combination with magnetic shielding calculations when aiming at information about the aromatic character of porphyrinoids, because the approaches do not provide very accurate information about molecular aromaticity for more complex molecules. Instead it is recommended to use current-density calculations in combination with numerical integration of current strengths, because this yields electron-delocalization pathways that show how electrons move around the molecular rings, when they are exposed to an external magnetic field.
Cβ′ bond of ring C, whereas the explicit current-density calculations of this work show that the ring current is generally stronger along the outer pathway of ring C than for the inner route.9,49,52,55 Furthermore, we show that all π-electrons of the pyrrolic rings participate in the electron delocalization pathway. For tropiporphyrin 4, the current-density analysis shows that the fused cycloheptatrienyl ring is antiaromatic. In general, the integration based current-density analysis provides accurate and reliable information about the aromatic character and the aromatic pathways of the studied multiring molecules. We suggest that one should not merely use spectroscopic data in combination with magnetic shielding calculations when aiming at information about the aromatic character of porphyrinoids, because the approaches do not provide very accurate information about molecular aromaticity for more complex molecules. Instead it is recommended to use current-density calculations in combination with numerical integration of current strengths, because this yields electron-delocalization pathways that show how electrons move around the molecular rings, when they are exposed to an external magnetic field.
Acknowledgements
This research was supported by the Academy of Finland through projects (137460 and 266227) and its Computational Science Research Programme (LASTU/258258). DS thanks Magnus Ehrnrooth Foundation, Swedish Cultural Foundation in Finland, Alexander von Humboldt Fundation and Fulbright Foundation for financial support during his sabbatical leave. CSC – the Finnish IT Center for Science – is acknowledged for computer time. H. F. thanks the Norwegian Research Council through the CoE Centre for Theoretical and Computational Chemistry (Grant No. 179568/V30 and 231571/F20) for support. This work had received support from the Norwegian Supercomputing Program (NOTUR) through a grant of computer time (Grant No. NN4654K).References
- A. Berlicka, P. Dutka, L. Szterenberg and L. Latos-Grażyński, Angew. Chem., Int. Ed., 2014, 53, 4885–4889 CrossRef CAS PubMed.
- S. Aronoff and M. Calvin, J. Org. Chem., 1943, 8, 205–223 CrossRef CAS.
- M. O. Senge, Angew. Chem., Int. Ed., 2011, 50, 4272–4277 CrossRef CAS PubMed.
- K. Berlin, Angew. Chem., Int. Ed., 1996, 35, 1820–1822 CrossRef CAS.
- T. D. Lash and S. T. Chaney, Chem. – Eur. J., 1996, 2, 944–948 CrossRef CAS.
- M. Pawlicki and L. Latos-Grażyński, Chem. Rec., 2006, 6, 64–78 CrossRef CAS PubMed.
- R. K. Pandey and G. Zheng, in Porphyrin Handbook, ed. K. M. S. K. M. Kadish and R. Guilard, Academic Press, San Diego, CA, 2000, vol. 6, pp. 157–230 Search PubMed.
- T. D. Lash, Eur. J. Org. Chem., 2007, 5461–5481 CrossRef CAS.
- D. Li and T. D. Lash, J. Org. Chem., 2014, 79, 7112–7121 CrossRef CAS PubMed.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- S. Taubert, D. Sundholm and J. Jusélius, J. Chem. Phys., 2011, 134, 054123 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- M. P. Johansson, J. Jusélius and D. Sundholm, Angew. Chem., Int. Ed., 2005, 44, 1843–1846 CrossRef CAS PubMed.
- J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2008, 10, 6630–6634 RSC.
- S. Taubert, J. Jusélius, D. Sundholm, W. Klopper and H. Fliegl, J. Phys. Chem. A, 2008, 112, 13584–13592 CrossRef CAS PubMed.
- S. Taubert, D. Sundholm and F. Pichierri, J. Org. Chem., 2010, 75, 5867–5874 CrossRef CAS PubMed.
- H. Fliegl, O. Lehtonen, D. Sundholm and V. R. I. Kaila, Phys. Chem. Chem. Phys., 2011, 13, 434–437 RSC.
- M. Kaipio, M. Patzschke, H. Fliegl, F. Pichierri and D. Sundholm, J. Phys. Chem. A, 2012, 116, 10257–10268 CrossRef CAS PubMed.
- D. Sundholm, Phys. Chem. Chem. Phys., 2013, 15, 9025–9028 RSC.
- H. Fliegl, D. Sundholm, S. Taubert and F. Pichierri, J. Phys. Chem. A, 2010, 114, 7153–7161 CrossRef CAS PubMed.
- H. Fliegl, D. Sundholm and F. Pichierri, Phys. Chem. Chem. Phys., 2011, 13, 20659–20665 RSC.
- H. Fliegl and D. Sundholm, J. Org. Chem., 2012, 77, 3408–3414 CrossRef CAS PubMed.
- H. Fliegl, N. Özcan, R. Mera-Adasme, F. Pichierri, J. Jusélius and D. Sundholm, Mol. Phys., 2013, 111, 1364–1372 CrossRef CAS.
- R. R. Valiev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2013, 117, 9062–9068 CrossRef CAS PubMed.
- R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2014, 16, 11010–11016 RSC.
- H. Fliegl, F. Pichierri and D. Sundholm, J. Phys. Chem. A, 2015, 119, 2344–2350 CrossRef CAS PubMed.
- R. R. Valiev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2015, 119, 1201–1207 CrossRef CAS PubMed.
- R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2015, 17, 14215–14222 RSC.
- H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676 CrossRef CAS PubMed.
- A. Balaban, P. von Ragué Schleyer and H. S. Rzepa, Chem. Rev., 2005, 105, 3436–3447 CrossRef CAS PubMed.
- T. Heine, C. Corminboeuf and G. Seifert, Chem. Rev., 2005, 105, 3889–3910 CrossRef CAS PubMed.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217–223 RSC.
- S. Pelloni, G. Monaco, P. Lazzeretti and R. Zanasi, Phys. Chem. Chem. Phys., 2011, 13, 20666–20672 RSC.
- P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88 CrossRef CAS.
- I. Morao, B. Lecea and F. P. Cossío, J. Org. Chem., 1997, 62, 7033–7036 CrossRef.
- J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 1999, 1, 3429–3435 RSC.
- J. O. C. Jiménez-Halla, E. Matito, J. Robles and M. Solá, J. Organomet. Chem., 2006, 691, 4359–4366 CrossRef.
- S. Pelloni and P. Lazzeretti, J. Phys. Chem. A, 2013, 117, 9083–9092 CrossRef CAS PubMed.
- Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, J. Chem. Theory Comput., 2013, 9, 4789–4796 CrossRef CAS PubMed.
- G. Monaco and R. Zanasi, J. Phys. Chem. A, 2014, 118, 1673–1683 CrossRef CAS PubMed.
- D. Du, H. Fliegl and D. Sundholm, J. Chin. Chem. Soc., 2016, 63, 93–100 CrossRef CAS.
- Y. C. Lin, D. Sundholm and J. Jusélius, J. Chem. Theory Comput., 2006, 2, 761–764 CrossRef CAS PubMed.
- S. Taubert, D. Sundholm and F. Pichierri, J. Org. Chem., 2009, 74, 6495–6502 CrossRef CAS PubMed.
- R. Islas, G. Martínez-Guajardo, J. O. C. Jiménez-Halla, M. Solá and G. Merino, J. Chem. Theory Comput., 2010, 6, 1131–1135 CrossRef CAS.
- A. C. Castro, E. Osorio, J. O. Jiménez-Halla, E. Matito, W. Tiznado and G. Merino, J. Chem. Theory Comput., 2010, 6, 2701–2750 CrossRef CAS PubMed.
- J. J. Torres, R. Islas, E. Osorio, J. G. Harrison, W. Tiznado and G. Merino, J. Phys. Chem. A, 2013, 117, 5529–5533 CrossRef CAS PubMed.
- T. D. Lash, Angew. Chem., Int. Ed., 1995, 34, 2533–2535 CrossRef CAS.
- T. D. Lash, M. J. Hayes, J. D. Spence, M. A. Muckey, G. M. Ferrence and L. F. Szczepura, J. Org. Chem., 2002, 67, 4860–4874 CrossRef CAS PubMed.
- D. I. AbuSalim and T. D. Lash, Org. Biomol. Chem., 2014, 12, 8719–8736 Search PubMed.
- T. D. Lash and M. J. J. Hayes, Angew. Chem., Int. Ed., 1997, 36, 840–842 CrossRef CAS.
- T. D. Lash, S. T. Chaney and D. T. Richter, J. Org. Chem., 1998, 63, 9076–9088 CrossRef CAS.
- S. R. Graham, D. A. Colby and T. D. Lash, Angew. Chem., Int. Ed., 2002, 41, 1371–1374 CrossRef CAS PubMed.
- T. D. Lash, D. A. Colby, S. R. Graham and S. T. Chaney, J. Org. Chem., 2004, 69, 8851–8864 CrossRef CAS PubMed.
- K. M. Bergman, G. M. Ferrence and T. D. Lash, J. Org. Chem., 2004, 69, 7888–7897 CrossRef CAS PubMed.
- T. D. Lash and S. T. Chaney, Tetrahedron Lett., 1996, 37, 8825–8828 CrossRef CAS.
- P. von Ragué Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef PubMed.
- M. K. Cyrañski, T. M. Krygowski, M. Wisiorowski, N. J. R. van Eikema Hommes and P. von Ragué Schleyer, Angew. Chem., Int. Ed., 1998, 37, 177–180 CrossRef.
- J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2000, 2, 2145–2151 RSC.
- E. Steiner and P. W. Fowler, ChemPhysChem, 2002, 3, 114–116 CrossRef CAS PubMed.
- E. Steiner, A. Soncini and P. W. Fowler, Org. Biomol. Chem., 2005, 4, 4053–4059 Search PubMed.
- J. I. Wu, I. Fernández and P. von Ragué Schleyer, J. Am. Chem. Soc., 2013, 135, 315–321 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. Häser, R. Ahlrichs, H. P. Baron, P. Weis and H. Horn, Theor. Chim. Acta, 1992, 83, 455–470 CrossRef.
- M. Kollwitz, M. Häser and J. Gauss, J. Chem. Phys., 1998, 108, 8295–8301 CrossRef CAS.
- S. Taubert, H. Konschin and D. Sundholm, Phys. Chem. Chem. Phys., 2005, 7, 2561–2569 RSC.
- R. Ditchfield, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- XMakemol, http://www.nongnu.org/xmakemol/.
- paint.net 4.0.6, http://www.getpaint.net/.
- Marvin 15.9.28, 2015, ChemAxon, http://www.chemaxon.com.
- PyNgl: Scientific visualization Python program package, http://www.pyngl.ucar.edu.
- ChemBioDraw Ultra 14.0 by PerkinElmer, http://scistore.cambridgesoft.com.
- gimp: GNU Image Manipulation Program, http://www.gimp.org.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Jusélius and D. Sundholm, J. Org. Chem., 2000, 65, 5233–5237 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp06987d |
| This journal is © the Owner Societies 2016 |