DOI:
10.1039/C5TC02025E
(Paper)
J. Mater. Chem. C, 2015,
3, 10534-10542
Compositions and thermoelectric properties of XNiSn (X = Ti, Zr, Hf) half-Heusler alloys
Received
6th July 2015
, Accepted 5th August 2015
First published on 5th August 2015
Abstract
Rietveld analysis of neutron powder diffraction data has been used to investigate the compositions of XNiSn (X = Ti, Zr, Hf) half-Heusler alloys prepared by solid state reactions. All samples containing Ti have 2–3% excess Ni, whereas the samples with X = Zr, Hf are almost stoichiometric. Samples with mixed X-metals are characterised by the presence of 3–4 distinct X1−xX′xNi1+ySn half-Heusler phases. Variable temperature and time dependent neutron powder diffraction for X = Ti and X = Ti0.5Hf0.5 demonstrates that both the amount of excess Ni and the phase distribution are stable up to at least 600 °C. Debye temperatures of 367(2) K and 317(2) K were obtained from the thermal displacement parameters. The samples containing Ti are characterised by a ∼0.15 eV bandgap and a monotonously decreasing Seebeck coefficient. The compositions with Zr and Hf have similar bandgap values but show ambipolar transitions. Analysis of the thermoelectric transport data of degenerately doped Ti0.5Zr0.5NiSn1−zSbz samples using a single parabolic band model demonstrates that the transport is limited by alloy scattering and yielded an effective carrier mass of 2.5(1) me.
Introduction
Half-Heuslers (HHs) show great promise in the field of thermoelectric waste heat recovery, in which they can be used to improve the energy efficiency of any heat-generating process.1 The performance of a thermoelectric material is determined by its figure of merit, zT = S2T/ρκ, where S is the Seebeck coefficient, ρ is the electrical resistivity, κ is the sum of the lattice (κlat) and electronic (κel) thermal conductivities, and T is the absolute temperature. The large power factors (S2/ρ) possessed by HHs make them an obvious choice for thermoelectrics research, but high κ values mean that alterations to the structure must be made to reduce κlat and achieve high zT values.2–6
Recently, phases on the XNiSn–XNi2Sn HH full-Heusler (FH) pseudo-binary have generated substantial interest (where X = Ti, Zr, Hf).3,5,6 The addition of excess Ni has been found to have a significant impact on the thermoelectric properties. In particular, large reductions in the thermal conductivity of TiNi1+ySn samples have been reported.7–13 In addition, simultaneously enhanced S and electrical conductivity (σ = 1/ρ) was reported for Zr0.25Hf0.75Ni1+ySn,14 and enhanced S with only a minor reduction in σ has been found in Ti0.1Zr0.9Ni1+ySn and p-type Ti0.5Hf0.5Co1+ySn0.9Sn0.1.15,16 Simultaneous improvements in S and σ are not expected in homogenous semiconductors, where they depend inversely on carrier concentration.1 The observation of this effect therefore suggests that potential barriers, due to FH nano-inclusions, filter out low energy carriers leading to an enhancement of S.17 Indeed, the formation of FH nano-inclusions within the HH matrix has been reported in many of these studies.8–10,13–16 However, not all samples containing excess Ni (y > 0) show enhancements of S and σ, and other reports observe only micro-inclusions of the FH phase.11,12 We recently reported an in-depth study of TiNiMySn (M = Co, Ni, and Cu) nanocomposites prepared via solid state reactions and showed that the excess metal is relatively homogeneously distributed with an upper limit <2 nm for any segregated TiNi2Sn FH inclusions.18 The absence of clear inclusions demonstrates that the degree of segregation is sensitively dependent on the sample processing, which is in keeping with the wide variety of nanostructures reported in the literature.3,6 Another topical issue in this field regards the low κ (=2–3 W m−1 K−1) that is sometimes observed in XNiSn and XCoSb samples with mixtures of Ti, Zr and Hf, and which is important to underpin ZT > 1.19–23 Recent studies have linked the low κ to phase segregation into multiple half-Heusler phases with different ratios of X-metals.6,21,24 However, our results for the Ti1−xZrxNiSn series indicate that this multiphase behaviour is kinetically controlled, and has a secondary impact on κ(T) after alloy scattering, suggesting that the presence of all three of Ti, Zr and Hf is needed.25 Other approaches aimed at minimising κlat include off-stoichiometric X9Ni7Sn8 (X = Ti, Zr) compositions that form a HH matrix and a number of segregated phases,26,27 addition of a Ti70.5Fe29.5 eutectic,28 InSb inclusions in TiCoSb,29,30 and phase segregation involving mixtures of HH phases.31
Neutron powder diffraction is a powerful tool to characterise metal-rich HH alloys due to the excellent scattering contrast between the elements present.7,18,32 In addition, the bulk nature of the technique means a representative average picture is obtained. For the TiNiMySn (M = Co, Ni, and Cu) nanocomposites it was possible to account for all excess metal present in the sample.18 In case of the M = Ni series, the excess Ni was divided over the matrix (nano-inclusions with diameter <2 nm) and over a distinct FH phase with the sum of excess Ni equal to the nominal y value. This analysis also allowed us to determine that Co substitutes in the matrix, while Cu is part of a nanosegregated FH phase. Here we have extended this approach to the high-zT XNiSn and X0.5X′0.5NiSn parent materials. This has enabled the accurate determination of the experimental compositions, and of the multiphase behaviour that occurs in these samples. In addition, we also present a detailed thermoelectric property analysis of degenerately and non-degenerately doped XNiSn and X0.5X′0.5NiSn compositions.
Experimental
The synthesis of the XNiSn and X0.5X′0.5NiSn (X, X′ = Ti, Zr or Hf) samples has been reported in ref. 25. Neutron powder diffraction data for these samples were collected on the upgraded POLARIS instrument at the ISIS facility, Rutherford Appleton Laboratory, UK. Powders were loaded into cylindrical sample cans and diffraction data were collected at room temperature for 300 µA h proton beam current to the ISIS target, corresponding to ∼2 hours neutron beam time. In addition, two samples were studied at elevated temperatures: TiNiSn (373 to 973 K in 100 K steps) and Ti0.5Hf0.5NiSn (293, 473, 673 and 873 K). The neutron scattering lengths are bTi = −3.4 fm, bZr = 7.2 fm, bHf = 7.7 fm, bNi = 10.3 fm and bSn = 6.2 fm. Crystal structure refinement was by the Rietveld method using the GSAS suite of programs and the EXPGUI graphical interface.33,34 Profile function three for time-of-flight data in GSAS was used to fit the peak shape. The thermoelectric characterisation for these samples was reported in ref. 25 but no data fitting was undertaken in that study.
Results
1. Room temperature structures
A convenient way to view the XNiSn half-Heusler structure is as a face-centred-cubic lattice of Sn, where all the octahedral holes are occupied by X and half the tetrahedral holes (herein Y1) are filled with Ni. This leaves half the tetrahedral holes empty (Y2). The Y2 sites are fully occupied in the Heusler structure, leading to an increase in space group symmetry (from F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m to Fm
3m to Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and lattice parameter (Δa ∼ 0.2 Å). TiNiSn is semiconducting with strong hybridisation between Ni and Sn s- and p-orbitals, while the valence and conduction bands are formed by hybridisation of the Ti and Ni d-orbitals.35 TiNi2Sn in contrast is metallic,35 and this difference in chemical bonding is responsible for the absence of solid solution formation.36–42
m) and lattice parameter (Δa ∼ 0.2 Å). TiNiSn is semiconducting with strong hybridisation between Ni and Sn s- and p-orbitals, while the valence and conduction bands are formed by hybridisation of the Ti and Ni d-orbitals.35 TiNi2Sn in contrast is metallic,35 and this difference in chemical bonding is responsible for the absence of solid solution formation.36–42
TiNiSn, ZrNiSn and HfNiSn.
The Rietveld fits to the POLARIS data are presented in Fig. 1. A single half-Heusler phase was used in the fits and the resulting lattice and atomic parameters are reported in Table 1. These agree well with previously reported values.25 Maintaining a stoichiometric TiNiSn model, with Ti, Ni and Sn on their expected sites (X, Y1, Z), results in χ2 = 8.8. Two models were subsequently identified that resulted in an improvement in χ2. The first of these involves 2% excess Ni on the vacant tetrahedral Y2 site. The second model has 3% inversion of Ti and Sn (i.e. Ti0.97Sn0.03NiSn0.97Ti0.03). Both models produce χ2 = 8.2 (χ2 = 7.9 from a LeBail fit). Larger degrees of inversion are needed for the previously reported TiNi1.04Sn (6% inversion) and TiNi1.06Sn (10% inversion) samples.7 A nominal TiNiSn0.95 sample was also prepared by standard solid state reaction and best-fit models were found for TiNi1.056(2)Sn or 9% Ti–Sn inversion. Furthermore, HfNiSn requires 30% inversion of Hf and Sn, or <1% excess Ni. ZrNiSn was found to be stoichiometric despite the presence of Zr5Sn4 and Ni2.67Sn2 secondary phases. The much smaller variation in Y2 site occupancies suggests that the presence of excess Ni is the most plausible interpretation of our data. This is in keeping with the covalent bonding in these structures and the large energetic cost for X/Sn inversion.39
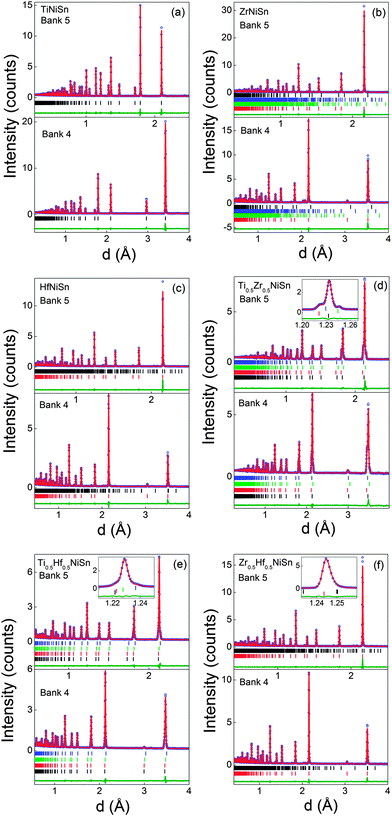 |
| | Fig. 1 Observed (circles), calculated (solid line) and difference Rietveld neutron powder diffraction profiles for (a) TiNiSn, (b) ZrNiSn, (c) HfNiSn, (d) Ti0.5Zr0.5NiSn, (e) Ti0.5Hf0.5NiSn and (f) Zr0.5Hf0.5NiSn. Bragg markers correspond to the half-Heusler phases used to fit the pattern (summarised in Tables 1 and 2), except for ZrNiSn where the markers are for ZrNiSn, Zr5Sn4, Ni2.67Sn2 and ZrNi2Sn (bottom to top). The insets in (d–f) illustrate the multiphase behaviour for samples with mixed X metals. Bank 5 and 4 are the backscattering and 90 degrees detector banks, respectively. | |
Table 1 Lattice parameter (a), fractional site occupancies (occ), thermal displacement parameters (Uiso/Å2) and fit statistics for the XNiSn (X = Ti, Zr, Hf) samples
| X |
Ti |
Zr |
Hf |
| X: 4a (0, 0, 0), Ni(1): 4c (¼, ¼, ¼), Ni(2): 4d (¾, ¾, ¾), Sn: 4b (½, ½, ½). ZrNiSn contains 0.93(7) wt% Zr5Sn4, 3.36(3) wt% Ni2.67Sn2 and 0.44(1) wt% ZrNi2Sn. HfNiSn contains 0.83(3) wt% HfO2. Bank 5, 4 and 3 are the backscattering, 90 degrees and low angle detector banks, respectively. |
|
a (Å) |
5.9298(1) |
6.1089(1) |
6.0795(1) |
| X |
occ |
1 |
1 |
1 |
|
U
iso
|
0.00494(7) |
0.0057(2) |
0.0047(5) |
| Ni(1) |
occ |
1 |
1 |
1 |
|
U
iso
|
0.00498(5) |
0.00461(6) |
0.0046(5) |
| Ni(2) |
occ |
0.024(1) |
0.002(1) |
0.009(2) |
|
U
iso
|
0.00498(5) |
0.00461(6) |
0.0046(5) |
| Sn |
occ |
1 |
1 |
1 |
|
U
iso
|
0.00407(5) |
0.0021(2) |
0.0036(5) |
| wt% |
100 |
95.00(8) |
99.17(3) |
|
|
|
χ
2
|
8.2 |
9.9 |
7.4 |
| wRp/% |
Bank 5 |
3.4 |
3.0 |
2.8 |
| Bank 4 |
2.0 |
2.4 |
2.2 |
| Bank 3 |
2.1 |
2.5 |
2.2 |
|
R
p/% |
Bank 5 |
4.2 |
4.2 |
5.1 |
| Bank 4 |
3.2 |
5.0 |
4.2 |
| Bank 3 |
3.6 |
3.0 |
3.0 |
|
R
f
2/% |
Bank 5 |
5.7 |
7.1 |
8.5 |
| Bank 4 |
6.2 |
6.0 |
7.3 |
| Bank 3 |
7.5 |
7.2 |
5.3 |
Ti0.5Zr0.5NiSn.
Our previous work demonstrated that the ingots with mixed X metals are not phase pure but contain multiple X1−xX′xNiSn half-Heusler phases.25 A total of 4 half-Heusler phases were used to fit the NPD data, as shown in the inset to Fig. 1d. The lattice and atomic parameters for the 4 phases are presented in Table 2. The Zr content of each phase was calculated from the lattice parameters using Vegard's law (xV) and by refining the X-site occupancy (xR). It was not possible to determine xR for the most minor phase, present at 3 wt%, and the occupancies were kept fixed at the xV values. The xR values are plotted against xV in Fig. 2a. From this figure, it may be seen that, for xV ≥ 0.5, there is good agreement between xR and xV. At lower values of xV however, the refined xV are somewhat larger than xR. This indicates a departure from Vegard's law with the xR indicating a lower Zr-fraction than that derived from the lattice parameter. This discrepancy does not lead to any significant difference in average composition of the multiphase samples. The highest resolution backscattering detector (bank 5) was used to get an estimate of any peak broadening caused by further compositional fluctuations (Δx).25 All profile function parameters, except γ1 which models microstrain, were kept fixed at the average value for the XNiSn end-members. For a cubic system, the microstrain can be easily related to a spread in x value,25 and the calculated values for Δx are tabulated in Table 2 and are shown in Fig. 3a. Refinement of the Y2 site occupancy revealed that Ni partially occupies the Y2 site in 2 of the 4 HH phases (Table 2). The largest excess of Ni (y = 0.052(2)) was found in the phase with xR = 0.153(3). The average composition of this sample was found to be Ti0.495(7)Zr0.505(7)Ni1.028(3)Sn, which is in good agreement with the nominal x value and indicates the presence of 3% excess Ni.
Table 2 Lattice parameters (a), weight percentages (wt%), fractional site occupancies (occ), thermal displacement parameters (Uiso/Å2), xV calculated from Vegard's law, xR obtained from the refined X-site occupancies, compositional spread (Δx), and fit statistics for the X1−xX′xNiSn phases present in the X0.5X′0.5NiSn samples (X, X′ = Ti, Zr, Hf)
|
a (Å) |
wt% |
|
X/X′ |
Ni(1) |
Ni(2) |
Sn |
x
V
|
x
R
|
Δx |
χ
2
|
Bank |
wRp |
R
p
|
R
f
2
|
| Zr0.5Hf0.5NiSn contains 1.1(1) wt% Ni2.67Sn2. |
| Ti0.5Zr0.5NiSn/fitted composition: Ti0.495(7)Zr0.505(7)Ni1.028(3)Sn |
| 5.9815(2) |
18.3(2) |
occ |
0.847(3)/0.153(3) |
1 |
0.052(2) |
1 |
0.29(1) |
0.153(3) |
0.12(1) |
5.5 |
|
|
|
|
|
|
U
iso
|
0.0052(1) |
0.0052(1) |
0.0052(1) |
0.0052(1) |
|
|
|
|
| 6.0240(2) |
19.7(7) |
occ |
0.53(1)/0.47(1) |
1 |
−0.003(8) |
1 |
0.5(1) |
0.47(1) |
0.10(1) |
5 |
2.8 |
4.6 |
5.9 |
|
|
U
iso
|
0.00213(4) |
0.00213(4) |
0.00213(4) |
0.00213(4) |
4 |
1.6 |
2.9 |
3.6 |
| 6.0406(1) |
59.2(7) |
occ |
0.412(6)/0.588(6) |
1 |
0.032(4) |
1 |
0.62(1) |
0.588(6) |
0.07(1) |
3 |
1.7 |
2.9 |
5.4 |
|
|
U
iso
|
0.00653(4) |
0.00653(4) |
0.00653(4) |
0.00653(4) |
|
|
|
|
| 6.1020(2) |
2.7(1) |
occ |
0.04/0.96 |
1 |
0 |
1 |
0.96(1) |
0.96 |
0.06(1) |
|
|
|
|
|
|
U
iso
|
0.0010(2) |
0.0010(2) |
0.0010(2) |
0.0010(2) |
|
|
|
|
|
|
| Ti0.5Hf0.5NiSn/fitted composition: Ti0.53(1)Hf0.47(1)Ni1.019(5)Sn |
| 5.9834(3) |
14(1) |
occ |
0.805(5)/0.195(5) |
1 |
0.030(4) |
1 |
0.36(1) |
0.195(5) |
0.12(1) |
6.0 |
|
|
|
|
|
|
U
iso
|
0.0050(2) |
0.0050(2) |
0.0050(2) |
0.0054(2) |
|
|
|
|
| 6.0046(3) |
23(1) |
occ |
0.46(2)/0.54(2) |
1 |
0.00(2) |
1 |
0.50(1) |
0.54(2) |
0.04(1) |
5 |
2.0 |
2.7 |
1.8 |
|
|
U
iso
|
0.00524(5) |
0.00524(5) |
0.00524(5) |
0.00524(5) |
4 |
1.5 |
2.6 |
4.8 |
| 6.0157(1) |
60.1(9) |
occ |
0.419(9)/0.581(9) |
1 |
0.024(6) |
1 |
0.57(1) |
0.581(9) |
0.03(1) |
3 |
2.0 |
2.5 |
2.8 |
|
|
U
iso
|
0.00524(5) |
0.00524(5) |
0.00524(5) |
0.00524(5) |
|
|
|
|
| 6.0604(3) |
3.0(8) |
occ |
0.13/0.87 |
1 |
0 |
1 |
0.87(1) |
0.87 |
0.08(1) |
|
|
|
|
|
|
U
iso
|
0.00007(7) |
0.00007(7) |
0.00007(7) |
0.00007(7) |
|
|
|
|
|
|
| Zr0.5Hf0.5NiSn/fitted composition: Zr0.59(4)Hf0.41(4)Ni1.002(3)Sn |
| 6.0926(1) |
98.9(1) |
occ |
0.59(4)/0.41(4) |
1 |
0.002(3) |
1 |
0.49(1) |
0.59(4) |
0.14(1) |
10.9 |
5 |
2.1 |
4.4 |
6.0 |
|
|
U
iso
|
0.0066(2) |
0.00495(6) |
0.00495(6) |
0.0017(2) |
4 |
2.0 |
3.1 |
5.1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
2.9 |
3.7 |
3.2 |
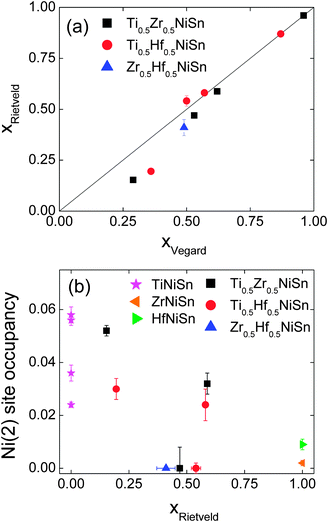 |
| | Fig. 2 (a) Fitted X-metal fractions (xR) against those calculated from Vegard's law (xV) (b) Ni(2) site occupancy for the X1−xX′xNi1+ySn phases present in the X0.5X′0.5NiSn samples (X, X′ = Ti, Zr, Hf). Additional TiNiSn data from ref. 7. | |
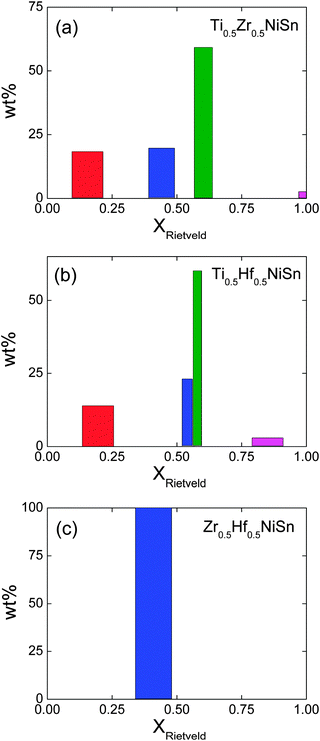 |
| | Fig. 3 Histograms of the phase distribution and compositional spread of the X1−xX′xNiSn phases present in the X0.5X′0.5NiSn samples (X = Ti, Zr, Hf). The centre and widths of the bars correspond to xR and Δx. | |
Ti0.5Hf0.5NiSn.
This sample shows similar multiphase behaviour to Ti0.5Zr0.5NiSn and was analysed analogously. The refined Hf occupancies were found to be xR = 0.195(5), 0.54(2), 0.581(9) and 0.87, where the last value was fixed to xV due to the low abundance of this phase. The xR values are in good agreement with xV for xV ≥ 0.5, with a small discrepancy for lower x, as seen for Ti0.5Zr0.5NiSn (Fig. 2a). The Δx values are comparable to those found in Ti0.5Zr0.5NiSn and are shown in Fig. 3b. Two of the HH phases were found to contain Ni on the Y2 site. The refined values are presented in Table 2 and the Ni content is plotted in Fig. 2b. The average composition was found to be Ti0.53(1)Hf0.47(1)Ni1.019(5)Sn.
Zr0.5Hf0.5NiSn.
The narrow range of unit cell parameters observed for this composition (due to the similar radii of Zr and Hf) means only one phase could be identified, instead of the three that were observable in the X-ray data (Fig. 1f).25 The lattice and atomic parameters are presented in Table 2. Refinement of the Y2 site occupancy suggested this sample is stoichiometric, and does not contain any excess Ni. The final fitted composition of this sample was found to be Zr0.59(4)Hf0.41(4)Ni1.002(3)Sn, consistent with the X-ray data,25 and the nominal composition.
2. Temperature dependence studies
TiNiSn.
The fitted lattice parameters, fractional site occupancies and fit statistics are presented in Table 3. The unit cell volume was found to increase linearly above 300 K, as illustrated in Fig. 4a. The volume expansion could be fitted by V(T) = V0 + A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) coth(θD/T), where A is a scale factor and θD is the Debye temperature. From this fit V0 = 205.4(1) Å3, A = 2.6(2) and θD = 347(22) K. This is consistent with literature values which put θD in the range 360–420 K.43 The temperature dependence of the thermal displacement parameters (Uiso) of each atom are plotted in Fig. 4b. The similar gradients and magnitudes indicate that all three atom types vibrate at around the same frequency. The values for Sn are slightly reduced compared with Ti and Ni due to its larger mass. Using the average slope and mass of TiNiSn a Debye temperature of 367(2) K was obtained,44 in excellent agreement with the value from the fit to cell volume, and the literature. The Ni occupancies on the Y1 and Y2 sites were also refined for each temperature step and remained constant within one estimated standard deviation (Table 3).
coth(θD/T), where A is a scale factor and θD is the Debye temperature. From this fit V0 = 205.4(1) Å3, A = 2.6(2) and θD = 347(22) K. This is consistent with literature values which put θD in the range 360–420 K.43 The temperature dependence of the thermal displacement parameters (Uiso) of each atom are plotted in Fig. 4b. The similar gradients and magnitudes indicate that all three atom types vibrate at around the same frequency. The values for Sn are slightly reduced compared with Ti and Ni due to its larger mass. Using the average slope and mass of TiNiSn a Debye temperature of 367(2) K was obtained,44 in excellent agreement with the value from the fit to cell volume, and the literature. The Ni occupancies on the Y1 and Y2 sites were also refined for each temperature step and remained constant within one estimated standard deviation (Table 3).
Table 3 Temperature evolution of the lattice parameter (a), thermal displacement parameters (Uiso/Å2), Y2 site occupancy (occ) and fit statistics for TiNiSn between 293 and 973 K
|
|
293 K |
373 K |
473 K |
573 K |
673 K |
773 K |
873 K |
973 K |
| The 293 K pattern was collected outside of the furnace. |
|
a (Å) |
5.9297(1) |
5.9333(1) |
5.9329(1) |
5.9453(1) |
5.9514(1) |
5.9576(1) |
5.9641(1) |
5.9710(1) |
| Ti |
U
iso
|
0.00495(7) |
0.0061(1) |
0.0078(1) |
0.0095(2) |
0.0107(2) |
0.0130(2) |
0.0142(3) |
0.0167(2) |
| Ni(1) |
U
iso
|
0.00499(5) |
0.00609(6) |
0.0078(1) |
0.00946(7) |
0.01099(9) |
0.01276(9) |
0.0147(2) |
0.0164(1) |
| Ni(2) |
occ |
0.022(1) |
0.019(1) |
0.019(1) |
0.018(1) |
0.019(1) |
0.015(1) |
0.020(1) |
0.015(1) |
|
U
iso
|
0.00499(5) |
0.00609(6) |
0.0078(1) |
0.00946(7) |
0.01099(9) |
0.01276(9) |
0.0147(2) |
0.0164(1) |
| Sn |
U
iso
|
0.0045(6) |
0.00527(9) |
0.00703(1) |
0.0066(9) |
0.0099(1) |
0.0119(2) |
0.0134(2) |
0.0155(1) |
|
|
|
χ
2
|
8.6 |
4.1 |
4.0 |
4.0 |
3.8 |
4.1 |
4.1 |
4.3 |
| wRp |
Bank 5 |
3.1 |
2.0 |
2.0 |
2.1 |
2.1 |
2.2 |
2.2 |
2.3 |
| Bank 4 |
2.0 |
1.4 |
1.3 |
1.3 |
1.2 |
1.2 |
1.2 |
1.4 |
| Bank 3 |
2.1 |
1.0 |
1.2 |
1.1 |
1.1 |
1.3 |
1.2 |
1.3 |
|
R
p
|
Bank 5 |
3.6 |
2.3 |
2.5 |
2.4 |
2.5 |
2.6 |
2.7 |
2.7 |
| Bank 4 |
3.2 |
2.8 |
2.3 |
2.3 |
2.3 |
2.1 |
2.0 |
2.2 |
| Bank 3 |
3.6 |
1.1 |
1.3 |
1.2 |
1.1 |
1.4 |
1.3 |
1.4 |
|
R
f
2
|
Bank 5 |
5.4 |
3.4 |
3.6 |
4.1 |
4.5 |
5.7 |
6.4 |
6.4 |
| Bank 4 |
6.2 |
4.3 |
4.7 |
7.8 |
7.5 |
8.3 |
8.9 |
10.7 |
| Bank 3 |
7.6 |
7.5 |
7.5 |
10.9 |
10.5 |
11.5 |
10.8 |
10.0 |
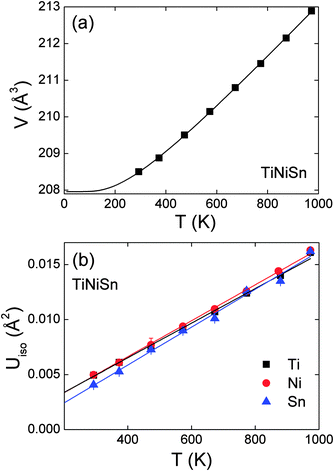 |
| | Fig. 4 (a) Temperature dependence of the unit cell volume for TiNiSn. The solid line is a fit (see manuscript text). (b) Temperature dependence of the thermal displacement parameters of Ti, Ni and Sn. | |
Ti0.5Hf0.5NiSn.
The fitted lattice parameters, weight fractions, site occupancies and fit statistics are presented in Table 4. The lattice parameters for each phase were found to increase linearly with temperature. The increase in temperature was found to have very little effect on the distribution of the phases in this sample. The Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hf ratio remained almost constant for each phase, while Ni(2) site occupancy was found to decrease somewhat at the highest measured temperatures. The weight fractions of each of the phases remained constant between 273 and 873 K. The overall composition and distribution of phases therefore do not change significantly with temperature. The temperature dependence of the average thermal displacement parameters for the two most abundant phases was used to estimate the Debye temperature, which was calculated to be 317(2) K.
Hf ratio remained almost constant for each phase, while Ni(2) site occupancy was found to decrease somewhat at the highest measured temperatures. The weight fractions of each of the phases remained constant between 273 and 873 K. The overall composition and distribution of phases therefore do not change significantly with temperature. The temperature dependence of the average thermal displacement parameters for the two most abundant phases was used to estimate the Debye temperature, which was calculated to be 317(2) K.
Table 4 Temperature evolution of the lattice parameters (a), fitted Hf fractions (x), Ni(2) site occupancy, weight percentages (wt%), thermal displacement parameters (Uiso/Å2) and fit statistics for the Ti1−xHfxNiSn phases present in the Ti0.5Hf0.5NiSn sample
| Phase |
293 K |
473 K |
673 K |
873 K |
|
Integrated proton beam current to ISIS target/µA h.
|
| 1 |
a (Å) |
5.9834(3) |
5.9950(3) |
6.0074(6) |
6.0192(5) |
|
x
|
0.195(5) |
0.223(5) |
0.210(9) |
0.206(8) |
| Ni(2) |
0.030(4) |
0.027(4) |
0.016(5) |
0.011(7) |
| Wt% |
14(1) |
16(1) |
16(1) |
15.5(2) |
|
U
iso
|
0.0050(2) |
0.0060(2) |
0.0088(2) |
0.0132(4) |
|
|
| 2 |
a (Å) |
6.0046(3) |
6.0164(2) |
6.0285(3) |
6.0394(4) |
|
x
|
0.54(3) |
0.559(9) |
0.57(1) |
0.59(2) |
| Ni(2) |
0.00(2) |
0 |
0 |
0 |
| Wt% |
23(1) |
27.6(7) |
29.8(9) |
25.2(1) |
|
U
iso
|
0.00524(5) |
0.00770(4) |
0.01068(5) |
0.01378(8) |
|
|
|
|
|
|
|
| 3 |
a (Å) |
6.0157(1) |
6.0262(1) |
6.0378(1) |
6.0490(1) |
|
x
|
0.581(9) |
0.588(4) |
0.610(5) |
0.592(6) |
| Ni(2) |
0.024(6) |
0.022(5) |
0 |
0 |
| Wt% |
60.1(9) |
54.0(7) |
51.8(9) |
56.3(1) |
|
U
iso
|
0.00524(5) |
0.00770(4) |
0.01068(5) |
0.01378(8) |
|
|
| 4 |
a (Å) |
6.0604(3) |
6.0691(4) |
6.0800(4) |
6.0919(7) |
|
x
|
0.87 |
0.87 |
0.87 |
0.87 |
| Ni(2) |
0 |
0 |
0 |
0 |
| Wt% |
3.0(8) |
2.8(1) |
2.9(1) |
2.9(2) |
|
U
iso
|
0.0001(3) |
0.0004(5) |
0.0021(6) |
0.0050(9) |
|
|
| Currenta |
450 |
200 |
200 |
75 |
|
χ
2
|
6.0 |
2.4 |
2.4 |
1.0 |
| wRp |
Bank 5 |
2.0 |
1.4 |
1.4 |
1.7 |
| Bank 4 |
1.5 |
1.0 |
1.3 |
1.4 |
| Bank 3 |
2.0 |
2.2 |
1.9 |
1.5 |
|
R
p
|
Bank 5 |
2.7 |
2.5 |
2.4 |
2.9 |
| Bank 4 |
2.6 |
1.6 |
2.8 |
3.3 |
| Bank 3 |
2.5 |
2.5 |
2.2 |
2.0 |
|
R
f
2
|
Bank 5 |
1.8 |
3.0 |
3.6 |
5.2 |
| Bank 4 |
4.8 |
8.8 |
9.8 |
7.0 |
| Bank 3 |
2.8 |
3.5 |
5.3 |
9.4 |
3. Thermoelectric properties
The use of band models to fit experimental thermoelectric data is increasingly common. The simplest of these models is the single parabolic band model which is most readily applied in the high temperature and degenerate semiconducting limit,45 where the chemical carrier concentration (n) is assumed constant. The ρ(T) of electron doped Ti0.5Zr0.5NiSn1−zSbz samples (z = 0.005, 0.01 and 0.02) is shown on a log–log plot in Fig. 5a. The slopes fall between 0.2–0.7, where values between 1–1.5 are expected for electron transport limited by acoustic phonon scattering. The lower values observed here are characteristic of alloy scattering.45 As both acoustic and alloy scattering are energy independent, an identical S(T) is expected,46 and the familiar expressions for S and n can be used:| | 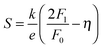 | (1) |
| | 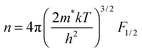 | (2) |
Here, k is Boltzmann's constant, e the electron charge, h is Planck's constant, m* is the effective carrier mass, η is the reduced Fermi level measured from the conduction band minimum (EF/kT), and Fj are the Fermi integrals, which were evaluated numerically (ε is the reduced energy):| | 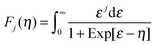 | (3) |
The magnitude of S is therefore only a function of η (eqn (1)), while m* can be evaluated using the η value gained from the experimental S, and the chemical carrier concentration (eqn (2)). The calculated carrier concentrations were (z = 0.005, 9.15 × 1025 m−3), (z = 0.01, 1.83 × 1026 m−3) and (z = 0.02, 3.66 × 1026 m−3) and the obtained m* values are 2.33 me (z = 0.005), 2.51 me (z = 0.01) and 2.64 me (z = 0.02) where me is the electron mass. These values are in good agreement with published data for ZrNi1+ySn HH alloys.47,48 As a further test of the validity of the SPB model we calculated the predicted temperature dependence of S using the constant carrier approximation, and these curves are plotted in Fig. 5b. There is a good agreement below 400 K, while S is overestimated above this temperature, which typically signals the presence of minority charge carriers. The ρ(T) and S(T) for the non-Sb doped (non-degenerate) samples containing Ti are shown in Fig. 5c and d. The ρ(T) follows a thermally activated temperature dependence over the entire measured temperature interval (300–730 K). The fitted bandgap values are Eg = 0.12–0.15 eV (see Table 5) which is much smaller than the 0.45 eV gap predicted from first principles calculations.49 The observation of reduced bandgaps is common for HHs,50 and points towards the presence of in-gap states due to structural disorder and/or excess Ni.36 Similar bandgap values are observed for SPS processed Ti0.5Zr0.5NiSn samples,51 demonstrating that these values are not affected strongly by porosity. The S(T) for these compositions shows a gradual monotonous decrease (Fig. 5d). By contrast, the S(T) for samples containing Zr and Hf are characterised by a maximum near 350 K (X = Zr) and 550 K (X = Zr0.5Hf0.5, Hf), followed by a rapid decrease (Fig. 5f). This rapid decrease is caused by the onset of minority carrier (p-type) conduction, which is also evident in the ρ(T) data (Fig. 5e). The maximum for X = Zr is lower than reported in the literature (550 K),52 and this may be linked to presence of impurity phases in this sample (Table 1). The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ(T) − 1/T data for the samples without Ti are shown in Fig. 5e, and reveals the presence of similar bandgap values below the onset of minority carrier conduction (0.07–0.16 eV, Table 5). In addition, the Goldsmid–Sharp formula was used to extract a value for the bandgap from the S(T) data.53 These are larger and fall between 0.3–0.4 eV (Table 5). The discrepancy between the bandgap values from ρ(T) and S(T) data has recently been discussed and results from the mobility difference between electrons and holes, and leads to overestimates when using the classical Goldsmid–Sharp equation.50 The bandgap values observed here are consistent with recently reported values of 0.13 eV for ZrNiSn from room temperature optical measurements.50
ρ(T) − 1/T data for the samples without Ti are shown in Fig. 5e, and reveals the presence of similar bandgap values below the onset of minority carrier conduction (0.07–0.16 eV, Table 5). In addition, the Goldsmid–Sharp formula was used to extract a value for the bandgap from the S(T) data.53 These are larger and fall between 0.3–0.4 eV (Table 5). The discrepancy between the bandgap values from ρ(T) and S(T) data has recently been discussed and results from the mobility difference between electrons and holes, and leads to overestimates when using the classical Goldsmid–Sharp equation.50 The bandgap values observed here are consistent with recently reported values of 0.13 eV for ZrNiSn from room temperature optical measurements.50
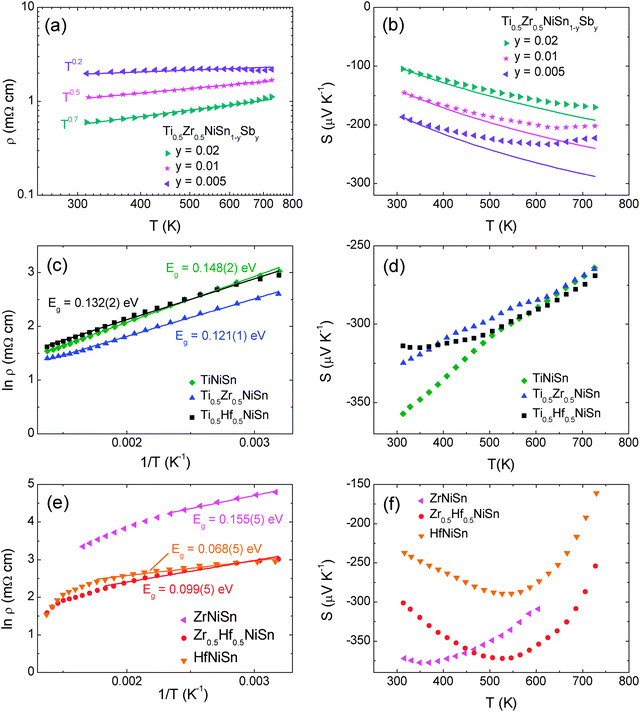 |
| | Fig. 5 Temperature dependence of the electrical resistivity and Seebeck coefficient for (a and b) degenerately doped Ti0.5Zr0.5NiSn1−zSbz (c and d) non-degenerate XNiSn samples containing X = Ti and (e and f) non-degenerate XNiSn samples with X = Zr, Hf. | |
Table 5 Summary of bandgap values and pre-exponential factors obtained from fits to electrical resistivity data, and thermal bandgap values obtained using the Goldsmid–Sharp formula53
| Composition |
Fitting range (K) |
E
g (eV) |
ρ
0 (mΩ cm) |
E
g = 2e|Smax|Tmax |
| TiNiSn |
300–730 |
0.148(2) |
1.43(8) |
|
| Ti0.5Zr0.5NiSn |
300–730 |
0.121(1) |
1.51(8) |
|
| Ti0.5Hf0.5NiSn |
300–730 |
0.132(2) |
1.80(9) |
|
| ZrNiSn |
300–450 |
0.155(5) |
13.7(2) |
0.271(8) |
| Zr0.5Hf0.5NiSn |
300–570 |
0.099(5) |
3.5(2) |
0.392(7) |
| HfNiSn |
300–570 |
0.068(5) |
6.0(2) |
0.310(5) |
Discussion
There is now substantial evidence confirming that there is no solubility of excess Ni in the HH structure, and that segregation into a HH matrix and FH inclusions occurs.3,6 We have previously reported extensive electron microscopy characterisation of a TiNi1.05Sn sample which was prepared in an identical manner to the samples discussed here (e.g. by solid state reactions without post synthesis processing).18 This revealed that the excess Ni is finely dispersed within the matrix with a limit <2 nm on the size of the nanoinclusions. We also demonstrated that ∼2% additional Ni was present in all TiNiMySn samples investigated. This was attributed to the stability of competing Ti–Sn binary phases. The observation of 2–3% excess Ni for the samples containing Ti, and the absence of excess Ni for samples with X = Zr, Hf (Tables 1 and 2), is in keeping with this earlier observation and emphasises the need for a tight control of the synthesis conditions. One of the most striking features of the transport data is the gradual decrease of S(T) for samples containing Ti, and the absence of an ambipolar transition (the onset of minority carrier conduction). This occurs for both TiNiSn and the multiphase samples, suggesting that the phase segregation has limited impact. Density functional theory calculations reveal similar bandstructures for X = Ti, Zr and Hf with an indirect gap of ∼0.45 eV between the Γ and X points,49 and it is therefore not immediately apparent why S(T) behaves differently. As the experimental bandgaps are also rather similar, it is tempting to link the absence of minority carrier conduction to the presence of electron doping from the 2–3% excess Ni in these samples. However, literature data reveals that the ambipolar transition survives in ZrNi1+ySn samples with 6% excess Ni,47,52 suggesting that there may not be a link to the amount of excess Ni, or that it may depend on the exact nature of the phase segregation. The ZrNi1+ySn samples were prepared from the melt and it is likely that this will cause a difference in the degree of segregation of the FH phases. This can have a significant impact on the properties: for example the changes in S(T) and ρ(T) in the TiNi1+ySn series with finely dispersed excess Ni are consistent with conventional doping,18 whereas enhancements in S due to carrier filtering were observed in hot-pressed compositions containing well-defined FH inclusions.14 Further work is needed to fully elucidate the difference in behaviour between the samples that contain Ti and those that do not. Another plausible explanation is that the difference in behaviour is linked to a microstructural effect that only occurs in the presence of Ti, and is not directly linked to either the multiphase behaviour or the presence of excess Ni. The S(T) for degenerately doped Ti0.5Zr0.5NiSn1−zSbz samples can be modelled adequately using a single parabolic band model with the mobility limited by alloy scattering. The observation of carrier transport limited by alloy scattering is reasonable as the compositional changes due to phase segregation of the X-site metals occur over relatively large lengthscales (>5 µm).20,21,25 These distances are greater than typical electron mean free paths, and are therefore not expected to impact strongly on the carrier transport.
Neutrons probe a larger sample volume than X-rays, and the phase distributions in the multiphase samples (Fig. 3) are significantly narrower than determined from X-ray data. The present data are more representative of the bulk, suggesting that 3–4 discrete phases are indeed present with the broadening of the individual HH X-ray and neutron profiles (quantified as Δx) at least partially due to microstrain effects and not solely linked to compositional variations. Some of the refined compositions fall outside of the thermodynamic limits for mixing of the X-metals,6 suggesting that the final observed phase distribution is kinetically controlled. The temperature-dependent neutron diffraction study into TiNiSn and Ti0.5Hf0.5NiSn showed no significant change in phase-distribution as the temperature was increased (Fig. 4, Tables 3 and 4). In addition to the temperature steps reported in Table 4, this sample was held at 600 °C for 6 hours and re-measured at regular intervals. The reflections remained the same shape throughout, indicating no change in the distribution. In terms of application this highlights that these materials show stability to prolonged exposure to high temperatures, which is of vital importance for thermoelectric materials. The variable temperature data also afforded the extraction of a reliable estimate of the Debye temperatures for TiNiSn (θD = 367(2) K) and Ti0.5Hf0.5NiSn (θD = 317(2) K).
The main conclusion is that XNiSn half-Heuslers samples are susceptible to phase segregation as exemplified by the presence of distinct half-Heusler compositions for samples with mixtures of X metals, and full-Heusler domains in samples containing Ti. The onset of minority carrier conduction observed for XNiSn samples with Zr and Hf is suppressed in the samples containing Ti.
Acknowledgements
The authors thank the EPSRC (grant EP/J000884/1 and EP/K036408/1), and the STFC for the provision of neutron beam time at ISIS. D. A. MacLaren is acknowledged for scientific discussions and preliminary TEM data.
References
-
Thermoelectrics and its Energy Harvesting, ed. D. M. Rowe, CRC Press, Boca Raton, 2012 Search PubMed.
-
H. Hohl, A. P. Ramirez, W. Kaefer, K. Fess, C. Thurner, C. Kloc and E. Bucher, Thermoelectric Materials – New Directions and Approaches, 1997, pp. 109–114 Search PubMed.
- J. W. G. Bos and R. A. Downie, J. Phys.: Condens. Matter, 2014, 26, 433201 CrossRef PubMed.
- S. Chen and Z. F. Ren, Mater. Today, 2013, 16, 387–395 CrossRef CAS PubMed.
- W. J. Xie, A. Weidenkaff, X. F. Tang, Q. J. Zhang, J. Poon and T. M. Tritt, Nanomaterials, 2012, 2, 379–412 CrossRef CAS PubMed.
- Y. Kimura and Y. W. Chai, JOM, 2015, 67, 233–245 CrossRef CAS.
- R. A. Downie, D. A. MacLaren, R. I. Smith and J. W. G. Bos, Chem. Commun., 2013, 49, 4184–4186 RSC.
- Y. W. Chai and Y. Kimura, Appl. Phys. Lett., 2012, 100, 033114 CrossRef PubMed.
- Y. W. Chai and Y. Kimura, Acta Mater., 2013, 61, 6684–6697 CrossRef CAS PubMed.
- H. Hazama, M. Matsubara, R. Asahi and T. Takeuchi, J. Appl. Phys., 2011, 110, 063710 CrossRef PubMed.
- C. S. Birkel, J. E. Douglas, B. R. Lettiere, G. Seward, N. Verma, Y. Zhang, T. M. Pollock, R. Seshadri and G. D. Stucky, Phys. Chem. Chem. Phys., 2013, 15, 6990–6997 RSC.
- J. E. Douglas, C. S. Birkel, M.-S. Miao, C. J. Torbet, G. D. Stucky, T. M. Pollock and R. Seshadri, Appl. Phys. Lett., 2012, 101, 183902 CrossRef PubMed.
- H. Hazama, R. Asahi, M. Matsubara and T. Takeuchi, J. Electron. Mater., 2010, 39, 1549–1553 CrossRef CAS.
- J. P. A. Makongo, D. K. Misra, X. Zhou, A. Pant, M. R. Shabetai, X. Su, C. Uher, K. L. Stokes and P. F. P. Poudeu, J. Am. Chem. Soc., 2011, 133, 18843–18852 CrossRef CAS PubMed.
- P. Sahoo, Y. Liu, J. P. A. Makongo, X.-L. Su, S. J. Kim, N. Takas, H. Chi, C. Uher, X. Pan and P. F. P. Poudeu, Nanoscale, 2013, 5, 9419–9427 RSC.
- Y. Liu, P. Sahoo, J. P. A. Makongo, X. Zhou, S.-J. Kim, H. Chi, C. Uher, X. Pan and P. F. P. Poudeu, J. Am. Chem. Soc., 2013, 135, 7486–7495 CrossRef CAS PubMed.
- S. V. Faleev and F. Léonard, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 214304 CrossRef.
- R. A. Downie, R. I. Smith, D. A. MacLaren and J. W. G. Bos, Chem. Mater., 2015, 27, 2449–2459 CrossRef CAS.
- S. Sakurada and N. Shutoh, Appl. Phys. Lett., 2005, 86, 082105 CrossRef PubMed.
- S. Populoh, M. H. Aguirre, O. C. Brunko, K. Galazka, Y. Lu and A. Weidenkaff, Scr. Mater., 2012, 66, 1073–1076 CrossRef CAS PubMed.
- M. Schwall and B. Balke, Phys. Chem. Chem. Phys., 2013, 15, 1868–1872 RSC.
- E. Rausch, B. Balke, T. Deschauer, S. Ouardi and C. Felser, APL Mater., 2015, 3, 041516 CrossRef PubMed.
- E. Rausch, B. Balke, S. Ouardi and C. Felser, Phys. Chem. Chem. Phys., 2014, 16, 25258–25262 RSC.
- H. Y. Geng and H. Zhang, J. Appl. Phys., 2014, 116, 033708 CrossRef PubMed.
- R. A. Downie, D. A. MacLaren and J. W. G. Bos, J. Mater. Chem. A, 2014, 2, 6107–6114 CAS.
- D. K. Misra, A. Bhardwaj and S. Singh, J. Mater. Chem. A, 2014, 2, 11913–11921 CAS.
- D. K. Misra, A. Rajput, A. Bhardwaj, N. S. Chauhan and S. Singh, Appl. Phys. Lett., 2015, 106, 103901 CrossRef PubMed.
- A. Bhardwaj and D. K. Misra, J. Mater. Chem. A, 2014, 2, 20980–20989 CAS.
- W. J. Xie, Y. G. Yan, S. Zhu, M. Zhou, S. Populoh, K. Galazka, S. J. Poon, A. Weidenkaff, J. He, X. F. Tang and T. M. Tritt, Acta Mater., 2013, 61, 2087–2094 CrossRef CAS PubMed.
- W. J. Xie, J. He, S. Zhu, X. L. Su, S. Y. Wang, T. Holgate, J. W. Graff, V. Ponnambalam, S. J. Poon, X. F. Tang, Q. J. Zhang and T. M. Tritt, Acta Mater., 2010, 58, 4705–4713 CrossRef CAS PubMed.
- T. Graf, P. Klaer, J. Barth, B. Balke, H. J. Elmers and C. Felser, Scr. Mater., 2010, 63, 1216–1219 CrossRef CAS PubMed.
- J. E. Douglas, P. A. Chater, C. M. Brown, T. M. Pollock and R. Seshadri, J. Appl. Phys., 2014, 116, 163514 CrossRef PubMed.
-
A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report LAUR, 2000, pp. 86–748 Search PubMed.
- B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS PubMed.
- D. T. Do, S. D. Mahanti and J. J. Pulikkoti, J. Phys.: Condens. Matter, 2014, 26, 275501 CrossRef PubMed.
- K. Kirievsky, Y. Gelbstein and D. Fuks, J. Solid State Chem., 2013, 203, 247–254 CrossRef CAS PubMed.
- K. Kirievsky, M. Shlimovich, D. Fuks and Y. Gelbstein, Phys. Chem. Chem. Phys., 2014, 16, 20023–20029 RSC.
- P. Larson, S. D. Mahanti and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 12754–12762 CrossRef CAS.
- V. V. Romaka, P. Rogl, L. Romaka, Y. Stadnyk, N. Melnychenko, A. Grytsiv, M. Falmbigl and N. Skryabina, J. Solid State Chem., 2013, 197, 103–112 CrossRef CAS PubMed.
- Y. V. Stadnyk and R. V. Skolozdra, Inorg. Mater., 1991, 27, 1884–1885 Search PubMed.
- J. E. Douglas, C. S. Birkel, N. Verma, V. M. Miller, M.-S. Miao, G. D. Stucky, T. M. Pollock and R. Seshadri, J. Appl. Phys., 2014, 115, 043720 CrossRef PubMed.
- P. Hermet, K. Niedziolka and P. Jund, RSC Adv., 2013, 3, 22176–22184 RSC.
-
B. C. Sales, D. G. Mandrus and B. C. Chakoumakos, in Recent Trends in Thermoelectrics Materials Research II, ed. T. M. Tritt, Academic Press, San Diego, 2001, pp. 1–34 Search PubMed.
-
A. F. May and G. J. Snyder, in Thermoelectrics and its Energy Harvesting, ed. D. M. Rowe, CRC press, Boca Raton, 2012 Search PubMed.
- W. Liu, H. Chi, H. Sun, Q. Zhang, K. Yin, X. Tang, Q. Zhang and C. Uher, Phys. Chem. Chem. Phys., 2014, 16, 6893–6897 RSC.
- H. H. Xie, H. Wang, C. G. Fu, Y. T. Liu, G. J. Snyder, X. B. Zhao and T. J. Zhu, Sci. Rep., 2014, 4, 6888 CrossRef CAS PubMed.
- H. H. Xie, H. Wang, Y. Z. Pei, C. G. Fu, X. H. Liu, G. J. Snyder, X. B. Zhao and T. J. Zhu, Adv. Funct. Mater., 2013, 23, 5123–5130 CrossRef CAS PubMed.
- S. Ogut and K. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 10443 CrossRef CAS.
- J. Schmitt, Z. M. Gibbs, G. J. Snyder and C. Felser, Mater. Horiz., 2015, 2, 68–75 RSC.
- R. A. Downie, S. R. Popuri, H. P. Ning, M. J. Reece and J. W. G. Bos, Materials, 2014, 7, 7093–7104 CrossRef PubMed.
- H.-H. Xie, J.-L. Mi, L.-P. Hu, N. Lock, M. Chirstensen, C.-G. Fu, B. B. Iversen, X.-B. Zhao and T.-J. Zhu, CrystEngComm, 2012, 14, 4467–4471 RSC.
- H. J. Goldsmid and J. W. Sharp, J. Electron. Mater., 1999, 28, 869–872 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m to Fm
3m to Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and lattice parameter (Δa ∼ 0.2 Å). TiNiSn is semiconducting with strong hybridisation between Ni and Sn s- and p-orbitals, while the valence and conduction bands are formed by hybridisation of the Ti and Ni d-orbitals.35 TiNi2Sn in contrast is metallic,35 and this difference in chemical bonding is responsible for the absence of solid solution formation.36–42
m) and lattice parameter (Δa ∼ 0.2 Å). TiNiSn is semiconducting with strong hybridisation between Ni and Sn s- and p-orbitals, while the valence and conduction bands are formed by hybridisation of the Ti and Ni d-orbitals.35 TiNi2Sn in contrast is metallic,35 and this difference in chemical bonding is responsible for the absence of solid solution formation.36–42


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) coth(θD/T), where A is a scale factor and θD is the Debye temperature. From this fit V0 = 205.4(1) Å3, A = 2.6(2) and θD = 347(22) K. This is consistent with literature values which put θD in the range 360–420 K.43 The temperature dependence of the thermal displacement parameters (Uiso) of each atom are plotted in Fig. 4b. The similar gradients and magnitudes indicate that all three atom types vibrate at around the same frequency. The values for Sn are slightly reduced compared with Ti and Ni due to its larger mass. Using the average slope and mass of TiNiSn a Debye temperature of 367(2) K was obtained,44 in excellent agreement with the value from the fit to cell volume, and the literature. The Ni occupancies on the Y1 and Y2 sites were also refined for each temperature step and remained constant within one estimated standard deviation (Table 3).
coth(θD/T), where A is a scale factor and θD is the Debye temperature. From this fit V0 = 205.4(1) Å3, A = 2.6(2) and θD = 347(22) K. This is consistent with literature values which put θD in the range 360–420 K.43 The temperature dependence of the thermal displacement parameters (Uiso) of each atom are plotted in Fig. 4b. The similar gradients and magnitudes indicate that all three atom types vibrate at around the same frequency. The values for Sn are slightly reduced compared with Ti and Ni due to its larger mass. Using the average slope and mass of TiNiSn a Debye temperature of 367(2) K was obtained,44 in excellent agreement with the value from the fit to cell volume, and the literature. The Ni occupancies on the Y1 and Y2 sites were also refined for each temperature step and remained constant within one estimated standard deviation (Table 3).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hf ratio remained almost constant for each phase, while Ni(2) site occupancy was found to decrease somewhat at the highest measured temperatures. The weight fractions of each of the phases remained constant between 273 and 873 K. The overall composition and distribution of phases therefore do not change significantly with temperature. The temperature dependence of the average thermal displacement parameters for the two most abundant phases was used to estimate the Debye temperature, which was calculated to be 317(2) K.
Hf ratio remained almost constant for each phase, while Ni(2) site occupancy was found to decrease somewhat at the highest measured temperatures. The weight fractions of each of the phases remained constant between 273 and 873 K. The overall composition and distribution of phases therefore do not change significantly with temperature. The temperature dependence of the average thermal displacement parameters for the two most abundant phases was used to estimate the Debye temperature, which was calculated to be 317(2) K.
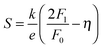
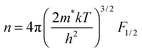
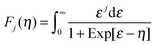
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ(T) − 1/T data for the samples without Ti are shown in Fig. 5e, and reveals the presence of similar bandgap values below the onset of minority carrier conduction (0.07–0.16 eV, Table 5). In addition, the Goldsmid–Sharp formula was used to extract a value for the bandgap from the S(T) data.53 These are larger and fall between 0.3–0.4 eV (Table 5). The discrepancy between the bandgap values from ρ(T) and S(T) data has recently been discussed and results from the mobility difference between electrons and holes, and leads to overestimates when using the classical Goldsmid–Sharp equation.50 The bandgap values observed here are consistent with recently reported values of 0.13 eV for ZrNiSn from room temperature optical measurements.50
ρ(T) − 1/T data for the samples without Ti are shown in Fig. 5e, and reveals the presence of similar bandgap values below the onset of minority carrier conduction (0.07–0.16 eV, Table 5). In addition, the Goldsmid–Sharp formula was used to extract a value for the bandgap from the S(T) data.53 These are larger and fall between 0.3–0.4 eV (Table 5). The discrepancy between the bandgap values from ρ(T) and S(T) data has recently been discussed and results from the mobility difference between electrons and holes, and leads to overestimates when using the classical Goldsmid–Sharp equation.50 The bandgap values observed here are consistent with recently reported values of 0.13 eV for ZrNiSn from room temperature optical measurements.50



