Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Curvature-sensing and generation by membrane proteins: a review
Hiroshi
Noguchi

Institute for Solid State Physics, University of Tokyo, Kashiwa, Chiba 277-8581, Japan. E-mail: noguchi@issp.u-tokyo.ac.jp
First published on 23rd April 2025
Abstract
Membrane proteins are crucial in regulating biomembrane shapes and controlling the dynamic changes in membrane morphology during essential cellular processes. These proteins can localize to regions with their preferred curvatures (curvature sensing) and induce localized membrane curvature. Thus, this review describes the recent theoretical development in membrane remodeling performed by membrane proteins. The mean-field theories of protein binding and the resulting membrane deformations are reviewed. The effects of hydrophobic insertions on the area-difference elasticity energy and that of intrinsically disordered protein domains on the membrane bending energy are discussed. For the crescent-shaped proteins, such as Bin/Amphiphysin/Rvs superfamily proteins, anisotropic protein bending energy and orientation-dependent excluded volume significantly contribute to curvature sensing and generation. Moreover, simulation studies of membrane deformations caused by protein binding are reviewed, including domain formation, budding, and tubulation.
1 Introduction
Cell membranes and organelles exhibit a variety of shapes. Various types of proteins are known to control dynamical changes in membrane morphology during essential cellular processes, such as endocytosis, exocytosis, vesicle transport, mitosis, and cell locomotion.1–7 During in vitro experiments, protein binding has been observed to induce membrane budding and tubulation. Additionally, membrane proteins can localize to membrane regions of specific curvature. These two phenomena are referred to as curvature generation and curvature sensing, respectively. This review focuses on the theoretical studies of protein behaviors with emphasis on thermal equilibrium and relaxation to the equilibrium. Non-equilibrium membrane dynamics, such as non-thermal fluctuations8–11 and wave propagations,12–18 are covered in our recent review.19 Moreover, because membrane simulation models and methods have previously been reviewed in ref. 20–26, this review primarily describes the mean-field theory and presents relevant simulation results without delving into detailed simulation methodologies.Section 2 provides an overview of the bending energy of lipid membranes and their morphology in the absence of proteins. Section 3 discusses curvature-sensing. Certain proteins exhibit laterally isotropic shapes in a membrane and bend the membrane isotropically. Section 3.1 presents the theoretical aspects of isotropic proteins, and Section 3.2 explores how intrinsically disordered protein (IDP) domains influence membrane bending properties. Section 3.3 addresses the behavior of anisotropic proteins. Crescent-shaped proteins, such as Bin/Amphiphysin/Rvs (BAR) superfamily proteins, induce membrane bending along their major protein axes. Section 3.4 examines protein binding to tethered vesicles and presents the estimation of protein bending properties. Section 4 focuses on curvature generation, with Sections 4.1 and 4.2 reviewing membrane deformations induced by the isotropic and anisotropic proteins, respectively. Section 4.3 discusses the membrane deformation by the adhesion of colloidal nanoparticles. Finally, Section 5 provides a summary and outlook.
2 Lipid membranes
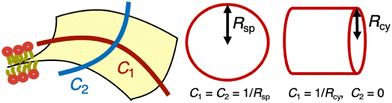
In a fluid phase, lipid membranes are laterally isotropic, and their bending energy can be expressed using the second-order expansion of the membrane curvature, known as the Canham–Helfrich model.27,28 | (1) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d denote the bending rigidity and saddle-splay modulus (also referred to as the Gaussian curvature modulus), respectively. The parameter Cmb denotes the spontaneous curvature. Note that the spontaneous curvature is often expressed as Hmb = Cmb/2, which is particularly useful in the analysis of spherical membranes, while Cmb is useful for cylindrical membranes. For lipid bilayers with symmetric leaflets, the membrane has zero spontaneous curvature (Cmb = 0). The last term in eqn (1) can be neglected when considering the shape transformation of vesicles with a fixed topology, owing to the Gauss–Bonnet theorem,
d denote the bending rigidity and saddle-splay modulus (also referred to as the Gaussian curvature modulus), respectively. The parameter Cmb denotes the spontaneous curvature. Note that the spontaneous curvature is often expressed as Hmb = Cmb/2, which is particularly useful in the analysis of spherical membranes, while Cmb is useful for cylindrical membranes. For lipid bilayers with symmetric leaflets, the membrane has zero spontaneous curvature (Cmb = 0). The last term in eqn (1) can be neglected when considering the shape transformation of vesicles with a fixed topology, owing to the Gauss–Bonnet theorem, 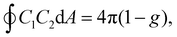 where g represents the genus of the vesicle. Lipid membranes typically exhibit a bending rigidity in the range of κd = 10–100 kBT29–32 and
where g represents the genus of the vesicle. Lipid membranes typically exhibit a bending rigidity in the range of κd = 10–100 kBT29–32 and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d/κd ≃ −133, where kBT is the thermal energy. In this review, we use κd = −
d/κd ≃ −133, where kBT is the thermal energy. In this review, we use κd = −![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d = 20 kBT and Cmb = 0, unless otherwise specified.
d = 20 kBT and Cmb = 0, unless otherwise specified.
In lipid membranes, the traverse movement of phospholipids between the two leaflets, known as flip–flop, occurs at an extremely slow rate, with half-lives ranging from hours to days.34 In contrast, amphiphilic molecules with small hydrophilic head groups, such as cholesterols, exhibit significantly faster flip–flop dynamics, occurring within seconds to minutes.35–37 In living cells, proteins facilitate flip–flop. Flippase and floppase proteins actively transport specific lipids from the outer to the inner leaflets (flip) or in the opposite direction (flop), respectively, through ATP hydrolysis, leading to an asymmetric lipid distribution. Conversely, scramblases mediate the bidirectional translocation of lipids, allowing the bilayer to relax toward a thermal-equilibrium lipid distribution.35 As a result, the number of lipids in each leaflet remains constant over typical experimental timescales, although it can relax with the addition of cholesterols,38,39 ultra-long-chain fatty acids,40,41 and scramblases. Consequently, the area difference  of the two leaflets in a liposome may differ from the lipid-preferred area difference ΔA0 = (Nout − Nin)alip, where Nout and Nin represent the numbers of lipids in the outer and inner leaflets, respectively, alip is the area per lipid, and h ≃ 2 nm denotes the distance between the centers of the two leaflets. In the area difference elasticity (ADE) model,42–44 the energy associated with the mismatch ΔA − ΔA0 is accounted for by a harmonic potential:
of the two leaflets in a liposome may differ from the lipid-preferred area difference ΔA0 = (Nout − Nin)alip, where Nout and Nin represent the numbers of lipids in the outer and inner leaflets, respectively, alip is the area per lipid, and h ≃ 2 nm denotes the distance between the centers of the two leaflets. In the area difference elasticity (ADE) model,42–44 the energy associated with the mismatch ΔA − ΔA0 is accounted for by a harmonic potential:
 | (2) |
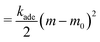 | (3) |
| = 8πkr(Δa − Δa0)2, | (4) |
Because the critical micelle concentration (CMC) of lipids is extremely low,46 the number of lipid molecules within a vesicle remains essentially constant over typical experimental timescales. Additionally, the internal volume is maintained nearly constant due to osmotic pressure, since water molecules can slowly permeate the lipid bilayer, whereas the penetration of ions or macromolecules is negligible. Under the constraints of a constant volume V and constant surface area A at Cmb = 0, the global energy minimum of Fcv0 corresponds to different vesicle shapes depending on the reduced volume V* = 3V/(4πRA3). In the mechanical (force) viewpoint, the stress caused by the bending energy is balanced by the surface tension (γ) and the osmotic pressure difference between the inner and outer solutions. For vesicles with genus g = 0, stomatocyte, discocyte, and prolate shapes achieve global energy minima within the ranges 0 < V* ≲ 0.59, 0.59 ≲ V* ≲ 0.65, and 0.65 ≲ V* < 1, respectively.42,47,48 These three shapes can coexist as (meta-)stable states at V* ≃ 0.6,49 and the prolate shape can persist as a meta-stable state even at V* ≲ 0.6, as illustrated in Fig. 2.50,51 Note that red blood cells have a discocyte shape with V* ≃ 0.6 in the physiological condition, and their membranes have shear elasticity due to the cytoskeletons underneath the membranes.52 When the ADE energy is included, additionally, branched tubular vesicles and budding (where spherical buds form on the outside of a spherical vesicle)42,53 emerge alongside the stomatocyte, discocyte, and prolate shapes. Notably, experimental observations have been well reproduced by this theoretical model.45 Furthermore, rapid changes in ΔA0 induced by chemical reactions and other factors can lead to the protrusion of bilayer sheets, reducing the area difference.54,55
 | ||
| Fig. 2 Stable and meta-stable shapes of vesicles in the Canham–Helfrich model (eqn (1)) with Cmb = 0.49,50 (a) Snapshots obtained by dynamically-triangulated MC simulations. Stomatocyte at V* = 0.5, discocyte at V* = 0.6, and prolate at V* = 0.5. (b) Area difference Δa of (meta-) stable shapes. Adapted from ref. 50 with permission from the Royal Society of Chemistry (2015). | ||
3 Curvature sensing
Peripheral and transmembrane proteins tend to accumulate in membrane regions that match their preferred curvatures. The surface densities of peripheral proteins are governed by the balance between the protein binding and unbinding processes in thermal equilibrium. In contrast, in typical in vitro experiments, the total number of transmembrane proteins within a vesicle remains fixed. These scenarios correspond to grand canonical and canonical ensembles in the membrane, respectively. While the choice between these two conditions does not affect average properties, such as surface protein density and alignment, it influences kinetics and fluctuations (the second derivatives of free energy).3.1 Theory of isotropic proteins
First, we discuss the curvature-sensing phenomenon of proteins with a laterally isotropic shape. The insertion of a hydrophobic α-helix and the anchoring of IDP domains do not exhibit a preferred bending direction. Moreover, proteins or protein assemblies possessing threefold, fivefold, or higher rotational symmetry exhibit laterally isotropic bending energy, when their asymmetric deformations are negligible.56 Several types of ion channels57,58 and G-protein coupled receptors (GPCRs),59–62 have rotationally symmetric structures. For instance, the trimer and pentamer of microbial rhodopsins exhibit threefold and fivefold symmetry, respectively.62 Furthermore, certain peripheral proteins, such as a clathrin monomer63 and annexin A5 trimer,64,65 also possess threefold symmetry.The presence of membrane-bound proteins can alter the membrane bending rigidity and spontaneous curvature relative to a bare (unbound) membrane. The bending energy of a vesicle can be expressed as66
 | (5) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi, and C0 = 2H0 denote the bending rigidity, saddle-splay modulus, and spontaneous curvature of the protein-occupied membrane, respectively, and ϕ represents the local protein density (area fraction, i.e., ϕ = 1 indicates complete coverage). This formulation accounts for the bending energy induced by the protein–membrane interactions. Additionally, inter-protein interactions – such as the steric effects arising from the brush region of IDP chains discussed in Section 3.2 – can further influence membrane rigidity and spontaneous curvature. In that case, κpi,
pi, and C0 = 2H0 denote the bending rigidity, saddle-splay modulus, and spontaneous curvature of the protein-occupied membrane, respectively, and ϕ represents the local protein density (area fraction, i.e., ϕ = 1 indicates complete coverage). This formulation accounts for the bending energy induced by the protein–membrane interactions. Additionally, inter-protein interactions – such as the steric effects arising from the brush region of IDP chains discussed in Section 3.2 – can further influence membrane rigidity and spontaneous curvature. In that case, κpi, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi, and C0 become functions of ϕ.66
pi, and C0 become functions of ϕ.66
At κpi > κd, the bending energy can also be expressed as Fcv1 = Fcv0 + Fpi with
 | (6) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi =
pi = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pa +
pa + ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d and C0 = [κpa/(κpa + κd)]C0a. This formulation is known as the curvature mismatch model, where κpa represents the additional bending rigidity by protein binding, while κpi accounts for the combined rigidity of the protein and the underlying membrane. The curvature mismatch model with
d and C0 = [κpa/(κpa + κd)]C0a. This formulation is known as the curvature mismatch model, where κpa represents the additional bending rigidity by protein binding, while κpi accounts for the combined rigidity of the protein and the underlying membrane. The curvature mismatch model with ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pa = 0 was used in ref. 67–69.
pa = 0 was used in ref. 67–69.
The total free energy F of a vesicle consists of the bending energy Fcv1, the inter-protein interaction energy, and the mixing entropy:
 | (7) |
The binding equilibrium of peripheral proteins is determined by minimizing J = F − μN, where μ is the binding chemical potential of the protein binding, and  is the number of the bound proteins. Consequently, the local protein density ϕ is given by ∂f/∂ϕ = μ/ap, where
is the number of the bound proteins. Consequently, the local protein density ϕ is given by ∂f/∂ϕ = μ/ap, where  . When the inter-protein interactions are negligible (b = 0), ϕ is expressed by a sigmoid function of μ:66
. When the inter-protein interactions are negligible (b = 0), ϕ is expressed by a sigmoid function of μ:66
 | (8) |
 | (9) |
This relation reflects the detailed balance between protein binding and unbinding at a local membrane region: ηub/ηb = exp(wb) for the kinetic equation dϕ/dt = ηb(1 − ϕ) − ηubϕ.70,71 For b ≠ 0, ϕ can be solved iteratively by replacing wb with wb + 2bϕap/kBT in eqn (8).66
For κpi > κd (κpa > 0), the protein density ϕ exhibits a peak at a finite curvature (referred to as the sensing curvature Hs, see Fig. 3(a)). The maximum value of ϕ increases from 0 to 1 with increasing μ. Notably, the protein binding differ between spherical and cylindrical membranes with the same mean curvature H, when ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi ≠
pi ≠ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d. The proteins bind more to spherical membranes compared to cylindrical membranes at (
d. The proteins bind more to spherical membranes compared to cylindrical membranes at (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi −
pi − ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d)/(κpi − κd) = −1 (see Fig. 3(a)). The sensing curvature Hs is obtained by solving dϕ/dH = 0 using eqn (8) under the conditions K = H2 for spherical membranes and K = 0 for cylindrical membranes:
d)/(κpi − κd) = −1 (see Fig. 3(a)). The sensing curvature Hs is obtained by solving dϕ/dH = 0 using eqn (8) under the conditions K = H2 for spherical membranes and K = 0 for cylindrical membranes:
 | (10) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi −
pi − ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d)/2 and κdif = κpi − κd for the spherical and cylindrical membranes, respectively. As κpi increases from κd to ∞, Hs decreases from ∞ to C0/(2 +
d)/2 and κdif = κpi − κd for the spherical and cylindrical membranes, respectively. As κpi increases from κd to ∞, Hs decreases from ∞ to C0/(2 + ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi/κpi) for spherical membranes and to C0/2 for cylindrical membranes (see Fig. 3(b)). It is important to note that ϕ(H) is mirror symmetric with respect to the sensing curvature for both cylindrical and spherical membranes (see Fig. 3(a)).
pi/κpi) for spherical membranes and to C0/2 for cylindrical membranes (see Fig. 3(b)). It is important to note that ϕ(H) is mirror symmetric with respect to the sensing curvature for both cylindrical and spherical membranes (see Fig. 3(a)).
 | ||
Fig. 3 Curvature sensing of isotropic proteins at C02ap = 0.04 (e.g., C0 = 0.02 nm−1 for ap = 100 nm2) and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi/κpi = pi/κpi = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d/κd = −1.66,70 (a) Protein density ϕ as a function of the local mean curvature H at κpi/κd = 0.5, 1, 2, and 4 for μ = 0. (b) Sensing curvature Hs and the maximum generation curvature Hg as a function of bending rigidity ratio κpi/κd. Hs and Hg are given by eqn (10) and (30) with ϕ = 1, respectively. The solid and dashed lines represent the data for spherical and cylindrical membranes, respectively. d/κd = −1.66,70 (a) Protein density ϕ as a function of the local mean curvature H at κpi/κd = 0.5, 1, 2, and 4 for μ = 0. (b) Sensing curvature Hs and the maximum generation curvature Hg as a function of bending rigidity ratio κpi/κd. Hs and Hg are given by eqn (10) and (30) with ϕ = 1, respectively. The solid and dashed lines represent the data for spherical and cylindrical membranes, respectively. | ||
In contrast, for κpi < κd, the bound membrane exhibits a lower bending rigidity compared to the bare membrane. This scenario may arise when the bound proteins (or other molecules) remodel the bound membrane. For example, a reduction in membrane thickness can lead to decreased bending rigidity. Interestingly, the proteins hold a negative curvature sensing at κpi < κd, where ϕ exhibits a minimum instead of a maximum (see the gray lines in Fig. 3(a)).70 In other words, the fraction of bare membrane, 1 − ϕ, reaches its maximum at the negative sensing curvature. Owing to the lower rigidity, the bound membranes bend passively to reduce the bending energy of bare membrane regions, sometimes even in the opposite direction to their spontaneous curvatures. Consequently, these proteins cannot induce membrane bending to their spontaneous curvatures. Therefore, a higher bending rigidity (κpi > κd) is required to bend membranes to a specific curvature.
For κpi = κd, ϕ follows a monotonic sigmoid function of H without any distinct peaks (see the green line in Fig. 3(a)). In several previous studies,72–75 the condition κpi = κd was set as a simplified model, and the following bending energy was used:
 | (11) |
This formulation corresponds to the condition of κpi = κd, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi =
pi = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d, and b = κdC02/2. The quadratic term (κdC02/2)ϕ2 is often neglected.76,77 Since this quadratic term is independent of membrane curvature and represents a pairwise inter-protein interaction, its inclusion in the bending energy is not recommended. Similarly, preaveraging both bending rigidity and spontaneous curvature as
d, and b = κdC02/2. The quadratic term (κdC02/2)ϕ2 is often neglected.76,77 Since this quadratic term is independent of membrane curvature and represents a pairwise inter-protein interaction, its inclusion in the bending energy is not recommended. Similarly, preaveraging both bending rigidity and spontaneous curvature as 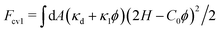 is not advisable, because it implicitly accounts for pairwise and three-body inter-protein interactions ((2κ1C0H + κdC02/2)ϕ2 and (κ1C02/2)ϕ3, respectively).70,78 Although the previous studies69,74,79 have compared the two models given by eqn (6) and (11) as distinct approaches, they are, in fact, the subsets of eqn (6) for κpi ≠ κd and κpi = κd, respectively.
is not advisable, because it implicitly accounts for pairwise and three-body inter-protein interactions ((2κ1C0H + κdC02/2)ϕ2 and (κ1C02/2)ϕ3, respectively).70,78 Although the previous studies69,74,79 have compared the two models given by eqn (6) and (11) as distinct approaches, they are, in fact, the subsets of eqn (6) for κpi ≠ κd and κpi = κd, respectively.
The chemical potential μ can be modulated by adjusting the bulk protein concentration ρ. For a dilute solution, it is expressed as μ(ρ) = μ(1) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ρ). In experiments, the ratio of surface protein densities at different curvatures has often been used, making the estimation of μ unnecessary. For a large spherical vesicle with RAC0 ≫ 1, the membrane can be approximated as flat (H = K = 0), and the protein density is given by ϕflat = 1/{1 + exp[(−μ + apκpiC02/2)/kBT]} for b = 0. Hence, for the protein density ϕcy in a cylindrical membrane with radius Rcy, eqn (8) can be rewritten as80
ln(ρ). In experiments, the ratio of surface protein densities at different curvatures has often been used, making the estimation of μ unnecessary. For a large spherical vesicle with RAC0 ≫ 1, the membrane can be approximated as flat (H = K = 0), and the protein density is given by ϕflat = 1/{1 + exp[(−μ + apκpiC02/2)/kBT]} for b = 0. Hence, for the protein density ϕcy in a cylindrical membrane with radius Rcy, eqn (8) can be rewritten as80
 | (12) |
In the low-density limit (ϕflat ≪ 1 and ϕcy ≪ 1), the density ratio is simplified to an exponential function as67,81
 | (13) |
3.2 Intrinsically disordered protein (IDP) domains
Many curvature-inducing proteins contain IDP domains. Stachowiak and coworkers have investigated the effects of varying the length of IDP domains in BAR and other proteins and have reported that the disordered domains facilitate curvature sensing and that the longer IDP chains promote the formation of small vesicles.82–85 A disordered domain behaves as a linear polymer chain in a good solvent,86 that is, its mean radius of gyration scales as 〈Rg〉 ∼ nνpoly, where 〈⋯〉 denotes the ensemble average, npoly represents the number of Kuhn segments, and ν = 0.6 is the scaling exponent for an excluded volume chain.87,88 The Kuhn length of IDP chains is approximately 0.8 nm.86 The interactions between membrane-anchored polymer chains and membrane have been extensively studied through theory,89–93 simulations,94–97 and experiments.98–102 The formation of spherical buds98,99,101 and membrane tubes99,100,102 have been observed experimentally. Polymer anchoring induces a positive spontaneous curvature of the membrane and increases the bending rigidity in a good solvent.At low polymer densities (referred to as the “mushroom regime”), the polymer chain exists in isolation on the membrane forming a mushroom-like distribution, where the inter-polymer interactions are negligible. In this regime, both the spontaneous curvature and bending rigidity increase linearly with the grafting density ϕpoly of the polymer chains. Analytically, the relations89,90
| κpiΔH0 = kh0kBTRendϕpoly, | (14) |
| Δκ = kκkBTRend2ϕpoly, | (15) |
Δ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) = − = −![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) κkBTRend2ϕpoly, κkBTRend2ϕpoly, | (16) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) represent the differences in the spontaneous curvatures, bending rigidities, and saddle-splay moduli between the polymer-decorated and bare membranes, respectively, and Rend represents the mean end-to-end distance of the polymer chain. These coefficients have been analytically derived using Green's function for ideal chains89,90 and have also been estimated by Monte Carlo (MC) simulations of single anchored polymer chains:94kh0 = 0.18 and 0.17; kκ = 0.21 and 0.2; and
represent the differences in the spontaneous curvatures, bending rigidities, and saddle-splay moduli between the polymer-decorated and bare membranes, respectively, and Rend represents the mean end-to-end distance of the polymer chain. These coefficients have been analytically derived using Green's function for ideal chains89,90 and have also been estimated by Monte Carlo (MC) simulations of single anchored polymer chains:94kh0 = 0.18 and 0.17; kκ = 0.21 and 0.2; and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) κ = 0.17 and 0.15; for ideal and excluded-volume chains, respectively.
κ = 0.17 and 0.15; for ideal and excluded-volume chains, respectively.
At a polymer density sufficiently higher than the overlap density (referred to as “brush regime”), the polymer chains extend perpendicularly from the membrane surface, forming a brush-like structure. In this regime, polymers grafting further enhance both the bending rigidity and spontaneous curvature of the membrane. In the limit of small curvature, the bending rigidity and saddle-splay modulus are given by90
 | (17) |
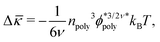 | (18) |
 is the polymer density normalized by the maximum coverage. Consequently, brush polymers increases the membrane rigidity in proportion to ϕ2.5poly, as show in Fig. 4.
is the polymer density normalized by the maximum coverage. Consequently, brush polymers increases the membrane rigidity in proportion to ϕ2.5poly, as show in Fig. 4.
 | ||
Fig. 4 Schematic graph of the bending modulus modification by IDP chains. The red and blue lines represent the differences in the bending rigidities (Δκ), and saddle-splay moduli (Δ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ) between the IDP-decorated and bare membranes, respectively. At sufficiently lower and higher densities than the overlap density (ϕoverlap), the IDP chains exhibit mushroom and brush shapes, respectively, as drawn in the inset. In the mushroom region, Δκ and Δ ) between the IDP-decorated and bare membranes, respectively. At sufficiently lower and higher densities than the overlap density (ϕoverlap), the IDP chains exhibit mushroom and brush shapes, respectively, as drawn in the inset. In the mushroom region, Δκ and Δ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) are expressed by eqn (15) and (16), respectively, with the coefficients for a good solvent.94 In the brush region, Δκ and Δ are expressed by eqn (15) and (16), respectively, with the coefficients for a good solvent.94 In the brush region, Δκ and Δ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) are expressed by eqn (17) and (18), respectively, in the small curvature limit.90 are expressed by eqn (17) and (18), respectively, in the small curvature limit.90 | ||
In addition, polymer grafting reduces the line tension of membrane edges, thereby stabilizing the microdomains with a size of the polymer-chain length.97 Furthermore, in a poor solvent environment, the polymer grafting can induce a negative spontaneous curvature, leading to the formation of a dimple-shaped membrane structure.96,103
3.3 Theory of anisotropic proteins
Here, we consider the binding of anisotropic proteins to membranes. A prominent example of anisotropic proteins is the BAR superfamily proteins, which features a banana-shaped binding domain known as the BAR domain. This binding domain is a dimer and holds twofold rotational symmetry. The BAR domain binds to the membrane, inducing curvature along the domain axis and generating cylindrical membrane tubes.1,3,73,104–109 The BAR domains have lengths from 13 to 27 nm.104 N-BAR and F-BAR domains have a positive curvature along the domain axis and I-BAR (Inverse-BAR) domains have a negative curvature. Some BAR proteins also have extra binding domains, such as phox homology (PX) and pleckstrin homology (PH) domains, and N-BAR and some extra domains have membrane insertion modules.105,110,111 These domains and modules can modify the bending energy of bound regions, with maintaining the rotational symmetry.Not all curvature-inducing proteins exhibit rotational symmetry. For example, dynamin,112–114 which has an asymmetric structure, forms helical assemblies that constrict membrane neck, leading to membrane fission. Similarly, melittin and amphipathic peptides115–118 bind to membranes, and their circular assemblies result in membrane pore formation. Recent coarse-grained simulation of a buckled membrane by Gómez-Llobregat and coworkers demonstrated the curvature sensing of three amphipathic peptides.119 They revealed that melittin and the amphipathic peptides LL-37 (PDB: 2k6O) exhibited asymmetric curvature sensing, meaning that their angular distribution relative to the buckled axis is not symmetric.
Several bending-energy models have been proposed to describe the behavior of anisotropic proteins. For the crescent-shaped symmetric proteins, such as BAR proteins, the bending energy can be expressed as70,120,121
 | (19) |
C![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m = C1 m = C1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(θpc) + C2 cos2(θpc) + C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(θpc) = H + D sin2(θpc) = H + D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2θpc), cos(2θpc), | (20) |
C![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) s = C1 s = C1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(θpc) + C2 sin2(θpc) + C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(θpc) = H − D cos2(θpc) = H − D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2θpc), cos(2θpc), | (21) |
A protein can comprise binding domains with distinct bending axes (where C![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) j denotes the membrane curvature along the axis of the j-th domain) and isotropic bending regions (IDP domains etc.). Consequently, the bending energy of a single protein is generally expressed as56
j denotes the membrane curvature along the axis of the j-th domain) and isotropic bending regions (IDP domains etc.). Consequently, the bending energy of a single protein is generally expressed as56
 | (22) |
= k1H2 + k2H + k3K + k4D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2θpc) + k5HD cos(2θpc) + k5HD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2θpc) + k6D2 cos(2θpc) + k6D2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(4θpc) + k7D cos(4θpc) + k7D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2θpc) + k8HD sin(2θpc) + k8HD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2θpc) + k9D2 sin(2θpc) + k9D2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(4θpc) + U0, sin(4θpc) + U0, | (23) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) paap for Fpi (compare eqn (6) and (23)). Proteins with twofold rotational or mirror symmetry can have the first six terms (k1–k6), while asymmetric proteins may exhibit all nine terms. The protein major axis can be chosen to be k7 = 0 in order to reduce the number of coefficients. To express asymmetry, k8 ≠ 0 or k9 ≠ 0 is needed at this axis. The protein model in eqn (19) is considered with Nax = 2 and Fpi = 0, assuming orthogonal axes where C
paap for Fpi (compare eqn (6) and (23)). Proteins with twofold rotational or mirror symmetry can have the first six terms (k1–k6), while asymmetric proteins may exhibit all nine terms. The protein major axis can be chosen to be k7 = 0 in order to reduce the number of coefficients. To express asymmetry, k8 ≠ 0 or k9 ≠ 0 is needed at this axis. The protein model in eqn (19) is considered with Nax = 2 and Fpi = 0, assuming orthogonal axes where C![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 = C
1 = C![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m and C
m and C![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2 = C
2 = C![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) s, and the coefficients are mapped accordingly as k1 = 3(κp + κs)ap/4, k2 = −(κpCp + κsCs)ap, k3 = −(κp + κs)ap/4, k4 = −(κpCp − κsCs)ap, k5 = (κp − κs)ap, and k6 = (κp + κs)ap/4.56 Akabori and Santangelo125 have added Uasy = kasy[D
s, and the coefficients are mapped accordingly as k1 = 3(κp + κs)ap/4, k2 = −(κpCp + κsCs)ap, k3 = −(κp + κs)ap/4, k4 = −(κpCp − κsCs)ap, k5 = (κp − κs)ap, and k6 = (κp + κs)ap/4.56 Akabori and Santangelo125 have added Uasy = kasy[D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(2θpc) − Casy]2 to eqn (19) in order to include an asymmetric bending effect. Their formulation corresponds to eqn (23) with k7 = −2kasyCasy and k8 = k9 = 0, modifying k1, k3, and k6. Kralj-Iglič and coworkers have considered the protein energy with a symmetric shape,126,127Up = ka(H − H0)2/2 + (ka + kb)[D2 − 2DD0
sin(2θpc) − Casy]2 to eqn (19) in order to include an asymmetric bending effect. Their formulation corresponds to eqn (23) with k7 = −2kasyCasy and k8 = k9 = 0, modifying k1, k3, and k6. Kralj-Iglič and coworkers have considered the protein energy with a symmetric shape,126,127Up = ka(H − H0)2/2 + (ka + kb)[D2 − 2DD0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2θpc) + D02]/4. The second term assumes an energy proportional to a rotational average of (d(C
cos(2θpc) + D02]/4. The second term assumes an energy proportional to a rotational average of (d(C![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − Cm)/dθ)2, where C
− Cm)/dθ)2, where C![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the normal membrane curvature at the angle θ, and Cm = Cm0 + Cm1
is the normal membrane curvature at the angle θ, and Cm = Cm0 + Cm1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2θ) is the angle-dependent spontaneous curvature. In this formulation, k1 = 3ka/4 + kb/4, k2 = −kaH0, k3 = −(ka + kb)/4, k4 = −(ka + kb)D0/2, and k5 = k6 = 0. They have also used the first term of eqn (19) for rod-like proteins (i.e., κs = 0).127 Fournier combined an anisotropic bending energy with the tilt energy of lipids for transmembrane proteins.128
cos(2θ) is the angle-dependent spontaneous curvature. In this formulation, k1 = 3ka/4 + kb/4, k2 = −kaH0, k3 = −(ka + kb)/4, k4 = −(ka + kb)D0/2, and k5 = k6 = 0. They have also used the first term of eqn (19) for rod-like proteins (i.e., κs = 0).127 Fournier combined an anisotropic bending energy with the tilt energy of lipids for transmembrane proteins.128
 . The binding ratio of proteins to a cylindrical membrane tube relative to a flat membrane is expressed as56
. The binding ratio of proteins to a cylindrical membrane tube relative to a flat membrane is expressed as56 | (24) |
Anisotropic proteins can adjust their lateral orientation to reduce their bending energy. Let us consider a crescent symmetric protein (eqn (19) with κs = 0) and its variants as simple anisotropic protein models. This crescent protein has the lowest bending energy at θpc = 0 (the protein orients in the azimuthal direction) in a wide cylinder (1/RcyCp ≤ 1), whereas tilt proteins have the lowest at  in a narrow cylinder (1/RcyCp > 1). Hence, the protein density exhibits peaks at these preferred orientations (see the red lines in Fig. 5(b) and (c)). The average density ϕcy also exhibits a peak at a membrane curvature slightly higher than 1/RcyCp = 1 (see Fig. 5(a)). Unlike isotropic proteins, ϕcy(Rcy) is not mirror symmetric and decreases gradually at larger curvatures, owing to the angular adjustment of proteins. When an isotropic bending energy component, Fpi, is added with a relative strength of 10% (κpi/κp = 0.1 and C0a = 0), the density profile of ϕcy approaches a mirror symmetric shape (see the green line in Fig. 5(a)). Some amphipathic peptides have a kink structure, which allows significant bending. To mimic this behavior, a kink is introduced at 20% of the protein length from the protein end; at the kink, the protein bends laterally at an angle of π/4. Owing to the resulting asymmetry, the angular distribution becomes skewed, with the highest peak appearing at θpc < 0 and θpc > 0 for the curvature ranges 1 < 1/RcyCp < 2 and 1/RcyCp > 2, respectively (see the blue lines in Fig. 5).56 A similar asymmetric angular distribution was reported in molecular simulation.119 The above discussion focuses on the binding of rigid proteins; however, the deformation of the binding domains can modify the protein density as demonstrated in ref. 56.
in a narrow cylinder (1/RcyCp > 1). Hence, the protein density exhibits peaks at these preferred orientations (see the red lines in Fig. 5(b) and (c)). The average density ϕcy also exhibits a peak at a membrane curvature slightly higher than 1/RcyCp = 1 (see Fig. 5(a)). Unlike isotropic proteins, ϕcy(Rcy) is not mirror symmetric and decreases gradually at larger curvatures, owing to the angular adjustment of proteins. When an isotropic bending energy component, Fpi, is added with a relative strength of 10% (κpi/κp = 0.1 and C0a = 0), the density profile of ϕcy approaches a mirror symmetric shape (see the green line in Fig. 5(a)). Some amphipathic peptides have a kink structure, which allows significant bending. To mimic this behavior, a kink is introduced at 20% of the protein length from the protein end; at the kink, the protein bends laterally at an angle of π/4. Owing to the resulting asymmetry, the angular distribution becomes skewed, with the highest peak appearing at θpc < 0 and θpc > 0 for the curvature ranges 1 < 1/RcyCp < 2 and 1/RcyCp > 2, respectively (see the blue lines in Fig. 5).56 A similar asymmetric angular distribution was reported in molecular simulation.119 The above discussion focuses on the binding of rigid proteins; however, the deformation of the binding domains can modify the protein density as demonstrated in ref. 56.
 | ||
| Fig. 5 Binding of anisotropic proteins in the low-density limit with Cp2ap = 0.2, κp = 50 kBT, and κs = 0.56 The red lines represent the data of a twofold rotationally symmetric protein (crescent-rod shape without kinks). The blue lines represent the data of an asymmetric protein, where the rod-shaped protein bends at a kink with an angle of π/4, positioned at 20% of the protein length from the end. The axis of the asymmetric protein is set to be θpeak = 0 at 1/Rcy ≪ 1. The green line represents the data of the twofold rotationally symmetric protein with an isotropic segment of κpi/κp = 0.1. (a) Binding density ϕcy on a cylindrical membrane with respect to the density ϕflat on a flat membrane. (b) Peak position of the angle θpc. The solid and dashed lines represent the first and second peaks, respectively. The inset shows the schematics of the top and side views of proteins. (c) Distribution of the angle θpc. The solid and dashed lines represent the data for 1/RcyCp = 3 and 0.8, respectively. | ||
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1
1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2/4, where
2/4, where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 are
1 are ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2 represent the lengths of the major and minor protein axes, respectively.
2 represent the lengths of the major and minor protein axes, respectively.
The free energy Fp of bound proteins is expressed as121
 | (25) |
 | (26) |
 | (27) |
| g = 1 − ϕ[b0 − b2Ssp(θps)]. | (28) |
 represent the symmetric and asymmetric components of the nematic tensor, respectively. The factor g accounts for the weight of the orientation-dependent excluded volume interaction, and Θ(x) denotes the unit step function. When two proteins are aligned parallel to each other, the excluded area Aexc between them is smaller compared to when they are oriented perpendicularly. This difference increases with increasing aspect ratio del =
represent the symmetric and asymmetric components of the nematic tensor, respectively. The factor g accounts for the weight of the orientation-dependent excluded volume interaction, and Θ(x) denotes the unit step function. When two proteins are aligned parallel to each other, the excluded area Aexc between them is smaller compared to when they are oriented perpendicularly. This difference increases with increasing aspect ratio del = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1/
1/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2. The area Aexc can be approximated as Aexc = [b0 − b2(cos2(θpp) − 1/2)]ap/λ, where θpp is the angle between the major axes of two proteins, and λ represents the packing ratio. The maximum density is given by ϕmax = 1/λ(b0 − b2/2).129
2. The area Aexc can be approximated as Aexc = [b0 − b2(cos2(θpp) − 1/2)]ap/λ, where θpp is the angle between the major axes of two proteins, and λ represents the packing ratio. The maximum density is given by ϕmax = 1/λ(b0 − b2/2).129
For a flat membrane, proteins exhibit an isotropic orientation at low densities and a first-order transition to a nematic order at high densities owing to the orientation-dependent excluded volume interactions.121 In this review, we consider the anisotropic bending energy described by eqn (19) with κs = 0 for Up. As the curvature 1/Rcy of a membrane tube increases, proteins tend to align in the azimuthal direction even in the dilute limit (see Fig. 5(c)), and the transition to the nematic state becomes continuous.
For narrow tubes with 1/Rcy > Cp, the preferred protein orientation tilts away from the azimuthal direction. At low ϕ, proteins tilted in both the left and right directions coexist equally (Fig. 5). However, at high protein densities, only one type of tilt direction dominates due to orientation-dependent excluded volume interactions. Thus, second-order and first-order transitions occur between these two states at medium and large curvatures, respectively.129
This theory well reproduces the simulation results for crescent protein rods on a membrane tube, when the proteins are isotropically distributed.129 However, the discrepancies arise when the proteins form a significant amount of clusters, since the current theory does not account for inter-protein attraction and assumes a homogeneous protein distribution.129
3.4 Binding to tethered vesicle
A vesicle held by a micropipette forms a narrow membrane tube (tether) under a pulling force applied by optical tweezers, as illustrated in Fig. 6(a).30,131–133 The tube radius can be controlled by adjusting the force strength. Tethered vesicles have been widely employed to study the curvature sensing of membrane proteins, including BAR proteins,67,69,72,79,134 ion channels,135,136 GPCRs,68 dynamin,137 annexins,138 and Ras proteins.139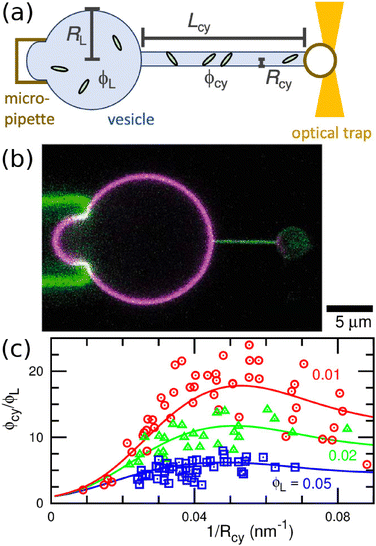 | ||
| Fig. 6 Binding of I-BAR domain of IRSp53 to tethered vesicle. (a) Schematic of the experimental setup. A cylindrical membrane tube (tether) is extended by an optical trap and micropipette. (b) Confocal image of a vesicle with a tube of Rcy = 25 nm. Green and magenta indicate the fluorescence for I-BARs and lipids, respectively. (c) Protein density ϕcy in the tube normalized by that of the large spherical region ϕL. Circles, triangles, and squares indicate the experimental data of ϕcy/ϕL for ϕL = 0.01, 0.02, and 0.05, respectively. The solid lines are obtained using fitting by the anisotropic protein model with κp/kBT = 82 and Cp = −0.047 nm−1. The experimental data in (b) and (c) are reproduced from ref. 67. Licensed under CC BY (2015). The plot in (c) is reproduced from ref. 80 with permission from the Royal Society of Chemistry (2023). | ||
Protein density in the membrane can be quantified using fluorescence intensity measurement, as shown in Fig. 6(b). For I-BAR domains, the density ratio ϕcy/ϕL between the membrane tube to large spherical regions reaches a peak at a tube curvature of approximately 0.05 nm−1 and gradually decreases at larger curvature (see Fig. 6(c)).67 This curvature dependence can be reproduced by the theory for elliptic proteins (eqn (25)–(28)) with κp/kBT = 82, Cp = −0.047 nm−1, and κs = 0.80 Note that the theory for isotropic proteins (eqn (12) or (13)) can reproduce each curve using different κpi and C067 but cannot simultaneously fit all three experimental curves.80 This finding strongly supports the anisotropic nature of the curvature sensing in I-BAR domains. Therefore, the tethered vesicle serves as a valuable tool not only for investigating curvature sensing but also for estimating the bending properties of various membrane proteins. However, the dependence on the saddle-splay modulus (k3 in eqn (23)) cannot be directly measured using the tethered vesicle, since K = 0 in the membrane tube. Instead, k3 can be estimated by comparing curvature sensing data from the membrane tubes and spherical vesicles with the same mean curvature (see Fig. 3). Curvature sensing has been observed through protein binding to spherical vesicles with various sizes,84,139,140 and the comparisons with the data in membrane tube were also reported in ref. 139 at small membrane curvatures. For the estimation of the protein properties, the sensing data at large curvatures are particularly significant, since the anisotropic characteristics become more pronounced in this regime (see Fig. 5(a)).
The force generated by the bending energy, while maintaining a fixed volume and surface area, is balanced with the external force fex at equilibrium. Under typical experimental conditions of the tethered vesicle, the membrane tube is extremely narrow, making the volume of the cylindrical tube negligible, as Rcy2Lcy/RA3 ≪ 1.81,141 In this limit condition, the vesicle shape is obtained from ∂Fcv1/∂Lcy = fex|Acy of the cylindrical tube with Acy = 2πRcyLcy.
For the binding of isotropic proteins, it is expressed as81
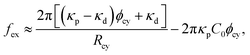 | (29) |
 | ||
| Fig. 7 Protein binding to a membrane tube pulled by an external force fex. Protein density ϕ and tube curvature 1/Rcy are shown in (a), (c) and in (b), (d), respectively. (a) and (b) Isotropic proteins for μ/kBT = −4, −2, −1, and 0 at κp/κd = 4 and apC02 = 0.16. (c) and (d) Crescent elliptic proteins for μ/kBT = −2, 0, and 2.5 at κp/kBT = 60, κs = 0, del = 3, and apCp2 = 0.26. The solid lines represent equilibrium states. The black dashed lines represent metastable and free-energy barrier states (van der Waals loops). The isotropic proteins exhibit a first-order transition twice at large μ.81 In contrast, the anisotropic proteins exhibit it only once at a small curvature.129 | ||
For the anisotropic proteins, the membrane curvature is obtained from the force balance as fex/2π = ∂fp/∂(1/Rcy)|ϕcy + κd/Rcy, where fp is given by eqn (26).80,129 The fex dependence curves of ϕcy and 1/Rcy are not symmetric, unlike for isotropic proteins (compare Fig. 7(c) and (d) with Fig. 7(a) and (b)). The density and curvature exhibit a weaker dependence on fex at fex > f0 owing to the protein tilting in narrow tubes, where f0 = 2πκdCp. Consequently, at high μ, the first-order transition occurs only once in wide tubes. This transition has been experimentally observed, showing the coexistence of high and low I-BAR density regions within the same membrane tube in ref. 67. The sensing curvature of anisotropic proteins is influenced not only by Cp but also by the protein density, as shown in Fig. 7(c) and (d).129
4 Curvature generation
4.1 Isotropic proteins
Curvature-inducing proteins alter the local membrane curvature, bringing it closer to their preferred curvatures. In the absence of constraints, the curvature Hg generated by isotropic proteins is determined by minimizing the free-energy, given by the condition dFcv1/dH = 0 using eqn (5):66 | (30) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi ≠
pi ≠ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d (see Fig. 3(b)). In the presence of constraints, the membrane may bend to a lesser extent than this generation curvature, since the constraints can suppress the membrane deformation.
d (see Fig. 3(b)). In the presence of constraints, the membrane may bend to a lesser extent than this generation curvature, since the constraints can suppress the membrane deformation.
In living cells, spherical buds typically form during vesicle formation. In clathrins-mediated endocytosis, clathrins assemble on the membrane, forming spherical buds with diameters ranging from 20 to 200-nm.4,142–144 Similarly, in the membrane trafficking between the endoplasmic reticulum and the Golgi apparatus, COPI and COPII coated vesicles with diameters ranging from 60 to 100-nm are generated through budding under typical conditions.5,145,146 These proteins can be considered as laterally isotropic, and their budding processes have been theoretically analyzed using a spherical-cap geometry147–149 and more detailed geometry.150
The budding of a vesicle can be understood using the mean-field theory with simplified geometries.66 A budded vesicle is modeled as small spheres connected to a large spherical membrane, as depicted in the inset of Fig. 8(c). Assuming that all buds have the same radius Rbud, the free energy minimum can be easily solved using eqn (7) for one degree of freedom, since the other two lengths can be determined by the area and volume constraints. A prolate vesicle can be modeled by a cylinder shape capped with two hemispheres. As the chemical potential μ increases, the protein density ϕbud in the buds increases greater than ϕL in the large spherical region, leading to the formation of a greater number of buds with a smaller radius (see Fig. 8). At a small spontaneous curvature (C0RA = 200), The number of buds increases continuously, whereas, at a large spontaneous curvature (C0RA = 300), a first-order transition occurs from a few buds with a large radius to many buds with a small radius, as shown in Fig. 8. Thus, many buds can suddenly form after a long incubation period at slightly higher than the transition point.
 | ||
Fig. 8 Budding of a vesicle induced by the binding of proteins with a spontaneous curvature C0 at V* = 0.95, κpi/κd = 4, and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pi/ pi/![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) d = 1.66 (a) Protein density on the vesicle surface in the absence of the ADE energy. The solid and dashed lines represent the densities in the buds ϕbud and spherical vesicle region ϕL, respectively. The blue and red lines indicate the continuous and discontinuous transitions at C0RA = 200 and 300, respectively. (b) Number nbud of buds. The blue and red lines represent the data at C0RA = 200 and 300, respectively, in the absence of the ADE energy (corresponding to the data shown in (a)). The green and magenta lines represent the data with the ADE energy in the presence and absence of protein insertion (the insertion area ratio of the protein γin = 0.02 and 0), respectively, at RA/h = 5000. (c) Free energy profiles at μ/kBT = −0.7, −0.65, and −0.6 (from top to bottom) at C0RA = 300 (corresponding to the red lines in (a)). Two minima for a few and many buds appear around the transition point. d = 1.66 (a) Protein density on the vesicle surface in the absence of the ADE energy. The solid and dashed lines represent the densities in the buds ϕbud and spherical vesicle region ϕL, respectively. The blue and red lines indicate the continuous and discontinuous transitions at C0RA = 200 and 300, respectively. (b) Number nbud of buds. The blue and red lines represent the data at C0RA = 200 and 300, respectively, in the absence of the ADE energy (corresponding to the data shown in (a)). The green and magenta lines represent the data with the ADE energy in the presence and absence of protein insertion (the insertion area ratio of the protein γin = 0.02 and 0), respectively, at RA/h = 5000. (c) Free energy profiles at μ/kBT = −0.7, −0.65, and −0.6 (from top to bottom) at C0RA = 300 (corresponding to the red lines in (a)). Two minima for a few and many buds appear around the transition point. | ||
This simplified geometrical framework can be easily applied to other shape transformations and is useful for investigating the effects of additional interactions. For instance, the ADE energy is incorporated into the budding process (see Fig. 8(b)). Initially, the ADE energy is considered to be relaxed in the prolate vesicle (ΔA = ΔA0 in the prolate). When the bound proteins do not change ΔA0, the ADE energy only slightly reduces the budding (see the magenta curve in Fig. 8(b)).66 However, the insertion of hydrophobic segments into the membrane can modify ΔA0. When the segments insert only the outer leaflet with the ratio γin of the inserted area (i.e.,  ), the budding can be promoted (see the green curve in Fig. 8(b)). The insertion can induce the budding even at C0 = 0 through the protein binding to the large spherical region.
), the budding can be promoted (see the green curve in Fig. 8(b)). The insertion can induce the budding even at C0 = 0 through the protein binding to the large spherical region.
Lipid membranes supported on a solid substrate are widely used as model systems for biological membranes, providing a valuable platform to study both protein functions and membrane properties.151–155 Boye and coworkers reported that the annexin proteins64,156,157 can detach lipid membranes from the substrate.158,159 Their observation revealed membrane rolling and budding from open edges, with variations depending on the types of annexins. The budding and vesicle formation observed in these experiments can be interpreted as the binding behavior of isotropic proteins. Fig. 9 shows the membrane detachment dynamics obtained by a meshless membrane simulation,160 in which particles with a diameter of σ self-assemble into one-layer sheets in a fluid phase. The bound proteins (represented as red particles) induce membrane bending, counteracting the adhesion to the substrate, leading to the formation of small vesicles from the membrane edge.
 | ||
| Fig. 9 Sequential snapshots of membrane detachment from a substrate induced by the binding of isotropic proteins at C0σ = 0.2, κpi/kBT = 34, κd/kBT = 16, and μ/kBT = 5.160 Detached membranes form small vesicles. A sliced snapshot from the side view is shown for the right bird's-eye view snapshot. The red and yellow spheres represent the membrane particles with and without the protein binding, respectively. In the side view, the light gray rectangle represents the substrate. | ||
Under conditions of high surface tension compared to the spontaneous curvature of the domain and the line tension of the domain boundary, curved domains do not fully close into spherical buds but instead adopt a spherical-cap shape. When these spherical-cap domains expand to cover most of the membrane surface, they organize into a hexagonal array, representing the closest packing configuration in 2D space, as shown in Fig. 10(a).71 As the binding chemical potential μ of proteins increases, the membrane undergoes a continuous transition from an unbound state to a hexagonal phase. This is followed by a first-order transition to the homogeneously bound phase, where the entire membrane becomes saturated with proteins.71
 | ||
| Fig. 10 Phase separation induced by binding of isotropic proteins. (a)–(c) Binding to upper and lower membrane surfaces at C0σ = ±0.1, κpi/kBT = 144, κd/kBT = 16, μu/kBT = 7.5, and μff = μd − μu.160 The red and green spheres represent membrane particles bound from the upper and lower surfaces, respectively. The yellow spheres represent unbound membrane particles. (a) Hexagonal pattern of the upper-bound domains in the unbound membrane at μd/kBT = 4. Lower bound particles are negligible. (b) Kagome-lattice pattern at μd/kBT = 6. The upper- and lower-bound domains form hexagonal and triangular shapes, respectively. (c) Checkerboard pattern at μd = μu. Both upper- and lower-bound domains form square shapes. (d) Beaded-necklace-shaped membrane tube induced by binding to the outer surface.81 The red and yellow spheres represent bound and unbound membrane particles, respectively. | ||
When proteins bind to both membrane surfaces from the upper and lower buffers, the membrane can form both convex and concave domains, as shown in Fig. 10(b) and (c).160,161 Under symmetric conditions, where the chemical potentials of the upper and lower surfaces are equal (μu = μd), the membrane exhibits distinct patterns depending on the chemical potential. At low chemical potentials, square domains arranged in a checkerboard pattern obtained, while at higher chemical potentials, striped patterns emerge. Small unbound membrane patches stabilize the vertices of the square domains (see Fig. 10(c)). When repulsive interactions are added between the unbound and bound membranes, these unbound patches expand and take on a square shape, and the bound domains adopt an octagonal shape, resembling the 4.8.8 tiling pattern.161 Under asymmetric conditions, where the chemical potential of the upper surface exceeds that of the lower surface (μu > μd), a kagome-lattice pattern can form. In this configuration, triangular concave domains are arranged within a hexagonal array of convex domains (see Fig. 10(b)). As the chemical-potential difference further increases, concave domains disappear and a hexagonal pattern of convex domains form (see Fig. 10(a)). Additionally, the transfer (flip–flop) of proteins between the two surfaces can be accounted for using the flip–flop chemical potential μff. At thermal equilibrium (μff = μd − μu), the flip–flop does not change the equilibrium behavior owing to the principle of detailed balance. However, under non-equilibrium conditions (μff ≠ μd − μu), the ballistic motion of biphasic domains and time-irreversible fluctuations of patterns can be observed.161
Phase separation can also occur in both spherical and cylindrical membranes. In spherical vesicles, the formation of hexagonal arrays of concave domains has been theoretically investigated.162 In cylindrical membrane, a 1D periodic pattern can emerge, in which round bound and narrow straight unbound domains alternate in a beaded-necklace-like arrangement (see Fig. 10(d)).81
Even in the absence of spontaneous-curvature differences between bound and unbound membranes, attraction between bound membrane regions can arise due to hydrophobic mismatch of transmembrane proteins and Casimir-like interactions in rigid proteins. The height of the transmembrane proteins can differ from the thickness of surrounding membrane,163–165 resulting in an effective attraction between proteins to reduce the hydrophobic mismatch.166–169 In thermal equilibrium, the membrane height fluctuations follow the relation 〈|hq|2〉 = kBT/(γq2 + κq4), where hq represents the Fourier transform of the membrane height in the Monge representation.170,171 Here, the surface tension γ corresponds to the mechanical frame tension conjugated to the projected membrane area.172 Rigid proteins with high bending rigidity κp suppress membrane fluctuations in their vicinity. As a result, protein assembly mitigates entropy loss, leading to a Casimir-like attractive interaction.71,173 This interaction is expressed in the leading order as 6 kBT(rp/r)4, where r is the inter-protein distance and rp represents the protein length. Consequently, the binding of rigid proteins induces a first-order transition between unbound and bound states.71 Additionally, Casimir-like interaction also arises between ligand–receptor pairs that connect adjacent membranes, effectively reducing the fluctuations in the membrane separation distance.174,175
4.2 Anisotropic proteins
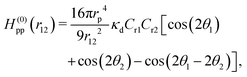 | (31) |
When two proteins bend the membrane in the same direction (Cr1Cr2 > 0), they exhibit an attractive interaction when oriented side-by-side (θ1 = θ2 = π/2) and a weaker repulsive interaction when aligned along the membrane axis (θ1 = 0 or θ2 = 0). In the side-by-side dimer configuration (i.e., θ1 = θ2 = π/2), the membrane experiences reduced deformation. This bending-energy reduction is the origin of this attraction. Conversely, when the proteins bend the membrane in the opposite directions (Cr1Cr2 < 0), the interactions are reversed. In this case, the proteins exhibit weak attraction when aligned along the membrane axis (θ1 = 0 or θ2 = 0) and repulsion when positioned side-by-side (θ1 = θ2 = π/2). Therefore, proteins with similar curvatures preferentially interact in a side-by-side configuration, whereas proteins with opposite curvatures prefer tip-to-tip alignment. These interactions have been quantitatively confirmed through the meshless membrane simulations.124 Furthermore, the Casimir-like interaction between straight rods exhibits a different angular dependence but decay over a shorter range, proportional to r12−4.181,182
For positive surface tensions (γ > 0), the bending energy dominates interactions on length scales shorter than 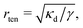 whereas surface tension effects become dominant at length scale greater than rten. As a result, the interaction energy changes from a bending-dominant regime to a tension-dominant regime at approximately r12 ≈ 3rten:124
whereas surface tension effects become dominant at length scale greater than rten. As a result, the interaction energy changes from a bending-dominant regime to a tension-dominant regime at approximately r12 ≈ 3rten:124
 | (32) |
 | (33) |
 | (34) |
In some coarse-grained simulations, the tip-to-tip assembly of crescent proteins on membranes has been reported.122,123 In these systems, proteins sink into the bound membrane by a strong protein-membrane attraction, resulting in a strongly negative spontaneous curvature perpendicular to the major axis of the crescent proteins. Consequently, the protein bending axis is perpendicular to the major axis, meaning that tip-to-tip alignment, from the perspective of the protein's shape, corresponds to side-to-side alignment when viewed from the bending axis.124
 | ||
| Fig. 11 Tubulation generated by BAR domains. (a) Confocal image of tubular invagination generated by the binding of I-BAR domains. Reproduced from ref. 109. Licensed under CC BY (2016). (b) N-BAR (amphiphysin/B1N1s)-coated tube with a diameter of 280 Å. 3D reconstruction from cryo-EM images. Reproduced from ref. 108. Licensed under CC BY (2015). (c) Tubulation simulated by a meshless membrane model.183 The BAR domain and membrane beneath are modeled as a linear chain of (red and yellow) particles with two kink (light blue and yellow) particles for the molecular chirality. In the upper panel, a protein rod is extracted to show the structure. The gray spheres represent the bare membrane particles. | ||
Tubulation and other membrane deformations have been realized using meshless membrane simulations (Fig. 11–14). In these simulations, the protein rods are modeled as linear chains consisting of ten membrane particles, with or without two kink particles to account for chirality, as shown in Fig. 11(c). The rod curvature Crodrrod ≃ 3 corresponds to that of BAR-PH domains,184 where rrod is the rod length. Additionally, excluded polymer chains, each containing npoly Kuhn segments to represent IDP domains, are incorporated, as shown in Fig. 13(a). Tubulation with a helical protein assembly can be effectively reproduced using meshless simulations of chiral protein rods (see Fig. 11(c)).183 While tubulation can also be induced by the achiral protein rods, the chirality has been shown to enhance the tubulation process.183
 | ||
| Fig. 12 Tubulation from a flat membrane by crescent-rod proteins at ϕrod = 0.4 and Crodrrod = 4.120 The proteins have the spontaneous curvatures Crod and Cs along the protein axis and perpendicular (side) direction, respectively, as shown at the middle bottom in (a). The initial state is an equilibrium state at Crod = Cs = 0, and the rod curvatures are tuned at t = 0. (a) The left panels show the sequential snapshots at t/τ = 0, 12.5, and 100 for a positive side curvature (Csrrod = 1). The right panels show the sequential snapshots at t/τ = 10, 100, and 200 for a negative side curvature (Csrrod = −1). The chains of spheres (upper and lower half surfaces are in red and yellow, respectively) represent the protein rods, and the gray spheres represent the bare membrane particles. (b) Time evolution of mean cluster height 〈zcl2〉1/2 normalized by the protein length rrod. The solid lines represent the data at the surface tension γrrod2kBT = 0, 6.25, and 12.5 for Csrrod = − 1. The dashed line represents the data at γ = 0 for Csrrod = 1. Reproduced from ref. 120. Licensed under CC BY (2016). | ||
 | ||
| Fig. 13 Tubulation and budding induced by crescent-rod proteins with anchoring excluded-volume chains at ϕrod = 0.24.185 (a) A protein comprising a crescent rod with two (light blue) kink particles (for chirality) and two excluded-volume chains of npoly particles, as a model of BAR proteins. (b) An array of short tubules at Crodrrod = 3 and npoly = 25. (c) Long tubules at Crodrrod = 3 and npoly = 100. (d) Ellipsoidal buds at Crod = 0 and npoly = 50. (e) Shish-kebab-shaped tubules at Crodrrod = −3 and npoly = 50. | ||
 | ||
| Fig. 14 Snapshots of vesicles with crescent protein rods. (a)–(d) A single type of protein is bound. Here, a protein is represented by a linear chain of ten spheres, whose upper and lower halves are in red and yellow, respectively. Unbound membrane particles are displayed in transparent gray. (a) Disk-shaped vesicle at ϕ = 0.167 and Crodrrod = 2.5. The proteins are in the disk edge.78,186 (b) Linear protein assembly at ϕ = 0.167 and Crodrrod = 3.75.78,186 (c) Tetrahedral vesicle at ϕ = 0.4 and Crodrrod = 2.5.78 (d) High-genus vesicle at ϕ = 0.8 and Crodrrod = 4.187 (e) and (f) Two types of proteins are bound with the densities ϕ1 = ϕ2 = 0.15.124 Two types of proteins are displayed in red and yellow and in blue and green, respectively. (e) Disk-shaped vesicle at Crod1rrod = 4 and Crod2rrod = 2. The proteins are phase-separated in the disk edge. (f) Vesicle with bumps at Crod1rrod = 3 and Crod2rrod = −3. The linear protein assemblies with opposite curvatures are alternately aligned side-by-side. | ||
Fig. 12 shows the tubulation dynamics of the achiral straight crescent rods.120 The same type of protein rods exhibit a membrane-mediated attractive interaction when aligned side-by-side, as discussed in Section 4.2.1. Consequently, these protein rods initially form linear assemblies perpendicular to their axis. Over time, the contacts of these assemblies lead to the development of a network structure at a sufficiently high protein densities. Eventually, tubules protrude from the network (see Fig. 12(a)). The stability of this network structure is influenced by the side curvature Cs of the proteins and the membrane surface tension γ. A negative side curvature Cs reduces the bending energy at network branch points, leading to slower tubulation compared to the case where Cs > 0 (compare the dashed and solid lines at γ = 0 in Fig. 12(b)). Since tubulation results in a reduction of the projected membrane surface area, increasing membrane tension γ inhibits tubulation (see three solid lines in Fig. 12(b)).73,183
The addition of the IDP domains can either promote or suppress tubulation, depending on the conditions.185 For a short IDP with npoly = 25, the tubulation dynamics slow down and become trapped in a short-tubule array, as shown in Fig. 13(b). In this case, the crowded IDP domains induce repulsion between tubules, preventing their fusion. Conversely, when npoly = 100, the IDP chains extend beyond the mean distance between tubules, allowing fusion and promoting tubule elongation in the vertical direction (see Fig. 13(c)). Thus, interactions between IDP chains and membranes enhance tubulation, while interactions between the IDP chains of neighboring tubules slow it down. In the absence of spontaneous curvature in the binding domains, IDP domains facilitate the formation of ellipsoidal buds, since the IDP chains gain more conformational entropy in vertically elongated shapes (see Fig. 13(d)). When IDPs are introduced to negatively bent crescent rods – where the binding domain and IDPs exhibit the opposite spontaneous curvatures – periodically bumped tubules are formed (see Fig. 13(e)). For short IDP chains, the proteins assemble into a network structure, resembling Fig. 12(a), on the membrane. This assembly causes the membrane to become rugged due to the bumped assemblies. Notably, a similar rugged vesicle has been observed in experiments involving a chimeric protein composed of I-BAR and IDP domains.85
At high Crod and increasing protein density, the length of the protein assembly exceeds the edge length of the disk-shaped vesicle. Initially, the vesicle elongates into an elongated elliptical shape, eventually, forming polyhedral structures, such as a tetrahedral vesicle shown in Fig. 14(c). In membrane tubes, this process results in polygonal deformations, with proteins assembling along the edge lines of the polygon vertices.70,78 Unlike the continuous transition described earlier, the transformations between polyhedral vesicles and between polygonal tubes are discontinuous.78 Notably, similar triangular membrane tubes have been observed in the inner mitochondrial membranes of astrocytes.188,189 At high Crod and protein density, excessive protein-induce stress can lead to membrane rupture, giving rise to high-genus vesicles (see Fig. 14(d)).187,190
When multiple types of proteins bind to a membrane, differences in their preferred curvatures can induce phase separation.124,191–193 When two types of proteins exhibit positive curvatures with different magnitudes, they can segregate into regions of large and small curvatures. In the case of a disk-shaped vesicle, proteins with larger curvature preferentially assemble at the corners of the triangular disk (see Fig. 14(e)). Conversely, when two types of proteins possess opposite curvatures, their 1D assemblies align alternately in a side-by-side arrangement, forming periodic bumps (see Fig. 14(f)).124 Within this alternating pattern, the different proteins establish tip-to-tip contact, which is consistent with the attractive interactions in the tip-to-tip direction described in Section 4.2.1. Notably, this alternating assembly can also occur in flat membranes; however, it is disassembled under high surface tension.124
Simulations showed that identical protein rods formed 1D linear assemblies through membrane-mediated interactions. The introduction of direct inter-protein interactions can modify the assemblies. The formation of helical tubular assemblies is further enhanced by direct attraction.183 Specific types of direct interactions may be necessary to accurately describe the assemblies of certain proteins. The endosomal sorting complex required for transport (ESCRT) forms a distinctive assembly, characterized by a spiral-spring-like structure on flat membranes and a helical tube configuration on cylindrical membranes.194–197 This spiral assembly is involved in endosomal fission. In dynamically triangulated membrane simulations,192,193,198,199 proteins are often represented as point-like inclusions with orientational degrees of freedom. In their models, protein interactions are governed by an orientation-dependent yet laterally isotropic potential. As a results, when the orientations and the distance between two proteins are fixed, the interaction energy remains identical for both side-by-side and tip-to-tip alignments. Owing to the attractive nature of this potential in both lateral directions, the resulting protein assemblies exhibit a thickness of a few proteins rather than forming a strict single-layer 1D structure.
4.3 Adhesion of nanoparticles
During phagocytosis, large objects, such as viruses and cell debris, are engulfed by the plasma membrane and internalized into the cell. The engulfment of colloidal nanoparticles has been extensively studied as a model system for phagocytosis, and nanoparticles are also widely considered as the carriers for drug delivery.200–203 Unlike curvature-inducing proteins, an adhesive spherical nanoparticle can become fully wrapped by the membrane;204–207 however, as surface tension increases, the membrane undergoes a first-order transition to a partially wrapped state.208 Similarly, liquid droplets can also be wrapped by the membrane, but in contrast, the partially wrapped droplets deform to satisfy the wetting conditions at the contact lines.209,210 For non-spherical particles, the wrapping process may be accompanied by changes in particle orientation.204,211,212Nanoparticles exhibit membrane-mediated interactions, similar to those observed in membrane proteins.204,213,214 Nanoparticles can induce the formation of membrane tubules, wrapping the nanoparticle assembly.215 Simulations of nanoparticles with crescent216 and hinge-like217 shapes have been conducted as model systems for protein binding, revealing orientational assemblies analogous to those formed by anisotropic proteins. Note that these nanoparticles have negative spontaneous curvatures along their minor axes due to their rounded shapes.
5 Summary and outlook
This review examined the curvature-sensing and generation mechanisms of membrane proteins. Laterally isotropic proteins are capable of sensing both the mean and Gaussian curvatures of membranes, with their curvature dependence well described by the mean-field theory. The IDP chains increase the bending rigidity and spontaneous curvature of membranes, while decreasing the saddle-splay modulus. The binding of isotropic proteins can lead to the formation of spherical buds and periodic patterns, such as hexagonal, kagome-lattice, checkerboard arrangements, and beaded necklace tubes. The curvatures generated by proteins play a crucial role in stabilizing these phase-separated patterns. Additionally, the insertion of hydrophobic segments can modify the area difference between the two leaflets of the bilayer within the ADE model, ultimately inducing membrane budding.The binding behavior of anisotropic proteins, such as those from the BAR superfamily proteins, depends not only on the membrane curvatures but also on protein orientations. Orientation-dependent excluded-volume interactions can drive an isotropic-to-nematic transition among the proteins. In the dilute limit, an isolated protein preferentially binds to wide cylindrical membrane tubes with its orientation aligned along the azimuthal or axial directions, whereas it binds to narrow tubes with two distinct tilted orientations. As protein density increases, these proteins undergo the first-order and second-order transitions from a state characterized by the coexistence of two tilt angles to an ordered phase with a single orientation angle, depending on the membrane curvature.
Anisotropic proteins are also capable of driving tubulation. Protein chirality enhances tubulation, whereas negative side curvature and positive surface tension counteract it. The IDP domains of BAR proteins promote tubulation while simultaneously inhibiting tubule fusion, leading to either accelerated or decelerated tubulation dynamics depending on the condition. Furthermore, anisotropic proteins can facilitate the formation of disk-shaped and polyhedral vesicles, polygonal tubes, and periodically bumped membranes.
For a quantitative understanding of the curvature sensing and generation, accurate estimation of protein bending properties is essential. This review described the estimation of bending properties of I-BAR domains through curvature-sensing studies using tethered vesicles. The same approach can be extended to other curvature-inducing proteins. To analyze the effects of Gaussian curvature, comparisons between cylindrical and spherical membranes with equivalent mean curvature are particularly important, especially at large curvatures. Additionally, the asymmetric protein shapes of proteins can be assessed by examining their orientation distributions in cylindrical and buckled membranes. Molecular dynamics simulations of proteins on a buckled membrane119,218 provide valuable insights into their curvature-sensing properties and behavior.
Data availability
No primary research results, software or code have been included as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI Grant Number JP24K06973.Notes and references
- H. T. McMahon and J. L. Gallop, Nature, 2005, 438, 590–596 CrossRef CAS.
- J. Zimmerberg and M. M. Kozlov, Nat. Rev. Mol. Cell Biol., 2006, 7, 9–19 CrossRef CAS PubMed.
- S. Suetsugu, S. Kurisu and T. Takenawa, Physiol. Rev., 2014, 94, 1219–1248 CrossRef CAS PubMed.
- M. Kaksonen and A. Roux, Nat. Rev. Mol. Cell Biol., 2018, 19, 313–326 CrossRef CAS.
- J. Béthune and F. T. Wieland, Annu. Rev. Biophys., 2018, 47, 63–83 CrossRef.
- T. Svitkina, Cold Spring Harbor Perspect. Biol., 2018, 10, a018267 CrossRef.
- J. Lutkenhaus, Trends Microbiol., 2012, 20, 411–418 CrossRef CAS.
- H. Turlier and T. Betz, Annu. Rev. Condens. Matter Phys., 2019, 10, 213–232 CrossRef.
- J.-B. Manneville, P. Bassereau, S. Ramaswamy and J. Prost, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021908 CrossRef CAS.
- P. Lenz, J.-F. Joanny, F. Jülicher and J. Prost, Phys. Rev. Lett., 2003, 91, 108104 CrossRef.
- H. Noguchi and O. Pierre-Louis, Sci. Rep., 2021, 11, 7985 CrossRef CAS.
- Z. Wu, M. Su, C. Tong, M. Wu and J. Liu, Nat. Commun., 2018, 9, 136 CrossRef PubMed.
- S. Takada, N. Yoshinaga, N. Doi and K. Fujiwara, Sci. Adv., 2022, 8, eabm8460 CrossRef CAS PubMed.
- B. Peleg, A. Disanza, G. Scita and N. Gov, PLoS One, 2011, 6, e18635 CrossRef CAS.
- N. Tamemoto and H. Noguchi, Sci. Rep., 2020, 10, 19582 CrossRef CAS PubMed.
- N. Tamemoto and H. Noguchi, Soft Matter, 2021, 17, 6589–6596 RSC.
- N. Tamemoto and H. Noguchi, Phys. Rev. E, 2022, 106, 024403 CrossRef CAS.
- H. Noguchi, Sci. Rep., 2023, 13, 6207 CrossRef CAS PubMed.
- H. Noguchi, ChemSystemsChem, 2025, 7, e202400042 CrossRef CAS.
- M. Müller, K. Katsov and M. Schick, Phys. Rep., 2006, 434, 113–176 CrossRef.
- M. Venturoli, M. M. Sperotto, M. Kranenburg and B. Smit, Phys. Rep., 2006, 437, 1–54 CrossRef CAS.
- H. Noguchi, J. Phys. Soc. Jpn., 2009, 78, 041007 CrossRef.
- W. Shinoda, R. DeVane and M. L. Klein, Curr. Opin. Struct. Biol., 2012, 22, 175–186 CrossRef CAS PubMed.
- W. Pezeshkian and S. J. Marrink, Curr. Opin. Cell Biol., 2021, 71, 103–111 CrossRef CAS.
- S. J. Marrink, L. Monticelli, M. N. Melo, R. Alessandri, D. P. Tieleman and P. C. T. Souza, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, 13, e1620 Search PubMed.
- A. K. Dasanna and D. A. Fedosov, Eur. Phys. J.: Spec. Top., 2024, 233, 3053–3071 Search PubMed.
- P. B. Canham, J. Theor. Biol., 1970, 26, 61–81 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., 1973, 28c, 693–703 CrossRef PubMed.
- M. A. S. Karal, M. M. Billah, M. Ahmed and M. K. Ahamed, Soft Matter, 2023, 19, 8285–8304 RSC.
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS.
- D. Marsh, Chem. Phys. Lipids, 2006, 144, 146–159 CrossRef CAS.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS.
- M. Hu, J. J. Briguglio and M. Deserno, Biophys. J., 2012, 102, 1403–1410 CrossRef CAS.
- R. D. Kornberg and H. M. McConnell, Biochemistry, 1971, 10, 1111–1120 CrossRef CAS PubMed.
- F.-X. Contreras, L. Sánchez-Magraner, A. Alonso and F. M. Goñi, FEBS Lett., 2009, 584, 1779–1786 CrossRef.
- J. A. Hamilton, Curr. Opin. Lipidol., 2003, 14, 263–271 CrossRef CAS.
- T. L. Steck, J. Ye and Y. Lange, Biophys. J., 2002, 83, 2118–2125 CrossRef CAS.
- R. J. Bruckner, S. S. Mansy, A. Ricardo, L. Mahadevan and J. W. Szostak, Biophys. J., 2009, 97, 3113–3122 CrossRef CAS PubMed.
- M. S. Miettinen and R. Lipowsky, Nano Lett., 2019, 19, 5011–5016 CrossRef CAS.
- K. Kawaguchi, K. M. Nakagawa, S. Nakagawa, H. Shindou, H. Nagao and H. Noguchi, J. Chem. Phys., 2020, 153, 165101 CrossRef CAS.
- K. Kawaguchi, H. Nagao, H. Shindou and H. Noguchi, J. Phys. Chem. B, 2022, 126, 9316–9324 CrossRef CAS PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- S. Svetina, ChemPhysChem, 2009, 10, 2769–2776 CrossRef CAS PubMed.
- S. Svetina and B. Žekš, Eur. Biophys. J., 1989, 17, 101–111 CrossRef CAS PubMed.
- A. Sakashita, N. Urakami, P. Ziherl and M. Imai, Soft Matter, 2012, 8, 8569–8581 RSC.
- C. Tanford, The hydrophobic effect: formation of micelles and biological membranes, Wiley, New York, 1980 Search PubMed.
- in Structure and Dynamics of Membranes, ed. R. Lipowsky and E. Sackmann, Elsevier Science, Amsterdam, 1995 Search PubMed.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS PubMed.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011901 CrossRef PubMed.
- H. Noguchi, A. Sakashita and M. Imai, Soft Matter, 2015, 11, 193–201 RSC.
- A. H. Bahrami and G. Hummer, ACS Nano, 2017, 11, 9558–9565 CrossRef CAS PubMed.
- H. W. G. Lim, M. Wortis and R. Mukhopadhyay, Lipid bilayers and red blood cells, Wiley-VCH, Weinheim, 2008 Search PubMed.
- P. Ziherl and S. Svetina, Europhys. Lett., 2005, 70, 690–696 CrossRef CAS.
- K. M. Nakagawa and H. Noguchi, Soft Matter, 2018, 14, 1397–1407 RSC.
- A. Sreekumari and R. Lipowsky, Soft Matter, 2022, 18, 6066–6078 RSC.
- H. Noguchi, Phys. Rev. E, 2024, 109, 024403 CrossRef CAS.
- S. F. Traynelis, L. P. Wollmuth, C. J. McBain, F. S. Menniti, K. M. Vance, K. K. Ogden, K. B. Hansen, H. Yuan, S. J. Myers and R. Dingledine, Pharmacol. Rev., 2010, 62, 405–496 CrossRef CAS PubMed.
- J. Syrjanen, K. Michalski, T. Kawate and H. Furukawa, J. Mol. Biol., 2021, 433, 166994 CrossRef CAS.
- O. P. Ernst, D. T. Lodowski, M. Elstner, P. Hegemann, L. S. Brown and H. Kandori, Chem. Rev., 2014, 114, 126–163 CrossRef CAS PubMed.
- T. Nagata and K. Inoue, J. Cell Sci., 2021, 134, jcs258989 CrossRef CAS.
- A. J. Venkatakrishnan, X. Deupi, G. Lebon, C. G. Tate, G. F. Schertler and M. M. Babu, Nature, 2013, 494, 185–194 CrossRef CAS PubMed.
- M. Shibata, K. Inoue, K. Ikeda, M. Konno, M. Singh, C. Kataoka, R. Abe-Yoshizumi, H. Kandori and T. Uchihashi, Sci. Rep., 2018, 8, 8262 CrossRef.
- J. H. Hurley, E. Boura, L.-A. Carlson and B. Różycki, Cell, 2010, 143, 875–887 CrossRef CAS PubMed.
- V. Gerke, C. E. Creutz and S. E. Moss, Nat. Rev. Mol. Cell Biol., 2005, 6, 449–461 CrossRef CAS.
- F. Oling, J. S. de Oliveira Santos, N. Govorukhina, C. Mazères-Dubut, W. Bergsma-Schutter, G. Oostergetel, W. Keegstra, O. Lambert, A. Lewit-Bentley and A. Brisson, J. Mol. Biol., 2000, 304, 561–573 CrossRef CAS PubMed.
- H. Noguchi, Phys. Rev. E, 2021, 104, 014410 CrossRef CAS.
- C. Prévost, H. Zhao, J. Manzi, E. Lemichez, P. Lappalainen, A. Callan-Jones and P. Bassereau, Nat. Commun., 2015, 6, 8529 CrossRef.
- K. R. Rosholm, N. Leijnse, A. Mantsiou, V. Tkach, S. L. Pedersen, V. F. Wirth, L. B. Oddershede, K. J. Jensen, K. L. Martinez, N. S. Hatzakis, P. M. Bendix, A. Callan-Jones and D. Stamou, Nat. Chem. Biol., 2017, 13, 724–729 CrossRef CAS PubMed.
- F.-C. Tsai, M. Simunovic, B. Sorre, A. Bertin, J. Manzi, A. Callan-Jones and P. Bassereau, Soft Matter, 2021, 17, 4254–4265 RSC.
- H. Noguchi, Int. J. Mod. Phys. B, 2022, 36, 2230002 CrossRef CAS.
- Q. Goutaland, F. van Wijland, J.-B. Fournier and H. Noguchi, Soft Matter, 2021, 17, 5560–5573 RSC.
- B. Sorre, A. Callan-Jones, J. Manzi, B. Goud, J. Prost, P. Bassereau and A. Roux, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 173–178 CrossRef CAS.
- Z. Shi and T. Baumgart, Nat. Commun., 2015, 6, 5974 CrossRef CAS.
- C. Tozzi, N. Walani and M. Arroyo, New J. Phys., 2019, 21, 093004 CrossRef CAS.
- T. V. Sachin Krishnan, S. L. Das and P. B. Sunil Kumar, Soft Matter, 2019, 15, 2071–2080 RSC.
- S. Ramaswamy, J. Toner and J. Prost, Phys. Rev. Lett., 2000, 84, 3494–3497 CrossRef CAS PubMed.
- R. Shlomovitz and N. S. Gov, Phys. Biol., 2009, 6, 046017 CrossRef CAS.
- H. Noguchi, J. Chem. Phys., 2015, 143, 243109 CrossRef.
- C. Has and S. L. Das, Biochim. Biophys. Acta, 2021, 1865, 129971 CrossRef CAS PubMed.
- H. Noguchi, N. Walani and M. Arroyo, Soft Matter, 2023, 19, 5300–5310 RSC.
- H. Noguchi, Soft Matter, 2021, 17, 10469–10478 RSC.
- J. C. Stachowiak, E. M. Schmid, C. J. Ryan, H. S. Ann, D. Y. Sasaki, M. B. Sherman, P. L. Geissler, D. A. Fletcher and C. C. Hayden, Nat. Cell Biol., 2012, 14, 944–949 CrossRef CAS PubMed.
- D. J. Busch, J. R. Houser, C. C. Hayden, M. B. Sherman, E. M. Lafer and J. C. Stachowiak, Nat. Commun., 2015, 6, 7875 CrossRef CAS PubMed.
- W. F. Zeno, W. T. Snead, A. S. Thatte and J. C. Stachowiak, Soft Matter, 2019, 15, 8706–8717 RSC.
- W. T. Snead, W. F. Zeno, G. Kago, R. W. Perkins, J. B. Richter, C. Zhao, E. M. Lafer and J. C. Stachowiak, J. Cell Biol., 2019, 218, 664–682 CrossRef CAS PubMed.
- H. Hofmann, A. Soranno, A. Borgia, K. Gast, D. Nettels and B. Schuler, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16155–16160 CrossRef CAS PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University, Oxford, 1986 Search PubMed.
- G. R. Strobl, The physics of polymers: concepts for understanding their structures and behavior, Springer, Berlin, 2nd edn, 1997 Search PubMed.
- R. Lipowsky, Europhys. Lett., 1995, 30, 197–202 CrossRef CAS.
- C. Hiergeist and R. Lipowsky, J. Phys. II, 1996, 6, 1465–1481 CrossRef CAS.
- T. Bickel, C. Jeppesen and C. M. Marques, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 33–43 CrossRef CAS.
- D. Marsh, R. Bartucci and L. Sportelli, Biochim. Biophys. Acta, 2003, 1615, 33–59 CrossRef CAS PubMed.
- T. Bickel and C. M. Marques, J. Nanosci. Nanotechnol., 2006, 6, 2386–2395 CrossRef CAS PubMed.
- T. Auth and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 051801 CrossRef PubMed.
- T. Auth and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 031904 CrossRef.
- M. Werner and J.-U. Sommer, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 383–392 CrossRef CAS.
- H. Wu, H. Shiba and H. Noguchi, Soft Matter, 2013, 9, 9907–9917 RSC.
- I. Tsafrir, D. Sagi, T. Arzi, M.-A. Guedeau-Boudeville, V. Frette, D. Kandel and J. Stavans, Phys. Rev. Lett., 2001, 86, 1138–1141 CrossRef CAS PubMed.
- I. Tsafrir, Y. Caspi, M.-A. Guedeau-Boudeville, T. Arzi and J. Stavans, Phys. Rev. Lett., 2003, 91, 138102 CrossRef.
- K. Akiyoshi, A. Itaya, S. I. M. Nomura, N. Ono and K. Yoshikawa, FEBS Lett., 2003, 534, 33–38 CrossRef CAS.
- V. Nikolov, R. Lipowsky and R. Dimova, Biophys. J., 2007, 92, 4356–4368 CrossRef CAS PubMed.
- A. Köth, D. Appelhans, D. Robertson, B. Tiersch and J. Koetz, Soft Matter, 2011, 7, 10581–10584 RSC.
- A. R. Evans, M. S. Turner and P. Sens, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 041907 CrossRef CAS PubMed.
- M. Masuda and N. Mochizuki, Semin. Cell Dev. Biol., 2010, 21, 391–398 CrossRef CAS PubMed.
- T. Itoh and P. De Camilli, Biochim. Biophys. Acta, 2006, 1761, 897–912 CrossRef CAS PubMed.
- C. Mim and V. M. Unger, Trends Biochem. Sci., 2012, 37, 526–533 CrossRef CAS PubMed.
- A. Frost, V. M. Unger and P. D. Camilli, Cell, 2009, 17, 191–196 CrossRef PubMed.
- J. Adam, N. Basnet and N. Mizuno, Sci. Rep., 2015, 5, 15452 CrossRef CAS PubMed.
- Y. F. Barooji, A. Rørvig-Lund, S. Semsey, S. N. S. Reihani and P. M. Bendix, Sci. Rep., 2016, 6, 30054 CrossRef CAS.
- M. A. Lemmon, Nat. Rev. Mol. Cell Biol., 2008, 9, 99–111 Search PubMed.
- M. Chandra, Y. K.-Y. Chin, C. Mas, J. R. Feathers, B. Paul, S. Datta, K.-E. Chen, X. Jia, Z. Yang, S. J. Norwood, B. Mohanty, A. Bugarcic, R. D. Teasdale, W. M. Henne, M. Mobli and B. M. Collins, Nat. Commun., 2019, 10, 1528 CrossRef.
- S. M. Ferguson and P. D. Camilli, Nat. Rev. Mol. Cell Biol., 2012, 13, 75–88 CrossRef CAS.
- B. Antonny, C. Burd, P. D. Camilli, E. Chen, O. Daumke, K. Faelber, M. Ford, V. A. Frolov, A. Frost, J. E. Hinshaw, T. Kirchhausen, M. M. Kozlov, M. Lenz, H. H. Low, H. McMahon, C. Merrifield, T. D. Pollard, P. J. Robinson, A. Roux and S. Schmid, EMBO J., 2016, 35, 2270–2284 CrossRef CAS.
- M. Pannuzzo, Z. A. McDargh and M. Deserno, eLife, 2018, 7, e39441 CrossRef.
- H. Sato and J. B. Feix, Biochim. Biophys. Acta, 2006, 1758, 1245–1256 CrossRef CAS PubMed.
- I. Rady, I. A. Siddiqui, M. Rady and H. Mukhtar, Cancer Lett., 2017, 402, 16–31 CrossRef CAS.
- S. Guha, J. Ghimire, E. Wu and W. C. Wimley, Chem. Rev., 2019, 119, 6040–6085 CrossRef CAS PubMed.
- Y. Miyazaki and W. Shinoda, Biochim. Biophys. Acta, 2022, 1864, 183955 CrossRef CAS.
- J. Gómez-Llobregat, F. Elías-Wolff and M. Lindén, Biophys. J., 2016, 110, 197–204 CrossRef.
- H. Noguchi, Sci. Rep., 2016, 6, 20935 CrossRef CAS.
- C. Tozzi, N. Walani, A.-L. L. Roux, P. Roca-Cusachs and M. Arroyo, Soft Matter, 2021, 17, 3367–3379 RSC.
- M. Simunovic, A. Srivastava and G. A. Voth, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20396–20401 Search PubMed.
- A. D. Olinger, E. J. Spangler, P. B. Sunil Kumar and M. Laradji, Faraday Discuss., 2016, 186, 265–275 RSC.
- H. Noguchi and J.-B. Fournier, Soft Matter, 2017, 13, 4099–4111 RSC.
- K. Akabori and C. D. Santangelo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061909 CrossRef PubMed.
- V. Kralj-Iglič, V. Heinrich, S. Svetina and B. Žekš, Eur. Phys. J. B, 1999, 10, 5–8 CrossRef.
- A. Iglič, T. Slivnika and V. Kralj-Iglič, J. Biomech., 2007, 40, 2492–2500 CrossRef PubMed.
- J.-B. Fournier, Phys. Rev. Lett., 1996, 76, 4436–4439 CrossRef CAS.
- H. Noguchi, C. Tozzi and M. Arroyo, Soft Matter, 2022, 18, 3384–3394 RSC.
- E. S. Nascimento, P. Palffy-Muhoray, J. M. Taylor, E. G. Virga and X. Zheng, Phys. Rev. E, 2017, 96, 022704 CrossRef.
- L. Bo and R. Waugh, Biophys. J., 1989, 55, 509–517 CrossRef CAS PubMed.
- E. Evans, H. Bowman, A. Leung, D. Needham and D. Tirrell, Science, 1996, 273, 933–935 CrossRef CAS.
- D. Cuvelier, I. Derényi, P. Bassereau and P. Nassoy, Biophys. J., 2005, 88, 2714–2726 CrossRef CAS.
- T. Baumgart, B. R. Capraro, C. Zhu and S. L. Das, Annu. Rev. Phys. Chem., 2011, 62, 483–506 CrossRef CAS PubMed.
- S. Aimon, A. Callan-Jones, A. Berthaud, M. Pinot, G. E. Toombes and P. Bassereau, Dev. Cell, 2014, 28, 212–218 CrossRef CAS.
- S. Yang, X. Miao, S. Arnold, B. Li, A. T. Ly, H. Wang, M. Wang, X. Guo, M. Pathak, W. Zhao, C. D. Cox and Z. Shi, Nat. Commun., 2022, 13, 7467 CrossRef CAS PubMed.
- A. Roux, G. Koster, M. Lenz, B. Sorre, J.-B. Manneville, P. Nassoy and P. Bassereau, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4141–4146 CrossRef CAS.
- G. Moreno-Pescador, C. D. Florentsen, H. Østbye, S. L. Sønder, T. L. Boye, E. L. Veje, A. K. Sonne, S. Semsey, J. Nylandsted, R. Daniels and P. M. Bendix, ACS Nano, 2019, 13, 6689–6701 CrossRef CAS.
- J. B. Larsen, K. R. Rosholm, C. Kennard, S. L. Pedersen, H. K. Munch, V. Tkach, J. J. Sakon, T. Bjørnholm, K. R. Weninger, P. M. Bendix, K. J. Jensen, N. S. Hatzakis, M. J. Uline and D. Stamou, ACS Cent. Sci., 2020, 6, 1159–1168 CrossRef CAS.
- N. S. Hatzakis, V. K. Bhatia, J. Larsen, K. L. Madsen, P.-Y. Bolinger, A. H. Kunding, J. Castillo, U. Gether, P. Hedegård and D. Stamou, Nat. Chem. Biol., 2009, 5, 835–841 CrossRef CAS.
- A.-S. Smith, E. Sackmann and U. Seifert, Phys. Rev. Lett., 2004, 92, 208101 CrossRef.
- H. T. McMahon and E. Boucrot, Nat. Rev. Mol. Cell Biol., 2011, 12, 517–533 CrossRef CAS PubMed.
- O. Avinoam, M. Schorb, C. J. Beese, J. A. G. Briggs and M. Kaksonen, Science, 2015, 348, 1369–1372 CrossRef CAS PubMed.
- M. Saleem, S. Morlot, A. Hohendahl, J. Manzi, M. Lenz and A. Roux, Nat. Commun., 2015, 6, 6249 CrossRef CAS PubMed.
- F. Brandizzi and C. Barlowe, Nat. Rev. Mol. Cell Biol., 2013, 14, 382–392 CrossRef CAS PubMed.
- M. Faini, R. Beck, F. T. Wieland and J. A. Briggs, Trends Cell Biol., 2013, 23, 279–288 CrossRef CAS PubMed.
- F. Frey and U. S. Schwarz, Phys. Rev. E, 2024, 110, 064403 CrossRef CAS.
- R. Lipowsky, J. Phys. II, 1992, 2, 1825–1840 CrossRef CAS.
- P. Sens, Phys. Rev. Lett., 2004, 93, 108103 CrossRef.
- L. Foret, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 42 CrossRef.
- M. Tanaka and E. Sackmann, Nature, 2005, 437, 656–663 CrossRef CAS PubMed.
- E. T. Castellana and P. S. Cremer, Surf. Sci. Rep., 2006, 61, 429–444 CrossRef CAS PubMed.
- A. S. Achalkumar, R. J. Bushby and S. D. Evans, Soft Matter, 2010, 6, 6036–6051 RSC.
- A. Alessandrini and P. Facci, Soft Matter, 2014, 10, 7145–7164 RSC.
- J. van Weerd, M. Karperien and P. Jonkheijm, Adv. Healthcare Mater., 2015, 4, 2743–2779 CrossRef CAS.
- A. Bouter, R. Carmeille, C. Gounou, F. Bouvet, S. A. Degrelle, D. Evain-Brion and A. R. Brisson, Placenta, 2015, 36, S43–S49 CrossRef CAS PubMed.
- A. D. Blazek, B. J. Paleo and N. Weisleder, Physiol., 2015, 30, 438–448 CrossRef CAS.
- T. L. Boye, K. Maeda, W. Pezeshkian, S. L. Sønder, S. C. Haeger, V. Gerke, A. C. Simonsen and J. Nylandsted, Nat. Commun., 2017, 8, 1623 CrossRef PubMed.
- T. L. Boye, J. C. Jeppesen, K. Maeda, W. Pezeshkian, V. Solovyeva, J. Nylandsted and A. C. Simonsen, Sci. Rep., 2018, 8, 10309 CrossRef PubMed.
- H. Noguchi, Soft Matter, 2019, 15, 8741–8748 RSC.
- H. Noguchi, Soft Matter, 2025, 21, 1113–1121 RSC.
- T. Auth and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031901 CrossRef PubMed.
- A. G. Lee, Biochim. Biophys. Acta, 2003, 1612, 1–40 CrossRef CAS PubMed.
- O. S. Andersen and R. E. Koeppe, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 107–130 CrossRef CAS PubMed.
- M. Venturoli, B. Smit and M. M. Sperotto, Biophys. J., 2005, 88, 1778–1798 Search PubMed.
- R. Phillips, T. Ursell, P. Wiggins and P. Sens, Nature, 2009, 459, 379–385 CrossRef CAS PubMed.
- F. J. de Meyer, M. Venturoli and B. Smit, Biophys. J., 2008, 95, 1851–1865 CrossRef.
- U. Schmidt, G. Guigas and M. Weiss, Phys. Rev. Lett., 2008, 101, 128104 CrossRef PubMed.
- J.-B. Fournier, Eur. Phys. J. B, 1999, 11, 261–272 CrossRef CAS.
- S. A. Safran, Statistical Thermodynamics of Surfaces, Interfaces, and Membranes, Addison-Wesley, Reading, MA, 1994 Search PubMed.
- R. Goetz, G. Gompper and R. Lipowsky, Phys. Rev. Lett., 1999, 82, 221–224 CrossRef CAS.
- H. Shiba, H. Noguchi and J.-B. Fournier, Soft Matter, 2016, 12, 2373–2380 RSC.
- M. Goulian, R. Bruinsma and P. Pincus, Europhys. Lett., 1993, 22, 145 CrossRef CAS.
- N. Weil and O. Farago, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 81–87 CrossRef CAS.
- H. Noguchi, EPL, 2013, 102, 68001 CrossRef.
- Y. Schweitzer and M. M. Kozlov, PLoS Comput. Biol., 2015, 11, e1004054 Search PubMed.
- T. Kohyama, J. Phys. Soc. Jpn., 2019, 88, 024008 CrossRef.
- P. G. Dommersnes and J.-B. Fournier, Eur. Phys. J. B, 1999, 12, 9–12 CrossRef CAS.
- P. G. Dommersnes and J.-B. Fournier, Biophys. J., 2002, 83, 2898–2905 CrossRef CAS PubMed.
- C. Yolcu, R. C. Haussman and M. Deserno, Adv. Colloid Interface Sci., 2014, 208, 89 Search PubMed.
- R. Golestanian, M. Goulian and M. Kardar, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6725 CrossRef CAS.
- A.-F. Bitbol, K. Sin Ronia and J.-B. Fournier, EPL, 2011, 96, 40013 Search PubMed.
- H. Noguchi, Sci. Rep., 2019, 9, 11721 CrossRef PubMed.
- G. Zhu, J. Chen, J. Liu, J. S. Brunzelle, B. Huang, N. Wakeham, S. Terzyan, X. Li, Z. Rao, G. Li and X. C. Zhang, EMBO J., 2007, 26, 3484–3493 CrossRef CAS PubMed.
- H. Noguchi, J. Chem. Phys., 2022, 157, 034901 CrossRef CAS.
- H. Noguchi, EPL, 2014, 108, 48001 CrossRef.
- H. Noguchi, Phys. Rev. E, 2016, 93, 052404 CrossRef.
- K. Blinzinger, N. B. Rewcastle and H. Hgaer, J. Cell Biol., 1965, 25, 293–303 CrossRef CAS PubMed.
- B. Fernandez, I. Suarez and C. Gianonatti, J. Anat., 1983, 137, 483–488 Search PubMed.
- G. S. Ayton, E. Lyman, V. Krishna, R. D. Swenson, C. Mim, V. M. Unger and G. A. Voth, Biophys. J., 2009, 97, 1616–1625 CrossRef CAS PubMed.
- H. Noguchi, Soft Matter, 2017, 13, 7771–7779 RSC.
- N. Ramakrishnan, P. B. Sunil Kumar and J. H. Ipsen, Biophys. J., 2013, 104, 1018–1028 CrossRef CAS.
- G. Kumar and A. Srivastava, J. Chem. Theory Comput., 2022, 18, 5659–5671 CrossRef CAS PubMed.
- N. Jukic, A. P. Perrino, L. Redondo-Morata and S. Scheuring, J. Biol. Chem., 2023, 299, 104575 CrossRef CAS.
- T. Wollert, C. Wunder, J. Lippincott-Schwartz and J. H. Hurley, Nature, 2009, 458, 172–177 CrossRef CAS.
- B. Meadowcroft, I. Palaia, A.-K. Pfitzner, A. Roux, B. Baum and A. Šarić, Phys. Rev. Lett., 2022, 129, 268101 CrossRef CAS PubMed.
- K. Azad, D. Guilligay, C. Boscheron, S. Maity, N. D. Franceschi, G. Sulbaran, G. Effantin, H. Wang, J.-P. Kleman, P. Bassereau, G. Schoehn, W. H. Roos, A. Desfosses and W. Weissenhorn, Nat. Struct. Mol. Biol., 2023, 30, 81–90 CrossRef CAS.
- N. Ramakrishnan, J. H. Ipsen and P. B. Sunil Kumar, Soft Matter, 2012, 8, 3058–3061 RSC.
- N. Ramakrishnan, R. P. Bradley, R. W. Tourdot and R. Radhakrishnan, J. Phys.: Condens. Matter, 2018, 30, 273001 CrossRef CAS.
- S. Behzadi, V. Serpooshan, W. Tao, M. A. Hamaly, M. Y. Alkawareek, E. C. Dreaden, D. Brown, A. M. Alkilany, O. C. Farokhzad and M. Mahmoudi, Chem. Soc. Rev., 2017, 46, 4218–4244 RSC.
- N. D. Donahue, H. Acar and S. Wilhelm, Adv. Drug Delivery Rev., 2019, 143, 68–96 Search PubMed.
- M. S. de Almeida, E. Susnik, B. Drasler, P. Taladriz-Blanco, A. Petri-Fink and B. Rothen-Rutishauser, Chem. Soc. Rev., 2021, 50, 5397–5434 RSC.
- M. J. Mitchell, M. M. Billingsley, R. M. Haley, M. E. Wechsler, N. A. Peppas and R. Langer, Nat. Rev. Drug Discovery, 2021, 20, 101–124 CrossRef CAS.
- S. Dasgupta, T. Auth and G. Gompper, J. Phys.: Condens. Matter, 2017, 29, 373003 CrossRef CAS PubMed.
- H. Noguchi and M. Takasu, Biophys. J., 2002, 83, 299–308 CrossRef CAS PubMed.
- Y. Li and N. Gu, J. Phys. Chem. B, 2010, 114, 2749–2754 CrossRef CAS PubMed.
- C. van der Wel, A. Vahid, A. Šarić, T. Idema, D. Heinrich and D. J. Kraft, Sci. Rep., 2016, 6, 32825 CrossRef CAS.
- M. Deserno and T. Bickel, Europhys. Lett., 2003, 62, 767–773 CrossRef CAS.
- R. Dimova and R. Lipowsky, Adv. Mater. Interfaces, 2017, 4, 1600451 CrossRef.
- V. Satarifard and R. Lipowsky, Nat. Commun., 2023, 6, 6 Search PubMed.
- S. Dasgupta, T. Auth, N. S. Gov, T. J. Satchwell, E. Hanssen, E. S. Zuccala, D. T. Riglar, A. M. Toye, T. Betz, J. Baum and G. Gompper, Biophys. J., 2014, 107, 43–54 CrossRef CAS.
- S. van der Ham, J. Agudo-Canalejo and H. R. Vutukuri, ACS Nano, 2024, 18, 10407–10416 CrossRef CAS.
- B. J. Reynwar, G. Ilya, V. A. Harmandaris, M. M. Müller, K. Kremer and M. Deserno, Nature, 2007, 447, 461–464 CrossRef CAS.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 108, 118101 CrossRef PubMed.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 109, 188101 CrossRef.
- X. Liu, F. Tian, T. Yue, X. Zhang and C. Zhong, Nanoscale, 2020, 12, 3029–3037 RSC.
- B. Li and S. M. Abel, J. Chem. Phys., 2024, 160, 194901 CrossRef CAS.
- M. I. Mahmood, H. Noguchi and K. Okazaki, Sci. Rep., 2019, 9, 14557 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |