View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence
DOI: 10.1039/D4QI01484G (Research Article) Inorg. Chem. Front., 2025, 12, 1059-1079

Enhancing blocking temperatures in {CrIII2DyIII2} butterfly SMMs: deciphering the role of exchange interactions and developing magneto-structural maps†

Abinash Swain a, Yasmin L. Whyatt b, Daniel Wielechowski c, Satheeshkumar Muthu a, Sophie L. Benjamin d, Keith S. Murray *c, Gopalan Rajaraman *a and Stuart K. Langley *e
aDepartment of Chemistry, IIT Bombay, Powai, Mumbai – 400076, India. E-mail: rajaraman@chem.iitb.ac.in
bDepartment of Chemistry, The University of Manchester, Manchester, UK
cSchool of Chemistry, Monash University, 17 Rainforest Walk, Clayton, Victoria 3800, Australia. E-mail: keith.murray@monash.edu
dSchool of Science and Technology, Nottingham Trent University, Nottingham NG11 8NS, UK
eDepartment of Natural Sciences, Manchester Metropolitan University, Manchester M1 5GD, England, UK. E-mail: S.Langley@mmu.ac.uk

Received 28th June 2024 , Accepted 18th September 2024

First published on 2nd October 2024

Abstract

A tetranuclear heterometallic butterfly-shaped complex of molecular formula; [CrIII2DyIII2(OMe)2(mdea)2(benz)4(NO3)2] (mdeaH2 = N-methyldiethanolamine, benz = benzoate) was reported by us and found to display single-molecule magnetism (SMM) behaviour with a Ueff = 54 cm−1 and well-resolved magnetisation hysteresis plots, with a blocking temperature, TB = 3.5 K. In the present study, fourteen related {CrIII2DyIII2} complexes have been synthesised, and their magnetic properties have been studied. The study probes how chemical changes in bridging ligands and coordination environment affect the SMM properties compared to the parent complex. We show that by making simple chemical modifications to the ligands, the Ueff and TB values change, with Ueff values ranging from 22 to 65 cm−1 and TB 1.8 K to 4.7 K. We also show that SMM behaviour can be turned off by manipulation of the coordination sphere around the DyIII ion. Based on these experimental results, we undertook a detailed theoretical study to understand why these changes occur. The theoretical studies further describe the mode of exchange mechanism in such complexes and how it controls the blocking temperature. Further, we have found that the exchange coupling between the DyIII–CrIII ions strongly influences the magnetic relaxation for this family of complexes, and interestingly, the exchange between the CrIII–CrIII centres plays a determining role in the overall SMM properties, which has been ignored in previous studies. We have derived a relation between the magnetic exchange and TB for such 3d–4f SMMs where exchange coupled states play a dominant role, revealing the blocking temperature is strongly correlated to the overall magnetic exchange. This clearly illustrates the importance of inducing strong exchange coupling to enhance not only the magnetisation reversal barrier but also TBvia quenching of zero-field quantum tunnelling of the magnetisation (QTM) in {3d–4f} type complexes.

Introduction

Single-molecule magnets (SMMs)1 offer the tantalising possibility of storing digital information on a single molecule and providing the ultimate high-density data storage platform.2 For this technology to become a reality, the temperature at which data can be stored must be addressed.3,4 Since the discovery of the first SMM in 1993, a {Mn12OAc}5 complex, which displays a magnetic blocking temperature (TB) of 4 K, huge improvements have been made, especially in the past few years, with the best-performing SMMs able to store digital information at temperatures 80 K.6 The driving force for these breakthroughs is due to a shift from synthesising complexes consisting of pure transition metal ions to harnessing the large anisotropy inherently present for lanthanide ions, with a major focus being on the DyIII ion.7–10 The recent increases in TB stem from the design of mononuclear lanthanide SMMs using a simple electrostatic approach.11,12 The approach for DyIII ions is simply prescribed using highly charged ligands on a single axis (i.e. a linear type geometry) while minimising ligands equatorial to the DyIII ion. This approach lays a blueprint for designing SMMs with extremely large anisotropy barriers (Ueff), hence allowing the electrons to retain their orientation at much higher temperatures than previously observed. For example, Goodwin et al.13 achieved remarkable increases in TB by fully conforming to this design in the isolation of the first dysprosocenium cation [Dy(C5H2tBu3)2]+, which is a sandwich complex with no equatorial ligands. They reported a Ueff = 1223 cm−1, with TB = 60 K.13 Several other dysprosocenium derivatives have subsequently been reported with a range of TB reported between 62 K to 80 K.6,13–15 While the use of lanthanide ions has pushed the field forward significantly, with molecules producing very large Ueff parameters, many problems have been highlighted in terms of the relaxation mechanism, especially the observations of fast quantum tunnelling of the magnetisation (QTM)16 which results in a loss of magnetisation via an under barrier process.6,14 With this in mind, while the best SMM limits the probability of QTM occurring, we need to understand how QTM can be controlled and minimised. One successful approach has been to use polynuclear lanthanide complexes, which introduce relatively strong magnetic exchange interactions between ions. This was most notably highlighted in N23− radical bridged LnIII dinuclear complexes.17,18 In general, exchange interactions (J) between LnIII ions are often <0.1 cm−1 due to the contracted nature of the magnetic orbitals.19,20 In the case of the radical bridged system, it is reported that the magnetic exchange interaction of JGd–rad = −27 cm−1 between the radical and GdIII ion and hysteresis was observed at TB = 14 K with a Ueff = 227 cm−1 for the TbIII analogue with little indication of QTM relaxation.21 While the radical-4f interactions are very strong in some cases, they are weaker in others, and this is correlated to the nature of the orbital that holds the unpaired electron at the radical centre with a strongly delocalised radical, leading to weaker exchange. However, the stability of the radical complexes is generally proportional to the delocalisation of spin density, with strong delocalisation leading to greater stability and, thus, weaker exchange coupling.22–24 Other alternative strategies that can be implemented to enhance the magnetic exchange is the introduction of direct metal–metal bonding, though these are very rare systems as they are very unstable.25,26 For comparatively stable molecules, there is scope for 4f metal ions coupled with 4d/5d ions, as the later have more diffuse orbitals.27 Furthermore 4f-radical exchange as high as +300 cm−1 has been observed in the lanthano fullerene class of molecules, paving the way forward for desired strong magnetic exchange interactions.28–30

Alternative avenues that have been explored include {3d–4f} assemblies where a suitable 3d metal ion is incorporated in the 4f cluster aggregation, with the aim being to induce relatively stronger exchange coupling compared to the {4f–4f} exchange.31–35 Among several {3d–4f} complexes reported, incorporating the CrIII ion seems more beneficial. Results suggest this boosts the exchange more strongly than any other transition metal ion while suppressing the QTM significantly.36,37 This was highlighted by some of us38–46 in a hetero-metallic tetra-nuclear complex of formula [CrIII2DyIII2(OMe)2(mdea)2(benz)4(NO3)2] (Fig. 1). This is a rare example of a lanthanide SMM that displays relatively strong magnetic exchange interactions and magnetic hysteresis with large coercive fields that were unprecedented in this class of compounds.


image file: d4qi01484g-f1.tif
Fig. 1 Structural representation of the {CrIII2DyIII2} butterfly complexes and structural formulae of the ligands.

While stronger exchange coupling underscores better SMMs in this {CrIII2DyIII2} class of compounds, a correlation between various structural alterations and the observed magnetic properties (such as exchange coupling, magnetisation reversal barrier and blocking temperature TB) is not established, and such an understanding is imperative to improve the performance of the SMMs both in this class of compounds but also in the other class of {M2Dy2} butterflies that perhaps make one of the largest family of complexes (∼500 structures in CCDC database) for SMMs among all poly-nuclear{3d–4f} complexes reported. Furthermore, in this class of complex, the geometry around the LnIII ions are generally preserved as square antiprismatic (pseudo-D4d), which is shown to yield large single-ion magnetic anisotropy, especially for the oblate type ions such as DyIII/TbIII/HoIIIetc.47,48 A quick glance at the Cambridge structural database reveals ∼500 such geometries where square antiprismatic geometries are preserved. As preserving geometries in polynuclear {3d–4f} classes is challenging, the butterfly {M2Ln2} core remains, perhaps, the most successful structural motif among {3d–4f} complexes that yield attractive SMM characteristics.40 Despite the vast amount of experimental data that are available, even a simple correlation of geometry/electronic structure to the experimental observables such as J, Ueff and TB is lacking. Particularly, there are several puzzling observations of very large Ueff values with no blocking temperature49 and moderate Ueff values with relatively large TB values,38–46,50 hinting at an absence of direct correlations between these two important SMM parameters. To answer such an intriguing observation in this area, we have synthesised, structurally, and magnetically characterised fifteen different {CrIII2DyIII2} complexes and used extensive theoretical studies (DFT and CASSCF/RASSI-SO/POLY_ANISO approach)51–54 thereby establishing several structural correlations to the observed magnetic properties.

We subdivide the fifteen reported complexes into four sections/groups where either the amine polyalcohol R group (category 1 and 2, structures 1–2d), bridging ligands (category 3, structures 3a–3g) or the coordination environment around the DyIII (category 4, structures 4a–4c) are altered as shown schematically in Scheme 1 along with the ligands employed (Fig. 1).


image file: d4qi01484g-s1.tif
Scheme 1 Synthesis route for all the butterfly complexes.

The fifteen complexes studied have the following formulae; [CrIII2DyIII2(OMe)2(mdea)2(benz)4(NO3)2] (1),39 [CrIII2DyIII2(OMe)2(dea)2(benz)4(MeOH)4](NO3)2 (2a) [CrIII2DyIII2(OMe)2(edea)2(benz)4(NO3)2] (2b), [CrIII2DyIII2(OMe)2(bdea)2(benz)4(NO3)2] (2c), [CrIII2DyIII2(OMe)2(teaH)2(benz)4(NO3)2(MeOH)2] (2d), [CrIII2DyIII2(OMe)2(mdea)2(2-Cl-benz)4(NO3)2] (3a), [CrIII2DyIII2(OMe)2(bdea)2(2,6-Cl-benz)4(NO3)2] (3b), [CrIII2DyIII2(OMe)2(mdea)2(2,4,6-Cl-benz)4(NO3)2] (3c), [CrIII2DyIII2(OMe)2(mdea)2(2-Cl-4,5-F-benz)4(NO3)2] (3d), [CrIII2DyIII2(OMe)2(mdea)2(2-CF3-benz)4(NO3)2] (3e), [CrIII2DyIII2(OMe)2(mdea)2(2-OMe-benz)4(NO3)2] (3f), [CrIII2DyIII2(OMe)2(tBudea)2(4-tBu-benz)4(NO3)2] (3g), [Cr2Dy2(OH)2(2,6-Cl-benz)4(teaH)2(MeOH)2(NO3)2](HNEt3)Cl (4a), [Cr2Dy2(OH)2(2,6-Cl-benz)4(bdea)2(DMF)2(NO3)2] (4b), [Cr2Dy2(OH)2(2,6-Cl-benz)4(mdea)2(DMF)2(NO3)2] (4c). [mdeaH2 = N-methyldiethanolamine, deaH2 = diethanolamine, edaH2 = ethyldiethanolamine, bdeaH2 = N-n-butyldiethanolamine, teaH3 = triethanolamine, tBudeaH2 = N-tbutyldiethanolamine, benz = benzoic acid and DMF = dimetylformamide]. The ligand formulae, along with the structures, are provided in Fig. 1. Using these groups of complexes, we explain the following: (i) which features influence the SMM behaviour of these complexes; (ii) the reason why QTM is minimised; (iii) optimisation of the SMM properties; (iv) how the nature and magnitude of the magnetic exchange interaction control the TB.

Experimental

General information

All reactions were carried out under aerobic conditions. Chemicals and solvents were obtained from commercial sources and used without further purification. Elemental analyses (CHN) were carried out by Campbell Microanalytical Laboratory, University of Otago, Dunedin, New Zealand.

The synthesis of all 14 complexes and representative infra-red spectra and PXRD analysis are shown for compounds 1 and 2a in the ESI.†

Crystal data collection and refinement

X-ray crystallographic measurements for compounds 1, 2c, 2d, 3a, 3e and 3f were collected with an Oxford Diffraction Supernova diffractometer using MoKα radiation. The data collection and data reduction were performed using CrysAlisPro; absorption corrections were applied using a multi-scan method.55 The data for 2a and 2b were performed using a Bruker Smart Apex X8 diffractometer with MoKα radiation. The data collection and integration were performed within SMART and SAINT+ software programs and corrected for absorption using the Bruker SADABS program.56 Measurements on complexes 3b, 3c, 4a, 4b and 4c were made using an Oxford Xcalibur diffractometer with MoKα radiation (λ = 0.71073 Å) and a Sapphire3 detector. The data collection and integration were performed within the CrysAlisPro software program. X-ray measurements for 3d and 3g were performed at 150(2) K at the Australian synchrotron MX1 beam-line. The data collection and integration were performed within Blu-Ice and XDS software programs.57,58 All complexes were all solved by direct methods (SHELXS-97), and refined (SHELXL-97) by full least matrix least-squares on all F2 data.59 Crystallographic data and refinement parameters for all these complexes are summarised in Tables S1a–1c.† Crystallographic details are available in the ESI† in CIF format. CCDC numbers 2268871–2268878.† See Tables S1a–1c† for experimental details. The structures of 1, 2a, 2b, 2c, 2d, 3d, and 3g have been published previously.39,45,46

Magnetic measurements

Direct current (dc) magnetic susceptibility measurements were carried out on a Quantum Design SQUID magnetometer MPMS-XL 7 operating between 1.8 and 300 K for dc-applied fields ranging from 0–5 T. Microcrystalline samples were dispersed in Vaseline in order to avoid torquing of the crystallites. The sample mulls were contained in a calibrated gelatine capsule held at the centre of a drinking straw that was fixed at the end of the sample rod. Alternating current (ac) susceptibility measurements were carried out on the same instrument utilising an oscillating ac field of 3.5 Oe and frequencies ranging from 0.1 to 1500 Hz. Hysteresis measurements were performed with an average sweep rate of 0.003 T s−1.

Computational details

The magnetic properties of this series of complexes were analysed through an ab initio study using the MOLCAS 8.0/8.2 suite of programs.60 The approach was of CASSCF/RASSI-SO/SINGLE_ANISO type calculations to determine the low-lying energy levels and magnetic properties of individual DyIII and CrIII ions.53,54,61–63 The estimated values of the exchange coupling between the Dy⋯Cr and Dy⋯Dy ions were performed in the Gaussian 16.0 C (ref. 64) suite of programs by considering the BS-DFT65 approach using the hybrid type hybrid B3LYP functional.66,67 Since first-order orbital momentum plays a distinctive role for DyIII it cannot be described in the single determinant, hence the BS-DFT involves the replacement of DyIII with GdIII, and the exchange value was then normalised with respect to the DyIII ion.68–70 The ab initio SINGLE_ANISO module also generates inputs to proceed for the POLY_ANISO module, which has been used to calculate the exchange parameter.71,72

Equation for J,

 
H = −JS1S2(1)

The calculations were performed on the obtained X-ray diffraction crystal structures without further optimisation. In calculating the single ion properties, other DyIII and CrIII ions were replaced by LuIII and ScIII, respectively, for the SINGLE_ANISO module. The Cholesky decomposition threshold was set to 5.0 × 10–8.73 The relativistic effects were taken into consideration by including the Doughlas–Kroll–Hess Hamiltonian.74 The active space for DyIII includes nine electrons in seven orbitals, and for CrIII, three electrons in five orbitals. For the RASSI-SO mixing, only 21 sextets were considered for DyIII since it has been well-established for Dy systems and for Cr, 10 quartets and 40 doublets have been taken into account.75 The SINGLE_ANISO module is used for the computation of local magnetic properties like the g-tensors and the magnetic axes of DyIII and CrIII centers. The basis set employed for the MOLCAS calculations is of ANO…RCC type, Dy. ANO-RCC…8s7p5d3f2g1h, Lu. ANO-RCC…7s6p4d2f, Sc. ANO-RCC…5s4p2d, O. ANO-RCC…3s2p, Cl. ANO-RCC…4s3p, F. ANO-RCC…4s3p, N. ANO-RCC…3s2p, C. ANO-RCC…3s2p, H. ANO-RCC…2s.76–78 The basis set for BS-DFT calculations is of CSDZ79 level basis set for GdIII with the addition of electron core potential for the metal centers taken from the EMSL80 library, and for the rest of the atoms, it was of TZV81 type. To compare the DFT obtained Jexch from the Gaussian calculations with the earlier reported DFT Jexch by Chibotaru et al. using the ORCA82 package, all the calculations have been repeated using the ORCA package with a similar model as that reported in 2013 on all the above complexes along with the parent complex using the same methodologies reported earlier.39

Results and discussion

Structural description and classification of the complexes

All of the fourteen newly characterised complexes have a {CrIII2DyIII2} butterfly motif similar to 1 (Fig. 2(a)).39 Complex 1 is described as a tetranuclear butterfly complex with the DyIII ions in the body positions and the CrIII ions lying in the outer wing positions. The DyIII and CrIII ions in the butterfly core are bridged by methoxide, benzoate and deprotonated amine polyalcohol ligands, whereas the DyIII ions are bridged only by methoxide ligands. The coordination sphere of each DyIII ion is completed by a chelating nitrate. The CrIII ions are six coordinated with an octahedral geometry, and the DyIII ions are eight coordinated with a square antiprismatic (SAP) geometry. With respect to the starting structure, we have classified these molecules into three types in order to have better comparison and insights according to the coordination around the DyIII ion and the types of ligands involved in the complex. These three types are classified as follows: (i) 2a–2d, (ii) 3a–3g and (iii) 4a–4c (Fig. S1†). See Fig. 2 for the representative examples 1, 2a, 3a and 4a.
image file: d4qi01484g-f2.tif
Fig. 2 Molecular structures of complex 1 (a),392a (b), 3a (c) and 4a (d), violet = Dy, cyan = Cr, grey = C, red = O, blue = N, green = Cl, hydrogen atoms were omitted for clarity, (e) schematic representation of the coordination environments.
Structural descriptions of 2a–2d. Complexes 2a–2d are iso-structural with the parent complex 1, and all crystalise in the monoclinic P21/n space group. The asymmetric unit for each consists of half of the complex (one CrIII and one DyIII ion), which lies upon an inversion center. Each complex differs in the aminopolyalcohol used (2a = deaH2, 2b = edeaH2, 2c = bdeaH2 and 2d = teaH3); however, the coordination to the metal ions remains the same in all cases, except we find that the coordination environment at the DyIII ion differs for 2a and 2d compared to 1. In the case of 2a, two MeOH molecules are coordinated at each DyIII site, whereas for 2d, one terminal nitrate and a MeOH are coordinated (Fig. S1†) instead of a chelating nitrate for 1. The geometry around the DyIII (SAP) and CrIII (octahedral) (Table 1) centers are the same with respect to 1.
Table 1 Selected bond parameters (bond length in Å and bond angles in °) around the DyIII ions for all the complexes. The terminology for the coordination environment has been provided in the ESI Fig. S2a–d†
Parameters 1 2a 2b 2c 2d 3a 3b 3c 3d 3e 3f 3g 4a 4b 4c
Parameters 1 2a 2b 2c 2d 3a 3b 3c 3d 3e 3f 3g 4a 4b 4c
Dy1–O1–Cr1 95.8 96.21 97.37 95.77 96.05 95.25 95.7 94.91 95 95.82 95.88 97.22 97.43 100.8 100.61
Dy1–O1′–Cr1′ 95.7 95.87 97.39 95.79 96.05 96.2 96.57 96.61 95.87 96.76 95.91 97.32 99.87 100.86 100.68
Dy1–O5–Cr1 102.75 103.06 102.97 102.72 104.3 102.81 103.2 103.45 102.77 102.47 102.61 103.74 102.73 104.42 105.85
Dy1–O4′–Cr1′ 103.3 104.6 102.24 103.71 104.53 102.52 103.87 104.16 102.34 102.5 102.3 104.05 105.95 107.73 107.03
Dy1–O1–Dy1′ 114.1 114.267 113.09 113.58 114.74 114.03 113.25 113.01 113.86 113.52 113.8 113.58 113.54 109.26 109.31
Dy1–Dy1 4.105 4.148 4.034 4.086 4.171 4.091 4.083 4.07 4.091 4.063 4.074 4.091 4.078 3.981 3.974
Dy1–Cr1 3.282 3.299 3.301 3.286 3.286 3.278 3.302 3.286 3.273 3.276 3.272 3.278 3.323 3.403 3.403
Dy1–Cr1′ 3.282 3.331 3.305 3.298 3.298 3.288 3.307 3.295 3.283 3.285 3.285 3.288 3.359 3.373 3.399
Cr1–Cr1′ 5.157 5.174 5.233 5.164 5.173 5.139 5.197 5.173 5.122 5.152 5.139 5.139 5.201 5.119 5.059
Dy1–O2 2.355 2.33 2.355 2.347 2.345 2.243 2.243 2.227 2.24 2.243 2.255 2.248 2.385 2.322 2.321
Dy1–O5 2.248 2.267 2.282 2.238 2.262 2.349 2.351 2.414 2.384 2.359 2.34 2.365 2.297 2.433 2.455
Dy1–O4′ 2.245 2.258 2.267 2.247 2.254 2.247 2.241 2.234 2.242 2.374 2.234 2.243 2.28 2.283 2.297
Dy1–O6′ 2.347 2.354 2.365 2.383 2.362 2.35 2.409 2.377 2.386 2.351 2.351 2.356 2.449 2.488 2.474
Dy1–O1 2.452 2.444 2.414 2.449 2.47 2.448 2.461 2.462 2.443 2.436 2.44 2.426 2.422 2.448 2.448
Dy1–O1′ 2.44 2.494 2.42 2.44 2.481 2.429 2.428 2.419 2.432 2.422 2.424 2.423 2.436 2.422 2.45
Dy1–O8 2.429 2.444 2.454 2.406 2.388 2.442 2.429 2.42 2.441 2.437 2.455 2.445 2.558 2.451 2.443
Dy1–O9 2.428 2.4 2.46 2.467 2.418 2.424 2.407 2.421 2.44 2.429 2.435 2.437 2.451 2.504 2.507
Dy1–O10 — — — — — — — — — — — — 2.427 2.353 2.374
Average 2.368 2.374 2.377 2.3721 2.372 2.366 2.371 2.372 2.376 2.3813 2.367 2.3679 2.412 2.411 2.419
Avg. Ax. 2.299 2.302 2.317 2.304 2.306 2.297 2.311 2.313 2.313 2.332 2.295 2.303 — — —
Avg. Eq. 2.43725 2.4455 2.437 2.4405 2.43925 2.43575 2.43125 2.4305 2.439 2.431 2.4385 2.43275 — — —
ESD 0.084 0.086 0.073 0.089 0.085 0.084 0.085 0.090 0.087 0.066 0.086 0.082 0.079 0.071 0.067
Deviation from ideal SAP (Dy-eight coordinated), TCTPR (Dy-nine coordinated) and O h (Cr-six coordinated) From SHAPE analysis
Dy 1.801 0.721 2.023 2.000 0.846 2.001 1.761 1.883 1.782 1.806 1.968 2.179 1.801(1.073) 0.721(0.590) 0.263
Cr 0.37 0.349 0.449 0.390 0.394 0.408 0.465 0.514 0.396 0.396 0.390 0.706 0.37(0.863) 0.349(0.744) 0.920

Structural descriptions of 3a–3g. Complexes 3a–3g are isostructural and crystallise in the triclinic P[1 with combining macron] space group, with the key difference compared to 1 is that the bridging benzoate ligands have been replaced by several different functionalised benzoates. These include Cl-based (3a–3c), Cl and F-based (3d) and CF3, OMe and tBu (3e, 3f and 3g, respectively) groups around the aromatic ring (Fig. 1 and S1†). The rationale for using these ligands was to test what effects electron withdrawing or donating groups and the steric effects that these ligands provide have on the magnetic behaviour and SMM properties of the complexes. For complexes 2a–2d and 3a–3g, the deviation from an ideal SAP geometry for DyIII and an ideal octahedral geometry for CrIII has been provided in Table 1, obtained from continuous SHAPE analysis.83
Structural descriptions of 4a–4c. For complexes 4a–4c, the bridging coordination environment is identical to 1, but the coordination environment at the DyIII ions was varied. Complexes 4a–4c now reveal a nine-coordinate environment with a chelating nitrate and the inclusion of an extra solvent molecule (4a (MeOH), 4b (DMF) and 4c (DMF)) at each DyIII site. In 4a, methanol ligands lie cis to each other at each DyIII site (Fig. 2d). Similarly, in 4b, a DMF ligand coordinates via the O-atom to the DyIII ions, which lie cis to each other. For 4c, again, DMF coordinates to the DyIII ions; however, the ligands are disposed of trans to each other (Fig. S1†). The nine-coordinate DyIII ions display a tricapped trigonal prismatic (TCTPR) geometry (Table 1), while the six-coordinate CrIII ions are octahedral (see Table 1 for SHAPE analysis).83

Magnetic properties

Direct current magnetic susceptibility measurements have been performed on powdered polycrystalline samples in the temperature range between 2 to 300 K under an applied field of 1 and 0.1 T. The χMT vs. temperature plots are shown in Fig. 3 for 2a, 3a, 4a and 4b and plots for the remaining molecules are shown in Fig. S3a and S3d.† The room temperature χMT value for each complex matches well with the calculated value for having two non-interacting CrIII (S = 3/2, g = 2, C = 1.875 cm3 K mol−1) and two DyIII (S = 5/2, L = 5, 6H15/2, g = 4/3, C = 14.17 cm3 K mol−1) ions of 32.09 cm3 K mol−1. For complexes 2a–2d and 3a–3g the χMT behaviour closely resembles that of complex 1 measured in dc fields of 0.1 T and 1 T.39 For example, for 2a at 0.1 T, as the temperature decreases from 300 K, the χMT values decrease gradually until reaching ∼30 K, then there is a small increase towards a maximum at ∼12 K followed by a sharp drop below 12 K down to 2 K. In the 1 T measurement, there is a continuous drop in the χMT value till 50 K; then it drops and plateaus before a further decrease occurs at low temperature. The slight decrease in the χMT values at high temperatures is attributed to the depopulation of mJ levels of the DyIII ions, whereas the increase/plateau below 50 K is due to the presence of non-negligible magnetic interaction between the DyIII–CrIII centers. As seen from Fig. 3 and S3a–3d,† we can see that the χMT values behave differently at low temperatures, and this is dependent on the nature of the exchange strength between the DyIII and CrIII centers; for each case, the behaviour is explained below, when discussing the theory of exchange.
image file: d4qi01484g-f3.tif
Fig. 3 The DC χMT vs. T and M vs. H isotherm (inset) plots for complexes 2a (a), 3a (b), 4a (c) and 4b (d).

For complexes 4a–4c, the χMT values decrease continually from 300 K as the temperature is reduced, decreasing more rapidly below ∼70 K (Fig. 3, bottom) with no increase or plateau. This behaviour is markedly different to that observed for 1, 2a–2d and 3a–3g. For 4a, however, a small rise is observed at very low temperatures (at 0.1 T), these differences are discussed below, vide infra.

The isothermal magnetisation curves for 1, 2a–2d and 3a–3g, plotted against the dc magnetic field (inset Fig. 3 and Fig. S3†), depict the presence of significant anisotropy for all the complexes. There is S-shaped behaviour in M when magnetised from zero field for the 2 K isotherms, which is indicative of hysteresis behaviour (see later). For 4a–4c, this behaviour is absent, with an increase in M occurring at all temperatures without reaching saturation.

Due to the likelihood of SMM behaviour for 1, 2a–2d and 3a–3g, alternating current magnetic measurements have been made on the powdered samples of all the complexes. All complexes display SMM behaviour with frequency and temperature-dependent out-of-phase susceptibility peaks observed. Representative plots of the in-phase (χ′M) and out-of-phase (χ′′M) vs. frequency (0.1–1500 Hz), Cole–Cole and ln(τ) vs. 1/T show good resolution and are shown for 2b in Fig. 4. At all temperatures studied (4.5–10 K), it was found that the relaxation is thermally activated, and plots of ln(τ) versus 1/T are linear, which suggests that an Orbach process is operative over the entire temperature and frequency range investigated. Fitting the data to the Arrhenius law [τ = τ0[thin space (1/6-em)]exp(Ueff/kBT)] yields an effective barrier to magnetisation reversal: Ueff = 79.1 K (ca. 54 cm−1) with τ0 = 3.4 × 10–8 s (R = 0.99) for 2b. This relaxation behaviour is observed for all complexes 1, 2a–2d and 3a–3g and analysed in a similar manner, and the respective Ueff are provided in the Table 2. The key observation for each complex is that even at the lowest temperatures, there is no crossover towards a QTM relaxation regime on the timescale of the ac experiment, which is extremely common for lanthanide-based SMMs. The Ueff and τ0 values for all the complexes are listed in Table 2.


image file: d4qi01484g-f4.tif
Fig. 4 Plots of in-phase (χ′M) (a) and out-of-phase (χ′M) vs. frequency (0.1–1500 Hz) (c), Cole–Cole (b) and ln(τ) vs.1/T (d) for 2b.
Table 2 DFT computed Jexch and the ab initio fitted Jtot/Jdip parameters for all the complexes together with Ueff, TB and HC values
Complex Gaussian Jexch BS-DFT MOLCAS_fitted U eff/K τ 0/s T B/K H c (1.8 K)/T
J Dy–Cr J Dy–Cr′ J Dy–Dy J Cr–Cr J totDy–Cr (JdipDy–Cr) J totDy–Dy (JdipDy–Dy) J totCr–Cr (JdipCr–Cr)
A total of four different exchanges values are given for JtotDy–Cr (two of them are in parenthesis for JdipDy–Cr). Since both the Dy(III) and Cr(III) centers are not equivalent to each other, they are resulting in different JtotDy–Cr exchange values, the same is applicable for dipolar exchange as well (JdipDy–Cr) provided in the parenthesis.
1 −0.88/−0.78 +0.03 +0.08 −4.0/−3.2(−3.22/−2.32) 0.04 (0.07) 0.10 (0.02) 76 5.1 × 10−8 3.7 2.7
2a −0.52/−0.80 +0.01 +0.04 −3.1/−3.15 (−2.30/−2.63) 0.03 (0.02) 0.06 (0.02) 60 2.3 × 10−7 3.5 2.1
2b −1.0/−0.70 +0.01 +0.06 −3.75/−3.80 (−2.80/−3.12) 0.02 (0.01) 0.04 (0.03) 77 3.4 × 10−8 4 2.5
2c −0.80/−0.86 +0.01 +0.07 −3.40/−3.50 (−2.54/−2.64) 0.02 (0.01) 0.03 (−0.04) 60 1.1 × 10−7 3.5 2.4
2d −0.51/−0.70 +0.01 +0.04 −2.90/−2.90 (−2.39/−2.20) 0.02 (−0.07) 0.03 (−0.01) 62 8.3 × 10−7 3.5 2.4
3a −0.55/−0.76 +0.01 +0.16 −4.25/−4.30 (−3.47/−3.75) 0.02 (0.01) 0.04 (−0.12) 85 4.8 × 10−8 3.5 No data
3b −0.55/−0.47 +0.01 +0.28 −4.20/−4.30 (−3.65/−3.83) 0.02 (0.01) 0.32 (0.04) 84 8.6 × 10−8 3.3 4.1
3c −0.91/−0.75 +0.01 +0.18 −4.40/−4.50 (−3.49/−3.75) 0.02 (0.01) 0.24 (0.06) 91 1.2 × 10−7 4.5 3.8
3d −0.98/−0.89 +0.01 +0.16 −4.10/−4.10 (−3.12/−3.21) 0.02 (0.01) 0.18 (0.02) 85 5.1 × 10−8 4.7 4.2
3e −0.95/−0.84 +0.01 +0.08 −3.90/−3.90 (−2.95/−3.06) 0.04 (0.03) 0.20 (0.12) 83 2.1 × 10−7 4.5 3.1
3f −0.94/−0.84 +0.03 +0.08 −3.80/−3.95 (−2.86/−3.11) 0.02 (0.05) 0.10 (0.02) 77 5.6 × 10−8 4 2.3
3g −0.88/−0.78 +0.03 +0.08 −3.10/−3.25 (−2.22/−2.47) 0.01 (0.04) 0.04 (−0.04) 63 3.8 × 10−8 3.1 2.2
4a −0.18/−0.57/−0.45 +0.04 +0.11 −1.80/−1.90 (−1.33/−1.75) 0.02 (−0.02) −0.02 (−0.09) 32 5.9 × 10−7 1.8
4b −0.27/−0.12 +0.01 −0.22 — — — n/a
4c −0.15–0.05 +0.004 −0.10 — — — n/a

For 4a–4c, the relaxation behaviour changes somewhat. Complexes 4b and 4c reveal no out-of-phase susceptibility signals above 1.8 K and, therefore, no SMM behaviour. For 4a, however, frequency and temperature-dependent out-of-phase susceptibility signals are found between 2–6.5 K, following a similar profile to those shown above (Fig. S5a–5n†) however after performing an Arrhenius analysis on the relaxation rates, we find that Ueff = 32 K (τ0 = 6.16 × 10–7 s), which is roughly half as small as seen in groups 1, 2 and 3.

Because of the relatively large thermal barriers and lack of observable QTM, we performed variable-field magnetisation measurements to probe the relaxation dynamics over a longer time scale and search for magnetic hysteresis. It was found that using sweep rates accessible with a conventional magnetometer (an average of 0.003 T s−1) on a polycrystalline sample, we were able to observe magnetic hysteresis for 1, 2a–2d and 3a–3g. Hysteresis plots are shown for 1, 2c, 3c, and 3d in Fig. 5 (see Fig. S4a and b† for the remaining complexes). From the data, we can clearly see open magnetic hysteresis loops with large coercive fields (Hc). In some cases, we observed some loss of magnetisation at a zero field, indicating QTM, which was not apparent on the much faster time scale of the dynamic AC experiment. Interestingly, we find that the coercive field and blocking temperature changes for each complex (Table 2). This must be indicative of structural modifications for each complex. In order to understand these results, we have performed theoretical DFT/ab initio calculations, which will be discussed next.


image file: d4qi01484g-f5.tif
Fig. 5 Plot of magnetization (M) versus field (H) for (a) 1, (b) 2c, (c) 3c and (d) 3d sweeping the field with an average sweep rate of 0.003 T s−1, at the temperatures indicated.

Theoretical studies

Ab initio calculations were performed on all complexes by taking the single crystal X-ray diffracted coordinates and employing the CASCCF/RASSI-SO/SINGLE_ANISO/POLY_ANISO module to obtain both the single-ion magnetic properties as well as the overall magnetic properties emanating from the exchanged coupled states. The computational methodologies are provided above in the Experimental section. For all complexes, the resulting single-ion magnetic properties, the low-lying Kramers doublets (KDs), along with the g-anisotropy are listed in the ESI Tables S3 and S4.†
Mechanism of magnetization relaxation for the single-ion DyIII centres. Employing the same level of basis set and methodologies for all fifteen complexes, including the starting complex 1, their single-ion anisotropic properties have been compared. For all complexes, the ground and 1st excited state anisotropy are found to be axial in nature (gzz ∼ 19.9, gxx = gyy ∼ 0), and the transverse component arises from the 2nd excited state (Table S4†). The computed energy levels of the KDs (up to n + 1 level with ‘n’ being the state via relaxation is facilitated) for all fifteen complexes are shown in Fig. 7 (see also Table S3 and Fig. S6† for the full energy level diagram).
Single-ion magnetic anisotropy of 2a–2d. The structural changes in the substituted polyamine-alcohol have a large effect on the crystal field splitting, which is due to both the structural and electronic effects offered by the substituents on the polyamine-alcohols; however, the former plays a dominant role as discussed below. It is interesting to note that increasing the size of the substituents from methyl to ethyl results in a decrease in the crystal field energy gap between the ground to the first excited state (136 cm−1 for 1vs. 109 cm−1 for 2b) (Fig. 7 and Table S3†). However, in contrast, a bulkier substituent like the n-butyl group increases the energy splitting (136 cm−1 for 1vs. 162 cm−1 for 2c) (Fig. 7, and Table S3†). For complex 2a (deaH2), an increase in the ground to 1st excited state energy (149 cm−1) is found compared to 1 (136 cm−1). The replacement of (mdea)2− to (dea)2− also changes the terminal coordination of the DyIII ion; for complexes 1, 2b and 2c a chelating nitrate group is coordinated to the DyIII ion, whereas for 2a, it is coordinated to two terminal MeOH groups. For complex 2d, when (mdea)2− is replaced by (teaH)2−, the ground to 1st excited state gap is found to be 177 cm−1, the largest among this group of complexes. The ground state anisotropy axis derived from POLY_ANISO fitting for 1 and 2a–2d for DyIII ions are shown in Fig. 6 and Fig. S1† and lie along the O-atoms of amine-polyalcohol groups (Fig. S1 and S8†) and lie parallel to each other. The same is true for both the CrIII centers, i.e. they lie parallel to each other (Fig. 6 and Fig. S1†). However, the arrangement of the anisotropy axes of DyIII and CrIII are anti-parallel to each other, which has been obtained from POLY_ANISO fitting (Fig. 6 and S1;†vide infra).
image file: d4qi01484g-f6.tif
Fig. 6 The arrangement of the ground state anisotropic axis obtained from the POLY_ANISO module for the complexes 1,392b, 3a and 4a. Green arrows represent the DyIII ions and the yellow arrows the CrIII ions.

image file: d4qi01484g-f7.tif
Fig. 7 The energy distribution of low lying Kramers doublets for all the complexes. The red square indicates the state for magnetic relaxation originating from the single DyIII centre.

To obtain a clearer picture of the structural vs. electronic effects, i.e. whether the changes in the geometry around the DyIII centre are due to different substitutions or are purely electronic in origin, we have modelled a similar complex to that of 1 by introducing a Cl group at the ortho position of the benzene ring (complex 1a, which resembles complex 3a Fig. S1†), however, keeping the bond parameters the same to that of 1. The calculations yield a slight enhancement of the overall KD splitting (by ∼1.95% see Table S3†) and nearly identical g-anisotropy to that of complex 1, however we find a substantial difference from complex 3a. This emphasises the importance of structural alterations that occurs due to the change in the functional group (98% vs. 2%) rather than the electronic structure of the functional group itself, as seen earlier in other systems.68

The magnetic relaxation dynamics were plotted for all complexes in Fig. 8 (2a, 3a, 4a and 4c) and in Fig. S7.† In all cases, magnetic relaxation occurs via the 2nd excited state through TA-QTM/Orbach process. The UDycal from the single DyIII ion ab initio calculations for 1, 2a–2d follows the order 2b (240 cm−1) < 1 (285 cm−1) < 2a (288 cm−1) < 2d (296 cm−1) < 2c (311 cm−1). As shown in Fig. 6 (Fig. S11†) the main anisotropy axis points towards the Dy–O bonds from the aminopolyalcohol ligands, thus a shorter Dy–O bond length would correspond to a stronger axial ligand field and hence a larger UDycal. The largest UDycal (2c) and smallest (2b) were found to correlate to the Dy–O bond length corresponding to the amine polyalcohol ligand (average 2.275 vs. 2.243 Å for 2b and 2c, respectively, see Table 1), with shorter distances yielding the largest UDycal and longer distances yielding the smallest UDycal in this family of complexes. The difference in distance observed is correlated to the electronic effect of the substituents, which alter the donor capability of the polyalcohol amine, which in turn is likely to change the donor nature of the oxygen arm. However, the bond length correlation does not hold true for the entire series, and neither it is found to correlate to the electronic nature of the substituents (inductive effects, etc.). This is essentially due to the minor variation in the bond length (of the order of ∼0.03 Å), causing significant variation in the magnetic behaviour. This demands a quantitative analysis based on the computed charges, which are discussed below.


image file: d4qi01484g-f8.tif
Fig. 8 The magnetic relaxation dynamics originating from the single DyIII centre for 2a (a), 3a (b), 4a (c) and 4b (d). Red dotted line indicates QTM(TA-QTM), solid blue line for TA, green line for Raman/Orbach Processes. Number above the line indicates the transition probabilities.
Single-ion magnetic anisotropy of 3a–3g. For this group of complexes, we have modified the functional groups at the benzoate bridging ligand, which would alter the donor capability of the corresponding oxygen atoms, and this has been performed in three ways: (i) for 3a, 3c, 3d–3f using (mdea)2− identical to 1 and alter the substituents around the aromatic ring of the benzoate ligand; (ii) for 3b keeping the n-butyl group intact similar to 2c and alter the 2,6-positions of the benzoate ligand with –Cl; (iii) for 3g employ a tert-butyl amine polyalcohol group along with tert-butyl substitution at the benzene ring. Thus 3b and 3g are expected to have mixed effects on both the functional groups, and a direct comparison or correlation to 1 is not possible. The ground and 1st excited state g-anisotropy are highly axial similar to 2a–2d. The 2nd excited state shows some transverse components (see Table S4†). The ground-to-first excited state energy gap for the KDs follows the ensuing order 3f (140 cm−1) < 3g (152 cm−1) < 3e (153 cm−1) < 3b (163 cm−1) < 3d (167 cm−1) < 3a (211 cm−1) < 3c (248 cm−1). For complexes 3a–3g, the ground state anisotropic axis lies along the O-atom of the amine polyalcohol group (with a deviation of 10–20°, see Fig. S8†).

All of these complexes have a larger ground to 1st excited state energy gap compared to 1. This is essentially due to the fact that the substitution at the benzoic position is expected to reduce the donation at the corresponding oxygen atom compared to the unsubstituted benzoate group in 1 (except for 3f and 3g, which increases the amount of electron density to the donor ligands). This reduction for the majority of complexes in the charge at the substituted benzoate oxygen atoms leads to weaker equatorial donation, which is known to destabilise the first excited KDs, leading to a larger gap (see Fig. S11†).

For complexes 3a–3g, relaxation occurs via the 2nd excited state except 3c, where it is predicted to occur via the 3rd excited state. The order of the computed UDycal values is found to follow the order 3g (277 cm−1) < 3f (286 cm−1) < 3e (312 cm−1) < 3b (327 cm−1) < 3d (336 cm−1) < 3a (394 cm−1) < 3c (613 cm−1) (Fig. 8, Fig. S6/S7 and Table S3†). It is clear from these calculations that the introduction of an electron-donating group such as OMe (complex 3f) at the ortho position or tert-Bu (complex 3g) at the para position of the benzoate ring causes a smaller crystal field splitting, in accordance with the expected electron-donating capability of the substituent groups (3f being a better electron donor through the π system than 3g through the σ donor system). Depending on the number and the position of the electron-withdrawing group, the ground-to-first-excited state gap varies for the other five complexes. If we compare the structures containing (mdea)2− as the amine polyalcohol (i.e.3a, 3c–3f), the largest UDycal is found for 3c while the smallest is found for 3f. This is attributed to the fact that for 3c, there are three –Cl groups substituted in the aromatic ring, offering a significant electron withdrawal effect, leading to a reduction in the donor capability of the corresponding oxygen compared to the (OMe)− group in 3f which enhances the donor strength of the equatorial oxygen. This is clearly reflected in the Dy–O bond distance, with a longer Dy–O bond found for 3c and a shorter one found for 3f (2.414 Å vs. 2.340 Å). As this oxygen lies in the equatorial position, lengthening of the bond leads to a larger UDycal value and vice versa. These effects are also reflected in the computed LoProp charges84 for the corresponding oxygen atoms (−0.668 vs. −0.723) for the O atoms of 3c and 3f, respectively (see Fig. S10 and S11†).

From the above analysis, it is clear, again, that the electronic factors of the substituents slightly alter the bond geometries, which has a consequential effect on the computed magnetic properties. For complexes 1, 2a–2d, and 3a–3g, which have eight oxygen donor atoms with a {DyO8} core, out of the eight O-atoms, two of the axial O-atoms from the aminepolyalcohol group and two of the equatorial O-atoms from the (NO3)− group (or MeOH for 2a) is primarily determining the strength of KDs energy splitting and hence the UDycal values. Another factor contributing to the difference in the observed UDycal values for these complexes are the amount of deformation of the {DyO8} core. This was indeed reflected in the observed LoProp charges on the surrounding O atoms and, hence on the crystal field parameters, leading to the largest observed UDycal values from the single DyIII center for 3c. The variation of the ground to 1st excited state energy splitting with respect to the difference in the percentage of axial and equatorial LoProp by taking the equal contribution of charges has been plotted in Fig. 9 (the difference of axial and equatorial LoProp charges/total charge × 100), and the detailed LoProp charge around each O-atom has been provided in Fig. S10 and S11 in ESI† for all the complexes. It has been noticed that a pseudo linear or sinusoidal correlation exists between the difference of axial to equatorial LoProp charge and the computed ground to 1st excited energy gap exist. The pseudo linear or sinusoidal behavior can be attributed to the fact that all these complexes are not completely structurally analogous to each other due to the wide variety of ligand systems (categories 1 to 3) having been employed. This reflects on the axial crystal field parameters B02 obtained from the Hamiltonian provided in eqn (S1) in the ESI† (HCF); a larger magnitude in B02 indicates a large axial approach of the ligand field, and the splitting between the low-lying KDs increases.85 For all the studied molecules, the crystal field parameters have been provided in Table S6 of the ESI.†


image file: d4qi01484g-f9.tif
Fig. 9 (a) Variation of ground to 1st excited state energy gap for all the complexes with respect to the percentage of axial and equatorial LoProp charges calculated from the CASSCF calculations. (b) 3D plot for axial LoProp vs. equatorial LoProp vs. ground to 1st excited state energy gap.
Single-ion magnetic anisotropy of 4a–4c. For the last set of complexes 4a–4c, there is an extra coordination site attached to the DyIII ions, and therefore the DyIII ion is nine coordinate with a {DyO9} motif. For all three complexes, the carboxylate is 2,6-dichlorobenzoate, which is the same as for complex 3b, with the amine polyalcohol ligands being (teaH)2− (4a), (bdea)2− (4b) and (mdea)2− (4c). For complex 4a, along with the chelating (NO3)−, a MeOH is coordinated to each DyIII ion. The MeOH ligands lie cis to each other. For complexes 4b and 4c, a chelating nitrate is present with a terminal DMF ligand at each DyIII ion, that lies cis and trans to each other, respectively. We find that despite moving from eight to nine coordinate environments, there is minimal change in the ground, 1st and 2nd excited g-anisotropy values (Table S4†); however, in comparison to the other complexes, the ground to 1st excited gap is reduced (Fig. 7 and Table S3†), and smaller UDycal values are found – 249 cm−1, 220 cm−1 and 208 cm−1 for 4a, 4b and 4c, respectively. The significant reduction in the ground-first excited state gap and the UDycal value compared to groups 1, 2 and 3 are due to the additional ligand. For 4a the extra MeOH ligand is found equatorial to the anisotropy axis, thus reducing the ground to 1st excited state gap. For 4b and 4c, however, the extra coordinated DMF ligand alters the position of one of the O-atoms of the polyalcohol ligand to lie equatorial compared to the other complexes where both the oxygen atoms lie along the axial direction (Fig. S11†). As these two amine polyalcohol O-atoms provide the shortest bond length and the strongest ligand field, moving one of the O-atoms to an equatorial position destabilises the first and second excited states leading to a drastic reduction in the UDycal value. Furthermore, as the geometry around the DyIII ion changes from a pseudo D4d square antiprismatic geometry, which is favoured for DyIII SMMs, the tunnelling contribution at the ground and excited states are larger (1.1 × 10–3 for 3bvs. 5.1 × 10–3 for 4b) leading to the suggestion of the absence of single-ion magnetic relaxation for this set of complexes.

The single aniso calculations indicate the axial approach of the ligand field and, hence, the contribution towards the overall energy barrier for magnetic relaxation. For the majority of complexes, the calculations predict good SMM behaviour, and this is found to be the case experimentally. The calculations also indicate the absence of SMM behaviour for 4b and 4c, which is also the case. The experimentally observed Ueff barrier in each molecule is, however, substantially less compared to the single ion-derived values (Table 2). Furthermore, there is no direct linear correlation between the observed UDycal and the experimental Ueff (see Fig. S12†). As it was revealed from complex 1 that there is a significant magnetic exchange interaction between the DyIII–CrIII ions, and the overall magnetic relaxation is strongly dependent on the exchanged coupled states, we, therefore, probe the influence of the exchange coupling on the SMM behaviour.

Mechanism of magnetization relaxation for the {CrIII2DyIII2} motif

To estimate the exchange coupling in these {CrIII2DyIII2} complexes, the following Hamiltonian was employed
 
image file: d4qi01484g-t1.tif(2)

The dipolar contribution to the magnetic exchange was computed using the dipolar Hamiltonian which is shown in eqn (S2).† There are three different exchange interactions that exist in these metal cores, which are between the DyIII–DyIII, DyIII–CrIII and CrIII–CrIII ions. In each molecule, there are six exchange pathways present, one between CrIII–CrIII, one between DyIII–DyIII and four between DyIII–CrIII (Fig. 10a). For the molecules where both the DyIII and CrIII centres are completely equivalent and can be attained by a 180° rotation, an equal value of JDy–Cr and JDy′–Cr′ is expected, whereas when they are not exactly equivalent, two different J values have been estimated (for complexes 2b, 4a and 4c).


image file: d4qi01484g-f10.tif
Fig. 10 (a) Mode of exchange coupling between the metal–metal centers in all the complexes. (b) The overlap between the 4f orbital of the lanthanide and the 3d orbitals of the Cr ion via the oxo bridges. The orange and blue lobes represent the α and β electron density for in the HS state and the green and gray lobes represents the α and β electron density in the broken symmetry states obtained from the density functional calculations.

The J values obtained from BS-DFT calculations using both Gaussian (B3LYP/TZVP) and Orca packages are provided in Table 2 and Table S5† (DFT spin density plots shown in Fig. S13†). For the Gaussian calculations, all six exchange interactions are taken into account simultaneously, whereas, for the ORCA calculations, the individual exchange terms between two paramagnetic centres have been calculated by substituting the other two centres with the diamagnetic metal centres, using the Hamiltonian provided in eqn (1). The fitted value using the POLY_ANISO module also follows the same Hamiltonian as eqn (1). The fitted values are provided in Table 2 along with the computed values (see Fig. S16† for the fitted χMT vs. T data).

In all the cases, the nature of the exchange between the CrIII and DyIII ions is antiferromagnetic in nature. This is due to the significant overlap of the 4f orbital (all seven 4f orbitals) of the lanthanide with the 3d orbitals of CrIII (dxy, dyz and dxz) (Fig. 10b, Sij ∼ 10–2 for 4fxyz with 3dxy). Further, as the unpaired electrons for the CrIII ions are in the t2g orbitals, they are less efficient in charge transfer to the 5d orbitals of the DyIII, which is established to be the primary contributor to the ferromagnetic part of the exchange.86,87 Thus, strong antiferromagnetic contributions and weaker ferromagnetic contributions lead to overall antiferromagnetic exchange. For all systems, the JDy–Dy′ exchange is ferromagnetic in nature and is found to be in the range of 0.01–0.04 cm−1. This is essentially correlated to the fact that the super-exchange mediates via two μ3 (OR)− groups with relatively acute Dy–O–Dy angles enforced by the butterfly geometry. For this angle, the exchange is expected to be ferromagnetic as per the earlier magneto-structural correlation established, affirming the computed data.88,89 The JDy–Cr exchange for groups 1, 2a–2d, 3a–3g, lie in the range of ∼−0.47 to −1 cm−1 (Table 2). The largest JDy–Cr exchange is observed for the 3a–3g series, followed by the 2a–2d. The smallest JDy–Cr exchange is found for 4a–4c and lies in the range −0.05–0.57 cm−1. These results correlate to the Dy–O bond lengths as well as the DyIII–Oamine–CrIII bond angles, which play a dominant role in determining the strength of magnetic exchange. A comparatively larger JDy–Cr exchange has been noticed for complexes 3c–3g, an intermediate-range for 1, 2a–2d and 3a–3b and a much smaller exchange for 4a–4c. This is due to the larger orbital overlap between the 4f orbitals of DyIII ion with the p orbitals of the bridging μ3-O, the carboxylate O-atom and the polyamine alcohol O-atom and the 3d orbital of the CrIII ion for 3c–3g (spin density on the oxygen 0.029–0.030, Fig. S11†) compared to the smaller overlap for the rest of the complexes. For 4a–4c, the JDy–Cr exchange is comparatively less (spin density on the oxygen 0.017 to 0.019) due to the increased bond length (average Dy–O 2.41 Å for 4a–4c and 2.36 to 2.38 Å for the eight coordinated complexes). The variation of JDy–Cr with respect to the DyIII–CrIII bond length and the DyIII–Oamine–CrIII angle has been plotted in Fig. 11 and Fig. S13, S14 and S18.† The Dy–O–Cr angle yields a quasi-linear regression suggesting that a larger Dy–O–Cr angle leads to ferromagnetic JDy–Cr exchange, while a smaller angle leads to antiferromagnetic exchange, though the Dy⋯Cr distance was also found to play a role in influencing the magnitude of the J value when the exchange gets strongly antiferromagnetic. In the weak antiferromagnetic region, J is found to be insensitive to the Dy⋯.Cr distance (see Fig. 11b). Except for 4b and 4c, for the rest of the complexes, the JCr–Cr is found to be ferromagnetic in nature and lies in the range of +0.04 to +0.28 cm−1. This interaction is very weak, as expected, as these are next-nearest-neighbour interactions, and the magnitude of the computed Js are found to be correlated to various geometric parameters, with the Cr⋯Cr distance being the prominent one. It also appears that the nature of CrIII–CrIII exchange influences the Ueff and TB along with the CrIII–DyIII exchange (see below). At low temperatures, this effect plays a dominant role and is observed experimentally in the χMT vs. T plots, hence quenching QTM and leading to SMM behaviour at zero field. Interestingly, this is further corroborated, as shown for complexes 4b and 4c, where an antiferromagnetic JCr–Cr leads to the absence of SMM behaviour. Very recently, Rentschler and co-workers reported a similar {CrIII2DyIII2} butterfly complex, where the two DyIII centres were replaced by two YIII centres and revealed a ferro-magnetic CrIII–CrIII interaction with hysteresis observed.90 For all fourteen complexes, the superexchange is relatively weaker than the dipolar interactions; however, they cannot be ignored. Including the superexchange along with the dipolar contribution is found to be crucial for reproducing the computed effective energy barrier from POLY_ANISO simulations in a way that aligns with experimental results. Further, the fits were found to be poor when exchange coupling interactions are excluded, suggesting that both contributions are crucial for their performance.


image file: d4qi01484g-f11.tif
Fig. 11 Variation of Jexch–Dy–Cr with respect to the Dy–O–Cr bond angle (a) and the variation of Jexch–Dy–Cr with respect to both Dy–Cr bond length and Dy–O–Cr bond angle represented in a 3D plot (b).

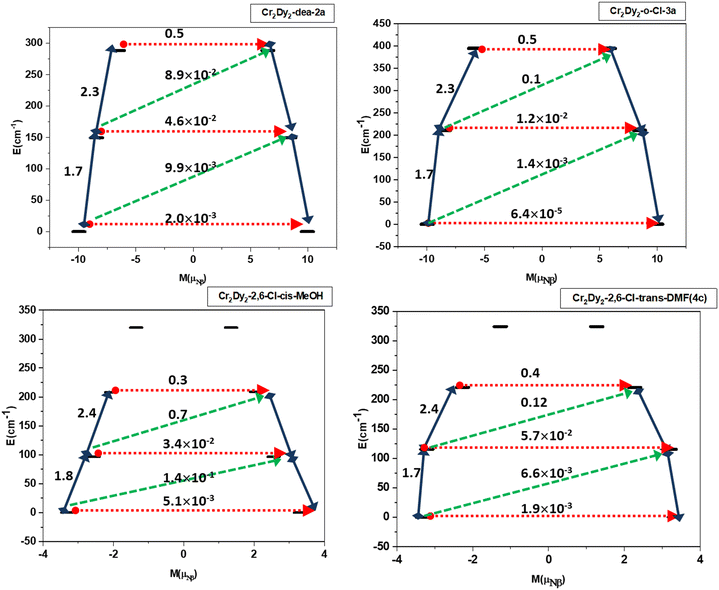
In all cases a nearly identical Ueff barrier has been derived using the POLY_ANISO module to that of the experimentally reported values (Fig. 12). With the low-lying doublet states, the resulting exchange spectrum is depicted in Fig. 12 and Fig. S17.† Each doublet's very modest tunnel splitting effectively suppresses the ground state and thermally assisted QTM (represented by the number on the top of each arrow). Therefore, it is anticipated that the excited states shown by the blue arrows in Fig. 12 will lead to the relaxation of magnetisation via a spin–phonon mechanism.


image file: d4qi01484g-f12.tif
Fig. 12 Poly_Aniso computed Ueff barrier heights for complexes 2a and 3a.

The relaxation path can be defined by connecting exchange states with the biggest transition magnetic moments, according to a recent proposal (blue numbers in Fig. 12).91

The calculated UDy−Crcal for the entire system by considering the exchanged coupled states has been plotted against the Ueff values, which gives a good linear fit (Fig. 13b). The magnitude of Jtot is plotted with respect to the observed Ueff and shows a linear correlation between exchange parameters and the observed Ueff. The relationship of Jtotvs. TB also holds true with a linear relationship between the Jtot and TB (Fig. 13c). The variation of the magnitude of total magnetic exchange, TB and the observed Ueff values has been plotted in Fig. 13d, which indicates a stronger exchange is playing a dominant role in achieving large TB and Ueff values. For complexes 1, 2a–2d and 3a–3g, a large dipolar coupling has been observed and, hence a large Jtot. The largest Jtot is found for 3a–3d, followed by 3e–3g and 2a–2d. Complex 2b is found to have the largest Jtot among 2a–2d. This is essentially reflected in the SMM behavior for all these complexes. A linear relation between the J values with Ueff and TB, holds true throughout the series of complexes. We show that the POLY_ANISO simulations help in the extraction of the barrier for magnetic relaxation (Ueff) for all these complexes, aligning with the experimentally obtained values. However, predicting the TB values from the exchange-coupled state is challenging, as TB is influenced by spin–phonon effects, hyperfine coupling, and inter-molecular interactions. However, it can be proposed that the observed hysteresis may result from the low-lying exchange-coupled states; as the overall total exchange (Jtot) is similar to the observed blocking temperatures (TB ∼ Jtot). While the correlation between the two factors is evident from the provided data, the reason for such a correlation, beyond the quenching of QTM at zero-field and exchange-bias effects, remains unclear. This warrants further study to improve the TB in this class of molecules.


image file: d4qi01484g-f13.tif
Fig. 13 (a) Variation of Jtot-Dy–Crvs. Ueff, (b) UDy−Crcalvs. Ueff, (c) Jtot-Dy–Crvs. TB and (d) dependence of Ueff and TB on Jtot-Dy–Cr represented in a 3D plot.

Conclusion

In summary, synthesis, characterisation and magnetic properties, along with detailed theoretical analysis, have been performed for fourteen {CrIII2DyIII2} butterfly complexes. Of the fourteen studied complexes, twelve were found to display SMM behaviour, and eleven revealed magnetic hysteresis above 3 K to 4.7 K with large coercive fields. These complexes are found to be some of the best 3d–4f SMMs reported. Various aspects have been explored in detail by computational methods in order to understand the magnetisation dynamics for these complexes. From the detailed experimental results combined with the theoretical studies, it has been revealed that;

(a) The crystal field splitting and the exchange coupling strongly originate from the structural parameters as compared to the electronic effects. Depending on the nature and bulkiness of the substituents, the bond parameters and geometry around the metal centres differ strongly, leading to different crystal field splitting as the axial approach of the ligand changes. In all of the above complexes, the ground state anisotropy axis lies along the oxygen of the polyamine-alcohol group, whereas the oxygen of (NO3)− (in some cases MeOH/DMF) lies in the equatorial plane. Substitution of various functional groups at various positions affects the Dy–O bond length and, hence the LoProp charges on the respective oxygens. Depending upon the magnitude of these LoProp charges on the oxygens, the ground to 1st excited energy gaps determine the overall UcalDy values.

(b) The nature of the JCr–Cr coupling plays a crucial role in determining the SMM behaviour for all complexes along with the magnitude of the JDy–Cr coupling. The single-ion calculated UDycalparameter indicates that all complexes are SMM at a single-ion level. However, complexes 2a–2d, 3a–3g shows SMM behaviour with a significant TB value. A detailed mechanism of magnetisation relaxation developed reveals that whenever the JCr–Cr exchange coupling is ferromagnetic, this results in the observation of SMM behaviour, and if it is antiferromagnetic (as in the case of 4b–4c), it lacks SMM characteristics.

(c) Depending on the bulkiness of the substituent, the bond angle between the Cr–O–Dy, and Dy–O–Dy changes, leading to different extents of orbital overlaps and, hence different exchange values with the angles playing a prominent role compared to other parameters in controlling the magnetic exchange. Quite interestingly, a near linear correlation between the TB values and |JDy–Cr| value was detected among the fourteen complexes reported suggesting that this particular exchange interaction is crucial in dictating not only the Ueff value but also TB values.

(d) Structural alterations that aim to alter this JDy–Cr to the strongest value yield the best TB values, offering design clues to improve the SMM characteristics in this family of complexes. Further, the substitution on the aromatic ring is found to be the more suitable approach to attain large Ueff and TB compared to the alternation in the polyamine alcohol group for such class of complexes, where the variation on the terminal DyIII coordination with more than eight coordination leads to the diminishing of SMM behaviour.

(e) The most suitable combination of transition metal (TM) and DyIII, along with suitable ligands, has been studied to optimise the SMM properties of butterfly complexes. Since the nature of TM–TM exchange interaction plays a dominating role, this can be further improved by enhancing this exchange e.g. by bringing into play the 4d and 5d TM ions which have more diffuse d orbitals. In our earlier report, however, 4d–4f exchange in a {Ru2Dy2} butterfly complex revealed a smaller Ueff and no TB was observed above 2 K, this contradicting SMM behaviour was due to poor exchange between the RuIII–DyIII center, likely due to a single unpaired electron residing on the RuIII center.27 However, similar polynuclear 3d–4f complexes have been reported with stronger 3d–4f ferromagnetic exchange containing CuII and DyIII ions,92,93 adapting these geometries/ions could pave the way for higher TB values. Furthermore, with such ferromagnetic exchange coupling between the 3d–4f metal centers, the 4f ions can also be varied to produce new series of SMMs involving lanthanide ions other than DyIII.

Data availability

The data supporting this article have been included as part of the ESI.†

Crystallographic details are available in the ESI† in CIF format. CCDC numbers 2268871–2268878.†

Conflicts of interest

There are no conflict of interest.

Acknowledgements

We thank DST and SERB (SB/SJF/2019-20/12; CRG/2022/001697) for funding. AS thanks UGC/CSIR for the fellowship. M. S acknowledges the financial support from the Prime Ministers Research Fellowship (PMRF). KSM thanks the Australian Research Council (DP110100525) for a Discovery grant.

References

  1. G. Christou, D. Gatteschi, D. N. Hendrickson and R. Sessoli, Single-molecule magnets, MRS Bull., 2000, 25, 66–71 CrossRef CAS.
  2. Y. Song, High density data storage: Principle, Technology, and Materials, World Scientific, 2009 Search PubMed.
  3. D. York, Magnetic blocking temperature, Earth Planet. Sci. Lett., 1978, 39, 94–97 CrossRef CAS.
  4. I. J. Bruvera, P. M. Zélis, M. P. Calatayud, G. F. Goya and F. H. Sánchez, Determination of the blocking temperature of magnetic nanoparticles: The good, the bad, and the ugly, J. Appl. Phys., 2015, 118, 184304 CrossRef.
  5. R. Sessoli, D. Gatteschi, A. Caneschi and M. Novak, Magnetic bistability in a metal-ion cluster, Nature, 1993, 365, 141–143 CrossRef CAS.
  6. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
  7. V. S. Parmar, D. P. Mills and R. E. Winpenny, Mononuclear Dysprosium Alkoxide and Aryloxide Single–Molecule Magnets, Chem. – Eur. J., 2021, 27, 7625–7645 CrossRef CAS.
  8. J. Lu, M. Guo and J. Tang, Recent Developments in Lanthanide Single–Molecule Magnets, Chem. – Asian J., 2017, 12, 2772–2779 CrossRef CAS PubMed.
  9. P. Zhang, L. Zhang and J. Tang, Lanthanide single molecule magnets: progress and perspective, Dalton Trans., 2015, 44, 3923–3929 RSC.
  10. D. N. Woodruff, R. E. Winpenny and R. A. Layfield, Lanthanide single-molecule magnets, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
  11. S.-D. Jiang and S.-X. Qin, Prediction of the quantised axis of rare-earth ions: the electrostatic model with displaced point charges, Inorg. Chem. Front., 2015, 2, 613–619 RSC.
  12. A. M. Ariciu, Use of Advanced EPR Methods for the Study of Lanthanide and Actinide complexes, The University ofManchester, United Kingdom, 2019 Search PubMed.
  13. C. A. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442 CrossRef CAS.
  14. K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, High-temperature magnetic blocking and magneto-structural correlations in a series of dysprosium(III) metallocenium single-molecule magnets, Chem. Sci., 2018, 9, 8492–8503 RSC.
  15. J. C. Vanjak, B. O. Wilkins, V. Vieru, N. S. Bhuvanesh, J. H. Reibenspies, C. D. Martin, L. F. Chibotaru and M. Nippe, A High-Performance Single-Molecule Magnet Utilising Dianionic Aminoborolide Ligands, J. Am. Chem. Soc., 2022, 144, 17743–17747 CrossRef CAS.
  16. D. Gatteschi and R. Sessoli, Quantum tunnelling of magnetisation and related phenomena in molecular materials, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS.
  17. S. K. Singh, M. F. Beg and G. Rajaraman, Role of Magnetic Exchange Interactions in the Magnetization Relaxation of {3d–4f} Single–Molecule Magnets: A Theoretical Perspective, Chem. – Eur. J., 2016, 22, 672–680 CrossRef CAS PubMed.
  18. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Strong exchange and magnetic blocking in N23−-radical-bridged lanthanide complexes, Nat. Chem., 2011, 3, 538–542 CrossRef CAS.
  19. P. H. Lin, T. J. Burchell, R. Clérac and M. Murugesu, Dinuclear Dysprosium(III) Single-Molecule Magnets with a Large Anisotropic Barrier, Angew. Chem., Int. Ed., 2008, 47, 8848–8851 CrossRef CAS.
  20. J. Long, F. Habib, P.-H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, Single-molecule magnet behaviour for an antiferromagnetically superexchange-coupled dinuclear dysprosium(III) complex, J. Am. Chem. Soc., 2011, 133, 5319–5328 CrossRef CAS PubMed.
  21. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, A N23− Radical-Bridged Terbium Complex Exhibiting Magnetic Hysteresis at 14 K, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS.
  22. L. Noodleman, C. Peng, D. Case and J.-M. Mouesca, Orbital interactions, electron delocalisation and spin coupling in iron-sulfur clusters, Coord. Chem. Rev., 1995, 144, 199–244 CrossRef CAS.
  23. E. Matito and M. Solà, The role of electronic delocalisation in transition metal complexes from the electron localisation function and the quantum theory of atoms in molecules viewpoints, Coord. Chem. Rev., 2009, 253, 647–665 CrossRef CAS.
  24. T. Gupta, T. Rajeshkumar and G. Rajaraman, Magnetic exchange in {Gd III–radical} complexes: method assessment, mechanism of coupling and magneto-structural correlations, Phys. Chem. Chem. Phys., 2014, 16, 14568–14577 RSC.
  25. A. Swain, A. Sen and G. Rajaraman, Are lanthanide-transition metal direct bonds a route to achieving new generation {3d–4f} SMMs?, Dalton Trans., 2021, 50, 16099–16109 RSC.
  26. C. A. Gould, K. R. McClain, D. Reta, J. G. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt and N. F. Chilton, Ultrahard magnetism from mixed-valence dilanthanide complexes with metal-metal bonding, Science, 2022, 375, 198–202 CrossRef CAS.
  27. A. Swain, R. Martin, K. R. Vignesh, G. Rajaraman, K. S. Murray and S. K. Langley, Enhancing the barrier height for magnetisation reversal in 4d/4f RuIII2LnIII2 “butterfly” single molecule magnets (Ln = Gd, Dy) via targeted structural alterations, Dalton Trans., 2021, 50, 12265–12274 RSC.
  28. M. K. Singh, N. Yadav and G. Rajaraman, Record high magnetic exchange and magnetisation blockade in Ln2@C79 N (Ln = Gd(III) and Dy(III)) molecules: a theoretical perspective, Chem. Commun., 2015, 51, 17732–17735 RSC.
  29. F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. Wolter, B. Büchner, S. M. Avdoshenko and A. A. Popov, Air-stable redox-active nanomagnets with lanthanide spins radical-bridged by a metal–metal bond, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed.
  30. Z. Hu, B.-W. Dong, Z. Liu, J.-J. Liu, J. Su, C. Yu, J. Xiong, D.-E. Shi, Y. Wang and B.-W. Wang, Endohedral Metallofullerene as Molecular High Spin Qubit: Diverse Rabi Cycles in Gd2@C79N, J. Am. Chem. Soc., 2018, 140, 1123–1130 CrossRef CAS PubMed.
  31. F. Pointillart, K. Bernot, R. Sessoli and D. Gatteschi, Effects of 3d–4f Magnetic Exchange Interactions on the Dynamics of the Magnetization of DyIII–MII–DyIII Trinuclear Clusters, Chem. – Eur. J., 2007, 13, 1602–1609 CrossRef PubMed.
  32. M. Andruh, J.-P. Costes, C. Diaz and S. Gao, 3d–4f combined chemistry: synthetic strategies and magnetic properties, Inorg. Chem., 2009, 48, 3342–3359 CrossRef CAS PubMed.
  33. K. N. Pantelis, K. H. Baka, J. Huang, C. P. Raptopoulou, V. Psycharis, K. R. Dunbar and T. C. Stamatatos, Linear versus Bent 3d/4f-Heterometallic Clusters: The Carboxylate Effect on the Metal Topology and Magnetic Properties of Two {MnIII2Dy2} Complexes Supported by N-Naphthalidene-o-Aminophenol, Cryst. Growth Des., 2023, 23, 5301–5313 CrossRef CAS.
  34. H.-H. Zou, L.-B. Sheng, F.-P. Liang, Z.-L. Chen and Y.-Q. Zhang, Experimental and theoretical investigations of four 3d–4f butterfly single-molecule magnets, Dalton Trans., 2015, 44, 18544–18552 RSC.
  35. G. P. Li, H.-Z. Tang, R.-C. Gao, Y.-Y. Wang, X. Sun and K. Zhang, Tuning Quantum Tunneling in Isomorphic {MII2DyIII2} “Butterfly” System via 3d-4f Magnetic Interaction, Cryst. Growth Des., 2023, 23, 1575–1580 CrossRef CAS.
  36. P. Shukla, S. Das, P. Bag and A. Dey, Magnetic materials based on heterometallic CrII/III–LnIII complexes, Inorg. Chem. Front., 2023, 10, 4322–4357 RSC.
  37. S. K. Langley, D. P. Wielechowski, N. F. Chilton, B. Moubaraki and K. S. Murray, A Family of {CrIII2LnIII2} Butterfly Complexes: Effect of the Lanthanide Ion on the Single-Molecule Magnet Properties, Inorg. Chem., 2015, 54, 10497–10503 CrossRef CAS PubMed.
  38. S. K. Langley, N. F. Chilton, L. Ungur, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Heterometallic Tetranuclear [LnIII2CoIII2] Complexes Including Suppression of Quantum Tunneling of Magnetization in the [DyIII2CoIII2] Single Molecule Magnet, Inorg. Chem., 2012, 51, 11873–11881 CrossRef CAS PubMed.
  39. S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, A {CrIII2DyIII2} single-molecule magnet: enhancing the blocking temperature through 3d magnetic exchange, Angew. Chem., Int. Ed., 2013, 52, 12014–12019 CrossRef CAS.
  40. S. K. Langley, L. Ungur, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Single-Molecule Magnetism in a Family of {CoIII2DyIII2} Butterfly Complexes: Effects of Ligand Replacement on the Dynamics of Magnetic Relaxation, Inorg. Chem., 2014, 53, 4303–4315 CrossRef CAS.
  41. S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Modulation of slow magnetic relaxation by tuning magnetic exchange in {Cr2Dy2} single molecule magnets, Chem. Sci., 2014, 5, 3246–3256 RSC.
  42. S. K. Langley, C. Le, L. Ungur, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, Heterometallic 3d–4f single-molecule magnets: ligand and metal ion influences on the magnetic relaxation, Inorg. Chem., 2015, 54, 3631–3642 CrossRef CAS.
  43. S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, The first 4d/4f single-molecule magnet containing a {RuIII2DyIII2} core, Chem. Commun., 2015, 51, 2044–2047 RSC.
  44. Y. Peng and A. K. Powell, What do 3d-4f butterflies tell us?, Coord. Chem. Rev., 2021, 426, 213490 CrossRef CAS.
  45. S. K. Langley, D. P. Wielechowski, B. Moubaraki, B. F. Abrahams and K. S. Murray, Magnetic Exchange Effects in {CrIII2DyIII2} Single Molecule Magnets Containing Alcoholamine Ligands, Aust. J. Chem., 2014, 67, 1581–1587 CrossRef CAS.
  46. S. K. Langley, D. P. Wielechowski, B. Moubaraki and K. S. Murray, Enhancing the magnetic blocking temperature and magnetic coercivity of {CrIII2LnIII2} single-molecule magnets via bridging ligand modification, Chem. Commun., 2016, 52, 10976–10979 RSC.
  47. J. D. Rinehart and J. R. Long, Exploiting single-ion anisotropy in the design of f-element single-molecule magnets, Chem. Sci., 2011, 2, 2078–2085 RSC.
  48. S. Dhers, J.-P. Costes, P. Guionneau, C. Paulsen, L. Vendier and J.-P. Sutter, On the importance of ferromagnetic exchange between transition metals in field-free SMMs: examples of ring-shaped hetero-trimetallic [(LnNi2){W(CN)8}]2 compounds, Chem. Commun., 2015, 51, 7875–7878 RSC.
  49. K. R. Vignesh, S. K. Langley, K. S. Murray and G. Rajaraman, Exploring the Influence of Diamagnetic Ions on the Mechanism of Magnetization Relaxation in {CoIII2LnIII2} (Ln = Dy, Tb, Ho) “Butterfly” Complexes, Inorg. Chem., 2017, 56, 2518–2532 CrossRef CAS PubMed.
  50. T. Kajiwara, M. Nakano, K. Takahashi, S. Takaishi and M. Yamashita, Structural design of easy-axis magnetic anisotropy and determination of anisotropic parameters of Ln(III)-Cu(II) single-molecule magnets, Chem. – Eur. J., 2011, 17, 196–205 CrossRef CAS PubMed.
  51. M. Orio, D. A. Pantazis and F. Neese, Density functional theory, Photosynth. Res., 2009, 102, 443–453 CrossRef CAS PubMed.
  52. E. Engel, Density functional theory, Springer, 2011 Search PubMed.
  53. P. A. Malmqvist and B. O. Roos, The CASSCF state interaction method, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
  54. L. F. Chibotaru and L. Ungur, Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS.
  55. Rigaku Oxford Diffraction, CrysAlis, Yarnton, England, 2009 Search PubMed.
  56. G. M. Sheldrick, SADABS, Program for Scaling and Correction of Area Detector Data, University of Göttingen, Germany, 1996.
  57. T. M. McPhillips, S. E. McPhillips, H.-J. Chiu, A. E. Cohen, A. M. Deacon, P. J. Ellis, E. Garman, A. Gonzalez, N. K. Sauter and R. P. Phizackerley, Blu-Ice and the Distributed Control System: software for data acquisition and instrument control at macromolecular crystallography beamlines, J. Synchrotron Radiat., 2002, 9, 401–406 CrossRef CAS PubMed.
  58. W. Kabsch, Automatic processing of rotation diffraction data from crystals of initially unknown symmetry and cell constants, J. Appl. Crystallogr., 1993, 26, 795–800 CrossRef CAS.
  59. G. M. Sheldrick, SHELXTL Version 5.1, Bruker AXS Inc., Madison, Wisconsin, USA, 1997.
  60. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. D. Vico, I. F. Galván, N. Ferré, L. M. Frutos and L. Gagliardi, MOLCAS 8: New capabilities for multiconfigurational quantum chemical calculations across the periodic table, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS.
  61. P. A. Malmqvist, B. O. Roos and B. Schimmelpfennig, The restricted active space (RAS) state interaction approach with spin–orbit coupling, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
  62. M. Böhme and W. Plass, How to link theory and experiment for single-chain magnets beyond the Ising model: magnetic properties modelled from ab initio calculations of molecular fragments, Chem. Sci., 2019, 10, 9189–9202 RSC.
  63. L. Ungur and L. F. Chibotaru, Ab initio crystal field for lanthanides, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS.
  64. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.02, Wallingford CT, 2009, 121, 150–166 Search PubMed.
  65. L. Noodleman, D. A. Case and A. Aizman, Broken symmetry analysis of spin coupling in iron-sulfur clusters, J. Am. Chem. Soc., 1988, 110, 1001–1005 CrossRef CAS.
  66. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behaviour, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed.
  67. W. Kohn, A. D. Becke and R. G. Parr, Density functional theory of electronic structure, J. Phys. Chem., 1996, 100, 12974–12980 CrossRef CAS.
  68. P. Kumar, S. Biswas, A. Swain, J. Acharya, V. Kumar, P. Kalita, J. F. Gonzalez, O. Cador, F. Pointillart and G. Rajaraman, Azide-Coordination in Homometallic Dinuclear Lanthanide(III) Complexes Containing Nonequivalent Lanthanide Metal Ions: Zero-Field SMM Behavior in the Dysprosium Analogue, Inorg. Chem., 2021, 60, 8530–8545 CrossRef CAS PubMed.
  69. T. Onishi, Y. Takano, Y. Kitagawa, T. Kawakami, Y. Yoshioka and K. Yamaguchi, Theoretical study of the magnetic interaction for M–O–M type metal oxides. Comparison of broken-symmetry approaches, Polyhedron, 2001, 20, 1177–1184 CrossRef CAS.
  70. T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Ab initio computations of effective exchange integrals for H–H, H–He–H and Mn2O2 complex: comparison of broken-symmetry approaches, Chem. Phys. Lett., 2000, 319, 223–230 CrossRef CAS.
  71. L. F. Chibotaru, L. Ungur and A. Soncini, The origin of nonmagnetic Kramers doublets in the ground state of dysprosium triangles: evidence for a toroidal magnetic moment, Angew. Chem., 2008, 120, 4194–4197 CrossRef.
  72. L. F. Chibotaru, L. Ungur, C. Aronica, H. Elmoll, G. Pilet and D. Luneau, Structure, Magnetism, and Theoretical Study of a Mixed-Valence CoII3CoIII4 Heptanuclear Wheel: Lack of SMM Behavior despite Negative Magnetic Anisotropy, J. Am. Chem. Soc., 2008, 130, 12445–12455 CrossRef CAS PubMed.
  73. H. Koch, A. Sánchez de Merás and T. B. Pedersen, Reduced scaling in electronic structure calculations using Cholesky decompositions, J. Chem. Phys., 2003, 118, 9481–9484 CrossRef CAS.
  74. M. Reiher, Douglas–Kroll–Hess Theory: a relativistic electrons-only theory for chemistry, Theor. Chem. Acc., 2006, 116, 241–252 Search PubMed.
  75. T. Gupta, M. K. Singh and G. Rajaraman, Role of Ab Initio calculations in the design and development of lanthanide based single molecule magnets, in Organometallic Magnets, 2019, pp. 281–354 Search PubMed.
  76. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, New relativistic ANO basis sets for transition metal atoms, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS.
  77. J. P. Zobel, P.-O. Widmark and V. Veryazov, The ANO-R basis set, J. Chem. Theory Comput., 2019, 16, 278–294 CrossRef.
  78. D. A. Pantazis and F. Neese, All-electron scalar relativistic basis sets for the lanthanides, J. Chem. Theory Comput., 2009, 5, 2229–2238 CrossRef CAS PubMed.
  79. T. R. Cundari and W. J. Stevens, Effective core potential methods for the lanthanides, J. Chem. Phys., 1993, 98, 5555–5565 CrossRef CAS.
  80. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, Basis set exchange: a community database for computational sciences, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
  81. A. Schäfer, C. Huber and R. Ahlrichs, Fully optimised contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
  82. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
  83. J. Cirera, E. Ruiz and S. Alvarez, Continuous shape measures as a stereochemical tool in organometallic chemistry, Organometallics, 2005, 24, 1556–1562 CrossRef.
  84. L. Gagliardi, R. Lindh and G. Karlström, Local properties of quantum chemical systems: The LoProp approach, J. Chem. Phys., 2004, 121, 4494–4500 CrossRef CAS PubMed.
  85. C. Rudowicz, Transformation relations for the conventional Okq and normalised O'kq Stevens operator equivalents with k = 1 to 6 and-k≤ q≤ k, J. Phys. Chem. C, 1985, 18, 1415 Search PubMed.
  86. K. S. Pedersen, G. Lorusso, J. J. Morales, T. Weyhermüller, S. Piligkos, S. K. Singh, D. Larsen, M. Schau-Magnussen, G. Rajaraman and M. Evangelisti, Fluoride-Bridged {GdIII3MIII2} (M=Cr, Fe, Ga) Molecular Magnetic Refrigerants, Angew. Chem., Int. Ed., 2014, 53, 2394–2397 CrossRef CAS.
  87. S. K. Singh, K. S. Pedersen, M. Sigrist, C. A. Thuesen, M. Schau-Magnussen, H. Mutka, S. Piligkos, H. Weihe, G. Rajaraman and J. Bendix, Angular dependence of the exchange interaction in fluoride-bridged Gd III–Cr III complexes, Chem. Commun., 2013, 49, 5583–5585 RSC.
  88. S. K. Singh, T. Rajeshkumar, V. Chandrasekhar and G. Rajaraman, Theoretical studies on {3d-Gd} and {3d-Gd-3d} complexes: Effect of metal substitution on the effective exchange interaction, Polyhedron, 2013, 66, 81–86 CrossRef CAS.
  89. T. Rajeshkumar, S. K. Singh and G. Rajaraman, A computational perspective on magnetic coupling, magneto-structural correlations and magneto-caloric effect of a ferromagnetically coupled {GdIII–GdIII} Pair, Polyhedron, 2013, 52, 1299–1305 CrossRef CAS.
  90. J. H. M. Ortiz, D. Cabrosi, L. M. Carrella, E. Rentschler and P. Alborés, SMM Behaviour of the Butterfly {CrIII2DyIII2} Pivalate Complex and Magneto–structurally Correlated Relaxation Thermal Barrier, Chem. – Eur. J., 2022, 28, e202201450 CrossRef.
  91. L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Interplay of strongly anisotropic metal ions in magnetic blocking of complexes, Inorg. Chem., 2013, 52, 6328–6337 CrossRef CAS.
  92. X. Zhao, G. Li, J. Ma and W. Liu, Two Octanuclear {Cu4Ln4} (Ln = Dy or Tb) Complexes with a Butterfly-Shaped Unit Exhibiting Zero-Field Single-Molecule Magnet Behavior, Inorg. Chem., 2020, 59, 2328–2336 CrossRef CAS PubMed.
  93. F. Mori, T. Nyui, T. Ishida, T. Nogami, K.-Y. Choi and H. Nojiri, Oximate-bridged trinuclear Dy− Cu− Dy complex behaving as a single-molecule magnet and its mechanistic investigation, J. Am. Chem. Soc., 2006, 128, 1440–1441 CrossRef CAS PubMed.

Footnote

† Electronic supplementary information (ESI) available. CCDC 2268871–2268878. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qi01484g
This journal is © the Partner Organisations 2025
Click here to see how this site uses Cookies. View our privacy policy here.