Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Calix[n]arene-based polyradicals: enhancing ferromagnetism by avoiding edge effects†
Daniel
Reta
 *ab,
Ibério de P. R.
Moreira
*ab,
Ibério de P. R.
Moreira
 a and
Francesc
Illas
a and
Francesc
Illas
 a
a
aDepartament de Ciència de Materials i Química Física & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, C/Martí i Franquès 1, 08028 Barcelona, Spain
bSchool of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: daniel.reta@manchester.ac.uk
First published on 11th August 2017
Abstract
Through-bond interacting organic polyradicals, rendered by customizable capacities of the state-of-the-art synthetic routes, are ideal systems to investigate spin topologies. Relying on Rajca and co-workers’ synthetic efforts, hereby we investigate the role of borders in the stability of the high-spin ground state in a series of realistic linear and ring-like arylmethyl polyradical derivatives. We show that, compared to their linear counterpart, the absence of borders in a ring-like arrangement of arylmethyl radicals imposes a larger number of spin-alternation rule violations, which strongly stabilizes the high-spin ground state. In addition, the structural flexibility of the investigated compounds translates into the existence of various structural energy minima for which the ferromagnetic ground state is always maintained. In view of the present results we propose these rings as possible candidates for the development of enhanced high spin single molecule toroics.
1. Introduction
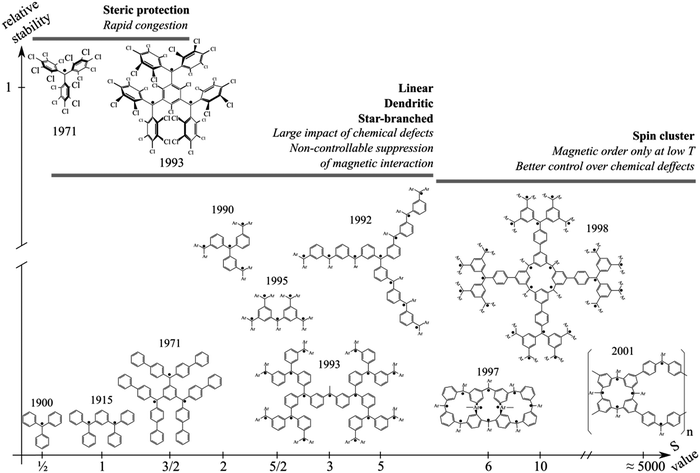
Ever since the synthesis of the triphenylmethyl radical by Gomberg,1 carbon-based π-conjugated polyradicals interacting through-bond have been considered as candidates for the practical realization of purely organic magnetism. Among the different coupling schemes enabling one to obtain extended structures from triarylmethyl-based building blocks, only a 1,3 (or meta)-connectivity between the radical centres ensures a preferential high-spin ground state, in agreement with well-known rules derived from topological arguments.2–5 This structural constraint in assembling the building blocks results in a limited number of possible structures such as linear, dendritic, star-branched or macrocyclic architectures, which indeed are expected to determine the macroscopic properties of the compounds.6–8Fig. 1 schematically summarizes the most significant experimental achievements obtained by exploiting a 1,3 (or meta)-connectivity using triarylmethyl-based radicals and classifies them as a function of the measured multiplicity of the ground state vs. relative stability. Here, relative stability is not a well-defined experimental property, but rather used for qualitatively comparing the most stable of these radicals. Fig. 1 also indicates the relationship between the adopted coupling scheme and the associated deficiencies. One of the main issues here is the lack of chemical stability of the carbon-based radicals, with dimerization, or other types of reactions, likely to result in loss of any magnetic property of interest. To protect the polyradical character of these compounds, two main synthetic strategies emerged. One is based on the idea that larger conjugation would result in a more pronounced delocalization of the unpaired electrons making them less reactive. Rajca and co-workers have led this branch with the refinement of the carbanion method and the development of spin clusters;9–11 see the lower part of Fig. 1. The second approach aims at sterically protecting the radical centre by introducing bulky chlorine atoms, resulting in the well-known perchlorotriphenylmethyl (PTM) radical originally synthesized by Ballester et al.12 Based on this, Veciana and coworkers have managed to synthesize di-13 and triradicals14 showing respectively stable triplet and quartet states in solution at room temperatures, as well as to synthesize and characterize a large series of multifunctional materials;15–19cf. the upper part of Fig. 1. Unfortunately, one cannot simultaneously take advantage of the two strategies simply because they are mutually exclusive due to steric congestion.20 As a result, no major experimental advance has been pursued in the field in the last decade. It is at this point when one can envisage exploiting the inherent structural flexibility21 present in these compounds so as to propose alternative approaches combining both a large conjugation and steric protection of the radical centres.
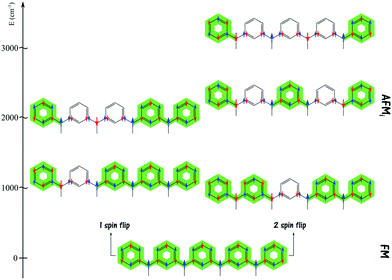
Relying on the ideas outlined above, it has been recently shown that a linear triarylmethyl-based polyradical molecule adopts a more stable helical conformation, which also promotes larger ferromagnetic interactions.22 However, the presence of edges in these high-spin ground state linear-like systems plays a detrimental role in ferromagnetism. This can be understood by simple arguments derived from the spin alternation rule schematically depicted in Fig. 2. Starting from a high spin arrangement with all spins up, the occurrence of a spin–flip in any of the radical centres leads to a situation that disrupts the spin-alternation rule forcing a spin frustration and a concomitant penalizing suppression of spin density in the adjacent phenyl rings. From theoretical and computational points of view, such a situation with one (or more) spin–flip can be represented by an antiferromagnetic solution (AFM). It is clear that the only region of the polyradical chain, either in a linear or helical conformation, where a spin flip imposes a minimum amount of disruptions is precisely at the edge. Consequently, the corresponding AFM solution will be stabilized which, again, is detrimental to an energetically isolated high spin ground state. Thus, to maintain a stable, ferromagnetic, high spin ground state, one should be able to equally penalize all AFM solutions and this is possible if one can get rid of the borders.
It is obvious that the most straightforward manner to remove edge effects in finite systems is by generating a ring-like structure. Inorganic chemistry has provided extraordinary relevant examples,23–33 but the localized nature of the magnetic centres and the presence of necessary bridging ligands often result in low-spin ground states and weak to moderate antiferromagnetic interactions. In organic chemistry, on the other hand, remarkable examples of ring-like molecules34–44 in the field of host–guest and supramolecular chemistry have been achieved. However, attempts to obtain organic magnetic rings are scarce. For the purpose of the present work, the most relevant example is precisely the tetraradical that led Rajca and co-workers to coin the spin cluster term.45 Despite their success, no further attempts have been reported to achieve more extended rings with a larger number of interacting radical centres, as the interest shifted towards the linkage of the tetraradical ring units.7 Other unrelated approaches consist of planar systems where the polyradical character arises from an equilibrium between quinoidal and aromatic forms,46,47 and of circular covalent organic frameworks (COFs) to which stable nitronyl radicals are covalently bound.48 Of particular significance for the present work is the concept of single molecule toroics (SMT),32 where on top of exchange interactions between centres, having a significant magnetic anisotropy is a key goal. Despite the fact that magnetic anisotropy is not expected in purely organic molecules, appropriate coordination with metallic centres appears as an effective manner to introduce such a property.49,50
Bearing in mind the structural flexibility of arylmethyl-derivatives and aiming at further investigating them as the most promising candidates to develop organic magnetism, we study a series of realistic, progressively bigger, circular-like, arylmethyl-based polyradicals. We then compare the magnetic features of these ring-like compounds to those of their associated linear and helical counterparts. Through a systematic theoretical study of their structural and magnetic features, we provide compelling evidence that a ring-like arrangement persistently presents comparatively more stable high-spin ground states, which is not affected by the ease to undergo conformational distortions. Additionally, the chemical stability of the investigated examples could be largely increased by promoting a favourable balance between steric protection and the associated strain.
2. Computational and theoretical details
All calculations have been carried out with the Gaussian09 suite of programs,51 using the B3LYP52 hybrid density functional within the unrestricted formalism and the Pople-type basis set 6-31G(d,p)53–55 for all atoms, including dispersion corrections as proposed by Grimme.56–58 All discussed structures have been fully optimized and characterized as stationary minima in the potential energy surface (PES) by explicitly calculating the hessian matrix and making sure that all frequencies were positive and the forces (numerically) zero. For N ≥ 12 systems (N is the number of radical centres), explicit calculation of hessian was not possible due to memory problems; however they fulfilled the convergence criteria in the optimization cycle. For complicated cases, the optimized geometry obtained using the semi-empirical method PM659 was used as a starting point for the B3LYP method. A further assessment of the employed method has been done by comparing the predicted structures and energy differences to different functionals and basis sets, for the 7-membered ring as a representative case. Thus, we selected the hybrid TPSS60meta-GGA functional, PBE061 and M06-2X62 hybrid functionals and the LC-ωPBE63–65 long range-corrected functional and the cc-pVTZ66 basis set.To gain information about the magnitude of energy change induced by spin flips from the high spin state a common strategy consists in mapping the low energy ferromagnetic and antiferromagnetic solutions to the corresponding expectation values of a given spin only model Hamiltonian. Most often the well-known Heisenberg–Dirac–Van Vleck (HDVV) model Hamiltonian as in eqn (1) is chosen
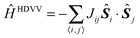 | (1) |
3. Linear, helical and circular oligomers: structure and magnetism
In order to analyse the impact of edge effects on the relative stability of FM solutions, we compare a series of oligomers in a linear, helical and ring conformation ranging from 4 to 15 radical centres. The linear and helical structures contain exactly the same number and type of atoms and therefore one can make use of absolute energies to discuss the relative properties. However, the ring arrangement possesses one less phenyl moiety and the discussion is then referred to relative energy differences per magnetic centre. For completeness, we also investigated the steric protection of the radical centres in some of the rings, by substituting the hydrogen atoms in the radical-bearing carbon by phenyl rings and in a subsequent step (for the smallest ring), by substituting all hydrogen atoms by chlorine atoms.Let us first discuss the results obtained for the linear and helical structures. Table 1(a) presents the energy difference between the FM ground state and the lowest (excited) AFM solution for the linear and helical conformations. As predicted by the simple topological arguments discussed in Fig. 2, it is found that the lowest AFM solutions always correspond to the arrangement of consecutive spin down densities at one of the edges (compare AFM(i) and AFM(i)* rows in Tables S2 and S3 in the ESI†). This follows from the fact that this type of AFM solution involves the minimum amount of spin alternation rule violations. Due to technical limitations on the control of the topology of the solution sought for, the solution presenting consecutive spin down densities at the edge was not possible to converge in a few cases (helical N = 8, 10, 13 and 14) despite extensive efforts made using different starting density and convergence control procedures. In any case, all converged solutions are presented in Table S3 (ESI†) thus providing a strong support to the conclusions reached in the present work. Table 1(a) also indicates the gain in stability (kcal mol−1) per magnetic centre due to the appearance of the helical conformation. As indicated before, the expressions to obtain the magnetic couplings can be found in Section 1 of the ESI.† For the linear molecules (Table S4 and Section 3 of the ESI†), the calculated exchange coupling constants remain practically the same throughout the series, where J1 is an order of magnitude larger than J2 and of opposed sign. The situation is less clear for the helical arrangement (Table S4 and Section 3 of the ESI†), as there is a significant variation in the magnitude and sign of the different two body terms with the number of centres. Additionally, depending on which DFT-computed energies are used to solve the spectrum, one finds a large variation in J3 and J4 (see Section 3 in the ESI†). The crucial point here is, however, the consistent prediction of a helical-induced stabilization of the FM ground state in all cases that can be safely addressed considering the HDVV spin model Hamiltonian to classify and compare the different spin solutions.
| (a) ΔEFM–AFM | ΔEL–H | (b) ΔEFM–AFM | ΔEFMi–FMj | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | Linear | Helical | 1 | 2 | 3 | 4 | 1 → 2 | 1 → 3 | 1 → 4 | |
| 4 | −291 | −175 | 2.3 | −572 | ||||||
| 5 | −283 | −165 | 3.1 | −387 | −454 | −353 | −8.2 | −17.0 | ||
| 6 | −194 | −86 | 3.6 | −367 | −27 | −17.5 | ||||
| 7 | −167 | −88 | 4.1 | −266 | −203 | −35.2 | ||||
| 8 | −145 | * | 4.4 | −283 | −270 | −269 | −209 | −1.3 | −24.0 | −34.2 |
| 9 | −130 | −51 | 4.7 | −228 | −205 | −184 | −213 | −1.0 | −6.6 | −17.4 |
| 10 | −117 | * | 4.9 | −205 | −233 | −180 | −1.1 | −25.6 | ||
| 12 | −97 | −44 | 5.2 | −178 | ||||||
| 13 | −90 | * | 5.3 | |||||||
| 14 | −83 | * | 5.4 | |||||||
| 15 | −133 | |||||||||
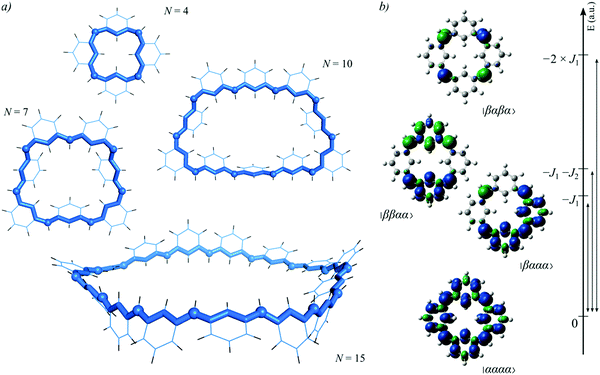
Using the data in Table 1(b), we focus now on the results for the ring-like structures. Table 1(b) presents (i) the energy differences between the ground ferromagnetic and the lowest AFM solutions (which correspond to consecutive beta-centres) at each of the different local minima found and (ii) the energy cost to change conformation among the different minima. Concerning the lowest energy structures, Fig. 3a depicts the corresponding geometries of four representative cases displaying N = 4, 7, 10 and 15 magnetic centres (see Table S5 in the ESI† for absolute energies associated with FM and AFM). The cases corresponding to N = 4 and N = 10 are of particular relevance due to reported experimental information. Thus, for N = 4 the optimized structure shows a 4-fold-symmetry, as experimentally found for phenyl-substituted calix[4]arene,45 and for N = 4 and 10 the adopted conformation of the inner rings resemble the ones reported for related closed-shell aza[1n]metacyclophanes.44 The N = 4 system also allows exemplifying the spin density associated with the FM and AFM solutions, as indicated in Fig. 3b. From this simple case, the spin densities of all possible AFM solutions for larger systems can be envisioned. As implicit in the previous discussion, these systems present an additional complexity arising from the multiple local minima that a ring structure can adopt. For instance, for N = 8 a total of four, well separated in energy, minima were characterized. Interestingly, for the largest molecular structure investigated (N = 15), the energy minimum structure is reminiscent of a Möbius strip and, despite the different degree of strain found in the different minima, the ground state always remains FM. This strongly supports the claim that these systems exhibit a robust FM ground state, a conclusion which, qualitatively speaking, can be considered independent of the DFT based-method used. In fact, the validity of the B3LYP functional with the standard Pople-type GTO basis set to describe these types of organic radicals has been extensively validated in previous theoretical21,71 and experimental72,73 works. Taken altogether, one can safely conclude that a more exhaustive investigation of the potential energy surfaces will not reveal a qualitatively different picture in terms of magnetic interactions and that the presented cases are sufficiently representative. To further justify this, Table S11 in Section 5 of the ESI† presents the results obtained with TPSS, PBE0, M06-2X and LC-ωPBE functionals together with the 6-31G(d,p) and triple-ζ polarized quality basis sets, for the 7-membered ring system. As shown for the m-xylylene diradical,71 the long-range separated functional predicts values off the trends, while the rest of the functionals behave in a more consistent way.
Having separately discussed linear-like and ring-like structures we now compare the results obtained for the two types of structures. For a given number of radical centres, the energy difference between the FM and lowest AFM solutions is always larger for the ring, as compared to either linear and helical arrangements; this proves that avoiding edge effects provides a clear strategy to stabilize high spin states in triarylmethyl polyradical derivatives. In fact, a single spin flip anywhere in the ring results in a state approximately 2400 cm−1 above the FM ground state, which is twice the difference found in the linear cases (see AFM1 rows in Table S2 vs. Table S5 in the ESI†). Interestingly, due to spin topology, while removing edge effects significantly stabilizes the FM solution, the magnetic coupling constant value J1 remains similar to the linear counterpart. This can be understood by comparing eqn (S2) and (S6) in the ESI.† However, J2 shows a considerable variation along the series. It is worth mentioning that, as in the case of the helical structures, the calculated magnetic coupling constants also show differences depending on which set of equations is used (Table S7 in Section 4 of the ESI†) which seem to indicate that the HDVV Hamiltonian used is a too crude spin model for this type of system. In this case, the apparent inconsistency can be traced to the rather irregular distribution of radical centres within the molecule, which makes the distances between the first and second nearest neighbours not always constant. The impact of the adopted conformation on the magnetic coupling constants is further investigated by calculating those values at the different conformers, as presented in Table S8 of the ESI.† For all investigated cases, J1 remains largely ferromagnetic although in some cases it experiences a noticeable decrease. On the other hand, J2 does switch from ferro- to antiferro- character depending on the conformation. Nevertheless, J1 is, in all cases, one order of magnitude larger than J2, thus retaining the dominant magnetic interaction. To conclude the study, a similar analysis was carried out on more realistic molecules where the steric protection of the radical centres is increased by (i) substituting the hydrogen atom in each carbon-based radical by a phenyl ring for N = 4, 5, 7, 8 or (ii) substituting all hydrogen atoms by chlorine atoms for N = 4 (see Table S9 in the ESI†). The general trends are the same but the absolute values of the magnetic coupling constants are smaller, due mainly to a larger delocalization of the unpaired spin density on the rings that do not participate in the exchange coupling. For instance, J1 drops from 2333 to 1637 cm−1 for the lowest stationary point found for N = 8 after replacing the hydrogen atoms in the radical centre by phenyl groups. Additionally, the fully chlorinated N = 4 case also shows a ferromagnetic ground state in both stationary points found, despite presenting a smaller J1 value. Finally, the relative energy position of the molecular orbitals does not depend on the size of the molecule and the steric protection of the radical centres does not significantly modify the HOMO–LUMO gap, which remains around 2 eV (see Fig. S2 in the ESI†). This is in contrast with what is predicted for planar arrangements of triarylmethyl-based polyradicals.74 Nevertheless, the important finding is that, irrespective of the HDVV used to map the different magnetic solution, removing edges significantly stabilizes the FM ground state, strongly suggesting that this may be a potential way to obtain polyradicals with robust ferromagnetism.
4. Conclusions
The present study shows that structurally stable, ring-like molecules derived from arylmethyl polyradicals display largely stabilized high-spin ground states as compared to their linear-like counterparts. The reason is the absence of borders, as predicted by simple spin topological arguments. Rajca and co-workers45 exploited the basic calix[4]arene to develop spin clusters through the linkage of these units, but syntheses of larger rings have not been reported.A meta-connectivity of the radical centres is crucial for two reasons: (i) it ensures high-spin ground states and (ii) offers a structural freedom, increasing with size, that alleviates possible strains imposed by the ring structures. In fact, the inner ring of all optimized structures presented in this work resembles previous experimentally reported geometries in related closed-shell aza[1n]metacyclophanes,44 which indicates the feasibility of the proposed molecules.
For ring structures with a given number of centres, several local structural minima are found. The preference for a high-spin ground state, the increased energy difference between FM and AFM solutions and the predicted HOMO–LUMO gap are not altered by the conformational richness. The calculated nearest neighbour (J1) coupling remains always the dominant term and exhibit robust ferromagnetic character.
Further stabilization of the reactive carbon-based radical centres can be achieved by steric protection, maintaining the main structural and magnetic characteristics. The ideal situation would then be to find a balance between steric congestion and stabilization of the radical centres.
To summarize, removal of edges by considering purely organic, through-bond interacting, meta-connected ring-like molecules derived from arylmethyl polyradicals appears as a realistic strategy to obtain very high-spin systems and move forward in the field of organic magnetism. Particularly, the investigated rings can be considered as potential candidates for the development of enhanced single-molecule toroics (SMT),32 owing to their extended conjugation within the molecule and the large ferromagnetic exchange interactions. Taken together, these findings call for efforts to attempt the synthesis of ring-like arylmethyl-based molecules, along a well-defined synthetic route.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Spanish MINECO/FEDER CTQ2015-64618-R and CTQ2016-76423-P grants and, in part, by Generalitat de Catalunya (grants 2014SGR97 and XRQTC) and by the NOMAD Center of Excellence project, which received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 676580. DR acknowledges additional funding from the Engineering and Physical Sciences Research Council (EP/P002560/1 grant). FI acknowledges additional support from the 2015 ICREA Academia Award for Excellence in University Research. The toroid of the image in table of content was created by Yassine Mrabet. This vector image was created with Inkscape. Under GFDL and CC BY-SA 3.0, via Wikimedia Commons.References
- M. Gomberg, J. Am. Chem. Soc., 1900, 22, 757–771 CrossRef.
- H. C. Longuet-Higgins, J. Chem. Phys., 1950, 18, 265–274 CrossRef CAS.
- A. A. Ovchinnikov, Theor. Chim. Acta, 1978, 47, 297–304 CrossRef CAS.
- W. T. Borden and E. R. Davidson, J. Am. Chem. Soc., 1977, 99, 4587–4594 CrossRef CAS.
- N. Mataga, Theor. Chim. Acta, 1968, 10, 372–376 CrossRef CAS.
- A. Rajca, Chem. Rev., 1994, 94, 871–893 CrossRef CAS.
- A. Rajca, Adv. Phys. Org. Chem., 2005, 40, 153–199 CrossRef CAS.
- N. M. Shishlov, Russ. Chem. Rev., 2007, 75, 863–884 CrossRef.
- A. Rajca, K. Lu and S. Rajca, J. Am. Chem. Soc., 1997, 119, 10335–10345 CrossRef CAS.
- S. Rajca, A. Rajca, J. Wongsriratanakul, P. Butler and S. M. Choi, J. Am. Chem. Soc., 2004, 126, 6972–6986 CrossRef CAS PubMed.
- A. Rajca, J. Wongsriratanakul and S. Rajca, Science, 2001, 294, 1503–1505 CrossRef CAS PubMed.
- M. Ballester, J. Riera-Figueras, J. Castaner, C. Badfa and J. M. Monso, J. Am. Chem. Soc., 1971, 93, 2215–2225 CrossRef CAS.
- J. Veciana, C. Rovira, M. I. Crespo, O. Armet, V. M. Domingo and F. Palacio, J. Am. Chem. Soc., 1991, 113, 2552–2561 CrossRef CAS.
- J. Veciana, C. Rovira, N. Ventosa, M. I. Crespo and F. Palacio, J. Am. Chem. Soc., 1993, 115, 57–64 CrossRef CAS.
- D. Maspoch, D. Ruiz-Molina and J. Veciana, Chem. Soc. Rev., 2007, 36, 770–818 RSC.
- N. Crivillers, M. Mas-Torrent, J. Vidal-Gancedo, J. Veciana and C. Rovira, J. Am. Chem. Soc., 2008, 130, 5499–5506 CrossRef CAS PubMed.
- M. Mas-Torrent, N. Crivillers, C. Rovira and J. Veciana, Chem. Rev., 2012, 112, 2506–2527 CrossRef CAS PubMed.
- C. Simão, M. Mas-Torrent, N. Crivillers, V. Lloveras, J. M. Artés, P. Gorostiza, J. Veciana and C. Rovira, Nat. Chem., 2011, 3, 359–364 CrossRef PubMed.
- I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303–349 RSC.
- D. Ruiz-Molina, J. Veciana, F. Palacio and C. Rovira, J. Org. Chem., 1997, 62, 9009–9017 CrossRef CAS.
- D. Reta Mañeru, I. de P. R. Moreira and F. Illas, Theor. Chem. Acc., 2015, 134, 18 CrossRef.
- D. Reta Mañeru, I. de P. R. Moreira and F. Illas, J. Am. Chem. Soc., 2016, 138, 5271–5275 CrossRef PubMed.
- M. L. Baker, G. A. Timco, S. Piligkos, J. S. Mathieson, H. Mutka, F. Tuna, P. Kozlowski, M. Antkowiak, T. Guidi, T. Gupta, H. Rath, R. J. Woolfson, G. Kamieniarz, R. G. Pritchard, H. Weihe, L. Cronin, G. Rajaraman, D. Collison, E. J. L. McInnes and R. E. P. Winpenny, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19113–19118 CrossRef CAS PubMed.
- M. Affronte, T. Guidi, R. Caciuffo, S. Carretta, G. Amoretti, J. Hinderer, I. Sheikin, A. G. M. Jansen, A. A. Smith, R. E. P. Winpenny, J. van Slageren and D. Gatteschi, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 104403 CrossRef.
- O. Cador, D. Gatteschi, R. Sessoli, A.-L. Barra, G. A. Timco and R. E. P. Winpenny, J. Magn. Magn. Mater., 2005, 290, 55–60 CrossRef.
- G. N. Newton, N. Hoshino, T. Matsumoto, T. Shiga, M. Nakano, H. Nojiri, W. Wernsdorfer, Y. Furukawa and H. Oshio, Chem. – Eur. J., 2016, 22, 14205–14212 CrossRef CAS PubMed.
- R. E. P. Winpenny, G. A. Timco, S. Marocchi, E. Garlatti, M. Albring, V. Bellini, F. Manghi, E. J. L. McInnes, R. Pritchard, F. Tuna, W. Wernsdorfer, G. Lorusso, G. Amoretti, S. Carretta and M. Affronte, Dalton Trans., 2016, 45, 16610–16615 RSC.
- T. Minato, K. Suzuki, K. Yamaguchi and N. Mizuno, Angew. Chem., Int. Ed., 2016, 55, 9630–9633 CrossRef CAS PubMed.
- S. Sanz, J. M. Frost, T. Rajeshkumar, S. J. Dalgarno, G. Rajaraman, W. Wernsdorfer, J. Schnack, P. J. Lusby and E. K. Brechin, Chem. – Eur. J., 2014, 20, 3010–3013 CrossRef CAS PubMed.
- J. van Slageren, S. Piligkos and F. Neese, Dalton Trans., 2010, 39, 4999–5004 RSC.
- P. Santini, S. Carretta, G. Amoretti, T. Guidi, R. Caciuffo, A. Caneschi, D. Rovai, Y. Qiu and J. R. D. Copley, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 184405 CrossRef.
- L. Ungur, S.-Y. Lin, J. Tang and L. F. Chibotaru, Chem. Soc. Rev., 2014, 43, 6894–6905 RSC.
- V. Chandrasekhar, S. Biswas, S. Das, J. Acharya, V. Kumar, J. Leusen, J. M. Herrera, P. Koegerler and E. Colacio, Chem. – Eur. J., 2017, 23, 5145–5170 CrossRef PubMed.
- A. Ikeda and S. Shinkai, Chem. Rev., 1997, 97, 1713–1734 CrossRef CAS PubMed.
- N. Morohashi, F. Narumi, N. Iki, T. Hattori and S. Miyano, Chem. Rev., 2006, 106, 5291–5316 CrossRef CAS PubMed.
- D. R. Stewart and C. D. Gutsche, J. Am. Chem. Soc., 1999, 121, 4136–4146 CrossRef CAS.
- C. D. Gutsche, Calixarenes, Royal Society of Chemistry, Cambridge, 2008 Search PubMed.
- F. Chen, T. Tanaka, Y. Hong, W. Kim, D. Kim and A. Osuka, Chem. – Eur. J., 2016, 22, 10597–10606 CrossRef CAS PubMed.
- Z.-A. Huang, C. Chen, X.-D. Yang, X.-B. Fan, W. Zhou, C.-H. Tung, L.-Z. Wu and H. Cong, J. Am. Chem. Soc., 2016, 138, 11144–11147 CrossRef CAS PubMed.
- T. Josse, J. De Winter, P. Gerbaux and O. Coulembier, Angew. Chem., Int. Ed., 2016, 55, 13944–13958 CrossRef CAS PubMed.
- T. Kim, N. Singh, J. Oh, E.-H. Kim, J. Jung, H. Kim and K.-W. Chi, J. Am. Chem. Soc., 2016, 138, 8368–8371 CrossRef CAS PubMed.
- G. Trinquier and J.-P. Malrieu, Chem. – Eur. J., 2015, 21, 814–828 CrossRef CAS PubMed.
- T. Ogoshi, T. Yamagishi and Y. Nakamoto, Chem. Rev., 2016, 116, 7937–8002 CrossRef CAS PubMed.
- M. Vale, M. Pink, S. Rajca and A. Rajca, J. Org. Chem., 2008, 73, 27–35 CrossRef CAS PubMed.
- A. Rajca, S. Rajca and S. R. Desai, J. Am. Chem. Soc., 1995, 117, 806–816 CrossRef CAS.
- S. Nobusue, H. Miyoshi, A. Shimizu, I. Hisaki, K. Fukuda, M. Nakano and Y. Tobe, Angew. Chem., Int. Ed., 2015, 54, 2090–2094 CrossRef CAS PubMed.
- S. Das, T. S. Herng, J. L. Zafra, P. M. Burrezo, M. Kitano, M. Ishida, T. Y. Gopalakrishna, P. Hu, A. Osuka, J. Casado, J. Ding, D. Casanova and J. Wu, J. Am. Chem. Soc., 2016, 138, 7782–7790 CrossRef CAS PubMed.
- B. K. Hughes, W. A. Braunecker, D. C. Bobela, S. U. Nanayakkara, O. G. Reid and J. C. Johnson, J. Phys. Chem. Lett., 2016, 7, 3660–3665 CrossRef CAS PubMed.
- T. Kusamoto, Y. Hattori, A. Tanushi and H. Nishihara, Inorg. Chem., 2015, 54, 4186–4188 CrossRef CAS PubMed.
- T. Kusamoto, S. Kimura and H. Nishihara, Chem. Lett., 2016, 45, 1057–1059 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921–2922 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. Stephen Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- O. A. Vydrov, J. Heyd, A. V Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 74106–74109 CrossRef PubMed.
- O. A. Vydrov, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2007, 126, 154109 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1024 CrossRef CAS.
- I. de P. R. Moreira and F. Illas, Phys. Chem. Chem. Phys., 2006, 8, 1645–1659 RSC.
- P. Rivero, I. de P. R. Moreira and F. Illas, J. Phys.: Conf. Ser., 2008, 117, 12025 CrossRef.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS PubMed.
- I. de P. R. Moreira, C. J. Calzado, J. P. Malrieu and F. Illas, New J. Phys., 2007, 9, 369 CrossRef.
- D. Reta Mañeru, A. K. Pal, I. D. P. R. Moreira, S. N. Datta and F. Illas, J. Chem. Theory Comput., 2014, 10, 335–345 CrossRef PubMed.
- R. Gaudenzi, E. Burzurí, D. Reta, I. de P. R. Moreira, S. T. Bromley, C. Rovira, J. Veciana and H. S. J. van der Zant, Nano Lett., 2016, 16, 2066–2071 CrossRef CAS PubMed.
- R. Gaudenzi, J. de Bruijckere, D. Reta, I. de P. R. Moreira, C. Rovira, J. Veciana, H. S. J. van der Zant and E. Burzurí, ACS Nano, 2017, 11, 5879–5883 CrossRef CAS PubMed.
- I. Alcón, D. Reta, I. de P. R. Moreira and S. T. Bromley, Chem. Sci., 2017, 8, 1027–1039 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp04145d |
| This journal is © the Owner Societies 2017 |