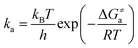DOI:
10.1039/D1MH00552A
(Communication)
Mater. Horiz., 2022,
9, 334-341
A computational scheme for evaluating the phosphorescence quantum efficiency: applied to blue-emitting tetradentate Pt(II) complexes†
Received
3rd April 2021
, Accepted 1st July 2021
First published on 2nd July 2021
Abstract
Phosphorescent organic light-emitting diodes (PhOLEDs) are leading candidates for displays or lighting technologies. Recently, blue phosphorescent tetradentate Pt(II) complexes have been attracting extensive attention due to their high phosphorescence quantum efficiency and numerous chemical structures on account of flexible ligand frames and modifications. Using quantum chemistry coupled with our thermal vibration correlation function (TVCF) formalism, we investigated the triplet excited state energy surface and the decay processes involving both direct vibrational relaxation and minimum energy crossing point (MECP) via the transition state (3TS) to the ground state (S0) for 16 recently experimentally reported blue-emitting tetradentate Pt(II) emitters containing fused 5/6/6 metallocycles. We found that (i) in most cases, the direct vibrational relaxation deactivations dominated the triplet non-radiative decay because either the 3TS is too high or the MECP is not reachable. Hence, results from the TVCF formalism agreed well with the experiments for the phosphorescence quantum efficiency; (ii) only when both 3TS and MECP are low, for instance, for PtON1-oMe, deactivations via MECP dominated the triplet non-radiative decay.
New concepts
Organometallic complexes have been widely applied in phosphorescent organic light-emitting diodes (PhOLEDs). It is essential to quantitatively predict phosphorescence quantum efficiencies for these light-emitting materials from a theoretical aspect. In this study, we quantitatively calculated all possible triplet decay rates for a series of newly developed blue-emitting tetradentate Pt(II) complexes under the framework of thermal vibration correlation function (TVCF) and transition state theory (TST). For blue-emitting organometallic complexes, it was generally believed that the metal-centered (MC) state is the leading deactivation channel. We found for the first time that commonly for newly developed Pt-complexes, deactivation channel via MC is usually prohibited due to either the transition state 3TS is too high or the minimum energy crossing point (MECP) is unreachable. Therefore, the TVCF framework can serve as an efficient and accurate tool in evaluating phosphorescence quantum efficiencies for blue-emitting tetradentate Pt complexes.
|
Introduction
Phosphorescent organic light-emitting diodes (PhOLEDs) are the most employed components in the organic electronics industry.1–3 Phosphorescent emitters, including cyclometalated Ir(III) and Pt(II) complexes, have attracted considerable attention due to the 100% electroluminescence internal quantum efficiency (IQE) caused by strong spin–orbit coupling effects that could efficiently harness both singlet and triplet excitons.4–6 However, the development of highly efficient deep-blue organometallic emitters is still of significant challenge, mainly due to their attainable metal-centered d–d quenching states.7,8 Recently, a rapid progress has been made in the development of efficient deep-blue OLEDs employing Pt(II) complexes that have met or even exceeded the performance of Ir(III) complexes in many aspects.9,10 On the one hand, Pt(II) complexes have demonstrated phosphorescence quantum efficiencies (Φp) close to unity and a short luminescence lifetime in the range of microseconds at room temperature, thus making them advantageous as phosphorescent emitters.11 On the other hand, square planar Pt(II) complexes have multiple chemical structures that could be assigned with various frames of ligands, including bidentate, tridentate, and tetradentate ligand scaffolds.12–14 Typically, Pt(II) complexes with bidentate or tridentate ligands suffer from low quantum efficiencies or poor stabilities owing to their readily distorted geometries or monoanionic ligands.15,16 In contrast, Pt(II) complexes with a tetradentate ligand frame, which afford rigid structural scaffolds, exhibit high Φp as well as good thermal and electrochemical stabilities.17 Given the diverse metallocycle arrangements, several types of tetradentate Pt(II) complexes have been developed by now. It is noteworthy to mention that tetradentate Pt(II) complexes with 5/6/5 or 5/5/6 fused metallocycles exhibit planar molecular geometries and are apt to form excimer emissions, enabling them to act as ideal emitters for single-doped white OLEDs.18 Correspondingly, tetradentate Pt(II) complexes with 5/6/6 or 6/6/6 fused metallocycles are more twisty in structure that prevent intermolecular interactions, thereby making them suitable for monochromic luminescence.19,20 In this study, sixteen blue-emitting tetradentate Pt(II) emitters containing fused 5/6/6 metallocycles that have been synthesized and characterized in experiments were chosen for theoretical investigations, as shown in Scheme 1.21–24 These tetradentate Pt(II) emitters are similar in structure yet different in monomeric photophysical properties.
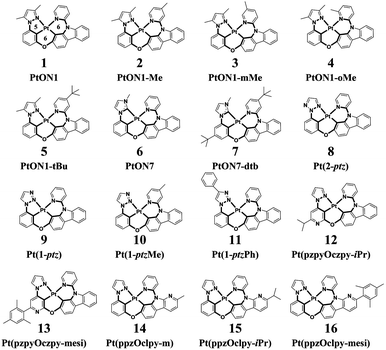 |
| | Scheme 1 Structures of 16 blue-emitting tetradentate Pt(II) emitters containing fused 5/6/6 metallocycles. (2-ptz = 2-phenyl-1,2,3-triazole; 1-ptz = 1-phenyl-1,2,3-triazole; ppz = phenyl-pyrazol; pzpy = pyrazol-pyridine; czpy = pyridyl-carbazole; clpy = pyridyl-carboline; iPr = iso propyl; mesi = mesityl) | |
The photophysical model adopted in this study is depicted in Scheme 2. The electro-pumped carriers form the lowest triplet excited state, which would undergo several processes. The radiative decay rate for a two-level system could be evaluated by the Einstein spontaneous emission rate as 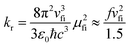 , which ranges ∼102−6 s−1 for phosphorescent with μfi (f), the cross spin–manifold transition electric dipole moment (oscillator strength) between the initial and final states to give rise to photon with transition energy νfi in wavenumber. When vibrational levels were considered, a more elaborated formula was given by eqn (1). Within the harmonic oscillator approximation, the non-radiative decay rates (knrTVCF) from the triplet emissive state (3ES) to the ground state (S0) can be evaluated via the thermal vibration correlation function (TVCF) rate theory, which was earlier developed by us, in combination with the quantum chemistry calculations for relevant molecular parameters. This theory has been demonstrated to be precise and efficient in numerous cases if the potential energy surface crossing effects can be ignored.25–28 For organometallic compounds, the metal-centered (3MC) states could play an essential role in triplet deactivations. Among the complexes considered in this study, the most significant geometry change in the processes of 3ES → 3MC → MECP is the variations in the dihedral angle N1–C1–N2–C2, and soft scans of the lowest triplet excited states over this dihedral angle in complex 1 are depicted in Fig. S1 (ESI†), which illustrates that the non-radiative decay including 3MC is beyond the harmonic region. In such cases, the additional non-radiative decay rate knrMC (beyond the harmonic region) should be considered and be quantitatively evaluated via a kinetic model, involving equilibration between 3ES and 3MC states before irreversible return to the S0 state.29,30 More details can be found under the “Methods” section. The calculated phosphorescence quantum efficiencies without and with considerations of knrMC are expressed as ΦpTVCF = kr/(kr + knrTVCF) and ΦpMC = kr/(kr + knrTVCF + knrMC), respectively. This study will show that only one complex, PtON1-oMe, possesses both low 3TS (transition states between 3ES and 3MC) and MECP, contributing considerably to the triplet deactivations. In principle, ΦpMC is more general than ΦpTVCF, but MC is much more complicated to evaluate. For the rest of the blue-emitting tetradentate Pt(II) complexes, phosphorescence efficiencies calculated via the TVCF framework (ΦpTVCF) are comparable with experimental measurements owing to their unreachable 3TS or MECP.
, which ranges ∼102−6 s−1 for phosphorescent with μfi (f), the cross spin–manifold transition electric dipole moment (oscillator strength) between the initial and final states to give rise to photon with transition energy νfi in wavenumber. When vibrational levels were considered, a more elaborated formula was given by eqn (1). Within the harmonic oscillator approximation, the non-radiative decay rates (knrTVCF) from the triplet emissive state (3ES) to the ground state (S0) can be evaluated via the thermal vibration correlation function (TVCF) rate theory, which was earlier developed by us, in combination with the quantum chemistry calculations for relevant molecular parameters. This theory has been demonstrated to be precise and efficient in numerous cases if the potential energy surface crossing effects can be ignored.25–28 For organometallic compounds, the metal-centered (3MC) states could play an essential role in triplet deactivations. Among the complexes considered in this study, the most significant geometry change in the processes of 3ES → 3MC → MECP is the variations in the dihedral angle N1–C1–N2–C2, and soft scans of the lowest triplet excited states over this dihedral angle in complex 1 are depicted in Fig. S1 (ESI†), which illustrates that the non-radiative decay including 3MC is beyond the harmonic region. In such cases, the additional non-radiative decay rate knrMC (beyond the harmonic region) should be considered and be quantitatively evaluated via a kinetic model, involving equilibration between 3ES and 3MC states before irreversible return to the S0 state.29,30 More details can be found under the “Methods” section. The calculated phosphorescence quantum efficiencies without and with considerations of knrMC are expressed as ΦpTVCF = kr/(kr + knrTVCF) and ΦpMC = kr/(kr + knrTVCF + knrMC), respectively. This study will show that only one complex, PtON1-oMe, possesses both low 3TS (transition states between 3ES and 3MC) and MECP, contributing considerably to the triplet deactivations. In principle, ΦpMC is more general than ΦpTVCF, but MC is much more complicated to evaluate. For the rest of the blue-emitting tetradentate Pt(II) complexes, phosphorescence efficiencies calculated via the TVCF framework (ΦpTVCF) are comparable with experimental measurements owing to their unreachable 3TS or MECP.
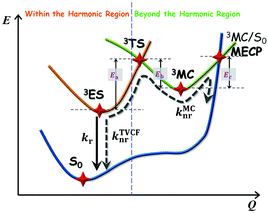 |
| | Scheme 2 Schematic representation of the competing excited-state deactivations of Pt(II) complexes. kr and knrTVCF are the radiative and non-radiative decay rates from the triplet emissive state (3ES) to the ground state (S0) within the harmonic region, and knrMC is the thermally activated nonradiative decay rate beyond the harmonic region. Ea, Eb, and Ec are the electronic energy barriers among 3ES, 3TS, 3MC, and MECP states (3TS represents the transition state between 3ES and 3MC states, and MECP is the S0/3MC minimum energy crossing point). | |
Methods
The vibrational relaxation decay rates of kr and knrTVCF are calculated via a home-built MOMAP program.31kr can be obtained by the integration over the whole range of the emission spectrum:32| | 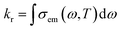 | (1) |
where| | 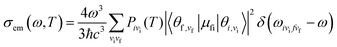 | (2) |
μfi = 〈Φf|![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) |Φf〉 is the electric transition dipole moment between the final and initial electronic states; Pivi is the Boltzmann distribution function for the initial state vibration manifold; Φ and θ are the electronic and vibrational wavefunctions, respectively. Under the Franck–Condon approximation, the emission spectra σe,m(ω,T) in TVCF formalism can be expressed as:
|Φf〉 is the electric transition dipole moment between the final and initial electronic states; Pivi is the Boltzmann distribution function for the initial state vibration manifold; Φ and θ are the electronic and vibrational wavefunctions, respectively. Under the Franck–Condon approximation, the emission spectra σe,m(ω,T) in TVCF formalism can be expressed as:| | 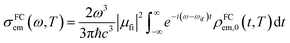 | (3) |
where ρem,0FC(t,T) is the TVCFs and can be formulated as 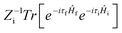 , which can be analytically solved by multidimensional Gaussian integrations; τi = −iβ − t/ħ; τf = t/ħ; β = (kBT)−1 and Ĥf (Ĥi) is the harmonic oscillator Hamiltonian of the final (initial) electronic states. As for knrTVCF, which is the non-radiative decay rate within the harmonic region, can be expressed as:26
, which can be analytically solved by multidimensional Gaussian integrations; τi = −iβ − t/ħ; τf = t/ħ; β = (kBT)−1 and Ĥf (Ĥi) is the harmonic oscillator Hamiltonian of the final (initial) electronic states. As for knrTVCF, which is the non-radiative decay rate within the harmonic region, can be expressed as:26| | 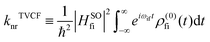 | (4) |
where HfiSO = 〈Φf|ĤSOC|Φi〉 is the spin–orbit coupling matrix between two electronic states; ρ(0)fi(t) is the same with ρFCem,0(t,T).
For the calculation of knrMC that is beyond the harmonic region, a kinetic model, which assumes equilibrium between the 3ES and 3MC states before irreversible return to the ground state, is employed as 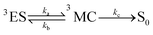 . Using the steady-state approximation, the kMCnr can be expressed as
. Using the steady-state approximation, the kMCnr can be expressed as
| | 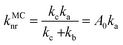 | (5) |
where
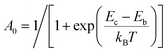
(
Eb and
Ec being the electronic energy barriers, as shown in
Scheme 2) and
ka can be evaluated
via the transition state theory (TST) Eyring equation as:
33| | 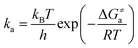 | (6) |
where Δ
Ga≠ is the Gibbs free energy of activation between
3ES and
3TS states, which was evaluated using the Shermo program;
34kB is the Boltzmann's constant,
h is the Planck's constant, and
T is the temperature (
T = 298 K).
As appeared in the above formula eqn ((1)–(6)), there contained numerous molecular parameters, including electronic structures and vibrational modes as well as their couplings. These were evaluated with the density functional theory (DFT) and time-dependent DFT (TDDFT), as implemented in the Gaussian16 software.35 Geometry optimizations were performed for the S0, 3ES, 3TS, and 3MC states, as well as the S0/3MC minimum energy crossing point (MECP) with the hybrid Perdew–Burke–Ernzerhof (PBE0)36 functional in combination with the third version of Grimme's atom pair–wise dispersion corrections with Becke–Johnson damping (D3BJ).37,38 The 3MC states are searched by rotating the aromatic rings containing the N–Pt coordination bond in the tetradentate ligand scaffold on account of strong electronic repulsion between the metal and nitrogen atom when the electronic excitation is of metal-centered character. The MECPs were optimized by the sobMECP program.39 All structural optimizations were carried out using a polarizable continuum model (PCM) taking solvent effects into account.40 The unrestricted formalism was used for the geometry optimizations of triplet states. Vibrational frequency calculations at the same level of the theory for geometry were conducted to affirm the nature of the stationary points of geometries. For S0, 3ES and 3MC minimum states, there was no imaginary frequency, while for 3TS states, there exists one mode with an imaginary frequency. The basis set combining with Stuttgart Dresden ECP (SDD)41 is chosen for heavy atom Pt(II), and the 6-31G** basis set is adopted for light atoms. Four kinds of functionals, namely PBE0, M06,42 M062X,42 and PBE38,37 were employed for triplet-emitting spectral calculations, and PBE38 was chosen as the most suitable one. All single-point calculations were calculated via PBE38 functional, with the same basis sets as optimizations. Spin–orbit coupling (SOC) of singlet and triplet states calculations are carried out with the PySOC package.43 The Dalton program44,45 was employed for the calculations of the 3ES → S0 transition dipole moment μfi at the B3LYP46,47/6-31g**/SDD theoretical level. The hole–electron distribution analysis for 3ES → S0 excitations was conducted by the Multiwfn program.48,49
Results and discussion
Triplet excitation properties
First, geometries of S0 and 3ES states for these 16 tetradentate Pt(II) complexes are optimized via PBE0 functional, which has been demonstrated accurately for Pt(II) complex optimizations in numerous documents.15,16,50 Next, triplet emission properties were evaluated with four different functionals. The triplet emission peaks in solutions of experimental and theoretical results are given in Table 1. It can be seen that PBE38 functional has the least mean absolute error (MAE), which was chosen for the triplet emission property calculations.
Table 1 Experimental and computational results of triplet emission peaks for 16 chosen Pt(II) complexes in solutions at their optimized 3ES geometries
|
|
λ
em
(nm,exp) |
λ
em
(eV,exp) |
λ
em (eV,PBE38) |
λ
em (eV,PBE0) |
λ
em (eV,m06) |
λ
em (eV,m062x) |
|
Experimental results of 1–7 are from ref. 21 in CH2Cl2, of 8–11 are from ref. 22 in 2-MeTHF, of 12 and 13 are from ref. 23 in CH2Cl2, of 14–16 are from ref. 24 in CH2Cl2, respectively.
|
|
1
|
478 |
2.5941 |
2.8404 |
2.4999 |
2.4919 |
3.1629 |
|
2
|
444 |
2.7928 |
2.6619 |
2.5875 |
2.5599 |
2.9569 |
|
3
|
476 |
2.6050 |
2.8471 |
2.5226 |
2.5089 |
3.1435 |
|
4
|
450 |
2.7556 |
2.9021 |
2.5990 |
2.5935 |
3.1989 |
|
5
|
444 |
2.7928 |
2.6644 |
2.5892 |
2.5601 |
2.9586 |
|
6
|
452 |
2.7434 |
2.8619 |
2.5300 |
2.5245 |
3.1861 |
|
7
|
446 |
2.7803 |
2.9303 |
2.5994 |
2.5926 |
3.2549 |
|
8
|
464 |
2.6724 |
2.7297 |
2.4607 |
2.4242 |
3.0889 |
|
9
|
468 |
2.6496 |
2.6723 |
2.4047 |
2.3648 |
3.0170 |
|
10
|
476 |
2.6050 |
2.6694 |
2.4008 |
2.3603 |
3.0135 |
|
11
|
480 |
2.5833 |
2.6206 |
2.3677 |
2.3287 |
2.9481 |
|
12
|
456 |
2.7193 |
2.6959 |
2.5326 |
2.4977 |
2.9637 |
|
13
|
458 |
2.7074 |
2.6659 |
2.5111 |
2.4753 |
2.9412 |
|
14
|
466 |
2.6609 |
2.4738 |
2.4228 |
2.3950 |
2.7571 |
|
15
|
464 |
2.6724 |
2.4747 |
2.4240 |
2.3943 |
2.7548 |
|
16
|
481 |
2.5780 |
2.3644 |
2.3083 |
2.2779 |
2.6343 |
|
MAE
|
0.1279 |
0.1993 |
0.2255 |
0.3051 |
The tetradentate ligand is divided into three parts, as shown in Fig. 1a, for the sake of analysis. Fig. 1b presents the calculated hole–electron distributions of 3ES → S0 excitations for Pt(II) complexes, where red represents the hole distribution and green represents the electron distribution. Transition characters of 3ES → S0 processes for these Pt(II) complexes are dominated by the triplet ligand to ligand charge transfer (3LLCT) or intraligand (3IL), mixed with metal to ligand charge transfer (3MLCT), as listed in Table 2. Comparing complexes 1–5, the introduction of an electron-donating group such as methyl or tertiary butyl on the para position of pyridine (just as 2 and 5) decreases charge distributions on the L1 part efficiently, whereas the introduction of a methyl group on the meta or ortho position of pyridine has no such effect. Note that introducing tertiary butyl on the para position of pyridine within complex 7, whereby the L3 part (imidazole carbene) is different from that (pyrazole) in complexes 1–5, cannot decrease electron distributions on the L1 part. The 3ES → S0 excitations listed in Table S1 (ESI†) show that coefficients in the configuration interaction expansions are higher than 10% for seven representative complexes. Comparing 2 and 7, it was found that both of them have an electron-donating group substituted on the para position of pyridine in the L1 part, although their spatial distributions of the highest occupied molecular orbital (HOMO) are similar, while their spatial distributions of the lowest unoccupied molecular orbital (LUMO) are quite different, as depicted in Fig. S2 (ESI†). For complex 2, the LUMO was diffused over the whole molecule, while for 7, it was more localized on the L1 partowing to the stronger electron-donating capability of imidazole carbene in complex 7 that prevented charge diffusions.
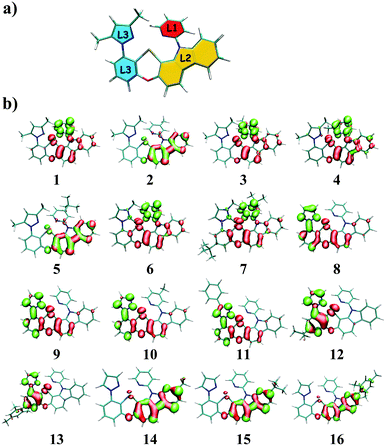 |
| | Fig. 1 (a) The tetradentate ligand was divided into three parts, namely L1 (red), L2 (yellow), and L3 (blue); (b) distributions of hole and electron of 3ES → S0 excitations for Pt(II) complexes in this study (isovalue = 0.002), where red represents the hole distribution and green represents the electron distribution. | |
Table 2 The electron–hole difference of atom Pt, L1, L2, and L3 parts of Pt(II) complexes as well as transition characters of 3ES → S0 processes. (3L2L1CT means charge transfer from L2 to L1; 3IL2 means intraligand character centered on the L2 part)
|
|
ΔPt % |
ΔL1 % |
ΔL2 % |
ΔL3 % |
Character |
|
1
|
−13.32 |
57.85 |
−39.48 |
0.28 |
3L2L1CT/3MLCT |
|
2
|
−2.31 |
5.61 |
1.06 |
−0.15 |
3IL2/3MLCT |
|
3
|
−12.57 |
56.26 |
−40.54 |
1.03 |
3L2L1CT/3MLCT |
|
4
|
−10.89 |
43.77 |
−30.18 |
1.81 |
3L2L1CT/3MLCT |
|
5
|
−2.61 |
5.81 |
1.07 |
−0.10 |
3IL2/3MLCT |
|
6
|
−10.87 |
49.73 |
−30.89 |
−1.32 |
3L2L1CT/3MLCT |
|
7
|
−12.97 |
45.79 |
−22.03 |
−4.01 |
3L2L1CT/3MLCT |
|
8
|
−7.81 |
1.31 |
−22.91 |
40.56 |
3L2L3CT/3MLCT |
|
9
|
−12.48 |
0.79 |
−24.67 |
46.43 |
3L2L3CT/3MLCT |
|
10
|
−12.52 |
0.03 |
−24.20 |
46.80 |
3L2L3CT/3MLCT |
|
11
|
−14.75 |
0.34 |
−20.64 |
43.40 |
3L2L3CT/3MLCT |
|
12
|
−14.33 |
−0.09 |
−3.11 |
21.62 |
3IL3/3MLCT |
|
13
|
−12.97 |
0.13 |
−2.72 |
19.90 |
3IL3/3MLCT |
|
14
|
−2.03 |
1.67 |
5.34 |
−1.31 |
3IL2/3MLCT |
|
15
|
−1.85 |
1.43 |
5.43 |
−1.40 |
3IL2/3MLCT |
|
16
|
−1.78 |
1.56 |
5.01 |
−1.61 |
3IL2/3MLCT |
When the pyrazole moiety in the L3 part was replaced with triazole, like complexes 8–11, the electron distribution was mainly concentrated on the L3 part. Comparing complexes 1 and 8, it was found that both of them were dominated by H → L transition in 3ES → S0 excitations, as shown in Table S1 (ESI†). However, on account of the stronger electron-withdrawing ability of triazole in complex 8, the spatial distribution of LUMO in 8 spread mainly over the L3 part, while the LUMO of 1 was primarily localized on the L1 part, as shown in Fig. S2 (ESI†).
For complexes 12 and 13, in which the phenyl moiety in the L3 part was replaced with pyridine, the electron distributions were also mainly localized on the L3 part. Since pyridine is more electron-withdrawing than phenyl, the LUMO of 12 is mainly distributed on the L3 part, as presented in Fig. S2 (ESI†). When the carbazole group in the L2 part was replaced by the carboline moiety, which is less electron-donating, the transitions of 3ES → S0 are typically concentrated on the L2 part, as exhibited in complexes 14–16.
Radiative and non-radiative decay within the harmonic region
The calculated kr and knrTVCFvia the TVCF framework are listed in Table 3. Critical parameters relating to kr and knrTVCF, including 3ES → S0 adiabatic energy difference (ΔEad), transition dipole moment (μtran.), spin–orbit coupling (SOC) and reorganization energies (Reorg.), are also laid out in Table 3. It can be seen that the calculated radiative decay rates kr (cal.) have the same order of magnitude of experimental results kr (exp.), which is in the range of 104 s−1–105 s−1, indicating the reliability of the TVCF method, which is the first principle without any empirical parameters.
Table 3 Calculated adiabatic energy difference between 3ES and S0 states (ΔEad), transition dipole of 3ES → S0 processes (μtran.), spin–orbit coupling between 3ES and S0 states (SOC), reorganization energies of 3ES → S0 processes (Reorg.), kr (cal.) and knrTVCF (cal.) of 3ES → S0 processes within the harmonic region, as well as experimental results of kr (exp.)
|
|
ΔEad (eV) |
μ
tran. (Debye) |
SOC (cm−1) |
Reorg. (cm−1) |
k
r (s−1, cal.) |
k
nr
TVCF (s−1, cal.) |
k
r
(s−1, exp.) |
|
Experimental results of 1–7 are from ref. 21 in CH2Cl2, of 8–11 are from ref. 22 in 2-MeTHF, of 12–13 are from ref. 23 in CH2Cl2, of 14–16 are from ref. 24 in CH2Cl2, respectively.
|
| 1 |
3.21 |
0.30 |
215 |
2144 |
3.16 × 105 |
3.19 × 103 |
2.15 × 105 |
| 2 |
2.99 |
0.20 |
68 |
2047 |
1.06 × 105 |
1.10 × 104 |
8.90 × 104 |
| 3 |
3.20 |
0.32 |
208 |
2096 |
3.39 × 105 |
9.33 × 104 |
2.34 × 105 |
| 4 |
3.22 |
0.36 |
121 |
1952 |
4.75 × 105 |
2.92 × 102 |
1.77 × 104 |
| 5 |
2.99 |
0.19 |
69 |
1787 |
9.88 × 104 |
1.12 × 104 |
1.07 × 105 |
| 6 |
3.18 |
0.24 |
121 |
1892 |
1.89 × 105 |
1.10 × 103 |
1.86 × 105 |
| 7 |
3.24 |
0.24 |
117 |
1788 |
2.07 × 105 |
3.53 × 104 |
1.57 × 105 |
| 8 |
3.04 |
0.33 |
118 |
2024 |
3.42 × 105 |
9.27 × 101 |
1.89 × 105 |
| 9 |
2.99 |
0.34 |
164 |
2063 |
3.42 × 105 |
6.61 × 102 |
2.77 × 105 |
| 10 |
2.99 |
0.35 |
171 |
2072 |
3.56 × 105 |
8.13 × 102 |
7.14 × 105 |
| 11 |
2.94 |
0.37 |
183 |
2091 |
3.73 × 105 |
1.14 × 104 |
2.70 × 105 |
| 12 |
2.81 |
0.33 |
81 |
1982 |
3.27 × 105 |
5.49 × 102 |
2.40 × 105 |
| 13 |
3.00 |
0.31 |
81 |
2203 |
2.77 × 105 |
7.80 × 102 |
2.40 × 105 |
| 14 |
2.86 |
0.08 |
54 |
2572 |
1.42 × 104 |
8.07 × 104 |
3.00 × 104 |
| 15 |
2.86 |
0.08 |
54 |
2585 |
1.42 × 104 |
2.85 × 104 |
8.00 × 104 |
| 16 |
2.78 |
0.08 |
49 |
3185 |
1.17 × 104 |
1.48 × 104 |
1.00 × 105 |
To investigate the processes of non-radiative decay within the harmonic region, the reorganization energies of 3ES → S0 are further decomposed into internal coordinates, namely bond lengths, bond angles and dihedral angles. The internal coordinates with the first five highest contributions to the total reorganization energies are depicted in Fig. S3 (ESI†). It is interesting to note that the area of these internal coordinate vibrations exactly corresponds to the electron distribution of each complex, as shown in Fig. 1b. For example, the electron distributions are focused on the L1 part in complex 1, so that its bond length stretching vibrations contributing the most to total reorganization energies were also located on the L1 region. There has been a general correlation between the absolute amount of charge transfer on metal Pt atom in 3ES → S0 processes (|ΔPt| %) and SOC values, except for complexes 12 and 13, as shown in Fig. 2. Comparing 10–13, although they have nearly the same |ΔPt| %, the SOC of 10 and 11 is more than two orders of magnitude larger than that of 12 and 13. It is because the excitation coefficients of H → L in 10 and 11 (∼0.8) are higher than that in 12 and 13 (∼0.6) in 3ES → S0 processes (see Table S2, ESI†), as SOC integrals are proportional to the excitation coefficients and coefficients of AO basis.51 Note that when the carbazole group in the L2 part was replaced by the carboline moiety as in 14–16, |ΔPt| % decreased the most, thus leading to small SOC. The reorganization energies of 3ES → S0 for these 16 blue-emitting tetradentate Pt(II) complexes were less than 0.4 eV, and together with SOC ranging from 49 cm−1 to 215 cm−1, their non-radiative decay rates of 3ES → S0 within the harmonic region were less than 105 s−1 (knrTVCF < 105 s−1).
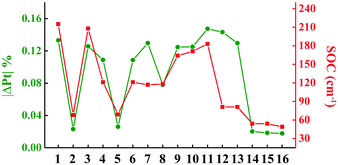 |
| | Fig. 2 Line graphs of calculated the absolute amount of charge transfer in 3ES → S0 processes on Pt atom (|ΔPt| %) and SOC values for 16 Pt(II) complexes. | |
Non-radiative decay beyond the harmonic region
As is known, the transfer of thermal population to the 3MC state state from the 3ES is an effective pathway for the nonradiative decay of organometallic complexes, so that the accessibility of the 3MC state can always be expected to have significant impacts on triplet deactivation processes. Herein, 3MC states for all 16 tetradentate Pt(II) complexes were optimized at first, and then 3TS states between 3ES and 3MC states were confirmed. For these 16 Pt(II) complexes, stable 3MC states could be found when rotating the pyridine ring in the L1 part, and the spin density of 3MC states is presented in Fig. S4 (ESI†). As the complexes investigated in this study were highly unsymmetric, more than one MC state should be considered.52 Therefore, for representative complexes 1 and 8–12, stable 3MC’ states of the rotating triazole ring in the L3 part were also found and are shown in Fig. S5 (ESI†). The structures of 3TS states were confirmed by the vibrational displacements of only one imaginary frequency, as depicted in Fig. S6 (ESI†). The displacement vectors of the imaginary frequency in Fig. S6 (ESI†) are all rotational vibrations of the pyridine ring in the L1 part, indicating the rationality of these 3TS states. In addition, the displacement vectors of the imaginary frequency in 3TS’ states for complexes 1, and 8–12 exhibited in Fig. S7 (ESI†) also indicate the reasonability of these 3TS’ states.
The calculated Gibbs free energies (ΔGa≠) for these Pt(II) complexes are listed in Table S3 (ESI†), and the bar graph depicted in Fig. 3 shows that complex 4 (i.e., PtON1-oMe) has the lowest val. According to eqn ((5) and (6)), ka and knrMC can be quantitatively calculated, and the results are listed in Table 4. Complexes except for 1, 3, 4, 6 and 7 have ka of not more than 104 s−1, which are uncompetitive with their kr and knrTVCF; therefore, deactivations via3TS and MECP can be ignored (ka′ was also uncompetitive with kr and knrTVCF for 8–12, as given in Table S4, ESI†). Although ka′ (2.85 × 106 s−1) for complex 1 was comparable to its ka (3.15 × 106 s−1), the MECP’ was so high in energy (Ec = 1.21 eV, as listed in Table S5, ESI†) that the calculated knrMC was only ∼10−14 s−1. Hence, the non-radiative decay via this channel not need be considered. As for 1, 3, 4, 6 and 7, the structures of MECP were optimized by increasing the torsion angle of the L1 part, as shown in Fig. S8 (ESI†). Comparing calculated ΦpTVCF andΦpMC with experimental measurements of Φp (exp.), as shown in Fig. 4, ΦpTVCF was in accordance with Φp (exp.) for the majority of these blue-emitting tetradentate Pt(II) complexes owing to either their high 3TS or unreachable MECP, deactivations via direct vibrational relaxation were dominant (see schematic case in Fig. 5a). Only for complex 4, whereby both 3TS and MECP are low in energy (as the schematic case shown in Fig. 5b), the deactivations beyond the harmonic region must be taken into account. Therefore, the TVCF framework was fairly accurate in the Φp predictions for most of these blue-emitting tetradentate Pt(II) complexes.
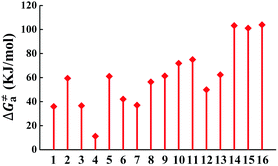 |
| | Fig. 3 Bar graph of the calculated Gibbs free energy (ΔGa≠) of activation energy between 3ES and 3TS. | |
Table 4 Calculated rates (ka) between 3ES and 3TS states, values of knrMC beyond the harmonic region, and calculated phosphorescent quantum yields without considerations of knrMC (ΦpTVCF) and with considerations of knrMC (ΦpMC), as well as experimental measurements Φp (exp.)
|
|
k
a (s−1,cal.) |
k
nr
MC
(s−1,cal.) |
Φ
p
TVCF % |
Φ
p
MC % |
Φ
p
(exp.) % |
|
“—” means there is no need to consider knrMC due to the small ka.
Experimental results of 1–7 are from ref. 21 in CH2Cl2, of 8–11 are from ref. 22 in 2-MeTHF, of 12 and 13 are from ref. 23 in CH2Cl2, of 14–16 are from ref. 24 in CH2Cl2, respectively.
|
|
1
|
3.15 × 106 |
1.95 × 104 |
98.78 |
93.11 |
71.00 |
|
2
|
2.41 × 102 |
— |
90.57 |
90.57 |
89.00 |
|
3
|
2.39 × 106 |
3.83 × 10−11 |
78.44 |
78.44 |
82.00 |
|
4
|
6.70 × 1010 |
8.06 × 105 |
99.94 |
37.05 |
45.00 |
|
5
|
1.22 × 102 |
— |
89.81 |
89.81 |
95.00 |
|
6
|
2.63 × 105 |
1.10 × 103 |
99.42 |
98.29 |
78.00 |
|
7
|
2.99 × 106 |
3.05 × 10−3 |
85.45 |
85.45 |
85.00 |
|
8
|
8.24 × 102 |
— |
99.97 |
99.97 |
100.00 |
|
9
|
1.12 × 102 |
— |
99.81 |
99.81 |
100.00 |
|
10
|
1.55 × 100 |
— |
99.77 |
99.77 |
100.00 |
|
11
|
4.51 × 10−1 |
— |
97.04 |
97.04 |
100.00 |
|
12
|
1.11 × 104 |
— |
99.83 |
99.83 |
95.00 |
|
13
|
7.44 × 101 |
— |
99.72 |
99.72 |
90.00 |
|
14
|
4.99 × 10−6 |
— |
14.95 |
14.95 |
34.00 |
|
15
|
1.20 × 10−5 |
— |
33.21 |
33.21 |
44.00 |
|
16
|
3.85 × 10−6 |
— |
44.20 |
44.20 |
33.00 |
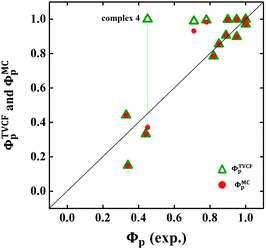 |
| | Fig. 4 Comparison between calculated ΦpTVCF (green hollow triangle) or ΦpMC (red solid circle) and experimental Φp (exp.) for 16 Pt(II) complexes. | |
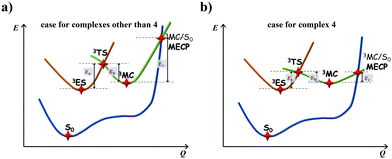 |
| | Fig. 5 Schematic representation of the competing excited-state deactivations of (a) complexes other than 4 that either 3TS is high or MECP is unreachable; (b) complex 4 that both 3TS and MECP are low in energy. | |
Conclusion
In summary, this study presents a computational scheme to evaluate the phosphorescence quantum efficiency by considering all possible triplet deactivation rates. It was applied to 16 blue-emitting tetradentate Pt(II) complexes characterized recently in experiments. Although all these Pt(II) complexes contained fused 5/6/6 metallocycles, their monomeric photophysical properties are dissimilar. Within the harmonic deactivation region, their 3ES → S0 transitions are 3LLCT or 3IL mixed with 3MLCT characters. The calculated kr of these complexes are in the range of 104 s−1–105 s−1, which is consistent with experiments, and the computed non-radiative decay rates within the harmonic region (knrTVCF) are less than 105 s−1. By going beyond the harmonic deactivation region, the structures of 3TS and 3MC are optimized for all complexes, and non-radiative decay rates knrMC are quantitatively calculated. It is noteworthy that for the majority of these tetradentate Pt(II) complexes, the phosphorescence quantum efficiencies within the harmonic region ΦpTVCF are in well accordance with experimental observations. Only for PtON1-oMe, with both 3TS and MECP low in energy, considering knrMC is necessary. Given the accuracy of the TVCF framework, potential valuable blue-emitting tetradentate Pt(II) complexes can be designed and screened out efficiently.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
This work is dedicated to Prof. Seth Marder, a brilliant mind in organic electronic materials chemistry, for his 60th birthday. ZS has been inspired by Seth's sharp mind and persistence in pursuit of science. This work is supported by the National Natural Science Foundation of China (Grant No. 21788102 and 21973099), the Ministry of Science and Technology of China (Grant No. 2017YFA0204501) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB12020200).
Notes and references
- C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048–5051 CrossRef CAS.
- Y. Chi and P.-T. Chou, Chem. Soc. Rev., 2010, 39, 638–655 RSC.
- V. W.-W. Yam, V. K.-M. Au and S. Y.-L. Leung, Chem. Rev., 2015, 115, 7589–7728 CrossRef CAS PubMed.
- I. Omae, Coord. Chem. Rev., 2016, 310, 154–169 CrossRef CAS.
- T. Fleetham, G. Li and J. Li, Adv. Mater., 2017, 29, 1601861 CrossRef PubMed.
- M. Mao, T.-L. Lam, W.-P. To, X. Lao, W. Liu, S. Xu, G. Cheng and C.-M. Che, Adv. Mater., 2021, 33, 2004873 CrossRef CAS PubMed.
- W.-S. Tai, L.-Y. Hsu, W.-Y. Hung, Y.-Y. Chen, C.-L. Ko, X. Zhou, Y. Yuan, A. K.-Y. Jen and Y. Chi, J. Mater. Chem. C, 2020, 8, 13590–13602 RSC.
- T. Fleetham, G. Li, L. Wen and J. Li, Adv. Mater., 2014, 26, 7116–7121 CrossRef CAS PubMed.
- X.-C. Hang, T. Fleetham, E. Turner, J. Brooks and J. Li, Angew. Chem., Int. Ed., 2013, 52, 6753–6756 CrossRef CAS PubMed.
- K. Li, Q. Wan, C. Yang, X.-Y. Chang, K.-H. Low and C.-M. Che, Angew. Chem., Int. Ed., 2018, 57, 14129–14133 CrossRef CAS PubMed.
- K. Li, G. S. Ming Tong, Q. Wan, G. Cheng, W.-Y. Tong, W.-H. Ang, W.-L. Kwong and C.-M. Che, Chem. Sci., 2016, 7, 1653–1673 RSC.
- W.-C. Chen, C. Sukpattanacharoen, W.-H. Chan, C.-C. Huang, H.-F. Hsu, D. Shen, W.-Y. Hung, N. Kungwan, D. Escudero, C.-S. Lee and Y. Chi, Adv. Funct. Mater., 2020, 30, 2002494 CrossRef CAS.
- S. K. Fung, T. Zou, B. Cao, T. Chen, W.-P. To, C. Yang, C.-N. Lok and C.-M. Che, Nat. Commun., 2016, 7, 10655 CrossRef CAS PubMed.
- G. Cheng, Y. Kwak, W.-P. To, T.-L. Lam, G. S. M. Tong, M.-K. Sit, S. Gong, B. Choi, W. Il Choi, C. Yang and C.-M. Che, ACS Appl. Mater. Interfaces, 2019, 11, 45161–45170 CrossRef CAS PubMed.
- A. Heil and C. M. Marian, Inorg. Chem., 2019, 58, 6123–6136 CrossRef CAS PubMed.
- W. H. Lam, E. S.-H. Lam and V. W.-W. Yam, J. Am. Chem. Soc., 2013, 135, 15135–15143 CrossRef CAS PubMed.
- A. Osipov, I. Kim, A. Odinokov, W.-J. Son, A. Yakubovich and H. Choi, J. Phys. Chem. C, 2020, 124, 12039–12048 CrossRef CAS.
- X. Wang, T. Peng, C. Nguyen, Z.-H. Lu, N. Wang, W. Wu, Q. Li and S. Wang, Adv. Funct. Mater., 2017, 27, 1604318 CrossRef.
- W. Zhang, J. Ma, G.-J. Liu, X.-Y. Liu, J. Fan and L.-S. Liao, J. Mater. Chem. C, 2017, 5, 9496–9503 RSC.
- Y. Wu, X. Tan, A. Lv, F. Yu, H. Ma, K. Shen, Z. Sun, F. Chen, Z.-K. Chen and X.-C. Hang, J. Phys. Chem. Lett., 2019, 10, 5105–5110 CrossRef CAS.
- G. Li, A. Wolfe, J. Brooks, Z.-Q. Zhu and J. Li, Inorg. Chem., 2017, 56, 8244–8256 CrossRef CAS PubMed.
- G. Li, X. Zhao, T. Fleetham, Q. Chen, F. Zhan, J. Zheng, Y.-F. Yang, W. Lou, Y. Yang, K. Fang, Z. Shao, Q. Zhang and Y. She, Chem. Mater., 2020, 32, 537–548 CrossRef CAS.
- L. Zhu, W. Xie, C. Qian, W. Xie, K. Shen, A. Lv, H. Ma, H. Li, X.-C. Hang, W. Li, S.-J. Su and W. Huang, Adv. Opt. Mater., 2020, 8, 2000406 CrossRef CAS.
- F. Yu, Y. Sheng, D. Wu, K. Qin, H. Li, G. Xie, Q. Xue, Z. Sun, Z. Lu, H. Ma and X.-C. Hang, Inorg. Chem., 2020, 59, 14493–14500 CrossRef CAS PubMed.
- Q. Peng, Y. Yi, Z. Shuai and J. Shao, J. Am. Chem. Soc., 2007, 129, 9333–9339 CrossRef CAS PubMed.
- Q. Peng, Y. Niu, Q. Shi, X. Gao and Z. Shuai, J. Chem. Theory Comput., 2013, 9, 1132–1143 CrossRef CAS PubMed.
- Q. Peng, Q. Shi, Y. Niu, Y. Yi, S. Sun, W. Li and Z. Shuai, J. Mater. Chem. C, 2016, 4, 6829–6838 RSC.
- Z. Shuai, Chin. J. Chem., 2020, 38, 1223–1232 CrossRef CAS.
- X. Zhang, D. Jacquemin, Q. Peng, Z. Shuai and D. Escudero, J. Phys. Chem. C, 2018, 122, 6340–6347 CrossRef CAS.
- D. Escudero, Chem. Sci., 2016, 7, 1262–1267 RSC.
- Y. Niu, W. Li, Q. Peng, H. Geng, Y. Yi, L. Wang, G. Nan, D. Wang and Z. Shuai, Mol. Phys., 2018, 116, 1078–1090 CrossRef CAS.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef CAS PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- T. Lu and Q. Chen, Comput. Theor. Chem., 2021, 1200 DOI:10.1016/j.comptc.2021.113249.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
-
T. Lu, sobMECP program, 2020, http://sobereva.com/286 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- X. Gao, S. Bai, D. Fazzi, T. Niehaus, M. Barbatti and W. Thiel, J. Chem. Theory Comput., 2017, 13, 515–524 CrossRef CAS PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CAS.
-
Dalton, a molecular electronic structure program, Release v2017.alpha, 2017, http://daltonprogram.org Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- Z. Liu, T. Lu and Q. Chen, Carbon, 2020, 165, 461–467 CrossRef CAS.
- G. S. M. Tong, P. K. Chow, W. P. To, W. M. Kwok and C. M. Che, Chem. – Eur. J., 2014, 6433–6443 CrossRef CAS PubMed.
- Q. Ou and J. E. Subotnik, J. Phys. Chem. C, 2013, 117, 19839–19849 CrossRef CAS.
- S. Arroliga-Rocha and D. Escudero, Inorg. Chem., 2018, 57, 12106–12112 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1mh00552a |
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  b and
Zhigang
Shuai
b and
Zhigang
Shuai
 *a
*a
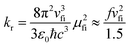 , which ranges ∼102−6 s−1 for phosphorescent with μfi (f), the cross spin–manifold transition electric dipole moment (oscillator strength) between the initial and final states to give rise to photon with transition energy νfi in wavenumber. When vibrational levels were considered, a more elaborated formula was given by eqn (1). Within the harmonic oscillator approximation, the non-radiative decay rates (knrTVCF) from the triplet emissive state (3ES) to the ground state (S0) can be evaluated via the thermal vibration correlation function (TVCF) rate theory, which was earlier developed by us, in combination with the quantum chemistry calculations for relevant molecular parameters. This theory has been demonstrated to be precise and efficient in numerous cases if the potential energy surface crossing effects can be ignored.25–28 For organometallic compounds, the metal-centered (3MC) states could play an essential role in triplet deactivations. Among the complexes considered in this study, the most significant geometry change in the processes of 3ES → 3MC → MECP is the variations in the dihedral angle N1–C1–N2–C2, and soft scans of the lowest triplet excited states over this dihedral angle in complex 1 are depicted in Fig. S1 (ESI†), which illustrates that the non-radiative decay including 3MC is beyond the harmonic region. In such cases, the additional non-radiative decay rate knrMC (beyond the harmonic region) should be considered and be quantitatively evaluated via a kinetic model, involving equilibration between 3ES and 3MC states before irreversible return to the S0 state.29,30 More details can be found under the “Methods” section. The calculated phosphorescence quantum efficiencies without and with considerations of knrMC are expressed as ΦpTVCF = kr/(kr + knrTVCF) and ΦpMC = kr/(kr + knrTVCF + knrMC), respectively. This study will show that only one complex, PtON1-oMe, possesses both low 3TS (transition states between 3ES and 3MC) and MECP, contributing considerably to the triplet deactivations. In principle, ΦpMC is more general than ΦpTVCF, but MC is much more complicated to evaluate. For the rest of the blue-emitting tetradentate Pt(II) complexes, phosphorescence efficiencies calculated via the TVCF framework (ΦpTVCF) are comparable with experimental measurements owing to their unreachable 3TS or MECP.
, which ranges ∼102−6 s−1 for phosphorescent with μfi (f), the cross spin–manifold transition electric dipole moment (oscillator strength) between the initial and final states to give rise to photon with transition energy νfi in wavenumber. When vibrational levels were considered, a more elaborated formula was given by eqn (1). Within the harmonic oscillator approximation, the non-radiative decay rates (knrTVCF) from the triplet emissive state (3ES) to the ground state (S0) can be evaluated via the thermal vibration correlation function (TVCF) rate theory, which was earlier developed by us, in combination with the quantum chemistry calculations for relevant molecular parameters. This theory has been demonstrated to be precise and efficient in numerous cases if the potential energy surface crossing effects can be ignored.25–28 For organometallic compounds, the metal-centered (3MC) states could play an essential role in triplet deactivations. Among the complexes considered in this study, the most significant geometry change in the processes of 3ES → 3MC → MECP is the variations in the dihedral angle N1–C1–N2–C2, and soft scans of the lowest triplet excited states over this dihedral angle in complex 1 are depicted in Fig. S1 (ESI†), which illustrates that the non-radiative decay including 3MC is beyond the harmonic region. In such cases, the additional non-radiative decay rate knrMC (beyond the harmonic region) should be considered and be quantitatively evaluated via a kinetic model, involving equilibration between 3ES and 3MC states before irreversible return to the S0 state.29,30 More details can be found under the “Methods” section. The calculated phosphorescence quantum efficiencies without and with considerations of knrMC are expressed as ΦpTVCF = kr/(kr + knrTVCF) and ΦpMC = kr/(kr + knrTVCF + knrMC), respectively. This study will show that only one complex, PtON1-oMe, possesses both low 3TS (transition states between 3ES and 3MC) and MECP, contributing considerably to the triplet deactivations. In principle, ΦpMC is more general than ΦpTVCF, but MC is much more complicated to evaluate. For the rest of the blue-emitting tetradentate Pt(II) complexes, phosphorescence efficiencies calculated via the TVCF framework (ΦpTVCF) are comparable with experimental measurements owing to their unreachable 3TS or MECP.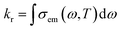
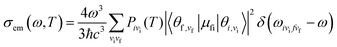
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) |Φf〉 is the electric transition dipole moment between the final and initial electronic states; Pivi is the Boltzmann distribution function for the initial state vibration manifold; Φ and θ are the electronic and vibrational wavefunctions, respectively. Under the Franck–Condon approximation, the emission spectra σe,m(ω,T) in TVCF formalism can be expressed as:
|Φf〉 is the electric transition dipole moment between the final and initial electronic states; Pivi is the Boltzmann distribution function for the initial state vibration manifold; Φ and θ are the electronic and vibrational wavefunctions, respectively. Under the Franck–Condon approximation, the emission spectra σe,m(ω,T) in TVCF formalism can be expressed as: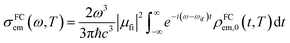
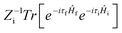 , which can be analytically solved by multidimensional Gaussian integrations; τi = −iβ − t/ħ; τf = t/ħ; β = (kBT)−1 and Ĥf (Ĥi) is the harmonic oscillator Hamiltonian of the final (initial) electronic states. As for knrTVCF, which is the non-radiative decay rate within the harmonic region, can be expressed as:26
, which can be analytically solved by multidimensional Gaussian integrations; τi = −iβ − t/ħ; τf = t/ħ; β = (kBT)−1 and Ĥf (Ĥi) is the harmonic oscillator Hamiltonian of the final (initial) electronic states. As for knrTVCF, which is the non-radiative decay rate within the harmonic region, can be expressed as:26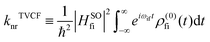
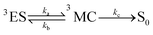 . Using the steady-state approximation, the kMCnr can be expressed as
. Using the steady-state approximation, the kMCnr can be expressed as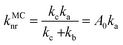
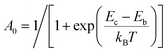 (Eb and Ec being the electronic energy barriers, as shown in Scheme 2) and ka can be evaluated via the transition state theory (TST) Eyring equation as:33
(Eb and Ec being the electronic energy barriers, as shown in Scheme 2) and ka can be evaluated via the transition state theory (TST) Eyring equation as:33