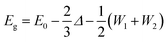Mg₃(Bi,Sb)₂ single crystals towards high thermoelectric performance

Abstract

The rapid growth of the thermoelectric cooler market makes the development of novel room temperature thermoelectric materials of great importance. Ternary n-type Mg₃(Bi,Sb)₂ alloys are promising alternatives to the state-of-the-art Bi₂(Te,Se)₃ alloys but grain boundary resistance is the most important limitation. n-type Mg₃(Bi,Sb)₂ single crystals with negligible grain boundaries are expected to have particularly high zT but have rarely been realized due to the demanding Mg-rich growth conditions required. Here, we report, for the first time, the thermoelectric properties of n-type Mg₃(Bi,Sb)₂ alloyed single crystals grown by a one-step Mg-flux method using sealed tantalum tubes. High weighted mobility ∼140 cm² V⁻¹ s⁻¹ and a high zT of 0.82 at 315 K are achieved in Y-doped Mg₃Bi_1.25Sb_0.75 single crystals. Through both experimental angle-resolved photoemission spectroscopy and theoretical calculations, we denote the origin of the high thermoelectric performance from a point of view of band widening effect and electronegativity, as well as the necessity to form high Bi/Sb ratio ternary Mg₃(Bi,Sb)₂ alloys. The present work paves the way for further development of Mg₃(Bi,Sb)₂ for near room temperature thermoelectric applications.

---

Broader context

There are only few thermoelectric materials show high performance in the temperature range of 300–500 K, especially for the n-type. Bi₂Te₃-based alloys have been the only commercialized thermoelectric alloys for more than 50 years. Searching for thermoelectric materials with high figure of merit at 300–500 K has great significance for low-grade waste-heat recovery and solid-state cooling. In recent years, n-type Mg₃(Bi,Sb)₂ ternary alloys are found to be promising as an alternative for the n-type Bi₂(Te,Se)₃ thermoelectric alloys. Successful growth of the single crystals of n-type Mg₃(Bi,Sb)₂ alloys can enable the investigation of band structure analysis by ARPES, as well as the grain boundary effect on the transport of charge carriers and phonons which greatly affect the room temperature thermoelectric figure of merit. These insights into the fundamental physics of Mg₃(Bi,Sb)₂ alloys could shed light on further strategies for enhancing the thermoelectric performance, and thus promote their application in waste-heat recovery and solid-state cooling.

Introduction

Thermoelectric materials possess great potential in waste heat recovery and as static state Peltier coolers, since they are able to convert heat into electricity and vice versa.^1,2 Application of thermoelectric technology near room temperature offers a great opportunity for energy saving and solid-state cooling.³ Wide application of thermoelectric technology is constrained by the energy conversion efficiency, which is closely related to the material's dimensionless figure of merit zT, defined as zT = α²σT/(κ_L + κ_e), where α, σ, κ_L, κ_e, and T are Seebeck coefficient, electrical conductivity, lattice thermal conductivity, electronic thermal conductivity, and absolute temperature, respectively.^4,5 To date, most good thermoelectric materials achieve peak zT values at middle-to-high temperatures.^6–11 Only a few materials exhibit high zT at or near room temperature, for example, the conventional (Bi,Sb)₂(Te,Se)₃ alloys,^12,13 MgAgSb,^14,15 and the very recently reported n-type Mg₃(Bi,Sb)₂ compounds.^16,17

The high zT in n-type Mg₃(Bi,Sb)₂ alloys stems from the high degeneracy of the conduction band, and the intrinsic low thermal conductivity due to soft and highly anharmonic transverse phonons.^18,19 However, only until recently n-type ternary polycrystalline samples are achieved due to the lack of understanding of the Mg vacancies acting as “electron killers”²⁰ as well as the importance of Bi alloying which advantages electron doping. The remarkable zT, which is greater than 1.5 at high temperatures (700 K),^20,21 has led to extensive studies on Mg₃(Bi,Sb)₂, in which excess Mg is commonly added to compensate for evaporation.^22–26 Then notably in 2018 grain size was found to significantly limit the room temperature mobility as well as the zT.²⁷ Thereafter, room temperature zT values have been considerably enhanced in coarse-grained samples by either increasing the sintering temperature or high temperature annealing.^16,17,28,29 Nevertheless, few n-type single crystals have been reported, and none for ternary solid solutions exhibiting high zT.^30,31

Previously reported Mg₃Bi₂ or Mg₃Sb₂ single crystals are binary compounds that cannot result in high zT. First, they exhibit p-type transport properties as grown under Mg-poor conditions,³² and must later be annealed under Mg-atmosphere to become n-type.³³ Second, even with annealing, it is difficult to obtain ternary Mg₃(Bi,Sb)₂ by starting with Bi or Sb as the flux, as it is difficult to control the Bi/Sb ratio; this results in binary compounds with maximum zT limited to 0.4 at 300 K.³³ Therefore, it would be of great significance to grow n-type ternary Mg₃(Bi,Sb)₂ single crystals for both the understanding of the thermoelectric transport and also further enhancement in the thermoelectric performance. This would enable the experimental investigations of the grain boundary effect (which was proved to inhibit charge carrier mobility at room temperature³⁴) in ternary Mg₃(Bi,Sb)₂ by directly removing the grain boundaries, according to which higher zT is expected for ternary Mg₃(Bi,Sb)₂ single crystals. Furthermore, the successful growth of single crystals provides an opportunity to unravel the band structure of Mg₃(Bi,Sb)₂ by angle-resolved photoemission spectroscopy (ARPES), which can give a deeper understanding of the origin of the excellent thermoelectric performance of Mg₃(Bi,Sb)₂.

In this work, we report the successful growth of n-type ternary Mg₃Bi_1.25Sb_0.75 and binary Mg₃Bi₂ and Mg₃Sb₂ single crystals using a Mg-flux method. A zT of 0.82 is achieved at 315 K in Y-doped Mg₃Bi_1.25Sb_0.75 single crystals, which is much higher than values seen for fine-grained polycrystalline samples. Moreover, the present n-type single crystals grown under the Mg-flux condition avoid adding uncontrollable Mg as in polycrystals, which would be advantageous for the stability of the single crystals. Furthermore, we investigate for the first time the band structure of this material with ARPES. The high thermoelectric performance of Mg₃(Bi,Sb)₂ can be attributed to the large band degeneracy since the lowest conduction band shifts off the high symmetry point. Notably, the alloying of Mg₃Bi₂ and Mg₃Sb₂ is essential for the high thermoelectric performance, not only because of the commonly known alloying effect in reducing thermal conductivity, but more importantly, because Mg₃Bi₂ contributes to higher mobility and Mg₃Sb₂ can enlarge the band gap to suppress the bipolar effect. The present work advances the understanding and development of the important Mg₃(Bi,Sb)₂ thermoelectric alloys in several significant respects, including the evolution of band structure with alloying, the effect of grain boundary on both charge carriers and phonons, as well as a time-saving one-step synthesis of n-type ternary single crystals with high zT at room temperature for cooling applications.

Experimental

Mg₃Bi₂, Mg₃Sb₂, and Mg₃Bi_1.25Sb_0.75 single crystals were grown using a flux method, employing Mg as the flux. Starting elements Mg (pieces, 99.8%), Bi (ingot, 99.9999%) and Sb (shot, 99.9999%) were weighed and mixed with molar ratios of Mg : Bi = 5 : 2, Mg : Sb = 8 : 2 and Mg : Bi : Sb = 11 : 3 : 1, respectively. Approximately 0.2 mol% of yttrium is added as an efficient n-type dopant (to occupy Mg sites) for optimizing electron concentration.^35,36 The mixtures were then sealed in tantalum tubes under a partial pressure of argon in a glove box, where a specially designed tantalum filter is used for the separation of grown crystals and the liquid flux during centrifugation. The tantalum tubes were then sealed in quartz tubes under partial argon pressure. Excess Mg melts prevent the reaction between Sb and Ta, and thus protect the Ta tube and filter. Temperature procedures are as follows: for Mg₃Bi₂, the sample was first heated up to 750 °C for over 30 h, kept for 48 h, then slowly cooled to 600 °C at the rate of 2 °C h⁻¹; for Mg₃Sb₂ and Mg₃Bi₂–Mg₃Sb₂ alloys, samples were first heated up to 900 °C for 30 h, kept for 48 h, then slowly cooled to 700 °C with a rate of 2 °C h⁻¹. Subsequently, single crystals were obtained by removing the liquid flux in a centrifugation process.

The orientation of the single crystals was determined by the backscattering Laue X-ray diffraction method. Chemical compositions were examined by scanning electron microscope (SEM) with an attached energy-dispersive X-ray spectrometer, and results agreed with the nominal compositions. Resistivity and Hall resistivity were measured simultaneously using a physical property measurement system (PPMS, Quantum Design) in the AC transport option. Seebeck coefficient was measured with PPMS, using the thermal transport option with one-heater and two-thermometer configurations. Thermal conductivity was measured in a home-built high vacuum cryostat using the standard four-contact steady-state method. The sample was glued onto the thermal bath with DeltaBond™ 152 adhesive, which is electrically insulating. Temperature gradient was measured with differential AuFe/Chromel thermocouples (Fig. S1, ESI†). All the transport properties were measured in the ab plane. Different samples are measured to check the consistency of the sample quality (Fig. S2, ESI†), since Seebeck coefficient is measured on a sample different from the piece used for resistivity and thermal conductivity measurements. ARPES experiments were carried out at the Berliner Elektronenspeicherring für Synchrotronstrahlung (BESSY) (beamline UE112-PGM-1) with a Scienta Omicron R8000 analyzer, and at beam line 13U of the National Synchrotron Radiation Laboratory with a Scienta Omicron DA30 analyzer. The single crystals were cleaved in situ below 15 K, under a pressure of ∼1 × 10⁻¹⁰ mbar.

The density functional theory (DFT) calculations were performed using projector-augmented wave method as implemented in the Vienna ab initio Simulation Package.^37,38 The exchange and correlation functional was treated by the Perdew–Burke–Ernzerhof (PBE)-generalized gradient approximation.³⁹ The Mg₃Bi_1.25Sb_0.75 was obtained by Special Quasirandom Structure method⁴⁰ in a supercell with 160 atoms (4 × 4 × 2 unit cell). The band structure calculations for Mg₃Bi₂, Mg₃Bi_1.25Sb_0.75 and Mg₃Sb₂ were conducted using the modified Becke–Johnson (mBJ) potential⁴¹ to get more accurate band gaps. Spin–orbit coupling was considered throughout this study. The energy and Hellmann–Feynman force convergences were less than 10⁻⁴ eV and 0.01 eV Å⁻¹, respectively. The Brillouin zones were sampled by an 11 × 11 × 7 Γ-centred k-mesh for the relaxations of Mg₃Bi₂ and Mg₃Sb₂ unit cells. The Fermi surface of Mg₃Bi₂ was calculated with a dense 40 × 40 × 25 k-mesh and plotted with XCrySDen.⁴² The band structure of Mg₃Bi_1.25Sb_0.75 was determined by adopting the band unfolding method.⁴³

Results and discussion

High zT in Mg₃Bi_1.25Sb_0.75 single crystal

n-Type ternary Mg₃(Bi,Sb)₂ single crystals are highly desired for achieving optimal thermoelectric performance at around room temperature. Firstly, only ternary Mg₃(Bi,Sb)₂ compounds show exceptional zT values, instead of binary Mg₃Bi₂ or Mg₃Sb₂. Secondly, zT of this system is found to be strongly affected by the grain size.²⁷Fig. 1(a) summarizes the grain size dependence of electron mobility (μ_H) and lattice thermal conductivity (κ_L) for n-type Mg₃(Bi₂,Sb)₂ polycrystalline samples reported in the literature.^{17,20,27,28,44–46} It is obvious that κ_L is nearly independent of grain size, whereas μ_H exhibits a significant increase with larger grain size. Therefore, the ratio of μ_H/κ_L exhibits a positive correlation with grain size. Along with the independence of Seebeck coefficient on grain boundaries, indicate that single crystals show great potential to exhibit higher zT values.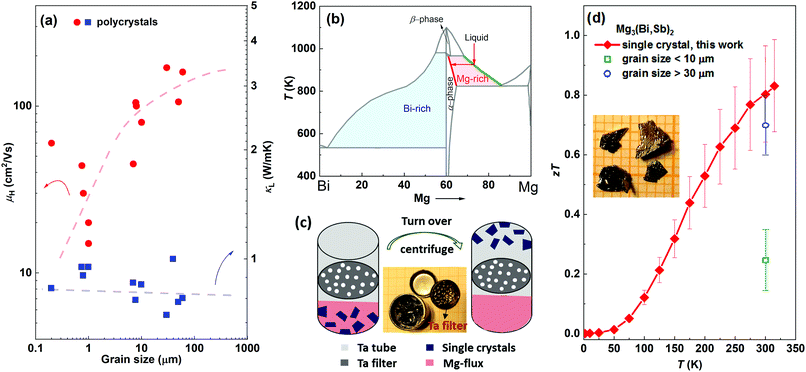

Fig. 1 (a) Charge carrier mobility and lattice thermal conductivity versus grain size for polycrystalline Mg₃(Bi,Sb)₂ samples, the data are collected from the literature.^{17,20,27,28,44–46} Although the data points are scattered, which can be due to different charge carrier concentration and Bi/Sb ratios, or the effects of differing amounts of excess Mg on the sample quality, the trends as guided by the dashed lines are clear. Schematics of (b) Mg–Bi phase diagram, (c) Mg-flux method using a Ta tube with self-designed Ta filter made from a Ta cap. (d) zT of Y-doped Mg₃Bi_1.25Sb_0.75 single crystal (an error bar of 20% is added), with a comparison to the Mg₃(Bi,Sb)₂ polycrystalline samples whose grain sizes are larger than 30 μm (blue) and below 10 μm (green).^{17,20,27,28,44–46} The inset image shows the single crystals.

The difficulties in growing n-type Mg₃(Bi₂,Sb)₂ single crystals lie in the complexity of the phase diagram and the high chemical reactivity of Mg. Taking Mg₃Bi₂ as an example (Mg₃Sb₂ is similar (Fig. S3, ESI†)), it is not a line compound and undergoes a phase transition from a high-temperature β-phase (cubic) to a low-temperature α-phase (trigonal) (Fig. 1(b)).⁴⁷ Hence, it would be difficult to grow high-quality α-phase single crystals (desired for thermoelectrics) using high-temperature methods, as the structural transition during cooling would lead to a multi-domain α-phase polycrystalline sample. Instead, a low-temperature flux method can avoid structural change by maintaining the growth temperature below the phase transition point. Previous studies using Bi- or Sb-flux methods only result in p-type (and only binary) single crystals because of the Mg-deficient environment.^32,48 A probable solution for growing n-type (both binary and ternary) single crystals involves using the Mg-flux method. However, this is extremely challenging since Mg is highly reactive with most conventional crucibles, including quartz, graphite, and the Al₂O₃ crucibles which are commonly used for flux growth. Tantalum metal, however, is stable in the presence of Mg melts, but there is no commercially available Ta filter for use with the molten flux method. To solve this problem, a self-designed tantalum filter was employed to separate the single crystals from the Mg-flux, as illustrated in Fig. 1(c).

The Ta filter setup and the use of Mg as the flux allowed the preparation of ternary alloyed Mg₃(Bi,Sb)₂ single crystals which should possess high zT. n-Type Mg₃Bi₂ and Mg₃Sb₂ single crystals were also successfully grown. The single crystals show a typical layered structure with widths ranging from a few millimeters to one centimeter and a thickness of ∼0.2 mm (Fig. 1(d)). The backscattering Laue XRD diffraction patterns show clear diffraction spots, indicating the high quality and crystallinity of the as-grown single crystals (Fig. S4, ESI†). Further SEM and EDX analysis demonstrate that the chemical compositions of Mg₃Bi₂ and Mg₃Sb₂ agree well with the stoichiometric compositions (Fig. S5, ESI†). The actual composition of the ternary compound is determined to be Mg₃Bi_1.25Sb_0.75 by the EDX analysis. It is worth noting that the compositions of the single crystals are very close to the Mg : X = 3 : 2 relationship (X = Bi, Sb), without the uncontrollable large excess of Mg seen in polycrystalline samples. Excess Mg impurities would reduce the stability due to its high reactivity, and also impair the thermoelectric performance.⁴⁹ Consequently, the high-quality n-type single crystal results in a high zT over 0.82 at 315 K for Y-doped Mg₃Bi_1.25Sb_0.75, as shown in Fig. 1(e). This zT value is much higher than that of the fine-grained polycrystalline samples and surpasses most coarse-grained samples, demonstrating that zT is closely related to the density of grain boundaries. Further zT enhancement is possible by tuning the Bi/Sb ratio and Fermi level. Moreover, the high thermoelectric performance of n-type Mg₃(Bi,Sb)₂ rivals that of n-type Bi₂(Te,Se)₃ samples,^50–53 which is of great significance since Bi₂(Te,Se)₃ is the only commercial n-type thermoelectric material used near room temperature.

Thermoelectric transport properties

The Y-doped Mg₃Bi_1.25Sb_0.75 and Mg₃Sb₂ crystals are n-type and show metallic transport behaviour down to the lowest temperatures measured (Fig. 2(a)). The Y-doped Mg₃Bi₂ displays a mixed conduction character of two types of charge carriers, in which the major carrier changes from hole to electron at temperatures above ∼200 K. Hence, only the carrier concentration above 200 K is given for Y-doped Mg₃Bi₂. All samples show a Hall electron concentration of ∼10¹⁹ cm⁻³ (Fig. 2(b)). In contrast, pure Mg₃Sb₂ (without Y doping) displays p-type semiconducting behavior (Fig. S6, ESI†), clarifying that Mg-excess growth condition cannot directly lead to n-type conduction but can only guarantee effective n-type doping, which is instructive for further research on this system.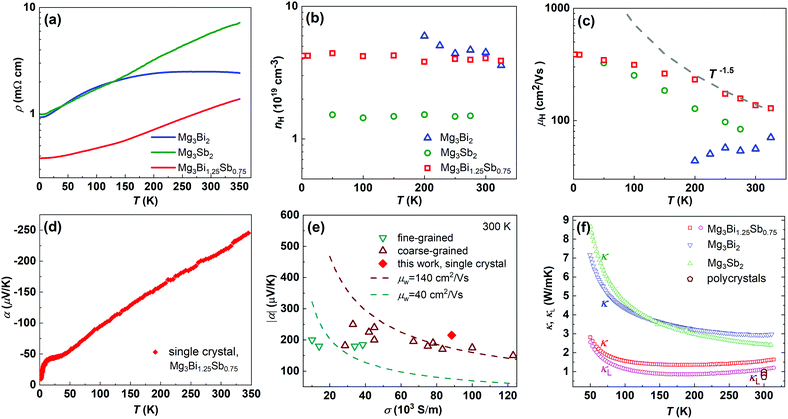

Fig. 2 Temperature dependence of (a) resistivity, (b) Hall charge carrier concentration, (c) Hall charge carrier mobility, (d) Seebeck coefficient, (e) conductivity dependence of Seebeck coefficient of Y-doped Mg₃Bi_1.25Sb_0.75 single crystal at 300 K, with a comparison to polycrystalline samples,^{16,17,20,23,26–28,44,46} and (f) temperature dependence of total and lattice thermal conductivity, with a comparison to the lattice thermal conductivity of polycrystalline samples.^{17,20,27,28,44–46}

The single crystal outperforms traditional polycrystals because of the higher mobility with comparable thermal conductivity. As shown in Fig. 2(c), the charge carrier mobility of Mg₃Bi_1.25Sb_0.75 and Mg₃Sb₂ single crystals exhibit a T^−1.5 dependence, indicating a phonon-dominated scattering mechanism. Notably, previously reported fine-grained (<10 μm) samples usually show lower mobility with decreasing temperature under 400 K,^20,27,44,45 which has been initially and widely attributed to the ionized impurity scattering mechanism. The present results demonstrate the absence of ionized impurity scattering in limiting low temperature charge carrier mobility for ternary Mg₃(Bi,Sb)₂ alloys. Nevertheless, the Seebeck coefficient (Fig. 2(d)) would be nearly independent on the grain size. As a result, the single crystal shows more than three times higher weighted mobility than that of the fine-grained samples, and also better than the coarse-grained samples, as shown in Fig. 2(e). Conversely, the thermal conductivity of the Mg₃Bi_1.25Sb_0.75 single crystal is still low, and is only slightly increased compared to the polycrystalline samples (Fig. 2(f)),^{17,20,27,28,44–46} directly demonstrating that grain boundaries have very small effect on the phonon transport. The higher weighted mobility, together with the comparably low thermal conductivity, leading to the excellent thermoelectric performance in single crystals.

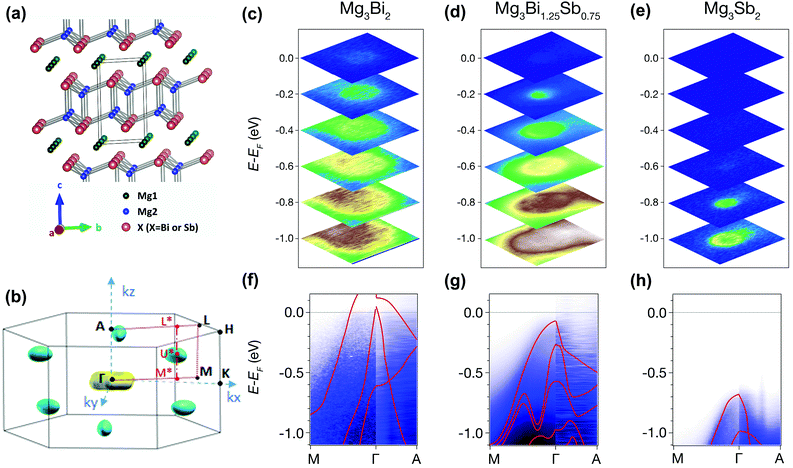
Band structure analysis by ARPES and DFT

The origin of the exceptional thermoelectric performance is further investigated by analyzing the electronic band structure. In addition to DFT calculations, the high-quality single crystals enable experimental investigation of the electronic structure by ARPES.⁵⁴ The crystal structure and corresponding Brillouin zone of Mg₃X₂ (X = Bi and Sb) are illustrated in Fig. 3(a) and (b). For ARPES experiments, the crystals were cleaved in situ along ab plane, corresponding to the k_x–k_y plane in the reciprocal space. For each sample, ARPES spectra were first measured along the Γ–M–K plane. As shown in Fig. 3(c)–(e), all three compounds show an obvious increase in the electron states with rising binding energy (absolute value of E − E_F), indicating the hole pockets at around the Γ point. From Mg₃Bi₂ to Mg₃Sb₂, the electron states near E_F disappear and the top of the valence band shifts dramatically to higher binding energy, leading to a significant expansion in the band gap. No obvious electron states were observed at lower binding energy, which may be due to the shift of the conduction band from the Γ–M–K plane. To further probe the conduction band, we changed the photon energy to acquire the ARPES spectra in the entire Γ–M–A–L plane; while no electron pockets were found (Fig. S7, ESI†), although all of the crystals have an electron density larger than 10¹⁹ cm⁻³.

Fig. 3 (a) Crystal structure and (b) Brillouin zone and Fermi surface of Mg₃X₂ system (X = Bi as an example). Series constant energy maps (c)–(e) and ARPES spectra along high symmetry directions (f)–(h); corresponding calculated band structures are overlaid (red lines) in (f)–(h).

The observation of conduction bands is very challenging. First, DFT calculations indicate that the lowest conduction band is located at U* (in the Γ*–M* direction), not at the high-symmetry points of the Brillouin zone. This, to some extent, makes it difficult to observe the conduction bands. Second, the E_F of the single crystals might not be high enough to guarantee that there are sufficient electron states to be observed by ARPES, suggesting the necessity of further n-type doping to elevate the E_F. Therefore, potassium deposition, generally employed to raise the E_F of samples during the ARPES experiments, was attempted for Mg₃(Bi,Sb)₂. Nonetheless, there was no obvious improvement of the E_F after several minutes of potassium deposition (Fig. S8, ESI†). These attempts demonstrate the difficulties in observing the electron pockets of the Mg₃Bi₂–Mg₃Sb₂ system with ARPES. Future ARPES experiments may require heavily-doped single crystals with higher E_F and larger electron density of states, with, for example, an electron density of ∼10²⁰ cm⁻³.

Nevertheless, the valence bands of all three compounds have been clearly observed along different directions. As shown in Fig. 3(f)–(h), the ARPES intensities along the Γ–M and Γ–A directions are resolved. The band dispersion in ARPES spectra along Γ–A is steeper than that along Γ–M, indicating a smaller effective mass (Fig. S9, ESI†) and higher hole velocity along the k_z direction, corresponding to the c-axis in real space. Moreover, the ARPES spectra observed for all three compounds are consistent with the calculated valence bands (red lines in Fig. 3(f)–(h)), corroborating the reliability of our DFT calculations.

A molecular orbital analysis was performed to develop an intuitive understanding of the enlargement of the band gap (as observed in ARPES) from the bonding interactions,⁵⁵ as depicted in Fig. 4(a) and (b). This schematic illustration sheds light on two important aspects. First, the band gap can be described as in the following equation:

where E_g is the band gap, E₀ is the energy difference between the bonding orbitals, Δ is the energy difference between p_z and p_x/p_y due to orbital splitting, and W₁ and W₂ are the band widths of the s and p orbitals, respectively. A smaller E_g is expected for Mg₃Bi₂ due to a smaller E₀, larger Δ and larger W₁, W₂, resulting from the lower electronegativity and the stronger spin orbit interaction of bismuth. Second, the larger band widening effect of the 6p orbit in Bi leads to a larger W₂, as well as W₁ though it is the 3s orbital of Mg due to the bonding interaction, and therefore a larger band curvature of Mg₃Bi₂, compared to 5p orbit of Sb (as shown by the energy vs. DOS figures in Fig. 4(a) and (b)). This explains the reduction in the effective mass and higher mobility for Mg₃Bi₂ than Mg₃Sb₂. Noteworthy, this is a contributing factor to the higher weighted mobility in ternary Mg₃Sb₂–Mg₃Bi₂ alloys¹⁷ with higher Bi content. Consequently, Bi/Sb ratio is significant for the band gap as well as the mobility and eventually electrical performance of Mg₃(Bi,Sb)₂ compounds.

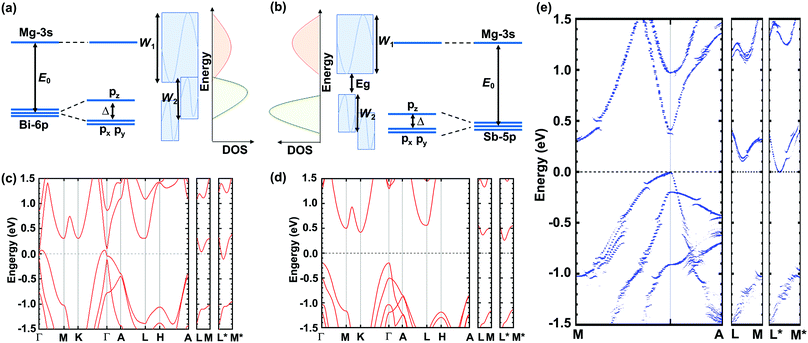Fig. 4 (a) and (b) Schematic illustration of band widening effect and (c)–(e) DFT-calculated band structures of Mg₃Bi₂, Mg₃Sb₂, and Mg₃Bi_1.25Sb_0.75, respectively.

Further DFT calculations resolve more details of the band evolution from Mg₃Bi₂ to Mg₃Sb₂, and therefore explain how the high thermoelectric performance of Mg₃(Bi,Sb)₂ is rooted in the band structure. The DFT-calculated band structures of Mg₃Bi₂, Mg₃Sb₂, and Mg₃Bi_1.25Sb_0.75 are shown in Fig. 4(c)–(e), respectively. The band gap values are slightly lower than that observed by ARPES, due to the typical underestimation of band gaps in DFT calculations. But the trend in band gap variation is identical, ranging from a negative band gap for Mg₃Bi₂, to a near-zero gap for Mg₃Bi_1.25Sb_0.75 and ∼0.45 eV for Mg₃Sb₂. More important, the conduction band minimum is located at U* (along L*–M*) for all of the compounds investigated, since it is mainly dominated by Mg–Mg bonding interactions^56,57 and is relatively independent of Bi or Sb composition. The shift of the conduction band bottom off a high symmetry point contributes to a large band degeneracy, favoring a large quality factor and also zT. Although the large band degeneracy that favors the high thermoelectric performance of Mg₃(Bi,Sb)₂ stems from the Mg–Mg interaction introduced off-high-symmetry-point conduction band, it is worth noting that the Bi/Sb ratio is also of great significance. This is because Mg₃Bi₂ can exhibit higher mobility, and Mg₃Sb₂ is needed to enlarge the band gap and suppress the detrimental bipolar effect. Therefore, at near room temperatures, we emphasize that larger Mg₃Bi₂ content is needed to achieve higher zT in Mg₃(Bi,Sb)₂, as long as the band gap is large enough to avoid intrinsic excitation. This ensures the high zT observed in the Y-doped Mg₃Bi_1.25Sb_0.75 single crystals studied here and also suggests future paths to better thermoelectric performance.

Conclusions

High-quality n-type ternary Mg₃(Bi,Sb)₂ single crystals are synthesized using a facile Mg-flux method. The single crystals show higher mobility and low lattice thermal conductivity comparable to that of polycrystalline samples, indicating the unfavourable nature of grain boundaries. A high zT over 0.82 at 315 K is achieved in a Y-doped Mg₃Bi_1.25Sb_0.75 single crystal, demonstrating its great potential in application of low-grade waste heat recovery and room temperature Peltier coolers. Moreover, ARPES combined with DFT calculations denote the band evolution from Mg₃Bi₂ to Mg₃Sb₂, and consequently indicate the need for a large Bi/Sb ratio for high thermoelectric performance of Mg₃(Bi,Sb)₂. These findings provide future avenues to higher thermoelectric performance.

Author contributions

Y. P. designed the experiment, synthesized the samples, measured the electrical transport properties; Y. M. conducted the ARPES; X. H. and C. H. measured the thermal conductivity; Y. Z., F. F. and J. Y. completed the DFT calculations; K. I. confirmed the Hall data; Y. P. and C. Fu wrote and edited the manuscript; G. J. S. analysed the experimental data and all authors edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation – 392228380) and the ERC Advanced “TOP-MAT” (742068). YP acknowledges the support from the Alexander von Humboldt Foundation. CH and XH acknowledge support from the European Research Council (ERC) under the European Unions’ Horizon 2020 research and innovation programme (647276-MARS-ERC-2014-CoG). JY acknowledges the support from National Natural Science Foundation of China (51761135127). GJS, KI acknowledge the support of award 70NANB19H005 from U.S. Department of Commerce, National Institute of Standards and Technology as part of the Center for Hierarchical Materials Design (CHiMaD). Open Access funding provided by the Max Planck Society.

References

1. F. J. DiSalvo, Science, 1999, 285, 703.
2. G. Snyder and E. Toberer, Nat. Mater., 2008, 7, 105–114.
3. M. Zebarjadi, K. Esfarjani, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2012, 5, 5147–5162.
4. D. M. Rowe, Thermoelectrics Handbook: Macro to Nano, CRC Press, 2006.
5. J.-F. Li, W.-S. Liu, L.-D. Zhao and M. Zhou, NPG Asia Mater., 2010, 2, 152–158.
6. Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69.
7. H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Nat. Mater., 2012, 11, 422–425.
8. C. Fu, S. Bai, Y. Liu, Y. Tang, L. Chen, X. Zhao and T. Zhu, Nat. Commun., 2015, 6, 8144.
9. L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377.
10. W. Zhao, Z. Liu, Z. Sun, Q. Zhang, P. Wei, X. Mu, H. Zhou, C. Li, S. Ma, D. He, P. Ji, W. Zhu, X. Nie, X. Su, X. Tang, B. Shen, X. Dong, J. Yang, Y. Liu and J. Shi, Nature, 2017, 549, 247–251.
11. W. He, D. Wang, H. Wu, Y. Xiao, Y. Zhang, D. He, Y. Feng, Y.-J. Hao, J.-F. Dong, R. Chetty, L. Hao, D. Chen, J. Qin, Q. Yang, X. Li, J.-M. Song, Y. Zhu, W. Xu, C. Niu, X. Li, G. Wang, C. Liu, M. Ohta, S. J. Pennycook, J. He, J.-F. Li and L.-D. Zhao, Science, 2019, 365, 1418–1424.
12. B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, Science, 2008, 320, 634–638.
13. Y. Pan, Y. Qiu, I. Witting, L. Zhang, C. Fu, J.-W. Li, Y. Huang, F.-H. Sun, J. He, G. J. Snyder, C. Felser and J.-F. Li, Energy Environ. Sci., 2019, 12, 624–630.
14. H. Zhao, J. Sui, Z. Tang, Y. Lan, Q. Jie, D. Kraemer, K. McEnaney, A. Guloy, G. Chen and Z. Ren, Nano Energy, 2014, 7, 97–103.
15. D. Kraemer, J. Sui, K. McEnaney, H. Zhao, Q. Jie, Z. F. Ren and G. Chen, Energy Environ. Sci., 2015, 8, 1299–1308.
16. J. Mao, H. Zhu, Z. Ding, Z. Liu, G. A. Gamage, G. Chen and Z. Ren, Science, 2019, 365, 495–498.
17. K. Imasato, S. D. Kang and G. J. Snyder, Energy Environ. Sci., 2019, 12, 965.
18. W. Peng, G. Petretto, G.-M. Rignanese, G. Hautier and A. Zevalkink, Joule, 2018, 2, 1879–1893.
19. J. Zhang, L. Song and B. B. Iversen, npj Comput. Mater., 2019, 5, 76.
20. H. Tamaki, H. K. Sato and T. Kanno, Adv. Mater., 2016, 28, 10182–10187.
21. J. Zhang, L. Song, S. H. Pedersen, H. Yin, L. T. Hung and B. B. Iversen, Nat. Commun., 2017, 8, 13901.
22. J. Zhang, L. Song, A. Mamakhel, M. R. V. Jørgensen and B. B. Iversen, Chem. Mater., 2017, 29, 5371–5383.
23. J. Shuai, J. Mao, S. Song, Q. Zhu, J. Sun, Y. Wang, R. He, J. Zhou, G. Chen, D. J. Singh and Z. Ren, Energy Environ. Sci., 2017, 10, 799–807.
24. S. Ohno, K. Imasato, S. Anand, H. Tamaki, S. D. Kang, P. Gorai, H. K. Sato, E. S. Toberer, T. Kanno and G. J. Snyder, Joule, 2018, 2, 141–154.
25. J. Mao, J. Shuai, S. Song, Y. Wu, R. Dally, J. Zhou, Z. Liu, J. Sun, Q. Zhang, C. dela Cruz, S. Wilson, Y. Pei, D. J. Singh, G. Chen, C.-W. Chu and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10548–10553.
26. K. Imasato, S. D. Kang, S. Ohno and G. J. Snyder, Mater. Horiz., 2018, 5, 59–64.
27. T. Kanno, H. Tamaki, H. K. Sato, S. D. Kang, S. Ohno, K. Imasato, J. J. Kuo, G. J. Snyder and Y. Miyazaki, Appl. Phys. Lett., 2018, 112, 033903.
28. M. Wood, J. J. Kuo, K. Imasato and G. J. Snyder, Adv. Mater., 2019, 31, 1902337.
29. X. Chen, S. Chang, J. Chen, P. Nan, X. Li, X. Chen, X. Zhu, B. Ge, W. Cai, J. Sui, S. Zheng, F. Wang, X. Chen and H. Zhao, 2018, arXiv preprint arXiv:1810.03356.
30. S. Kim, C. Kim, Y.-K. Hong, T. Onimaru, K. Suekuni, T. Takabatake and M.-H. Jung, J. Mater. Chem. A, 2014, 2, 12311–12316.
31. S. H. Kim, C. M. Kim, Y.-K. Hong, K. I. Sim, J. H. Kim, T. Onimaru, T. Takabatake and M.-H. Jung, Mater. Res. Express, 2015, 2, 055903.
32. J. Xin, G. Li, G. Auffermann, H. Borrmann, W. Schnelle, J. Gooth, X. Zhao, T. Zhu, C. Felser and C. Fu, Mater. Today Phys., 2018, 7, 61–68.
33. K. Imasato, C. Fu, Y. Pan, M. Wood, J. J. Kuo, C. Felser and G. J. Snyder, Adv. Mater., 2020, 32, 1908218.
34. J. J. Kuo, S. D. Kang, K. Imasato, H. Tamaki, S. Ohno, T. Kanno and G. J. Snyder, Energy Environ. Sci., 2018, 11, 429–434.
35. P. Gorai, E. S. Toberer and V. Stevanovic, J. Appl. Phys., 2019, 125, 025105.
36. X. Shi, T. Zhao, X. Zhang, C. Sun, Z. Chen, S. Lin, W. Li, H. Gu and Y. Pei, Adv. Mater., 2019, 31, 1903387.
37. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
38. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 77, 3865.
40. A. van de Walle, P. Tiwary, M. de Jong, D. L. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L. Q. Chen and Z.-K. Liu, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2013, 42, 13.
41. F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401.
42. A. Kokalj, J. Mol. Graphics Modell., 1999, 17, 215.
43. P. V. C. Medeiros, S. Stafström and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 041407.
44. J. Shuai, B. Ge, J. Mao, S. Song, Y. Wang and Z. Ren, J. Am. Chem. Soc., 2018, 140, 1910–1915.
45. X. Chen, H. Wu, J. Cui, Y. Xiao, Y. Zhang, J. He, Y. Chen, J. Cao, W. Cai, S. J. Pennycook, Z. Liu, L.-D. Zhao and J. Sui, Nano Energy, 2018, 52, 246–255.
46. X. Shi, C. Sun, Z. Bu, X. Zhang, Y. Wu, S. Lin, W. Li, A. Faghaninia, A. Jain and Y. Pei, Adv. Sci., 2019, 6, 1802286.
47. A. A. Nayeb-Hashemi and J. B. Clark, Bull. Alloy Phase Diagrams, 1985, 6, 528–533.
48. T.-R. Chang, I. Pletikosic, T. Kong, G. Bian, A. Huang, J. Denlinger, S. K. Kushwaha, B. Sinkovic, H.-T. Jeng, T. Valla, W. Xie and R. J. Cava, Adv. Sci., 2019, 6, 1800897.
49. K. Imasato, S. Ohno, S. D. Kang and G. J. Snyder, Appl. Phys. Lett. Mater., 2018, 6, 016106.
50. Y. Pan, T.-R. Wei, C.-F. Wu and J.-F. Li, J. Mater. Chem. C, 2015, 3, 10583.
51. L. Hu, T. Zhu, X. Liu and X. Zhao, Adv. Funct. Mater., 2014, 24, 5211–5218.
52. Y. Pan and J.-F. Li, NPG Asia Mater., 2016, 8, e275.
53. G. S. Nolas, J. Sharp and J. Goldsmid, Thermoelectrics: Basic Principles and New Materials Developments, Springer Science & Business Media, 2013.
54. C. Fu, M. Yao, X. Chen, L. Z. Maulana, X. Li, J. Yang, K. Imasato, F. Zhu, G. Li, G. Auffermann, U. Burkhardt, W. Schnelle, J. Zhou, T. Zhu, X. Zhao, M. Shi, M. Dressel, A. V. Pronin, G. J. Snyder and C. Felser, Adv. Sci., 2020, 7, 1902409.
55. W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem., Int. Ed., 2016, 55, 6826.
56. X. Sun, X. Li, J. Yang, J. Xi, R. Nelson, C. Ertural, R. Dronskowski, W. Liu, G. J. Snyder, D. J. Singh and W. Zhang, J. Comput. Chem., 2019, 9999, 1–8.
57. M. Wood, K. Imasato, S. Anand, J. Yang and G. J. Snyder, J. Mater. Chem. A, 2020, 4, 2033.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee00838a

‡ These authors contributed equally.

---