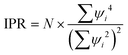Reducing hot carrier cooling rate in metal halide perovskites through lead vacancies: time-domain ab initio analysis†
Junguang
Hu
a,
Ning
Li
a,
Junping
Xie
b,
Yong
Pei
b,
Oleg V.
Prezhdo
 *c and
Wei
Li
*c and
Wei
Li
 *a
*a
aSchool of Chemistry and Materials Science, Hunan Agricultural University, Changsha, PR China. E-mail: weili@hunau.edu.cn
bDepartment of Chemistry, Key Laboratory of Environmentally Friendly Chemistry and Applications of Ministry of Education, Xiangtan University, Xiangtan 411105, China
cDepartment of Chemistry, University of Southern California, Los Angeles, California 90089, USA. E-mail: prezhdo@usc.edu
First published on 23rd May 2024
Abstract
Hybrid organic–inorganic perovskites are promising for optoelectronic applications, yet the impact of intrinsic defects on hot carrier dynamics remains poorly understood. Here, we investigate hot carrier dynamics in methylammonium lead triiodide (MAPbI3) perovskite containing Pb vacancies, a prevalent defect type, using ab initio nonadiabatic molecular dynamics. We observe pronounced slower hot carrier cooling in Pb vacancy-containing MAPbI3 compared to pristine system. In particular, the hot hole cooling in the Pb vacancy system is approximately an order of magnitude slower than that of pristine perovskite for states situated ∼0.5 eV below the top of the valence bands. This deceleration arises primarily from reduced nonadiabatic couplings due to charge state localization and suppressed fluctuations of the inorganic sub-lattice, facilitated by the enhanced rotational disorder of MA cations in the presence of Pb vacancies. Additionally, Pb vacancies introduce intraband defect states capable of trapping photogenerated hot holes, further delaying the hot carrier cooling process. The absence of trap-assisted hot carrier cooling dynamics in hybrid perovskite is consistent with the well-established consensus of defect tolerance in these materials. Our findings provide crucial insights into defect-mediated hot carrier dynamics in hybrid perovskites, holding significant implications for advancing the development of perovskite solar cells and related devices through defect engineering.
1. Introduction
Metal halide perovskites (MHPs) have attracted considerable attention as emerging semiconductor materials in recent years, particularly for next-generation solar cells, owing to their remarkable performance.1–4 The reported power conversion efficiency (PCE) for perovskite solar cells (PSCs) has rapidly evolved from 3.8%5 to 25.8%6 within just a few years. This advance is attributed to their distinctive photophysical properties. However, further improvements in PSC efficiency are impeded by various energy loss channels for the photo-excited carriers. To address this challenge, an unconventional strategy is to slow down the relaxation process of carriers with excess energy, known as hot carriers (HCs), generated by above-bandgap excitation. HCs relax to band extrema by dissipating their excess energy to the lattice via charge-phonon scattering. Rapid HC cooling severely undermines the extraction and utilization of photogenerated carrier energy.7 Therefore, reducing the carrier thermalization rate is crucial for achieving higher performance in optoelectronic applications relying on HCs, such as hot carrier solar cells, etc.Extensive research efforts have been dedicated to understanding the mechanisms and dynamics of HC cooling in MHPs.8–12 Early studies revealed that carrier thermalization in MHPs occurs on an ultrafast timescale (within hundreds of femtoseconds), making HC extraction extremely challenging.13 Recent findings have shown that MHPs exhibit slow HC cooling dynamics, which is linked to various photophysical mechanisms such as hot phonon bottleneck, Auger heating, polaron formation, and band filling effect.14–17 These findings have initiated hot discussions about the potential of PSCs utilizing hot carriers. Several studies have regulated HC cooling rates through doping or chemical engineering to facilitate efficient HC extraction and utilization. It was reported that HC relaxation in MHPs can be slowed down by inclusion of dipolar A-site cations,18–21 mixing halogen atoms,22,23 alloying divalent metal ions (e.g., Zn2+ or Sn2+),24–28 incorporation of alkali cations,29 surface passivation treatments,30,31 manipulations of dielectric confinement, and Rashba band splitting.32 Furthermore, other works have explored the size, dimensionality, and shape dependence of HC cooling dynamics using first-principles calculations.33 However, less attention has been given to controlling HC cooling via defect engineering. Existing literature on this topic is scarce, with a focus mainly on halide interstitial and vacancy defects.34,35 Notably, Pb vacancies (PbV) are prevalent defects observed in perovskite materials due to their low formation energy under Pb-poor/I-rich chemical conditions. The presence of PbV in MAPbI3 based perovskites has been experimentally identified using positron annihilation lifetime spectroscopy.36,37 Previous studies have indicated that PbV can change localization of photoexcited electron and hole states, thereby suppressing radiative and nonradiative electron–hole recombination processes in MHPs.38,39–41 Understanding the extent to which HC cooling dynamics can be manipulated by PbV is urgently needed, underscoring the importance of further in-depth theoretical investigations.
In this work, using ab initio NA–MD simulations, we investigated in detail the HC cooling dynamics of MAPbI3 perovskites with and without PbV. Our results demonstrate that PbV induces a slowdown in HC cooling dynamics. The presence of PbV disrupts the structural symmetry and localize charge density distributions, resulting in reduced overlap between states within valence band (VB) and conduction band (CB). The decreased thermal motion of inorganic atoms, facilitated by PbV, decreases fluctuations of excited state energies, leading to weaker electron-vibrational interaction. Reduced wavefunction overlaps and smaller nuclear displacements contribute the weakened nonadiabatic (NA) couplings, consequently reducing the HC cooling rate. Additionally, without creating mid-gap defect states, PbV introduces intraband defect levels inside VB. These defect states are capable of trapping holes with the trapped holes staying longer at defect sites, impeding the relaxation of hot holes towards the band edge. Furthermore, hot electron and hole relaxations are facilitated exclusively by low-frequency modes. The synergistic effects of these aspects lead to a 10-fold decrease in the hole relaxation rate in the presence of PbV under moderate excitation energy, whereas the change in the electron relaxation rate is less pronounced. These results highlight the beneficial role of PbV in HC cooling dynamics, which is important for further development of PSCs.
2. Computational methodology
Geometry optimization, static electronic structure calculation, and adiabatic molecular dynamics (MD) simulations were carried out with the VASP code.42,43 The exchange–correlation interaction was described using the Perdew–Burke–Ernzerhof (PBE) functional in the generalized gradient approximation (GGA) with a plane-wave basis set. The plane-wave energy cutoff was set to 400 eV. For geometry optimization, Γ-centered 2 × 2 × 1 Monkhorst–Pack k-point mesh was employed, while the electronic properties were calculated with a denser 4 × 4 × 2 k-point mesh for more accurate results. During the geometry optimization, all atoms were allowed to move while maintaining the fixed lattice vectors. The optimization was deemed finished when all ion forces were smaller than 0.01 eV Å−1. The energy convergence criterion for the self-consistency cycle of solving the Kohn–Sham equations was set to 10−4 eV. Dispersion interactions were account for using the DFT-D3 scheme proposed by Grimme et al.44 Subsequently, the systems were heated to 300 K using repeated velocity rescaling, followed by a 5 ps MD production run in the microcanonical ensemble (NVE) with a time step of 1 fs. The electronic properties of the MD configurations were re-computed for each MD configuration to obtain the time-dependent adiabatic energies and NA couplings, forming vibronic Hamiltonian matrices. These time-dependent data were further utilized for NA–MD simulations employing the fewest switches surface hopping (FSSH) algorithm under the classical path approximation, implemented in the PYXAID code.45,46 50 geometries were randomly sampled from the adiabatic MD trajectories and used as initial conditions in the NA–MD calculations. The results were averaged over 1000 stochastic realizations of the surface hopping simulation to achieve convergence. A detailed description of NA–MD methodology can be found elsewhere.45,46 The method has been widely used to model carrier trapping, relaxation, and recombination in various nanoscale systems.22,47–593. Results and discussion
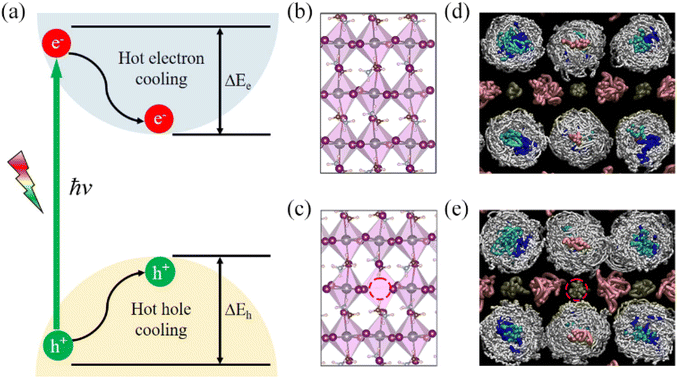
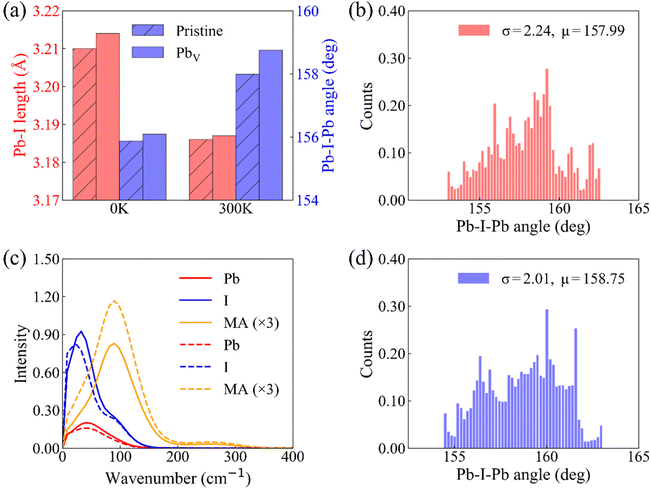
Fig. 1a illustrates the fundamental photophysical processes governing HC cooling dynamics in semiconductors. To model HC cooling dynamics, we constructed a large supercell based on a 2 × 2 × 2 expansion of the tetragonal MAPbI3 unit cell with experimental lattice constants, containing 384 atoms in total. The PbV defect is created by removing a Pb atom from the pristine supercell structure. Fig. 1b and c present the optimized structures of MAPbI3 perovskites with and without PbV, respectively. It is clear that the pristine system shows large octahedral distortion from the ideal perovskite structure, a well-known characteristic feature for the tetragonal MAPbI3 perovskite. The presence of PbV decreases this distortion, leading to a reduction in the tilting of the [PbI6]4− octahedron. This structural adjustment is accompanied by an elongation of the Pb–I bonds and an increase in the Pb–I–Pb bond angles, as summarized in Fig. 2a and Table S1.† We observe the same phenomenon for the structures averaged over 5 ps MD trajectories. The structural reorganization induced by PbV results in internal strain relaxation, leading to a more ordered arrangement of inorganic sub-lattice to accommodate the additional space created by the vacancies. The internal strain relaxation via vacancy defect formation has been also reported in oxide perovskites.60,61 During MD simulation, all atoms exhibit fluctuations around their equilibrium positions, confirming thermal stability of both structures. MA cations display more pronounced fluctuations compared to the inorganic lattice, attributed to their lighter mass relative to Pb and I atoms. Notably, the MA fluctuation is enhanced in the defective system, Fig. 1d and e. This rotational motion of MA cations influences the dynamical behavior of the inorganic sub-lattice, modulating the optoelectronic properties of the MAPbI3 perovskite.In order to understand how PbV influences the lattice dynamics, we computed the root-mean-square (RMS) displacement of each atomic species, as listed in Table S2.† The RMS data indicate that Pb vacancies slightly enhance the motion of MA cations while suppressing the vibrations of Pb and I atoms. This phenomenon likely stems from the enhanced rotational disorder of MA cations facilitated by the additional spatial freedom afforded by PbV. In turn, this imposes steric hindrance, constraining fluctuations of the inorganic sub-lattice. The observation is further supported by the statistical analysis of the Pb–I–Pb angles, Fig. 2b and d. We extend our analysis to the vibrational density of states (VDOS) obtained by Fourier transforming the velocity autocorrelation function from a 5 ps MD trajectory at 300 K, Fig. 2c. The VDOS is projected onto individual species of interests including Pb, I, and organic cation. Such an analysis has been widely used to reveal the structure and dynamic behavior of a system, especially hybrid perovskites.62–64 We focus exclusively on the low-frequency modes in the range of 0–400 cm−1, predominately associated with vibrations of the inorganic components, albeit with a significant contribution from organic cation motion. Our results reveal that while the intensity of vibrational modes associated with the Pb and I components exhibits a slight decrease, those involving MA cations demonstrate a notable increase in the Pb vacancy system compared to the pristine system. This finding further supports the argument that the dynamical fluctuation of the inorganic sub-lattice is restricted by the rotational disorder of the organic cations. Moreover, the enhanced rotational disorder of the organic cations in the presence of PbV may decrease the possible formation of hydrogen bonding, thereby further reducing the octahedral tilting. It is noteworthy that the “locking” effect of the MA cations on the inorganic sub-lattice has previously been reported in the context of temperature effects in hybrid perovskites.3,65 The above analysis reveals the intricate interplay between structural dynamics and defect-induced perturbation in hybrid perovskites.
Band structures and projected density of states (pDOS) for pristine and Pb-vacancy-containing systems are shown in Fig. S1a and b.† The band structures illustrate that the direct band gap between the VB maximum (VBM) and CB minimum (CBM) at the G-point for pristine MAPbI3 is approximately 1.62 eV, consistent with experiment.66 Analysis of the pDOS suggests that the VB is predominantly composed of I-5p states with a minor contribution from Pb-6s states, while the CB is primarily comprised of Pb-6p states. The relaxation of hot holes and electrons mainly involves the vibrational motion of Pb and I atoms, respectively, driving charge–phonon interactions. The Crystal Orbital Hamilton Population (COHP) analysis, presented in Fig. S2,† further suggests that the VBM is dominated by the anti-bonding hybridization of Pb-6s/I-5p states, whereas the CBM consists of non-bonding Pb-6p orbitals with negligible coupling to I-5p. Consequently, VB levels are more sensitive to changes in the inorganic framework, including variations in the Pb–I–Pb bond angle and Pb–I bond length. Although MA cations do not directly contribute to states near the band edges, they indirectly influence HC dynamics through electrostatic and steric interactions with the inorganic Pb–I lattice. The analysis of pDOS reveals an asymmetric distribution, with the pDOS of VB higher than CB, indicating a denser distribution of states in the former. While a denser DOS in the VB typically accelerates hole relaxation relative to electrons, this may not always hold true, particularly in the presence of defects, as we shall discuss below. PbV slightly increases the band gap by approximately 0.06 eV without introducing mid-gap states. The removal of Pb atoms disrupts Pb–I bonds, creating defect states originating from the dangling bonds of surrounding I atoms. These defect levels, located between the VBM and the I-5p atomic orbital level, as illustrated by the diagram for the interaction between Pb and I atomic orbitals in Fig. S1c,† form intra-band defect states characterized by flat energy dispersion profiles, indicative of localized trap states.
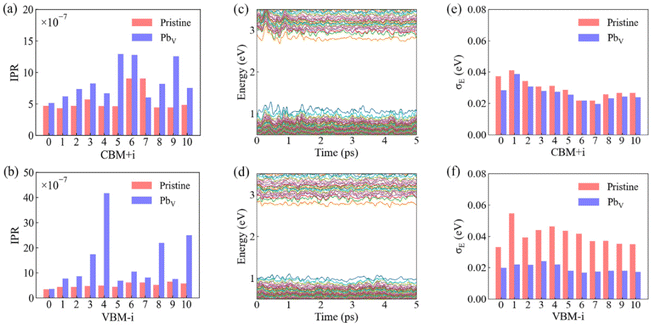
To quantify the orbital localization, we calculated the inverse participation ratio (IPR) of Kohn–Sham states based on the optimized ground state structures for both systems. The IPR is defined as:
We proceed to analyze the time evolution of Kohn–Sham orbital energies and the standard deviations of these energies, as shown in Fig. 3c and d. Vibrations of lattice atoms modulates the electronic energy levels, creates electron–phonon coupling, and drives transitions between electronic states. The inherent softness of the perovskite lattice results in substantial fluctuations in VB and CB levels, reaching magnitudes comparable to or several times that of kBT (∼0.026 eV). The presence of PbV reduces the fluctuations of the VB and CB levels, as indicated by the smaller standard deviation data calculated for each orbital, Fig. 3e and f. This reduction stems from the decreased amplitude of Pb and I motion induced by PbV. NA electron–phonon coupling reflects wavefunction sensitivity to nuclear motion, and can be related to the second derivative of the energy levels along an MD trajectory. Consequently, the degree of fluctuations in orbital levels serves as an indicator of the relative strength of NA couplings. It is anticipated that PbV should decrease NA coupling compared to the pristine system. The calculated standard deviations for VB levels generally surpass those for CB levels, indicating stronger electron–phonon couplings for states in the VB than the CB. This disparity arises because VB states are formed by an anti-bonding hybridization of Pb-s/I-p atomic orbitals, making them more sensitive to structural changes of the inorganic sub-lattice.
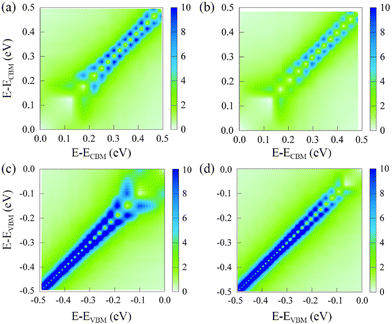
Nonadiabatic couplings play a critical role in influencing the HC cooling process. According to the definition of the NA coupling, it is related to wavefunction overlap, nuclear velocity, and energy difference between initial and final states. Here we have calculated the average absolute values of the NA couplings between states in VB or CB. Fig. 4 presents 2D maps of the NA coupling for the pristine and defective systems. The sub-diagonal matrix elements represent the NA coupling between adjacent states. Strong coupling values along the sub-diagonal lines indicate an enhanced tendency for non-radiative transitions between nearby states with similar energies. Conversely, NA couplings between states separated by large energy gaps yield smaller values, consistent with the expected inverse relationship between coupling strength and energy gap. However, direct NA transitions between low energy and high energy states within VB or CB remain possible due to non-zero coupling values away from the sub-diagonal lines. Notably, NA couplings between VB states generally exceed those between CB states. This difference can be attributed to the larger density of states in the VB, resulting in denser electronic states and smaller energy spacings. Importantly, we observe that PbV leads to a reduction in NA couplings between states within both VB and CB compared to pristine MAPbI3. This reduction in the NA coupling strength can be attributed to decreased nuclear velocities associated with weaker fluctuations of the Pb–I framework and smaller overlap of Kohn–Sham orbitals stemming from the localized charge density distributions. The observed differences in the NA couplings are expected to modulate HC relaxation dynamics, underscoring the significance of defect-induced structural perturbations.
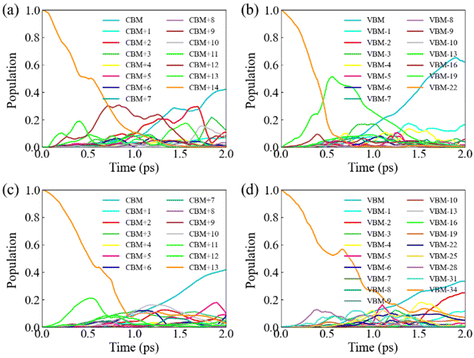
Next, we discuss HC cooling dynamics for pristine and defective systems. We use NA–MD simulation in the single-particle description and ignore the electron–hole Coulomb interaction given the small exciton binding energy in these perovskite materials. The approximation allows for a separate treatment of the hot electron and hot hole relaxation processes. The population decay for each excited state is presented in Tables S7–S10.† To facilitate comparison, Fig. 5 illustrates the time-dependent excited state population following initial excitation to states with excess energy ΔE ≈ 0.5 eV relative to band edges. The lifetimes (τ) are obtained by fitting the population decays using an exponential function, exp(−t/τ). First of all, we find that hot carrier cooling primarily occurs through state-to-state transitions, as evidenced by the considerable population of intermediate states. We emphasize that the HC cooling can also include other relaxation channels due to non-negligible coupling values between states separated by large energy gaps. In pristine MAPbI3, HC relaxation occurs on a timescale of 89 fs and 572 fs for holes and electrons, respectively, which are in agreement with the timescales measured by experimental transient absorption spectroscopy.13 The faster hole relaxation relative to electron relaxation can be attributed to the stronger NA coupling between states within the VB, arising from the higher DOS and smaller energy spacings. This is consistent with the previous work by Kawai et al. who demonstrated that large DOS facilitates rapid carrier cooling using many body perturbation theory calculations.67 Interestingly, Pb vacancies substantially extend the lifetime of hot hole cooling (820 fs), while showing only a slight increase for hot electron cooling (645 fs) compared to the pristine system. The slower hot hole cooling with respect to the hot electron cooling in defective perovskite is in contrast to the trend observed in pristine perovskite. This is because PbV introduces intra-band defect states that are capable of trapping holes within the VB, slowing down hole relaxation towards the band edge, though NA couplings between states in both VB and CB are reduced in the presence of Pb vacancies. Longer carrier cooling time is important for efficient HC harvesting.
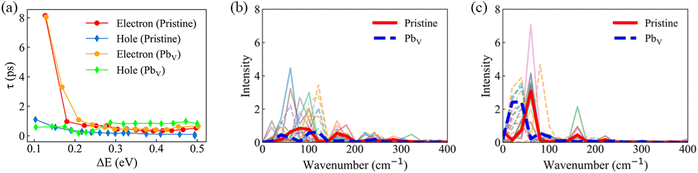
We further studied the HC cooling dynamics as a function of excess energy for the considered systems, Fig. 6a. Overall, all cooling processes happen within a time scale of few picoseconds. Our results show a clear dependence of the HC cooling time on excess energy for the studied systems. From Fig. 6a, hot electron relaxation is more sensitive to the excess energy than hot hole relaxation. Particularly, for pristine MAPbI3, higher excitation energy leads to faster electron relaxation, consistent with report of a hot-phonon bottleneck observed at low excitation pump fluences.68 The observation can be explained by the significantly denser states in the CB in higher energy regions, providing more relaxation channels for HCs, Fig. 3c and d. The electron relaxation dynamics exhibit a similar excitation energy dependence in the defective system as in the pristine system. However, hot hole relaxation displays longer relaxation times with increasing excitation energy, especially for excess energies exceeding ∼0.28 eV. The hot hole cooling rates are relatively similar between the pristine and defective systems when the excess energy is less than ∼0.28 eV. This behavior can be attributed to the presence of intra-band trap states and to the reduced NA couplings in the VB. The absence of accelerated trap-assisted HC cooling is also in agreement with the experimental observation.69 The NA–MD results offer valuable insights into HC dynamics at varying excitation energies with and without the presence of Pb vacancies.
In order to examine the phonon modes driving the HC cooling process, in Fig. 6b and c we present the power spectra obtained by performing Fourier transform of autocorrelation functions of time-dependent orbital energies. The heights of the peaks of the power spectra characterize the strengths of electron–phonon coupling for the given phonon modes. Our analysis reveals that the power spectra for both electron and hole relaxations are predominantly influenced by low-frequency modes in the range of 0–200 cm−1, with minor contributions from high-frequency modes between 200–400 cm−1. Notably, holes exhibit more pronounced coupling to modes in the 0–100 cm−1 range compared to electrons, indicating a stronger charge–phonon interaction during hole relaxation. The phonon modes below 100 cm−1 are primarily attributed to Pb–I stretching and bending, as identified through Raman spectroscopy.70 These modes determine NA couplings because they originate from the inorganic sub-lattice that supports charge carriers. The modes for frequencies larger than 130 cm−1 arise mainly from vibrational motions of the organic cations. In particular, the signals around 200 cm−1 are due to the torsional mode of the MA cation.70,71 Furthermore, the introduction of PbV induces a red-shift and suppression of low-frequency phonon modes for both electron and hole relaxations. This phenomenon aligns intuitively with our analysis of the stiffness of the inorganic network. The above results highlight the importance of Pb vacancies in tunning the vibrational characteristics and, correspondingly, the electron–phonon interactions responsible for HC cooling.
The exceptional performance of the MAPbI3 perovskite can be attributed to defect-tolerance, that is, shallow-level defects have low formation energies, while deep-level defects are hard to form. Deep-level defects serve as nonradiative electron–hole recombination centers, significantly deteriorating the performance of solar cells. In contrast, shallow level defects are generally considered benign. Through our investigations, we have revealed that Pb vacancies do not generate mid-gap states, rather, they contribute to enhancing the PSCs performance by delaying the cooling dynamics of hot carriers. We propose that shallow-level defects play a crucial role in decreasing the HC cooling rate by localizing charge density within VB or CB, decreasing wavefunction overlap, reducing the electronic density of states near the band edges, and stiffening the lattice dynamics. This explanation is supported by experimental observations demonstrating the absence of accelerated trap-assisted hot carrier cooling in hybrid perovskites.69 The favorable defect properties in hybrid perovskites stem not only from the high formation energies of deep-level defects but also from the beneficial behavior of shallow defects in HC cooling dynamics. While our study focuses on PbV in MHPs, the insights gained from our work are applicable to other common defects, such as halide interstitials. Recent works indicate that negatively charged iodine interstitial defects introduce localized intra-band states within CB, disrupting band degeneracy, decreasing nonadiabatic couplings, and subsequently slowing down hot electron cooling,34 which is in qualitative agreement with the analyses presented in this work. These findings contribute to a deeper understanding of the well-established defect-tolerance reported for hybrid perovskites, thereby advancing their potential for various optoelectronic applications.
4. Conclusions
In summary, we have elucidated the influence of PbV on the dynamics of hot carriers in the MAPbI3 perovskite using ab initio NA–MD simulations. The detailed mechanism and timescale of hot carrier dynamics are established in this work. Our findings reveal that PbV induce internal strain relaxation and structural reorganization, leading to elongation of Pb–I bond lengths and alteration of Pb–I–Pb bond angles. This renders the VB more susceptible to thermally induced structural changes. Additionally, Pb vacancies promote rotational disorder of MA cations, constraining the dynamic fluctuations of the inorganic sub-lattice that supports charge carriers. Consequently, both VB and CB exhibit weaker fluctuations in energy levels. Pb vacancies reduce the nonadiabatic couplings because of the charge state localization resulting from structural perturbations and the reduced nuclear velocity. For pristine perovskite, hot electrons and holes with an excess energy of approximately 0.5 eV relax within a sub-ps timescale, consistent with recent experimental observations. Notably, hole relaxation occurs at a faster rate than electron relaxation in the pristine system. PbV slows down the hot carrier cooling process, particularly affecting hot holes, which can be attributed to the reduced nonadiabatic coupling and the trapping of hot holes by intraband defect states introduced by PbV. Furthermore, Pb vacancies lead to weaker electron-vibrational interaction due to the suppressed motion of Pb and I atoms. Importantly, the absence of trap-assisted hot carrier cooling dynamics observed in our study aligns with ultrafast spectroscopy experiments on MHPs and supports the widely accepted notion of defect tolerance in these materials. Our theoretical insights provide a comprehensive understanding of the commonly present Pb vacancies and their role in the fundamental mechanisms governing hot carrier dynamics of halide perovskites. This knowledge can aid in the design of high-efficiency PSCs and related devices through targeted defect engineering strategies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
W. L. acknowledges the financial support of the National Natural Science Foundation of China (No. 22373033) and the Science and Technology Innovation Program of Hunan Province (No. 2021RC3089). Y. P. acknowledges the support of the National Natural Science Foundation of China (Grant No. 22373082) and the Science and Technology Innovation Program of Hunan Province (2023RC1055). N. L. acknowledges the Innovation and Entrepreneurship Training Program for Undergraduates (No. D202305231555195730). O. V. P. acknowledges support of the US Department of Energy (grant DE-SC0014429).References
- J. T. DuBose and P. V. Kamat, Energy Versus Electron Transfer: Managing Excited-State Interactions in Perovskite Nanocrystal–Molecular Hybrids, Chem. Rev., 2022, 122(15), 12475–12494, DOI:10.1021/acs.chemrev.2c00172.
- J. Y. Kim, J.-W. Lee, H. S. Jung, H. Shin and N.-G. Park, High-Efficiency Perovskite Solar Cells, Chem. Rev., 2020, 120(15), 7867–7918, DOI:10.1021/acs.chemrev.0c00107.
- J. Zhan, J. Yang, X. Xie, O. V. Prezhdo and W. Li, Interplay of Structural Fluctuations and Charge Carrier Dynamics Is Key for High Performance of Hybrid Lead Halide Perovskites, Inorg. Chem. Front., 2022, 9, 5549, 10.1039/D2QI01482C.
- J. W. Yang, Y. J. Ahn, D. K. Cho, J. Y. Kim and H. W. Jang, Halide Perovskite Photovoltaic-Electrocatalysis for Solar Fuel Generation, Inorg. Chem. Front., 2023, 10(13), 3781–3807, 10.1039/D3QI00714F.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131(17), 6050–6051, DOI:10.1021/ja809598r.
- H. Min, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim, M. G. Kim, T. J. Shin and S. Il Seok, Perovskite, Solar Cells with Atomically Coherent Interlayers on SnO2 Electrodes, Nature, 2021, 598(7881), 444–450, DOI:10.1038/s41586-021-03964-8.
- A. Mahata, E. Mosconi, D. Meggiolaro, S. Fantacci and F. De Angelis, Rationalizing, Electron–Phonon Interactions and Hot Carriers Cooling in 2D to 3D Metal Halide Perovskites, Adv. Energy Mater., 2023, 2303405, DOI:10.1002/aenm.202303405.
- M. Li, J. Fu, Q. Xu and T. C. Sum, Slow Hot-Carrier Cooling in Halide Perovskites: Prospects for Hot-Carrier Solar Cells, Adv. Mater., 2019, 31(47), 1802486, DOI:10.1002/adma.201802486.
- J. Fu, Q. Xu, G. Han, B. Wu, C. H. A. Huan, M. L. Leek and T. C. Sum, Hot Carrier Cooling Mechanisms in Halide Perovskites, Nat. Commun., 2017, 8(1), 1300, DOI:10.1038/s41467-017-01360-3.
- I. Ahmed, L. Shi, H. Pasanen, P. Vivo, P. Maity, M. Hatamvand and Y. Zhan, There Is Plenty of Room at the Top: Generation of Hot Charge Carriers and Their Applications in Perovskite and Other Semiconductor-Based Optoelectronic Devices, Light: Sci. Appl., 2021, 10(1), 174, DOI:10.1038/s41377-021-00609-3.
- A. O. El-Ballouli, O. M. Bakr and O. F. Mohammed, Structurally Tunable Two-Dimensional Layered Perovskites: From Confinement and Enhanced Charge Transport to Prolonged Hot Carrier Cooling Dynamics, J. Phys. Chem. Lett., 2020, 11(14), 5705–5718, DOI:10.1021/acs.jpclett.0c00359.
- C. Ding, F. Liu, Y. Zhang, D. Hirotani, X. Rin, S. Hayase, T. Minemoto, T. Masuda, R. Wang and Q. Shen, Photoexcited Hot and Cold Electron and Hole Dynamics at FAPbI3 Perovskite Quantum Dots/Metal Oxide Heterojunctions Used for Stable Perovskite Quantum Dot Solar Cells, Nano Energy, 2020, 67, 104267, DOI:10.1016/j.nanoen.2019.104267.
- G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar and T. C. Sum, Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3, Science, 2013, 342(6156), 344–347, DOI:10.1126/science.1243167.
- L. Dai, J. Ye and N. C. Greenham, Thermalization and Relaxation Mediated by Phonon Management in Tin-Lead Perovskites, Light: Sci. Appl., 2023, 12(1), 208, DOI:10.1038/s41377-023-01236-w.
- L. Dai, Z. Deng, F. Auras, H. Goodwin, Z. Zhang, J. C. Walmsley, P. D. Bristowe, F. Deschler and N. C. Greenham, Slow Carrier Relaxation in Tin-Based Perovskite Nanocrystals, Nat. Photonics, 2021, 15(9), 696–702, DOI:10.1038/s41566-021-00847-2.
- S. A. Bretschneider, I. Ivanov, H. I. Wang, K. Miyata, X. Zhu and M. Bonn, Quantifying Polaron Formation and Charge Carrier Cooling in Lead-Iodide Perovskites, Adv. Mater., 2018, 30(29), 1707312, DOI:10.1002/adma.201707312.
- P. P. Joshi, S. F. Maehrlein and X. Zhu, Dynamic Screening and Slow Cooling of Hot Carriers in Lead Halide Perovskites, Adv. Mater., 2019, 31(47), 1803054, DOI:10.1002/adma.201803054.
- J. Chen, M. E. Messing, K. Zheng and T. Pullerits, Cation-Dependent Hot Carrier Cooling in Halide Perovskite Nanocrystals, J. Am. Chem. Soc., 2019, 141(8), 3532–3540, DOI:10.1021/jacs.8b11867.
- M. E. Madjet, G. R. Berdiyorov, F. El-Mellouhi, F. H. Alharbi, A. V. Akimov and S. Kais, Cation Effect on Hot Carrier Cooling in Halide Perovskite Materials, J. Phys. Chem. Lett., 2017, 8(18), 4439–4445, DOI:10.1021/acs.jpclett.7b01732.
- D. Ghosh, C. M. Perez, O. Prezhdo, W. Nie, S. Tretiak and A. J. Neukirch, Impact of Composition Engineering on Charge Carrier Cooling in Hybrid Perovskites: Computational Insights, J. Mater. Chem. C, 2022, 10(25), 9563–9572, 10.1039/D2TC01413K.
- L. J. M. van de Ven, E. K. Tekelenburg, M. Pitaro, J. Pinna and M. A. Loi, Cation Influence on Hot-Carrier Relaxation in Tin Triiodide Perovskite Thin Films, ACS Energy Lett., 2024, 9(3), 992–999, DOI:10.1021/acsenergylett.4c00055.
- M. E.-A. Madjet, A. V. Akimov, F. El-Mellouhi, G. R. Berdiyorov, S. Ashhab, N. Tabet and S. Kais, Enhancing the Carrier Thermalization Time in Organometallic Perovskites by Halide Mixing, Phys. Chem. Chem. Phys., 2016, 18(7), 5219–5231, 10.1039/C5CP06603D.
- L. T. Mix, D. Ghosh, J. Tisdale, M.-C. Lee, K. R. O'Neal, N. Sirica, A. J. Neukirch, W. Nie, A. J. Taylor, R. P. Prasankumar, S. Tretiak and D. A. Yarotski, Hot Carrier Cooling and Recombination Dynamics of Chlorine-Doped Hybrid Perovskite Single Crystals, J. Phys. Chem. Lett., 2020, 11(19), 8430–8436, DOI:10.1021/acs.jpclett.0c02243.
- S. D. Verma, Q. Gu, A. Sadhanala, V. Venugopalan and A. Rao, Slow Carrier Cooling in Hybrid Pb–Sn Halide Perovskites, ACS Energy Lett., 2019, 4(3), 736–740, DOI:10.1021/acsenergylett.9b00251.
- Q. Wei, J. Yin, O. M. Bakr, Z. Wang, C. Wang, O. F. Mohammed, M. Li and G. Xing, Effect of Zinc-Doping on the Reduction of the Hot-Carrier Cooling Rate in Halide Perovskites, Angew. Chem., Int. Ed., 2021, 60(19), 10957–10963, DOI:10.1002/anie.202100099.
- W. Yan, C. Li, C. Peng, S. Tan, J. Zhang, H. Jiang, F. Xin, F. Yue and Z. Zhou, Hot-Carrier Cooling Regulation for Mixed Sn-Pb Perovskite Solar Cells, Adv. Mater., 2024, 36, 2312170, DOI:10.1002/adma.202312170.
- M. Monti, K. D. G. I. Jayawardena, E. Butler-Caddle, R. M. I. Bandara, J. M. Woolley, M. Staniforth, S. R. P. Silva and J. Lloyd-Hughes, Hot Carriers in Mixed Pb-Sn Halide Perovskite Semiconductors Cool Slowly While Retaining Their Electrical Mobility, Phys. Rev. B, 2020, 102(24), 245204, DOI:10.1103/PhysRevB.102.245204.
- N. Mondal, B. P. Carwithen and A. A. Bakulin, Alloying Metal Cations in Perovskite Nanocrystals Is a New Route to Controlling Hot Carrier Cooling, Light: Sci. Appl., 2023, 12(1), 276, DOI:10.1038/s41377-023-01316-x.
- T. Wang, L. Jin, J. Hidalgo, W. Chu, J. M. Snaider, S. Deng, T. Zhu, B. Lai, O. Prezhdo, J.-P. Correa-Baena and L. Huang, Protecting Hot Carriers by Tuning Hybrid Perovskite Structures with Alkali Cations, Sci. Adv., 2020, 6(43), eabb1336, DOI:10.1126/sciadv.abb1336.
- A. Forde, T. Inerbaev, E. K. Hobbie and D. S. Kilin, Excited-State Dynamics of a CsPbBr3 Nanocrystal Terminated with Binary Ligands: Sparse Density of States with Giant Spin–Orbit Coupling Suppresses Carrier Cooling, J. Am. Chem. Soc., 2019, 141(10), 4388–4397, DOI:10.1021/jacs.8b13385.
- A. Das, K. Marjit, S. Ghosh, D. Ghosh and A. Patra, Slowing Down the Hot Carrier Relaxation Dynamics of CsPbX3 Nanocrystals by the Surface Passivation Strategy, J. Phys. Chem. C, 2023, 127(31), 15385–15394, DOI:10.1021/acs.jpcc.3c03728.
- J. Yin, R. Naphade, P. Maity, L. Gutiérrez-Arzaluz, D. Almalawi, I. S. Roqan, J.-L. Brédas, O. M. Bakr and O. F. Mohammed, Manipulation of Hot Carrier Cooling Dynamics in Two-Dimensional Dion–Jacobson Hybrid Perovskites via Rashba Band Splitting, Nat. Commun., 2021, 12(1), 3995, DOI:10.1038/s41467-021-24258-7.
- S. C. Boehme, S. Brinck, J. ten Maes, N. Yazdani, F. Zapata, K. Chen, V. Wood, J. M. Hodgkiss, Z. Hens, P. Geiregat and I. Infante, Phonon-Mediated and Weakly Size-Dependent Electron and Hole Cooling in CsPbBr3 Nanocrystals Revealed by Atomistic Simulations and Ultrafast Spectroscopy, Nano Lett., 2020, 20(3), 1819–1829, DOI:10.1021/acs.nanolett.9b05051.
- Z. Zhou, J. He, T. Frauenheim, O. V. Prezhdo and J. Wang, Control of Hot Carrier Cooling in Lead Halide Perovskites by Point Defects, J. Am. Chem. Soc., 2022, 144(39), 18126–18134, DOI:10.1021/jacs.2c08487.
- S. Banerjee, J. Kang, X. Zhang and L.-W. Wang, The Effects of Interstitial Iodine in Hybrid Perovskite Hot Carrier Cooling: A Non-Adiabatic Molecular Dynamics Study, J. Chem. Phys., 2020, 152(9), 091102, DOI:10.1063/1.5132595.
- D. J. Keeble, J. Wiktor, S. K. Pathak, L. J. Phillips, M. Dickmann, K. Durose, H. J. Snaith and W. Egger, Identification of Lead Vacancy Defects in Lead Halide Perovskites, Nat. Commun., 2021, 12(1), 5566, DOI:10.1038/s41467-021-25937-1.
- S. Moshat, P. P. Ray, S. Sil, J. Dhar and D. Sanyal, Positron Annihilation Studies of Methylammonium Lead Bromide Perovskite, Phys. Scr., 2023, 98(3), 035822, DOI:10.1088/1402-4896/acb6c2.
- A. Forde and D. Kilin, Defect Tolerance Mechanism Revealed! Influence of Polaron Occupied Surface Trap States on CsPbBr3 Nanocrystal Photoluminescence: Ab Initio Excited-State Dynamics, J. Chem. Theory Comput., 2021, 17(11), 7224–7236, DOI:10.1021/acs.jctc.1c00691.
- D. J. Vogel, T. M. Inerbaev and D. S. Kilin, Role of Lead Vacancies for Optoelectronic Properties of Lead-Halide Perovskites, J. Phys. Chem. C, 2018, 122(10), 5216–5226, DOI:10.1021/acs.jpcc.7b05375.
- Y. Gao, M. Zhang, X. Zhang and G. Lu, Decreasing Exciton Binding Energy in Two-Dimensional Halide Perovskites by Lead Vacancies, J. Phys. Chem. Lett., 2019, 10(14), 3820–3827, DOI:10.1021/acs.jpclett.9b01093.
- J. He and R. Long, Lead Vacancy Can Explain the Suppressed Nonradiative Electron–Hole Recombination in FAPbI3 Perovskite under Iodine-Rich Conditions: A Time-Domain Ab Initio Study, J. Phys. Chem. Lett., 2018, 9(22), 6489–6495, DOI:10.1021/acs.jpclett.8b03095.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- G. Kresse and J. Furthmüller, Efficiency of Ab initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104, DOI:10.1063/1.3382344.
- A. V. Akimov and O. V. Prezhdo, Advanced Capabilities of the PYXAID Program: Integration Schemes, Decoherence Effects, Multiexcitonic States, and Field-Matter Interaction, J. Chem. Theory Comput., 2014, 10(2), 789–804, DOI:10.1021/ct400934c.
- A. V. Akimov and O. V. Prezhdo, The PYXAID Program for Non-Adiabatic Molecular Dynamics in Condensed Matter Systems, J. Chem. Theory Comput., 2013, 9(11), 4959–4972, DOI:10.1021/ct400641n.
- Z. Zhou, J. Liu, R. Long, L. Li, L. Guo and O. V. Prezhdo, Control of Charge Carriers Trapping and Relaxation in Hematite by Oxygen Vacancy Charge: Ab Initio Non-Adiabatic Molecular Dynamics, J. Am. Chem. Soc., 2017, 139(19), 6707–6717, DOI:10.1021/jacs.7b02121.
- Z. Wang, P. Altmann, C. Gadermaier, Y. Yang, W. Li, L. Ghirardini, C. Trovatello, M. Finazzi, L. Duò, M. Celebrano, R. Long, D. Akinwande, O. V. Prezhdo, G. Cerullo and S. Dal Conte, Phonon-Mediated Interlayer Charge Separation and, Recombination in a MoSe 2 /WSe 2 Heterostructure, Nano Lett., 2021, 21(5), 2165–2173, DOI:10.1021/acs.nanolett.0c04955.
- W. Stier, W. R. Duncan and O. V. Prezhdo, Thermally Assisted Sub-10 Fs Electron Transfer in Dye-Sensitized Nanocrystalline TiO2 Solar Cells, Adv. Mater., 2004, 16(3), 240–244, DOI:10.1002/adma.200306027.
- A. Nijamudheen and A. V. Akimov, Excited-State Dynamics in Two-Dimensional Heterostructures: SiR/TiO 2 and GeR/TiO 2 (R = H, Me) as Promising Photocatalysts, J. Phys. Chem. C, 2017, 121(12), 6520–6532, DOI:10.1021/acs.jpcc.7b00545.
- W. Li, Y. She, A. S. Vasenko and O. V. Prezhdo, Ab Initio Nonadiabatic Molecular Dynamics of Charge Carriers in Metal Halide Perovskites, Nanoscale, 2021, 13(23), 10239–10265, 10.1039/D1NR01990B.
- W. Li, R. Long, Z. Hou, J. Tang and O. V. Prezhdo, Influence of Encapsulated Water on Luminescence Energy, Line Width, and Lifetime of Carbon Nanotubes: Time Domain Ab Initio Analysis, J. Phys. Chem. Lett., 2018, 9(14), 4006–4013, DOI:10.1021/acs.jpclett.8b02049.
- W. Li, J. Liu, F.-Q. Bai, H.-X. Zhang and O. V. Prezhdo, Hole Trapping by Iodine Interstitial Defects Decreases Free Carrier Losses in Perovskite Solar Cells: A Time-Domain Ab Initio Study, ACS Energy Lett., 2017, 2(6), 1270–1278, DOI:10.1021/acsenergylett.7b00183.
- L. Li, R. Long, T. Bertolini and O. V. Prezhdo, Sulfur Adatom and Vacancy Accelerate Charge Recombination in MoS 2 but by Different Mechanisms: Time-Domain Ab Initio Analysis, Nano Lett., 2017, 17(12), 7962–7967, DOI:10.1021/acs.nanolett.7b04374.
- J. He, A. S. Vasenko, R. Long and O. V. Prezhdo, Halide Composition Controls Electron–Hole Recombination in Cesium–Lead Halide Perovskite Quantum Dots: A Time Domain Ab Initio Study, J. Phys. Chem. Lett., 2018, 9(8), 1872–1879, DOI:10.1021/acs.jpclett.8b00446.
- C. Cheng, W.-H. Fang, R. Long and O. V. Prezhdo, Water Splitting with a Single-Atom Cu/TiO 2 Photocatalyst: Atomistic Origin of High Efficiency and Proposed Enhancement by Spin Selection, JACS Au, 2021, 1(5), 550–559, DOI:10.1021/jacsau.1c00004.
- A. V. Akimov, R. Asahi, R. Jinnouchi and O. V. Prezhdo, What Makes the Photocatalytic CO 2 Reduction on N-Doped Ta 2 O 5 Efficient: Insights from Nonadiabatic Molecular Dynamics, J. Am. Chem. Soc., 2015, 137(35), 11517–11525, DOI:10.1021/jacs.5b07454.
- W. Li, T. Xue, C. Mora-Perez and O. V. Prezhdo, Ab Initio Quantum Dynamics of Plasmonic Charge Carriers, Trends Chem., 2023, 5(8), 634–645, DOI:10.1016/j.trechm.2023.02.010.
- W. Li and A. V. Akimov, How Good Is the Vibronic Hamiltonian Repetition Approach for Long-Time Nonadiabatic Molecular Dynamics?, J. Phys. Chem. Lett., 2022, 13(41), 9688–9694, DOI:10.1021/acs.jpclett.2c02765.
- U. Aschauer, R. Pfenninger, S. M. Selbach, T. Grande and N. A. Spaldin, Strain-Controlled Oxygen Vacancy Formation and Ordering in CaMnO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(5), 054111, DOI:10.1103/PhysRevB.88.054111.
- M. I. Saidaminov, J. Kim, A. Jain, R. Quintero-Bermudez, H. Tan, G. Long, F. Tan, A. Johnston, Y. Zhao, O. Voznyy and E. H. Sargent, Suppression of Atomic Vacancies via Incorporation of Isovalent Small Ions to Increase the Stability of Halide Perovskite Solar Cells in Ambient Air, Nat. Energy, 2018, 3(8), 648–654, DOI:10.1038/s41560-018-0192-2.
- P. Zhang, B. Chang, T. Xue, R.-X. Ding, C.-J. Tong, Z. Hou and W. Li, Mixed Sulfur/Selenium Anions Weaken Electron-Vibrational Interaction in Cu2ZnSn(S,Se)4 Photoabsorber, J. Phys. Chem. Lett., 2023, 14(1), 107–115, DOI:10.1021/acs.jpclett.2c03631.
- P. Zhang, T. Xue, Z. Wang, W. Wei, X. Xie, R. Jia and W. Li, MoSe2/C60 Heterojunction May Be Efficient for Photovoltaic Applications: Time-Domain Ab Initio Analysis of Interfacial Charge Separation and Recombination Dynamics, Inorg. Chem. Front., 2023, 10(24), 7238–7250, 10.1039/D3QI01105D.
- A. Garrote-Márquez, L. Lodeiro, R. Suresh, N. Cruz Hernández, R. Grau-Crespo and E. Menéndez-Proupin, Hydrogen Bonds in Lead Halide Perovskites: Insights from Ab Initio Molecular Dynamics, J. Phys. Chem. C, 2023, 127(32), 15901–15910, DOI:10.1021/acs.jpcc.3c02376.
- W. Li, J. Tang, D. Casanova and O. V. Prezhdo, Time-Domain Ab Initio Analysis Rationalizes the Unusual Temperature Dependence of Charge Carrier Relaxation in Lead Halide Perovskite, ACS Energy Lett., 2018, 3, 2713–2720, DOI:10.1021/acsenergylett.8b01608.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Formamidinium Lead Trihalide: A Broadly Tunable Perovskite for Efficient Planar Heterojunction Solar Cells, Energy Environ. Sci., 2014, 7(3), 982–988, 10.1039/C3EE43822H.
- H. Kawai, G. Giorgi, A. Marini and K. Yamashita, The Mechanism of Slow Hot-Hole Cooling in Lead-Iodide Perovskite: First-Principles Calculation on Carrier Lifetime from Electron–Phonon Interaction, Nano Lett., 2015, 15(5), 3103–3108, DOI:10.1021/acs.nanolett.5b00109.
- H. Li, Q. Wang, Y. Oteki, C. Ding, D. Liu, Y. Guo, Y. Li, Y. Wei, D. Wang, Y. Yang, T. Masuda, M. Chen, Z. Zhang, T. Sogabe, S. Hayase, Y. Okada, S. Iikubo and Q. Shen, Enhanced Hot-Phonon Bottleneck Effect on Slowing Hot Carrier Cooling in Metal Halide Perovskite Quantum Dots with Alloyed A-Site, Adv. Mater., 2023, 35(38), 2301834, DOI:10.1002/adma.202301834.
- S. A. Bretschneider, F. Laquai and M. Bonn, Trap-Free Hot Carrier Relaxation in Lead–Halide Perovskite Films, J. Phys. Chem. C, 2017, 121(21), 11201–11206, DOI:10.1021/acs.jpcc.7b03992.
- C. Quarti, G. Grancini, E. Mosconi, P. Bruno, J. M. Ball, M. M. Lee, H. J. Snaith, A. Petrozza and F. De Angelis, The, Raman Spectrum of the CH 3 NH 3 PbI 3 Hybrid Perovskite: Interplay of Theory and Experiment, J. Phys. Chem. Lett., 2014, 5(2), 279–284, DOI:10.1021/jz402589q.
- A. M. A. Leguy, A. R. Goñi, J. M. Frost, J. Skelton, F. Brivio, X. Rodríguez-Martínez, O. J. Weber, A. Pallipurath, M. I. Alonso, M. Campoy-Quiles, M. T. Weller, J. Nelson, A. Walsh and P. R. F. Barnes, Dynamic Disorder, Phonon Lifetimes, and, the Assignment of Modes to the Vibrational Spectra of Methylammonium Lead Halide Perovskites, Phys. Chem. Chem. Phys., 2016, 18(39), 27051–27066, 10.1039/C6CP03474H.
Footnote |
| † Electronic supplementary information (ESI) available: Band structures and projected density of states. The crystal orbital Hamilton population analysis. Root-mean-square displacement velocities for each atomic species. The calculated Pb–I bond lengths and Pb–I–Pb bond angles. Charge density distributions for valence band and conduction bands state. Population decay plots for each excited state. See DOI: https://doi.org/10.1039/d4qi00833b |
| This journal is © the Partner Organisations 2024 |