Open Access Article
Open Access ArticleLA-ICP-MS/MS-based Rb–Sr isotope mapping for geochronology
Martin
Kutzschbach
 *a and
Johannes
Glodny
*a and
Johannes
Glodny
 b
b
aTechnische Universität Berlin, Chair of Applied Geochemistry, 10587 Berlin, Germany. E-mail: m.kutzschbach@tu-berlin.de
bGFZ German Research Centre for Geosciences, 14473 Potsdam, Germany
First published on 9th January 2024
Abstract
This study introduces a new approach for in situ Rb–Sr dating that utilizes rapid line scans instead of static spot ablation, enabling the creation of two-dimensional 87Rb/86Sr and 87Sr/86Sr isotope ratio and Rb–Sr age maps. The data acquisition is conducted utilizing an ICP-MS/MS instrument with N2O as the reaction gas, coupled to a 193 nm excimer laser via a low-aerosol-dispersion interface. This configuration allows for high repetition rates (>100 Hz) and sensitivities, enabling data acquisition at a high scanning speed and small laser beam size (3–4 μm). Notably, this approach requires just about 1/30 of the sample volume typically utilized in conventional spot ablation mode, while achieving similar levels of precision and accuracy. Line scan ablation is tested and compared to spot ablation on age-homogeneous crystalline muscovite and biotite, for which reference Rb–Sr age data is acquired through ID-TIMS. Results show that a key requirement for accurate Rb–Sr ages based on line scan analyses is matrix correction using chemically matched crystalline mica. By presenting Rb–Sr age maps of three naturally deformed mica samples, we highlight the potential of Rb–Sr mapping for extracting age data from rocks that exhibit complex metamorphic-metasomatic histories and microscale dynamic recrystallization. Additionally, we show that quantitative elemental information (Al, Fe, Si, Li) can be collected alongside Rb–Sr isotope data. This advancement offers a distinctly more insightful assessment of isotope mobility in natural systems, the timing of element enrichment processes and enables, in high-Rb/Sr rock systems, precise and accurate isotopic dating of intricate geological processes at small scales.
1. Introduction
Rb–Sr dating relies on the beta decay of 87Rb to 87Sr with an 87Rb half-life of 49.61 ± 0.16 billion years.1 This decay system has been discovered already in 1937, and was later extensively used for isotopic dating of almost any kind of Rb-bearing geologic materials. The attractiveness of the Rb–Sr geochronometer lies in its wide applicability, as both elements occur in most crustal lithologies and are present in μg g−1-levels in the majority of rock forming minerals. The contrasting geochemical behavior of Rb and Sr often leads to highly contrasting Rb/Sr ratios between minerals of a given rock, and, in consequence, to large inter-mineral contrasts of Sr isotopic compositions that facilitate precise dating of geologic processes. Rb–Sr mineral data have successfully been used to date crystallization of magmatic rocks as well as high-grade metamorphic processes like eclogitization of subducted crust.2,3 Moreover, Rb–Sr dating can also provide age constraints on secondary events such as hydrothermal alteration, hydrothermal vein formation, or deformational events that can cause isotope mobility during fluid-mediated recrystallization or recrystallization as a response to intracrystalline deformation during accommodation of strain in ductile shear zones.4–8 Rb–Sr isotopic dating mainly relies on minerals with high Rb/Sr elemental ratios. These minerals are typically K-rich phases, like the phlogopite–annite solid solution series (biotite), different types of potassic white mica, and K-feldspar. In the classic approach, either whole rock powders or mineral separates are dissolved, followed by wet-chemical separation of Rb and Sr from each other and from the matrix, to avoid the isobaric interference of 87Rb and 87Sr during mass spectrometric analysis of Sr isotopic compositions. Only recently laser ablation-ICP-MS-based analytical methodologies have been developed for in situ dating of Rb-rich mineral phases such as mica or K-feldspar.9–11Unlike the well-established in situ40Ar–39Ar dating technique, which focuses on the same minerals,12–14in situ Rb–Sr dating offers several distinct advantages. Notably, it eliminates the need for access to irradiation facilities, which can be both time-consuming and costly, and involves handling radioactive materials. In contrast, in situ Rb–Sr dating is significantly less demanding in terms of instrumentation and sample preparation, making it a cost-effective and versatile option that can be implemented in various laboratory settings. Additionally, this method allows for a rapid sample turnaround, enhancing its potential as a widely accessible dating tool suitable for a diverse range of geological targets. The two essential components of suitable laboratory equipment comprise (1) a laser for in situ sampling of the target material and (2) a mass spectrometer capable of (quasi) simultaneously analysing a minimum of three nuclides: 85Rb or 87Rb, 87Sr, and 86Sr or 88Sr throughout the sample ablation process. Notably, achieving the necessary mass resolution for effectively distinguishing between 87Rb and 87Sr (M/ΔM ∼ 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) surpasses the capabilities of any commercially accessible mass spectrometer, so that the use of a collision/reaction cell (CRC) is required. Within the CRC, reactive gases (O2, SF6, N2O, CH3F) form Sr-molecule ions such as SrF+ or SrO+ that can be measured free of the 87Rb-interference.9,15–18 Interference from mononuclide ions on mass shifted Sr-molecule ions (e.g.104Pd+ on 88Sr16O+) is in turn avoided by applying a pre-CRC mass filter (either quadrupole-based or through Wien filtering). This technique obviates the need for time-consuming offline chemical separation of Rb and Sr by classic cation-exchange chromatography. However, this approach currently reaches its limits when it comes to dating of geologically young (Cenozoic) assemblages or to K-phases with particularly low Rb/Sr ratios, like white mica populations rich in non-radiogenic Sr. Here, precise age information depends upon the extremely precise determination of Sr isotopic compositions not only for mica but also for accompanying mineral phases, a task that requires mass spectrometers featuring multicollection (TIMS, MC-ICP-MS).
000) surpasses the capabilities of any commercially accessible mass spectrometer, so that the use of a collision/reaction cell (CRC) is required. Within the CRC, reactive gases (O2, SF6, N2O, CH3F) form Sr-molecule ions such as SrF+ or SrO+ that can be measured free of the 87Rb-interference.9,15–18 Interference from mononuclide ions on mass shifted Sr-molecule ions (e.g.104Pd+ on 88Sr16O+) is in turn avoided by applying a pre-CRC mass filter (either quadrupole-based or through Wien filtering). This technique obviates the need for time-consuming offline chemical separation of Rb and Sr by classic cation-exchange chromatography. However, this approach currently reaches its limits when it comes to dating of geologically young (Cenozoic) assemblages or to K-phases with particularly low Rb/Sr ratios, like white mica populations rich in non-radiogenic Sr. Here, precise age information depends upon the extremely precise determination of Sr isotopic compositions not only for mica but also for accompanying mineral phases, a task that requires mass spectrometers featuring multicollection (TIMS, MC-ICP-MS).
Traditionally, Rb–Sr ages are obtained by constructing multi-point isochrons through analyses of co-genetic phases with contrasting Rb/Sr ratios.19 It is also possible to obtain model ages with an accuracy and precision of 1–3% from single spot in situ analyses using laser ablation (LA), provided that either (1) the grains show high Rb/Sr ratios and correspondingly very high 87Sr/86Sr ratios or (2) a reasonable guess of the initial 87Sr/86Sr ratio can be made.20 Most recently, the isochron approach was applied to single spot dating using high-precision LA-MC-ICP-MS/MS analyses, which allows precise single spot dating (2–4%) without prior knowledge of the initial 87Sr/86Sr ratio.21 So far, in situ Rb–Sr dating relies on placing rather large single laser spots (50–100 μm)20,21 on the phase of interest. To obtain a reasonable level of uncertainty for 87Rb/86Sr and 87Sr/86Sr ratios (typically around 1–3% and 0.5–1% when using quadrupole instruments), the ablation interval is chosen long enough to enable the recording of multiple mass sweeps (n > 100). Due to the destructive nature of the ablation process, this results in ablation pits that are a few tens of μm deep. However, large ablations depths are problematic in fine grained rocks or when aiming to date small (μm scale) secondary features, like reaction rims on larger grains, local shear bands, or localized domains of fluid-induced recrystallization.
In this contribution, we present a novel technique that enables in situ Rb–Sr dating with minimal sample material extraction. This approach uses line rasters instead of conventional single spot ablation, resembling the well-established image-based dating techniques utilized in carbonate and zircon U–Pb dating.22–24 By applying a low-aerosol dispersion system, sampling at significantly greater repetition rates (>100 Hz) is enabled, so that large Rb–Sr maps can be produced from multiple line scans in a reasonable amount of time and, most importantly, at μm-scale resolution and high precision and accuracy but with only a fraction of the material that is used for conventional spot dating. By using examples of naturally deformed mica we show that this technique opens up new avenues to study isotope mobility in nature, to derive precise and accurate ages from rocks showing textural disequilibria, and to date particularly small-scale features like localized dynamic recrystallization in shear bands at the micrometer scale.
2. Material and methods
2.1. Single crystal mica reference materials
To correct for elemental and mass-dependent isotopic fractionation, reference materials (RM) with a well-known and homogeneous 87Rb/86Sr and 87Sr/86Sr distribution are applied. For in situ Rb–Sr dating, NIST 610 glass25 and MicaMg-NP9,26 are the most widely used.15,20,21,27,28 The latter is a finely ground pressed powder of phlogopite from a pyroxenite from southern Madagascar that displays a homogeneous age signal (519.4 ± 6.5 Ma).9 Although these RM are frequently used in geochronological applications, none provides a proper matrix match to single-crystal mica, which is also the case for the recently tested fused mica mineral glasses.29 It has been shown that a lack of matrix match between RM and sample may negatively affect dating accuracy. Systematic matrix age biases of as much as 10% have been observed.29–31We therefore produced secondary reference materials with well-known ages, determined by isotope dilution thermal ionization mass spectrometry (ID-TIMS) at the GFZ Potsdam. The aim was to establish an additional set of mica reference materials with good matrix match to both natural K-white mica (muscovite–phengite) and natural K-(Mg, Fe2+) solid solution series (phlogopite–annite, ‘biotite’)
2.2. Natural mica from metamorphic rocks
Rb–Sr age mapping was undertaken on natural muscovite and biotite from three locations (Fig. 1).2.3. LA-ICP-MS/MS isotope ratio, Rb–Sr age and elemental maps
Elemental and isotope ratio mapping on mica from mylonite and metapegmatites were performed at the MAGMA Lab of the TU Berlin during three sessions (GÄD08, WIL1A and GER2B, corresponding to the sample names) using an Agilent 8900 ICP-MS/MS coupled to an Analyte Excite 193 nm excimer laser (Teledyne Photon Machines). Prior to analysis, the reaction cell is flushed for at least 12 hours with N2O (25%) to reduce instrumental drift.9 For introduction of N2O into the Agilent 8900 CRC, the 4th cell gas mass flow controller is used, where a flow rate of 100% corresponds to ∼1.07 ml min−1. The aerosol rapid introduction system ARIS (Teledyne Photon Machines) was used in combination with a low-volume adapter from Glass Expansion. Helium (99.999%) was used as a carrier gas with a total flow rate of 0.95 l min−1 (0.5 l min−1 cell flow, 0.45 l min−1 cup flow) and small amounts (3 ml min−1) of high-purity N2 (99.999%) were admixed to increase sensitivity. After plasma ignition and initialization of He flow, m/z = 42 (e.g., 14N14N14N+) and m/z = 31 (e.g., 15N16O+) were recorded to monitor the amount of air entrained in the interface tubing and ablation cell. After count rates were stable and below 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps for m/z = 31 and 42, the Ar nebulizer gas and He carrier gas flows were tuned to achieve m/z = 248/232 ratios of <0.1% (ThO/Th) and m/z = 232/238 ratios of 100 ± 1% (Th/U), while ablating NIST 610 in line scans and in single quadrupole mode. An automatic lens tune was performed on NIST 610 to maximize sensitivity in the mid-mass range with m/z = 88 (Sr) as the sensitivity monitor. Laser parameters for the sensitivity and gas flow tuning were 50 Hz repetition rate, 5 μm circular spot size, and 4 J cm−2 fluence.
000 cps for m/z = 31 and 42, the Ar nebulizer gas and He carrier gas flows were tuned to achieve m/z = 248/232 ratios of <0.1% (ThO/Th) and m/z = 232/238 ratios of 100 ± 1% (Th/U), while ablating NIST 610 in line scans and in single quadrupole mode. An automatic lens tune was performed on NIST 610 to maximize sensitivity in the mid-mass range with m/z = 88 (Sr) as the sensitivity monitor. Laser parameters for the sensitivity and gas flow tuning were 50 Hz repetition rate, 5 μm circular spot size, and 4 J cm−2 fluence.
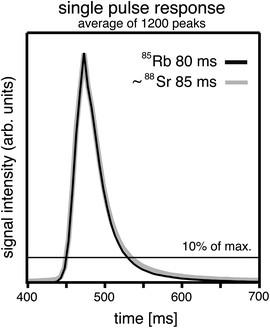
After sensitivity and carrier gas flow tuning, the ICP was switched to MS/MS mode. To resolve the isobaric interference of 87Rb and 87Sr, Sr isotopes were measured as SrO+ molecular ions in mass shift mode using an N2O-filled reaction cell. Throughout this paper we use the notation “∼yX” with y being the atomic mass of element X to refer to a +16 oxygen mass shift of that particular isotope (e.g. ∼88Sr, refers to 88Sr16O). Flow rates of N2O were tuned to yield maximum counts on m/z = 104 (∼88Sr) and were between 15 and 19%. Typically, the ∼88Sr/(88Sr + ∼88Sr) ratio was 0.97. Counts on m/z = 101 (∼85Rb) where checked and suggested negligible formation of RbO+ (typically 1 count per second). After a second sensitivity tune in MS/MS mode the single pulse response (SPR), i.e., the combined wash-in and wash-out time, was determined by (1) ablating NIST 610 at 1 Hz and dosage 1 in line scan mode and recording m/z = 85 (Rb) and m/z = 104 (∼88Sr) at a dwell time of 5 ms and (2) averaging the full width at 10% of the maximum of 1200 single pulses. Usually, 85Rb and ∼88Sr yielded similar SPR (Fig. 2 and Table 1). The last tuning step was tuning of pulse–analog (P/A) factors to correct for the non-linear response across the pulse to analog switch of the detector, which appears between 1 and 2 million counts per second (cps) or, more precisely, at count rates of 10 million cps multiplied by the respective P/A factor (J. Hansmann, Agilent, personal communication). P/A tuning is done by switching the ICP from time-resolved analysis (TRA) to spectrum mode, opt-in “independent P/A factor” in the mass hunter configuration and “P/A factor adjustment” and then running several line scans with different spot diameter as calibration standards on NIST610. Resulting P/A factors were between ∼0.15 and 0.17, varied between sessions and also displayed a certain relative difference between Sr isotopes (typically 1–2% difference). It should be noted that for all mappings all ∼ySr nuclides are acquired in pulse mode, whereas 85Rb is acquired in pulse mode in NIST610, Phalaborwa biotite, GER2B, WIL1A and GÄD08 and in analog mode in SagaB biotite and Harvard 98973 muscovite (https://doi.org/10.26434/chemrxiv-2023-273lw-v2).
| Session | Line scan (mapping) | Spots | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GÄD08 | GER2B | WIL1A | GÄD08 | GE2B/WIL1A | Homogeneity | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a Dosage refers to the number of laser shots applied within the diameter of the laser beam during its vertical movement. Q1 and Q2 denote the quadrupoles before and after the collision-reaction cell, respectively. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Date | 22/03/2022 | 28/06/2022 | 29/06/2022 | 30/05/2023 | 08/08/2022 | 23/05/2022 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Spot size (μm) | 3 | 4 | 3 | 65 | 65 | 65 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fluence (J cm−2) | 5.0 | 5.0 | 5.0 | 5.0 | 5.0 | 5.0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| He (l min−1) | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N2 (ml min−1) | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SPR 85Rb (ms) | 136 | 80 | 80 | — | — | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SPR ∼88Sr (ms) | 112 | 85 | 85 | — | — | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dosage | 10 | 10 | 10 | — | — | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Repetition rate (Hz) | 50 | 118 | 118 | 10 Hz | 10 Hz | 10 Hz | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Scan speed (μm s−1) | 15.0 | 47.2 | 35.4 | — | — | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Mapping time (h) | 1.5 | 8.0 | 7.0 | 60 s per shot | 60 s per shot | 60 s per shot | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Element | m/z Q1 | m/z Q2 | Dwell time (ms) | Dwell time (ms) | ||||
|---|---|---|---|---|---|---|---|---|
| Li | 7 | 7 | — | 10 | 20 | 1 | 1 | 1 |
| Na | 23 | 23 | — | — | — | 1 | 1 | 1 |
| Mg | 24 | 24 | — | — | — | 1 | 1 | 1 |
| Al | 27 | 27 | — | 1 | 1 | 1 | 1 | 1 |
| Si | 28 | 60 | 1 | 1 | 1 | 1 | 1 | 1 |
| K | 39 | 39 | — | — | — | 1 | 1 | 1 |
| Ca | 44 | 44 | — | — | — | 1 | 1 | 1 |
| Ti | 47 | 63 | — | — | — | 1 | 1 | 1 |
| Fe | 57 | 57 | — | 1 | 1.8 | 1 | 1 | 1 |
| Rb | 85 | 85 | 10 | 10 | 10 | 50 | 50 | 50 |
| Sr | 86 | 102 | — | — | — | 70 | 70 | 100 |
| Sr | 87 | 103 | 109.7 | 35 | 24.6 | 70 | 70 | 100 |
| Sr | 88 | 104 | 10.4 | 10 | 10 | 70 | 70 | — |
| Total sweep time (ms) | 140.10 | 85.00 | 85.40 | 294 | 294 | 283 | ||
For mapping sessions, the following mass channels were recorded: m/z = 7 (Li), m/z = 27 (Al), m/z = 60 (∼28Si), m/z = 57 (Fe), m/z = 85 (Rb), m/z = 103 (∼87Sr), m/z = 104 (∼88Sr). Dwell times, repetition rate and scan speed (Table 1) were optimized on test line scans on target grains to suppress aliasing and carry-over effects and to obtain a signal/noise ratio >10 for each mass channel. Grains were mapped with a 3–4 μm round spot at a fluence of 5.0 J cm−2 by using a raster of unidirectional scans with no overlap between lines and a 2 s pause after each line. The total penetration depth of the laser is estimated to between 1 and 2 μm based on the 10-fold degree of spot overlap (dosage in Table 1) and assuming 100–200 nm ablation per laser shot. At regular intervals (∼every 120 minutes), a set of reference materials (RM) was ablated in 30–40 s long line scans (total of 6–15 scans per RM and session). Reference materials were NIST610 as the primary calibration standard and the in-house secondary RM, which are single crystal mica, namely SagaB biotite, Phalaborwa biotite and Harvard 98973 muscovite. In run GÄD08, the pressed mica nanopowder MicaMg9,26 has been measured in addition. A comprehensive overview of the essential ICP and laser settings used in each session is presented in Tables 1 and 2.
| Session | Line | Spots | ||||
|---|---|---|---|---|---|---|
| GÄD08 | GER2B | WIL1A | GÄD08 | GER2B/WIL1A | Homogeneity | |
| Plasma | ||||||
| RF power (W) | 1450 | 1400 | 1400 | 1400 | 1450 | 1400 |
| RF matching (V) | 0.86 | 0.88 | 0.90 | 0.86 | 0.87 | 0.87 |
| Sample depth (mm) | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 5.0 |
| Nebulizer gas (l min−1) | 0.6 | 0.6 | 0.6 | 0.6 | 0.55 | 0.8 |
| Plasma gas (l min−1) | 15 | 15 | 15 | 15 | 15 | 15 |
| Auxiliary gas (l min−1) | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Lenses | ||||||
| Extract 1 (V) | −11.5 | −12.0 | −12.0 | −9.6 | −12.0 | −12.0 |
| Extract 2 (V) | −250 | −250 | −250 | −245 | −250 | −240 |
| Omega bias (V) | −135 | −130 | −145 | −140 | −145 | −140 |
| Omega lens (V) | 6.8 | 7.0 | 6.2 | 7.4 | 6.2 | 6.8 |
| Q1 entrance (V) | −50 | −50 | −50 | −50 | −50 | −50 |
| Q1 exit (V) | 0.0 | −1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Cell focus (V) | 2.0 | 2.0 | 2.0 | 3.0 | 4.0 | 4.0 |
| Cell entrance (V) | −40 | −40 | −40 | −40 | −40 | −40 |
| Cell exit (V) | −60 | −60 | −60 | −60 | −60 | −60 |
| Deflect (V) | −1.2 | −0.8 | −0.8 | −0.8 | −0.4 | −0.8 |
| Plate bias (V) | −50 | −50 | −50 | −50 | −50 | −50 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Q1 | ||||||
| Q1 bias (V) | −1.0 | −2.0 | −2.0 | −2.0 | −1.0 | −1.0 |
| Q1 prefilter bias (V) | −5.5 | −9.5 | −6.0 | −8.5 | −6.0 | −5.5 |
| Q1 postfilter bias (V) | −9.0 | −7.0 | −9.0 | −3.0 | −9.0 | −5.0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Cell | ||||||
| N2O gas flow (%) | 15 | 19 | 19 | 18 | 14 | 15 |
| OctP bias (V) | −8.0 | −8.0 | −8.0 | −8.0 | −8.0 | −8.0 |
| OctP RF (V) | 140 | 150 | 180 | 180 | 180 | 180 |
| Axial acceleration (V) | 2.00 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| Energy discrimination (V) | −7.0 | −7.0 | −7.0 | −7.0 | −7.0 | −7.0 |
2.4. LA-ICP-MS/MS isotope ratios, Rb–Sr and concentrations by single spot ablation
Following the initial mapping process, the mica samples underwent a re-investigation using conventional analysis, employing static spot ablation to validate the accuracy of the mapped age distribution (Fig. 1). This verification procedure was conducted in two separate sessions, namely “GER2B/Wil1A spot” and “GÄD08 spot”. Moreover, the single crystal reference materials were analyzed during an additional session by randomly placing 28–30 spots across the single crystal to assess both the composition and the uniformity of the Rb–Sr age signal. This session is referred to as “homogeneity”. The same interface tubing is used for the aerosol transport, but another higher volume glass adapter from Glass Expansion is installed before the ICP plasma inlet as a signal smoothing device. The tuning procedure was identical to the mapping sessions and the following mass channels were recorded m/z = 7 (Li), m/z = 23 (Na), m/z = 24 (Mg), m/z = 27 (Al), m/z = 39 (K), m/z = 44 (Ca), m/z = 57 (Fe), m/z = 60 (∼28Si), m/z = 63 (∼47Ti) m/z = 85 (Rb), m/z = 102 (∼86Sr) m/z = 103 (∼87Sr), m/z = 104 (∼88Sr) with dwell times compiled in Table 1. While 85Rb was acquired in analog mode, ∼86Sr and ∼87Sr were always acquired in pulse mode. In NIST610, ∼88Sr is acquired in analog mode but in pulse mode for all mica samples, hence being the only non-P/A matched nuclide during spot analysis (https://doi.org/10.26434/chemrxiv-2023-273lw-v2). Spot analyses of GER2B, Wil1A, and GER2B were bracketed by analyses of NIST610, SagaB, Harvard 98973, Phalaborwa and MicaMg RMs. Spot size was 65 μm at a repetition rate of 10 Hz and a fluence of 5.0 J cm−2. One spot analysis comprised 30 seconds of gas blank and a 30-second period to allow for complete wash-out of the aerosol. The length of the actual ablation interval was 40 s during “GER2B/Wil1A spot”, and “GÄD08 spot” and 60 s during “homogeneity”.2.5. Data reduction strategy for elemental concentrations and phase assignment
Elemental and isotopic concentrations are processed using the software HDIP (version 1.6, Teledyne Photon Machines). The background was fitted using a cubic spline function for each mass channel and drift is corrected linearly using NIST610 as a drift monitor. For the elemental concentration maps, each mass sweep is transformed into a quadratic pixel and is calibrated using NIST610 line scan analyses. The assignment of pixels to specific mineral phases (muscovite, biotite, quartz, plagioclase, K-Fsp) is achieved using the labeled segments tool within HDIP. This tool provides flexibility in pixel selection, allowing manual selection, cluster analyses based on a k-means algorithm, or user-defined thresholds using logical operators. In the case of the k-means algorithm, a predefined number of clusters is necessary, which we determined based on the expected mineral phases. For instance, in the GER2B dataset, we used 3 clusters for quartz, plagioclase, and muscovite, while in the GÄD 08 dataset, 4 clusters were utilized to represent quartz, plagioclase, muscovite, and biotite. The k-means algorithm partitions the data points into clusters by assigning each point to the cluster whose mean (centroid) is closest to the point. This iterative process refines cluster assignments by recalculating centroids and reassigning data points until the clusters' positions converge and remain stable. To account for mixed analyses occurring at grain boundaries, an additional cluster per map was added. The clusters were generated by taking into account specific mass channels (28Si, 85Rb, 88Sr, 87Sr for GÄD08 and 7Li, 27Al, 28Si, 85Rb, 88Sr, 87Sr for GER2B). However, in the case of the WIL1A mapping, the compositional variability of muscovite and the appearance of K-Fsp as an additional phase posed challenges for the k-means filter. Therefore, we opted for the logical operators tool, where specific thresholds were defined for each of the four phases.Muscovite: 87Sr < 5 μg g−1, Rb > 50 μg g−1, Fe < 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μg g−1.
000 μg g−1.
Plagioclase: 88Sr > 3 μg g−1, Rb < 20 μg g−1, Fe < 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μg g−1.
000 μg g−1.
Biotite: Fe > 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μg g−1.
000 μg g−1.
K-Fsp: 88Sr > 40 μg g−1, Rb > 10 μg g−1.
In a last step, all pixels assigned to mica were normalized to SiO2 concentrations of 45.2 wt%, corresponding to Kal3Si3O10(OH)1.8F0.2 stoichiometry. The mean normalization factor from all mica pixels was also applied to all non-mica pixels. This procedure introduces a systematic error to the biotite composition, whose SiO2 concentration deviates slightly from muscovite (e.g. 41.6 wt% considering K(Mg2.5Fe0.5)AlSi3O10(OH)1.8F0.2 stoichiometry). However, elemental and isotopic ratios or relative compositional changes within a map remain unaffected.
Concentrations obtained during spot analyses were calibrated on NIST 610 and normalized to a sum of SiO2 + Al2O3 + TiO2 + FeO + MgO + CaO + Na2O + K2O = 95%, assuming H2O + F = 5 wt%. The compositions obtained for Phalaborwa biotite, Harvard 98973 muscovite and SagaB biotite during session homogeneity are displayed in Table 3.
| Phalaborwa biotite (n = 29) | SagaB biotite (n = 28) | Harvard 98973 (n = 30) | LOD (ppm) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 2s | Mean | 2s | Mean | 2s | Dyar et al.33 (2001) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a Major element composition for Harvard 98973 data of Dyar et al. (2001)33 are from GFZ electron microprobe session, except Li2O, which is from the PIGE session. The limit of detection (LOD) for LA-ICP-MS data is calculated after Longerich et al. (1996).45 Elemental and isotopic concentrations normalized to SiO2 + Al2O3 + TiO2 + FeO + MgO + CaO + Na2O + K2O = 95%. Expected age of Phalaborwa biotite is from Wu et al. (2011).32 SagaB and Harvard 98973 expected ages are based on ID-TIMS analyses presented in this study. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SiO2 (wt%) | 42.28 | 0.40 | 38.44 | 0.28 | 45.80 | 0.22 | 45.67 (0.28) | 1.02 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Al2O3 (wt%) | 7.66 | 1.60 | 11.56 | 0.36 | 32.83 | 0.38 | 30.58 (0.34) | 0.05 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TiO2 (wt%) | 0.70 | 8.52 | 2.98 | 0.78 | 0.03 | 9.50 | 0.08 (0.02) | 0.13 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| FeO (wt%) | 10.80 | 1.98 | 27.41 | 0.92 | 4.91 | 2.18 | 6.65 (0.48) | 0.85 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| MgO (wt%) | 22.27 | 1.12 | 4.38 | 1.02 | 0.01 | 4.08 | 0.02 (0.02) | 0.04 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CaO (wt%) | <LOD | 0.07 | 53.20 | <LOD | 0.00 (0.00) | 151 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Na2O (wt%) | 0.037 | 5.40 | 0.42 | 6.70 | 0.52 | 3.50 | 0.38 (0.08) | 0.29 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| K2O (wt%) | 11.26 | 1.52 | 9.75 | 0.70 | 10.90 | 0.34 | 10.14 (0.17) | 0.70 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Li (μg g−1) | 9.77 | 7.10 | 0.44 | 2.96 | 1886 | 6.68 | 1998 (18.61) | 0.15 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Rb (μg g−1) | 791.8 | 1.16 | 3862 | 0.58 | 3826 | 1.20 | 0.0070 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86Sr (μg g−1) | 0.023 | 28.38 | 0.073 | 7.30 | 0.009 | 10.02 | 0.00004 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87Sr (μg g−1) | 5.83 | 0.92 | 4.069 | 0.66 | 3.600 | 1.14 | 0.00008 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87Sr/87Rb | 0.02596 | 0.39 | 0.00379 | 0.32 | 0.00341 | 0.33 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Expected age (Ma) | 2062 ± 2 | 295.4 ± 1.4 | 266.8 ± 1.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.6. Data reduction strategy and uncertainty propagation for LA-ICP-MS/MS based Rb–Sr ages
The data reduction and uncertainty propagation strategy for line, map and spot derived Rb–Sr ages largely follows the recommendations by Horstwood et al. (2016)37 and Rösel & Zack (2022).20 An overview of the workflow is summarized in Fig. 3. | ||
| Fig. 3 Schematic illustration of the data reduction and uncertainty propagation workflow. For further information see text. | ||
For line scan/mapping analyses the background was subtracted for each mass channel using a cubic spline function in HDIP. Drift is linearly corrected using NIST610 as a drift monitor. Background and drift correction for spot analyses is performed using an in-house Excel spreadsheet. Here, the background of the Rb and Sr mass channels was fitted for each individual spot by subtracting the mean gas blank signal obtained in the time interval 1–26 s before ablation was initiated. No downhole fractionation correction was applied.
After transferring each channel from counts to counts per second based on the applied dwell times (Table 2), “raw” isotope ratios were calculated for each individual mass sweep (e.g. ∼87Sr/∼88Sr and ∼85Rb/∼88Sr). Mean isotope ratios and their respective standard deviations (SD) and standard errors (SE; SE = SD/√n with n being the number of mass sweeps) are then calculated based on a “mean of ratios” approach.38 For spot analyses all mass sweeps within the first ∼10 seconds of the ablation interval were discarded to allow for stabilization of the signal. This interval was held constant for each individual spot during a particular session. No such cut-off was applied for line scan analyses. Calibration factors are derived based on replicate analyses (either spot or line scans) on NIST610 glass to correct for mass bias. “Raw” isotope ratios (e.g. ∼87Sr/∼88Sr and 85Rb/∼88Sr) were transferred into “true” isotope ratios (e.g.87Sr/86Sr and 87Rb/86Sr ratios) by applying the following and analogous equations:
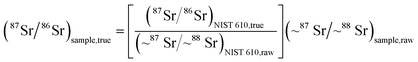 | (1) |
For the true Rb–Sr isotope ratios of NIST 610 the following working values are used: 87Rb/86Sr = 2.3300 and 87Sr/86Sr = 0.709699.15,25
Ages are calculated based on the isochron equation:19
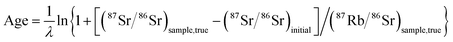 | (2) |
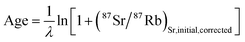 | (3) |
Given that:
| [(87Sr/86Sr)sample,true − (87Sr/86Sr)initial]/(87Rb/86Sr)sample,true = [1 + (87Sr/87Rb)Sr,initial,corrected] | (4) |
An essential aspect during data reduction is the uncertainty of the common Sr correction (γ), which corrects for the amount of common 87Sr (87Src) that did not form via in situ radioactive decay of 87Rb. We implemented the procedure proposed by Rösel & Zack (2022),20 treating γ as a systematic uncertainty that is calculated by weighting the uncertainty of (87Sr/86Sr)initial to the magnitude of the common Sr correction [eqn (9) in Rösel & Zack (2022)].20 In case the fraction of 87Src is low enough (<∼1%), a common Sr correction is not required and ages are directly calculated from the (87Sr/86Rb)true ratios:
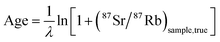 | (5) |
This way ages are calculated for each of the spot analyses and line scans, both of which consist of multiple mass sweeps. For line scan analyses on NIST610 the number of mass sweeps is between 280 and 580, depending on dwell times and length of the line scans (Table 5). For spot analysis, the number of mass sweeps is either 97 (sessions “GER2B/Wil1A” and “GÄD08”) or 151 (session “homogeneity”).
| Sample | Rb [μg g−1] | Sr [μg g−1] | 87Rb/86Sr | ±2s (%) | 87Sr/86Sr | ±2sm (%) |
|---|---|---|---|---|---|---|
| SagaB: 295.4 ± 1.4 Ma; Sr ini. = 0.7049 ± 0.0014; MSWD = 1.7 | ||||||
| Biotite | 3043 | 5.22 | 5331 | 0.5 | 22.7375 | 0.0024 |
| Feldspar | 402 | 55 | 21.32 | 1.5 | 0.793036 | 0.0017 |
| Bt + feldspar | 2502 | 24.2 | 340.0 | 1.5 | 2.12442 | 0.0020 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Harvard 98973: 266.8 ± 1.6 Ma; Sr ini. = 0.720 ± 0.011; MSWD = 0.12 | ||||||
| Musc 1 | 3666 | 3.98 | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 860 |
1.5 | 197.872 | 0.0405 |
| Musc 2 | 4268 | 4.57 | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575 575 |
2.4 | 205.646 | 0.0160 |
| Musc 3 | 3639 | 3.96 | 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 847 847 |
0.74 | 254.067 | 0.0620 |
| Assumed ini. | 0.0001 | 100 | 0.72 | Assumed 1.5 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Phalaborwa: 2058.2 ± 7.0 Ma; Sr ini. = 0.707671 ± 0.000035; MSWD = 2.6 | ||||||
| Apatite | 0.03 | 3751 | 0.00002 | 1.5 | 0.707672 | 0.0012 |
| Biotite 1 | 654 | 12.5 | 262.48 | 0.5 | 8.34328 | 0.0040 |
| Biotite 2 | 635 | 21.1 | 116.59 | 0.5 | 4.11875 | 0.0019 |
| Session | ∼87Sr/∼88Sr | 87Sr/86Sr | 2SE (%) | 85Rb/∼88Sr | 87Rb/86Sr | 2SE (%) | ∼87Sr/85Rb | 87Sr/87Rb | 2SE (%) |
|---|---|---|---|---|---|---|---|---|---|
| GÄD08 (40 s line scan) | 0.9014 | 0.7130 | 2.56 | 0.7004 | 2.4051 | 1.62 | 1.28698 | 0.29637 | 1.63 |
| 0.8971 | 0.7096 | 2.24 | 0.6788 | 2.3309 | 1.38 | 1.32160 | 0.30434 | 1.59 | |
| 0.8931 | 0.7064 | 2.48 | 0.6600 | 2.2664 | 1.48 | 1.35318 | 0.31162 | 1.69 | |
| 0.8995 | 0.7115 | 2.23 | 0.6767 | 2.3237 | 1.32 | 1.32924 | 0.30610 | 1.62 | |
| 0.8965 | 0.7091 | 2.13 | 0.6752 | 2.3186 | 1.31 | 1.32775 | 0.30576 | 1.51 | |
| 0.8959 | 0.7086 | 2.17 | 0.6801 | 2.3354 | 1.39 | 1.31731 | 0.30336 | 1.54 | |
| Mean | 0.8973 | 0.6785 | 1.32268 | ||||||
| 2SE (%) | 0.27 | 1.56 | 1.33 | ||||||
| Expected | 0.7097 | 2.3300 | 0.30459 | ||||||
| Calibration factor | 0.7910 | 3.4339 | 0.23028 | ||||||
| GER2B (40 s line scan) | 0.2941 | 0.7145 | 0.62 | 0.6313 | 2.3246 | 0.92 | 0.46586 | 0.30731 | 0.60 |
| 0.2894 | 0.7031 | 0.67 | 0.6147 | 2.2635 | 0.80 | 0.47080 | 0.31057 | 0.48 | |
| 0.2918 | 0.7089 | 0.69 | 0.6386 | 2.3515 | 0.81 | 0.45694 | 0.30143 | 0.51 | |
| 0.2911 | 0.7072 | 0.53 | 0.6293 | 2.3172 | 0.65 | 0.46258 | 0.30515 | 0.41 | |
| 0.2913 | 0.7077 | 0.51 | 0.6298 | 2.3191 | 0.63 | 0.46253 | 0.30511 | 0.39 | |
| 0.2913 | 0.7077 | 0.52 | 0.6298 | 2.3191 | 0.66 | 0.46253 | 0.30511 | 0.44 | |
| 0.2916 | 0.7084 | 1.76 | 0.6555 | 2.4137 | 3.16 | 0.44485 | 0.29345 | 1.63 | |
| 0.2919 | 0.7091 | 0.49 | 0.6276 | 2.3110 | 0.69 | 0.46511 | 0.30681 | 0.47 | |
| 0.2922 | 0.7099 | 0.54 | 0.6312 | 2.3242 | 0.66 | 0.46293 | 0.30538 | 0.41 | |
| 0.2921 | 0.7096 | 0.55 | 0.6324 | 2.3286 | 0.65 | 0.46189 | 0.30469 | 0.42 | |
| 0.2919 | 0.7091 | 0.57 | 0.6313 | 2.3246 | 0.69 | 0.46238 | 0.30502 | 0.42 | |
| 0.2919 | 0.7091 | 0.52 | 0.6297 | 2.3187 | 0.71 | 0.46355 | 0.30579 | 0.50 | |
| 0.2934 | 0.7128 | 0.51 | 0.6356 | 2.3404 | 0.64 | 0.46161 | 0.30451 | 0.42 | |
| 0.2932 | 0.7123 | 0.55 | 0.6332 | 2.3316 | 0.66 | 0.46304 | 0.30545 | 0.57 | |
| 0.2948 | 0.7162 | 0.50 | 0.6416 | 2.3625 | 0.62 | 0.45948 | 0.30310 | 0.41 | |
| Mean | 0.2921 | 0.6328 | 0.46174 | ||||||
| 2SE (%) | 0.24 | 0.70 | 0.62 | ||||||
| Expected | 0.7097 | 2.3300 | 0.30459 | ||||||
| Calibration factor | 2.4294 | 3.6822 | 0.65966 | ||||||
| WIL1A (50 s line scan) | 0.2054 | 0.7082 | 0.60 | 0.6391 | 2.3234 | 0.61 | 0.32139 | 0.30479 | 0.58 |
| 0.2055 | 0.7085 | 0.57 | 0.6393 | 2.3241 | 0.60 | 0.32145 | 0.30484 | 0.58 | |
| 0.2055 | 0.7085 | 0.57 | 0.6400 | 2.3266 | 0.67 | 0.32109 | 0.30451 | 0.95 | |
| 0.2059 | 0.7099 | 0.49 | 0.6423 | 2.3350 | 0.57 | 0.32057 | 0.30401 | 0.56 | |
| 0.2056 | 0.7088 | 0.54 | 0.6403 | 2.3277 | 0.61 | 0.32110 | 0.30452 | 0.50 | |
| 0.2057 | 0.7092 | 0.49 | 0.6415 | 2.3321 | 0.54 | 0.32065 | 0.30409 | 0.50 | |
| 0.2057 | 0.7092 | 0.53 | 0.6424 | 2.3354 | 0.54 | 0.32021 | 0.30367 | 0.52 | |
| 0.2057 | 0.7092 | 0.53 | 0.6417 | 2.3328 | 0.57 | 0.32055 | 0.30400 | 0.54 | |
| 0.2061 | 0.7106 | 0.54 | 0.6416 | 2.3324 | 0.55 | 0.32123 | 0.30464 | 0.53 | |
| 0.2059 | 0.7099 | 0.56 | 0.6425 | 2.3357 | 0.56 | 0.32047 | 0.30392 | 0.59 | |
| 0.2064 | 0.7116 | 0.57 | 0.6442 | 2.3419 | 0.62 | 0.32040 | 0.30385 | 0.71 | |
| 0.2057 | 0.7092 | 0.55 | 0.6415 | 2.3321 | 0.59 | 0.32065 | 0.30409 | 0.58 | |
| 0.2065 | 0.7120 | 0.51 | 0.6448 | 2.3441 | 0.60 | 0.32025 | 0.30371 | 0.54 | |
| 0.2065 | 0.7120 | 0.56 | 0.6445 | 2.3430 | 0.65 | 0.32040 | 0.30386 | 0.55 | |
| 0.2056 | 0.7088 | 0.51 | 0.6282 | 2.2837 | 0.65 | 0.32728 | 0.31038 | 0.52 | |
| Mean | 0.2058 | 0.6409 | 0.32118 | ||||||
| 2SE (%) | 0.09 | 0.31 | 0.28 | ||||||
| Expected | 0.7097 | 2.3300 | 0.30459 | ||||||
| Calibration factor | 3.4477 | 3.6354 | 0.94835 |
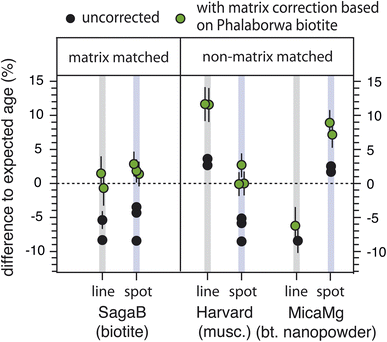
In both line and spot mode acquisition, the NIST610 calibrated ages of the mica RM were offset with respect to their expected ages by up to ∼11% (Fig. 4 and Table 7). This bias is in the order of magnitude that has been observed in other studies,29–31 where it is ascribed to matrix effects resulting from the use of a non-matrix matched primary reference material (e.g. NIST610 glass or pressed nanopowder Mica-Mg). It has been suggested to correct for that matrix-induced bias by co-analyzing a matrix-matched, i.e. crystalline mica with known age.30 We adapted this approach by calculating matrix correction factors (MCF):
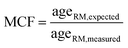 | (6) |
| Agematrix corrected = MCF × ageNIST calibrated | (7) |
| ∼87Sr/∼86Sr | 87Sr/86Sr | 2SE (‰) | 85Rb/∼86Sr | 87Rb/86Sr | 2SE (‰) | ∼87Sr/85Rb | 87Sr/87Rb | 2SE (‰) | |
|---|---|---|---|---|---|---|---|---|---|
| GER2B/WIL1A (spots) | 0.72853 | 0.7096 | 0.63 | 8.25120 | 2.3445 | 0.72 | 0.08836 | 0.30343 | 0.69 |
| 0.72888 | 0.7099 | 0.67 | 8.18057 | 2.3244 | 0.90 | 0.08924 | 0.30647 | 0.99 | |
| 0.72764 | 0.7087 | 0.68 | 8.16421 | 2.3197 | 0.82 | 0.08921 | 0.30635 | 0.81 | |
| 0.72717 | 0.7083 | 0.96 | 8.27992 | 2.3526 | 1.44 | 0.08794 | 0.30199 | 1.27 | |
| 0.73017 | 0.7112 | 1.11 | 8.26125 | 2.3473 | 1.50 | 0.08852 | 0.30399 | 1.41 | |
| 0.73008 | 0.7111 | 1.06 | 8.20448 | 2.3312 | 1.14 | 0.08896 | 0.30549 | 1.16 | |
| 0.72607 | 0.7072 | 0.94 | 8.15324 | 2.3166 | 1.28 | 0.08888 | 0.30522 | 1.21 | |
| 0.72807 | 0.7091 | 0.99 | 8.16681 | 2.3205 | 1.28 | 0.08899 | 0.30559 | 1.32 | |
| 0.72567 | 0.7068 | 1.03 | 8.16689 | 2.3205 | 1.40 | 0.08874 | 0.30474 | 1.42 | |
| 0.73381 | 0.7147 | 1.44 | 8.18843 | 2.3266 | 2.24 | 0.08974 | 0.30816 | 2.09 | |
| 0.72715 | 0.7082 | 1.26 | 8.20666 | 2.3318 | 1.92 | 0.08849 | 0.30387 | 1.76 | |
| 0.73112 | 0.7121 | 1.09 | 8.20293 | 2.3307 | 1.58 | 0.08880 | 0.30495 | 1.46 | |
| 0.72937 | 0.7104 | 0.93 | 8.23217 | 2.3391 | 1.24 | 0.08791 | 0.30187 | 1.25 | |
| 0.72815 | 0.7092 | 0.90 | 8.13048 | 2.3102 | 1.22 | 0.08883 | 0.30504 | 1.21 | |
| 0.72782 | 0.7089 | 0.90 | 8.21518 | 2.3342 | 1.20 | 0.08787 | 0.30173 | 1.20 | |
| Mean | 0.72865 | 8.20029 | 0.08870 | ||||||
| 2SE (%) | 0.15 | 0.27 | 0.31 | ||||||
| Expected | 0.7097 | 2.3300 | 0.30459 | ||||||
| Calibration factor | 0.97400 | 0.28414 | 3.43406 | ||||||
| GÄD08 (spots) | 0.72528 | 0.7125 | 1.03 | 5.63831 | 2.3437 | 1.49 | 0.12912 | 0.30432 | 1.46 |
| 0.71951 | 0.7068 | 1.14 | 5.57035 | 2.3154 | 1.51 | 0.12968 | 0.30564 | 1.41 | |
| 0.72135 | 0.7086 | 0.82 | 5.53829 | 2.3021 | 1.31 | 0.13072 | 0.30808 | 1.36 | |
| 0.72498 | 0.7122 | 0.88 | 5.63313 | 2.3415 | 1.36 | 0.12915 | 0.30439 | 1.42 | |
| 0.72325 | 0.7105 | 0.90 | 5.67350 | 2.3583 | 1.27 | 0.12773 | 0.30105 | 1.17 | |
| 0.72197 | 0.7092 | 0.86 | 5.62590 | 2.3385 | 1.01 | 0.12846 | 0.30276 | 1.07 | |
| 0.72421 | 0.7114 | 0.57 | 5.59656 | 2.3263 | 0.92 | 0.12948 | 0.30516 | 0.91 | |
| 0.71996 | 0.7073 | 0.73 | 5.60574 | 2.3301 | 1.01 | 0.12863 | 0.30315 | 1.02 | |
| 0.71901 | 0.7063 | 0.77 | 5.57798 | 2.3186 | 1.22 | 0.12940 | 0.30498 | 1.23 | |
| 0.71986 | 0.7072 | 1.15 | 5.61409 | 2.3336 | 1.59 | 0.12883 | 0.30362 | 1.49 | |
| 0.72475 | 0.7120 | 0.90 | 5.60244 | 2.3287 | 1.44 | 0.12994 | 0.30624 | 1.45 | |
| 0.72435 | 0.7116 | 1.05 | 5.59543 | 2.3258 | 1.42 | 0.12970 | 0.30567 | 1.29 | |
| 0.72262 | 0.7099 | 1.06 | 5.61006 | 2.3319 | 1.37 | 0.12902 | 0.30408 | 1.36 | |
| 0.72295 | 0.7102 | 1.11 | 5.61255 | 2.3329 | 1.53 | 0.12922 | 0.30454 | 1.52 | |
| 0.72243 | 0.7097 | 0.92 | 5.58758 | 2.3226 | 1.28 | 0.12949 | 0.30519 | 1.22 | |
| Mean | 0.72243 | 5.60546 | 0.12924 | ||||||
| 2SE (%) | 0.15 | 0.29 | 0.28 | ||||||
| Expected | 0.7097 | 2.3300 | 0.30459 | ||||||
| Calibration factor | 0.98238 | 0.41567 | 2.35684 | ||||||
| Homogeneity (spots) | 0.7228 | 0.7087 | 0.48 | 6.131607 | 2.3218 | 0.82 | 0.11817 | 0.30554 | 0.94 |
| 0.7239 | 0.7097 | 0.49 | 6.179168 | 2.3399 | 0.87 | 0.11747 | 0.30371 | 0.97 | |
| 0.7247 | 0.7105 | 0.42 | 6.196586 | 2.3464 | 0.86 | 0.11727 | 0.30320 | 0.92 | |
| 0.7262 | 0.7120 | 0.49 | 6.208785 | 2.3511 | 0.75 | 0.11717 | 0.30294 | 0.83 | |
| 0.7261 | 0.7119 | 0.48 | 6.155889 | 2.3310 | 0.85 | 0.11826 | 0.30576 | 1.00 | |
| 0.7213 | 0.7071 | 0.46 | 6.131273 | 2.3217 | 0.94 | 0.11796 | 0.30499 | 0.94 | |
| 0.7238 | 0.7096 | 0.49 | 6.193627 | 2.3453 | 0.90 | 0.11710 | 0.30277 | 0.94 | |
| 0.7261 | 0.7119 | 0.47 | 6.130510 | 2.3214 | 0.89 | 0.11867 | 0.30682 | 0.91 | |
| 0.7245 | 0.7103 | 0.55 | 6.132414 | 2.3221 | 0.96 | 0.11841 | 0.30614 | 0.95 | |
| 0.7237 | 0.7096 | 0.38 | 6.109771 | 2.3136 | 0.69 | 0.11849 | 0.30635 | 0.73 | |
| 0.7252 | 0.7110 | 0.53 | 6.101410 | 2.3104 | 0.73 | 0.11888 | 0.30736 | 0.77 | |
| 0.7227 | 0.7085 | 0.41 | 6.086960 | 2.3049 | 0.81 | 0.11885 | 0.30728 | 0.90 | |
| 0.7229 | 0.7087 | 0.49 | 6.190817 | 2.3443 | 0.96 | 0.11696 | 0.30240 | 1.06 | |
| 0.7225 | 0.7083 | 0.44 | 6.099260 | 2.3096 | 0.89 | 0.11857 | 0.30657 | 0.95 | |
| 0.7208 | 0.7067 | 0.50 | 6.127270 | 2.3202 | 0.89 | 0.11772 | 0.30437 | 0.90 | |
| 0.7237 | 0.7095 | 0.52 | 6.149925 | 2.3288 | 0.86 | 0.11768 | 0.30426 | 0.84 | |
| 0.7232 | 0.7090 | 0.50 | 6.132032 | 2.3220 | 0.82 | 0.11795 | 0.30497 | 0.89 | |
| 0.7278 | 0.7135 | 0.70 | 6.160059 | 2.3326 | 0.95 | 0.11825 | 0.30574 | 1.11 | |
| 0.7226 | 0.7084 | 0.44 | 6.243558 | 2.3642 | 0.96 | 0.11580 | 0.29941 | 1.00 | |
| 0.7238 | 0.7096 | 0.52 | 6.155113 | 2.3307 | 0.93 | 0.11767 | 0.30422 | 1.06 | |
| 0.7234 | 0.7092 | 0.50 | 6.200097 | 2.3478 | 0.90 | 0.11667 | 0.30165 | 0.91 | |
| Mean | 0.72389 | 6.15315 | 0.11781 | ||||||
| 2SE (%) | 0.10 | 0.29 | 0.29 | ||||||
| Expected | 0.7097 | 2.3300 | 0.30459 | ||||||
| Calibration factor | 0.98039 | 0.37867 | 2.58548 |
| Line scan (this study) | Rb–Sr age (Ma) | 2sx (%) | Rb–Sr age (Ma) matrix corrected | 2s* (%) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Session | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a For Harvard 98973, SagaB and Phalaborwa, ages are calculated without a common Sr correction due to the high amount of 87Sr using eqn (3). Ages for MicaMg are calculated using eqn (2) with (87Sr/86Sr)initial = 0.72607 ± 0.0007.9 Single spot ages of Högsbo, La Posta, Mt Dromedary and McClure Mountain are from Rösel & Zack (2022).20 All ages are indicated as weighted means. 2sx denotes the uncertainty on the weighted mean calculated using random uncertainties. 2s* denotes the total uncertainty resulting from propagating all random and systematic uncertainties. Matrix correction for single spot and line scan ages presented in our study is based on Phalaborwa biotite. Expected ages for Phalaborwa are from Wu et al. (2011);32 for MicaMg from Hogmalm et al. (2017);9 for Högsbo from Romer & Smeds (1994);43 for La Posta from Zack & Hogmalm (2016);15 for Mt Dromedary from Williams et al. (1982);46 for McClure Mountain from Schoene & Bowring (2006).47 For SagaB and Harvard 98973 expected ages are based on ID-TIMS data presented in this study. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Phalaborwa (age = 2062 ± 2 Ma)
87
Rb/
86
Sr = 350–42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GÄD08 (n = 6) | 2013 | 0.8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Accuracy (%) | −2.38 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GER2B (n = 15) | 1902 | 0.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Accuracy (%) | −7.76 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| WIL1A (n = 15) | 1919 | 1.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Accuracy (%) | −6.94 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
SagaB (age = 295.4 ± 1.4 Ma)
87
Rb/
86
Sr = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–270 000–270![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GER2B (n = 15) | 270.2 | 0.8 | 293.0 | 2.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Accuracy (%) | −8.53 | −0.81 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| WIL1A (n = 15) | 278.8 | 1.2 | 299.5 | 2.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Accuracy (%) | −5.62 | 1.38 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Harvard 98973 (age 266.8 ± 1.6 Ma)
87
Rb/
86
Sr = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–44 000–44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GER2B (n = 15) | 273.9 | 0.6 | 296.9 | 2.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Accuracy (%) | 2.66 | 11.30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| WIL1A (n = 15) | 276.6 | 0.8 | 297.2 | 2.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Accuracy (%) | 3.67 | 11.39 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| MicaMg (age = 519.4 ± 6.5 Ma) 87 Rb/ 86 Sr = 154.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GÄD08 (n = 6) | 475.3 | 1.7 | 486.9 | 2.8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Accuracy (%) | −8.49 | −6.26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Single spot (this study) | Rb–Sr age (Ma) | 2sx (%) | Rb–Sr age (Ma) matrix corrected | 2s* (%) |
|---|---|---|---|---|
| Session | ||||
Phalaborwa (age = 2062 ± 2 Ma)
87
Rb/
86
Sr = 350–42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||||
| GER2B/WIL1A (n = 15) | 1939.3 | 0.5 | ||
| Accuracy (%) | −5.95 | |||
| GÄD08 (n = 15) | 1960.9 | 0.4 | ||
| Accuracy (%) | −4.90 | |||
| Homogeneity (n = 29) | 1834.2 | 0.4 | ||
| Accuracy (%) | −11.05 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
SagaB (age = 295.4 ± 1.4 Ma)
87
Rb/
86
Sr = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–270 000–270![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||||
| GER2B/WIL1A (n = 15) | 282.8 | 0.5 | 300.7 | 1.7 |
| Accuracy (%) | −4.27 | 1.79 | ||
| GÄD08 (n = 15) | 284.5 | 0.7 | 299.2 | 1.9 |
| Accuracy (%) | −3.69 | 1.29 | ||
| Homogeneity (n = 28) | 270.4 | 0.3 | 304.0 | 1.8 |
| Accuracy (%) | −8.45 | 2.92 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
Harvard 98973 (age = 266.8 ± 1.6 Ma)
87
Rb/
86
Sr = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–44 000–44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||||
| GER2B/WIL1A (n = 15) | 250.7 | 0.4 | 266.5 | 1.7 |
| Accuracy (%) | −6.05 | −0.11 | ||
| GÄD08 (n = 15) | 253.9 | 0.4 | 267.0 | 1.8 |
| Accuracy (%) | −4.97 | 0.07 | ||
| Homogeneity (n = 30) | 243.9 | 0.3 | 274.2 | 1.8 |
| Accuracy (%) | −8.79 | 2.79 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| MicaMg (age = 519.4 ± 6.5 Ma) 87 Rb/ 86 Sr = 154.6 | ||||
| GÄD08 (n = 15) | 529.2 | 0.7 | 556.5 | 1.9 |
| Accuracy (%) | 1.89 | 7.14 | ||
| GER2B/WIL1A (n = 15) | 532.7 | 0.7 | 566.4 | 1.9 |
| Accuracy (%) | 2.56 | 9.05 | ||
| Single spot (Rösel & Zack 2022)20 | Rb–Sr age (Ma) | 2sx (%) |
|---|---|---|
| Session | ||
Högsbo (age = 1029 Ma)
87
Rb/
86
Sr = 3440–24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||
191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 003 (n = 12) 003 (n = 12) |
1037.8 | 0.7 |
| Accuracy (%) | 0.86 | |
191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 (n = 9) 128 (n = 9) |
1037.0 | 0.7 |
| Accuracy (%) | 0.78 | |
203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 021 (n = 14) 021 (n = 14) |
1002.8 | 0.7 |
| Accuracy (%) | −2.54 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| La Posta (age = 91.6 Ma) 87 Rb/ 86 Sr = 408–1239 | ||
180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 (n = 27) 220 (n = 27) |
88.7 | 1.5 |
| Accuracy (%) | −3.17 | |
191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 (n = 7) 128 (n = 7) |
90.0 | 2.1 |
| Accuracy (%) | −1.75 | |
203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 021 (n = 7) 021 (n = 7) |
91.0 | 2.3 |
| Accuracy (%) | −0.66 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Mt Dromedary (age = 100.4 Ma) 87 Rb/ 86 Sr = 55–171.1 | ||
191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 003 (n = 7) 003 (n = 7) |
99.1 | 3.0 |
| Accuracy (%) | −1.28 | |
191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 (n = 9) 128 (n = 9) |
100.3 | 2.5 |
| Accuracy (%) | −0.10 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| McClure Mt (age = 523.98 Ma) 87 Rb/ 86 Sr = 110–940 | ||
191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 003 (n = 7) 003 (n = 7) |
511.5 | 1.0 |
| Accuracy (%) | −2.38 | |
191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 (n = 8) 128 (n = 8) |
513.7 | 1.1 |
| Accuracy (%) | −1.96 | |
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 321 (n = 10) 321 (n = 10) |
518.5 | 1.0 |
| Accuracy (%) | −1.05 | |
The total uncertainty (s*) of a single spot or line scan is calculated by adding the random uncertainty and all systematic uncertainties in quadrature:
| 2s* = srandom2 + γ2 + sλ2 + sy2 + sage,RM2 + εhomo2 + ε′2 | (8) |
Two-dimensional Rb–Sr age maps were created using HDIP. During this procedure, the 87Rb/86Sr and 87Sr/86Sr ratios, which had been calibrated with NIST610 and obtained in a single mass sweep, were converted into quadratic pixels. The pixel sizes were adjusted to correspond to the laser spot dimensions (3 μm for session GÄD08/WIL1A and 4 μm for session GER 2B). The numerical values of the pixels were then assigned to a color scale for visualization (Fig. 5). We employed the viridis color scheme, which features blue and yellow sequences, making it suitable for both color-blind individuals and black and white presentations. Finally, for each pixel which corresponds to a single mass sweep, an age is calculated by applying the Rb–Sr isochron equation (eqn (2)), which has been implemented in the HDIP channel calculator tool. The random uncertainty (srandom) of a single mass sweep (or pixel) is estimated by the standard deviation (SD) of the 87Rb/86Sr and 87Sr/86Sr ratios obtained during a single line scan on NIST610 (Fig. 5 and Table 5). For the GÄD08 session we have obtained a mean ratio uncertainty of 39% (2SD) on 87Rb/86Sr and 24% (2SD) on 87Sr/86Sr. For the subsequent sessions GER2B and WIL1A, NIST610 was polished with 1 μm diamond paste, significantly improving the uncertainty (mean 2SD uncertainty on 87Sr/86Sr = 12–13% and mean 2SD uncertainty on 87Rb/86Sr = 14.4–15.2%). Both of the latter isotope ratio uncertainties are similar to the uncertainties obtained in spot ablation mode (Table 6).
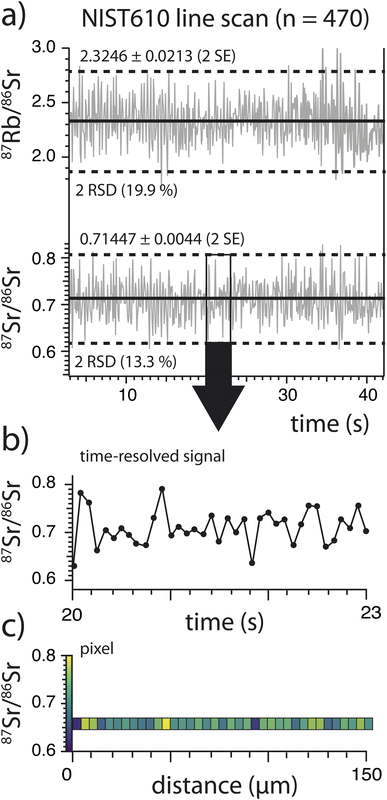 | ||
| Fig. 5 (a) Single line scan on NIST610 acquired during the mapping session of GER2B (analyses #1 in Table 5). (b) Blow-up of 87Sr/86Sr ratios within a short time segment (3 s) within that line scan. Each point within the time-resolved signal corresponds to a single mass sweep (n = 470, for the whole line scan). (c) To obtain 2D maps of 87Sr/86Sr, 87Rb/86Sr isotope ratios and ultimately ages, these values were transferred to colored pixel using the viridis color scheme. | ||
To further improve the measurement uncertainty on Rb–Sr ages, multiple pixels were pooled. This is accomplished through a meticulous user-driven selection of pixel segments employing the Rb–Sr age map as a reference to identify regions that represent homogeneous age populations. This way the mixed analyses of multiple age populations, as seen for example in the GER2B map (Fig. 6) is avoided. In sample GÄD08, which consists of co-genetic and apparently age homogeneous muscovite and biotite, we additionally analyzed segments comprising all biotite and muscovite pixel as assigned by the k-means algorithm (Fig. 7, see Section 2.5).
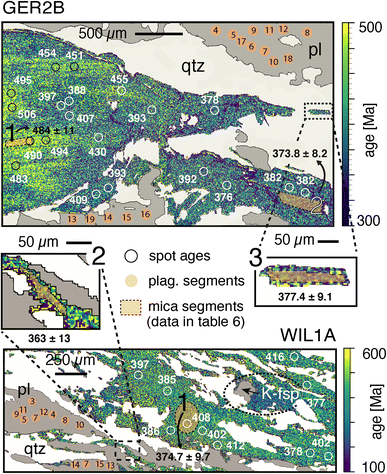 | ||
| Fig. 6 Rb–Sr age maps of deformed muscovite from two metapegmatites (GER2B and Wil1A) from the Western Bohemian Massif in NE Bavaria (Germany) consisting mainly of white mica and plagioclase. Different segments have been defined for plagioclase and mica for which isotope and age information is obtained (Tables 8 and 9). Image pixel size is 3 μm for WIL1A and 4 μm for GER2B. Values adjacent to the black and white circles indicate the single spot ages that have been acquired post mapping. For segments referring to mica, ages and uncertainties (95% conf.) in Ma are indicated. All ages are with matrix correction based on Harvard 98973 muscovite. | ||
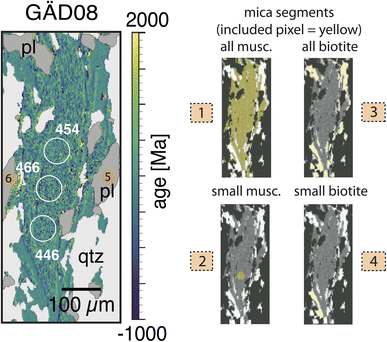 | ||
| Fig. 7 Rb–Sr age map of a mylonitic mica schist (GÄD08) from the Middle Seve Nappe near Ankarede, Jämtland (Sweden) consisting mainly of muscovite, biotite and plagioclase. Image pixel size is 3 μm. Different segments have been assigned for mica and biotite, with segment #1 and #3 comprising all muscovite and biotite pixel, respectively. Segments #2 and #4 comprise a smaller subset. Two segments #5 and #6 are assigned to plagioclase. White circles indicate Rb–Sr ages obtained from single spot analyses with matrix correction based on Harvard 98973. Isotopic and age data for the segments is compiled in Tables 8 and 9. | ||
To finally extract the ages from the resulting pixel segments we applied two approaches (Fig. 8 and Table 9). The first one is calculating the weighted mean age of all pixels using the IsoplotR software40 and taking into account the estimated random uncertainty of a single mass sweep (see above). The second approach is to create histograms from all single pixel ages within a segment and fitting a Gaussian probability distribution to it, with the age corresponding to the Gaussian mean. Both histograms and Gaussian fitting are performed using the Igor Pro software (version 8.04) and applying the Freedman–Daiconis algorithm to calculate the bin width. The resulting ages were again matrix corrected, and all systematic uncertainties were added in quadrature (see eqn (8)). Since GER2B and WIL1A are muscovites, a MCF based on RM Harvard 98973 is applied. For GÄD08, which contains muscovite and biotite, a Phalaborwa biotite-based MCF is used for matrix correction.
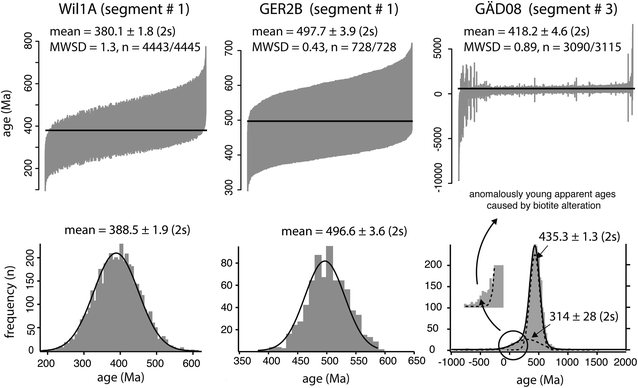 | ||
| Fig. 8 Rb–Sr ages of selected mica segments within the Rb–Sr age maps (Fig. 5 and 6) expressed as either the weighted means (top) or the mean of a Gaussian fit to the age histograms (bottom). The latter have been generated using the Igor Pro software (version 8.04) and applying the Freedman–Daiconis method to calculate the bin width. The (87Sr/86Sr)initial is anchored to the values obtained from plagioclase analyses (Table 8). Ages displayed are without matrix correction. Matrix corrected ages are compiled in Table 9. For WIL1A (segment #1) and GER2B (segment #3) both approaches yield similar means and uncertainties. For GÄD08 segment #3, which comprises all biotite-assigned pixel, the Gaussian mean yields a higher age compared to the weighted mean. This is explained by the presence of anomalously low apparent ages caused by biotite alteration, visible as a shoulder on the lower-age side of the main age peak. | ||
| Sample | Segment # | Description | n pixel | 87Rb/86Sr | 2SE (abs) | 87Sr/86Sr | 2SE (abs) |
|---|---|---|---|---|---|---|---|
| GÄD08 | 1 | All muscovite | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 880 |
22.6977 | 0.2574 | 0.9009 | 0.0026 |
| 2 | Small muscovite | 247 | 16.2712 | 0.1494 | 0.8463 | 0.0074 | |
| 3 | All biotite | 3115 | 283.9290 | 3.6264 | 2.5282 | 0.0253 | |
| 4 | Small biotite | 528 | 301.9315 | 6.6887 | 2.6483 | 0.0524 | |
| 5 | Plagioclase | 91 | 0.0209 | 0.0034 | 0.73982 | 0.0141 | |
| 6 | Plagioclase | 33 | 0.0415 | 0.0124 | 0.73849 | 0.0202 | |
| GER2B | 1 | Muscovite old core domain | 728 | 364.5206 | 0.9001 | 3.2830 | 0.0102 |
| 2 | Muscovite new (large) | 2515 | 416.9389 | 1.0787 | 2.9717 | 0.0069 | |
| 3 | Muscovite new (small) | 200 | 476.5435 | 4.8434 | 3.3480 | 0.0275 | |
| 4 | Plagioclase | 311 | 0.2086 | 0.0494 | 0.74828 | 0.0103 | |
| 5 | Plagioclase | 311 | 0.5803 | 0.094 | 0.71875 | 0.0096 | |
| 6 | Plagioclase | 330 | 3.0187 | 0.514 | 0.74263 | 0.0141 | |
| 7 | Plagioclase | 332 | 2.2074 | 0.5278 | 0.74739 | 0.0134 | |
| 8 | Plagioclase | 311 | 2.7003 | 1.0446 | 0.75779 | 0.0163 | |
| 9 | Plagioclase | 311 | 2.2078 | 0.5622 | 0.73119 | 0.0129 | |
| 10 | Plagioclase | 311 | 0.6851 | 0.0938 | 0.73138 | 0.0108 | |
| 11 | Plagioclase | 311 | 0.5853 | 0.1332 | 0.72526 | 0.0138 | |
| 12 | Plagioclase | 332 | 1.2544 | 0.3022 | 0.73971 | 0.0162 | |
| 13 | Plagioclase | 311 | 1.0809 | 0.2174 | 0.74634 | 0.0101 | |
| 14 | Plagioclase | 311 | 0.1868 | 0.039 | 0.7216 | 0.0089 | |
| 15 | Plagioclase | 332 | 0.1599 | 0.0228 | 0.72169 | 0.0095 | |
| 16 | Plagioclase | 311 | 0.3122 | 0.1132 | 0.72488 | 0.01 | |
| 17 | Plagioclase | 373 | 1.7964 | 0.3244 | 0.73659 | 0.0088 | |
| 18 | Plagioclase | 345 | 5.4221 | 1.662 | 0.78052 | 0.017 | |
| 19 | Plagioclase | 332 | 4.1518 | 0.8982 | 0.74333 | 0.0122 | |
| WIL1A | 1 | Muscovite shear zone (large) | 4445 | 150.5048 | 0.9742 | 1.5222 | 0.0094 |
| 2 | Muscovite shear zone (small) | 216 | 185.4582 | 0.8914 | 1.7341 | 0.0056 | |
| 3 | Plagioclase | 373 | 0.19798 | 0.04556 | 0.74537 | 0.0142 | |
| 4 | Plagioclase | 373 | 1.6672 | 0.31774 | 0.73652 | 0.0152 | |
| 5 | Plagioclase | 397 | 0.07997 | 0.04546 | 0.72325 | 0.0128 | |
| 6 | Plagioclase | 347 | 0.03425 | 0.0314 | 0.73985 | 0.0143 | |
| 7 | Plagioclase | 366 | 0.72295 | 0.16136 | 0.72975 | 0.015 | |
| 8 | Plagioclase | 311 | 0.64183 | 0.17836 | 0.74466 | 0.0161 | |
| 9 | Plagioclase | 311 | 0.18682 | 0.0448 | 0.74264 | 0.0153 | |
| 10 | Plagioclase | 311 | 7.02967 | 0.69448 | 0.76065 | 0.0225 | |
| 11 | Plagioclase | 311 | 0.31599 | 0.1363 | 0.73881 | 0.0149 | |
| 12 | Plagioclase | 345 | 0.6681 | 0.14396 | 0.73282 | 0.0156 | |
| 13 | Plagioclase | 311 | 0.10586 | 0.02704 | 0.73492 | 0.0139 | |
| 14 | Plagioclase | 311 | 0.04974 | 0.01838 | 0.7353 | 0.0152 | |
| 15 | Plagioclase | 311 | 0.01382 | 0.02084 | 0.71214 | 0.0153 |
| Sample | Segment # | Description | Gaussian mean | Weighted mean | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age (Ma) | 2sx (%) | Matrix corrected | 2s* (%) | Age (Ma) | 2sx (%) | Matrix corrected | 2s* (%) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a 2sx denotes the uncertainty on the weighted/Gaussian mean. 2s* denotes the total uncertainty resulting from propagating all random and systematic uncertainties. The initial Sr-isotope composition is obtained from plagioclase analyses within the same sample. *Matrix correction based on Phalaborwa biotite, i.e., here there is no chemical matrix match between mica RM and sample. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GER2B | 1 | Muscovite old core | 496.6 | 0.7 | 483.7 | 2.3 | 497.7 | 0.8 | 484.8 | 2.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (87Sr/86Sr)initial | 2 | Muscovite new (large) | 383.7 | 0.4 | 373.8 | 2.2 | 382.7 | 0.4 | 372.8 | 2.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.7148 ± 0.0094 | 3 | Muscovite new (small) | 387.4 | 1.0 | 377.4 | 2.4 | 392.8 | 1.5 | 382.6 | 2.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| WIL1A | 1 | Muscovite shear zone (large) | 388.5 | 0.5 | 374.7 | 2.6 | 380.1 | 0.5 | 366.6 | 2.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (87Sr/86Sr)initial | 2 | Muscovite shear zone (small) | 376.1 | 2.4 | 362.8 | 3.5 | 375.6 | 1.9 | 362.3 | 3.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.712 ± 0.015 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GÄD08 | 1 | All muscovite | 424.7 | 0.7 | 435.0* | 6.8 | 397.5 | 2.5 | 407.2* | 7.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (87Sr/86Sr)initial | 2 | Small muscovite | 389.2 | 26.5 | 398.7* | 27.3 | 378.5 | 24.0 | 387.7* | 24.9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.739 ± 0.011 | 3 | All biotite | Peak 1: 435.3 | 0.3 | 445.9 | 2.5 | 418.2 | 1.2 | 426.2 | 2.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Peak 2: 314 | 8.9 | 321.6 | 9.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Small biotite | 427.2 | 1.4 | 437.6 | 2.8 | 414.8 | 2.8 | 424.9 | 3.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The initial Sr-isotope values for GÄD08, GER2B and WIL1A are obtained by averaging the 87Sr/86Sr over several small segments within plagioclase contained in the same mapping (Fig. 6 and 7). To derive the initial 87Sr/86Sr, the plagioclase segment with the smallest 87Sr/86Sr ratio is chosen (Table 8) to account for post-crystallization mobility of radiogenic Sr in pegmatites,5,41 which is of particular importance for rocks with high Rb/Sr ratios. The final (87Sr/86Sr)initial is calculated from that segment by correcting for the amount of radiogenic 87Sr based on the expected ages and the measured 87Rb/86Sr using IsoplotR.40 For all mica RM, the fraction of common 87Sr is low enough (0.2–1.3%) to neglect a common Sr correction. For mica-Mg pressed nanopowder (87Sr/86Sr)initial is 0.72607 ± 0.0007.9
2.7. ID-TIMS dating of SagaB, Harvard 98973 and Phalaborwa mica RM
For the secondary reference materials Phalaborwa and SagaB, kg-sized samples of the original rock were available. Mica and apatite or feldspar used for analysis were parts of particularly clear domains of individual crystals. In the case of Harvard 98973, we used different aliquots of white mica, combined with a small turbid feldspar crystal that was left from the original preparation of reference material. Rb–Sr isotopic data were generated at GFZ Potsdam using a Thermo Scientific TRITON thermal ionization mass spectrometer and a set of mixed 87Rb–84Sr tracers. Sr was measured in dynamic multicollection mode, and Rb isotope-dilution analysis was done in static multicollection mode. The 87Sr/86Sr obtained for NIST SRM 987 reference material during the period of analytical work was 0.710245 ± 0.000008 (2 s; n = 10). For age calculation, in case of feldspar and apatite, standard 2 s uncertainties of ±0.005% for 87Sr/86Sr and of ±1.5% for 87Rb/86Sr ratios were assigned to the results. Individual analytical uncertainties were generally smaller than these values. For mica 87Rb/86Sr ratios, uncertainty estimates are based on the standard error of several (3 to 6) independent isotope dilution analyses of Rb concentrations, combined with uncertainties of the Rb instrumental mass fractionation correction factor and of the Sr isotope dilution analysis. For mica 87Sr/86Sr ratios, we used either a standard uncertainty of ±0.005% or, if higher, the individual analytical uncertainties. Analytical procedures for sample dissolution and separation of Rb from Sr are described in more detail elsewhere.42 Uncertainties of isotope and age data are quoted at 2 s. The program Isoplot39 was used to calculate regression lines. The 87Rb decay constant was the one recommended by Villa and co-workers.1Age results are as follows: for Phalaborwa, we obtained an age of 2058.2 ± 7.0 Ma (MSWD = 2.6; initial 87Sr/86Sr = 0.707671 ± 0.000035), based on data for apatite and two biotite crystal fragments. For SagaB, the Rb–Sr age based on biotite, a biotite-feldspar aggregate and feldspar is 295.4 ± 1.4 Ma (MSWD = 1.7, initial 87Sr/86Sr = 0.7049 ± 0.0014). Both these results are in agreement with published U–Pb data (better than ±1%; see Section 2.1 for references). The model age determined here for RM Harvard 98973 is 266.8 ± 1.6 Ma (MSWD = 0.12; assumed initial 87Sr/86Sr = 0.720 ± 0.011), an age that is well within the range of ages of other pegmatite bodies in its regional pegmatite field. The turbid feldspar crystal that we analyzed alongside the Harvard 98973 mica fractions calculates to an impossibly low, apparently sub-primordial initial Sr isotopic composition, an effect that indicates some secondary overprint of that feldspar. Therefore, this analysis is not taken into further consideration. Calculation of the Rb–Sr model age for Harvard 98973 is, due to the extremely radiogenic 87Sr/86Sr signature of the mica, almost insensitive to the model initial 87Sr/86Sr ratio. We therefore consider the above Harvard 98973 model age as equally robust as the Rb–Sr ages obtained for SagaB and Phalaborwa. All ID-TIMS results are compiled in Table 4.
3. Results & discussion
3.1. Isotopic homogeneity of the secondary mica RM
An integral part of the data reduction scheme involves matrix correction by co-analysis of a matrix matched single crystalline mica RM (SagaB biotite, Harvard 98973 muscovite and Phalaborwa biotite). Hence, it is crucial to assess the isotopic homogeneity of the mica RM. This was done by randomly placing 28–30 LA-ICP-MS/MS spot analyses across the epoxy mounted crystal/rock fragments, which were at least 1 × 1 cm in size (images available at https://doi.org/10.5281/chemrxiv.8245448). The variability in both 87Sr/86Sr is 87Rb/86Sr is rather large (13–28%, 2SE, https://doi.org/10.26434/chemrxiv-2023-273lw-v2) and reflects the Rb/Sr variability within natural mica. For comparison, the isotope ratio variability for NIST610 obtained in session “homogeneity” is 0.1% (2SE) for 87Sr/86Sr and 0.3% (2SE) for 87Rb/86Sr. Hence, the mica RM are not suited to correct for mass bias on 87Sr/86Sr and 87Rb/86Sr ratios. In contrast, the 87Sr/87Rb ratios are reproducible within <1% (2SE) in each of the three mica RM (https://doi.org/10.26434/chemrxiv-2023-273lw-v2). Since SagaB, Harvard 98973 and Phalaborwa are characterized by a high proportion of radiogenic 87Sr (98.7–99.8%; Table 3), precise knowledge of the initial Sr isotope ratio is not required and a common Sr correction can be suspended.20 Hence, the good reproducibility on 87Sr/87Rb directly implies a good reproducibility of the Rb–Sr age signal (see Section 2.6). The uncertainty of the weighted mean 87Sr/87Rb ratio is below 0.4% (2sx, Table 3), if outliers are accepted (0 for Harvard 98973, 1 for SagaB and 2 for Phalaborwa). It is noteworthy that this uncertainty (Table 7) is similar to the one obtained by Rösel & Zack (2022),20 which can be considered a benchmark study for single-spot Rb–Sr dating. They reported 0.7% (2sx, n = 9–14) for the Högsbo muscovite (87Rb/86Sr = 3440–24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), which has an expected age of 1029 ± 1.7 Ma (ref. 43) and shares a similar Rb/Sr range to the mica RM analyzed in this study (Table 7). However, excess scatter has been detected (1.2% in Harvard 98973, 1.4% in SagaB and 1.7% in Phalaborwa biotite; https://doi.org/10.26434/chemrxiv-2023-273lw-v2), suggesting some degree of inhomogeneity in 87Sr/87Rb ratios beyond the analytical uncertainty. In the uncertainty workflow this excess variance (εhomo) is treated as a systematic uncertainty. It is incorporated in quadrature into the uncertainties associated with all ages calculated using the MCF derived from any of the three secondary mica RM.
000), which has an expected age of 1029 ± 1.7 Ma (ref. 43) and shares a similar Rb/Sr range to the mica RM analyzed in this study (Table 7). However, excess scatter has been detected (1.2% in Harvard 98973, 1.4% in SagaB and 1.7% in Phalaborwa biotite; https://doi.org/10.26434/chemrxiv-2023-273lw-v2), suggesting some degree of inhomogeneity in 87Sr/87Rb ratios beyond the analytical uncertainty. In the uncertainty workflow this excess variance (εhomo) is treated as a systematic uncertainty. It is incorporated in quadrature into the uncertainties associated with all ages calculated using the MCF derived from any of the three secondary mica RM.
3.2. Measurement uncertainty and accuracy by line scan vs. static spot ablation
This study presents Rb–Sr age maps generated using an innovative line scan ablation technique, employing small beam sizes, high scanning speeds, repetition rates, and shallow ablation depth. To evaluate the effectiveness of this method in comparison to the conventional static spot mode ablation, it is crucial to analyze and compare both measurement uncertainty and accuracy. The following assessment is based on repeated analyses of the secondary mica RM during the three spot and three line mode sessions and considers the propagation of all random and systematic uncertainties, as detailed in Section 2.6 and illustrated in Fig. 4 and Table 7.In this study, we define accuracy as the degree of similarity between the measured ages and the expected ages, quantified as the relative deviation (in %). For all mica RM investigated in this study, high-precision ID-TIMS data is available (Table 4), providing reliable expected ages. In all spot ablation sessions, an improved accuracy of <3.0% is obtained for dating of Harvard 98987 muscovite (−0.1–2.9%) and SagaB biotite by applying a Phalaborwa biotite-based MCF (Fig. 4 and Table 7) compared to the accuracy obtained for non-matrix matched ages (−3.7% to −11.05%). In the case of MicaMg-pressed nanopowder, the matrix correction has the opposite effect and leads to a decrease in accuracy from <2.6% (without matrix correction) to <9.1% (with Phalaborwa-based matrix correction). This observation supports earlier conclusions on the general matrix mismatch between crystalline mica and pressed mica nanopowders.21,27,29
For line scan ablation-based age determinations, application of a Phalaborwa biotite-based MCF leads to a good accuracy for SagaB biotite (−0.8–1.4%, Fig. 4 and Table 7), whereas for Harvard 98973 muscovite, the accuracy even decreases compared to the non-matrix corrected ages (from 2.7–3.7% to 11.3–11.4%). This implies that both a structural AND a chemical matrix match between the secondary mica RM and unknown sample material are crucial. This is somehow different to spot mode ablation, where accurate ages seem to mainly rely on a structural matrix match, i.e. muscovite secondary RM can be equally well used for matrix correction of biotites (Fig. 4).
The total propagated uncertainty on matrix corrected ages obtained during line scan analyses is slightly worse compared to spot mode (1.7–1.9% vs. 2.3–2.8%, Table 7). This is mainly owed to the higher 87Sr/87Rb ratio uncertainty in line compared to spot mode (2sx = 0.5–1.7% vs. 0.3–0.7%, Table 7) and the higher long-term excess variance on 87Sr/87Rb ratios (1.4% in line mode vs. 0% in spot mode; https://doi.org/10.26434/chemrxiv-2023-273lw-v2). In contrast, the average accuracy is ∼1% better in line mode compared to spot mode when employing matrix correction with chemically matched mica RM. The level of accuracy achieved remains unaffected by the non P/A-matched acquisition of 85Rb. Specifically, the Phalaborwa biotite-based MCF, when utilizing 85Rb in analog mode, consistently provides the anticipated Rb–Sr age for SagaB biotite, for which 85Rb has been acquired in pulse mode. Therefore, the P/A tuning is regarded accurate for 85Rb. It is important to note that data acquisition in line scan mode only requires a fraction of the sample volume. A single 50 s line scan on NIST610 during the WIL1A mapping session consists of 5900 shots with a 3 μm beam, while a single spot analysis during session “GER2B/WilA” consists of 400 shots with a 65 μm beam. Assuming a constant ablation depth per shot, this results in a ∼31.8 times more sample volume during a single spot analysis as opposed to line scan analyses.
3.3. LA-ICP-MS/MS-based Rb–Sr age mapping
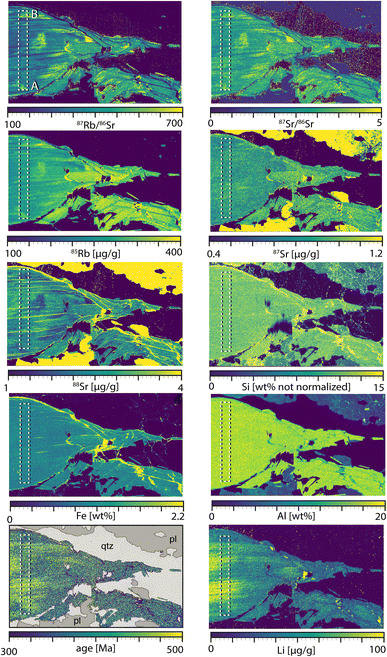 | ||
| Fig. 9 Elemental, isotopic, isotope ratio and Rb–Sr age distribution of sample GER2B. All concentration maps have been normalized to Si (see Methods section). Hence for Si, only non-normalized concentrations are shown. The dotted square denotes the location of the transect shown in Fig. 10. | ||
For a more detailed assessment of the element and age distribution we inspected a ∼1.3 mm transect across the core region of the large deformed muscovite (Fig. 10). In this context, we observe two distinct types of domains exhibiting partial age reset. One is marked by a noticeable rise in Rb concentration, with an increase of 50–100 μg g−1 in Rb and a corresponding ∼20 μg g−1 decrease in Li concentration (depicted as blue regions in Fig. 10). In contrast, the other domain experiencing age reduction shows a slight decrease in Rb concentration coupled with an increase in Li concentrations. Given that both Rb and Li have a strong affinity for fluids, we propose that the former domains, exhibiting a significant age reset, record element and isotope mobility induced by fluid activity. The latter type of partial age reset, we tentatively attribute to element and isotope mobility occurring during dry volume diffusion.
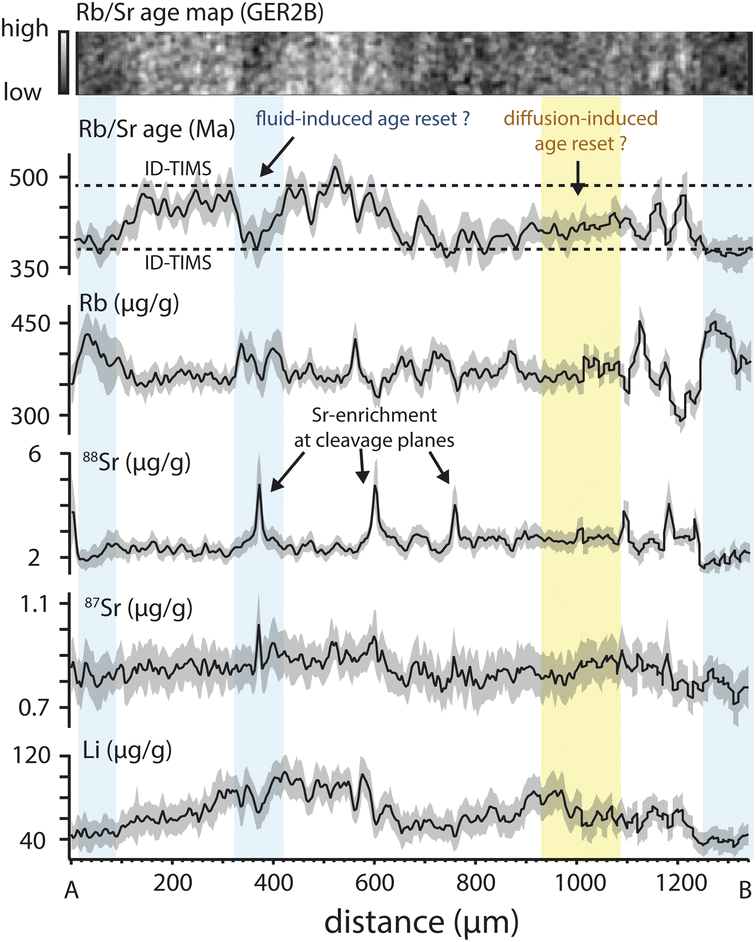 | ||
| Fig. 10 Distribution of Rb–Sr age, selected elements and isotopes along a transect (A and B, see Fig. 9) perpendicular to the cleavage of the large deformed muscovite crystal displayed in Fig. 6 and 9. Shown are mean values ± 1SD of all pixel perpendicular to the transect. Blue regions are interpreted as domains affected by fluid-induced age reset. The yellow domain highlights age reset likely caused by dry volume diffusion (see text). The lower and upper age range as constrained by ID-TIMS analyses is indicated by dotted lines. Sr occasionally shows strong enrichment along cleavage planes also visible in the elemental distribution maps in Fig. 9. | ||
To constrain and compare the total age range displayed in the Rb–Sr age map to the ID-TIMS-based ages, we defined three segments: one in the oldest domains of the large mica core, one containing a larger (200 × 500 μm) and one a smaller (50 × 150 μm) newly crystallized mica. For the old segment, both matrix-corrected weighted mean and Gaussian mean approaches yield comparable results (485 ± 11 Ma vs. 484 ± 11 Ma, Table 9) and are in agreement with the ID-TIMS age of the pegmatite crystallization of GER2B (482 ± 5 Ma,5Fig. 11). The Gaussian and weighted mean ages for the latter two segments also agree within their uncertainty covering a range of 373–383 Ma and are in line with the ID-TIMS age of the deformation event (377 to ∼382 Ma (ref. 5)). As anticipated, the uncertainty in the weighted means (2sx) rises proportionally with the square root of the number of pixels (2515 pixels result in 0.4% uncertainty, while 200 pixels yield 1.0–1.5% uncertainty). Nevertheless, after accounting for all external uncertainties, the enhancement in measurement precision is somewhat mitigated (2515 pixels lead to 2.1–2.2% uncertainty, whereas 200 pixels result in 2.4–2.5% uncertainty).
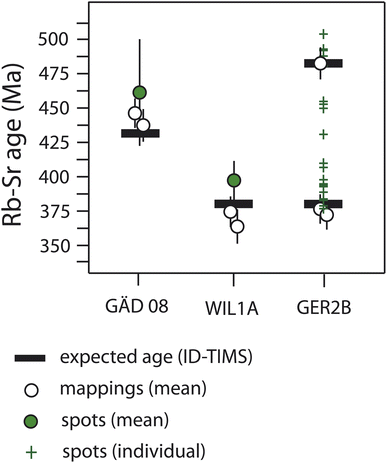 | ||
| Fig. 11 Comparison of matrix corrected Rb–Sr mica ages obtained from the segments defined in Fig. 5 and 6, matrix corrected Rb–Sr spot ages and expected ages as based on ID-TIMS Rb–Sr multimineral isochron data (see Section 2.1). All data is based on muscovite analyses, except mapping data for GÄD08, which is based on biotite analyses. | ||
Some regions within the Rb–Sr map display anomalously low ages, in particular around a larger K-feldspar crystal, which is identified by the quantitative chemical mapping (Fig. 6, https://doi.org/10.26434/chemrxiv-2023-273lw-v2). This is interpreted as an artefact from mixed K-Fsp/mica analyses, for which mica-based matrix correction does not correctly account for the Rb/Sr fractionation behavior of K-feldspar.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880) and biotite (n = 3115) pixel and two segments are smaller subsets of these populations (n = 247 for muscovite and n = 528 for biotite, Fig. 7). In general, the uncertainty on the weighted mean (2sx) for muscovite (26.5% for 247 pixel) is considerably higher compared to biotite (1.4% for 528 pixel). The higher analytical age uncertainty for muscovite is due to its lower 87Sr/86Sr ratios. During common Sr correction, a constant value for (87Sr/86Sr)initial is subtracted from (87Sr/86Sr)sample,true ratios of individual pixels (eqn (4)). As the value of (87Sr/86Sr)sample,true approaches (87Sr/86Sr)initial the relative variability in the (87Sr/86Rb)Sr,initial,corrected ratios—and consequently the Rb–Sr ages—becomes more amplified (see eqn (3)). This is also reflected by the higher age noise displayed by muscovite pixel (Fig. 7). Nevertheless, by pooling a larger number of pixels, e.g. all 11.880 muscovite pixels, we are able to attain a reasonable weighted mean uncertainty of 0.7% (Table 9). However, it's worth noting that the total uncertainty is significantly influenced by the common Sr correction (γ), which tends to be higher for lower 87Sr/86Sr ratios.20 As a result, even when all muscovite pixels are included, the total uncertainty is reduced but remains at 6.8% (Table 9). For both muscovite and biotite, matrix correction is based on Phalaborwa biotite and hence is not matrix matched with respect to the muscovite in GÄD08. However, within the limits of uncertainty, both muscovite segments match the ID-TIMS derived Rb–Sr ages (Table 9).
880) and biotite (n = 3115) pixel and two segments are smaller subsets of these populations (n = 247 for muscovite and n = 528 for biotite, Fig. 7). In general, the uncertainty on the weighted mean (2sx) for muscovite (26.5% for 247 pixel) is considerably higher compared to biotite (1.4% for 528 pixel). The higher analytical age uncertainty for muscovite is due to its lower 87Sr/86Sr ratios. During common Sr correction, a constant value for (87Sr/86Sr)initial is subtracted from (87Sr/86Sr)sample,true ratios of individual pixels (eqn (4)). As the value of (87Sr/86Sr)sample,true approaches (87Sr/86Sr)initial the relative variability in the (87Sr/86Rb)Sr,initial,corrected ratios—and consequently the Rb–Sr ages—becomes more amplified (see eqn (3)). This is also reflected by the higher age noise displayed by muscovite pixel (Fig. 7). Nevertheless, by pooling a larger number of pixels, e.g. all 11.880 muscovite pixels, we are able to attain a reasonable weighted mean uncertainty of 0.7% (Table 9). However, it's worth noting that the total uncertainty is significantly influenced by the common Sr correction (γ), which tends to be higher for lower 87Sr/86Sr ratios.20 As a result, even when all muscovite pixels are included, the total uncertainty is reduced but remains at 6.8% (Table 9). For both muscovite and biotite, matrix correction is based on Phalaborwa biotite and hence is not matrix matched with respect to the muscovite in GÄD08. However, within the limits of uncertainty, both muscovite segments match the ID-TIMS derived Rb–Sr ages (Table 9).
For biotite, improved total uncertainties are achieved and both, small and large segments, yield ages in agreement with ID-TIMS data (425 ± 15 Ma and 426 ± 10 Ma for the weighted mean approach). Interestingly, the age distribution of the “all biotite” segment exhibits an intriguing skewness towards younger ages (Fig. 8). To account for the asymmetry of the histogram, two Gaussians probability distributions were used for fitting. The main age peak displays an age of 446 ± 11 Ma and is assigned to the main deformation event at 431.7 ± 3.1 Ma.36 The peak that fits the population of anomalously young apparent ages at 322 ± 30 Ma is interpreted to reflect fluid alteration leading to chloritization of biotite and hence partially reset ages.44 This is supported by Rb–Sr data presented by Bender and co-workers,36 which yield lower mean ages for the apatite plus biotite isochron (421.7 ± 6.2 Ma) compared to the age defined by the feldspar and muscovite fractions (431.7 ± 3.1 Ma). The detection of a younger age population within the age distribution displayed by biotite in the Rb–Sr map is likely a result of the small laser beam size of 3 μm. This beam size enables precise sampling of altered biotite domains. In contrast, both ID-TIMS analyses and conventional spot ablation with larger beam sizes more likely lead to mixed analyses of pristine and altered biotite, which imposes problems in interpreting the obtained ages.
3.4. Single spot Rb–Sr ages
Since in single spot mode, both ∼86Sr and ∼88Sr were recorded instead of only ∼88Sr in line scan mode, ages obtained using either Sr-isotope can be compared. The age range displayed by the single spots on GER2B based on ∼86Sr (youngest age 376 ± 22; oldest age: 505 ± 28 Ma, Fig. 11) encompasses the age range constrained by ID-TIMS. However, if ∼88Sr is used for age calculation, individual spot ages are up to 5–18 Ma years older (Table 10), indicating an adverse impact on accuracy. This is also exemplified by the weighted mean age of all spot analyses obtained for WIL1A and GÄD08, for which only ∼86Sr-based ages (396 ± 14 Ma and 462 ± 39 Ma) are in agreement with the expected ages (377–382 Ma and 431.7 ± 3.1 Ma).5,36 Since in spot mode, the acquisition of ∼88Sr is not P/A matched in NIST610 and muscovite as opposed to ∼86Sr, the observed bias points to a failure of the employed P/A tuning procedure (see Methods section) for ∼ySr nuclides. This is somewhat disappointing given the better total uncertainty of ∼88Sr vs. ∼86Sr-based single spot ages (Table 10), due to the higher natural abundance of 88Sr as compared to 86Sr.| Sample | Nuclides: 85Rb, ∼86Sr, ∼87Sr | Nuclides: 85Rb, ∼88Sr, ∼87Sr | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age (Ma) | Age matrix corrected (Ma) | 2s* (%) | Age (Ma) | Age matrix corrected (Ma) | 2s* (%) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a (87Sr/86Sr)initial is anchored to the indicated value, which is obtained from plagioclase analyses within the same sample. Matrix correction is based on Harvard 98973 muscovite. Spot locations are indicated in Fig. 6 and 7. There, only ages based on ∼86Sr are shown. b Nuclides used for calculating the single spot ages. * spots obtained within the mapped area. The other spots are obtained on two adjacent mica grains. 2sx denotes the uncertainty on the weighted/Gaussian mean. 2s* denotes the total uncertainty resulting from propagating all random and systematic uncertainties. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GER2B | 460 | 489 | 6.9 | 474 | 505 | 2.8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 464 | 493 | 5.3 | 469 | 499 | 2.3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (87Sr/86Sr)ini | 454 | 483 | 5.8 | 466 | 496 | 2.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.7148 ± 0.0094 | 465 | 495 | 5.4 | 482 | 513 | 2.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 475 | 505 | 5.5 | 490 | 522 | 2.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 364 | 388 | 6.3 | 380 | 404 | 2.3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 382 | 406 | 5.0 | 386 | 411 | 2.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 373 | 397 | 6.0 | 387 | 411 | 2.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 426 | 454 | 5.8 | 440 | 468 | 2.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 423 | 451 | 5.8 | 435 | 463 | 2.3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 404 | 430 | 4.9 | 409 | 435 | 2.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 428 | 455 | 5.2 | 434 | 462 | 2.4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 370 | 393 | 5.1 | 380 | 405 | 2.3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 368 | 392 | 5.9 | 379 | 403 | 2.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 353 | 376 | 5.7 | 365 | 389 | 2.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 355 | 378 | 5.3 | 365 | 388 | 2.4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 359 | 382 | 5.1 | 366 | 389 | 2.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 359 | 382 | 5.0 | 374 | 398 | 2.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 369 | 393 | 6.4 | 379 | 404 | 2.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 384 | 409 | 5.8 | 390 | 415 | 2.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| WIL1A | 378 | 402 | 4.1 | 393 | 418 | 3.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 384 | 408 | 3.8 | 395 | 420 | 3.0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (87Sr/86Sr)ini | 362 | 385 | 4.6 | 369 | 392 | 3.7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.712 ± 0.015 | 373 | 397 | 4.9 | 388 | 412 | 3.8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 378 | 402 | 4.3 | 395 | 420 | 3.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 355 | 378 | 4.2 | 373 | 397 | 3.0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 354 | 377 | 5.3 | 371 | 395 | 3.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 390 | 415 | 4.3 | 408 | 434 | 4.0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 362 | 386 | 4.5 | 389 | 414 | 3.8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 387 | 412 | 4.5 | 405 | 431 | 4.1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Weighted mean (WIL1A) | 396.3 | 411 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| MWSD | 2.5 | 3.7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2sx (%) | 2.5 | 2.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2s* (%) | 3.4 | 3.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GÄD08 | 434 | 456 | 7.0 | 494 | 519 | 6.0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 463 | 487 | 6.8 | 527 | 554 | 5.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (87Sr/86Sr)ini | 444 | 466 | 8.2 | 538 | 566 | 6.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.739 ± 0.011 | 437 | 460 | 7.3 | 494 | 519 | 6.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 448 | 471 | 6.5 | 503 | 528 | 5.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 422 | 455 | 8.1 | 500 | 525 | 6.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 429 | 451 | 9.5 | 543 | 570 | 7.3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 432 | 454 | 10.5 | 556 | 585 | 7.9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | 432 | 454 | 10.5 | 556 | 585 | 7.9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | 424 | 446 | 8.6 | 498 | 523 | 7.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | 443 | 465 | 10.1 | 570 | 599 | 7.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Weighted mean (GÄD08) | 462.0 | 543.0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| MWSD | 0.42 | 1.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2sx (%) | 2.4 | 2.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2s* (%) | 8.4 | 6.9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
As suggested by Rösel & Zack (2022)20 the total uncertainty for both individual and pooled spot ages is a function of the 87Sr/86Sr ratio. Muscovite in GÄD08 exhibits the lowest 87Sr/86Sr ratios (0.85–0.90) and hence also the highest single spot age uncertainty (6.5–10.5%). In contrast, in Wil1A and GER2B (87Sr/86Sr = 1.5–3.3) the single spot uncertainty is considerably lower (3.8–6.9%).
4. Conclusions & outlook
This study demonstrates that precise and accurate Rb–Sr ages can be obtained based on Rb–Sr isotope mapping with μm-scale spatial resolution using much smaller sample volumes than required for conventional spot ablation. This technique opens new possibilities for geochronological applications. It allows for the dating of μm-sized shear zones and small crystals that are either tightly intergrown with other phases or too small for conventional spot analyses. This includes the analysis of usually small detrital mica grains, which is a promising approach for sedimentary provenance analysis.20Another notable strength of Rb–Sr mapping lies in its capacity to identify and pool homogeneous age populations, which is essential for meaningful weighted mean age determinations.37 This is particularly important, given the presence of sharp intracrystalline age gradients (∼100 Ma over 20–30 μm) and larger domains displaying partial age reset (Fig. 10). These μm-scale age variations correspond to the identification of multiple age populations in natural biotite, as observed in the time-resolved signal of a single spot ablation interval.21 While increasing the size of a particular age population segment improves the weighted mean uncertainty, the obtainable total uncertainty of the Rb–Sr age is limited by the propagation of the uncertainty of the initial Sr correction and other systematic uncertainties. In this respect, the availability of matrix-matched, homogeneous, and well characterized RM as well as an accurate and precise determination of the initial 87Sr/86Sr is crucial. Furthermore, it is imperative to ensure a P/A match for mass-shifted Sr-ions, given the absence of a viable software-based P/A tuning method. Developing alternative routines for P/A factor determination and correction for P/A mismatch will advance analytical accuracy and precision.
As shown, the quadrupole-based mapping approach not only provides age data but also offers valuable quantitative elemental information. This dual capability enhances our understanding of the formation and timing of economically important ore deposits, encompassing even light elements like lithium. Analyzing these lighter elements alongside Rb/Sr poses challenges, particularly when employing a Wien field to restrict the mass range transmitted to the CRC.21 Rb–Sr age maps are also highly promising for thermochronology applications, as they allow to constrain diffusion profiles and to distinguish diffusion (at static conditions) from fluid-induced age resetting or dynamic recrystallization. This capability is pivotal for the much-needed re-evaluation of true diffusion-related closure temperatures in natural biotite and muscovite.
Data availability
Supplementary data can be accessed through the ChemRxiv® server (https://doi.org/10.26434/chemrxiv-2023-273lw-v2). Here both raw and corrected isotope ratios of reference materials and samples of all six sessions are available as well the uncertainty components and the P/A configuration for 85Rb and ∼ySr nuclides. Furthermore, an excel sheet including the Rb/Sr isotope ratios and Rb–Sr ages of every individual pixel within the mica segments outlined in the mapping is included. Additionally, high-resolution, unedited elemental, isotope ratio, and Rb–Sr age maps of all mappings are provided.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Uwe Dittmann prepared high-quality polished thin sections. Michael Wiedenbeck provided both Harvard 98973 muscovite and a block of Phalaborwa biotite apatitite, and facilitated the sampling of SagaB. Thomas Neumann granted access to the LA-ICP-MS/MS laboratory of the TU Berlin, which is funded by the large scale research instrumentation program of the German Research Foundation (project number 432099368). Uwe Ring organized the sampling campaign for GÄD08. The manuscript was significantly improved through constructive comments from three anonymous reviewers. The manuscript was handled by Emma Stephen and Derya Kara Fisher. All these contributions are gratefully acknowledged.References
- I. M. Villa, P. De Bièvre, N. E. Holden and P. R. Renne, IUPAC-IUGS recommendation on the half-life of 87Rb, Geochim. Cosmochim. Acta, 2015, 164, 382–385 CrossRef CAS.
- U. Kramm, L. N. Kogarko, V. A. Kononova and H. Vartiainen, The Kola Alkaline Province of the CIS and Finland: Precise Rb-Sr Ages Define 380–360 Ma Age Range for All Magmatism, Lithos, 1993, 30(1), 33–44 CrossRef CAS.
- J. Glodny, B. Bingen, H. Austrheim, J. F. Molina and A. Rusin, Precise eclogitization ages deduced from Rb/Sr mineral systematics: the Maksyutov complex, Southern Urals, Russia, Geochim. Cosmochim. Acta, 2002, 66(7), 1221–1235 CrossRef CAS.
- S. M. ten Grotenhuis, R. A. J. Trouw and C. W. Passchier, Evolution of mica fish in mylonitic rocks, Tectonophysics, 2003, 372, 1–21 CrossRef CAS.
- J. Glodny, B. Grauert, J. Fiala, Z. Vejnar and A. Krohe, Metapegmatites in the western Bohemian massif: ages of crystallization and metamorphic overprint, as constrained by U-Pb zircon, monazite, garnet, columbite and Rb-Sr muscovite date, Geol. Rundsch., 1998, 87, 124–134 CrossRef CAS.
- W. Müller, D. Aerden and A. Halliday, Isotopic Dating of Strain Fringe Increments: Duration and Rates of Deformation in Shear Zones, Science, 2000, 288, 2195–2198 CrossRef PubMed.
- R. Halama, J. Glodny, M. Konrad-Schmolke and M. Sudo, Rb-Sr and in situ 40Ar/39Ar dating of exhumation-related shearing and fluid-induced recrystallization in the Sesia zone, Geosphere, 2018, 14, 1425–1450 CrossRef.
- J. Glodny and U. Ring, The Cycladic Blueschist Unit of the Hellenic subduction orogen: protracted high-pressure metamorphism, decompression, and reimbrication of a diachronous nappe stack, Earth-Sci. Rev., 2022, 224, 103883 CrossRef.
- K. J. Hogmalm, T. Zack, A. K.-O. Karlsson, A. S. L. Sjöqvist and D. Garbe-Schönberg, In situ Rb-Sr and K-Ca dating by LA-ICP-MS/MS: an evaluation of N2O and SF6 as reaction gases, J. Anal. At. Spectrom., 2017, 32, 305–313 RSC.
- H. Drake, C. Heim, N. M. W. Roberts, T. Zack, M. Tillberg, C. Brosman, M. Ivarsson, M. J. Whitehouse and M. E. Åström, Isotopic evidence for microbial production and consumption of methane in the upper continental crust throughout the phanerozoic eon, Earth Planet. Sci. Lett., 2017, 470, 108–118 CrossRef CAS.
- M. Tillberg, H. Drake, T. Zack, E. Kooijman, M. J. Whitehouse and M. E. Åström, In situ Rb/Sr dating of slickenfibres in deep crystalline basement faults, Sci. Rep., 2020, 10, 562 CrossRef CAS PubMed.
- D. York, C. M. Hall, Y. Yanase, J. A. Hanes and W. J. Kenyon, 40Ar/39Ar dating of terrestrial minerals with a continuous laser, Geophys. Res. Lett., 1981, 8(11), 1136–1138 CrossRef CAS.
- H. von Eynatten, R. Gaupp and J. R. Wijbrans, 40Ar/39Ar laserprobe dating of detrital white micas from Cretaceous sediments of the Eastern Alps: evidence for Variscan high-pressure metamorphism and implications for Alpine orogeny, Geology, 1996, 24, 691–694 CrossRef CAS.
- D. V. Popov and R. A. Spikings, Diffusion vs. fluid alteration in alkali feldspar 40Ar/39Ar thermochronology: does cross-correlation of log(r/r0) and age spectra validate thermal histories?, Chem. Geol., 2020, 539, 119506 CrossRef CAS.
- T. Zack and K. J. Hogmalm, Laser ablation Rb/Sr dating by online separation of Rb and Sr in an oxygen-filled reaction cell, Chem. Geol., 2016, 437, 120–133 CrossRef CAS.
- E. Bolea-Fernandez, S. J. M. Van Malderen, L. Balcaen, M. Resano and F. Vanhaecke, Laser ablation-tandem ICP-mass spectrometry (LA-ICP-MS/MS) for direct Sr isotopic analysis of solid samples with high Rb/Sr ratios, J. Anal. At. Spectrom., 2016, 31, 464–472 RSC.
- L. J. Moens, F. F. Vanhaecke, D. R. Bandura, V. I. Baranov and S. D. Tanner, Elimination of isobaric interferences in ICP-MS, using ion-molecule reaction chemistry: Rb/Sr age determination of magmatic rocks, a case study, J. Anal. At. Spectrom., 2001, 16, 991–994 RSC.
- D. R. Bandura, V. Baranov, A. Litherland and S. D. Tanner, Gas-phase ion-molecule reactions for resolution of atomic isobars: AMS and ICP-MS perspectives, Int. J. Mass Sepctrom., 2006, 255–256, 312–327 CrossRef CAS.
- L. O. Nicolaysen, Graphic interpretation of discordant age measurements on metamorphic rocks, Ann. N. Y. Acad. Sci., 1961, 91, 198–206 CrossRef.
- D. Rösel and T. Zack, LA-ICP-MS/MS Single-Spot Rb-Sr Dating, Geostand. Geoanal. Res., 2022, 46(143), 168 Search PubMed.
- A. M. Cruz-Uribe, G. Craig, J. M. Garber, B. Paul, C. Arkula and C. Bouman, Single Spot Rb/Sr Isochron Dating of Biotite by LA-MC-ICP-MS/MS, Geostand. Geoanal. Res., 2023, 47, 795–809 CrossRef CAS.
- K. Drost, D. M. Chew, J. A. Petrus, F. Scholze, J. D. Woodhead, J. W. Schneider and D. A. T. Harper, An Image Mapping Approach to U-Pb LA-ICP-MS Carbonate Dating and Applications to Direct Dating of Carbonate Sedimentation, Geochem., Geophys., Geosyst., 2018, 19, 4631–4648 CrossRef CAS.
- D. M. Chew, J. A. Petrus, G. G. Kenny and N. McEvoy, Rapid high-resolution U-Pb LA-Q-ICPMS age mapping of zircon, J. Anal. At. Spectrom., 2017, 32, 262–276 RSC.
- D. Chew, K. Drost, J. Marsh and J. A. Petrus, LA-ICP-MS imaging in geosciences and its applications to geochronology, Chem. Geol., 2021, 559, 119917 CrossRef CAS.
- J. D. Woodhead and J. M. Hergt, Strontium, neodymium and lead isotope analyses of NIST glass certified reference materials: SRM 610, 612, 614, Geostand. Newsl., 2001, 25, 261–266 CrossRef CAS.
- Y. Jegal, C. Zimmermann, L. Reisberg, D. Yeghicheyan, C. Cloquet, C. Peiffert, M. Gerardin, E. Deloule and J. Mercadier, Characterisation of reference materials for in situ Rb-Sr dating by LA-ICP-MS/MS, Geostand. Geoanal. Res., 2022, 46, 645–671 CrossRef CAS.
- S.-S. Li, M. Santosh, J. Farkaš, A. Redaa, S. Ganguly, S. W. Kim, C. Zhang, S. Gilbert and T. Zack, Coupled U-Pb and Rb-Sr laser ablation geochronology trace Archean to Proterozoic crustal evolution in the Dharwar Craton, India, Precambrian Res., 2020, 343, 105709 CrossRef CAS.
- H. K. Olierook, K. Rankenburg, S. Ulrich, C. L. Kirkland, N. J. Evans, S. Brown, B. I. McInnes, A. Prent, J. Gillespie and B. McDonald, Resolving multiple geological events using in situ Rb-Sr geochronology: implications for metallogenesis at Tropicana, Western Australia, Geochronology, 2020, 2, 283–303 CrossRef.
- A. Redaa, J. Farkaš, S. Gilbert, A. S. Collins, S. Löhr, D. Casegh, M. Forster, M. Blades and T. Zack, Testing Nano-Powder and Fused-Glass Mineral Reference Materials for In Situ Dating of Glauconite, Phlogopite, Biotite and Feldspar via LA-ICP-MS/MS, Geostand. Geoanal. Res., 2023, 47, 23–48 CrossRef CAS.
- A. Redaa, J. Farkaš, S. Gilbert, A. S. Collins, B. Wade, S. Löhr, T. Zack and D. Garbe-Schönberg, Assessment of elemental fractionation and matrix effects during in situ Rb-Sr dating of phlogopite by LA-ICP-MS/MS: implications for the accuracy and precision of mineral ages, J. Anal. At. Spectrom., 2021, 36, 322–344 RSC.
- L. Gorojovsky and O. Alard, Optimisation of laser and mass spectrometer parameters for the in situ analysis of Rb/Sr ratios by LA-ICP-MS/MS, J. Anal. At. Spectrom., 2020, 35, 2322–2336 RSC.
- F. Y. Wu, Y. H. Yang, Q. L. Li, R. H. Mitchell, J. B. Dawson, G. Brandl and M. Yuhara, In situ determination of U–Pb ages and Sr–Nd–Hf isotopic constraints on the petrogenesis of the Phalaborwa carbonatite complex, South Africa, Lithos, 2011, 127(1–2), 309–322 CrossRef CAS.
- M. D. Dyar, M. Wiedenbeck, D. Robertson, L. R. Cross, J. S. Delaney, K. Ferguson, C. A. Francis, E. S. Grew, C. V. Guidotti, R. L. Hervig, J. M. Hughes, J. Husler, W. Leeman, A. V. McGuire, D. Rhede, H. Rothe, R. L. Paul, I. Richards and M. Yates, Reference minerals for the microanalysis of light elements, Geostand. Newsl., 2001, 25, 441–463 CrossRef CAS.
- K. L. Webber, W. B. Simmons, A. U. Falster and S. L. Hanson, Anatectic pegmatites of the Oxford County pegmatite field, Maine, USA, Can. Mineral., 2019, 57(5), 811–815 CrossRef.
- S. Dahlgren, F. Corfu and L. Heaman, Datering av plutoner og pegmatitter i Larvik pluton-kompleks, sydlige Oslo Graben, ved hjelp av U-Pb isotoper i zirkon og baddeleyitt, Norsk Bergverksmuseum Skrift, 1998, 14, 32–39 Search PubMed.
- H. Bender, J. Glodny and U. Ring, Absolute Timing of Caledonian orogenic wedge assembly, Central Sweden, constrained by Rb-Sr mutli-mineral isochron data, Lithos, 2019, 334–345, 339–359 CrossRef.
- S. A. Horstwood, J. Košler, G. Gehrels, S. E. Jacksoin, N. M. McLean, C. Paton, N. J. Pearson, K. Sircombe, P. Sylvester, P. Vermeesch, J. F. Bowring, D. J. Condon and B. Schoene, Community-Derived Standards for LA-ICP-MS U-(Th-)Pb Geochronology – Uncertainty Propagation, Age Interpretation and Data Reporting, Geostand. Geoanal. Res., 2016, 40, 311–332 CrossRef.
- C. M. Fisher, H. P. Longerich, S. E. Jackson and J. M. Hanchar, Data acquisition and calculation of U-Pb isotopic analyses using laser ablation (single collector) inductively coupled plasma mass spectrometry, J. Anal. At. Spectrom., 2010, 25, 1905–1920 RSC.
- K. R. Ludwig, User's Manual for Isoplot 3.00: A Geochronological Toolkit for Microsoft Excel, Berkeley Geochronological Center, Berkeley, special publication 4, 2003, pp. 1–70 Search PubMed.
- P. Vermeesch, IsoplotR: a free and open toolbox for geochronology, Geosci. Front., 2018, 9, 1479–1493 CrossRef CAS.
- D. Küster, Rb–Sr isotope systematics of muscovite from Pan-African granitic pegmatites of western and northeastern Africa, Mineral. Petrol., 1995, 55, 71–83 CrossRef.
- J. Glodny, U. Ring and A. Kühn, Coeval high-pressure metamorphism, thrusting, strike-slip, and extensional shearing in the Tauern Window, Eastern Alps, Tectonics, 2008, 27(4) CrossRef.
- R. L. Romer and S.-A. Smeds, Implications of U-Pb ages of columbite-tantalites from granitic pegmatites for the Palaeoproterozoic accrection of 1.90-1.85 Ga magmatic arcs to the Baltic Shield, Precambrian Res., 1994, 67, 141–158 CrossRef CAS.
- B. J. A. Willigers, K. Mezger and J. A. Baker, Development of high precision Rb-Sr phlogopite and biotite geochronology; an alternative to 40Ar/39Ar tri-octahedral mica dating, Chem. Geol., 2004, 213, 339–358 CrossRef CAS.
- H. P. Longerich, S. E. Jackson and D. Günther, Laser ablation inductively coupled plasma mass spectrometric transient signal data acquisition and analyte concentration calculation, J. Anal. At. Spectrom., 1996, 11, 899–904 RSC.
- I. S. Williams, N. W. Tetley, W. Compston and I. McDougall, A comparison of K-Ar and Rb-Sr ages of rapidly cooled igneous rocks: two points in the Palaeozoic time scale re-evaluated, J. Geol. Soc. London, 1982, 139, 557–568 CrossRef CAS.
- B. Schoene and S. A. Bowring, U-Pb systematics of the McClure Mountain syenite: thermochronological constraints on the age of the 40Ar/39Ar standard MMhb, Contrib. Mineral. Petrol., 2006, 151, 615–630 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |