Open Access Article
Open Access ArticleIdentifying structure–absorption relationships and predicting absorption strength of non-fullerene acceptors for organic photovoltaics†
Jun
Yan‡
 a,
Xabier
Rodríguez-Martínez‡
*bc,
Drew
Pearce
a,
Hana
Douglas
a,
Danai
Bili
a,
Mohammed
Azzouzi
a,
Flurin
Eisner
a,
Xabier
Rodríguez-Martínez‡
*bc,
Drew
Pearce
a,
Hana
Douglas
a,
Danai
Bili
a,
Mohammed
Azzouzi
a,
Flurin
Eisner
 a,
Alise
Virbule
a,
Elham
Rezasoltani
a,
Valentina
Belova
a,
Alise
Virbule
a,
Elham
Rezasoltani
a,
Valentina
Belova
 c,
Bernhard
Dörling
c,
Sheridan
Few
af,
Anna A.
Szumska
a,
Xueyan
Hou
a,
Guichuan
Zhang
d,
Hin-Lap
Yip
de,
Mariano
Campoy-Quiles
c,
Bernhard
Dörling
c,
Sheridan
Few
af,
Anna A.
Szumska
a,
Xueyan
Hou
a,
Guichuan
Zhang
d,
Hin-Lap
Yip
de,
Mariano
Campoy-Quiles
 *c and
Jenny
Nelson
*c and
Jenny
Nelson
 *a
*a
aDepartment of Physics, Imperial College London, SW7 2AZ, London, UK. E-mail: jenny.nelson@imperial.ac.uk
bElectronic and Photonic Materials (EFM), Department of Physics, Chemistry and Biology (IFM), Linköping University, Linköping, SE 581 83, Sweden. E-mail: xabier.rodriguez.martinez@liu.se
cInstituto de Ciencia de Materiales de Barcelona, ICMAB-CSIC, Campus UAB, Bellaterra 08193, Spain. E-mail: mcampoy@icmab.es
dInstitute of Polymer Optoelectronic Materials and Devices, State Key Laboratory of Luminescent Materials and Devices, South China University of Technology, Guangzhou 510640, P. R. China
eDepartment of Materials Science and Engineering, City University of Hong Kong, Tat Chee Avenue, Kowloon, Hong Kong
fSustainability Research Institute, School of Earth and Environment, University of Leeds, LS2 9JT, Leeds, UK
First published on 20th May 2022
Abstract
Non-fullerene acceptors (NFAs) are excellent light harvesters, yet the origin of their high optical extinction is not well understood. In this work, we investigate the absorption strength of NFAs by building a database of time-dependent density functional theory (TDDFT) calculations of ∼500 π-conjugated molecules. The calculations are first validated by comparison with experimental measurements in solution and solid state using common fullerene and non-fullerene acceptors. We find that the molar extinction coefficient (εd,max) shows reasonable agreement between calculation in vacuum and experiment for molecules in solution, highlighting the effectiveness of TDDFT for predicting optical properties of organic π-conjugated molecules. We then perform a statistical analysis based on molecular descriptors to identify which features are important in defining the absorption strength. This allows us to identify structural features that are correlated with high absorption strength in NFAs and could be used to guide molecular design: highly absorbing NFAs should possess a planar, linear, and fully conjugated molecular backbone with highly polarisable heteroatoms. We then exploit a random decision forest algorithm to draw predictions for εd,max using a computational framework based on extended tight-binding Hamiltonians, which shows reasonable predicting accuracy with lower computational cost than TDDFT. This work provides a general understanding of the relationship between molecular structure and absorption strength in π-conjugated organic molecules, including NFAs, while introducing predictive machine-learning models of low computational cost.
Broader contextOrganic π-conjugated semiconductors (OSCs) work as the main light harvesters in organic photovoltaics (OPVs). Their synthetic versatility converts them onto suitable candidates for rational molecular design based on high-throughput screening techniques. Significant advances in the efficiency of OPVs (exceeding 19% in single junctions under 1 sun) have been made by trial-and-error with new but increasingly diverse materials, primarily non-fullerene acceptors (NFAs) and mostly owing to their high absorption strength. However, the reasons for that superior light harvesting performance remain elusive, thus preventing the molecular tailoring of NFAs with further enhanced light harvesting capabilities toward breakthrough OPV efficiencies. A statistical analysis of time-dependent density functional theory calculations and machine learning (ML) models reveal that molecular linearity, planarity, polarizability, and number of π-conjugated carbon atoms correlate strongly with the absorption strength of OSCs. A structure–absorption strength relationship is established to introduce design rules for highly absorbing OSCs. ML models, in combination with extended tight-binding Hamiltonians, are shown to predict the absorption strength of OSCs. As a result, this work contributes to an improved understanding of the absorption strength of π-conjugated organic molecules in general while suggesting ways to design highly absorbing NFAs that maximize the light harvesting capabilities for solar energy conversion. |
1. Introduction
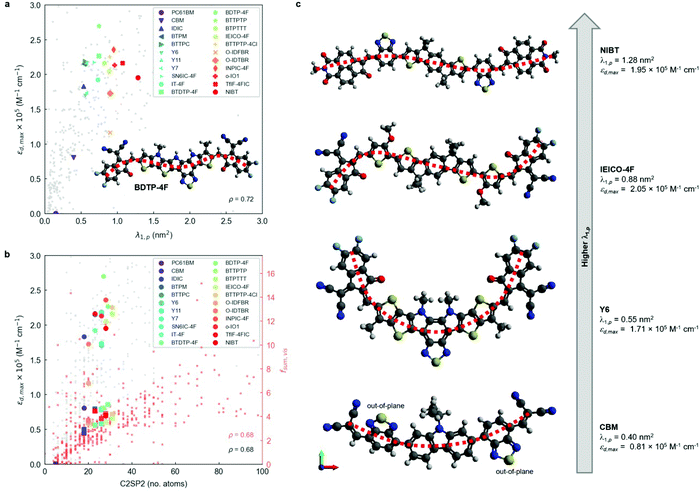
Organic photovoltaic (OPV) energy conversion is a promising option among next generation renewable and sustainable energy technologies for a low-carbon energy future.1–3 OPV has shown promising potential for various applications, such as indoor photovoltaics (PV),4–6 semi-transparent solar windows,7,8 PV greenhouses,9 and off-grid power supply.10 Recent OPV devices based on non-fullerene acceptors (NFAs) have demonstrated certified power conversion efficiencies (PCEs) exceeding 19% in a single junction configuration,11 approaching the efficiencies observed in inorganic semiconductor PV technologies such as crystalline silicon and perovskite solar cells, and far higher than values thought attainable in OPV when using fullerene derivatives as the electron-acceptors.12 The startling progress led by NFAs can be attributed to various advantages over fullerene derivatives, such as band-gap tunability, sharp absorption onset, high emission, high absorption, and low energy losses.13–15 Among these advantages, the absorption strength of state-of-the-art NFAs is particularly outstanding, as exemplified in Fig. 1c (a detailed list of chemical names and nomenclatures is provided in Note S1, ESI†).16 For instance, Y6 shows a maximum extinction coefficient (κmax) over 1.5 in the visible part of the electromagnetic spectrum, as compared to less than 0.75 for fullerene derivatives (PC61BM and PC71BM). A high extinction coefficient increases the chance of high quantum efficiency and photogenerated current density, and makes it possible to fabricate highly absorbing OPV films with just a few tens of nanometre-thick photoactive layers. In comparison with workhorse fullerene acceptors, OPV devices based on highly absorbing NFAs could be made comparably thinner than the former, which exponentially raises the output power per weight (i.e. the specific weight in W g−1) of OPV devices17 and might be an effective route toward lower production costs (as less material could employed to achieve an equivalent PCE) and even increase device thermal stability.18 Moreover, through detailed balance between photon absorption and emission,19,20 high absorption strength in principle should lead to high emission from the NFAs, while strong NFA emission is believed to be a key reason for NFA-based OPVs to possess low nonradiative voltage losses.21–25 Despite the clear advantage of strong photo-absorption of NFAs over fullerene derivatives, the phenomenon has attracted much less attention than other properties of NFAs.21–23,25–28 Conceptually, symmetry rules (i.e., the Laporte rule) can explain the qualitative difference between NFAs and fullerene derivatives in terms of absorption strength, yet such rules cannot predict differences in absorption strength among structures for which the lowest transitions are symmetry allowed. The features empirically and theoretically proposed29,30 to lead to strong absorption in π-conjugated polymers are molecular stiffness, linearity, extended π-conjugation and large molecular size. It is therefore of interest to establish whether the same (or other) molecular features are quantitatively associated or not with increased absorption strength in NFAs, while seeking molecular design rules to drive absorption and performance higher in new molecules.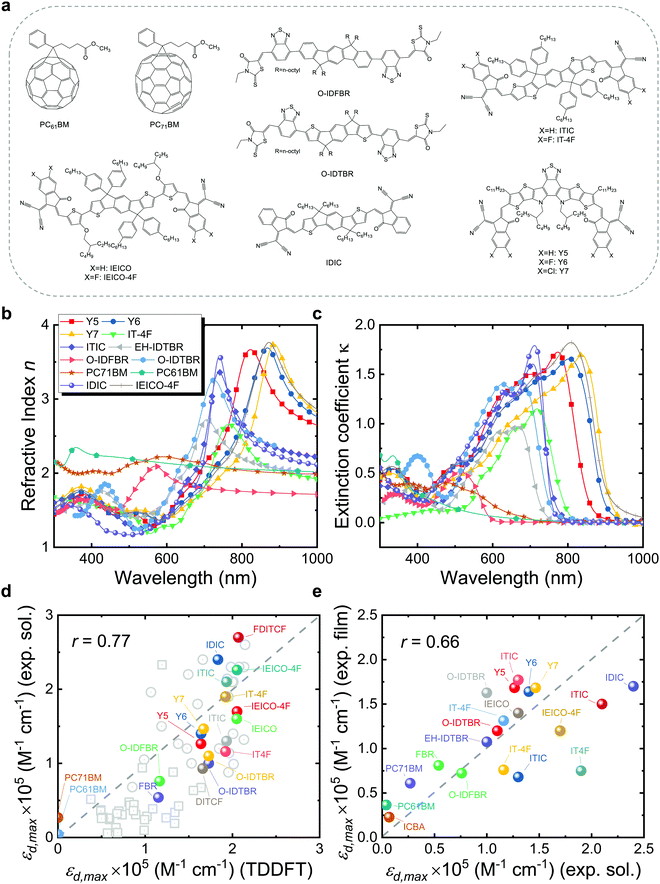 | ||
| Fig. 1 (a) Molecular structures of typical organic acceptors, including PC61BM, PC71BM, O-IDFBR, O-IDTBR, ITIC, IT-4F, IDIC, IEICO, IEICO-4F, Y5, Y6, and Y7. (b) Refractive index and (c) extinction coefficient of a larger set of typical organic acceptor thin films measured using VASE. (d) Experimental εd,max in solution versus calculated εd,max in vacuum using TDDFT of a set of ∼80 π-conjugated molecules. (e) Estimated experimental εd,max in film (solid state) versus that in solution using eqn (3). Panel (d) contains a subset of well-known NFA molecules that are highlighted in colour. All TDDFT results in panel (d) were performed using the functional B3LYP and basis set 6-311+G(d,p), except for the ones (grey squares) taken from ref. 69 that are based on the LRC-wPBEh functional and 6-311+G(d) basis set. We also note here that the side chains of molecules are replaced by H atoms or methyl groups in the calculations as they are computationally expensive and do not contribute to the π-conjugation, hence electronic transitions.29 The experimental data of εd,max in film are converted from maximum values of extinction coefficients shown in panel (c) using eqn (3), while solution data are collected from literature, noting that different values may be present for the same material as retrieved from different sources. Grey dashed lines indicate the perfect match between x and y axis. The data required for generating panels (d) and (e) in this figure are presented in the ESI.† | ||
Excited state calculations based on quantum chemistry methods, such as time-dependent density functional theory (TDDFT),8,29,31–33 Hartree–Fock method,34ab initio Monte Carlo method,35 second order Møllier–Plesset theory (MP2),36 and coupled cluster method,37 have been applied to predict the electronic and optical properties of molecules. Among them, TDDFT is the most widely applied method for excited state calculations, and has shown reasonable accuracy in calculating and predicting the trends in absorption strength of organic molecules,29,31 as also demonstrated in this work. However, the rapid scaling of computation time with molecular size has been the real obstacle limiting the applicability of TDDFT for excited state calculations on molecules with hundreds of atoms. Given the size and diverse structure of modern NFAs, faster and more efficient methods are therefore needed to establish the relationship between excited-state and molecular properties in NFAs.
The emergence of artificial intelligence (AI) has made it possible to study quantitative structure–property relationships (QSPRs) in molecules with massively improved computational efficiency. As the most popular branch of AI, machine-learning (ML) has attracted much attention in materials science over the last decade, and has been widely applied for material property prediction and material discovery.38–41 Recently, ML has also gained popularity in OPV scenarios,42–52 yet existing ML studies related to OPVs have been primarily focused either on the energetics42,43,53–56 or directly on PCE,42,48,57–64 with little attention paid to the absorption strength of the photoactive materials.65,66 Moreover, there are no ML studies explicitly focused on the absorption strength of NFAs beyond the identification of moieties of frequent appearance in highly absorbing molecules.42 However, QSPR and ML models have been successfully applied to investigate the absorption strength of fluorophores or dyes typically employed in bioimaging, showing encouraging results.30,67,68 Therefore, it is appealing to apply ML methods in combination with QSPR models to investigate the origin of the large absorption strength in state-of-the-art NFAs.
Here, we present an experimental, TDDFT, QSPR, statistical and ML study of the absorption strength of NFAs to identify the key chemical and structural features that lead to high optical absorption in state-of-the-art NFAs. We exploit a database of nearly 500 unique organic molecules (or 3500 calculations) generated using DFT and TDDFT over several years. We obtain good quantitative agreement between TDDFT calculations of absorption strength and experimental values for state-of-the-art NFAs and fullerenes, which supports the use of TDDFT results for further statistical and QSPR modelling. Accordingly, we extract molecular information from the DFT-optimized geometries by computing nearly 6000 molecular descriptors and first looking for correlations with the absorption strength. The strongest correlations are found between experimentally measured maximum molar extinction coefficient (εd,max) and two main molecular descriptors from calculations: λ1,p and C2SP2, which describe the size of the molecule in the direction of maximal atomic polarizability, and the number of sp2 hybridized carbon atoms that are bound to two other carbons (C2), respectively. These quantities can be related to a few key material features leading to high absorption strength: linearity, planarity, and extension of the π-conjugation in the form of fused and closed-ring moieties, in good agreement with previous ML reports on fluorophores and dyes.30 We further identify several moieties and paired combinations thereof that are frequently found in highly absorbing NFAs, corresponding to thieno[3,2-b]thiophene (TT), thiophene (T), 2-(5,6-difluoro-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (2FIC), 2-(3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (IC) and indaceno[1,2-b:5,6-b′]dithiophene (IDT). These form a catalogue of molecular design rules to further enhance the absorption strength of organic π-conjugated molecules, such as next-generation NFAs. We then train and test an ensemble learning method, namely a random decision forest (RF), to predict εd,max and provide further information about the most important features in the modelling of absorption strength in organic π-conjugated molecules. Finally, we explore the possibility to predict εd,max while using a cheaper molecular geometry optimization method based on semiempirical extended tight-binding (xTB) Hamiltonians instead of the expensive DFT approach. We do so by training a RF with our TDDFT database and proving its predictive properties in terms of εd,max when interpolated using xTB-optimized geometries. This approach shows application potential in high-throughput screening studies in combination with generative molecular models.
2. Results and discussion
2.1. Experimental validation of calculated absorption strength using TDDFT
Quantifying how well the TDDFT derived excited state properties agree with the experimental measurements in terms of absorption strength is of utmost importance to validate our theoretical calculations and support further conclusions extracted thereof. Accordingly, we first evaluate the agreement between TDDFT calculations and experimental data in terms of the absorption strength. We compare the absorption strength of a broad catalogue (∼10 molecules) of NFA molecules and widely studied fullerene derivatives (PC61BM and PC71BM, with their molecular structures shown in Fig. 1a) as obtained from TDDFT calculations, with a variety of optical measurements in both solution and solid state. For the most representative NFAs examined, we verify that their frontier molecular orbital energy levels as retrieved from TDDFT calculations are properly aligned, relative to those of a set of common polymer donors, for the NFAs to act as electron acceptor in a bulk heterojunction blend with those donors (Fig. S1, ESI†). The measured refractive index (n) and extinction coefficient (κ) of those molecules in thin film obtained using our variable-angle spectroscopic ellipsometry (VASE) measurements are shown in Fig. 1b and c. Solution state data shown in Fig. 1d and e are collected from a variety of literature references as detailed in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1
As a metric for absorption strength, we initially consider several candidates such as the oscillator strength (fosc), the absorption coefficient (α) or the imaginary part of the dielectric function (ε2). In this work, we eventually focus on the maximum molar extinction coefficient (εd,max, M−1 cm−1) of NFAs as it shows the best agreement between experimental and theoretical data, as we demonstrate below. εd,max constitutes a typical experimental measurement in solution that can also be accessed from myriad literature references. Note that the usual calculations based on single molecules using TDDFT cannot account for solid state effects as they are performed for isolated molecules in vacuum or surrounded by an isotropic medium (such as a solvent using the polarizable-continuum-solvent-model, PCM, Fig. S2, ESI†). The derivation of the theoretical εd is provided in the Methods section, which results in a mathematical expression for εd,max as
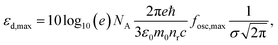 | (1) |
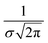 , where σ is the Gaussian width and assumed to be 0.1 eV for a common organic pi-conjugated molecule.
, where σ is the Gaussian width and assumed to be 0.1 eV for a common organic pi-conjugated molecule.
The experimental εd,max from solution can be obtained using the optical density (OD) measurements performed using UV-visible spectroscopy, via
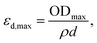 | (2) |
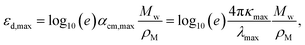 | (3) |
Fig. 1d presents the results of the comparison between experimental εd,max in solution and theoretical εd,max calculated from single molecules using TDDFT in vacuum. A brief discussion of the solvent effect on the absorption strength and the reasons why we choose a vacuum medium are provided in Fig. S2 (ESI†). Despite the scattering of data points, we observe the occurrence of a monotonic relationship between solution and calculated εd,max with a Pearson correlation coefficient (r) of 0.77. Interestingly, such correlation is no longer observed when quantifying the absorption strength in terms of αmax neither when adding further data points from literature on π-conjugated fluorophores to our statistical analysis (Fig. S3a (ESI†), r = 0.30), which is believed to be caused by the differences in molecular weight; in that case, only εd,max is found to follow a monotonic trend (Fig. S3b, ESI†). Some of the material assumptions on refractive index and density required to obtain αmax values might be responsible for the observed mismatch. It is worth noting that, expectedly, the correlation between solid state (film) and solution (r = 0.66, Fig. 1e) or calculated εd,max (r = 0.61, Fig. 1e) is not as good as that from solution data versus calculated εd,max (r = 0.77, Fig. 1d, neither for αmax as shown in Fig. S4, ESI†). Such discrepancy is attributed to solid-state effects such as aggregation effects,15 intermolecular orientation,70,71 and side chain interactions,72 which are not considered in single molecule excited state calculations.29 The observed trend that a highly absorbing material in solution will produce highly absorbing films is, nonetheless, generally valid and thus solution data are relevant for devices. Since the NFAs analysed here have a rather similar number of π-electrons (nπ), the corresponding εd,max per π-electron (Fig. S6, ESI†) shows a similar trend as that in Fig. 1d, e, and Fig. S4 (ESI†). Despite the simplicity of single molecule excited state calculations, these data show that using TDDFT calculations of the excited state to deliver εd,max can provide a reasonably good approximation to experimental measurements. Moreover, dealing with TDDFT calculations gives us room to correlate key molecular properties, such as molecular size and shape (aspect ratio), linearity, planarity, grafted side chain positions, or functional groups, to the absorption strength using molecular descriptors. These observations provide a foundation from molecular structures to identify the origin and further extend the high optical extinction of NFAs through chemical design rules, as we show in the upcoming sections.
2.2. Statistical analysis of the TDDFT absorption strength dataset
The experimental validation of the TDDFT calculations in NFAs supports the use of such results to build an extended database of optimized molecular geometries and excited state properties. The dataset is built by collecting thousands of molecular geometries generated over the last years in our group, making up a total of 3515 calculations on small molecules and oligomers. The distribution of number of atoms in a molecule is shown in Fig. S7 (ESI†) with a majority lying between 50 and 100 atoms. This database is sufficiently diverse to allow us to detect correlations and chemical/structural design rules that could explain and/or further enhance optical absorption in conjugated small molecules.Then, we introduce several target features related with absorption strength, starting from the maximum oscillator strength of any calculated transition (fmax); the maximum oscillator strength of any transition in the visible electromagnetic window (herein constrained between 300–1200 nm or 1–4 eV for its relevance in solar energy harvesting applications) (fmax,vis); and the sum of oscillator strengths of all transitions in the visible window, fsum,vis. These three features are also evaluated per nπ for the molecule, i.e., fmax/nπ, fmax,vis/nπ and fsum,vis/nπ. We then consider the maximum absorption coefficient (αmax) obtained using eqn (1) and (3); the maximum of the imaginary part of the dielectric function (ε2,max);29 and εd,max. Finally, we compute the spectral overlap between the OD (dα(E), where d is set to a typical film thickness value of 100 nm and α(E) derives from the Gaussian-broadened spectrum of f in the visible spectral range taking a standard deviation of 0.1 eV) and the AM1.5G solar photon flux spectrum (ΦAM1.5G), namely 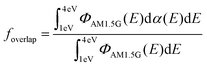 .
.
These features, together with their corresponding histograms (Fig. S14, ESI†) in terms of Spearman's rank correlation coefficients (ρ), are explained in more detail in Note S2 (ESI†). Molecular descriptors are calculated using up to four different open-source packages73–76 (Note S2, ESI†) to generate a (curated) collection of 3239 entries (including 40 electronic descriptors derived from the TDDFT calculations, namely the energy of the molecular orbitals ranging from HOMO−19 to LUMO+19). Then, we scan for statistical correlations between those descriptors and all target features introduced above, from which we consider as highly correlated descriptors those showing ρ ≥ 0.7 as threshold. However, since some descriptors are calculated in groups or families where weighting factors are varied among atomic masses, van der Waals volumes, electronegativities, ionization potentials or polarizabilities, we usually encounter sets of multicollinear descriptors that show very similar trends with respect to the target feature. Accordingly, to drop redundant (collinear) descriptors we classify them into clusters to select the most representative candidate of each bundle (i.e., cluster). This serves us to simplify the identification of characteristic and well-correlated descriptors families. The clustering algorithm applied to analyse multicollinear descriptors based on ρ and r values is further described in Note S3 (ESI†).
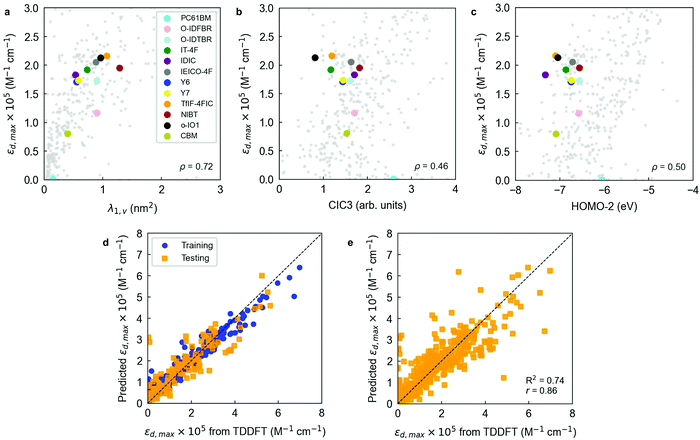
After running the clusterization of descriptors on all target features, we identify strong correlations with molecular descriptors for fmax, fsum,vis and εd,max (i.e., implicitly fmax,vis). For the remaining target variables (foverlap, αmax, ε2,max, fmax/nπ, fmax,vis/nπ and fsum,vis/nπ), we do not identify molecular descriptors with ρ above the threshold value (0.7) and they are generally below 0.6 units, see Fig. S14 (ESI†). The lack of correlation for foverlap could be justified by the existence of a gas-to-solid shift in the corresponding absorption spectrum, which prevents proper matching of the Gaussian-broadened absorption features with the solar photon flux. Regarding αmax and ε2,max, the estimation of these values from TDDFT calculations requires taking generalized assumptions on several materials properties (such as density or refractive index) that might be enough to disturb the underlying trends in our heterogeneous material database. For the quantities normalised by the number of pi electrons, i.e. fmax/nπ, fmax,vis/nπ and fsum,vis/nπ, the weak correlation is expected since normalization tends to deviate from linear correlations depending on the straightness of the molecule.29 Due to the strong correlation between size of the molecule and oscillator strength as discussed below based on C2SP2, the normalised quantity is believed to be a secondary factor, therefore not clear correlations are observed. In the successful correlation cases (i.e. fmax, fsum,vis and εd,max) and with the given thresholds of 0.7 units for ρ and r, we identify a single feature cluster lead by the λ1,p descriptor in the case of fmax and εd,max (Fig. 2a). For fsum,vis, a threshold ρ of 0.68 reveals C2SP2 as a rather descriptive molecular feature (Fig. 2b). Interestingly, C2SP2 is also found in the main cluster represented by λ1,p in fmax and εd,max, and we could not identify any strong correlations between the absorption strength (in any of its proposed metrics) and electronic descriptors (from HOMO−19 to LUMO+19 energy levels). Note that εd,max values in excess of 2.5 × 105 M−1 cm−1 in Fig. 2a and b are mostly attributed to artificially straight conjugated oligomers with >10 monomers contained in our database, for which the straightness, hence high εd,max, are unlikely to be maintained in the experimental solid state scenario. In fact, only the exemplary and asymmetric NFA known as BDTP-4F (inset of Fig. 2a)77,78 surpasses that threshold with a record εd,max in our NFA dataset (2.7 × 105 M−1 cm−1, and 2.4 × 105 M−1 cm−1 measured in CHCl3 solution).77
λ 1,p is part of a bundle of three-dimensional molecular size and shape descriptors known as weighted holistic invariant molecular (WHIM) descriptors.79–81 These can be interpreted as a generalized search for the principal axes with respect to a defined atomic property.82 In this particular case, λ1,p is obtained by performing a principal component analysis (PCA) on the centred atomic coordinates of the molecule using a covariance matrix (sjk) that is weighted by the atomic polarizabilities (pi):
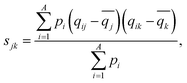 | (4) |
![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) is their average value.82 After diagonalization of the polarizability-weighted covariance matrix, the first eigenvalue (λ1,p) quantifies the size of the molecule in the direction of maximal polarizability variance. Interestingly, the third eigenvalue (λ3,p) approaches zero in planar molecules as a result of absence of variance in the out-of-plane (z) direction.82 On the other hand, C2SP2, which is not in the WHIM group, accounts for the number of doubly bound carbon atoms (sp2 hybridized, SP2) bound to two other carbons (C2), thus constituting a two-dimensional descriptor of fast computation. The correlation between C2SP2 and absorption strength can be relatively easier to understand, as C2SP2 to some extent represents the size of the conjugated molecule. Enlarging the size of the molecule increases the total number of π-electrons, which controls the total oscillator strength following the Thomas–Reiche–Kuhn rule. For the molecules that are extended along one direction, such as linear oligomers, increasing the size should enhance the oscillator strength of the first transition,29i.e. the dominant one.
is their average value.82 After diagonalization of the polarizability-weighted covariance matrix, the first eigenvalue (λ1,p) quantifies the size of the molecule in the direction of maximal polarizability variance. Interestingly, the third eigenvalue (λ3,p) approaches zero in planar molecules as a result of absence of variance in the out-of-plane (z) direction.82 On the other hand, C2SP2, which is not in the WHIM group, accounts for the number of doubly bound carbon atoms (sp2 hybridized, SP2) bound to two other carbons (C2), thus constituting a two-dimensional descriptor of fast computation. The correlation between C2SP2 and absorption strength can be relatively easier to understand, as C2SP2 to some extent represents the size of the conjugated molecule. Enlarging the size of the molecule increases the total number of π-electrons, which controls the total oscillator strength following the Thomas–Reiche–Kuhn rule. For the molecules that are extended along one direction, such as linear oligomers, increasing the size should enhance the oscillator strength of the first transition,29i.e. the dominant one.
To further interpret these two magnitudes (λ1,p and C2SP2) as the main correlated descriptors with εd,max and fsum,vis, we inspect the DFT-optimized geometries of archetypal NFAs (Fig. 2c). The observed trend suggests that optical extinction monotonically increases with λ1,p (Fig. 2a) in molecules having most of their polarizable atoms arranged along a main axis, i.e., linear molecules. While CBM shows large torsion angles mainly affecting the 2,1,3-benzothiadiazole (BT) moieties (thus making the molecule non-planar and increasing λ3,p, see Fig. S15, ESI†), Y6 shows a characteristic curved geometry that limits its εd,max despite showing improved planarity. The NFA with the highest λ1,p (NIBT) shows both linearity and planarity, with most of the more polarizable atoms (mainly C and S) lying along the principal polarizable axis of the molecule. Thus, in terms of molecular geometry, the absorption strength of NFAs could be further enhanced by distributing most of the atomic polarizability along a main axis while keeping good planarity and minimizing curvature. However, λ1,p is not the sole molecular descriptor governing absorption strength, as BDTP-4F shows ca. 40% lower λ1,p (0.75 nm2) yet ca. 40% higher εd,max than NIBT (Fig. 2a), which suggests that the molecular symmetry of NFAs could be another important factor affecting εd,max. Our preliminary investigations on this issue indicate that molecular asymmetry, as quantified by the WHIM symmetry index Gu, might drive absorption strength higher (Fig. S16a, ESI†), yet we require a larger NFA database including more asymmetric molecules to further explore such an observation. Also, we acknowledge that this observation might be biased by the systematic omission of side chains in the TDDFT calculations. By comparing λ1,p in a selection of small molecule acceptors geometrically optimized with and without side chains (Fig. S17a, ESI†), we observe that in most cases the addition of side chains either decreases λ1,p slightly or keeps it invariant. Still, the positive correlation of λ1,p with respect to εd,max is maintained (Fig. S17b, ESI†). Furthermore, the presence of naphthalene imide derivatives in the molecular structure of NIBT could be hindering further increase of the absorption strength with λ1,p, as suggested by our statistical analysis of frequent moieties in the selection of good light harvesters (presented in the next section). On the other hand, an increase of nπ in the molecule in the form of closed-ring conjugated moieties will systematically increase C2SP2 and accordingly fsum,vis. These findings support the previously known design rules in terms of molecular linearity and π-conjugation enabling large oscillator strength in organic small molecules and polymers, and are consistent with a recent study on chromophores.30 In particular, trans-conjugated polymer stereoisomers are known to possess higher optical extinction due to their increased straightness and persistence length,29 which agrees with our observations on exemplary curved (Y6) and more linear (NIBT) NFAs.
The energy of the first optical transition (E1) is also of practical importance in light harvesters such as NFAs as the lower energy part of the solar spectrum, down to ∼1 eV, contains a higher photon flux density. Our results show the number of heteroatoms in the molecule as the most correlated feature with (ρ = −0.72, Fig. S18a, ESI†) while forming a single feature cluster, yet neither λ1,p nor C2SP2 show strong correlations with E1. This fact prevents the introduction of molecular design rules targeted at E1 using λ1,p or C2SP2. However, we acknowledge a negative correlation between E1 and fosc,max among common NFAs that suggests further room for absorption strength increase as E1 is reduced (Fig. S19, ESI†).
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )/σk, where k is the number of high-absorbing molecules containing certain moiety; is its expected value, defined as pK/P where K corresponds to the number of molecules in the entire dataset containing that same moiety; and
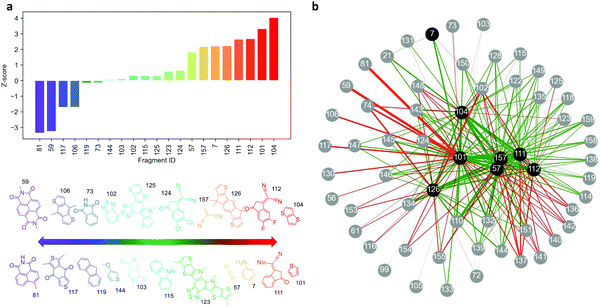
)/σk, where k is the number of high-absorbing molecules containing certain moiety; is its expected value, defined as pK/P where K corresponds to the number of molecules in the entire dataset containing that same moiety; and 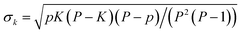 is the standard deviation of the hypergeometric distribution. Z-scores will indicate (in units of σk) which moieties are overrepresented or underrepresented in the subset of high-performing molecules with respect to the expected values when looking at the entire dataset. Our results (Fig. 3) suggest that thieno[3,2-b]thiophene (TT), thiophene (T), 2-(5,6-difluoro-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (2FIC), 2-(3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (IC), indaceno[1,2-b:5,6-b′]dithiophene (IDT), 2-methylene malononitrile, cyanide, and aniline are particularly frequent in highly absorbing molecules. Interestingly, four of those molecular fragments (TT, T, 2FIC and IC) are contained in the chemical structure of the workhorse NFA Y6 (Fig. 2c). Contrarily, naphthalene imide derivatives, as typically encountered in n-type small molecules and conjugated polymers; 4H,8H-benzo[1,2-c:4,5-c′]dithiophene-4,8-dione and benzo[1,2-b:4,5-b′]dithiophene fragments are mostly underrepresented in the selection of high-performing light harvesters.
is the standard deviation of the hypergeometric distribution. Z-scores will indicate (in units of σk) which moieties are overrepresented or underrepresented in the subset of high-performing molecules with respect to the expected values when looking at the entire dataset. Our results (Fig. 3) suggest that thieno[3,2-b]thiophene (TT), thiophene (T), 2-(5,6-difluoro-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (2FIC), 2-(3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (IC), indaceno[1,2-b:5,6-b′]dithiophene (IDT), 2-methylene malononitrile, cyanide, and aniline are particularly frequent in highly absorbing molecules. Interestingly, four of those molecular fragments (TT, T, 2FIC and IC) are contained in the chemical structure of the workhorse NFA Y6 (Fig. 2c). Contrarily, naphthalene imide derivatives, as typically encountered in n-type small molecules and conjugated polymers; 4H,8H-benzo[1,2-c:4,5-c′]dithiophene-4,8-dione and benzo[1,2-b:4,5-b′]dithiophene fragments are mostly underrepresented in the selection of high-performing light harvesters.
We further study the existing correlation between pairs of moieties to understand in which way the different molecular fragments should (or should not) be combined to retrieve highly-absorbing molecules. Our analysis starts by creating molecular subsets determined by the presence of a given moiety, which acts as source node (coloured in black) in the network graph shown in Fig. 3b. Within that subset, we identify the high-absorbing molecules (fosc,max > 2.5) and compute the Z-scores of their moieties (child nodes, coloured in grey in Fig. 3b) with respect to the molecules of the entire molecular subset. As per the network shown in Fig. 3b, the absolute Z-scores will determine the width of the edges connecting the nodes (moieties) and its sign the colour of the edge (green for positive Z-score [overrepresentation] and red for negative Z-score [underrepresentation]). Therefore, green and thick edges connect pairs of molecules that are more frequently found in high-absorbing molecules whereas thick and red edges indicate combinations of moieties that lead to less absorbing molecules. In this analysis, we set up 8 different source nodes corresponding to the most overrepresented moieties observed in Fig. 3a. As a result, Fig. 3b can be interpreted as a catalogue of design rules relating pairs of moieties with high oscillator strength in π-conjugated small molecules.
2.3. Machine-learning modelling of the absorption strength
Besides providing useful chemical insights from a material design perspective, molecular descriptors can be exploited to feed regression models and draw predictions on certain target features, forming the so-called quantitative structure–property relationship (QSPR) and quantitative structure–activity relationship (QSAR) models.79,80,82,83 In the present study, we train and test several ML models fed with molecular and electronic descriptors obtained from TDDFT calculations to predict the value of εd,max in conjugated small molecules and oligomers. Finally, we propose exploiting such ML model (trained with TDDFT data) to predict εd,max in molecules optimized using a semi-empirical quantum chemistry method, i.e. xTB.84 This renders possible thanks to the geometrical similarity of the TDDFT and xTB ground state conformers, which lead to similar (geometrical) descriptors values; and the calibration of their corresponding energy levels, as per the required inputs of the ML model herein employed. Therefore, further molecular candidates beyond the pristine dataset could be geometrically optimized using solely xTB Hamiltonians and their absorption strength predicted using such ML model. This approach effectively bypasses the use of TDDFT calculations when screening the absorption strength of novel molecules, which results in less demanding computations and higher throughput. The present ML workflow will open the possibility to accelerate the screening of high-performing molecular candidates with low-to-moderate computational requirements (further discussed in Note S5, ESI†).Accordingly, we deploy a state-of-the-art ML method, namely a RF, to aid in both aspects: feature selection and building of εd,max models of higher accuracy. RFs constitute one of the simplest and most widely applied ML methods in molecular screening and data mining studies.30,43,46,86 They are particularly appealing for their straightforward implementation through open-source Python libraries such as Scikit-Learn,87 and also for their inherent robustness against overfitting and fast optimization. RFs are formed by an ensemble of decision trees (estimators) that are executed in parallel and independently from each other. Decision trees serve to classify data by starting from a single root node that is subsequently divided into child nodes, the latter being chosen randomly among the input features. At every node splitting step (i.e., decision making), the algorithm selects the pathway that minimizes the mean square error (MSE). Eventually, when every tree reaches its maximum extension (which is set arbitrarily via model hyperparameters), the predictions of all trees are averaged (ensembled), hence constituting the final predicted value of the RF. At this stage, myriad cross-validation (CV) techniques exist to evaluate the quality of the model and help in the tuning of hyperparameters. CV methods can estimate the ML model performance, evaluate potential over- or underfitting, and quantify how accurate the model is on drawing predictions on unseen data. In this work, we adopt two common cross-validation schemes, namely a repeated holdout CV; and a leave-one-out cross-validation (LOOCV). On the one hand, in a repeated holdout CV the pristine dataset is randomly split onto two distinct subsets, namely the training (here gathering 70% of the data) and testing (the remaining fraction of data, i.e. 30%) subsets. The model is trained and tested on the respective subsets, and the corresponding statistical metrics (R2, r, MSE, etc.) annotated. Eventually, the process is repeated k times (10-fold in this work), and all metrics are averaged to evaluate the ML model performance (its CV score). On the other hand, in a LOOCV the holdout process is taken to the extreme as the testing subset consists of a single data point while the remaining data is used in the training step. The process runs recursively for all data, thus eventually all data points are used for training and testing in the LOOCV protocol. Yet being computationally expensive, a LOOCV results in a more accurate estimate of model performance.
Table S1 (ESI†) includes the performance of an out-of-the-box RF model trained and cross-validated using 300 trees (estimators). Exemplary comparisons between the two previous baseline models (1-nearest neighbor and linear regression) and the out-of-the-box RF model are found in Fig. S20 (ESI†). The RF models indicate that scoring functions (R2, r) well above 0.6–0.8 are feasible upon careful feature selection and further optimization of the RF regressor. Feature selection in RFs is usually performed by filtering variables based on their feature importance, which is a metric that accounts for how much a feature decreases the weighted variance in the node splitting steps of the decision trees. This property enables feature ranking to then apply myriad algorithms to filter out the least important variables as seen by the RF regressor. In this work, we perform a recursive feature elimination (RFE) procedure to the initial library of 3239 descriptors as described in Note S2 (ESI†). In a RFE protocol, a significant fraction of the initial population of features is dropped in successive training steps of the RF ensemble. Features are dropped based on their corresponding feature importance until reaching an arbitrarily low number of input variables, hence simplifying the original model. Our RFE analysis shows that a threshold average R2 of 0.70 is achieved using a 12-variable model (R2 = 0.70 ± 0.05, r = 0.84 ± 0.03), which outperforms the RF model presented earlier while including a drastic reduction in the number of variables (from 3239 to 12). The sweet spot in model accuracy and number of degrees of freedom is found for the 10-variable model, which shows the maximum average Radj2 (0.67 ± 0.06).
Notably, a threshold R2 of 0.60 is already achieved training a 3-parameter RF model (R2 = 0.63 ± 0.06, Radj2 = 0.62 ± 0.06, r = 0.80 ± 0.03), which is particularly appealing given its simplicity. The resulting three-variable model includes one three-dimensional descriptor (λ1,v or WHIM_45, as computed by the RDKit library, Fig. 4a), one two-dimensional descriptor (CIC3, as computed by PaDEL software, Fig. 4b) and one electronic descriptor, in this case the energy level of the second molecular orbital below the frontier HOMO (HOMO−2, Fig. 4c). λ1,v refers to the first eigenvalue of the covariance matrix weighted by the atomic van der Waals volumes; thus, λ1,v is included in the multicollinear feature cluster represented by λ1,p that we previously and statistically identified, showing nearly perfect correlation (r = 0.99) with λ1,p. Accordingly, λ1,v can be exchanged by λ1,p without loss of performance in the RF model. This finding confirms that the linearity of the molecule (either quantified in terms of polarizabilities or van der Waals volumes) plays a key role in determining its absorption strength in the form of εd,max. On the other hand, CIC3 is a graph-based, third-order neighbourhood symmetry index82 which lacks a straightforward interpretation due to its mathematical complexity. We observe, however, that it linearly scales as log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, with A being the total number of vertices (atoms) in the graph (molecule)82 thus likely reflecting the size of π-conjugation as per the characteristics of our dataset. The interpretation of HOMO−2 as an important descriptor is more challenging, and it is not possible to substitute it by a different descriptor without a noticeable drop in the model performance (excepting HOMO−1, which shows r = 0.96).
A, with A being the total number of vertices (atoms) in the graph (molecule)82 thus likely reflecting the size of π-conjugation as per the characteristics of our dataset. The interpretation of HOMO−2 as an important descriptor is more challenging, and it is not possible to substitute it by a different descriptor without a noticeable drop in the model performance (excepting HOMO−1, which shows r = 0.96).
Interestingly, electronic descriptors (in particular) are required for the RF models to achieve their highest potential and scoring despite we have not observed strong correlations in our earlier statistical analysis. To probe it, we have performed the same RFE protocol yet skipping the set of electronic descriptors among the input features. Our results show that the top performing RF models (selecting 29 variables and getting R2 = 0.58 ± 0.06, Radj2 = 0.48 ± 0.07, r = 0.78 ± 0.04; or selecting 9 variables to obtain Radj2 = 0.52 ± 0.06, see Fig. S13, ESI†) are yet behind the scorings recorded when the electronic descriptors are included in the list of features. Note that the performance without electronic descriptors is lower than the 3-parameter model that includes HOMO−2 as descriptor, highlighting its positive effect on the performance of the RF regressor.
Molecular fingerprints have also been extensively exploited as input vectorial descriptors in statistical and ML models focused on feature prediction.42,88–90 Molecular fingerprints are usually represented as bit activation vectors of arbitrary length and degree of complexity, representing the absence or presence of certain molecular (bonding) pattern, moiety, functional group, or atom. In this work, we exploit the RDKit library to generate moiety fingerprints, MACCS keys, Morgan fingerprints, path-based or topological fingerprints, E-state fingerprints, and Coulomb vectors. These fingerprints are quickly computed and serve to complement and improve the learning process of the ML models employed herein.
To better analyse the influence of the different fingerprint vectors in improving the RF scoring, we trained and cross-validated the 3-parameter RF model previously found in combination with all fingerprint vectors generated. The results shown in Table S2 (ESI†) indicate that by adding a Morgan fingerprint vector of 64 bits to the initial set of input features the model performance can be substantially improved: R2 increases by 10% (relative), and r by another (relative) 5% (see Fig. 4d). Therefore, Morgan fingerprints are particularly suitable to fine-tune the training and prediction accuracy of εd,max in RF models although lacking of a straightforward physical interpretation. Additional refinement of the RF hyperparameters results in further improved models. We performed this optimization through a randomized search (in 350 iterations) of the hyperparameters controlling the number of estimators in the RF, the minimum number of samples per leaf node and the minimum number of samples required to split an internal node, which constitute the main adjustable hyperparameters of the RF algorithm. These results are shown in Table S3 (ESI†), together with the scoring obtained in a rigorous LOOCV of the optimized RF model (Fig. 4e). As an alternative ensemble of decision trees, we have also tested and optimized an Extra Trees (ET) regressor in Scikit-Learn. Its performance is, however, very close to that attained in the workhorse RF regressor (Table S3 and Fig. S21, ESI†).
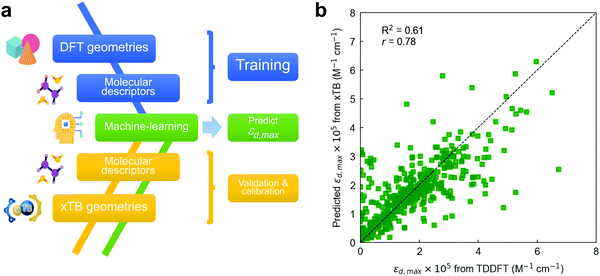 | ||
| Fig. 5 (a) ML workflow used in this work to draw εd,max predictions. A RF model is trained on TDDFT data and interpolated (validated) on xTB geometries, including also their corresponding molecular descriptors. To improve the accuracy of the model, energy levels obtained using the GFN2-xTB Hamiltonian require calibration with TDDFT values (Fig. S23, ESI†). (b) Leave-one-out interpolation of the resulting RF model using three input molecular descriptors (including calibrated energy levels) and a 64-bit Morgan fingerprint vector. | ||
Nevertheless, the dissimilarity between xTB- and DFT-optimized molecular geometries might have a direct impact on the value of the (three-dimensional) molecular descriptors, and hence on the final accuracy of the interpolated ML model if some of those are included. Accordingly, we have first quantitatively compared both sets of molecular (non-electronic) descriptors by computing r in all of them and found that the median of their distributions is very close to unity in all cases (Fig. S22, ESI†). Based on this finding, we proceed by training the RF model with TDDFT-derived descriptors and exploring how well the model interpolates when fed with xTB-derived descriptors. Fig. S23a (ESI†) shows a leave-one-out interpolation of a RF model trained using TDDFT data and interpolated on GFN2-xTB-optimized molecules, descriptors and energy levels.84,91,92 In this kind of model validation, all TDDFT data is used in the training step excepting that for a single molecule, for which we retrieve its corresponding xTB-optimized geometry and descriptors as the sole interpolation (testing) dataset; this procedure is subsequently repeated for all molecules. Thus, the model performance is assessed by comparing the actual TDDFT-derived εd,max of the molecules (x-axis in Fig. 5b) with that predicted by a RF model trained with TDDFT data and interpolated using xTB-derived descriptors (y-axis in Fig. 5b). This is useful to evaluate whether such RF model fed with TDDFT data could be exploited to predict εd,max in unseen molecules that are geometrically optimized through xTB Hamiltonians.
Our first model takes as inputs the three molecular descriptors found previously to be the most important features in the RF model together with their corresponding (64-bit) Morgan fingerprints. The scoring of the LOOCV in this preliminary model (R2 = 0.53, r = 0.74) is limited due to the existence of a mismatch between the absolute energy levels retrieved by either DFT (B3LYP) or GFN2-xTB methods (Fig. S23b, ESI†). Thus, the RF model trained on TDDFT data needs proper calibration of the energy levels obtained through GFN2-xTB, which we perform using either a linear regression, a support vector regressor (SVR) or an additional RF model (Fig. S23c, ESI†). By applying such calibration on the HOMO−2 energy levels, we obtain the champion RF model (R2 = 0.61, r = 0.78) shown in Fig. 5b using three molecular descriptors and a 64-bit Morgan fingerprint vector. Hence, Fig. 5b shows that molecular databases of xTB-optimized geometries could be exploited in combination with TDDFT-trained ML models to predict the absorption strength (εd,max) at significantly lower computational cost and with reasonable accuracy. The statistical analysis and ML modelling framework introduced here is thus expected to show large potential in the high-throughput screening of highly absorbing molecular candidates in combination with generative models (autoencoders and neural networks) as part of future work in the group.
3. Conclusion
We have demonstrated that TDDFT calculations agree reasonably well with the experimental maximum molar extinction coefficient (εd,max) in solution state by exploiting a database of TDDFT-optimized small molecular acceptors (NFAs) and donor oligomers collected over the years. This finding supports further analysis of the molecular dataset to identify structure–absorption relationships by means of statistical and machine-learning (ML) methods. Through the exploration of molecular descriptors, we identify two features that are strongly correlated with εd,max, namely the linearity and planarity of the molecule in the direction of maximum atomic polarizability variance; and the number of sp2-hybridized carbon atoms bonded to two other carbons included in the molecule. These further suggest design rules that highly absorbing organic π-conjugated molecules (such as NFAs) should follow, namely a fully conjugated, planar and linear molecular backbone with more polarisable heteroatoms. We further identify that moieties such as thieno[3,2-b]thiophene (TT), thiophene (T), 2-(5,6-difluoro-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (2FIC), 2-(3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (IC) and indaceno[1,2-b:5,6-b′]dithiophene (IDT) appear more frequently in molecules with the highest absorption strength. Finally, we demonstrate the feasibility of random decision forests (RFs) trained with a few (3) molecular descriptors and 64-bit Morgan fingerprint vectors to predict in molecular geometries optimized by a computationally less demanding method such as extended tight-binding (xTB). This approach shows the ability to bypass thorough TDDFT calculations, thus facilitating high-throughput screening of absorption strength in organic π-conjugated molecules in combination with generative molecular models.4. Outlook
This work was motivated by the search for molecular design rules to enable higher PCE in organic solar cells. Although maximizing light absorption for a given optical band gap is a key requirement to enable record PCE, many additional physical processes contribute to photovoltaic performance but are not considered directly in the present work, namely, exciton diffusion, charge transfer, charge separation, charge transport and charge recombination. To date, there is no holistic modelling framework nor are there sufficient data to relate these multiple processes to device performance via chemical structure. However, developments in AI and ML methods are likely to advance the status of models for multiple property–device performance relationships in the coming years.Nevertheless, understanding how light harvesting alone can be maximized by smart molecular design is significant for improving several different aspects of OPV performance. Light absorption is the primary step towards charge generation and is therefore strongly related to the macroscopic short-circuit current density of the device. According to the reciprocity relation between absorption and emission,20 high absorption should in principle lead to strong emission, therefore reducing the nonradiative energy losses, and benefitting the open-circuit voltage. In addition, high absorption allows the fabrication of thin devices, therefore facilitating charge extraction and enhancing fill factor.93 Moreover, based on the causality principle, high absorption strength would lead to higher refractive index, which takes the first interference maximum of electric field to lower thicknesses, resulting in large light harvesting potential in thinner devices. Therefore, designing highly absorbing organic π-conjugated molecules has the potential to enhance different aspects relating to the performance of OPVs in conjunction with the proposed predictive ML model.
A separate aspect for future work is the impact of solid-state molecular interactions on light absorption. This paper concerns the optical absorption of isolated molecules while applications normally require thin films of molecules. Although intermolecular interactions can strongly impact the strength as well as the spectrum of thin film absorption,94 this has been neglected in the present study due to the lack of a suitable database of computations and the lack of solid state packing information. In the future, ML approaches could be used to better understand and predict how solid state interactions affect optical absorption, and thereby improve molecular design rules. Such advances may be enabled by the growing capability in computational structure prediction as well as improved understanding of the impact of intermolecular interactions on excited state properties.
5. Experimental and theoretical methods
Excited state calculation database and experimental εd,max database: TDDFT results in this study are based on the functional B3LYP and were performed by present and past group members in Prof. Jenny Nelson's group at Imperial College London, making up more than 3500 entries (corresponding to 479 unique molecules). The majority of experimental solid state thin film εd,max values for NFAs shown in Fig. 1a–c were measured using variable-angle spectroscopic ellipsometry (VASE) for the present study. Neat films were deposited from solution by either spin- or blade-coating on glass substrates at distinct thicknesses (typically ranging from 30 to 150 nm). Ellipsometry data were acquired at three to five angles of incidence (55°–75°) using a Sopralab GES-5E rotating polarizer spectroscopic ellipsometer (SEMILAB) coupled to a charge-coupled device (CCD) detector. Experimental solution εd,max were mostly collected from literature with a majority of data taken from ref. 95, and Y5, Y6, and Y7 measured using UV-visible spectroscopy. The complete database and sources are presented in the ESI.†Theoretical description of molar extinction coefficient (εd): to calculate the molar extinction coefficient εd, let us start with defining the absorption coefficient α in a quantum picture (we stay with SI units for the moment). The absorption coefficient for transition from state 1 to state 2 can be defined as19,96
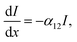 | (5) |
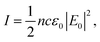 | (6) |
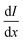 is equal to the rate of loss of energy density from the field
is equal to the rate of loss of energy density from the field 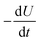 , and the latter is the product of transition rate Γ12 and transition energy ħω12, and we have
, and the latter is the product of transition rate Γ12 and transition energy ħω12, and we have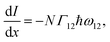 | (7) |
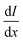 and I in the definition of α12 we get
and I in the definition of α12 we get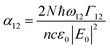 | (8) |
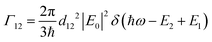 | (9) |
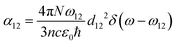 | (10) |
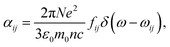 | (11) |
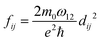 . Integrating over all transitions, we have
. Integrating over all transitions, we have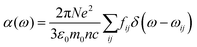 | (12) |
| I(d) = I0e−αd = I010−OD | (13) |
| OD = ρεdd, | (14) |
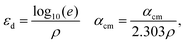 | (15) |
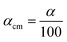 . ρ is moles of molecules per dm3. We now have
. ρ is moles of molecules per dm3. We now have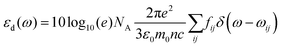 | (16) |
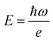 , rather than angular frequency, so it is easier to consider the magnitude, and finally we have εd in the unit of M−1 cm−1.
, rather than angular frequency, so it is easier to consider the magnitude, and finally we have εd in the unit of M−1 cm−1.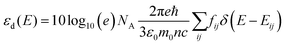 | (17) |
Converting complex refractive index from solid state ellipsometry measurements to εd: using ellipsometry measurements from film (solid state), we can extract the complex refractive index, η
| η = n + iκ | (18) |
 | (19) |
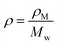 , we have
, we have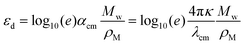 | (20) |
Author contributions
J. Y. and X. R.-M. contributed equally to this work and drafted the paper. J. Y. performed DFT and TDDFT calculations, absorption strength analysis, and data collection. X. R.-M. performed the statistical analysis and machine-learning study. D. P., H. D., D. B., M. A., A. V., S. F., A. A. S., and X. H. shared their DFT/TDDFT calculation results. F. E. prepared thin films of NFAs for VASE measurements. X. R.-M., V. B., and B. D. did VASE measurements. E. R. did UV-vis measurements of Y5, Y6, and Y7 in solution. G. Z. and H.-L. Y. provided Y5, Y6, and Y7. All authors gave critical review on this work. J. N. and M. C.-Q. supervised this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. N., J. Y., D. P., M. A., F. E., and E. R. thank the European Research Council for support under the European Union's Horizon 2020 research and innovation program (Grant Agreement No. 742708 and 648901). The authors at ICMAB acknowledge financial support from the Spanish Ministry of Science and Innovation through the Severo Ochoa” Program for Centers of Excellence in R&D (No. CEX2019-000917-S), and project PGC2018-095411-B-I00. E. R. is grateful to the Fonds de Recherche du Quebec-Nature et technologies (FRQNT) for a postdoctoral fellowship and acknowledges financial support from the European Cooperation in Science and Technology. M. A. thanks the Engineering and Physical Sciences Research Council (EPSRC) for support via doctoral studentships. F. E. thanks the Engineering and Physical Sciences Research Council (EPSRC) for support via the Post-Doctoral Prize Fellowship. X. R.-M. acknowledges Prof. Olle Inganäs and the Knut and Allice Wallenberg Foundation for funding of his current postdoctoral position. H.-L. Yip thanks the support from Guangdong Major Project of Basic and Applied Basic Research (2019B030302007). The TOC figure and Fig. 5a in the manuscript include freely available resources from http://Flaticon.com. J. Y. thank Xiaodan Ge for her support.References
- J. Nelson, Mater. Today, 2011, 14, 462–470 CrossRef CAS.
- G. Li, R. Zhu and Y. Yang, Nat. Photonics, 2012, 6, 153–161 CrossRef CAS.
- A. J. Heeger, Adv. Mater., 2014, 26, 10–28 CrossRef CAS PubMed.
- M. Mainville and M. Leclerc, ACS Energy Lett., 2020, 5, 1186–1197 CrossRef CAS.
- H. K.-H. Lee, J. Wu, J. Barbé, S. M. Jain, S. Wood, E. M. Speller, Z. Li, F. A. Castro, J. R. Durrant and W. C. Tsoi, J. Mater. Chem. A, 2018, 6, 5618–5626 RSC.
- Y. Cui, Y. Wang, J. Bergqvist, H. Yao, Y. Xu, B. Gao, C. Yang, S. Zhang, O. Inganäs, F. Gao and J. Hou, Nat. Energy, 2019, 4, 768–775 CrossRef CAS.
- Y. Li, J. D. Lin, X. Che, Y. Qu, F. Liu, L. S. Liao and S. R. Forrest, J. Am. Chem. Soc., 2017, 139, 17114–17119 CrossRef CAS PubMed.
- S. Difley and T. Van Voorhis, J. Chem. Theory Comput., 2011, 7, 594–601 CrossRef CAS.
- C. J.-M. Emmott, J. A. Röhr, M. Campoy-Quiles, T. Kirchartz, A. Urbina, N. J. Ekins-Daukes and J. Nelson, Energy Environ. Sci., 2015, 8, 1317–1328 RSC.
- C. J.-M. Emmott, D. Moia, P. Sandwell, N. Ekins-Daukes, M. Hösel, L. Lukoschek, C. Amarasinghe, F. C. Krebs and J. Nelson, Sol. Energy Mater. Sol. Cells, 2016, 149, 284–293 CrossRef CAS.
- L. Zhu, M. Zhang, J. Xu, C. Li, J. Yan, G. Zhou, W. Zhong, T. Hao, J. Song, X. Xue, Z. Zhou, R. Zeng, H. Zhu, C.-C. Chen, R. C.-I. MacKenzie, Y. Zou, J. Nelson, Y. Zhang, Y. Sun and F. Liu, Nat. Mater., 2022, 1–8, DOI:10.1038/s41563-022-01244-y.
- J. Zhao, Y. Li, G. Yang, K. Jiang, H. Lin, H. Ade, W. Ma and H. Yan, Nat. Energy, 2016, 1, 15027 CrossRef CAS.
- P. Cheng, G. Li, X. Zhan and Y. Yang, Nat. Photonics, 2018, 12, 131–142 CrossRef CAS.
- Y. Wang, J. Lee, X. Hou, C. Labanti, J. Yan, E. Mazzolini, A. Parhar, J. Nelson, J. Kim and Z. Li, Adv. Energy Mater., 2021, 11, 2003002 CrossRef CAS.
- J. Hou, O. Inganäs, R. H. Friend and F. Gao, Nat. Mater., 2018, 17, 119–128 CrossRef CAS PubMed.
- J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H.-L. Yip, T.-K. Lau, X. Lu, C. Zhu, H. Peng, P. A. Johnson, M. Leclerc, Y. Cao, J. Ulanski, Y. Li and Y. Zou, Joule, 2019, 3, 1140–1151 CrossRef CAS.
- M. Kaltenbrunner, M. S. White, E. D. Głowacki, T. Sekitani, T. Someya, N. S. Sariciftci and S. Bauer, Nat. Commun., 2012, 3, 1–7 Search PubMed.
- W. Yang, W. Wang, Y. Wang, R. Sun, J. Guo, H. Li, M. Shi, J. Guo, Y. Wu, T. Wang, G. Lu, C. J. Brabec, Y. Li and J. Min, Joule, 2021, 5, 1209–1230 CrossRef.
- J. Nelson, The Physics of Solar Cells, Imperial College Press, 2003 Search PubMed.
- U. Rau, Phys. Rev. B, 2007, 76, 085303 CrossRef.
- M. Azzouzi, J. Yan, T. Kirchartz, K. Liu, J. Wang, H. Wu and J. Nelson, Phys. Rev. X, 2018, 8, 031055 CAS.
- F. D. Eisner, M. Azzouzi, Z. Fei, X. Hou, T. D. Anthopoulos, T. J.-S. J.-S. Dennis, M. Heeney and J. Nelson, J. Am. Chem. Soc., 2019, 141, 6362–6374 CrossRef CAS PubMed.
- J. Yan, E. Rezasoltani, M. Azzouzi, F. Eisner and J. Nelson, Nat. Commun., 2021, 12, 3642 CrossRef CAS.
- A. Classen, C. L. Chochos, L. Lüer, V. G. Gregoriou, J. Wortmann, A. Osvet, K. Forberich, I. McCulloch, T. Heumüller and C. J. Brabec, Nat. Energy, 2020, 5, 711–719 CrossRef CAS.
- X.-K. Chen, D. Qian, Y. Wang, T. Kirchartz, W. Tress, H. Yao, J. Yuan, M. Hülsbeck, M. Zhang, Y. Zou, Y. Sun, Y. Li, J. Hou, O. Inganäs, V. Coropceanu, J.-L. Bredas and F. Gao, Nat. Energy, 2021, 6, 799–806 CrossRef CAS.
- J. Benduhn, K. Tvingstedt, F. Piersimoni, S. Ullbrich, Y. Fan, M. Tropiano, K. A.-A. McGarry, O. Zeika, M. K.-K. Riede, C. J.-J. Douglas, S. Barlow, S. R.-R. Marder, D. Neher, D. Spoltore and K. Vandewal, Nat. Energy, 2017, 2, 17053 CrossRef CAS.
- X.-K. Chen, V. Coropceanu, J.-L. Bredas and J.-L. Bredas, Nat. Commun., 2018, 9, 5295 CrossRef CAS PubMed.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. S. Chen, S. Li, J. Liu, S. S. Chen, J. Zhang, X.-K. K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J.-L. L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed.
- M. S. Vezie, S. Few, I. Meager, G. Pieridou, B. Dörling, R. S. Ashraf, A. R. Goñi, H. Bronstein, I. McCulloch, S. C. Hayes, M. Campoy-Quiles and J. Nelson, Nat. Mater., 2016, 15, 746–753 CrossRef CAS.
- B. Kang, C. Seok and J. Lee, J. Chem. Inf. Model., 2020, 60, 5984–5994 CrossRef CAS PubMed.
- S. Few, J. M. Frost, J. Kirkpatrick and J. Nelson, J. Phys. Chem. C, 2014, 118, 8253–8261 CrossRef CAS.
- Y. Yi, V. Coropceanu and J.-L. Brédas, J. Mater. Chem., 2011, 21, 1479 RSC.
- T. Liu and A. Troisi, J. Phys. Chem. C, 2011, 115, 2406–2415 CrossRef CAS.
- J. C. Slater, Phys. Rev., 1951, 81, 385 CrossRef CAS.
- B. L. Hammond, W. A. Lester and P. J. Reynolds, Monte Carlo Methods in Ab Initio Quantum Chemistry, World Scientific, 1994, vol. 1 Search PubMed.
- R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6648–6653 CrossRef CAS PubMed.
- Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O’Neill, R. A. DiStasio Jr, R. C. Lochan, T. Wang, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Yeh Lin, T. Van Voorhis, S. Hung Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. Min Rhee, J. Ritchie, E. Rosta, C. David Sherrill, A. C. Simmonett, J. E. Subotnik, H. Lee Woodcock III, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer III, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 3172–3191 RSC.
- P. Raccuglia, K. C. Elbert, P. D.-F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73–76 CrossRef CAS PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS.
- J. Westermayr and P. Marquetand, Chem. Rev., 2021, 121, 9873–9926 CrossRef CAS PubMed.
- F. Häse, L. M. Roch, P. Friederich and A. Aspuru-Guzik, Nat. Commun., 2020, 11, 1–11 CrossRef PubMed.
- S. A. Lopez, B. Sanchez-Lengeling, J. de Goes Soares and A. Aspuru-Guzik, Joule, 2017, 1, 857–870 CrossRef CAS.
- H. Sahu, W. Rao, A. Troisi and H. Ma, Adv. Energy Mater., 2018, 8, 1–9 Search PubMed.
- W. K. Tatum, D. Torrejon, A. B. Resing, J. W. Onorato and C. K. Luscombe, Comput. Mater. Sci., 2021, 197, 110599 CrossRef.
- N. Majeed, M. Saladina, M. Krompiec, S. Greedy, C. Deibel and R. C.-I. MacKenzie, Adv. Funct. Mater., 2019, 1907259 Search PubMed.
- X. Rodríguez-Martínez, E. Pascual-San-José, Z. Fei, M. Heeney, R. Guimerà and M. Campoy-Quiles, Energy Environ. Sci., 2021, 14, 986–994 RSC.
- X. Rodríguez-Martínez, E. Pascual-San-José and M. Campoy-Quiles, Energy Environ. Sci., 2021, 14, 3301–3322 RSC.
- K. Kranthiraja and A. Saeki, Adv. Funct. Mater., 2021, 31, 1–11 Search PubMed.
- E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, Annu. Rev. Mater. Res., 2015, 45, 195–216 CrossRef CAS.
- J. Hachmann, R. Olivares-amaya, S. Atahan-evrenk, C. Amador-bedolla, R. S. Sanchez-carrera, A. Gold-parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2011, 2, 2241–2251 CrossRef CAS.
- A. Mahmood and J.-L. Wang, Energy Environ. Sci., 2021, 14, 90–105 RSC.
- P. Malhotra, S. Biswas, F.-C. Chen and G. D. Sharma, Sol. Energy, 2021, 228, 175–186 CrossRef CAS.
- A. Kuzmich, D. Padula, H. Ma and A. Troisi, Energy Environ. Sci., 2017, 10, 395–401 RSC.
- I. Y. Kanal, S. G. Owens, J. S. Bechtel and G. R. Hutchison, J. Phys. Chem. Lett., 2013, 4, 1613–1623 CrossRef CAS PubMed.
- L. Wilbraham, E. Berardo, L. Turcani, K. E. Jelfs and M. A. Zwijnenburg, J. Chem. Inf. Model., 2018, 58, 2450–2459 CrossRef CAS PubMed.
- E. O. Pyzer-Knapp, K. Li and A. Aspuru-Guzik, Adv. Funct. Mater., 2015, 25, 6495–6502 CrossRef CAS.
- J. Hachmann, R. Olivares-Amaya, A. Jinich, A. L. Appleton, M. A. Blood-Forsythe, L. R. Seress, C. Román-Salgado, K. Trepte, S. Atahan-Evrenk, S. Er, S. Shrestha, R. Mondal, A. Sokolov, Z. Bao and A. Aspuru-Guzik, Energy Environ. Sci., 2014, 7, 698–704 RSC.
- N. Bérubé, V. Gosselin, J. Gaudreau and M. Côté, J. Phys. Chem. C, 2013, 117, 7964–7972 CrossRef.
- S. Nagasawa, E. Al-Naamani and A. Saeki, J. Phys. Chem. Lett., 2018, 9, 2639–2646 CrossRef CAS PubMed.
- Y. Huang, J. Zhang, E. S. Jiang, Y. Oya, A. Saeki, G. Kikugawa, T. Okabe, T. Okabe, F. S. Ohuchi and F. S. Ohuchi, J. Phys. Chem. C, 2020, 124, 12871–12882 CrossRef CAS.
- W. Sun, M. Li, Y. Li, Z. Wu, Y. Sun, S. Lu, Z. Xiao, B. Zhao and K. Sun, Adv. Theory Simul., 2019, 2, 1–9 Search PubMed.
- R. Olivares-Amaya, C. Amador-Bedolla, J. Hachmann, S. Atahan-Evrenk, R. S. Sánchez-Carrera, L. Vogt and A. Aspuru-Guzik, Energy Environ. Sci., 2011, 4, 4849–4861 RSC.
- H. Sahu, F. Yang, X. Ye, J. Ma, W. Fang and H. Ma, J. Mater. Chem. A, 2019, 7, 17480–17488 RSC.
- D. Padula, J. D.-D. Simpson and A. Troisi, Mater. Horiz., 2019, 6, 343–349 RSC.
- L. Simine, T. C. Allen and P. J. Rossky, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 13945–13948 CrossRef CAS PubMed.
- J. F. Joung, M. Han, J. Hwang, M. Jeong, D. H. Choi and S. Park, JACS Au, 2021, 1, 427–438 CrossRef CAS PubMed.
- S. Ye, W. Hu, X. Li, J. Zhang, K. Zhong, G. Zhang, Y. Luo, S. Mukamel and J. Jiang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 201821044 Search PubMed.
- C. Nantasenamat, C. Isarankura-Na-Ayudhya, N. Tansila, T. Naenna and V. Prachayasittikul, J. Comput. Chem., 2007, 28, 1275–1289 CrossRef CAS PubMed.
- E. J. Beard, G. Sivaraman, Á. Vázquez-Mayagoitia, V. Vishwanath and J. M. Cole, Sci. Data, 2019, 6, 307 CrossRef PubMed.
- S. Varghese and S. Das, J. Phys. Chem. Lett., 2011, 2, 863–873 CrossRef CAS PubMed.
- C. L. Donley, J. Zaumseil, J. W. Andreasen, M. M. Nielsen, H. Sirringhaus, R. H. Friend and J. S. Kim, J. Am. Chem. Soc., 2005, 127, 12890–12899 CrossRef CAS PubMed.
- P. J. Brown, D. S. Thomas, A. Köhler, J. S. Wilson, J.-S. S. Kim, C. M. Ramsdale, H. Sirringhaus and R. H. Friend, Phys. Rev. B, 2003, 67, 064203 CrossRef.
- C. W. Yap, J. Comput. Chem., 2011, 32, 1466–1474 CrossRef CAS PubMed.
- D.-S. Cao, Q.-S. Xu, Q.-N. Hu and Y.-Z. Liang, Bioinformatics, 2013, 29, 1092–1094 CrossRef CAS PubMed.
- H. Moriwaki, Y.-S. Tian, N. Kawashita and T. Takagi, J. Cheminform., 2018, 10, 4 CrossRef PubMed.
- RDKit: Open-Source Cheminformatics Software.
- Z. Luo, R. Ma, Y. Xiao, T. Liu, H. Sun, M. Su, Q. Guo, G. Li, W. Gao, Y. Chen, Y. Zou, X. Guo, M. Zhang, X. Lu, H. Yan and C. Yang, Small, 2020, 16, 2001942 CrossRef CAS PubMed.
- M. Y. Mehboob, M. Adnan, R. Hussain and Z. Irshad, Synth. Met., 2021, 277, 116800 CrossRef CAS.
- R. Todeschini, M. Lasagni and E. Marengo, J. Chemom., 1994, 8, 263–272 CrossRef CAS.
- R. Todeschini and P. Gramatica, 3D QSAR in Drug Design, Kluwer Academic Publishers, Dordrecht, 1998, pp. 355–380 Search PubMed.
- R. Todeschini and P. Gramatica, Quant. Struct. Relationships, 1997, 16, 113–119 CrossRef CAS.
- R. Todeschini and V. Consonni, Molecular Descriptors for Chemoinformatics, Wiley, 2nd edn, 2009, vol. 41 Search PubMed.
- R. Todeschini and V. Consonni, Handbook of Molecular Descriptors, Wiley, 2000 Search PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- N. Artrith, K. T. Butler, F.-X. Coudert, S. Han, O. Isayev, A. Jain and A. Walsh, Nat. Chem., 2021, 13, 505–508 CrossRef CAS PubMed.
- M. Lee, Adv. Energy Mater., 2019, 1900891 CrossRef.
- F. Pedregosa, R. Weiss, M. Brucher, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- L. H. Hall and L. B. Kier, J. Chem. Inf. Comput. Sci., 1995, 35, 1039–1045 CrossRef CAS.
- D. C. Elton, Z. Boukouvalas, M. S. Butrico, M. D. Fuge and P. W. Chung, Sci. Rep., 2018, 8, 9059 CrossRef PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- F. Deledalle, T. Kirchartz, M. S. Vezie, M. Campoy-Quiles, P. S. Tuladhar, J. Nelson and J. R. Durrant, Phys. Rev. X, 2015, 5, 1–13 CAS.
- F. C. Spano, Acc. Chem. Res., 2010, 43, 429–439 CrossRef CAS PubMed.
- G. Forti, A. Nitti, P. Osw, G. Bianchi, R. Po and D. Pasini, Int. J. Mol. Sci., 2020, 21, 8085 CrossRef CAS PubMed.
- L. A.-A. Pettersson, L. S. Roman and O. Inganäs, J. Appl. Phys., 1999, 86, 487–496 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ee00887d |
| ‡ J. Y. and X. R.-M. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |