Open Access Article
Open Access ArticleFemtosecond stimulated Raman spectroscopy – guided library mining leads to efficient singlet fission in rubrene derivatives†
Kajari
Bera
 ,
Christopher J.
Douglas
,
Christopher J.
Douglas
 and
Renee R.
Frontiera
and
Renee R.
Frontiera
 *
*
Department of Chemistry, University of Minnesota, Minneapolis, MN 55455, USA. E-mail: rrf@umn.edu; Tel: +1612-624-2501
First published on 4th October 2021
Abstract
Chromophores undergoing singlet fission are promising candidates for harnessing solar energy as they can generate a pair of charge carriers by the absorption of one photon. However, photovoltaic devices employing singlet fission are still lacking practical applications due to the limitations within the existing molecules undergoing singlet fission. Chemical modifications to acenes can lead to efficient singlet fission devices, but the influence of changes to molecular structure on the rate of singlet fission is challenging to model and predict. Using femtosecond stimulated Raman spectroscopy we have previously demonstrated that the triplet separation process during singlet fission in crystalline rubrene is associated with the loss of electron density from its tetracene core. Based on this knowledge, we mined a library of new rubrene derivatives with electron withdrawing substituents that prime the molecules for efficient singlet fission, without impacting their crystal packing. Our rationally chosen crystalline chromophores exhibit significantly improved singlet fission rates. This study demonstrates the utility and strength of a structurally sensitive spectroscopic technique in providing insights to spectroscopy-guided materials selection and design guidelines that go beyond energy arguments to design new singlet fission-capable chromophores.
Introduction
The theoretical efficiency of solar energy conversion to electrical energy for a single p–n junction solar cell is limited to ∼34% as calculated by Shockley and Queisser.1 Although this limit takes into account the energy losses due to fill factor and charge recombination, the largest reason for this limit is due to spectral losses. A strategy to overcome spectral losses is to manufacture semiconductors based on organic molecules that can better utilize the solar spectrum by increasing the charge per photon ratio. One such process is singlet fission (SF), where one photon is used to generate two triplet excitons, leading to external quantum efficiency exceeding 100%.2,3 Ultrafast spectroscopic measurements have demonstrated that SF is a multistep process comprising an excited singlet exciton S1 converting into a distinct intermediate of a neighboring pair of triplets coupled with an overall singlet character, called a correlated triplet pair 1(T1T1),4–9 undergoing subsequent loss of the electronic coherence to form 1(T1⋯T1) and finally spin relaxation leading to two individual isolated triplets T1.6,9–15 Thus, SF generates two charge carriers at the expense of a single photon through a spin-allowed ultrafast process. Customized organic chromophores undergoing SF have the ability to push the boundary of photovoltaic power conversion efficiency from 34% to 45% and thus has inspired new methods to fabricate photovoltaic devices.16,17 However, solar cells based on SF have yet to deliver on this promise, with observed power conversion efficiency maximum of only 5.1% due to energy loss mechanisms.18 Therefore, we need strategic material design models for advancing compounds capable of undergoing SF to achieve efficiency much closer to the theoretically modeled limit.The major obstacle in the development of SF devices is the scarcity of materials capable of undergoing SF with near unit efficiency while also possessing other desirable qualities such as solution processability, photochemical stability and large extinction coefficients.19,20 This lack of materials is partly due to the limited knowledge about the molecular design principles to develop tunable SF-capable systems, resulting in slow and unproductive trial-and-error approaches. Computational-guided design is challenging due to difficulty in modeling the complex multiexcitonic states with several different crossing potential energy surfaces and spins. The small number of available chromophores is compounded by the difficulty in designing congeners or derivatives with similar molecular and electronic structures that also have similar solid-state packing structures. The only way to reach a consensus is by examining a wider set of materials. Thus, the primary interest in this field has been to understand the photophysical mechanism of SF with the aim of rationally designing materials to increase the commercial viability of SF. Examples of rationally selecting materials, particularly congeners of molecules known for SF properties, are exceptionally rare.
In order to design materials undergoing efficient and rapid SF, crystal packing needs to be optimized. Many experimental and theoretical studies have focused on the connection between electronic and vibronic couplings with SF dynamics to design systems for highly efficient SF process.5,10,15,21–27 However, the relationship between SF efficiency and molecular structure is challenging to explore, and correlations between the molecular structural changes and its effects on the SF rates and yields remain unclear. Thus, there is a need to construct a comprehensive set of measurement-guided design protocols based on the structural dynamic studies on known SF molecules to develop principles for the synthesis or selection of new and more efficient SF systems.
To address the above-mentioned challenges about rational designing of materials guided by spectroscopic measurements, we couple prior vibrational spectroscopic knowledge and synthetic protocols, and packing knowledge to identify and screen potential candidates for SF. Although transient absorption spectroscopy is the most popular technique to quantify and demonstrate SF, obtaining direct structural information using this technique can be challenging. Vibrational spectroscopies are compelling probes because they can directly probe nuclear motions, thereby monitoring the structural changes in molecules undergoing singlet fission.28 We have thus previously investigated the structural evolution in crystalline rubrene, the tetraphenyl tetracene derivative shown in Fig. 1a, during SF with femtosecond stimulated Raman spectroscopy (FSRS). Rubrene is one of the most studied organic semiconductors because of its unique optoelectronic properties, such as high charge carrier mobility and long exciton diffusion lengths,29–32 and the fact that it undergoes efficient SF in its crystalline orthorhombic form.33–40 Early studies established that SF is the most prominent decay path of the excited singlet excitons in crystalline rubrene,30,36,39 where the correlated triplet pair is formed within 20 fs and has a lifetime of 2 ps before separating into two individual triplets.40
A large number of rubrene congeners have been crystallized, and even more have been synthesized. Limiting a Chemical Abstract Search (SciFinder) to substituted 5,6,11,12-tetraphenyltetracenes (rubrene) revealed over 350 structures with the 5,6,11,12-tetraaryltetracene core.41 Limiting the candidates to those proven by X-ray crystallography to adopt conformations and solid-state packing similar to orthorhombic rubrene reduces the number of candidates by an order of magnitude, but still provides a daunting number of candidates. One of us has developed syntheses that allow for late-stage diversification of the rubrene structure;42 new compounds of this class can be readily prepared by a variety of methods.43–47 Without predictive structural and mechanistic models however, selecting candidates to study SF from this library of rubrenes amounts to ‘guess-and-check’ work. The prospect of proposing the synthesis of new rubrenes for SF is similarly a guesswork. Ideally, a model for the structural and electronic changes involved in rubrene's SF process guide our mining of candidates from the known rubrene library and aid in the design of new targets for synthesis.
We previously conducted a study highlighting the changes in the molecular structure of rubrene during the SF process.48 FSRS is an ultrafast vibrational spectroscopic technique that is used to investigate the structural dynamics in a chemical reaction by monitoring the vibrational modes of the system with high temporal and spectral resolution.49–54 Our FSRS measurements indicated that the separation of the correlated triplet pair into two individual triplets is accompanied with the loss of electron density from the tetracene core in crystalline rubrene.48 Building off on our crystalline rubrene FSR spectral analysis and interpretation during SF, here we hypothesize that rubrene derivatives with reduced amount of electron density in the tetracene core will facilitate the triplet separation process faster, which will be experimentally manifested as smaller extent of structural reorganization in the FSR data of the derivatives.
Assessing this hypothesis requires a system in which the electron density over the tetracene backbone in parent rubrene can be controlled, for example by introducing substituents in the peripheral phenyl groups in rubrene moiety. Fortunately, Douglas and co-workers have previously engineered and characterized a series of rubrene derivatives with the electron withdrawing CF3 substituent.42,55 In this work we study two potential candidates for SF from the database of synthesized rubrene derivatives by Douglas and co-workers: di-CF3 di-CH3 rubrene (FM-rubrene) and di-CF3 rubrene (F-rubrene), where the functional groups are on the para position of the phenyl rings as shown in Fig. 1.42 The presence of electron withdrawing groups in the phenyl rings reduces the electron density over the tetracene core in the rubrene derivatives, which is in accordance with the criteria to test our proposition.
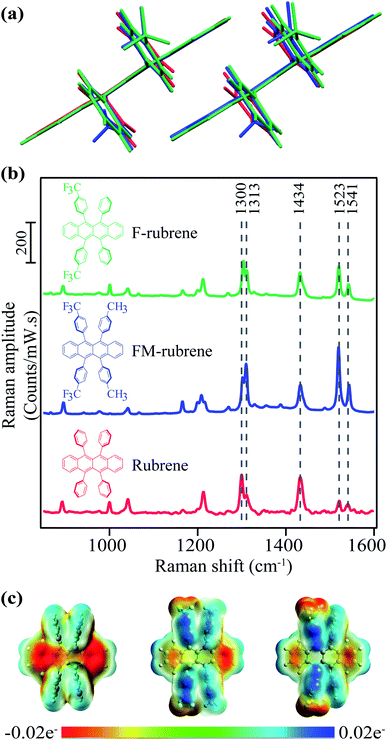
Comparing rubrene with the FM-rubrene and F-rubrene derivatives, the substitution has little impact on the crystal packing distances between tetracene pi-faces or the electronic energy of the crystalline excited states. Our material selection should allow us to look at SF in a series of related molecules, giving insight into intrinsic structure–property relationships. FM-rubrene and F-rubrene have comparable electronic state energies to that of rubrene, indicating that SF should occur in both derivatives.56 Although these rubrene derivatives have not been previously investigated for SF experimentally, thin films of these derivatives have been shown to have longer exciton diffusion length as compared to rubrene, indicating enhanced electronic coupling, a desirable property for optoelectronics and SF.57 The tetracene core in FM-rubrene and F-rubrene is planar and the π-stacking packing motif of rubrene is maintained in crystals of these derivatives, demonstrating that there is little change in packing between the rubrene analogues. Computational studies on FM-rubrene and F-rubrene showed an increased wave function overlap due to the noncovalent interactions provided by substituents, which leads to large favorable electronic couplings of the excited states for SF.56 Thus, we selectively chose FM-rubrene and F-rubrene based on the energetics of their orbitals and their similarity in the crystal packing with rubrene, which indicates that SF should occur in both FM-rubrene and F-rubrene. We used crystals of rubrene, FM-rubrene and F-rubrene rather than thin films due to the controlled morphology available with crystal growth which is important to study SF, as well as relevance to the substantial body of literature on organic semiconducting behavior in high quality single crystals. In this investigation, we aim to establish the practical applicability of spectroscopy-guided screening to identify and provide synthetic designing principles for chromophores with efficient SF properties that go beyond the simple energy arguments.
Experimental method and setup
Sample preparation and characterization
We grew crystalline rubrene via a physical vapor deposition (PVT) method using our home-built setup.48 FM-rubrene and F-rubrene powder was prepared as previously described,42 and we grew their single crystals via slow solvent evaporation method (CH2Cl2/isopropanol, see ESI† for additional details). We obtained 2–3 mm long and wide, plate-shaped, red-colored FM-rubrene and F-rubrene crystals and mounted them separately onto 1 mm thick glass coverslips. We present detailed crystal growth methods in the ESI.† We measured the absorption spectra of the crystals using a commercial instrument and plot the profiles in ESI Fig. S1.† We obtained the spontaneous Raman spectra of the crystals using 785 nm excitation on a home-built setup.Femtosecond stimulated Raman spectroscopy
We measured time-resolved FSRS experiments on our home-built optical setup, described elsewhere.48,58–61 In short, we used the fundamental output of 4.6 W at 800 nm from a 1 kHz repetition rate Ti:sapphire regenerative amplifier (Coherent model Libra-F-1K-HE-110) to generate the Raman pump, Raman probe and actinic pulses for the FSRS experiments. We focused 2.5 mW of the 800 nm fundamental output through a 2 mm sapphire crystal to generate a white light continuum and then compressed it with a fused silica prism pair to generate the femtosecond broadband Raman probe. We used two different setups to generate Raman pump pulses for the experiments presented in this article. We used a custom grating filter to generate the Raman pump pulse for rubrene FSRS data and a custom etalon (TecOptics) to produce Raman pump pulse centered at 807 nm for FM-rubrene and F-rubrene FSRS experiments. We generated the actinic pulse using a home-built non-collinear optical parametric amplification (NOPA) system to produce pulses with a central wavelength of 536 nm and full-width half maximum of 14 nm to collect time-resolved data in crystalline rubrene and a 533 nm actinic pulse with 10 nm full-width half maximum for crystalline FM-rubrene and F-rubrene FSR experiments, shown in Fig. S2.† We performed the time-resolved experiments on different days with different alignments, which resulted in slightly different actinic pulse central wavelength. We used a newly installed pulse shaper (Fastlite Dazzler™) and an SF10 prism pair compressor for compression and dispersion compensation in the actinic pulse for the FM-rubrene and F-rubrene FSR measurements.We sent all the three pulses to the sample through an inverted Olympus IX 73 microscope and collected the stimulated Raman signal with a Princeton Instruments PIXIS 100F CCD array detector. The laser beams are normal to the ab plane in rubrene and FM-rubrene, and ac plane in F-rubrene crystals. We modulated the time delay between the pulses using a motorized stage for the time-resolved FSR data. We measured the cross-correlation of the actinic pump and Raman probe pulses by the optical Kerr effect with a 2 mm cuvette of cyclohexane and found them to be 120 ± 3 fs with the 533 nm actinic pulse for FM-rubrene and F-rubrene studies and 250 ± 2 fs with 536 nm actinic pulse for rubrene FSR data. The better cross-correlation during the FM-rubrene and F-rubrene FSR measurements is attributed to better compression of the actinic pulse by the newly mounted pulse shaper (Dazzler). Given the high signal to noise ratio in our FSR data, we can resolve changes in frequency less than 2 cm−1 apart. We present the detailed experimental procedure in the ESI.†
In this study, we use previously published results for crystalline rubrene48 and have broadened the set of chromophores examined here to provide new insights for molecular structure designing guidelines to obtain more efficient SF systems for their use in optoelectronics.
Computational calculations
We optimized the ground state geometries (S0) with flat conformation of rubrene, FM-rubrene and F-rubrene in the gas-phase using density functional theory (DFT) with B3LYP functional and 6-31g(d,p) basis set on Gaussian 16 (version C.01) program package.42,62 We computed the harmonic vibrational frequencies of the optimized geometries to confirm a minimum without any imaginary frequency had been reached. We performed the natural bond orbital (NBO) analysis at B3LYP/6-31g(d,p) level using NBO 3.1 program implemented in the Gaussian 16 package to compare the charge distribution in ground singlet state of rubrene, FM-rubrene and F-rubrene. We optimized the lowest-energy triplet state geometries (T1) of all three molecules by DFT at the (U)B3LYP/6-31g(d,p) level of theory in gas-phase single molecule.Results and discussion
To investigate the effect of reduced electron density in the tetracene backbone of rubrene on SF dynamics while keeping the crystallographic parameters similar, we rationally selected FM-rubrene and F-rubrene for this study. We present the crystallographic parameters of rubrene, FM-rubrene and F-rubrene in Table 1 demonstrating that the three motifs pack quite similarly in crystals.57 We overlaid the dimers of rubrene and its analogues from the crystallographic data in Fig. 1a to show that there exists minimal change in the crystallographic packing between all three of them, so any difference observed in SF dynamics is only due to the changed electron density in the tetracene core. We plot the steady-state absorption spectra of rubrene, FM-rubrene and F-rubrene in Fig. S1,† which depicts clear vibronic signatures in all the crystalline systems.| Lattice | a (Å) | b (Å) | c (Å) | d (Å) | |
|---|---|---|---|---|---|
| Rubrene | Orthorhombic | 26.79 | 14.21 | 7.17 | 5.46 |
| FM-rubrene | Orthorhombic | 34.14 | 14.05 | 7.14 | 5.89 |
| F-rubrene | Orthorhombic | 31.18 | 14.21 | 7.12 | 5.73 |
We collected ground state spontaneous Raman spectra of crystalline rubrene, FM-rubrene and F-rubrene with a 785 nm excitation to probe the effect of chemical substitution on the vibrational modes and present it in Fig. 1b. All three moieties possess the same vibrational modes in the fingerprint region. We have labeled select Raman modes in Fig. 1b between 1300–1541 cm−1, which correspond to C–C stretching and C–H wagging motions in the tetracene core of all the three molecules, based on our DFT frequency calculations.
Since the structural rearrangement observed during SF in crystalline rubrene was previously established to be associated with the loss of electron density in the tetracene core,48 we aimed to quantify the effect of the electron withdrawing groups on the charge distribution in the tetracene core within the rubrene derivatives. We performed natural bond orbital (NBO) analysis on the optimized ground state singlet geometries of rubrene, FM-rubrene and F-rubrene. The natural charges from the NBO population analysis on the tetracene backbone in rubrene, FM-rubrene and F-rubrene are 0 e−, 0.012 e− and 0.016 e− respectively. These values indicate that the tetracene core in rubrene has the most electron density followed by FM-rubrene and then F-rubrene. To visually inspect this charge distribution over the rubrene series, we display the electrostatic potential (ESP) maps in Fig. 1c. The ESP plot shows the density of electrons within a molecule on a surface that encompasses the molecule. Red depicts high electron density and blue depicts low density. Based on the ESP plots, we observe that the negative ESP is localized more on the tetracene backbone in rubrene, followed by FM-rubrene and then F-rubrene. The ESP maps along with NBO analysis demonstrates that the electron density over the tetracene backbone is reduced while going from rubrene to FM-rubrene and to F-rubrene.
Although the rubrene series have similar crystallographic packing and ground state vibrational bands, the key difference between these three molecules is the tetracene core electron density. This indicates the importance of studying excited state dynamics where the transient spectral changes between the three can be significant and those spectral differences can be attributed as the function of the tetracene core electron density. Based on our aforementioned hypothesis and the electron density distribution calculations, we here predict that F-rubrene should undergo the least structural rearrangement and thus the fastest SF rate.
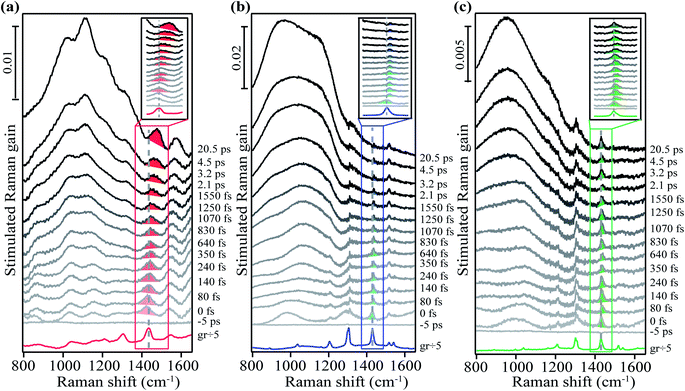
To test our prediction, we used time-resolved FSRS to examine the excited state structural evolution during SF and triplet separation process in crystalline rubrene and rubrene derivatives. We compare these newly measured derivatives to the previously published experimental data of crystalline rubrene.48 A raw FSR spectrum contains contributions from both the ground state and excited state features. Thus, to extract only the excited state information, we subtracted the FSR spectra collected in the ground state without the actinic pulse from the spectra collected at a given time delay after photoexcitation with the actinic pulse. We present this one-to-one subtracted FSR data of crystalline rubrene, FM-rubrene and F-rubrene in Fig. S3.† We observe large bleach features of the ground state modes in the excited state spectra due to the fact that there are fewer molecules in the ground state after photoexcitation. These bleach features in the excited state spectra required the addition of a scaled ground state spectra to be able to extract features exclusive to the excited states. Therefore, we added fraction of the ground state spectrum back to the excited state spectra until ground state bleach was no longer observed (kinetics shown in Fig. S4†) for rubrene, FM-rubrene and F-rubrene FSR data in Fig. 2.
We used a grating filter as the source to generate the Raman pump pulse for the FSR data of rubrene in Fig. 2a and an etalon as the source for the FSR data of FM-rubrene and F-rubrene in Fig. 2b and c, which lead to differences in the linewidths between the measurements. As a control, we collected the FSR data of crystalline FM-rubrene using the grating filter as the source to generate Raman pump pulse (Fig. S5–S7†) and we observe similar excited state dynamics as we observe with the etalon. Therefore, we can confidently compare the three data sets presented in Fig. 2 to understand how the dynamics of SF and triplet separation process differ among the rubrene derivatives. While the excited state dynamics in FM-rubrene are similar using grating filter and etalon-derived Raman pump pulses, we continued using the etalon system to study the excited state dynamics in F-rubrene because the etalon provides better spectral resolution, necessary here to observe small changes in vibrational frequencies. The traces at the bottom of the three data sets in Fig. 2 correspond to the ground state stimulated Raman spectrum of crystalline rubrene, FM-rubrene and F-rubrene, each scaled by a factor of 1/5 for clear pictorial representation. In this study we mainly focus on the broad features below 1200 cm−1 and the shaded region vibrational peaks around 1430 cm−1 in all three crystals.
From Fig. 2, we observe broad long-lived features below 1200 cm−1 region in the FSR data of crystalline rubrene, FM-rubrene and F-rubrene. From our previous FSR study on crystalline rubrene we assigned this broad feature to an electronic signature of the separated triplets during the SF process by comparing the dynamics of this broad feature with the transient absorption data in rubrene (Fig. S8†).48 Interestingly, the FSR data of crystalline FM-rubrene and F-rubrene in Fig. 2b and c also display broad long-lived features below 1200 cm−1. We observe similar broad features in the transient absorption data for crystalline FM-rubrene and F-rubrene in Fig. S8,† which is indicative of excited state absorption. Since rubrene does not undergo SF in solution,36 as a control we measured the transient absorption data of FM-rubrene in solution, presented in Fig. S9.† We do not witness these broad long-lived features in the transient absorption data of FM-rubrene solution as seen in its crystalline counterpart. This implies that the origin of those broad long-lived features in FSR spectra of FM-rubrene and F-rubrene are similar to the long-lived triplet states in crystalline rubrene. Given that the energetics of the electronic states in FM-rubrene and F-rubrene satisfy the energy criteria for SF56 and the similarity of spectral dynamics between rubrene and the derivatives, we believe that FM-rubrene and F-rubrene undergo SF and form long-lived triplets. Therefore, we assigned these broad long-lived spectral features to electronic transient absorption signatures of the separated triplets generated through the SF process in FM-rubrene and F-rubrene.
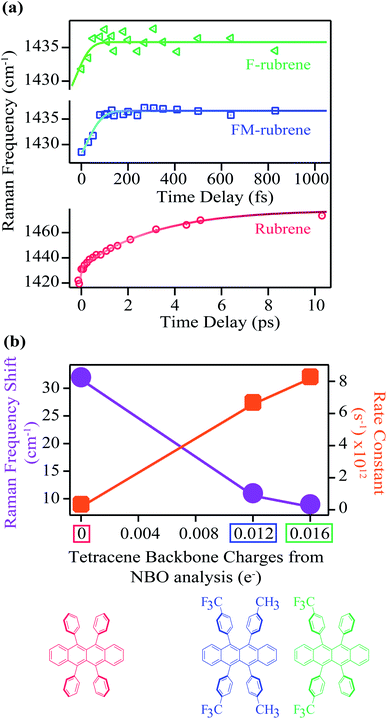
In addition to triplet features, we observe that the Raman mode shaded in red for crystalline rubrene FSR data in Fig. 2a undergoes a spectral evolution with a time constant of 3.3 ± 0.2 ps. This mode appears at a frequency of 1430 cm−1 around time zero and then blueshifts to a frequency of 1462 cm−1 by 3 ps as shown in Fig. 3a and S10.† In ultrafast spectroscopy, a shift in vibrational mode implies a structural rearrangement.54,63–65 Since the time constant associated with the frequency shift of the 1430 cm−1 mode is longer than the 2 ps correlated triplet pair lifetime in crystalline rubrene,40 we previously assigned this structural evolution to dynamics during the triplet pair separation 1(T⋯T).48
The 1430 cm−1 mode in the ground state Raman spectrum of rubrene corresponds to C–C stretching and C–H wagging motions of the tetracene core in rubrene. Since the 1430 cm−1 vibrational mode blueshifts after photoexcitation, the shift in frequency we observe in the excited state spectra is associated with the structural rearrangement of the tetracene core during the triplet separation process in crystalline rubrene. We previously assigned this spectral evolution of the 1430 cm−1 to higher frequencies to be accompanied by the loss of electron density in the tetracene backbone during the correlated triplet pair separation into two individual triplets in crystalline rubrene.48 Therefore, we expect a correlation between the structural rearrangement during the correlated triplet pair separation and the frequency shift along the rubrene series: the smaller the structural rearrangement, the smaller the frequency shift, and the less energy lost during the whole fission process. Since FM-rubrene and F-rubrene have less electron density in their tetracene core than rubrene, we expect to observe smaller and faster frequency shifts in the vibrational mode in the derivatives compared to rubrene, where F-rubrene is expected to be the fastest to separate the correlated triplet pair into individual triplets.
Excitingly, we obtained similar behavior of the frequency evolution for the 1430 cm−1 vibrational mode in crystals of FM-rubrene and F-rubrene as observed in crystalline rubrene, as shown in the FSR data in Fig. 2b and c respectively. To extract information on the transient evolution of the Raman vibration, we fit the Raman mode around 1430 cm−1 at different time delays after photoexcitation with a Gaussian spectral function. We notice that the intensity evolution of the 1430 cm−1 mode is different within the three crystals and this difference in intensity evolution of the 1430 cm−1 mode is due to differences in the resonance conditions of the excited states in the three derivatives. We plot the dynamics of the fitted peak frequency around 1430 cm−1 region as a function of time for rubrene, FM-rubrene and F-rubrene in Fig. 3a. The experimental error bars for the frequency fits are contained within the markers. We fit the spectral peak frequencies to a biexponential decay convoluted with the cross-correlation between the actinic pulse and the Raman probe to obtain the kinetics. We considered a potential triexponential decay function to fit our results. This yielded similar results, but with more poorly fitted time constants. See the ESI (Fig. S10†) for additional discussion. We have propagated the error in the instrument response function during the deconvolution process and obtained the time constants (τ1) associated with the kinetic fits for rubrene, FM-rubrene and F-rubrene as 3.3 ± 0.2 ps, 150 ± 20 fs and less than 120 ± 40 fs, respectively. The time constants of the spectral evolution for FM-rubrene and F-rubrene approaches our instrumental response function of 120 ± 3 fs in the experiments. A time constant of tens of nanoseconds, corresponding to long-lived triplets, was held constant to fit the transient spectral evolution of the feature around 1430 cm−1. Using the time constants from the kinetic fits, we quantify that the 1430 cm−1 at time zero displays a shift of ∼32 cm−1 by 3 ps in rubrene, ∼11 cm−1 by 150 fs in FM-rubrene and ∼9 cm−1 in less than 120 fs in F-rubrene. Within error, the time constants for FM-rubrene and F-rubrene are not significantly different. However, we have measured multiple F-rubrene and FM-rubrene crystals, and in all cases, we observe faster dynamics in F-rubrene compared to that in FM-rubrene. Thus, the trend of frequency shift and the associated time constants is qualitatively followed where F-rubrene displays a smaller frequency shift on a relatively faster time scale than FM-rubrene.
The stimulated Raman signal obtained by employing a broadband Raman pump and a narrowband Raman pulse offers a high spectral resolution of vibrational features and information on the time dependent vibrational frequencies integrated over the dephasing vibrational time. The signal observed in FSRS experiments do not represent instantaneous vibrational frequencies present in the sample only at the moment when the probe arrives, but the signal comprises of all the vibrational frequencies present in the sample over the course of the vibrational dephasing time.66,67 This means that the FSRS spectrum obtained at a time point of 100 fs contains information on 100 fs + ΔT, where ΔT is the vibrational dephasing time convoluted with the Raman pump pulse. The center peak frequencies observed experimentally at the early time points in our FSRS data in Fig. 3a are not the instantaneous frequencies. However, the relative shifts of the 1430 cm−1 mode in the fluorinated rubrene derivatives, while small, are reproducible across samples and thus qualitatively holds true.
The frequency upshifts observed in Fig. 3a are not intuitively correlated with bond stiffening or weakening. However, based on our previous computational and experimental studies, we found out that the blue shift is associated with the electron density change after photoexcitation during SF.48 The amount of frequency shift observed experimentally is related to the extent of structural rearrangement occurring within the molecules during the correlated triplet pair separation process while undergoing SF. This structural rearrangement is in turn associated with the loss of electron density over the tetracene core in the rubrene series during the loss of electronic coherence of the correlated triplet pair. Thus, to extract the relationship between the electron charge distribution in the ground state of the rubrene series with spectral evolution, we plot the total experimentally observed shift in frequency of the Raman mode around 1430 cm−1 from our FSRS data and the rate (1/τ1) of this frequency shift as a function of the NBO charges on the tetracene core in the rubrene derivatives in Fig. 3b. We observe an inverse relationship between the frequency shift and the tetracene backbone being more positive along the rubrene series. We also found a direct correlation between the rate constant of the frequency shifts with the presence of less electron density between the tetracene cores in rubrene, FM-rubrene and F-rubrene. The rate constant of this frequency shift is proportional to the rate of SF and thus, our results reveal that the FM-rubrene and F-rubrene exhibit SF rates higher than rubrene, with F-rubrene undergoing slightly faster SF than FM-rubrene. This demonstrates a one-to-one correlation between the charge distribution over tetracene core in the three molecules and the experimentally observed structural rearrangement and rate of triplet pair separation via SF.
Here, we have associated the spectral evolution to the structural rearrangement during the triplet pair separation 1(T⋯T) in rubrene, FM-rubrene and F-rubrene based on their time constants.40,48 As we are limited by our instrument response function of 120 fs and given that the frequency evolution time-constants in FM-rubrene and F-rubrene are on ultrafast timescales of 150 fs and 120 fs respectively, it can be assumed that this frequency evolution observed in FM-rubrene and F-rubrene correspond to the entire process of the system going from S1 → 1(TT) → 1(T⋯T). However, dissecting the individual steps would call for shorter instrumental response functions. Additionally, the time constants associated with the spectral evolution of the 1430 cm−1 Raman mode, which we have attributed to the structural evolution dynamics during the triplet pair separation 1(T⋯T), is faster than the growth of the separated triplet signatures from the transient absorption data in Fig. S11.† A possible explanation for the time gap between the vibrational structural evolution of the triplet pair separation and the electronic feature appearance from uncoupled triplets could be due to other processes that occur simultaneously with the triplet formation, such as triplet–triplet annihilation or other relaxation processes. We note that differences between time constants observed in transient absorption microscopy and FSRS have been observed in all previously published singlet fission studies involving using FSRS to probe dynamics in single crystals,48,59 and thus we emphasize the relative comparison between the FSRS results here rather than the absolute numbers. Most importantly, we observe that the structural changes in FM-rubrene and F-rubrene is indeed to a lesser extent than that observed in rubrene during the SF process, as predicted by our model.
To correlate the observed experimental structural reorganization with the molecular structural properties in the rubrene derivatives, we draw attention to our NBO calculations. From the NBO analysis, F-rubrene and FM-rubrene have less electron density in their tetracene core compared to rubrene, and therefore, the derivative structures are closer to their triplet state structures to begin with. Since F-rubrene possess the minimum amount of electron density in its tetracene core among the rubrene series, it displays the smallest frequency shift, and thereby undergoes the least and fastest structural reorganization to form the individual triplets because its ground state structure is pre-primed to that of the final triplet structure. Hence, less energy is lost in restructuring the molecules in F-rubrene while separating the correlated triplet pair, a favorable property for SF as this reduces the thermalization loss. Therefore, we have successfully utilized our spectroscopic knowledge to predict and screen the molecular structure of the rubrene derivatives such that they are pre-deposited to the product structure, which is the triplet structure during SF in this scenario. Additionally, the observed correlation between the frequency shift and the tetracene core electron density suggests that the electron density shifts away from the tetracene core into the phenyl groups during the separation of correlated triplet pairs in rubrene and its derivatives. This time-resolved study thus provides new insights regarding the directionality of the electron density movements during SF within the rubrene derivatives series.
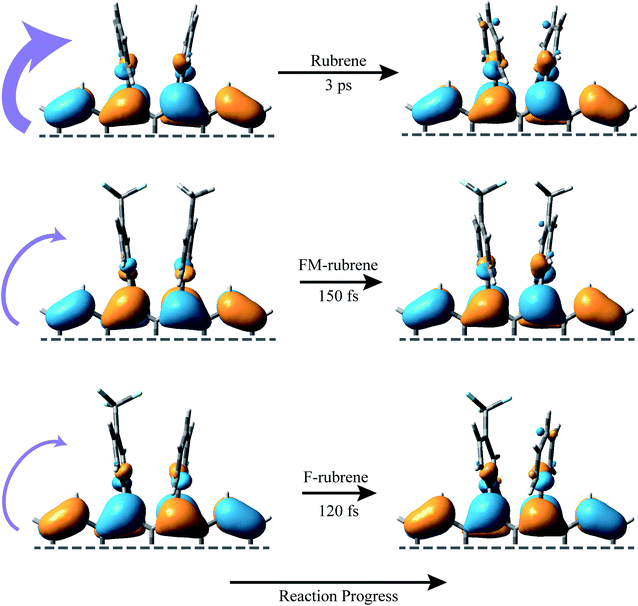
Fig. 4 represents a schematic illustration of the structural changes in rubrene, FM-rubrene and F-rubrene during the triplet pair separation process via SF. We graphed the frontier molecular orbitals consisting the highest occupied molecular orbital (HOMO) of the ground singlet state and singly occupied molecular orbital (SOMO) of the triplet state in rubrene, FM-rubrene and F-rubrene obtained from our DFT calculations in Fig. 4. Analyzing the optimized geometries in the ground singlet and first triplet structures indicate that rubrene, FM-rubrene and F-rubrene undergo less changes in their structures while going from singlet to triplet geometry. This is in agreement with the little change we observe in the vibrational dynamics between the singlet and triplet states suggesting that the structure of the triplets and singlets are quite similar. Analyzing these optimized geometries further supports our experimental results that FM-rubrene and F-rubrene undergo less changes in their structures while going from singlet to triplet geometry than rubrene. Also, comparing the molecular orbitals of the SOMO of triplet and HOMO of ground singlet state confirms that the electron density indeed shifts from the tetracene backbone into the edges of the peripheryl phenyl groups during the triplet generation process, as depicted by the curved purple arrows in Fig. 4. Therefore, the time-resolved studies in partner with the theoretical calculations together support that the electron density moves away from the tetracene core into the side phenyl groups during the separation of the correlated triplet pair in rubrene and its derivatives.
One limitation in the current FSRS crystalline rubrene data is the fewer data points in the ultrafast regime. It might seem from Fig. 3a and S10† that rubrene also displays a ∼12 cm−1 frequency shift near time zero on ultrafast time scale of less than 1 ps, similar to the ∼11 cm−1 shift in FM-rubrene within 150 fs and ∼9 cm−1 frequency shift in F-rubrene within 120 fs. This would suggest that this fast time-constant dynamics is a common relaxation step between rubrene and the derivatives, and that the absence of the slow time constant of 3 ps in FM-rubrene and F-rubrene is the deciding factor resulting in the fast SF process in rubrene derivatives. However, our current data and their fits with bi- and tri-exponentials suggest that the relaxation process associated with the structural rearrangement during triplet separation process in rubrene takes about 3 ps whereas it takes ∼150 fs in FM-rubrene and ∼120 fs that in F-rubrene.
In summary, we used the insights gained from FSRS studies about structural changes during SF in crystalline rubrene to screen promising candidates for efficient SF process. We compared the crystal structures and measured spontaneous Raman spectra of rubrene, FM-rubrene and F-rubrene to show their similarities. We then performed FSRS on crystalline rubrene, FM-rubrene and F-rubrene and observed that after the systems absorb light, placing the wavepackets on the excited state Franck–Condon surface, all three chromophores relaxes displaying spectral signatures of long-lived triplets generated via SF. We provide the first ever experimental evidence for these rubrene derivatives to undergo efficient SF. Among the three molecules, F-rubrene displays the fastest rate of SF, which is a favorable property to generate excitons for further harvesting into photovoltaics. Hence, we conclude that we have selected pre-primed molecular structures of rubrene derivatives, guided by spectroscopic data, to undergo more efficient SF. Our results not only define the structural changes within molecules during SF but bridges the gap between spectroscopic results and translating these results to practical application regarding efficient SF systems. This study expands upon our previous spectroscopic knowledge, proving that controlling the electron density in the tetracene core synthetically leads to significant improvement in the SF rate. Moving forward, we plan to explore this spectroscopy-guided experimental control of synthesis with other acene derivatives, particularly those containing electron withdrawing functional groups on the peripheral aryl groups, provided the molecular packing in the crystal remains the same. These studies will help achieve the end goal of utilizing current spectroscopic knowledge to formulate and realize design guidelines for new and efficient SF systems.
Conclusion
In conclusion, we have successfully used FSRS to understand the effect of chemical modification on SF and our results indicate that both our carefully chosen rubrene derivatives, FM-rubrene and F-rubrene, undergo SF. We observe a shift in the frequency of a vibrational mode during triplet separation process in our time-resolved FSR data, which is associated with the loss of electron density from the tetracene backbone into the peripheryl phenyl groups in crystalline rubrene and its derivatives. By intentionally reducing the electron density over the tetracene core in the rubrene derivatives, we have now designed the system to have a structure which is much closer to the final structure for efficient SF. Thus, we observe less structural reorganization in rubrene derivatives and a faster rate of SF in F-rubrene followed by FM-rubrene compared to parent rubrene. Less structural reordering leads to lower energy losses, thereby reducing thermalization loss mechanism for efficient SF. We have created a predictive model based on spectroscopic techniques for the design and identification of rubrene derivatives that show increased SF rates. Our work shows that the long-held promise of spectroscopy-informed small molecule design for organic optoelectronic materials can be realized in rubrene-based singlet fission systems. This will inspire spectroscopic measurements-guided intelligent engineering and syntheses of future materials within SF chromophores and other similar families.Data availability
All data is freely available through the Data Repository for University of Minnesota (DRUM), at persistent identifier https://hdl.handle.net/11299/224735.Author contributions
K. B. and R. R. F. conceived and designed the project. K. B. carried out the spectroscopic measurements. K. B., C. J. D. and R. R. F. wrote and revised the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work is supported by Department of Energy DE-SC0018203 and the Doctoral Dissertation Fellowship award from University of Minnesota. The authors thank Dr Billy Ogden, Dr Zhuoran Zhang, and Margaret Clapham for the crude samples of FM-rubrene and F-rubrene, and Dr Federico Coppola for helpful discussions on calculations. The authors also acknowledge the Minnesota Supercomputing Institute (MSI) at the University of Minnesota for providing resources that contributed to the research reported in this paper.References
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, Science, 2013, 340, 334–337 CrossRef CAS.
- O. E. Semonin, J. M. Luther, S. Choi, H. Y. Chen, J. Gao, A. J. Nozik and M. C. Beard, Science, 2011, 334, 1530–1533 CrossRef CAS.
- G. D. Scholes, J. Phys. Chem. A, 2015, 119, 12699–12705 CrossRef CAS.
- A. A. Bakulin, S. E. Morgan, T. B. Kehoe, M. W. B. B. Wilson, A. W. Chin, D. Zigmantas, D. Egorova and A. Rao, Nat. Chem., 2016, 8, 16–23 CrossRef CAS.
- N. R. Monahan, D. Sun, H. Tamura, K. W. Williams, B. Xu, Y. Zhong, B. Kumar, C. Nuckolls, A. R. Harutyunyan, G. Chen, H.-L. Dai, D. Beljonne, Y. Rao and X.-Y. Zhu, Nat. Chem., 2017, 9, 341–346 CrossRef CAS PubMed.
- S. N. Sanders, A. B. Pun, K. R. Parenti, E. Kumarasamy, L. M. Yablon, M. Y. Sfeir and L. M. Campos, Chem, 2019, 5, 1988–2005 CAS.
- K. Miyata, F. S. Conrad-Burton, F. L. Geyer and X.-Y. Zhu, Chem. Rev., 2019, 119, 4261–4292 CrossRef CAS PubMed.
- C. K. Yong, A. J. Musser, S. L. Bayliss, S. Lukman, H. Tamura, O. Bubnova, R. K. Hallani, A. Meneau, R. Resel, M. Maruyama, S. Hotta, L. M. Herz, D. Beljonne, J. E. Anthony, J. Clark and H. Sirringhaus, Nat. Commun., 2017, 8, 15953 CrossRef CAS PubMed.
- J. Zheng, Y. Xie, S. Jiang and Z. Lan, J. Phys. Chem. C, 2016, 120, 1375–1389 CrossRef CAS.
- C. Grieco, E. R. Kennehan, A. Rimshaw, M. M. Payne, J. E. Anthony and J. B. Asbury, J. Phys. Chem. Lett., 2017, 8, 5700–5706 CrossRef CAS.
- N. Monahan and X.-Y. Zhu, Annu. Rev. Phys. Chem., 2015, 66, 601–618 CrossRef CAS.
- G. B. Piland, J. J. Burdett, R. J. Dillon and C. J. Bardeen, J. Phys. Chem. Lett., 2014, 5, 2312–2319 CrossRef CAS PubMed.
- T. Sakuma, H. Sakai, Y. Araki, T. Mori, T. Wada, N. V. Tkachenko and T. Hasobe, J. Phys. Chem. A, 2016, 120, 1867–1875 CrossRef CAS.
- A. J. Musser, M. Liebel, C. Schnedermann, T. Wende, T. B. Kehoe, A. Rao and P. Kukura, Nat. Phys., 2015, 11, 352–357 Search PubMed.
- M. C. Hanna and A. J. Nozik, J. Appl. Phys., 2006, 100, 074510 CrossRef.
- M. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- M. Einzinger, T. Wu, J. F. Kompalla, H. L. Smith, C. F. Perkinson, L. Nienhaus, S. Wieghold, D. N. Congreve, A. Kahn, M. G. Bawendi and M. A. Baldo, Nature, 2019, 571, 90–94 CrossRef CAS PubMed.
- Q. Ye and C. Chi, Chem. Mater., 2014, 26, 4046–4056 CrossRef CAS.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS.
- W.-L. Chan, M. Ligges, A. Jailaubekov, L. Kaake, L. Miaja-Avila and X.-Y. Zhu, Science, 2011, 334, 1541–1545 CrossRef CAS PubMed.
- K. Miyata, Y. Kurashige, K. Watanabe, T. Sugimoto, S. Takahashi, S. Tanaka, J. Takeya, T. Yanai and Y. Matsumoto, Nat. Chem., 2017, 9, 983–989 CrossRef CAS PubMed.
- A. B. Kolomeisky, X. Feng and A. I. Krylov, J. Phys. Chem. C, 2014, 118, 5188–5195 CrossRef CAS.
- S. Ito, T. Nagami and M. Nakano, J. Photochem. Photobiol., C, 2018, 34, 85–120 CrossRef CAS.
- M. K. Gish, N. A. Pace, G. Rumbles and J. C. Johnson, J. Phys. Chem. C, 2019, 123, 3923–3934 CrossRef CAS.
- K. M. Felter and F. C. Grozema, J. Phys. Chem. Lett., 2019, 10, 7208–7214 CrossRef CAS PubMed.
- K. C. Krishnapriya, A. J. Musser and S. Patil, ACS Energy Lett., 2019, 4, 192–202 CrossRef CAS.
- K. Bera, S. Y. Kwang and R. R. Frontiera, J. Phys. Chem. C, 2020, 124, 25163–25174 CrossRef CAS.
- A. K. Pandey and J. M. Nunzi, Adv. Mater., 2007, 19, 3613–3617 CrossRef CAS.
- H. Najafov, B. Lee, Q. Zhou, L. C. Feldman and V. Podzorov, Nat. Mater., 2010, 9, 938–943 CrossRef CAS PubMed.
- R. Zeis, C. Besnard, T. Siegrist, C. Schlockermann, X. Chi and C. Kloc, Chem. Mater., 2006, 18, 244–248 CrossRef CAS.
- P. Irkhin and I. Biaggio, Phys. Rev. Lett., 2011, 107, 017402 CrossRef.
- M. Ullah, S. D. Yambem, E. G. Moore, E. B. Namdas and A. K. Pandey, Adv. Electron. Mater., 2015, 1, 1500229–1500238 CrossRef.
- V. Jankus, E. W. Snedden, D. W. Bright, E. Arac, D. Dai and A. P. Monkman, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 224202 CrossRef.
- H. Tsunoyama and A. Nakajima, J. Phys. Chem. C, 2017, 121, 20680–20686 CrossRef CAS.
- L. Ma, K. Zhang, C. Kloc, H. Sun, M. E. Michel-Beyerle and G. G. Gurzadyan, Phys. Chem. Chem. Phys., 2012, 14, 8307–8312 RSC.
- Y. Zhang, Y. Lei, Q. Zhang and Z. Xiong, Org. Electron., 2014, 15, 577–581 CrossRef CAS.
- L. Ma, K. Zhang, C. Kloc, H. Sun, C. Soci, M. E. Michel-Beyerle and G. G. Gurzadyan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 201203 CrossRef.
- L. Ma, G. Galstyan, K. Zhang, C. Kloc, H. Sun, C. Soci, M. E. Michel-Beyerle and G. G. Gurzadyan, J. Chem. Phys., 2013, 138, 184508 CrossRef.
- I. Breen, R. Tempelaar, L. A. Bizimana, B. Kloss, D. R. Reichman, D. B. Turner, R. David, D. B. Turner, D. R. Reichman and D. B. Turner, J. Am. Chem. Soc., 2017, 139, 11745–11751 CrossRef CAS PubMed.
- A SciFinder search was conducted on May 22, 2020 using rubrene as the starting structure. Ring fusions on the tetracene core were excluded. The search was also refined to exclude metal-containing substances and structures without references (accessed May 22, 2020).
- K. A. McGarry, W. Xie, C. Sutton, C. Risko, Y. Wu, V. G. Young, J. L. Brédas, C. D. Frisbie and C. J. Douglas, Chem. Mater., 2013, 25, 2254–2263 CrossRef CAS.
- Y. Sakamoto and T. Suzuki, J. Org. Chem., 2017, 82, 8111–8116 CrossRef CAS PubMed.
- D. Braga, A. Jaafari, L. Miozzo, M. Moret, S. Rizzato, A. Papagni and A. Yassar, Eur. J. Inorg. Chem., 2011, 2011, 4160–4169 CrossRef CAS.
- J. A. Dodge, J. D. Bain and A. R. Chamberlin, J. Org. Chem., 1990, 55, 4190–4198 CrossRef CAS.
- A. S. Paraskar, A. R. Reddy, A. Patra, Y. H. Wijsboom, O. Gidron, L. J. W. Shimon, G. Leitus and M. Bendikov, Chem.–Eur. J., 2008, 14, 10639–10647 CrossRef CAS.
- M. L. Clapham, E. C. Murphy and C. J. Douglas, Synthesis, 2021, 53, 461–474 CrossRef CAS.
- K. Bera, C. J. Douglas and R. R. Frontiera, J. Phys. Chem. Lett., 2017, 8, 5929–5934 CrossRef CAS PubMed.
- P. Kukura, D. W. McCamant and R. A. Mathies, Annu. Rev. Phys. Chem., 2007, 58, 461–488 CrossRef CAS PubMed.
- P. Kukura, S. Yoon and R. A. Mathies, Anal. Chem., 2006, 78, 5952–5959 CrossRef CAS.
- D. W. McCamant, P. Kukura, S. Yoon and R. A. Mathies, Rev. Sci. Instrum., 2004, 75, 4971–4980 CrossRef CAS.
- D. R. Dietze and R. A. Mathies, ChemPhysChem, 2016, 17, 1224–1251 CrossRef CAS.
- A. E. Bragg, W. Yu, J. Zhou and T. Magnanelli, J. Phys. Chem. Lett., 2016, 7, 3990–4000 CrossRef CAS.
- F. Provencher, N. Bérubé, A. W. Parker, G. M. Greetham, M. Towrie, C. Hellmann, M. Côté, N. Stingelin, C. Silva and S. C. Hayes, Nat. Commun., 2014, 5, 4288 CrossRef CAS.
- W. A. Ogden, S. Ghosh, M. J. Bruzek, K. A. McGarry, L. Balhorn, V. Young, L. J. Purvis, S. E. Wegwerth, Z. Zhang, N. A. Serratore, C. J. Cramer, L. Gagliardi and C. J. Douglas, Cryst. Growth Des., 2017, 17, 643–658 CrossRef CAS.
- C. Sutton, N. R. Tummala, D. Beljonne and J. L. Brédas, Chem. Mater., 2017, 29, 2777–2787 CrossRef CAS.
- T. K. Mullenbach, K. A. McGarry, W. A. Luhman, C. J. Douglas and R. J. Holmes, Adv. Mater., 2013, 25, 3689–3693 CrossRef CAS.
- A. A. Cassabaum, W. R. Silva, C. C. Rich and R. R. Frontiera, J. Phys. Chem. C, 2019, 123, 12563–12572 CrossRef CAS.
- S. M. Hart, W. R. Silva and R. R. Frontiera, Chem. Sci., 2018, 9, 1242–1250 RSC.
- W. R. Silva and R. R. Frontiera, Phys. Chem. Chem. Phys., 2016, 18, 20290–20297 RSC.
- K. Bera, S. Y. Kwang, A. A. Cassabaum, C. C. Rich and R. R. Frontiera, J. Phys. Chem. A, 2019, 123, 7932–7939 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell and D. J. Montgo, Gaussian 16, Revision C.01, https://gaussian.com/citation/, 2020, accessed 6 March Search PubMed.
- P. Kukura, D. W. McCamant, S. Yoon, D. B. Wandschneider and R. A. Mathies, Science, 2005, 310, 1006–1009 CrossRef CAS.
- C. Fang, R. R. Frontiera, R. Tran and R. A. Mathies, Nature, 2009, 462, 200–204 CrossRef CAS PubMed.
- R. R. Frontiera, J. Dasgupta and R. A. Mathies, J. Am. Chem. Soc., 2009, 131, 15630–15632 CrossRef CAS PubMed.
- S. Mukamel and J. D. Biggs, J. Chem. Phys., 2011, 134, 161101 CrossRef.
- D. W. McCamant, J. Phys. Chem. B, 2011, 115, 9299–9305 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed experimental procedures, absorption spectra of crystals, actinic pulse profile, raw FSR data of crystalline rubrene, FM-rubrene and F-rubrene, ground state addition kinetics, transient absorption data, FSR of crystalline FM-rubrene with grating filter, transient absorption of FM-rubrene solution, coordinates of optimized singlet and triplet state geometries. See DOI: 10.1039/d1sc04251c |
| This journal is © The Royal Society of Chemistry 2021 |