Open Access Article
Open Access ArticleTowards controlling the reversibility of anionic redox in transition metal oxides for high-energy Li-ion positive electrodes†
Yang
Yu
*a,
Pinar
Karayaylali‡
b,
Dimosthenis
Sokaras
c,
Livia
Giordano
bd,
Ronghui
Kou
e,
Cheng-Jun
Sun
e,
Filippo
Maglia
 f,
Roland
Jung
f,
Forrest S.
Gittleson
g and
Yang
Shao-Horn
f,
Roland
Jung
f,
Forrest S.
Gittleson
g and
Yang
Shao-Horn
 *abd
*abd
aDepartment of Materials Science and Engineering, MIT, Cambridge, MA 02139, USA. E-mail: yuy@mit.edu; shaohorn@mit.edu
bDepartment of Mechanical Engineering, MIT, Cambridge, MA 02139, USA
cSLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
dResearch Laboratory of Electronics, MIT, Cambridge, MA 02139, USA
eAdvanced Photon Source, Argonne National Laboratory, Argonne, IL 60439, USA
fBMW Group, Petuelring 130, 80788 Munich, Germany
gBMW Group Technology Office USA, 2606 Bayshore Parkway, Mountain View, California 94043, USA
First published on 26th February 2021
Abstract
Anionic redox in positive electrode materials in Li-ion batteries provides an additional redox couple besides conventional metal redox, which can be harvested to further boost the energy density of current Li-ion batteries. However, the requirement for the reversible anionic redox activity remains under debate, hindering the rational design of new materials with reversible anionic redox. In this work, we employed differential electrochemical mass spectrometry (DEMS) to monitor the release of oxygen and to quantify the reversibility of the anionic redox of Li2Ru0.75M0.25O3 (M = Ti, Cr, Mn, Fe, Ru, Sn, Pt, Ir) upon first charge. X-ray absorption spectroscopy, coupled with density functional theory (DFT) calculations, show that various substituents have a minimal effect on the nominal metal redox, yet more ionic substituents and reduced metal–oxygen covalency introduce irreversible oxygen redox, accompanied with easier distortion of the M–O octahedron and a smaller barrier for forming an oxygen dimer within the octahedron. Therefore, a strong metal–oxygen covalency is needed to enhance the reversible oxygen redox. We proposed an electron–phonon-coupled descriptor for the reversibility of oxygen redox, laying the foundation for high-throughput screening of novel materials that enable reversible anionic redox activity.
Broader contextLi-rich positive electrodes exhibiting anionic redox have enhanced the energy densities of Li-ion batteries, yet there is no clear understanding of the factors controlling the reversibility of the anionic redox process and enhancing the cycling stability of these materials. In this work, by employing 3d, 4d and 5d transition metal substituted Li2RuO3 oxides, we observe that the energetic overlap between the metal and oxygen density of states dictates the rigidity of the oxide sublattice upon lithium deintercalation. Therefore, a large metal–oxygen covalency is necessary for increasing the thermodynamic barrier to form molecular oxygen and to stabilize the oxygen redox intermediates, which is also the key to less disorder introduced in the M–O octahedron upon lithium deintercalation, as shown by X-ray absorption spectroscopies. The experimental oxygen redox reversibility quantified through mass spectrometry thus directly scales with the metal–oxygen covalency and lattice rigidity upon lithium removal. An electron–phonon-coupled descriptor for anionic redox reversibility is proposed, providing opportunities for further screening of low-cost, high-energy electrode materials leveraging anionic redox, to further improve the energy density of Li-ion batteries. |
1. Introduction
Positive electrode materials used in commercial lithium-ion batteries are based on layered LiMO2 (M = Co, Ni, Mn), where the reversible redox of 3d transition metals, including Co3+/Co4+,1,2 Ni2+/Ni4+ (or Ni3+/Ni4+)3–5 and Mn3+/Mn4+,6,7 can deliver capacities of up to 200 mA h g−1. Thackeray et al.8,9 have synthesized Li2MnO3-derived materials such as Li(LixMnyNizCo1−x−y−z)O2 (Li-rich Mn-rich NMC)10–14 which have shown enhanced discharge capacities of ∼300 mA h g−1, coming from cationic redox as well as lattice oxygen redox.12,13,15,16 The cycling stability of Li-rich Mn-rich NMC shows a significant voltage decay as well as a capacity fade over subsequent cycles, which is related to diminishing oxygen redox upon extended cycling.10,17 Fundamental understanding for the origin of oxygen redox is needed for the development of novel and non-noble oxides that employ reversible oxygen redox to boost the capacity and energy density of Li-ion batteries.15,18–21Li2MO3 (M = Ru and Ir)22–25 has been used as a model system to understand oxygen redox in oxides. Li2RuO322,24,26 and Li2IrO325,27 show reversible capacities with a two-electron transfer process and high cycling stability. For example, Tarascon and co-workers have shown that Li2Ru1−xMnxO324 and Li2Ru1−xSnxO311,22 deliver first discharge capacities as high as 250 mA h g−1, and capacity retention capabilities higher than 80% after 100 cycles. The capacity corresponding to the second electron transfer has been attributed to reversible lattice oxygen oxidation into peroxo- and superoxo-like species in the bulk.26,28 Currently, there are two schools of seemingly contradictory thought on the requirement for reversible anionic redox. In the first school of thought, the reversible oxygen redox is proposed to scale with the ionicity of the metal–oxygen bond. Yabuuchi et al.29,30 have reported that increasing the ionicity of the transition metal and oxygen bond can reduce the overlap between the metal and oxygen electronic density-of-states (DOS),29 forbidding the oxidation of oxygen ion to molecular oxygen. This thinking is exemplified in the superior cycling stability of more ionic oxides Li1.2Ti0.4Mn0.4O2 and the more depressed oxygen evolution of this material upon charging to 4.8 VLi, compared with those of Li1.2Ti0.4Fe0.4O2.29 Further support comes from density functional theory (DFT) calculation results by Doublet et al.,20,31 where it has been shown that as the charge transfer gap decreases, the covalency of the transition metal and oxygen increases. As a result, this lower charge transfer gap induces more oxygen character at the Fermi level, resulting in a larger degree of charge compensation coming from the oxygen, shortening of the O–O bond, and eventually leading to irreversible oxygen release.20 A certain ionicity between metal and oxygen is needed to maintain reversible oxygen redox.20
The second school of thought argues that more reversible anionic redox activity comes from a more covalent interaction between the transition metal and oxygen bond in the oxide. Saubanère et al.28 have reported from crystal orbital overlap population (COOP) analysis that greater covalent bonding between Ru and O in Li2−xRuO3 stabilizes the peroxo-like species upon oxidation more than that in Li2−xMnO3. This idea has also been further explored by Bruce and coworkers.16 In this work, an O K-edge resonant inelastic X-ray scattering (RIXS) study on Li-rich Mn-rich NMC showed an electronic structure fingerprint, which was assigned to the formation of oxygen-localized electron holes, where these researchers concluded that the reversibility of the anionic redox relies on more delocalized M–O bonds from higher M–O covalency. In our previous work by combining X-ray absorption and emission spectra as well as excited states calculations on charged Li2−xRuO3,32 we were able to pinpoint the experimental electronic fingerprint of (O–O) σ* states coordinated with Ru d states in core-level spectroscopies. Such type of signature is missing in charged Li2−xMnO3,32,33 which suffers irreversible oxygen redox and molecular oxygen evolution, again highlighting the importance of metal–oxygen covalency in stabilizing anionic redox. In our follow-up work,33 we showed that such Ru–O covalency results in phonon hardening in the oxide lattice upon lithium deintercalation, resulting in a more stable oxygen sublattice towards oxygen redox intermediates, inducing more reversible oxygen redox. In this work, we hypothesize that the larger degree of overlap between the transition metal and oxygen electronic states introduces a more rigid oxygen sublattice upon lithium deintercalation, resulting in a more reversible oxygen redox.
In this study, for the systematic examination of the role of M–O covalency in reversible anionic redox, we employ Li2RuO3 as the host lattice to substitute in different transition metal elements, to slightly tune the covalency between the transition metal and oxygen. We characterize the redox behavior and structural changes using X-ray absorption spectroscopy (XAS). Coupled with differential electrochemical mass spectrometry (DEMS) measurements and electrochemistry, we are able to identify the reversible component of anionic redox in each of the substituted materials and quantify the reversibility of the anionic redox. Through DFT calculations, an electron–phonon-coupled descriptor for the reversibility of anionic redox is then proposed, which allows for future high-throughput screening of next generation high-energy density Li-ion positive electrode materials.
2. Result and discussion
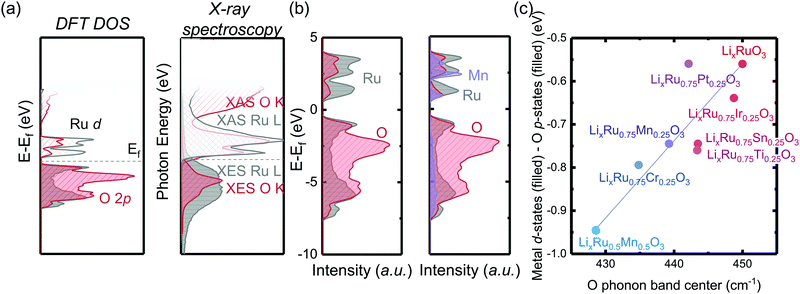
Coupled electronic and phononic trend in M-substituted Li2RuO3
By substituting different transition metal elements into the Li2RuO3 host lattice, the oxygen phonon band center of delithiated LiRuxM1−xO3, which describes the oxygen lattice integrity upon lithium deintercalation, has a strong positive correlation with the metal–oxygen covalency, characterized by the energetic overlap between metal d states and O p electronic states. From DFT calculations of the projected density of states (pDOS) and experimental density of states from X-ray spectroscopies in Fig. 1(a), Ru has a large degree of overlap with the oxygen states, which is quite different from 3d transition metals such as Mn, where in Li2MnO3 it is primarily the nonbonding oxygen, without the presence of Mn states, pinned at the Fermi level, as shown in previous work.33 The larger degree of overlap between Ru and O electronic states is also manifested when we compare the computed pDOS of Li2RuO3 and substituted Li2Ru0.75Mn0.25O3 in Fig. 1(b), whereby introducing Mn substituents, the total metal d band center of the transition metal shifts downwards, reducing the energetic overlap between oxygen and the transition metal. Such a decrease of energetic overlap between the transition metal and oxygen at the Fermi level induces a more flexible lattice upon lithium deintercalation, as shown in Fig. 1(c). As we decrease the energetic overlap between metal and oxygen near the Fermi level, the O phonon band center of metal oxides upon lithium deintercalation also shifts toward lower frequency, marking a less rigid M–O framework in the delithiated oxides. In our previous works,33 Li2(Ru,Ir)O3, which exhibits reversible lattice oxygen redox, in comparison with Li2(Mn,Sn)O3, which releases molecular oxygen upon lithium deintercalation, shows a larger degree of energetic overlap at the Fermi level, leading to more covalent M–O bonds as well as a hardened oxide lattice upon lithium deintercalation. Therefore, we propose that the lattice oxygen redox reversibility scales directly with the metal oxygen energetic overlap near the Fermi level as well as the oxygen phonon band center upon lithium deintercalation. To test this hypothesis, in the next section we will discuss quantification methods of the reversibility of anionic redox and qualify our hypothesis based on substituted Li2RuxM1−xO3 (M = Ti, Cr, Mn, Fe, Ru, Sn, Ir, Pt).Greater oxygen redox reversibility in M-substituted Li2RuO3 with increasing metal–oxygen covalency and oxygen lattice hardening
To evaluate the reversibility of anionic redox, DEMS measurements were conducted on the composite Li2RuxM1−xO3 electrodes to detect the evolution of molecular oxygen, where by substituting different transition metal elements, the amount of oxygen evolved in general increases with more electronegative substituents (Fig. 2). DEMS data reveal similar onset potentials and amounts of CO2 outgassing for the charged composite Li2RuxM1−xO3 (M = Ti, Cr, Mn, Fe, Ru, Sn, Ir, Pt) electrodes (Fig. 2 and Fig. S1, ESI†), which are typically attributed to the decomposition of the electrolyte at high potentials.34,35 The similar amount of CO2 evolution across different chemistries is rooted in the same amount of electrolyte in the cell and similar surface area of the positive electrode active materials. The voltage onset of CO2 evolution around 4.1 VLi is comparable to other Ru based systems such as Li1.2Ni0.2Ru0.6O2 reported in the literature,36 yet is not detected in Li2Ru0.75Sn0.25O2 in Sathiya et al.22 due to the potential insensitivity of their measurement and a lower amount of electrolyte used in the cell. Such CO2 potential onset occurs slightly earlier than that for 3d-based Li-rich systems, which is around 4.5 VLi for Li-rich NMC Li1.17[Ni0.22Co0.12Mn0.66]0.83O2,34 Li1.2Ni0.2Mn0.6O237 and disordered rock-salt Li2Mn2/3Nb1/3O2F.38 While the oxygen evolution profile varies drastically across different chemistries, for Li2RuxM1−xO3 (M = Ru, Pt, Ir, Ti) with relatively more covalent metal–oxygen interactions, we observe a similar oxygen evolution profile, where after the onset of oxygen evolution, there is a continuous and steady-rate oxygen evolution without any obvious peak feature (Fig. S1, ESI†). Materials represented by Li2RuxM1−xO3 (M = Cr, Mn, Fe, Sn) with slightly less covalent M–O bonds have a much more well-defined oxygen evolution peak, with an onset at a higher state-of-charge compared with the other materials, also with a relatively larger amount of oxygen evolved (Fig. 2). The oxygen evolution profile we observed in Li2Ru0.75Sn0.25O2 is also very close to what was observed by Sathiya et al.22 However, the difference in oxygen evolution profiles, which seems to depend on the electronic structures of the oxides, is not pointed out in previous works on the Li-rich systems and requires more detailed studies in the future to understand the physical origin.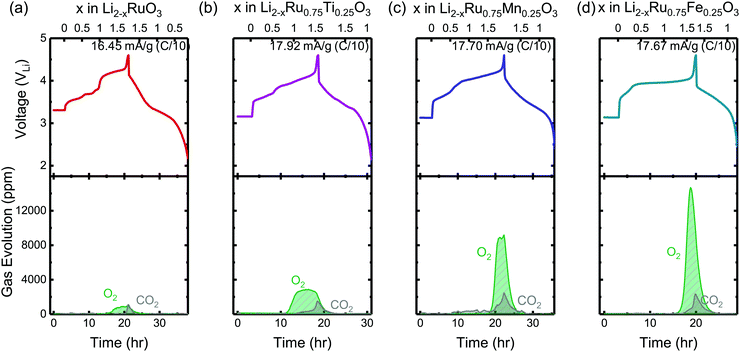 | ||
| Fig. 2 The charge and discharge voltage profiles (top panels) of (a) Li2RuO3, (b) Li2Ru0.75Ti0.25O3, (c) Li2Ru0.75Mn0.25O3 and (d) Li2Ru0.75Fe0.25O3 composite electrodes in two-electrode cells with lithium as the counter electrode as well as the concentration of CO2 and O2 (ppm) detected upon charging from DEMS (bottom panels). The cell volume is controlled around 6 cm3 and the cell is pressurized with argon to 22 psi with a flushing interval of 10 min. The electrodes were charged at a C/10 rate (∼16.45–17.92 mA g−1) during DEMS measurements with current density labeled on the right corner of the top panels. The DEMS data of other substituted systems Li2RuxM1−xO3 (M = Ir, Sn, Pt, Cr, Mn) are shown in Fig. S1 (ESI†). | ||
The reversibility of the anionic redox activity defined in this work is shown to increase for more covalent metal substituted Li2RuxM1−xO3 (M = Ti, Cr, Mn, Fe, Ru, Sn, Pt, Ir) and a more rigid oxygen lattice upon lithium deintercalation. To quantify the reversibility of the anionic redox process experimentally, we here first define the anionic reversibility figure of merit as 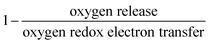 , where oxygen release could be measured as the integrated total oxygen released during the first charge cycle, as measured by DEMS (detailed methods and quantification methods are discussed in the Methodology section), and the electron transfer can be obtained by integrating the dQ/dV curve for the second plateau, which has been shown in earlier works11,32 associated with oxygen redox, upon first charge (shown in Methods in details). The larger this figure of merit, suggesting a smaller oxygen release with respect to the total electron transfer associated with oxygen, the more reversible is the anionic redox. Such a definition can more effectively decouple the oxygen redox from the metal redox, where one could alternatively define a such figure of merit by using
, where oxygen release could be measured as the integrated total oxygen released during the first charge cycle, as measured by DEMS (detailed methods and quantification methods are discussed in the Methodology section), and the electron transfer can be obtained by integrating the dQ/dV curve for the second plateau, which has been shown in earlier works11,32 associated with oxygen redox, upon first charge (shown in Methods in details). The larger this figure of merit, suggesting a smaller oxygen release with respect to the total electron transfer associated with oxygen, the more reversible is the anionic redox. Such a definition can more effectively decouple the oxygen redox from the metal redox, where one could alternatively define a such figure of merit by using  , yet such definition introduces the complexity that substituent metals and Ru might also be reduced in addition to oxygen redox upon discharge,11,15,17,22 where the discharge profile typically has one convoluted plateau.11 As a result, this definition would introduce more complexity in separating the metal reduction and oxygen reduction process upon discharge.11 In the definition employed in our work, we only use the information from the first charge, and the high-voltage plateau has been shown clearly to be related to the oxygen-redox plateau in previous work,11,32 which is quite easy to separate from the cationic redox that is represented by the lower-voltage plateau.11,22,27,32 Here we examine this defined figure of merit as a function of the computed energetic difference between filled M d and O p states and the O phononic band center in Fig. 3(a) and (b). As we increase the distance between the metal d states and oxygen p states, we are decreasing the covalency and bond strength between metal and oxygen around the Fermi level, resulting in less reversible oxygen redox activity. (Fig. 3(a)) This decrease of bond covalency between M and O is also evident in the simultaneous drop in the stiffness of the M–O framework upon lithium extraction (Fig 1(c)), inducing a lower oxygen phonon band center for the delithiated oxides. This coupling between the electronic structure and lattice dynamics has shown that the reversibility of the anionic redox also trends nicely with the oxygen phonon band center, where a softer oxygen lattice upon lithium removal induces generally more irreversible oxygen redox behavior. It is worth noting that lithium deintercalation from Li1MO3 to Li0.5MO3 results in a softening of the oxygen lattice for most of the substituted systems. We believe that such an observation is due to the incapability of the transition metals to be further oxidized from 5+ to 6+ in an octahedral environment,32,39 therefore the oxide lattice become less rigid upon lithium deintercalation,33 which is the case for M = Ti, Mn, Ru, Sn. However, for the case of the Cr-substituted system, Cr can be oxidized all the way up to 6+ in solid state,40 further increasing the covalency between M–O and the oxide lattice stiffness, pushing up the oxygen phonon band center. Moreover, the oxygen phonon band center for Li0.5CrO3 is also shifted upwards by the high frequency of the short O–O vibration upon lithium deintercalation as shown in Fig. S3(c) (ESI†). Furthermore, the observed trend is not dependent on the method we use to calculate the electron transfer correlated with the oxygen redox. If we calculate the oxygen redox electron transfer by alternatively integrating the total electrons transferred after the onset of oxygen gas evolution, the reversibility still trends with the electronic structure and phononic descriptors as shown in Fig. S5 (ESI†).
, yet such definition introduces the complexity that substituent metals and Ru might also be reduced in addition to oxygen redox upon discharge,11,15,17,22 where the discharge profile typically has one convoluted plateau.11 As a result, this definition would introduce more complexity in separating the metal reduction and oxygen reduction process upon discharge.11 In the definition employed in our work, we only use the information from the first charge, and the high-voltage plateau has been shown clearly to be related to the oxygen-redox plateau in previous work,11,32 which is quite easy to separate from the cationic redox that is represented by the lower-voltage plateau.11,22,27,32 Here we examine this defined figure of merit as a function of the computed energetic difference between filled M d and O p states and the O phononic band center in Fig. 3(a) and (b). As we increase the distance between the metal d states and oxygen p states, we are decreasing the covalency and bond strength between metal and oxygen around the Fermi level, resulting in less reversible oxygen redox activity. (Fig. 3(a)) This decrease of bond covalency between M and O is also evident in the simultaneous drop in the stiffness of the M–O framework upon lithium extraction (Fig 1(c)), inducing a lower oxygen phonon band center for the delithiated oxides. This coupling between the electronic structure and lattice dynamics has shown that the reversibility of the anionic redox also trends nicely with the oxygen phonon band center, where a softer oxygen lattice upon lithium removal induces generally more irreversible oxygen redox behavior. It is worth noting that lithium deintercalation from Li1MO3 to Li0.5MO3 results in a softening of the oxygen lattice for most of the substituted systems. We believe that such an observation is due to the incapability of the transition metals to be further oxidized from 5+ to 6+ in an octahedral environment,32,39 therefore the oxide lattice become less rigid upon lithium deintercalation,33 which is the case for M = Ti, Mn, Ru, Sn. However, for the case of the Cr-substituted system, Cr can be oxidized all the way up to 6+ in solid state,40 further increasing the covalency between M–O and the oxide lattice stiffness, pushing up the oxygen phonon band center. Moreover, the oxygen phonon band center for Li0.5CrO3 is also shifted upwards by the high frequency of the short O–O vibration upon lithium deintercalation as shown in Fig. S3(c) (ESI†). Furthermore, the observed trend is not dependent on the method we use to calculate the electron transfer correlated with the oxygen redox. If we calculate the oxygen redox electron transfer by alternatively integrating the total electrons transferred after the onset of oxygen gas evolution, the reversibility still trends with the electronic structure and phononic descriptors as shown in Fig. S5 (ESI†).
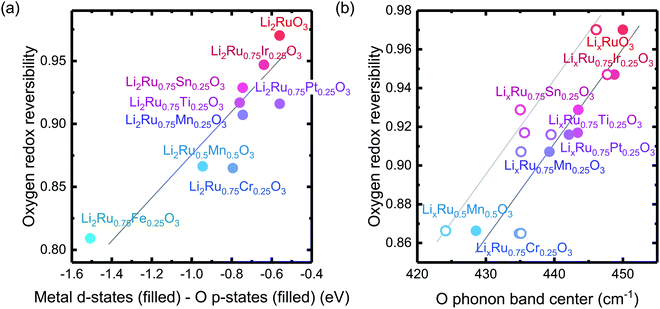 | ||
Fig. 3 Oxygen redox reversibility 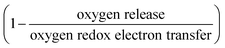 as a function of (a) DFT calculated M d–O p states (eV) and (b) oxygen phonon band center of Li2Ru0.75Fe0.25O3, Li2Ru0.75Mn0.25O3, Li2Ru0.75Pt0.25O3, Li2Ru0.75Sn0.25O3, Li2RuO3, Li2Ru0.75Ir0.25O3, Li2Ru0.75Ti0.25O3, Li2Ru0.75Cr0.25O3, Li2Ru0.5Mn0.5O3, where the raw DEMS spectra and the corresponding electrochemical profile of those compounds to calculate the reversibility figure of merit are shown in Fig. S1 (ESI†). The open circles represent the calculated O phonon band center of Li0.5Ru0.75M0.25O3 and the closed circles represent the calculated O phonon band center of Li1Ru0.75M0.25O3. The raw electronic pDOS of those compounds to calculate the M d–O p states are shown in Fig. S2 (ESI†). The oxygen phonon band center is obtained from our previous work33 and additional calculations are shown in Fig. S3 and S4 (ESI†), where for the substituted compounds, the phonon band center is taken as the weighted sum of the two endpoint compounds to simplify the calculations, as shown in previous work.41 The methodology of calculating the figure of merit is shown in the Methods section. The trend still stands as we switch to another method of integrating the charge based on the DEMS information, as shown in Fig. S5 (ESI†). The oxygen redox reversibility follows a linear trend with M–O covalency, described by the electronic structure, as well as the rigidity of the delithiated oxides lattice, as described by the phonon structure. A more covalent metal oxide induces a more rigid lattice upon lithium intercalation, resulting in a more reversible oxygen redox. as a function of (a) DFT calculated M d–O p states (eV) and (b) oxygen phonon band center of Li2Ru0.75Fe0.25O3, Li2Ru0.75Mn0.25O3, Li2Ru0.75Pt0.25O3, Li2Ru0.75Sn0.25O3, Li2RuO3, Li2Ru0.75Ir0.25O3, Li2Ru0.75Ti0.25O3, Li2Ru0.75Cr0.25O3, Li2Ru0.5Mn0.5O3, where the raw DEMS spectra and the corresponding electrochemical profile of those compounds to calculate the reversibility figure of merit are shown in Fig. S1 (ESI†). The open circles represent the calculated O phonon band center of Li0.5Ru0.75M0.25O3 and the closed circles represent the calculated O phonon band center of Li1Ru0.75M0.25O3. The raw electronic pDOS of those compounds to calculate the M d–O p states are shown in Fig. S2 (ESI†). The oxygen phonon band center is obtained from our previous work33 and additional calculations are shown in Fig. S3 and S4 (ESI†), where for the substituted compounds, the phonon band center is taken as the weighted sum of the two endpoint compounds to simplify the calculations, as shown in previous work.41 The methodology of calculating the figure of merit is shown in the Methods section. The trend still stands as we switch to another method of integrating the charge based on the DEMS information, as shown in Fig. S5 (ESI†). The oxygen redox reversibility follows a linear trend with M–O covalency, described by the electronic structure, as well as the rigidity of the delithiated oxides lattice, as described by the phonon structure. A more covalent metal oxide induces a more rigid lattice upon lithium intercalation, resulting in a more reversible oxygen redox. | ||
Ru/metal and oxygen redox from XAS of Li2−xRu0.75M0.25O3 (M = Mn, Ti, Fe)
To further understand the underlying mechanism for the observed trend, XAS was conducted on Ru and other transition metal substituents to reveal the redox process and structural evolution upon lithium deintercalation. XAS Ru L3-edge data for Li2−xRu0.75M0.25O3 (M = Mn, Ti and Fe) revealed comparable oxidation of Ru to that of Li2−xRuO3 with lithium de-intercalation, as shown in Fig. 4(a)–(c), respectively. The spectra of oxide-only Li2−xRu0.75M0.25O3 (M = Mn, Ti and Fe) pellets are comprised of two major features:42 one at a lower photon energy, corresponding to the MO interaction with electrons with t2g parentage, and the other at a higher photon energy, corresponding to the MO interaction with electrons with eg parentage, which are similar to those reported previously for Li2−xRuO3.32 The onset energy of Ru L3-edge for Li2−xRu0.75M0.25O3 (M = Mn, Ti and Fe) was found to shift towards a higher photon energy (upon removing ∼0.8 Li for Mn and Fe substitution and ∼0.5 Li for Ti substitution), indicating Ru oxidation during the first plateau, and then a shift towards a lower photon energy with further lithium de-intercalation, as shown in Fig. 4(d). This trend found for the onset energy of the Ru L3-edge of charged Li2−xRu0.75M0.25O3 is similar to that of Li2−xRuO3 reported previously,32 which has been attributed to Ru oxidation followed by reductive coupling triggered by lattice oxygen redox.22,27,32 This consistent Ru redox trend across different layered chemistries studied in this work highlights the limitation of the Ru redox, where Ru4+ is only able to be oxidized to Ru5+ upon removing 1 e−/Ru, followed by Ru reduction upon further oxidation associated with oxygen redox. Moreover, as observed in our previous work,32 such observed Ru redox process is not dependent on the quantification methods that we employ to represent the Ru oxidation state. Further support of this observed redox process comes from the analysis of the t2g/eg peak ratio (Fig. 4(e)) and t2g–eg splitting (Fig. S7, ESI†) as well as the white-line centroid (Fig. S8, ESI†). From those analyses, Ru was first oxidized, accompanied by a larger t2g/eg peak ratio and t2g–eg splitting, with the pre-peak centroid shifting towards a higher photon energy; Ru was then reduced after removing ∼0.8 Li, coupled with a smaller t2g/eg peak ratio and t2g–eg splitting (Fig. S7, ESI†), and the centroid shifted back to a lower photon energy (Fig. S8, ESI†). As we pointed out in a previous study,32 such reductive coupling observed in Ru is not necessarily the sole result of molecular oxygen evolution (Fig. 4(d)), as the amount of oxygen released cannot explain such a large degree of metal reduction. Moreover, the oxygen release onset observed in the DEMS measurements is at a higher state-of-charge than was observed for the inflection point of the Ru L-edge energy of the charged oxides. Furthermore, different metal substituted systems exhibit drastically different amounts of oxygen release, where Li2−xRu0.75Fe0.25O3 evolves ∼0.16 mol O2 per f.u., in contrast with Li2−xRuO3, which evolves 0.02 mol O2 per f.u., yet the degree of Ru backshift observed in those systems upon lithium deintercalation is quite close, at around 0.15 eV. Therefore, the Ru reduction/backshift upon lithium removal in the second plateau is not necessarily the result of molecular oxygen evolution, but more of lattice oxygen redox. It is interesting to note, as we pointed out previously,32 that lattice oxygen redox results in a broadening of the eg peak towards a high photon energy. By quantifying the FWHM of the eg peak through peak fitting (Fig. S12, ESI†), we observe that there is a sharp increase in the eg peak width upon removing 1 e−/Ru after entering the high-voltage plateau, further verifying the assumption that the high-voltage plateau represents the lattice oxygen redox pointed out in previous publications.11,32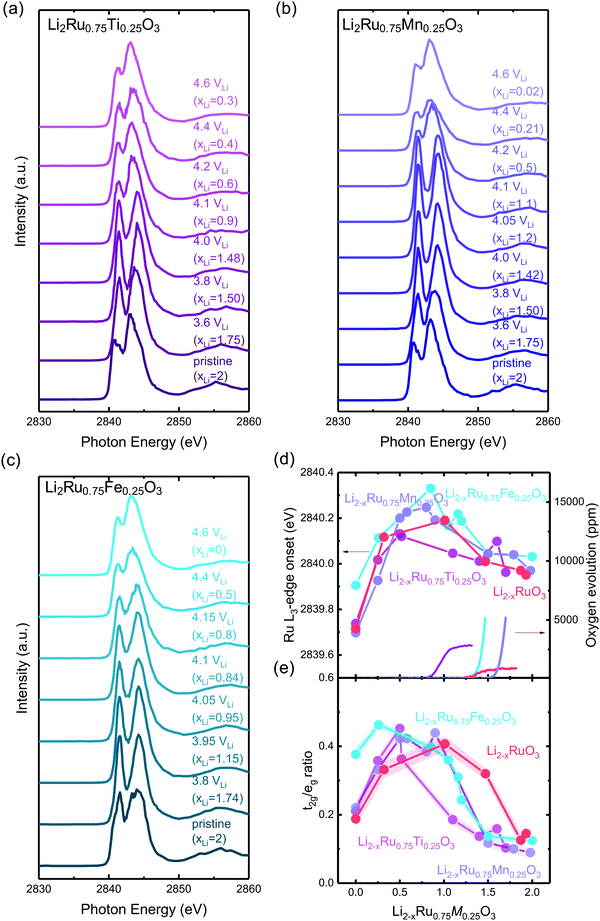 | ||
| Fig. 4 Ru L3-edge spectra of (a) Li2Ru0.75Ti0.25O3 pristine and charged pellets to 3.6, 3.8, 4.0, 4.1, 4.2, 4.4, 4.6 VLi, (b) Li2Ru0.75Mn0.25O3 pristine and charged oxide-only pellets to 3.6, 3.8, 4.0, 4.05, 4.1, 4.2, 4.4, 4.6 VLi and (c) Li2Ru0.75Fe0.25O3 pristine and charged pellets to 3.8, 3.95, 4.05, 4.1, 4.15, 4.4, 4.6 VLi, where the quantification of the Ru oxidation states using the edge onset and t2g/eg ratio is shown in (d) and (e), respectively. The t2g and eg areas are determined by fitting two Gaussian peaks with a linear background removed. Quantification of the Ru oxidation state using an alternative method with t2g and eg centroids are shown in Fig. S7 and S8 (ESI†), where we have shown similar oxidation and reduction trends to that shown in (d). Details of the Gaussian fitting are shown in Fig. S9–S11 (ESI†). The quantification of previously reported Li2RuO332 is also shown for comparison for the substituted systems in (d) and (e), where the edge onset is manually shifted by 0.7 eV for better comparison because Li2RuO3 and Li2Ru0.75M0.25O3 (M = Ti, Mn, Fe) were measured at two different beamtimes, and there is a slight shift in the beam energy. | ||
Hard X-ray XAS on the transition metal K-edge shows minimal involvement of the substituted metals in Li2Ru0.75M0.25O3 (M = Mn, Ti, Fe). XAS of Ti and Mn in the substituted systems shows a similar slight reduction upon charging in Li2Ru0.75M0.25O3 (M = Mn, Ti), whereas Fe K-edge data show a slight oxidation of Fe3+ upon Li removal in Li2Ru0.75Fe0.25O3 (Fig. S13, ESI†). As we remove Li from the oxide-only pellets of Li2Ru0.75M0.25O3 (M = Mn, Ti), we observe a slight shift towards a lower photon energy, which is captured in the quantification of the oxidation state using the edge onset in Fig. S6(c) (ESI†), indicating a slight reduction of Mn or Ti upon charging. As a result, due to the incapability of both Mn4+ and Ti4+ being further oxidized in the octahedral environment, we observed minimal changes in the oxidation state of Mn and Ti upon removing most of the Li in the lattice (Fig. S13(b) and (d), ESI†). On the other hand, in the Fe system, due to the instability of Fe4+ in the solid-state, the pristine Li2Ru0.75Fe0.25O3 shows an oxidation state of Fe3+. Upon lithium deintercalation by removing around 1.75 Li per f.u. in Li2Ru0.75Fe0.25O3, there is a clear oxidation, yet such oxidation of Fe is quite subtle, reaching an edge of 7124.3 eV at half-rise, compared with an edge of around 7128–7129 eV, which is roughly the theoretical Fe4+ edge onset by linear extrapolation of the edge energy of Fe2+ and Fe3+. As a result, even though the charged Li2Ru0.75Fe0.25O3 shows a slightly different trend in Fe oxidation compared with Mn and Ti in charged Li2Ru0.75Mn0.25O3 and Li2Ru0.75Ti0.25O3, the degree of involvement of those transition metals in redox is negligible compared to Ru in those substituted systems, as shown in Fig. 4.
Disorder in the first-shell M–O coordination from metal K-edge EXAFS of Li2−xRu0.75M0.25O3
Transition metal K-edge extended X-ray absorption fine structure spectroscopy (EXAFS) reveals a significant reduction in intensity in the first-shell coordination of Ti–O and Fe–O in Li2−xRu0.75M0.25O3 (M = Ti and Fe) with lithium de-intercalation in Fig. 5(b) and (d), respectively, in contrast to that of Ru–O in Li2−xRuO3 and Mn–O in Li2−xRu0.75Mn0.25O3 in Fig. 5(a) and (c), respectively. Fourier-transformed spectra in the R-space (Fig. 5(a)–(d)) show two major contributions, one located at a reduced distance of around 1.5 Å, representing M–O coordination, and the other located at a reduced distance of around 2.5 Å, representing M–M coordination. Similarly, Fourier-transformed Ti K-edge EXAFS of Li2−xRu0.75Ti0.25O3 (Fig. 5(b)) and Fourier-transformed Fe K-edge EXAFS of Li2−xRu0.75Fe0.25O3 (Fig. 5(d)) reveal significant decreases in the Ti–O and Fe–O coordination upon charging, respectively. On the other hand, substituting Ru with Mn in Li2−xRuO3 led to an insignificant reduction in the Mn–O coordination in the first shell from Mn K-edge EXAFS, as shown in Fig. 5(c), having a slight reduction of Mn–O coordination by ∼20% in intensity upon lithium removal in charged Li2−xRu0.75Mn0.25O3. The insignificant reduction in the Mn–O coordination in the first shell of Li2−xRu0.75Mn0.25O3 is accompanied with minimal changes observed in the Ru–O coordination in the Fourier-transformed Ru K-edge EXAFS of Li2−xRu0.75Mn0.25O3 in Fig. S19(a) (ESI†), compared with that in Li2−xRuO3 (Fig. 5(a)).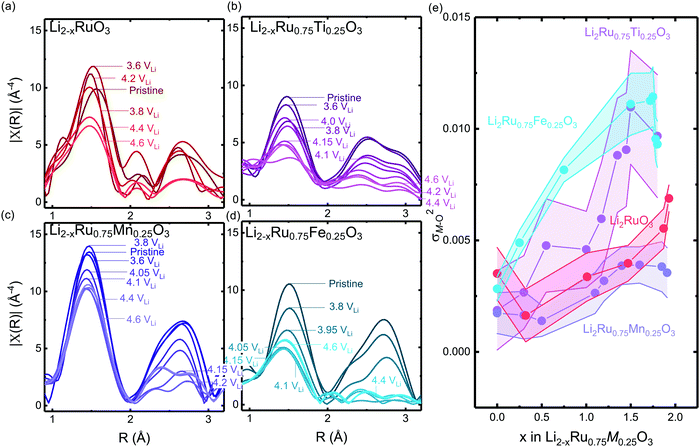 | ||
| Fig. 5 (a) Fourier-transformed Ru K-edge EXAFS spectra in the R space of pristine Li2−xRuO3 and pellets charged to 3.6 (xLi = 1.68), 3.8 (xLi = 0.99), 4.2 (xLi = 0.53), 4.4 (xLi = 0.13), 4.6 VLi (xLi = 0.07). (b) Fourier-transformed Ti K-edge EXAFS spectra in the R space of oxide-only pristine Li2−xRu0.75Ti0.25O3 and pellets charged to 3.6 (xLi = 1.7), 3.8 (xLi = 1.45), 4.0 (xLi = 1), 4.1 (xLi = 0.83), 4.15 (xLi = 0.65), 4.2 (xLi = 0.55), 4.4 (xLi = 0.5), 4.6 VLi (xLi = 0.2), where the k-space raw data are shown in Fig. S14(a) (ESI†). (c) Fourier-transformed Mn K-edge EXAFS spectra in the R space of oxide-only pristine Li2Ru0.75Mn0.25O3 and pellets charged to 3.6 (xLi = 1.7), 3.8 (xLi = 1.5), 4.05 (xLi = 0.9), 4.1 (xLi = 0.8), 4.15 (xLi = 0.6), 4.2 (xLi = 0.4), 4.4 (xLi = 0.15), 4.6 VLi (xLi = 0.09), where the k-space raw data are shown in Fig. S14(b) and the detailed fitting parameter is shown in Table S3 (ESI†). (d) Fourier-transformed Fe K-edge EXAFS spectra in the R space of pristine Li2Ru0.75Fe0.25O3 and pellets charged to 3.8 (xLi = 1.75), 3.95 (xLi = 1.25), 4.05 (xLi = 0.5), 4.1 (xLi = 0.28), 4.15 (xLi = 0.25), 4.4 (xLi = 0.22), 4.6 VLi (xLi = 0.2), where the k-space raw data are shown in Fig. S14(c) (ESI†). (e) Fitted pseudo Debye–Waller factor of Ru–O, Ti–O, Mn–O and Fe–O from the EXAFS data shown in (a)–(d), and the detailed fitting results are summarized in Fig. S15–S18 (ESI†), respectively, and in Tables S1–S4 (ESI†). Here, Li2Ru0.75Ti0.25O3 and Li2Ru0.75Fe0.25O3 show a significant reduction in the M–O peak intensity compared with Li2Ru0.75Mn0.25O3 at a high state-of-charge, which is responsible for the difference in the increase of the pseudo Debye–Waller factor. | ||
The decrease in the M–O intensity43–45 and metal–oxygen coordination in the first shell (MO6) for Ti–O (Fig. 5(b)) can be attributed to the considerable disordering in the first-shell introduced by lithium deintercalation, compared with Mn–O (Fig. 5(c)). The creation of considerable oxygen vacancies cannot be used to explain the observed large reduction in Ti–O in comparison with Mn–O coordination in the EXAFS spectra. Li2−xRu0.75Ti0.25O3 (with an oxygen release of 0.08 mol O2/moloxide) has an oxygen evolution that is very comparable to Li2−xRu0.75Mn0.25O3 (with an oxygen release of 0.12 mol O2/moloxide) based on the DEMS measurements shown in Fig. 2. If we assume that the oxygen vacancies created were distributed uniformly throughout the bulk of particles instead of being concentrated near the surface region, the similarity in the amount of oxygen evolved cannot explain the drastic difference in M–O contribution evolution upon charge. Moreover, the transition metal vacancy induced by metal dissolution as a parasitic reaction upon charging can also not be the likely reason for the difference observed in the metal K-edge EXAFS, because previous studies have shown that it is more difficult to dissolve Ti4+ in comparison with Mn4+ by substituting Ti into 0.5Li2MnO3–0.5LiNi0.5Mn0.5O2.46 Therefore, the increased reduction in the first-shell Ti–O coordination can be attributed to a greater pseudo Debye–Waller factor of M–O coordination extracted from the EXAFS spectra for Li2−xRu0.75Ti0.25O3 than Li2RuO3 and Li2−xRu0.75Mn0.25O3 (Fig. 5(a) and (c)), coming from a distorted M–O octahedron upon lithium deintercalation. On the other hand, for charged Li2−xRu0.75Fe0.25O3, which evolves a more significant amount of oxygen (∼0.16 mol per f.u.) compared with other systems studied by EXAFS, the more significant reduction in the Fe–O contribution in Fe EXAFS spectra compared with Mn and Ru based systems might be the compounded result of oxygen vacancy creations and octahedral distortion. To verify the hypothesis on the differences in tendency toward octahedral distortion across different substituted Li2−xRu0.75M0.25O3 upon lithium deintercalation, the systematic tuning of oxygen framework distortion is studied using DFT in the next section.
Tuning of the O–O distance shows evidence of two competing mechanisms of irreversible oxygen redox
Computational tuning of the oxygen–oxygen distance in Li0Ru0.75M0.25O3 (M = Ti, Mn, Ru) shows that by introducing less covalent substitutions from Ru to Ti or Mn, the barrier of forming oxygen dimers within the MO octahedron is reduced. Moreover, the observed more depressed M–O contribution in the Ti-substituted system at high states-of-charge from EXAFS comes from an easier MO octahedral distortion for Ti compared with Ru and Mn. Here, we employed the fully delithiated structures as the starting structures, where we selected an oxygen–oxygen pair, either within the oxygen octahedron or across two layers (shown schematically in Fig. 6(a) and (b) insets), where we forced that pair to have a fixed shorter distance, while allowing the other atoms in the unit cell to relax. Therefore, we are able to probe the barrier of O–O bond formation either within the MO octahedron or across the layer in the substituted systems. As we tune the oxygen–oxygen distance within the octahedron in Li2Ru0.75M0.25O3 (M = Mn, Ti, Ru), the Mn-substituted case shows a relatively big barrier of around 0.6 eV towards a reduction in bond distance to 1.3 Å. Such a dimerization barrier with Li2Ru0.75Mn0.25O3 lies roughly between the two end-point compounds Li2RuO3 (red circle) and Li2MnO3 (grey circle) in Fig. 6(a). Compared with Li2Ru0.75Mn0.25O3, Li2Ru0.75Ti0.25O3 basically shows the absence of such a barrier for octahedral distortion, which is the root cause of the increase in the Ti–O first shell disorder upon lithium deintercalation in charged Li2Ru0.75Ti0.25O3 as observed in EXAFS (Fig. 5(b) and (e)). On the other hand, imposing such a short oxygen–oxygen distance across the layer (across different octahedrons) (Fig. 6(b)) induces a less obvious metal substituent dependency, where Ti shows a slightly higher barrier towards forming shorter oxygen bonds across the layer. Therefore, we can generalize that materials with a slightly smaller degree of metal and oxygen DOS overlap near the Fermi level have a higher tendency to form an O–O dimer within the octahedron due to less-directional M–O bonding.47,48 As summarized in Fig. 6(c), the barrier of forming O–O within the M–O octahedron is highly dependent on the energetic overlap between metal and oxygen DOS center of mass distance, whereas the barrier to forming an O–O bond across different layers is weakly dependent on the transition metal substituents introduced in the system. Therefore, as we decrease the energetic overlap between the transition metal and oxygen, there is a transition from forming the O–O dimer across the layer towards forming O–O bonds within the octahedron. As a result, as we decrease the M–O energetic overlap, we are decreasing the overall energetic barrier to form shorter O–O bonds, inducing a higher tendency in forming molecular oxygen and a less reversible anionic redox. This observation explains the linear dependence of the oxygen redox reversibility on both the electronic DOS overlap as well as the oxygen phonon band center, observed in Fig. 3(a) and (b), respectively.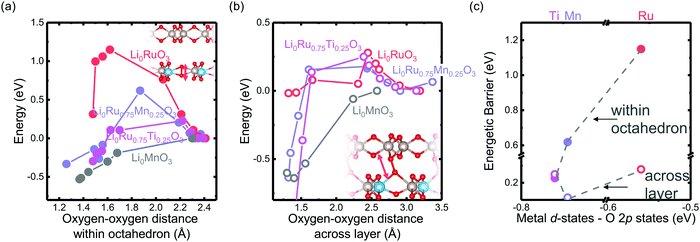 | ||
| Fig. 6 Computed energetic evolution as a function of the oxygen–oxygen distance (a) within the octahedron and (b) across the layer in Li0Ru0.75M0.25O3 (M = Mn, Ti, Ru) and Li0MnO3 from the literature,33 where the insets show schematics of the structures. The Li0MnO3 data from previous work are normalized by a factor of four due to the inclusion of four dimers created in the super cell compared with only one dimer created in this work. (c) The barrier of Li2Ru0.75M0.25O3 (M = Mn, Ti, Ru). Here we can see that, compared with the Ti-substituted case, Mn has a higher barrier to forming the oxygen dimer within the octahedron due to the rigidity of the metal–oxygen lattice, where the barrier of dimerization across the layer does not show a strong dependence of the energetic overlap between the M d states and O p states. | ||
Insights into design guidelines for novel high-energy positive electrode materials
The observations in this work again highlight the importance of maintaining the large degree of energetic overlap between the metal and oxygen DOS near the Fermi level for introducing a rigid lattice upon lithium deintercalation and a higher barrier to irreversible oxygen dimers. This requirement poses two clear strategies in designing new, Li-rich, high-energy electrode materials. The first strategy relies on using less correlated and more delocalized transition metal ions (4d and 5d transition metals) which have some degree of redox capability upon lithium deintercalation. Such transition metals include previously explored Ru4+,22–24,36 Ir4+,25,27 and Mo4+/3+,49 which show promising performance, as well as those not yet explored such as Rh4+. From what we have observed in this study, early 4d and 5d transition metals would not be good candidates as due to the absence of d electrons, since there are no accessible metal states around the Fermi level, leading to the de-coordination of oxygen redox intermediates. However, a single transition metal redox center poses a large limitation on redox center choice and cost challenges related to those feasible noble transition metals. Therefore, another strategy for the design of reversible anionic redox positive electrodes involves substituting 3d Li-rich positive electrodes with less correlated transition metals such as Ru4+, Ir4+, Mo4+/3+, and W3+ to introduce a larger degree of energetic overlap between M and O to increase the barrier to oxygen dimerization. The integration of Mo3+ and Ru4+ into the Li-rich Li1.2Ni0.2Mn0.6O2 has been previously explored experimentally and computationally,50 and was shown to have much more improved reversibility compared with pristine Li1.2Ni0.2Mn0.6O2. To systematically explore the substitution options that improve the oxygen redox reversibility beyond chemical intuition, a high-throughput computational and/or experimental approach are needed for identifying oxide compositions with a large degree of energetic overlap between the transition metal and oxygen in future studies.3. Conclusions
In our work, we examined an electronic and phononic descriptor for the anionic redox activity of the Li2Ru0.75M0.25O3 (M = Ti, Cr, Mn, Fe, Ru, Sn, Pt, Ir) system. Through DEMS measurements, coupled with electrochemistry profiles, we proposed a methodology to quantify the reversibility of anionic redox based on the ratio of oxygen release with respect to oxygen electron transfer. We demonstrated that for the substituted systems, the electronic structure is coupled with the rigidity of the oxide sublattice upon lithium deintercalation, where a larger degree of energetic overlap between the transition metal and oxygen induces a more rigid oxygen lattice upon lithium deintercalation from phonon calculations. As a result, the reversibility of anionic redox scales with the degree of overlap between the M d and O 2p states of the oxides. Employing EXAFS measurements and DFT calculations, we observed that such a trend is rooted in the more ionic substituents with a smaller energetic overlap between the M d and O 2p states being able to introduce easier distortion of M–O octahedron, thus giving a smaller barrier to forming an oxygen dimer within the octahedron, thus inducing oxygen release and irreversible oxygen redox. Moreover, the barrier to forming oxygen dimer across different layers show minimal metal dependence. As a result, as we increase the separation between metal and oxygen DOS below the Fermi level, there is a transition from the preference towards forming O–O bonds across the layer to forming O–O bonds within the octahedron. A more ionic substituent introduces a decrease in the oxygen dimerization barrier and a less reversible oxygen redox. Therefore, an optimized M d–O p DOS distance is needed for the harvesting of reversible anionic activity. Through this study, we were able to propose some new design strategies that can potentially induce more reversible anionic redox, providing guidance for future rational high-energy electrode exploration.4. Methods
Experimental methods
Composite electrodes for DEMS measurements were prepared by mixing the active material (80% mass fraction), 10% acetylene black (AB) and 10% polyvinylidene fluoride (PVDF) (Solvay 6020) dispersed in N-methyl-2-pyrrolidone (NMP) using a Fritsch Minimill 23 homogenizer. The resulting slurry was then blade-coated onto a stainless steel 304 mesh with an opening of 0.0012′′ with a wire diameter of 0.008′′ with an aluminium sheet underneath, and with a gap of 15 μ m. The electrodes were then dried and separated from the aluminium sheet underneath and punched into 15 mm diameter discs. The DEMS electrodes were pressed at 4.53 T cm−2 under a hydraulic press. Finally, the electrodes were dried completely at 120 °C under vacuum for 12 h before being transferred into an argon-filled glovebox (<0.5 ppm of H2O and O2). The active loading of the composite electrodes for the DEMS experiments was around 10 mg cm−2, which is higher than the usual loading of common composite electrodes to ensure that enough gaseous species were evolved to be detected during cycling.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 ethylene carbonate (EC)
7 ethylene carbonate (EC)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl methyl carbonate (EMC) electrolyte (BASF)). After assembly, the cells rested for 6 h prior to measurement and then were charged with different end-of-charge potentials at a rate of ∼1.6–1.9 mA g−1, depending on the specific chemistry. This rate of charge corresponds to a rate of C/100 based on the theoretical capacity calculated assuming one lithium extraction per Li2RuxM1−xO3. The cell was held at the end-of-charge potential for 5 h before disassembly inside the glovebox.
ethyl methyl carbonate (EMC) electrolyte (BASF)). After assembly, the cells rested for 6 h prior to measurement and then were charged with different end-of-charge potentials at a rate of ∼1.6–1.9 mA g−1, depending on the specific chemistry. This rate of charge corresponds to a rate of C/100 based on the theoretical capacity calculated assuming one lithium extraction per Li2RuxM1−xO3. The cell was held at the end-of-charge potential for 5 h before disassembly inside the glovebox.
Quantification of the reversibility of anionic redox
In our definition of the figure of merit, the quantification of electrons transferred from oxygen redox is obtained through the electrochemistry profile upon first charge obtained from the DEMS measurement. As shown schematically in Fig. S6(a) (ESI†) the dQ/dV is obtained from the electrochemistry profile. All the charges are integrated after around 3.9 VLi. The exception applies to Li2Ru0.75Cr0.25O3 and Li2Ru0.75Fe0.25O3, where the peaks at ca. 4.1 VLi and 4.0 VLi are not integrated due to the presence of Cr3+ and Fe3+, respectively, where the Cr3+/4+,5+ and Fe3+/4+ redox potential is around 4.0–4.1 VLi.54,55Alternatively, we have also shown that the quantification of electrons transferred from oxygen redox can be defined strictly as all the charges after the O2 gas onset upon first charge, which is also shown schematically in Fig. S6(b) (ESI†), and such a type of quantification method does not alter the trend in Fig. 3 as we observed in Fig. S5 (ESI†).
High-energy resolution fluorescence detected Ru L3-edge XAS was conducted at the Stanford Synchrotron Radiation Lightsource (SSRL) at the SLAC National Accelerator Laboratory Station 6-2b. The measurements were performed with a high-resolution tender X-ray spectrometer developed on a dispersive Johansson geometry in a 500 mm Rowland circle using a Si(111) analyzer.56 The spectrometer recorded in dispersive mode the overall Ru Lα emission line; for extracting the HERFD spectrum, the peak intensity of the Lα emission line is plotted as a function of the incident photon energy. By using the Si(111) monochromator of the SSRL beamline 6-2, an overall energy resolution of 0.6 eV was achieved enabling the sharpening of the Ru-L3 XAS features when compared with conventional X-ray absorption spectroscopy, i.e., total fluorescence yield or transmission mode XAS. The incident beam was about 400 μm × 800 μm (FWHM) and the photon flux ∼1012 s−1. The dried electrode material was mixed with sucrose to minimize any self-absorption effects across the very intense Ru L3-edge resonances, resulting in pressed pellets with an active material mass fraction concentration of 0.5%.
Transition metal Ti, Fe, Mn K-edge EXAFS was conducted at beamline 6-2b of SSRL in fluorescence mode with an active material mass fraction of around 1.5%, diluted with sucrose, using a Si(111) analyzer. The spectra are aligned using the Si(111) glitches. Ru K-edge EXAFS was conducted at beamline 20-BM-B of Advanced Photon Source (APS) in Argonne National Laboratory in transmission mode with an active material concentration of 10 wt%, where a Ru metal foil was used as the reference. All spectroscopy data were normalized and processed using the ATHENA software package.57 The EXAFS fitting was conducted using a k-space window of 3 Å−1 to 11 Å−1, and an R-space window of 1 to 3 Å to include both the first and second coordination shell of the metal center for Mn- and Fe-substituted cases. The EXAFS fitting was conducted using a k-space window of 3 Å−1 to 10 Å−1, and an R-space window of 1.1 to 3.1 Å to include both the first and second coordination shell of the metal center for Ti-substituted cases to avoid the impact of spurious interaction observed around 0.9 Å in the EXAFS spectra in R space. To have a more consistent estimation of the pseudo Debye–Waller factor, the coordination number S02 is fixed to be same as the pristine oxide for the fitting of charged oxides. The details of the fitting are shown in Tables S1–S4 (ESI†).
Computational methods
The computed M d–O 2p difference was based on the difference of center of mass of the metal d states from −10 to 0 eV versus the Fermi level and that of the oxygen p states from −10 to 0 eV versus the Fermi level. Most of the computed phonon density-of-states is taken from previous work by calculating the center of mass of the oxygen projected non-imaginary phonon density of states.33 For the substituted compounds, the phonon density-of-states is taken as the weighted sum of the two end compounds, as employed in previous work.41 We did not include Li2Ru0.75Fe0.25O3 because the phonon density of states of Li1Fe5+O3 and Li0.5Fe5.5+O3 results in a significant amount of imaginary frequency and most of the modes are not well converged. The observed imaginary frequency comes from the instability of Fe5+ and above at room temperature and 0 K, which can only be synthesized through high pressure and high temperature synthesis.63 Therefore, we did not include the phonon datapoint from LixRu0.75Fe0.25O3 (x = 1 and 0.5) due to the unstable nature of Fe5+ and phononic imaginary modes in the layered structure.
Computational tuning of the oxygen–oxygen dimer was conducted on the fully delithiated structures where the oxygen–oxygen distance of a specific oxygen–oxygen pair was either within the octahedron or across the layer. This specific oxygen pair was not allowed to relax during computation while the other atoms as well as the cell volume and cell shape are allowed to relax to full degree of freedom.
Author contributions
Conceptualization: Y. Y. and Y. S.-H. Methodology: Y. Y., P. K., D. S., R. K., C.-J. S. and Y. S.-H. Investigation: Y. Y., P. K., D. S., R. K., C.-J. S. and Y. S.-H. Writing: Y. Y. and Y. S.-H. Review & editing: Y. Y., P. K., D. S., L. G., R. K., C.-J. S., R. J., F. G., F. M. and Y. S.-H. Supervision: Y. S.-H. Funding acquisition: Y. S.-H.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work made use of the MRSEC Shared Experimental Facilities at MIT, supported by the National Science Foundation under award number DMR-1419807. Research at MIT related to this work was supported financially by BMW and MIT-Indonesia Seed Fund. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This work also used resources of the Extreme Science and Engineering Discovery Environment (XSEDE),64 which is supported by National Science Foundation grant number ACI-1548562. Use of the Stanford Synchrotron Radiation Lightsource (SSRL), SLAC National Accelerator Laboratory, was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences (contract no. DE-AC02-76SF00515). Part of the instrument used for this study was supported by U.S. Department of Energy, Office of Energy Efficiency & Renewable Energy, Solar Energy Technology Office BRIDGE Program. This research used resources of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science by Argonne National Laboratory, and was supported by the U.S.DOE under Contract No. DE-AC02-06CH11357, and the Canadian Light Source and its funding partners. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. The authors are thankful for the supply of the Pt precursors from Tanaka Precious Metal.References
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789 CrossRef CAS.
- W.-S. Yoon, K.-B. Kim, M.-G. Kim, M.-K. Lee, H.-J. Shin, J.-M. Lee, J.-S. Lee and C.-H. Yo, J. Phys. Chem. B, 2002, 106, 2526–2532 CrossRef CAS.
- M. Broussely, F. Perton, P. Biensan, J. M. Bodet, J. Labat, A. Lecerf, C. Delmas, A. Rougier and J. P. Peres, J. Power Sources, 1995, 54, 109–114 CrossRef CAS.
- C. Delmas, I. Saadoune and A. Rougier, J. Power Sources, 1993, 44, 595–602 CrossRef CAS.
- H.-J. Noh, S. Youn, C. S. Yoon and Y.-K. Sun, J. Power Sources, 2013, 233, 121–130 CrossRef CAS.
- I. Koetschau, M. N. Richard, J. R. Dahn, J. B. Soupart and J. C. Rousche, J. Electrochem. Soc., 1995, 142, 2906–2910 CrossRef CAS.
- Y. Shao-Horn, S. A. Hackney, A. R. Armstrong, P. G. Bruce, R. Gitzendanner, C. S. Johnson and M. M. Thackeray, J. Electrochem. Soc., 1999, 146, 2404–2412 CrossRef CAS.
- M. M. Thackeray, S.-H. Kang, C. S. Johnson, J. T. Vaughey and R. Benedek, and S. Hackney, J. Mater. Chem., 2007, 17, 3112–3125 RSC.
- M. M. Thackeray, C. S. Johnson, J. T. Vaughey, N. Li and S. A. Hackney, J. Mater. Chem., 2005, 15, 2257–2267 RSC.
- C. S. Johnson, N. Li, C. Lefief, J. T. Vaughey and M. M. Thackeray, Chem. Mater., 2008, 20, 6095–6106 CrossRef CAS.
- G. Assat, A. Iadecola, C. Delacourt, R. Dedryvère and J.-M. Tarascon, Chem. Mater., 2017, 29, 9714–9724 CrossRef CAS.
- W. E. Gent, K. Lim, Y. Liang, Q. Li, T. Barnes, S.-J. Ahn, K. H. Stone, M. McIntire, J. Hong and J. H. Song, Nat. Commun., 2017, 8, 2091 CrossRef PubMed.
- C. S. Johnson, N. Li, C. Lefief and M. M. Thackeray, Electrochem. Commun., 2007, 9, 787–795 CrossRef CAS.
- C. S. Johnson, J. S. Kim, C. Lefief, N. Li, J. T. Vaughey and M. M. Thackeray, Electrochem. Commun., 2004, 6, 1085–1091 CrossRef CAS.
- K. Dai, J. Wu, Z. Zhuo, Q. Li, S. Sallis, J. Mao, G. Ai, C. Sun, Z. Li, W. E. Gent, W. C. Chueh, Y. Chuang, R. Zeng, Z. Shen, F. Pan, S. Yan, L. F. J. Piper, Z. Hussain, G. Liu and W. Yang, Joule, 2019, 3, 518–541 CrossRef CAS.
- K. Luo, M. R. Roberts, R. Hao, N. Guerrini, D. M. Pickup, Y.-S. Liu, K. Edström, J. Guo, A. V. Chadwick and L. C. Duda, Nat. Chem., 2016, 8, 684 CrossRef CAS PubMed.
- E. Hu, X. Yu, R. Lin, X. Bi, J. Lu, S. Bak, K.-W. Nam, H. L. Xin, C. Jaye and D. A. Fischer, Nat. Energy, 2018, 3, 690 CrossRef CAS.
- G. Assat and J.-M. Tarascon, Nat. Energy, 2018, 1 Search PubMed.
- A. Grimaud, W. T. Hong, Y. Shao-Horn and J.-M. Tarascon, Nat. Mater., 2016, 15, 121 CrossRef CAS PubMed.
- M. B. Yahia, J. Vergnet, M. Saubanère and M.-L. Doublet, Nat. Mater., 2019, 18, 496–502 CrossRef PubMed.
- C. Zhan, Z. Yao, J. Lu, L. Ma, V. A. Maroni, L. Li, E. Lee, E. E. Alp, T. Wu and J. Wen, Nat. Energy, 2017, 2, 963 CrossRef CAS.
- M. Sathiya, A. M. Abakumov, D. Foix, G. Rousse, K. Ramesha, M. Saubanère, M. L. Doublet, H. Vezin, C. P. Laisa and A. S. Prakash, Nat. Mater., 2015, 14, 230 CrossRef CAS PubMed.
- M. Sathiya, J.-B. Leriche, E. Salager, D. Gourier, J.-M. Tarascon and H. Vezin, Nat. Commun., 2015, 6, 6276 CrossRef CAS PubMed.
- M. Sathiya, K. Ramesha, G. Rousse, D. Foix, D. Gonbeau, A. S. Prakash, M. L. Doublet, K. Hemalatha and J.-M. Tarascon, Chem. Mater., 2013, 25, 1121–1131 CrossRef CAS.
- E. McCalla, A. M. Abakumov, M. Saubanère, D. Foix, E. J. Berg, G. Rousse, M.-L. Doublet, D. Gonbeau, P. Novák and G. Van Tendeloo, Science, 2015, 350, 1516–1521 CrossRef CAS PubMed.
- M. Sathiya, G. Rousse, K. Ramesha, C. P. Laisa, H. Vezin, M. T. Sougrati, M.-L. Doublet, D. Foix, D. Gonbeau and W. Walker, Nat. Mater., 2013, 12, 827–835 CrossRef CAS PubMed.
- J. Hong, W. E. Gent, P. Xiao, K. Lim, D.-H. Seo, J. Wu, P. M. Csernica, C. J. Takacs, D. Nordlund and C.-J. Sun, Nat. Mater., 2019, 1 Search PubMed.
- M. Saubanère, E. McCalla, J.-M. Tarascon and M.-L. Doublet, Energy Environ. Sci., 2016, 9, 984–991 RSC.
- N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi and A. Nakao, Nat. Commun., 2016, 7, 13814 CrossRef CAS PubMed.
- N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki and T. Inamasu, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7650–7655 CrossRef CAS PubMed.
- Y. Xie, M. Saubanere and M.-L. Doublet, Energy Environ. Sci., 2017, 10, 266–274 RSC.
- Y. Yu, P. Karayaylali, S. H. Nowak, L. Giordano, M. Gauthier, W. Hong, R. Kou, Q. Li, J. Vinson and T. Kroll, Chem. Mater., 2019, 31, 7864–7876 CrossRef CAS PubMed.
- N. Charles, Y. Yu, L. Giordano, R. Jung, F. Maglia and Y. Shao-Horn, Chem. Mater., 2020, 32, 5502–5514 CrossRef CAS.
- J. Wandt, A. T. Freiberg, A. Ogrodnik and H. A. Gasteiger, Mater. Today, 2018, 21, 825–833 CrossRef CAS.
- R. Jung, M. Metzger, F. Maglia, C. Stinner and H. A. Gasteiger, J. Electrochem. Soc., 2017, 164, A1361–A1377 CrossRef CAS.
- J. Xu, M. Sun, R. Qiao, S. E. Renfrew, L. Ma, T. Wu, S. Hwang, D. Nordlund, D. Su and K. Amine, Nat. Commun., 2018, 9, 947 CrossRef PubMed.
- F. Wu, G.-T. Kim, T. Diemant, M. Kuenzel, A. R. Schür, X. Gao, B. Qin, D. Alwast, Z. Jusys and R. J. Behm, et al. , Adv. Energy Mater., 2020, 10, 2001830 CrossRef CAS.
- J. Lee, D. A. Kitchaev, D.-H. Kwon, C.-W. Lee, J. K. Papp, Y.-S. Liu, Z. Lun, R. J. Clément, T. Shi and B. D. McCloskey, et al. , Nature, 2018, 556, 185–190 CrossRef CAS PubMed.
- B. Ammundsen and J. Paulsen, Adv. Mater., 2001, 13, 943–956 CrossRef CAS.
- Y. Lyu, N. Zhao, E. Hu, R. Xiao, X. Yu, L. Gu, X.-Q. Yang and H. Li, Chem. Mater., 2015, 27, 5238–5252 CrossRef CAS.
- S. Muy, J. C. Bachman, L. Giordano, H.-H. Chang, D. L. Abernathy, D. Bansal, O. Delaire, S. Hori, R. Kanno and F. Maglia, et al. , Energy Environ. Sci., 2018, 11, 850–859 RSC.
- Z. Hu, H. Von Lips, M. Golden, J. Fink, G. Kaindl, F. De Groot, S. Ebbinghaus and A. Reller, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 5262 CrossRef CAS.
- M. Risch, A. Grimaud, K. J. May, K. A. Stoerzinger, T. J. Chen, A. N. Mansour and Y. Shao-Horn, J. Phys. Chem. C, 2013, 117, 8628–8635 CrossRef CAS.
- M. Risch, K. A. Stoerzinger, B. Han, T. Z. Regier, D. Peak, S. Y. Sayed, C. Wei, Z. Xu and Y. Shao-Horn, J. Phys. Chem. C, 2017, 121, 17682–17692 CrossRef CAS.
- S. Calvin, XAFS for Everyone, CRC Press, 2013, pp. 345–362 Search PubMed.
- S. Yamamoto, H. Noguchi and W. Zhao, J. Power Sources, 2015, 278, 76–86 CrossRef CAS.
- A. Urban, A. Abdellahi, S. Dacek, N. Artrith and G. Ceder, Phys. Rev. Lett., 2017, 119, 176402 CrossRef PubMed.
- D.-H. Seo, J. Lee, A. Urban, R. Malik, S. Kang and G. Ceder, Nat. Chem., 2016, 8, 692–697 CrossRef CAS PubMed.
- S. Hoshino, A. M. Glushenkov, S. Ichikawa, T. Ozaki, T. Inamasu and N. Yabuuchi, ACS Energy Lett., 2017, 2, 733–738 CrossRef CAS.
- T. A. Wynn, C. Fang, M. Zhang, H. Liu, D. M. Davies, X. Wang, D. Lau, J. Z. Lee, B.-Y. Huang and K.-Z. Fung, et al. , J. Mater. Chem. A, 2018, 6, 24651–24659 RSC.
- A. James and J. B. Goodenough, J. Solid State Chem., 1988, 74, 287–294 CrossRef CAS.
- B. D. McCloskey, D. S. Bethune, R. M. Shelby, G. Girishkumar and A. C. Luntz, J. Phys. Chem. Lett., 2011, 2, 1161–1166 CrossRef CAS PubMed.
- J. R. Harding, PhD thesis, Massachusetts Institute of Technology, 2015.
- S. Komaba, C. Takei, T. Nakayama, A. Ogata and N. Yabuuchi, Electrochem. Commun., 2010, 12, 355–358 CrossRef CAS.
- Y. Sakurai, H. Arai, S. Okada and J. Yamaki, J. Power Sources, 1997, 68, 711–715 CrossRef CAS.
- S. Nowak, R. Armenta, C. Schwartz, A. Gallo, B. Abraham, A. Garcia-Esparza, E. Biasin, A. Prado, A. Maciel and D. Zhang, et al. , Rev. Sci. Instrum., 2020, 91, 033101 CrossRef CAS PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- P. Xiong, H. Seki, H. Guo, Y. Hosaka, T. Saito, M. Mizumaki and Y. Shimakawa, Inorg. Chem., 2016, 55, 6218–6222 CrossRef CAS PubMed.
- J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazlewood, S. Lathrop, D. Lifka and G. D. Peterson, Comput. Sci. Eng., 2014, 16, 62–74 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee03765f |
| ‡ Current address: Faurecia Clean Mobility, Biberbachstraße 9, 86154, Augsburg, Germany. |
| This journal is © The Royal Society of Chemistry 2021 |