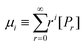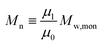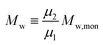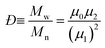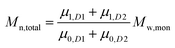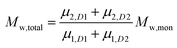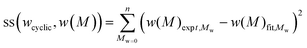DOI:
10.1039/D0PY01277G
(Paper)
Polym. Chem., 2020,
11, 7354-7361
Analysis of cyclic polymer purity by size exclusion chromatography: a model system†
Received
6th September 2020
, Accepted 27th October 2020
First published on 27th October 2020
Abstract
Because cyclic polymers have intriguing physical properties, considerable synthetic strategies have been developed to create a wide variety of cyclic architectures. One of the most utilized cyclization procedures is via ring-closure of a difunctional linear polymer using the copper catalyzed azide–alkyne cycloaddition (CuAAC) ‘click’ reaction. However, quantifying the percentage of mono-cyclic species (i.e. formed directly from the starting α,ω-linear polymer) still remains a challenge even with access to a variety of characterization techniques, including NMR, MALDI-ToF, size exclusion chromatography (SEC) and liquid chromatography at the critical condition (LCCC). Here, we demonstrated that SEC in combination with the log-normal distribution (LND) method and minimization of the sum of squares of the weighted residuals to fit the distribution provided an analytical method for the accurate analysis of cyclic purity. The key to the SEC analysis method relies on quantification of the hydrodynamic shift from linear to mono-cyclic. The technique developed in this work has wide applicability for the characterization of complex polymer architectures and compositions (and can be easily applied to sequence controlled polymers).
Introduction
The unique physical properties of cyclic polymers in bulk and solution make simple and complex cyclic topologies of significant interest across many disciplines of science.1,2 A lack of chain ends and a more compact configuration significantly improves the stability of biological cyclic macromolecules, including peptides, proteins and DNA, against enzymatic degradation and denaturation.3 Many highly potent toxins in nature have cyclic topological constituents (e.g., venom from the black mamba snake has an LD50 subcutaneous of 0.32 mg kg−1, which can kill humans in less than 30 min4). It is, therefore, not surprising that therapeutic companies synthesize cyclic peptides and proteins for better pharmacological outcomes. For example, the copper catalyzed azide–alkyne cycloaddition (CuAAC) reaction to cyclize hairpin decoy oligonucleotides produced greater enzymatic stability and enhanced cell uptake.5 When applying cyclic polymers to non-biological applications, Kapnistos et al.6 showed in a seminal paper that the viscoelastic properties in the melt of cyclic polystyrene in its ‘pure’ form (i.e., “as pure as currently possible”) showed no plateau modulus. It was postulated that the complex dynamics of the double-folded cyclic loops could be described by the lattice-animal model. More importantly, doping the ‘pure’ cyclic with even a small amount of linear impurity (volume fraction of 0.0007) significantly influenced the viscoelastic properties to have similar properties to that of the linear polymer. Liquid chromatography at the critical condition (LCCC)7–12 was used to purify their cyclic polymers of high molecular weights (i.e. 161![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and 198
000 g mol−1 and 198![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1), and showed excellent separation and resolution between linear and cyclic polystyrene at high molecular weights.
000 g mol−1), and showed excellent separation and resolution between linear and cyclic polystyrene at high molecular weights.
In recent years, the CuAAC coupling reaction has produced low molecular weight cyclic polymers via the ring closure method.1,13 Low molecular weight α,ω-functionalized linear polymers are more amenable to cyclization as quantitatively described by the Jacobson-Stockmayer equation,14,15 in which the probability of cyclization decreases with the power law dependence of −3/2 with increasing chain length. Our group has further elaborated on this method, creating a wide variety of complex topologies made from cyclic polymer building blocks,15–20 and their physical properties examined both in solution and bulk.21–23 With the ever increasing use of the CuAAC ‘click’ reaction to produce a variety of cyclic polymers via the ring closure method, purity of the resultant cyclic becomes critically important. The ring closure method, depending upon the reaction conditions, will produce the desired mono-cyclic species (consisting of only one triazol ring in the cyclic) and the additional undesired starting linear, linear and cyclic multiblocks (i.e. multiple triazols in the cyclic) polymer species.15,24 The main methods to characterize these species are size exclusion chromatography (SEC), MALDI-ToF, NMR, and in a few cases LCCC. Each characterization tool has its limitations.25–27 The LCCC method requires non-trivial optimization of the conditions, and at molecular weights of less than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 found not to be satisfactory for the quantitation of cyclic polystyrene based on the critical adsorption point (CAP) of linear precursors.12,28 When using the CAP for cyclic polymer, however, good resolution and cyclic purity were found.28 It was noted that linear species with higher molecular weights after the CuAAC reaction interfere with the LCCC analysis regardless of which CAP method was used as these lie between the starting linear and mono-cyclic polymer peaks, and thus need to be minimized.
000 g mol−1 found not to be satisfactory for the quantitation of cyclic polystyrene based on the critical adsorption point (CAP) of linear precursors.12,28 When using the CAP for cyclic polymer, however, good resolution and cyclic purity were found.28 It was noted that linear species with higher molecular weights after the CuAAC reaction interfere with the LCCC analysis regardless of which CAP method was used as these lie between the starting linear and mono-cyclic polymer peaks, and thus need to be minimized.
The universally used analysis technique by researchers for the characterization of cyclic polymers is SEC due to the clear and observable shift in the molecular weight distribution (MWD) from linear to cyclic when using only the refractive index detector. SEC is also readily available in most if not all polymer laboratories and is quite straightforward to derive molecular weight distribution data. The disadvantage of SEC for quantifying cyclic polymer is the significant overlap in the SEC chromatograms with linear species, and hence the difficulty in determining cyclic purity. One advantage of SEC is that all higher molecular weight linear and cyclic multiblocks do not interfere with the mono-cyclic distribution. In our own work, we quantified the amounts of mono-cyclic to other species by fitting (or deconvolution of) the MWD from SEC by analysis using the log-normal distribution (LND) model.29 This procedure allowed quantification of the weight fractions of all (or most) species in the polymer MWD after ring closure. We found that the peak molecular weight (Mp) of the cyclic was 0.76 times less than that of the Mp of the linear polymer using refractive index and a polystyrene calibration curve.19 The fitting procedure used visual inspection of the fit to the experimental MWD by changing the weight fraction of each possible species. Although visualization gave satisfactory results, removing this visual subjectivity would provide greater accuracy. To accomplish this, we use here a simple method based on minimizing the sum of squares of the weighted residuals to determine the relative weight fractions of polymer species. Cyclization of an α,ω-functionalized linear polystyrene (l-PSTY) with an alkyne and azide end-groups, using the Cu-catalyzed azide/alkyne cycloaddition (CuAAC) reaction, produced a mono-cyclic polystyrene (c-PSTY) as shown in Scheme 1.15 The sensitivity and accuracy of SEC/LND method was determined by doping the cyclic non-purified polymer after the ‘click’ reaction with different amounts of linear starting polymer (l-PSTY). The work presented here validated the accuracy of the SEC/LND method for low molecular weight cyclic polymers in the absence of other direct characterization techniques, and suggests the applicability of this technique to characterization of precision-made complex polymer architectures30,31 and sequence controlled polymers.32
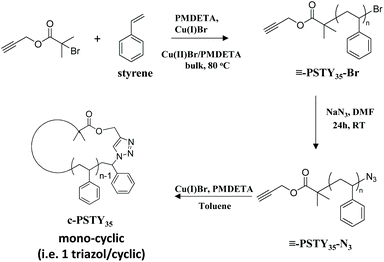 |
| | Scheme 1 Synthetic route for the cyclization of polystyrene (c-PSTY). | |
Experimental
Materials
The following reagents were used as received: alumina, activated basic (Aldrich: Brockmann I, standard grade, ∼150 mesh, 58 Å), magnesium sulfate, anhydrous (MgSO4: Scharlau, extra pure), copper(II)bromide (Aldrich, 99%), silica gel 60 (230–400 mesh ATM (SDS)), sodium hydrogen carbonate (Merck, AR grade), triethylamine (TEA: Fluka, 98%), 2-bromo-2-methylpropionyl bromide (Aldrich, 98%), propargyl alcohol (Aldrich, 99%), PMDETA (Aldrich, 99%), sodium azide (NaN3: Aldrich, ≥99.5%), TLC plates (silica gel 60 F254). Styrene (Aldrich, >99%) was passed through a basic alumina column to remove inhibitor, and then used in the polymerizations.
Nuclear magnetic resonance (NMR)
All NMR spectra were recorded on a Bruker DRX 400 MHz spectrometer using an external lock (CDCl3) and referenced to the residual nondeuterated solvent (CHCl3).
Size exclusion chromatography (SEC)
All polymer samples were dried prior to analysis in a vacuum oven at 50 °C for 24 h. The dried polymer was dissolved in tetrahydrofuran (THF) to a concentration of ∼20 mg mL−1 and then filtered through a 0.45 μm PTFE syringe filter. Analysis of the molecular weight distributions of the polymers was accomplished using a Waters 2695 separations module, fitted with a Waters 410 refractive index detector maintained at 35 °C, a Waters 996 photodiode array detector, and two Ultrastyragel linear columns (7.8 × 300 mm) arranged in series. These columns were maintained at 40 °C for all analyses and are capable of separating polymers in the molecular weight range of 500–4 million g mol−1 with high resolution. All samples were eluted at a flow rate of 1.0 mL min−1. Calibration was performed using narrow molecular weight PSTY standards (Đ ≤ 1.1) ranging from 500 to 2 million g mol−1. Data acquisition was performed using Empower software, and molecular weights were calculated relative to polystyrene standards.
Attenuated total reflectance-Fourier transform spectroscopy (ATR-FTIR)
ATR-FTIR spectra were obtained using a horizontal, single bounce, diamond ATR accessory on a Nicolet Nexus 870 FT-IR. Spectra were recorded between 4000 and 500 cm−1 for 128 scans. Solids were pressed directly onto the diamond internal reflection element of the ATR without further sample preparation.
Synthesis of CuBr2/PMDETA complex
Copper(II)bromide (CuBr2, 4.1 g, 1.84 × 10−2 mol) was stirred in MeOH (200 mL) until complete dissolution was achieved. PMDETA (3.2 g, 1.85 × 10−2) was added dropwise to this solution, and then stirred for an additional 60 min at room temperature. The reaction mixture was concentrated to ∼30 mL, and 20 mL of diethyl ether was added to the solution at which point the complex started to precipitate. The precipitated complex was collected by vacuum filtration, washed with diethyl ether and dried in a vacuum for 24 h at 25 °C.
Synthesis of propargyl 2-bromoisobutyrate (initiator)
2-Bromo-2-methylpropionyl bromide (6.61 mL, 53.48 mmol) dissolved in DCM (50 mL) at room temperature was added dropwise to a stirred solution of propargyl alcohol (2.08 mL, 35.67 mmol) and TEA (8 mL) in DCM (100 mL) at 0 °C. This reaction mixture was stirred at room temperature overnight. The resulting solution was washed with saturated aqueous NaHCO3 and brine, dried over MgSO4, filtered, and concentrated by rotary-evaporation. The resulting material was purified by a silica chromatography with petroleum spirit/ethyl acetate (10/1, v/v) as the eluent to obtain propargyl 2-bromoisobutyrate as a clear, colorless oil (yield = 75.28%, 5.13 g, 28.86 mmol). 1H NMR (CDCl3, 298 K, 400 MHz): δ 4.76 (d, 2H, J = 2.48 Hz, CH2O), 2.50 (t, 1H, J = 2.40 Hz, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH), and 1.95 (s, 6H, (CH3)2C). 13C NMR (CDCl3, 298 K, 400 MHz): 170.9, 76.9, 75.4, 54.9, 53.4, 30.6.
CH), and 1.95 (s, 6H, (CH3)2C). 13C NMR (CDCl3, 298 K, 400 MHz): 170.9, 76.9, 75.4, 54.9, 53.4, 30.6.
Synthesis of ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) -PSTY35-Br
-PSTY35-Br
The CuBr2/PMDETA complex (77.05 mg, 0.19 mmol), styrene (9.13 g, 87.71 mmol), PMDETA (0.203 mL, 0.97 mmol), and initiator (199.92 mg, 0.97 mmol) were added to a 50 mL Schlenk flask equipped with a magnetic stirrer, and then purged with argon for 30 min to remove oxygen. Cu(I)Br (138.64 mg, 0.97 mmol) was added to the polymerization mixture above under an argon blanket, degassed for a further 5 min, and placed into a temperature-controlled oil bath at 80 °C. A sample was taken at approximately 4 h to determine conversion; if conversion was close to 50%, the polymerization mixture quenched in an ice bath and diluted with CHCl3 (at ∼3 fold to the reaction mixture volume). The reaction could be left longer, if required, to reach ∼50% conversion. To the polymer solution, neutral Al2O3 (∼1.5 g) was added to complex with copper salts under Argon, and the mixture passed through an activated neutral alumina column. The resultant solution was concentrated by rotary-evaporation, the polymer recovered by precipitation into a large volume of MeOH (∼20-fold excess to polymer solution), and vacuum filtration. The polymer without drying was used directly in the next azidation step. A fraction of this polymer (∼0.2 g) was dried in a vacuum at 25 °C for 10 h to obtain a white powder for NMR and SEC characterization (Mn = 3670 and Đ = 1.11 based on a PSTY calibration curve).
Synthesis of ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) -PSTY35-N3
-PSTY35-N3
The polymer (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e002.gif) -PSTY35-Br), with a mass based on conversion, was dissolved in DMF (40 mL) and NaN3 (1.10 g, 19.6 mmol, ∼20 equiv. to initiator) under Argon at 25 °C for 24 h. The reaction solution was concentrated by an airflow to approximately a third of its original volume, precipitated into MeOH (20-fold excess to polymer solution), recovered by vacuum filtration, and washed with H2O and MeOH. The azide polymer was dried in vacuo at 25 °C for 24 h to obtain a white powder (approximately 4 g), which was characterized by NMR and SEC (Mn = 3690 and Đ = 1.10 based on a PSTY calibration curve).
-PSTY35-Br), with a mass based on conversion, was dissolved in DMF (40 mL) and NaN3 (1.10 g, 19.6 mmol, ∼20 equiv. to initiator) under Argon at 25 °C for 24 h. The reaction solution was concentrated by an airflow to approximately a third of its original volume, precipitated into MeOH (20-fold excess to polymer solution), recovered by vacuum filtration, and washed with H2O and MeOH. The azide polymer was dried in vacuo at 25 °C for 24 h to obtain a white powder (approximately 4 g), which was characterized by NMR and SEC (Mn = 3690 and Đ = 1.10 based on a PSTY calibration curve).
Synthesis of c-PSTY35
A degassed (30 min purging) solution of PMDETA (0.846 mL, 4.05 mmol) in 15 mL of dry toluene was added via a double tip needle to a dry Schlenk flask under argon containing CuBr (582.30 mg, 4.06 mmol) over a 5 min period. Formation of the CuBr/PMDETA complex was observed in the formation of a clear solution. To this solution, we added a solution of linear ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) -PSTY35-N3 (0.30 g, 0.08 mmol) in 15 mL of dry toluene via a syringe pump at a rate of 0.2 mL min−1. After complete addition of the polymer solution (i.e. 70 min), the reaction mixture was stirred for a further 3 h. Toluene was evaporated from the solution using an airflow, the remaining polymer was dissolved in DCM, and passed through an activated basic alumina column. The polymer was recovered by precipitation into MeOH (20-fold excess to polymer solution) and then filtered with the aid of a vacuum. The polymer was dried under vacuum at 25 °C for 24 h, resulting in the crude cyclic polymer (∼0.27 g) as white powder (Mn = 2950, Đ = 1.26 based on PSTY calibration curve).
-PSTY35-N3 (0.30 g, 0.08 mmol) in 15 mL of dry toluene via a syringe pump at a rate of 0.2 mL min−1. After complete addition of the polymer solution (i.e. 70 min), the reaction mixture was stirred for a further 3 h. Toluene was evaporated from the solution using an airflow, the remaining polymer was dissolved in DCM, and passed through an activated basic alumina column. The polymer was recovered by precipitation into MeOH (20-fold excess to polymer solution) and then filtered with the aid of a vacuum. The polymer was dried under vacuum at 25 °C for 24 h, resulting in the crude cyclic polymer (∼0.27 g) as white powder (Mn = 2950, Đ = 1.26 based on PSTY calibration curve).
Results and discussion
An in-depth analysis of the SEC chromatograms can be used to determine the purity of the cyclic polymer; a methodology used by our group in a quantitative manner to provide evidence for cyclic formation. Intuitively, a decrease in the apparent Mw (or decrease in hydrodynamic volume) may suggest high cyclic purity, but the absolute change (or Mp,cyclic/Mp,linear) from pure linear to pure cyclic is the key parameter to quantify the amount of cyclic after ring closure. This value can be determined from the change in the peak molecular weight Mp when using the weight distribution (i.e. w(M)), and was found that after CuAAC cyclization and purification by preparative SEC was Mp,cyclic = 0.76 Mp,linear.19 Here, the CuAAC cyclization method to produce c-PSTY showed a clear shift in hydrodynamic volume in the SEC traces using a refractive index detector and a linear polystyrene calibration curve (Fig. 1). The resultant cyclic product was not further purified. First, l-PSTY (red solid line) was analyzed by the LND method (dotted curve), and the best fit with a Gaussian distribution was using an Mn of 3674 and dispersity index (Đ) of 1.068. The purity of difunctional l-PSTY that would lead exclusively to mono-cyclic c-PSTY was 93.5%, with the other 6.5% consisting of high molecular cyclic or linear polymers. Using the value of 0.76 for the shift in molecular weight, the fit of the cyclic product with a Gaussian distribution was excellent (Mn = 2799, Đ = 1.068) with a purity of 94%, no linear starting material and only 6% higher molecular weight polymer species. This data suggests that our cyclization procedure was near quantitative.
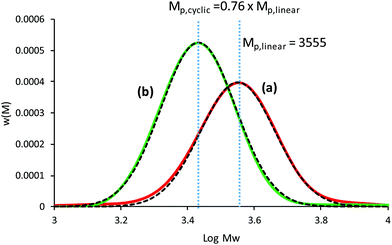 |
| | Fig. 1 SEC chromatograms of the cyclization of linear PSTY35. (A) before, and (B) after CuAAC coupling reaction. Dashed lines represent the fit using the LND method using for linear Mn = 3674 and Đ = 1.068. The cyclic polymer was fit using Mp,cyclic = 0.76 Mp,linear (i.e. Mn = 2799, Đ = 1.068). | |
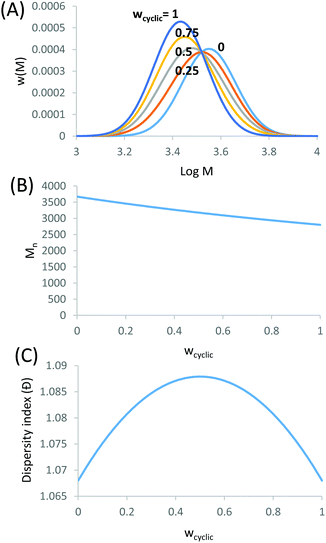
We demonstrate that the SEC/LND method29,33 is quite powerful to determine the weight fraction of linear in the cyclic product. A theoretical MWD simulated using the LND method and an Mp shift of 0.76 for a variety of linear and cyclic mixtures was shown in Fig. 2A. No matter the weight fraction of c-PSTY (wcyclic; from 0.25, 0.5 and 0.75), we observed no separation between the linear and cyclic MWDs; that is, all distributions were monomodal. To determine the Mn and Đ of these mixtures we used the method of moments. The generalized equation for the different moments is as follows:
| | 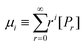 | (1) |
where
μ is the moment,
i is the moment order (
i.e. zeroth, first order, second order…),
r is the chainlength of the polymer, and
Pr is the concentration of polymer chains at chainlength
r. It can be seen that the zeroth moment (
i = 0) represents the concentration of polymer chains of the whole distribution, and the first moment (
i = 0) represents the concentration of monomer units within the polymer. Calculation of the first three moment orders allows the number-average (
Mn) and weight average (
Mw) of the MWD as shown below.
| | 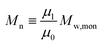 | (2) |
| | 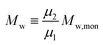 | (3) |
| | 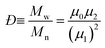 | (4) |
 |
| | Fig. 2 Theoretical mixture of linear and cyclic distributions. (A) SEC distributions using the Mn and Đ for linear and cyclic from Fig. 1. (B) Mn for the mixture of linear and cyclic determined from the method-of-moments. (C) Đ for the mixture of linear and cyclic determined from the method-of-moments. Where wcyclic is the weight fraction of cyclic to linear. | |
To add two different MWDs, we can use the above equations to determine the moment order of each distribution since the Mn and Mw of each distribution and its concentration within the total MWD (i.e. both distributions added together) are known:
| | 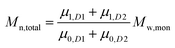 | (5) |
| | 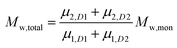 | (6) |
where
D1 and
D2 represents distributions 1 and 2.
The addition of the linear (Mn = 3674, Đ = 1.068) and cyclic (Mn = 2799, Đ = 1.068) MWDs using the method of moments at varying ratios of linear to cyclic showed a linear decrease in Mn as the weight fraction of cyclic increased (Fig. 2B). In a real MWD system, which usually contains high molecular weight species, such an analysis would lead to large errors. A more subtle method to discriminate between the two MWDs may be observed from a change in the dispersity index. As observed in Fig. 2C, Đ increased to a maximum at weight fraction of 0.5, and then decreased to a value of Đ of the pure cyclic polymer. Thus, although the MWDs from Fig. 2A were all monomodal, the subtle change in both the Mn and Đ of these mixtures provided some insight into determining the ratio of linear to cyclic. This has been long neglected in previous work, relying only on an observable shift in elution volume (or time) to justify cyclic formation.34–38 As shown above, much of the cyclic polymer synthesized in the literature may possibly include large amounts of starting linear or other polymer species. This finding may also apply to characterization of other complex topologically and compositionally different polymers.
In testing the accuracy of the SEC/LND method, we used the linear and cyclic described above as a model system. The weight fractions of cyclic was experimentally determined from the addition of stock solutions of linear and cyclic polymers (see Table 1). Care was taken in pipetting in the various ratios of solutions, but it should be noted that errors can arise due to instrumental error from the balance, pipette and even evaporation of THF from the stock solutions. A simple method to determine the true weight fraction of cyclic was to add the MWDs of the c-PSTY and l-PSTY and match this to the experimental MWD at a specific weight fraction of each polymer species. To find the optimal weight fraction, we minimized the residual sum of squares (ss)39 between the fit and experimental MWDs using a computer program (see ESI for the computer code†). The sum of the data points of the ss was determined as follows:
| | 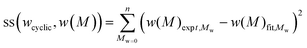 | (7) |
where
wcyclic is the weight fraction of cyclic (and
wlinear = 1 −
wcyclic),
w(
M) is the intensity of the weight-average MWD at
M. The computer code used very small step sizes of 0.001 for
wcyclic from 0 to 1. To account for any base line drift in the SEC, we also included a scaling factor to provide the best fit especially at the peak maximum.
Table 1 Stock solutions used to prepare cyclic and linear polymer at targeted ratios and the fits to experimental data and the SEC/LND model
| Polymer |
Linear |
Cyclic |
Cyclic (wt%) |
| |
Stock solution (mg mL−1) |
V
THF (μL) |
Masslinear (mg) |
Stock solution (mg mL−1) |
V
THF (μL) |
Masscyclic (mg) |
Target (%) |
Expt.a (%) |
Expt.b(accounting for pure cyclic) (%) |
LND fitc (%) |
|
The experimental was determined by adding the cyclic and linear distributions and using the ss simulation.
The experimental distribution accounting for the amount of pure cyclic.
LND fit using the ss.
|
| PSTY35-A |
4.378 |
200 |
0.9461 |
9.4612 |
100 |
0.9461 |
49.72 |
49.40 |
49.53 |
51.67 |
| PSTY35-B |
80 |
0.3827 |
160 |
1.5138 |
79.82 |
77.87 |
77.96 |
80.93 |
| PSTY35-C |
40 |
0.1913 |
180 |
1.7030 |
89.90 |
91.34 |
91.38 |
94.86 |
| PSTY35-D |
1.0257 |
100 |
0.1026 |
190 |
1.7976 |
94.60 |
95.56 |
95.58 |
99.20 |
| PSTY35-E |
80 |
0.0821 |
192 |
1.8166 |
95.68 |
98.58 |
98.59 |
100.00 |
| PSTY35-F |
60 |
0.0615 |
194 |
1.8355 |
96.76 |
99.56 |
99.56 |
99.14 |
| PSTY35-G |
40 |
0.0410 |
196 |
1.8544 |
97.84 |
99.95 |
99.95 |
98.42 |
| PSTY35-H |
0.0939 |
200 |
0.0188 |
198 |
1.8733 |
99.01 |
96.41 |
96.43 |
97.63 |
| PSTY35-I |
100 |
0.0094 |
199 |
1.8828 |
99.50 |
100.00 |
100.00 |
100.00 |
| PSTY35-J |
50 |
0.0047 |
199.5 |
1.8875 |
99.75 |
98.41 |
98.42 |
99.63 |
The simulated fit using the cyclic weight fraction determined from the residual sum of squares matched to all the experimental SEC chromatograms (see Fig. 3, which showed selected distributions covering a range of wcyclic). The fit at the peak of the distribution was also in good agreement with the experimental SEC traces, with the peak max approaching that of the pure cyclic at higher weight fractions. This fit provided the true weight fraction of l-PSTY doped into c-PSTY and was found to be slightly different to the targeted values due to the associated instrumental error. Regardless, the fitting of the two distributions provided a better and more accurate method to determine the ratio of linear to cyclic. It should be noted that wcyclic determined in this case was for the full distribution of both linear and cyclic, including the high molecular weight species.
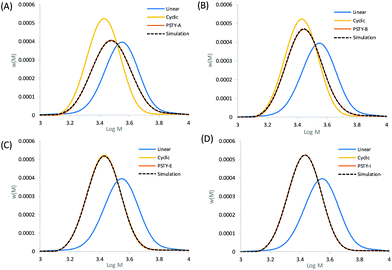 |
| | Fig. 3 Experimental SEC traces of mixtures of linear and cyclic (see Table 1). (A) PSTY-A with targeted wcyclic = 49.72%, (B) PSTY-B with targeted wcyclic = 77.96%, (C) PSTY-E with targeted wcyclic = 95.68%, and (D) PSTY-I with targeted wcyclic = 99.50%. The dashed lines are the fit using the ss to determine wcyclic calculated from fitting the experimental linear and cyclic distributions to the experimental distribution. | |
The Gaussian distributions for both the linear and cyclic polymers (as found from Fig. 1) were then used to find the optimal wcyclic for the different ratios of doped linear (i.e. distributions A–J) using the residual sum of squares. This procedure was similar to the addition of the two distributions above. The fits using the LND method and the weight fraction determined by ss was excellent for all distributions (Fig. 4). As expected, the fit at high molecular weight (M > 103.8) was poor due to the high molecular weight species in both the linear and cyclic distributions. The weight fraction of pure cyclic found by the LND method was higher at lower weight fractions of cyclic and higher as the weight fraction approached 1. For distribution E, there was a non-quantifiable amount of linear (i.e. wcyclic ∼1). To compare the weight fraction values found by the LND method with those from the added distribution method (i.e.Fig. 3), the amount of non-pure linear and cyclic species was taken into account to determine the true weight fraction of pure linear and cyclic from the added distribution (see Table 1). It can be seen that there is still a small difference between the values from the LND and the added distribution methods as shown in Fig. 5. The difference was greatest at a weight fraction of ∼0.5 (4%) and decreased to less than 2% with a further increase in wcyclic. The data showed that SEC coupled with the LND method provided an accurate analysis of cyclic purity. We believe that the greater difference at intermediate weight fractions (e.g. 0.5–0.9) was most probably due to the increase in dispersity of the mixture (see Fig. 2C), and therefore a greater susceptible to minor baseline drifts in the SEC chromatograms.
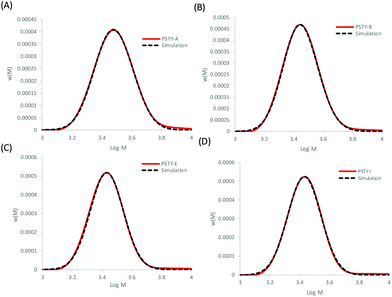 |
| | Fig. 4 Fitting the experimental linear and cyclic mixture with the individual linear and cyclic distributions found by ss and using the LND distributions in Fig. 1 (dashed lines). (A) PSTY-A with targeted wcyclic = 49.72%, (B) PSTY-B with targeted wcyclic = 77.96%, (C) PSTY-E with targeted wcyclic = 95.68%, and (D) PSTY-I with targeted wcyclic = 99.50%. | |
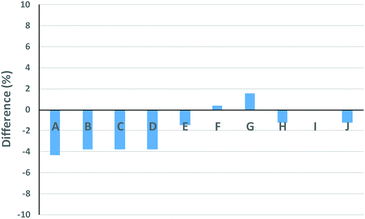 |
| | Fig. 5 Difference between the wcyclic found from the experimental mixed distributions and wcyclic from the LND (see Table 1). | |
Conclusions
In summary, the SEC/LND method successfully determined the amount of linear impurity after cyclization by the ring closure procedure. Using a polystyrene model system, we targeted varying ratios of linear to cyclic from stock solutions of c-PSTY and l-PSTY solutions. The mixtures were analyzed through the fit by ss and visualization of the fit from addition of two distributions using the found wcyclic. The weight fraction of cyclic was different from that targeted but was similar to the values of wcyclic found by the SEC/LND method. Taken together, the data supports that the use of the SEC coupled with the LND method provides an accurate and quantitative method to determine the amount of linear impurity in the cyclic. The key parameter of hydrodynamic shift is a requirement for the successful use of the SEC/LND method not only for polystyrene cyclic but all other low molecular weight polymers.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The acknowledgements come at the end of an article after the conclusions and before the notes and references.
Notes and references
- Z. F. Jia and M. J. Monteiro, Cyclic Polymers: Methods and Strategies, J. Polym. Sci., Part A: Polym. Chem., 2012, 50(11), 2085–2097 CrossRef CAS.
- F. M. Haque and S. M. Grayson, The synthesis, properties and potential applications of cyclic polymers, Nat. Chem., 2020, 12(5), 433–444 CrossRef CAS.
- D. J. Craik, N. L. Daly, T. Bond and C. Waine, Plant cyclotides: A unique family of cyclic and knotted proteins that defines the cyclic cystine knot structural motif, J. Mol. Biol., 1999, 294(5), 1327–1336 CrossRef CAS.
- D. J. Craik and C. I. Schroeder, Peptides from Mamba Venom as Pain Killers, Angew. Chem., Int. Ed., 2013, 52(11), 3071–3073 CrossRef CAS.
- A. H. El-Sagheer and T. Brown, Synthesis, Serum Stability and Cell Uptake of Cyclic and Hairpin Decoy Oligonucleotides for TCF/LEF and GLI Transcription Factors, Int. J. Pept. Res. Ther., 2008, 14(4), 367–372 CrossRef CAS.
- M. Kapnistos, M. Lang, D. Vlassopoulos, W. Pyckhout-Hintzen, D. Richter, D. Cho, T. Chang and M. Rubinstein, Unexpected power-law stress relaxation of entangled ring polymers, Nat. Mater., 2008, 7(12), 997–1002 CrossRef CAS.
- H. C. Lee, H. Lee, W. Lee, T. H. Chang and J. Roovers, Fractionation of cyclic polystyrene from linear precursor by HPLC at the chromatographic critical condition, Macromolecules, 2000, 33(22), 8119–8121 CrossRef CAS.
- B. Lepoittevin, M.-A. Dourges, M. Masure, P. Hemery, K. Baran and H. Cramail, Synthesis and Characterization of Ring-Shaped Polystyrenes, Macromolecules, 2000, 33(22), 8218–8224 CrossRef CAS.
- R. D. Adams and S. B. Falloon, The Catalytic Cyclooligomerization of Thietane by Trirhenium Cluster Complexes. A New Route to Polythiaether Macrocycles, J. Am. Chem. Soc., 1994, 116(23), 10540–10547 CrossRef CAS.
- S. E. Cabaniss, Q. H. Zhou, P. A. Maurice, Y. P. Chin and G. R. Aiken, A log-normal distribution model for the molecular weight of aquatic fulvic acids, Environ. Sci. Technol., 2000, 34(6), 1103–1109 CrossRef CAS.
- K. P. Chan, Y.-F. Wang, A. S. Hay, X. L. Hronowski and R. J. Cotter, Synthesis and Characterization of Novel Cyclic (Aryl Ether Ketone)s, Cyclic (Aryl Ether Phthalazine)s, and Cyclic (Aryl Ether Isoquinoline)s, Macromolecules, 1995, 28(20), 6705–6717 CrossRef CAS.
- D. Cho, K. Masuoka, K. Koguchi, T. Asari, D. Kawaguchi, A. Takano and Y. Matsushita, Preparation and characterization of cyclic polystyrenes, Polym. J., 2005, 37(7), 506–511 CrossRef CAS.
- B. A. Laurent and S. M. Grayson, An efficient route to well-defined macrocyclic polymers via “Click” cyclization, J. Am. Chem. Soc., 2006, 128(13), 4238–4239 CrossRef CAS.
- H. Jacobson and W. H. Stockmayer, Intramolecular reaction in polycondensations. I. The theory of linear systems, J. Chem. Phys., 1950, 18, 1600–1606 CrossRef CAS.
- D. E. Lonsdale, C. A. Bell and M. J. Monteiro, Strategy for Rapid and High-Purity Monocyclic Polymers by CuAAC “Click” Reactions, Macromolecules, 2010, 43(7), 3331–3339 CrossRef CAS.
- D. E. Lonsdale and M. J. Monteiro, Various polystyrene topologies built from tailored cyclic polystyrene via CuAAC reactions, Chem. Commun., 2010, 46(42), 7945–7947 RSC.
- J. Kulis, Z. F. Jia and M. J. Monteiro, One-Pot Synthesis of Mikto Three-Arm AB(2) Stars Constructed from Linear and Macrocyclic Polymer Chains, Macromolecules, 2012, 45(15), 5956–5966 CrossRef CAS.
- Z. F. Jia, D. E. Lonsdale, J. Kulis and M. J. Monteiro, Construction of a 3-Miktoarm Star from Cyclic Polymers, ACS Macro Lett., 2012, 1(6), 780–783 CrossRef CAS.
- M. D. Hossain, Z. F. Jia and M. J. Monteiro, Complex Polymer Topologies Built from Tailored Multifunctional
Cyclic Polymers, Macromolecules, 2014, 47(15), 4955–4970 CrossRef CAS.
- F. Amir, M. D. Hossain, Z. F. Jia and M. J. Monteiro, Precise grafting of macrocyclics and dendrons to a linear polymer chain, Polym. Chem., 2016, 7(43), 6598–6607 RSC.
- M. D. Hossain, J. C. Reid, D. R. Lu, Z. F. Jia, D. J. Searles and M. J. Monteiro, Influence of Constraints within a Cyclic Polymer on Solution Properties, Biomacromolecules, 2018, 19(2), 616–625 CrossRef CAS.
- A. Pipertzis, M. D. Hossain, M. J. Monteiro and G. Floudas, Segmental Dynamics in Multicyclic Polystyrenes, Macromolecules, 2018, 51(4), 1488–1497 CrossRef CAS.
- Z. C. Yan, M. D. Hossain, M. J. Monteiro and D. Vlassopoulos, Viscoelastic Properties of Unentangled Multicyclic Polystyrenes, Polymers, 2018, 10(9), 973–985 CrossRef.
- D. E. Lonsdale and M. J. Monteiro, Kinetic Simulations for Cyclization of alpha,omega-Telechelic Polymers, J. Polym. Sci., Part A: Polym. Chem., 2010, 48(20), 4496–4503 CrossRef CAS.
- J. N. Hoskins, S. Trimpin and S. M. Grayson, Architectural Differentiation of Linear and Cyclic Polymeric Isomers by Ion Mobility Spectrometry-Mass Spectrometry, Macromolecules, 2011, 44(17), 6915–6918 CrossRef CAS.
- A. M. Yol, D. Dabney, S. F. Wang, B. A. Laurent, M. D. Foster, R. P. Quirk, S. M. Grayson and C. Wesdemiotis, Differentiation of Linear and Cyclic Polymer Architectures by MALDI Tandem Mass Spectrometry (MALDI-MS2), J. Am. Soc. Mass Spectrom., 2013, 24(1), 74–82 CrossRef CAS.
- B. A. Laurent and S. M. Grayson, Synthetic approaches for the preparation of cyclic polymers, Chem. Soc. Rev., 2009, 38(8), 2202–2213 RSC.
- L. F. Gao, J. Oh, Y. F. Tu and T. Chang, Preparation of low molecular weight cyclic polystyrenes with high purity via liquid chromatography at the critical condition, Polymer, 2018, 135, 279–284 CrossRef CAS.
- M. J. Monteiro, Fitting molecular weight distributions using a log-normal distribution model, Eur. Polym. J., 2015, 65, 197–201 CrossRef CAS.
- M. Gavrilov, F. Amir, J. Kulis, M. D. Hossain, Z. F. Jia and M. J. Monteiro, Densely Packed Multicyclic Polymers, ACS Macro Lett., 2017, 6(9), 1036–1041 CrossRef CAS.
- M. N. Holerca, M. Peterca, B. E. Partridge, Q. Xiao, G. Lligadas, M. J. Monteiro and V. Percec, Monodisperse Macromolecules by Self-Interrupted Living Polymerization, J. Am. Chem. Soc., 2020, 142(36), 15265–15270 CrossRef CAS.
- F. Amir, Z. F. Jia and M. J. Monteiro, Sequence Control of Macromers via Iterative Sequential and Exponential Growth, J. Am. Chem. Soc., 2016, 138(51), 16600–16603 CrossRef CAS.
- M. J. Monteiro and M. Gavrilov, Characterization of hetero-block copolymers by the log-normal distribution model, Polym. Chem., 2016, 7(17), 2992–3002 RSC.
- J. Zhao, Y. Zhou, Y. Zhou, N. Zhou, X. Pan, Z. Zhang and X. Zhu, A straightforward approach for the one-pot synthesis of cyclic polymers from RAFT polymers via thiol–Michael addition, Polym. Chem., 2016, 7(9), 1782–1791 RSC.
- H. Shen and G. Wang, A versatile flash cyclization technique assisted by microreactor, Polym. Chem., 2017, 8(36), 5554–5560 RSC.
- S. Zhang, X. Cheng, J. Wang, Z. Zhang, W. Zhang and X. Zhu, Synthesis of a cyclic-brush polymer with a high grafting density using activated ester chemistry via the “grafting onto” approach, Polym. Chem., 2018, 9(41), 5155–5163 RSC.
- T. Yamamoto, S. Yagyu and Y. Tezuka, Light- and Heat-Triggered Reversible
Linear-Cyclic Topological Conversion of Telechelic Polymers with Anthryl End Groups, J. Am. Chem. Soc., 2016, 138(11), 3904–3911 CrossRef CAS.
- M. A. Cortez, W. T. Godbey, Y. Fang, M. E. Payne, B. J. Cafferty, K. A. Kosakowska and S. M. Grayson, The Synthesis of Cyclic Poly(ethylene imine) and Exact Linear Analogues: An Evaluation of Gene Delivery Comparing Polymer Architectures, J. Am. Chem. Soc., 2015, 137(20), 6541–6549 CrossRef CAS.
- A. M. vanHerk and T. Droge, Nonlinear least squares fitting applied to copolymerization modeling, Macromol. Theory Simul., 1997, 6(6), 1263–1276 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Computer code to distribution fitting. See DOI: 10.1039/d0py01277g |
| ‡ Current address: College of Science and Engineering, Flinders University, Sturt Road, Bedford Park, South Australia 5042, Australia |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  ,
Sung-Po R.
Chen
,
Zhongfan
Jia‡
,
Sung-Po R.
Chen
,
Zhongfan
Jia‡
 and
Michael J.
Monteiro
and
Michael J.
Monteiro
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and 198
000 g mol−1 and 198![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1), and showed excellent separation and resolution between linear and cyclic polystyrene at high molecular weights.
000 g mol−1), and showed excellent separation and resolution between linear and cyclic polystyrene at high molecular weights.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 found not to be satisfactory for the quantitation of cyclic polystyrene based on the critical adsorption point (CAP) of linear precursors.12,28 When using the CAP for cyclic polymer, however, good resolution and cyclic purity were found.28 It was noted that linear species with higher molecular weights after the CuAAC reaction interfere with the LCCC analysis regardless of which CAP method was used as these lie between the starting linear and mono-cyclic polymer peaks, and thus need to be minimized.
000 g mol−1 found not to be satisfactory for the quantitation of cyclic polystyrene based on the critical adsorption point (CAP) of linear precursors.12,28 When using the CAP for cyclic polymer, however, good resolution and cyclic purity were found.28 It was noted that linear species with higher molecular weights after the CuAAC reaction interfere with the LCCC analysis regardless of which CAP method was used as these lie between the starting linear and mono-cyclic polymer peaks, and thus need to be minimized.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH), and 1.95 (s, 6H, (CH3)2C). 13C NMR (CDCl3, 298 K, 400 MHz): 170.9, 76.9, 75.4, 54.9, 53.4, 30.6.
CH), and 1.95 (s, 6H, (CH3)2C). 13C NMR (CDCl3, 298 K, 400 MHz): 170.9, 76.9, 75.4, 54.9, 53.4, 30.6.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) -PSTY35-Br
-PSTY35-Br![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) -PSTY35-N3
-PSTY35-N3![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e002.gif) -PSTY35-Br), with a mass based on conversion, was dissolved in DMF (40 mL) and NaN3 (1.10 g, 19.6 mmol, ∼20 equiv. to initiator) under Argon at 25 °C for 24 h. The reaction solution was concentrated by an airflow to approximately a third of its original volume, precipitated into MeOH (20-fold excess to polymer solution), recovered by vacuum filtration, and washed with H2O and MeOH. The azide polymer was dried in vacuo at 25 °C for 24 h to obtain a white powder (approximately 4 g), which was characterized by NMR and SEC (Mn = 3690 and Đ = 1.10 based on a PSTY calibration curve).
-PSTY35-Br), with a mass based on conversion, was dissolved in DMF (40 mL) and NaN3 (1.10 g, 19.6 mmol, ∼20 equiv. to initiator) under Argon at 25 °C for 24 h. The reaction solution was concentrated by an airflow to approximately a third of its original volume, precipitated into MeOH (20-fold excess to polymer solution), recovered by vacuum filtration, and washed with H2O and MeOH. The azide polymer was dried in vacuo at 25 °C for 24 h to obtain a white powder (approximately 4 g), which was characterized by NMR and SEC (Mn = 3690 and Đ = 1.10 based on a PSTY calibration curve).
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) -PSTY35-N3 (0.30 g, 0.08 mmol) in 15 mL of dry toluene via a syringe pump at a rate of 0.2 mL min−1. After complete addition of the polymer solution (i.e. 70 min), the reaction mixture was stirred for a further 3 h. Toluene was evaporated from the solution using an airflow, the remaining polymer was dissolved in DCM, and passed through an activated basic alumina column. The polymer was recovered by precipitation into MeOH (20-fold excess to polymer solution) and then filtered with the aid of a vacuum. The polymer was dried under vacuum at 25 °C for 24 h, resulting in the crude cyclic polymer (∼0.27 g) as white powder (Mn = 2950, Đ = 1.26 based on PSTY calibration curve).
-PSTY35-N3 (0.30 g, 0.08 mmol) in 15 mL of dry toluene via a syringe pump at a rate of 0.2 mL min−1. After complete addition of the polymer solution (i.e. 70 min), the reaction mixture was stirred for a further 3 h. Toluene was evaporated from the solution using an airflow, the remaining polymer was dissolved in DCM, and passed through an activated basic alumina column. The polymer was recovered by precipitation into MeOH (20-fold excess to polymer solution) and then filtered with the aid of a vacuum. The polymer was dried under vacuum at 25 °C for 24 h, resulting in the crude cyclic polymer (∼0.27 g) as white powder (Mn = 2950, Đ = 1.26 based on PSTY calibration curve).